Deep Ensembles and Multisensor Data for Global LCZ Mapping: Insights from So2Sat LCZ42

Abstract

Classifying multiband images acquired by advanced sensors, including those mounted on satellites, is a central task in remote sensing and environmental monitoring. These sensors generate high-dimensional outputs rich in spectral and spatial information, enabling detailed analyses of Earth’s surface. However, the complexity of such data presents substantial challenges to achieving both accuracy and efficiency. To address these challenges, we tested the ensemble learning framework based on ResNet50, MobileNetV2, and DenseNet201, each trained on distinct three-channel representations of the input to capture complementary features. Training is conducted on the LCZ42 dataset of 400,673 paired Sentinel-1 SAR and Sentinel-2 multispectral image patches annotated with Local Climate Zone (LCZ) labels. Experiments show that our best ensemble surpasses several recent state-of-the-art methods on the LCZ42 benchmark.

1. Introduction

Multiband images represent data across multiple spectral or feature dimensions, offering substantially more information than traditional grayscale or RGB images. By capturing diverse characteristics that extend beyond the visible spectrum or conventional feature space, these images deliver a richer and more detailed depiction of the underlying phenomena. Their growing prevalence across numerous disciplines reflects their value for advanced analytical applications, particularly those requiring high precision. This expanded informational capacity enables sophisticated classification tasks in fields such as remote sensing, medical imaging, industrial inspection, and scientific research [1].

The classification of multiband images presents both distinctive challenges and significant opportunities. While their high dimensionality often contains essential features for distinguishing between classes, it also introduces noise, redundancy, and considerable computational demands. To mitigate these issues, researchers have advanced diverse methodologies in feature extraction, dimensionality reduction, and classification, each designed to achieve an optimal balance between accuracy and computational efficiency.

Computational strategies for classifying multiband images encompass both traditional machine learning methods and neural network-based approaches. Traditional machine learning techniques, whether supervised or unsupervised, typically employ linear or nonlinear transformations to extract salient and intrinsic features [2]. Among these, Principal Component Analysis (PCA) is widely adopted as a dimensionality-reduction technique that preserves essential variance, making it a standard preprocessing step in classical machine learning and pattern recognition. However, PCA assumes linearity in the data, which can result in the loss of critical nonlinear relationships inherent in the original feature space. To address this limitation, Ref. [2] introduced three PCA variants for multiband image classification: Kernel PCA (KPCA), Kernel Entropy Component Analysis (KECA), and Fuzzy PCA (FPCA). While FPCA demonstrated lower performance than KPCA and KECA, it offered the advantage of reduced space complexity. The high computational demands typical of multiband image classification have also motivated hybrid approaches. For example, Ref. [3] proposed combining PCA with Local Binary Patterns (LBPs) to improve efficiency, while [4] developed a local neighborhood structure-preserving embedding method that incorporates prior label information.

Building on these developments, more recent studies have introduced methods aimed at further enhancing classification performance and overcoming the limitations of conventional approaches. Subpixel Component Analysis (SCA), proposed in [5], delivered a high-performance framework for multiband image analysis. In [6], an adaptive strategy was developed to automatically determine the optimal number of superpixels, improving segmentation quality and downstream accuracy. Addressing the linearity constraint of PCA, Ref. [7] introduced a tree-based classifier capable of handling nonlinear datasets, while [8] applied gradient boosting decision tree regression to achieve robust predictive performance. Although many studies have concentrated solely on spectral features, Ref. [9] demonstrated that integrating both spectral and spatial information within tree-based models can yield exceptional classification results.

In addition to explorations into dimensionality-reduction and feature-extraction techniques, researchers have also investigated a variety of classification algorithms for multiband images. As far as traditional classifiers are concerned, several studies have applied K-means clustering methods to this task [10,11,12], while others have employed support vector machines (SVMs) [13,14,15]. Notably, Ref. [14] enhanced SVM classification by incorporating a genetic algorithm, thereby optimizing performance through evolutionary feature selection.

Beyond traditional classifiers, numerous studies have applied Convolutional Neural Networks (CNNs) directly to multiband and hyperspectral image classification, exploiting their capacity to extract hierarchical spectral–spatial features. Architectures range from one-dimensional CNNs (1D-CNNs), which operate exclusively along the spectral dimension by convolving spectral signatures, to two-dimensional CNNs (2D-CNNs) applied to spatial patches or to dimensionality-reduced representations such as principal components, and three-dimensional CNNs (3D-CNNs) that jointly model spectral and spatial information through volumetric kernels. More precisely, recent designs employ a sequential factorization of convolutional operators, applying 3D convolutions in early layers, 2D convolutions in intermediate layers, and lightweight 1D/pointwise operations later to exploit the complementary strengths of each operator. Early 3D kernels capture joint spectral–spatial correlations and reduce spectral redundancy, 2D kernels then learn higher-level spatial abstractions from the compacted spectral features, and 1D/pointwise layers provide efficient channel mixing and dimensionality reduction. This factorization often preserves or improves classification accuracy while substantially reducing parameter count and FLOPs compared with naively stacking 3D convolutions. For example, Hu et al. [16] implemented a 1D-CNN for image classification using the spectral domain, while Ahmad [17] developed a fast 3D-CNN for simultaneous spectral–spatial analysis. Hybrid approaches that integrate multiple CNN forms have also proven effective; the HybridSN architecture combines a 3D-CNN front-end with a 2D-CNN back-end to exploit both local spectral–spatial and higher-level spatial features [18]. Other works have focused on enhancing CNN input representations. Notably, the authors of [19] proposed a feature-extraction method based on multiscale covariance maps (MCMs) to fuse spectral and spatial information prior to CNN classification, significantly improving accuracy on benchmark datasets. More recent designs employ sequential 3D, 2D, and 1D convolutions to achieve robust classification with reduced computational overhead [20]. A Lightweight 1D CNN for In-Orbit Hyperspectral Segmentation proposed by Justo et al. [21] demonstrated high accuracy with minimal parameters for satellite-based segmentation, and an Adaptive Pixel Attention Network [22] introduced an adaptive attention mechanism to enhance spectral–spatial learning within CNN architectures. Collectively, these studies confirm that CNN-based segmentators/classifiers, even when used independently of ensembles, continue to deliver competitive or state-of-the-art performance in multiband image segmentation/classification.

Ensembling is a well-established strategy in machine learning that integrates the outputs of multiple models to enhance predictive performance, robustness, and generalization capability. By aggregating diverse learners, ensemble methods mitigate the limitations inherent in individual models, thereby reducing both variance and bias while improving overall accuracy. Among the various ensemble learning paradigms, Random Forest (RF) is particularly prominent; it constructs multiple decision trees from randomly selected subsets of the training data and feature space, and aggregates their outputs for final prediction. In the context of multiband image classification, an exponentially weighted RF approach was investigated in [23]. Comparative analysis conducted by [24] evaluated several traditional classifiers—Support Vector Machines (SVM), k-Nearest Neighbors (KNN), Decision Trees (DT), and RF, using Principal Component Analysis (PCA) and Minimum Noise Fraction (MNF) as preprocessing transformations to reduce noise. Their findings indicated that RF achieved the highest computational efficiency among the tested classifiers. A further contribution to robust and efficient classification was presented in [25], which proposed a methodology integrating PCA, Local Binary Pattern (LBP), and a Back Propagation Neural Network (BPNN) to achieve improved accuracy in multiband image analysis.

Ensemble strategies built from convolutional backbones have gained traction for hyperspectral and multiband image classification, chiefly to boost robustness under label noise, limited annotations, and distribution shift. Recent research has explored distilling knowledge from ensembles of deep networks into compact students to counter noisy supervision while maintaining classification accuracy [26]. Earlier contributions, such as [27], demonstrated that deep ensembles, comprising heterogeneous CNN base classifiers combined via a supervised fusion layer and augmented through weight-level Gaussian noise injection, enhance both hyperspectral classification and unmixing tasks, outperforming single CNN models and classical voting/averaging ensembles. Broader surveys and methodology exemplars in 2025 further emphasize deep ensembling of multiband CNNs by integrating varied architectures (e.g., ResNet50, MobileNetV2, DenseNet201, attention-based CNNs) trained on complementary feature subsets, achieving state-of-the-art performance on datasets like EuroSAT, LCZ42, and planktic foraminifera classification [28]. Collectively, these studies affirm that CNN-based ensembles via teacher–student distillation, multi-model aggregation, and architecture-level heterogeneity deliver consistently more reliable and widely generalizable classification outcomes than standalone CNNs across modern hyperspectral benchmarks.

While methodological advances such as deep ensembles and hybrid architectures have driven substantial gains in multiband image classification, meaningful progress ultimately depends on evaluating these systems under consistent and well-defined conditions. Given the critical role of standardized assessment, the availability of carefully designed benchmarks is essential for measuring and comparing competing methods. The accuracy of such systems can vary substantially depending on the dataset and test protocol employed. A persistent challenge in the field is the heterogeneity of evaluation practices, with different studies often relying on distinct datasets and inconsistent protocols, which hampers direct performance comparison. This lack of standardization can lead to considerable variability in reported results, making it difficult to draw reliable conclusions about relative model effectiveness. Encouragingly, specific datasets, such as the LCZ42 dataset adopted in this study, now provide clearly defined evaluation protocols, enabling reproducible experimentation and facilitating fair, transparent comparisons across multiband classification systems.

The So2Sat LCZ42 dataset [29], comprising 400,673 paired Sentinel-1 SAR and Sentinel-2 multispectral image patches labeled across 17 Local Climate Zone (LCZ) classes (10 built and 7 natural), constitutes a vital benchmark in this regard. These patches span 42 major urban agglomerations along with 10 additional smaller regions globally and were annotated over six months by 15 remote sensing experts subject to a rigorous quality assessment that yielded an overall labeling confidence of 85%. Importantly, So2Sat LCZ42 provides a clearly defined evaluation protocol, including spatially distinct training, validation, and test splits, enabling reproducible experimentation and transparent comparison of multiband classification systems.

Taking advantage of such a rigorously curated and consistently evaluated benchmark provides a robust foundation for assessing the effectiveness of advanced classification strategies. Building on this foundation, the present study investigates methods for constructing an ensemble of neural networks, with a comparative analysis of three widely adopted architectures: ResNet50 (RN), MobileNetV2 (MN), and DenseNet201 (DN), all pretrained on the ImageNet dataset. The ensemble is formed using the sum rule, wherein each constituent network is independently trained on a distinct three-channel image generated from the original multiband input. Experimental results demonstrate that the proposed system attains state-of-the-art (SOTA) performance. The goal of this work is to illustrate how a relatively simple ensemble method, based on the sum rule, and a well-known pre-trained neural network architecture, can achieve state-of-the-art (SOTA) performance on a large-scale dataset. In LCZ42 dataset, the training and test sets are drawn from geographically distinct locations, making the evaluation results fairly comparable to those of human experts. It is worth recalling that in the LCZ42 dataset, the agreement among human labels is about 85%, indicating that the classification task is challenging even for trained professionals.

This work, therefore, focuses on demonstrating the practical benefits of an ensemble approach applied to multiband imagery, using well-established CNN backbones and straightforward preprocessing to produce complementary three-channel representations. Our goal is not to design a lightweight network or propose a novel architecture, but rather to show that simple techniques for generating three-channel representations from multiband images can lead to SOTA performance. This performance, however, comes at the cost of increased computational requirements compared to methods based on a single architecture. Nonetheless, as our experimental results show, the processing time remains relatively limited given the intended applications. Clearly, we are not targeting embedded systems or on-board satellite classification; instead, we focus on server-side analyses, e.g., assessing satellite imagery over a given region or country to monitor forest coverage changes over time. In such contexts, the use of modern GPU clusters is assumed, enabling our more complex system, comprising multiple neural networks, to perform classification within a few hours.

The remainder of this paper is organized as follows. Section 2 describes the materials and methods, including the dataset, network architectures, strategies for generating three-channel images, and the ensemble strategy. Section 3 presents the experimental results and performance analysis. Finally, Section 4 concludes the paper with a summary of the main findings, a discussion of their implications, and potential directions for future research.

The code of the proposed approach will be available at https://github.com/LorisNanni/Leveraging-Deep-Ensembles-and-Multisensor-Data-for-Global-LCZ-Mapping-Insights-from-So2Sat-LCZ42 (accessed on 16 September 2025)

2. Materials and Methods

In the following subsections, we present the dataset used, the various strategies adopted to generate three-channel images, and a brief description of the neural networks and the ensemble method employed for classification.

2.1. LCZ42 Dataset

As indicated in the introduction, the So2Sat LCZ42 dataset encompasses Local Climate Zone (LCZ) annotations for approximately 400,000 paired Sentinel-1 synthetic aperture radar (SAR) and Sentinel-2 multispectral image patches. These image patches collectively represent 42 major urban agglomerations along with 10 additional smaller regions distributed across the globe. The annotation process, conducted over six months by a team of 15 domain experts, was subjected to a rigorous quality control protocol, the agreement among human labels is about 85%. The dataset is publicly available at http://doi.org/10.14459/2018mp1483140 (accessed on 20 July 2025).

The classification scheme employed adheres to the standard Local Climate Zone (LCZ) framework and comprises 17 categories: 10 built-type classes and seven natural-type classes. These categories are delineated on the basis of climate-relevant surface properties at the local scale, incorporating three-dimensional structural attributes (e.g., building and tree height and density), surface cover characteristics (e.g., vegetation or impervious materials), and anthropogenic factors (e.g., human-induced heat emissions). Representative examples are provided in Figure 1. The selected urban agglomerations, together with the additional regions, encompass all inhabited continents with the sole exception of Antarctica.

Figure 1. Visual comparison of some RGB images.

The Sentinel-2 multispectral data in So2Sat LCZ42 include 10 real-valued spectral bands:

• Band B2—10 m Ground Sampling Distance (GSD);
• Band B3—10 m GSD;
• Band B4—10 m GSD;
• Band B5—upsampled to 10 m from 20 m GSD;
• Band B6—upsampled to 10 m from 20 m GSD;
• Band B7—upsampled to 10 m from 20 m GSD;
• Band B8—10 m GSD;
• Band B8a—upsampled to 10 m from 20 m GSD;
• Band B11—upsampled to 10 m from 20 m GSD;
• Band B12—upsampled to 10 m from 20 m GSD.

The Sentinel-1 SAR component consists of 8 real-valued bands:

• Real part of the unfiltered VH channel;
• Imaginary part of the unfiltered VH channel;
• Real part of the unfiltered VV channel;
• Imaginary part of the unfiltered VV channel;
• Intensity of the refined Lee-filtered VH channel;
• Intensity of the refined Lee-filtered VV channel;
• Real part of the refined Lee-filtered covariance matrix off-diagonal element;
• Imaginary part of the refined Lee-filtered covariance matrix off-diagonal element.

The SAR imagery provides high-resolution, dual-polarization (VV and VH) radar backscatter data acquired by the Sentinel-1 satellite. These measurements capture structural and textural characteristics of both urban and non-urban environments. Unlike optical data, SAR observations are advantageous in cloudy or nighttime conditions, and they are particularly effective in identifying manufactured structures due to their sensitivity to surface roughness and geometry.

For machine learning applications, the dataset is partitioned into three subsets: a training set, a testing set, and a validation set, containing 352,366; 24,188; and 24,119 paired image patches, respectively, each consisting of multispectral and synthetic aperture radar data. The training set comprises image patches from 32 cities along with the 10 additional smaller regions. The remaining 10 cities—selected to represent a range of continents and cultural contexts—are reserved for testing and validation. Within each of these cities, every LCZ class label is divided into western and eastern halves, which are assigned to the testing and validation sets, respectively. This partitioning ensures that all three subsets are geographically disjoint, even though the testing and validation sets originate from the same group of cities.

To preserve the integrity of the evaluation, the validation set was not utilized, as it contains imagery originating from the same geographic regions as the test set. Instead, the test set was treated as a fully independent dataset, with its constituent cities entirely excluded from all phases of system development, including training and parameter tuning. This protocol, widely employed in the literature, mitigates the risk of data leakage and supports a fair and unbiased assessment of model performance.

For preprocessing, all multispectral image channels were normalized to the range [0, 255]. Given that the raw channel values lie within [0, 2.8], each image was rescaled using the transformation

$$Image={\displaystyle \frac{Image}{2.8/255}}.$$

Synthetic Aperture Radar (SAR) images were likewise normalized to [0, 255] through a two-stage procedure involving threshold-based clipping followed by linear scaling. First, to constrain the dynamic range and reduce the influence of extreme values, all pixel intensities exceeding 0.5 were clipped to 0.5, while those below −0.5 were clipped to −0.5. The resulting clipped data were then linearly mapped to [0, 255] according to

$$Image=\left(Image+0.5\right)\times 255.$$

Finally, the normalized images were converted to 8-bit unsigned integers, thereby reducing memory requirements and preparing the data for subsequent processing steps.

2.2. CNN Ensemble Learning (EL)

As noted in the introduction, the theoretical foundation of ensemble learning (EL) rests on the principle that the aggregation of multiple models has the potential to yield enhanced accuracy and greater reliability in predictive performance. The efficacy of an ensemble is maximized when its constituent models demonstrate substantial diversity. Within the framework presented here, the outputs of the classifiers are combined with the sum rule. Among decision fusion strategies, the sum rule is one of the most effective and robust operators. Compared to the product rule, it avoids the drawback that a single zero probability from one classifier nullifies the entire fused score. Empirical studies have shown that the sum rule generally performs better than voting, product, or even weighted-sum rules under reasonable assumptions on classifier calibration.

In the experiments presented below, the best performance is achieved by combining different DenseNet201 models trained using both multispectral and synthetic aperture radar images.

2.3. Ensemble Classifiers

In this study, we employ three convolutional neural network (CNN) architectures: ResNet-50 (RN) [30], DenseNet-201 (DN) [31], and MobileNetV2 (MN) [32], each pretrained on the ImageNet dataset and accessible through MATLAB 2025a. ResNet-50 is a deep CNN with 50 layers, distinguished by its incorporation of residual, or skip, connections. These connections effectively address the vanishing gradient problem, thereby enabling the efficient training of very deep models. The architecture is organized into bottleneck residual blocks incorporating batch normalization and ReLU activations, rendering it particularly effective for large-scale image classification and feature extraction tasks. DenseNet-201, by contrast, is a 201-layer CNN characterized by its dense connectivity pattern, wherein each layer receives as input the feature maps of all preceding layers. This design facilitates extensive feature reuse, reduces parameter redundancy, enhances gradient propagation, and improves overall training efficiency. MobileNetV2 represents a lightweight CNN optimized for deployment on mobile and edge devices. It employs depthwise separable convolutions alongside inverted residual blocks with linear bottlenecks, thereby significantly reducing computational overhead while maintaining competitive accuracy. Its streamlined architecture makes it especially well-suited for real-time applications constrained by limited processing resources. For each of these pretrained networks, we adapt the classification head prior to fine-tuning the models for the present task [33].

The ResNet-50, DenseNet-201, and MobileNetV2 architectures are subjected to fine-tuning over ten epochs with a learning rate of 0.001 and a batch size of 30, using stochastic gradient descent (SGD) as the optimization algorithm. This configuration balances convergence stability with computational efficiency, ensuring that the networks adapt effectively to the target dataset while mitigating risks of divergence or overfitting [34]. Data augmentation techniques are not employed in this study, as the size of the original dataset is deemed sufficiently large to ensure robust training and to avoid increasing the computational time required to train the tested networks.

2.4. Three-Channel Image Creation

Because the pretrained networks employed in this study require RGB images as input, the initial stage of our processing pipeline involves transforming the multiband Sentinel-2 dataset into a format compatible with conventional CNN architectures. In the Random (Rand) approach, three channels are selected at random from the available spectral bands of each multiband image. The RandomOneRGB (RandRGB) approach builds upon the empirical observation that RGB channels typically achieve superior performance relative to other spectral bands [28]. In this method, two channels are randomly sampled from the complete set of thirteen bands, while the third is randomly drawn from the RGB subset (R, G, or B). Since these transformed images are intended for use in an ensemble framework, the selection procedure is deliberately unconstrained. Consequently, it is possible for a network within the ensemble to be trained on images containing duplicated channels, for instance, a representation such as RRR, where all three input channels correspond to the red band.

For synthetic aperture radar (SAR) images, where RGB channels are not available, we apply two approaches:

• Rand: the random method just described.
• RandS: a method in which two channels are randomly extracted from Sentinel-2, and the third channel is randomly selected from Sentinel-1 (SAR data). This method generates inputs consisting of two Sentinel-2 channels and one SAR channel from Sentinel-1.

In our prior work [28], we evaluated a range of considerably more sophisticated strategies for transforming multiband images into three-band representations. Despite their methodological complexity, all such approaches produced inferior results when compared to the straightforward ensemble strategy advanced in the present study. We further investigated architectures explicitly designed to process multiband inputs, including both CNNs and Transformers. Empirical evidence from these experiments consistently demonstrated that neither multiband-specific architectures nor Transformer-based models provide performance gains over an ensemble of DenseNet models pretrained on ImageNet. Notably, the DenseNet ensemble not only surpassed the accuracy of our earlier methods but also achieved state-of-the-art results without relying on any assumptions regarding the composition or distribution of the test set.

The only published approaches that surpass our method in performance are those that either employ semi-supervised learning or explicitly incorporate assumptions regarding the validation or test set. Examples include techniques such as class reweighting, which adjusts decision boundaries on the basis of classification difficulty between specific pairs of classes, that is, in cases where certain classes exhibit a high degree of similarity. By contrast, the approach presented in this study introduces no such assumptions and relies exclusively on the training data.

It is essential to recognize that the ensemble method proposed in this study could, in principle, be combined with semi-supervised techniques or with strategies that explicitly account for the relative difficulty of class discrimination, such as treating certain classes differently when they exhibit a high degree of similarity. Such extensions, however, lie beyond the scope of the present work. Our objective has been to design and evaluate a method that is entirely fair with respect to test set usage. Specifically, the test set is kept strictly isolated from the training process and is not used to guide model selection, parameter tuning, or any form of adjustment. This strict separation reinforces the methodological rigor of the evaluation and ensures that the reported comparisons approximate as closely as possible the conditions under which a human operator would be assessed.

3. Results

In this study, the performance of the classification models is assessed using four standard metrics: precision, recall, F1-score, and accuracy. Precision quantifies the fraction of correctly identified positive cases relative to all instances predicted as positive. In contrast, recall captures the proportion of true positive cases successfully identified out of all actual positives. The F1-score serves as a balanced measure by computing the harmonic mean of precision and recall, thereby integrating both aspects into a single indicator. Accuracy, by contrast, reflects the overall proportion of correctly classified samples across the entire dataset. Formally, given the counts of True Positives (TP), False Positives (FP), True Negatives (TN), and False Negatives (FN), these metrics are expressed as follows:

$$\begin{gathered} \mathrm{Precision}={\displaystyle \frac{\mathit{TP}}{\mathit{TP}+\mathit{FP}}} \\ \mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}={\displaystyle \frac{\mathit{TP}}{\mathit{TP}+\mathit{FN}}} \\ \mathrm{F}1\text{-}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}={\displaystyle \frac{2(\mathit{Precision}\times \mathit{Recall})}{\mathit{Precision}+\mathit{Recall}}}={\displaystyle \frac{2\mathit{TP}}{2\mathit{TP}+\mathit{FP}+\mathit{FN}}} \\ \mathrm{Accuracy}=100\times {\displaystyle \frac{\mathit{TP}+\mathit{TN}}{\mathit{TP}+\mathit{TN}+\mathit{FP}+\mathit{FN}}} \end{gathered}$$

The following methods are compared in Table 1:

Table 1. Comparison among our ensembles, ‘---’ means that due to computation time those tests have not been performed. Bold is the best performance.

Net	SA_RGB	10 RGB	10 Rand	10 RandRGB	10 RandS	5 Rand + 5 RandRGB	10 Rand + 10 RandRGB	10 Rand + 10 RandRGB + 10 SAR	10 Rand + 10 RandRGB + 10 RandS
RN	62.77	64.33	71.21	70.97	---	70.80	71.61	72.46	---
MN	61.52	64.01	70.01	70.91	---	69.98	71.11	71.62	---
DN	63.89	66.20	72.51	72.68	71.84	72.44	73.03	73.42	73.58

• SA_RGB: stand-alone network trained using RGB images;
• K RGB: sum rule between K nets trained using RGB images;
• K Rand: sum rule between K networks trained using Rand images;
• K RandRGB: sum rule between K networks trained using RandRGB images;
• K SAR: sum rule between K networks trained using SAR images;
• K RandS: sum rule between K networks trained using RandS images;
• A + B: sum rule between A and B.

We also attempted to combine the DenseNet topology with the other architectures evaluated in this study, as well as with those examined in our previous work. In none of these cases was superior performance achieved. This finding is significant, as it demonstrates that a single topology is sufficient to attain state-of-the-art performance.

The first result evident from Table 1 is that the performance of a single network trained on RGB images is lower than that of the ensemble. The use of SAR images yields a slight improvement in performance. The RandRGB strategy does not clearly surpass Rand, which is particularly noteworthy given that, when assessed individually, the RGB bands are the most effective. The best-performing architecture is DenseNet-201.

In Table 2, we compare our best-performing ensemble with the current state of the art. It is important to note that [35] introduced a prior knowledge coupling (PKC) module. This module was constructed by evaluating system performance on the validation set, which, crucially, was derived from the same cities as the test set. Consequently, the incorporation of this module results in a non-equivalent evaluation protocol comparison with our method, as we do not exploit any information from the validation set. In contrast, in our approach, the test set comprises an entirely independent collection of cities. The proposed framework in [36] enables the seamless integration of multispectral and synthetic aperture radar (SAR) data through an attention-based mechanism. To further improve classification accuracy, this framework employs semi-supervised learning that utilizes information from unlabeled image data. The network is trained on both labeled and pseudo-labeled samples, which jointly guide the learning process. Thus, comparisons with [36] are likewise inequitable.

Table 2. Classification accuracy of the different methodologies on the LCZ dataset.

Approach	Year	Accuracy
Proposed Method	2025	73.58
Vit	2025	62.85
[29]	2020	61.10
[37]	2020	69.40
[38]	2023	63.00
[39]	2023	67.87
[40]	2023	68.51
[41]	2023	70.00
[42]	2024	63.01
[35] without PKC *	2024	71.10
[35] with PKC *	2024	73.80
[36] (semi supervised)	2024	74.42
[43]	2025	64.95
[28]	2025	72.79

* Among the approaches reported in [35], our method is solely comparable to the version without PKC, as previously explained.

Excluding the works discussed above, in all cases where the comparison between our ensemble and the existing literature follows a strictly equivalent evaluation protocol, our proposed ensemble achieves state-of-the-art performance on the LCZ42 dataset.

For a more detailed comparison, we report the performance of the Vision Transformer (large model) (Vit) trained on RGB images using the same learning rate and batch size as the CNN. Its performance is comparable to that of the CNN.

Figure 2 presents the “number of classifiers” (i.e., size of the ensemble) vs. accuracy plot, obtained by varying the number of test rejected patterns. As a rejection criterion, we considered the difference between the two highest output scores, i.e., between the two classes deemed most probable by the ensemble. The rejected patterns are assumed to be subsequently classified by human experts. Supposing that

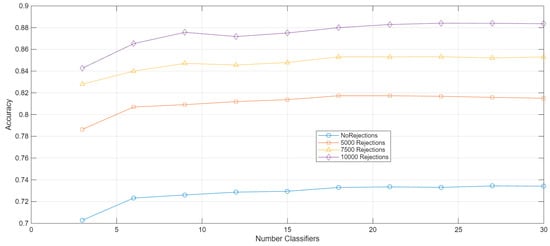
Figure 2. Plot of ensemble size (i.e., number of classifiers) versus accuracy, obtained by varying the number of rejected test patterns.

• θ1(x) is the highest score among the different classes given a pattern x,
• θ2(x) is the second highest score of that pattern,
• θ(x) = θ1(x) − θ2(x), then our rejection criterion is as follows:

If θ(x) > τ, the pattern is assigned to a class;

Otherwise, it is rejected (classified by a human expert).

It is worth noting that an accuracy of 85% is considered comparable to human-level performance. The plot demonstrates that such accuracy can be achieved with an ensemble significantly smaller than the full one, rejection of 7500 test patterns (i.e., fixing τ for getting a rejection rate of ~0.3). It is evident that our system can significantly reduce the manual effort required for the classification task.

It should also be noted that the ensemble size increases in increments of three classifiers: for each triplet of Rand, RandRGB, and SAR models, the corresponding performance is reported.

Next, we present the confusion matrices of our ensemble model, with and without SAR data, in order to illustrate the contribution of SAR imagery to overall performance (Figure 3). We then provide a comparison between the method proposed in this paper and our earlier approach, using all previously introduced performance indicators (Table 3). This comparison demonstrates that the new ensemble consistently outperforms our former method across all evaluation metrics.

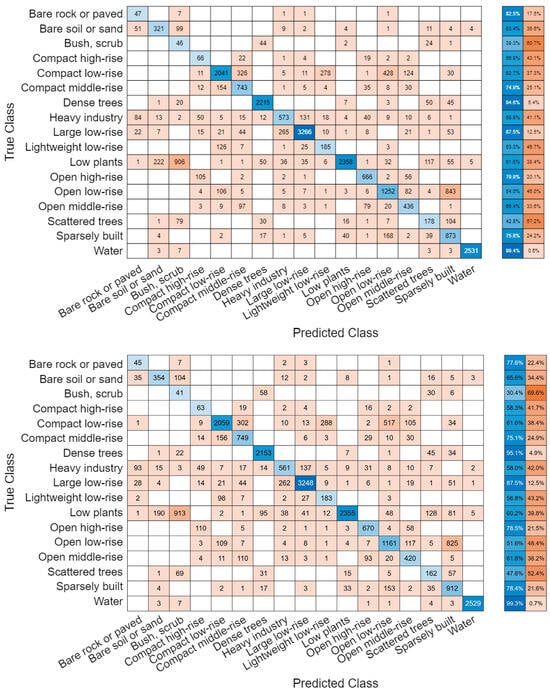
Figure 3. Confusion matrices: with SAR data (top), without SAR data (bottom).

Table 3. Comparison considering different performance indicators; bold is the best performance.

Approach	Accuracy	F1	Precision	Recall
Proposed Method	73.58	0.608	0.679	0.598
[28]	72.79	0.600	0.672	0.590

A key distinction is that the present approach relies on a single network topology, making it considerably easier to implement than our earlier method. In our previous work, we employed multiple network architectures and diverse strategies for processing multispectral images, including a mixture of three-channel models and models capable of handling multichannel data, which together produced a more complex pipeline. In contrast, the method proposed here is simple: it employs a pre-trained DenseNet, available in virtually any programming framework, together with straightforward strategies for converting multispectral images into three-channel inputs. Consequently, the implementation is not only simpler than our earlier work but also less complex than most state-of-the-art (SOTA) approaches.

Of note is that our method does not require the tuning of critical hyperparameters, which renders it straightforward to reproduce. When employing the official GitHub repositories of other methods, reproducing the reported results is often unfeasible, often due to undocumented or incorrectly reported hyperparameter values. Our method avoids such reproducibility issues.

The primary limitation of the proposed approach lies in the higher inference and computational cost incurred by the use of an ensemble. Nevertheless, this trade-off yields substantially more robust performance.

By analyzing the confusion matrices, it is clear that the errors are concentrated in a few specific classes. For example, the misclassification rate between “Open Low-Rise” and “Sparsely Built” is very high. The same occurs between “Low Plants” and “Bush, Scrub.” It is also interesting to note that “Compact Low-Rise” is often incorrectly classified as another class. Clearly, these classes are highly similar to each other: distinguishing, for instance, between “Compact Low-Rise” and “Compact Middle-Rise” is not easy even for a human observer.

Moreover, analysis of the two confusion matrices reveals that the incorporation of SAR imagery yields a generally beneficial effect across all classes. While no single class exhibits a pronounced performance gain, SAR data contribute to a moderate yet consistent improvement throughout the entire set of classes.

Figure 4 shows some examples of images obtained using different combinations of Sentinel-2 bands, other samples are available at https://custom-scripts.sentinel-hub.com/custom-scripts/sentinel-2/composites/ (accessed on 16 September 2025), to create three-channel images:

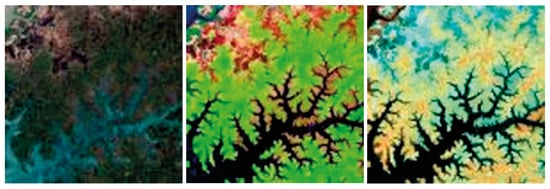
Figure 4. Comparison between different 3-channel images: (left): RGB; (center): band 11, band 12 and ‘red’; (right): band 8, 11 and 12.

• Standard RGB image;
• Bands 11, 12 and the red channel, short wave infrared (SWIR) bands 11 and 12 can help scientists estimate how much water is present in plants and soil, as water reflects SWIR wavelengths;
• Bands, 8, 11 and 12.

Even though our ensembles are straightforward to construct, their performance is comparable to, and in some cases surpasses, that of current state-of-the-art approaches. The principal limitation of the proposed ensemble method lies in its increased computational demands. Nonetheless, even when using a Titan RTX 24-GB GPU NVIDIA, Santa Clara, CA, USA, released in 2018, equipped with 4608 CUDA cores (for reference, the current NVIDIA 5090 features 21,760 CUDA cores), a batch of 10,000 images can be classified by the pre-trained DenseNet201 in 97.19 s.

Each pattern corresponds to a 32 × 32 pixel image patch, representing a physical area of 320 m × 320 m. At this resolution, the entire territory of Italy consists of approximately 2,942,578 patches. Considering the whole ensemble of 30 DenseNet models, it is possible to classify Italy, in its entirety, using patches of the exact resolution and size as those in the LCZ dataset within 10 days, even when relying on an old-generation GPU that is far from comparable to current architectures. Moreover, as previously discussed (see Figure 2), it is not necessary to employ all 30 models; a smaller subset is sufficient. It should also be noted that our experiments were conducted on a single GPU with 5000 CUDA cores. In many real-world applications, access to multiple modern GPUs or even GPU clusters is not a constraint. Consequently, processing time does not represent a significant limitation. For instance, using a cluster of four NVIDIA 5090 GPUs together with an ensemble of 18 models would enable classification of the entire Italian territory in just a few hours.

For other applications, such as edge or satellite computing, several strategies can be adopted to reduce the computational burden while maintaining competitive performance with CNNs [44,45]. One such strategy is knowledge distillation [45], a widely employed technique for compressing an ensemble into a single, smaller model. In this approach, the knowledge of the ensemble is transferred to a more efficient student network by training it to mimic the ensemble’s predictions, typically through the use of a softened softmax output. This method substantially reduces inference time while preserving much of the accuracy of the original ensemble.

Another effective strategy is quantization [46]. This technique reduces the precision of network weights and activations from 32-bit floating-point values to lower-bit formats, such as 16-bit or 8-bit integers. Quantization can yield significant speedups with only minimal degradation in accuracy.

A further approach involves evaluating only a dynamic subset of models within the ensemble rather than executing the complete set. Input-dependent strategies, such as gating networks or adaptive inference, enable selective model execution, thereby lowering computational demands while maintaining accuracy at a competitive level.

3.1. Further Validation

In addition to the fixed three-channel configuration, we performed further experiments using custom architectures based on ResNet50 (selected to reduce computational complexity compared to DenseNet201) that take all available spectral bands as input. This model achieved an accuracy of 63.24%, only slightly outperforming a ResNet50 trained on RGB images.

A more interesting result was obtained by implementing a ResNet50 variant in which a subset of bands was selected using Pudil’s search strategy [47], with the selection performed through 5-fold cross-validation on the training data. This approach yielded an accuracy of 67.08%, outperforming the standard ResNet-50 but still falling short of the proposed ensemble’s performance. This finding highlights the potential of band selection methods, which we plan to further explore in future work for designing ensembles based on different band subsets.

Furthermore, we extended our comparison by including two Transformer-based architectures. Specifically, we adopted a model that first extracts multiscale spatial and spectral features via a 3D CNN backbone and subsequently processes them through a Transformer encoder, as detailed in our previous work [28]. An ensemble of 10 such Transformer models achieved an accuracy of 69.1%, which, although lower than the accuracy of the proposed DenseNet201 ensemble, remains competitive. Finally, we adapted this Transformer-based model to handle all Sentinel-2 channels, obtaining an accuracy of 66.75%. While these models offer improvements over the stand-alone networks, they also require substantially higher training time and computational resources. Nevertheless, given their promising performance, we plan to investigate in future work the integration of Transformer-based architectures with DenseNet-like models for enhanced spectral–spatial learning.

Now, we report additional results obtained by varying the SAR clipping threshold parameter. It is important to note that no overfitting was introduced in this process. The threshold value was selected empirically based on visual inspection, aiming to remove evident outliers while maintaining overall stability. When using threshold values close to the selected one, the performance remains essentially unchanged; in some cases, a slight improvement is observed. Using the threshold of 0.5 employed in this paper, RandS (DenseNet) achieves an accuracy of 71.84%. With a threshold of 0.75, the accuracy increases to 71.96%, and with a threshold of 1.00%, it decreases to 71.57%.

As already emphasized, however, our objective is not to over-optimize the system. It is worth emphasizing that this minor improvement is evident in the test set: tuning the clipping threshold directly on test data would clearly constitute overfitting, which is precisely what needs to be avoided.

Next, we report results obtained by testing different loss functions, specifically, class-balanced [48] and focal loss [49] on ensemble ‘10 Rand’ coupled with DenseNet201 model. The results show comparable performance across the different loss formulations. This outcome is consistent with the fact that the dataset is not strongly imbalanced, except for a few classes, such as bush and scrub. Class-balanced loss improves the performance to 72.69% and the focal loss to 72.76%, representing only a marginal improvement. Moreover, this improvement should be validated using k-fold cross-validation on the training data, rather than by checking performance on the test set.

Moreover, we have included results obtained by increasing the training set size using MixUp [50] and RandAugment [51]. These data augmentation strategies were applied both independently, effectively doubling the size of the training set. Due to the resulting increase in computational complexity, we were unable to extend these experiments further. Nevertheless, it is worth noting that both augmentation methods led to a slight performance improvement for the stand-alone DenseNet201 model. MixUp increases the performance by +0.23% and RandAugment by +0.36%. Both approaches use the suggested parameters of the original paper/code.

Running an ensemble of 30 DenseNets combined with data augmentation is currently not computationally feasible. However, we have identified this direction as future work, with the goal of developing a lightweight DenseNet variant that can be effectively integrated with self-supervised pretraining and data augmentation strategies.

We also conducted additional experiments following the approach proposed in [52], which applies linear post-training quantization to facilitate model deployment on resource-constrained devices, such as edge or IoT systems, it decreases the performance of our proposed approach to 71.6%, clearly lower, but it could be interesting in some applications, considering the drastically lower inference time.

Self-Supervised Test

Specifically, we conducted an additional experiment involving self-supervised pretraining on a large-scale unlabeled dataset of Sentinel-1 and Sentinel-2 imagery, namely SSL4EO-S12 [53]. Following the approach described in that work, we used 10% of the available data to limit computational costs (as also done in the original paper, where experiments were performed using both 10% and 100% of the dataset). The objective of this stage was to learn rich, general-purpose representations of Sentinel data distributions without relying on labeled data.

In the subsequent supervised fine-tuning stage, we trained the network on our labeled dataset for the classification task, following the same training pipeline previously described, but initializing the model with the pretrained weights obtained from SSL4EO-S12. This step aims to enhance the model’s sensitivity to the spectral and spatial characteristics of Sentinel imagery.

Given the high computational demands of this procedure, we performed these experiments using ResNet50 (since applying the same process to DenseNet201 was computationally infeasible). The results show that ensembles of 10 ResNet50 networks, trained under this regime using Rand, achieve improved performance (72.11% compared to 71.21%), while increasing the ensemble to 30 models did not yield further gains.

Mean and standard deviation of accuracy, F1-score, Precision, and Recall of the self-supervised stand-alone ResNet50-based approaches are reported in Table 4.

Table 4. Comparison, mean and standard deviation, considering different performance indicators.

Accuracy	F1	Precision	Recall
65.76 ± 0.043	53.00 ± 0.047	56.07 ± 0.042	53.28 ± 0.044

4. Conclusions

Although classification with multiple neural networks is computationally demanding, our focus on optimizing accuracy yielded notable gains. As demonstrated, the proposed ensemble approach for multiband imagery delivers performance that surpasses current state-of-the-art methods, thereby establishing the model as a highly effective tool for the intended tasks. The marked improvements across key performance indicators, relative to individual networks, validate the computational overhead and underscore the superiority of a robust ensemble strategy over single-network solutions for image classification.

Our work addresses critical gaps in the field in two main respects. First, it bridges model architectures by combining the strengths of standard CNNs, thereby not only achieving state-of-the-art performance but also providing a more accessible alternative to methods that depend exclusively on highly complex or custom-designed networks. Second, it ensures ease and availability of implementation, as all source code used in this study is freely accessible on GitHub; this enhances reproducibility and makes the methods more accessible to both researchers and practitioners, directly addressing the challenge that many state-of-the-art approaches are difficult to deploy or replicate. In sum, our contribution advances the technical state of the art in multichannel image classification while simultaneously delivering a practical advantage: the proposed method is straightforward to implement and more readily deployable in real-world, cloud-based environments.

In future work, we intend to extend the promising results of this study in several directions. One line of development involves expanding the range of model architectures: while our current ensemble integrates standard CNNs with custom designs, exploring alternative deep learning paradigms, such as transformer-based models or graph neural networks, may better capture the intricate spectral and spatial dependencies of multiband data, and we plan to design new architectures capable of jointly processing multispectral and synthetic aperture radar imagery.

Another future development will involve selecting the bands to build the ensemble instead of using a random selection. For instance, one could choose networks trained with specific combinations of bands to maximize the diversity and the amount of information contributed by each individual network in the ensemble.

Another possible approach is to modify Densenet so that its input is not limited to three channels but extended to k channels, where k is a subset of the total number of available bands; each network in the ensemble would then be trained on a different number of channels.

Finally, building on our previous work, we could explore combining a Transformer-based architecture with a Densenet-based one. However, considering the computational cost of Densenet, it will be necessary to design a lightweight version of it in order to integrate it effectively with Transformer-based ideas.

Another avenue concerns domain adaptation and transfer learning, which could enhance the ability of the ensemble framework to generalize across diverse sensor types and imaging conditions, while also facilitating rapid adjustment to new datasets in dynamic environmental monitoring contexts. We also aim to incorporate temporal dynamics by extending the framework to process time-series multiband imagery, consequently enabling the analysis of land-cover evolution and ecological change and increasing the framework’s relevance for real-time applications. Finally, we will explore scalability and operational deployment, optimizing the system for real-time performance through distributed computing or edge-based implementations, which would substantially increase its applicability in remote sensing practice. Collectively, these efforts are designed to address current limitations and advance toward more versatile and resilient models for multiband image classification.