Abstract
Metal hydrides are emerging hydrogen-storage materials that have attracted much attention for their stability and practicality. The novel magnesium-based metal hydride Mg2CsH9 was investigated using the CALYPSO software (version 7.0). First-principles predictive methods were then employed to investigate the structural, mechanical, electronic, optical, and hydrogen-storage properties of Mg2CsH9 and its alkali metal substitution structure Mg2RbH9. The negative formation energy, compliance with the Born stability criterion, and absence of imaginary modes in the phonon spectrum collectively confirm the thermodynamic, mechanical, and dynamic stability of Mg2XH9 (X = Cs, Rb), fulfilling the basic criteria for practical hydrogen-storage applications. Mg2RbH9 is particularly outstanding in terms of its hydrogen-storage capacity, with a gravimetric capacity of 6.34 wt% and a volumetric capacity as high as 92.70 g H2/L, surpassing many conventional materials. The pronounced anisotropic characteristics of both compounds further enhance their practicality and adaptability to complex working conditions. An analysis of Poisson’s ratio revealed that the chemical bonding in both compounds is predominantly ionic. The details of the band structures and density of states indicate that Mg2CsH9 and Mg2RbH9 are semiconductors. Their optical properties confirm them as being high-refractive-index materials.
1. Introduction
Carbon combustion and inefficient fossil fuel utilization are the primary causes of a ~35% increase in CO2 emissions [1]. Consequently, the growing global emphasis on sustainable development has made clean energy a focus of interest in the energy sector [2,3,4,5,6,7]. Hydrides, long regarded as promising energy carriers, have attracted increasing attention for their high calorific value and zero pollutant emissions [8]. Their outstanding degree of applicability and environmental compatibility compared with other proposed fuels, makes them a choice material for energy storage [9]. For stationary power systems and portable devices, hydrides offer significant advantages in terms of safety, environmental performance, and cost-effectiveness [10].
However, hydrogen faces numerous technical challenges to its industrialization as a sustainable energy source. Current extensive research efforts aim to discover novel materials with a high hydrogen capacity and a suitable operating temperature range to meet industrial requirements [11]. The superior safety of metal hydrides with regard to compressed or liquefied hydrogen has been demonstrated in recent years, leading to their inclusion in commercial supply chains. Their practical usability is enhanced by their ability to release hydrogen under ideal conditions of ambient temperature and pressure [6,12]. However, metals, hydrides, hydroxides, and their alloys or composites still exhibit certain drawbacks such as relatively weak resistance to corrosive influences from environmental factors like temperature, oxygen, and electromagnetic radiation. In contrast, oxide compounds demonstrate significantly higher stability when used up to 1000 °C [13]. Considering the various available hydrogen-storage materials, magnesium-based hydrides have unique advantages that make them some of the most promising candidates. Magnesium exhibits a high hydrogen- storage capacity (7.65 wt% gravimetric and 110 g H2/L volumetric) and is abundant in the Earth’s crust, promising conditions for cost-effective large-scale applications [14]. Cs atoms, which are also uniquely advantageous in hydrogen-storage material design, are characterized by the largest atomic radius (265 pm). The hydrogen storage capacity of cesium-containing hydrogen storage structures can be significantly enhanced by expanding the lattice spacing and optimizing hydrogen adsorption sites [15]. Similarly, the double-perovskite structure has displayed remarkable hydrogen-storage capability. For example, the hydrogen capacities of Mg2FeH6 and Be2FeH6 are 5.43 and 7.9 wt%, respectively, highlighting their potential as hydrogen-storage materials [16]. Similarly, Be2CrH6 and Be2MnH6 exhibit 7.9 and 7.6 wt% hydrogen contents, respectively, making them strong candidates for onboard hydrogen-storage in new energy vehicles [17].
To screen for novel materials with high hydrogen density, we increased the number of hydrogen atoms within the magnesium-based perovskite framework. Subsequently, leveraging the large atomic radius of cesium (Cs), we introduced Cs atoms to expand the structural space. Finally, we employed the particle swarm optimization crystal structure analysis software (CALYPSO7.0) [18] to search for Mg2CsH9-type structures. Density functional theory (DFT) calculations confirmed that both the Mg2CsH9 structure obtained through structural search and the Mg2RbH9 structure derived via alkali metal substitution exhibited stability and demonstrated excellent hydrogen storage performance. In addition, optical properties such as transmittance, reflectivity, and absorption are closely related to the electronic structure, hydrogenation state, and kinetic behavior of hydrogen-storage materials. The present study therefore also analyzed the optical properties. In both compounds, the incorporation of specific metal atoms (Cs/Rb) into the Mg-H framework may weaken the strong ionic Mg-H bonds, potentially reducing the desorption energy barrier and lowering the required hydrogen release temperature. This mechanism suggests a potential pathway for addressing current energy storage challenges.
2. Computational Details
The variable cellular crystal structure of Mg2CsH9 was simulated using the CALYPSO code, a widely used tool whose reliability for stable crystal structure prediction has been verified in various systems [19,20]. During the prediction process, the number of individuals in each generation was set to 30, and the initial structure was constructed randomly within the symmetry constraints. A total of 50 generations were set to ensure that the structural evolution met the convergence criteria. The structural, electronic, elastic, dynamic, and optical properties of Mg2XH9 (X = Cs, Rb) were then predicted using the Vienna Ab initio Simulation Package (VASP5.4.4) [21] based on density functional theory (DFT) [22]. Exchange and correlation effects in electron–electron interactions were described using the generalized gradient approximation (GGA) combined with the Perdew–Burke–Ernzerhof functional (PBE) [23]. A plane-wave cutoff energy of 600 eV was applied, and a 6 × 6 × 6 Monkhorst-Pack k-point grid was used to ensure sufficient convergence of the total energy, with a precision of 1 × 10−5 eV [24,25]. All structures were subjected to lattice optimization and fully relaxed throughout the computational process. The phonon dispersion curves were computed using the Phonopy(version 2.12) package, employing a 2 × 2 × 2 supercell to evaluate the dynamic stability of the materials.
3. Results and Discussion
3.1. Structural Stability and Hydrogen Storage Performance
Mg2XH9 adopts a cubic structure with space group Pn (No. 201). The spatial structure of Mg2XH9 (X = Cs, Rb) is shown in Figure 1a. Views along the [111] directions are displayed in Figure 1b, where 18 hydrogen atoms form hydrogen cages surrounding the X atom. Specific atomic fractional coordinates are provided in Appendix A. The formation energies of Mg2XH9 (X = Cs, Rb) were calculated using the following formula [26]:
where E(Mg2XH9) represents the total energy of Mg2XH9, and E(Mg), E(X), and E(H) represent, respectively, the average energies of each Mg, X, and H atom in their elemental crystal forms. The formation energies of the two compounds (see Table 1) were negative, confirming their thermodynamic stability.
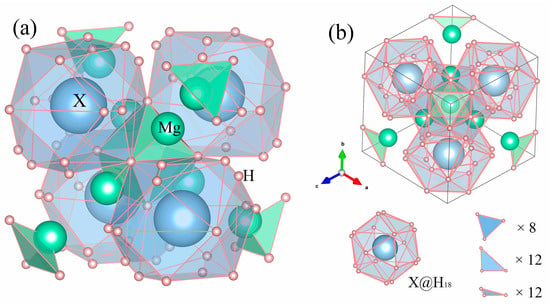
Figure 1.
(a) Crystal structures of Mg2XH9 (X = Cs, Rb) compounds and (b) Mg2XH9 (X = Cs, Rb) viewed along the [111] direction.

Table 1.
The possible decomposition pathways and relative formation energies Ef (eV/atom) of these Mg2XH9 structures.
To further evaluate the thermodynamic stability of these ternary compounds, we searched the Open Quantum Materials Database (OQMD) for relevant stable compounds and constructed decomposition reaction pathways for the Mg2XH9 structures. The relative formation energy (Ef) was calculated to assess stability: If Ef < 0, the structure is thermodynamically stable and likely synthesizable via the proposed pathway. If Ef > 0, the structure has lower thermodynamic stability and risks decomposition. As shown in Table 1, all Ef values were negative, confirming that these two structures are thermodynamically stable and potentially synthesizable from related compounds.
Mg2XH9 adopts a cubic crystal structure with three independent elastic constants (C11, C12, and C44) and its mechanical stability was assessed using the Born criteria [27]:
As shown in Table 2, both metal hydrides satisfy the stability criteria expressed in Equation (2), confirming their mechanical stability. In cubic crystals, uniaxial compression along the x-axis is represented by C11, whereas resistance to deformation under pure shear stress is represented by C44. The C11 values of both hydrides were higher than their corresponding C44 values, indicating that their resistance to uniaxial compression was greater than that to shear deformation.

Table 2.
Optimized lattice constants, volume, formation energies, elastic constants, gravimetric hydrogen capacity, volumetric hydrogen capacity, and desorption temperature of the compounds Mg2XH9 (X = Cs, Rb).
Phonon dispersion spectra are key indicators of the dynamical stability of materials. As shown in Figure 2, the phonon frequencies of both compounds were non-negative throughout the Brillouin zone. Imaginary frequencies below zero were not observed within the Brillouin zone, thereby confirming the dynamical stability of Mg2CsH9 and Mg2RbH9.
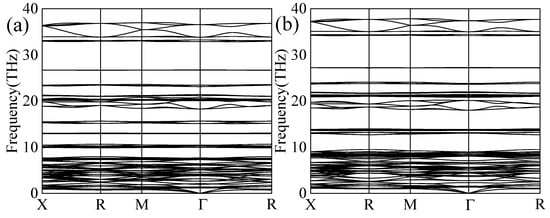
Figure 2.
Phonon spectra of (a) Mg2CsH9 and (b) Mg2RbH9.
To evaluate the hydrogen-storage performance of Mg2XH9, the gravimetric hydrogen-storage capacity was assessed based on the following formula [28]:
where n denotes the atomic ratio between hydrogen atoms and the host material (Mg2X), and and are the molar masses of hydrogen and the host material (Mg2X), respectively. The hydrogen-storage capacity of Mg2RbH9 was 6.34 wt%, demonstrating significant potential compared with common hydrogen-storage materials such as NaAlH4 (5.6 wt%) [29] and LaNi5H6 (1.4 wt%) [30], thus Mg2RbH9 demonstrates significant potential as a hydrogen-storage material.
Volumetric storage capacity, which quantifies the amount of hydrogen stored within a specific volume, is a key parameter for evaluating the hydrogen storage capability of materials [31]. Its mathematical expression is given as follows:
where denotes the number of absorbed hydrogen atoms, represents the molecular weight of hydrogen, V(L) indicates the absorbent volume (i.e., the cubic unit cell volume in Table 2), and is Avogadro’s number. As shown in Table 2, Mg2RbH9 exhibited a higher hydrogen-storage capacity due to its smaller volume, which is determined by the cation size (Rb+). Larger cation sizes lead to increased unit cell volumes, and consequently, a lower volumetric storage capacity.
During desorption, thermodynamic and kinetic factors act synergistically to influence the desorption rate and temperature. The desorption temperature, a key parameter for characterizing hydrogen-storage, is the temperature at which hydrogen becomes released from solid hydrides [32]. Its value is primarily calculated as:
where ∆Hf (see Table 2) and ∆S represent, respectively, the formation enthalpy of solid hydride and the entropy change of hydrogen (approximately −130.7 J/mol) [33]. The ideal temperature range is typically between 233 and 333 K [34]. The calculation results presented in Table 2, show that the desorption temperatures of both Mg2CsH9 and Mg2RbH9 fall within this ideal range. The values of 285.69 K or 282 K in Table 2 suggest that these structures may release hydrogen at room temperature. Therefore, the materials should be stored in environments slightly below or under pressure regulation to suppress hydrogen release. This property makes them suitable for mobile devices requiring rapid low-temperature hydrogen release, avoiding risks associated with high-temperature operations.
3.2. Mechanical Properties
The calculation of elastic constants facilitates the assessment of material stiffness, brittleness, ductility, mechanical stability, and elastic anisotropy. In VASP-based calculations, elastic constants are determined using the stress-strain method to comprehensively analyze the mechanical properties of the metal hydrides. Typically, elastic moduli include the bulk modulus, Young’s modulus, shear modulus, and Poisson’s ratio, which are calculated using the following formulas [35,36]:
When investigating mechanical properties, the bulk modulus (B), Young’s modulus (E), and shear modulus (G) characterize a material’s resistance to volumetric compression, elastic deformation, and shear strain, respectively. As shown in Table 3, Mg2RbH9 exhibits a high resistance to compression. The ductility and brittleness of materials can be assessed using the Pugh ratio (B/G). When B/G > 1.75, the material is considered ductile, whereas B/G < 1.75 indicates brittleness. The calculated B/G values for Mg2CsH9 (1.46) and Mg2RbH9 (1.52) were both below this critical value, confirming their brittle nature. This observation is consistent with the commonly reported low B/G ratios in metal hydrides [34]. Notably, the brittle characteristics of these compounds have significant engineering relevance in the context of the safe handling and transportation of hydrogen storage systems. Further analysis based on Poisson’s ratio indicates that the ν values of Mg2CsH9 (0.221) and Mg2RbH9 (0.23) are both close to 0.25, suggesting that their chemical structures are predominantly governed by ionic bonding. This result agrees well with the theoretical predictions derived from the charge-density distribution calculations.

Table 3.
Calculated bulk modulus, Young’s modulus, shear modulus, elastic anisotropy, B/G ratio, Poisson’s ratio, Vickers hardness, melting temperature, machinability index, average sound velocity, and Debye temperature for the Mg2XH9 (X = Cs, Rb) structures.
The elastic anisotropy factor can be expressed using the three independent elastic constants C11, C12, and C44, as defined by the following equation.
As shown in Table 3, the anisotropy factor of the metal hydrides Mg2XH9 deviate from 1, indicating elastic anisotropy.
Vickers hardness, melting point, and machinability index () are key indicators used for assessing mechanical properties, as they not only reflect structural strength but also play decisive roles in practical applicability. To evaluate the mechanical properties, Vickers hardness (based on the Chen model), melting temperature, and machinability index, are estimated using the following formulas [37,38,39]:
The parameter k is defined as the ratio of shear modulus to bulk modulus (i.e., k = G/B). Based on the data in Table 3, the comparable melting points and hardness values of Mg2CsH9 and Mg2RbH9 confirm their virtually equivalent crystal structural strength and thermal stability. The machinability index , which correlates with machinability, exhibits a direct proportionality to mechanical processability enhancement [40,41,42,43,44]. As shown in Table 3, it can be reasonably inferred that Mg2RbH9 shows superior processability compared with Mg2CsH9.
To further understand the structural stability of the materials, the Debye temperature was also calculated using the following formula [45]:
where h denotes the Planck constant, k is the Boltzmann constant, n is the number of atoms per unit cell, V is the crystal volume, and is the average sound velocity. The Debye temperature generally reflects the highest excited state of the atomic vibrational energy levels in a crystal, and its value is closely associated with the chemical bond strength, lattice dynamic characteristics, and thermal transport properties. A high Debye temperature implies strong interatomic bonding and intense internal interactions within the system [46]. The results in Table 3 suggest that Mg2RbH9 exhibits tighter internal atomic bonding, demonstrating superior structural cohesion performance.
3.3. Electronic Band Structure and Density of States
To investigate the electronic properties of the magnesium-based alkaline metal hydrides Mg2XH9 (X = Cs, Rb), we calculated their band structures using the GGA functional and the Heyd–Scuseria–Ernzherof (HSE06) hybrid functional in VASP [47,48]. The HSE06 hybrid functional is beneficial for accurately determining the band gap of Mg2XH9. The calculation results indicate that both materials exhibit direct band gap characteristics, as illustrated in Figure 3. Using the GGA method, the Mg2CsH9 band gap was calculated to be 0.87 eV, whereas that of Mg2RbH9 was significantly lower at 0.67 eV. The HSE06 hybrid functional accurately determined the band gap as 1.65 eV (Mg2CsH9) and 1.12 eV (Mg2RbH9). The narrowing of the band gap implied a lower electron transition barrier [49], which was identified as a critical factor for enhancing hydrogen-storage performance. This indicates the enhanced potential of Mg2RbH9 for application as a hydrogen-storage material. Notably, the Fermi level (marked by the red dashed lines) was biased toward the valence band maximum in both cases. Combined with the hole concentration analysis, both materials were identified as p-type semiconductors. This carrier characteristic could potentially optimize the hydrogen-storage performance through a hole-conduction mechanism.
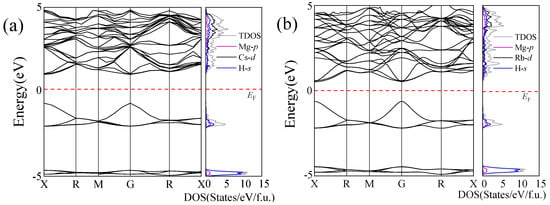
Figure 3.
Electronic band structures and density of states of (a) Mg2CsH9 and (b) Mg2RbH9 calculated using the HSE06 method. EF denotes the Fermi level.
As illustrated in Figure 3, the electronic structure of the Mg2XH9 (X = Cs, Rb) compounds shows the valence bands being predominantly dominated by the s-orbitals of hydrogen atoms, indicating their decisive role in the electronic structure of the valence. The conduction band region is primarily dominated by the d-orbital of the X atoms (Cs/Rb), whereas the p-orbital of the Mg atoms participates only marginally in low-energy regions. The highly electronegative X atoms dominate the formation of the conduction band, whereas hydrogen atoms maintain lattice stability through strong ionic bonding.
As illustrated in Figure 4, the electron localization function (ELF) analysis showed that Mg2XH9 (X = Cs, Rb) exhibits pronounced high electron density regions (ELF ≈ 1) surrounding hydrogen atoms in the (111) crystallographic plane. A pronounced electron localization gradient between the X (Cs/Rb) and H atoms indicates strong localized characteristics in H-X bonding. Bader charge analysis indicates that, on average, each H atom gains approximately 0.473 e from Mg and X atoms (X = Cs) or 0.427 e from Mg and X atoms (X = Rb), which is consistent with the high electron density distribution around H atoms observed in the ELF mapping. The highly localized electron clouds (ELF > 0.8) surrounding the H atoms, combined with significant charge transfer (>0.85 e), collectively demonstrate the ionic hybrid bonding characteristics of the Mg-X-H system. This electronic-scale evidence provides fundamental insights into the structural stability of the materials [50,51].
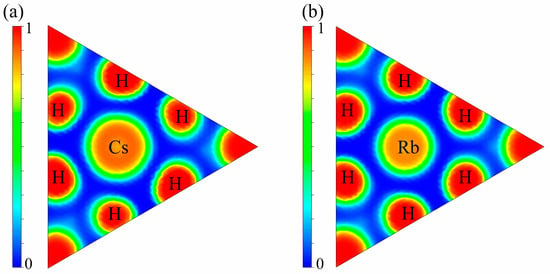
Figure 4.
Electronic localization function (ELF) along the [111] direction of (a) Mg2CsH9 and (b) Mg2RbH9.
3.4. Optical Properties
The optical properties of Mg2XH9 (X = Cs, Rb) were comprehensively analyzed and described, focusing on their dielectric function, refractive index, absorption, reflectivity, and energy-loss function.
The dielectric function was calculated as [52,53]:
The real part of the dielectric function , which characterizes the polarizability and dispersion relations in surface electromagnetic responses (Figure 5a), displayed a higher peak value for Mg2CsH9 (approximately 8.6) compared with Mg2RbH9 (approximately 7.9) within the low-frequency region (0–10 eV), indicating a stronger polarization response to low-frequency electric fields in Mg2CsH9. The imaginary part , which reflects the light absorption capacity through electronic band transitions (Figure 5b), displayed peaks around 7.8 and 7.2 for Mg2CsH9 and Mg2RbH9, respectively. This confirms the superior low-frequency photon absorption efficiency in Mg2CsH9, which correlates with the electron transition characteristics of H-X bonds. In the high-energy region (10–20 eV), the real part of the dielectric function for both materials approached 1 (the vacuum dielectric constant), while the imaginary part decayed to near zero. This behavior originates from truncation effects in the calculation, which exclude high-energy interband transitions such as inner-shell electronic excitations. In real materials, plasmon resonance (>15 eV) should exist in this energy range, but the independent-particle approximation (IPA) fails to account for such many-body effects.
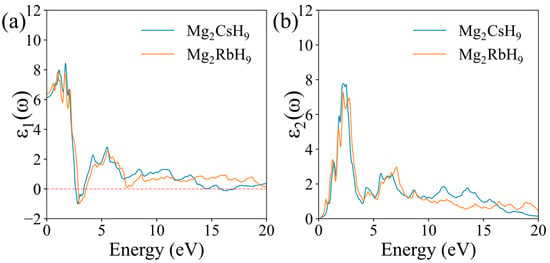
Figure 5.
Calculated dielectric functions of Mg2XH9: (a) real part; (b) imaginary part.
The absorption coefficients of Mg2CsH9 and Mg2RbH9, shown in Figure 6a, were zero in the energy range below their respective band-gaps (0.62 eV and 0.59 eV, respectively), which confirms their semiconducting nature. With increasing photon energy, the absorption peaks were primarily distributed in the UV region (>3.1 eV), indicating a strong tendency of Mg2CsH9 and Mg2RbH9 to absorb UV light.
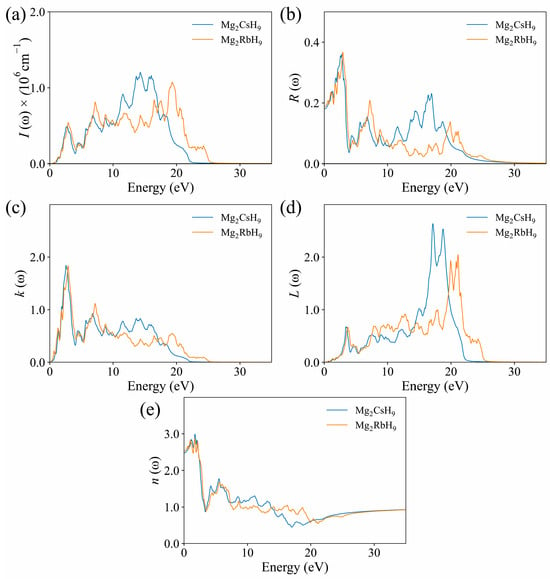
Figure 6.
Calculated optical properties of Mg2XH9: (a) absorption coefficient I(ω); (b) reflectivity R(ω); (c) extinction coefficient K(ω); (d) energy loss spectrum L(ω); and (e) refractive index n(ω).
As shown in Figure 6b, the initial reflectivity values of Mg2CsH9 and Mg2RbH9 were approximately 0.19 and 0.18, respectively. With increasing photon energy, the maximum reflectivity of Mg2CsH9 reached approximately 0.36 at 3.2 eV, whereas that of Mg2RbH9 peaked at approximately 0.38 at 3.4 eV. In the visible light-region, the reflectivity of Mg2CsH9 was higher than that of Mg2RbH9; however, in the far-ultraviolet region, Mg2RbH9 was more reflective. When the photon energy exceeded 27 eV, the reflectivity of both materials approached zero, indicating enhanced transparency to high-energy photons, which is consistent with the attenuation behavior of dielectric responses.
The extinction coefficients K(ω), presented in Figure 6c, displayed peaks at approximately 1.85 for Mg2CsH9 and 1.83 for Mg2RbH9, indicating minor differences between the two hydrides. The similarity in these peak values suggests a comparable degree of interaction between the incident photon radiation and each material. With increasing photon energy, the extinction coefficient showed an overall decreasing trend, indicating a weakened attenuation effect in the high-energy region, which favors light propagation within the material.
The energy-loss function for Mg2CsH9, presented in Figure 6d, showed a double-peak structure at 16.8 eV (L = 2.75) and 18.9 eV (L = 2.52), while the loss peaks of Mg2RbH9 shifted toward the higher-energy region, appearing at 21.2 eV (L = 1.92) and 22.8 eV (L = 2.08). The overall energy-loss intensity for Mg2CsH9 was approximately 30% higher than that for Mg2RbH9, indicating more pronounced collective electron oscillations (plasmons). This may be attributed to the enhanced polarization of the electron cloud induced by the larger radius of the Cs atom. At 0 eV, both substances had a loss function value of 0. The optical and electrical characteristics of these compounds make them suitable for use in LEDs and solar cells.
Figure 6e illustrates the variation of the refractive index n(ω) of the two hydrides. The static refractive index n(0) was approximately 2.5, which meets the requirements for high-refractive-index optical materials (n > 2.0). In the range of 7.5–20 eV, the fluctuation amplitude of the refractive index of Mg2RbH9 (Δn = 0.4) was smaller than that of Mg2RbH9 (Δn = 0.8), indicating a more stable optical response. When the photon energy exceeded 25 eV, n(ω) for both materials approached 1, consistent with the dielectric response of a vacuum and confirming the physical mechanism of dielectric polarization loss in the high-energy region.
4. Conclusions
Based on first-principles methods, the thermodynamic, hydrogen-storage, mechanical, electronic, and optical properties of magnesium-based alkali metal hydrides Mg2XH9 (X = Cs, Rb) were predicted. According to the Born stability criteria, both hydrides are mechanically stable. The Poisson’s ratio values confirmed that bonding in both compounds is predominantly ionic. The results also indicate that these alkali metal hydrides exhibit elastic anisotropy. The band structure analyses revealed their semiconducting nature, while the density of state analysis revealed that the s-orbitals of hydrogen atoms primarily influence the valence band, whereas the conduction band is mainly contributed by the d-orbital of X atoms, with smaller contributions from Mg atoms. The hydrogen-storage performance analysis revealed that Mg2RbH9 has a high storage capacity of 6.34 wt%. The optical properties showed that Mg2XH9 (X = Cs, Rb) exhibit favorable refractive indices, thereby classifying them as high-refractive-index materials. Theoretically, Mg2RbH9 demonstrates excellent mechanical, electronic, and hydrogen-storage properties, suggesting its strong potential as a candidate for future solid-state hydrogen-storage applications.
Author Contributions
Conceptualization, Q.W.; Methodology, W.L. and Q.W.; Software, W.L. and M.Z.; Validation, W.L. and Q.W.; Formal analysis, J.L. and X.J.; Investigation, W.L. and Q.W.; Resources, Q.W.; Data curation, W.L.; Writing—original draft preparation, W.L.; Writing—review and editing, Q.W. and M.Z.; Visualization, X.Z.; Supervision, Q.W.; Project administration, Q.W.; Funding acquisition, Q.W. and M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the National Natural Science Foundation of China (Grant Nos.: 11965005 and 11964026) and the Natural Science Basic Research Plan in Shaanxi Province of China (Grant No.: 2025JC-YBMS-027).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Atomic fractional coordinates for Mg2XH9 (X = Cs, Rb) in the Pn
phase (Space Group No. 201).
Table A1.
Atomic fractional coordinates for Mg2XH9 (X = Cs, Rb) in the Pn
phase (Space Group No. 201).
| Phases | Pressure (GPa) | Lattice Parameters | Atoms | Wyckoff Positions (Fractional) | ||
|---|---|---|---|---|---|---|
| x | y | z | ||||
| Pn Mg2CsH9 | 0 | a = 8.8667 | Cs (4b) | 0.2500 | 0.2500 | 0.2500 |
| Mg (8e) | 0.8571 | 0.8571 | 0.8571 | |||
| H (24h) | 0.5302 | 0.9691 | 0.7240 | |||
| H (12f) | 0.7701 | 0.0000 | 0.0000 | |||
| Pn Mg2RbH9 | 0 | a = 8.6630 | Rb (4b) | 0.2500 | 0.2500 | 0.2500 |
| Mg (8e) | 0.8552 | 0.8552 | 0.8552 | |||
| H (24j) | 0.5314 | 0.9686 | 0.7500 | |||
| H (12g) | 0.7644 | 0.0000 | –0.0000 | |||
References
- Khan, M.I.; Al-Ghamdi, S.G. Hydrogen economy for sustainable development in GCC countries: A SWOT analysis considering current situation, challenges, and prospects. Int. J. Hydrogen Energy 2023, 48, 10315–10344. [Google Scholar] [CrossRef]
- Le, T.T.; Sharma, P.; Bora, B.J.; Tran, V.D.; Truong, T.H.; Le, H.C.; Nguyen, P.Q.P. Fueling the future: A comprehensive review of hydrogen energy systems and their challenges. Int. J. Hydrogen Energy 2024, 54, 791–816. [Google Scholar] [CrossRef]
- Allendorf, M.D.; Stavila, V.; Snider, J.L.; Witman, M.; Bowden, M.E.; Brooks, K.; Tran, B.L.; Autrey, T. Challenges to developing materials for the transport and storage of hydrogen. Nat. Chem. 2022, 14, 1214–1223. [Google Scholar] [CrossRef]
- Schlapbach, L.; Züttel, A. Hydrogen-storage materials for mobile applications. Nature 2001, 414, 353–358. [Google Scholar] [CrossRef]
- Mohammadi, A.; Ikeda, Y.; Edalati, P.; Mito, M.; Grabowski, B.; Li, H.-W.; Edalati, K. High-entropy hydrides for fast and reversible hydrogen storage at room temperature: Binding-energy engineering via first-principles calculations and experiments. Acta Mater. 2022, 236, 118117. [Google Scholar] [CrossRef]
- Von Colbe, J.B.; Ares, J.R.; Barale, J.; Baricco, M.; Buckley, C.; Capurso, G.; Gallandat, N.; Grant, D.M.; Guzik, M.N.; Jacob, I.; et al. Application of hydrides in hydrogen storage and compression: Achievements, outlook and perspectives. Int. J. Hydrogen Energy 2019, 44, 7780–7808. [Google Scholar] [CrossRef]
- Jain, A.; Shin, Y.; Persson, K.A. Computational predictions of energy materials using density functional theory. Nat. Rev. Mater. 2016, 1, 15004. [Google Scholar] [CrossRef]
- Al, S.; Kurkcu, C.; Yamcicier, C. High pressure phase transitions and physical properties of Li2MgH4; implications for hydrogen storage. Int. J. Hydrogen Energy 2020, 45, 4720–4730. [Google Scholar] [CrossRef]
- Chu, S.; Cui, Y.; Liu, N. The path towards sustainable energy. Nat. Mater. 2017, 16, 16–22. [Google Scholar] [CrossRef] [PubMed]
- Aminudin, M.; Kamarudin, S.; Lim, B.; Majilan, E.H.; Masdar, M.S.; Shaari, N. An overview: Current progress on hydrogen fuel cell vehicles. Int. J. Hydrogen Energy 2023, 48, 4371–4388. [Google Scholar] [CrossRef]
- Al, S.; Yortanl, M.; Mete, E. Lithium metal hydrides (Li2CaH4 and Li2SrH4) for hydrogen storage; mechanical, electronic, and optical properties. Int. J. Hydrogen Energy 2020, 45, 18782–18788. [Google Scholar] [CrossRef]
- Nivedhitha, K.S.; Beena, T.; Banapurmath, N.R.; Umarfarooq, M.A.; Ramasamy, V.; Soudagar, M.E.M.; Ağbulut, Ü. Advances in hydrogen storage with metal hydrides: Mechanisms, materials, and challenges. Int. J. Hydrogen Energy 2024, 61, 1259–1273. [Google Scholar] [CrossRef]
- Trukhanov, A.V.; Turchenko, V.O.; Bobrikov, I.A.; Trukhanov, S.V.; Kazakevich, I.S.; Balagurov, A.M. Crystal structure and magnetic properties of the BaFe12-xAlxO19 (x = 0.1–1.2) solid solutions. J. Magn. Magn. Mater. 2015, 393, 253–259. [Google Scholar] [CrossRef]
- Noreus, D.; Olsson, L. The structure and dynamics of hydrogen in Mg2NiH4 studied by elastic and inelastic neutron scattering. J. Chem. Phys. 1983, 78, 2419–2427. [Google Scholar] [CrossRef]
- Kaiser, A.; Renzler, M.; Kranabetter, L.; Schwärzler, M.; Parajuli, R.; Echt, O.; Scheier, P. On enhanced hydrogen adsorption on alkali (cesium) doped C60 and effects of the quantum nature of the H2 molecule on physisorption energies. Int. J. Hydrogen Energy 2017, 42, 3078–3086. [Google Scholar] [CrossRef]
- Hakami, O.; Alathlawi, H.J. Study of mechanical, optoelectronic, and thermoelectric characteristics of Be/Mg ions based double perovskites A2FeH6 (A = Be, Mg) for hydrogen storage applications. Int. J. Hydrogen Energy 2024, 83, 307–316. [Google Scholar] [CrossRef]
- Zelai, T. Study of magnetic, thermoelectric, and mechanical properties of double perovskites Be2XH6 (X = Cr and Mn) for spintronic and hydrogen-storage applications. Inorg. Chem. Commun. 2024, 165, 112579. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, W.; Chen, L.; Zhang, Y.; Wang, H.; Zhang, M.; Wei, Q. Structural, strength and fracture mechanisms of superconducting transition metal nitrides TM3N5 (TM = W and Mo). Phys. Chem. Chem. Phys. 2025, 27, 6134–6145. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wei, Q.; Luo, J.; Jia, X.; Zhang, M.; Zhu, X.; Wei, B. Pressure-induced phase transitions and electronic structure evolution of Ba4Au. Materials 2025, 18, 3728. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Le Page, Y.; Saxe, P. Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress. Phys. Rev. B 2002, 65, 104104. [Google Scholar] [CrossRef]
- Mera, A.; Rehman, M.A. First-principles investigation for the hydrogen storage properties of AeSiH3 (Ae = Li, K, Na, Mg) perovskite-type hydrides. Int. J. Hydrogen Energy 2024, 50, 1435–1447. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Gencer, A.; Surucu, G. Investigation of structural, electronic and lattice dynamical properties of XNiH3 (X = Li, Na and K) perovskite type hydrides and their hydrogen storage applications. Int. J. Hydrogen Energy 2019, 44, 15173–15182. [Google Scholar] [CrossRef]
- Sandrock, G.; Gross, K.; Thomas, G.; Jensen, C.; Meeker, D.; Takara, S. Engineering considerations in the use of catalyzed sodium alanates for hydrogen storage. J. Alloys Compd. 2002, 330–332, 696–701. [Google Scholar] [CrossRef]
- Noreus, D.; Olsson, L.G.; Werner, P.-E. The structure and dynamics of hydrogen in LaNi5H6 studied by elastic and inelastic neutron scattering. J. Phys. F Met. Phys. 1983, 13, 715–727. [Google Scholar] [CrossRef]
- Baaddi, M.; Chami, R.; Baalla, O.; El Quaoubi, S.; Saadi, A.; Omari, L.E.H.; Chafi, M. The effect of strain on hydrogen storage characteristics in K2NaAlH6 double perovskite hydride through first principle method. Environ. Sci. Pollut. Res. 2024, 31, 62056–62064. [Google Scholar] [CrossRef]
- Lakhal, M.; Bhihi, M.; Labrim, H.; Benyoussef, A.; Naji, S.; Belhaj, A.; Khalil, B.; Abdellaoui, M.; Mounkachi, O.; Loulidi, M.; et al. Kinetic Monte Carlo and density functional study of hydrogen diffusion in magnesium hydride MgH2. Int. J. Hydrogen Energy 2013, 38, 8350–8356. [Google Scholar] [CrossRef]
- Züttel, A.; Wenger, P.; Rentsch, S.; Sudan, P.; Mauron, P.; Emmenegger, C. LiBH4: A new hydrogen storage material. J. Power Sources 2003, 118, 1–7. [Google Scholar] [CrossRef]
- Kudiiarov, V.; Lyu, J.; Semyonov, O.; Lider, A.; Chaemchuen, S.; Verpoort, F. Prospects of hybrid materials composed of MOFs and hydride-forming metal nanoparticles for light-duty vehicle hydrogen storage. Appl. Mater. Today 2021, 25, 101208. [Google Scholar] [CrossRef]
- Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, M.G.; Jia, X.F.; Wei, Q. Stable structures and properties of Ru2Al5. Chin. Phys. B 2025, 34, 016301. [Google Scholar] [CrossRef]
- Chen, X.Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
- Sun, Z.; Music, D.; Ahuja, R.; Schneider, J.M. Theoretical investigation of the bonding and elastic properties of nanolayered ternary nitrides. Phys. Rev. B 2005, 71, 193402. [Google Scholar] [CrossRef]
- Fine, M.E.; Brown, L.D.; Marcus, H.L. Elastic constants versus melting temperature in metals. Scr. Metall. 1984, 18, 951–956. [Google Scholar] [CrossRef]
- Hadi, M.A.; Christopoulos, S.R.G.; Naqib, S.H.; Chroneos, A.; Fitzpatrick, M.E.; Islam, A.K.M.A. Physical properties and defect processes of M3SnC2 (M = Ti, Zr, Hf) MAX phases: Effect of M-elements. J. Alloys Compd. 2018, 748, 804–813. [Google Scholar] [CrossRef]
- Roknuzzaman, M.; Hadi, M.A.; Abden, M.J.; Nasir, M.T.; Islam, A.K.M.A.; Ali, M.S.; Ostrikov, K.; Naqib, S.H. Physical properties of predicted Ti2CdN versus existing Ti2CdC MAX phase: An ab initio study. Comput. Mater. Sci. 2016, 113, 148–153. [Google Scholar] [CrossRef]
- Chowdhury, A.; Ali, M.A.; Hossain, M.M.; Uddin, M.M.; Naqib, S.H.; Islam, A.K.M.A. Predicted MAX phase Sc2InC: Dynamical stability, vibrational and optical properties. Phys. Status Solidi B 2018, 255, 1700235. [Google Scholar] [CrossRef]
- Ali, M.; Hossain, M.; Uddin, M.; Hossain, M.A.; Islam, A.K.M.A.; Naqib, S.H. Physical properties of new MAX phase borides M2SB (M = Zr, Hf and Nb) in comparison with conventional MAX phase carbides M2SC (M = Zr, Hf and Nb): Comprehensive insights. J. Mater. Res. Technol. 2021, 11, 1000–1018. [Google Scholar] [CrossRef]
- Ali, M.; Hossain, M.; Uddin, M.; Islam, A.K.M.A.; Jana, D.; Naqib, S.H. DFT insights into new B-containing 212 MAX phases: Hf2AB2 (A = In, Sn). J. Alloys Compd. 2021, 860, 158408. [Google Scholar] [CrossRef]
- Wei, Q.; Yang, J.X.; Jia, X.F.; Luo, J.; Zhang, M.G.; Zhu, X.M. Crystal structures, mechanical properties, and electronic structure analysis of ternary FeCrAl alloys. Phys. Lett. A 2025, 533, 130228. [Google Scholar] [CrossRef]
- Bashir, A.I.; Arif, H.; Azam, S.; Irfan, M.; Khan, N. First-principles quantum computations to investigate prospects of Mg2FeH6 for optoelectronics and hydrogen-storage applications. Int. J. Hydrogen Energy 2023, 48, 23930–23942. [Google Scholar] [CrossRef]
- Chen, Q.Y.; Huang, F.J.; Ruan, J.Q.; Zhao, Y.F.; Zhang, X.F.; Xiong, K.; He, Y. Two-dimensional Pm1 Ca3N2, Ba3P2, and Ba3As2: Promising stable narrow-gap semiconductors for infrared and broadband photodetectors. Phys. Rev. Appl. 2024, 22, 034013. [Google Scholar] [CrossRef]
- Ali, M.; Bibi, Z.; Younis, M.W.; Mubashir, M.; Iqbal, M.; Ali, M.U.; Iqbal, M.A. An accurate prediction of electronic structure, mechanical stability and optical response of BaCuF3 fluoroperovskite for solar cell application. Sol. Energy 2024, 267, 112199. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Lobanovski, L.S.; Bushinsky, M.V.; Khomchenko, V.A.; Fedotova, V.V.; Troyanchuk, I.O.; Szymczak, H. Microstructure evolution and magnetoresistance of the A-site ordered Ba-doped manganites. Semiconductors 2007, 41, 507–511. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Trukhanov, A.V.; Vasiliev, A.N.; Balagurov, A.M.; Szymczak, H. Magnetic state of the structurally separated anion-deficient La0.70Sr0.30MnO2.85 manganite. J. Exp. Theor. Phys. 2011, 113, 819–825. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Turchenko, V.A.; Trukhanov, S.V.; Kostishin, V.G.; Damay, F.; Porcher, F.; Klygach, D.S.; Vakhitov, M.G.; Lyakhov, D.; Michels, D.; Bozzo, B.; et al. Features of structure, magnetic state and electrodynamic performance of SrFe12-xInxO19. Sci. Rep. 2021, 11, 18342. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).