Extraction of Corrosion Damage Features of Serviced Cable Based on Three-Dimensional Point Cloud Technology
Abstract
1. Introduction
- (1)
- The corrosion wire specimens analyzed in this study were sourced from cable replacements in a 27-year-service-life cable-stayed bridge, rather than artificially accelerated corrosion samples. This provenance ensures the resultant data exhibits superior field-relevance and authentic degradation characteristics reflective of actual infrastructure service conditions.
- (2)
- Advanced non-contact 3D laser scanning technology was utilized to reconstruct morphological models of corroded steel wires, thereby characterizing the surface features of corroded wires. The implemented methodology has undergone validation and exhibits high measurement accuracy.
- (3)
- Kolmogorov–Smirnov (K–S) tests were employed to analyze the probability distribution models of corrosion characteristics.
2. Engineering Background and Methodology
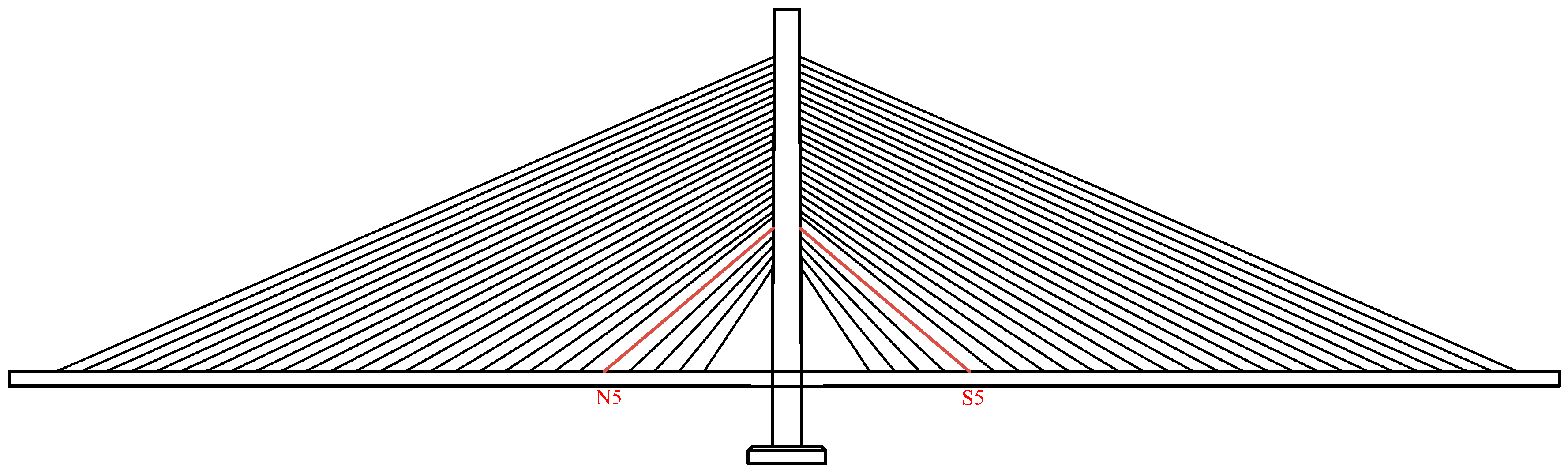
2.1. Engineering Background
2.2. Methodology
2.3. Wire Rust Removal
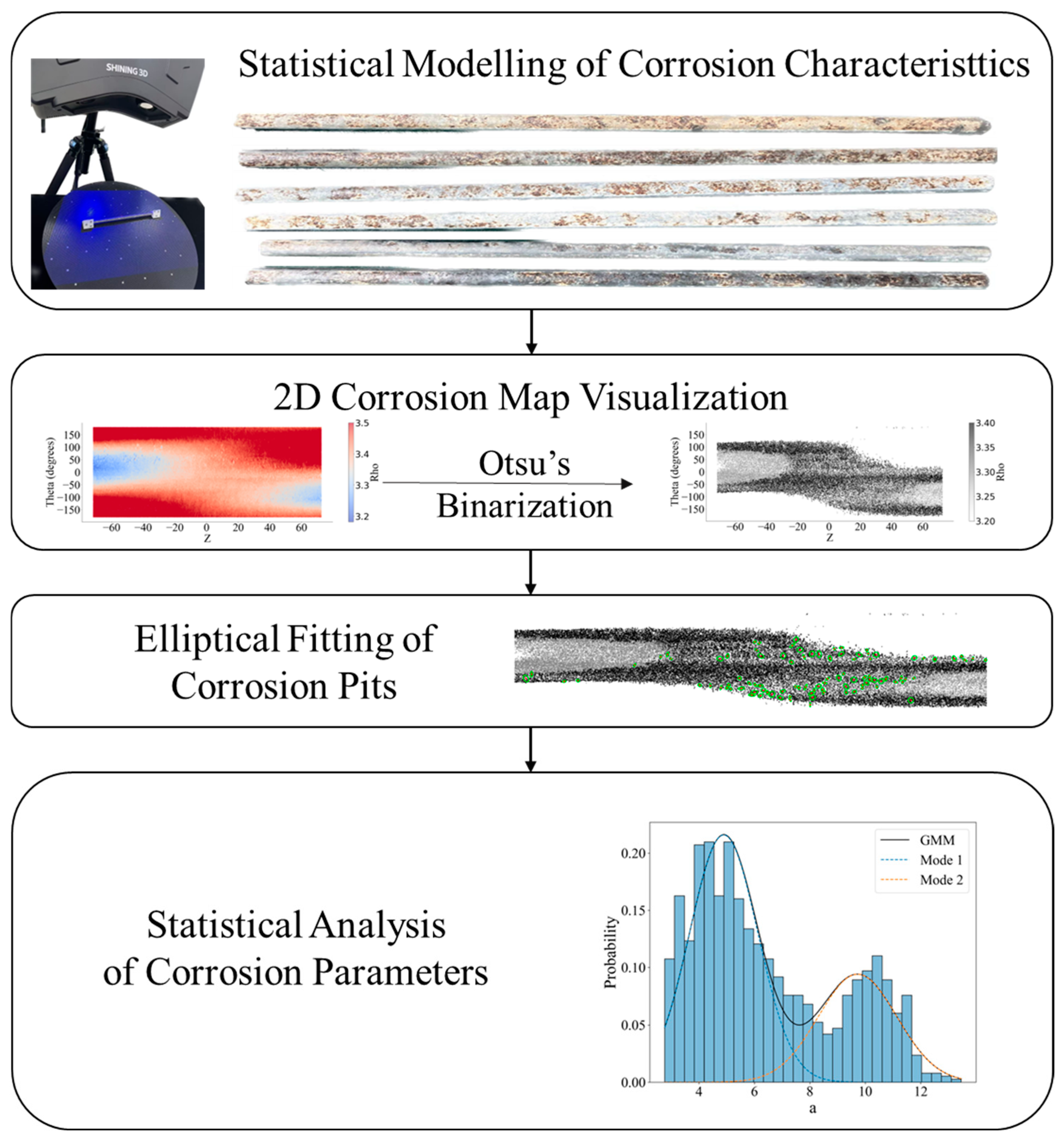
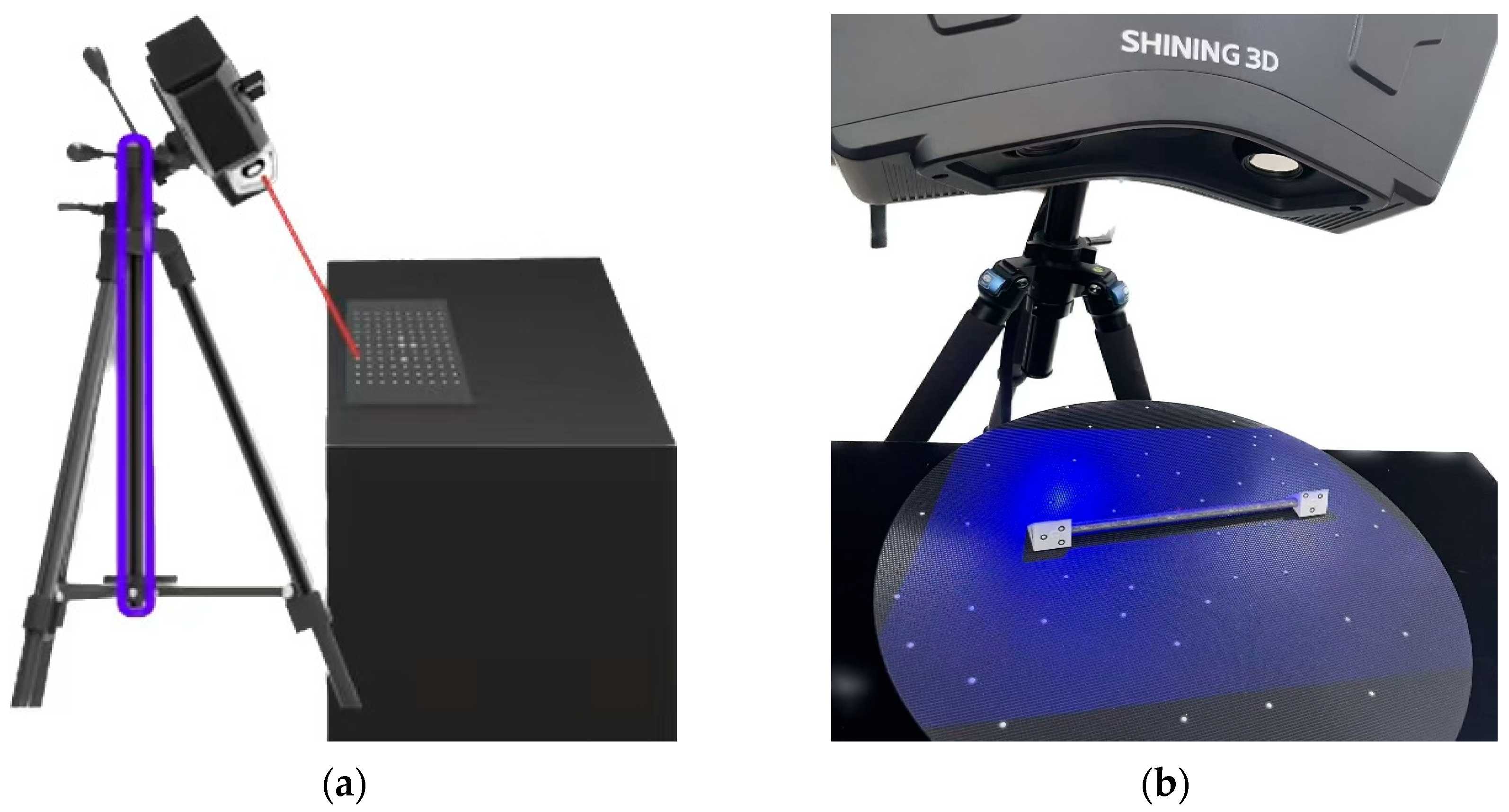
2.4. Three-Dimensional Scanning
3. Corrosion Feature Extraction
3.1. Binarization and the Otsu Method
3.2. Elliptical Fitting of a Corrosion Pit
4. Wire Corrosion Characteristics
4.1. Basic Parameters
4.2. Sharpness and Defect Parameters
5. Discussion
6. Conclusions
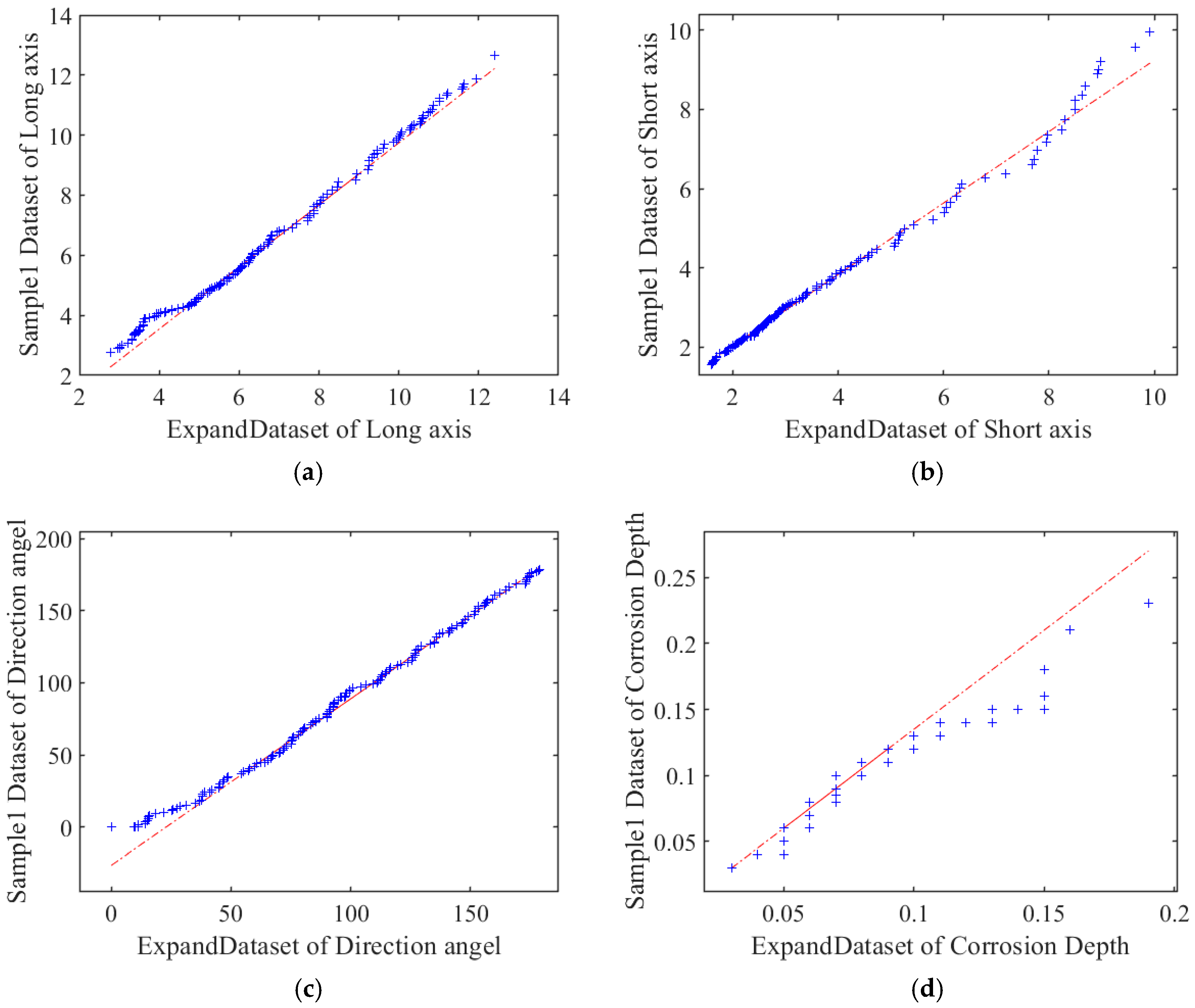
- The direction angle (θ) does not conform to any standard probability distribution.
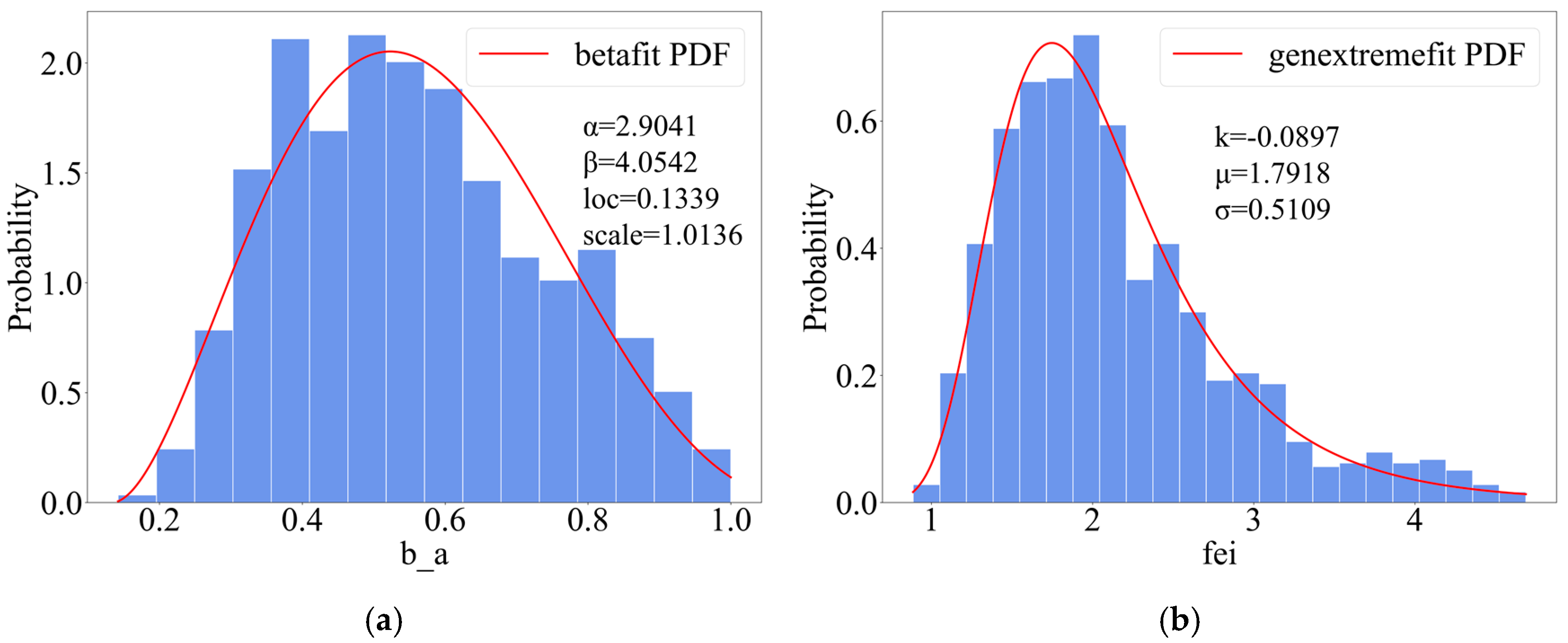
- The width (b) and defect parameter (Φ) follow a generalized extreme value distribution.
- The aspect ratio (b/a) fits a Beta distribution.
- The pit length (a) and depth (d) are well described by a Gaussian mixture model.
- These findings provide a valuable statistical foundation for characterizing the distribution of corrosion pits on in-service wires.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Duan, Y.; Wu, S.; Zhang, H.; Zhang, R.; Yun, C.; Cheng, J.; Wang, S. Development of corrosion-fatigue analysis method of cable hangers in tied-arch bridges considering train-bridge interaction. Eng. Struct. 2024, 315, 118484. [Google Scholar] [CrossRef]
- Sui, X.; Zhang, R.; Duan, Y.; Luo, Y.; Yun, C. Detection of wire breakage in steel strands using a roving magnetostrictive guided wave detector and outlier analysis. Smart Struct. Syst. 2025, 35, 53–64. [Google Scholar] [CrossRef]
- Tang, Z.F.; Sui, X.D.; Duan, Y.F.; Zhang, P.; Yun, C.B. Guided wave-based cable damage detection using wave energy transmission and reflection. Struct. Control Health Monit. 2021, 28, e2688. [Google Scholar] [CrossRef]
- Wu, L.; Cui, C.; Xie, Y.; Zhang, Q.; Liu, J. Investigating parameters and ultimate load-bearing performance of novel anchor-box type cable Girder anchoring structure for large-span cable-stayed bridges. Eng. Struct. 2024, 313, 118289. [Google Scholar] [CrossRef]
- Zhou, L.; Yao, G.; Zeng, G.; He, Z.; Gou, X.; He, X.; Liu, M. Cellular Automata-Based Experimental Study on the Evolution of Corrosion Damage in Bridge Cable Steel Wire. Buildings 2024, 14, 3354. [Google Scholar] [CrossRef]
- Lan, C.; Feng, A.; Zhang, Y.; Ma, J.; Wang, J.; Li, H. Evaluation of corrosion fatigue life for high-strength steel wires. J. Constr. Steel Res. 2024, 217, 108666. [Google Scholar] [CrossRef]
- Suzumura, K.; Nakamura, S. Environmental factors affecting corrosion of galvanized steel wires. J. Mater. Civ. Eng. 2004, 16, 1–7. [Google Scholar] [CrossRef]
- Watson, S.; Stafford, D. Cables in trouble. Civ. Eng. 1988, 58, 38–41. [Google Scholar]
- Chen, J.; Diao, B.; He, J.; Pang, S.; Guan, X. Equivalent surface defect model for fatigue life prediction of steel reinforcing bars with pitting corrosion. Int. J. Fatigue 2018, 110, 153–161. [Google Scholar] [CrossRef]
- Asadi, Z.S.; Melchers, R.E. Clustering of corrosion pit depths for buried cast iron pipes. Corros. Sci. 2018, 140, 92–98. [Google Scholar] [CrossRef]
- Li, S.; Xu, Y.; Zhu, S.; Guan, X.; Bao, Y. Probabilistic deterioration model of high-strength steel wires and its application to bridge cables. Struct. Infrastruct. Eng. 2015, 11, 1240–1249. [Google Scholar] [CrossRef]
- Chen, Y.; Qin, W.; Wang, Q.; Tan, H. Influence of corrosion pit on the tensile mechanical properties of a multi-layered wire rope strand. Constr. Build. Mater. 2021, 302, 124387. [Google Scholar] [CrossRef]
- Wu, S.; Guo, J.; Shi, G.; Li, J.; Lu, C. Laboratory-Based Investigation into Stress Corrosion Cracking of Cable Bolts. Materials 2019, 12, 2146. [Google Scholar] [CrossRef]
- Liu, X.; Han, W.; Yuan, Y.; Chen, X.; Xie, Q. Corrosion fatigue assessment and reliability analysis of short suspender of suspension bridge depending on refined traffic and wind load condition. Eng. Struct. 2021, 234, 111950. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, T.; Yu, X.; Niu, S.; Correia, J. Corrosion Fatigue Assessment of Bridge Cables Based on Equivalent Initial Flaw Size Model. Appl. Sci. 2023, 13, 10212. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, W.; Zheng, Y. Experimental Study on Corrosion Fatigue Performance of High-Strength Steel Wire with Initial Defect for Bridge Cable. Appl. Sci. 2020, 10, 2293. [Google Scholar] [CrossRef]
- Cui, C.; Chen, A.; Ma, R. An improved continuum damage mechanics model for evaluating corrosion-fatigue life of high-strength steel wires in the real service environment. Int. J. Fatigue 2020, 135, 105540. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, T.; Hebdon, M.H.; Han, W. Measurement and Comparative Study on Movements of Suspenders in Long-Span Suspension Bridges. J. Bridge Eng. 2019, 24, 04019026. [Google Scholar] [CrossRef]
- Lu, N.; Liu, Y.; Beer, M. System reliability evaluation of in-service cable-stayed bridges subjected to cable degradation. Struct. Infrastruct. Eng. 2018, 14, 1486–1498. [Google Scholar] [CrossRef]
- Sun, H.; Xu, J.; Chen, W.; Yang, J. Time-Dependent Effect of Corrosion on the Mechanical Characteristics of Stay Cable. J. Bridge Eng. 2018, 23, 04018019. [Google Scholar] [CrossRef]
- Bing, H.; Li, S. Point cloud data-driven modelling of high-strength steel wire corrosion pits considering orientation features. Constr. Build. Mater. 2024, 449, 138451. [Google Scholar] [CrossRef]
- Talebi, M.; Zeinoddini, M.; Elchalakani, M.; Gharebaghi, S.A.; Jadidi, P. Pseudo-random artificial corrosion morphologies for ultimate strength analysis of corroded steel tubulars. Structures 2022, 40, 902–919. [Google Scholar] [CrossRef]
- Burstein, G.; Daymond, B. The remarkable passivity of austenitic stainless steel in sulphuric acid solution and the effect of repetitive temperature cycling. Corros. Sci. 2009, 51, 2249–2252. [Google Scholar] [CrossRef]
- Pistorius, P.; Burstein, G. Growth of corrosion pits on stainless steel in chloride solution containing dilute sulphate. Corros. Sci. 1992, 33, 1885–1897. [Google Scholar] [CrossRef]
- Wu, K.; Jung, W.-S.; Byeon, J.-W. In-situ monitoring of pitting corrosion on vertically positioned 304 stainless steel by analyzing acoustic-emission energy parameter. Corros. Sci. 2016, 105, 8–16. [Google Scholar] [CrossRef]
- Codaro, E.; Nakazato, R.; Horovistiz, A.; Ribeiro, L.; Ribeiro, R.; Hein, L. An image processing method for morphology characterization and pitting corrosion evaluation. Mater. Sci. Eng. A 2002, 334, 298–306. [Google Scholar] [CrossRef]
- Feliciano, F.F.; Leta, F.R.; Mainier, F.B. Texture digital analysis for corrosion monitoring. Corros. Sci. 2015, 93, 138–147. [Google Scholar] [CrossRef]
- Gutierrez-Padilla, M.D.; Bielefeldt, A.; Ovtchinnikou, S.; Pellegrino, J.; Silverstein, J. Simple scanner-based image analysis for corrosion testing: Concrete application. J. Mater. Process. Technol. 2009, 209, 51–57. [Google Scholar] [CrossRef]
- Zhang, W.; Liang, C. Prediction of pitting corrosion mass loss for 304 stainless steel by image processing and BP neural network. J. Iron Steel Res. Int. 2005, 12, 59–62. [Google Scholar]
- Salgado, J.A.M.; Chavarín, J.U.; Cruz, D.M. Observation of Copper Corrosion Oxide Products Reduction in Metallic Samples by Means of Digital Image Correlation. Int. J. Electrochem. Sci. 2012, 7, 1107–1117. [Google Scholar] [CrossRef]
- Xu, Y.; Li, H.; Li, S.; Guan, X.; Lan, C. 3-D modelling and statistical properties of surface pits of corroded wire based on image processing technique. Corros. Sci. 2016, 111, 275–287. [Google Scholar] [CrossRef]
- Vincent, L. Morphological grayscale reconstruction in image analysis: Applications and efficient algorithms. IEEE Trans. Image Process. 1993, 2, 176–201. [Google Scholar] [CrossRef] [PubMed]
- Choi, K.; Kim, S. Morphological analysis and classification of types of surface corrosion damage by digital image processing. Corros. Sci. 2005, 47, 1–15. [Google Scholar] [CrossRef]
- Yan, K.; Liu, G.; Li, Q.; Jiang, C.; Ren, T.; Li, Z.; Xie, L.; Wang, L. Corrosion characteristics and evaluation of galvanized high-strength steel wire for bridge cables based on 3D laser scanning and image recognition. Constr. Build. Mater. 2024, 422, 135845. [Google Scholar] [CrossRef]
- Fang, K.; Li, S.; Chen, Z.; Li, H. Geometric characteristics of corrosion pits on high-strength steel wires in bridge cables under applied stress. Struct. Infrastruct. Eng. 2021, 17, 34–48. [Google Scholar] [CrossRef]
- Xu, S.-H.; Wang, Y.-D. Estimating the effects of corrosion pits on the fatigue life of steel plate based on the 3D profile. Int. J. Fatigue 2015, 72, 27–41. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, S.; Wang, H.; Li, A. Predicting the residual strength and deformability of corroded steel plate based on the corrosion morphology. Constr. Build. Mater. 2017, 152, 777–793. [Google Scholar] [CrossRef]
- Yuan, Y.; Liu, X.; Pu, G.; Wang, T.; Guo, Q. Corrosion features and time-dependent corrosion model of Galfan coating of high strength steel wires. Constr. Build. Mater. 2021, 313, 125534. [Google Scholar] [CrossRef]
- Li, S.; Xu, Y.; Li, H.; Guan, X. Uniform and Pitting Corrosion Modeling for High-Strength Bridge Wires. J. Bridge Eng. 2014, 19, 04014025. [Google Scholar] [CrossRef]
- Chen, A.; Yang, Y.; Ma, R.; Li, L.; Tian, H.; Pan, Z. Experimental study of corrosion effects on high-strength steel wires considering strain influence. Constr. Build. Mater. 2020, 240, 117910. [Google Scholar] [CrossRef]
- Harvey, P.S.; Gavin, H. Assessing the Accuracy of Vision-Based Accelerometry. Exp. Mech. 2014, 54, 273–277. [Google Scholar] [CrossRef]
- He, Z.; Xu, W. Deep learning and image preprocessing-based crack repair trace and secondary crack classification detection method for concrete bridges. Struct. Infrastruct. Eng. 2024, 1–17. [Google Scholar] [CrossRef]
- Ruffels, A.; Gonzalez, I.; Karoumi, R. Model-free damage detection of a laboratory bridge using artificial neural networks. J. Civ. Struct. Health Monit. 2020, 10, 183–195. [Google Scholar] [CrossRef]
- JTGT 5122-2021; Technical Specifications for Maintenance of Highway Cable-Supported Bridge. China Communications Press Co., Ltd.: Beijing, China, 2021.
- ISO 8407:1991; Corrosion of Metals and Alloys-Removal of Corrosion Products from Corrosion Test Specimens. International Organization for Standardization: Geneva, Switzerland, 1991.
- Kapur, J.N.; Sahoo, P.K.; Wong, A.K.C. A New Method for Gray-Level Picture Thresholding Using the Entropy of the Histogram. Comput. Vis. Graph. Image Process. 1985, 29, 273–285. [Google Scholar] [CrossRef]
- Murakami, Y.; Endo, M. Effects of Hardness and Crack Geometry on ΔKth of Small Cracks. J. Soc. Mater. Sci. Jpn. 1986, 35, 911–917. [Google Scholar] [CrossRef]
- Fang, K.; Liu, Z.; Zhang, X.; Zha, X. A Stochastic Modeling Method for Three-Dimensional Corrosion Pits of Bridge Cable Wires and Its Application. Corrosion 2024, 80, 808–817. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Wang, H.; Miao, C. Experimental and numerical study of the fatigue properties of stress-corroded steel wires for bridge cables. Int. J. Fatigue 2023, 177, 107939. [Google Scholar] [CrossRef]
- Li, R.; Wang, H.; Miao, C.; Ni, Y.; Zhang, Z. Experimental and numerical study on the degradation law of mechanical properties of stress-corrosion steel wire for bridge cables. J. Constr. Steel Res. 2024, 212, 108294. [Google Scholar] [CrossRef]
- Li, R.; Wang, H.; Yuan, Z.; Miao, C.; Liu, Y. Evolution law of corrosion characteristics and time-dependent reliability analysis for service life prediction of corroded bridge cables. Eng. Struct. 2025, 327, 119667. [Google Scholar] [CrossRef]
- Wang, Q.; Yao, G.; Yu, X.; He, X.; Qu, Y.; Yang, S.; Hou, M.; Zhang, T.; Yan, G. Evolution of cable corrosion characteristics and life reliability analysis for cable stayed bridges. Int. J. Fatigue 2025, 197, 108960. [Google Scholar] [CrossRef]
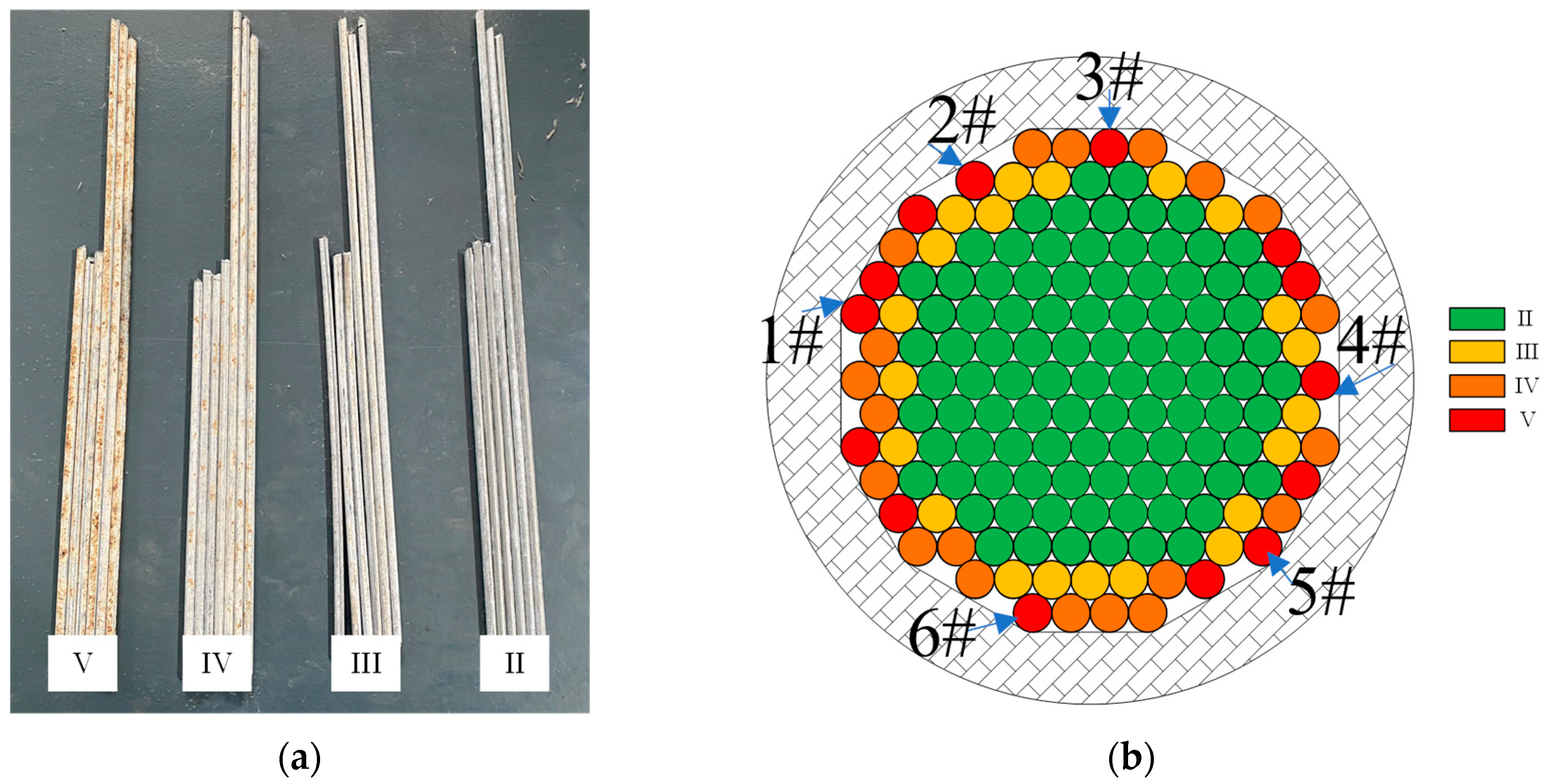



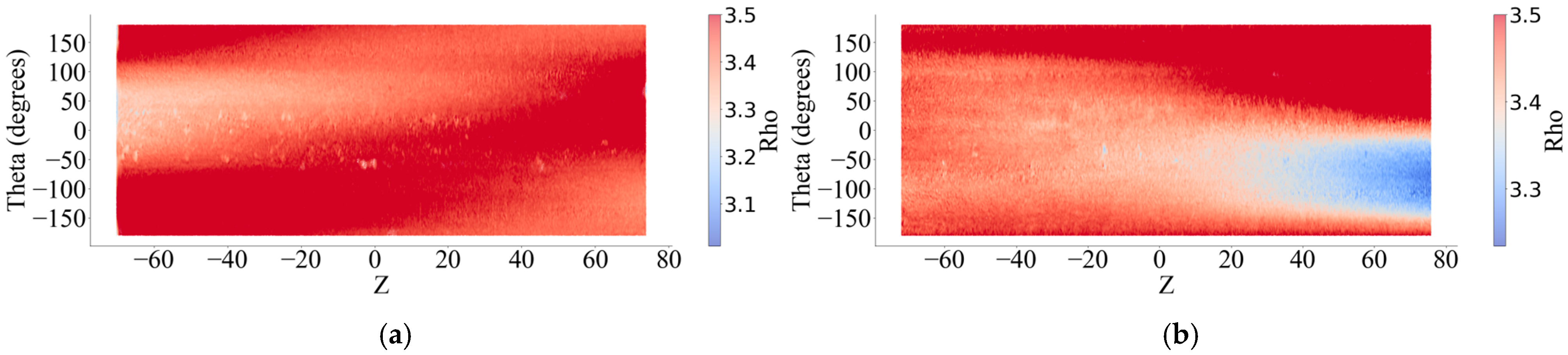
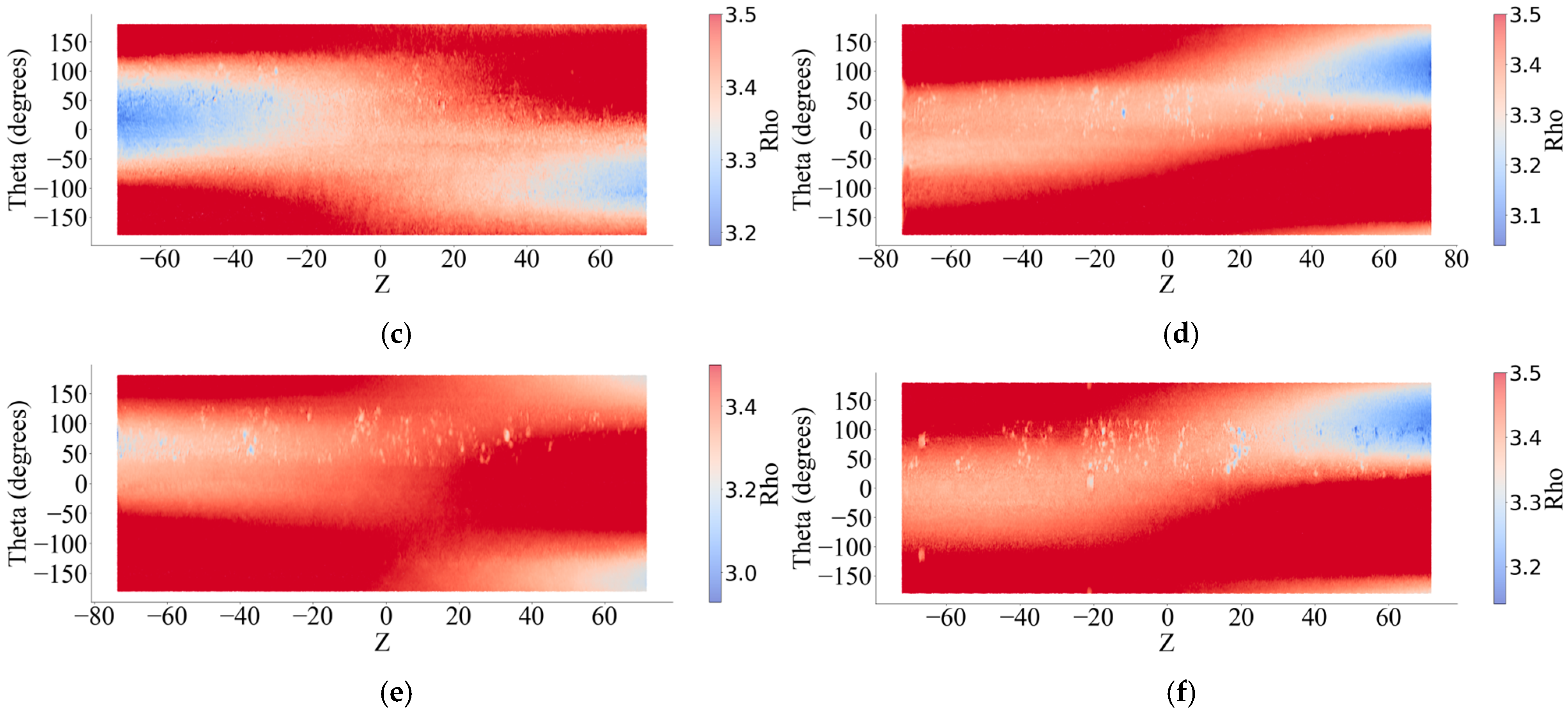
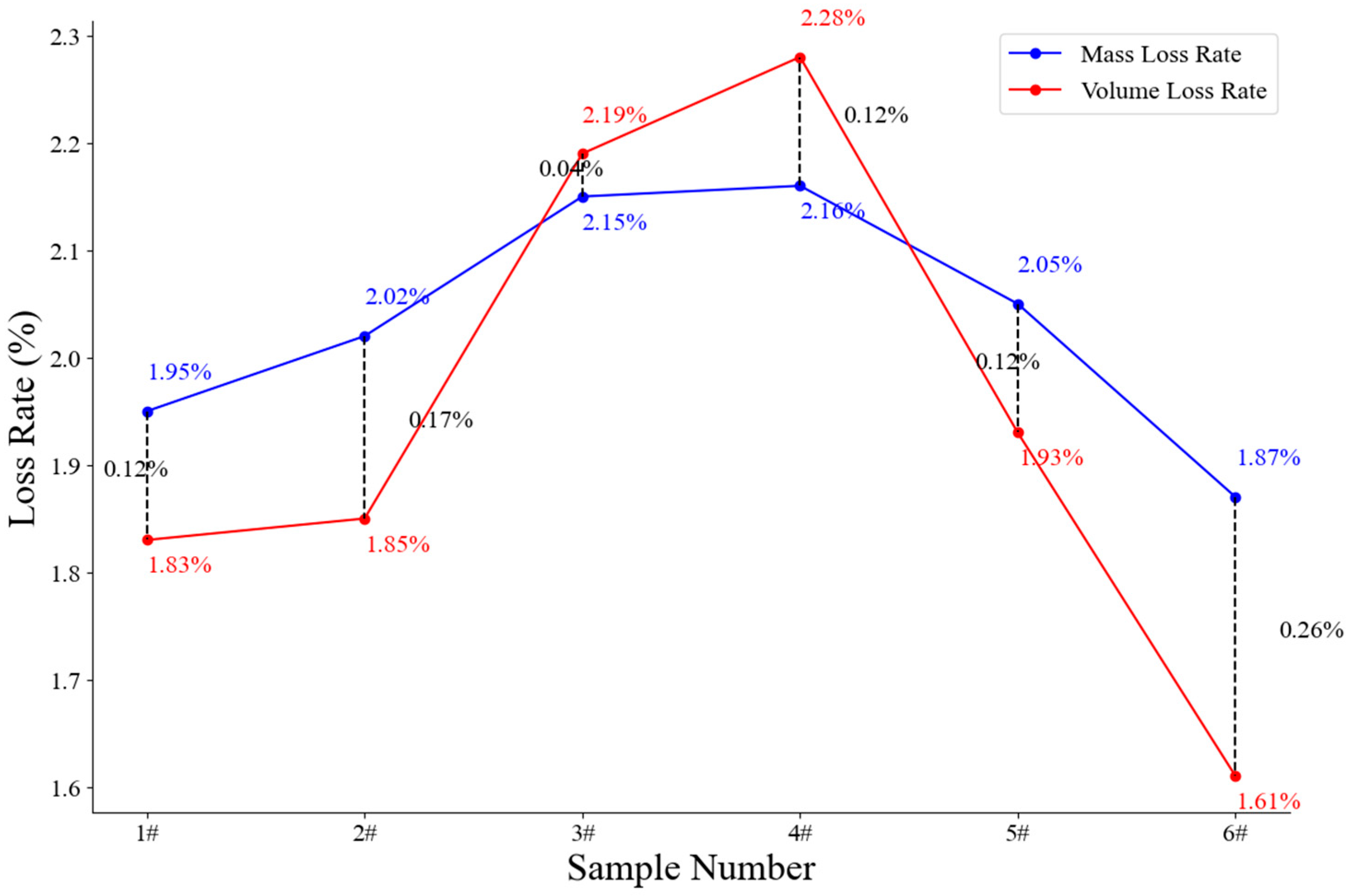

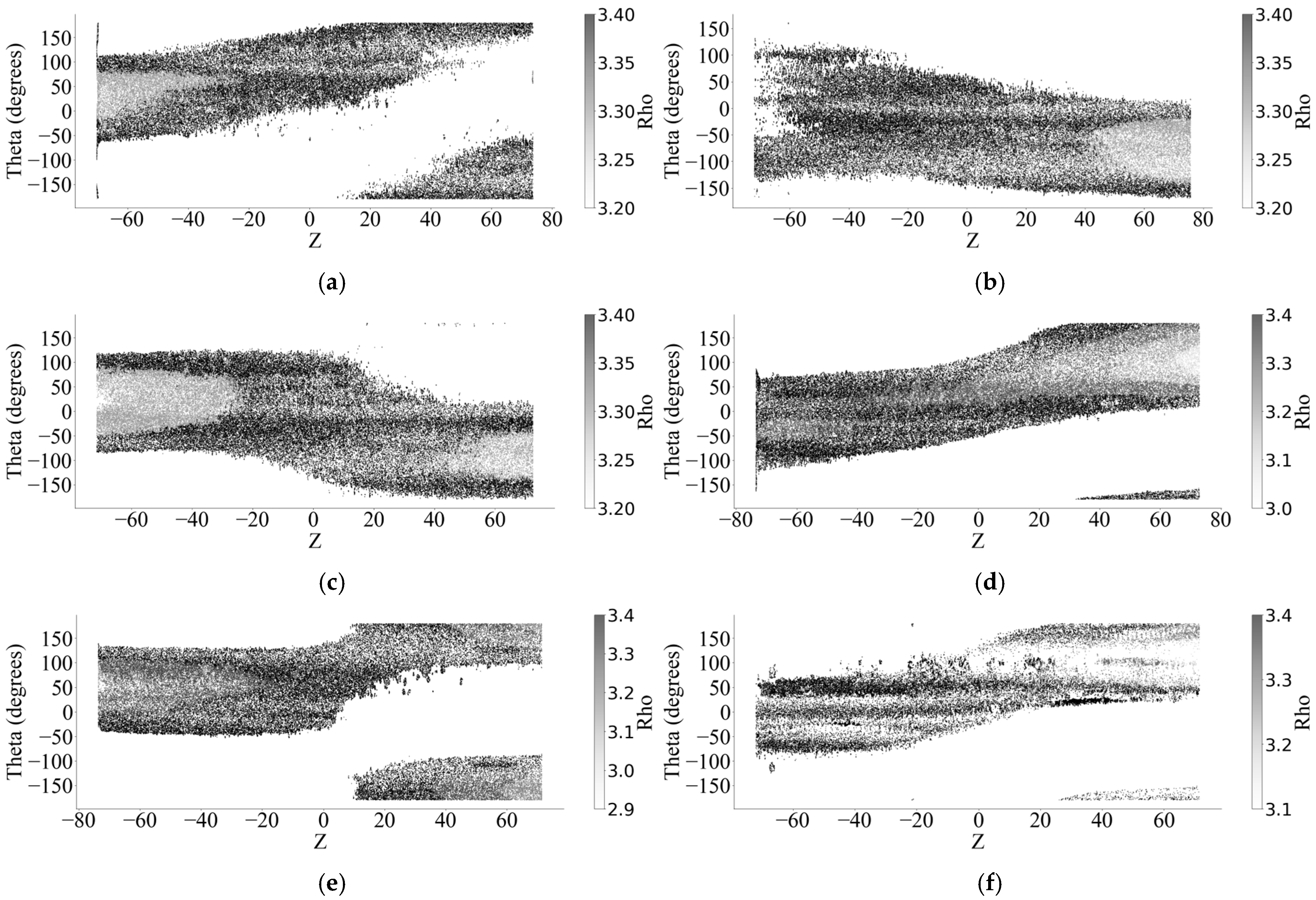

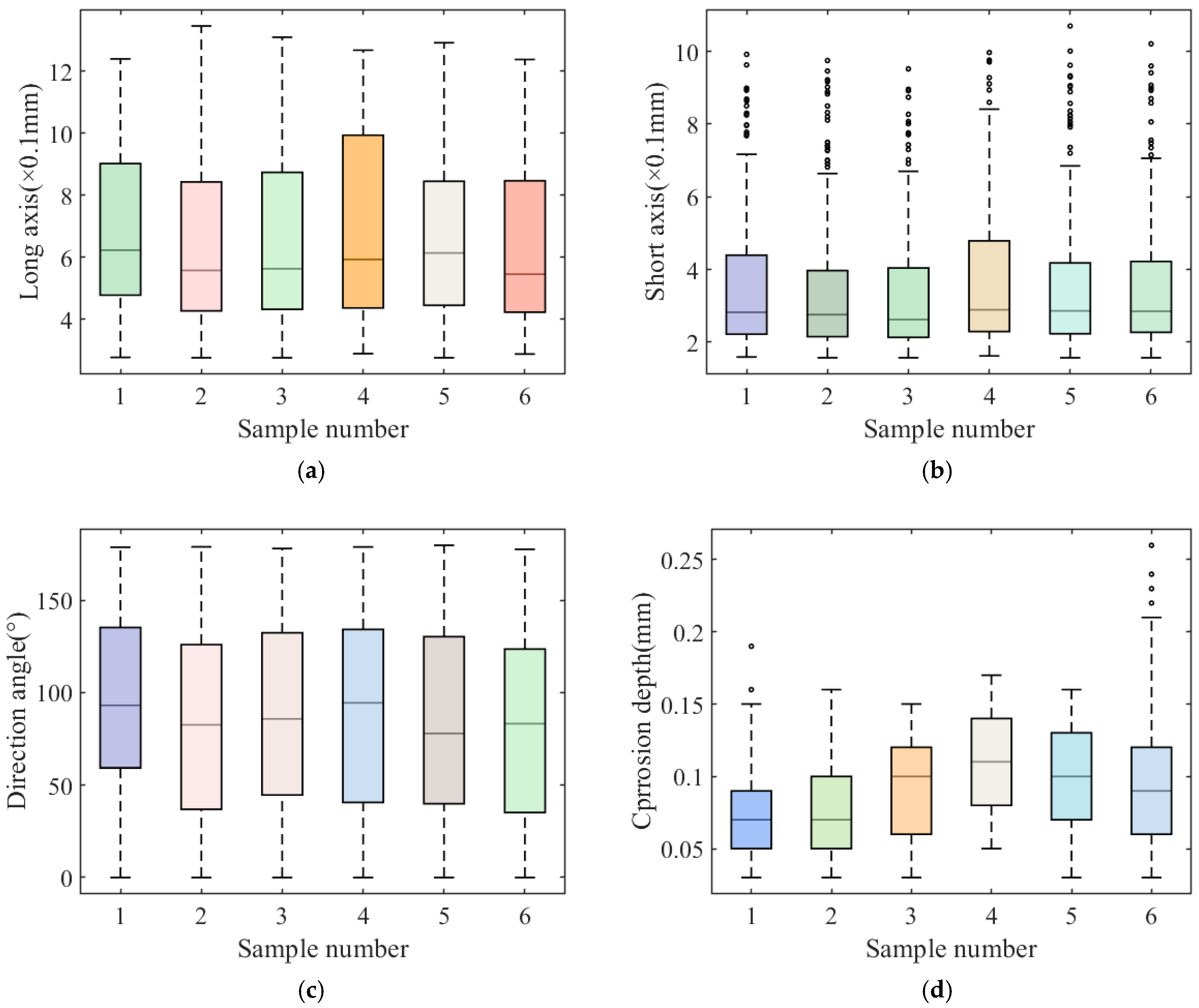
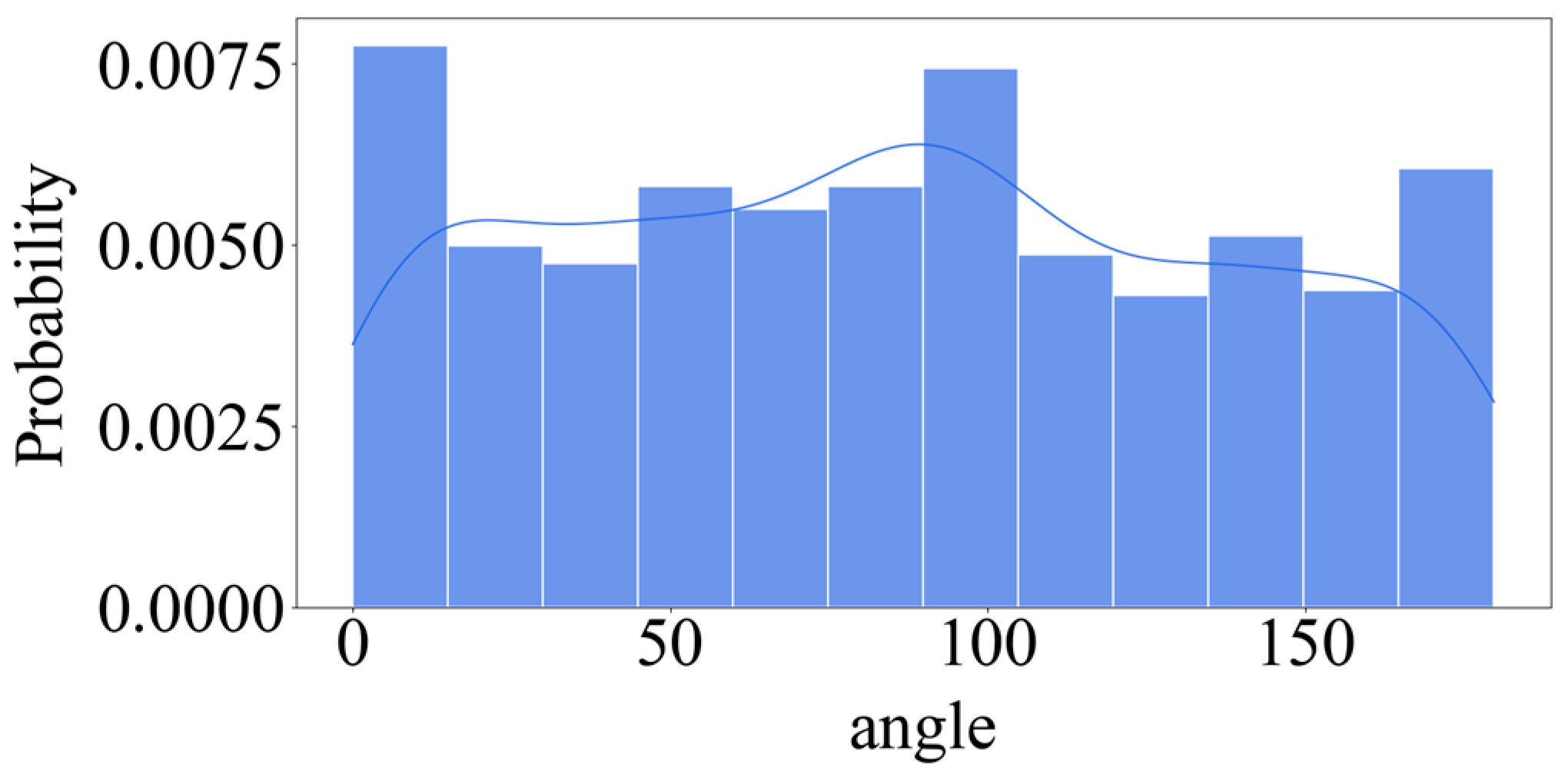
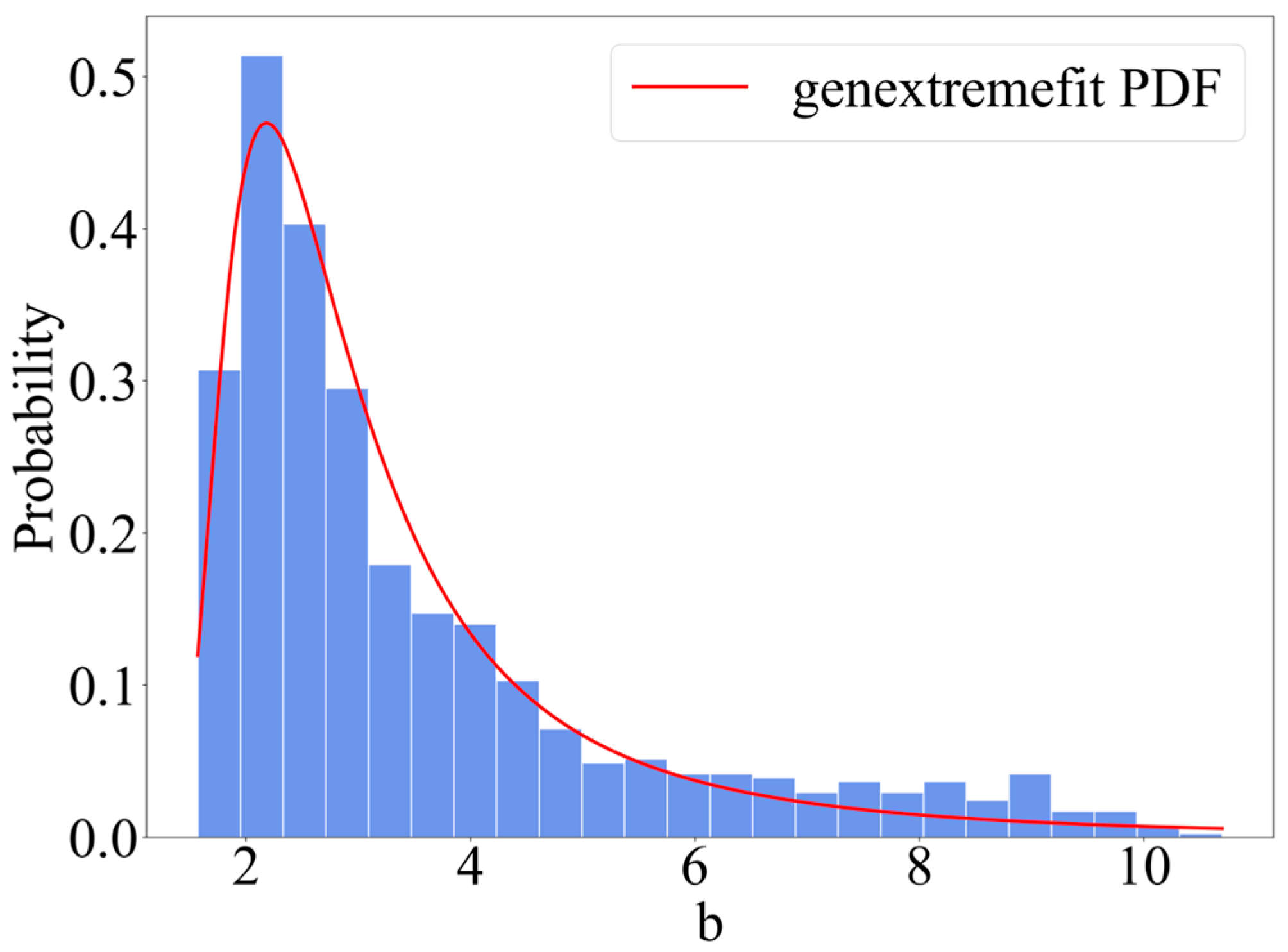
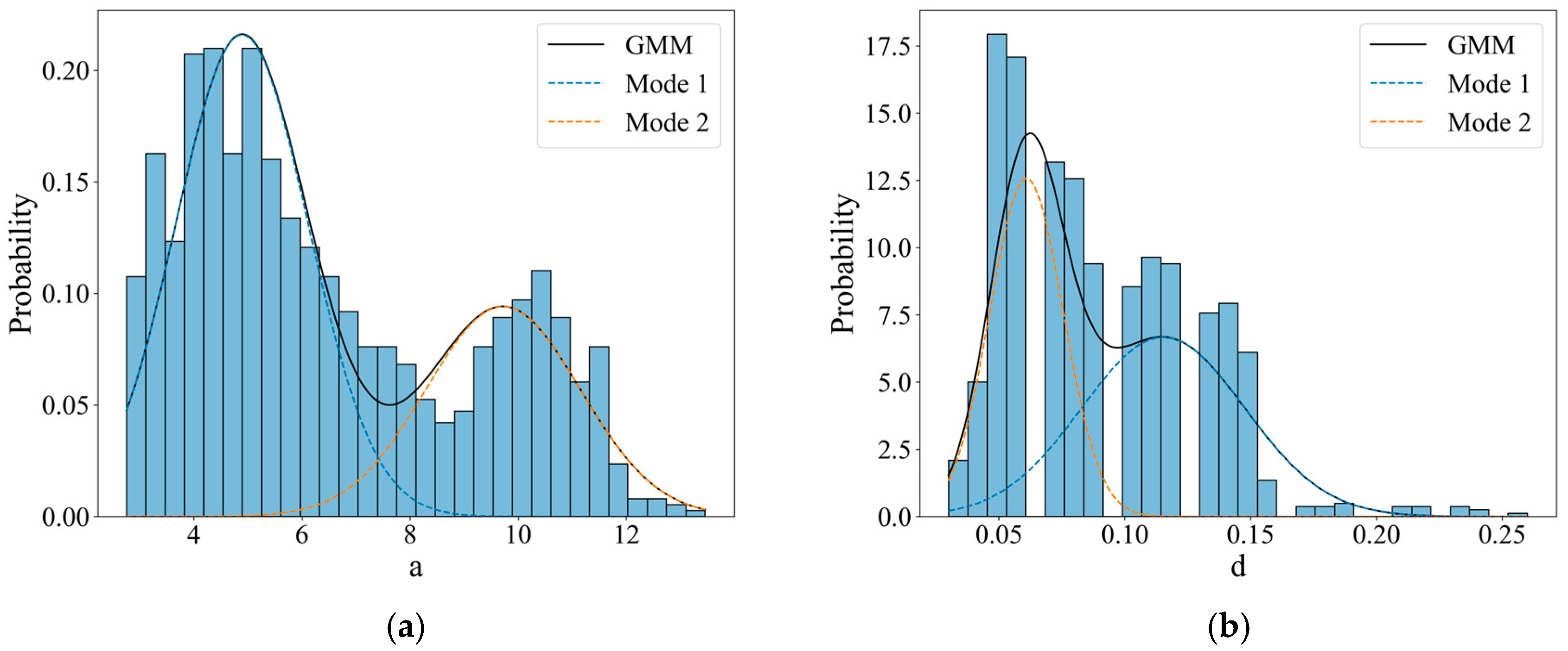
| Specimen Number | Mass Before Rust Removal | Mass After Rust Removal | Quality Loss Rate (%) |
|---|---|---|---|
| 1# | 56.157 | 55.062 | 1.95 |
| 2# | 58.392 | 57.215 | 2.02 |
| 3# | 57.144 | 55.913 | 2.15 |
| 4# | 57.311 | 56.073 | 2.16 |
| 5# | 57.257 | 56.083 | 2.05 |
| 6# | 56.394 | 55.240 | 2.05 |
| 2 | 0.663880 | 4.892641 | 1.226885 | |
| 0.336120 | 9.721610 | 1.425726 | ||
| 2 | 0.540497 | 0.115243 | 0.032355 | |
| 0.459503 | 0.060918 | 0.014593 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, T.; Cheng, S.; He, H.; Feng, K.; Zhu, J. Extraction of Corrosion Damage Features of Serviced Cable Based on Three-Dimensional Point Cloud Technology. Materials 2025, 18, 3611. https://doi.org/10.3390/ma18153611
Zhu T, Cheng S, He H, Feng K, Zhu J. Extraction of Corrosion Damage Features of Serviced Cable Based on Three-Dimensional Point Cloud Technology. Materials. 2025; 18(15):3611. https://doi.org/10.3390/ma18153611
Chicago/Turabian StyleZhu, Tong, Shoushan Cheng, Haifang He, Kun Feng, and Jinran Zhu. 2025. "Extraction of Corrosion Damage Features of Serviced Cable Based on Three-Dimensional Point Cloud Technology" Materials 18, no. 15: 3611. https://doi.org/10.3390/ma18153611
APA StyleZhu, T., Cheng, S., He, H., Feng, K., & Zhu, J. (2025). Extraction of Corrosion Damage Features of Serviced Cable Based on Three-Dimensional Point Cloud Technology. Materials, 18(15), 3611. https://doi.org/10.3390/ma18153611







