Study and Evaluation of Equivalent Conductivities of [SiO(OH)3]− and [SiO2(OH)2]2− in NaOH-Na2SiO3-H2O Solutions at 277.85 K to 308.45 K
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Conductivity Measurements
2.3. Data Processing
3. Conductivity Models
4. Results and Discussion
4.1. Validation of the Conductivity Model for NaOH Solution
4.2. Validation of the Conductivity Model with Electrolytes
4.3. Calculation of and from Conductivities of Solutions
5. Error Analysis
5.1. The Regression Analysis
5.2. Experimental Error
5.3. Limitation of the Superposition of Conductivity Model for Mixed Electrolytes
6. Conclusions
- (1)
- EIS spectrum is an efficient and precise tool to measure the conductivity of aqueous solutions at specific temperatures (277.65 K to 308.45 K), without the facilitation of equivalent circuits.
- (2)
- The conductivity estimated by McCleskey’s conductivity model for , proposed in 2011 [49], excesses the published data and the one deduced from Robinson–Stokes conductivity model at different temperatures (278.15 K to 303.15 K). It is found that in a mixed electrolyte solution, if the concentration of a composition is much less than the rest, the bulk electrical conductivity can be calculated by the superposition of the contribution of this composition and the conductivity of the background electrolytes. The conductivity of this composition can be calculated by Kohlrausch’s law of the independent migration of ions. The calibrated McCleskey’s conductivity model for NaOH shows high accuracy. The conductivity model for mixed electrolytes (Equation (11)) closely matches measured conductivities of solutions and solutions at investigated temperature and concentration range.
- (3)
- With the established model (Equation (11)), the equivalent conductivity of and were calculated with the least-square method. Their temperature dependence (277.85 K to 308.45 K) can be, respectively, approximated to Equations (18) and (19). The maximum deviation of conductivity in aqueous solutions is ±0.265 mS/cm.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shivaprasad, K.N.; Yang, H.-M.; Singh, J.K. A path to carbon neutrality in construction: An overview of recent progress in recycled cement usage. J. CO2 Util. 2024, 83, 102816. [Google Scholar] [CrossRef]
- Scrivener, K.; Ouzia, A.; Juilland, P.; Kunhi Mohamed, A. Advances in understanding cement hydration mechanisms. Cem. Concr. Res. 2019, 124, 105823. [Google Scholar] [CrossRef]
- Pustovgar, E.; Sangodkar, R.P.; Andreev, A.S.; Palacios, M.; Chmelka, B.F.; Flatt, R.J.; d’Espinose de Lacaillerie, J.-B. Understanding silicate hydration from quantitative analyses of hydrating tricalcium silicates. Nat. Commun. 2016, 7, 10952. [Google Scholar] [CrossRef]
- Li, Y.; Pan, H.; Li, Z. Ab initio metadynamics simulations on the formation of calcium silicate aqua complexes prior to the nuleation of calcium silicate hydrate. Cem. Concr. Res. 2022, 156, 106767. [Google Scholar] [CrossRef]
- Bellmann, F.; Damidot, D.; Moser, B.; Skibsted, J. Improved evidence for the existence of an intermediate phase during hydration of tricalcium silicate. Cem. Concr. Res. 2010, 40, 875–884. [Google Scholar] [CrossRef]
- Yang, K.; White, C.E. Modeling of aqueous species interaction energies prior to nucleation in cement-based gel systems. Cem. Concr. Res. 2021, 139, 106266. [Google Scholar] [CrossRef]
- Lian, X.; Peng, Z.-H.; Shen, L.-T.; Qi, T.-G.; Zhou, Q.-S.; Li, X.-B.; Liu, G.-H. Properties of low-modulus sodium silicate solution in alkali system. Trans. Nonferrous Met. Soc. China 2021, 31, 3918–3928. [Google Scholar] [CrossRef]
- Zaytsev, I.D.; Aseev, G.G. Properties of Aqueous Solutions of Electrolytes; CRC Press: Boca Raton, FL, USA, 1992. [Google Scholar]
- Harman, R.W. Aqueous Solutions of Sodium Silicates. I. J. Phys. Chem. 1925, 29, 1155–1168. [Google Scholar] [CrossRef]
- Ukihashi, H. Study on the Electric Conductivity of Sodium Silicate Aqueous Solution. I. Bull. Chem. Soc. Jpn. 1956, 29, 537–541. [Google Scholar] [CrossRef]
- Lothenbach, B.; Kulik, D.A.; Matschei, T.; Balonis, M.; Baquerizo, L.; Dilnesa, B.; Miron, G.D.; Myers, R.J. Cemdata18: A chemical thermodynamic database for hydrated Portland cements and alkali-activated materials. Cem. Concr. Res. 2019, 115, 472–506. [Google Scholar] [CrossRef]
- Rumble, J.R.; Bruno, T.J.; Doa, M.J. CRC Handbook of Chemistry and Physics: A Ready-Reference Book of Chemical and Physical Data; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Zeebe, R.E. On the molecular diffusion coefficients of dissolved CO2, HCO3−, and CO32− and their dependence on isotopic mass. Geochim. Cosmochim. Acta 2011, 75, 2483–2498. [Google Scholar] [CrossRef]
- Rebreanu, L.; Vanderborght, J.-P.; Chou, L. The diffusion coefficient of dissolved silica revisited. Mar. Chem. 2008, 112, 230–233. [Google Scholar] [CrossRef]
- Yokoyama, T. Diffusivity of dissolved silica in rock pore water at 25 °C as characterized by through-diffusion experiments. Water Resour. Res. 2013, 49, 8299–8309. [Google Scholar] [CrossRef]
- Qiu, X.; Chen, J.; Ye, G.; De Schutter, G. A 3D reactive transport model for simulation of the chemical reaction process of ASR at microscale. Cem. Concr. Res. 2022, 151, 106640. [Google Scholar] [CrossRef]
- Huang, H. Thermodynamics of Autogenous Self-Healing in Cementitious Materials. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2014. [Google Scholar]
- Damidot, D.; Nonat, A.; Barret, P. Kinetics of Tricalcium Silicate Hydration in Diluted Suspensions by Microcalorimetric Measurements. J. Am. Ceram. Soc. 1990, 73, 3319–3322. [Google Scholar] [CrossRef]
- Damidot, D.; Nonat, A. C3S hydration in diluted and stirred suspensions: (I) study of the two kinetic steps. Adv. Cem. Res. 1994, 6, 27–35. [Google Scholar] [CrossRef]
- Damidot, D.; Nonat, A. C3S hydration in diluted and stirred suspension: (II) properties of C–S–H precipitated during the two kinetic steps. Adv. Cem. Res. 1994, 6, 83–91. [Google Scholar] [CrossRef]
- Damidot, D.; Nonat, A.; Barret, P.; Bertrandie, D.; Zanni, H.; Rassem, R. C3S hydration in diluted and stirred suspenSIons: (III) NMR study of C-S-H precipitated during the two kinetic steps. Adv. Cem. Res. 1995, 7, 1–8. [Google Scholar] [CrossRef]
- Picker, A. Influence of Polymers on Nucleation and Assembly of Calcium Silicate Hydrates. Ph.D. Thesis, University of Konstanz, Konstanz, Germany, 2013. [Google Scholar]
- Mills, R.; Lobo, V.M.M. Self-Diffusion in Electrolyte Solutions: A Critical Examination of Data Compiled from the Literature; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Wiegand, C. Specification for 1.06392.0000 Sodium Carbonate Anhydrous for Analysis EMSURE® ISO. Available online: https://www.sigmaaldrich.com/BE/en/specification-sheet/SPEC/MDA/CHEM/1.06392/1063920000 (accessed on 13 September 2019).
- ISO 1692:1976; Sodium and Potassium Silicates for Industrial Use—Determination of Total Alkalinity—Titrimetric Method. International Organization for Standardization: Geneva, Switzerland, 1976.
- ISO 1690:1976; Sodium and Potassium Silicates for Industrial Use—Determination of Silica Content—Gravimetric Method by Insolubilization. International Organization for Standardization: Geneva, Switzerland, 1976.
- Item Number: 1.09137 Sodium Hydroxide Volumetric Solution. Available online: https://www.sigmaaldrich.com/deepweb/assets/sigmaaldrich/product/documents/386/648/109137dat.pdf (accessed on 13 March 2021).
- Taylor, B.N.; Kuyatt, C.E. Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results; US Department of Commerce, Technology Administration, National Institute of Standards and Technology: Gaithersburg, MD, USA, 1994.
- Kulik, D.; Wagner, T. Part 4. Calculation of Activity Coefficients in Built-In TSolMod Library Functions of the GEM-Selektor Code. In 4. GEMS TSolMod Built-In Activity Models v.3.2. Available online: https://gems.web.psi.ch/TSolMod/doc/pdf/Activity-Coeffs.pdf (accessed on 13 March 2021).
- Maccà, C. The current usage of selectivity coefficients for the characterization of ion-selective electrodes: A critical survey of the 2000/2001 literature. Electroanalysis 2003, 15, 997–1010. [Google Scholar] [CrossRef]
- Patrick, J.; Emmanuel, G. Hindered Calcium Hydroxide Nucleation and Growth as Mechanism Responsible for Tricalcium Silicate Retardation in Presence of Sucrose. ACI Symp. Publ. 2019, 329, 143–154. [Google Scholar]
- Krautwurst, N. Nucleation of Calcium Silicate Hydrate in Aqueous Solution and the Influence of Biomolecules on Cement Hydration. Ph.D. Thesis, Johannes Gutenberg-Universität Mainz, Mainz, Germany, 2017. [Google Scholar]
- Goward, G.R. Standard Operating Procedure: Gamry Potentiostat; McMaster University: Hamilton, ON, Canada, 2018. [Google Scholar]
- Robinson, R.A.; Stokes, R.H. Electrolyte Solutions; Dover Publications: Mineola, NY, USA, 2002. [Google Scholar]
- Boroujeni, S.N.; Maribo-Mogensen, B.; Liang, X.D.; Kontogeorgis, G.M. Novel Model for Predicting the Electrical Conductivity of Multisalt Electrolyte Solutions. J. Phys. Chem. B 2024, 128, 536–550. [Google Scholar] [CrossRef] [PubMed]
- Boroujeni, S.N.; Maribo-Mogensen, B.; Liang, X.D.; Kontogeorgis, G.M. New Electrical Conductivity Model for Electrolyte Solutions Based on the Debye-Huckel-Onsager Theory. J. Phys. Chem. B 2023, 127, 9954–9975. [Google Scholar] [CrossRef] [PubMed]
- Kohlrausch, F. Ueber Concentrations-Verschiebungen durch Electrolyse im Inneren von Lösungen und Lösungsgemischen. Ann. Phys. 1897, 298, 209–239. [Google Scholar] [CrossRef]
- Atkins, P.; Paula, J.d. Physical Chemistry; W.H. Freeman and Company: New York, NY, USA, 2010. [Google Scholar]
- Law, J.; Rennie, R. A Dictionary of Chemistry; Oxford University Press: Oxford, UK, 2020. [Google Scholar]
- Rumble, J.R. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Stokes, R.H. The Electrophoretic Corrections to the Diffusion Coefficient of an Electrolyte Solution. J. Am. Chem. Soc. 1953, 75, 4563–4566. [Google Scholar] [CrossRef]
- Robinson, R.A.; Stokes, R.H. The Variation of Equivalent Conductance with Concentration and Temperature. J. Am. Chem. Soc. 1954, 76, 1991–1994. [Google Scholar] [CrossRef]
- Woo, A.L.-W. Conductance Studies of Concentrated Solutions of Sodium Hydroxide and Potassium Hydroxide Electrolytes. Master’s Thesis, South Dakota State University, Brookings, SD, USA, 1968. [Google Scholar]
- Quint, J.; Viallard, A. The relaxation field for the general case of electrolyte mixtures. J. Solut. Chem. 1978, 7, 137–153. [Google Scholar] [CrossRef]
- Vink, H. Electrolytic conductivity of mixed electrolyte solutions. Berichte Bunsenges. Phys. Chem. 1994, 98, 1039–1045. [Google Scholar] [CrossRef]
- Lee, W.H.; Wheaton, R.J. Conductance of symmetrical, unsymmetrical and mixed electrolytes. Part 1.—Relaxation terms. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1978, 74, 743–766. [Google Scholar] [CrossRef]
- Lee, W.H.; Wheaton, R.J. Conductance of symmetrical, unsymmetrical and mixed electrolytes. Part 2.—Hydrodynamic terms and complete conductance equation. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1978, 74, 1456–1482. [Google Scholar] [CrossRef]
- McCleskey, R.B.; Nordstrom, D.K.; Ryan, J.N. Comparison of electrical conductivity calculation methods for natural waters. Limnol. Oceanogr. Methods 2012, 10, 952–967. [Google Scholar] [CrossRef]
- McCleskey, R.B. Electrical Conductivity of Electrolytes Found In Natural Waters from (5 to 90) °C. J. Chem. Eng. Data 2011, 56, 317–327. [Google Scholar] [CrossRef]
- Krautwurst, N.; Nicoleau, L.; Dietzsch, M.; Lieberwirth, I.; Labbez, C.; Fernandez-Martinez, A.; Van Driessche, A.E.S.; Barton, B.; Leukel, S.; Tremel, W. Two-Step Nucleation Process of Calcium Silicate Hydrate, the Nanobrick of Cement. Chem. Mater. 2018, 30, 2895–2904. [Google Scholar] [CrossRef]
- Patrick, J.; Emmanuel, G. Impact of sucrose on dissolution and nucleation. In Proceedings of the the 14th International Congress on the Chemistry of Cement, Beijing, China, 13–16 October 2015. [Google Scholar]
- DeWane, H.J.; Hamer, W.J. Electrochemical Data Part X. In Electrolytic Conductivity of Aqueous Solutions of the Alkali Metal Hydroxides; National Bureau of Standards Report; NASA: Washington, DC, USA, 1968. [Google Scholar]
- Marsh, K.; Stokes, R. The conductance of dilute aqueous sodium hydroxide solutions from 15° to 75°. Aust. J. Chem. 1964, 17, 740–749. [Google Scholar] [CrossRef]
- Wishaw, B.F.; Stokes, R.H. The Diffusion Coefficients and Conductances of Some Concentrated Electrolyte Solutions at 25°. J. Am. Chem. Soc. 1954, 76, 2065–2071. [Google Scholar] [CrossRef]
- Table of Diffusion Coefficients. 2020. Available online: https://www.aqion.de/site/diffusion-coefficients (accessed on 5 December 2020).
- Johnston, J. The Change of the Equivalent Conductance of Ions with the Temperature. J. Am. Chem. Soc. 1909, 31, 1010–1020. [Google Scholar] [CrossRef][Green Version]
- Light, T.S.; Licht, S.L. Conductivity and resistivity of water from the melting to critical point. Anal. Chem. 1987, 59, 2327–2330. [Google Scholar] [CrossRef]
- Light, T.S.; Licht, S.; Bevilacqua, A.C.; Morash, K.R. The Fundamental Conductivity and Resistivity of Water. Electrochem. Solid-State Lett. 2005, 8, E16. [Google Scholar] [CrossRef]
- Vlaev, L.; Tavlieva, M.; Barthel, J. Temperature and Concentration Dependences of the Electrical Conductance, Diffuson and Kinetic Parameters of Sodium Selenite Solutions in Ordinary and Heavy Water. J. Solut. Chem. 2007, 36, 447–465. [Google Scholar] [CrossRef]
- Kalugin, O.N.; Agieienko, V.N.; Otroshko, N.A.; Moroz, V.V. Ionic association and solvation in solutions of magnesium and nickel perchlorates in acetonitrile. Russ. J. Phys. Chem. A 2009, 83, 231–237. [Google Scholar] [CrossRef]
- Greenberg, S.A. The Nature of the Silicate Species in Sodium Silicate Solutions. J. Am. Chem. Soc. 1958, 80, 6508–6511. [Google Scholar] [CrossRef]
- Kunihiko, K.; Takusei, H. The Self-diffusion Coefficients of Carbon Dioxide, Hydrogen Carbonate Ions and Carbonate Ions in Aqueous Solutions. Bull. Chem. Soc. Jpn. 1963, 36, 1372. [Google Scholar]
- Gebauer, D.; Völkel, A.; Cölfen, H. Stable Prenucleation Calcium Carbonate Clusters. Science 2008, 322, 1819–1822. [Google Scholar] [CrossRef]
- Applin, K.R. The diffusion of dissolved silica in dilute aqueous solution. Geochim. Cosmochim. Acta 1987, 51, 2147–2151. [Google Scholar] [CrossRef]
- Fanning, K.A.; Pilson, M.E.Q. The diffusion of dissolved silica out of deep-sea sediments. J. Geophys. Res. 1974, 79, 1293–1297. [Google Scholar] [CrossRef]
- House, W.A.; Denison, F.H.; Warwick, M.S.; Zhmud, B.V. Dissolution of silica and the development of concentration profiles in freshwater sediments. Appl. Geochem. 2000, 15, 425–438. [Google Scholar] [CrossRef]
- Shock, E.L.; Sassani, D.C.; Wills, M.; Sverjensky, D.A. Inorganic species in geologic fluids: Correlations among standard molal thermodynamic properties of aqueous ions and hydroxide complexes. Geochim. Cosmochim. Acta 1997, 61, 907–950. [Google Scholar] [CrossRef] [PubMed]
- Sverjensky, D.A.; Shock, E.L.; Helgeson, H.C. Prediction of the thermodynamic properties of aqueous metal complexes to 1000 °C and 5 kb. Geochim. Cosmochim. Acta 1997, 61, 1359–1412. [Google Scholar] [CrossRef] [PubMed]
- Possolo, A.; Hibbert, D.B.; Stohner, J.; Bodnar, O.; Meija, J. A brief guide to measurement uncertainty (IUPAC Technical Report). Pure Appl. Chem. 2024, 96, 113–134. [Google Scholar] [CrossRef]
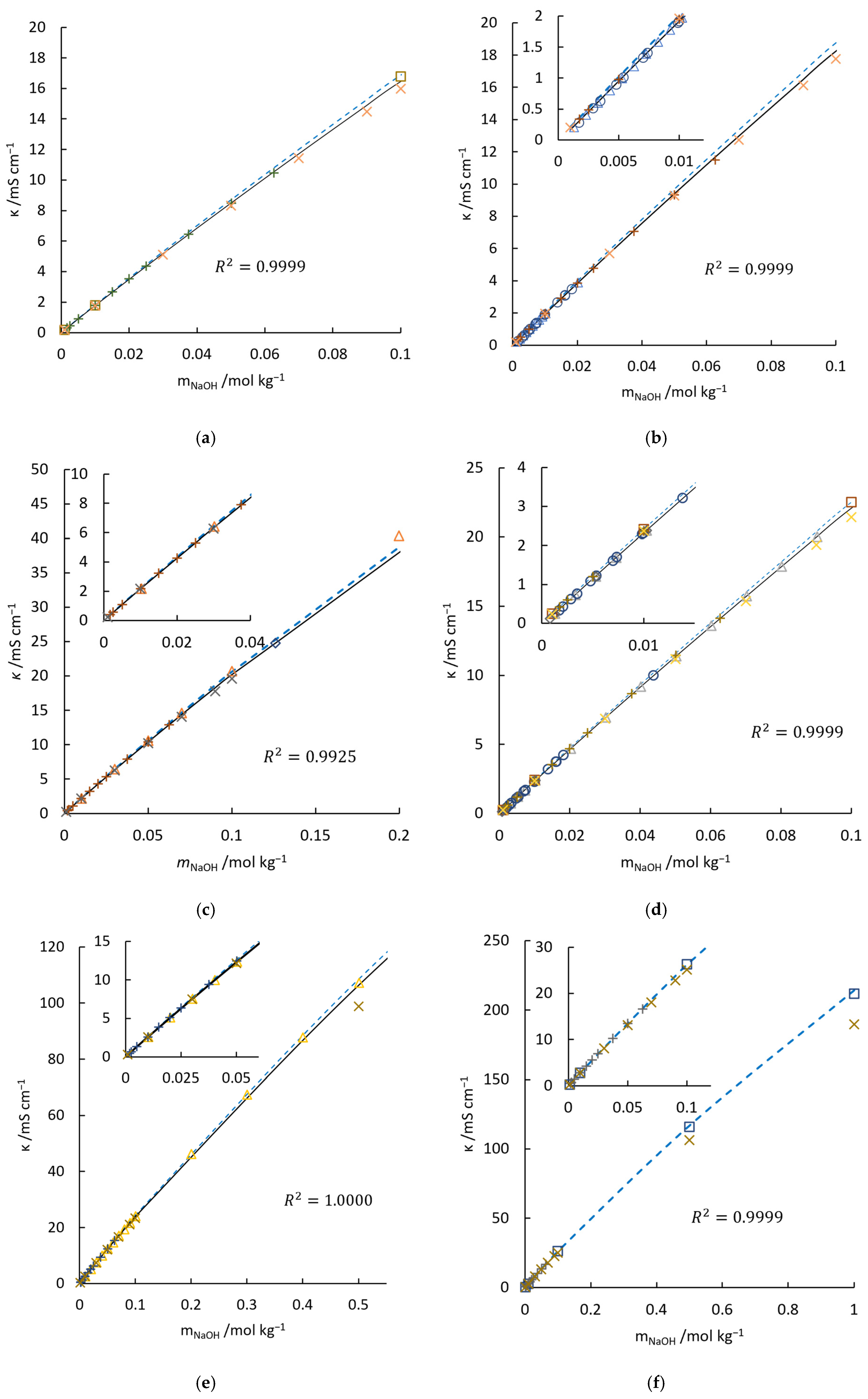
 , [12];
, [12];  , [34];
, [34];  , [23]; ꟷ, [34].
, [23]; ꟷ, [34].
 , [12];
, [12];  , [34];
, [34];  , [23]; ꟷ, [34].
, [23]; ꟷ, [34].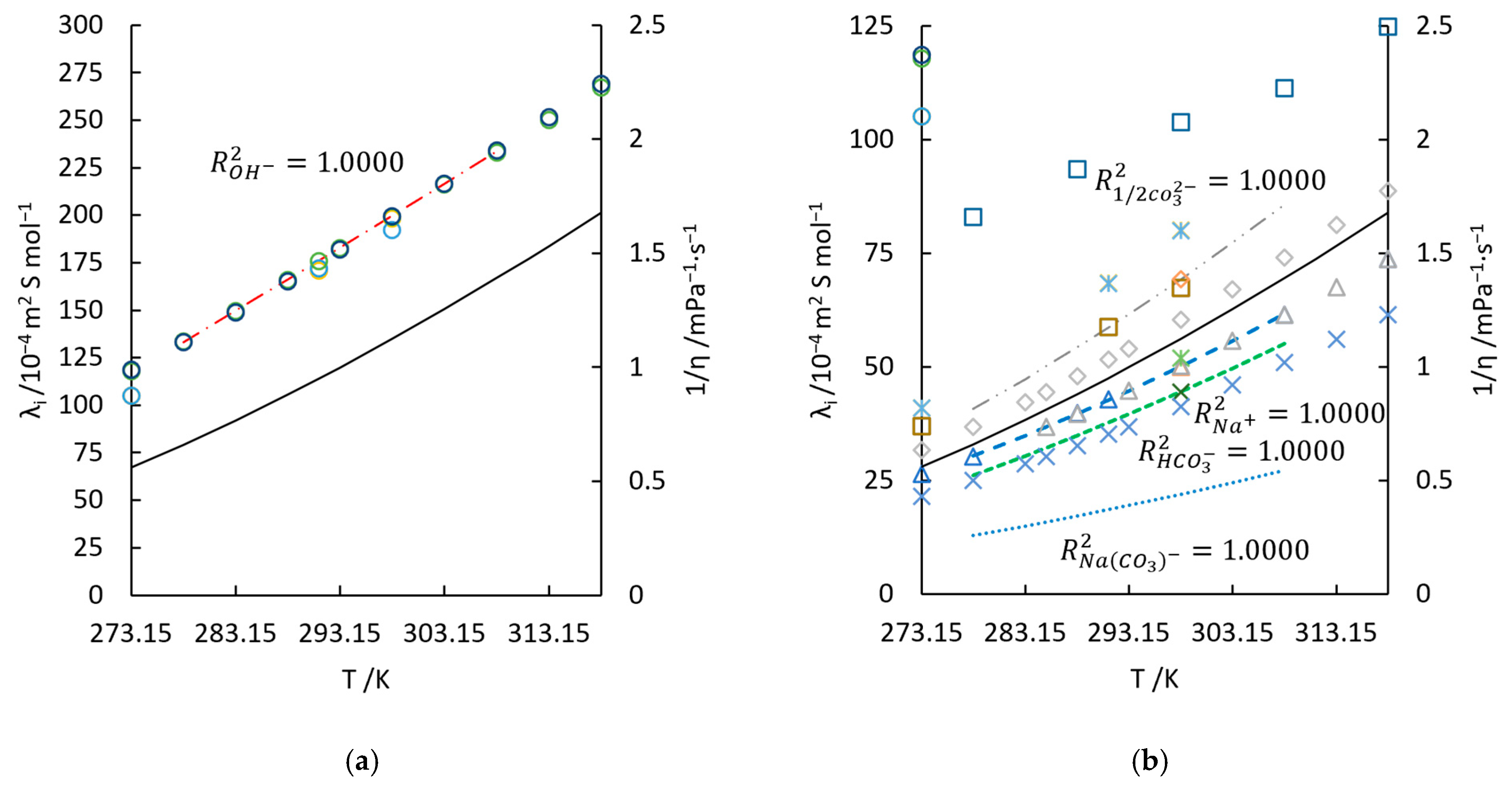

 amount of SiO2@; ◊, amount of .
amount of SiO2@; ◊, amount of .
 amount of SiO2@; ◊, amount of .
amount of SiO2@; ◊, amount of .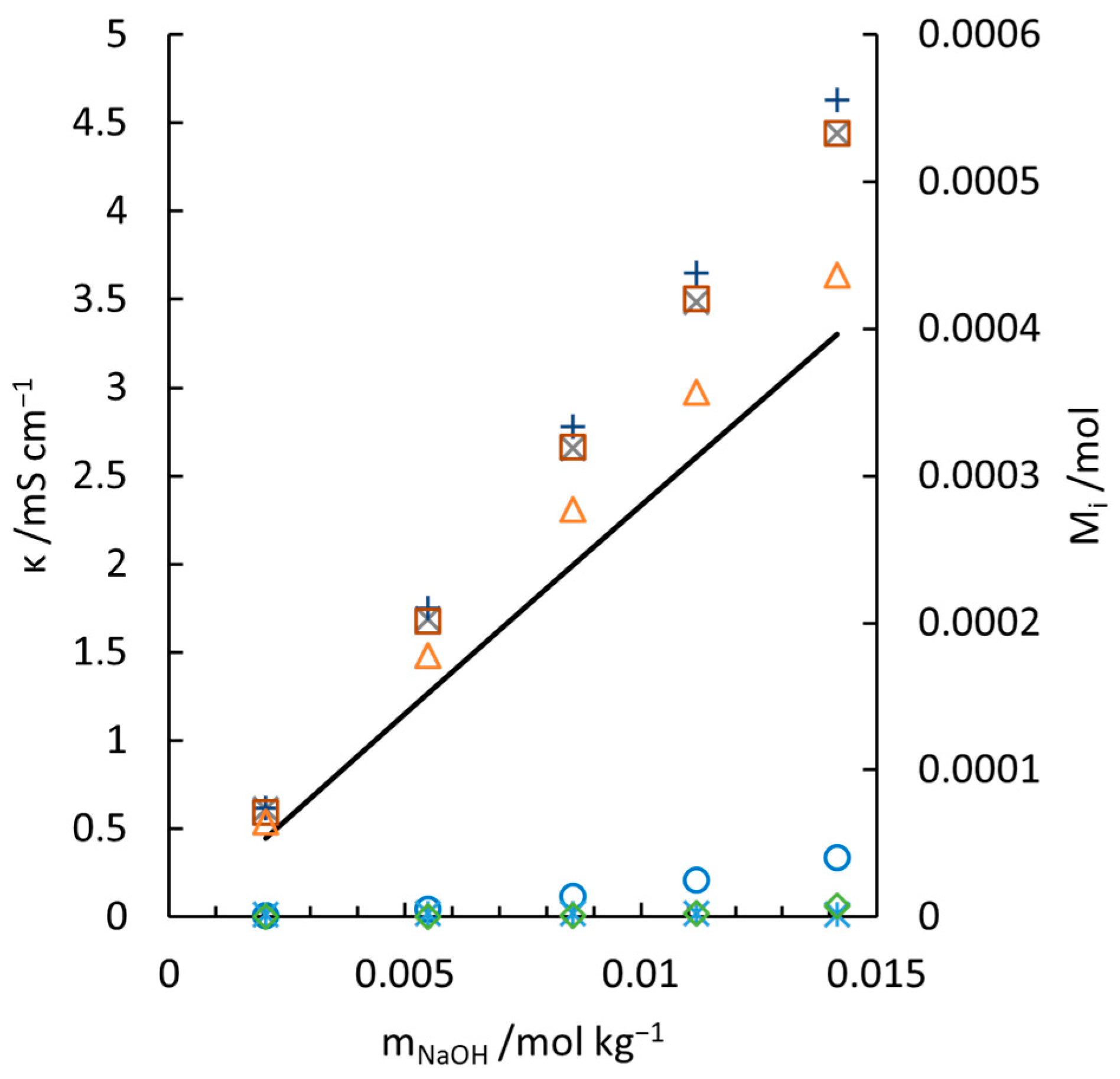
| Substance | IUPAC Name | CAS Registry Number | Origin | Purity | Method of Purity Determination | |
|---|---|---|---|---|---|---|
| Sodium carbonate | 105.99 | 497-19-8 | Merck KGaA (Darmstadt, Germany) | >99.9% [24] | Acidimetric method (calculated on dried substance). | |
| Sodium metasilicate pentahydrate | 212.14 | 10213-79-3 | VWR chemicals (Leuven, Belgium) | >98.08% | Titrimetric method, showed in ISO 1692 [25] and ISO 1690 [26]. | |
| Sodium hydroxide solution (1.04 mol/kg) | 40.00 | 1310-72-3 | Merck KGaA | 99.5% to 100.5% (±0.3%) [27] | Volumetric titration at 293.15 K | |
| Potassium chloride solution (3.31 mol/kg) | 74.55 | 7447-40-7 | Metrohm (Herisau, Switzerland) | 100.1% * | Potentiometric measurement at 298.0 ± 0.2 K |
| No. | ||||||
|---|---|---|---|---|---|---|
| K1 | 277.65 | 33.2542 | 0 | 0 | 0 | 0.010, 0.030, 0.050, 0.100, 0.150, 0.250, 0.400 |
| K2 | 293.55 | 33.2171 | 0 | 0 | 0 | 0.080, 0.150, 0.250, 0.300, 0.600, 1.000, 1.300, 1.600, 2.000 |
| K3 | 308.45 | 33.2282 | 0 | 0 | 0 | 0.150, 0.300, 0.700, 1.000, 1.300, 2.000, 3.000, 6.000, 10.000 |
| N1 | 277.65 | 33.0969 | 0 | 0 | 0.050, 0.100, 0.150, 0.250, 0.500, 0.750 | 0 |
| N2 | 282.55 | 33.2010 | 0 | 0 | 0.100, 0.250, 0.500, 0.750, 1.000 | 0 |
| N3 | 287.55 | 33.3148 | 0 | 0 | 0.100, 0.250, 0.500, 0.750, 1.000, 2.000 | 0 |
| N4 | 293.55 | 33.2000 | 0 | 0 | 0.250, 0.500, 0.750, 1.000, 2.000 | 0 |
| N5 | 298.55 | 33.0630 | 0 | 0 | 0.250, 0.500, 0.750, 1.000, 2.000 | 0 |
| N6 | 303.45 | 33.2332 | 0 | 0 | 0.500, 0.750, 1.000, 2.000, 3.000, 4.000 | 0 |
| N7 | 308.15 | 33.2820 | 0 | 0 | 0.750, 1.000, 2.000, 3.000, 4.000 | 0 |
| C1 | 277.65 | 33.2691 | 0.0178 | 0 | 0.050, 0.100, 0.150, 0.250, 0.500, 0.750, 1.000 | 0 |
| C2 | 282.65 | 33.2604 | 0.0176 | 0 | 0.100, 0.250, 0.501, 0.750, 1.000, 2.000 | 0 |
| C3 | 293.55 | 33.2553 | 0.0176 | 0 | 0.250, 0.500, 0.750, 1.000, 2.000, 3.000 | 0 |
| C4 | 308.45 | 33.2682 | 0.0179 | 0 | 0.750, 1.000, 2.000, 3.000, 4.000, 6.000 | 0 |
| S0 | 298.55 | 33.2507 | 0 | 0.0142, 0.0394, 0.0630, 0.0838, 0.1081 | 0 | 0 |
| S1 | 277.85 | 33.2713 | 0 | 0.0352 | 0.050, 0.100, 0.150, 0.250, 0.500, 0.750 | 0 |
| S2 | 282.65 | 33.0836 | 0 | 0.0352 | 0.100, 0.250, 0.500, 0.750, 1.000 | 0 |
| S3 | 287.65 | 33.1705 | 0 | 0.0352 | 0.100, 0.250, 0.500, 0.750, 1.000, 2.000 | 0 |
| S4 | 293.55 | 33.2451 | 0 | 0.0352 | 0.250, 0.500, 0.750, 1.000, 2.000 | 0 |
| S5 | 298.55 | 33.2514 | 0 | 0.0352 | 0.250, 0.500, 0.750, 1.000, 2.000 | 0 |
| S6 | 303.45 | 32.7884 | 0 | 0.0352 | 0.500, 0.750, 1.000, 2.000, 3.000, 4.000 | 0 |
| S7 | 308.45 | 33.2020 | 0 | 0.0352 | 0.750, 1.000, 2.000, 3.000, 4.000 | 0 |
| 278.15 | 283.15 | 288.15 | 293.15 | 298.15 | 303.15 | 308.15 | |
|---|---|---|---|---|---|---|---|
| 0.975 | 0.975 | 0.980 | 0.982 () | 0.980 | |||
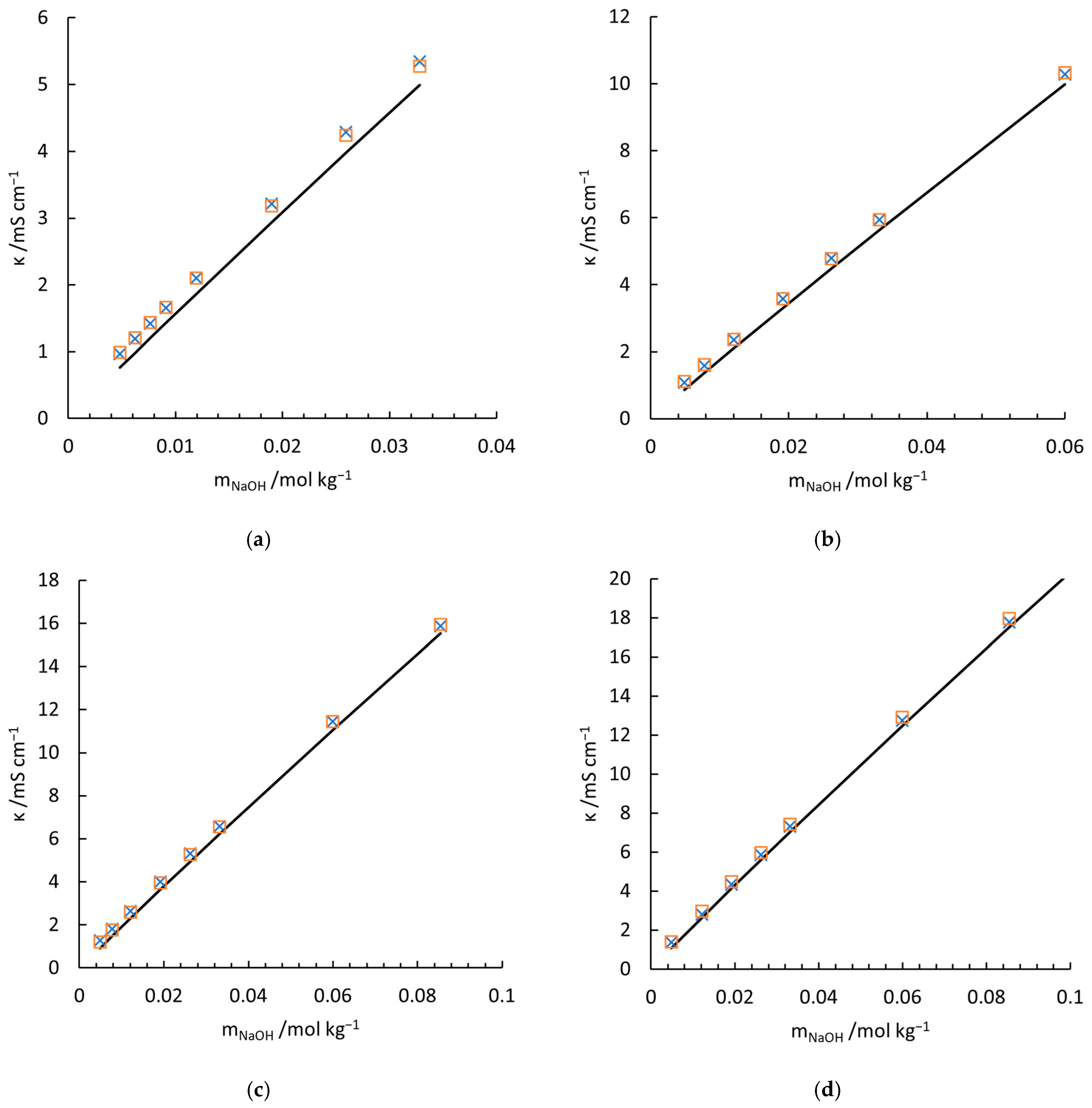
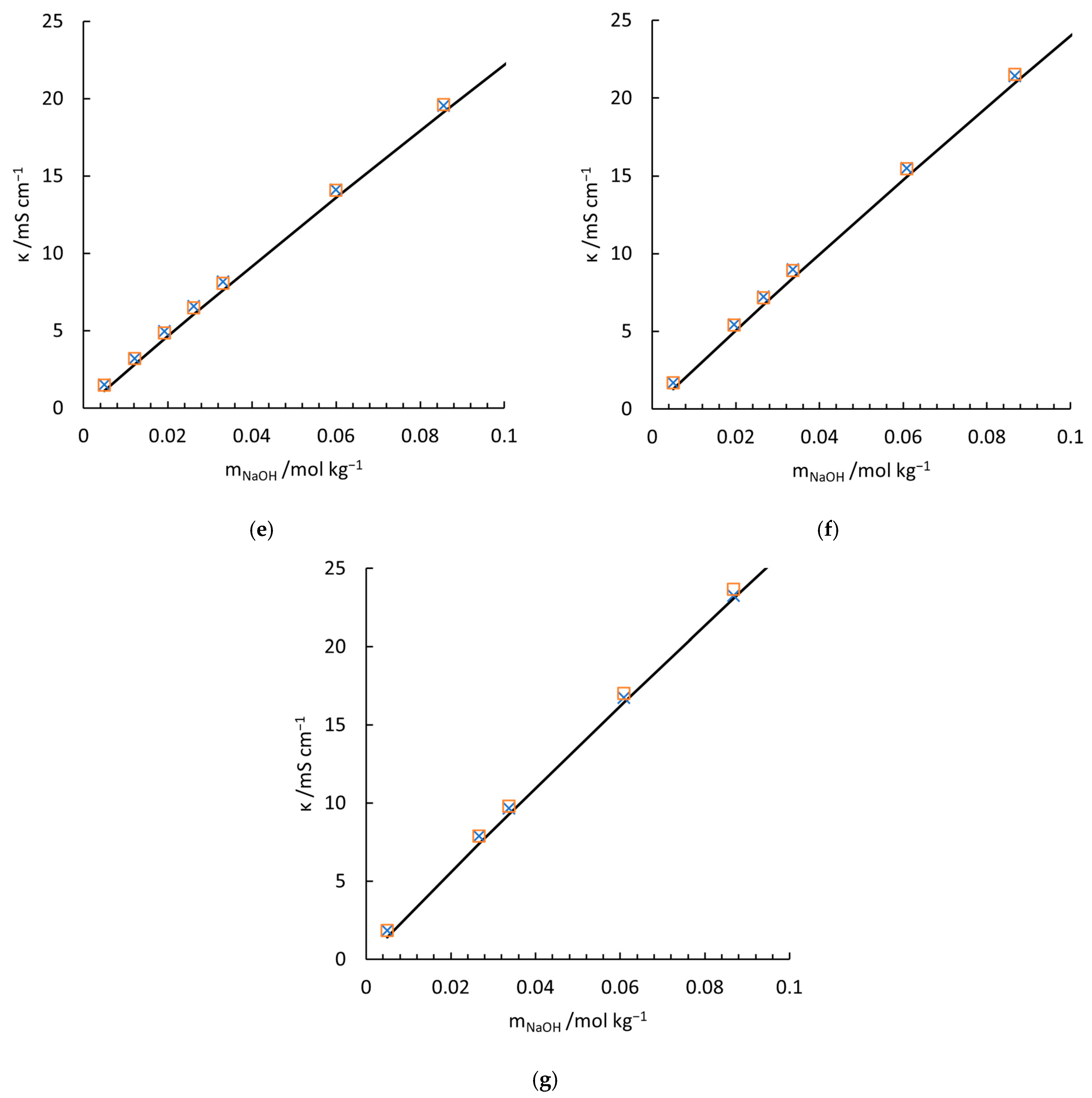
| 0.9993 | 0.9999 | 0.9999 | 0.9925 | 0.9999 | 1.0000 | 0.9999 |
| C (1.56) | N | O | F | |||
|---|---|---|---|---|---|---|
44.50 | 69.30 | / | / | / | / | / |
| Si | P (1.58) | S (1.54) | Cl | |||
| Tetrahedral, | Tetrahedral, | Tetrahedral, | Tetrahedral, | Tetrahedral, | ||
| Si-O 162 pm | S-O 149 pm | Cl-O 144 pm | ||||
| 36.00 | 57.00 | 52.00 | 80.00 | 67.30 | ||
| /K | 277.85 | 282.65 | 287.65 | 293.65 | 298.55 | 303.45 | 308.45 |
|---|---|---|---|---|---|---|---|
| 12.66 | 14.03 | 17.01 | 18.41 | 21.20 | 24.09 | 26.03 | |
| 19.78 | 21.92 | 26.57 | 28.77 | 33.12 | 37.64 | 40.66 | |
| ±0.048 | ±0.03 | ±0.061 | ±0.157 | ±0.093 | ±0.065 | ±0.265 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.; Ye, G.; De Schutter, G. Study and Evaluation of Equivalent Conductivities of [SiO(OH)3]− and [SiO2(OH)2]2− in NaOH-Na2SiO3-H2O Solutions at 277.85 K to 308.45 K. Materials 2025, 18, 2996. https://doi.org/10.3390/ma18132996
Yang K, Ye G, De Schutter G. Study and Evaluation of Equivalent Conductivities of [SiO(OH)3]− and [SiO2(OH)2]2− in NaOH-Na2SiO3-H2O Solutions at 277.85 K to 308.45 K. Materials. 2025; 18(13):2996. https://doi.org/10.3390/ma18132996
Chicago/Turabian StyleYang, Kai, Guang Ye, and Geert De Schutter. 2025. "Study and Evaluation of Equivalent Conductivities of [SiO(OH)3]− and [SiO2(OH)2]2− in NaOH-Na2SiO3-H2O Solutions at 277.85 K to 308.45 K" Materials 18, no. 13: 2996. https://doi.org/10.3390/ma18132996
APA StyleYang, K., Ye, G., & De Schutter, G. (2025). Study and Evaluation of Equivalent Conductivities of [SiO(OH)3]− and [SiO2(OH)2]2− in NaOH-Na2SiO3-H2O Solutions at 277.85 K to 308.45 K. Materials, 18(13), 2996. https://doi.org/10.3390/ma18132996







