Glauber’s Salt Composites for HVAC Applications: A Study on the Use of the T-History Method with a Modified Data Evaluation Methodology
Abstract
1. Introduction
2. Materials and Methodology
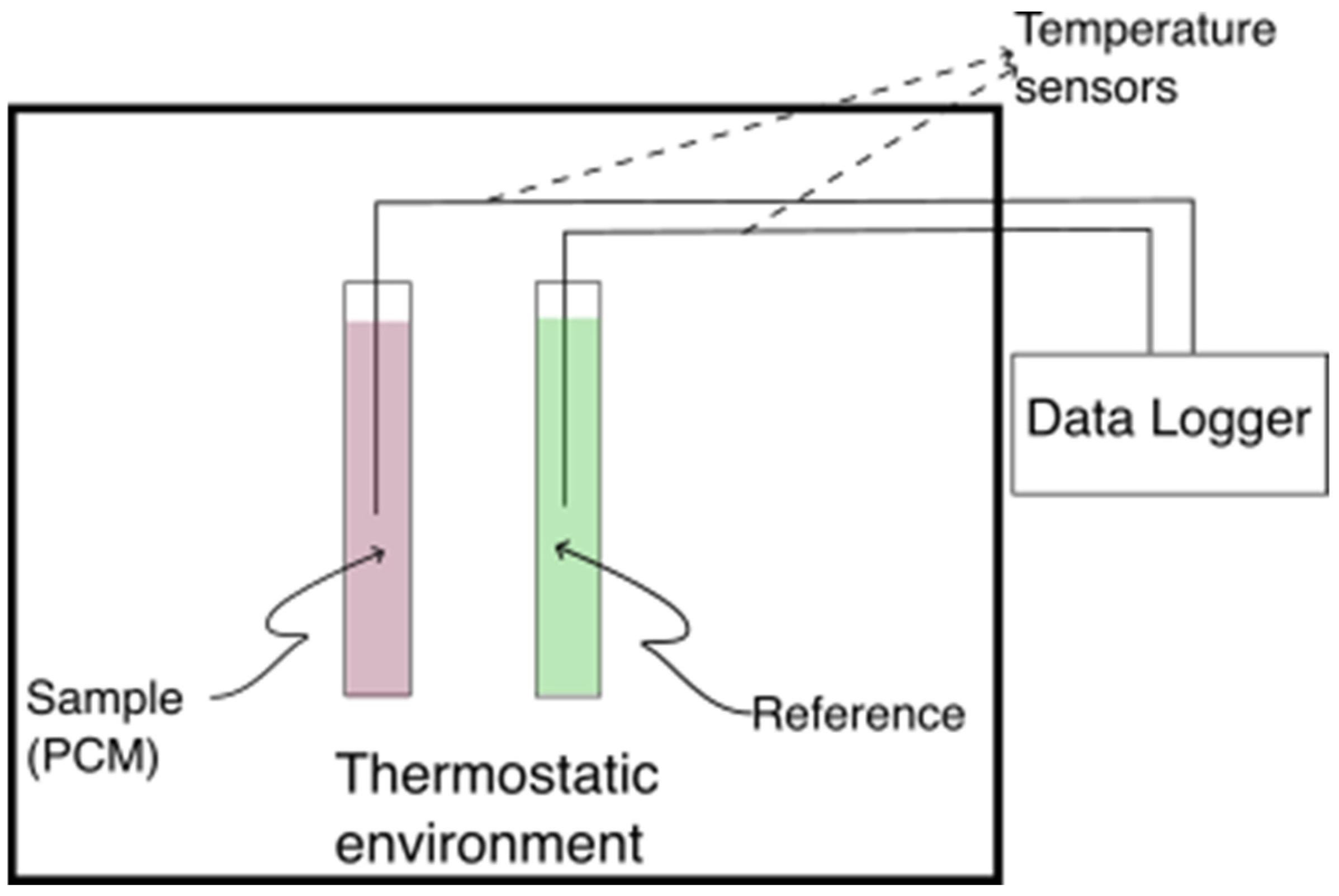
2.1. Experimental Setup
2.2. Temperature Uncertainty Estimation
2.3. PCM Preparation
2.4. Data Evaluation Methodology
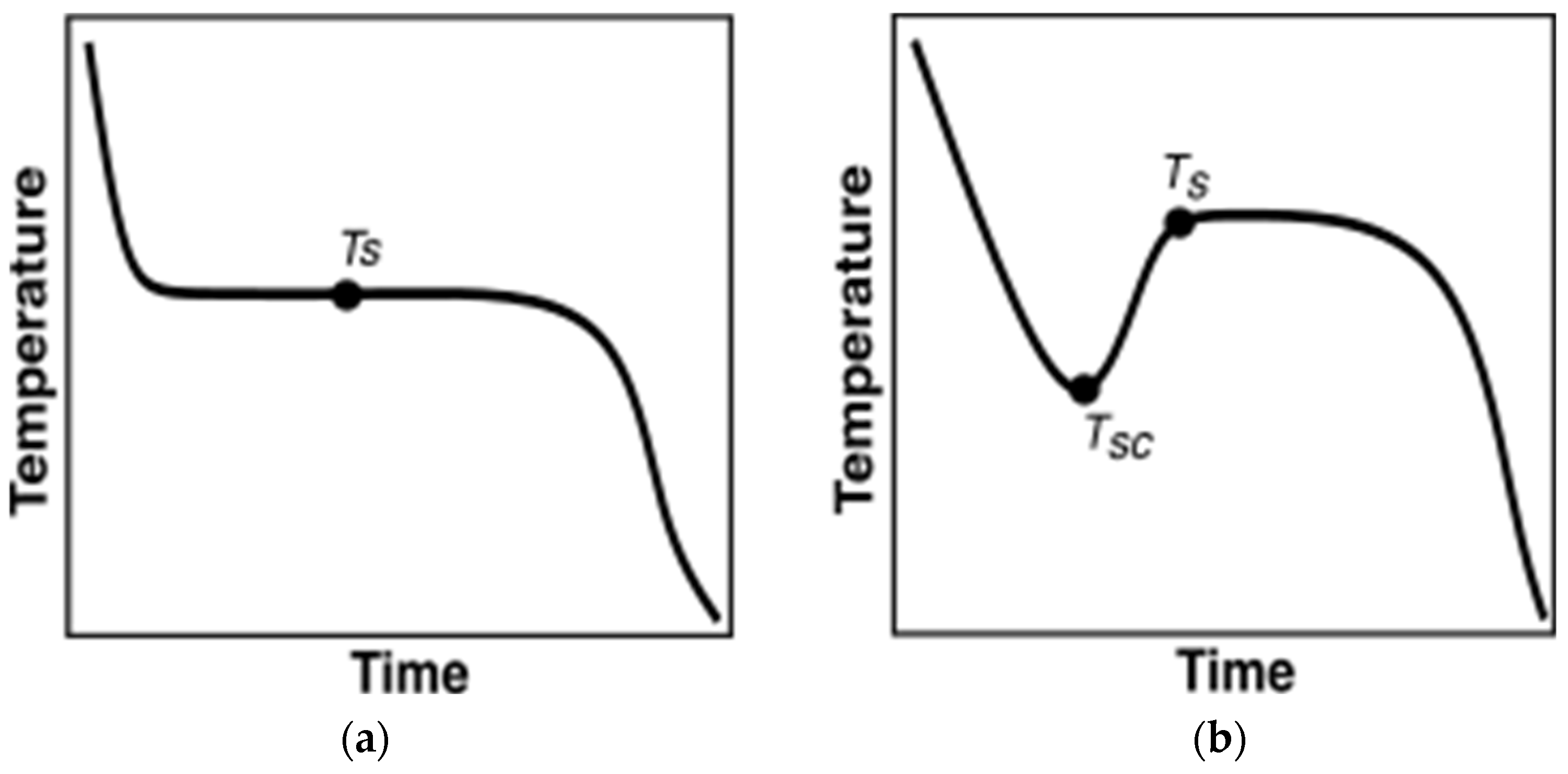
2.4.1. Current Data Evaluation Methodologies
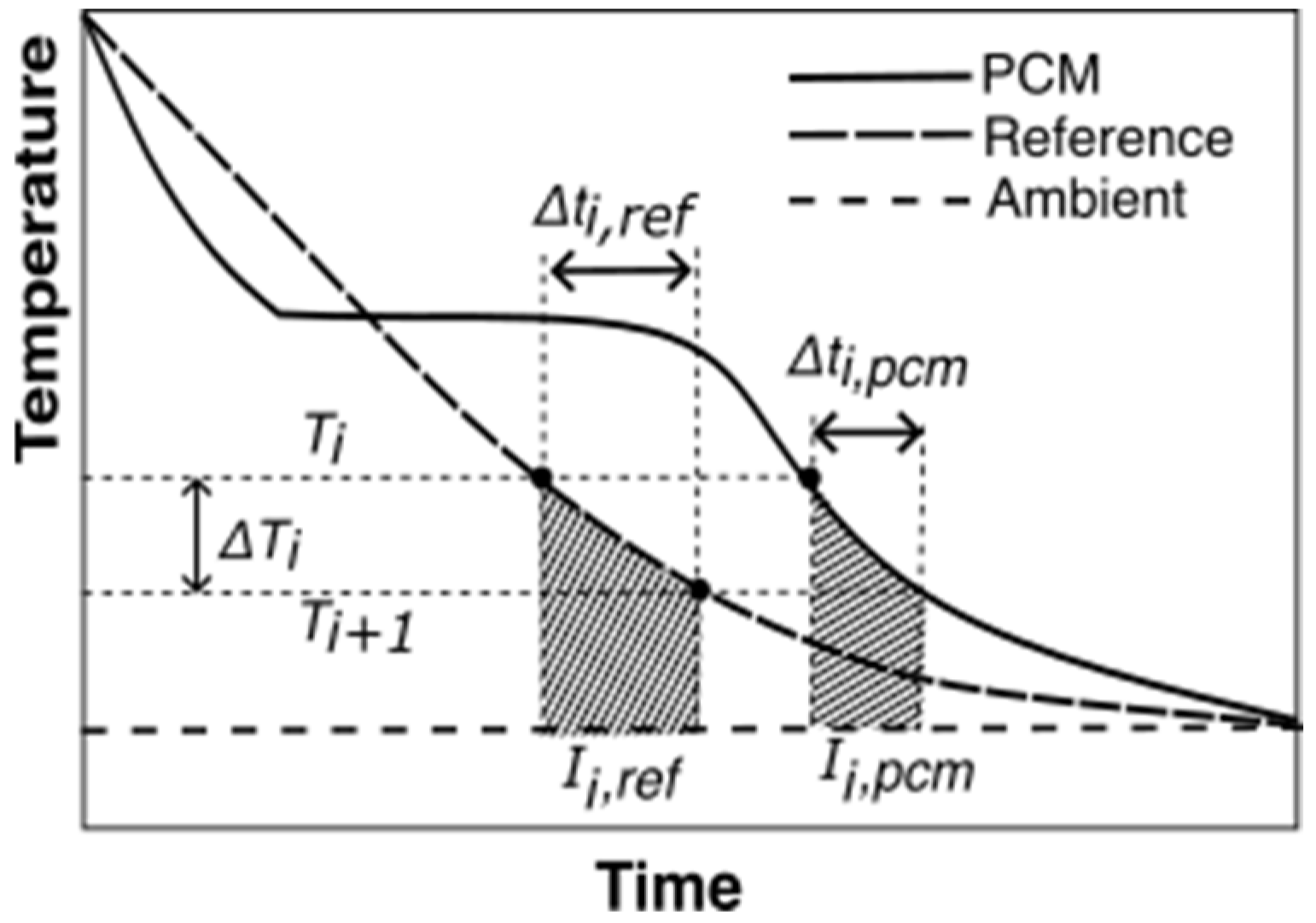
2.4.2. Proposed Data Evaluation Methodology
3. Results and Discussion
3.1. Validation of Proposed Methodology with n-Hexadecane’s Data Reported in the Literature
3.2. Salt Hydrate Composites
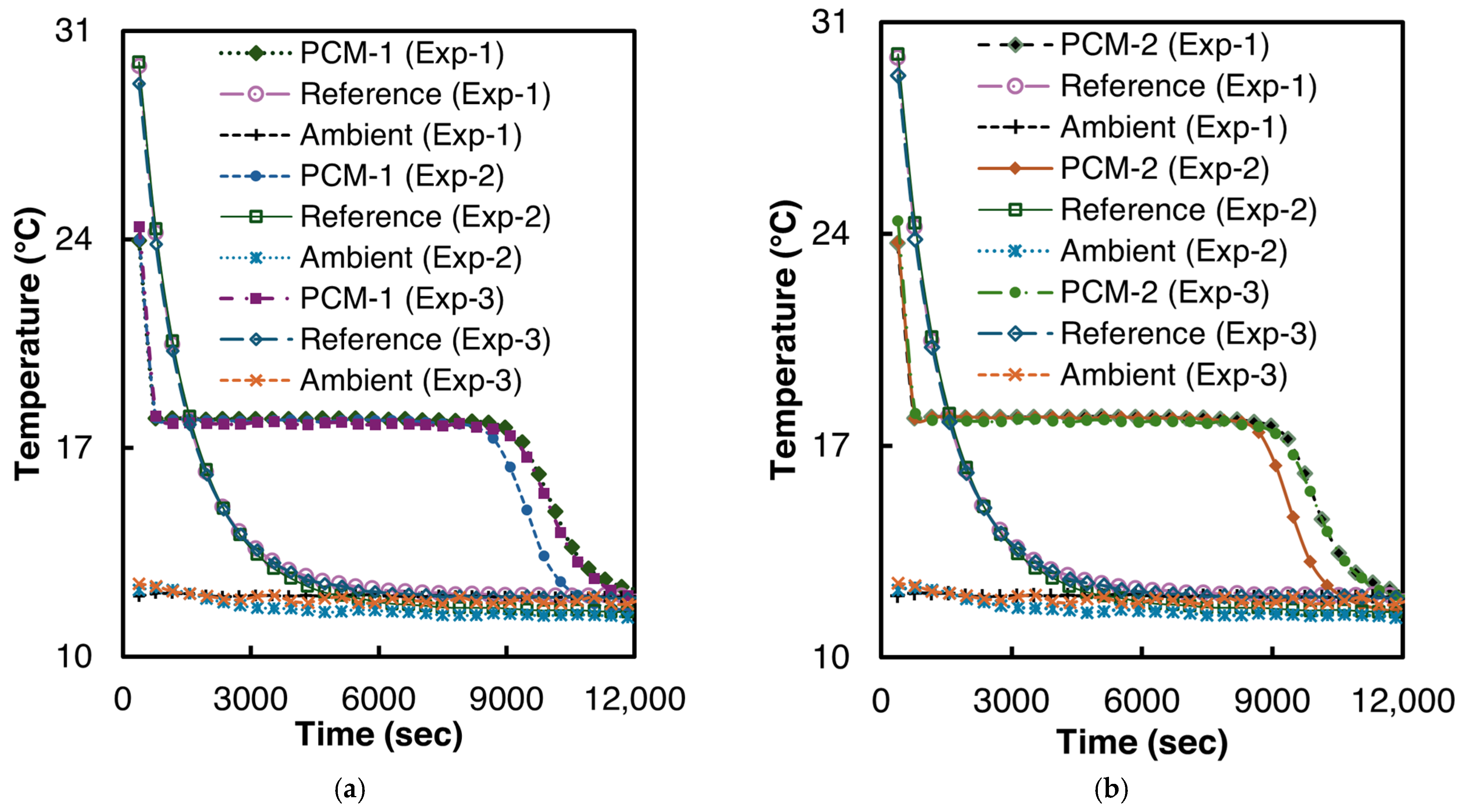
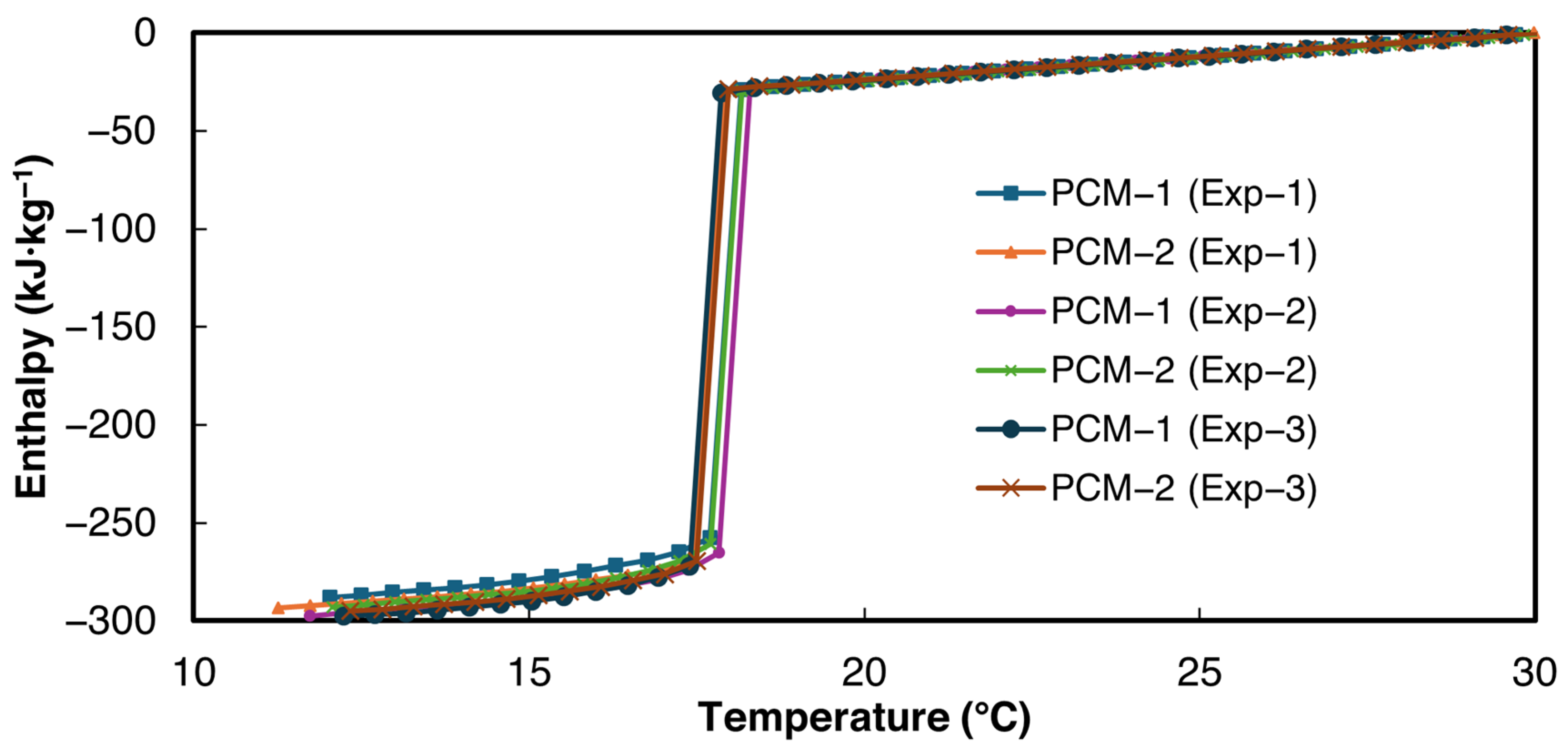
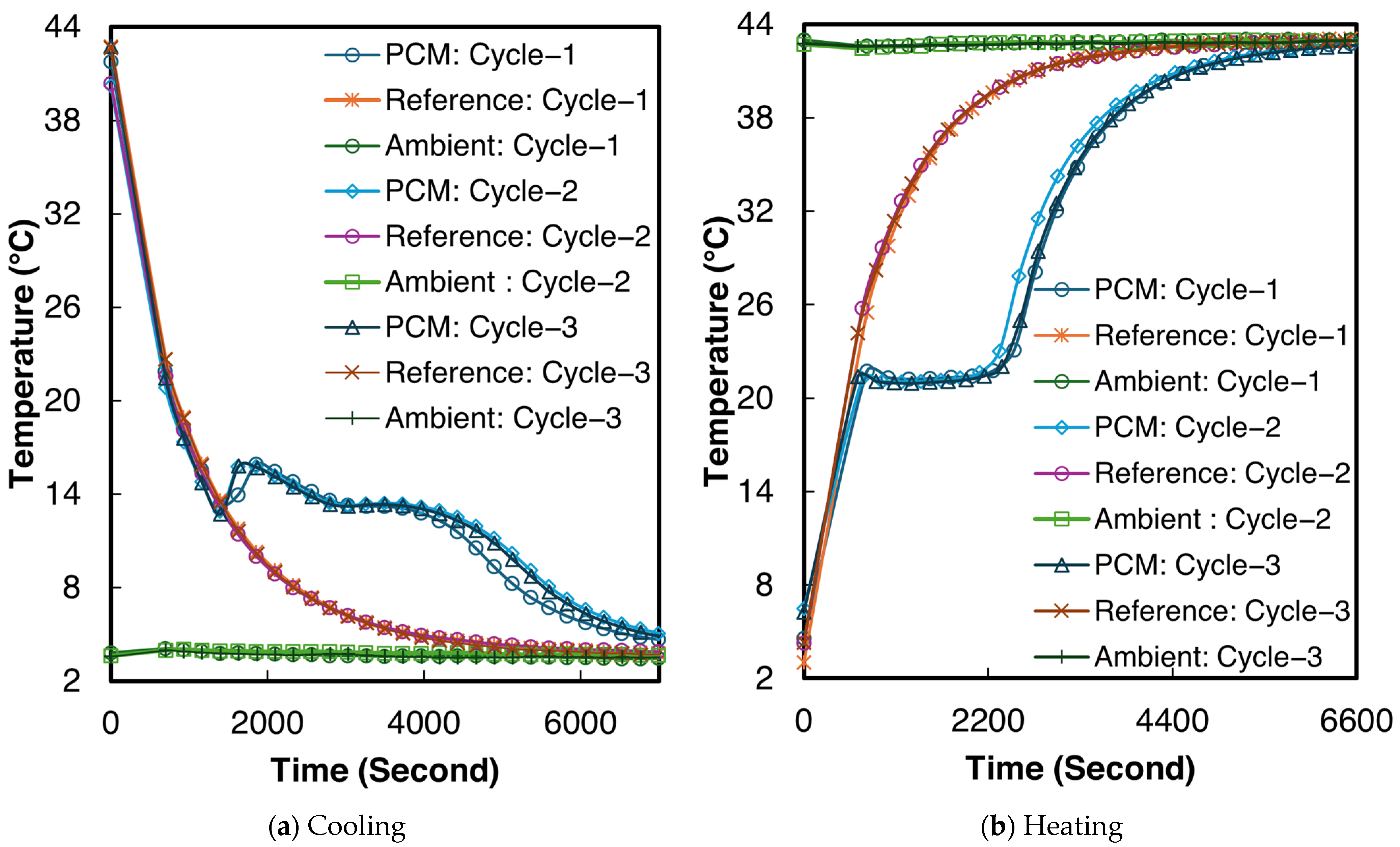
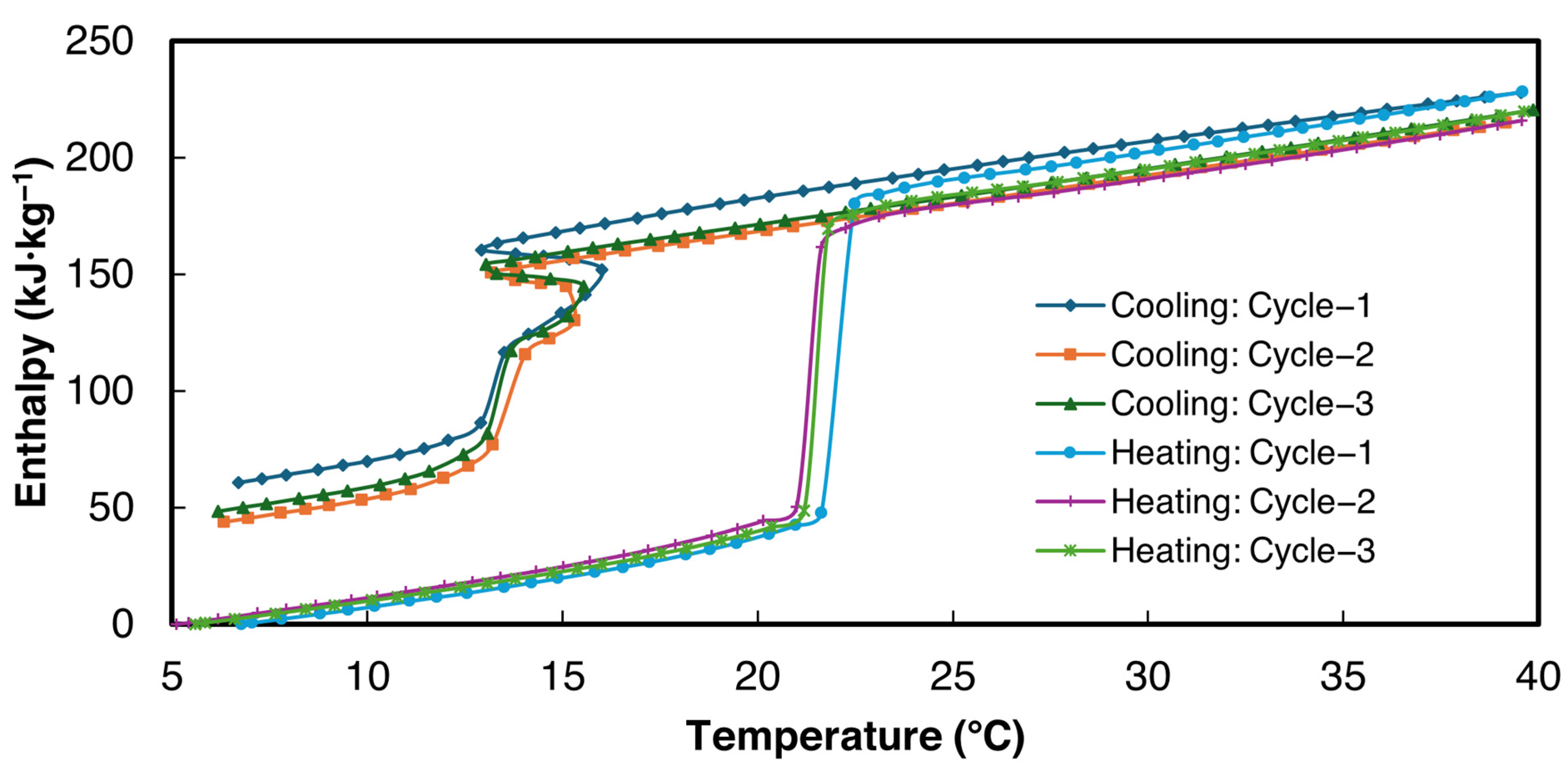
3.2.1. 1E-3SPA
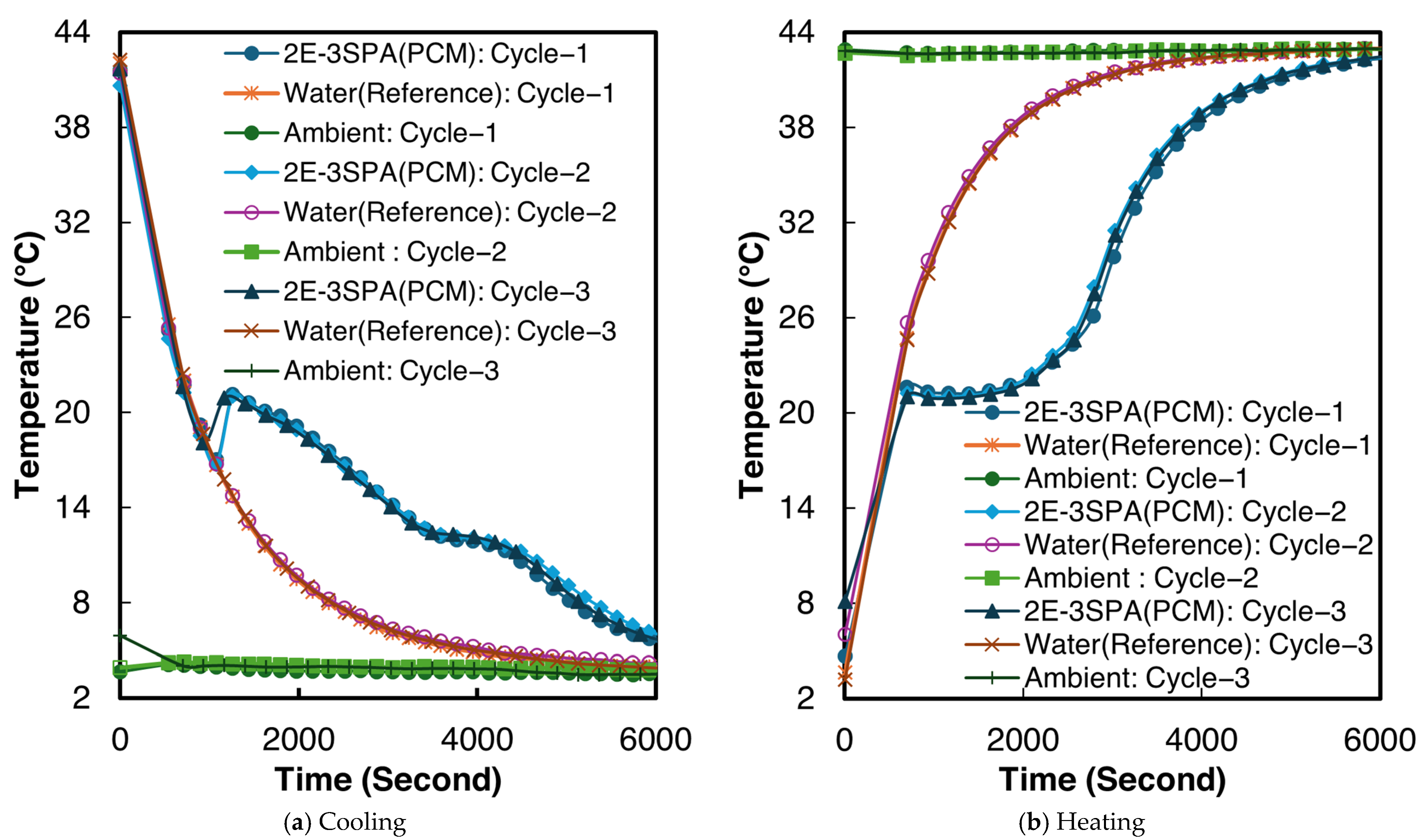
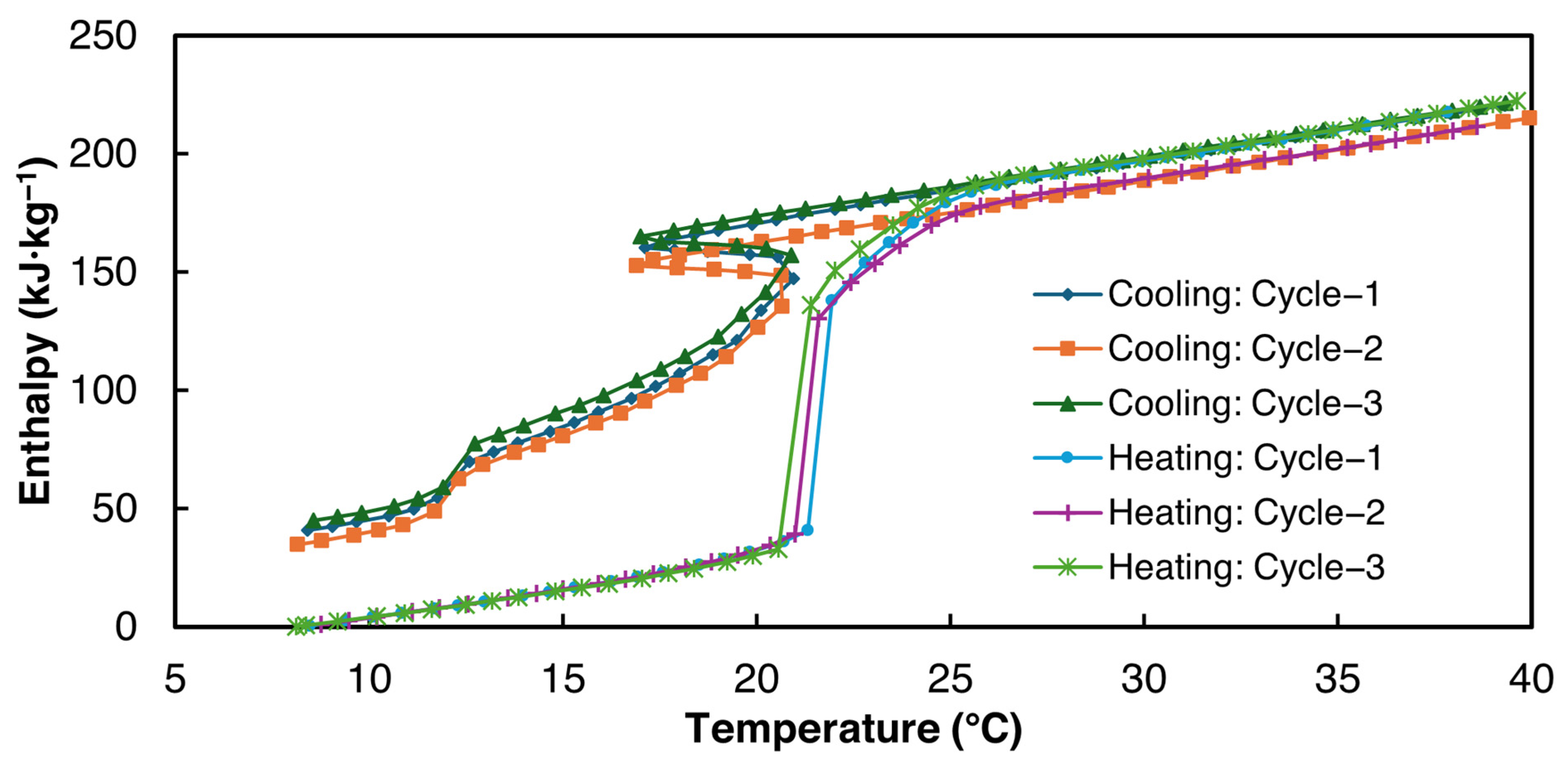
3.2.2. 2E-3SPA
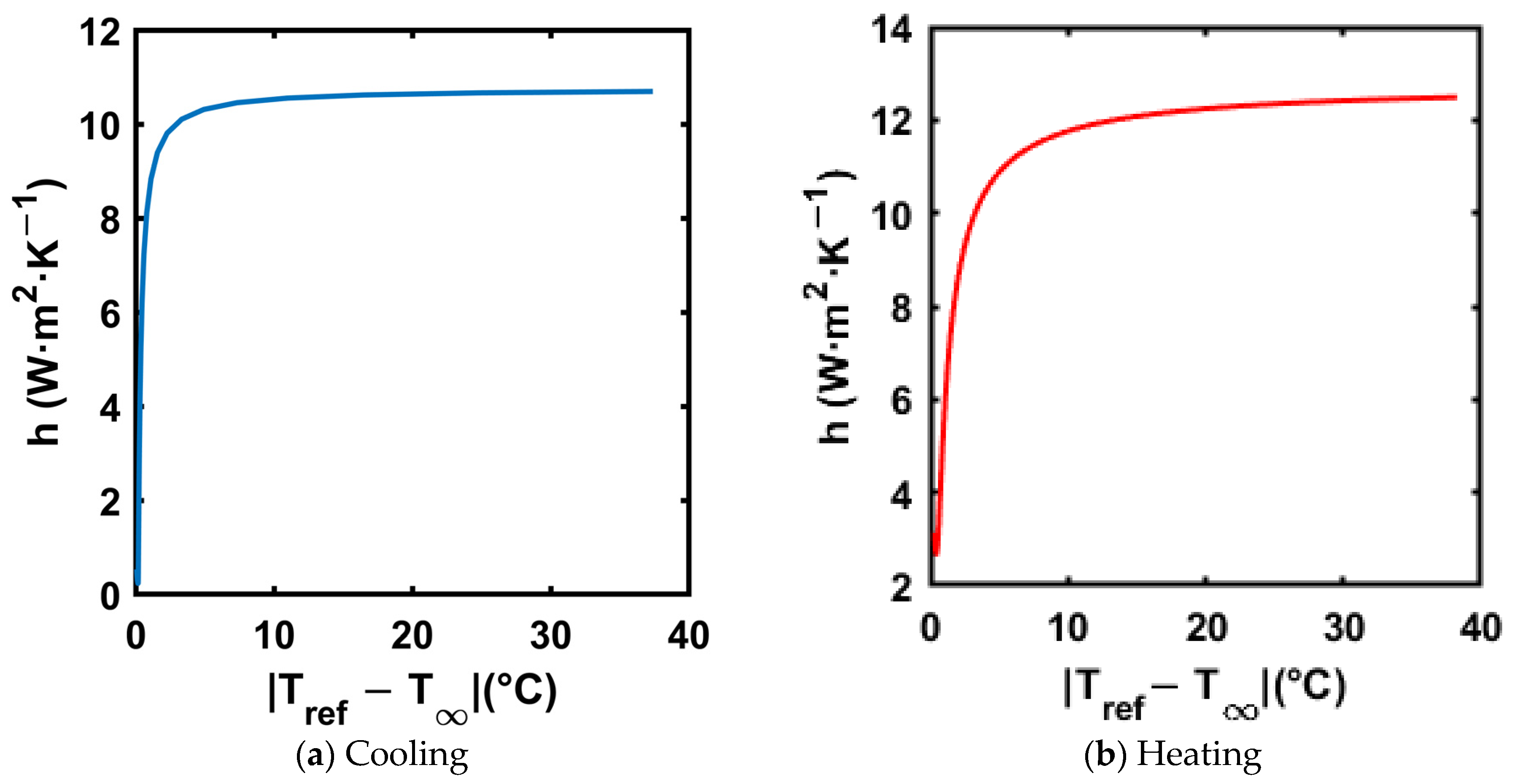
3.3. Calculating Convective Heat Transfer Coefficient
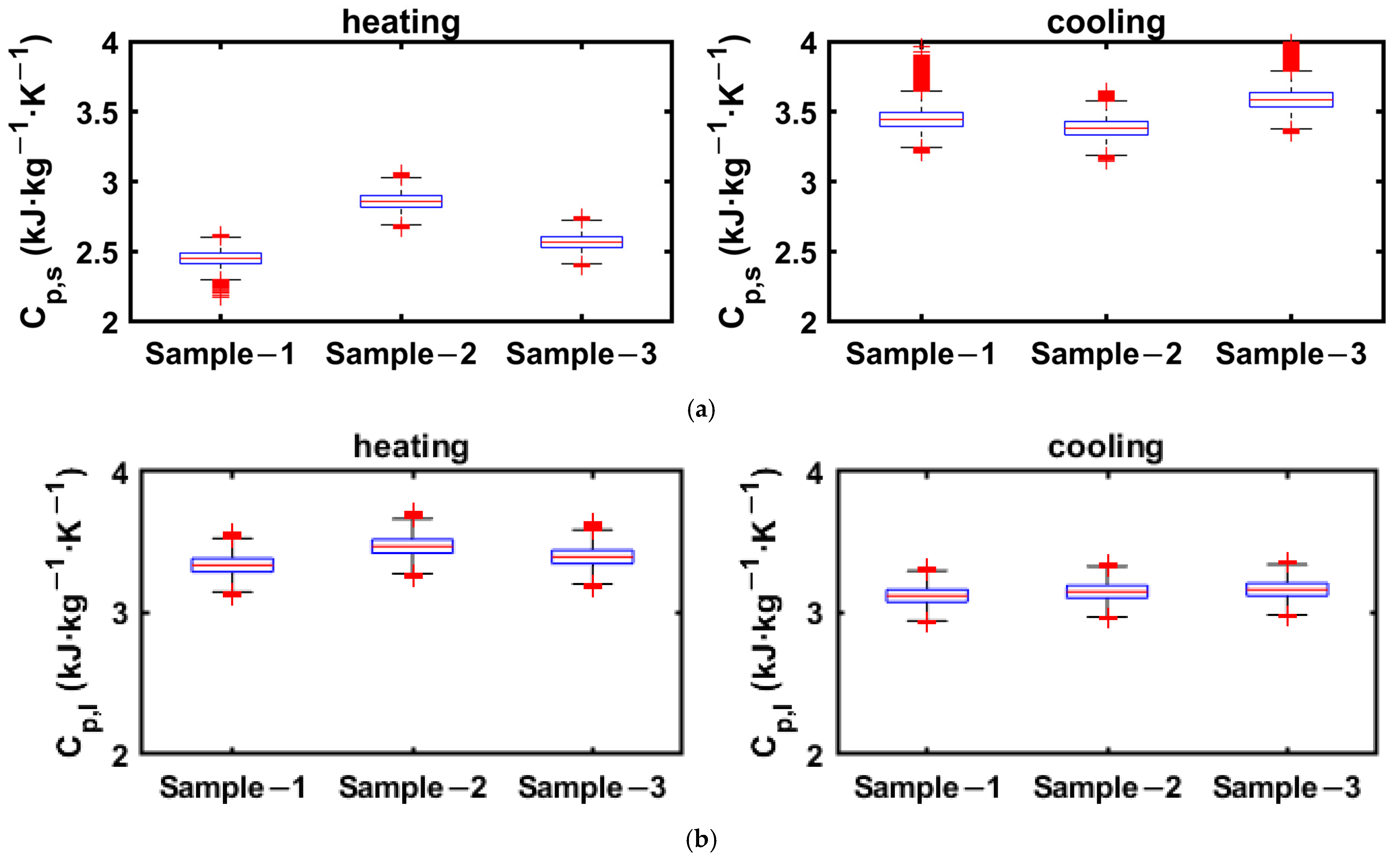
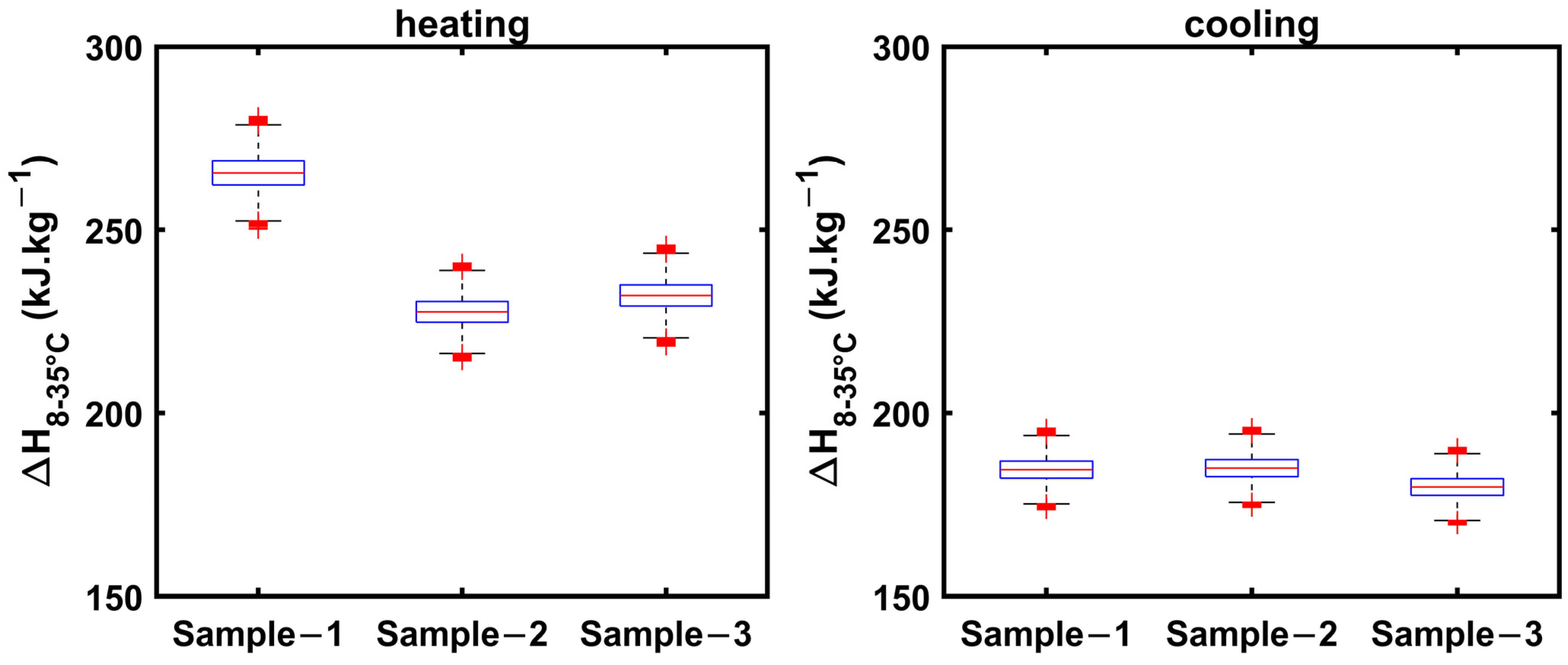
3.4. Uncertainty Analysis
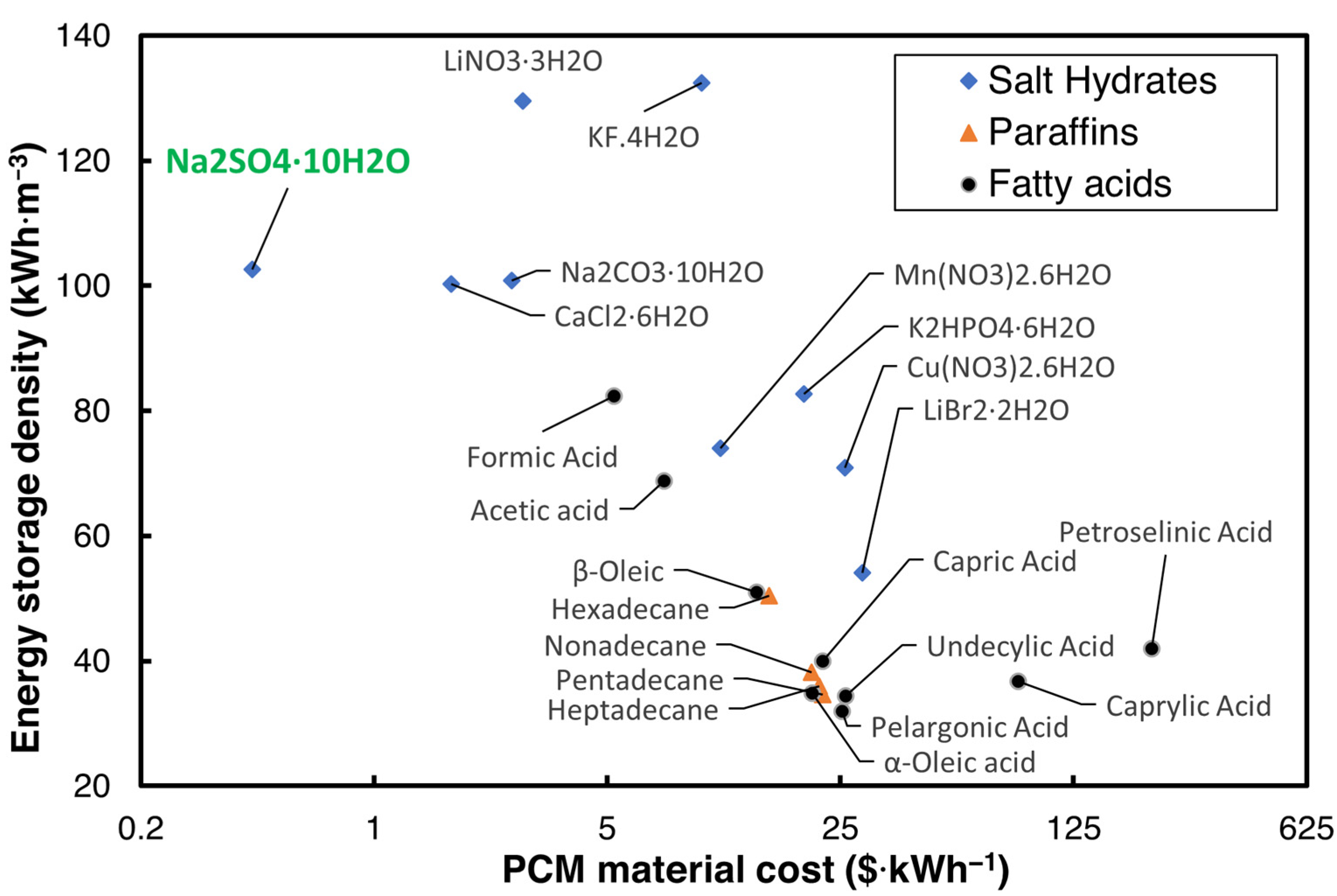
3.5. Comparison of the Volumetric Energy Densities with State of the Art
4. Conclusions and Future Work
- A modified data evaluation methodology was introduced to analyze the T-history data and obtain the enthalpy–temperature curves of the above-mentioned composite PCMs using Marin’s method. The modified methodology is built upon the physics-driven principles of heat transfer, suitable for PCMs demonstrating significant supercooling.
- Using the proposed methodology, we found the following:
- 1E-3SPA was found to have 139.1 kJ·kg−1 of latent heat with a melting onset temperature of 21 °C and a supercooling degree of 1.5 °C. However, it exhibited a large hysteresis of 7.7 °C, making it a less favorable PCM despite its lower cost.
- 2E-3SPA was found to have 170.9 kJ·kg−1 of latent heat with a melting temperature of 21 °C and a supercooling degree of 2 °C. It showed a low hysteresis of 2 °C, making it a favorable PCM for HVAC applications. Moreover, the melting range of 2E-3SPA falls in the optimum melting temperature of PCMs for HVAC applications such as data centers.
- The volumetric energy storage density of 2E-3SPA is 282 MJ·m−3, which is very close to the United States’ DOE target of 288 MJ·m−3 and is also closer to the volumetric energy storage densities of several commercial PCMs with similar melting ranges.
- It can be concluded that the temperature characteristics and energy and bulk thermophysical properties are sensitive to the amount of NaCl in the composite.
- Uncertainty estimation of the enthalpy and specific heat of both 1E-3SPA and 2E-3SPA was carried out using Monte Carlo simulations. The maximum deviation in the estimation of specific heat was ±0.3 kJ·kg−1·K−1, and in the estimation of the enthalpy increase from 8 to 35 °C, it was ±15 kJ·kg−1. It was found that the uncertainty in temperature estimation has the greatest impact on the uncertainty in estimating the PCM thermophysical properties. Thus, reduced uncertainty in temperature can reduce the uncertainties of the estimations further.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Proportionality constant in the power law curve fit | |
| Outer surface area of the test tube (m2) | |
| Power law coefficient (−) | |
| Biot number | |
| Offset in the power law curve fit (W) | |
| Specific heat (kJ·kg−1·K−1) | |
| Elemental change in time (second) | |
| Elemental change in temperature (°C) | |
| Convective heat transfer coefficient (W·m−2·K−1) | |
| Step enthalpy change (kJ·kg−1) | |
| Enthalpy (kJ·kg−1) | |
| Latent heat of fusion (kJ·kg−1) | |
| Reference enthalpy (kJ·kg−1) | |
| Area under the temperature–time curve (°C-sec) | |
| Thermal conductivity (W·m−1·K−1) | |
| Mass (gram) | |
| N | Number of PCM intervals |
| Heat flow rate (W) | |
| Inner radius of the test tube (mm) | |
| Outer radius of the test tube (mm) | |
| Thermal resistance (°C·W−1) | |
| Time (second) | |
| Duration of the interval (second) | |
| Temperature (°C) | |
| Average temperature (°C) | |
| Melting temperature (°C) | |
| Solidification temperature (°C) | |
| Supercooling temperature (°C) | |
| Step change in temperature (°C) | |
| Minimum allowed temperature interval (°C) | |
| Greek Symbols: | |
| Standard uncertainty in temperature measurement (°C) | |
| Subscripts: | |
| Ambient | |
| Average | |
| Conduction | |
| Convection | |
| Interval | |
| Liquid | |
| Melting point | |
| Phase change material | |
| Reference | |
| Solid | |
| Sensor | |
| Test tube | |
| Abbreviations: | |
| CFD | Computational fluid dynamics |
| CMC | Carboxymethyl cellulose |
| DOE | Department of Energy |
| DSC | Digital scanning calorimetry |
| FEA | Finite element analysis |
| HVAC | Heating, ventilation, and air conditioning |
| IQR | Interquartile range |
| JCGM | Joint Committee for Guides in Metrology |
| PAM | Polyacrylamide |
| PCM | Phase change material |
| Probability density function | |
| SAT | Sodium acetate trihydrate |
| SLM | Shape language modeling |
| SPA | Sodium polyacrylate |
| SSD | Sodium sulfate decahydrate |
| TES | Thermal energy storage |
References
- El Mankibi, M.; Stathopoulos, N.; Rezaï, N.; Zoubir, A. Optimization of an Air-PCM heat exchanger and elaboration of peak power reduction strategies. Energy Build. 2015, 106, 74–86. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, S.; Xiao, F.; Gao, D. Peak load shifting control using different cold thermal energy storage facilities in commercial buildings: A review. Energy Convers. Manag. 2013, 71, 101–114. [Google Scholar] [CrossRef]
- Yamaha, M.; Misaki, S. The Evaluation of Peak Shaving by a Thermal Storage System Using Phase-Change Materials in Air Distribution Systems. HVACR Res. 2006, 12, 861–869. [Google Scholar] [CrossRef]
- Erdemir, D.; Dincer, I. Potential use of thermal energy storage for shifting cooling and heating load to off-peak load: A case study for residential building in Canada. Energy Storage 2020, 2, e125. [Google Scholar] [CrossRef]
- Odukomaiya, A.; Woods, J.; James, N.; Kaur, S.; Gluesenkamp, K.R.; Kumar, N.; Mumme, S.; Jackson, R.; Prasher, R. Addressing energy storage needs at lower cost via on-site thermal energy storage in buildings †. Energy Environ. Sci. 2021, 14, 5315. [Google Scholar] [CrossRef]
- Izadi, M.; Afsharpanah, F.; Mohadjer, A.; Shobi, M.O.; Ajarostaghi, S.S.M.; Minelli, F. Performance enhancement of a shell-and-coil ice storage enclosure for air conditioning using spiral longitudinal fins: A numerical approach. Heliyon 2025, 11, e42786. [Google Scholar] [CrossRef]
- Sanaye, S.; Shirazi, A. Thermo-economic optimization of an ice thermal energy storage system for air-conditioning applications. Energy Build. 2013, 60, 100–109. [Google Scholar] [CrossRef]
- Song, X.; Zhu, T.; Liu, L.; Cao, Z. Study on optimal ice storage capacity of ice thermal storage system and its influence factors. Energy Convers. Manag. 2018, 164, 288–300. [Google Scholar] [CrossRef]
- Ljungdahl, V.; Taha, K.; Dallaire, J.; Kieseritzky, E.; Pawelz, F.; Jradi, M.; Veje, C. Phase change material based ventilation module-Numerical study and experimental validation of serial design. Energy 2021, 234, 121209. [Google Scholar] [CrossRef]
- Nie, B.; She, X.; Du, Z.; Xie, C.; Li, Y.; He, Z.; Ding, Y. System performance and economic assessment of a thermal energy storage based air-conditioning unit for transport applications. Appl. Energy 2019, 251, 113254. [Google Scholar] [CrossRef]
- Saffari, M.; de Gracia, A.; Fernández, C.; Cabeza, L.F. Simulation-based optimization of PCM melting temperature to improve the energy performance in buildings. Appl. Energy 2017, 202, 420–434. [Google Scholar] [CrossRef]
- Thermal Energy Storage-Buildings. n.d. Available online: https://www.energy.gov/eere/buildings/thermal-energy-storage (accessed on 5 August 2024).
- Hirschey, J.R.; Kumar, N.; Turnaoglu, T.; Gluesenkamp, K.R.; Graham, S. Review of Low-Cost Organic and Inorganic Phase Change Materials with Phase Change Temperature Between 0 °C and 65 °C; Purdue University: West Lafayette, IN, USA, 2021. [Google Scholar]
- Telkes, M. Nucleation of Supersaturated Inorganic Salt Solutions. Ind. Eng. Chem. 1952, 44, 1308–1310. [Google Scholar] [CrossRef]
- Marks, S. An investigation of the thermal energy storage capacity of Glauber’s salt with respect to thermal cycling. Sol. Energy 1980, 25, 255–258. [Google Scholar] [CrossRef]
- Purohit, B.K.; Sistla, V.S. Inorganic salt hydrate for thermal energy storage application: A review. Energy Storage 2021, 3, e212. [Google Scholar] [CrossRef]
- Randriambololona, A.M.; Manepalli, V.; McAfee, R.C.; Ojha, B.; Miraftab-Salo, R.; Guye, K.; Lee, H.; Graham, S.; Agonafer, D. Three-Component Composite Phase Change Material (PCM) for Electronics Subject to Transient/Pulsed Heat Loads. IEEE Trans. Compon. Packag. Manuf. Technol. 2024, 14, 2248–2257. [Google Scholar] [CrossRef]
- Deepa, A.S.; Tewari, A. Phase transition behaviour of hydrated Glauber’s salt based phase change materials and the effect of ionic salt additives: A molecular dynamics study. Comput. Mater. Sci. 2022, 203, 111112. [Google Scholar] [CrossRef]
- Akamo, D.; Hirschey, J.; Turnaoglu, T.; LaClair, T.; Gluesenkamp, K.; Goswami, M.; Rios, O. Salt Hydrate Eutectic Mixtures for Near Ambient Thermal Energy Storage Applications; Purdue University: West Lafayette, IN, USA, 2022. [Google Scholar]
- Fang, Y.; Su, J.; Tang, Y.; Liang, X.; Wang, S.; Gao, X.; Zhang, Z. Form-stable Na2SO4 10H2O-Na2HPO4 12H2O eutectic/hydrophilic fumed silica composite phase change material with low supercooling and low thermal conductivity for indoor thermal comfort improvement. Int. J. Energy Res. 2020, 44, 3171–3182. [Google Scholar] [CrossRef]
- Hou, P.; Mao, J.; Chen, F.; Li, Y.; Dong, X. Preparation and Thermal Performance Enhancement of Low Temperature Eutectic Composite Phase Change Materials Based on Na2SO4·10H2O. Materials 2018, 11, 2230. [Google Scholar] [CrossRef]
- Jiang, Z.; Tie, S. Preparation and thermal properties of Glauber’s salt-based phase-change materials for Qinghai–Tibet Plateau solar greenhouses. Int. J. Mod. Phys. B 2017, 31, 1744085. [Google Scholar] [CrossRef]
- Olson, L.; Lothian, C.; Ådén, U.; Lagercrantz, H.; Robertson, N.J.; Setterwall, F. Phase-Changing Glauber Salt Solution for Medical Applications in the 28–32 °C Interval. Materials 2021, 14, 7106. [Google Scholar] [CrossRef]
- Ryu, H.W.; Woo, S.W.; Shin, B.C.; Kim, S.D. Prevention of supercooling and stabilization of inorganic salt hydrates as latent heat storage materials. Sol. Energy Mater. Sol. Cells 1992, 27, 161–172. [Google Scholar] [CrossRef]
- Yinping, Z.; Yi, J. A simple method, the -history method, of determining the heat of fusion, specific heat and thermal conductivity of phase-change materials. Meas. Sci. Technol. 1999, 10, 201–205. [Google Scholar] [CrossRef]
- Lovelyn Theresa, I.; Velraj, R. Thermophysical characterization and comparison of PCMs using DSC and T-History experimental setup. Mater. Res. Express 2019, 6, 125527. [Google Scholar] [CrossRef]
- García-Romero, A.; Diarce, G.; Ibarretxe, J.; Urresti, A.; Sala, J.M. Influence of the experimental conditions on the subcooling of Glauber’s salt when used as PCM. Sol. Energy Mater. Sol. Cells 2012, 102, 189–195. [Google Scholar] [CrossRef]
- Marin, J.M.; Zalba, B.N.; Cabeza, L.F.; Mehling, H. Determination of enthalpy temperature curves of phase change materials with the temperature-history method: Improvement to temperature dependent properties. Meas. Sci. Technol. 2003, 14, 184–189. [Google Scholar] [CrossRef]
- Kumarasamy, K.; An, J.; Yang, J.; Yang, E.-H. Novel CFD-based numerical schemes for conduction dominant encapsulated phase change materials (EPCM) with temperature hysteresis for thermal energy storage applications. Energy 2017, 132, 31–40. [Google Scholar] [CrossRef]
- Solé, A.; Miró, L.; Barreneche, C.; Martorell, I.; Cabeza, L.F. Review of the T -history method to determine thermophysical properties of phase change materials (PCM). Renew. Sustain. Energy Rev. 2013, 26, 425–436. [Google Scholar] [CrossRef]
- Kailkhura, G.; Mandel, R.; Shooshtari, A.; Ohadi, M. A 1D Reduced-Order Model (ROM) for a Novel Latent Thermal Energy Storage System. Energies 2022, 15, 5124. [Google Scholar] [CrossRef]
- Gowreesunker, B.L.; Tassou, S.A.; Kolokotroni, M. Improved simulation of phase change processes in applications where conduction is the dominant heat transfer mode. Energy Build. 2012, 47, 353–359. [Google Scholar] [CrossRef]
- Sandnes, B.; Rekstad, J. Supercooling salt hydrates: Stored enthalpy as a function of temperature. Sol. Energy 2006, 80, 616–625. [Google Scholar] [CrossRef]
- Kravvaritis, E.D.; Antonopoulos, K.A.; Tzivanidis, C. Improvements to the measurement of the thermal properties of phase change materials. Meas. Sci. Technol. 2010, 21, 045103. [Google Scholar] [CrossRef]
- D’Avignon, K.; Kummert, M. Assessment of T-History Method Variants to Obtain Enthalpy–Temperature Curves for Phase Change Materials with Significant Subcooling. J. Therm. Sci. Eng. Appl. 2015, 7, 041015. [Google Scholar] [CrossRef]
- RAL. Phase Change Material Quality Assurance (RAL-GZ896). 2013. Available online: www.ral-guetezeichen.de (accessed on 1 May 2025).
- Tan, P.; Brütting, M.; Vidi, S.; Ebert, H.-P.; Johansson, P.; Kalagasidis, A.S. Characterizing phase change materials using the T-History method: On the factors influencing the accuracy and precision of the enthalpy-temperature curve. Thermochim. Acta 2018, 666, 212–228. [Google Scholar] [CrossRef]
- Badenhorst, H.; Cabeza, L.F. Critical analysis of the T-history method: A fundamental approach. Thermochim. Acta 2017, 650, 95–105. [Google Scholar] [CrossRef]
- Incropera, F.P. Fundamentals of Heat and Mass Transfer; Wiley: Hoboken, NJ, USA, 2007; Available online: https://books.google.com/books?id=_P9QAAAAMAAJ (accessed on 1 May 2025).
- Babar, O.A.; Arora, V.K.; Nema, P.K. Selection of phase change material for solar thermal storage application: A comparative study. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 355. [Google Scholar] [CrossRef]
- Lázaro, A.; Günther, E.; Mehling, H.; Hiebler, S.; Marín, J.M.; Zalba, B. Verification of a T-history installation to measure enthalpy versus temperature curves of phase change materials. Meas. Sci. Technol. 2006, 17, 2168–2174. [Google Scholar] [CrossRef]
- Rolka, P.; Kwidzinski, R.; Przybylinski, T.; Tomaszewski, A. Thermal Characterization of Medium-Temperature Phase Change Materials (PCMs) for Thermal Energy Storage Using the T-History Method. Materials 2021, 14, 7371. [Google Scholar] [CrossRef]
- De Paola, M.; Arcuri, N.; Calabrò, V.; De Simone, M. Thermal and Stability Investigation of Phase Change Material Dispersions for Thermal Energy Storage by T-History and Optical Methods. Energies 2017, 10, 354. [Google Scholar] [CrossRef]
- Stanković, S.B.; Kyriacou, P.A. Improved measurement technique for the characterization of organic and inorganic phase change materials using the T-history method. Appl. Energy 2013, 109, 433–440. [Google Scholar] [CrossRef]
- Ayyagari, V.; Kailkhura, G.; Mandel, R.; Shooshtari, A.; Ohadi, M. Performance Characterization of a Novel Low-Cost Additively Manufactured PCM-Air Polymer Composite Thermal Energy Storage. In Proceedings of the 2022 21st IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), San Diego, CA, USA, 31 May–3 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–9. [Google Scholar] [CrossRef]
- Kim, S.; Chang, S.J.; Chung, O.; Jeong, S.-G.; Kim, S. Thermal characteristics of mortar containing hexadecane/xGnP SSPCM and energy storage behaviors of envelopes integrated with enhanced heat storage composites for energy efficient buildings. Energy Build. 2014, 70, 472–479. [Google Scholar] [CrossRef]
- Rezaei, H.; Ghomsheh, M.J.; Kowsary, F.; Ahmadi, P. Performance assessment of a range-extended electric vehicle under real driving conditions using novel PCM-based HVAC system. Sustain. Energy Technol. Assess. 2021, 47, 101527. [Google Scholar] [CrossRef]
- De Paola, M.G.; Lopresto, C.G.; Arcuri, N.; Calabrò, V. T-history method: The importance of the cooling chamber to evaluate the thermal properties of Glauber’s salt-based phase change materials. Meas. Sci. Technol. 2021, 32, 035601. [Google Scholar] [CrossRef]
- Vélez, C.; Khayet, M.; De Zárate, J.M.O. Temperature-dependent thermal properties of solid/liquid phase change even-numbered n-alkanes: N-Hexadecane, n-octadecane and n-eicosane. Appl. Energy 2015, 143, 383–394. [Google Scholar] [CrossRef]
- Hong, H.; Kim, S.K.; Kim, Y.-S. Accuracy improvement of T-history method for measuring heat of fusion of various materials. Int. J. Refrig. 2004, 27, 360–366. [Google Scholar] [CrossRef]
- Kumar, N.; Hirschey, J.; LaClair, T.J.; Gluesenkamp, K.R.; Graham, S. Review of stability and thermal conductivity enhancements for salt hydrates. J. Energy Storage 2019, 24, 100794. [Google Scholar] [CrossRef]
- Joint Committee for Guides in Metrology (JCGM). Evaluation of Measurement Data-Supplement 1 to the “Guide to the Expression of Uncertainty in Measurement”-Propagation of Distributions Using a Monte Carlo Method: JCGM 101:2008; Joint Committee for Guides in Metrology: Sèvres, France, 2008. [Google Scholar]
- Rubitherm Phase Change Material. n.d. Available online: https://www.rubitherm.eu/en/productCategories.html (accessed on 1 May 2025).
- ClimSel C24 Data Sheet. n.d. Available online: https://climator.com/wp-content/uploads/2024/06/Prodblad-ClimSel-C24-230816.pdf (accessed on 1 May 2025).


| Ref. | [14] | [19] | [20] | [21] | [22] | [23] | [24] |
| Method | DSC | ||||||
| Base PCM | Pure SSD | 50 wt.% SSD | 20 wt.% SSD | 82 wt.% SSD | 74.5 wt.% SSD | SSD | 93 wt.% SSD |
| Melting point suppressing agent | - | 50 wt.% Na2CO3·10H2O | 80 wt.% Na2HPO4·12H2O | 5 wt.% KCl | 10 wt.% KCl and 10 wt.% NaCl | 5% wt.% NaCl | - |
| Nucleating agent | - | - | 2.5 wt.% Na2SiO3.9H2O | 5 wt.% borax | 3 wt.% borax | - | 4 wt.% borax |
| Thickener | - | - | 30 wt.% SiO2 | 5 wt.% PAM | 1.5 wt.% CMC | CMC | 3 wt.% SPA |
| Thermal conductivity enhancer | - | - | - | 3 wt.% expanded graphite | 1 wt.% carbon | - | - |
| (°C) | 32 | 25 | 25 | 23.6 | 13.4 | 25 | 32 |
| (kJ·kg−1) | 238 | 187 | 143 | 111 | 128 | - | 227 |
| PCM type | Pure | Eutectic | Composite | ||||
| Component | Parameter | Value |
|---|---|---|
| Thermocouple | Type | K |
| Probe length (mm) | 150 | |
| Probe diameter (mm) | 1.5 | |
| Tip diameter (mm) | 0.2 | |
| Test tube | Material | Borosilicate |
| Outer diameter (mm) | 12.7 | |
| Wall thickness (mm) | 1 | |
| Length (mm) | 100 |
| Uncertainty Component | Standard Uncertainty (°C) |
|---|---|
| Reference probe accuracy | 0.015 |
| Reference readout accuracy | 0.002 |
| Reference probe drift | 0.0025 |
| Thermocouple standard deviation | 0.067 |
| External cold junction standard deviation | 0.003 |
| Standard deviation of the calibration bath | 0.002 |
| DAQ measurement accuracy | 0.02 |
| Radial temperature uncertainty | 0.02 |
| Maximum deviation in temperature from the curve fit | 0.22 |
| Composite PCM | Content | Function | % by Weight |
|---|---|---|---|
| 1E-3SPA | Anhydrous Na2SO4 | Base salt | 35.7 |
| Anhydrous borax | Nucleating agent | 2.8 | |
| NaCl | Melting point suppression | 12.0 | |
| SPA | Thickener | 3.0 | |
| Distilled water | Hydration | 46.5 | |
| 2E-3SPA | Anhydrous Na2SO4 | Base salt | 37.2 |
| Anhydrous borax | Nucleating agent | 2.8 | |
| NaCl | Melting point suppression | 9.0 | |
| SPA | Thickener | 3.0 | |
| Distilled water | Hydration | 48.0 |
| Parameter | Current Work T-History | Velez et al. [49] DSC |
|---|---|---|
| Latent heat: Solidification (kJ·kg−1) | 234 ± 4.5 | 237 |
| Solid-state specific heat (kJ·kg−1·K−1) | 2.48 ± 0.04 | - |
| Liquid-state specific heat (kJ·kg−1·K−1) | 2.38 ± 0.01 | 2.22 |
| Deviation in latent heat (%) | −1.2 | |
| Deviation in liquid-state specific heat (%) | 8 | |
| Temperature (°C) | Sample 1 | Sample 2 | Sample 3 | Average ± 95% Confidence Limit |
|---|---|---|---|---|
| Melting onset | 21.3 | 21.4 | 21.2 | 21.3 ± 0.2 |
| Melting end | 26.7 | 25.5 | 26.4 | 26.2 ± 1.3 |
| Supercooling | 12.6 | 12.9 | 12.8 | 12.8 ± 0.3 |
| Solidification | 14.2 | 14.5 | 14.0 | 14.2 ± 0.5 |
| Solidification end | 9.5 | 9.3 | 9.6 | 9.4 ± 0.3 |
| Temperature hysteresis | 7.2 | 7.0 | 7.2 | 7.1 ± 0.3 |
| Thermal Property | Sample 1 | Sample 2 | Sample 3 | Average ± 95% Confidence Limit |
|---|---|---|---|---|
| Latent heat: Melting (kJ·kg−1) | 149.5 | 140.4 | 127.4 | 139.1 ± 22.5 |
| Latent heat: Solidification (kJ·kg−1) | 100.6 | 100.5 | 100.8 | 100.6 ± 0.3 |
| Solid-phase specific heat (kJ·kg−1·K−1) | 2.9 | 2.9 | 2.9 | 2.9 ± 0.1 |
| Liquid-phase specific heat (kJ·kg−1·K−1) | 3.3 | 3.4 | 3.4 | 3.4 ± 0.1 |
| Enthalpy hysteresis (kJ·kg−1) | 50.8 | 48.7 | 37 | 45.5 ± 15.1 |
| Temperature (°C) | Sample 1 | Sample 2 | Sample 3 | Average ± 95% Confidence Limit |
|---|---|---|---|---|
| Melting onset | 21.5 | 21.4 | 21.3 | 21.4 ± 0.2 |
| Melting end | 28.0 | 28.2 | 27.5 | 27.9 ± 0.7 |
| Supercooling | 17.5 | 17.0 | 18.2 | 17.6 ± 1.3 |
| Solidification | 18.9 | 19.3 | 20.1 | 19.4 ± 1.3 |
| Solidification end | 9.7 | 9.2 | 9.8 | 9.6 ± 0.7 |
| Temperature Hysteresis | 2.6 | 2.2 | 1.2 | 2 ± 1.5 |
| Thermal Property | Sample 1 | Sample 2 | Sample 3 | Average ± 95% Confidence Limit |
|---|---|---|---|---|
| Latent heat: Melting (kJ·kg−1) | 205.5 | 162.6 | 144.7 | 170.9 ± 63.4 |
| Latent heat: Solidification (kJ·kg−1) | 123.4 | 125.5 | 120.2 | 123.0 ± 5.4 |
| Solid-phase specific heat (kJ·kg−1·K−1) | 2.53 | 3.11 | 2.74 | 2.8 ± 0.6 |
| Liquid-phase specific heat (kJ·kg−1·K−1) | 3.5 | 3.5 | 3.4 | 3.5 ± 0.1 |
| Enthalpy hysteresis (kJ·kg−1) | 80 | 62.2 | 55.3 | 65.8 ± 25.8 |
| Input Quantities | Probability Density Function (PDF) | PDF Parameters |
|---|---|---|
| Normal | Mean = 0 °C, Standard deviation = 0.23 °C | |
| Rectangular | ±0.1 g | |
| Rectangular | ±0.1 J·g−1·K−1 |
| Quantity | Estimated Value | Measurement Uncertainty |
|---|---|---|
| (kJ·kg−1·K−1) | 2.6 | ±0.3 |
| (kJ·kg−1·K−1) | 3.4 | |
| (kJ·kg−1): Heating | 241.74 | ±15 |
| (kJ·kg−1): Cooling | 183.10 | ±13 |
| Property | 1E-3SPA | 2E-3SPA |
|---|---|---|
| Melting onset temperature (°C) | 21.3 ± 0.2 | 21.4 ± 0.2 |
| Melting end temperature (°C) | 26.2 ± 1.3 | 27.9 ± 0.7 |
| Degree of supercooling (°C) | 1.6 ± 0.8 | 1.9 ± 2.6 |
| Solidification temperature (°C) | 14.2 ± 0.5 | 19.4 ± 1.3 |
| Solidification end temperature (°C) | 9.4 ± 0.3 | 9.6 ± 0.7 |
| Temperature hysteresis (°C) | 7.1 ± 0.3 | 2 ± 1.5 |
| Latent heat of fusion (kJ·kg−1) | 139 ± 22.5 | 171 ± 63.4 |
| Latent heat of crystallization (kJ·kg−1) | 101± 0.3 | 123 ± 5.4 |
| Solid-phase specific heat (kJ·kg−1·K−1) | 2.9 ± 0.1 | 2.8 ± 0.6 |
| Liquid-phase specific heat (kJ·kg−1·K−1) | 3.4 ± 0.1 | 3.5 ± 0.1 |
| Vol. energy storage density (MJ·m−3) | 230 | 282 |
| PCM | Category | PCM Data Category | Volumetric Energy Storage Density (MJ·m−3) |
|---|---|---|---|
| 1E-3SPA | Salt hydrate | Current study | 230 |
| 2E-3SPA | 282 | ||
| RT25HC [53] | Paraffin | Commercial | 204 |
| SP25E2 [53] | Salt hydrate | 288 | |
| Climsel C24 [54] | Salt hydrate | 176 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayyagari, V.; Shooshtari, A.; Ohadi, M. Glauber’s Salt Composites for HVAC Applications: A Study on the Use of the T-History Method with a Modified Data Evaluation Methodology. Materials 2025, 18, 2998. https://doi.org/10.3390/ma18132998
Ayyagari V, Shooshtari A, Ohadi M. Glauber’s Salt Composites for HVAC Applications: A Study on the Use of the T-History Method with a Modified Data Evaluation Methodology. Materials. 2025; 18(13):2998. https://doi.org/10.3390/ma18132998
Chicago/Turabian StyleAyyagari, Veeresh, Amir Shooshtari, and Michael Ohadi. 2025. "Glauber’s Salt Composites for HVAC Applications: A Study on the Use of the T-History Method with a Modified Data Evaluation Methodology" Materials 18, no. 13: 2998. https://doi.org/10.3390/ma18132998
APA StyleAyyagari, V., Shooshtari, A., & Ohadi, M. (2025). Glauber’s Salt Composites for HVAC Applications: A Study on the Use of the T-History Method with a Modified Data Evaluation Methodology. Materials, 18(13), 2998. https://doi.org/10.3390/ma18132998








