Dynamic Compressive Behavior and Fracture Mechanisms of Binary Mineral Admixture-Modified Concrete
Abstract
1. Introduction
2. Experimental Investigation
2.1. Specimen Preparation
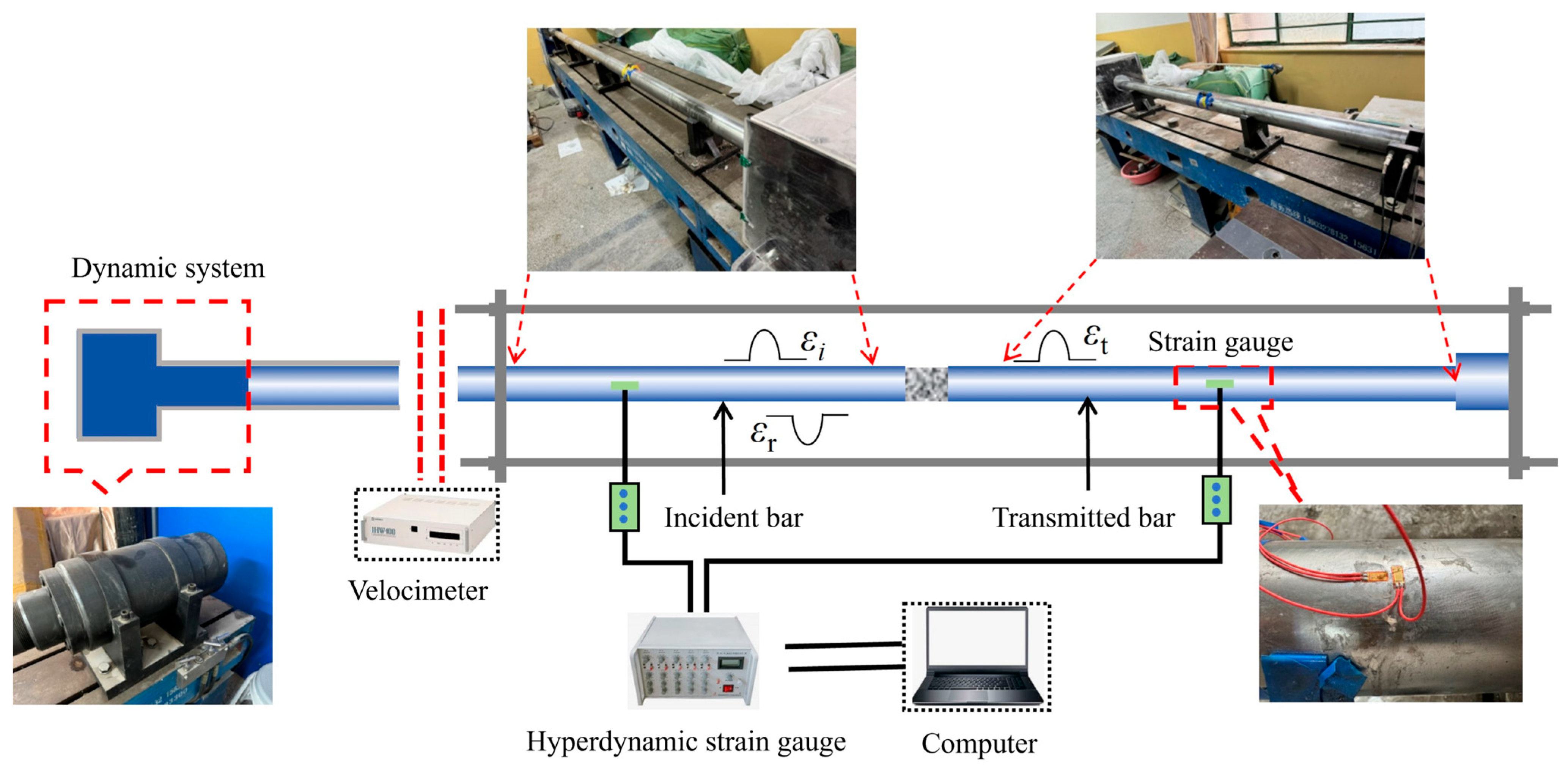
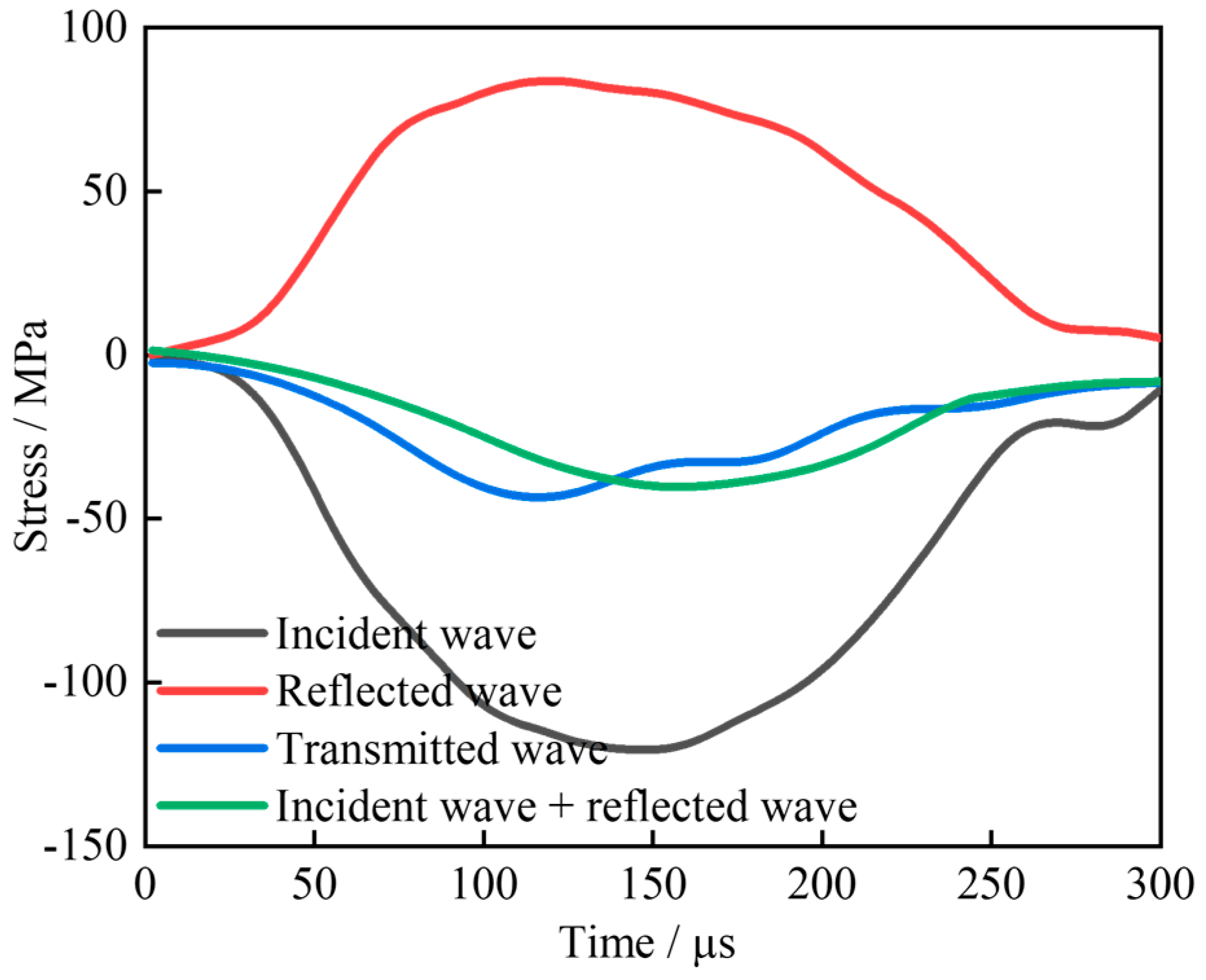
2.2. Experimental Method
3. Experimental Results
3.1. Microstructure
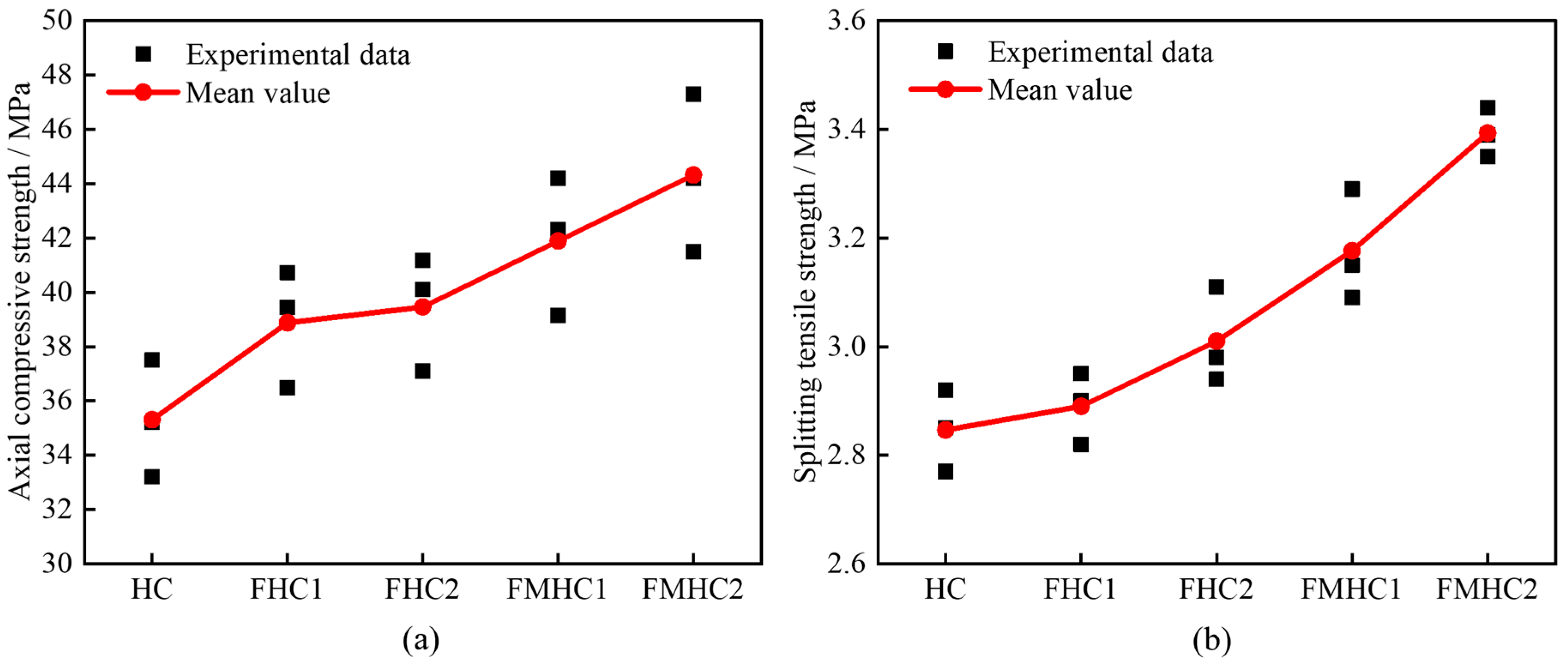
3.2. Static Test Results
3.3. Dynamics Test Results
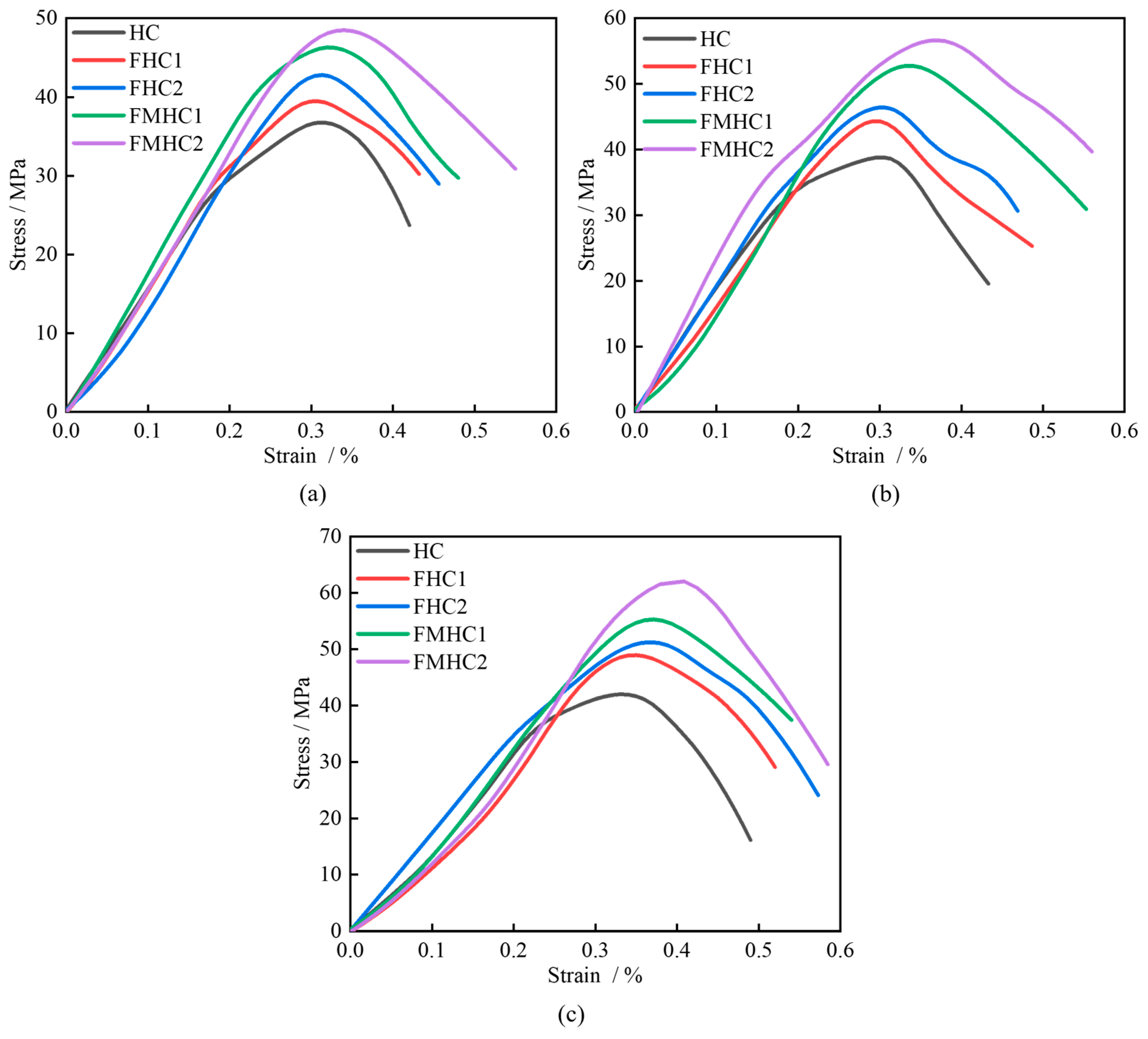
3.3.1. Dynamic Stress–Strain Curves
3.3.2. Energy Characterization
3.3.3. Damage Morphology
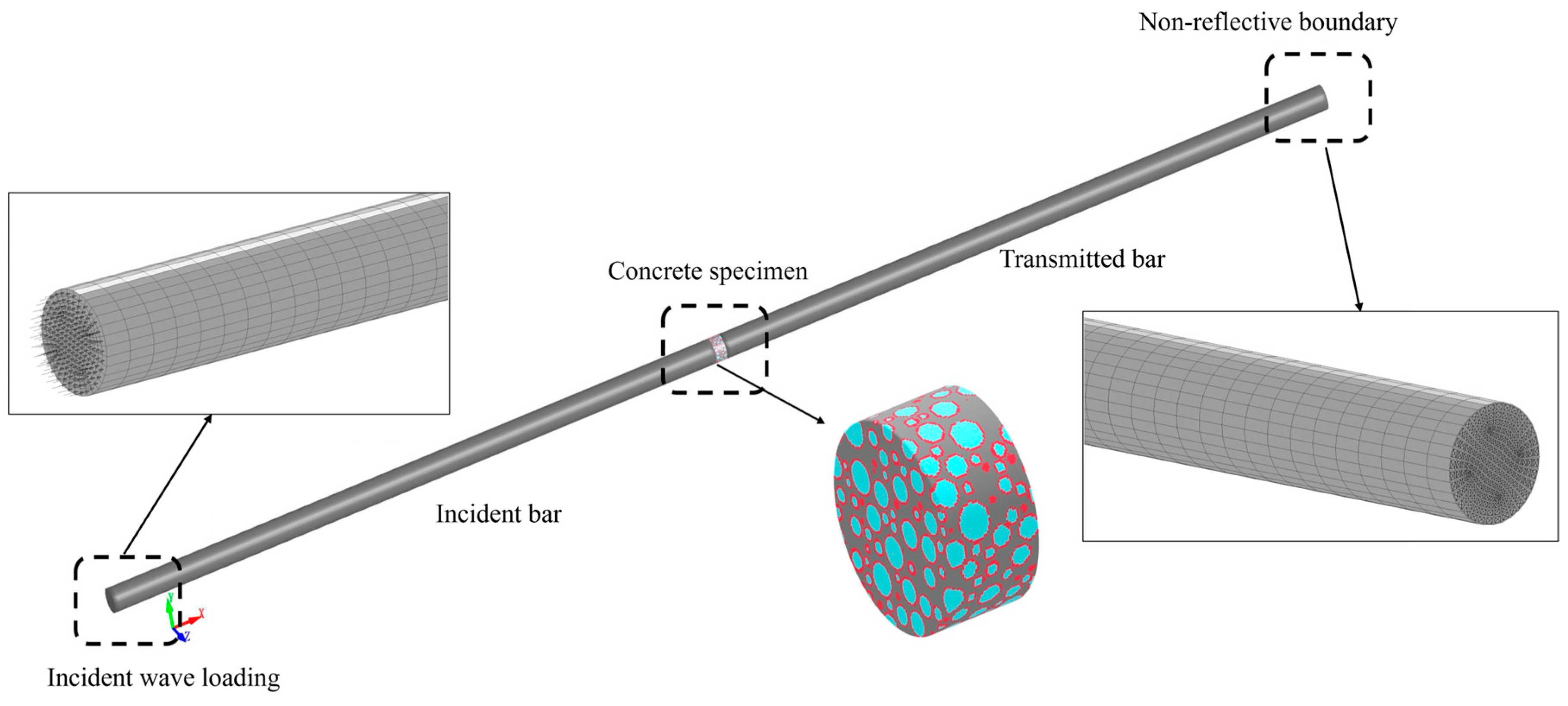
4. Numerical Simulation
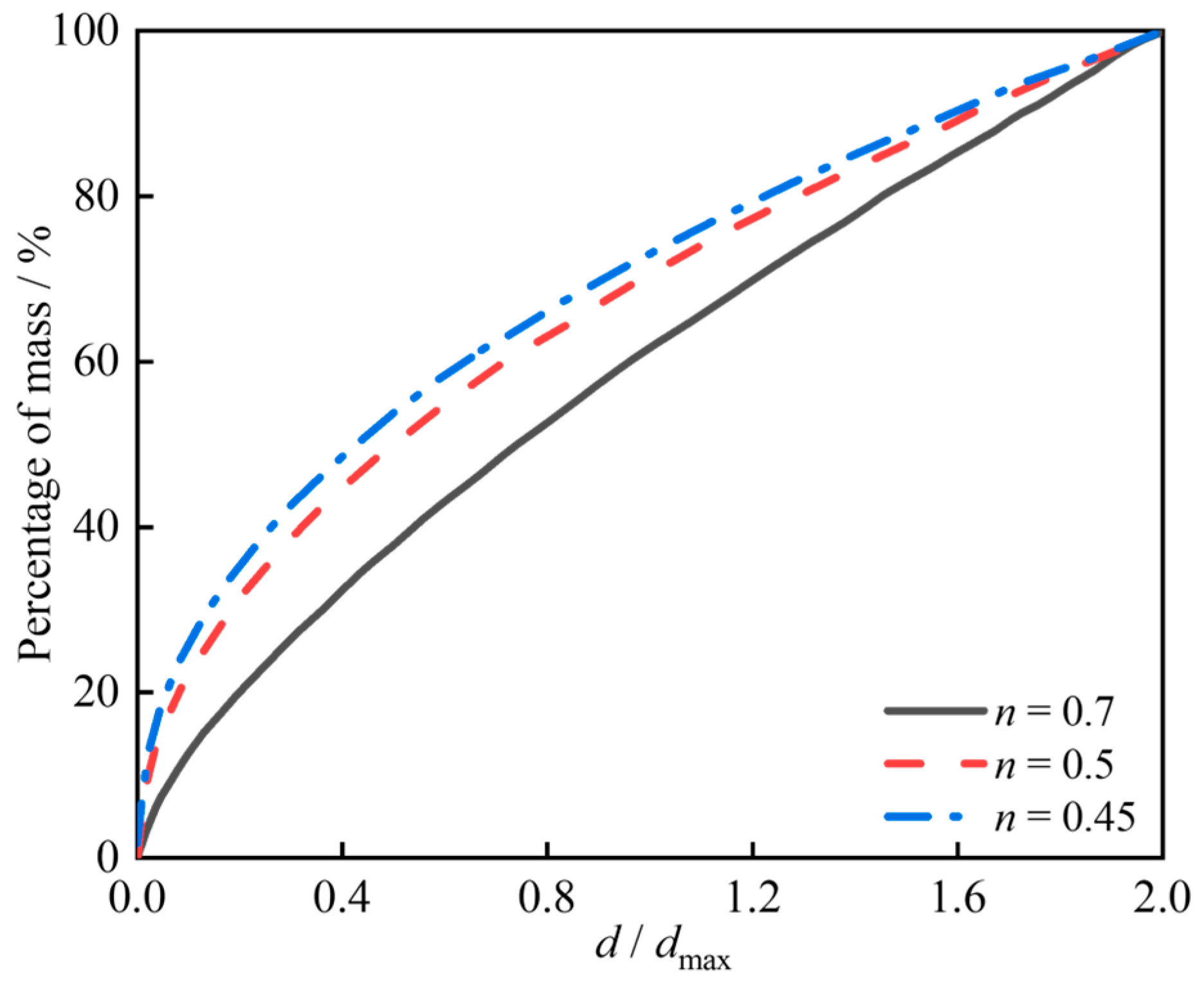
4.1. Modeling of Mesoscale Aggregates
4.2. Determination of Material Parameters
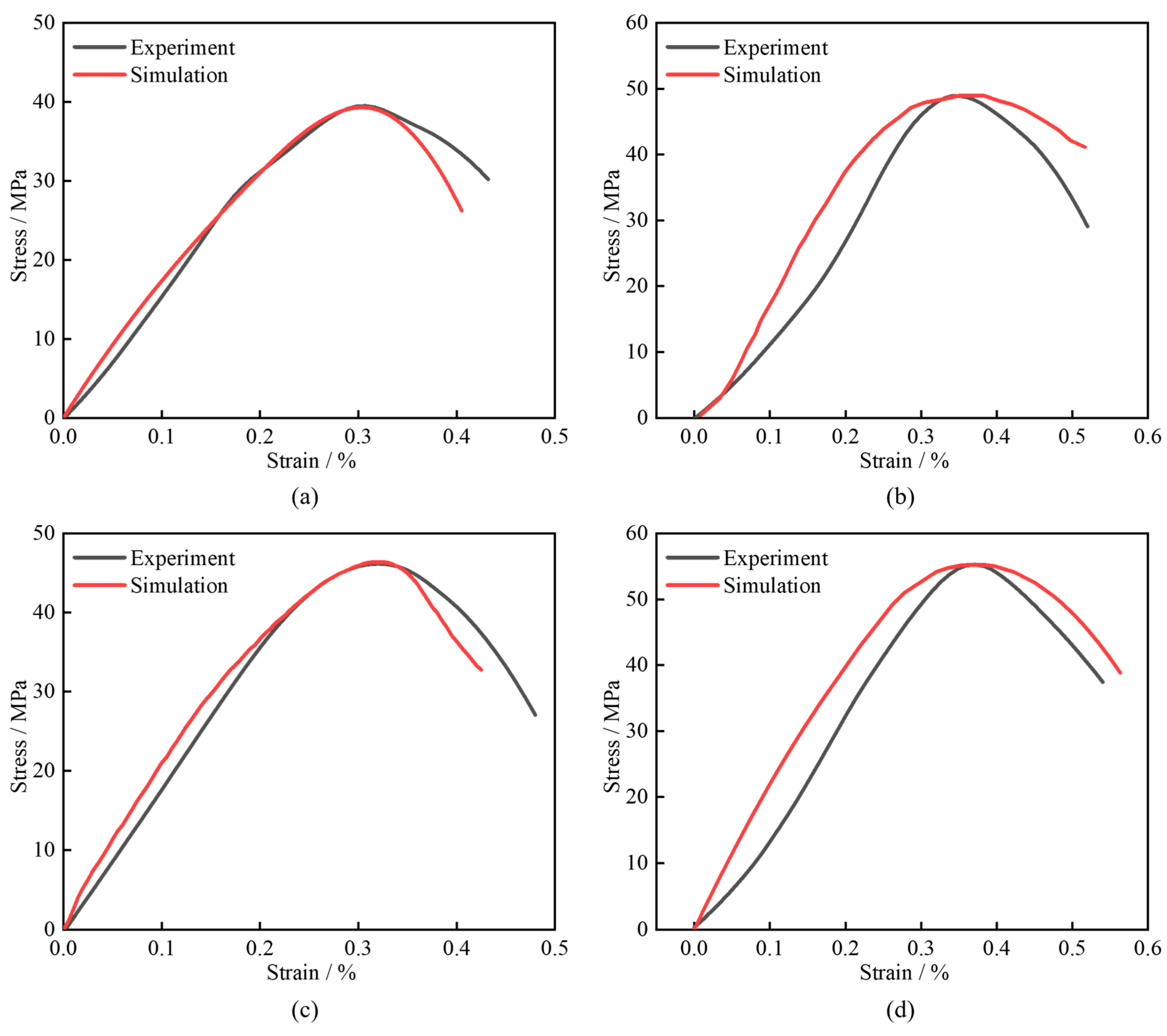
4.3. Validation of Numerical Model of SHPB
4.4. Simulation Results
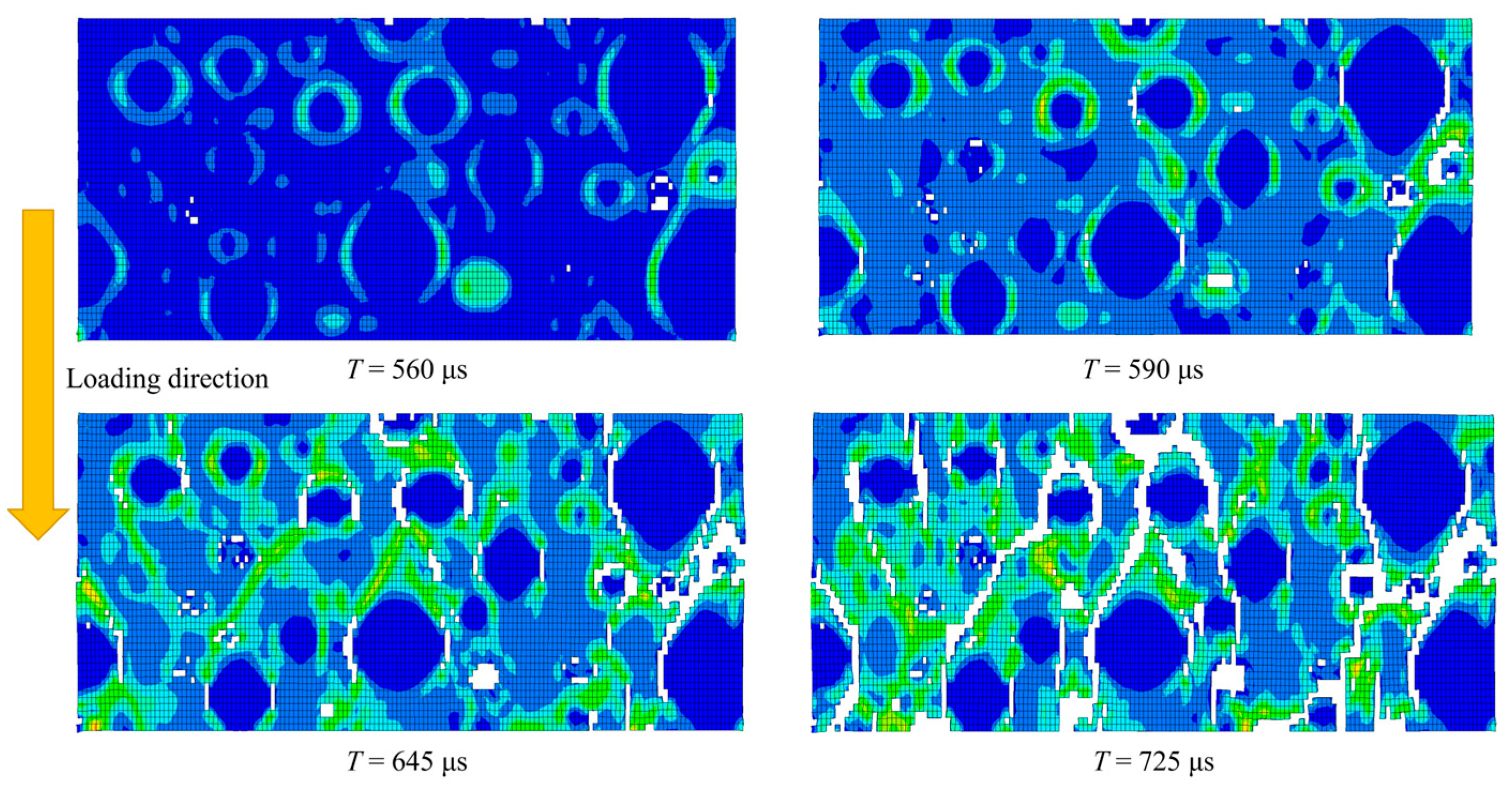
4.4.1. Damage Morphology
4.4.2. Energy Characterization
5. Discussion
6. Conclusions
- (1)
- The synergistic effect between slag powder and fly ash further optimizes the gel system structure, thereby comprehensively enhancing the stability of concrete’s internal microstructure. Concrete specimens incorporating binary mineral admixture demonstrate higher peak stresses in static compression tests and exhibit greater slopes during the elastic phase of splitting stress–strain curves. Compared to HC, the FHC1, FHC2, FMHC1, and FMHC2 specimens show respective increases of 10.11%, 11.75%, 18.63%, and 25.52% in average axial compressive strength, along with corresponding improvements of 1.40%, 5.61%, 11.58%, and 18.95% in average splitting tensile strength.
- (2)
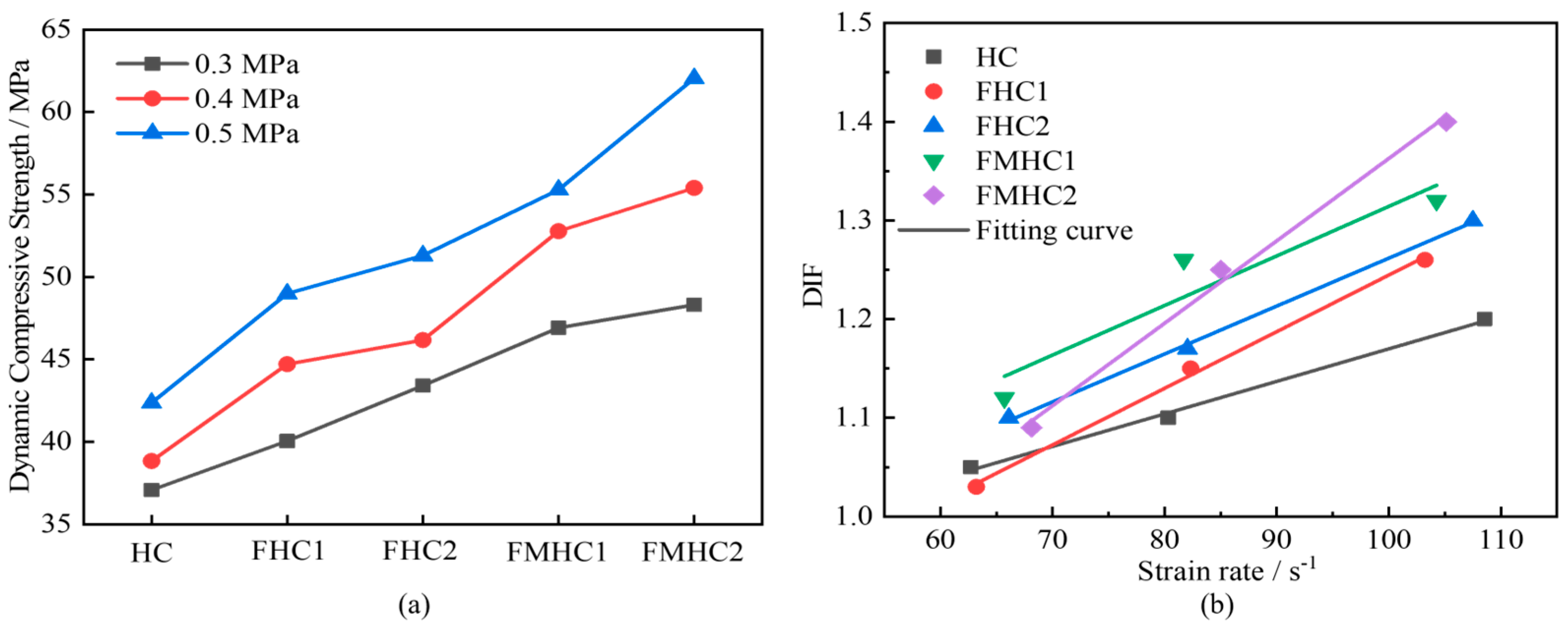
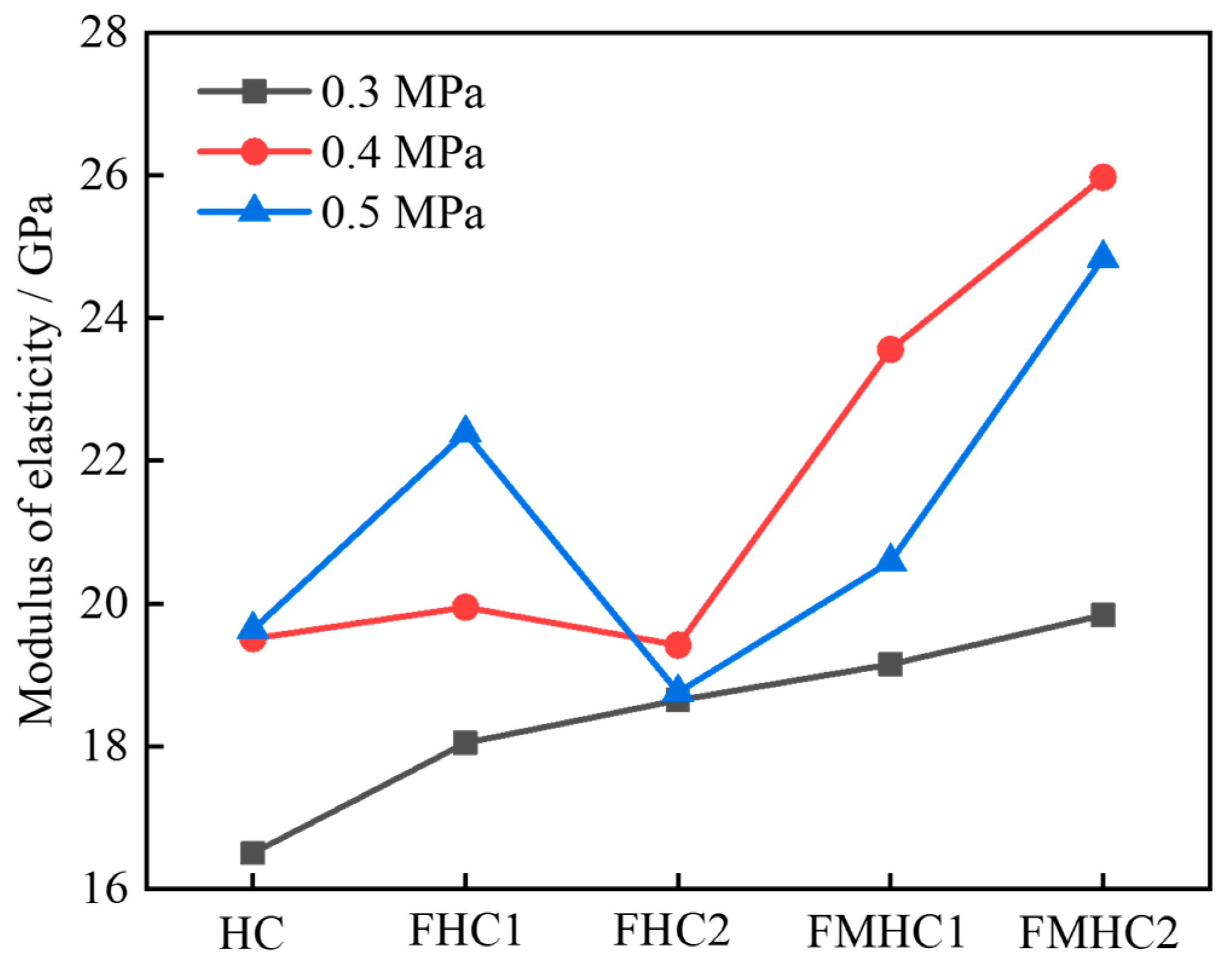
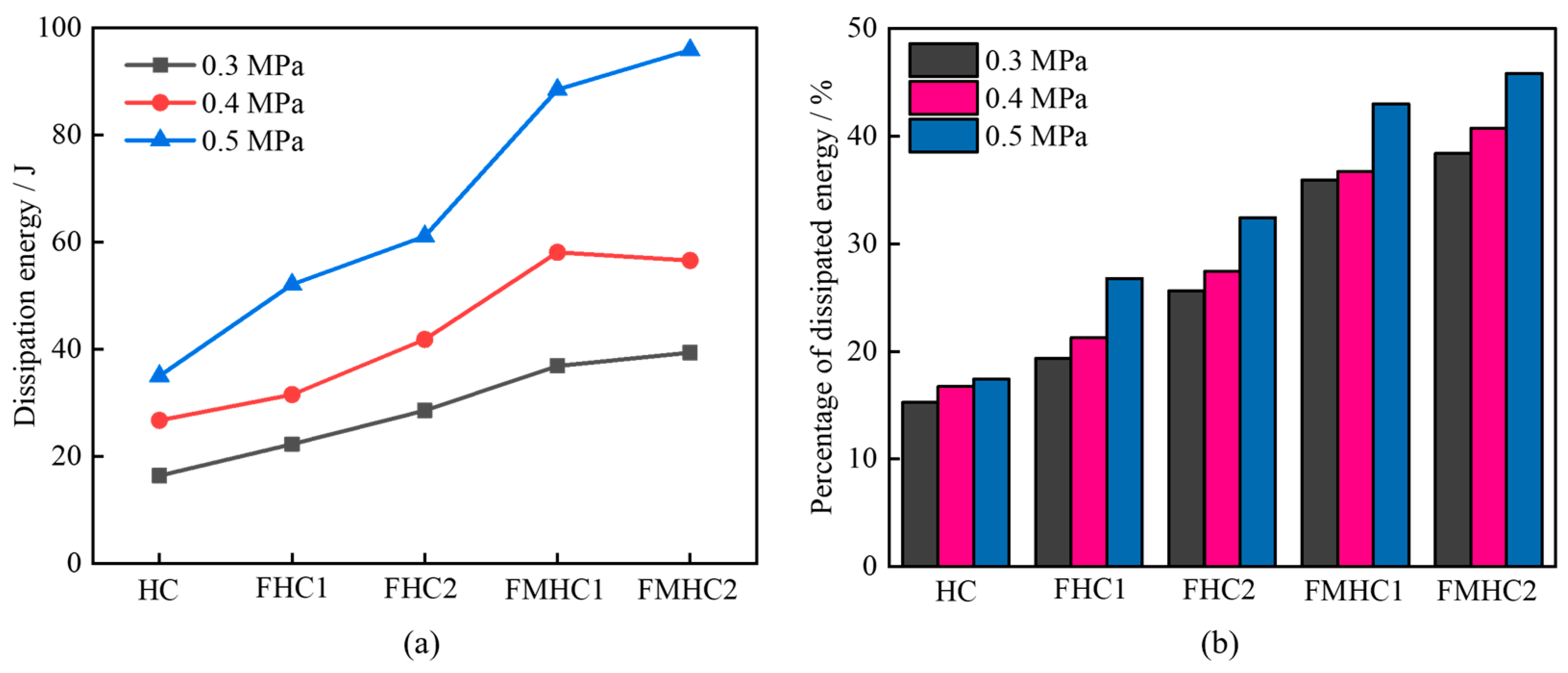
- All specimens exhibited strain rate enhancement characteristics as the strain rate increased. As the admixture approach transitioned from non-admixture to single admixture and subsequently to binary admixture, the dynamic strength, elastic modulus, and DIF of concrete increased progressively. Both the energy dissipation capacity and its proportion relative to total energy absorption showed continuous enhancement.
- (3)
- Comparative analysis demonstrates that the simulated stress–strain curves, failure modes, and fracture processes show good agreement with experimental results; this effectively verifies both the scientific validity of the mesoscale concrete model’s multiscale modeling approach and the reliability of the numerical simulations. The findings establish a robust basis for investigating critical micromechanical behaviors of concrete materials, including damage accumulation mechanisms and dynamic crack propagation laws under complex multi-field coupling conditions.
- (4)
- From an energy perspective, the mortar matrix exhibits the highest internal energy peaks, followed by the ITZ, with aggregate particles showing the lowest values. The mortar matrix and ITZ serve as primary contributors to energy dissipation under dynamic loading, whereas aggregate particles demonstrate relatively lower damage levels due to their weak internal energy absorption capacity. Compared to FHC1, FMHC1’s mesoscale structure can more effectively convert externally applied energy into stored internal energy while minimizing kinetic energy losses, thereby achieving superior dynamic compressive energy dissipation capacity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kopecskó, K.; Hajdu, M.; Khalaf, A.; Merta, I. Fresh and hardened properties for a wide range of geopolymer binders—an optimization process. Clean. Eng. Technol. 2024, 21, 100770. [Google Scholar] [CrossRef]
- Yan, G.; Hu, J.; Chen, M.; Ma, Y.; Huang, H.; Zhang, Z.; Wei, J.; Shi, C.; Yu, Q. Performance evaluation of reinforced slag-fly ash-ceramic waste powders ternary geopolymer concrete under chloride ingress environment. Constr. Build. Mater. 2025, 478, 141447. [Google Scholar] [CrossRef]
- Ge, L.; Li, H.; Xue, X.; Liu, S. Study on microstructure, mechanical properties and chloride ion binding of sea sand reactive powder concrete by multi-mineral admixture system. Powder Technol. 2025, 454, 120738. [Google Scholar] [CrossRef]
- Chang, H.; Li, C.; Wang, X.; Wang, J.; Wang, Y.; Qu, M.; Liu, J. Effect of composite mineral admixtures on self-healing properties of mortar. Mater. Rep. 2023, 37, 62–68. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Jiang, S. Early-age Cracking behavior of self-compacting concrete mixed with fly ash and slag. J. Shenyang Jianzhu Univ. (Nat. Sci.) 2022, 38, 1104–1113. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, X. Influence of steel slag-superfine blast furnace slag composite mineral admixture on the properties of mortar and concrete. Adv. Civ. Eng. 2021, 2021, 9983019. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, Q.; Zhao, Y. Study on the effect of double mineral admixtures on the properties of high water materials. J. Phys. Conf. Ser. 2024, 2720, 012018. [Google Scholar] [CrossRef]
- Zhang, N.; Fu, Q.; Wang, J.; Lu, L.; Luo, Q.; Xing, F. Compressive strength and chloride permeability of cement-based materials with high-volume compound mineral admixtures. Adv. Cem. Res. 2024, 36, 531–539. [Google Scholar] [CrossRef]
- Moghaddam, F.; Sirivivatnanon, V.; Vessalas, K. The effect of fly ash fineness on heat of hydration, microstructure, flow and compressive strength of blended cement pastes. Case Stud. Constr. Mater. 2019, 10, e00218. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, J.; Wang, L.; Liu, R.; Pang, B. Effect of fly ash with different particle size distributions on the properties and microstructure of concrete. J. Mater. Eng. Perform. 2020, 29, 6631–6639. [Google Scholar] [CrossRef]
- Dong, C.; Zong, Z.; Tang, L.; Guo, Z.; Chen, C. Mechanical properties of recycled self-compacting concrete with large volume mineral admixtures. J. Nanjing Tech Univ. (Nat. Sci. Ed.) 2023, 45, 434–443. [Google Scholar] [CrossRef]
- Luo, T.; Wang, Q.; Zhuang, S. Effects of ultra-fine ground granulated blast-furnace slag on initial setting time, fluidity and rheological properties of cement pastes. Powder Technol. 2019, 345, 54–63. [Google Scholar] [CrossRef]
- Yang, J.; Zeng, J.; He, X.; Hu, H.; Su, Y.; Bai, H.; Tan, H. Eco-friendly UHPC prepared from high volume wet-grinded ultrafine GGBS slurry. Constr. Build. Mater. 2021, 308, 125057. [Google Scholar] [CrossRef]
- Cheng, M.; Zhang, J.; Duan, X.; Zhu, J. Experimental study on mechanical properties of concrete reinforced with hybrid fiber and fly ash subjected to freeze-thaw cycles. Sci. Technol. Eng. 2020, 20, 11288–11294. [Google Scholar] [CrossRef]
- Yu, Y.; Gunasekara, C.; Elakneswaran, Y.; Robert, D.; Law, D.W.; Setunge, S. Correlating strength development with hydration characteristics for multi-blend fly ash concrete. J. Build. Eng. 2025, 13, 112076. [Google Scholar] [CrossRef]
- Duan, S.; Wu, H.; Liao, H.; Cheng, F. Design and experimental study of a blended cement containing high-volume solid waste activated ultrafine powder. Constr. Build. Mater. 2021, 303, 124–134. [Google Scholar] [CrossRef]
- Hu, H.; Wang, Z.; Shi, C.; Fan, X.; Qin, H.; Li, H. Study on properties of high-strength concrete with ultrafine mineral admixtures. Concrete 2022, 1, 106–111. [Google Scholar] [CrossRef]
- Huang, D.; Yuan, Q.; Chen, P.; Tian, X.; Peng, H. Effect of activator properties on drying shrinkage of alkali-activated fly ash and slag. J. Build. Eng. 2022, 62, 105341. [Google Scholar] [CrossRef]
- Feng, K.N.; Ruan, D.; Pan, Z.; Collins, F.; Bai, Y.; Wang, C.M.; Duan, W.H. Mechanical behavior of geopolymer concrete subjected to high strain rate compressive loadings. Mater. Struct. 2015, 48, 671–681. [Google Scholar] [CrossRef]
- Lian, C.; Wang, Y.; Liu, S.; Hao, H.; Hao, Y. Experimental study on dynamic mechanical properties of fly ash and slag based alkali-activated concrete. Constr. Build. Mater. 2023, 364, 129912. [Google Scholar] [CrossRef]
- Zou, H.; Cui, S.; Zhao, K.; Cheng, J.; Zheng, Z.; Li, S.; Zhang, Y. Dynamic mechanical properties and microstructure of ultrafine slag powder cement paste utilizing solid waste industrial tailings powder and fly ash. Process Saf. Environ. Prot. 2024, 191, 813–827. [Google Scholar] [CrossRef]
- Chen, X.; Yu, H.; Ma, H.; Wu, Z.; Fan, H.; Gao, Y.; Zhang, J.; Tu, Y.; Wu, J. 3D mesoscopic investigation on the biaxial mechanical behavior and failure criteria of coral aggregate concrete based on biaxial strength theory. Constr. Build. Mater. 2024, 451, 138920. [Google Scholar] [CrossRef]
- Guo, R.; Dong, J.; Ma, L.; Long, Z.; Xu, F.; Yin, C. Three-dimensional mesoscopic investigation on the dynamic compressive behavior of coral sand concrete with reinforced granite coarse aggregate (GCA). Compos. Struct. 2025, 352, 118650. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, C.; Yu, M.; Ran, Q.; Liu, L. Dynamic compressive behavior and energy absorption of SFRC. J. Build. Eng. 2025, 106, 112554. [Google Scholar] [CrossRef]
- Li, R.; Mu, C.; Zhang, Y.; Ma, L.; Zhou, H.; Wang, F.; Li, B.; Xie, Q. Dynamic mechanical performance of SCAC with various CCRL coarse aggregate: Experimental and numerical investigation. Constr. Build. Mater. 2025, 461, 139784. [Google Scholar] [CrossRef]
- GB/T 41054-2021; Technical Specification for High Performance Concrete. China Architecture and Building Press: Beijing, China, 2021. (In Chinese)
- Li, Z.; Zhang, X.; Liu, F.; Su, J.; Zhao, Q.; Liu, L. Effect of replacement of limestone slag powder with fly ash and direct coal liquefaction residue on the rheological properties of asphalt mastic. Constr. Build. Mater. 2024, 412, 134803. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y.; Wang, X.; Jin, Q.; Wu, Y.; Qu, Y.; Zhao, Z. Erosion resistance performance of marine concrete with red mud, slag and fly ash. Case Stud. Constr. Mater. 2025, 22, e04418. [Google Scholar] [CrossRef]
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. China Architecture and Building Press: Beijing, China, 2019. (In Chinese)
- Gutiérrez, R.; Ramírez, M.; Sánchez, S.; Santos, S. Experimental verification of the boundary conditions in the success of the Brazilian test with loading arcs. An uncertainty approach using concrete disks. Int. J. Rock. Mech. Min. 2020, 132, 104380. [Google Scholar] [CrossRef]
- Liu, L.; Cai, Y.; Chen, X.; Liang, J.; Xu, Z. Study on high temperature dynamic characteristics and mesoscopic simulation of HFRC under dynamic and static combined loading. Structures 2024, 60, 105824. [Google Scholar] [CrossRef]
- Huang, R.; Guan, Z.; Qin, J.; Wen, Y.; Lai, Z. Strain rate effect of concrete based on split Hopkinson pressure bar (SHPB) test. J. Build. Eng. 2024, 86, 108856. [Google Scholar] [CrossRef]
- Zhou, Y.; Zou, S.; Wen, J.; Zhang, Y. Study on the damage behavior and energy dissipation characteristics of basalt fiber concrete using SHPB device. Constr. Build. Mater. 2023, 368, 130413. [Google Scholar] [CrossRef]
- Fan, L.; Chen, D.; Zhong, W.; Zhang, Y. Influence of interface inclination angle and load impact velocity on dynamic splitting tensile behavior and dissipated energy of geopolymer-concrete composites. Constr. Build. Mater. 2023, 403, 133112. [Google Scholar] [CrossRef]
- Feng, S.; Zhou, Y.; Li, Q. Damage behavior and energy absorption characteristics of foamed concrete under dynamic load. Constr. Build. Mater. 2022, 357, 129340. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, W.; Gao, F.; Ge, Z.; Yang, M.; Fang, H.; Šavija, B. Rheology, shrinkage, mechanical properties and microstructure of ultra-light-weight concrete with fly ash cenospheres. J. Build. Eng. 2024, 98, 111258. [Google Scholar] [CrossRef]
- Wang, R.; Yao, Z.; Fang, Y.; Wang, J. Stat dynamic and static mechanical properties and Microstructure of frozen shaft lining imitation steel fiber reinforced concrete. Bull. Chin. Ceram. Soc. 2024, 43, 2835–2847. [Google Scholar] [CrossRef]
- Li, Q.; Mao, S.; Sun, B.; Yao, M. Experimental study on carbonization performance of concrete with large proportion of double mineral admixtures. Archit. Sci. 2024, 40, 66–71. [Google Scholar] [CrossRef]
- Cao, A.; Ma, Y.; Li, Z.; Du, X.; Li, G.; Wang, A. Study of the influence of desert sand-mineral admixture on the abrasion resistance of concrete. Materials 2025, 18, 446. [Google Scholar] [CrossRef]
- Chen, X.; Yu, H.; Ma, H.; Zhang, J.; Wu, Z.; Yue, C.; Zhang, M. 3D mesoscopic study on the triaxial compressive mechanical behavior and constitutive relationship of coral aggregate concrete. J. Build. Eng. 2025, 104, 112299. [Google Scholar] [CrossRef]
- Mao, L.; Hu, Z.; Xia, J.; Feng, G.; Azim, I.; Yang, J.; Liu, Q. Multi-phase modelling of electrochemical rehabilitation for ASR and chloride affected concrete composites. Compos. Struct. 2019, 208, 233–243. [Google Scholar] [CrossRef]
- He, J.; Mazlan, D.; Abu Bakar, B.H.; Chen, L. Difference in dynamic direct tensile failure mechanism between homogeneous mortar and three-dimensional mesoscopic concrete based on the split Hopkinson tension bar. Finite Elem. Anal. Des. 2024, 242, 104277. [Google Scholar] [CrossRef]
- Qiu, X.; Liu, X.; Hu, A.; Li, H.; Wang, Y. Research on numerical simulation of coal dynamic RHT constitutive model. J. China Coal Soc. 2024, 49, 261–273. [Google Scholar] [CrossRef]
- Liu, P.; Zhou, X.; Qian, Q.; Berto, F.; Zhou, L. Dynamic splitting tensile properties of concrete and cement mortar. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 635–856. [Google Scholar] [CrossRef]
- Wu, Z.; Fan, H.; Zhang, J.; Yu, H.; Da, B. Impact characterization of coral aggregate reinforced concrete beam: A 3D numerical study. J. Build. Eng. 2024, 91, 1109597. [Google Scholar] [CrossRef]









| SiO2 | Al2O3 | Fe2O3 | CaO | MgO | TiO2 | Na2O | SO3 | K2O | |
|---|---|---|---|---|---|---|---|---|---|
| Cement | 23.89 | 12.22 | 3.14 | 49.78 | 4.10 | 0.54 | 0.10 | 3.54 | 0.55 |
| Fly ash | 40.93 | 23.53 | 7.23 | 20.11 | 3.21 | 0.62 | 0.33 | 3.98 | 0.41 |
| Slag powder | 33.15 | 12.28 | 1.05 | 40.23 | 7.75 | 1.56 | 0.53 | 2.71 | 0.23 |
| Density (kg/m3) | Modulus of Elasticity (GPa) | Compressive Strength (MPa) | Tensile Strength (MPa) | Poisson’s Ratio |
|---|---|---|---|---|
| 2660 | 20.7 | 92.0 | 11.5 | 0.32 |
| NO. | Water | Cement | Fly Ash | Slag Powder | Fine Aggregate | Coarse Aggregate | Water/Binder Ratio |
|---|---|---|---|---|---|---|---|
| HC | 160 | 450 | 0 | 0 | 675 | 1090 | 0.36 |
| FHC1 | 160 | 360 | 90 | 0 | 675 | 1090 | 0.36 |
| FHC2 | 160 | 270 | 180 | 0 | 675 | 1090 | 0.36 |
| FMHC1 | 160 | 270 | 135 | 45 | 675 | 1090 | 0.36 |
| FMHC2 | 160 | 270 | 90 | 90 | 675 | 1090 | 0.36 |
| Test Group | Strain Rate (s−1) | Incident Energy (J) | Dissipated Energy (J) | Percentage of Dissipated Energy (%) |
|---|---|---|---|---|
| HC-0.3 | 62.72 | 107.67 | 16.42 | 15.25 |
| FHC1-0.3 | 63.21 | 115.26 | 22.29 | 19.34 |
| FHC2-0.3 | 66.11 | 111.51 | 28.58 | 25.63 |
| FMHC1-0.3 | 65.71 | 102.67 | 36.90 | 35.94 |
| FMHC2-0.3 | 68.13 | 102.56 | 39.38 | 38.40 |
| HC-0.4 | 80.32 | 160.06 | 26.75 | 16.71 |
| FHC1-0.4 | 82.33 | 148.30 | 31.54 | 21.27 |
| FHC2-0.4 | 82.05 | 152.61 | 41.86 | 27.43 |
| FMHC1-0.4 | 81.71 | 158.21 | 58.11 | 36.73 |
| FMHC2-0.4 | 85.02 | 138.91 | 56.60 | 40.75 |
| HC-0.5 | 108.56 | 200.79 | 35.02 | 17.44 |
| FHC1-0.5 | 103.24 | 194.58 | 52.11 | 26.78 |
| FHC2-0.5 | 107.51 | 188.45 | 61.13 | 32.44 |
| FMHC1-0.5 | 104.26 | 205.77 | 88.52 | 43.02 |
| FMHC2-0.5 | 105.13 | 209.13 | 95.90 | 45.86 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Compressive strength | 92.0 MPa | Failure surface parameter | 1.6 |
| Relative tensile strength | 0.13 | Failure surface parameter | 0.61 |
| Relative shear strength | 0.30 | Tensile and shear meridian | 0.68 |
| Elastic shear modulus | 8.30 GPa | Lode angle dependence factor | 0.01 |
| Compressive yield surface parameter | 0.53 | Reference compressive strain rate | 3 × 10−5 s−1 |
| Tensile yield surface parameter | 0.7 | Reference tensile strain rate | 3 × 10−6 s−1 |
| Shear modulus reduction factor | 0.50 | Critical compressive strain rate | 3 × 10−19 s−1 |
| Damage parameter | 0.04 | Critical tensile strain rate | 3 × 10−19 s−1 |
| Damage parameter | 1.0 | Compressive strain rate exponent | 0.015 |
| Minimum damaged strain | 0.01 | Tensile strain rate exponent | 0.020 |
| Residual surface parameter | 2.24 | Crush pressure | 30 MPa |
| Residual surface parameter | 0.85 | Compaction pressure | 6 GPa |
| Component | HC | FHC1 | FMHC1 |
|---|---|---|---|
| Quasi-Static Compressive Strength/(MPa) | |||
| Mortar | 30.50 | 33.75 | 38.24 |
| ITZ | 24.40 | 27.00 | 30.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bu, J.; Liu, Q.; Zhang, L.; Li, S.; Zhang, L. Dynamic Compressive Behavior and Fracture Mechanisms of Binary Mineral Admixture-Modified Concrete. Materials 2025, 18, 2883. https://doi.org/10.3390/ma18122883
Bu J, Liu Q, Zhang L, Li S, Zhang L. Dynamic Compressive Behavior and Fracture Mechanisms of Binary Mineral Admixture-Modified Concrete. Materials. 2025; 18(12):2883. https://doi.org/10.3390/ma18122883
Chicago/Turabian StyleBu, Jianqing, Qin Liu, Longwei Zhang, Shujie Li, and Liping Zhang. 2025. "Dynamic Compressive Behavior and Fracture Mechanisms of Binary Mineral Admixture-Modified Concrete" Materials 18, no. 12: 2883. https://doi.org/10.3390/ma18122883
APA StyleBu, J., Liu, Q., Zhang, L., Li, S., & Zhang, L. (2025). Dynamic Compressive Behavior and Fracture Mechanisms of Binary Mineral Admixture-Modified Concrete. Materials, 18(12), 2883. https://doi.org/10.3390/ma18122883





