Design and Performance Analysis of a Tower Solar Energy S-CO₂ Brayton Cycle Tri-Generation System

Abstract

Against the backdrop of global energy transition and increasingly severe environmental conditions, developing clean and efficient energy systems has become crucial. This study aims to investigate a solar tower receiver tri-generation (STRT) system combining supercritical CO₂ (S-CO₂) Brayton cycle and organic Rankine cycle (ORC), with the objective of achieving the production of electricity, hydrogen, and oxygen. The modeling of the STRT system is completed by using Ebsilon, and the performance of the STRT system is analyzed. The results show that the output power and efficiency of the S-CO₂ Brayton cycle are 62.29 MW and 48.3%, respectively. The net power and efficiency of ORC are 8.02 MW and 16.35%. The hydrogen and oxygen production rates of the STRT system are 183.8 kg·h⁻¹ and 1470.4 kg·h⁻¹, respectively. The STRT system shows stable and effective operation performance throughout the year. Through the exergy analysis, the exergy losses and exergy efficiencies of different components of the STRT system are obtained. The solar tower has the largest exergy loss (218.85 MW) and the lowest exergy efficiency (63%). The levelized electricity cost and the levelized hydrogen cost of the STRT system are 0.0788 USD·kWh⁻¹ and 2.97 USD·kg⁻¹ with a recovery period of 8.05 years, which reveal the economic competitiveness of the STRT system.

1. Introduction

With the development of the world economy and industry technology, energy plays an increasingly indispensable role [1]. Nowadays, in the face of increasingly severe environmental problems, traditional energy is facing great challenges [2]. At present, the main sources of energy consumed by the world are still fossil fuels, which can cause serious pollution to the environment. Therefore, environmentally friendly and efficient renewable energy sources are urgently needed to address these issues [3].

Solar energy, as a clean energy source, features abundant reserves, wide distribution, and environmental friendliness, and has remarkable advantages among many renewable energy sources [4]. Solar power generation mainly includes two types, which are concentrated solar thermal power (CSP) [5] and photovoltaic power generation [6,7]. Solar thermal power generation can not only be combined with other heat sources, but can also be integrated with thermal storage systems [8]. The supercritical CO₂ (S-CO₂) Brayton cycle, as a power generation module, is widely adopted in many future solar power systems due to its advantages such as high energy conversion efficiency, compact structure, and small footprint [9]. The solar S-CO₂ Brayton system combines solar thermal power generation with the S-CO₂ Brayton cycle, improving the comprehensive energy utilization efficiency [10].

Many studies on S-CO₂ Brayton cycles driven by CSP have been conducted. Lykas et al. [11] comprehensively studied a polygeneration system driven by both solar energy and biomass. The results showed that the energy efficiency at the optimal operation point was 37.89%, and the exergy efficiency was 20.86%. The yearly energy efficiency and exergy efficiency were 32.52% and 18.51%, respectively. Chen and Romero et al. [12] compared several solar S-CO₂ Brayton systems and optimized the system by using genetic algorithms. The results indicated that simple re-generation cycle and re-compression cycles were the most effective S-CO₂ Brayton systems when they were integrated with high-temperature CSP systems. Zaharil et al. [13] conducted a thermodynamic analysis on a solar-driven S-CO₂ Brayton cycle and desalination system. The results demonstrated that the decrease in the direct normal irradiance (DNI) would lead to a reduction in the exergy efficiency of the system, and the system had an optimal efficiency when the pressure ratio was 3.1. Liu et al. [14] conducted a comprehensive analysis of the S-CO₂ Brayton cycle and two dual pressure organic Rankine cycles (ORCs) from various perspectives. The results revealed that the total energy efficiency was 16.7%, the total exergy efficiency was 17.9%, and the recovery period was 4.38 years. Liu et al. [15] performed an advanced exergy analysis of the S-CO₂ Brayton cycle. The results indicated that half of the exergy loss of each component was caused by the interaction between the components. Xingyan et al. [16] compared and optimized four different configurations of the S-CO₂ Brayton cycles. The results indicated that the intercooling cycle exhibited the highest thermal efficiency under medium- and low-loads, while the re-heating cycle showed the highest thermal efficiency under high loads. Tafur-Escanta et al. [17] conducted an effect analysis of three various CO₂-based mixed working fluids on operation performance of CSP driven S-CO₂ Brayton cycle power plant. Results revealed that when the mixed fluid composed by CO₂ and hexane was used, the Brayton cycle with two re-heaters had the optimal operation performance, leading to a cycle efficiency of 51.3%. Nieto et al. [18] carried out economic and dynamic analyses on a tower solar collector (TSC) driven S-CO₂ Brayton cycle power system with thermo-chemical energy storage. They found that when the solar multiple was 2.6, and the discharging duration was 24 h, the power plant had the optimal performance, with an electric efficiency of 39%. Alves and Maia [19] conducted optimization works on TSC-driven S-CO₂ Brayton cycle power plants in five various areas of Brazil. Results indicated that when the gas turbine inlet temperature and thermal input were 565.0 °C and 206.8 MW, respectively, the power plant had the highest cycle efficiency, which was 48.4%.

This paper proposes a solar tower receiver tri-generation (STRT) system that combines the S-CO₂ Brayton cycle with ORC. The STRT system integrates multiple energy conversion systems to achieve the collaborative production of electric power, hydrogen, and oxygen. Electric power is generated by the S-CO₂ Brayton cycle, while hydrogen and oxygen are produced by using a proton exchange membrane water electrolyzer (PEMWE) equipment. The operation process of STRT system is simulated by using Ebsilon software (Version: Professional 13 P2), and calculations are carried out for the entire year under non-design conditions. The system performance is evaluated in terms of exergy and economy. The main purpose of this study is to provide references for the research methods and development of the S-CO₂ Brayton cycle multigeneration systems driven by solar tower. For the following contents of this paper, Section 2 presents the configuration, basic working principle, and design methods of the STRT system, simulation model, and formulas for exergy and economic analyses are introduced in Section 3, operation, exergy and economic performance evaluation results of the STRT system are presented in Section 4, and Section 5 serves as the conclusions section.

2. STRT System Design

2.1. Overall Design

The STRT system primarily consists of the TSC system, S-CO₂ Brayton cycle, and ORC driven hydrogen production (ORCHP) system. The TSC system is primarily composed of heliostats field, solar tower receiver, and two thermal energy storage tanks (TESTs), with the working fluid consisting of 67% KCl and 33% MgCl₂. The TSC system transfers heat to the S-CO₂ Brayton cycle through two main heat exchangers (MHXs). This cycle adopts re-compression and re-heat combined configuration, which maximizes the utilization of the heat supplied by the MHXs to achieve high-efficiency energy conversion and ultimately converts thermal energy into electric power output. The ORC uses hexane as the working fluid and recovers waste heat from the TSC system through an evaporator (EVA). Hexane is vaporized into steam by heating, and then drives turbine (TUB) and power generator (G2) for power generation. All the power generated by ORC is supplied to the PEMWE, where water is split into hydrogen and oxygen through an electrochemical reaction.

Figure 1 shows the working flow diagram of STRT system, where the heliostat field collects and reflects sunlight onto the receiver at the top of solar tower. The molten salt heats the S-CO₂ through high-pressure and low-pressure main heat exchangers (HP- and LP-MHXs). The molten salt, after being heated in the receiver (State 1), flows into the two MHXs (States 2 and 3), and the excess molten salt will flow into the hot heat storage (HHS) tank. Then the molten salt flows into the cold heat storage (CHS) tank after being utilized by MHXs (States 4 and 5). As the molten salt out from the LP-MHX still has a certain amount of heat, to fully utilize the heat, the molten salt is transported to the EVA (State 6) and exchanges heat with hexane before returning to the solar tower receiver (State 7). To achieve cascaded energy utilization, the high-temperature S-CO₂ does work through high-pressure and low-pressure gas turbines (HP- and LP-GTs) in turn (States 8 and 10), and then sequentially flows through various components of the S-CO₂ Brayton cycle (States 9, 11–18) before finally returning to the HP-MHX (State 19). The hexane heated by the EVA will drive the TUB (State 20), which drives G2 to produce electric power. Then, the electric power is transported to the PEMWE (State 26).

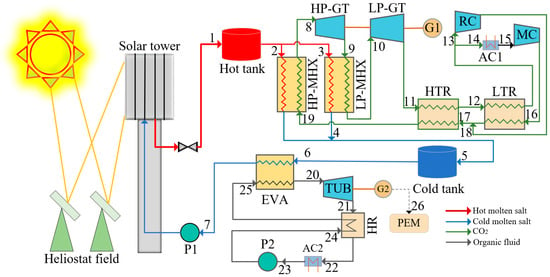
Figure 1. Abridged general view of STRT system.

2.2. TSC System

The TSC system consists of heliostat field, solar tower, molten salt pipeline, and TESTs. The heliostat field tracks the sun, reflects sunlight onto the receiver at the top of solar tower, and heats the molten salt inside the receiver. The TESTs store heat during periods of sufficient sunlight and releases heat when sunlight is insufficient, ensuring uninterrupted operation of the STRT system and a stable power supply throughout the day. Based on different energy utilization methods, the heliostat field area is divided into three parts, including the parts for S-CO₂ Brayton cycle, ORCHP system, and TESTs. The calculation formulas are shown below [20]:

$$A_{\mathrm{BC}}={\displaystyle \frac{Q_{\mathrm{BC}}}{DN{I}_{\mathrm{m}}\cdot {\eta }_{\mathrm{field}}\cdot {\eta }_{\mathrm{receiver}}\cdot {\eta }_{\mathrm{hex}1}}}$$

(1)

$$A_{\mathrm{ORC}}={\displaystyle \frac{Q_{\mathrm{ORC}}}{DN{I}_{\mathrm{m}}\cdot {\eta }_{\mathrm{field}}\cdot {\eta }_{\mathrm{receiver}}\cdot {\eta }_{\mathrm{hex}2}}}$$

(2)

$$A_{\mathrm{TSC}}={\displaystyle \frac{Q_{\mathrm{TSC}}}{DN{I}_1\cdot {\eta }_{\mathrm{field}}\cdot {\eta }_{\mathrm{receiver}}\cdot {\eta }_{\mathrm{hs}}\cdot t_{\mathrm{hs}}}}$$

(3)

$$A_{\mathrm{Total}}=A_{\mathrm{BC}}+A_{\mathrm{ORC}}+A_{\mathrm{TSC}}$$

(4)

$$M_{\mathrm{s}}={\displaystyle \frac{A_{\mathrm{Total}}}{A_{\mathrm{BC}}}}$$

(5)

where Q_BC and Q_ORC are the heat transferred from the TSC system to the S-CO₂ Brayton cycle and ORC, respectively. Q_TSC is the heat storage capacity of HHS tank under rated operation conditions. DNI_m and DNI₁ are the rated and daily average solar radiation intensities, respectively. η_field is the optical reflectivity of heliostat field. η_receiver is the heat absorption efficiency of tower solar receiver. η_hex1 is the total heat transfer efficiency of HP- and LP-MHXs. η_hex2 is the heat transfer efficiency of EVA. η_hs and t_hs are the charging efficiency and charging time of the HHS tank, respectively. A_Total is the total area of the heliostat field required by STRT system. M_s is the solar multiple. The calculation results show that A_BC, A_ORC, A_TSC and A_Total are 235,164.6 m², 101,853.9 m², 527,420.4 m², and 864,439.0 m², respectively.

The acquisition of solar energy relies on sunlight, which is affected by factors such as day/night alternation and weather conditions. Therefore, it is necessary to add TESTs to CSP plants. Currently, there are two commonly used TEST system types, which are single and double TESTs. This study adopts the double TEST system for the STRT system. The TESTs employ the mixture composed of 67% KCl and 33% MgCl₂ as the working fluid [21]. The physical properties of the mixture are [22]

$${\rho }_{\mathrm{MS}}=2363.84-0.474\cdot T$$

(6)

$${\mu }_{\mathrm{MS}}=12.0513\times {10}^{-3}-2.018\times {10}^{-5}T+1.0689\times {10}^{-8}{T}^2-1.5853\times {10}^{-10}{T}^3$$

(7)

$$k_{\mathrm{MS}}=0.26774+4.8387\times {10}^{-4}T$$

(8)

where T is the working fluid temperature. ρ_MS, μ_MS, and k_MS represent the density, dynamic viscosity, and thermal conductivity of working fluid. The constant–pressure specific heat capacity c_p,MS is taken as 1.150 kJ·(kg·K)⁻¹ at all temperatures [23].

Under the design condition, the TEST system of STRT system adopts a charging duration of 10 h and a discharging duration of 14 h. Formulas for the TEST system include

$${\eta }_{\mathrm{E}}={\displaystyle \frac{E}{Q_{\mathrm{BC}}}}$$

(9)

$${\eta }_{\mathrm{ORC}}={\displaystyle \frac{E_{\mathrm{ORC}}}{Q_{\mathrm{ORC}}}}$$

(10)

$$Q_{\mathrm{TSC}}={\displaystyle \frac{E}{{\eta }_{\mathrm{E}}\cdot {\eta }_{\mathrm{hs}}\cdot {\eta }_{\mathrm{p}}}}{t}_{\mathrm{hr}}$$

(11)

$$m_{\mathrm{MS}}={\displaystyle \frac{Q_{\mathrm{TSC}}}{C_{\mathrm{p},\mathrm{MS}}\cdot \Delta T}}$$

(12)

$$V_{\mathrm{TSC}}={\displaystyle \frac{m_{\mathrm{MS}}}{{\rho }_{\mathrm{MS}}}}$$

(13)

where E and η_E are the output power and efficiency of the S-CO₂ Brayton cycle at the design point. E_ORC and η_ORC are the net electric power and cycle efficiency of ORC at the design point. m_MS refers to the quality of working fluid in the HHS tank while ensuring stable system operation. ΔT is the temperature difference between the HHS and CHS tanks. V_TSC is the HHS tank volume. η_p is the pipeline efficiency of TSC system. t_hr is the discharging duration of HHS tank. The parameters of TESTs of the STRT system are shown in Table 1.

Table 1. Parameters of TESTs.

Parameter	Value
Hot molten salt temperature	680.0 °C
Cold molten salt temperature	474.0 °C
Working temperature difference	206.0 °C
Hot molten salt density	2041.5 kg·m−3
Cold molten salt density	1396.2 kg·m−3
Molten salt quality	2.96 × 108 kg
Heat storage quantity	7.02 × 109 kJ
HHS tank volume	1.45 × 104 m3
Charging efficiency	96.0%
Discharging efficiency	93.0%
Average heat loss	5.0%
Charging duration	10.0 h
Discharging duration	14.0 h

2.3. Brayton Cycle

The STRT system adopts an S-CO₂ Brayton cycle as the power cycle, which combines re-heating and re-compression. The re-heating process applies a staged expansion principle, dividing the expansion into two stages. Between the two expansion stages, the working fluid is re-heated by the LP-MHX using molten salt, achieving cascaded heating that improves energy utilization efficiency. The re-compression process utilizes two-stage re-generation with HTR and LTR. After coming out from the LTR, the working fluid is split into two streams, one stream of which flows directly into the HTR after passing through the RC, while the other stream enters the LTR after going through AC1 and MC. This configuration reduces the temperature difference between the hot and cold sides of the re-generators, enabling more efficient heat transfer and improving the total thermal efficiency of the cycle. Table 2 shows the relevant parameters of the S-CO₂ Brayton cycle of STRT system, and Table 3 provides some brief performance introductions of some components in the Brayton cycle. Figure 2 presents the thermophysical parameters of S-CO₂ under the operation pressure range of 20.0~24.0 MPa [24].

Table 2. Parameters of Brayton cycle.

Parameter	Value
Operation pressure of S-CO2	20.0 MPa
Inlet S-CO2 temperature of MC	32.0 °C
Splitting ratio of MC	0.52
Inlet S-CO2 pressure of MC	8.00 MPa
Mass flow rate of S-CO2	600.0 kg·s−1

Table 3. Brief performance introductions of some components in Brayton cycle.

Component	Equipment Type	Performance
GT	Axial flow turbine	Efficiency = 0.961
MC	Centrifugal compressor	Power consumption = 6320.2 kW
RC	Centrifugal compressor	Power consumption = 18,731.7 kW
HTR	Printed circuit heat exchanger	Pinch temperature difference = 20.27 K
LTR	Printed circuit heat exchanger	Pinch temperature difference = 10.86 K

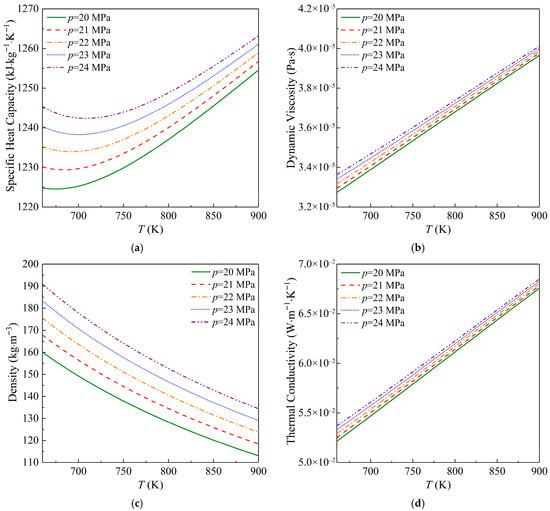
Figure 2. Thermophysical parameters of S-CO₂ under the operation pressure range of 20.0~24.0 MPa: (a) specific heat capacity, (b) dynamic viscosity, (c) density, and (d) thermal conductivity.

2.4. ORCHP System

In the STRT system, the ORCHP system generates hydrogen and oxygen through the PEMWE, and the electricity required for the operation of PEMWE is provided by ORC. In the ORC, hexane is utilized as the working fluid [25,26]. After being heated in the EVA, the working fluid expands through the TUB to drive G2 for power generation. Following heat recovery in the HR, the organic fluid sequentially passes through AC2 and P2, thereby completing a full cycle. The working pressure and mass flow rate of ORC are 4.0 MPa and 180.0 kg·s⁻¹, respectively.

Hexane is selected as the working fluid for ORC due to some of its advantages compared with other organic fluids [27]. For instance, hexane has relatively good thermodynamic properties, which can improve the overall performance of the system. Meanwhile, it belongs to dry working fluid and is not able to easily enter the wet steam zone during the expansion process, which can protect the steam turbine and effectively ensure the stable operation of the equipment. In addition, the ozone depletion potential of hexane is zero, and its global warming potential is also at a relatively low level, with a small impact on the environment. Figure 3 presents the thermophysical parameters of hexane under the operation pressure range of 3.0~4.0 MPa.

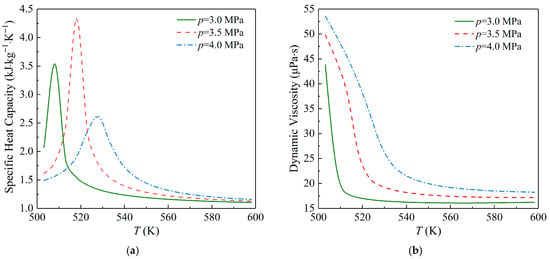
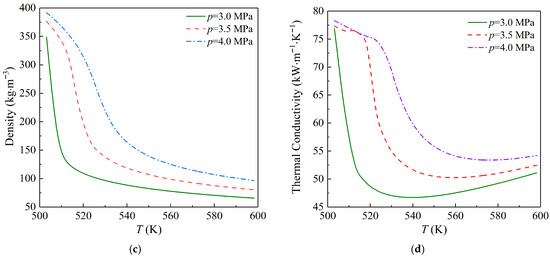
Figure 3. Thermophysical parameters of hexane under the operation pressure range of 3.0~4.0 MPa: (a) specific heat capacity, (b) dynamic viscosity, (c) density, and (d) thermal conductivity.

To address flammability and materials concerns brought by the usage of hexane, some safety measures should be adopted. For instance, inert gas should be used for protection, sealing design, and explosion-proof equipment, and a leak detection system should be adopted. Meanwhile, it is necessary to control the pinch temperature difference in the system to ensure the stability of the cycle.

3. Research Methods

3.1. Simulation Model

This study adopts Ebsilon to construct the simulation model [28]. Ebsilon is a software that can calculate and simulate various types of power generation systems based on thermodynamic principles and thermal equilibrium principles. The software can enable efficient calculations of different kinds of systems, analyze energy flow, conversion and destruction within the system, perform calculations for both design and off-design conditions, and demonstrate the operation characteristics of a system under various scenarios.

Based on the above system principles, Ebsilon (Version: Professional 13 P2) is used to simulate and model the STRT system. Figure 4 presents the STRT system model developed in Ebsilon. For simulations of the STRT system, Span–Wagner state formulas are used to calculate the enthalpy, entropy, and other parameters of CO₂, and properties of hexane are calculated by using thermodynamic models adapted to hydrocarbon working fluids in the REFPROP property database within Ebsilon. Through system simulation and calculation, the operation, exergy, and economic performances of the STRT system are investigated.

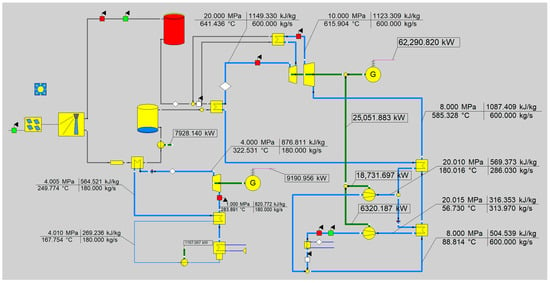
Figure 4. Simulation model of the STRT system.

To verify the quality and reliability of the Ebsilon-based model, a TSC system mentioned in Reference [29], a double-stage compressed S-CO₂ Brayton cycle mentioned in Reference [30], and an ORC mentioned in Reference [31] are used for verification. Models of the TSC system, S-CO₂ Brayton cycle, and ORC are constructed using Ebsilon, and the models are simulated with the same parameters. The simulation results are presented in Table 4. According to the results, the simulation outcomes of the Ebsilon-based models are basically consistent with the reference values in the literature, with only some components showing small discrepancies. This implies that the accuracy and reliability of Ebsilon are verified.

Table 4. Verification results of Ebsilon.

Section	Item	Referenced Value	This Work
TSC system [29]	Optical efficiency of heliostats/%	73.4	74.1
	Receiver efficiency/%	87.3	87.9
S-CO2 Brayton cycle [30]	Inlet temperature of GT/°C	500.0	500.0
	Inlet pressure of GT/MPa	20.0	20.0
	Inlet temperature of MC/°C	32.0	31.9
	Inlet pressure of MC/MPa	7.59	7.60
	Splitting ratio of RC	0.36	0.36
	Brayton cycle efficiency	39.5%	39.3%
ORC [31]	ST inlet temperature/°C	148.8	149.2
	ST inlet pressure/MPa	2.1	2.1
	Mass flow rate of working fluid/kg·s−1	60.79	60.79
	ST outlet pressure/MPa	0.4	0.4
	Output power/kW	3238.0	3235.6

3.2. Formulas for Exergy Evaluation

For the STRT system, to highlight the location where irreversibility of energy conversion occurs, the exergy loss and exergy efficiency of each component in the system are evaluated based on the second law of thermodynamics [32,33].

The formulas for calculating the exergy loss and exergy efficiency of the TSC system are

$$E_{\mathrm{x},\mathrm{TSC}}=E_{\mathrm{x},\mathrm{r}}-m_{\mathrm{TSC}}\cdot \left[\left(h_{\mathrm{b}}-h_{\mathrm{a}}\right)-T_0\cdot \left(s_{\mathrm{b}}-s_{\mathrm{a}}\right)\right]$$

(14)

$${\eta }_{\mathrm{x},\mathrm{TSC}}={\displaystyle \frac{m_{\mathrm{TSC}}\cdot \left[\left(h_{\mathrm{b}}-h_{\mathrm{a}}\right)-T_0\cdot \left(s_{\mathrm{b}}-s_{\mathrm{a}}\right)\right]}{E_{\mathrm{x},\mathrm{r}}}}$$

(15)

where E_x,r is the available energy absorbed by the TSC. m_TSC is the mass flow rate of molten salt in the TSC system. h_b and h_a are the enthalpy values at the outlet and inlet of the TSC. The ambient temperature T₀ is set to 25.0 °C. s_b and s_a are the entropy values at the outlet and inlet of solar receiver.

The exergy loss formula of an HX is

$$E_{\mathrm{x},\mathrm{hx}}=\left(E_{\mathrm{x},\mathrm{hot},\mathrm{in}}-E_{\mathrm{x},\mathrm{hot},\mathrm{out}}\right)-\left(E_{\mathrm{x},\mathrm{cold},\mathrm{in}}-E_{\mathrm{x},\mathrm{cold},\mathrm{out}}\right)$$

(16)

where E_x,hot,in and E_x,hot,out are the inlet and outlet exergies of hot fluid in the HX, and E_x,cold,in and E_x,cold,out are those of cold fluid in the HX.

The exergy loss formulas of the compressor and ST are

$$E_{\mathrm{x},\mathrm{com}}=W_{\mathrm{com}}+E_{\mathrm{x},\mathrm{com},\mathrm{in}}-E_{\mathrm{x},\mathrm{com},\mathrm{out}}$$

(17)

$$E_{\mathrm{x},\mathrm{st}}=E_{\mathrm{x},\mathrm{st},\mathrm{in}}-E_{\mathrm{x},\mathrm{st},\mathrm{out}}-W_{\mathrm{st}}$$

(18)

where W_com is the power consumption of compressor. E_x,com,in and E_x,com,out are the inlet and outlet exergies of compressor. E_x,st,in and E_x,st,out are the inlet and outlet exergies of ST. W_st is the output power of ST.

The formulas for the exergy loss and exergy efficiency of other components in the S-CO₂ Brayton cycle and ORC can be calculated as

$$E_{\mathrm{x}}={\displaystyle \sum E_{\mathrm{x},\mathrm{in}}-}{\displaystyle \sum E_{\mathrm{x},\mathrm{out}}}$$

(19)

$${\eta }_{\mathrm{x}}={\displaystyle \frac{E_{\mathrm{x},\mathrm{out}}}{E_{\mathrm{x},\mathrm{in}}}}$$

(20)

3.3. Formulas for Economic Evaluation

The economic evaluation of the STRT system is mainly based on the levelized costs, net proceeds, and recovery period [34]. Levelized electricity cost (LEC) is

$$LEC={\displaystyle \frac{R\cdot C_{\mathrm{BC}}+C_{\mathrm{BC},\mathrm{th}}+OM{C}_{\mathrm{F}}}{E_{\mathrm{yearly}}}}+OM{C}_{\mathrm{V}}$$

(21)

where R is the discount rate. C_BC and C_BC,th are the component costs and thermal costs of the S-CO₂ Brayton cycle, respectively. OMC_F and OMC_V are fixed and variable operating and maintenance costs for the S-CO₂ Brayton cycle and TSC system. E_yearly is the power generation of the S-CO₂ Brayton cycle every year.

The levelized hydrogen cost (LHC) is

$$LHC={\displaystyle \frac{C_{\mathrm{ORC}}+C_{\mathrm{ORC},\mathrm{th}}+C_{\mathrm{ORC},\mathrm{op}}}{t_{\mathrm{ser}}\cdot M_{\mathrm{h},\mathrm{yearly}}}}$$

(22)

where C_ORC and C_ORC,th are the component costs and thermal costs of ORCHP system. C_ORC,op is the operation costs of ORC. t_ser is the service life of STRT system. M_h,yearly is the hydrogen production of STRT system every year.

For cost calculations of typical items of STRT system, formulas are presented in Table 5 [35,36]. In Table 5, H_hx, H_reg, and H_cooler are conductance values of the heat exchanger, re-generator, and pre-cooler. W_tur is the output power of GT. W_com and P_pemwe are the power consumptions of the compressor and PEMWE, respectively. h_tow is the height of the solar tower. C_employee is the average salary. N_employee is the number of employees. α is the welfare coefficient. C_fuel is the fuel costs, which is 0.0 for the STRT system. C₁, C₂, and C₃ are the cost coefficients of the heliostats, molten salt, and TEST system, respectively.

Table 5. Some detailed cost calculation formulas [34,35].

Item	Formula
Heat exchanger	$C_{\mathrm{hx}}=3500\cdot H_{\mathrm{hx}}$	(23)
GT	$C_{\mathrm{tur}}=7790\cdot {(W_{\mathrm{tur}})}^{0.6842}$	(24)
Re-generator	$C_{\mathrm{reg}}=1250\cdot H_{\mathrm{reg}}$	(25)
Compressor	$C_{\mathrm{com}}=6898\cdot {(W_{\mathrm{com}})}^{0.7856}$	(26)
Pre-cooler	$C_{\mathrm{cooler}}=2300\cdot H_{\mathrm{cooler}}$	(27)
Heliostats	$C_{\mathrm{hel}}=C_1\cdot A_{\mathrm{Total}}$	(28)
Solar tower	$C_{\mathrm{tower}}=0.78232\times {10}^6\exp (0.01130\cdot h_{\mathrm{tow}})$	(29)
TEST	$C_{\mathrm{tsc}}=C_3\cdot V_{\mathrm{TSC}}$	(30)
Heat transfer fluid	$C_{\mathrm{ms}}=C_2\cdot M_{\mathrm{MS}}$	(31)
PEMWE	$C_{\mathrm{pemwe}}=1000\cdot P_{\mathrm{pemwe}}$	(32)
Fixed operating and maintenance costs	$OM{C}_{\mathrm{F}}=C_{\mathrm{fix}}+C_{\mathrm{fuel}}+C_{\mathrm{operation}}$	(33)
Fixed maintenance costs	$C_{\mathrm{fix}}=1\%\left(C_{\mathrm{BC}}+C_{\mathrm{ORC}}\right)$	(34)
Employee costs	$C_{\mathrm{operation}}=C_{\mathrm{employee}}\cdot N_{\mathrm{employee}}\cdot \left(1+\alpha \right)$	(35)

Table 5. Some detailed cost calculation formulas [34,35].

Item	Formula
Heat exchanger	$C_{\mathrm{hx}}=3500\cdot H_{\mathrm{hx}}$	(23)
GT	$C_{\mathrm{tur}}=7790\cdot {(W_{\mathrm{tur}})}^{0.6842}$	(24)
Re-generator	$C_{\mathrm{reg}}=1250\cdot H_{\mathrm{reg}}$	(25)
Compressor	$C_{\mathrm{com}}=6898\cdot {(W_{\mathrm{com}})}^{0.7856}$	(26)
Pre-cooler	$C_{\mathrm{cooler}}=2300\cdot H_{\mathrm{cooler}}$	(27)
Heliostats	$C_{\mathrm{hel}}=C_1\cdot A_{\mathrm{Total}}$	(28)
Solar tower	$C_{\mathrm{tower}}=0.78232\times {10}^6\exp (0.01130\cdot h_{\mathrm{tow}})$	(29)
TEST	$C_{\mathrm{tsc}}=C_3\cdot V_{\mathrm{TSC}}$	(30)
Heat transfer fluid	$C_{\mathrm{ms}}=C_2\cdot M_{\mathrm{MS}}$	(31)
PEMWE	$C_{\mathrm{pemwe}}=1000\cdot P_{\mathrm{pemwe}}$	(32)
Fixed operating and maintenance costs	$OM{C}_{\mathrm{F}}=C_{\mathrm{fix}}+C_{\mathrm{fuel}}+C_{\mathrm{operation}}$	(33)
Fixed maintenance costs	$C_{\mathrm{fix}}=1\%\left(C_{\mathrm{BC}}+C_{\mathrm{ORC}}\right)$	(34)
Employee costs	$C_{\mathrm{operation}}=C_{\mathrm{employee}}\cdot N_{\mathrm{employee}}\cdot \left(1+\alpha \right)$	(35)

The net proceeds of the STRT system are

$$C_{\mathrm{np}}=t_{\mathrm{ser}}\times \left[\left(P_{\mathrm{E}}-LEC\right)\times E_{\mathrm{yearly}}+\left(P_{\mathrm{h}}-LHC\right)\times M_{\mathrm{h},\mathrm{yearly}}+P_{\mathrm{o}}\times M_{\mathrm{o},\mathrm{yearly}}\right]$$

(36)

where P_E, P_h, and P_o are the selling prices of electricity, hydrogen, and oxygen, respectively. M_o,yearly is the oxygen production of the STRT system every year.

The cost recovery period of STRT system is

$$R_{\mathrm{rec}}={\displaystyle \frac{C_{\mathrm{Total}}}{C_{\mathrm{np}}}}$$

(37)

where C_Total represents the total investment cost of the STRT system.

4. Results and Discussion

4.1. Operation Simulation Results

4.1.1. Design Conditions

Based on the STRT system model constructed in Ebsilon, under design conditions, DNI_m is 900.0 W·m⁻². the external temperature is 25.0 °C, and the atmospheric pressure is 0.101 MPa. The operation process of the STRT system is simulated and calculated under design operation conditions. Table 6 shows the simulation results of the STRT system.

Table 6. Simulation results of STRT system under design conditions.

Item	Value
S-CO2 mass flow rate	600.0 kg·s−1
Inlet pressure of high-pressure GT	20.0 MPa
Inlet pressure of MC	8.0 MPa
Inlet temperature of high-pressure GT	641.4 °C
Inlet temperature of MC	32.00 °C
Power consumed by MC	6.32 MW
Power consumed by RC	18.73 MW
Output power of Brayton cycle	62.29 MW
Heat transfer in MHX	128.97 MW
Brayton cycle efficiency	48.3%
Splitting ratio of MC	0.52
Inlet temperature of ORC TUB	322.5 °C
Inlet pressure of ORC TUB	4 MPa
Mass flow rate of hexane	180 kg·s−1
Net power of ORC	8.02 MW
ORC efficiency	16.35%
Hydrogen production rate	183.8 kg·h−1
Oxygen production rate	1470.4 kg·h−1

Results show that under design conditions, the electric power of the S-CO₂ Brayton cycle is 62.29 MW, with a cycle efficiency of 48.3%. The ORC, serving as the bottoming cycle for the entire system, recovers the waste heat from the S-CO₂ Brayton cycle. Its net power is 8.02 MW, and its cycle efficiency is 16.35%. All the electricity generated by ORC is transported to PEMWE to produce hydrogen and oxygen, with a hydrogen production rate of 183.8 kg·h⁻¹ and an oxygen production rate of 1470.4 kg·h⁻¹.

The results of this paper are compared with those of other multigeneration systems, and the comparison results are shown in Table 7. In Table 7, normalized parameters are obtained through dividing production rates or output power by the total solar concentrator field area of each multigeneration system. Due to the differences in the structures, principles, and unit capacities of these multigeneration systems, their product categories and normalized production capacities are also different.

Table 7. Comparison of this work and some other typical solar multigeneration systems.

Reference	Solar Collector	Normalized Water Production Rate	Normalized Hydrogen Production Rate	Normalized Output Power	Brayton Cycle Efficiency
This work	Solar tower	--	2.13 × 10−4 kg·h−1·m−2	7.21 × 10−5 MW·m−2	0.483
Bozgeyik et al. (2022, [37])	Parabolic trough	1.57 × 10−3 t·h−1·m−2	5.59 × 10−4 kg·h−1·m−2	--	--
Abbaspour et al. (2024, [38])	Solar tower	--	2.36 × 10−3 kg·h−1·m−2	5.63 × 10−5 MW·m−2	--
Shabani et al. (2024, [39])	Parabolic trough	1.19 × 10−3 t·h−1·m−2	7.78 × 10−4 kg·h−1·m−2	3.05 × 10−5 MW·m−2	0.501
Wang et al. (2021, [40])	Solar tower	4.26 × 10−4 t·h−1·m−2	--	5.38 × 10−5 MW·m−2	0.366

4.1.2. Off-Design Conditions

To analyze the operation characteristics of the STRT system under actual weather conditions, the system is simulated throughout the year based on the changes in daily DNI. There can be many different operation strategies for a certain solar multigeneration system, and the operation strategy for the STRT system in this study is as follows:

(1)

During the period of 7:00 to 17:00, when the DNI is sufficient, the Brayton cycle and ORCHP system operate at 100% rated level. In the case of insufficient DNI, the two systems operate at 50% rated level if the working fluid level state in the HHS tank can be in 2.0%~98.0%.

(2)

During the period of 17:00 to 7:00, when the working fluid level state in the HHS tank can be in 2.0%~98.0%, the Brayton cycle and ORCHP system operated at 50% rated level.

(3)

When the working fluid level state in the HHS tank is in 2.0%~98.0%, if there is excess solar radiation, the HHS tank should be charged, and if the solar heat is insufficient, the HHS tank should be discharged. When the working fluid level state in the HHS tank is greater than or equal to 98.0%, the HHS tank should not be charged even if there is excess solar radiation, so that the pressure in the HHS tank does not exceed the limit. When the working fluid level state in the HHS tank is smaller than or equal to 2.0%, the HHS tank should not be discharged.

(4)

When both the DNI and the working fluid in the HHS tank are insufficient simultaneously, the STRT system stops running. Here, insufficient working fluid in the HHS tank refers to that the working fluid level state in the HHS tank is smaller than or equal to 2.0%.

Based on the operation strategy and actual sunlight data, a year-round simulation of the STRT system is conducted. The DNI and temperature data are selected from a typical year in Lanzhou City (36°03′ N, 103°49′ E) of China. Figure 5 shows the normalized simulation results of the STRT system for seven consecutive days in February. Results show that during days with sufficient DNI, the electric power and hydrogen production rate of the STRT system remain at 62.29 MW and 183.8 kg·h⁻¹. During days and nights when DNI is low and the working fluid in the HHS tank is sufficient, the output powers of the Brayton cycle and ORC are 50% of the rated level. When the solar radiation and working fluid are both insufficient, the STRT system is shut down. The working fluid level in the HHS tank is jointly affected by DNI and heat consumed by the STRT system. Therefore, it is concluded that the TSC system, S-CO₂ Brayton cycle, and ORCHP system are able to achieve long-term stable operation under the formulated operation strategy.

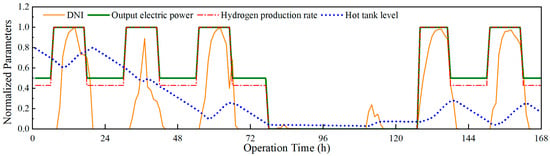
Figure 5. Simulation results of operation process of STRT system for seven consecutive days.

Table 8 and Figure 6 show the operation results of STRT system for electric power, hydrogen, and oxygen productions in a year. W_e,BC represents the electric power generation of the Brayton cycle. W_e,ORC represents the net power generation of ORC. And M_h,ORC and M_o,ORC represent the hydrogen and oxygen productions of the ORCHP system. Results show that the whole system produces the highest amounts of electricity, hydrogen and oxygen in July, which are 32,835.43 MWh, 82,503.17 kg and 660,025.35 kg, respectively. For the whole year, the power output of STRT system is 371,069.12 MWh, and the hydrogen and oxygen productions are 939,295.7 kg and 7,514,365.57 kg. These data basically match the evaluation results of STRT system under design operating conditions.

Table 8. Annual operation performance of STRT system.

Month	We,BC/MWh	We,ORC/MWh	Mh,ORC/kg	Mo,ORC/kg
Jan.	31,280.34	4177.38	79,032.29	632,258.33
Feb.	24,348.37	3243.64	64,989.78	519,918.25
Mar.	30,136.53	3972.04	73,982.29	591,858.31
Apr.	31,900.22	4181.73	79,776.76	638,214.08
May.	32,769.23	4357.47	82,489.17	659,913.35
Jun.	31,466.18	4184.51	79,780.20	638,241.57
Jul.	32,835.43	4366.27	82,503.17	660,025.35
Aug.	32,266.08	4295.50	81,548.68	652,389.42
Sep.	31,370.15	4171.74	79,778.20	638,225.57
Oct.	31,398.34	4189.89	79,639.69	637,117.56
Nov.	30,572.99	4075.52	77,871.21	622,969.71
Dec.	30,725.27	4109.26	77,904.26	623,234.05
Annual	371,069.12	49,324.96	939,295.70	7,514,365.57

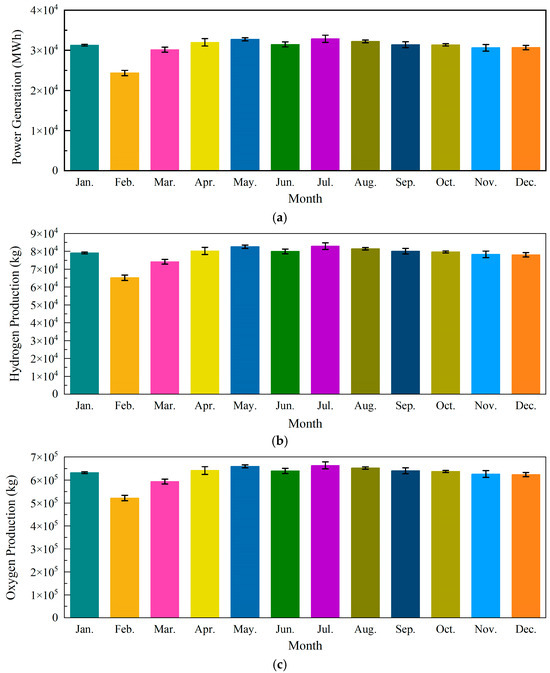
Figure 6. Annual operation performance of STRT system: (a) W_e,BC, (b) M_h,ORC, and (c) M_o,ORC.

4.2. Exergy Evaluation Results

In the exergy evaluation of STRT system, based on the second law of thermodynamics, the exergy losses and exergy efficiencies of various components in the STRT system are analyzed using the equations of Section 3.2 as well as Ebsilon. Results are shown in Figure 7 and Table 9.

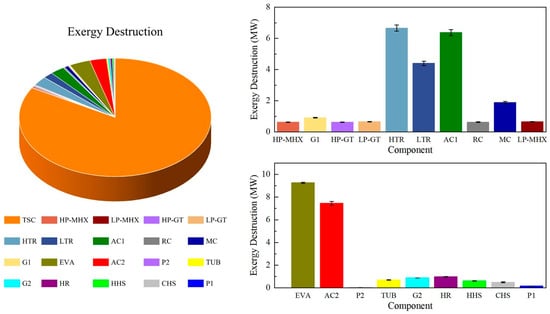
Figure 7. Exergy loss distribution of STRT system.

Table 9. Exergy performance of STRT system.

Item	Value
	Exergy Loss	Exergy Efficiency
TSC	218.85 MW	62.5%
HP-MHX	0.62 MW	99.4%
LP-MHX	0.65 MW	99.4%
HP-GT	0.62 MW	98.5%
LP-GT	0.65 MW	98.3%
HTR	6.66 MW	97.5%
LTR	4.40 MW	95.0%
AC1	6.37 MW	90.3%
RC	0.63 MW	99.0%
MC	1.89 MW	99.0%
G1	0.91 MW	98.7%
EVA	9.25 MW	72.9%
AC2	7.42 MW	84.3%
TUB	0.70 MW	93.1%
G2	0.88 MW	91.3%
HR	0.97 MW	98.0%
HHS	4.25 MW	74.0%
CHS	3.15 MW	74.00%
P1	0.16 MW	99.8%
Total	269.04 MW	22.3%

Table 9 shows the exergy losses and exergy efficiencies of typical components of STRT system. HHS, CHS, and P1 represent the HHS tank, CHS tank, and pump in the TSC system, respectively. Results show that the TSC has the largest exergy loss (218.85 MW). At the same time, it has an exergy efficiency of only 63%, which is also the lowest. The large exergy loss in the TSC is mainly brought by two aspects, which are the optical loss of TSC, and thermal conduction, radiation, and convection heat losses of the solar tower. To decrease the exergy loss of the TSC, the design and structural materials of the TSC should be improved. For instance, heliostat material with higher reflectance should be utilized, and TSC tube materials with larger absorptance should be developed. EVA has the second highest level of exergy loss (9.25 MW), while AC1 and AC2 have similar levels of exergy losses (i.e., 6.37 MW and 7.42 MW). Hence, there is certain potential for improvement in energy utilization for these components.

4.3. Economic Evaluation Results

The economic evaluation of STRT system is based on the theoretical framework of levelized cost of energy. Under this framework, a dynamic discount analysis is conducted on STRT system with considering fixed investment cost, operation and maintenance cost, thermal cost, and equipment depreciation cost. The economic evaluation of the STRT system mainly calculates the levelized costs, net proceeds, and recovery period. Table 10 shows some initial parameters for the economic evaluation. For the whole system, the discount rate is 0.1, the external power required for the ORCHP system is 0.0. The service life of STRT system is 25 years. Table 11 shows the economic evaluation results.

Table 10. Parameters for economic analysis of STRT system.

Section	Item	Value
Solar power section	Eyearly	379,449.98 MWh
	CBC	86,284,335.8 USD
	CBC,th	121,035,302.4 USD
	OMCF	7,661,542.4 USD
	OMCV	0.004 USD·kWh−1
ORC section	Mh,yearly	1,008,782.9 kg
	Mo,yearly	8,070,263.8 kg
	CORC,th	52,422,514.8 USD
	CORC	22,527,466.4 USD

Table 11. Results for economic evaluation of STRT system.

Item	Value
LEC	0.0788 USD·kWh−1
LHC	2.97 USD·kg−1
Net proceeds of selling electricity	810,672,651.9 USD
Net proceeds of selling hydrogen and oxygen	89,279,886.0 USD
Recovery period	8.05 years

Results reveal that LEC of STRT system is 0.0788 USD·kWh⁻¹, and LHC is 2.97 USD·kg⁻¹. A review of the literature [41] shows that the cost of hydrogen production from electrolytic water in the United States ranges from 2.0 USD·kg⁻¹ to 12.0 USD·kg⁻¹. Those indicate that LHC of STRT system is relatively reasonable and economically competitive. The net proceeds and recovery period of STRT system are calculated when the selling prices of electricity, hydrogen, and oxygen are chosen to be 0.164 USD·kWh⁻¹, 6.00 USD·kg⁻¹, and 0.064 USD·kg⁻¹, respectively. According to the economic evaluation, the net proceeds of selling electricity is about 8.11 × 10⁸ USD, and that of selling hydrogen and oxygen is about 8.93 × 10⁷ USD. The recovery period of the entire STRT system is 8.05 years.

5. Conclusions

To contribute to the goal of achieving carbon peaking and carbon neutrality, this study proposes a novel STRT system utilizing the S-CO₂ Brayton cycle and ORC, which is designed to produce electric power, hydrogen, and oxygen. The STRT system consists of the TSC system, S-CO₂ Brayton cycle, and ORC powered hydrogen production system. By using Ebsilon, evaluations of operation, exergic, and economic performances are conducted for the STRT system. Main results are concluded as follows:

(a)

The operation simulation results reveal that the S-CO₂ Brayton cycle has an electric power of 62.29 MW and a cycle efficiency of 48.29%. Hydrogen and oxygen production rates of the STRT system are 183.8 kg·h⁻¹ and 1470.4 kg·h⁻¹, respectively. The STRT system can achieve long-term and stable operation.

(b)

The exergy analysis results show that the TSC had the highest exergy loss of 218.85 MW and the lowest exergy efficiency of 63%. The overall exergy efficiency of the STRT system is 25%.

(c)

The economic analysis shows that the levelized electricity and hydrogen costs of the STRT system are 0.0788 USD·kWh⁻¹ and 2.97 USD·kg⁻¹, respectively. The net proceeds of selling electricity and selling hydrogen and oxygen are 8.11 × 10⁸ USD and 8.93 × 10⁷ USD, respectively, and the recovery period is 8.05 years.

For further research, dynamic simulations of the STRT system should be conducted to evaluate the dynamic characteristics of the system. In addition, advanced exergy analysis is also meaningful for the deep understanding and optimization works of the STRT system. Moreover, the optimization study on operation strategy of the STRT system is also a further research work in the future.