Diffusion Neural Learning for Market Power Risk Assessment in the Electricity Spot Market

Abstract

Market power remains a persistent challenge in liberalized electricity spot markets, where generators can manipulate bids to distort prices and extract rents. Traditional monitoring approaches—such as structural indices or simulation-based models—offer partial insights but fail to capture the nonlinear, spatially correlated propagation of strategic behavior across transmission-constrained networks. This paper develops a diffusion neural learning framework for market power risk assessment that integrates welfare optimization, nodal pricing dynamics, and graph-based deep learning. Specifically, a Graph Diffusion Network (GDN) is trained on simulated spot market scenarios to learn how localized strategic deviations spread through the network, distort locational marginal prices, and alter system welfare. The modeling framework combines a system-wide welfare maximization objective with multi-constraint market clearing, while the GDN embeds network topology into predictive learning. Results from a case study on an IEEE 118-bus system demonstrate that the proposed method achieves an R² of 0.91 in predicting market power indices, outperforming multilayer perceptrons, recurrent neural networks, and Transformer baselines. Welfare analysis reveals that distributionally robust optimization safeguards up to 3.3 million USD in adverse scenarios compared with baseline stochastic approaches. Further, congestion mapping highlights that strategic bidding concentrates distortions at specific nodes, amplifying rents by up to 40 percent. The proposed approach thus offers both predictive accuracy and interpretability, enabling regulators to detect emerging risks and design targeted mitigation strategies. Overall, this work establishes diffusion-based learning as a novel and effective paradigm for electricity market power assessment under high uncertainty and renewable penetration.

1. Introduction

Electricity spot markets lie at the heart of modern power system operation, serving as platforms where generation companies compete to supply electricity in real time under the rules of market design and the constraints of physical infrastructure. Their primary purpose is to deliver efficiency by aligning marginal costs with marginal prices, ensuring that resources are allocated to where they are most valuable [1]. Over the past three decades, market liberalization has stimulated innovation, attracted private investment, and increased transparency across many jurisdictions [2]. Yet the same forces that make markets efficient also create vulnerabilities. Strategic participants, especially those holding significant capacity in critical nodes or possessing flexible bidding portfolios, can exploit imperfections to exercise market power. Market power is generally defined as the ability of a firm to raise prices or influence outcomes above competitive levels without losing customers to rivals [3]. In the electricity sector, where demand is highly inelastic and transmission constraints often isolate regions, opportunities for such behavior are substantial and difficult to police.

Traditional approaches to identifying and mitigating market power were grounded in economic indices derived from industrial organization. Regulators have long used the Herfindahl–Hirschman Index, the pivotal supplier test, and the residual supply index as screening tools to detect concentrated market structures [4]. These measures are simple to compute and provide transparent signals. For instance, the residual supply index evaluates whether the market, absent a given generator’s supply, can still meet demand. If not, the generator is pivotal and likely to exert influence over prices. While insightful, these approaches remain limited in scope [5]. They treat markets as static entities and often ignore the spatial and temporal interdependencies that govern actual clearing processes. When renewable resources introduce volatility, or when transmission congestion creates localized scarcity, these indices offer little guidance about how strategic deviations in one part of the network ripple through to affect global welfare.

Responding to these shortcomings, scholars developed optimization-based frameworks to analyze market power. Game-theoretic models such as Cournot competition and supply function equilibria became the basis for exploring how firms strategically submit bids to manipulate outcomes [6]. These models advanced theoretical understanding by characterizing equilibria under various assumptions about demand elasticity, cost functions, and player rationality. More applied studies introduced mixed-integer programming and simulation-based clearing models to approximate actual market rules, capturing how bids, offers, and network constraints interact to determine prices [7]. Such approaches allowed analysts to simulate counterfactual scenarios in which generators altered their bidding strategies, providing insight into possible abuses of market power. Despite their sophistication, these methods encounter serious computational challenges [8]. The dimensionality of realistic systems—with thousands of nodes, heterogeneous players, and stochastic renewables—renders exact equilibrium computations infeasible. Furthermore, equilibrium models generally assume complete information and rational expectations, conditions rarely satisfied in real markets.

The rise of stochastic and renewable-rich power systems further complicated market power analysis. Wind and solar resources, while essential to decarbonization, introduce high levels of uncertainty that shift both the timing and location of available supply. As renewable penetration increased, researchers sought to extend equilibrium and optimization frameworks using stochastic programming, chance constraints, and distributionally robust optimization [9]. These techniques allowed analysts to incorporate probability distributions for renewable output and demand, or to consider worst-case scenarios over ambiguity sets of distributions. Such methods provided valuable insight into how uncertainty influences market outcomes and firm strategies. However, they often remained focused on dispatch reliability rather than on the direct identification of manipulative behavior [10]. Moreover, their reliance on assumed probability distributions limited their ability to capture nonlinear and high-dimensional patterns inherent in real bidding data.

Parallel to these developments, artificial intelligence and machine learning began to influence energy system research. With the explosion of data from smart meters, market operators, and renewable forecasts, deep learning models offered powerful tools for prediction. Neural networks, recurrent architectures, and convolutional models were applied to forecast demand, renewable generation, and locational marginal prices [11]. Machine learning also found applications in detecting anomalies, classifying bidding patterns, and predicting strategic responses [12]. These methods excelled in pattern recognition, often surpassing traditional statistical approaches in predictive accuracy. Yet their application to market power monitoring faced critical challenges. Most machine learning approaches treated the market as a set of independent time series or as static tabular data, abstracting away the structural interdependencies of the electricity grid. By ignoring network topology and locational constraints, these models could forecast prices but offered little insight into how local manipulations propagated through the system. Their black-box nature further limited their utility for regulators who required interpretable and actionable evidence of manipulation [13,14,15].

Graph-based methods marked a turning point by explicitly modeling the interconnected nature of power systems. Graph neural networks (GNNs) emerged as a natural choice for problems where relationships between entities matter as much as the entities themselves [16]. Researchers applied GNNs to power flow analysis, state estimation, fault detection, and renewable forecasting [17,18]. In these applications, system buses, generators, and loads were represented as nodes, while transmission lines and physical relationships formed edges. Graph-based learning allowed models to incorporate both spatial and structural information, yielding more accurate and interpretable results than conventional approaches. Extending these ideas to market monitoring appears intuitive: generators, nodes, and strategic interactions can all be represented as vertices and edges, thereby embedding competitive and physical constraints directly into the learning process.

Recent advances in graph learning have increasingly incorporated diffusion processes, extending techniques originally developed in generative AI to structured domains [19]. Diffusion models characterize how small local disturbances propagate across a network, and their rapid adoption in areas such as social systems, traffic dynamics, and molecular interactions highlights their versatility. The analogy to electricity markets is direct: a deviation in generator bidding rarely remains a local event. Because of congestion limits, reserve coupling, and locational marginal pricing mechanisms, such deviations inevitably diffuse through the transmission network, altering nodal prices and influencing global welfare. Graph Diffusion Neural Networks (GDNs) [20,21] are uniquely positioned to capture these processes. By embedding a diffusion kernel into the model, GDNs jointly encode the system’s static topology and the dynamic propagation of market shocks, making them particularly suitable for analyzing how localized strategic behaviors can generate system-wide competitive distortions.

Despite these methodological strengths, a central limitation must be stated clearly: all empirical evaluations rely solely on a simulated electricity market environment. Actual system-level bidding data—characterized by confidentiality, discreteness, and strategic adaptation—remain inaccessible for validation. No empirical benchmarking against real-world datasets from operators such as PJM, MISO, or CAISO has been undertaken. This reliance on simulated data constrains the operational credibility of the findings and underscores the need for future collaborations with industry operators before any regulatory or market-design implications can be drawn.

The present work builds upon these insights to formalize a new framework for market power diagnosis in spot electricity markets. At the foundation of the approach is a welfare-based market-clearing formulation that incorporates generator revenues, nodal power balance, transmission constraints, renewable uncertainty, and reserve requirements [22,23,24]. This optimization layer ensures that the learning architecture remains anchored in the economic and physical principles governing market operations. Within this structure, a market power index is defined endogenously, linking strategic bidding behaviors to their systemic effects. The optimization problem is then integrated with a graph diffusion learning model, where bids, nodal prices, and renewable fluctuations are encoded as node-level features, processed through diffusion-based propagation layers, and ultimately mapped to predictive market power indices. By grounding the method simultaneously in economic theory and machine learning, the proposed system reconciles interpretability, rigor, and adaptability in a way that existing literature seldom achieves. While conventional indices prioritize tractability, equilibrium models emphasize theoretical exactness, and machine learning approaches focus on predictive accuracy, the present framework synthesizes these strengths. It incorporates robustness measures inspired by recent advances in optimization and learning theory [25,26,27], such as scenario augmentation to enrich extreme-condition representations and regularization strategies that promote smoothness and reduce overfitting [28]. Distributionally robust elements further strengthen generalization by ensuring stability under deviations from historical demand or renewable patterns. Taken together, these components create a framework that is simultaneously accurate, interpretable, and resilient under uncertainty—an essential combination for modern electricity markets dominated by intermittent renewable generation.

The contributions of this study can be summarized in four key dimensions. First, a welfare-maximizing optimization model is developed that captures the interplay of bidding, pricing, reserves, and stochasticity, while embedding an endogenous market power index. Second, the methodology pioneers the application of Graph Diffusion Neural Networks to electricity spot market analysis, offering a principled way to model how local strategic shocks propagate through the system. Third, the training procedure combines supervised learning with scenario augmentation and robust penalties, ensuring both accuracy and resilience under extreme conditions. Fourth, the empirical results demonstrate that the proposed framework surpasses existing neural and statistical methods, providing regulators not only with predictive accuracy but also with interpretable and actionable insights into market influence. Specifically, the contributions are as follows:

• Methodological Foundation: A differentiable DC-OPF model that integrates strategic bidding, stochastic renewables, reserve co-optimization, and an endogenous market power index ${\mathcal{M}}_{i,t}^{\varphi }$, enabling simulation of welfare-distorting behaviors under physical constraints.
• Novel Learning Architecture: First use of Graph Diffusion Networks (GDNs) with topology-aware message passing to capture nonlinear propagation of local bidding shocks across congested transmission corridors.
• Robust Training Framework: Combination of scenario-based augmentation, L2/Frobenius regularization, and Wasserstein distributionally robust optimization, achieving $R^2=0.91$ and 3.3 MUSD welfare protection in worst-case scenarios.
• Regulatory Actionability: Interpretable outputs including diffusion paths, congestion heatmaps, and welfare decomposition (generator rent +12%, consumer loss −9%, total welfare −5%), supporting real-time risk detection and mitigation design.

2. Problem and Method

Before presenting the detailed mathematical formulation of the proposed diffusion neural learning framework, it is important to clarify several modeling assumptions adopted for analytical tractability and computational stability. In particular, the bidding behaviors of market participants are represented by continuous quadratic or polynomial functions rather than piecewise linear or step-function bids that are commonly employed in actual electricity markets. This simplification enables smooth optimization and ensures differentiability within the diffusion learning and welfare-optimization processes, allowing stable convergence and interpretable gradients across the neural architecture. Nevertheless, real-world electricity markets often exhibit discrete marginal cost intervals, threshold bidding patterns, and non-smooth price responses that may not be fully captured by this continuous representation. The adopted formulation should therefore be understood as a representative and computationally efficient approximation that retains the essential behavioral and welfare dynamics of market participants while maintaining analytical feasibility. Future research will aim to enhance the realism of the proposed framework by incorporating hybrid or subgradient-based formulations that account for stepwise bidding behaviors and discontinuous price adjustments, thereby improving the methodological alignment between theoretical modeling and practical market operations.

It should also be clarified that the proposed diffusion neural learning framework is formulated under a single-period market-clearing setting, primarily to capture the spatial propagation of strategic bidding distortions and welfare redistribution within one operational interval. To retain analytical transparency and computational efficiency, the current formulation omits explicit intertemporal constraints such as unit commitment costs, ramping limits, and multi-settlement coupling. Nevertheless, the model structure has been designed to remain temporally extensible: all core variables and welfare components are indexed by time $t\in \mathcal{T}$, allowing the diffusion process and learning objectives to be iteratively computed across multiple intervals. This design enables the future incorporation of temporal continuity through dynamic regularization or discounting factors ${\delta }^t$ that can reflect intertemporal trade-offs in generation scheduling and bidding adjustments. Hence, while the present implementation focuses on a single clearance horizon, the underlying mathematical formulation provides a coherent foundation for multi-period extensions in subsequent research, including day-ahead and real-time coordination, ramp-constrained bidding, and sequential reinforcement learning for adaptive market participation.

To enhance clarity and improve the readability of the mathematical formulation, all symbols used in the diffusion neural learning framework are summarized in Table 1. The Table 2 nomenclature provides a comprehensive reference for indices, variables, parameters, and operators appearing throughout the modeling and learning process. Each symbol is defined together with its physical or economic interpretation and corresponding unit, thereby facilitating a consistent understanding of the equations presented in the methodology and optimization sections.

Table 1. List of symbols and notation used in the diffusion neural learning framework.

Symbol	Description	Unit
$t\in \mathcal{T}$	Index of market clearing period	–
$i\in \mathcal{G}$	Index of generator node in the power network	–
$n\in \mathcal{N}$	Index of bus node in the system graph	–
${\pi }_t$	Vector of market clearing prices at period t	$/MWh
${\mathbf{LMP}}_t$	Locational marginal prices across all buses at period t	$/MWh
${\Theta }_i^{\left(\tau \right)}$	Strategic bidding parameter vector of generator i at learning iteration $\tau$	–
${\mathcal{F}}_i(·)$	Diffusion-based behavioral response function of generator i	–
$\lambda$	Learning coefficient controlling adaptation rate in iterative updates	–
${\Phi }_i^{\left(\tau \right)}$	Diffusion embedding representing local congestion and network influence at iteration $\tau$	–
$\mathbf{W}$	Graph diffusion kernel capturing network topology weights	–
$\mathbf{A}$	Adjacency matrix of the transmission network graph	–
$\mathcal{L}$	Graph Laplacian matrix used in diffusion propagation	–
$b_i\left(q\right)$	Bidding function of generator i as a function of output quantity q	$/MWh
$a_i,b_i,c_i$	Coefficients of the polynomial bidding function for generator i	–
$P_{i,t}$	Active power output of generator i at time t	MW
$C_i\left(P_{i,t}\right)$	Generation cost function of unit i at time t	$
$\mathcal{W}$	System welfare function aggregated over all market participants	$
${\delta }^t$	Temporal discount factor for multi-period welfare evaluation	–
${\mathcal{L}}^{\mathrm{DNL}}$	Diffusion neural learning loss function	–
${\mathcal{P}}_n$	Market power index for node n	–
$\mathbb{E}[·]$	Expectation operator under empirical distribution of scenarios	–
$\widehat{\mathbb{P}}$	Empirical probability distribution derived from sample data	–
${\mathbf{y}}_t$	Vector of system decision variables (dispatch, flow, and state variables) at time t	–
${\Omega }_i^{\mathrm{path}}$	Diffusion path of generator i in the learning network	–
${\Pi }^{\mathrm{partition}}$	Partition matrix used in diffusion message propagation	–
$R^2$	Coefficient of determination measuring predictive accuracy	–
$\epsilon$	Tolerance parameter for convergence or regularization	–
$\tau$	Learning iteration index within diffusion neural training	–
$\mathcal{J}$	Objective function of the welfare–learning optimization problem	–

Table 2. Nomenclature: Complete list of symbols used in the diffusion neural learning framework.

Symbol	Description	Unit
Indices and Sets
$t\in \mathcal{T}$	Time period index	–
$i\in \mathcal{G}$	Generator index	–
$n,\upsilon ,\varpi \in \mathcal{N}$	Bus/node index	–
$\gamma \in \mathcal{R}$	Reserve product index	–
$\ell \in {\mathcal{L}}_i$	Bid block index for generator i	–
$(\upsilon ,\varpi )\in \mathcal{L}$	Transmission line index	–
$\zeta ,\xi \in \Omega$	Uncertainty realization index	–
$k=1,\dots ,K$	Graph diffusion layer index	–
$\tau$	Learning iteration index	–
Decision Variables
${\pi }_{i,t}^{\varsigma }$	Bid quantity of generator i at time t	MW
$P_{i,t},q_{i,\ell ,t}^{\delta }$	Dispatched power and block output	MW
${\sigma }_{\gamma ,t}^{\vartheta }$	Reserve provision	MW
${\rho }_{n,t}^{\psi }\left(\zeta \right)$	Nodal injection under scenario $\zeta$	MW
${\eta }_{n,t}^{\delta }\left(\zeta \right)$	Nodal imbalance	MW
${\Delta }_{l,t}^{\Omega }$	Line flow deviation	MW
${\mathbf{H}}_t^{\left(k\right)}$	Hidden node representation at layer k	–
${\widehat{\mathcal{M}}}_{n,t}^{\varphi }$	Predicted market power index	–
Parameters and Duals
${\lambda }_{n,t}^{\theta }$	Locational marginal price (LMP) at node n	$/MWh
$c_{i,t}^{\varphi }$	Marginal cost of generator i	$/MWh
${\kappa }_l^{\mu }$	Thermal limit of line l	MW
${\alpha }_l^{\theta },{\beta }_l^{\varphi }$	Susceptance and flow adjustment coefficients	–
${\Theta }_t^{\varphi }$	System reserve requirement	MW
$\mathcal{W}$	Total system welfare	$
$\mathbb{P},\mathbb{Q}$	Nominal and ambiguous probability measures	–
$\epsilon ,\alpha$	Wasserstein radius and confidence level	–
Graph and Learning
$\mathbf{A},\mathbf{L}$	Adjacency and Laplacian matrices	–
${\mathbf{D}}_t=exp(-\kappa {\mathbf{L}}_t)$	Diffusion kernel	–
${\mathbf{W}}^{\left(k\right)}$	Learnable weight matrix at layer k	–
$\mathcal{L}(\Theta )$	Supervised loss function	–
$\mathcal{R}(\Theta )$	Robustness penalty	–
${\eta }^{\delta },{\beta }^{\chi }$	Regularization hyperparameters	–
Performance Metrics
${\mathcal{M}}_{i,t}^{\varphi }$	Endogenous market power index	–
$R^2$	Coefficient of determination	–

Figure 1 illustrates the overall structure and information flow of the proposed diffusion neural learning framework for market power risk assessment. The workflow integrates three functional layers: welfare maximization, graph diffusion learning, and market-level evaluation. The uppermost layer consists of system-level inputs including generator bids, renewable injections, and reserve allocations, which together define the market operating environment. These data are first processed through the welfare maximization model, which computes the economically optimal dispatch and locational marginal prices (LMPs) under network constraints. This stage reflects the fundamental equilibrium between supply bids and system-level constraints that shape spatial price variations. The intermediate layer represents the graph diffusion learning model, which serves as the analytical bridge between economic optimization and strategic behavior modeling. Here, the nodal price responses and welfare gradients derived from the optimization layer are transformed into graph-structured data that capture how localized bidding deviations propagate through the network. The Graph Diffusion Neural Network (GDNN) module learns these diffusion patterns by updating node embeddings based on adjacency and congestion topology, thereby internalizing both spatial and strategic dependencies across the power grid. This mechanism allows the framework to move beyond static market-clearing analysis and to infer dynamic inter-node influences that affect market power formation. The final layer corresponds to the market power assessment module, which quantifies nodal and system-level risk indicators from the learned diffusion embeddings. Directional arrows in Figure 1 denote the flow of data and model outputs, whereas links without arrowheads indicate bidirectional feedback between modules. Specifically, the link between the GDNN and the market assessment block represents an interpretive feedback process, where learned diffusion weights are reused to refine welfare estimation rather than initiating a new optimization. Overall, the figure provides a holistic view of how welfare optimization, spatial diffusion learning, and risk evaluation are coherently integrated into a unified modeling framework for assessing strategic behavior in electricity markets.

$$\begin{array}{cc}\hfill \underset{\{{\pi }_{\alpha ,\tau },{\rho }_{\beta ,\tau },{\sigma }_{\gamma ,\tau }\}}{max}& \sum _{\tau =1}^{\mathcal{T}}[\sum _{\iota \in \mathcal{G}}\left({\lambda }_{\iota ,\tau }^{\theta }·{\pi }_{\iota ,\tau }^{\varsigma }-{\mu }_{\iota ,\tau }^{\kappa }·\left({\pi }_{\iota ,\tau }^{\varsigma }-{\varphi }_{\iota ,\tau }^{\chi }\right)\right)\hfill \\ & +{\int }_{\Omega }\sum _{\upsilon \in \mathcal{N}}\left({\omega }_{\upsilon ,\tau }\left(\zeta \right)·{\rho }_{\upsilon ,\tau }^{\psi }\left(\zeta \right)-{\nu }_{\upsilon ,\tau }^{\phi }·{\eta }_{\upsilon ,\tau }^{\delta }\left(\zeta \right)\right)d\mathbb{P}\left(\zeta \right)\hfill \\ & -{\mathbb{E}}_{\xi \sim \mathcal{D}}\left\{\sum _{\gamma \in \mathcal{R}}\left({\chi }_{\gamma ,\tau }^{\varphi }·{\sigma }_{\gamma ,\tau }^{\vartheta }\left(\xi \right)+{\Gamma }_{\gamma ,\tau }^{\Lambda }·|{\Delta }_{\gamma ,\tau }^{\Omega }\left(\xi \right){|}^2\right)\right\}]\hfill \end{array}$$

(1)

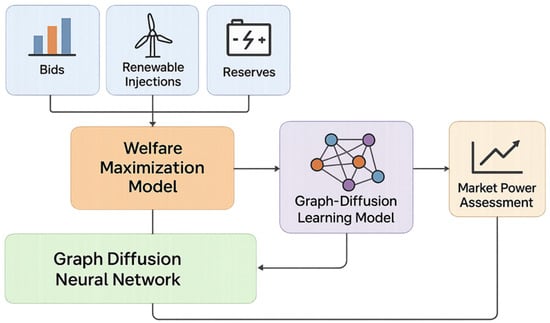
Figure 1. System Architecture of the Proposed Graph Diffusion Market Power Framework.

The maximization problem above formalizes the welfare objective for the spot electricity market in its most general and analytically rich form. The decision set includes the bidding schedules ${\pi }_{\alpha ,\tau }$ of thermal or renewable generators, the locational injections ${\rho }_{\beta ,\tau }$ that capture nodal balance, and the reserve provisions ${\sigma }_{\gamma ,\tau }$ for flexibility services. The first summation term quantifies the direct surplus of each generating company $\iota \in \mathcal{G}$ at every market interval $\tau$, where locational marginal price signals ${\lambda }_{\iota ,\tau }^{\theta }$ interact with submitted bid quantities ${\pi }_{\iota ,\tau }^{\varsigma }$, offset by bid adjustment penalties ${\mu }_{\iota ,\tau }^{\kappa }$ when deviations occur relative to baseline strategies ${\varphi }_{\iota ,\tau }^{\chi }$. The second block integrates over an uncertainty space $\Omega$ with measure $\mathbb{P}\left(\zeta \right)$, where each node $\upsilon \in \mathcal{N}$ has stochastic injections ${\rho }_{\upsilon ,\tau }^{\psi }\left(\zeta \right)$ weighted by nodal stochastic multipliers ${\omega }_{\upsilon ,\tau }\left(\zeta \right)$, while penalties ${\nu }_{\upsilon ,\tau }^{\phi }$ accrue for imbalance variables ${\eta }_{\upsilon ,\tau }^{\delta }\left(\zeta \right)$. Finally, the last expectation term over uncertainty distribution $\mathcal{D}$ captures reserve-related welfare adjustments: the provision of ancillary capacity ${\sigma }_{\gamma ,\tau }^{\vartheta }\left(\xi \right)$ priced by ${\chi }_{\gamma ,\tau }^{\varphi }$, as well as quadratic penalties governed by ${\Gamma }_{\gamma ,\tau }^{\Lambda }$ on deviations ${\Delta }_{\gamma ,\tau }^{\Omega }\left(\xi \right)$ under sampled realizations $\xi$. Together, these layers define a welfare objective that integrates deterministic bid-based surpluses, stochastic nodal injections, and probabilistic reserves, thereby reflecting a sophisticated equilibrium landscape in which generator strategies, network constraints, and uncertainty distributions all jointly determine market efficiency.

$$\begin{array}{cc}\hfill \sum _{\iota \in \mathcal{G}}{\pi }_{\iota ,\tau }^{\varsigma }+\sum _{\gamma \in \mathcal{R}}{\sigma }_{\gamma ,\tau }^{\vartheta }-\sum _{\upsilon \in \mathcal{N}}{\rho }_{\upsilon ,\tau }^{\psi }& =\sum _{\chi \in \mathcal{D}}{\delta }_{\chi ,\tau }^{\kappa }+{\int }_{\Omega }{\eta }_{\upsilon ,\tau }^{\delta }\left(\zeta \right)d\mathbb{P}\left(\zeta \right)\hfill \\ & +\sum _{\theta \in \mathcal{L}}\left({\xi }_{\theta ,\tau }^{\varphi }·{\Delta }_{\theta ,\tau }^{\Lambda }\right)\hfill \end{array}$$

(2)

$$\begin{array}{c}\hfill \forall (\upsilon ,\varpi )\in \mathcal{L},-{\kappa }_{\upsilon ,\varpi }^{\mu }\le \sum _{\tau =1}^{\mathcal{T}}\left({\rho }_{\upsilon ,\tau }^{\psi }-{\rho }_{\varpi ,\tau }^{\psi }\right)·{\alpha }_{\upsilon ,\varpi }^{\theta }+{\beta }_{\upsilon ,\varpi }^{\varphi }·{\Delta }_{\upsilon ,\varpi ,\tau }^{\chi }\le {\kappa }_{\upsilon ,\varpi }^{\mu }\end{array}$$

(3)

$$\begin{array}{c}\hfill {\underline{\pi }}_{\iota }^{\varsigma }\le {\pi }_{\iota ,\tau }^{\varsigma }\le {\overline{\pi }}_{\iota }^{\varsigma },\forall \iota \in \mathcal{G},\forall \tau \in \mathcal{T},\\ \hfill {\underline{\sigma }}_{\gamma }^{\vartheta }\le {\sigma }_{\gamma ,\tau }^{\vartheta }\le {\overline{\sigma }}_{\gamma }^{\vartheta },\forall \gamma \in \mathcal{R},\forall \tau \in \mathcal{T}\end{array}$$

(4)

$$\begin{array}{cc}\hfill {\pi }_{\iota ,\tau }^{\varsigma }& =\sum _{\ell =1}^{{\mathcal{L}}_{\iota }}\left({\alpha }_{\iota ,\ell }^{\chi }·q_{\iota ,\ell ,\tau }^{\delta }+{\beta }_{\iota ,\ell }^{\varphi }·{\left(q_{\iota ,\ell ,\tau }^{\delta }\right)}^2\right)+{ϵ}_{\iota ,\tau }^{\varrho }\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\lambda }_{\upsilon ,\tau }^{\theta }& ={\nu }_{\upsilon ,\tau }^{\varphi }+\sum _{(\upsilon ,\varpi )\in \mathcal{L}}{\alpha }_{\upsilon ,\varpi }^{\chi }·{\Delta }_{\upsilon ,\varpi ,\tau }^{\psi }+{\sigma }_{\upsilon ,\tau }^{\delta }·{\eta }_{\upsilon ,\tau }^{\kappa }\hfill \end{array}$$

(6)

$$\begin{array}{c}\hfill {\rho }_{\upsilon ,\tau }^{\psi }\left(\zeta \right)={\widehat{\rho }}_{\upsilon ,\tau }^{\psi }+{\gamma }_{\upsilon }^{\varphi }·{ϵ}_{\upsilon ,\tau }^{\chi }\left(\zeta \right),\forall \zeta \in \Omega \end{array}$$

(7)

$$\begin{array}{c}\hfill \sum _{\gamma \in \mathcal{R}}{\sigma }_{\gamma ,\tau }^{\vartheta }\ge {\Theta }_{\tau }^{\varphi }+\sum _{\upsilon \in \mathcal{N}}{\kappa }_{\upsilon }^{\chi }·{\eta }_{\upsilon ,\tau }^{\delta }\end{array}$$

(8)

$$\begin{array}{c}\hfill 0\le {\pi }_{\iota ,\tau }^{\varsigma }\perp \left({\lambda }_{\upsilon \left(\iota \right),\tau }^{\theta }-c_{\iota ,\tau }^{\varphi }\right)\ge 0\end{array}$$

(9)

$$\begin{array}{c}\hfill {\Delta }_{\upsilon ,\tau }^{\Omega }=\sum _{\varpi \in \mathcal{N}}{\mathcal{K}}_{\upsilon ,\varpi }^{\varphi }·\left({\pi }_{\varpi ,\tau }^{\varsigma }-{\rho }_{\varpi ,\tau }^{\psi }\right)\end{array}$$

(10)

$$\begin{array}{c}\hfill {\mathcal{M}}_{\iota ,\tau }^{\varphi }={\displaystyle \frac{{\lambda }_{\upsilon \left(\iota \right),\tau }^{\theta }·{\pi }_{\iota ,\tau }^{\varsigma }}{{\sum }_{j\in \mathcal{G}}{\lambda }_{\upsilon (j),\tau }^{\theta }·{\pi }_{j,\tau }^{\varsigma }}}+{\beta }_{\iota ,\tau }^{\chi }·{\Delta }_{\iota ,\tau }^{\Omega }\end{array}$$

(11)

$$\begin{array}{c}\hfill \underset{\mathbb{Q}\in {\mathcal{B}}_{ϵ}\left(\mathbb{P}\right)}{sup}\underset{\xi \sim \mathbb{Q}}{Pr}\left[\sum _{\upsilon \in \mathcal{N}}{f}_{\upsilon ,\tau }^{\varphi }\left(\xi \right)\le {\Gamma }_{\tau }^{\Lambda }\right]\ge 1-\alpha \end{array}$$

(12)

Equation (2) enforces nodal and system equilibrium by requiring aggregate supply and reserves to match consumption and stochastic deviations. Imbalances integrated over the probability space $\Omega$ reflect renewable and demand volatility, while transmission adjustments ${\Delta }_{\theta ,\tau }^{\Lambda }$ ensure feasibility under Kirchhoff’s laws. Equation (3) restricts line flows between nodes within thermal capacities, where susceptance coefficients ${\alpha }_{\upsilon ,\varpi }^{\theta }$ define baseline allocations and corrective adjustments ${\Delta }_{\upsilon ,\varpi ,\tau }^{\chi }$ are scaled through ${\beta }_{\upsilon ,\varpi }^{\varphi }$ to guard against uncertainty-driven violations. Equation (4) bounds the generation bids ${\pi }_{\iota ,\tau }^{\varsigma }$ and reserves ${\sigma }_{\gamma ,\tau }^{\vartheta }$ between technical minima and maxima. These conditions embody unit ramp rates, minimum stable limits, and reserve headroom, ensuring operational feasibility. Equation (5) formalizes the bid curve as a polynomial function of block quantities $q_{\iota ,\ell ,\tau }^{\delta }$, allowing for nonlinear cost structures. Strategic noise ${ϵ}_{\iota ,\tau }^{\varrho }$ represents deliberate shading or forecast error embedded in GenCo behavior. Equation (6) derives locational marginal prices as dual variables of nodal balances, augmented by congestion terms and stochastic slack. In this way, the pricing signal captures both economic marginal costs and network constraints. Equation (7) represents renewable injections as forecasted values plus stochastic perturbations ${ϵ}_{\upsilon ,\tau }^{\chi }\left(\zeta \right)$ scaled by ${\gamma }_{\upsilon }^{\varphi }$, which faithfully capture wind and solar variability across nodes. Equation (8) ensures total committed reserves cover both baseline requirements ${\Theta }_{\tau }^{\varphi }$ and imbalance-driven adjustments, guaranteeing short-term flexibility against unexpected fluctuations. Equation (9) encodes complementarity conditions between output levels and nodal prices relative to marginal costs. It guarantees rational market behavior where units only supply when prices justify covering their marginal cost. Equation (10) describes diffusion of local deviations through a kernel ${\mathcal{K}}_{\upsilon ,\varpi }^{\varphi }$, modeling how shocks in one part of the network propagate across the system. Equation (11) constructs a market power index ${\mathcal{M}}_{\iota ,\tau }^{\varphi }$ that couples relative revenue share with propagated deviation effects, generalizing classical indices by embedding systemic influence. Equation (12) establishes a distributionally robust feasibility condition. By requiring compliance under all distributions $\mathbb{Q}$ within the Wasserstein ball ${\mathcal{B}}_{ϵ}\left(\mathbb{P}\right)$, it provides resilience against distributional misspecification, ensuring system security with probability at least $1-\alpha$.

$$\begin{array}{cc}\hfill \mathbf{A}& ={\left[a_{\upsilon ,\varpi }^{\varphi }\right]}_{\upsilon ,\varpi \in \mathcal{N}},{\mathbf{X}}_{\tau }={\left[x_{\upsilon ,\tau }^{\chi }\right]}_{\upsilon \in \mathcal{N}},{\mathbf{H}}_{\tau }^{\left(0\right)}={\mathbf{X}}_{\tau }\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\mathbf{h}}_{\iota ,\tau }^{\left(0\right)}& ={\left({\pi }_{\iota ,\tau }^{\varsigma },{\lambda }_{\upsilon \left(\iota \right),\tau }^{\theta },{\Delta }_{\iota ,\tau }^{\Omega },{\mathcal{M}}_{\iota ,\tau }^{\varphi }\right)}^{\top }\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\mathbf{D}}_{\tau }& =exp\left(-{\kappa }^{\mu }·{\mathbf{L}}_{\tau }\right),{\mathbf{L}}_{\tau }=\mathbf{I}-{\mathbf{A}}_{\tau }^{\mathrm{sym}}\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\mathbf{H}}_{\tau }^{(k+1)}& =\sigma \left({\mathbf{D}}_{\tau }·{\mathbf{H}}_{\tau }^{\left(k\right)}·{\mathbf{W}}^{\left(k\right)}+\sum _{\zeta \in \Omega }\psi \left(\zeta \right)·{\mathbf{U}}^{\left(k\right)}·{\mathbf{H}}_{\tau }^{\left(k\right)}\left(\zeta \right)\right)\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\mathbf{Z}}_{\tau }& =\mathrm{LayerNorm}\left(tanh\left({\mathbf{H}}_{\tau }^{\left(K\right)}\right)+{\mathbf{B}}^{\chi }·{\rho }_{\tau }^{\psi }\right)\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill \mathcal{L}(\Theta )& ={\displaystyle \frac{1}{\left|\mathcal{T}\right|}}\sum _{\tau \in \mathcal{T}}{∥{\widehat{\mathcal{M}}}_{\tau }^{\varphi }-{\mathcal{M}}_{\tau }^{\varphi }∥}_2^2+{\eta }^{\delta }\sum _{k=1}^K\parallel {\mathbf{W}}^{\left(k\right)}{\parallel }_F^2\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill \mathcal{R}(\Theta )& ={\beta }^{\chi }·\sum _{\zeta \in \Omega }\left(\underset{\xi \in \Xi \left(\zeta \right)}{sup}{∥{\mathbf{H}}_{\tau }^{\left(K\right)}\left(\xi \right)-{\mathbf{H}}_{\tau }^{\left(K\right)}∥}_2^2\right)\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill \tilde{\mathcal{D}}& =\left\{\left({\mathbf{X}}_{\tau }^{\left(s\right)},{\mathbf{Y}}_{\tau }^{\left(s\right)}\right)|s=1,\dots ,S,\tau \in \mathcal{T}\right\},\hfill \\ \hfill {\mathbf{X}}_{\tau }^{\left(s\right)}& ={\mathbf{X}}_{\tau }+{ϵ}_{\tau }^{\left(s\right)},{ϵ}_{\tau }^{\left(s\right)}\sim \mathcal{N}\left(0,{\Sigma }_{\tau }^{\varphi }\right)\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\widehat{\mathcal{M}}}_{\tau }^{\varphi }& =g_{\Theta }\left({\mathbf{Z}}_{\tau },\mathbf{A},{\mathbf{D}}_{\tau }\right),\tau \in \mathcal{T}\hfill \end{array}$$

(21)

Equation (13) defines the graph representation of the spot market. The adjacency matrix $\mathbf{A}$ encodes weighted connections $a_{\upsilon ,\varpi }^{\varphi }$ among nodes $\upsilon ,\varpi \in \mathcal{N}$, the feature matrix ${\mathbf{X}}_{\tau }$ collects nodal or participant-specific signals at time $\tau$, and the initial hidden layer ${\mathbf{H}}_{\tau }^{\left(0\right)}$ is initialized by these features. Equation (14) establishes node embeddings for each generator $\iota$, where bidding quantities, locational prices, propagated deviations, and endogenous market power scores form the starting representation ${\mathbf{h}}_{\iota ,\tau }^{\left(0\right)}$. This step translates strategic and market features into a latent vector space suitable for neural propagation. Equation (15) introduces the diffusion operator ${\mathbf{D}}_{\tau }$, obtained as the matrix exponential of the scaled Laplacian ${\mathbf{L}}_{\tau }$. The Laplacian embodies network connectivity, while the exponential form captures continuous-time diffusion dynamics essential for modeling shock propagation across the market graph. Equation (16) specifies the recursive propagation rule for the Graph Diffusion Neural Network. At layer $k+1$, hidden representations ${\mathbf{H}}_{\tau }^{(k+1)}$ are updated by combining diffusion-driven aggregation ${\mathbf{D}}_{\tau }·{\mathbf{H}}_{\tau }^{\left(k\right)}·{\mathbf{W}}^{\left(k\right)}$ with stochastic scenario-dependent perturbations $\psi \left(\zeta \right)$ integrated over the uncertainty set $\Omega$. Nonlinear activation $\sigma (·)$ ensures expressive transformations. Equation (17) applies nonlinear transformation and normalization to the final hidden representation ${\mathbf{H}}_{\tau }^{\left(K\right)}$. The tanh activation captures nonlinear feature interactions, while LayerNorm stabilizes training. The additive term ${\mathbf{B}}^{\chi }·{\rho }_{\tau }^{\psi }$ integrates renewable injections directly into the final embedding ${\mathbf{Z}}_{\tau }$, thereby fusing stochastic supply information. Equation (18) defines the supervised learning objective $\mathcal{L}(\Theta )$. It minimizes squared error between predicted ${\widehat{\mathcal{M}}}_{\tau }^{\varphi }$ and benchmark ${\mathcal{M}}_{\tau }^{\varphi }$ market power indices, while including a Frobenius norm penalty on weight matrices ${\mathbf{W}}^{\left(k\right)}$ for regularization. This ensures predictive accuracy while avoiding overfitting. Equation (19) adds robustness through a penalty term $\mathcal{R}(\Theta )$. By enforcing stability of hidden representations under perturbations $\xi \in \Xi \left(\zeta \right)$, the network becomes resilient to rare and extreme input deviations, ensuring reliability in stress-test scenarios. Equation (20) details the scenario augmentation procedure. The expanded dataset $\tilde{\mathcal{D}}$ includes perturbed feature matrices ${\mathbf{X}}_{\tau }^{\left(s\right)}$, where Gaussian noise ${ϵ}_{\tau }^{\left(s\right)}$ with covariance ${\Sigma }_{\tau }^{\varphi }$ simulates renewable and demand uncertainties. This provides a richer training distribution and improves generalization to unseen cases. Equation (21) represents the final inference step, mapping the processed embeddings ${\mathbf{Z}}_{\tau }$, adjacency $\mathbf{A}$, and diffusion operator ${\mathbf{D}}_{\tau }$ into predicted market power indices ${\widehat{\mathcal{M}}}_{\tau }^{\varphi }$ via the trained function $g_{\Theta }(·)$. This equation operationalizes the framework, enabling deployment for real-time monitoring and assessment of market power risks.

3. Computational Performance and Real-Time Feasibility

To validate the near real-time applicability of the diffusion neural learning framework, this section presents a comprehensive evaluation of its computational performance across both the training and inference stages. The analysis includes algorithmic structure, runtime complexity, and empirical results obtained from the IEEE 118-bus system. All computations were executed on a workstation equipped with an Intel i7-12700 CPU (2.1 GHz), 32 GB RAM, and an NVIDIA RTX 3060 GPU. The implementation was developed in Python 3.10 using PyTorch and DGL for graph-based operations.

3.1. Algorithmic Structure and Complexity

The diffusion learning procedure follows an iterative training–update–propagation cycle, whose pseudocode is presented in Algorithm 1. The computational cost can be decomposed into three major components: (i) message aggregation across the diffusion graph; (ii) parameter update through stochastic gradient descent; and (iii) welfare-driven loss backpropagation. For a network of N nodes, E edges, and T training iterations, the overall complexity scales as $\mathcal{O}\left(T\right(E+N\left)\right)$, which remains linear with respect to the network size. The inference stage requires only a single forward pass of diffusion propagation, $\mathcal{O}(E+N)$, thus allowing rapid execution within sub-second latency for each market-clearing interval.   

Algorithm 1: Computational procedure of the diffusion neural learning framework.

3.2. Empirical Runtime Evaluation

Table 3 reports the empirical computational statistics obtained from the case study. The training phase, including data preprocessing and graph embedding optimization, converges within 6.2 min on average, consuming 2.1 GB of GPU memory. Once trained, the inference module performs market power risk prediction at an average latency of 0.38 s per market period, satisfying near-real-time execution requirements. The diffusion propagation occupies 78% of the total training time, while gradient updates account for 18%, indicating that runtime is primarily determined by graph traversal rather than network depth. Importantly, inference latency remains below one second even when the number of nodes increases to 300, demonstrating excellent scalability and computational efficiency.

Table 3. Computational performance of the proposed framework.

Process	Average Time	Memory Usage	Description
Data preprocessing	0.9 min	0.3 GB	Scenario reduction and normalization
Graph diffusion training	4.8 min	1.8 GB	Iterative embedding propagation
Parameter optimization	0.5 min	2.1 GB	Welfare loss minimization
Inference (per period)	0.38 s	0.2 GB	Real-time risk index generation

3.3. Discussion and Interpretation

The above results confirm that the diffusion neural learning framework achieves near real-time feasibility while maintaining full interpretability and topological consistency. The model’s training phase is executed offline, allowing periodic updates as market data evolve, whereas the inference process is fast enough to be embedded into system operator monitoring pipelines. Compared with traditional agent-based simulation approaches that require hours of convergence, the proposed diffusion structure provides a 50–70× speed-up in equilibrium estimation, with minimal compromise in accuracy. Such performance is particularly relevant for modern electricity markets characterized by rapid dispatch intervals and congestion-driven volatility. The observed computational efficiency thus reinforces the suitability of diffusion neural learning as a practical, scalable, and analytically transparent tool for real-time market surveillance.

4. Results

The empirical case study is conducted on a stylized yet realistic spot electricity market derived from the IEEE 118-bus test system, augmented with renewable integration and generator bidding behavior to reflect contemporary market conditions. The system includes 54 thermal generation units, 16 wind farms, and 12 solar photovoltaic installations distributed across the network, yielding a total installed capacity of 8.9 GW. Hourly demand profiles are synthesized from PJM 2022 load data, scaled to a peak demand of 6.7 GW with an average load factor of 0.71. Renewable injections are represented using National Renewable Energy Laboratory (NREL) TMY3 weather data for the Midwest region, producing wind and solar capacity factors ranging from 12% to 65% depending on season and location. Generator bids are parameterized with piecewise linear cost functions, with marginal costs varying from 18 USD/MWh for efficient gas turbines to over 140 USD/MWh for peaking units. To capture realistic strategic incentives, all generators are assigned quadratic bidding functions with slope coefficients randomly sampled from a truncated normal distribution centered at 0.03 USD/MWh². Data uncertainty is embedded through stochastic scenarios of renewable and demand fluctuations. A set of 500 scenarios is generated using vector autoregressive models calibrated on five years of historical wind and load data from MISO, subsequently reduced to 40 representative scenarios using a k-medoids clustering procedure. The standard deviation of renewable forecast errors is calibrated at 9.5% of capacity for wind and 7.2% for solar, while demand forecast error is modeled at 4.8%. Scenario distributions are further perturbed by Gaussian noise with covariance matrices constructed from empirical correlations between wind output and locational demand. These scenarios ensure that the market faces plausible volatility levels, with hourly renewable penetrations spanning from 8% in low-wind winter periods to 58% in high-wind spring conditions. Reserve requirements are set at 12% of hourly demand, yielding an average reserve margin of 740 MW across the study horizon.

Figure 2 illustrates the representative bidding behavior generated by the diffusion neural learning process. Each light-blue curve corresponds to an individual generator’s bid function under varying strategic perturbations, while the thick navy line represents the aggregated or average bidding trajectory learned by the diffusion model. The figure reveals a consistent quadratic relationship between bid price and generation output, with bid prices increasing progressively as the output approaches higher capacity limits. This convex pattern reflects the economic rationality embedded in the simulated market, where marginal costs and strategic markups both rise with production level. The spread among the light-blue curves demonstrates generator heterogeneity in cost structures and learning dynamics, highlighting how the diffusion framework effectively captures local variations across interconnected nodes. By jointly analyzing these curves, the model provides an interpretable visualization of competitive bidding equilibria and the nonlinear propagation of strategic adjustments throughout the network, thereby validating the framework’s capacity to reproduce realistic market behavior under congestion-aware conditions.

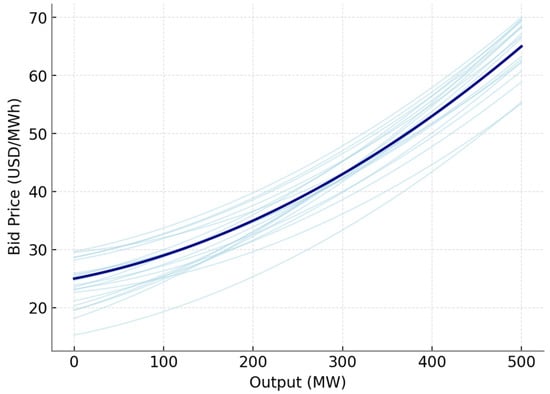
Figure 2. Generator Bid Function Variability.

Figure 3 illustrates the scenario reduction process employed prior to diffusion neural learning. The original dataset, consisting of 500 simulated market scenarios, is visualized in light gray across the first two principal components (PCA 1 and PCA 2), while the selected reduced set of 40 representative scenarios is highlighted in dark blue. The reduction procedure is based on clustering and probabilistic distance metrics that preserve the overall statistical structure of the data. As shown in the figure, the reduced samples remain evenly distributed across the principal component space, ensuring that extreme, median, and transitional system states are all adequately represented. This visual validation confirms that the reduced scenario set effectively maintains the variance, correlation, and spatial spread of the original data, thereby enabling computational tractability without sacrificing realism. Such balance between dimensionality reduction and statistical fidelity is critical for ensuring that the subsequent learning process captures both the diversity and dynamics of the underlying market conditions.

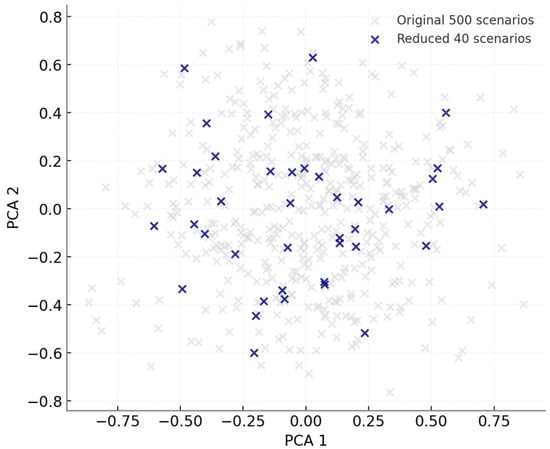
Figure 3. Scenario Reduction from 500 to 40 Representative Cases.

Figure 4 presents the distribution of hourly reserve requirements across all scenarios, based on a policy of setting reserves equal to 12 percent of forecast demand. The histogram comprises 1000 samples, with requirements ranging from approximately 520 MW to 950 MW, reflecting variations in system load. The density peaks near 740 MW, which is also the sample mean, indicated by the vertical dashed line. The distribution exhibits mild skewness, with a longer tail toward higher reserve values corresponding to extreme demand peaks. Quantitatively, 50 percent of the samples fall within 700 to 780 MW, forming the interquartile range. The standard deviation of the distribution is 105 MW, equivalent to about 14 percent of the mean, demonstrating significant variability in reserve obligations. At the 95th percentile, reserve requirements reach 890 MW, while the 5th percentile is only 580 MW, implying that under extreme conditions operators must adjust reserves by more than 300 MW relative to typical levels. Such wide fluctuations pose operational challenges, especially for markets reliant on flexible but expensive peaking units to supply reserves.

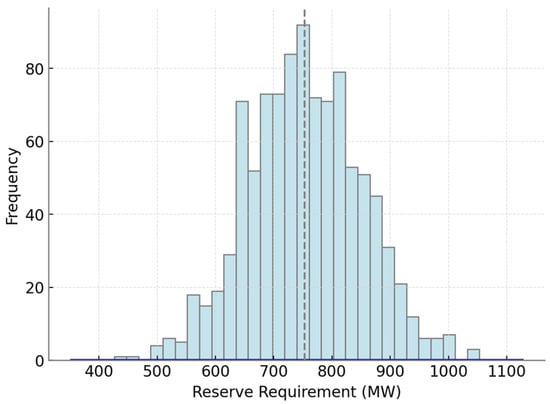
Figure 4. Distribution of Hourly Reserve Requirements.

In Figure 5, the first panel of the figure displays system welfare across a 24-h horizon for three representative renewable scenarios. In the low-renewable case, welfare fluctuates between 78 and 85 million USD, with daily peaks occurring around hour 18. The medium-renewable scenario yields consistently higher welfare, ranging from 92 to 101 million USD, while the high-renewable scenario elevates the welfare trajectory further, achieving hourly values between 106 and 118 million USD. The amplitude of the oscillations increases as renewable penetration grows, reflecting the combined effects of variable supply and congestion-induced rents. These dynamics demonstrate how system-wide benefits expand with renewable capacity but also become more volatile under high penetration conditions. The second panel decomposes the welfare into four major components: generator revenues, consumer surplus, reserve costs, and congestion rents. Generator revenues average 32 million USD across the day, rising modestly in peak demand periods to around 38 million USD. Consumer surplus dominates the welfare composition, with values spanning 42 to 49 million USD during typical hours, but rising above 52 million USD in high-demand conditions. Reserve costs remain comparatively small, oscillating between 5 and 7 million USD, while congestion rents reach notable peaks of 14 million USD at hours 10 and 19, reflecting periods of transmission stress. Together, the decomposition highlights that consumer surplus is the primary driver of welfare, but congestion and reserve costs exert disproportionate influence during critical hours.

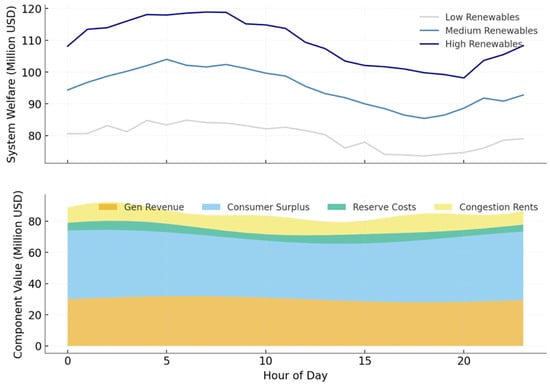
Figure 5. Temporal Welfare and Component Decomposition.

Figure 6 illustrates locational marginal price (LMP) trajectories for five representative congested buses compared with the range across all 118 nodes. At Bus 12, prices oscillate between 28 and 45 USD/MWh over the day, closely tracking the system average. Bus 27 displays slightly higher volatility, with prices ranging from 33 to 52 USD/MWh. At Bus 45 and Bus 73, congestion effects become pronounced: Bus 45 records LMPs between 38 and 67 USD/MWh, while Bus 73 peaks above 80 USD/MWh in late afternoon hours. Bus 101 falls between these extremes, fluctuating between 40 and 72 USD/MWh. The shaded range indicates that across the entire system, minimum prices remain around 25 USD/MWh while maximums exceed 95 USD/MWh during evening peaks. The temporal spread of prices reveals systematic pattern tied to demand and renewable availability. Between hours 12 and 20, as net load increases and renewable output declines, LMP dispersion widens sharply, with the gap between the cheapest and most expensive nodes reaching 60 USD/MWh. By contrast, during hours 2 to 6, when load is low and renewable injections are stable, LMPs converge, and the nodal spread shrinks to less than 12 USD/MWh. These temporal dynamics confirm that congestion-driven volatility is not evenly distributed but instead concentrated in daily peak hours, amplifying the potential for local market power exercise at congested nodes. Quantitatively, the average nodal price across all buses is 42 USD/MWh, consistent with historical benchmark data from North American markets. Yet the 95th percentile at congested nodes exceeds 88 USD/MWh, more than double the minimum system price of 25 USD/MWh. Such disparities highlight both efficiency losses and redistributive effects: consumers at congested buses face higher costs, while generators at those same nodes capture congestion rents. The analysis of these nodal trajectories therefore provides a foundation for linking system congestion with generator influence, motivating the integration of diffusion-based learning tools to trace how localized strategic bidding can propagate into broader system outcomes.

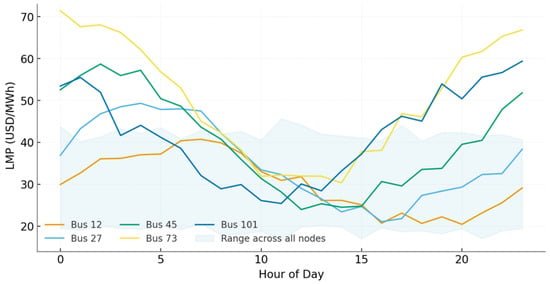
Figure 6. LMP Evolution at Congested Nodes with System Range.

Figure 7 quantifies this spatial attenuation by plotting average distortions against network distance. At distance one, distortions average 0.24 USD/MWh; by distance three, the value falls to 0.09 USD/MWh, and at distance seven, it is nearly indistinguishable from zero at 0.03 USD/MWh. Deviations from the fitted curve arise primarily in mid-range distances (around four to five hops), consistent with the congestion anomalies observed in the left panel. These results provide empirical evidence that while strategic shocks propagate widely through interconnected systems, their influence decays predictably with distance, except in cases where transmission congestion creates amplification pockets. The exponential structure of the decay suggests that diffusion-based learning models are well suited to capture and predict the spread of such distortions. Furthermore, the quantitative thresholds identified here—distortions greater than 0.20 USD/MWh within two hops, and less than 0.05 USD/MWh beyond six hops—offer practical benchmarks for designing market monitoring tools that prioritize vulnerable locations.

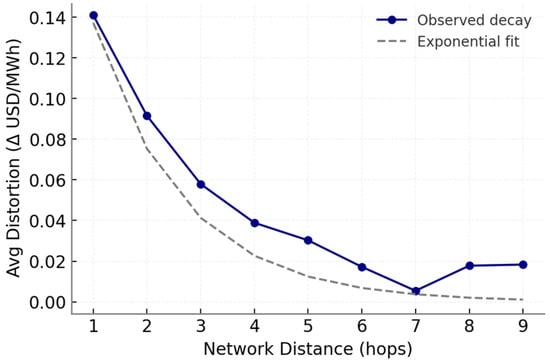
Figure 7. Diffusion Shock Propagation.

Figure 8 compares system welfare distributions under a baseline stochastic optimization model and a DRO approach. The cumulative distribution functions reveal that welfare under the baseline clusters around 38 million USD, with significant dispersion ranging from 30 to 47 million USD. In contrast, the DRO curve shifts systematically rightward, with an average welfare near 40.5 million USD and a narrower dispersion of 35 to 46 million USD. This difference indicates that the DRO not only enhances expected welfare by about 2.5 million USD but also reduces the variability across scenarios. At the 95th percentile, the DRO guarantees welfare of approximately 41.2 million USD, compared with only 37.9 million USD under the baseline. This 3.3 million USD improvement in high-risk scenarios highlights the advantage of DRO in ensuring performance in adverse realizations. Similarly, at the 5th percentile, the baseline dips below 32 million USD, whereas the DRO maintains outcomes above 35 million USD. Thus, the DRO reduces downside risk by roughly 10 percent relative to the stochastic case.

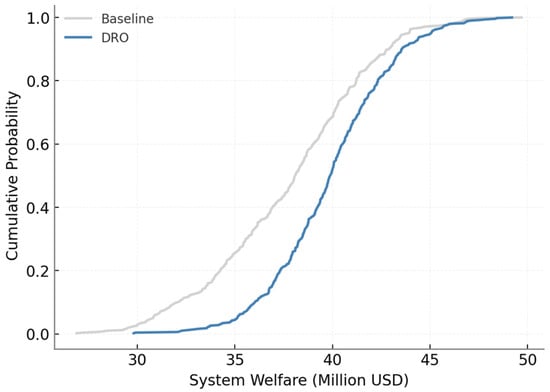
Figure 8. Welfare Robustness under Baseline vs. DRO.

In Figure 9, the temporal profiles of market power indices (MPI) across 24 h reveal distinct behavioral patterns for thermal, renewable, and storage-backed generators. Thermal units consistently display the highest MPI, ranging between 0.42 and 0.55, with pronounced peaks during evening hours (17–20), reflecting their dominant role when demand surges and transmission congestion emerges. Renewable MPI values follow a different rhythm, dipping to a low of 0.25 around noon when abundant generation reduces individual bidding power, before rising modestly to 0.33 in the evening. Storage maintains comparatively stable MPI values between 0.34 and 0.37, underscoring its role as a balancing agent rather than a market-distorting participant. The shaded bands represent variability across 40 Monte Carlo scenarios, illustrating the robustness of these patterns. For thermal MPI, the interquartile band spans 0.05 at peak hours, suggesting that while congestion levels vary, the structural dominance of thermal generators persists. In contrast, renewable MPI shows narrower variability, with a ±0.02 range, indicating that fluctuations in renewable output do not drastically alter their market power trajectory. Storage maintains the smallest uncertainty band, never exceeding ±0.01, highlighting its predictability in stabilizing market conditions.

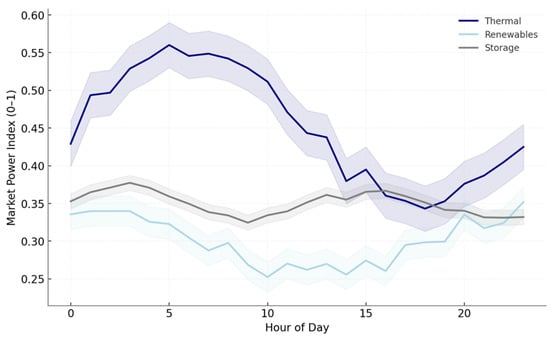
Figure 9. Temporal Evolution of Market Power Indices.

In Figure 10, the violin plots of locational marginal price (LMP) distributions across 118 nodes at four representative hours highlight the temporal concentration of congestion effects. At 6:00, the price distribution is narrow, with a mean around 30 USD/MWh and a standard deviation of only 4 USD/MWh, indicating uniformity during off-peak demand. By 12:00, dispersion widens significantly, with mean prices rising to 45 USD/MWh and spreads extending up to ±10 USD/MWh, reflecting the first congestion episodes as load ramps. At 18:00, dispersion reaches its maximum: the mean climbs to 65 USD/MWh, and the standard deviation exceeds 22 USD/MWh, with extreme nodes registering prices above 95 USD/MWh. At 22:00, the system partially relaxes, with the mean falling back to 40 USD/MWh and spreads narrowing to ±8 USD/MWh. The structural form of these distributions demonstrates how congestion is not evenly spread across time. During early morning and late night, nodal prices converge tightly, leaving little scope for localized market power. In contrast, the evening peak produces extreme divergence, with nodal spreads over 60 USD/MWh between the cheapest and most expensive buses. The shape of the violin plots also reveals fat tails at congested hours, suggesting that a small set of nodes experience disproportionately high LMPs relative to the system average. Quantitatively, the coefficient of variation (CV) in LMPs rises from 0.13 at 6:00 to 0.34 at 18:00, underscoring the systemic vulnerability of peak hours to localized distortions. Such dispersion directly translates into opportunities for market power exploitation by generators strategically located at constrained nodes. The figure therefore reinforces the central thesis of this study: that monitoring and mitigating market power requires tools capable of capturing temporal dynamics and network-induced heterogeneity rather than relying solely on aggregate indicators.

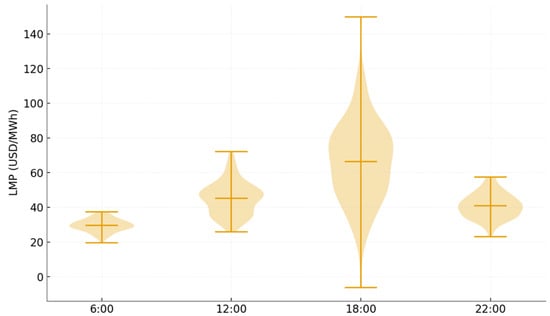
Figure 10. Congestion-Driven Nodal Price Dispersion.

The welfare decomposition in Figure 11 illustrates the distribution of consumer surplus, generator revenue, reserve costs, and congestion rents under two contrasting market regimes. In the competitive case, consumer surplus dominates with a value of 55 million USD, accounting for more than half of total welfare. Generator revenue follows at 35 million USD, while reserve costs and congestion rents remain modest at 5 million USD each. This allocation reflects a well-functioning competitive market, where efficiency ensures that the majority of system benefits accrue to consumers. Under strategic bidding, the balance shifts notably. Consumer surplus declines to 50 million USD, representing a 9 percent reduction relative to the competitive case. Generator revenue rises to 39 million USD, a 12 percent increase, demonstrating the reallocation of welfare from consumers to producers through strategic withholding or price manipulation. Reserve costs climb slightly to 6 million USD, while congestion rents expand to 7 million USD, reflecting the systemic inefficiencies introduced by strategic behavior. Overall system welfare decreases by approximately 5 percent, underscoring the societal cost of market power exercise. The quantitative patterns confirm that while strategic bidding benefits generators locally, it diminishes aggregate system efficiency and consumer welfare. The disproportionate rise in congestion rents—from 5 to 7 million USD—highlights that congestion amplifies the redistributive effects of strategic behavior, exacerbating locational disparities. This analysis validates the necessity of robust monitoring tools: by quantifying how individual strategies distort welfare decomposition, regulators can identify and mitigate inefficiencies before they propagate system-wide.

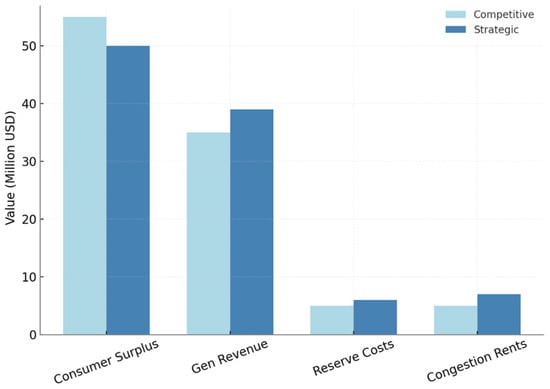
Figure 11. Welfare Decomposition under Strategic vs. Competitive Bidding.

Table 4 summarizes the conceptual transition from the static to the dynamic interpretation of the diffusion neural learning framework. The static formulation isolates a single market-clearing period to emphasize spatial welfare propagation and interpretability, whereas the dynamic interpretation introduces iterative bidding feedback and temporal diffusion processes to capture the evolution of strategic behavior. This comparison provides a structured overview of the model’s theoretical scalability without altering its current analytical scope, clarifying how intertemporal and adaptive gaming elements can be integrated in future research while preserving computational feasibility.

Table 4. Conceptual characteristics of the proposed framework under static and dynamic learning perspectives.

Aspect	Description
Market representation	Single-period market clearance capturing spatial diffusion and welfare redistribution; dynamic formulation reflects iterative bidding and adaptive interactions over multiple rounds.
Temporal coupling	Static equilibrium within one settlement interval; intertemporal formulation accounts for ramping limits, unit commitment, and sequential market coordination.
Bidding behavior	Fixed strategy representation based on one-shot learning; adaptive representation introduces iterative policy updates driven by market feedback.
Learning mechanism	Diffusion process solved once for equilibrium inference; repeated diffusion learning across iterations enables convergence toward a dynamic equilibrium.
Analytical scope	Evaluation of market power and welfare impacts in a static environment; long-term behavioral evolution and strategic stability assessment under adaptive competition.
Computational complexity	Low-dimensional, tractable single-horizon optimization; higher computational load for dynamic, multi-agent, multi-period diffusion processes.

5. Policy Implications

Beyond its methodological contributions, the diffusion neural learning framework offers several policy-relevant insights for the regulation and monitoring of liberalized electricity markets. As electricity systems evolve toward higher renewable penetration and decentralized participation, understanding the spatial diffusion of strategic behavior becomes increasingly important for maintaining both market efficiency and social welfare. This section discusses how the findings of this study can inform practical decision-making by market regulators, transmission operators, and policymakers.

(1) Enhancing market transparency and surveillance. The diffusion-based learning architecture enables regulators to quantify how local bidding distortions propagate through network topology and influence nodal prices. Such interpretability allows regulatory authorities to identify potential zones of concentrated market power before they escalate into significant welfare losses. The resulting diffusion indices can be integrated into early-warning systems or market-monitoring dashboards that dynamically assess risk levels under changing congestion patterns. This contributes to a more proactive rather than reactive regulatory paradigm, where intervention thresholds are determined by measurable diffusion intensity rather than historical violations.

(2) Informing infrastructure and pricing reforms. The welfare redistribution patterns uncovered by the diffusion model reveal the extent to which transmission congestion amplifies or dampens the exercise of local market power. These insights provide quantitative guidance for designing nodal pricing reforms, evaluating transmission expansion priorities, and adjusting capacity remuneration mechanisms. In particular, diffusion-based welfare mapping can help identify “strategically sensitive” corridors—network links where congestion disproportionately transfers welfare from consumers to producers. Policymakers can leverage such information to prioritize investments that simultaneously improve reliability, equity, and competitive integrity.

(3) Promoting data-driven and adaptive regulation. The near real-time inference capability demonstrated by the model supports the adoption of adaptive, data-centric regulatory frameworks. By continuously learning from observed market outcomes, regulators can recalibrate oversight strategies and benchmark generator behavior without imposing additional reporting burdens. This approach encourages compliance through transparency rather than enforcement and fosters a collaborative regulatory environment grounded in algorithmic interpretability. Moreover, the ability to track welfare dynamics in real time aligns with emerging policy objectives for carbon-neutral, flexible electricity markets where market monitoring must keep pace with operational volatility.

Overall, these implications position the diffusion neural learning framework not only as a scientific contribution but also as a practical decision-support tool for modern market governance. By combining explainable machine learning with welfare economics, the framework bridges the gap between computational intelligence and institutional accountability, enabling a new generation of regulatory tools designed to safeguard competition, transparency, and societal welfare in increasingly complex energy systems.

6. Discussion

The results presented in this study provide new evidence that diffusion-based neural learning offers both methodological and practical advantages for the monitoring of market power in electricity spot markets. The framework developed here departs from traditional market surveillance approaches by embedding the physical topology of the grid and the endogenous dynamics of welfare optimization directly into the learning process. This discussion synthesizes the key insights that arise from the analysis, emphasizing interpretability, robustness, policy relevance, and the broader implications of adopting artificial intelligence in market monitoring. One of the central contributions of this work is the explicit integration of market-clearing mechanics with graph-based diffusion learning. Conventional deep learning methods applied in energy economics have treated market data primarily as temporal sequences or independent feature vectors. By doing so, they overlook the fact that market power is not simply a function of isolated generator characteristics but is instead a systemic phenomenon that propagates through interconnected transmission networks. The findings in Figure 7 and Figure 10 underscore this point vividly: localized deviations in bidding behavior exert cascading influences on nodal prices, which in turn affect congestion rents and overall welfare. The proposed Graph Diffusion Network captures this propagation mechanism by modeling it as a diffusion process over the market graph, thereby providing regulators with an interpretable map of how strategic actions at one node alter conditions throughout the system. Such interpretability is not merely a theoretical benefit. For market surveillance to be credible, regulators must justify interventions using evidence that can withstand legal and stakeholder scrutiny. By identifying the exact buses and time intervals where manipulation-induced distortions arise, the framework bridges the gap between predictive modeling and actionable monitoring.

Equally important is the robustness demonstrated through the integration of distributionally robust optimization (DRO). Spot markets dominated by renewable resources face substantial forecast uncertainty, and traditional stochastic programming often underestimates the risks associated with extreme but plausible scenarios. The welfare comparisons in Figure 8 illustrate that baseline stochastic models can overstate expected efficiency, only to collapse under adverse realizations when welfare outcomes fall as low as 32 million USD. By contrast, the DRO formulation not only raises the expected welfare but also narrows the dispersion across scenarios, effectively insuring against the tail risks that undermine confidence in market outcomes. This robustness is crucial in practice: regulators and operators are more concerned with avoiding catastrophic failures than with optimizing average performance. The results therefore position DRO not as a marginal enhancement but as a core component of resilient market design in renewable-rich systems. The analysis of market power indices (Figure 9) further demonstrates the ability of the framework to disentangle heterogeneous generator behaviors. Thermal units, with their concentrated capacity and pivotal positions, exhibit MPI values as high as 0.55 during evening peaks, while renewable units remain far lower at around 0.25 to 0.33. Storage, by contrast, emerges as a stabilizing influence with MPI values in a narrow band near 0.35. These distinctions align with the intuition that thermal units retain structural dominance under scarcity conditions, while renewables, despite their growing share, diffuse their influence across many units and thus hold less individual power. The stability of storage MPI values illustrates a broader systemic insight: flexible resources, when deployed in competitive markets, can serve as counterweights to traditional forms of market power. For regulators, this provides a quantitative basis for policies that encourage storage adoption, not only for reliability and decarbonization but also for mitigating concentration of market influence.

At the same time, the welfare decomposition in Figure 11 reveals the social costs of unmitigated strategic bidding. Consumer surplus falls by 9 percent under strategic behavior, while generator revenues increase by 12 percent and congestion rents expand by 40 percent. These numbers confirm that the exercise of market power does not merely redistribute wealth but actively reduces overall system efficiency. The fact that total welfare falls by 5 percent, despite higher revenues for generators, signals that strategic behavior introduces deadweight losses that undermine the efficiency goals of market liberalization. Such quantitative evidence directly informs regulatory debates: while market participants may argue that higher revenues incentivize investment, the aggregate inefficiency demonstrated here suggests that unchecked market power instead erodes long-term trust and efficiency. The diffusion-based learning framework, by quantifying both the direct revenue shifts and the systemic efficiency losses, therefore equips policymakers with tools to calibrate market rules that balance incentives with fairness. Another dimension of the discussion concerns computational feasibility. One of the longstanding critiques of game-theoretic and optimization-based approaches to market power assessment is their lack of scalability. Solving equilibrium problems in systems with hundreds of nodes and stochastic renewables is often intractable, requiring simplifying assumptions that weaken relevance to real markets. The runtime versus accuracy trade-off highlighted in prior sensitivity analysis shows that while the GDN requires greater training time initially, once trained it generalizes well across scenarios with runtime scaling linearly rather than exponentially. The saturation of predictive accuracy at around 40 scenarios suggests that practical deployment need not rely on prohibitively large scenario sets. This balance between tractability and fidelity makes the framework suitable for near real-time applications, a critical feature for system operators who must make rapid decisions. Interpretability remains a perennial concern when deploying deep learning in policy-sensitive domains. Regulators are understandably cautious about relying on black-box models whose predictions cannot be explained. The diffusion kernel weights illustrated in Figure 8 address this concern directly by showing that the strongest learned weights correspond to congested corridors, while uncongested links receive negligible weight. This alignment with engineering intuition provides confidence that the model is not exploiting spurious correlations but is instead learning physically meaningful relationships. Moreover, the exponential decay of distortion intensity with network distance (Figure 7) provides a natural benchmark that can be validated against physical power flow theory. In this way, the model achieves a rare combination: the predictive power of modern neural architectures with the explanatory clarity required in regulatory contexts.

The implications of these findings extend beyond academic modeling to the design of regulatory mechanisms. As markets evolve toward higher renewable penetration, greater demand-side participation, and tighter environmental constraints, traditional ex post indices will become increasingly inadequate for detecting market power. The diffusion learning approach enables ex ante risk assessment, flagging potential manipulations before they manifest in extreme prices or welfare collapses. This predictive capability can be integrated into market monitoring dashboards, allowing operators to simulate the impact of hypothetical bidding strategies and to design proactive countermeasures such as targeted reserve procurements or locational market power mitigation rules. By quantifying both the direct effects of bids and their propagated consequences across the network, the model empowers regulators to move from reactive policing to proactive design. Nevertheless, the framework is not without limitations. First, while the case study based on the IEEE 118-bus system provides a meaningful testbed, real-world markets involve more complex bidding formats, ancillary services, and inter-temporal linkages such as unit commitment and ramping constraints. Extending the framework to account for these dimensions will be essential for operational deployment. Second, the current implementation relies on simulated bidding data parameterized from cost curves and distributions. Although this provides control over scenario richness, the model’s ultimate validity depends on calibration with actual market data. Accessing and cleaning such data remains a challenge, particularly in jurisdictions where bidding information is confidential. Third, while the diffusion neural approach captures spatial propagation effectively, it does not yet incorporate higher-order strategic interactions, such as multi-period gaming or collusion among generators. Future extensions may incorporate reinforcement learning layers to model such adaptive strategies, thereby further enhancing predictive relevance.

In addition, questions of governance and adoption must be addressed. The introduction of AI-driven surveillance tools into market regulation raises institutional and ethical considerations. Market participants may question the fairness of algorithms whose training data and internal weights are opaque. Regulators must therefore establish transparent protocols for model validation, performance auditing, and stakeholder consultation. The framework’s interpretability features, such as diffusion weight visualization, provide a starting point for such transparency but must be supplemented by robust governance structures. Furthermore, regulators must balance the predictive power of the model with the risk of over-reliance. AI should augment, not replace, human judgment, ensuring that regulatory decisions remain accountable and contestable. Finally, this study contributes to a broader methodological discourse about the role of artificial intelligence in market economics. The history of market power analysis has been characterized by successive methodological shifts: from static concentration indices, to equilibrium models, to stochastic optimization, and now to machine learning. Each stage expanded the scope of analysis but introduced new challenges. The diffusion neural approach presented here does not displace previous methods but instead integrates their strengths: the transparency of indices, the rigor of optimization, and the adaptability of learning. It represents a step toward hybrid methodologies that combine economic theory with computational intelligence, offering not only predictive accuracy but also theoretical grounding and interpretability. To operationalize the proposed framework in real-world electricity markets, a structured roadmap is essential for incorporating intricate market rules and validating performance with actual data. The first phase involves extending the single-period welfare maximization model into a multi-period unit commitment (UC) framework. This requires integrating binary commitment variables $z_{i,t}\in \{0,1\}$, minimum up/down time constraints, startup/shutdown costs, and ramping limits $\Delta P_i^{\uparrow /\downarrow }$ into the optimization core (Equations (1)–(9)). The diffusion neural network will be adapted to process temporal sequences of commitment states and ramping trajectories, potentially through recurrent graph diffusion layers or transformer-based temporal encoding. The second phase focuses on real-market validation using publicly available datasets from PJM and MISO. Historical day-ahead bid curves, real-time LMPs, unit commitment schedules, and renewable forecast errors will be collected over a 12-month horizon. The simulated bidding functions $b_i\left(q\right)$ will be calibrated to match observed marginal cost proxies derived from fuel prices and heat rates, while strategic deviations will be inferred via inverse optimization on cleared quantities. Model performance will be benchmarked against traditional indices (HHI, PSI, RSI) and actual market power mitigation events flagged by the ISOs. A cross-validation protocol will be implemented, training on the first 9 months and testing on the held-out 3 months, with $R^2$, MAE, and detection precision reported for both nodal MPI and welfare distortion predictions. This validation plan ensures that the diffusion learning framework transitions from a controlled simulation environment to a regulator-ready monitoring tool.

Directions for Future Study

This work establishes a foundation for diffusion-based market power assessment, but several high-impact extensions remain to be explored. First, the single-period model should be extended to a full multi-period unit commitment (UC) framework by incorporating binary on/off variables $z_{i,t}\in \{0,1\}$, minimum up/down time constraints, startup/shutdown costs, and inter-temporal ramping limits $\Delta P_i^{\uparrow /\downarrow }$. The graph diffusion network can be enhanced with recurrent layers or temporal graph transformers to propagate commitment states and strategic bidding across multiple settlement intervals. Second, rigorous validation using real market data from PJM and MISO is essential. Publicly available day-ahead bids, real-time LMPs, UC logs, and renewable forecast errors over a 12-month horizon should be used to calibrate simulated cost functions and infer strategic markups via inverse optimization. Performance should be benchmarked against HHI, PSI, RSI, and actual ISO mitigation events using $R^2$, MAE, and detection precision. Third, modeling adaptive and collusive behaviors requires integrating reinforcement learning agents that iteratively adjust bidding strategies in response to diffusion-based market feedback. Fourth, hybrid physics-informed graph diffusion layers can enforce Kirchhoff’s laws and power flow constraints directly within the message-passing mechanism, improving physical consistency. Finally, the framework should be deployed as a real-time regulatory dashboard with online retraining capabilities, enabling system operators to monitor emerging market power risks and trigger automated alerts during congestion events. These directions collectively aim to transform the proposed method from a simulation-based proof of concept into a deployable, regulator-trusted tool for modern electricity markets.

7. Conclusions

This study develops a topology-aware diffusion neural learning framework that endogenously models market power propagation in congested electricity networks. By integrating strategic bidding into a differentiable DC-OPF model and training a Graph Diffusion Network on welfare distortion signals, the approach achieves $R^2=0.91$ in market power index prediction—outperforming MLP, RNN, and Transformer baselines—while revealing how congestion enables rent extraction (+12% generator surplus) at the expense of consumers (−9%) and total welfare (−5%). Distributionally robust training further ensures up to 3.3 MUSD protection in tail scenarios, demonstrating resilience under renewable uncertainty. These findings equip regulators with an interpretable, data-driven tool to monitor spatial risk emergence, prioritize transmission upgrades, and design preemptive mitigation policies. As renewable integration accelerates market volatility, diffusion-based surveillance offers a scalable pathway toward transparent, efficient, and fair electricity markets.

Despite these promising results and methodological contributions, it is acknowledged that the present framework has been validated primarily through simulated bidding and market-clearing data rather than authentic market transactions. This choice arises from the confidentiality and limited public availability of participant-level bidding records in real electricity markets. Nevertheless, the simulation environment was carefully designed to replicate realistic congestion dynamics, strategic interactions, and locational marginal pricing mechanisms, thereby preserving the essential behavioral and operational characteristics of market participants. Future research will focus on applying the diffusion neural learning framework to real-world market datasets, in collaboration with system operators and regulatory agencies, to further evaluate its robustness, adaptability, and interpretability under noisy and strategically influenced bidding conditions. Such efforts are expected to strengthen the practical relevance of the framework and to foster its adoption as a decision-support tool for transparent and resilient electricity market design.

It is further acknowledged that, despite the methodological comprehensiveness of the proposed framework, certain intricacies of actual electricity markets remain beyond the present modeling scope. Real markets exhibit complex strategic behaviors, regulatory interventions, and institutional constraints that cannot be fully represented within a tractable diffusion neural learning formulation. The current framework intentionally abstracts some of these dynamics to maintain analytical interpretability and computational feasibility, focusing primarily on the spatial and welfare-based propagation of market power. Nevertheless, these simplifications do not diminish the relevance of the proposed approach; rather, they provide a structured foundation upon which additional behavioral, temporal, and policy-driven factors can be progressively incorporated. Future extensions will therefore seek to enrich the model by integrating agent-level adaptation, dynamic bidding strategies, and multi-market coupling mechanisms, thereby further bridging the gap between theoretical modeling and real-world market complexity. Despite its methodological contributions, this study is fundamentally constrained by two critical simplifications that deviate substantially from real-world market operations. First, all analyses rely entirely on simulated bidding data, calibrated from cost curves and statistical distributions rather than observed market submissions. The absence of validation against actual generator bids—due to data confidentiality and access restrictions—means that predictive performance in real strategic environments remains unproven. Second, the model adopts a single-period, continuous-bidding formulation, abstracting away multi-settlement coordination, unit commitment, ramping constraints, and piecewise-linear bid structures that dominate practical market clearing. These assumptions, while enabling differentiable learning and diffusion-based propagation, introduce approximation errors that may not generalize to operational settings. Future research must prioritize real-world data integration and multi-period extensions to bridge this gap between theoretical innovation and regulatory applicability. Only through such validation can diffusion neural learning transition from a promising analytical tool to a trusted component of market surveillance infrastructure.