Algorithmic Design of Modular Two-Layer Multiphase Windings Based on Number Theory

Abstract

Many electromechanical specialists have attempted to move away from the classical method of designing windings of electrical machines using the star of slot electromotive forces, but their approaches are not always simple or universal. This article proposes a straightforward algorithmic method of winding synthesis based on number theory, which makes it possible to compute the distribution table of symmetrical multiphase, multimodular windings. Analytical expressions are provided for determining the assignment of coils to the corresponding phases, phase zones, and winding modules by sampling coils from a closed-ring structure. The method allows one to determine the direction of coil connections within a phase and covers both overlapping and non-overlapping windings. Three characteristic cases of the relationship between the number of coils and the number of pole pairs in multiphase alternating-current electrical machines are analyzed from the perspective of number theory. Conditions for implementing symmetrical windings are presented. The distribution factors of modular windings for higher field harmonics are evaluated. To validate the approach, examples of application and experimental results are provided.

1. Introduction

In recent years, increased attention has been given to novel types of electrical machines—particularly multipole and multiphase machines—which enable reliable operation under rapidly changing load conditions found in direct-drive servo systems, electric transportation, and other applications. These are primarily fractional-slot electrical machines with concentrated or non-overlapping windings [1,2,3,4,5,6].

Such design solutions make it possible to reduce torque ripple, decrease the magnitude of losses in the armature winding, improve reliability and fault tolerance, lower the mutual inductance between phases and between individual winding coils, influence the filtering properties of the winding with respect to higher field harmonics, and extend the speed range toward ultra-low values [7,8,9,10,11].

Many publications have been devoted to the synthesis of multiphase windings of alternating-current machines and to the determination of their winding factors, with authors striving for simplicity and universality. This study examines the principles of constructing multiphase double-layer windings from the perspective of number theory. These principles make it possible to obtain a greater variety of possible configurations, as well as to use the winding material more efficiently due to shorter end connections. This is particularly characteristic of double-layer non-overlapping windings.

Figure 1 shows two possible variants of non-overlapping windings. The presented investigations are applied to the so-called modular electrical machines with different numbers of modules. Structurally, these consist of galvanically unconnected windings whose magnetomotive forces (MMFs) interact with a predominantly single magnetic flux of the inductor, typically equipped with permanent magnets.

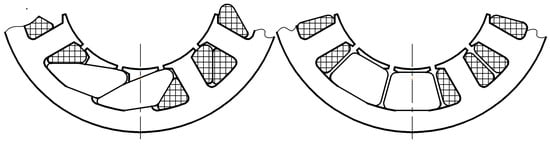
Figure 1. Fragments of armatures with double-layer non-overlapping windings.

The first works on the design of windings for electrical machines date back more than a century and belong to the pioneers of electromechanics—E. Arnold, R. Richter, and W. Kauders (W. Klím) [6,8]. They laid the foundation and developed the systematic method of designing windings for both direct-current and alternating-current machines. The principle of constructing a winding diagram lies in achieving the maximum value of phase electromotive forces (EMFs), based on the given number of slots Z, number of poles 2p, and the selected winding pitch. Today, for constructing diagrams of multiphase armature windings of alternating-current machines, the classical approach is traditionally applied—this is based on constructing the star of slot EMFs [2,12,13].

To build the star of slot EMFs, a phasor fan of electromotive force vectors is drawn. The origins of the vectors coincide at a single point, while the vectors themselves are shifted relative to one another by an angle α = 360°p/Z. For applying this principle to the construction of double-layer symmetrical windings, it is convenient to use the concept of a coil EMF star. It does not differ from slot EMF star, provided that the EMF vector of a coil is assumed to coincide not with the symmetry axis of the coil, but with the EMF direction of the slot—for example, the left side of the coil.

Thus, for single-layer windings (number of coils S = Z/2) and double-layer windings (S = Z), regardless of the pitch shortening, the EMF star will have an identical appearance, differing only in the number of vectors. This makes it possible to divide the coils into zones for a single-zone (ζ = 1) or double-zone (ζ = 2) phase [14], with the width of the phase zone usually equal to 360/(m ζ) electrical degrees (where m is the number of phases of the winding).

Figure 2 shows an example of an EMF star of a double-zone two-phase (m = 2) winding for the case of S = 16 coils (slots) and p = 7 pole pairs (α = 360 × 7/16 = 157.5 electrical degrees).

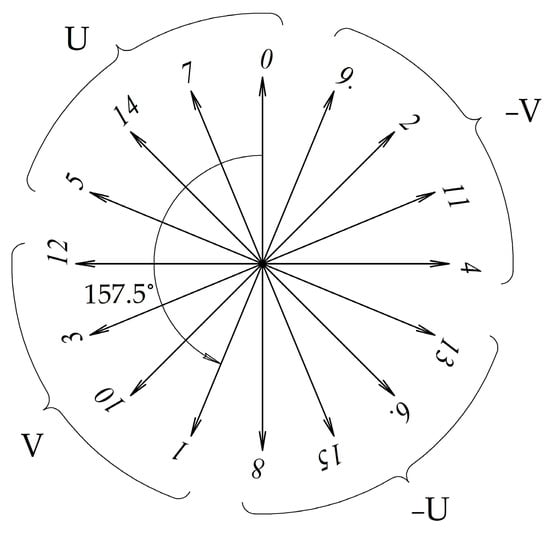
Figure 2. Coil EMF star for a winding with Z = 16, p = 7, m = 2, ζ = 2.

This is sufficient for constructing the winding diagram. The coils of one phase (e.g., zones U and −U) are connected either in series or in parallel; however, the coils of zone −U are connected in opposition to the coils of zone U.

Such an approach requires heuristic principles for selecting the structure of phases, requiring the graphical construction of the EMF star, which complicates the mathematical formalization of winding diagram design. Several attempts have been made to algorithmize the construction of simple winding diagrams [8,12,15]. However, these methods are not straightforward, do not cover all relevant cases, and do not account for modular structures. For example, the theory of symmetrical winding distributions [1] treats separately the cases of an even and an odd number of phases. Of particular interest is the study [8], which uses a tabular framework to mathematically describe winding configurations without relying on the slot-EMF star and allows coil transfers between zones to improve EMF harmonic content. The proposed classification of multiphase winding configurations [13] makes it possible to systematize and simplify the processing of complex multiphase systems. The article [16] presents a new tool for winding analysis using tensors, which, in the form of multidimensional tables, describe the interrelation among several concepts related to electrical machine windings.

The use of modular electrical machine constructions is now well documented in recent scientific studies [17,18,19]. Structurally, an indivisible electrical machine contains two or more separate, predominantly three-phase windings (modules) and a single magnetic system of the inductor. The armature core may be magnetically isolated for each module or shared among all machine modules. Each module operates with its own inverter, synchronized according to the current rotor position, either with one or several rotor position sensors or by a sensorless method [20].

The modular concept of drive design often makes it possible to reduce inverter currents, disconnect faulty phases or modules, and continue limited operation under partial load, which is acceptable in electric vehicle drives [21]. For modular machines, discrete scaling can also be applied to set a required power level without changing the machine’s design—simply by connecting or disconnecting individual modules [7,22].

Research on algorithmization of winding design aims to ensure high-quality performance indicators, i.e., maximizing the winding factor for the fundamental spatial harmonic of the field and improving the filtering properties of the winding to reduce or eliminate higher-order parasitic harmonics [1,5,10,23,24]. Particularly interesting and promising from this perspective are studies on electrical machines with star-polygonal windings [4,25]. Their main advantages include a significant reduction in higher-order EMF harmonics due to mutual compensation, and therefore an improvement in the sinusoidal quality of the EMF, reduction in losses and noise, and more efficient use of active materials.

Often, violation of symmetry conditions prevents the implementation of a perfectly symmetrical winding. In such cases, to expand the range of slot/pole combinations, some researchers propose disymmetrical (with certain symmetry violations) or asymmetrical designs [3,26], along with evaluation of the degree of asymmetry [3]. There is also the possibility of constructing symmetrical armature windings of permanent magnet synchronous machines (PMSMs) for otherwise unsuitable slot/pole ratios by employing multilayer winding configurations [4,23,27,28,29,30]. However, such windings are more complex to manufacture technologically.

Based on the conducted review, it has been established that existing methods for the synthesis of windings of permanent magnet synchronous motors (PMSMs) do not fully ensure comprehensive analysis, simplicity, and universality, nor do they allow for the synthesis of modular windings. Therefore, there is a pressing need to formalize and optimize a new algorithm.

The aim of this study is to establish, based on number theory, the regularities of assigning armature coils to the phase zone of a single-zone or double-zone winding, to the corresponding phase, and to the module of a multimodular winding, as well as to determine the direction of winding of the coils (direct or reverse) using analytical algorithms.

Structurally, the article consists of the above introduction with a literature review, research background, explanation of its relevance, and the statement of objectives; Section 2, which describes the algorithm for synthesizing symmetrical modular windings and considers three variants of the relationship between the number of coil sections and pole pairs; Section 3, which presents a universal formula for determining the distribution coefficients of modular windings for the fundamental and higher harmonics, along with an analysis of the winding’s filtering properties. To verify the research results, Section 4 and Section 5 provide examples of applying the algorithmic synthesis method, compare the results with the EMF star-based method, and present the experimental studies of a multimodule permanent-magnet synchronous machine. The article concludes with final remarks, a description of the patent obtained by the co-authors, and the list of references.

2. Algorithm for the Synthesis of Symmetrical Windings

Existing theories of winding construction [1,2] use the category of the greatest common divisor d between the number of coils S and the number of pole pairs p. In general, from the perspective of constructing symmetrical windings, we consider three possible cases of the relationship between the numbers S and p.

2.1. Case d = p

This is the first case, when the number S is divisible by the number p without a remainder. In this situation, all coils (or groups of coils) of one phase are magnetically located at the same angle to the pole, and the star of coil EMFs has m vectors repeated p times. Such windings can easily be divided into d identical modules without any shift in the magnetomotive forces of the modules.

The condition for implementing the winding in this case is that the ratio S/p must be a multiple of the number of phases m for odd m, and of twice the number of phases 2m for even m. It should be noted that windings with an even number of phases can only be double-zone.

In Figure 3, as an example, the winding diagram and the star of coil EMFs are shown for the case of S = 12 coils, p = 4 pole pairs, and the greatest common divisor between S and p, namely d = p = 4.

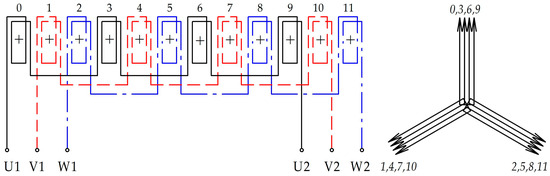
Figure 3. Winding diagram and coil EMF star S = 12, d = p = 4.

2.2. Case d = 1

The second case, opposite to the one described above, occurs when the number S is not divisible by the number p without remainder and has no common divisors other than unity. This case requires a more detailed examination. Here, the star of coil EMFs consists of S vectors uniformly distributed around the circle (each coil is magnetically shifted by 360/S electrical degrees), which ensures the lowest level of EMF pulsations and, consequently, of current and electromagnetic torque.

The symmetry of the structure of a multiphase non-overlapping winding is ensured by the divisibility of the number of coils S by the product of the number of phases m and the number of modules χ (for modules that are magnetically shifted relative to each other by an angle θ = 360/(m ζ χ) electrical degrees), and by the absence of common divisors between the number of coils S and the number of pole pairs p. The phase zones are formed by sampling coils from the closed-ring structure S with a step of

$$y={\displaystyle \frac{S k\pm 1}{p}}.$$

(1)

The sign “+” or “−” in (1) determines the direction of traversal along the circumference of the armature bore for identifying the next coil, adjacent in magnetic relation [14].

Based on the Chinese Remainder Theorem [31], it can be shown that for a cyclic S-group and coprime numbers p and S, there always exists a number $\mathrm{k}$ that satisfies Equation (1). Moreover, there are two such numbers—k₁ and k₂—which fulfill the condition k₁ + k₂ = p, and the numbers y₁ and y₂ from (1) satisfy y₁ + y₂ = S. One pair, y₁ and k₁, forms a right-handed winding with direct phase sequence, while the other pair, y₂ and k₂, forms a left-handed winding with reverse phase sequence.

To ensure the shortest length of jumpers between sections, one should select the number $\mathrm{y}$f, or which y < 0.5S, and the required phase sequence order is achieved by changing the connection order of the winding phase terminals.

The number of coils of the phase zone l is defined by the expression

$$l={\displaystyle \frac{S n+i}{y}},$$

(2)

where k—the smallest positive integer for which the step y becomes an integer;

n—a non-negative integer for which l is an integer;

i—the number of the coil according to its physical arrangement along the circumference of the armature bore [14].

The belonging of coil i to phase zone g = $\overline{0,m\zeta -1}$ is determined by the expression:

$$g(i)=\zeta \mathrm{Int}\left({\displaystyle \frac{l}{t}}\right)+\mathrm{Int}\left(\zeta \mathrm{Fr}\left({\displaystyle \frac{l}{t}}\right)\right),$$

(3)

where ζ = 1 or ζ = 2 for single-zone or double-zone winding, respectively;

Int—operator for extracting the integer part of a number;

t = S/m—the number of coils per phase;

Fr—operator for extracting the fractional part of a number.

The belonging of coil i to phase j = $\overline{0,m-1}$ is determined by the expression

$$j(i)=\mathrm{Int}\left(m \mathrm{Fr}{\displaystyle \frac{g\left(i\right)}{m \chi }}\right),$$

(4)

where χ—the number of armature winding modules.

The belonging of coil i to module u = $\overline{0,v-1}$ is determined by the expression

$$u(i)=v \mathrm{Fr}{\displaystyle \frac{g\left(i\right)}{\chi }}.$$

(5)

The winding direction of coil i for an odd number of phases m can be determined by the sign of the expression

$$\mathrm{sign}(i)={\left(-1\right)}^{\mathrm{Int}{\displaystyle \frac{2\cdot g\left(i\right)}{\chi \zeta }}},$$

(6)

However, a universal formula is applicable for any number of phases.

$$\mathrm{sign}(i)={\left(-1\right)}^{\mathrm{Int}{\displaystyle \frac{\left(1+2\mathrm{Fr}\left(m/2\right)\right)\cdot g\left(i\right)}{\chi \zeta }}}.$$

(7)

Using the numbering obtained in this way, the winding coils are connected to the corresponding phases of a given module either in the direct or reverse direction according to the determined winding direction, resulting in a multiphase winding of a modular alternating-current electrical machine. The order of coil connection follows the increasing (or decreasing) sequence of their numbers i, which minimizes the length of end connections and thereby reduces energy losses in the winding and the overall size of the electrical machine.

The starts of individual module phases (and, correspondingly, their ends) for an odd number of phases m are usually positioned evenly along coil EMF star vectors, corresponding to a conventionally two-pole electrical machine (360 electrical degrees). For an even number of phases, they are arranged evenly along half of the star (180 electrical degrees). For ease of manufacturing or for compact placement of terminals, symmetry can be intentionally broken by shifting the starts (and ends) of any phase to another coil within the selection j(i) of that phase, while preserving the traversal direction around the coils.

The starts of identically named phases of different modules, when arranged symmetrically, are shifted by the angular width of the phase zone

$$\theta ={\displaystyle \frac{360}{m \varsigma \chi }}.$$

(8)

As an example of applying the proposed method for constructing a multiphase winding, Table 1 presents the calculated structural parameters of a two-phase (m = 2), two-module (χ = 2), double-zone (ζ = 2) winding with S = 16 coils, p = 7 pole pairs, and a coil sampling step of

$$y={\displaystyle \frac{S k-1}{p}}={\displaystyle \frac{16\cdot 4-1}{7}}=9$$

Table 1. Calculated structure of a two-phase, double-layer winding (S = 16, p = 7, χ = 2, ζ = 2).

i	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
n	0	5	1	6	2	7	3	8	4	0	5	1	6	2	7	3
l(i)	0	9	2	11	4	13	6	15	8	1	10	3	12	5	14	7
g(i)	0	4	1	5	2	6	3	7	4	0	5	1	6	2	7	3
j(i)	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
u(i)	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
sign	1	−1	1	−1	1	−1	1	−1	−1	1	−1	1	−1	1	−1	1

Figure 4 shows the winding diagram corresponding to the parameters listed in Table 1, indicating the numbering of the coil positions in the armature (i), the winding direction of the coils (+—clockwise,−—counterclockwise), as well as 0U1, 0U2, 1U1, 1U2 and 0V1, 0V2, 1V1, 1V2—the starts and ends of the zero and first modules of phases U and V, respectively. For clarity, Figure 3 also shows the star of coil EMFs, indicating their belonging to phase j, zone g, and module u.

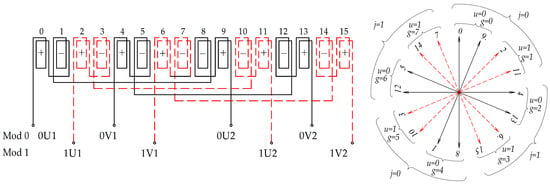
Figure 4. Diagram of a two-module, two-phase, double-zone winding with p = 7 and S = 16, and the coil EMF star.

2.3. Case 1 < d < p

Finally, the third case, intermediate between the two previously described, should be considered—when S and p have common divisors and the greatest of them satisfies 1 < d < p.

In this case, the star of coil EMFs has S/d vectors evenly distributed around the circle, repeated d times, superimposed. This allows the winding to be divided into χ = d independent modules without any angular magnetic shift relative to each other. Furthermore, a double-zone winding allows the number of modules without angular shift to be doubled, regardless of the value of d. All relations (1)–(8) remain valid.

In summary, it should be noted that the condition for constructing a symmetrical winding is that the number of coils S must be divisible by the product of d, m, and χ.

Regardless of the relationship between S and p, the coil pitch y_s is equal to or close to (in the case of pitch shortening) the pole pitch τ = S/2p. Hence, the number of poles should not exceed the number of coils (2p < S) for a non-overlapping, end-winding “coil-tooth” type winding (Figure 1) with a coil pitch y_s = 1. Reducing the number of poles of a non-overlapping winding is undesirable, as it leads to an increase in the yoke thickness of the magnetic cores, a reduction in the winding shortening factor, although the coil distribution factor in the phase zone changes very little (approximately 0.96 for a three-phase, double-zone, single-module (χ = 1) winding) (see Table 2). Approaching the lower theoretical limit of the number of poles for such a winding, 2p = S/2, at which it ceases to be non-overlapping (y_s > 1), worsens the ratio between the active length of the coil and the end-winding length, and increases copper losses.

Table 2. Results of determining the distribution factors for higher harmonics of a double-layer winding with the number of coils S = 36, phases m = 3, phase zones ζ = 2, modules χ = 1, and number of pole pairs p = $\overline{1, 20}$.

S	p	d	S/d	Kdν=1	ys	Kpν=1	Kwν=1	Kdν=3	Kpν=3	Kwν=3	Kdν=5	Kpν=5	Kwν=5	Kdν=7	Kpν=7	Kwν=7	Kdν=9	Kpν=9	Kwν=9
36	20	4	9	0.960	1	0.985	0.945	0.667	0.866	0.577	0.218	0.643	0.140	−0.177	0.342	0.061	−0.333	0	0
36	19	1	36	0.956	1	0.996	0.953	0.644	0.966	0.622	0.197	0.906	0.179	−0.145	0.819	0.119	−0.236	0.707	0.167
36	18	18	2	The winding is not implemented due to violation of symmetry conditions
36	17	1	36	0.956	1	0.996	0.953	0.644	0.966	0.622	0.197	0.906	0.179	−0.145	0.819	0.119	−0.236	0.707	0.167
36	16	4	9	0.960	1	0.985	0.945	0.667	0.866	0.577	0.218	0.643	0.140	−0.177	0.342	0.061	−0.333	0	0
36	15	3	12	0.966	1	0.966	0.933	0.707	0.707	0.500	0.259	0.259	0.067	−0.259	0.259	0.067	−0.707	0.707	0.5
36	14	2	18	0.960	1	0.940	0.902	0.667	0.500	0.333	0.218	0.174	0.038	−0.177	0.766	0.136	−0.333	1	0.333
36	13	1	36	0.956	1	0.906	0.867	0.644	0.259	0.167	0.197	0.574	0.113	−0.145	0.996	0.145	−0.236	0.707	0.167
36	12	12	3	1	1	0.866	0.866	1	0	0	1	0.866	0.866	1	0.866	0.866	1	0	0
36	11	1	36	0.956	1	0.819	0.783	0.644	0.259	0.167	0.197	0.996	0.196	−0.145	0.423	0.061	−0.236	0.707	0.167
36	10	2	18	0.960	1	0.766	0.735	0.667	0.500	0.333	0.218	0.940	0.204	−0.177	0.174	0.031	−0.333	1	0.333
36	9	9	4	The winding is not implemented due to violation of symmetry conditions
36	8	4	9	0.960	2	0.985	0.945	0.667	0.866	0.577	0.218	0.643	0.140	−0.177	0.342	0.061	−0.333	0	0
36	7	1	36	0.956	2	0.940	0.898	0.644	0.500	0.322	0.197	0.174	0.034	−0.145	0.766	0.111	−0.236	1	0.236
36	6	6	6	1	3	1	1	1	1	1	1	1	1	1	1	1	1	1	1
36	5	1	36	0.956	3	0.966	0.924	0.644	0.707	0.455	0.197	0.259	0.051	−0.145	0.259	0.038	−0.236	0.707	0.167
36	4	4	9	0.960	4	0.985	0.945	0.667	0.866	0.577	0.218	0.643	0.140	−0.177	0.342	0.061	−0.333	0	0
36	3	3	12	0.966	6	1	0.966	0.707	1	0.707	0.259	1	0.259	−0.259	1	0.259	−0.707	1	0.707
36	2	2	18	0.960	9	1	0.960	0.667	1	0.667	0.218	1	0.218	−0.177	1	0.177	−0.333	1	0.333
36	1	1	36	0.956	12	1	0.956	0.644	1	0.644	0.197	1	0.197	−0.145	1	0.145	−0.236	1	0.236

Notes. 1. The coil pitch $y_s$ is chosen as the value closest to the pole pitch $\tau$ to achieve the highest winding factor. Values $y_s=1$ correspond to configurations with non-overlapping windings. 2. The distribution factors calculated using (9) were verified by the graph–analytical method, defined as the ratio of the geometric sum of the EMF vectors of a phase zone to their algebraic sum.

Equations (1)–(7) are based on the equations originally developed for single-module windings [14], adapted through an empirical search process grounded in practical experience and observations, rather than on any pre-established theoretical models.

The proposed synthesis method allows the algorithmization and formalization of the construction process of non-overlapping windings of alternating-current electrical machines and extends its applicability to modular, multipole electrical machines [14,30].

3. Distribution Factors of Modular Windings

It is also necessary to consider the filtering properties of the winding phases with respect to higher-order harmonics of the magnetic field.

For odd harmonics of the magnetic field, the coil distribution factor in the phase zone for the ν-th harmonic is determined by the well-known formula [2]

$$K_{p \nu }={\displaystyle \frac{\sin q\nu \frac{\gamma }{2}}{q\sin \nu \frac{\gamma }{2}}},$$

(9)

where $q=\left[3-{\left(-1\right)}^{S/d}\right]{\displaystyle \frac{S}{2dm\varsigma \chi }}$—the equivalent number of uniformly distributed EMF vectors over the angular sector of the phase zone of a module;

ν—the order of the EMF harmonic;

$\gamma =\left[3+{\left(-1\right)}^{S/d}\right]{\displaystyle \frac{90d}{S}}$—the equivalent angle (electrical degrees) between two adjacent vectors on the coil EMF star diagram.

When characterizing the distribution factors of a phase for higher harmonics, it should be noted that their values for odd harmonics that are multiples of three are several times greater than for other odd harmonics, and the ability of the winding phase to filter higher EMF harmonics is better. An exception is made by windings with poor filtering properties, from the first and third cases considered above, where the common divisor d is not a prime number. This can be seen from the example of the distribution factors of phases for higher harmonics of a three-phase, two-zone, single-module (χ = 1), double-layer winding with the number of coils S = 36 and p = $\overline{1, 20}$ (Table 2).

Despite the fact that the third harmonic of the field may be significant, and a single phase filters it weakly, in a three-phase winding connected in a star configuration, the EMF pulsations of this harmonic do not cause current pulsations because the third EMF harmonics of a three-phase winding are in phase, which is well known [2]. When connected in a delta configuration, however, third-harmonic currents circulate within the winding, causing additional losses.

As for even higher harmonics of the magnetic field, they are absent in a symmetrically designed inductor due to the property of the magnetic field distribution being an odd function. However, they may exist in the presence of an uneven air gap under the poles, unequal pole widths, or nonuniform pole distribution around the periphery, especially with a small number of poles, as well as due to other structural inaccuracies or technological factors. In such cases, the filtering properties of the winding come into effect, since the distribution factor of coils in a phase for even harmonics is equal to zero, except for windings in which the common divisor d between the number of coils S and the number of pole pairs p is not a prime number.

4. Examples of Applying the Winding Synthesis Algorithm

A practically significant example is the application of this algorithmic method in research on autonomous-vehicle drives. One of the research directions involved the development and analysis of a universal multi-module permanent-magnet synchronous motor with 36 slots (Z = 36).

To design the winding scheme of a two-module χ = 2 three-phase synchronous machine with a shift of the resultant magnetomotive forces (MMFs) of the modules by θ = 30° el. (and θ = 20° el. for the three-module case, χ = 3), the above-described number theory-based method was applied, which lends itself well to algorithmization.

For this purpose, it is necessary to determine the belonging of each coil to the corresponding phase zone, phase, and module according to Formulas (3)–(5), as well as the connection direction of the coil according to (6) or (7). The calculation results for the two-module χ = 2 and three-module χ = 3 three-phase double-layer windings are presented in Table 3 and Table 4. The corresponding winding schemes are shown in Figure 5 and Figure 6.

Table 3. Calculation results for PMSM with χ = 2 and θ = 30°.

i	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35
n	0	10	1	11	2	12	3	13	4	14	5	15	6	16	7	17	8	18	9	0	10	1	11	2	12	3	13	4	14	5	15	6	16	7	17	8
l(i)	0	19	2	21	4	23	6	25	8	27	10	29	12	31	14	33	16	35	18	1	20	3	22	5	24	7	26	9	28	11	30	13	32	15	34	17
g(i)	0	6	0	7	1	7	2	8	2	9	3	9	4	10	4	11	5	11	6	0	6	1	7	1	8	2	8	3	9	3	10	4	10	5	11	5
+/−	1	−1	1	−1	1	−1	−1	1	−1	1	−1	1	1	−1	1	−1	1	−1	−1	1	−1	1	−1	1	1	−1	1	−1	1	−1	−1	1	−1	1	−1	1
u(i)	0	0	0	1	1	1	0	0	0	1	1	1	0	0	0	1	1	1	0	0	0	1	1	1	0	0	0	1	1	1	0	0	0	1	1	1
j(i)	0	0	0	0	0	0	1	1	1	1	1	1	2	2	2	2	2	2	0	0	0	0	0	0	1	1	1	1	1	1	2	2	2	2	2	2

Table 4. Calculation results for PMSM with χ = 3 and θ = 20°.

i	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35
n	0	10	1	11	2	12	3	13	4	14	5	15	6	16	7	17	8	18	9	0	10	1	11	2	12	3	13	4	14	5	15	6	16	7	17	8
l(i)	0	19	2	21	4	23	6	25	8	27	10	29	12	31	14	33	16	35	18	1	20	3	22	5	24	7	26	9	28	11	30	13	32	15	34	17
g(i)	0	9	1	10	2	11	3	12	4	13	5	14	6	15	7	16	8	17	9	0	10	1	11	2	12	3	13	4	14	5	15	6	16	7	17	8
+/−	1	−1	1	−1	1	−1	−1	1	−1	1	−1	1	1	−1	1	−1	1	−1	−1	1	−1	1	−1	1	1	−1	1	−1	1	−1	−1	1	−1	1	−1	1
u(i)	0	0	1	1	2	2	0	0	1	1	2	2	0	0	1	1	2	2	0	0	1	1	2	2	0	0	1	1	2	2	0	0	1	1	2	2
j(i)	0	0	0	0	0	0	1	1	1	1	1	1	2	2	2	2	2	2	0	0	0	0	0	0	1	1	1	1	1	1	2	2	2	2	2	2

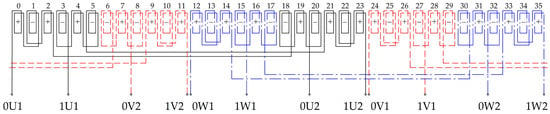
Figure 5. Winding diagram PMSM with χ = 2 and θ = 30°.

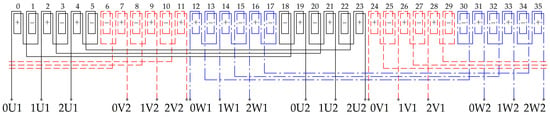
Figure 6. Winding diagram PMSM with χ = 3 and θ = 20°.

Above, the numbering of the coils corresponds to their physical arrangement in the stator of the electrical machine. The “+” and “−” signs indicate the connection direction of the coils in each module. The stars of the coil EMFs presented in Figure 6 and Figure 7 verify the proposed algorithmic method for the given two-module and three-module synchronous machines.

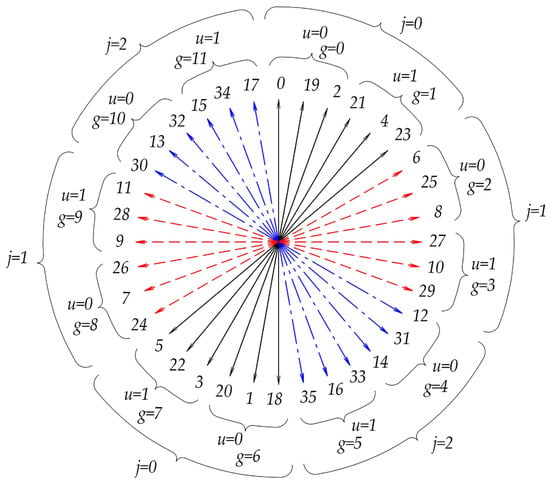
Figure 7. The coil EMFs star PMSM with χ = 2 and θ = 30°.

The algorithmic synthesis method does not require constructing the coil EMF star. Figure 7 and Figure 8 are provided solely for comparison and verification of the proposed algorithm.

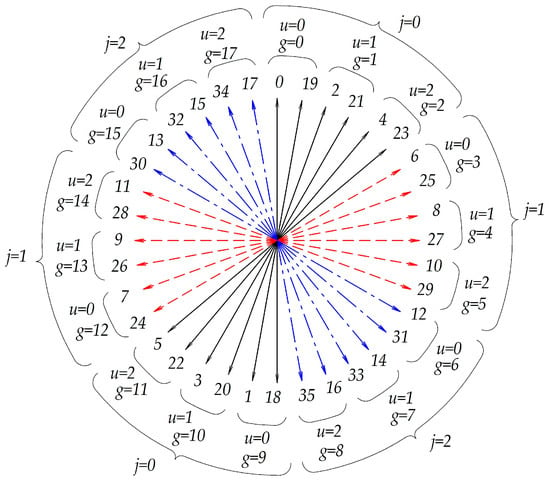
Figure 8. The coil EMFs star with χ = 3 and θ = 20°.

5. Experimental Studies

The purpose of the experiment was to determine the resultant winding factors of the phase windings for the first five odd EMF harmonics of a modular permanent magnet synchronous machine (PMSM) and to compare the obtained values with those calculated using the proposed algorithm (Section 2).

To achieve this, an experimental setup was used (Figure 9). It consists of the PMSM under study, a load/drive DC commutator machine, a support device, and measurement and switching equipment. Figure 10 shows the components of the test machine and the measuring concentric coil with a diametral pitch, placed on the inner surface of the stator.

Figure 9. Experimental setup: 1—test machine; 2—drive motor; 3—coupling; 4—frame.

Figure 10. Rotor (inductor) (a) and stator (armature) (b) with a diametral-pitch measuring coil (pos. 1).

The dimensions, winding data, and magnetic properties of the materials used in the test machine are given in Table 5.

Table 5. Input data of the test machine.

Parameter	Value
Active part dimensions:
length of stator and rotor cores, mm	140
stator bore diameter, mm	92
outer diameter of stator core, mm	138
air gap, mm	1
rotor pole height, mm	3.5
Materials:
stator core steel grade	M270-50A
permanent magnet material grade	N38SH
remanent flux density, T	1.2
coercivity force, kA/m	900
Winding data:
number of phases	3 × 2
number of stator core slots	36
number of poles	34
coil pitch (tooth pitches)	1
number of series turns per phase	62 × 2

The stator winding diagram of the test machine, with a shift of θ = 30° between the resultant MMFs of the modules, is shown in Figure 5.

The experimental procedure was as follows. The test machine was rotated by the drive motor and operated in generator mode at no load. In this mode, the EMF of the measuring coil and the phase EMF of a single module were recorded. The EMFs obtained in this way were decomposed into a Fourier series. The series was limited to the first eight odd harmonics, from the 1st to the 15th.

The resultant winding factor was determined as the ratio of the amplitudes of harmonics of a given order of the phase EMFs to the corresponding amplitudes of the EMF of the diametral-pitch measuring coil

$$k_{w\nu }={\displaystyle \frac{E_{mf\nu }^{\prime }}{E_{md\nu }}},$$

(10)

where $E_{mf\nu }^{\prime }$—amplitude of the ν-th harmonic of the phase EMF of the modular machine, normalized to the number of turns of the measuring coil;

$E_{md\nu }$—amplitude of the ν-th harmonic of the EMF of the diametral-pitch measuring coil.

The oscilloscope traces of the corresponding EMFs are shown in Figure 11a. The amplitudes of the higher odd harmonics of the EMF (except the first) of the diametral-pitch measuring coil and the normalized phase EMF are shown in Figure 11b. The numerical comparison results for the 1st, 3rd, 5th, and 7th harmonics are presented in Table 6.

Figure 11. (a) EMF oscilloscope traces: CH1—measuring coil, CH2—phase EMF of one module; (b) frequency spectrum of the amplitudes of higher harmonic EMFs.

Table 6. Comparison of winding factor values (χ = 1).

Parameter	Harmonic Order
	1	3	5	7
$E_{mf\nu }^{\prime }$, V	1.4213	0.0195	0.0119	2.0463 × 10−3
$E_{md\nu }$, V	1.4413	0.0704	0.0268	9.7331 × 10−3
$k_{w\nu }$ (experiment)	0.9859	0.2765	0.4438	0.2102
$k_{w\nu }$ (calculation)	0.9525	0.6220	0.1787	0.1190

The analysis of the obtained results indicates an almost complete agreement between the calculated winding factor for the first harmonic of the EMF and its experimentally measured value. For higher harmonics, however, a significant discrepancy is observed. This can be explained by several factors, including the specific design of the stator winding of the modular machine, whose end turns do not overlap (y_s = 1, Figure 1). Higher-order magnetic field harmonics of the tooth order, whose frequencies in this machine are comparable to the fundamental harmonic, can drastically alter the filtering properties of the stator windings [22]. The effect of the spatial arrangement of the coils in the slots is also apparently not accounted for in the proposed analytical method for defining $k_{w\nu }$.

Other reasons for the differences in winding factor values for higher harmonics may include the influence of local saturation in the stator core tooth zones, discrepancies between the actual width of the measuring coil and its calculated value, and the accuracy of the measurement equipment used.

Despite these circumstances, the experimentally obtained winding factor for the first harmonic of the EMF confirms the correctness of the analytical algorithm proposed in Section 2 and serves as validation of its adequacy.

6. Conclusions

• The algorithmic method based on number theory is simple to apply and suitable for formalizing and automating the synthesis of the structure of multi-phase, multi-module, two-layer windings, as well as for preliminary engineering analysis.
• The star of coil EMFs should be used only for illustrative theoretical generalizations, teaching, explanations, and comparisons.
• The use of coil EMFs, rather than slot EMFs, is universal. The star of coil EMFs has S/d vectors evenly distributed, which are repeated d-fold, allowing the winding to be divided into d separate modules without angular displacement.
• A necessary condition for constructing a symmetrical AC winding is that the number of slots S be a multiple of the product of the number of phases m, the number of modules χ, and the divisor d.
• Using windings with S and p ratios that have a common divisor d > 1 is undesirable, as it increases EMF and electromagnetic torque ripples and deteriorates the filtering properties of the winding for higher harmonics if d is not a prime number.
• A two-zone winding allows doubling the number of modules without angular displacement, regardless of the S/d ratio.
• Using modular windings with angularly shifted modules increases the winding factor.
• Future research will focus on generalizing the algorithmic design method to single-layer, mixed single–double-layer, and multilayer windings.

7. Patents

As a result of the work presented in this manuscript, a patent was obtained: Kharchyshyn, B.M.; Shchur, I.Z.; Makarchuk, O.V.; Khai, M.V. Method of constructing non-cross windings of multipole electrical machines of alternating current. Ukrainian Patent No. 129784, 30 July 2025, Bulletin No. 31/2025.