Abstract
This paper proposes a novel optimization framework for Magnetic Gear Compound Machines (MGCMs) that integrates parameter grouping and surrogate modeling to address challenges of high-dimensional design spaces and conflicting objectives. The core methodological contribution is a new parameter grouping strategy employing sensitivity analysis and partial correlation coefficients, which systematically classifies design parameters into high-, medium-, and low-impact groups. This approach achieves a 60% reduction in optimization dimensionality while preserving essential electromagnetic relationships. Latin Hypercube Sampling (LHS) is coupled with high-fidelity Maxwell 2D transient simulations to construct an accurate Kriging surrogate model, which is then integrated with the NSGA-III algorithm for efficient Pareto front identification. Comprehensive simulations demonstrate the framework’s exceptional performance. The sensitivity-based optimized design achieves an 85.5% reduction in inner rotor torque ripple (0.091), maintains 90.3% of the original torque output (475.100 N·m), and preserves 94.8% of the induced electromotive force (399.578 V), yielding an optimal objective function value of −0.901 that indicates superior overall performance improvement. In comparison, the correlation-based approach provides an 84.5% torque ripple reduction (0.097) with 97.7% torque retention (514.166 N·m) and 86.0% voltage preservation (362.739 V), corresponding to an objective function value of −0.841. Both grouping strategies significantly reduce computational cost by approximately 60% compared to conventional single-stage optimization methods. This research establishes an effective optimization paradigm for MGCMs, successfully resolving the fundamental trade-off between power density maximization and operational stability, with promising applications in electric propulsion and renewable energy systems.
1. Introduction
MGCMs have emerged as promising solutions for demanding applications where high reliability, maintenance-free operation, and precise torque control are critical [1]. These include electric vehicle traction systems requiring high torque density and minimal acoustic noise, tidal energy generators operating in harsh marine environments with limited maintenance access, and industrial servo drives demanding precise motion control with minimal torque ripple. However, the multi-objective design optimization of MGCMs presents significant challenges due to conflicting performance requirements and computational complexity, necessitating advanced optimization methodologies to fully exploit their potential in these practical applications.
MG has emerged as viable alternatives to their mechanical counterparts, offering superior transmission performance via the flux modulation effect [2]. These concentric MGs typically employ sandwiched, harmonic, or planetary configurations [3] that facilitate seamless integration with permanent magnet synchronous machines. The flux modulation-based architecture enables effective interaction between multiple components and electrical excitation systems, establishing a robust foundation for advanced electromechanical energy conversion.
Substantial progress has been achieved in developing innovative machine topologies through MG integration. Pioneering work by Chau et al. introduced a 2 kW magnetic-geared PM brushless motor for electric vehicle applications [4], with subsequent research achieving 85% efficiency in optimized in-wheel drive systems [5]. Various integration strategies have been explored, including side-by-side configurations for applications with adequate axial space [6] and spoke-type PM rotor designs that enhance magnetic coupling through flux concentration. Advanced implementations incorporating double-layer spoke-type PM arrangements with Halbach arrays have demonstrated improved harmonic characteristics and reduced torque ripple in tidal power generation [7]. Alternative architectures such as wound-modulator magnetic-geared compound permanent magnet machines show considerable potential for wind power generation systems [8]. Collectively, these investigations establish that concentric MG integration predominantly yields double-rotor structures with enhanced performance metrics.
The pseudo-direct-drive (PDD) compound permanent magnet machine constitutes another competitive topology, delivering substantial improvements in continuous torque density and operational efficiency [9]. This configuration incorporates a concentric MG within a conventional high-speed PMSM while implementing innovative magnetic circuit designs [10]. Prototype PDD machines for traction applications have demonstrated exceptional performance, achieving torque densities exceeding 100 N·m/L with peak efficiencies surpassing 95% [11]. Structural enhancements, including split-tooth designs, have further augmented torque density, while consequent-pole configurations for stationary magnet arrays have significantly increased torque per unit magnet volume [12,13].
Concurrently with these topological developments, notable advances have been made in PM design and optimization methodologies. Recent innovations combining unequal-thickness PMs with 90° Halbach arrays have enhanced the sinusoidal quality of radial and tangential magnetic flux waveforms by 19% while reducing torque ripple by over 20% [14]. Parallel improvements in modulator ring design incorporate multi-tooth protrusion structures that suppress 5th and 7th harmonics by 23% through circumferential flux guidance, complemented by non-uniform modulation schemes utilizing width-graded teeth and V-shaped magnetic barriers. These developments collectively increase output torque by 15% while reducing torque ripple by 42% [15].
The domain of motor multi-objective optimization has progressed significantly through the integration of surrogate modeling and intelligent optimization algorithms. The Kriging model has established itself as a predominant surrogate framework due to its robust performance in nonlinear high-dimensional fitting, consistently yielding coefficients of determination () exceeding 0.92. Representative implementations include the optimization of Flux-Focusing Halbach Coaxial Machines, where LHS with 200 design points reduced computational costs by 81% while achieving volumetric torque densities of 411 kN·m/m3 [16]. Genetic Aggregation Response Surface Methodology, which combines second-order polynomial regression with BP neural networks, has attained parameter optimization errors as low as 3.2% in five-phase permanent magnet motors [17]. The NSGA-III algorithm remains a leading multi-objective optimization technique, recognized for its superior Pareto front distribution. For example, it has facilitated a 15% increase in torque density accompanied by a 12% reduction in torque ripple in dual-structure permanent magnet motors [18]. Recent algorithmic enhancements focus on convergence acceleration, exemplified by Improved Dragonfly Algorithms employing Tent chaotic mapping, which reduce optimization iterations by 30% through dynamic parameter adjustment [19].
Despite these advancements, a integrated optimization framework specifically designed for MGCM applications remains underdeveloped. This research addresses this gap by introducing an innovative parameter grouping and surrogate modeling approach. The principal innovations of this work are twofold. First, this study presents the systematic investigation of multi-objective optimization methods specifically for Magnetic Gear Compound Machines (MGCMs), establishing a comprehensive methodology and workflow that addresses a significant research gap in this domain. Second, This research introduce a comparative framework employing multiple optimization strategies, including initial model determination based on parameter impacts on objective functions, single-stage optimization, sensitivity-based grouping, and correlation-based grouping utilizing partial correlation coefficients. Notably, the correlation-based grouping approach with partial correlation coefficients represents a methodological advancement that effectively captures nonlinear parameter interactions in MGCMs, providing a novel technical pathway for their optimization design.
2. Magnetic Gear Compound Machine Structure and Parameters
The MGCM is an advanced electromechanical system that synergistically integrates MG technology with PMSG functionality into a unified energy conversion architecture. As illustrated in Figure 1, the MGCM employs a four-layer concentric topology comprising: (1) an outer rotor serving as the primary torque input, (2) an intermediate flux modulator ring for magnetic field regulation, (3) an inner rotor functioning as the PM excitation source, and (4) a stationary stator housing the armature windings. This configuration establishes two distinct functional domains: the outer rotor-modulator-inner rotor assembly forms a MG unit for contactless speed/torque conversion, while the inner rotor and stator constitute the PMSG unit that transforms mechanical input into electrical output [20,21].
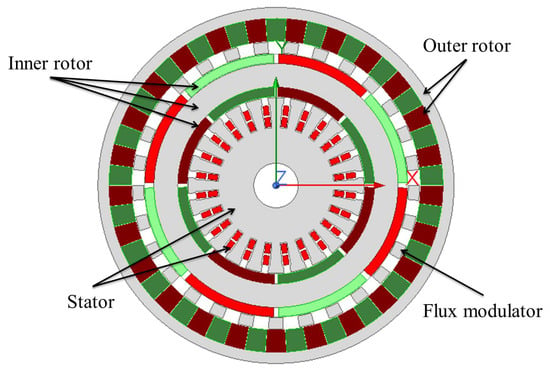
Figure 1.
Topology of the MGCM.
The operational principle is governed by the magnetic field modulation relationship:
where and denote the numbers of inner and outer rotor pole pairs, respectively, and represents the number of modulation segments.
The present design adopts an optimized asymmetric pole configuration (, , ) that satisfies (1), enabling effective coupling between the low-speed 25-pole pair field and the high-speed 4-pole pair field through 29 modulation segments [22]. For the integrated PMSG subsystem, electromagnetic synchronization requires matching the stator winding pole pairs () with the rotor poles (), implemented using a 24-slot stator configuration to ensure optimal magnetic circuit performance and harmonic suppression. The complete set of critical design parameters is provided in Table 1 for system implementation and performance evaluation.

Table 1.
Main Design Parameters of the MGCM.
The electromagnetic performance of the MGCM is governed by interactions among its four core components. While outer rotor and modulator parameters significantly impact torque transmission efficiency [23], this work focuses specifically on the power generation subsystem. Although these components indirectly influence PMSG electrical outputs—including voltage waveform quality, conversion efficiency, and power quality—through mechanical input effects, this work concentrates on the direct relationships between generator performance and both the inner rotor’s PM configuration (as excitation source) and stator geometry (incorporating winding distribution, slot-pole combination, and magnetic circuit design). The parametric optimization uses initial values and variation ranges provided in Table 2, established through electromagnetic analysis and design principles to ensure physical realizability and performance potential.

Table 2.
Initial Values and Allowable Variation Ranges of Optimization Parameters.
3. Objective Functions and Constraints
The MGCG constitutes a sophisticated electromechanical energy conversion system where power generation performance is primarily determined by the amplitude of the induced EMF () in the stator windings. Under fixed radial dimension constraints, maximizing becomes the principal optimization objective for enhancing power generation capacity [24]. The energy conversion process occurs in two sequential stages: (1) mechanical input undergoes speed/torque conversion through the MG unit with transmission ratio , and (2) electromechanical conversion takes place within the PMSG subsystem. This dual-stage operation requires simultaneous optimization of both the MG’s torque transmission efficiency and the PMSG’s electromagnetic performance.
To address these requirements, this study formulate a multi-objective optimization framework incorporating four critical performance metrics [25,26]: outer rotor torque ripple (), indicative of input-side mechanical vibration and acoustic noise; inner rotor torque ripple (), directly influencing electromagnetic vibration and output power quality; inner rotor average torque (), determining the system’s power output capability; and stator-induced EMF amplitude (), governing output voltage characteristics.
The torque ripple and average torque are formally defined as:
where denotes the maximum torque, represents the minimum torque, signifies the average torque, n is the calculation index and N indicates the total number of calculations.
Due to the high torque transmission efficiency inherent in MG systems, the average torques of the inner and outer rotors satisfy:
Consequently, only is used to represent the overall torque transmission capability of the system [27].
To mitigate the influence of disparate physical dimensions and orders of magnitude between objectives, the objective function is normalized using per unit transformation [28]:
where the subscript ‘ref’ denotes the base value of each parameter, typically corresponding to the initial design value or the rated value.
The multi-objective optimization employs NSGA-III to simultaneously optimize four separate normalized objectives without scalarization:
where the negative signs for and indicate maximization objectives.
After obtaining the Pareto-optimal set, a weighted scoring method is applied for final solution selection based on engineering priorities:
These are subject to:
where and denote the weighting coefficients for each objective, determined through sensitivity analysis to balance the competing objectives [29]. Based on comprehensive sensitivity studies and engineering priorities for MGCM applications, the weighting coefficients are set as , , , and , reflecting the greater emphasis on torque retention and induced EMF performance while maintaining acceptable torque ripple levels.
Constraints are primarily established around the objective functions and optimization parameters:
4. Multi-Objective Optimization Design Methodology
4.1. Parameter Grouping Strategy
To address the high-dimensional optimization challenges in the MGCM’s parameter space, this study employs an advanced parameter grouping strategy for effective dimensionality reduction. Utilizing sensitivity analysis and correlation analysis, design parameters are systematically classified into three distinct categories—high, medium, and low influence—based on their relative impact on system performance. As illustrated in Figure 2, this methodology significantly reduces optimization complexity while preserving essential design relationships, thereby enhancing computational efficiency without compromising solution quality [30].
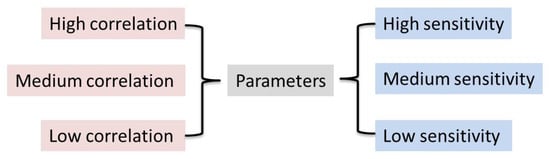
Figure 2.
Schematic diagram of the parameter grouping strategy.
Sensitivity analysis quantifies the independent influence of each parameter on the objective function. To eliminate dimensional discrepancies across different objective functions, this study adopts a normalized sensitivity calculation formula expressed as:
where represents the sensitivity coefficient of the i-th parameter . Parameters are categorized into high, medium, and low sensitivity groups according to the magnitude of .
Correlation analysis employs the Pearson correlation coefficient to evaluate linear associations between parameters:
where denotes the j-th objective function.
The conventional Pearson coefficient is susceptible to confounding effects from parameter interference. Consequently, this paper introduces the partial correlation coefficient [31] to isolate the influence of other variables:
where z represents the set of control variables, specifically encompassing all design parameters except x. Based on the values of , parameters are classified into high, medium, and low correlation groups.
4.2. Multi-Stage Optimization Process
Based on the grouping results, a sequential optimization framework is implemented, as depicted in Figure 3. Each optimization stage comprises five distinct steps:
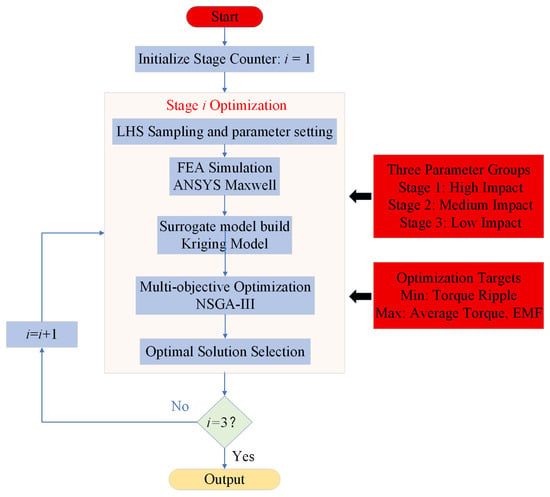
Figure 3.
Sequential optimization framework.
- (1)
- Parameter Sampling:LHS [32] generates experimental designs that uniformly fill the design space of each parameter group. For the k-th optimization stage with parameter set , fixed parameters follow the assignment rule: if (), the optimized value is utilized; if (), the initial value is maintained. This procedure generates a representative sample set that ensures comprehensive exploration of the design space while respecting the sequential optimization structure.
- (2)
- Surrogate Model Construction: A Kriging metamodel [33] is constructed to approximate the input-output relationship. The model consists of two components: a deterministic global trend and a stochastic process capturing local variations:The Gaussian process term follows a normal distribution , where is the correlation matrix parameterized by . The model parameters are estimated via maximum likelihood estimation, and prediction accuracy is validated against hold-out samples, achieving R2 values consistent with reported electrical machine optimization studies [34].
- (3)
- Pareto Front Search: The NSGA-III algorithm is applied to solve the multi-objective optimization problem defined in (9), which considers four separate normalized objectives. The algorithm identifies the Pareto-optimal set representing the best trade-offs among the competing objectives without artificial scalarization [35,36].
- (4)
- Optimal Solution Decision: From the obtained Pareto front, the final design solution is selected using the weighted scoring approach in (10). This ensures that the selected solution aligns with specific application requirements while maintaining the diversity of the Pareto-optimal set.
The proposed optimization framework exhibits strong generalization capability across different MGCM configurations. The core methodology of parameter grouping combined with surrogate modeling is fundamentally transferable to various magnetic gear machine topologies, including axial-flux, double-stator, and flux-modulation variants. While specific parameter sensitivity rankings may vary with topology changes, the underlying grouping principle and optimization workflow maintain their effectiveness. This adaptability ensures the framework’s utility beyond the specific MGCM configuration studied in this work.
5. Optimization Results and Analysis
5.1. Parameter Grouping Results
A comprehensive parameter sensitivity analysis was conducted by systematically evaluating each design variable across its full operational range while maintaining other parameters at baseline values. The methodology employed uniform sampling of 11 discrete points (indexed ) spanning from minimum to maximum allowable values for each parameter to ensure complete design space coverage. Through sequential single-variable perturbation and subsequent FEA simulations, the relationships between individual parameters and system performance metrics were rigorously quantified, with the complete sensitivity characteristics shown in Figure 4.
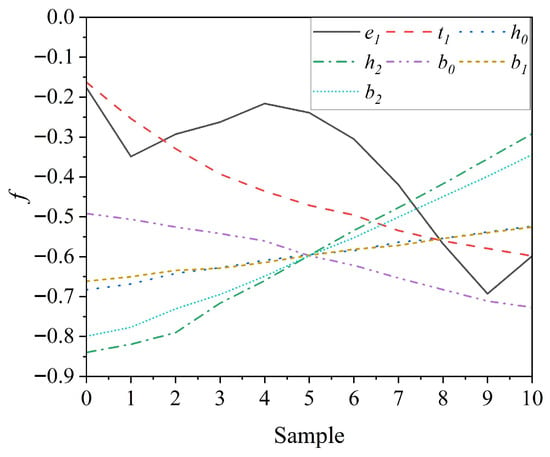
Figure 4.
Sensitivity analysis results for design parameters.
The analysis reveals distinct parametric influence patterns: parameters and exhibit inverse correlation with the objective function, indicating performance improvement with increasing values, while , , , and demonstrate direct proportionality, suggesting performance degradation at higher values. Parameter displays nonlinear oscillatory behavior with an overall decreasing trend, reflecting significant electromagnetic interactions. Based on these findings, the maximum values of and , the minimum values of , , , , and the 9th sampling point of were selected as the initial model configuration.
Quantitative sensitivity evaluation using standardized metrics produced the normalized sensitivity coefficients presented in Table 3, enabling systematic parameter classification into three influence groups: high-sensitivity (), including and , which dominate system performance; medium-sensitivity (), comprising and ; and low-sensitivity (), including , , , which exhibit minimal impact.

Table 3.
Normalized Sensitivity Coefficients for Design Parameters.
The sensitivity analysis reveals the relative influence of each parameter on the objective function, but understanding the physical mechanisms behind these sensitivities is crucial for design insight. The most sensitive parameter, the inner rotor embrace (), controls the pole-arc to pole-pitch ratio, directly affecting the magnetic flux distribution and harmonic content. A higher increases the fundamental flux component, enhancing torque, but also intensifies slot harmonics that increase torque ripple. The slot body height () ranks second in sensitivity, as it determines the winding space and thus the current loading capacity, but also influences the magnetic saturation in the stator teeth. The inner rotor thickness () and slot bottom width () exhibit moderate sensitivity, with balancing the magnetic path length and mechanical integrity, and affecting the flux distribution in the stator yoke and heat dissipation. These physical interpretations explain the sensitivity rankings and highlight the complex trade-offs in MGCM design.
A comprehensive correlation analysis was performed using both Pearson correlation coefficients and partial correlation coefficients (Figure 5) to quantify parameter relationships. Significant discrepancies were observed between these measures, particularly for parameter , which exhibits notable influence across multiple performance metrics, indicating substantial parameter interdependencies. Partial correlation analysis, which isolates direct effects by controlling other variables, provides more accurate influence classification: (1) and form a high-correlation group () dominating electromagnetic performance; (2) and constitute a medium-correlation group () with secondary influence; and (3) remaining parameters show negligible direct correlations ().
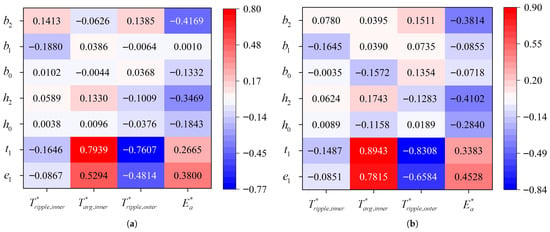
Figure 5.
Correlation analysis of design parameters: (a) Pearson correlation coefficients; (b) partial correlation coefficients.
The final parameter grouping results are summarized in Table 4. To validate the effectiveness of the proposed grouping methodology, non-grouped single-stage optimization approaches were employed as control benchmarks.

Table 4.
Final Parameter Grouping Results Based on Sensitivity and Correlation Analyses.
5.2. Optimization Result Analysis
Comparative evaluation of optimization strategies reveals distinct performance characteristics between sensitivity-based and correlation-based grouping methods, as evidenced by the Pareto fronts presented in Figure 6. Both approaches yield viable yet qualitatively different solutions, reflecting their respective methodological emphases. The sensitivity-based method achieves a 38.7% larger hypervolume, indicating broader design space exploration, while the correlation-based approach demonstrates alternative optimization pathways. This distinction is particularly evident in the three-dimensional objective space (inner rotor torque ripple, average torque, and induced EMF), where the sensitivity method exhibits a spread 1.5–2.3 times wider than the correlation method across objective axes. Outer rotor torque ripple was excluded from visualization due to minimal variation ( across solutions), enabling clearer interpretation of fundamental trade-offs. The differential performance between the two approaches originates from their distinct analytical foundations: the sensitivity method focuses on individual parameter impacts on objectives, whereas the correlation method emphasizes inter-parameter relationships. Both strategies provide valuable insights for multi-objective decision-making, offering complementary perspectives on MGCM system optimization.
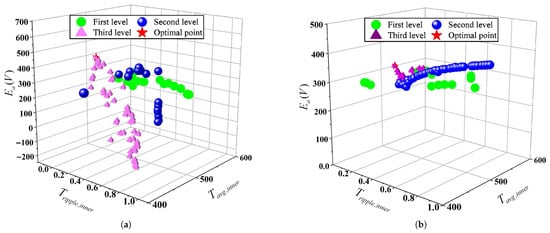
Figure 6.
Three-dimensional Pareto front showing inner rotor torque ripple (), average torque (, N·m), and induced EMF (, V). Outer rotor torque ripple is omitted due to minimal variation (<2.3%) across all solutions: (a) sensitivity-based grouping; (b) correlation-based grouping.
The Pareto fronts presented in this study were obtained using MATLAB 2018b’s gamultiobj function with the following settings: the population size was 200, there were a maximum of 200 generations per optimization stage, and the optimization process terminated when the change in objective function values remained below the threshold of 1 .
Using an appropriately weighted objective function prioritizing electrical energy production, finite element validation confirms substantial performance improvements across all optimized designs, as illustrated in Figure 7 and Figure 8. Comparative analysis reveals that both sensitivity- and correlation-based grouping strategies yield significant torque ripple reductions while effectively maintaining average torque output. Outer rotor torque ripple is consistently minimized across all configurations, with the correlation-based approach exhibiting notably stable transmission characteristics. Three-phase output waveforms verify proper electromagnetic operation, with the sensitivity-optimized design showing improved harmonic performance compared to conventional single-stage optimization. Induced EMF analysis further demonstrates that the sensitivity-based model achieves an effective balance between voltage retention and torque performance enhancement. These results collectively validate the capability of the proposed parameter grouping strategies to successfully manage design trade-offs between torque quality, power output, and voltage characteristics in MGCM systems.
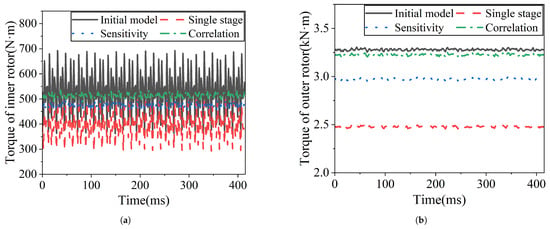
Figure 7.
Torque characteristics comparison: (a) Inner rotor torque (N·m) versus time (ms). (b) Outer rotor torque (kN·m) versus time (ms).
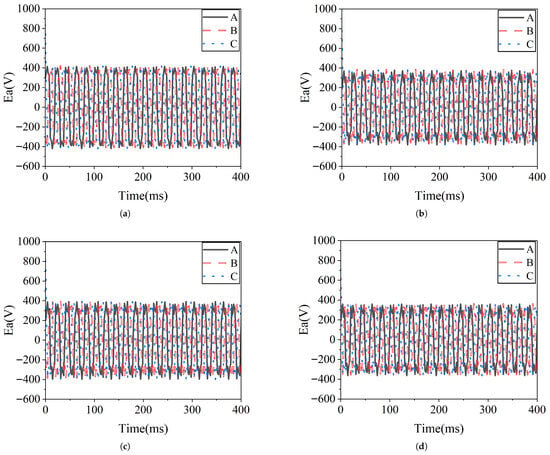
Figure 8.
Induced EMF waveforms (V) versus time (ms) for different optimization approaches: (a) Initial model. (b) Single-stage optimization. (c) Sensitivity-based grouping. (d) Correlation-based grouping.
The quantitative performance evaluation presented in Table 5 highlights distinct optimization outcomes across different approaches. The initial model achieves impressive torque output (526.237 N·m) and EMF (421.716 V) but suffers from excessive torque ripple (0.627), significantly compromising operational stability. This is reflected in its objective function value of −0.811, indicating suboptimal overall performance.

Table 5.
Comparative performance evaluation of different optimization approaches.
The single-stage optimization model demonstrates poor performance across most metrics, with significant discrepancies between predicted and FEA-validated results. The surrogate model predicts a torque output of 552.062 N·m, but FEA validation reveals an actual value of only 395.022 N·m—a substantial overestimation of 39.7%. Similarly, the predicted EMF of 548.187 V deviates from the FEA-validated 383.719 V by 42.9%. These large errors stem from the inherent limitations of surrogate modeling in high-dimensional spaces. Despite employing 1000 FEA samples for surrogate construction, the sampling density remains insufficient to accurately capture the complex parameter interactions in the 7-dimensional design space, resulting in significant surrogate model errors that misguide the optimization process toward suboptimal solutions.
In contrast, both grouped optimization approaches demonstrate substantial improvements in surrogate model accuracy through dimensional reduction. The sensitivity-based method shows excellent agreement between predicted and FEA-validated results, with torque prediction error of only 0.03% (474.939 N·m predicted vs. 475.100 N·m validated) and EMF error of 6.5%. The correlation-based approach similarly achieves high accuracy with torque prediction error of 0.02% (514.085 N·m predicted vs. 514.166 N·m validated). The superior predictive capability of grouped approaches validates their effectiveness: although each stage uses only 100 samples, the reduced parameter dimensionality (2–3 parameters per stage) ensures adequate sampling density for accurate surrogate modeling. This dimensional reduction enables more precise capture of parameter effects and interactions within each subgroup, ultimately leading to better optimization outcomes.
Comparative analysis of optimization results reveals distinct performance characteristics among different approaches. The sensitivity-based grouping achieves the best overall performance with objective function value f = −0.901, featuring the lowest torque ripple (0.091) while maintaining good torque output (475.100 N·m) and EMF (399.578 V). The correlation-based grouping provides superior torque retention (514.166 N·m, 97.7% of initial) with acceptable torque ripple (0.097), making it suitable for torque-critical applications. In comparison, the single-stage approach yields the poorest results across all metrics, with high torque ripple (0.518), reduced torque output (395.022 N·m), and the worst objective function value (f = −0.674), confirming the limitations of conventional optimization in high-dimensional MGCM problems.
The computational advantage of the grouped approach is significant. The single-stage method requires 1000 FEA simulations to explore the 7-dimensional parameter space, while the grouped approach achieves better results with only 400 simulations (100 for grouping analysis plus 300 for three optimization stages), representing a 60% reduction in computational cost. Considering that each FEA simulation requires approximately 4 min to complete, the single-stage optimization demands about 67 h of computation time, whereas the grouped approach reduces this to approximately 27 h. This efficiency gain stems from the fundamental advantage of dimensional reduction: by decomposing the problem into smaller subspaces, each with 2–3 parameters, the sampling density increases exponentially, enabling more accurate surrogate modeling despite fewer total samples.
5.3. Magnetic Field Distribution and Radial Magnetic Field Analysis
The optimized parameters obtained in the previous section were incorporated into the finite element simulation program to compute the motor’s magnetic field distribution, as shown in Figure 9. The results indicate that the magnetic field distributions obtained using the four different methods are generally similar. However, the single-stage optimization exhibits relatively lower magnetic field intensity with fewer magnetic saturation regions. The other three methods demonstrate comparable magnetic saturation characteristics.
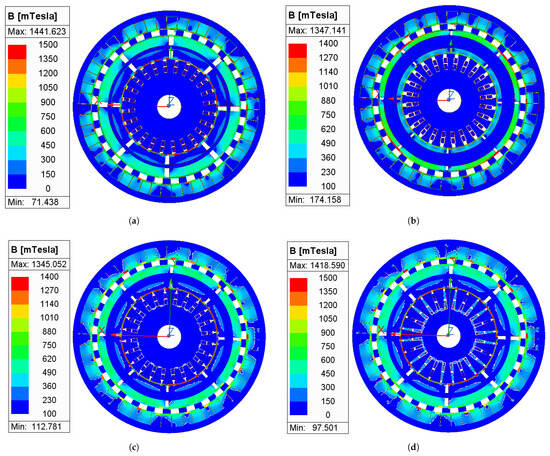
Figure 9.
Magnetic field distribution (mTesla) in the MGCM for different optimization approaches. (a) Initial model. (b) Single-stage optimization. (c) Sensitivity-based grouping. (d) Correlation-based grouping.
Further analysis was conducted on the radial magnetic fields in the first and second air gaps, with results presented in Figure 10. The radial magnetic field in the first air gap demonstrates essentially identical variation trends and magnitudes across all four methods. For the second air gap, while the variation patterns remain consistent, the initial model and correlation-based grouping approach exhibit comparable radial magnetic field strengths that exceed those of the other two methods, with the single-stage optimization showing the lowest magnitude.
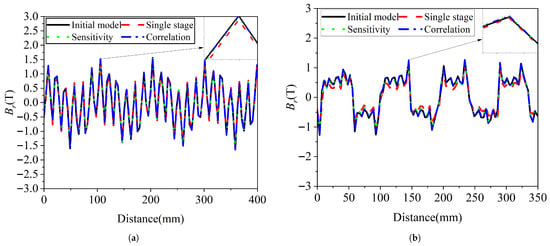
Figure 10.
Radial magnetic flux density (Tesla) versus circumferential position in air gap (mm): (a) First air gap. (b) Second air gap.
Fourier decomposition of the radial magnetic fields in both air gaps was performed, with results illustrated in Figure 11. The analysis reveals significant harmonic components at the 4th, 12th, 17th, and 25th orders in the first air gap, while the second air gap exhibits prominent harmonics at the 4th, 8th, 12th, 20th, and 29th orders. These harmonic characteristics align well with the operational principles of magnetic field modulated machines.
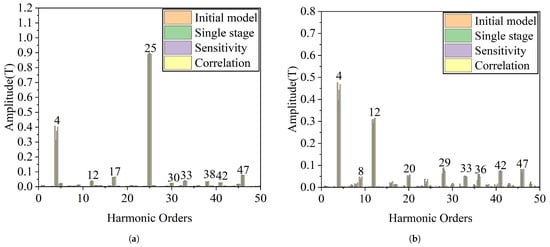
Figure 11.
Fourier harmonic analysis of radial magnetic fields showing amplitude (T) versus harmonic order: (a) First air gap. (b) Second air gap.
To address potential concerns about thermal impact and overall efficiency, this study analyzed the core losses and eddy current losses of the optimized designs through simplified simulations. Figure 12 presents a comparative analysis of loss characteristics for different optimization approaches.
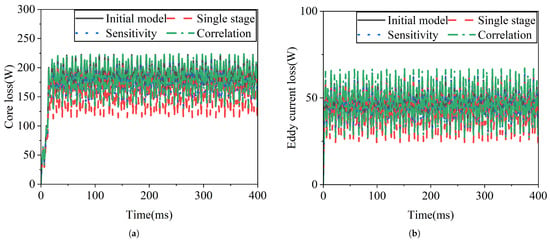
Figure 12.
Loss characteristics’ comparison: (a) Core loss distribution. (b) Eddy current loss distribution.
The analysis reveals that all optimization approaches exhibit similar core loss and eddy current loss distributions. The variations in both core losses and eddy current losses across different optimized designs are minimal, demonstrating that the parameter optimization process maintains stable thermal and loss performance. This consistency ensures that the improvements in electromagnetic performance—such as reduced torque ripple and maintained torque output—are achieved without compromising the overall efficiency of the MGCM system.
6. Conclusions
This research establishes fundamental contributions to MGCM optimization through several key innovations. Primarily, the study develops the comprehensive multi-objective optimization framework specifically tailored for Magnetic Gear Compound Machines, encompassing the complete process from parameter analysis and surrogate modeling to multi-objective optimization. Additionally, a parameter grouping method based on partial correlation coefficients is introduced, accurately capturing complex coupling relationships among MGCM parameters. Through systematic comparison of various strategies—including single-stage optimization, sensitivity-based grouping, and correlation-based grouping—the research demonstrates the differential impacts of these approaches on Pareto fronts, providing multiple viable optimization pathways for engineering practice. These contributions establish a methodological foundation for MGCM optimization design.
The integration of Kriging surrogate modeling with the NSGA-III algorithm demonstrates remarkable computational efficiency, reducing FEA requirements by 60% while maintaining high prediction accuracy. The optimized MGCM configurations demonstrate distinct performance characteristics: the sensitivity-based approach achieves 85.5% torque ripple reduction with 90.3% torque retention and 94.8% voltage preservation (f = −0.901), while the correlation-based method provides 84.5% ripple reduction with 97.7% torque retention and 86.0% voltage preservation (f = −0.841). Both approaches successfully stabilize outer rotor torque ripple below 5%, with the sensitivity-based method demonstrating superior overall performance balance. These results conclusively demonstrate the framework’s capability to resolve the critical trade-off between power density maximization and vibration suppression that has long challenged MGCM designers, while providing alternative optimization pathways based on different performance priorities.
The comparative analysis between sensitivity-based and correlation-based grouping strategies should be interpreted within the context of the specific weighting scheme () employed for final solution selection from the Pareto front. Under this weighting scheme that emphasizes torque retention and EMF performance, the sensitivity-based grouping achieves better overall comprehensive performance (f = −0.901). It is important to emphasize that both grouping strategies generate distinct Pareto-optimal sets, each containing solutions with different performance trade-offs. The optimal choice between these strategies depends on the specific weighting preferences and application requirements, with both methods providing valuable alternative design pathways for MGCM optimization.
The optimization framework demonstrates excellent generalization potential across different MGCM topologies, with the parameter grouping strategy providing a universal approach for managing design complexity in magnetic gear machines. This methodological foundation ensures broad applicability in electromechanical system optimization.
Future work will focus on extending this framework to incorporate thermo-mechanical coupled field analysis, further enhancing operational reliability under diverse loading conditions, and exploring applications in emerging domains such as aerospace propulsion and marine renewable energy systems. Additionally, experimental validation through MGCM prototyping will be conducted to verify the optimization results and reinforce the practical applicability of the proposed methodology.
Author Contributions
Conceptualization, B.Z. and Y.X.; methodology, B.Z. and J.Z.; software, B.Z. and K.Y.; validation, J.Z. and B.Q.; formal analysis, B.Z. and Y.X.; investigation, X.P. and X.S.; resources, Y.X. and X.Z.; data curation, B.Z. and X.P.; writing—original draft preparation, B.Z.; writing—review and editing, J.Z., Y.X. and X.Z.; visualization, B.Z. and X.P.; supervision, Y.X. and X.Z.; project administration, Y.X.; funding acquisition, B.Q. and K.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the China Postdoctoral Science Foundation under Grant No. 2024M761012, the Henan Province Science and Technology Research Project under Grant No. 242102220020, and the Henan Province Higher Education Institutions Key Scientific Research Project under Grant No. 24B470003.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to restrictions related to ongoing research and potential commercial applications.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| MGCM | Magnetic Gear Compound Machine |
| MG | Magnetic Gear |
| PM | Permanent Magnet |
| PMSG | Permanent Magnet Synchronous Generator |
| PDD | Pseudo-Direct-Drive |
| EMF | Electromotive Force |
| LHS | Latin Hypercube Sampling |
| FEA | Finite Element Analysis |
| NSGA-III | Non-dominated Sorting Genetic Algorithm III |
References
- Wang, L.; Yu, S.; Liu, H.; Gao, X. Design of High Torque Density Magnetic Gear Composite Motor for Electric Vehicles. In Proceedings of the 2023 IEEE 6th Student Conference on Electrical Machines and Systems (SCEMS), Wuhan, China, 1–3 December 2023; pp. 1–5. [Google Scholar]
- Atallah, K.; Howe, D. A Novel High-Performance Magnetic Gear. IEEE Trans. Magn. 2001, 37, 2844–2846. [Google Scholar] [CrossRef]
- Tlali, P.M.; Wang, R.J.; Gerber, S. Magnetic Gear Technologies: A Review. In Proceedings of the International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 544–550. [Google Scholar]
- Chau, K.T.; Zhang, D.; Jiang, J.Z.; Liu, C.; Zhang, Y. Design of a Magnetic-Geared Outer-Rotor Permanent-Magnet Brushless Motor for Electric Vehicles. IEEE Trans. Magn. 2007, 43, 2504–2506. [Google Scholar] [CrossRef]
- Ito, K.; Kadomatsu, T.; Nakamura, K. Efficiency Improvement of In-Wheel Magnetic Geared Motor and Feasibility Study for Walking Support Machines. In Proceedings of the IEEE International Electric Machines and Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; pp. 1818–1823. [Google Scholar]
- Jungmayr, G.; Marth, E.; Segon, G. Magnetic-Geared Motor in Side-by-Side Arrangement—Concept and Design. In Proceedings of the IEEE International Electric Machines and Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; pp. 847–853. [Google Scholar]
- Jing, L.; Liu, W.; Tang, W.; Qu, R. Design and Optimization of Coaxial Magnetic Gear with Double-Layer PMs and Spoke Structure for Tidal Power Generation. IEEE/ASME Trans. Mechatronics 2023, 28, 3263–3271. [Google Scholar] [CrossRef]
- Jian, L.; Xu, G.; Gong, Y.; Song, J.; Liang, J.; Chang, M. Electromagnetic Design and Analysis of a Novel Magnetic-Gear-Integrated Wind Power Generator Using Time-Stepping Finite Element Method. Prog. Electromagn. Res. 2011, 113, 351–367. [Google Scholar] [CrossRef]
- Atallah, K.; Rens, J.; Mezani, S.; Howe, D. A Novel “Pseudo” Direct-Drive Brushless Permanent Magnet Machine. IEEE Trans. Magn. 2008, 44, 4349–4352. [Google Scholar] [CrossRef]
- Dragan, R.S.; Clark, R.E.; Hussain, E.K.; Atallah, K.; Odavic, M. Magnetically Geared Pseudo Direct Drive for Safety Critical Applications. IEEE Trans. Ind. Appl. 2019, 55, 1239–1249. [Google Scholar] [CrossRef]
- Magnomatics. Pseudo Direct Drive—Traction Motor. Available online: https://www.magnomatics.com/pdd-traction-motor (accessed on 1 January 2024).
- Gan, Q.; Fang, Y.; Pfister, P.D. A Novel Concentrated-Winding Vernier Pseudo-Direct-Drive Permanent-Magnet Machine. IEEE Trans. Magn. 2022, 58, 8201505. [Google Scholar] [CrossRef]
- Yin, X.; Fang, Y.; Pfister, P.D. High-Torque-Density Pseudo-Direct-Drive Permanent-Magnet Machine with Less Magnet. IEEE Trans. Ind. Electron. 2018, 65, 37–44. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, W.; Cheng, J.; Zhao, J.; Qian, F. Design and Optimization of Axial Field Flux-Switching Magnetic Gear Composite Motor Based on Varying-Network Magnetic Circuit. IEEE Access 2023, 11, 53749–53759. [Google Scholar] [CrossRef]
- Xu, Z.; Zhu, Z.; Liu, R.; Chen, S. Design of an Eccentric Pole Type Magnetic Geared Composite Motor. In Proceedings of the 30th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Nanjing, China, 26–28 November 2024; pp. 1–5. [Google Scholar]
- Bramerdorfer, G.; Zăvoianu, A.C. Surrogate-Based Multi-Objective Optimization of Electrical Machine Designs Facilitating Tolerance Analysis. IEEE Trans. Magn. 2017, 53, 8203211. [Google Scholar] [CrossRef]
- Ma, Y.; Ching, T.W.; Fu, W.N.; Niu, S. Multi-Objective Optimization of a Direct-Drive Dual-Structure Permanent Magnet Machine. IEEE Trans. Magn. 2019, 55, 8203504. [Google Scholar] [CrossRef]
- Cui, X.; Li, Y.; Fan, J.; Wang, T.; Zheng, Y. A Hybrid Improved Dragonfly Algorithm for Feature Selection. IEEE Access 2020, 8, 155619–155629. [Google Scholar] [CrossRef]
- Shan, S.; Wang, G.G. Survey of Modeling and Optimization Strategies to Solve High-Dimensional Design Problems with Computationally-Expensive Black-Box Functions. Struct. Multidiscip. Optim. 2010, 41, 219–241. [Google Scholar] [CrossRef]
- Chau, K.T.; Chan, C.C.; Liu, C. Overview of Permanent-Magnet Brushless Drives for Electric and Hybrid Electric Vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2246–2257. [Google Scholar] [CrossRef]
- Lee, J.I.; Kim, D.H.; Park, M.R.; Lim, M.S. Design and Analysis of the Coaxial Magnetic Gear Considering the Electromagnetic Performance and Mechanical Stress. IEEE Trans. Appl. Supercond. 2020, 30, 5203505. [Google Scholar] [CrossRef]
- Lee, J.I.; Kim, D.H.; Park, M.R.; Lim, M.S. Electromagnetic Performance Analysis and Experimental Verification Considering the End Effect of Linear Magnetic Gears Using Subdomain-Based Analytical Method. IEEE Trans. Magn. 2021, 57, 8203505. [Google Scholar] [CrossRef]
- Ling, Z.; Ji, J.; Zeng, T.; Zhao, W. Design Optimization and Comparison of Linear Magnetic Actuators under Different Topologies. Chin. J. Elect. Eng. 2020, 6, 41–51. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D. Electrical Machines and Drives for Electric, Hybrid, and Fuel Cell Vehicles. Proc. IEEE 2007, 95, 746–765. [Google Scholar] [CrossRef]
- Wu, Z.; Su, G.J. High-Performance Permanent Magnet Machine Drive for Electric Vehicle Applications Using a Current Source Inverter. In Proceedings of the 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008; pp. 2812–2817. [Google Scholar]
- Dai, L.; Gao, J.; Niu, S.; Huang, S. Multi-Electromagnetic Performance Optimization of Double-Layer Interior Permanent Magnet Synchronous Machine. IEEE Trans. Ind. Electron. 2024, 71, 14535–14545. [Google Scholar] [CrossRef]
- Jian, L.; Chau, K.T.; Gong, Y.; Jiang, J.Z.; Yu, C.; Li, W. Comparison of Coaxial Magnetic Gears with Different Topologies. IEEE Trans. Magn. 2009, 45, 4526–4529. [Google Scholar] [CrossRef]
- Lu, Y.; Kai, Y.; Songjun, S.; Yixiao, L.; Fei, X.; Cheng, L. Study on the Influence of a Combined-Halbach Array for the Axial Flux Permanent Magnet Electrical Machine with Yokeless and Segmented Armature. IEEE Trans. Magn. 2024, 60, 8201505. [Google Scholar] [CrossRef]
- Jara, E.C. Multi-Objective Optimization by Using Evolutionary Algorithms: The p-Optimality Criteria. IEEE Trans. Evol. Comput. 2014, 18, 167–179. [Google Scholar] [CrossRef]
- Simpson, T.; Poplinski, J.; Koch, P.; Allen, J. Metamodels for Computer-Based Engineering Design: Survey and Recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, J.; Xia, Y.; Zhu, X. Research on a Two-Stage Multi-Objective Optimization Design Method for Permanent Magnet Synchronous Motors Utilizing Partial Correlation Coefficients for Parameter Screening. IEEE Access 2025, 13, 143479–143488. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, G.; Zhang, J.; Gao, Y.; Hua, W.; Wang, Y. An Improved Kriging Surrogate Model Method With High Robustness for Electrical Machine Optimization. IEEE Trans. Ind. Appl. 2024, 60, 6799–6810. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Marler, R.; Arora, J. Survey of Multi-Objective Optimization Methods for Engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).