Coordinated Active and Reactive Power Control of VSC-HVDC for Enhancing Static Voltage Stability in AC/DC Systems
Abstract
1. Introduction
- Based on the theory of minimum modulus eigenvalue analysis, a numerical analysis method suitable for quantifying the static voltage stability margin of AC/DC power systems is proposed.
- The power coupling relationship between the sending-end and receiving-end converters of VSC-HVDC is taken into account to improve analysis accuracy.
- Through the coordinated control of active and reactive power in the VSC-HVDC converter station, the static voltage stability of the AC/DC power system has been effectively enhanced under the premise of meeting the actual operation constraints.
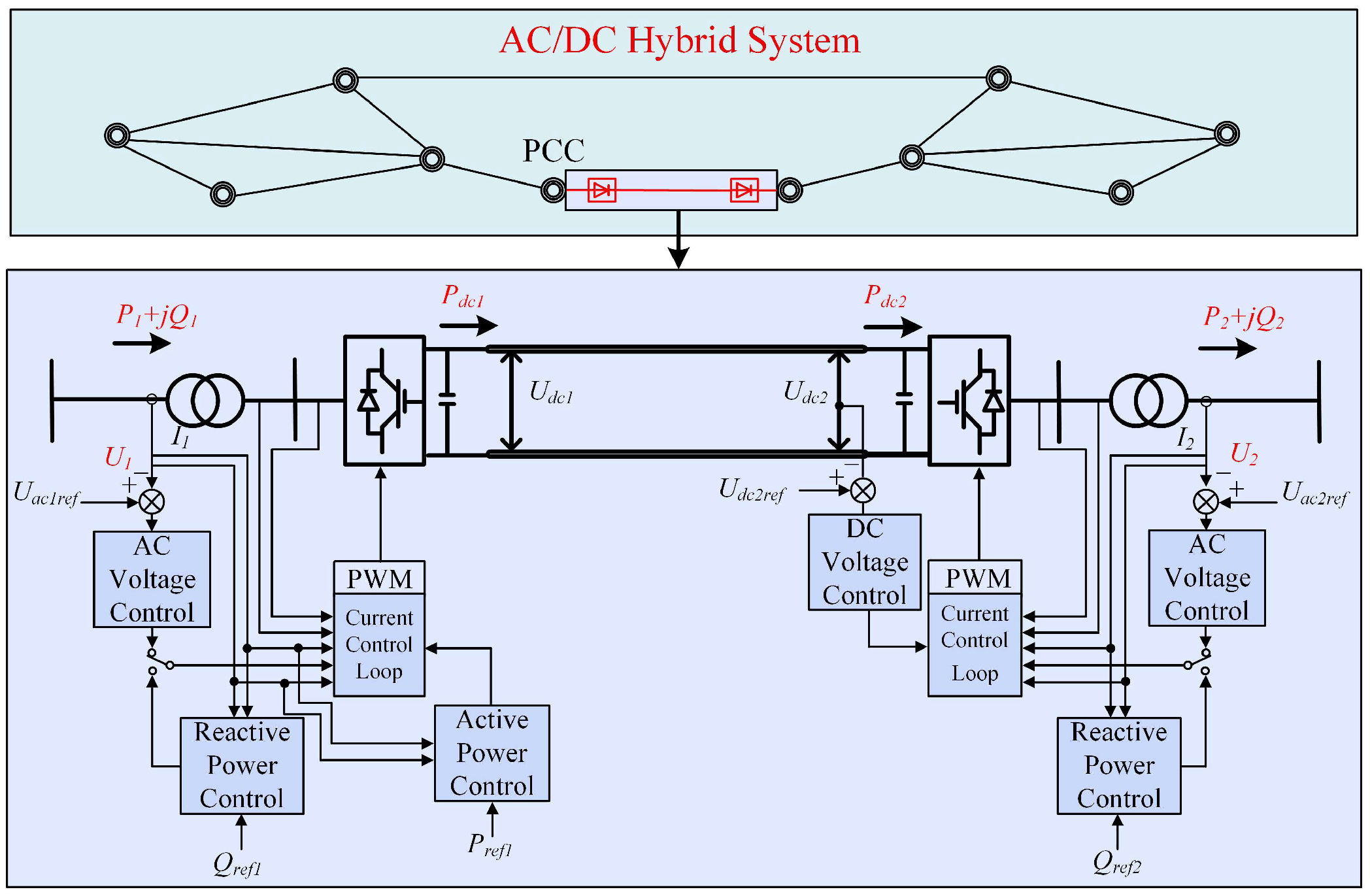
2. Static Voltage Stability Analysis of AC/DC System
2.1. Power Flow Solution Methods for the AC/DC System
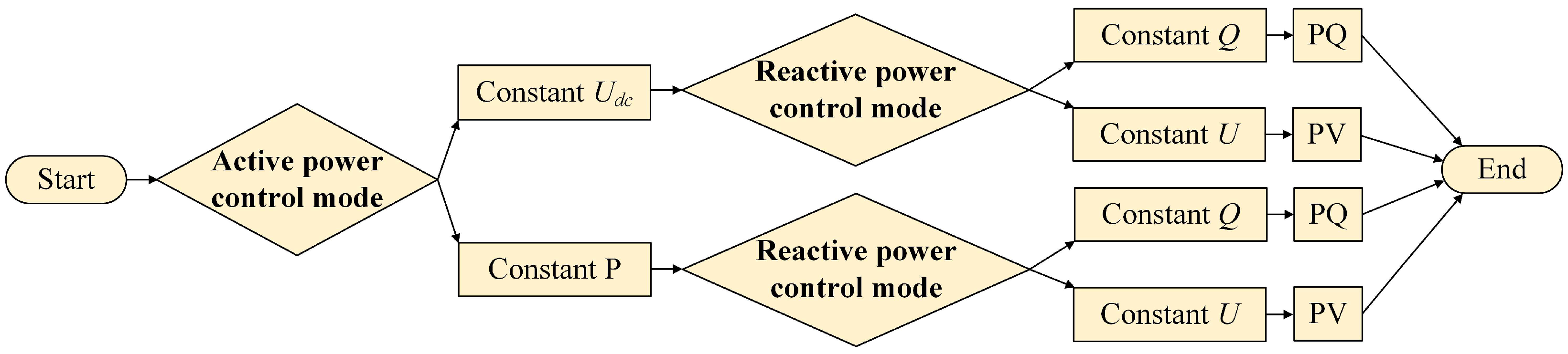
2.1.1. The Power Relationship Between VSC-HVDC and AC System
2.1.2. Power Flow Solution Method Considering Converter Station Losses
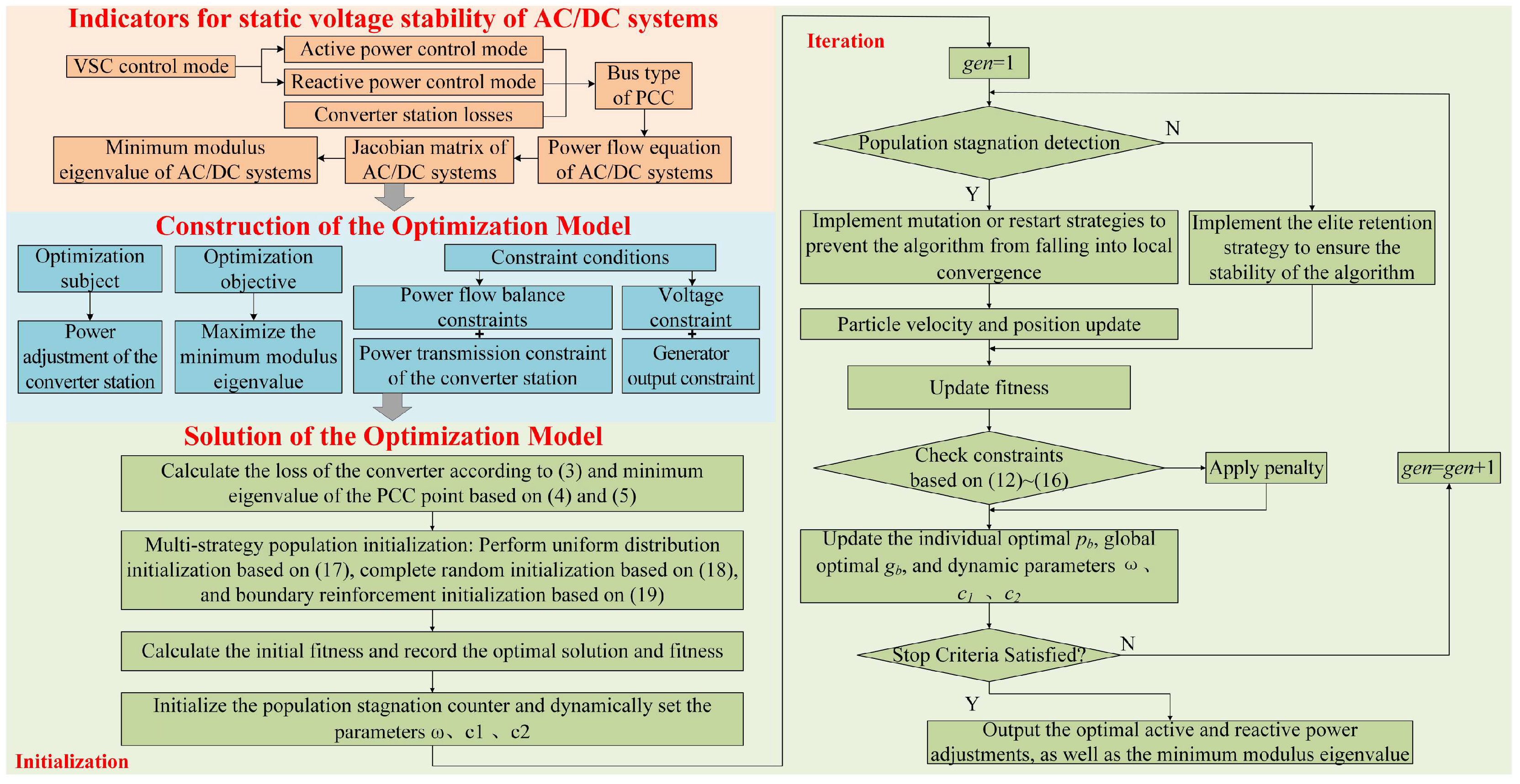
2.2. Static Voltage Stability Analysis of AC/DC Systems Based on the Minimum Modulus Eigenvalue
3. Optimization Model to Cooperatively Control Active and Reactive Power for VSC-HVDC
3.1. Construction of the Optimization Model
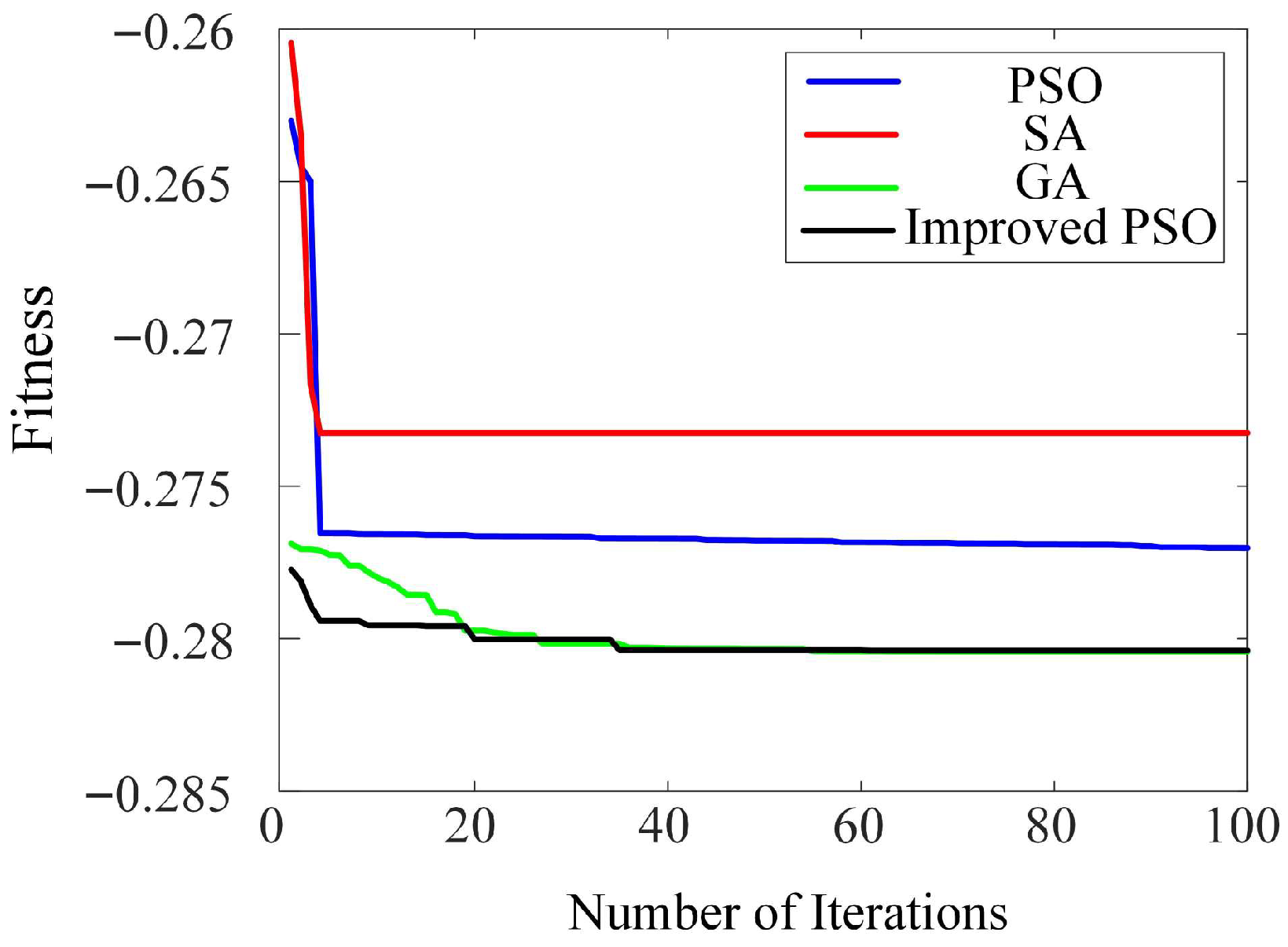
3.2. Solution of the Optimization Model
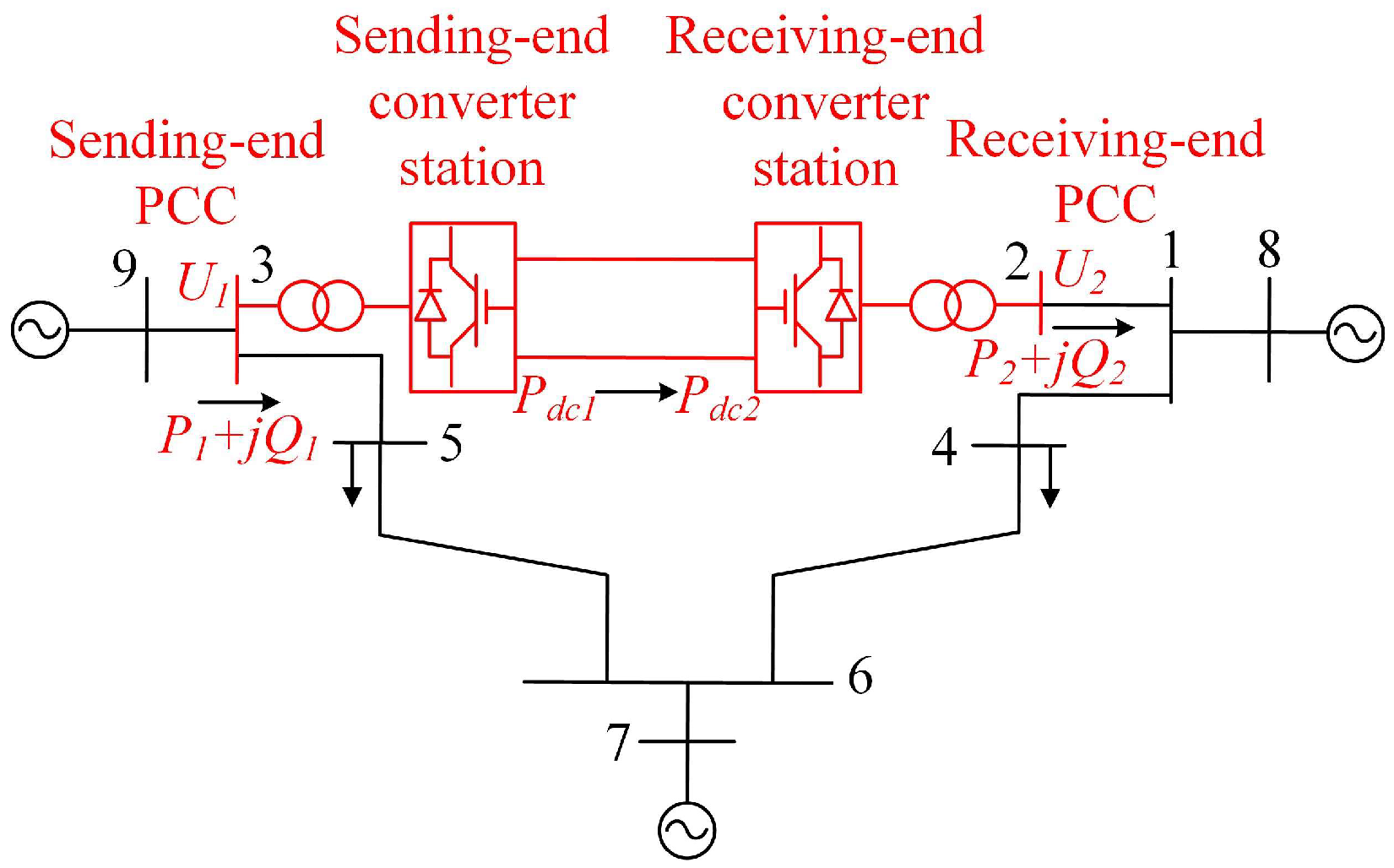
4. Case Study
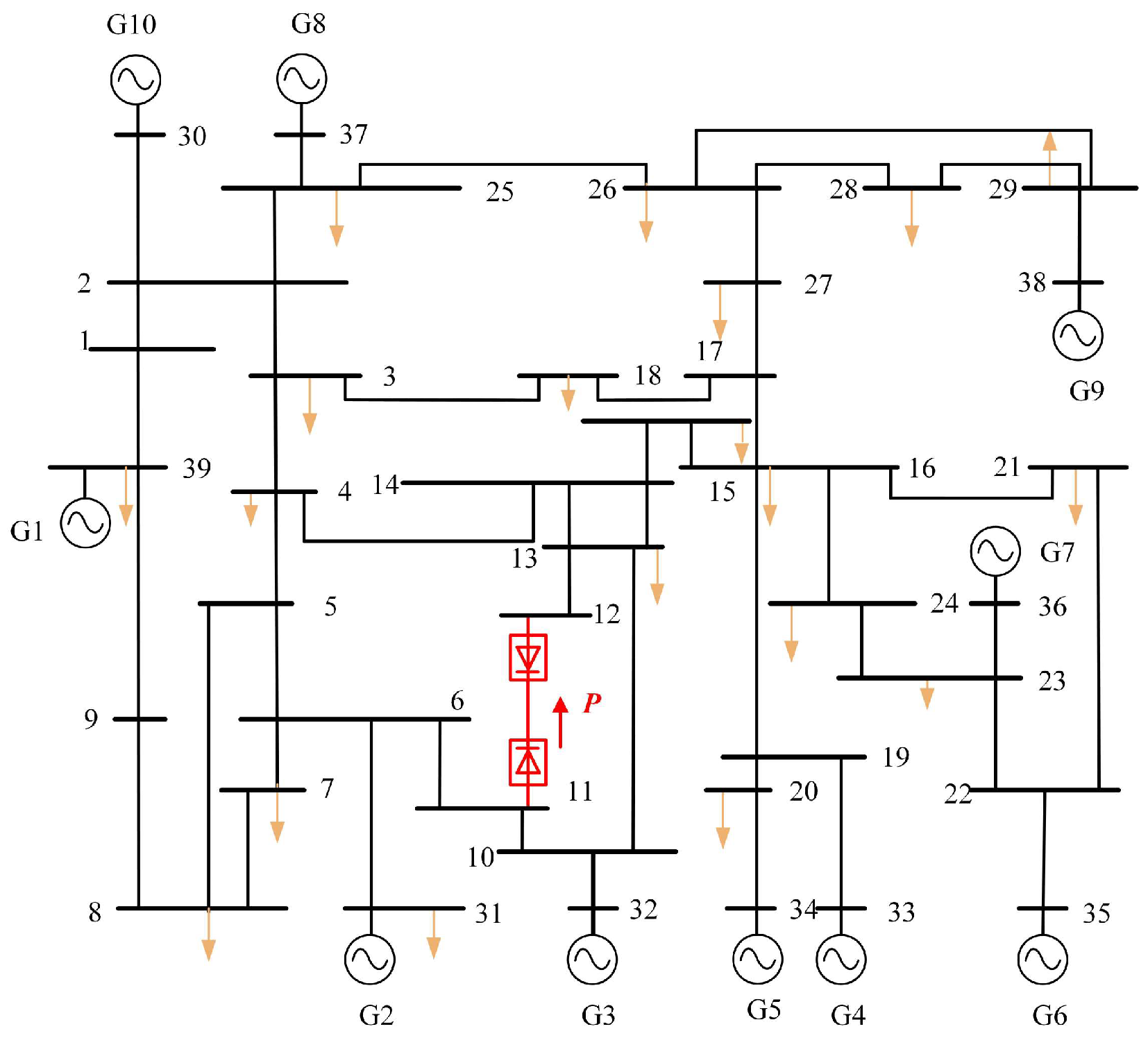
4.1. System Under Study
4.2. Fitting and Verification of VSC-HVDC Converter Loss Function
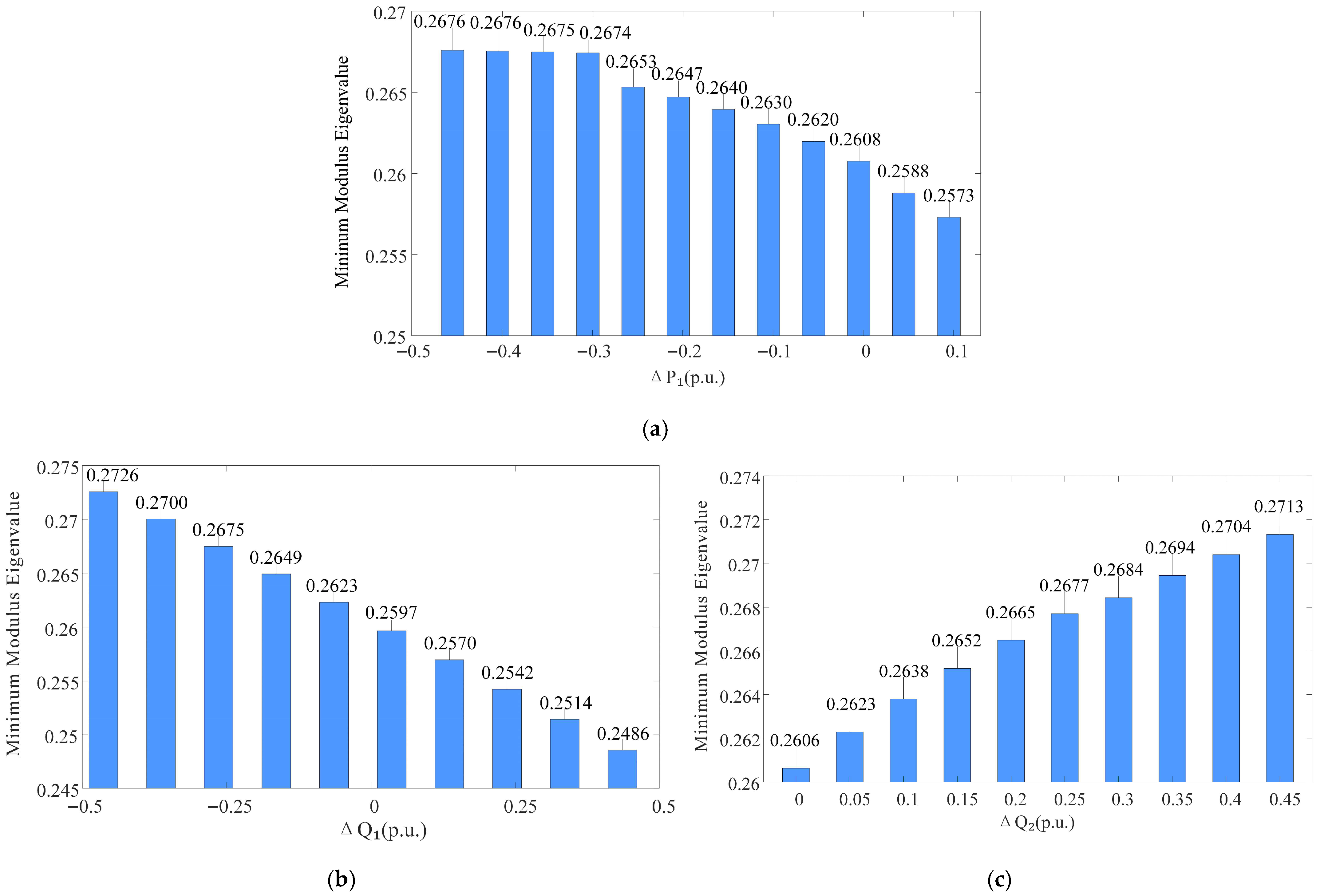
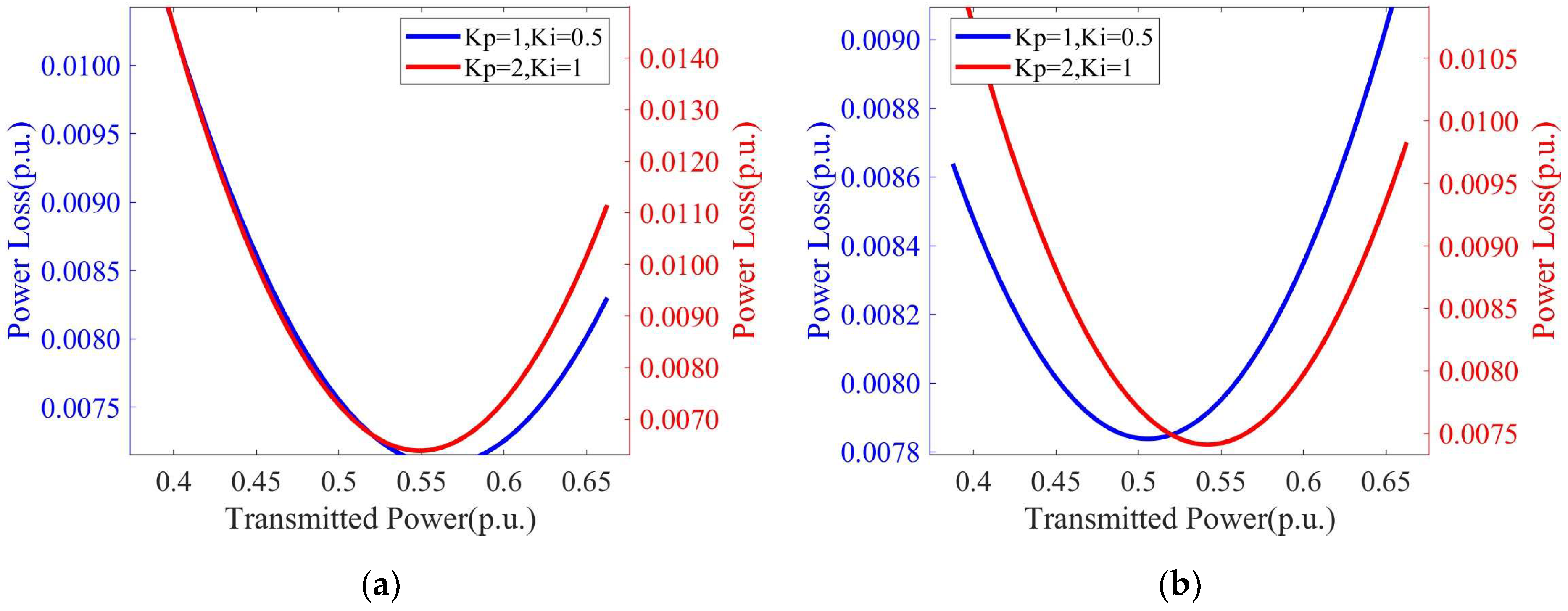
4.3. Influence of Active and Reactive Power Variation on the System’s Static Voltage Stability
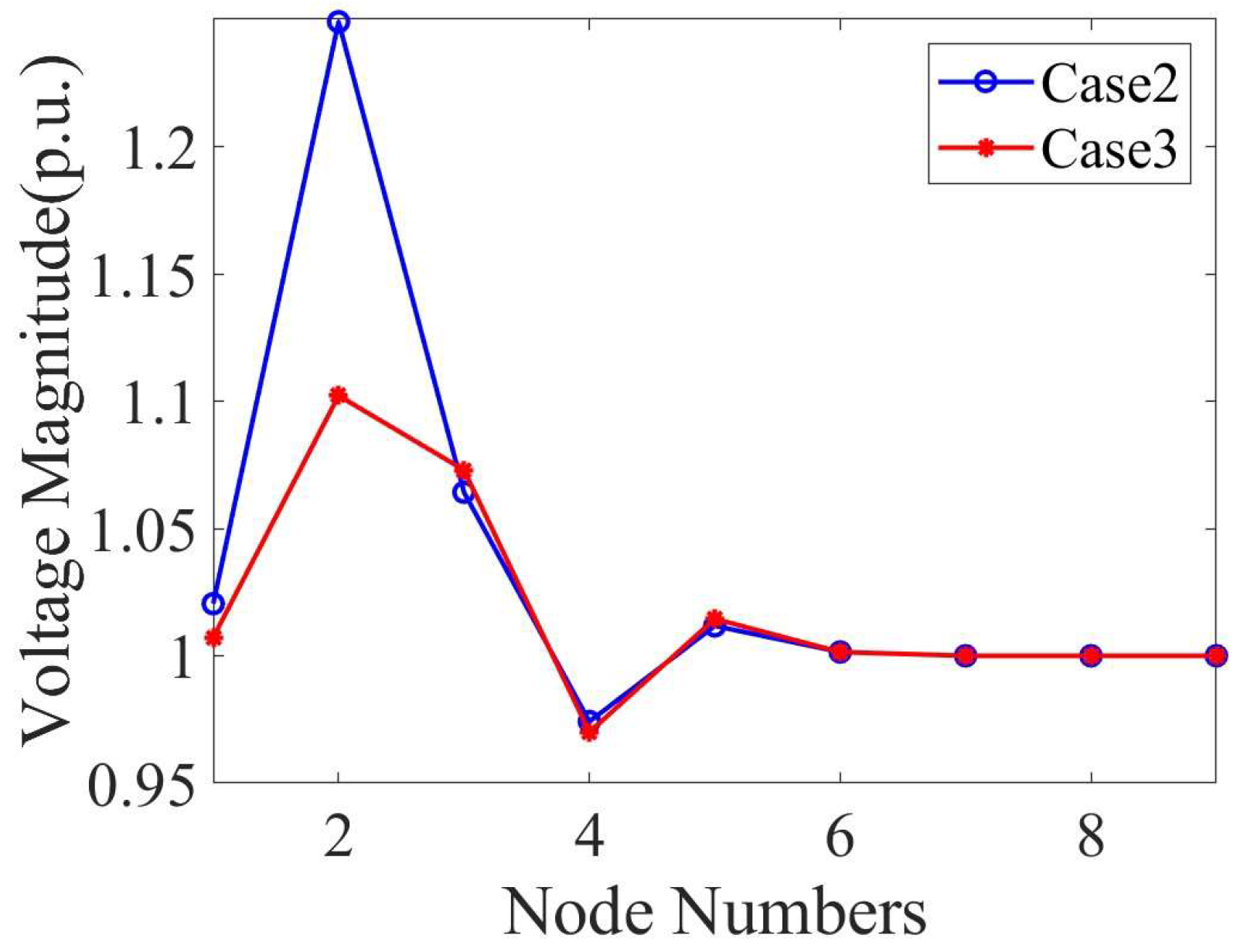
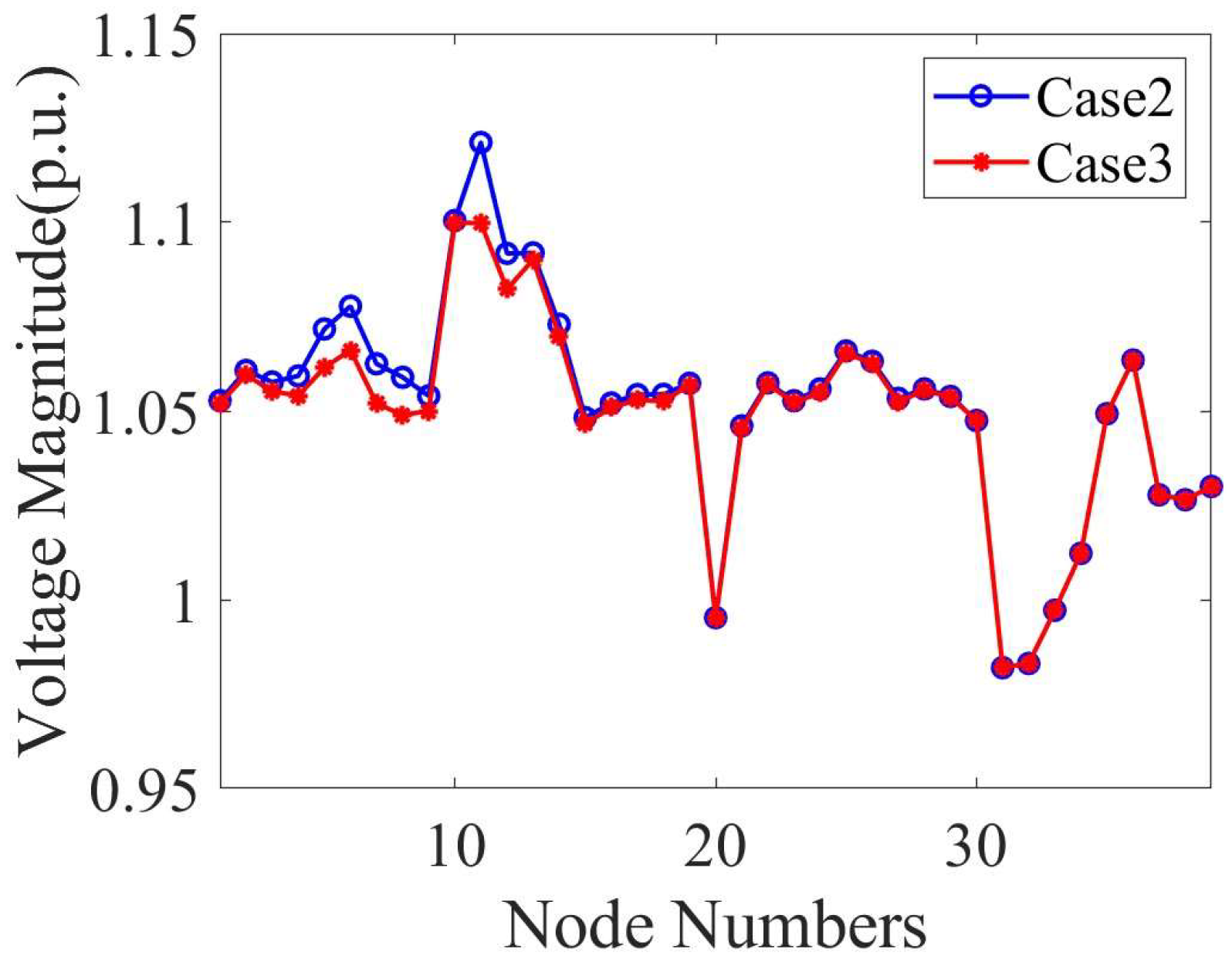
4.4. Performance of Coordinated Active and Reactive Power Control in the IEEE 9-Bus System
4.5. The Impact of DC Voltage Gain on System Voltage Stability
4.6. Performance of Coordinated Active and Reactive Power Control in the IEEE 39-Bus System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| VSC-HVDC | Voltage source converter—high-voltage direct current transmission |
| PCC | Point of common coupling |
| PSO | Particle swarm optimization |
Nomenclature
| Symbol | Definition | Unit/Description |
| Ploss | The converter station losses | Dimensionless (p.u.) |
| a | Loss parameter | Dimensionless |
| b | Loss parameter | Dimensionless |
| c | Loss parameter | Dimensionless |
| Is | The current flowing through the converter station | Dimensionless (p.u.) |
| Ps | The active power injected into the converter station | Dimensionless (p.u.) |
| Qs | The reactive power injected into the converter station | Dimensionless (p.u.) |
| Us | The PCC voltage of the converter station | Dimensionless (p.u.) |
| J | Jacobian matrix | Dimensionless (feature vector) |
| λmin | Minimum modulus eigenvalue | Dimensionless |
| ∆P1 | The active and reactive power adjustment of the sending-end converter station | Dimensionless (p.u.) |
| ∆Q1 | The reactive and reactive power adjustment of the sending-end converter station | Dimensionless (p.u.) |
| ∆Q2 | The reactive and reactive power adjustment of the receiving -end converter station | Dimensionless (p.u.) |
| Ui | The voltage at bus i in the sending-end system | Dimensionless (p.u.) |
| SGi | The apparent power of generator i in the sending-end system | kW |
| S | The transmission power limit of the VSC-HVDC system | kW |
| c1 | Cognitive coefficient | Dimensionless |
| c2 | Social coefficient | Dimensionless |
| ω | Inertia weight | Dimensionless |
| pop | Particle position | Dimensionless |
| sizepop | Number of particles | Dimensionless |
| kp | DC voltage proportional gain | Dimensionless |
| ki | DC voltage integral gain | Dimensionless |
References
- Zhang, G.; Ren, J.; Zeng, Y.; Liu, F.; Wang, S.; Jia, H. Security assessment method for inertia and frequency stability of high proportional renewable energy system. Int. J. Electr. Power Energy Syst. 2023, 153, 109309. [Google Scholar] [CrossRef]
- Wang, B.; Kou, Y.; Zhang, D.; Zhang, Q.; Li, H.; Lu, Z.; Qiao, Y. Voltage strength assessment of sending/receiving systems with a high proportion of new energy and HVDC. Appl. Syst. Innov. 2025, 8, 120. [Google Scholar] [CrossRef]
- Zafari, L.; Liu, Y.; Ukil, A.; Nair, N.-K.C. Advances in HVDC systems: Aspects, principles, and a comprehensive review of signal processing techniques for fault detection. Energies 2025, 18, 3106. [Google Scholar] [CrossRef]
- Stan, A.; Costinaș, S.; Ion, G. Overview and assessment of HVDC current applications and future trends. Energies 2022, 15, 1193. [Google Scholar] [CrossRef]
- Kumar, D.; Shireen, W.; Ram, N. Grid integration of offshore wind energy: A review on fault ride through techniques for MMC-HVDC systems. Energies 2024, 17, 5308. [Google Scholar] [CrossRef]
- Rao, H.; Zhou, Y.; Li, W.; Zou, C.; Wang, Z. Engineering application and development prospect of VSC-HVDC transmission technology. Autom. Electr. Power Syst. 2023, 47, 1–11. (In Chinese) [Google Scholar]
- Benato, R.; Gardan, G.; Milano, F. Effect of uniformly distributed parameter line models on the evaluation of PV curves and of the maximum loading condition. IEEE Trans. Power Syst. 2022, 37, 4974–4977. [Google Scholar] [CrossRef]
- Qiu, Y.; Wu, H.; Zhou, Y.; Song, Y. Global parametric polynomial approximation of static voltage stability region boundaries. IEEE Trans. Power Syst. 2017, 32, 2362–2371. [Google Scholar] [CrossRef]
- Khan, N.H.; Wang, Y.; Tian, D.; Jamal, R.; Kamel, S.; Ebeed, M. Optimal siting and sizing of SSSC using modified salp swarm algorithm considering optimal reactive power dispatch problem. IEEE Access 2021, 9, 49249–49266. [Google Scholar] [CrossRef]
- Xu, Q.; Guo, J.; Pan, X.; Sun, X.; Xu, H. Extraction of influencing variables for power system static stability indicators based on reciprocal information entropy causal inference. In Proceedings of the 2024 9th Asia Conference on Power and Electrical Engineering (ACPEE), Shanghai, China, 11–13 April 2024; pp. 2509–2513. [Google Scholar]
- Lu, J.; Qiu, J.; Feng, J.; Xu, K.; Xing, C.; Xin, Q. Analysis of the Voltage Stability Margin of the Sending-end Grid for the Large-scale PV Cluster Transmission by VSC-HVDC. In Proceedings of the 2025 IEEE International Conference on Power Systems and Smart Grid Technologies (PSSGT), Chongqing, China, 11–13 April 2025; IEEE: New York, NY, USA, 2025; pp. 123–128. [Google Scholar]
- Ma, J.; Zeng, Y.; Sheng, H.; Zhang, Z. Static voltage stability evaluation method based on equivalent power index. Power Syst. Technol. 2025, 49, 2347–2355. (In Chinese) [Google Scholar]
- Chen, G.; Liu, L.; Song, P.; Du, Y. Chaotic improved PSO-based multi-objective optimization for minimization of power losses and L index in power systems. Energy Convers. Manag. 2014, 86, 548–560. [Google Scholar] [CrossRef]
- Liu, X.; Tan, Z.; Yuan, Z.; Liu, Y. Combination weighting-based method for access point optimization of offshore wind farm. Energy Rep. 2022, 8, 900–907. [Google Scholar] [CrossRef]
- Kessel, P.; Glavitsch, H. Estimating the voltage stability of a power system. IEEE Trans. Power Deliv. 1986, 1, 346–354. [Google Scholar] [CrossRef]
- Rehman, B.; Liu, C.; Wei, W.; Fu, C.; Li, H. Applications of eigenvalues in installation of multi-infeed HVDC system for voltage stability. Int. Trans. Elect. Energy Syst. 2020, 30, e12645. [Google Scholar] [CrossRef]
- Yan, M.; Xu, L.; Zhang, X.; Wang, G.; Huang, Y. Robust day-ahead scheduling method for multi-infeed HVDC systems considering static voltage stability constraints. In Proceedings of the 4th Energy Conversion and Economics Annual Forum (ECE Forum 2024), Beijing, China, 14–15 December 2024; pp. 774–781. [Google Scholar]
- Zhao, L.; Wang, Z.; Sheng, H.; Li, Y.; Wang, X.; Wang, Y.; Yu, H. Optimal Configuration Model for Large Capacity Synchronous Condenser Considering Transient Voltage Stability in Multiple UHV DC Receiving End Grids. Energies 2024, 17, 5346. [Google Scholar] [CrossRef]
- Guo, X.; Tang, J.; Shu, T.; Peng, S.; Xie, K. Static voltage stability assessment on hybrid alternating current/voltage source converter-multiple terminal direct current system using improved modal analysis. Trans. China Electrotech. Soc. 2021, 36, 3741–3752. (In Chinese) [Google Scholar]
- Chen, H.; Huang, Y.; Jiang, T.; Li, X.; Li, G. Voltage stability analysis and control for AC/DC system with VSC-HVDC. Power Syst. Technol. 2017, 41, 2429–2435. (In Chinese) [Google Scholar]
- Urquidez, O.A.; Xie, L. Singular value sensitivity based optimal control of embedded VSC-HVDC for steady-state voltage stability enhancement. IEEE Trans. Power Syst. 2016, 31, 216–225. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, L.; Liao, S.; Xu, J.; Cheng, F. A static voltage stability enhancement method for power systems with a high proportion of voltage source converters. IEEE Trans. Power Syst. 2025, 40, 4019–4032. [Google Scholar] [CrossRef]
- Guo, J.; Zou, L.; Pan, X.; Zhang, N.; Jia, Y.; Sun, X.; Xie, Z.; Li, W. Research on coordinated active and reactive power control of VSC-HVDC connected renewable energy system for enhancing static voltage stability. In Proceedings of the 2025 IEEE 3rd International Conference on Power Science and Technology (ICPST), Kunming, China, 16–18 May 2025; pp. 1568–1573. [Google Scholar]
- Wu, X. Research on Electromechanical Transient Modeling and Voltage Support of VSC-HVDC Systems. Master’s Thesis, Zhejiang University, Hangzhou, China, 2023. (In Chinese). [Google Scholar]
- Wu, X.; Qu, H.; Xin, W.; Wang, M. An efficient model of hybrid AC/DC grid power flow based on the simplified VSC station model. In Proceedings of the 2023 8th Asia Conference on Power and Electrical Engineering (ACPEE), Tianjin, China, 14–16 April 2023; pp. 329–333. [Google Scholar]
- Li, Z.; Yu, J.; Wu, Q.H. Approximate linear power flow using logarithmic transform of voltage magnitudes with reactive power and transmission loss consideration. IEEE Trans. Power Syst. 2018, 33, 4593–4603. [Google Scholar] [CrossRef]
- Xu, Q.; Pan, X.; Guo, J.; Zhang, H.; Li, W.; Sun, X. Clustering of operating scenarios for new energy power systems based on the variables affecting static voltage stability. In Proceedings of the 2024 IEEE PES 16th Asia-Pacific Power and Energy Engineering Conference (APPEEC), Nanjing, China, 25–27 October 2024; pp. 1–5. [Google Scholar]
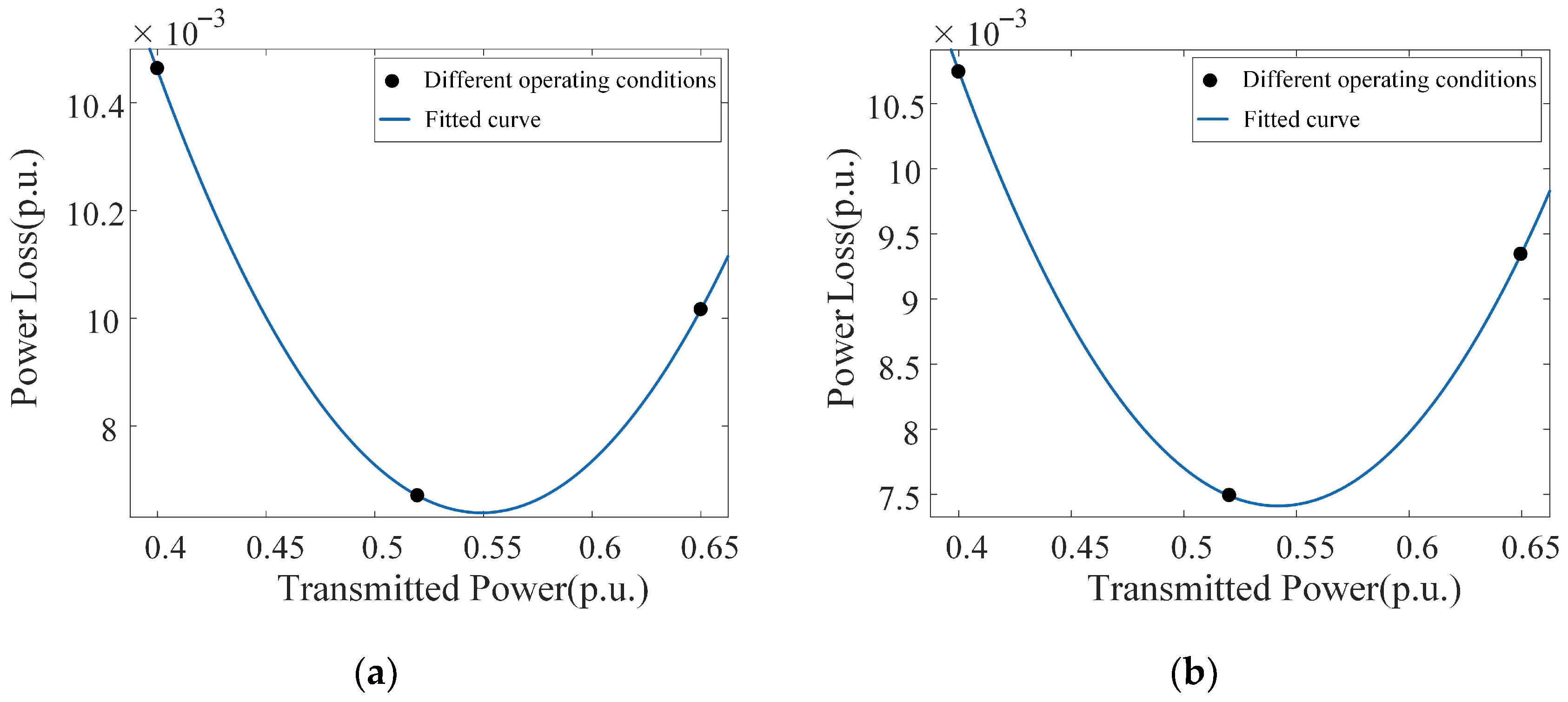
| Sending-End Converter Station | Receiving-End Converter Station | ||||
|---|---|---|---|---|---|
| a1 | b1 | c1 | a2 | b2 | c2 |
| 0.3698 | −0.4060 | 0.1179 | 0.1660 | −0.1799 | 0.0561 |
| Sending-End Converter Station | Receiving-End Converter Station | ||||
|---|---|---|---|---|---|
| Simulation loss (p.u.) | Calculation loss (p.u.) | Error (%) | Simulation loss (p.u.) | Calculation loss (p.u.) | Error (%) |
| 0.00724 | 0.00735 | 1.52 | 0.00756 | 0.00765 | 1.19 |
| Active-Power Adjustment ∆P1 | Reactive-Power Adjustment ∆Q1 | Reactive-Power Adjustment ∆Q2 | Minimum Modulus Eigenvalue of the System | |
|---|---|---|---|---|
| Case 1 | −0.2646 | / | / | 0.2632 |
| Case 2 | / | −0.6201 | 0.2732 | 0.2732 |
| Case 3 | −0.2989 | −0.8576 | 0.1588 | 0.2802 |
| Active-Power Adjustment ∆P1 | Reactive-Power Adjustment ∆Q1 | Reactive-Power Adjustment ∆Q2 | Minimum Modulus Eigenvalue of the System | |
|---|---|---|---|---|
| Case 1 | −0.2989 | −0.8576 | 0.1588 | 0.2803 |
| Case 2 | −0.2738 | −0.8477 | 0.1581 | 0.2797 |
| Active-Power Adjustment ∆P1 | Reactive-Power Adjustment ∆Q1 | Reactive-Power Adjustment ∆Q2 | Minimum Modulus Eigenvalue of the System | |
|---|---|---|---|---|
| Case 1 | −0.2878 | / | / | 0.5791 |
| Case 2 | / | −0.5229 | 0.4728 | 0.6253 |
| Case 3 | −0.2979 | −0.4847 | 0.4514 | 0.6348 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Zou, L.; Zhang, N.; Jia, Y.; Pan, X.; Sun, X. Coordinated Active and Reactive Power Control of VSC-HVDC for Enhancing Static Voltage Stability in AC/DC Systems. Energies 2025, 18, 6127. https://doi.org/10.3390/en18236127
Guo J, Zou L, Zhang N, Jia Y, Pan X, Sun X. Coordinated Active and Reactive Power Control of VSC-HVDC for Enhancing Static Voltage Stability in AC/DC Systems. Energies. 2025; 18(23):6127. https://doi.org/10.3390/en18236127
Chicago/Turabian StyleGuo, Jinpeng, Luo Zou, Ningyu Zhang, Yuqiao Jia, Xueping Pan, and Xiaorong Sun. 2025. "Coordinated Active and Reactive Power Control of VSC-HVDC for Enhancing Static Voltage Stability in AC/DC Systems" Energies 18, no. 23: 6127. https://doi.org/10.3390/en18236127
APA StyleGuo, J., Zou, L., Zhang, N., Jia, Y., Pan, X., & Sun, X. (2025). Coordinated Active and Reactive Power Control of VSC-HVDC for Enhancing Static Voltage Stability in AC/DC Systems. Energies, 18(23), 6127. https://doi.org/10.3390/en18236127







