Transient Stability-Constrained Optimal Power Flow Model Based on CatBoost-DF and ISOA

Abstract

Traditional transient stability-constrained optimal power flow (TSCOPF) methods rely on solving complex nonlinear differential equations, resulting in high computational demands and lengthy processing times. To address these issues, this paper proposes a TSCOPF model based on a cascaded CatBoost model (CatBoost-DF) and an improved seagull optimization algorithm (ISOA). First, a TSCOPF model is constructed. Second, the CatBoost-DF model is developed to establish a mapping relationship between the dynamic characteristics of the power system and the power angle of generators. The trained CatBoost-DF model is then employed as a surrogate model to handle transient stability constraints, thereby avoiding the computation of complex differential-algebraic equations traditionally required in transient stability constraint analysis. Then, the ISOA is employed to iteratively solve the TSCOPF model. This enables timely adjustment of generator output when transient instability risks arise, preventing accidents while maintaining system economic efficiency. Finally, simulations conducted on the IEEE 39 bus system demonstrate that this method effectively safeguards both system security and economic performance.

1. Introduction

The safe and stable operation of power systems is a critical guarantee for industrial production and people’s livelihoods. However, with the continuous expansion of power system scale, particularly due to complex network structures and the integration of numerous generating units, the system’s dynamic characteristics have become increasingly intricate, thereby heightening the risk of transient stability loss [1,2,3]. Transient stability loss is a key factor contributing to the frequent occurrence of large-scale accidents, and efficient transient stability-constrained optimal power flow (TSCOPF) methods represent a vital approach to addressing this issue [4,5,6].

Traditional TSCOPF methods typically rely on complex nonlinear differential and algebraic equations to describe the dynamic behavior of power systems [7]. Among these, classical approaches for handling transient stability constraints primarily include time-domain simulation methods [8], direct methods [9], and judgment methods based on post-fault system responses. Although these methods offer high computational accuracy and engineering applicability, they generally suffer from limitations of low computational efficiency and time-consuming processing. In recent years, the advancement of machine learning has brought new opportunities to power system analysis, effectively addressing the shortcomings of classical methods. Machine learning approaches possess the capability to mine data features, enabling the establishment of mapping relationships between input characteristics and outputs [10]. Reference [11] proposes a novel neural network-based dimensionality reduction method for data preprocessing, followed by applying an extreme learning machine (ELM) to the reconstructed data for transient stability assessment. Reference [12] proposes a transient stability assessment method based on extreme gradient boosting (XGBoost) and factorization machines (FM). The aforementioned research aimed to develop transient stability assessment models using machine learning algorithms. However, these models featured simple structures and insufficient accuracy. Compared to traditional machine learning approaches, deep learning methods progressively extract higher-level features from raw data across multiple layers, offering advantages such as robust feature extraction capabilities and superior convergence properties [13]. Reference [14] proposes a squeeze-excitation (SE)-enhanced attention mechanism for graph convolutional neural networks (SE-GCN). By embedding power grid topology and explicitly accounting for network topographical effects, this model enables deep feature extraction and learning on graphs for rapid transient stability assessment. Reference [15] proposes an active transfer learning method based on the deep belief network (DBN) model. Reference [16] proposes a transient stability assessment model based on a spatio-temporal generalized learning system (STBLS). Reference [17] introduces an interpretable deep learning transient stability assessment model that combines the powerful nonlinear modeling capabilities of deep neural networks with the interpretability of decision trees (DT). Although these studies have employed deep learning techniques to develop higher-precision transient stability assessment models, most of these models exist as standalone evaluation modules and have not yet been systematically integrated into the TSCOPF optimization framework to enable rapid characterization and solution of transient stability constraints.

The aforementioned research focuses on enhancing the performance of transient stability assessment through data-driven approaches. On the other hand, in the optimization solution phase, intelligent optimization algorithms have been widely applied to solve TSCOPF models due to their flexibility in handling complex nonlinear problems [18]. Reference [19] used the Butterfly Optimization Algorithm (BOA) to solve the Optimal Power Flow (OPF) problem in power systems; however, further improvement is needed to obtain better solutions within a reasonable time. In this paper, the Sobol sequence initialization and nonlinear control parameters are introduced to enhance population diversity and search efficiency, while the Lévy flight strategy helps the algorithm escape from local optima. As a result, the improved Seagull Optimization Algorithm (ISOA) can still converge rapidly and achieve lower generation costs and higher stability margins in a larger IEEE 39 bus system. Reference [20] proposed a bio-inspired Multi-Objective Artificial Hummingbird Algorithm (MOAHA) to address the OPF problem in power systems, but it suffers from insufficient population diversity and premature convergence. In contrast, our ISOA employs Sobol sequence initialization and the Lévy flight strategy to effectively enhance global exploration ability, and uses the CatBoost-DF surrogate model to replace complex transient stability calculations, fundamentally reducing the number of iterations and computation time. Reference [21] applied a Multi-Objective Particle Swarm Optimization (MOPSO) algorithm to handle conflicting objectives in the OPF problem and used fuzzy set theory to select a compromise solution. In contrast, our proposed ISOA directly searches for Pareto-optimal solutions while balancing exploration and exploitation, without requiring additional fuzzy decision mechanisms. Combined with the CatBoost-DF surrogate model, the algorithm not only optimizes static economic indicators but also enables early warning and prevention of transient instability, effectively improving system security and real-time control capability. In summary, compared with the cited metaheuristic algorithm studies, the proposed method—through the integration of a deep surrogate model and an improved swarm intelligence algorithm—demonstrates more significant advantages in terms of algorithm diversity, convergence speed, adaptability to complex constraints, and scalability for large-scale power systems.

To address the aforementioned issues, this paper proposes a TSCPOF model integrating a cascaded CatBoost model (CatBoost-DF) and an improved seagull optimization algorithm (ISOA). This method achieves coordinated system safety, stability, and economic operation by optimizing generator output under anticipated fault scenarios, effectively enhancing the computational efficiency and decision reliability of traditional TSCOPF models.

2. TSCOPF Model

2.1. Objective Function

The objective function is the minimum generation cost of the generator, with the following formula:

$$f=\min {\displaystyle \sum _{i=1}^{S_G}\left(A_i{P}_i^2+B_i{P}_i+C_i\right)}$$

(1)

where $S_G$ is controllable generator set; $P_i$ represents active power output of the $i$-th generator; $A_i$, $B_i$, and $C_i$ represent the cost coefficients for the $i$-th generator.

2.2. Power Flow Constraints

The power flow constraints are given as follows:

$$\left\{\begin{array}{l}{P}_{Gi}=P_{Di}+V_i{\displaystyle {\sum }_{j=1}^{S_N}{V}_j\left(G_{ij}\cos {\theta }_{ij}+B_{ij}\sin {\theta }_{ij}\right)}\\ Q_{Gi}=Q_{Di}+V_i{\displaystyle {\sum }_{j=1}^{S_N}{V}_j\left(G_{ij}\sin {\theta }_{ij}-B_{ij}\cos {\theta }_{ij}\right)}\end{array}\right.$$

(2)

where $P_G$ and $P_D$ represent the active power of the generator and load, respectively; $Q_G$ and $Q_D$ represent the reactive power of the generator and load, respectively; $V_i$ is the voltage amplitude at node $i$; $S_N$ represents the total number of nodes; ${\theta }_{ij}$ represents phase angle difference between nodes $i$ and $j$; $G_{ij}$ and $B_{ij}$ represent the conductance and conductance between nodes $i$ and $j$, respectively.

2.3. Inequality Constraints

The inequality constraints in power grid operation include generator output constraints, bus voltage constraints, and line thermal stability constraints:

$$\left\{\begin{array}{l}{P}_{Gi,\min }\le P_{Gi}\le P_{Gi,\max }\\ Q_{Gi,\min }\le Q_{Gi}\le Q_{Gi,\max }\end{array}\right.,i\in S_G$$

(3)

$$V_{i,\min }\le V_i\le V_{i,\max } , i\in S_N$$

(4)

$$S_{ij,\min }\le S_{ij}\le S_{ij,\max } , \left(i,j\right)\in S_l$$

(5)

where $P_{Gi,\min }$, $P_{Gi,\max }$, $Q_{Gi,\min }$, and $Q_{Gi,\max }$ represent the minimum and maximum values of the generator’s active and reactive power outputs, respectively; $V_{i,\min }$ and $V_{i,\max }$ represent the minimum and maximum values of the bus voltage amplitude, respectively; $S_{ij,\min }$ and $S_{ij,\max }$ represent the minimum and maximum values for thermal stability of the line, respectively; $S_G$ represents the number of dispatchable generators; $S_l$ denotes the total number of system lines.

2.4. Transient Stability Constraints

Transient stability constraints can be described by differential Equation (6) and algebraic Equation (7):

$${\displaystyle \frac{dx}{dt}}=f\left(x,j,\lambda \right)$$

(6)

$$h\left(x,y,\lambda \right)=0$$

(7)

where $x$ is the state variable; $y$ is the algebraic variable; $\lambda$ is the control variable.

Solving nonlinear differential-algebraic equations involves complex computations and is time-consuming. Therefore, this paper employs the CatBoost-DF transient stability assessment model to replace the intricate solution process. The CatBoost-DF algorithm enables rapid and accurate estimation of system transient stability, significantly reducing the computational load associated with addressing transient stability constraints in power systems.

3. Handling Transient Stability Constraints Using the CatBoost-DF Model

3.1. Transient Stability Index

This paper employs the transient stability index (TSI) to quantitatively evaluate the dynamic stability of power systems. This metric characterizes the system’s stability margin by analyzing the maximum deviation of the generator rotor angle during transient processes. Its mathematical expression is:

$$T_{SI}={\displaystyle \frac{360-\left|{\delta }_{\max }\right|}{360+\left|{\delta }_{\max }\right|}}\times 100$$

(8)

where ${\delta }_{\max }$ is the maximum difference between the rotor angles of any two generators.

3.2. CatBoost-DF Model

CatBoost, as an enhanced gradient boosting decision tree (GBDT) algorithm [22], demonstrates exceptional data adaptability. It effectively handles diverse data types, including categorical features, and maintains high predictive accuracy even in the presence of noise and outliers, showcasing strong model robustness [23].

To further enhance CatBoost’s capability in characterizing complex power system functions and achieve layer-by-layer learning of input features, this paper constructs the CatBoost-DF model by referencing the multi-grained cascade forest (DF) framework [24]. Compared to random forests, CatBoost offers advantages such as overfitting resistance and high adaptability. The structure of the CatBoost-DF model is illustrated in Figure 1.

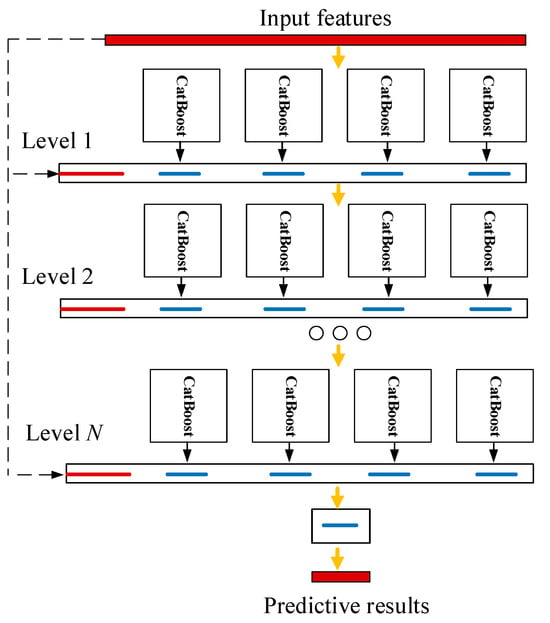
Figure 1. CatBoost-DF model architecture diagram.

Input features utilize variables reflecting the dynamic state of the power system, including generator active and reactive power, node voltage magnitude and phase angle, and load active and reactive power. The raw feature vector $\mathit{X}\in {\mathit{R}}^M$ is input into the first layer, where $M$ represents the feature dimension. Four CatBoost models process data in parallel:

$$h_1^i={\xi }_1^i\left(X\right),i=1,2,3,4$$

(9)

where $h_1^i$ is the output of the $i$-th CatBoost model in the first layer; $\xi$ represents the CatBoost model.

The output vector of the first layer is:

$${\mathit{h}}_1={\left. [h_1^1,h_1^2,h_1^3,h_1^4\right]}^{\mathrm{T}}$$

(10)

The input vector for the second layer consists of the original feature vector and all outputs from the first layer:

$${\mathit{X}}_2=Concat(\mathit{X},{\mathit{h}}_1)\in {\mathit{R}}^{M+4}$$

(11)

where $Concat(·)$ represents concatenation along the feature dimension.

The output vector of the second layer is:

$${\mathit{h}}_2={\xi }_2\left(Concat\left(\mathit{X},{\mathit{h}}_1\right)\right)$$

(12)

Similarly, if the evaluation accuracy of the current layer exceeds that of the previous layer, continue adding cascading layers; otherwise, halt the expansion. When the cascading structure terminates at layer $N$ according to the above criteria, this layer constitutes the model’s final prediction layer. The output vector can be expressed as:

$${\mathit{h}}_N={\xi }_N\left(Concat(\mathit{X},{\mathit{h}}_1,\cdot \cdot \cdot ,{\mathit{h}}_{N-1})\right)$$

(13)

Finally, the weighted sum yields the final $T_{SI}$ prediction value:

$$y=T_{SI}={\displaystyle \sum _j^4{w}_j\cdot h_l^j+b}$$

(14)

where $w_j$ represents the weight corresponding to the output of the $j$-th CatBoost model in the $N$-th layer, and $b$ represents the bias term.

Embed the trained model as a “proxy” into the TSCOPF model, incorporating the model’s prediction results as part of the constraint function. Based on the transient stability constraints from CatBoost-DF:

$${\Theta }^{\mathrm{CatBoost}-\mathrm{DF}}\left(X\right)>\epsilon$$

(15)

where $\Theta \left(\cdot \right)$ represents the correlation latent function of the trained CatBoost-DF model; $\epsilon$ represents the transient stability margin threshold.

4. TSCOPF Model Based on CatBoost-DF and ISOA

4.1. Improved Seagull Optimization Algorithm

When applying the traditional seagull optimization algorithm (SOA) [25] to solve the TSCOPF problem, issues such as insufficient exploration capability, slow convergence speed with low accuracy, and susceptibility to local optima arise [26]. To address these challenges, this paper proposes algorithmic enhancements. First, the population is initialized using the Sobol sequence [27] to enhance diversity. Then introduce nonlinear parameter $\widehat{A}$ [28] to enhance the algorithm’s optimization performance. Finally, a Levy flight strategy [29] is employed to help the algorithm escape local optima.

The initial population is initialized based on the Sobol sequence. The initial positions of the seagull population are:

$$X_n=LB+S_i\times \left(UB-LB\right)$$

(16)

where $LB$ and $UB$ denote the lower and upper bounds of the value range; $S_i$ is a random number in the interval [0, 1].

The mathematical formula for nonlinear parameter $\widehat{A}$ is as follows:

$$\widehat{A}=f_c\times {\left(1-{\displaystyle \frac{t}{T_{\max }}}\right)}^{\left(2\times {\displaystyle \frac{t}{T_{\max }}}\right)}$$

(17)

where the initial value of the parameter $f_c$ is set to 2; $t$ represents the current iteration count; $T_{\max }$ denotes the maximum iteration count.

The Levy flight strategy is a random walk search strategy that enhances the algorithm’s ability to escape local optima. It is expressed as follows:

$$Levy(\lambda )={\displaystyle \frac{\alpha \mu }{{\left|\beta \right|}^{\frac{1}{\lambda }}}}$$

(18)

$$\mu ={\left({\displaystyle \frac{\mathsf{\Gamma }\left(1+\lambda \right)\times \sin \left(\frac{\pi \lambda }{2}\right)}{\mathsf{\Gamma }\left(1+\lambda \right)\times \lambda \times 2^{\frac{\left(\lambda -1\right)}{2}}}}\right)}^{{\displaystyle \frac{1}{\lambda }}}$$

(19)

where $\lambda \in \left(0,2\right)$, typically set to 1.5; $\alpha ,\beta ~\left(0,{\sigma }^2\right)$.

4.2. TSCOPF Optimization Process

This paper introduces the CatBoost-DF transient stability assessment model to replace complex differential-algebraic transient stability constraints. The ISOA is employed for rapid and accurate model solution. The TSCOPF flowchart is shown in Figure 2, comprising two main components:

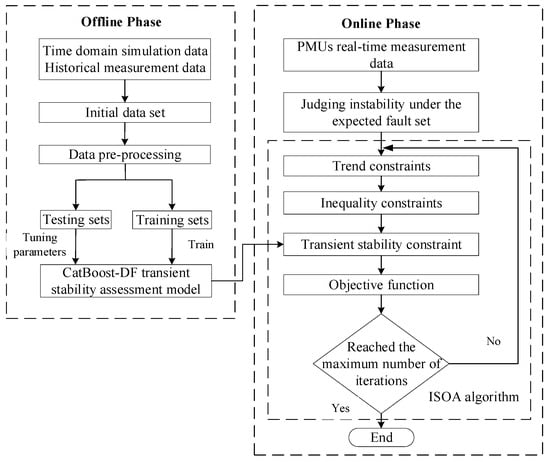
Figure 2. TSCOPF optimization process.

(1)

Offline Phase

First, based on time domain simulations combined with historical measurements, the six dynamic characteristics proposed in Section 3.2 are extracted. Then, time domain simulations were conducted using the PSASP simulation software. By varying generator output levels and load sizes and randomly combining them with predefined fault sets, the transient stability index from Equation (8) was calculated to obtain the initial sample set. Outliers in the initial sample set were handled, and the preprocessed data was randomly split into training and testing sets (8:2 ratio). The CatBoost-DF model was trained and tested on these sets respectively. After model training, the transient stability constraints in the traditional TSCOPF model were replaced.

(2)

Online Phase

By collecting real-time power system measurement data through phasor measurement units (PMUs), the system adjusts the active power output of synchronous generators based on the ISOA when instability is predicted under anticipated fault conditions. This process solves for the optimal operating point to maintain system stability.

The specific steps for solving the TSCOPF model using the ISOA are as follows:

Step 1: Initialize the population positions based on the Sobol sequence as shown in Equation (16), and set parameters such as the maximum iteration count $T_{\max }$;

Step 2: Process power flow constraints (2) and inequality constraints (3)–(5) using Matpower, and handle transient stability constraints based on the trained CatBoost-DF model;

Step 3: Calculate the fitness value of each seagull based on the objective function. Rank each seagull according to its fitness value, eliminating the weaker ones while retaining the stronger ones. Simultaneously, introduce the Levy flight strategy as shown in Equations (18) and (19) to help the algorithm escape local optima and update the optimal value;

Step 4: Determine whether the maximum iteration count has been reached. If so, output the globally optimal solution of ISOA as the TSCOPF adjustment plan. If not, return to Step 2 to continue the iterative solution process.

5. Simulation Analysis

5.1. Sample Set Generation

This paper conducts simulation tests on an IEEE 39 bus system, which comprises 10 generators, 39 nodes, and 46 transmission buses. Its topology is shown in Figure 3.

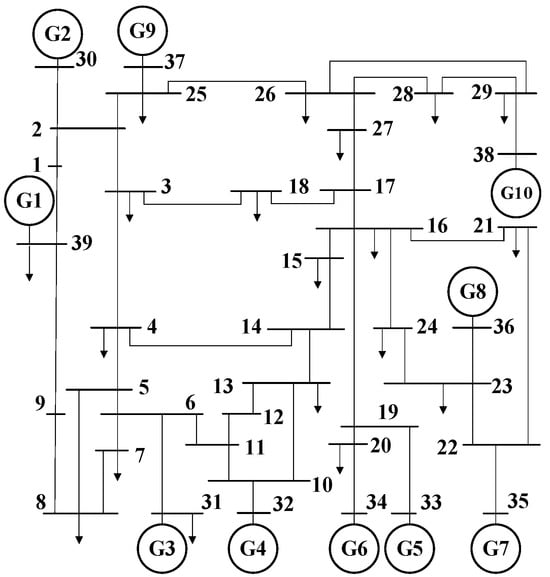
Figure 3. IEEE 39 bus schematic diagram.

This study employs MATLAB R2020a and PSASP 7.4.1 for simulation research and provides sampled data. The equipment configuration consists of an Intel Core i7 3.40-GHz CPU with 8 GB RAM. To generate diverse samples, simulations were conducted at a sampling frequency of 100 Hz, with a total simulation duration of 20 s. The load and generator active power output range is 80% to 120%, with the generator voltage amplitude fluctuating between 1.0 and 1.05 (p.u.). To comprehensively evaluate the transient stability of the system under various fault scenarios, this paper selects eight lines from the entire network as potential fault lines. Multiple fault types are defined to simulate the disturbance patterns that may occur in actual systems, as shown in Table 1. By combining different operating parameters with fault scenarios, a total of 6561 simulations were conducted, yielding 6561 independent simulation cases. After outlier processing of the simulation data, approximately 95% of the data was retained. Ultimately, the processed data was randomly divided into training and test sets, with a ratio of approximately 8:2.

Table 1. Anticipated fault set.

Fault Number	Faulty Circuit	Fault Type
1	1–2	Single-phase ground fault
2	3–18	Three-phase short circuit
3	4–14	Three-phase short circuit
4	16–21	Two-phase short circuit
5	16–17	Single-phase open circuit
6	17–27	Three-phase open circuit
7	25–26	Three-phase short circuit
8	9–39	Single-phase ground fault

5.2. Performance Comparison of CatBoost-DF Model

When evaluating the performance of the model, a confusion matrix is adopted to conduct a comprehensive assessment of the transient stability evaluation model. The confusion matrix is shown in Table 2.

Table 2. Confusion matrix.

Status	Assess Stability	Assess Instability
ActualStability	TP	FN
ActualInstability	FP	TN

This paper introduces the accuracy rate $A_{cc}$, precision rate $P_r$, recall rate $R_e$ and $F_1$-score as evaluation metrics. The specific formulas are as follows:

$$A_{cc}={\displaystyle \frac{T_p+T_N}{T_P+T_N+F_P+F_N}}\times 100\%$$

(20)

$$P_r={\displaystyle \frac{T_P}{T_N+F_N}}\times 100\%$$

(21)

$$R_e={\displaystyle \frac{T_N}{T_N+F_P}}\times 100\%$$

(22)

$$F_1={\displaystyle \frac{2\times P_r\times R_e}{P_r+R_e}}$$

(23)

To validate the performance of the CatBoost-DF model in transient stability assessment, we compared it with several machine learning algorithms, including CatBoost, LSTM, SVM, and DT. The results are shown in Table 3. Experiments demonstrate that CatBoost-DF achieves the best performance due to its cascade structure, with an accuracy 1.54% higher than that of the CatBoost model. Although the LSTM model can capture features through its deep architecture and performs better than SVM and DT, its accuracy and $F_1$-score are still lower than those of CatBoost-DF. In contrast, the simpler structures of SVM and DT make them prone to overfitting, resulting in relatively poor evaluation performance.

Table 3. Model performance comparison.

Model	Acc (%)	F1-Score
CatBoost-DF	98.85	0.9883
CatBoost	97.35	0.9722
LSTM	97.06	0.9701
SVM	94.38	0.9426
DT	93.55	0.9346

5.3. Algorithm Performance Comparison

This paper verifies the performance advantages of ISOA by comparing it with the traditional Seagull Optimization Algorithm (SOA), Genetic Algorithm (GA), and Particle Swarm Optimization Algorithm (PSO). The expected failure is set to 1, the population size to 50, and the number of iterations to 150. The convergence curves of different algorithms are shown in Figure 4.

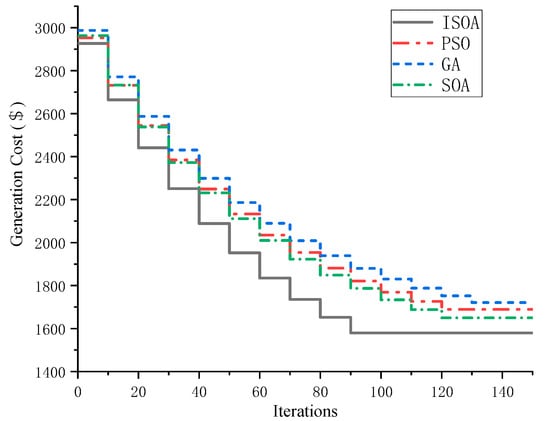
Figure 4. Algorithm convergence curve.

As can be seen from Figure 4, ISOA reaches its final convergence after 80 iterations, while PSO, SOA and GA algorithms all require at least 100 iterations to achieve their final convergence. In addition, the total adjustment cost of ISOA is lower than that of other algorithms. Therefore, the ISOA outperforms the other three algorithms in both convergence speed and accuracy.

Given the random nature of metaheuristic algorithms, to verify the performance advantages of the ISOA in a more scientific and rigorous manner, this paper followed the evaluation criteria for metaheuristic algorithms. Under uniform population sizes and consistent termination rules, 30 independent replicate experiments were conducted for ISOA, PSO, GA, and SOA. The statistical results are shown in Table 4.

Table 4. Algorithm performance statistical analysis.

Performance Metrics	ISOA	SOA	PSO	GA
Optimal cost ($)	1578.45	1645.87	1673.97	1700.21
Worst cost ($)	1586.91	1670.24	1707.56	1744.16
Average cost ($)	1583.27	1657.61	1689.15	1721.88
Cost standard deviation ($)	2.15	5.78	9.41	11.05
Average iterations	85	111	118	127
Iterations standard deviation	5.2	10.3	16.8	19.3

As shown in Table 4, from the cost-related metrics, it is evident that ISOA not only achieved the lowest average cost across 30 runs but also exhibited a significantly smaller standard deviation compared to other algorithms. This demonstrates that ISOA not only delivers the highest solution accuracy but also possesses exceptional robustness and stability. The iteration count metric demonstrates that ISOA converges to high-quality solutions at the fastest average speed while exhibiting the smallest standard deviation in iteration counts. This indicates a highly stable and predictable convergence process, whereas the other three algorithms converge slowly with significant fluctuations.

5.4. Analysis of the Optimization Effect of the TSCOPF Model

Taking anticipated fault 2 as an example, when the TSCOPF optimization scheme is not adopted, transient instability occurs in the power system. Based on the method proposed in this paper, the PMUs collects the measurement data of the power system in real time. The CatBoost-DF model detects the risk of transient instability in the system and adjusts the active power output of the generator in advance to prevent the occurrence of transient instability. The comparison of the active power output of each generator before and after control is shown in Table 5.

Table 5. Generator active power output status.

Generator	Before Optimization (MW)	After Optimization (MW)	Active Power Regulation (MW)	Total Adjustment Volume (MW)
G1	536.85	521.75	−15.10	275.89
G2	695.24	663.16	−32.08
G3	668.35	685.83	17.48
G4	672.89	708.71	35.82
G5	730.53	754.87	24.34
G6	854.94	835.12	−19.82
G7	334.79	384.31	49.52
G8	342.82	370.02	27.2
G9	546.27	503.49	−42.78
G10	583.46	595.21	11.75

When three-phase short circuits occur in the IEEE 39 bus system at fault lines 3–18 and 4–14, the scheme proposed in this paper is adopted to optimize the system operation and increase the transient stability margin of the system. The TSI values of the system before and after optimization are shown in Table 6.

Table 6. TSI comparison before and after optimization.

Fault Number	TSI
	Before Optimization	After Optimization
2	−99.11	67.92
3	−98.77	61.72

As shown in Table 6, before optimization, when a fault occurred in the line, the system TSI was less than 0, and at this time, the system experienced transient instability. After preventive control by the method proposed in this paper, the system TSI was greater than 0, and no transient instability occurred in the system. This indicates that the method proposed in this paper can improve the stability of the system.

To further verify the effectiveness of the proposed method, the power angle curves of the generator before and after TSCOPF optimization were plotted, respectively, when the anticipated faults 2 and 3 occurred, as shown in Figure 5 and Figure 6.

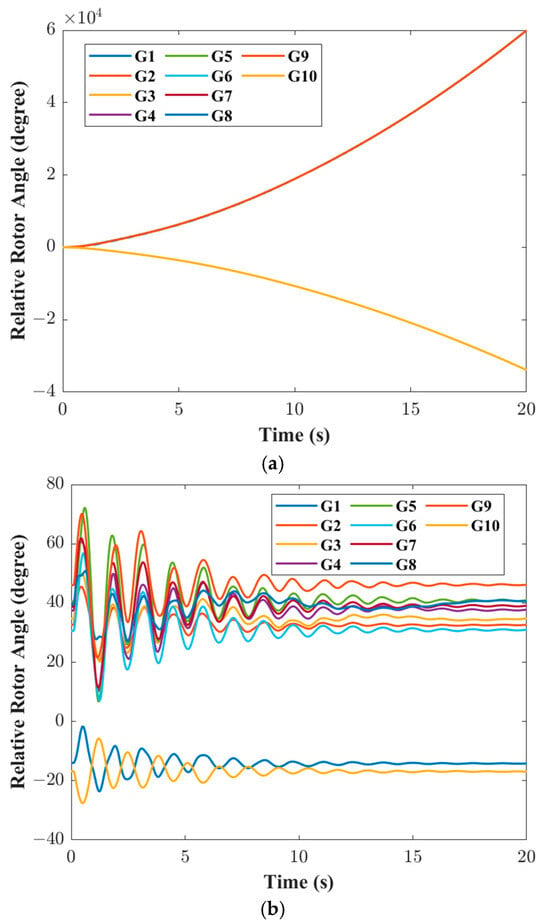
Figure 5. Generator power angle curve. (a) Anticipated fault 2 before optimization; (b) Anticipated fault 2 after optimization.

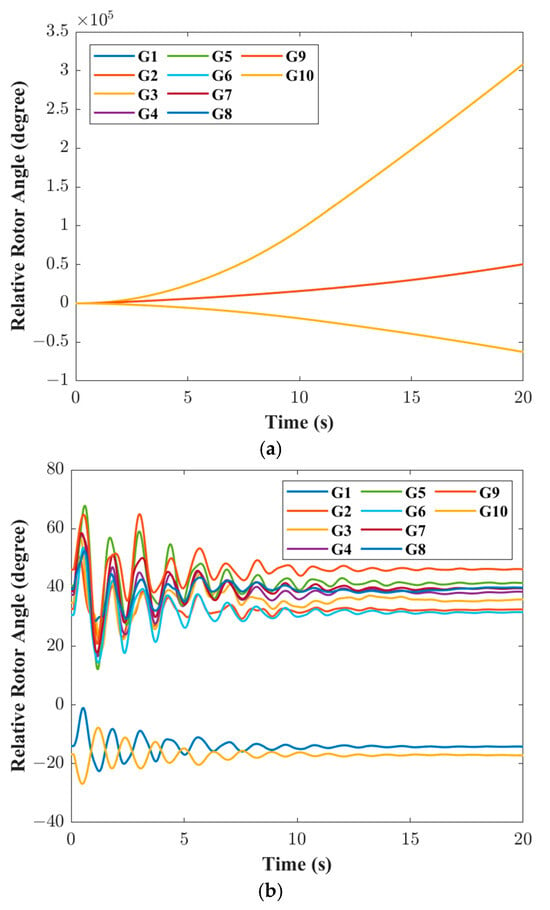
Figure 6. Generator power angle curve. (a) Anticipated fault 3 before optimization; (b) Anticipated fault 3 after optimization.

As can be seen from Figure 5a and Figure 6a, when a system failure occurs, the power angle of the generator continues to diverges, and the maximum power angle difference far exceeds the threshold, resulting in transient instability of the system. As can be seen from Figure 5b and Figure 6b, based on the method proposed in this paper to optimize the system operation, the generator power angle gradually stabilizes after a period of disturbance, with the maximum power angle difference being less than the threshold, and no transient instability occurs in the system. Therefore, the method proposed in this paper can prevent the continuous increase in the generator power angle difference when the system malfunctions, ensuring the safety of the system.

5.5. Performance Comparison of Different TSCOPF Models

To verify the superiority of the model proposed in this paper, this paper compares three models as follows:

Model 1: The time domain simulation method is adopted to solve the computational transient stability constraints, and the ISOA is utilized to solve TSCOPF;

Model 2: The CatBoost-DF model is adopted to handle the transient stability constraints, and the interior point method is utilized to solve TSCOPF;

Model 3: The CatBoost-DF model is adopted to handle the transient stability constraints, and the ISOA is utilized to solve TSCOPF.

When the system experiences the anticipated fault 2, the transient stability index drops to −99.11, indicating that the system has lost its transient stability. To address this unstable scenario, three different methods were, respectively, adopted to solve the TSCOPF problem. The comparison of the optimization results of each method is detailed in Table 7.

Table 7. Performance comparison of three TSCOPF models.

Model	Optimized TSI	Calculation Time (s)	Generation Cost ($)
Model 1	68.34	402.91	1607
Model 2	65.71	62.34	1779
Model 3	67.92	38.27	1583

As can be seen from Table 7, Model 1 adopts the time domain simulation method to handle the transient stability constraints. The optimized system has a relatively high $T_{SI}$ and good transient stability. However, the required computing time is too long, making it difficult to meet the online prediction requirements. Model 2 and Model 3 adopt the CatBoost-DF model to handle the transient stability constraints, effectively shortening the computing time. Compared with Method 2, Method 3 uses the ISOA to solve TSCOPF. In terms of system stability, computing time and power generation cost after optimization, it is superior to the interior point method, indicating that the algorithm has strong global search ability and local optimization ability. Therefore, the model proposed in this paper ensures the stability of the power system while taking into account its economy.

6. Conclusions

In order to ensure the safety and economy of power system operation, this paper proposes a TSCOPF model based on CatBoost-DF and ISOA. Through simulation analysis and comparative experiments, the following conclusions are obtained:

(1) The constructed CatBoost-DF model, with its deep feature extraction and high-precision prediction capabilities, builds an efficient and accurate transient stability assessment tool. It is embedded as a surrogate model in the TSCOPF framework, effectively replacing the solution of complex differential algebraic equations. It provides key technical support for achieving online safety monitoring and rapid early warning of the power system.

(2) The TSCOPF model was solved by using ISOA. Compared with other swarm intelligence optimization algorithms, ISOA has better performance in convergence speed and accuracy, ensuring the economic operation of the power system.

(3) Under identical hardware and computational scenarios, when evaluating system stability using optimized T_SI, online availability via total computation time, and TSCOPF model economics through generation cost, CatBoost-DF maintains values close to the time-domain simulation T_SI (67.92 and 68.34, respectively) while reducing computation time from 402.91 s to 38.27 s (approximately a 90.5% decrease), outperforming both CatBoost-DF+ interior point method in speed and stability (T_SI improvement of 2.21, acceleration of approximately 38.6%). It also exhibits the lowest generation cost among the three models (reducing costs by 1.5% and 11% compared to Model 1 and Model 2, respectively), thereby constituting the optimal accuracy–speed tradeoff solution for online scenarios.

(4) The TSCOPF model that integrates CatBoost-DF and ISOA achieves a good balance in terms of computational efficiency, optimization accuracy and economy compared with the traditional model. This method can quickly adjust the generator output when the risk of transient instability is detected, guiding the system from the instability edge to the stable operation domain, thereby reliably ensuring the safe and stable operation of the power system and achieving better economic benefits.