Extending the Frequency Bandwidth of a Tristable Electromagnetic Energy Harvester Through the Use of Stoppers

Abstract

This study investigated a nonlinear tristable electromagnetic vibration energy harvester enhanced with adjustable mechanical stoppers. The stoppers were designed to limit yoke displacement and prevent sticking in the outer stable positions. The research aimed to extend the operational frequency bandwidth and improve the stability of energy conversion under variable excitation conditions. A comprehensive experimental setup based on a PXI measurement platform was developed to analyze the system’s electrical and mechanical responses. The study examined the influence of stopper spacing, vibration acceleration, and electrical load on the frequency–voltage characteristics and beam strain. The results showed that introducing adjustable stoppers eliminated the sticking phenomenon and broadened the effective operational bandwidth to a total range of 14 Hz under excitation frequencies between 10 and 50 Hz, while maintaining structural safety. The findings confirmed that the proper selection of stopper distance enabled adaptive tuning of the harvester’s dynamic behavior and power output, increasing the average voltage by approximately 50% compared with the configuration without stoppers. The proposed approach improved the autonomy and reliability of self-powered sensor nodes and other low-power electronic systems for Internet of Things (IoT) and condition monitoring applications.

1. Introduction

The progressive integration of the physical world of production machinery with virtual technologies currently forms the foundation of modern industrial development. The implementation of integrated control and data analytics solutions enables reductions in manufacturing costs, increased process flexibility, and customization according to individual customer needs. However, realizing this model requires the use of advanced automation components such as actuators, sensors, and data processing and transmission systems [1,2]. At the same time, the rapid development of microelectromechanical systems (MEMS) and the Internet of Things (IoT) has led to the widespread adoption of low-power electronic devices, including wireless microsensor nodes used in applications such as structural health monitoring, safety systems, aerospace telemetry, medical diagnostics, and environmental monitoring [3,4,5,6]. Nevertheless, dynamic digitalization and miniaturization of electronic devices have resulted in a significant increase in energy demand, which still largely relies on conventional sources. An additional limitation is the use of traditional batteries in sensor systems, whose short lifespan necessitates frequent replacement, leading to increased operating costs, reduced reliability in hard-to-access environments, and a substantial environmental burden due to insufficient recycling processes of lithium and alkaline batteries [7,8,9].

In response to these challenges, the concept of energy harvesting—the conversion of energy generated by natural or incidental phenomena such as mechanical vibrations, fluid flows, thermal gradients, or electromagnetic radiation into electrical energy—has gained increasing importance [4,10,11]. Such solutions can enhance the autonomy of low-power electronic systems. Among various ambient energy sources, mechanical vibrations attract particular attention, as they constitute a widely available form of microenergy present both in everyday environments and in numerous industrial processes [12]. The ability to convert this energy into electricity enables the powering of a wide range of low-power measurement, monitoring, and diagnostic devices operating autonomously in distributed applications [1,13,14,15,16]. This, in turn, leads to a considerable extension of device lifetime and, in many cases, eliminates the need for a wired power supply—an essential step toward the development of autonomous and energy-efficient systems of the future [11,17].

Energy obtained from vibrations can be converted into electrical energy through several mechanisms, including electromagnetic [18,19,20], piezoelectric [21,22,23,24,25], triboelectric [3,26,27], and electrostatic methods [28]. Among them, traditional electromagnetic generators stand out due to their simple construction and low fabrication cost. However, their linear resonance-based designs are characterized by a narrow operational frequency bandwidth, limiting their efficiency under variable excitation frequencies typical of real-world environments. Effective energy harvesting occurs only when the excitation frequency matches the resonance frequency; any deviation causes a sharp drop in output power [29]. To overcome this limitation, intensive research has been conducted on nonlinear and broadband vibration energy harvesters [2,30]. These approaches include the introduction of nonlinear springs, frequency tuning, multimodal structures, frequency up-conversion mechanisms, and impact-based methods [31,32,33]. Among them, impact-based (collision-type) designs have proven particularly promising, as the introduction of mechanical stoppers or additional elastic elements enables a notable extension of the operating bandwidth and improvement of conversion efficiency. Studies have shown that both the position of the stopper and frequency up-conversion mechanisms have a crucial influence on the electrical performance of the generator [34,35].

The effectiveness of such devices depends not only on their operating principles or adopted dynamic models but also on the proper design of structural components and material selection. In the case of miniature energy harvesters, an individualized design approach is required, in which the optimal matching of geometry and material properties of energy-converting elements plays a critical role [36,37]. Of particular importance is the analysis of the vibrating cantilever beam—a key component determining the natural frequencies, deflection amplitudes, and conversion efficiency. Its shape, stiffness, and stress distribution directly influence the energy parameters and operational stability of the system [1,17,38], while material properties (such as Young’s modulus, damping, and density) determine the resonance frequency and dynamic response under operational conditions [19,25]. The literature indicates that in systems with single- or double-sided stoppers and frequency up-conversion mechanisms, not only the dynamic response but also the stress state of load-bearing components changes significantly [39]. Therefore, the cantilever beam requires dedicated mechanical investigations to assess the influence of stopper position on stress concentration. Neglecting this verification may lead to accelerated fatigue degradation, modal parameter drift, power reduction, and mechanical failure [40,41,42]. Conscious selection of beam geometry, material properties, and stopper characteristics is essential to achieve a broad operational bandwidth while maintaining controlled stress levels and ensuring structural reliability.

This study presents a comprehensive investigation of the influence of various stoppers on the characteristics of a nonlinear tristable energy harvester, aiming to eliminate design drawbacks and extend its operational bandwidth. Voltage characteristics were determined across a wide range of excitation accelerations and load resistances, resulting in curves that enabled evaluation of load matching and the effect of stoppers on conversion efficiency. Additionally, strain measurements were performed for all examined operating configurations using strain-gauge techniques. Since strain is proportional to beam deflection, these measurements allow real-time monitoring of the potential energy well in which the yoke with permanent magnets is currently located.

Unlike previously reported stopper-assisted bistable or tristable harvesters [3,39,40], the proposed design introduces adjustable mechanical stoppers that can be tuned to control the yoke displacement and suppress sticking in the outer potential wells. This adjustable spacing enables passive, broadband tuning of the dynamic response without additional magnetic force or external frequency-tracking mechanisms. The resulting system achieves up to 14 Hz operational bandwidth and improved voltage stability, representing a meaningful advancement in the design of tristable electromagnetic harvesters for practical IoT power sources.

2. Tristable Electromagnetic Energy Harvester

This study investigates an electromagnetic energy harvester designed for powering low-power electronic systems. The harvester consists of a flat composite beam reinforced with glass fiber, which acts as a spring and is clamped at one end to a vibration source. A yoke with permanent magnets is mounted at the free end of the beam (Figure 1). Two fixed coils, connected in parallel, are positioned near the yoke, where an electric voltage is induced as the beam oscillates. Additional permanent magnets embedded in the supporting structure are used to introduce magnetic nonlinearity into the system [36,43].

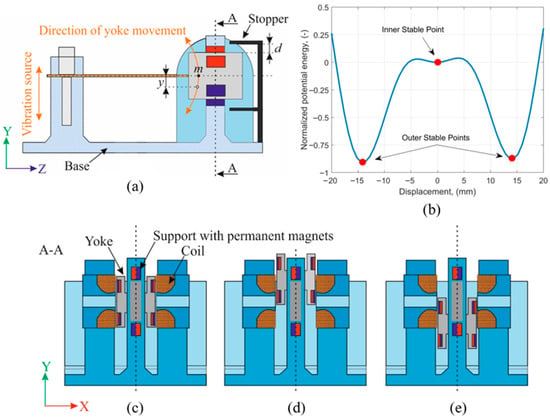
Figure 1. CAD diagram of the nonlinear tristable vibration energy harvester (a), Potential energy landscape of the vibration energy harvester (b), Yoke resting in the inner stable point (c), Yoke resting in the upper stable point (d), Yoke resting in the lower stable point (e).

The mathematical model of the nonlinear electromagnetic microgenerator is described by the following equations:

$$m{\displaystyle \frac{d^{2}y\left(t\right)}{d{t}^2}}+c{\displaystyle \frac{dy\left(t\right)}{dt}}+ky\left(t\right)+F_{mag}\left(y\right)+{\displaystyle \frac{\partial \mathsf{\lambda }\left(y\right)}{\partial y}}i=m{a}_{\mathrm{v}\mathrm{i}\mathrm{b}}\left(t\right)-mg$$

(1)

$$L_{\mathrm{c}}{\displaystyle \frac{di\left(t\right)}{dt}}={\displaystyle \frac{\partial \mathsf{\lambda }\left(y\right)}{\partial y}}{\displaystyle \frac{dy\left(t\right)}{dt}}-\left(R_{\mathrm{L}}+R_{\mathrm{c}}\right)i$$

(2)

where: $m$—mass of the vibrating part, $c$—damping coefficient, $k$—stiffness coefficient, $F_{mag}$—magnetic force, $y$—displacement of the vibrating part, $a_{\mathrm{v}\mathrm{i}\mathrm{b}}$—external vibration acceleration, $g$—gravitational acceleration, $\mathsf{\lambda }$—magnetic flux linkage associated with the coil winding, $i$—current flowing through the coil, $L_{\mathrm{c}}$—coil inductance, $R_{\mathrm{c}}$—coil resistance, $R_{\mathrm{L}}$—load resistance, $t$—time.

The governing Equations (1) and (2) assume small base displacement and linear viscous damping, with temperature effects considered negligible. The tristable potential shown in Figure 1b arises from the superposition of the beam’s elastic energy and the repulsive magnetic potential between opposing poles, creating three distinct equilibrium positions. Owing to the nonlinear magnetic force dependent on the yoke displacement, the system exhibits stable equilibrium points that strongly influence its dynamic behavior. To account for this behavior, the local minima of the potential energy as a function of displacement must be determined. The total potential energy comprises the elastic energy of the flat beam, the gravitational potential energy, and the magnetic potential energy, and can be written as follows:

$$U\left(y\right)={\displaystyle \frac{1}{2}}k{y}^2+mgy-\int F_{mag}\left(y\right)dy$$

(3)

The potential energy curve as a function of displacement is illustrated in Figure 1. The magnetic force was calculated using the finite element method (FEM).

Based on the analysis of previous research, the authors proposed the use of mechanical stoppers to limit the maximum displacement of the yoke. When the yoke collides with the metallic arm of the stopper, a contact force is generated, comprising both the elastic response of the material and frictional effects. This interaction further enriches the system dynamics by introducing impact-related nonlinearities. During the experiments, the distance between the yoke and the stoppers was gradually increased along the Y-axis by an increment denoted as d. The experiments were performed for three excitation acceleration values: 2.5 m/s², 5 m/s², and 7.5 m/s², which were selected as representative for vibration-based energy harvesters and allowed an assessment of the influence of increasing vibration amplitude on the system characteristics. Additionally, various electrical load conditions were considered by changing the load resistance, simulating different operating scenarios of the energy harvester. The combined effects of beam elasticity, magnetic nonlinearity, and yoke–stopper contact interactions enabled the achievement of a broad operational bandwidth, which increased with the amplitude and acceleration of the vibrations.

3. Experimental Setup

The experimental setup used to investigate the electromagnetic energy harvester is shown in Figure 2. The system was equipped with a laboratory computer integrated with a National Instruments PXI-based modular measurement system. The core element of the data acquisition system was a multichannel NI PXIe-6368 measurement card (ArtisanTG, Champaign, IL, USA, X Series), which enabled precise excitation control of the tested harvester, generation of control signals with adjustable frequency and amplitude, and simultaneous acquisition of voltage signals induced in the harvester coils with high resolution (16-bit) and a sampling rate of up to 2 MS/s per channel [44]. This configuration ensures time synchronization between input and output channels, allowing accurate dynamic analysis of phenomena occurring in the system. To measure mechanical loads and strain, an NI PXI-9237 module was used, dedicated to strain-gauge bridge configurations in quarter-, half-, and full-bridge arrangements. This module provides stable bridge excitation, digital temperature compensation, noise filtering, and high measurement resolution through a 24-bit ADC, as well as synchronous operation with other PXI modules [45]. Prior to testing, all electrical channels were calibrated using a reference voltage generator and a precision resistor network, while strain bridges were verified against a reference bridge. The expanded measurement uncertainty was estimated as ±2.5% for voltage and ±3% for strain. The test beam was instrumented with foil strain gauges connected in a full-bridge configuration, enabling the recording of bending stresses generated during its motion under dynamic conditions. The strain gauges were placed at three points along the beam, with the highest readings obtained from the gauge located near the clamping point of the beam to the housing (Figure 2). The setup was further complemented by a precision decade resistor, allowing smooth adjustment of the harvester’s electrical load. This feature made it possible to simulate various operating conditions and optimize the device performance. The entire system was controlled via the LabVIEW environment, enabling automation of measurement procedures, real-time data acquisition, and comprehensive analysis of the collected results. The experiments were conducted at room temperature (20 ± 1 °C). The excitation frequency was linearly swept up and down between 10 Hz and 50 Hz within a 50-s cycle. These parameters ensured stable data acquisition and minimized transient effects.

Figure 2. Desktop (1), PXIe-8861 embedded controller housed in a PXIe-1092 chassis (2), Resistance decade box (3), Nonlinear electromagnetic vibration energy harvester whose beam was instrumented with TF-3-2x/120-type strain gauges (4), PXIe-6368 multifunction data acquisition (DAQ) module (5), PXI-9237 strain/bridge input module (6), Vibration source (7).

4. Extending the Frequency Bandwidth Through the Use of Stoppers

Since the presented harvester is a tristable system (Figure 1), it tends to become trapped in the outer stable positions, particularly at high vibration acceleration levels. This issue is illustrated in Figure 3, which shows the time-domain waveforms of voltage and beam strain for a vibration acceleration of 7.5 m/s². As can be observed, both during decreasing and increasing excitation frequencies, the yoke becomes stuck when the beam reaches its limit strain (displacement), which effectively results in a complete loss of voltage generation. Another drawback is that, after the vibrations cease, the yoke does not return to the central stable position, and upon reapplying excitation, no voltage is generated either. To mitigate the described problem, mechanical stoppers were applied to the yokes (as shown in Figure 1). Their introduction limits the motion of the yokes and prevents them from sticking to the outer stable positions. In this study, adjustable stoppers were used, allowing the investigation of how the distance between the stoppers and the yokes in the resting position affects the frequency response characteristics of the system.

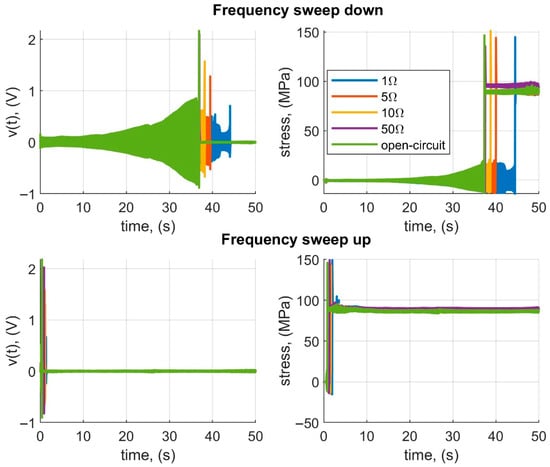
Figure 3. Time-domain waveforms of voltage and beam strain illustrating the “sticking” of the yoke to the outer stable position—without stoppers.

Initially, measurements of the frequency–response characteristics of voltage amplitude were performed for an increasing vibration frequency from 10 Hz to 50 Hz, followed by measurements for a decreasing frequency from 50 Hz to 10 Hz. The root mean square (RMS) value of vibration acceleration was set to 2.5 m/s². Figure 4 presents a comparison of the obtained results for different stopper distances and load resistances. In this case, the maximum stopper distance was set to 4 mm, since for larger distances the yokes no longer collided with the stoppers. The solid line represents the characteristics obtained during increasing frequency, while the dashed line corresponds to decreasing frequency. Additionally, in each plot, a dotted red line marks the level of 0.5 V, indicating the minimum voltage amplitude required to convert the generated signal into a usable charging signal for autonomous measurement systems. This threshold also defines the effective bandwidth, i.e., the frequency range in which the generated voltage is equal to or greater than this value. The presented characteristics show that for stopper distances of 3 mm and 4 mm, a broader operational frequency band is obtained for the 50 Ω load and for the open-circuit condition compared with the system without stoppers, particularly during the frequency-increasing sweep.

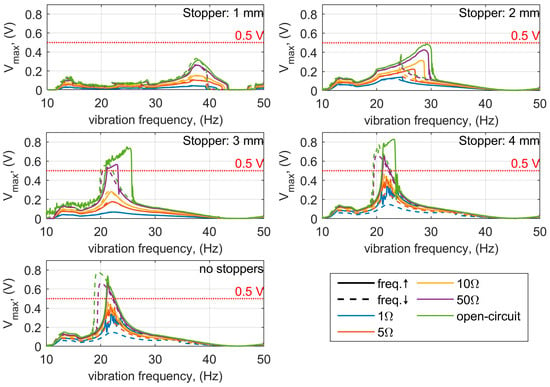
Figure 4. Frequency response characteristics at an RMS vibration acceleration of 2.5 m/s² for various stopper distances, load resistances, and frequency sweep directions.

To analyze parameters such as the bandwidth and the average voltage amplitude within that range, a parallel plot was created (Figure 5). This plot shows that, during increasing vibration frequency, the widest bandwidth is achieved for a stopper distance of 3 mm and a load resistance of 50 Ω, amounting to 2 Hz. Under the same configuration but for decreasing frequency, the bandwidth equals approximately 1.2 Hz. The average voltage amplitudes within these bands are 0.54 V and 0.5 V, respectively. The widest bandwidth for decreasing frequency, equal to 2.6 Hz, is obtained for a 4 mm stopper distance and a 50 Ω resistance.

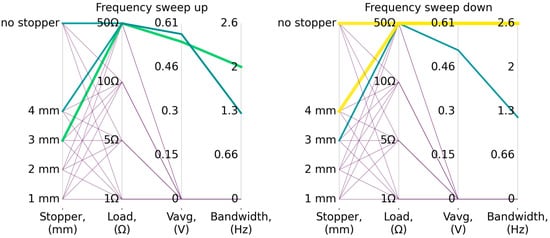
Figure 5. Parallel plot showing the relationship between the bandwidth and the average voltage amplitude within that band as a function of stopper distance and load resistance—RMS vibration acceleration of 2.5 m/s².

A notable improvement was observed when the vibration acceleration was increased to 5 m/s², as illustrated in Figure 6. For stopper distances ranging from 2 mm to 5 mm, the operational bandwidths were broader compared with the system without stoppers. Additionally, it can be noted that the smaller the stopper distance, the more the resonant frequency shifts toward higher frequencies. This effect results from the stiffening of the system caused by collisions between the yokes and the stoppers. In the open-circuit condition without stoppers, the yokes became stuck in the outer stable position.

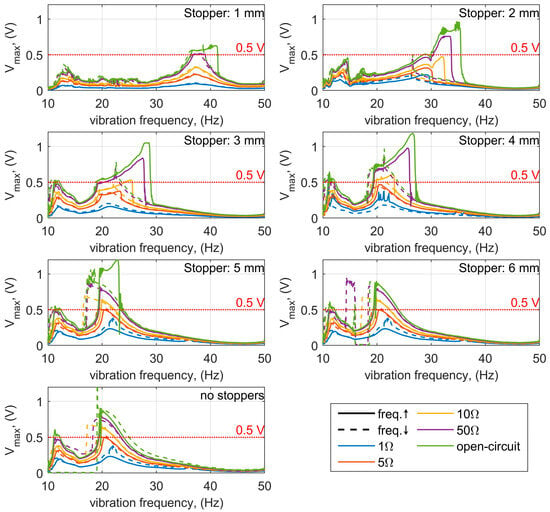
Figure 6. Frequency response characteristics at an RMS vibration acceleration of 5 m/s² for various stopper distances, load resistances, and frequency sweep directions.

The parallel plot (Figure 7) shows that the widest bandwidth, equal to 7.5 Hz, occurs during the increasing frequency sweep for a stopper distance of 3 mm and a load resistance of 50 Ω. For the decreasing frequency sweep, the best configuration yields a bandwidth of 7 Hz at a stopper distance of 6 mm and load resistance of 50 Ω. At higher excitation levels, it can also be observed that the characteristics corresponding to lower load resistances (from 5 Ω) may exceed the 0.5 V threshold.

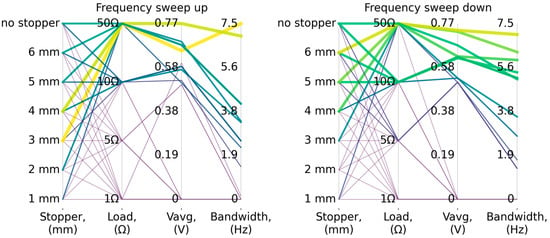
Figure 7. Parallel plot showing the relationship between the bandwidth and the average voltage amplitude within that band as a function of stopper distance and load resistance—RMS vibration acceleration of 5 m/s².

The frequency response characteristics for an RMS vibration acceleration of 7.5 m/s² are presented in Figure 8. As can be observed, the use of stoppers allows not only a broadening of the operational bandwidth but also an increase in the output voltage. All tested stopper distances significantly improve the system performance compared with the configuration without stoppers, in which the yokes became stuck in the outer stable positions for every load condition.

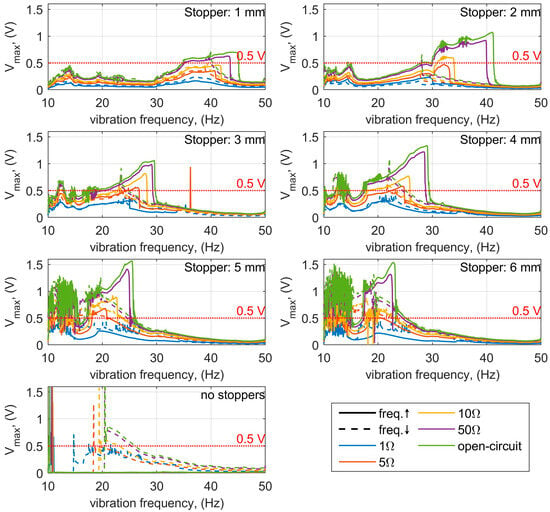
Figure 8. Frequency response characteristics at an RMS vibration acceleration of 7.5 m/s² for various stopper distances, load resistances, and frequency sweep directions.

From the parallel plot (Figure 9), it can be concluded that the investigated system can achieve a bandwidth of up to 14 Hz, both during increasing and decreasing vibration frequency sweeps. A wide bandwidth and a relatively high average voltage amplitude within this range can be obtained for load resistances from 5 Ω. For stopper distances of 5 mm and 6 mm with a 5 Ω load, the operational frequency range extends approximately from 5 Hz to 11 Hz. Similarly, for stopper distances of 3, 4, 5, and 6 mm with a 10 Ω load, the bandwidth extends from approximately 6 Hz to 13 Hz.

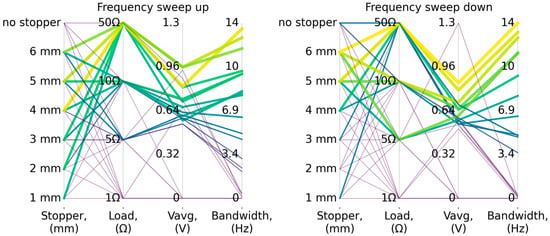
Figure 9. Parallel plot showing the relationship between the bandwidth and the average voltage amplitude within that band as a function of stopper distance and load resistance—RMS vibration acceleration of 7.5 m/s².

Figure 10 presents a comparison of the best frequency–voltage characteristics in terms of the frequency bandwidth. The optimal stopper distances are compared with configurations without stoppers. For each vibration acceleration level considered, the optimal stopper distances were obtained for a load resistance of 50 Ω. In addition, for each voltage characteristic, the frequency response of the beam strain envelope is shown. This allows identification of operating points at which the system is pulled toward the outer stable positions, since the strain is proportional to the displacement of the yokes. A noticeable bandwidth extension can already be observed at an RMS vibration acceleration of 2.5 m/s² for the increasing frequency sweep. The use of stoppers stiffens the system during impacts, which shifts the resonance toward higher frequencies, resulting in a broader operational bandwidth. When the yoke contacts the stopper, the instantaneous contact stiffness rises sharply. This interaction between the magnetic and mechanical nonlinearities produces a restoring force that broadens the frequency response, as similarly described in [31,32]. This phenomenon becomes more pronounced at higher acceleration levels. The advantages of using stoppers are particularly evident at an acceleration of 7.5 m/s², as they prevent the yokes from sticking to the outer stable positions. As can be seen, in the system without stoppers, the attraction of the yokes to an outer stable point causes them to remain trapped, preventing further voltage generation. The vibration energy delivered at the tested acceleration levels is insufficient for the yokes to overcome the potential energy barrier and return to the central stable position. By applying stoppers with appropriate spacing, the frequency bandwidth is greatly extended as the vibration acceleration increases. It can also be observed that the optimal stopper distance differs for increasing and decreasing frequency sweeps. Therefore, when designing a harvester for a specific practical application—considering the target frequency range, desired voltage level, and frequency sweep direction—the stopper distance should be selected based on an appropriate compromise between the bandwidths obtained for both increasing and decreasing frequencies. The maximum beam stresses are approximately 15, 40, and 50 MPa for excitation accelerations of 2.5 m/s², 5 m/s², and 7.5 m/s², respectively. Future work will focus on determining the fatigue strength and wear at the stopper–yoke interface. Table 1 presents a comparison of the achieved bandwidth and output parameters with those reported in the literature.

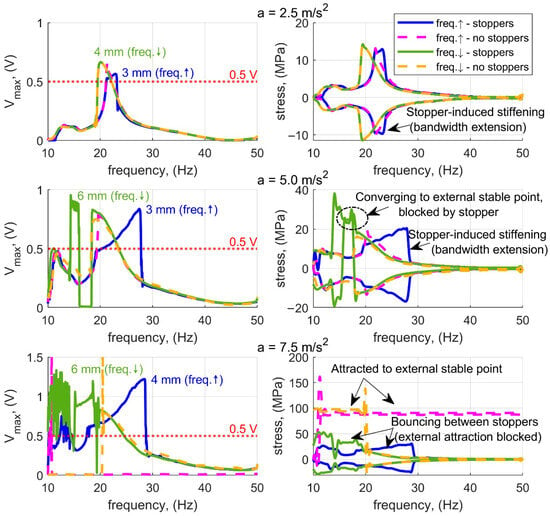
Figure 10. Frequency response characteristics of voltage amplitude and beam strain envelopes for different vibration accelerations, compared for the optimal stopper distances in terms of bandwidth and for the configuration without stoppers (optimal bandwidths obtained for a load resistance of 50 Ω).

Table 1. Comparison of bandwidth and voltage with recent energy harvesters.

Reference	Harvester Type	Bandwidth (Hz)	Output
[3]	Piezo-triboelectric with mechanical stoppers	6.9	1.2 V piezoelectric + 15.59 triboelectric, max 680 µW
[39]	Piezoelectric (2-DOF) with mechanical stoppers	11	94.82 V, max 713 µW
This work	Tristable electromagnetic with mechanical stoppers	14	0.96 V avg, 3.6 mW avg

5. Conclusions

This study experimentally investigated a tristable electromagnetic vibration energy harvester equipped with mechanical stoppers designed to limit the displacement of the yoke. The results clearly demonstrated that the proper design and positioning of the stoppers considerably improve the overall performance and reliability of the system.

The conducted measurements and analyses led to the following key conclusions:

• Influence of stoppers on system performance:
  The implementation of adjustable stoppers has a direct and measurable impact on the output parameters of the harvester. By appropriately setting the stopper distance, it is possible to effectively tune both the bandwidth and the average output voltage, enabling flexible adaptation of the harvester to environments with variable excitation frequencies.
• Elimination of yoke sticking:
  One of the major achievements of this work is the complete removal of the sticking phenomenon, in which the yokes previously became trapped in the outer stable positions. This effect, observed in systems without stoppers, caused the disappearance of voltage generation and reduced operational reliability. The application of stoppers prevents this behavior and ensures stable operation even at high vibration amplitudes.
• Bandwidth enhancement:
  The use of mechanical stoppers resulted in a notable extension of the operational frequency range—up to 14 Hz in the optimal configurations at higher excitation levels. The introduction of adjustable stoppers increased the effective operational bandwidth for excitation levels of 5 m/s² and 7.5 m/s². At 2.5 m/s², the optimal stopper configuration produced performance comparable to the system without stoppers, yielding a bandwidth of 2.6 Hz and an average output voltage of 0.61 V. For 5 m/s², the bandwidth expanded from 5 Hz to 7.5 Hz (a 1.5× increase) and the mean voltage rose from 0.70 V to 0.77 V (a 1.1× improvement). At 7.5 m/s², the bandwidth broadened from 6 Hz to 14 Hz (a 2.3× increase) and the mean voltage increased from 0.55 V to 0.85 V (a 1.5× improvement). These results confirm that proper selection of stopper spacing not only stabilizes the dynamic behavior of the system but also enhances its broadband energy conversion capability.

The findings indicate that the integration of mechanical stoppers can substantially enhance the autonomy and reliability of power sources for low-power electronic devices, such as monitoring sensors and IoT nodes. Improved frequency adaptability and robust operation under variable excitation conditions make this concept particularly promising for self-powered systems operating in unpredictable vibration environments.

Future work will focus on fatigue analysis, optimization of stopper geometry through numerical simulations, and integration with energy storage modules.