Potential Properties and Applications of Wires with Helical Structure in High-Voltage Overhead Power Lines and PV Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Analyzed Structure
2.2. Numerical Model and Properties
3. Results and Discussion
3.1. Calculation Setup and Parameters
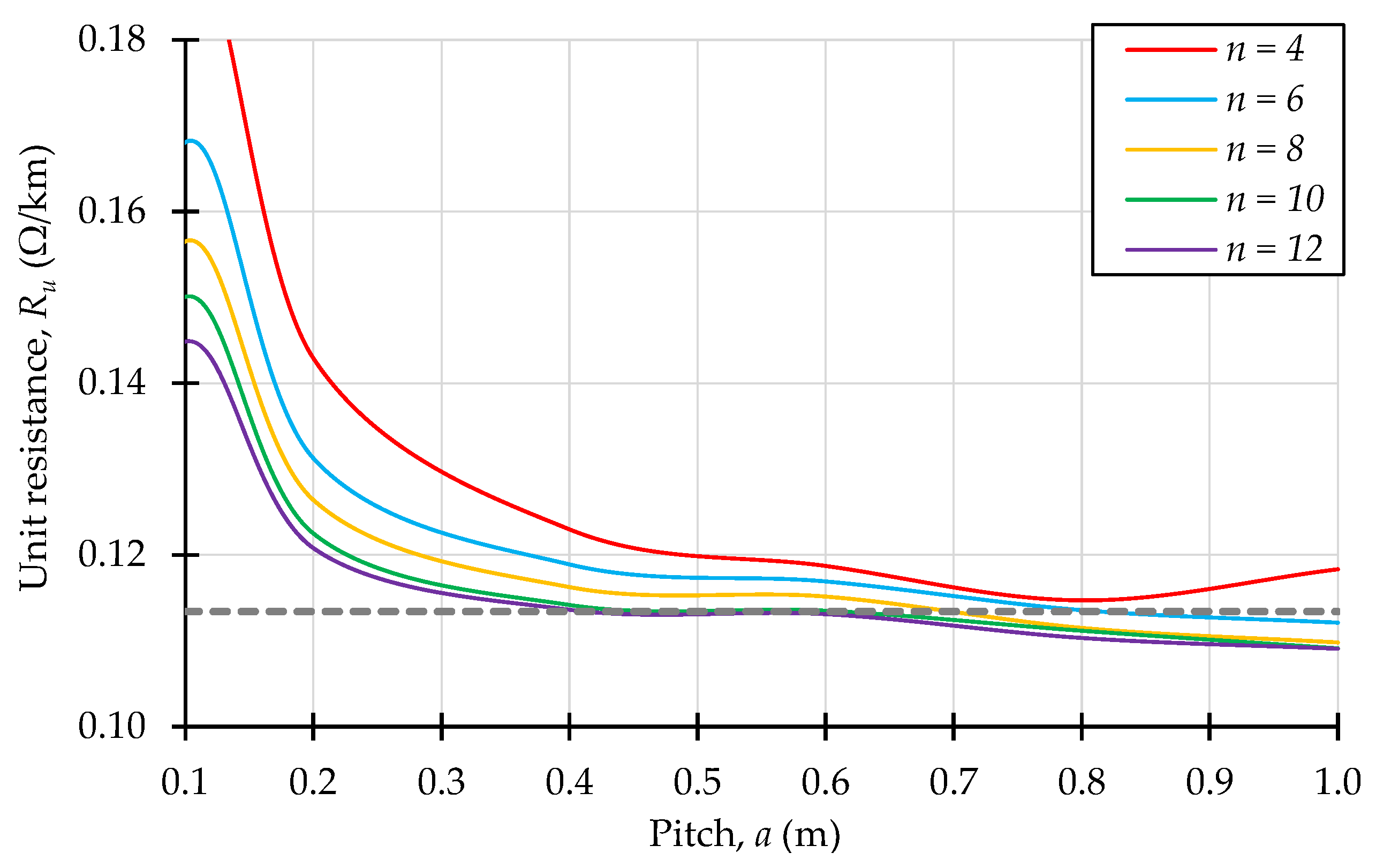
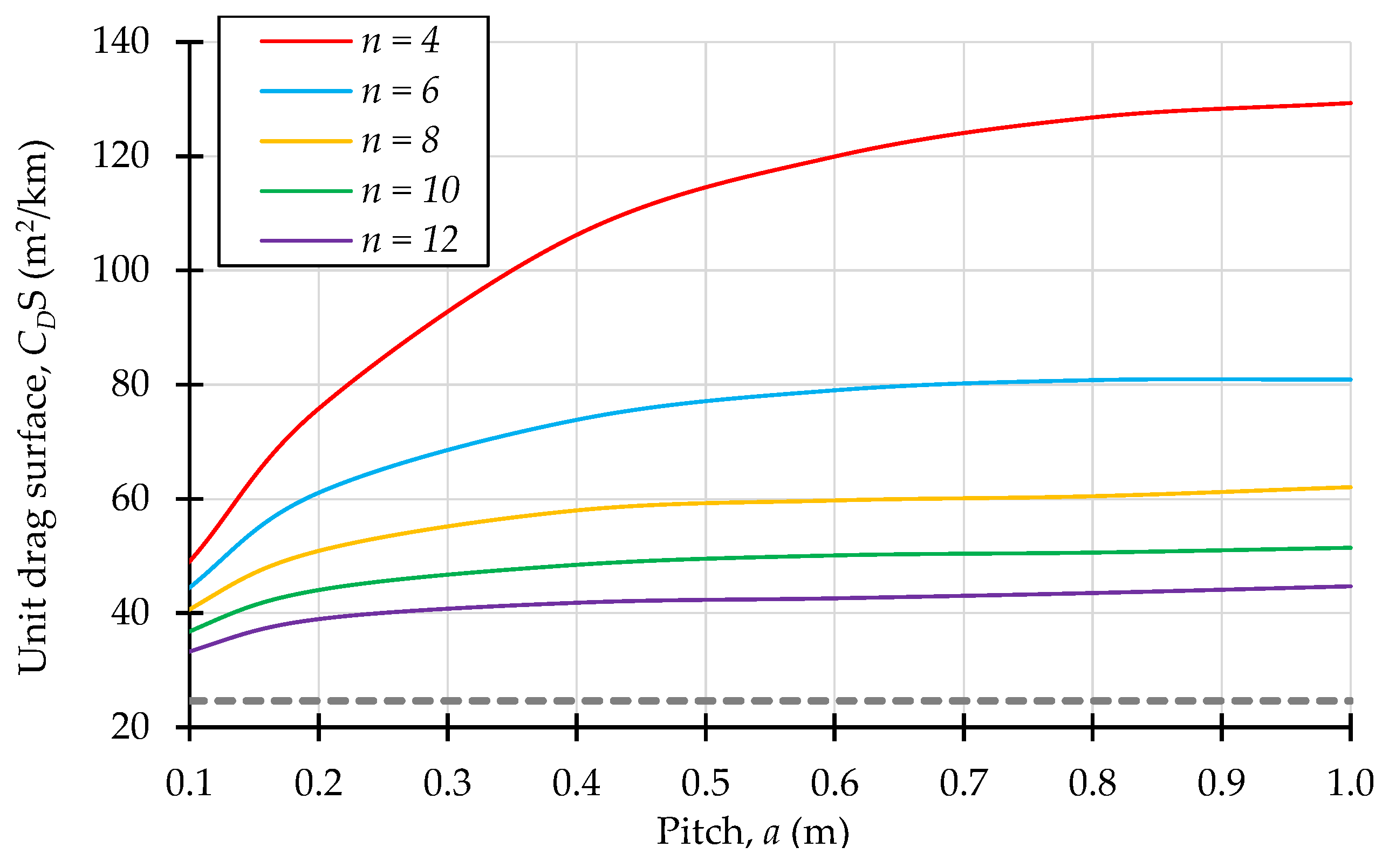
3.2. Selection of Optimal Structure
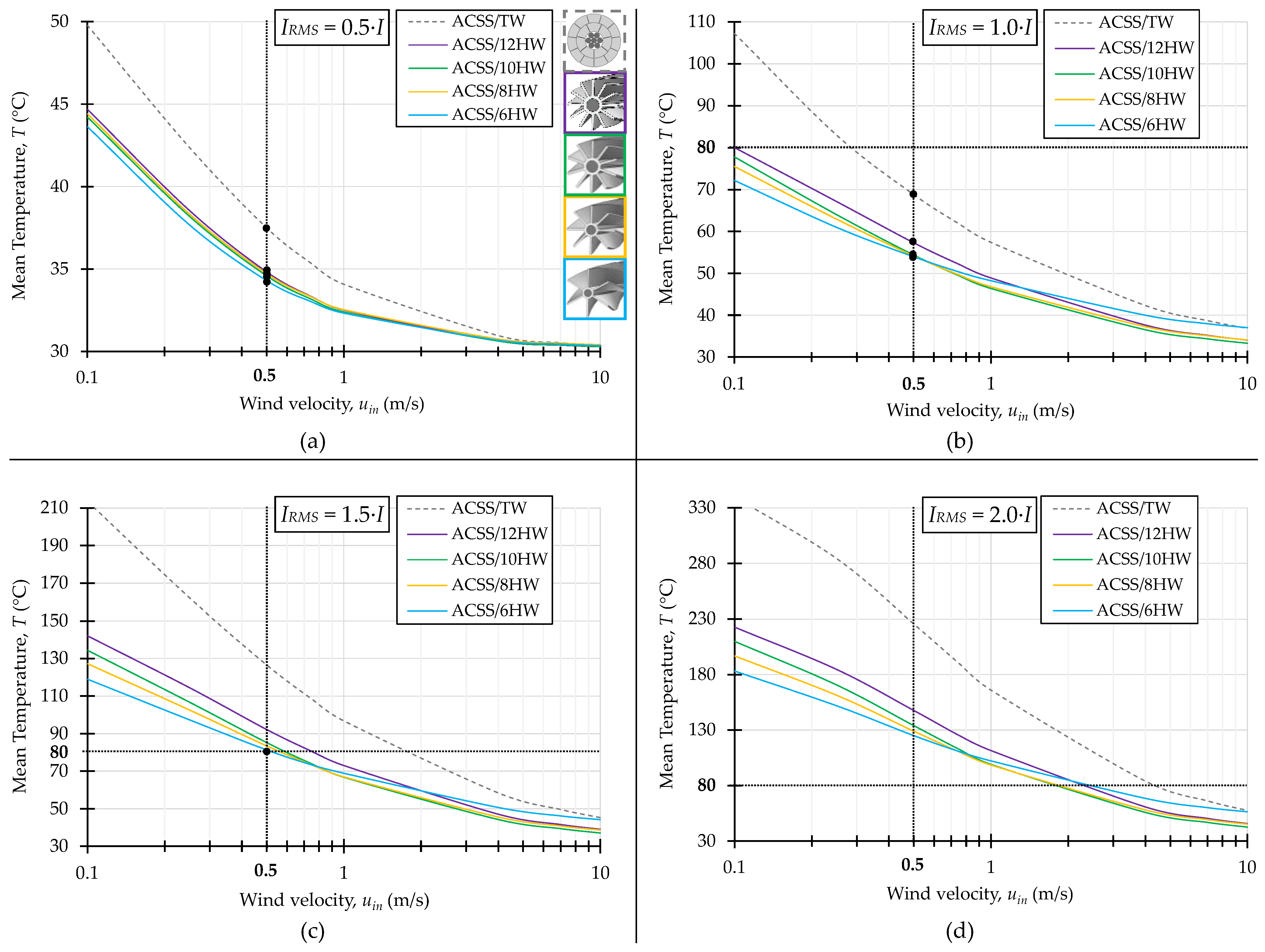
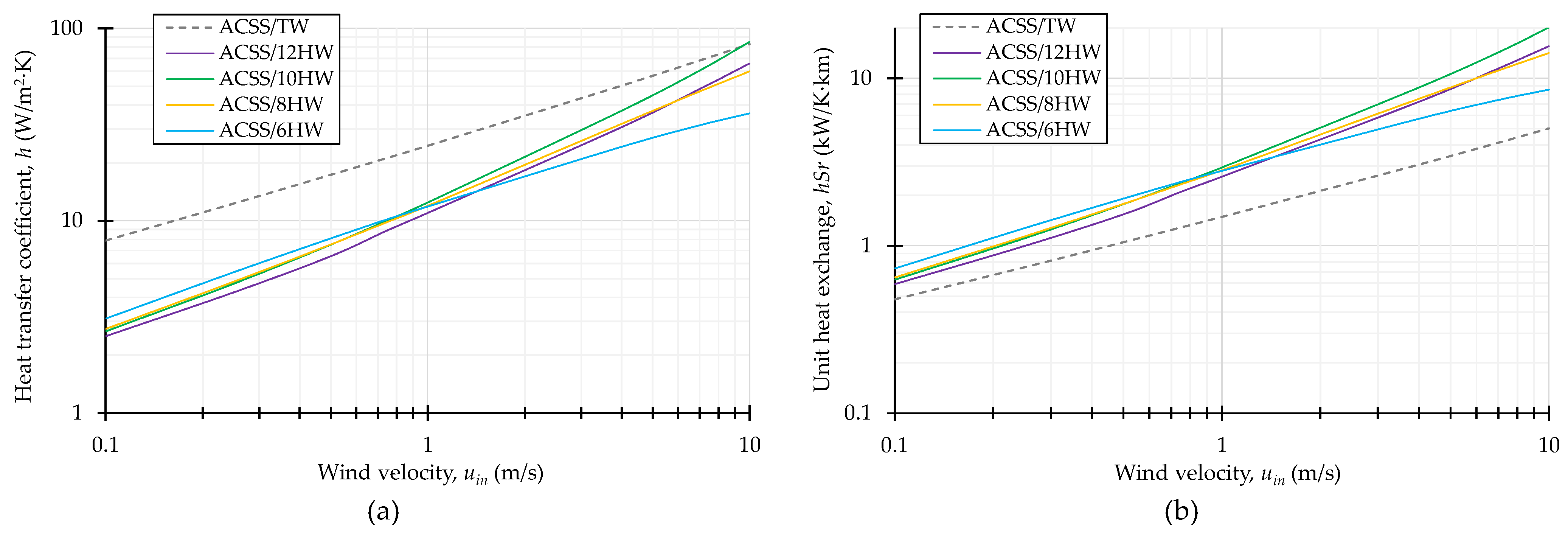
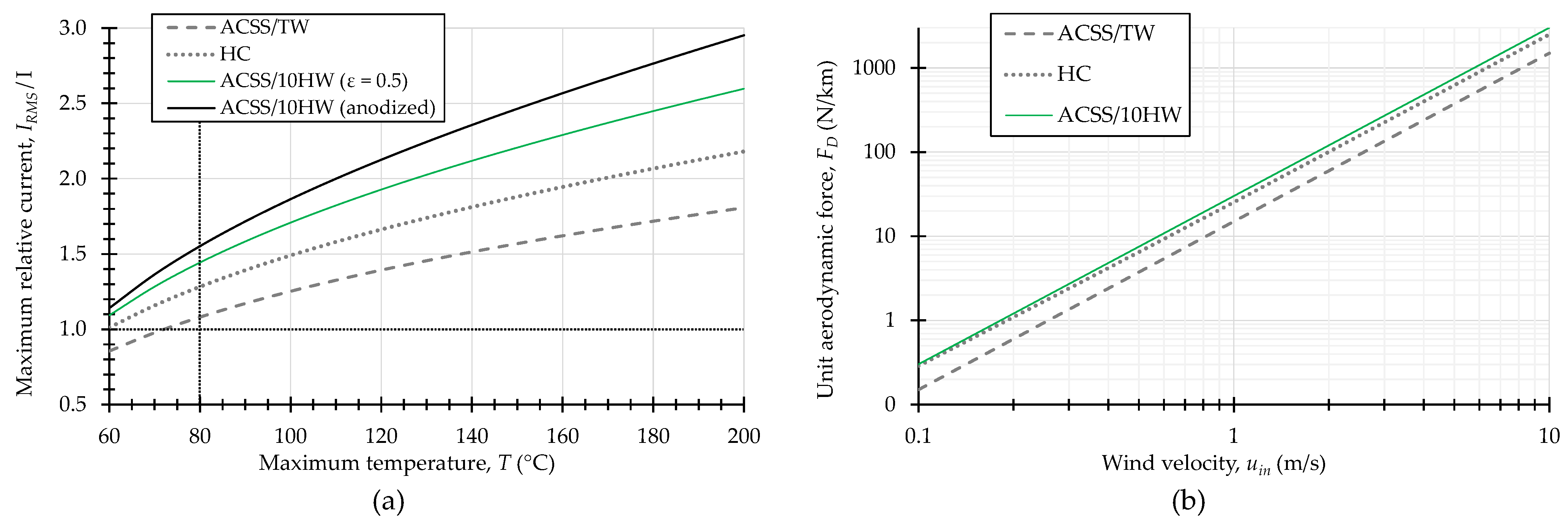
3.3. Cooling Efficiency of Helical Conductor
- Only half of the conductor was lit by the solar light; hence, half of G was used,
- η = ε, according to Kirchhoff’s law of thermal radiation,
- A coefficient of radiative heating k was introduced to take into account that helices radiate the heat not only into surrounding open space, but also that some part of the radiated energy returns to neighboring helices,
- Sr can be analytically calculated using Equations (1) and (2),
- Ru can be found numerically or analytically.
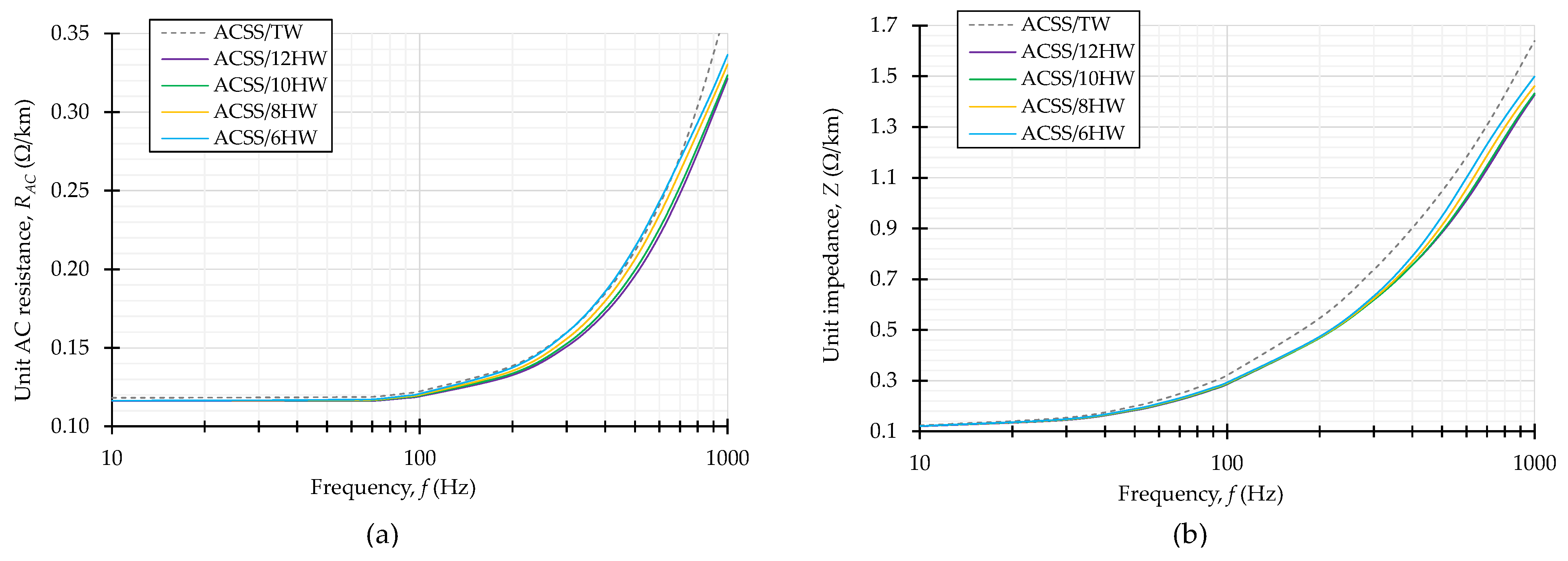
3.4. Analysis of Optimal Structure
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- De Santis, D.; James, B.D.; Houchins, C.; Saur, G.; Lyubovsky, M. Cost of long-distance energy transmission by different carriers. iScience 2021, 24, 103495. [Google Scholar] [CrossRef]
- Prasad Rao, K.P.; Srinivasa Varma, P. Analysis of very long distance AC power transmission line. In Proceedings of the 2017 International Conference on Electrical, Electronics, Communication, Computer, and Optimization Techniques (ICEECCOT), Mysuru, India, 15–16 December 2017. [Google Scholar]
- Wu, X.; Yang, X.; Shen, H.; Zhou, Q. Research on the Long-distance Transmission. Energy Power Eng. 2013, 5, 1293–1297. [Google Scholar] [CrossRef]
- Dwivedi, A.; Rajbhar, P.; Tiwari, N.M. Long Distance Power Transfer Technique: A Review. J. Robot. Mechatron. 2019, 3, 208–214. [Google Scholar] [CrossRef]
- Lienert, P.; Sutterlin, B.; Siegrist, M. Public acceptance of high-voltage power lines: The influence of information provision on undergrounding. Energy Policy 2018, 112, 305–315. [Google Scholar] [CrossRef]
- Yin, J.; Wei, Q.; Shao, D.; Luo, Z.; Ji, L. The impacts of power transmission and transformation projects on ecological corridors and landscape connectivity: A case study of Shandong province, China. Sci. Rep. 2025, 15, 6709. [Google Scholar] [CrossRef]
- Tempesta, T.; Vecchiato, D.; Girardi, P. The landscape benefits of the burial of high voltage power lines: A study in rural areas of Italy. Landsc. Urban Plan. 2014, 126, 53–64. [Google Scholar] [CrossRef]
- Nowak, W.; Tarko, R. Analysis of electrical shock hazard caused by electromagnetic coupling effects in parallel overhead high-voltage power lines. IET Gener. Transm. Distrib. 2018, 12, 3398–3404. [Google Scholar] [CrossRef]
- Hoger, M.; Regul’a, M.; Roch, M. Investigating the impacts of high voltage powerlines on ground current fields. Transp. Res. Proc. 2023, 74, 900–907. [Google Scholar] [CrossRef]
- Chojnacki, A.Ł. Modelling the influence of atmospheric conditions represented by wind, precipitation and air temperature on the intensity of failure and restoration time of medium-voltage power lines. Sustain. Energy Grids Netw. 2025, 42, 101652. [Google Scholar] [CrossRef]
- Larsen, P.H. A method to estimate the costs and benefits of undergrounding electricity transmission and distribution lines. Energy Econ. 2016, 60, 47–61. [Google Scholar] [CrossRef]
- Rambonilaza, T.; Dube, J.; Ay, J.-S. External costs of high-voltage overhead transmission lines: Evidence from a causal approach in rural France. Environ. Impact Assess. Rev. 2024, 109, 107639. [Google Scholar] [CrossRef]
- Fenrick, S.A.; Getachew, L. Cost and reliability comparisons of underground and overhead power lines. Util. Policy 2012, 20, 31–37. [Google Scholar] [CrossRef]
- Nuchprayoon, S.; Chaichana, A. Cost evaluation of current uprating of overhead transmission lines using ACSR and HTLS conductors. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017. [Google Scholar]
- Gębczyk, K.; Chojnacki, A.Ł.; Grąkowski, Ł.; Banasik, K. Comparative analysis of the costs of medium voltage overhead and cable lines failure. Przegląd Elektrotechniczny 2020, 96, 84–90. [Google Scholar] [CrossRef]
- Cost Analysis of Electrical Conductors: A Comprehensive Study. Available online: https://elkamehr.com/en/cost-analysis-of-electrical-conductors-a-comprehensive-study/ (accessed on 11 September 2025).
- Strielkowski, W.; Civín, L.; Tarkhanova, E.; Tvaronavičienė, M.; Petrenko, Y. Renewable Energy in the Sustainable Development of Electrical Power Sector: A Review. Energies 2021, 14, 8240. [Google Scholar] [CrossRef]
- Qin, B.; Wang, H.; Liao, Y.; Li, H.; Ding, T.; Wang, Z.; Li, F.; Liu, D. Challenges and opportunities for long-distance renewable energy transmission in China. Sustain. Energy Technol. Assess. 2024, 69, 103925. [Google Scholar] [CrossRef]
- Tian, J.; Culley, S.A.; Maier, H.R.; Zecchin, A.C. Is renewable energy sustainable? Potential relationships between renewable energy production and the Sustainable Development Goals. npj Clim. Action 2024, 3, 35. [Google Scholar] [CrossRef]
- Loschel, A.; Managi, S. Recent Advances in Energy Demand Analysis—Insights for Industry and Households. Resour. Energy Econ. 2019, 56, 1–5. [Google Scholar] [CrossRef]
- Hina, H.; Abbas, F.; Qayyum, U. Selecting correct functional form in consumption function: Analysis of energy demand at household level. PLoS ONE 2022, 17, e0270222. [Google Scholar] [CrossRef]
- Malka, L.; Bidaj, F.; Kuriqi, A.; Jaku, A.; Roçi, R.; Gebremedhin, A. Energy system analysis with a focus on future energy demand projections: The case of Norway. Energy 2023, 272, 127107. [Google Scholar] [CrossRef]
- Al-Yasiri, A.J. Global Energy Demand For Different Energy Sources: Current Status and Future Prospects. Akkad J. Contemp. Econ. Stud. 2021, 1, 35. [Google Scholar] [CrossRef]
- Rani, S.; Jayapragash, R. Review on electric mobility: Trends, challenges and opportunities. Results Eng. 2024, 23, 102631. [Google Scholar] [CrossRef]
- Muratori, M.; Alexander, M.; Arent, D.; Bazilian, M.; Cazzola, P.; Dede, E.M.; Farrell, J.; Gearhart, C.; Greene, D.; Jenn, A.; et al. The rise of electric vehicles—2020 status and future expectations. Prog. Energy 2021, 3, 022002. [Google Scholar] [CrossRef]
- Adamo, A.; Martin, H.; de la Hoz, J.; Rubio, J. A Review of Worldwide Strategies for Promoting High-Temperature Heat Pumps. Appl. Sci. 2025, 15, 839. [Google Scholar] [CrossRef]
- Akbarzadeh, S.; Sefidgar, Z.; Valipour, M.S.; Elmegaard, B.; Arabkoohsar, A. A comprehensive review of research and applied studies on bifunctional heat pumps supplying heating and cooling. Appl. Therm. Eng. 2024, 257, 124280. [Google Scholar] [CrossRef]
- Kishore, T.S.; Selvaraj, M.; Singal, S.K. Methodology for cost estimation of overhead power transmission lines. Int. J. Power Energy Convers. 2017, 8, 132–145. [Google Scholar] [CrossRef]
- Larruskain Eskobal, D.M.; Zamora, I.; Abarrategui, O.; Iraolagoitia, A.; Gutiérrez, M.D.; Loroño, E.; de la Bodega, F. Power transmission capacity upgrade for overhead lines. Renew. Energy Power Qual. J. 2006, 4, 132–145. [Google Scholar] [CrossRef]
- Lequien, F.; Auzoux, Q.; Moine, G.; Rousseau, M.; Pasquier-Tilliette, S.; Holande, A.; Ammi, S.; Heurtault, S.; Prieur, P. Characterization of an aluminum conductor steel reinforced (ACSR) after 60 years of operation. Eng. Fail. Anal. 2021, 120, 105039. [Google Scholar] [CrossRef]
- Kanálik, M.; Margitová, A.; Urbanský, J.; Beňa, L. Temperature Calculation of Overhead Power Line Conductors According to the CIGRE Technical Brochure 207. In Proceedings of the 2019 20th International Scientific Conference on Electric Power Engineering (EPE), Kouty nad Desnou, Czech Republic, 15–17 May 2019. [Google Scholar]
- Riba, J.-R.; Liu, Y.; Moreno-Eguilaz, M. Analyzing the role of emissivity in stranded conductors for overhead power lines. Int. J. Elec. Power Energy Syst. 2024, 159, 110027. [Google Scholar] [CrossRef]
- Practical Considerations for ACSR Cable Selection. Available online: https://cable-uni.com/cases/cable-news/practical-considerations-for-acsr-cable-selection.html (accessed on 11 September 2025).
- Power System Engineering & Technology Development Central Electricity Authority. Guidelines for Rationalised Use of High Performance Conductors. Available online: https://cea.nic.in/old/reports/others/ps/psetd/guidelines_conductors.pdf (accessed on 11 September 2025).
- Seppa, T.; Deve, H.; Watt, G.; Didier, B.; Yonezawa, K.; Hoffman, S.; Iglesias, J.; Brahe, B.; Ueda, S.; Lundquist, J.; et al. Conseil international des grands réseaux électriques. In Guide for Qualifying High Temperature Conductors for Use on Overhead Transmission Lines; CIGRÉ: Paris, France, 2010. [Google Scholar]
- Thrash, F.R. ACSS/TW-an improved high temperature conductor for upgrading existing lines or new construction. In Proceedings of the 2001 Power Engineering Society Summer Meeting Conference Proceedings (Cat. No.01CH37262), Vancouver, Canada, 15–19 July 2001. [Google Scholar]
- de Miranda, T.B.; Kalombo, R.B.; Araújo, J.A.; de Almeida Ferreira, J.L. Self-damping of conductors AAC, AAAC and ACSR with respect of H/W parameter. In Proceedings of the 25th ABCM International Congress of Mechanical Engineering, Uberlandia, Brazil, 20–25 October 2019. [Google Scholar]
- Mohtar, S.N.; Jamal, N.; Sulaiman, M. Analysis of all aluminum conductor (AAC) and all aluminum alloy conductor (AAAC). In Proceedings of the 2004 IEEE Region 10 Conference TENCON 2004, Chiang Mai, Thailand, 21–24 November 2004. [Google Scholar]
- Zainuddin, N.M.; Rahman, M.S.A.; Kadir, Z.; Nik Ali, N.H.B.; Zanyar, A.; Osman, M.; Mansor, M.; Ariffin, A.H.; Rahman, M.S.A.; Nor, S.F.H.; et al. Review of Thermal Stress and Condition Monitoring Technologies for Overhead Transmission Lines: Issues and Challenges. IEEE Access 2020, 8, 120053–120081. [Google Scholar] [CrossRef]
- Smyrak, B. Analysis of the quality of aluminum overhead conductors after 30 years of operation. Eng. Fail. Anal. 2023, 154, 107600. [Google Scholar] [CrossRef]
- Miyazaki, H.; Kitamura, S. Temperature distribution within an ACSR conductor during large current flow. Electr. Eng. Jpn. 2002, 140, 38–45. [Google Scholar] [CrossRef]
- Pawlak, U.; Pawlak, M. Type of Material in the Pipes Overhead Power Lines Impact on the Distribution on the Size of the Overhang and the Tension. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, 022058. [Google Scholar] [CrossRef]
- Margita, F.; Beňa, Ľ.; Malska, W.; Pijarski, P. Possibilities of Increasing the Ampacity of Overhead Lines Using High-Temperature Low-Sag Conductors in the Electric Power System of the Slovak Republic. Appl. Sci. 2024, 14, 7846. [Google Scholar] [CrossRef]
- Riba, J.-R.; Bogarra, S.; Gómez-Pau, Á.; Moreno-Eguilaz, M. Uprating of Transmission Lines by Means of HTLS Conductors for Sustainable Growth: Challenges, Opportunities, and Research Needs. Renew. Sustain. Energy Rev. 2020, 134, 110334. [Google Scholar] [CrossRef]
- Evoenergy. Overhead Distribution Line Design Manual. Available online: https://www.evoenergy.com.au/-/media/Project/Evoenergy/EVO/Documents/Manuals/PO07132-Overhead-Line-Distribution-Design-Manual.pdf (accessed on 11 September 2025).
- Gołębiowski, J.; Zaręba, M. Analytical modelling of the transient thermal field of a tubular bus in nominal rating. COMPEL 2019, 38, 642–656. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, L.Y.; Zhang, L.M.; Huang, S.H.; Du, B.X.; Wang, F. PD characteristics in PTFE insulated tubular busbar models measured with HFCT and acoustic sensor. In Proceedings of the 2015 IEEE 11th International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Sydney, Australia, 19–22 July 2015. [Google Scholar]
- Paul, V.J. A Review of Geometry Investigations of Helicoids. IOP Conf. Ser. Mater. Sci. Eng. 2018, 371, 012029. [Google Scholar] [CrossRef]
- Kasap, S.O. Principles of Electronic Materials and Devices; McGraw–Hill: Boston, MA, USA, 2006; pp. 127–129. [Google Scholar]
- Steckiewicz, A.; Konopka, K.; Choroszucho, A.; Stankiewicz, J.M. Temperature Measurement at Curved Surfaces Using 3D Printed Planar Resistance Temperature Detectors. Electronics 2021, 10, 1100. [Google Scholar] [CrossRef]
- Soucek, O.; Martinec, Z.; Velimsky, J. Vector potential formulation of a quasi-static EM induction problem: Existence, uniqueness and stability of the weak solution. Int. J. Geomath. 2011, 2, 265–279. [Google Scholar] [CrossRef]
- Roslan, S.N.; Hoe, Y.S. Numerical Solutions of 2D Poisson Equation Using Finite Element Method and Finite Difference Method. Proc. Sci. Math. 2024, 23, 99–107. [Google Scholar]
- COMSOL. Linearized Navier-Stokes Model. Available online: https://doc.comsol.com/5.4/doc/com.comsol.help.aco/aco_ug_aero.07.026.html (accessed on 11 September 2025).
- EN 50540:2010; Conductors for Overhead Lines—Aluminium Conductors Steel Supported (ACSS). CENELEC: Brussels, Belgium, 2010. Available online: https://standards.cencenelec.eu/ords/f?p=CENELEC:110:::::FSP_PROJECT,FSP_ORG_ID:45725,1258751&cs=1576CA9F8F5D3514BF2E5A7EC91AE1FA9 (accessed on 11 September 2025).
- Midal Cables. CONDUCTOR DATA SHEET Aluminum Conductors Steel Supported-Trapezoidal (ACSS/TW). Available online: https://www.midalcable.com/storage/products/acsstw/acsstw-metric.PDF (accessed on 11 September 2025).
- Alberdi, R.; Fernandez, E.; Albizu, I.; Bedialauneta, M.T.; Fernandez, R. Overhead Line Ampacity Forecasting and a Methodology for Assessing Risk and Line Capacity Utilization. Int. J. Electr. Power Energy Syst. 2021, 133, 107305. [Google Scholar] [CrossRef]
- Katona, T.; Bartsch, A. Estimation of wind speed over lakes in Central Europe using spaceborne C-band SAR. Eur. J. Remote Sens. 2018, 51, 921–931. [Google Scholar] [CrossRef]
- Araźny, A.; Przybylak, R.; Vizi, Z.; Kejna, M.; Maszewski, R.; Uscka-Kowalkowska, J. Mean and extreme wind velocities in Central Europe 1951-2005 (on the basis of data from NCEP/NCAR reanalysis project). Geogr. Pol. 2007, 80, 69–78. [Google Scholar]
- Eguchi, Y.; Kikuchi, N.; Kawabata, K.; Yukinoc, T.; Ishikubo, Y. Drag reduction mechanism and aerodynamic characteristics of a newly developed overhead electric wire. Wind. Eng. Ind. Aerodyn. 2002, 90, 293–304. [Google Scholar] [CrossRef]
- Li, D.Q.; Li, Z.; Liu, Z.; Liu, L.; Yang, C.L.; Fan, W.; Yang, L.Y.; Si, J.J. Application Research on Drag Reduced Conductors for Electric Power Transmission Lines in Strong Wind Areas. MATEC Web Conf. 2014, 44, 01093. [Google Scholar] [CrossRef]
- Park, J.; Son, K.; Lee, J.; Kim, D.; Chung, W. Effects of Anodizing Conditions on Thermal Properties of Al 20XX Alloys for Aircraft. Symmetry 2021, 13, 433. [Google Scholar] [CrossRef]
- Gustavsen, A.; Berdahl, P.H. Spectral Emissivity of Anodized Aluminum and the Thermal Transmittance of Aluminum Window Frames. J. Build. Phys. 2003, 3, 0103. [Google Scholar]
- Riba, J.-R. Studying the breakdown electric field in uniform and non-uniform air gaps. Eur. J. Phys. 2024, 45, 045205. [Google Scholar] [CrossRef]
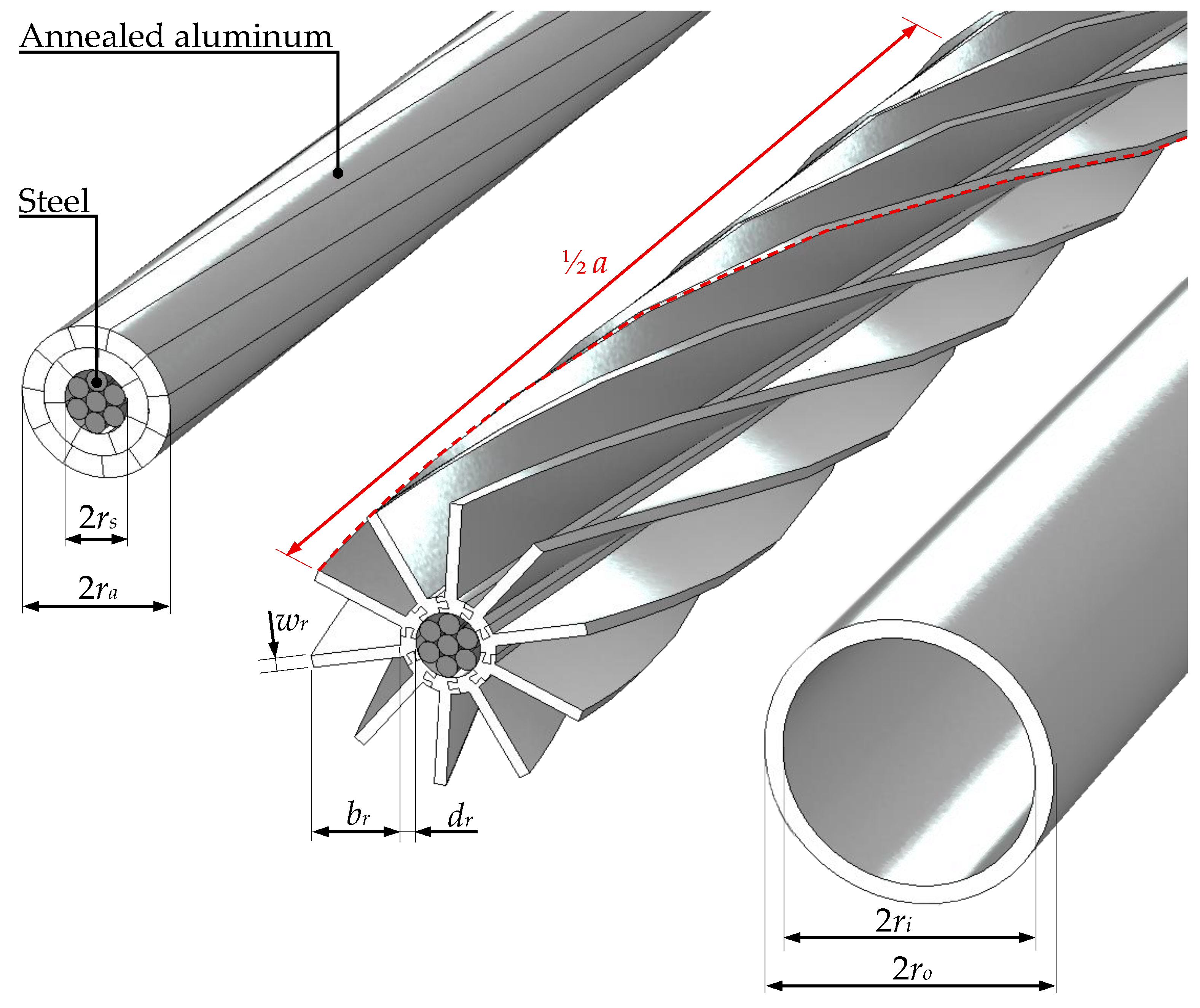

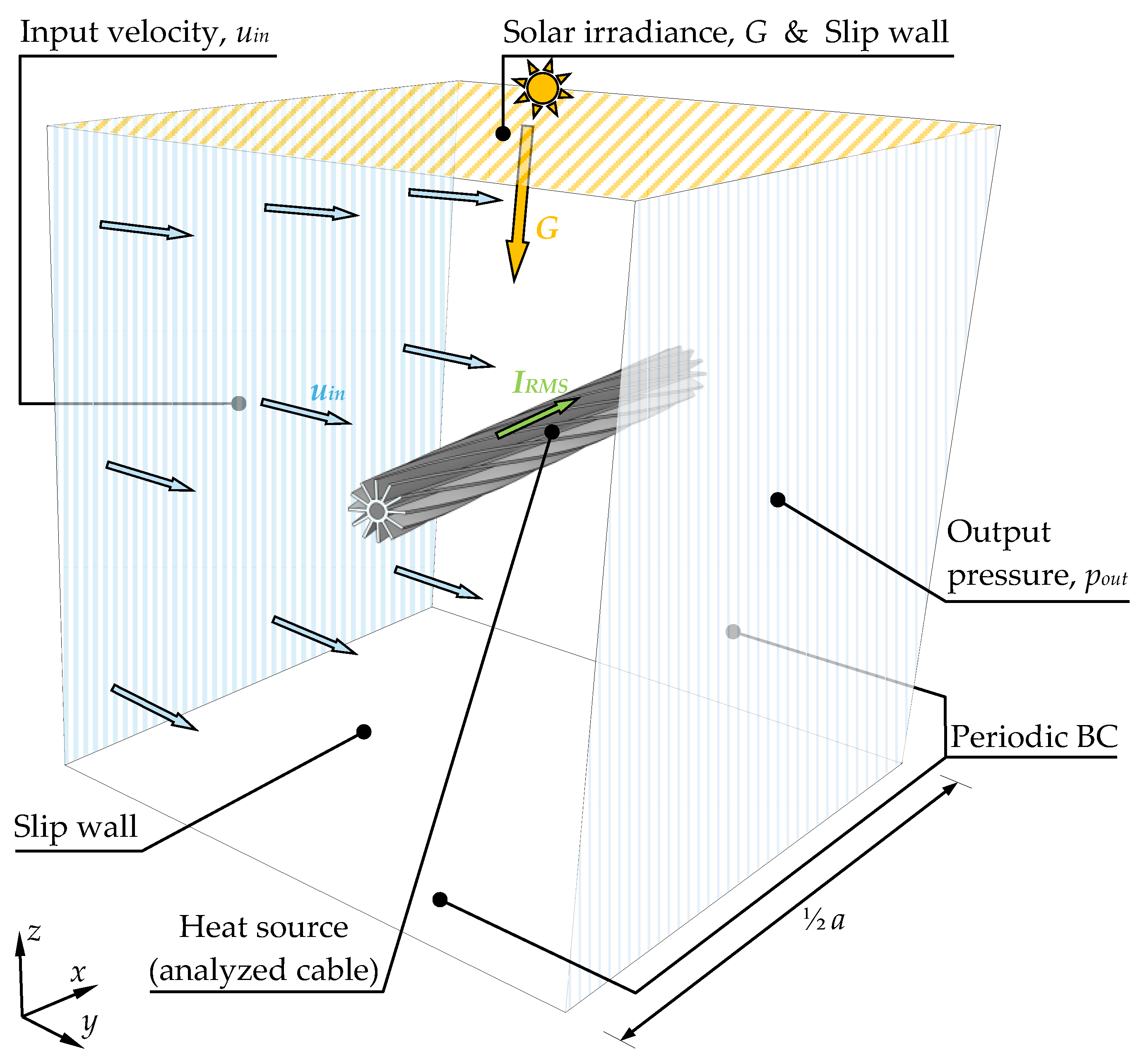
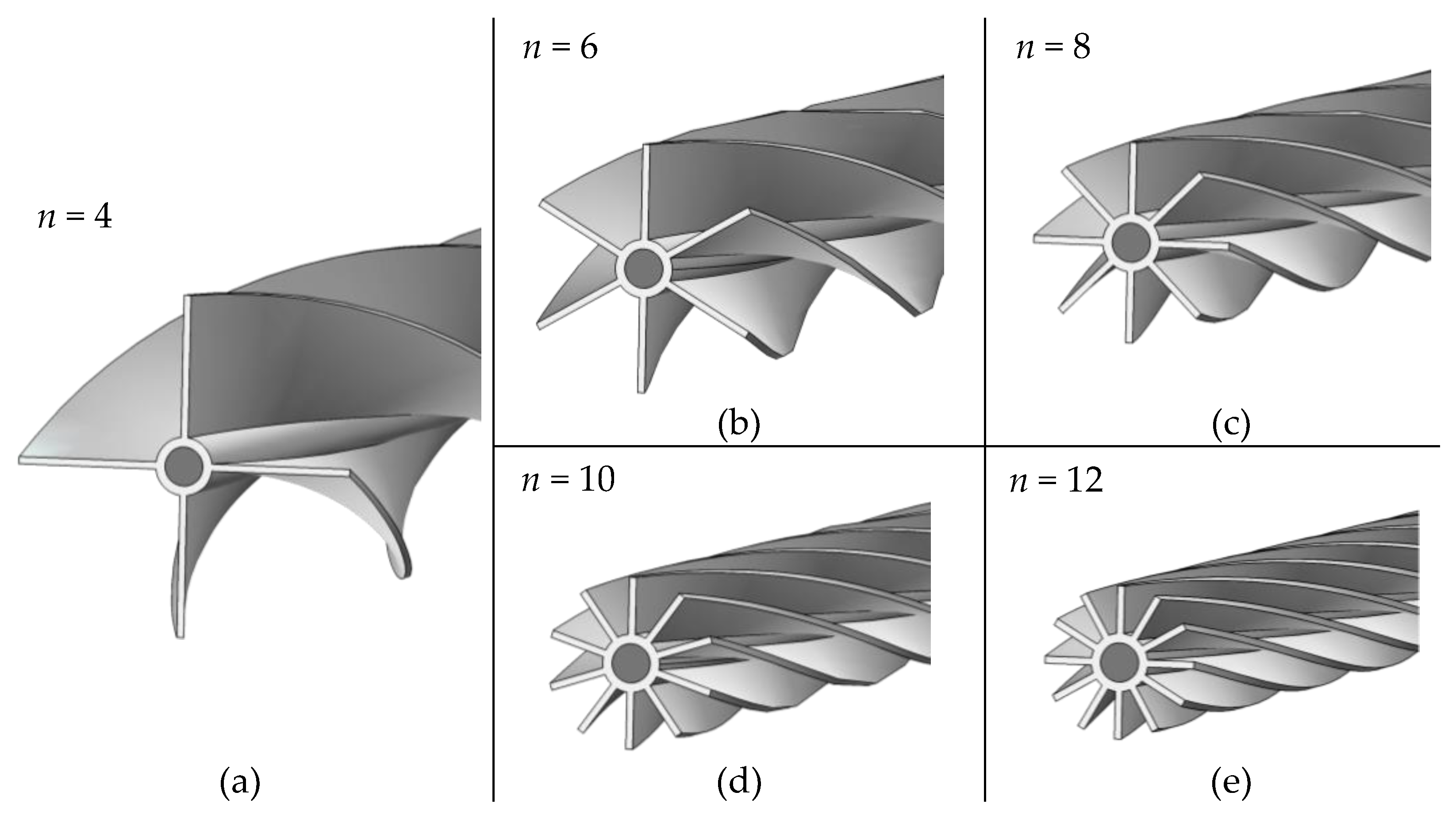


| Name | Symbol | Value | Unit |
|---|---|---|---|
| Ambient temperature | Tamb | 303.15 | K |
| Reference temperature | T0 | 293.15 | K |
| Solar irradiance | G | 1000 | W/m2 |
| Emissivity (aluminum) | ε | 0.5 | – |
| Density (air) | gair | 1.22 | kg/m3 |
| Density (aluminum) | ga | 2700 | kg/m3 |
| Density (steel) | gs | 7850 | kg/m3 |
| Heat capacity (air) | Cp,air | 1000 | J/kg·K |
| Heat capacity (aluminum) | Cp,a | 900 | J/kg·K |
| Heat capacity (steel) | Cp,s | 470 | J/kg·K |
| Thermal conductivity (air) | λair | 0.0266 | W/m·K |
| Thermal conductivity (aluminum) | λa | 234.2 | W/m·K |
| Thermal conductivity (steel) | λs | 50 | W/m·K |
| Heat capacity ratio (air) | γ | 1.4 | – |
| Dynamic viscosity (air) | ν | 19.5·× 10−6 | Pa·s |
| Relative permeability (aluminum, air) | μa | 1 | – |
| Relative permeability (steel) | μs | 100 | – |
| Electrical resistivity (aluminum) | ρ0,a | 2.83·× 10−8 | Ω·m |
| Electrical resistivity (steel) | ρ0,s | 1.7·× 10−7 | Ω·m |
| Temperature coefficient (aluminum) | αa | 0.00408 | 1/K |
| Temperature coefficient (steel) | αs | 0.003 | 1/K |
| Cross-section (aluminum) | Aa | 240 | mm2 |
| Cross-section (steel) | As | 39.2 | mm2 |
| Radius of steel support | rs | 4.05 | mm |
| Width of helix | wr | 1.5 | mm |
| Thickness of inner tube | dr | 2 | mm |
| No. | Pitch, a (m) | Number of Helices, n | Unit Weight, mu (kg/km) | Relative Difference Δm | Unit Resistance, Ru (Ω/km) | Relative Difference ΔR |
|---|---|---|---|---|---|---|
| I | 0.50 | 10 | 662.757 | −0.30% | 0.1136 | 0.18% |
| II | 0.52 | 12 | 662.875 | −0.29% | 0.1137 | 0.26% |
| III | 0.62 | 12 | 664.345 | −0.07% | 0.1128 | −0.53% |
| IV | 0.65 | 10 | 664.275 | −0.08% | 0.1126 | −0.71% |
| V | 0.70 | 8 | 667.242 | 0.37% | 0.1126 | −0.71% |
| VI | 0.75 | 4 | 665.454 | 0.10% | 0.1106 | −2.47% |
| VII | 0.78 | 6 | 664.821 | 0.01% | 0.1143 | 0.79% |
| No. | Name | Number of Helices, n | Radiative Heating Coefficient, k |
|---|---|---|---|
| I | ACSS/10HW | 10 | 0.195 |
| II | ACSS/12HW | 12 | 0.200 |
| V | ACSS/8HW | 8 | 0.159 |
| VII | ACSS/6HW | 6 | 0.198 |
| – | ACSS/TW | – | 0 |
| Name | Mechanical Reinforcement | Transport and Installation | Ampacity at 80 °C, 0.5 m/s | Ampacity at 110 °C, 0.5 m/s | Aerodynamic Load |
|---|---|---|---|---|---|
| ACSS/TW | steel (can be changed to composite) | easy | 669 A | 822 A | lowest |
| HC | none | more difficult | 793 A | 980 A | nearly twice as ACSS/TW |
| ACSS/10HW | steel | more difficult | 895 A | 1130 A | twice as ACSS/TW |
| ACCC/10HW | composite strand/fibers | much more difficult | 962 A | 1240 A | twice as ACSS/TW |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steckiewicz, A.; Zajkowski, M.; Jovanovic, A. Potential Properties and Applications of Wires with Helical Structure in High-Voltage Overhead Power Lines and PV Systems. Energies 2025, 18, 6008. https://doi.org/10.3390/en18226008
Steckiewicz A, Zajkowski M, Jovanovic A. Potential Properties and Applications of Wires with Helical Structure in High-Voltage Overhead Power Lines and PV Systems. Energies. 2025; 18(22):6008. https://doi.org/10.3390/en18226008
Chicago/Turabian StyleSteckiewicz, Adam, Maciej Zajkowski, and Andrijana Jovanovic. 2025. "Potential Properties and Applications of Wires with Helical Structure in High-Voltage Overhead Power Lines and PV Systems" Energies 18, no. 22: 6008. https://doi.org/10.3390/en18226008
APA StyleSteckiewicz, A., Zajkowski, M., & Jovanovic, A. (2025). Potential Properties and Applications of Wires with Helical Structure in High-Voltage Overhead Power Lines and PV Systems. Energies, 18(22), 6008. https://doi.org/10.3390/en18226008







