Fairness–Performance Trade-Offs in Active Power Curtailment for Radial Distribution Grids with Battery Energy Storage

Abstract

The increasing integration of decentralized technologies such as photovoltaic (PV) systems and electric vehicles (EVs) poses significant challenges to the reliable operation of radial distribution grids. In this paper, we study Active Power Curtailment (APC), which is a cost-effective method that maintains grid safety by temporarily reducing power injections. However, APC can place disproportional curtailment burden on grid buses that may in fact undermine the continuous adoption of PVs and EVs. In this work, we propose different novel APC methods that incorporate fairness properties for radial grids with PVs, EVs, and battery energy storage systems (BESSs). In addition, we integrate BESSs and show their benefits in lowering APC levels and achieving better PV and EV utilization while enhancing fairness. The proposed APC designs allow for fast decision making and can be generalized to unseen grids. To do so, a two-step solution is adopted, where in the first step, a reinforcement learning (RL)-based agent determines uniform per-feeder APC and BESS actions, and in the second step, heuristic controllers disaggregate these actions into tailored per-bus decisions while incorporating fairness features. Through simulations, the controllers are shown to mitigate over $99\%$ of constraint violations and significantly enhance fairness in curtailment distribution. BESSs are shown to improve the violations count and APC trade-off, leaning towards reduced APC percentages. Finally, we exemplify how the solution generalizes effectively to unseen grid configurations.

1. Introduction

The reliable operation of electric power systems depends on their ability to maintain stability and avoid service interruptions by keeping voltages and ampacities within safe operating margins. The complexity of this task is increasing as distribution grids are being transformed by the rapid uptake of decentralized, uncertain, and variable technologies such as photovoltaic (PV) generation and electric vehicles (EVs). EV charging clusters can exacerbate local voltage drops during peak demand periods [1], while PV systems can cause overvoltages when generation exceeds consumption [2]. Managing these emerging challenges in view of the increasing grid scales requires control strategies that can handle uncertain and rapidly changing power injections while remaining cost-effective and operationally simple. A portfolio of solutions can be collected from the literature to ensure the reliability of power grids in the presence of PVs and EVs. Common approaches to reduce voltage constraint violations include the use of On-Load Tap Changer control [3,4], reactive power control [5], Hybrid Transformers [6], and Active Power Curtailment (APC) [7].

In this work, we focus on APC, which remains a widely applied and cost-effective method for maintaining safe grid operation by dynamically reducing active power injections based on temporal demands/generation. APC is essential for preventing violations of grid safety constraints; yet, if applied without consideration of fairness, it risks creating constant inequities among grid prosumers undermining public acceptance of distributed energy integration and electromobility. Indeed, in our previous work in [8], the results of the sensitivity analysis have shown that the APC levels are minimized when curtailing specific buses that are the farthest from the PCC, indicating the risks of being constantly unfair to particular grid participants. Embedding fairness principles into APC is, therefore, crucial to fairly split curtailment burden across grid participants while maintaining overall low curtailment percentages.

In parallel, battery energy storage systems (BESSs) are emerging as a critical resource to mitigate these challenges and reduce APC levels. By absorbing surplus PV output and supplying energy during charging peaks, BESSs can substantially reduce the need for curtailment and provide flexibility that supports grid security. Although the combination of APC with battery control has been studied in the literature, showing the possibilities of reducing APC levels brought about by BESSs, it has hardly been seen together with fairness considerations as far as PVs, EVs and BESSs are concerned. This is exactly the gap we aim to fill in this work by proposing APC strategies in power grids including PVs, EVs, and BESSs and considering impacts on fairness and showing emerging fairness–performance trade-offs. In addition, to align with the increasing scales of future power grids, the proposed APC policies are based on reinforcement learning (RL) to enable fast decision making and are designed so that they are generalizable, i.e., they can be applied to unseen grids without re-training while maintaining satisfactory performance.

The contributions of this paper can be summarized as follows:

• We develop an APC strategy for radial distribution grids with PVs, EVs, and BESSs that determines optimal curtailments for PV generation and EV demand per bus. The APC strategy is based on our previous work in [8] and consists of two steps, namely, one step that applies RL to determine uniform per-feeder curtailments and a second step that applies heuristic disaggregators to determine tailored per-bus curtailments. The novelty of the proposed scheme in this work compared to the existing one lies in the consideration of fairness in per-bus curtailments while not impacting the generalization and low complexity properties of the two-step approach as well as the integration of BESSs that can further enhance fairness and performance.
• Fairness is intelligently incorporated into the heuristic design of the disaggregation step and not imposed as a hard constraint that would have required explicit system modeling, impeding generalization to unseen grids, and would have led to increased computational complexity which would require solving complex optimization problems. BESSs decisions are incorporated via RL-based decision making and have guaranteed fairness per feeder.
• We have performed extensive evaluations and comparisons of the proposed solution approach with emphasis on validating its fairness properties as well as the advantages brought by the integration of BESSs. In summary, fairness in curtailments is significantly enhanced, thus encouraging the integration of EVs and PVs at all buses independently of their location, and with BESSs the trade-off between fairness and performance further improves.

The rest of the paper is organized as follows. Section 2 positions our work within the related literature. Section 3 explains the considered system, formulates the problem, and details the fairness metrics that will be incorporated into our approach. Section 4 presents the RL-based solution approach. Section 5 includes all the numerical evaluations and comparisons and assesses the generalization properties of the proposed method. Finally, Section 6 discusses conclusive remarks and future steps.

2. Related Works

The APC method has been widely studied in the literature to ensure satisfaction of voltage and current constraints in power grids by limiting active power injection at the buses. Common approaches include droop-based methods [9], OPF with linearized grid models [10], non-convex AC OPF solutions [9], and model predictive control [11]. Recent studies such as [7,8,12] have focused on machine learning and reinforcement learning approaches that do not require a grid model, offering significant potential for generalization and computational tractability. Specifically, in our previous work [7], an RL-based solution for voltage regulation in radial low-voltage grids with high penetration of PVs and EVs was proposed. The approach uses a per-feeder aggregated state and action representation, which enables generalization possibilities. The solution was enhanced in [8] with disaggregation heuristics based on a sensitivity analysis study. However, these techniques tend to penalize buses located farther from the PCC, raising fairness concerns. The present work builds upon the approach in [8], while explicitly addressing these fairness issues.

Ensuring fairness in APC is critical to encourage sustainability and continuous adoption of renewable generation and electromobility by sharing the burden proportionally and avoiding constant impact on specific buses/producers. Due to its importance, fairness in APC has been studied in the literature. The work in [13] proposes an online feedback optimization approach to minimize curtailment needs while satisfying operational constraints. A modification of the voltage sensitivity matrix is suggested to provide fair solutions. In [14], three notions of fairness are studied, a linearized OPF formulation is proposed for each, and their impacts on MV/LV distribution grids are assessed. Furthermore, [15] proposes an ADMM-based algorithm for Volt–Var Control (VVC), which addresses fairness in APC for PVs. Jointly controlling VVC and APC minimizes the number of voltage violations, however, increases the communication burden. In [16], a heuristic control algorithm, inspired by a sensitivity analysis, aims to suggest similar curtailment percentage for all PVs and achieve fairness. A decentralized control method for Volt–Var–Watt control of PV inverters with minimal communication requirements is studied in [17]. By limiting the curtailment, the proportional fairness metrics are improved. An RL-based approach for controlling PV inverters which considers fairness is presented in [12], where fairness is incorporated into the reward of the RL agent. Similarly, the work in [18] employs an RL agent to ensure grid operational limits satisfaction for unbalanced three-phase networks with a reward formulated to account for fairness.

The aforementioned works considering fairness in APC ([12,13,14,15,16,17]) do not include EVs in their proposed control schemes. However, the increasing EV adoption may be exploited to reduce the curtailment needs in PV-dominated grids [19]. In this spirit, in [20], the EV batteries are controlled along with APC for PVs to mitigate voltage rises above operational limits. In addition, in [21], a droop-based EV charging strategy along with APC is proposed to improve the economic and environmental benefits in a low-voltage distribution network. The vehicle-to-grid (V2G) capability that is studied in previous works ([20,21]) emerges as a promising direction to enhance the utilization of EV batteries. However, it requires explicit modeling of EV arrivals and departures, impeding the potential of generalizability to different grids and loads for the control strategies. The works above often consider fairness regarding PV curtailment but neglect fairness with respect to EV charging. In [22], a max–min fairness notion regarding charging delay is formulated as a mixed-integer program. A distributed algorithm is proposed that iteratively solves linear programs to approximate the optimal solution efficiently. A fairness-focused approach on EV charging is presented on [23]. The suggested heuristic algorithm, augmented with a forecasting model to predict the departure time of EVs, balances evenly the possibilities of EVs to reach their desirable charging levels. In [24], a hierarchical framework is suggested, where the system operator considers both grid operational constraints and fairness in the allocation of maximum charging power among EV aggregators. At the lower level, a multi-agent RL approach is incorporated to manage the charging of individual EVs. However, the fairness is enforced at the upper level by solving an OPF problem, which is computationally demanding.

Another approach attracting increasing research interest is the combination of battery energy storage systems (BESSs) with APC which aims to improve curtailment percentages. The popularity of BESSs is increasing as battery investment costs are decreasing [25] in combination with their low operational costs [26]. The study in [27] demonstrates that jointly controlling PV inverters and BESSs can significantly reduce the APC level, yielding financial benefits. In [28], traditional volt–var and volt–watt techniques are used to control BESSs along with APC. The study focuses on optimal BESS sizing and shows that the inclusion of BESS allows higher PV adoption without compromising the power grid’s reliability. However, the literature lacks studies on joint considerations of APC in the presence of BESSs while accounting for fairness both in terms of PVs and EVs curtailments as well as of BESSs control. In our previous work [29], we studied the problem of distributed batteries control using multi-agent RL and considering fairness issues among batteries. In comparison to [29], the current paper additionally studies fair APC for PV generation and EV demands.

In this paper, we propose diverse APC schemes for distribution grids including PVs, EVs, and BESSs. The studied APC schemes are based on RL and are designed with generalization properties so that they can be applied in different grid topologies and under different loads without re-training. This is achieved via a two-step solution approach: first, an RL agent makes uniform per-feeder decisions, and then, heuristic controllers disaggregate the decisions into tailored per-bus PV and EV curtailments. We focus on enhancing the disaggregation with fairness properties based on fairness criteria such as those in [13], while not impacting the generalization and low complexity properties of the solution. We thoroughly study the emerging trade-off between fairness and performance achieved for the different designs. Moreover, we integrate BESSs control in our framework to further improve the performance–fairness trade-off. Experiments demonstrate that the augmented framework that includes BESSs can also be generalized to unseen grids without re-training.

3. System Model and Problem Formulation

3.1. System Model

We consider a low-voltage distribution grid with a radial structure and model it as a graph consisting of the set $\mathcal{N}$ of PQ buses and the set $\mathcal{L}$ of lines. A single bus, with ID 0, is set as both the slack bus and the Point of Common Coupling (PCC) between the low-voltage and the upper-level grid. The operation of the upper-level grid is outside the scope of this work. Because of its radial structure, the grid can be organized into F feeders, each directly connected to the PCC. We denote the set of feeders by $\mathcal{F}$. The buses and lines belonging to the feeder f form the sets ${\mathcal{N}}_f=\{(f,1),\dots ,(f,N_f)\}\subset \mathcal{N}$ and ${\mathcal{L}}_f=\{(f,1),\dots ,(f,L_f)\}\subset \mathcal{L}$, respectively. We assume that indices are ordered with increasing geometric distance from the PCC, i.e., if $i<j$, then $(f,i)$ is closer from or equally distant to the PCC as $(f,j)$. Buses located farther from the PCC than a given bus, in terms of geometric distance, are referred to as ‘downstream’, while those closer to the PCC are considered ‘upstream’. We also denote by ${\mathcal{N}}_f^{EV},{\mathcal{N}}_f^{PV}$, and ${\mathcal{N}}_f^{BESS}$ the subsets of buses in feeder f where an EV, a PV, or a BESS is connected, respectively.

The control horizon is discretized into T time slots, each with a duration of $\mathsf{\Delta }t$. Let t stand for the time index with $t\in \mathcal{T}=\{1,\dots ,T\}\in \mathbb{N}$. The voltage magnitude on bus n of the feeder f is referred to as $U_{f,n}\left(t\right)$ and the maximum current magnitude along the line l of feeder f is denoted by $I_{f,l}\left(t\right)$. For convenience, we use $\mathbf{U}\left(t\right)$ and $\mathbf{I}\left(t\right)$ to represent the collection of voltage and current magnitude values along the whole grid. The total apparent power at bus $(f,n)\in {\mathcal{N}}_f$ is calculated as

$$S_{f,n}(t,a_{f,n}^{EV},a_{f,n}^{PV},a_{f,n}^{BESS})=S_{f,n}^H\left(t\right)+S_{f,n}^{EV}(t,a_{f,n}^{EV})+S_{f,n}^{PV}(t,a_{f,n}^{PV})+S_{f,n}^{BESS}(t,a_{f,n}^{BESS}),$$

(1)

where $S_{f,n}^H\left(t\right)=P_{f,n}^{H,d}\left(t\right)+j·Q_{f,n}^{H,d}\left(t\right)$ is the inflexible household (H) power injection at bus n of feeder f with P denoting the active power and Q the reactive power, respectively. $S_{f,n}^X(t,a_{f,n}^X)=a_{f,n}^X·P_{f,n}^{X,d}\left(t\right)+j·Q_{f,n}^{X,d}\left(t\right),X\in \{EV,PV\}$ is the EV or PV apparent power injection at bus n of feeder f. $P_{f,n}^{X,d}\left(t\right)$ denotes the active power demand and $a_{f,n}^X\in [0,1]$ the controllable curtailment action, that is, the ratio of the active power allowed to the demand of EVs and PVs. Positive values of power correspond to consumption, while negative values correspond to generation. Similarly, $S_{f,n}^{BESS}(t,a_{f,n}^{BESS})=a_{f,n}^{BESS}·{\overline{P}}_{f,n}^{BESS}=P_{f,n}^{BESS}\left(t\right)$ is the apparent power injection of the battery located at bus n of feeder f, which is considered fully controllable through the variable $a_{f,n}^{BESS}\in [-1,1]$, which is the ratio of battery’s applied power injection to its maximum power limit ${\overline{P}}_{f,n}^{BESS}$. Battery’s reactive power is omitted for simplicity as reactive power control is out of the scope of this work.

The grid dynamics are determined through the set of nonlinear power flow equations, which couple the bus voltages $\mathbf{U}\left(t\right)$ and line currents $\mathbf{I}\left(t\right)$ with the power injections at each bus and the network parameters. The voltage and current values should be constrained to ensure the grid’s safe operation; thus the following constraints are defined:

$$\begin{array}{cc}\hfill & U_{f,n}\left(t\right)\in [\underline{U},\overline{U}],\forall f\in \mathcal{F},\forall (f,n)\in {\mathcal{N}}_f,\forall t\in \mathcal{T},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & I_{f,l}\left(t\right)\in [0,\overline{I}],\forall f\in \mathcal{F},\forall (f,l)\in {\mathcal{L}}_f,\forall t\in \mathcal{T},\hfill \end{array}$$

(3)

where $[\underline{U},\overline{U}]$ is the interval of safe operation with respect to voltage magnitudes and $[0,\overline{I}]$ is the interval of safe operation with respect to current magnitudes.

Regarding the battery model, we follow similar lines as in [30]. The battery’s state-of-charge (SoC) value is denoted as $So{C}_{f,n}\left(t\right)$, with ${\eta }_{f,n}^{ch}\le 1$ and ${\eta }_{f,n}^{dis}\le 1$ being the battery’s charging and discharging efficiency coefficients, respectively. $E_{f,n}^{max}$ is the maximum energy capacity of the battery. The following set of equations and constraints determines the battery’s operation:

$$\begin{array}{cc}\hfill So{C}_{f,n}\left(t\right)& =So{C}_{f,n}(t-1)+{\eta }_{f,n}^{ch}·{\displaystyle \frac{max\{P_{f,n}^{BESS}\left(t\right),0\}}{E_{f,n}^{max}}}·\mathsf{\Delta }t+{\displaystyle \frac{min\{P_{f,n}^{BESS}\left(t\right),0\}}{{\eta }_{f,n}^{dis}·E_{f,n}^{max}}}·\mathsf{\Delta }t,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill So{C}_{f,n}^{min}& \le So{C}_{f,n}\left(t\right)\le So{C}_{f,n}^{max},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill -{\overline{P}}_{f,n}^{BESS}& \le P_{f,n}^{BESS}\left(t\right)\le {\overline{P}}_{f,n}^{BESS},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill So{C}_{f,n}\left(T\right)& =So{C}_{f,n}\left(0\right)\forall f\in \mathcal{F},\forall (f,n)\in {\mathcal{N}}_f,\forall t\in \mathcal{T}.\hfill \end{array}$$

(7)

Equation (4) is the battery’s SoC evolution equation, whereas (5) and (6) impose the state-of-charge and active power bounds, respectively. Equation (7) ensures that the battery’s SoC at the end of the control horizon is equal to its initial SoC value, $So{C}_{f,n}\left(0\right)$, i.e., at the beginning of the control horizon, which is considered a given.

3.2. Problem Formulation

The aim of controlling the EV, PV, and BESS power injections is to achieve a safe grid operation by minimizing voltage and current constraints violations while minimizing curtailments of PV generation and EV demand. This is a similar problem as the one tackled in our previous work in [7] with the difference being that controllable batteries are also included, which introduce time dependencies among optimization variables via their SoC evolution equation (Equation (4)). Under ideal conditions that the values of the uncertain quantities over time (i.e., consuming loads and PV generation) are given by an oracle, our grid control problem can be expressed as the following optimization problem:

$$\begin{gathered} \begin{array}{c}\underset{\mathbf{a}\left(t\right),\mathbf{U}\left(t\right),\mathbf{I}\left(t\right)}{min}\sum _{t=1}^T\sum _{f=1}^F[w_1\sum _{n=1}^{N_f}{\varphi }_1\left(U_{f,n}\left(t\right)\right)+w_2\sum _{n=1}^{N_f}{\varphi }_2\left(U_{f,n}\left(t\right)\right)+w_3\sum _{l=1}^{L_f}{\varphi }_3\left(I_{f,l}\left(t\right)\right) \\ +w_4\sum _{n=1}^{N_f}\left(1-a_{f,n}^{EV}\left(t\right)\right)+w_5\sum _{n=1}^{N_f}\left(1-a_{f,n}^{PV}\left(t\right)\right)] \\ \mathrm{s}.\mathrm{t}.\mathrm{the} \mathrm{power} \mathrm{flow} \mathrm{equations} \mathrm{with} \mathrm{power} \mathrm{injections}\end{array} \end{gathered}$$

(8)

$$\begin{array}{c}\hfill S_{f,n}(t,a_{f,n}^{EV},a_{f,n}^{PV},a_{f,n}^{BESS}),\forall t\in \mathcal{T},\forall f\in \mathcal{F},\forall (f,n)\in {\mathcal{N}}_f,\end{array}$$

(9)

$$\begin{array}{cc}\hfill & \left(4\right)–\left(7\right),\forall t\in \mathcal{T},\forall f\in \mathcal{F},\forall (f,n)\in {\mathcal{N}}_f^{BESS},\hfill \end{array}$$

(10)

where $\mathbf{a}\left(t\right)={\left[a_{1,1}^{EV}\left(t\right),a_{1,1}^{PV}\left(t\right),a_{1,1}^{BESS}\left(t\right),\dots ,a_{F,N_f}^{EV}\left(t\right),a_{F,N_f}^{PV}\left(t\right),a_{F,N_f}^{BESS}\left(t\right)\right]}^T$ is the vector of controllable quantities and $w_1,w_2,w_3,w_4,w_5\in [0,1]$ are the weights of the individual objectives. Voltage and current constraints violations are penalized via the functions ${\varphi }_1\left(U_{f,n}\left(t\right)\right)=max\left(0, U_{f,n}\left(t\right)-\overline{U}\right)$, ${\varphi }_2\left(U_{f,n}\left(t\right)\right)=max\left(0, \underline{U}-U_{f,n}\left(t\right)\right)$, ${\varphi }_3\left(I_{f,l}\left(t\right)\right)=max\left(0, I_{f,l}\left(t\right)-\overline{I}\right)$, which correspond to soft form expressions of the constraints (2) and (3). The last two terms of the objective in (8) aim to minimize the APC for both EVs and PVs so as to maximize the satisfaction of EV charging demands and PV utilization. The non-linearity of power flow equations implies that the problem at hand is non-convex.

In this work, we design causal grid controllers that perform APC jointly with battery control. Causality means that decisions are based solely on currently known information. This work enhances and extends our previous works in [7,8] by additionally adopting BESSs and introducing fairness criteria in curtailment decisions. In particular, we design an RL-based solution of (8)–(10) as well as heuristic APC controllers that integrate fair BESSs control and fairness among buses in the APC process. We aim at designing controllers that can be generalized in different grid topologies and loads without re-training. Moreover, we evaluate the performance of the heuristic controllers in terms of safety constraints violations, amount of curtailed power, and fairness regarding the per-bus PV and EV-demand curtailment quantities.

3.3. Fairness Criteria

In this section, we mathematically formulate the fairness criteria considered in this work for the APC process. Starting with PVs, an often-used definition of fairness in the context of PVs’ APC is proportional fair generation. This criterion is widely adopted in the literature, for instance, in [13,14,17]. According to proportional fair generation, the ratio of curtailed power to maximum generation should be equal across buses that belong to the same feeder. In other words,

$$a_{f,n_i}^{PV}\left(t\right)=a_{f,n_j}^{PV}\left(t\right),\forall f\in \mathcal{F},\forall \{(f,n_i),(f,n_j)\}\in {\mathcal{N}}_f^{PV}\times {\mathcal{N}}_f^{PV}.$$

(11)

A similar fairness condition is adopted for the EV curtailment, i.e.,

$$a_{f,n_i}^{EV}\left(t\right)=a_{f,n_j}^{EV}\left(t\right),\forall f\in \mathcal{F},\forall \{(f,n_i),(f,n_j)\}\in {\mathcal{N}}_f^{EV}\times {\mathcal{N}}_f^{EV}.$$

(12)

Contrary to existing works in the literature, e.g., ref. [22], we apply a more generalizable EV fairness condition that is aligned with our target of designing a solution approach that can be generalized to different grid topologies and loads. For instance, the EV fairness criterion used in [22] involves the charging time of each EV, thus, requiring knowledge of the detailed EV charging model, whereas (12) does not demand information tailored to each EV. Note that these fairness conditions are not directly imposed on the proposed controllers, but they are indirectly accounted for through parameter tuning or other design features, as will be detailed in the following section. This is essential for maintaining the computational complexity low and real-time suitable. Imposing the fairness conditions as hard constraints requires solving an optimal power flow for the whole grid, which is hard to scale in very fast time scales.

4. Solution Approach

We develop a heuristic and causal solution to the problem stated in Section 3.2 that consists of two steps. The first step uses a trained RL agent to determine uniform per-feeder curtailment and battery power decisions. In other words, it determines for each feeder f three curtailment coefficient values: the first applies to all EVs in ${\mathcal{N}}_f^{EV}$, the second for all PVs in ${\mathcal{N}}_f^{PV}$, and the third one to all batteries in ${\mathcal{N}}_f^{BESS}$. The second step uses heuristic controllers that disaggregate the per-feeder coefficients to per-bus coefficients while accounting for the fairness criteria in Section 3.3 among different buses. This methodology is illustrated in Figure 1.

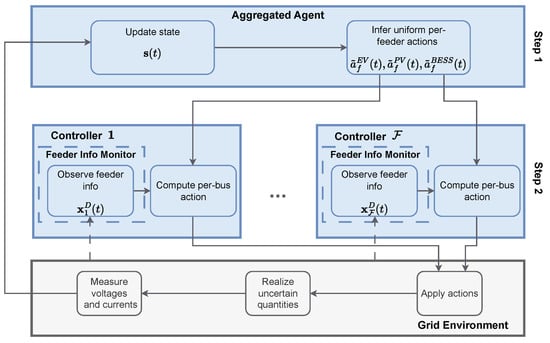
Figure 1. Two-step APC and BESS control solution.

Before describing the controllers of each step, we state the assumptions regarding their operation. Each controller has access to the system state, denoted by $\mathbf{s}\left(t\right)$, which includes overvoltage, undervoltage, and overcurrent violation quantities from previous time steps, the current SoC values of the BESSs, and the current time step index. For the controllers of the second step, depending on their design, additional state information may be required, and this is contained in the vector ${\mathbf{x}}_f^D\left(t\right)$ defined for each feeder $f\in \mathcal{F}$. Examples of such additional information are the location of each bus or forecasts of future PV and EV realizations.

4.1. RL Agent for the First Solution Step: Aggregated Agent

In this section, we design the RL-based agent of the first step that requires as input only aggregated information per feeder and outputs uniform per-feeder curtailment coefficients. The proposed agent is an extension of the RL agent of our previous work in [7], denoted as Aggregated Agent (AA) to include BESSs. The evaluation of [7] has demonstrated that the AA enhances training efficiency due to its relatively low dimensionality of state and action spaces and can be applied to grids with similar topologies and load patterns without requiring re-training. The aggregation of the state and the action spaces per feeder is the key feature of the AA that enables its good generalization properties. In the current design, we leverage the advantages of the previously developed AA agent and enhance its state and action spaces with batteries SoC values and uniform per-feeder BESSs power decisions, correspondingly. Regarding the BESSs, we assume that those belonging to the same feeder have identical characteristics and that their initial SoC values are the same. Thus, a uniform action is always applicable. Next, we describe in detail the Markov Decision Process (MDP) formulation that is used for the AA.

State: The state of the agent is formulated as

$$\begin{array}{cc}\hfill \mathbf{s}\left(t\right)=& [\overline{\mathbf{U}}(t-h-1),\dots ,\overline{\mathbf{U}}(t-1),\underline{\mathbf{U}}(t-h-1),\dots ,\underline{\mathbf{U}}(t-1),\hfill \\ & \overline{\mathbf{I}}(t-h-1),\dots ,\overline{\mathbf{I}}(t-1),\widetilde{\mathbf{SoC}}(t-1),t],\hfill \end{array}$$

(13)

where (i) $\overline{\mathbf{U}}\left(t\right)=[{\overline{U}}_1\left(t\right),\dots ,{\overline{U}}_F\left(t\right)]$, with ${\overline{U}}_f\left(t\right)={max}_{n\in {\mathcal{N}}_f}\left\{U_{f,n}\left(t\right)\right\}$, $\forall f\in \mathcal{F}$, (ii) $\underline{\mathbf{U}}\left(t\right)=[{\underline{U}}_1\left(t\right),\dots ,{\underline{U}}_F\left(t\right)]$, with ${\underline{U}}_f\left(t\right)={max}_{n\in {\mathcal{N}}_f}\left\{U_{f,n}\left(t\right)\right\}$, $\forall f\in \mathcal{F}$, (iii) $\overline{\mathbf{I}}\left(t\right)=[{\overline{I}}_1\left(t\right),\dots ,{\overline{I}}_F\left(t\right)]$, with ${\overline{I}}_f\left(t\right)={max}_{l\in {\mathcal{L}}_f}\left\{I_{f,l}\left(t\right)\right\}$, $\forall f\in \mathcal{F}$, and (iv) $\widetilde{\mathbf{SoC}}\left(t\right)=[{\widetilde{SoC}}_1\left(t\right),\dots ,{\widetilde{SoC}}_F\left(t\right)]$, where ${\widetilde{SoC}}_f\left(t\right)$ is the average SoC value of the batteries belonging to feeder f and h is the historical window size. Historical data for h prior time steps to $t-1$ are included to improve the agent’s forecasting capabilities by capturing violation patterns.

Action: The AA agent suggests a uniform action for each feeder, i.e., the same action is applied to all buses that belong to the same feeder. Thus, the action space is

$$\begin{array}{c}\hfill \tilde{\mathbf{a}}\left(t\right)=[{\tilde{a}}_1^{EV}\left(t\right),\dots ,{\tilde{a}}_F^{EV}\left(t\right),{\tilde{a}}_1^{PV}\left(t\right),\dots ,{\tilde{a}}_F^{PV}\left(t\right),{\overline{a}}_1^{BESS}\left(t\right),\dots ,{\overline{a}}_F^{BESS}\left(t\right)],\end{array}$$

(14)

and an action projection mechanism may then adjust ${\overline{a}}_f^{BESS}\left(t\right)$ to ${\tilde{a}}_f^{BESS}\left(t\right)$ in order to satisfy the constraints (5)–(7). The action applied to bus n of feeder f is $a_{f,n}^X\left(t\right)={\tilde{a}}_f^X\left(t\right)$, $X\in \{EV,PV,BESS\}$, if $(f,n)\in {\mathcal{N}}_f^X$. Note that, in case there are no EVs in a feeder, then the corresponding action is omitted from the action space. Similarly for PVs and BESSs.

Transition Process and Reward Function: After the action is decided based on the current state observation, the uncertain quantities for time t (i.e., the PV generation value, the EV demand, and other consumption loads) get realized and can be observed. Then, the voltage and current values for time t are derived through power flow calculations which inputs the action at t and the PV, EV, and load realizations at t. The reward function corresponds to the part of the objective function (8) corresponding to time t, i.e.,

$$\begin{array}{cc}\hfill r\left(t\right)=& -w_1{\displaystyle \sum _{f=1}^F}{\varphi }_1\left({\overline{U}}_f\left(t\right)\right)-w_2{\displaystyle \sum _{f=1}^F}{\varphi }_2\left({\underline{U}}_f\left(t\right)\right)-w_3{\displaystyle \sum _{f=1}^F}{\varphi }_3\left({\overline{I}}_f\left(t\right)\right)\hfill \\ & -w_4{\displaystyle \sum _{f=1}^F}(1-{\tilde{a}}_f^{EV}\left(t\right))-w_5{\displaystyle \sum _{f=1}^F}(1-{\tilde{a}}_f^{PV}\left(t\right)).\hfill \end{array}$$

(15)

The AA is trained through the Soft Actor–Critic (SAC) algorithm [31], which is an RL algorithm well-suited for continuous action spaces.

A feature of AA worth mentioning is that applying a uniform action per-feeder satisfies the fairness conditions in Section 3.3. Thus, the AA is considered fair by design. That is why we have not explicitly included the fairness criteria in our problem formulation. In the following, we present the heuristic controllers of step 2 that disaggregate the uniform per-feeder RL actions to per-bus decisions.

4.2. Heuristic Controllers for the Second Solution Step: Disaggregators

In this section, we briefly describe the disaggregators developed in [8], which take as input the uniform per-feeder action produced by the RL agent in the first step and compute individualized actions for each PV and EV, based on the location of their corresponding bus. Furthermore, in this paper, we propose two enhanced versions of these disaggregators with improved performance and fairness in several scenarios. Disaggregation is applied solely to determine per-bus PV and EV curtailments, while the battery decisions from the first step remain unchanged; in other words, a uniform per-feeder action is applied to the BESSs. This choice is motivated by the temporal interdependencies introduced in the problem by the batteries affecting the satisfaction of hard constraints and which, upon disaggregation, may introduce inconsistencies in the actual impact of the AA uniform decision. Despite this choice being considered limiting, our evaluations demonstrate that the inclusion of BESSs improves the cost performance of the disaggregators while maintaining fairness.

The key design principle of the disaggregators is obtained from a sensitivity analysis presented in [8] which has shown that buses farther from the PCC have a higher impact on voltage magnitudes as their power injection affects the voltages of all upstream buses, i.e., the buses closer to the PCC.

LD disaggregator: The first disaggregator is referred to as the Linear Disaggregator (LD). A per-bus action, $a_{f,n}^X\left(t\right),\forall (f,n)\in {\mathcal{N}}_f^X,X\in \{EV,PV\}$, is determined such that ${\displaystyle \frac{{\sum }_{(f,n)\in {\mathcal{N}}_f^X}{a}_{f,n}^X\left(t\right)}{|{\mathcal{N}}_f^X|}}={\tilde{a}}_f^X\left(t\right)$, i.e., the mean value of curtailment multipliers is equal to the uniform action of the AA (solution of step 1). The exact value of $a_{f,n}^X\left(t\right)$ at bus $(f,n)\in {\mathcal{N}}_f^X$ for $X\in \{EV,PV\}$ is given as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill n_f^{ref,X}& ={\displaystyle \frac{1}{2}}\left(\left|N_f^X\right|-1\right),\hfill \\ \hfill \mathsf{\Delta }{\overline{a}}_f^X\left(t\right)& =min\left\{1-{\tilde{a}}_f^X\left(t\right),{\tilde{a}}_f^X\left(t\right)\right\},\hfill \\ \hfill \mathsf{\Delta }{a}_{f,n}^X\left(t\right)& =\left\{\begin{array}{c}{m}_s^X·\left(reindex\left(X,f,n\right)-n_f^{ref,X}\right),\mathrm{if}\left|m_s^X·\left(reindex\left(X,f,n\right)-n_f^{ref,X}\right)\right|\le \mathsf{\Delta }{\overline{a}}_f^X\left(t\right),\hfill \\ \mathrm{sign}\left(m_s^X·\left(reindex(X,f,n)-n_f^{ref,X}\right)\right)·\mathsf{\Delta }{\overline{a}}_f^X\left(t\right),\mathrm{otherwise},\hfill \end{array}\right.\hfill \\ \hfill a_{f,n}^X\left(t\right)& ={\tilde{a}}_f^X\left(t\right)+\mathsf{\Delta }{a}_{f,n}^X\left(t\right),\hfill \end{array}\end{array}$$

(16)

where $\mathsf{\Delta }{a}_{f,n}^X\left(t\right)$ denotes the offset of the disaggregated from the uniform AA actions, $m_s^X<0$ is a parameter of the LD controller that corresponds to the slope of the linear disaggregation, and $\mathsf{\Delta }{\overline{a}}_f^X\left(t\right)$ is an upper bound on the absolute value of the offset $\mathsf{\Delta }{a}_{f,n}^X\left(t\right)$. $reindex(X,f,n)$ is an auxiliary function that calculates the relative index of $(f,n)$ in the set ${\mathcal{N}}_f^X$, i.e., it returns k if $(f,n)$ is the k-th nearest bus to the PCC among those in ${\mathcal{N}}_f^X$. Note that the reference bus $n_f^{ref,X}$ may be a virtual bus located between two actual buses when the cardinality of ${\mathcal{N}}_f^X$ is even. The absolute value of the offset $\mathsf{\Delta }{a}_{f,n}^X\left(t\right)$ is equal for buses located at equal distances from the reference bus $n_f^{ref,X}$. The definition of $\mathsf{\Delta }{\overline{a}}_f^X\left(t\right)$ ensures that $a_{f,n}^X\left(t\right)\in [0,1],\forall (f,n)\in {\mathcal{N}}_f^X$.

PBD disaggregator: The second disaggregator is denoted as the Power-Based Disaggregator (PBD). PBD allows the same PV generation or EV consumption as the AA would have permitted by its uniform action. To achieve this, PBD uses the additional information vector $x_f^D\left(t\right)$ with entries forecasts of the per-bus next-time-step generation and consumption denoted as $P_{f,n}^{H,p}\left(t\right)$, $P_{f,n}^{EV,p}\left(t\right)$, and $P_{f,n}^{PV,p}\left(t\right)$ for household demand of EVs and PVs, respectively. Initially, PBD sets $a_{f,n}^X\left(t\right)=1,\forall (f,n)\in {\mathcal{N}}_f^X,X\in \{PV,EV\}$. Then, it checks if generation or consumption dominates the feeder when no curtailment action is applied and curtails solely PV or EV power, respectively. If the quantity ${\sum }_{(f,n)\in {\mathcal{N}}_f}{P}_{f,n}^{H,p}\left(t\right)+{\sum }_{(f,n)\in {\mathcal{N}}_f^{EV}}{P}_{f,n}^{EV,p}\left(t\right)+{\sum }_{(f,n)\in {\mathcal{N}}_f^{PV}}{P}_{f,n}^{PV,p}\left(t\right)+{\sum }_{(f,n)\in {\mathcal{N}}_f^{BESS}}{\tilde{a}}_{f,n}^{BESS}\left(t\right)·{\overline{P}}_{f,n}^{BESS}$ is positive, then consumption dominates the grid. In this case, PBD greedily curtails EV demand starting from the bus that is located the farthest from the PCC by setting $a_{f,n}^{EV}\left(t\right)=0$ and continues upstream towards the PCC until the allowed EV consumption becomes equal to the AA’s one, i.e., until the following condition holds:

$$\sum _{n\in {\mathcal{N}}_f^{EV}}{a}_{f,n}^{EV}\left(t\right)P_{f,n}^{EV,p}\left(t\right)={\tilde{a}}_f^{EV}\left(t\right)\sum _{n\in {\mathcal{N}}_f^{EV}}{P}_{f,n}^{EV,p}\left(t\right).$$

(17)

When generation dominates the feeder, PBD curtails only PVs in the same way as with the EVs above until the following condition is fulfilled:

$$\sum _{n\in {\mathcal{N}}_f^{PV}}{a}_{f,n}^{PV}\left(t\right)P_{f,n}^{PV,p}\left(t\right)={\tilde{a}}_f^{PV}\left(t\right)\sum _{n\in {\mathcal{N}}_f^{PV}}{P}_{f,n}^{PV,p}\left(t\right).$$

(18)

CPBD disaggregator: In this paper, we propose a variation in PBD, called Constraint PBD (CPBD), which aims to enhance PBD’s fairness properties in line with the fairness criteria of Section 3.3. CPBD restricts the per-bus curtailment by minimum and maximum quantities that depend on the uniform action given by the AA. In particular, in CPBD the curtailment multipliers are constrained by

$$(1-ϵ)·{\tilde{a}}_f^X\left(t\right)\le a_{f,n}^X\left(t\right)\le (1+ϵ)·{\tilde{a}}_f^X\left(t\right),$$

(19)

where $ϵ\ge 0$ is a parameter that determines the maximum relative deviation from the uniform action. To determine such curtailment multipliers, we initially set $a_{f,n}^X\left(t\right)=1,\forall (f,n)\in {\mathcal{N}}_f^X,X\in \{PV,EV\}$. Then, we set $a_{f,n}^X\left(t\right)=min\{(1+ϵ)·{\tilde{a}}_f^X\left(t\right),1\},\forall n\in {\mathcal{N}}_f^X,\forall f\in \mathcal{F}$, where X is $EV$ when consumption dominates without curtailment and $PV$ otherwise. Then, CPBD starts the curtailment from the bus the farthest from the PCC, but the action is set equal to $a_{f,n}^X\left(t\right)=(1-ϵ)·{\tilde{a}}_f^X\left(t\right)$ instead of zero, set by PBD. Curtailment stops at the bus where one of the conditions (17) or (18) becomes valid for dominating consumption or generation, respectively.

EPBD disaggregator: An alternative way to improve fairness in the utilization of the feeders is to consider the bus export. In this respect, we propose the Export-considering PBD (EPBD) disaggregator. EPBD curtails either PVs or EVs, depending on whether the feeder is dominated by generation or consumption (without curtailment), respectively. Then, starting from the bus the farthest from the PCC, it curtails PV power or EV power for each bus (depending on the decision above) until the corresponding bus’ power export is zero. Curtailment stops when one of the conditions (17), (18) becomes active or at the bus $(f,1)$ that is closest to the PCC. In the case that consumption (generation) dominates the grid but locally at a bus $(f,n)$, there is dominating generation (consumption), no curtailment is applied at the corresponding bus, i.e., $a_{f,n}^X\left(t\right)=1,X\in \{EV,PV\}$.

In Figure 2, the individual per-bus actions derived from the proposed disaggregators are depicted and compared using a toy example. Consider a single-feeder network consisting of 10 buses, where the PV generation is equal to 20 kW and the EV demand is equal to 10 kW for each bus. BESSs are not included in this example. The AA suggests the uniform actions ${\tilde{a}}_f^{EV}\left(t\right)=0.7$ and ${\tilde{a}}_f^{PV}\left(t\right)=0.6$, and these actions are applied to all buses. The LD controller, the slope of which is set to $m_s^{EV}=m_s^{PV}=-0.1$ in this example, suggests actions that decrease linearly with the distance from PCC and curtails both PVs and EVs at each bus. Contrarily, the remaining disaggregators penalize only PV generation as it exceeds the EV demand without curtailment. PBD curtails all PV generation for buses 7–10 (the farthest ones from the PCC) and allows the total PV generation from the remaining buses. On the contrary, CPBD with parameter $ϵ$ set to $0.35$ suggests the minimum acceptable action of $(1-ϵ)·{\tilde{a}}_f^{PV}\left(t\right)=0.39$ for the last five buses (6–10) and the maximum one, which is equal to $(1+ϵ)·{\tilde{a}}_f^{PV}=0.81$, for the remaining ones. Lastly, the EPBD sets the curtailment multiplier $a_{f,n}^{PV}\left(t\right)$ equal to $0.5$ for the buses with index $n\ge 3$ and all other multipliers to 1. Thus, for buses with $n\ge 3$, the allowed PV generation is equal to their local EV demand, setting their export to the grid to zero. Buses 1 and 2 remain unaffected as the condition (18) is fulfilled already without curtailing PV from them.

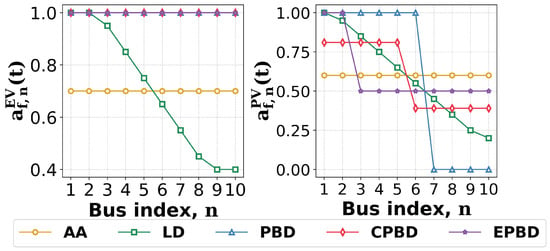
Figure 2. Toy example illustrating the disaggregation decisions of the different controllers for solution step 2.

Rules-Based Curtailment (RBC): RBC is inspired by droop-based control and is proposed in our previous work [8]. In this section, we provide a brief overview of how it works, and as an enhancement to its version in [8], we show how per-bus fairness is incorporated in the APC process and how BESSs control is included.

For BESSs, RBC applies the uniform action computed by the AA and corresponding to their feeder. For EVs and PVs, curtailments are computed based on the heuristic scheme explained below. Notice that the RBC curtailments for PVs and EVs are computed in a future myopic way, and thus, BESSs time interdependencies and future SoC constraints cannot be easily encoded within the RBC framework, and that is why AA is used for BESSs. However, a simplified version of the AA can be trained to control the BESSs along with the RBC. The state and the reward of the simplified AA remain the same as those used in Section 4.1, but the action vector includes only the BESSs uniform per-feeder power decisions, i.e.,

$$\begin{array}{c}\hfill \tilde{a}\left(t\right)=[{\overline{a}}_1^{BESS}\left(t\right),\dots ,{\overline{a}}_F^{BESS}\left(t\right)],\end{array}$$

(20)

along with the action projection (so that constraints (5)–(7) are satisfied) to compute ${\tilde{a}}_f^{BESS}\left(t\right),\forall f\in \mathcal{F}$. In this way, by reducing the action space, training becomes faster and more efficient. During the training of AA, RBC is executed in the environment to decide the APC of PVs and EVs. In this way, the agent controlling BESSs is expected to learn the dynamics corresponding to RBC and to improve the performance of the method.

For PVs and EVs, RBC suggests curtailment actions proportional to the deviation in voltages and currents from RBC bounds, which are tighter than grid operational limits. When a violation occurs at a bus indexed by n or at a line indexed by l, all downstream buses, as well as $\eta$ upstream buses, should share the curtailment amount of the RBC. The choice of curtailing all the downstream buses is aligned with the sensitivity analysis of [8], whereas the parameter $\eta$ is exploited in the current work to improve the fairness of the controller as with $\eta \ge 1$ more buses sharing the penalty.

RBC uses tightened bounds to compute violations, namely, ${\underline{U}}^{RBC}\ge \underline{U}$, ${\overline{U}}^{RBC}\le \overline{U}$ for the voltage lower and upper limits and ${\overline{I}}^{RBC}\le \overline{I}$ for the ampacity upper constraint. In particular, for the bus n of feeder $f\in \mathcal{F}$, the violation quantities are calculated as

$$\begin{array}{cc}\hfill \mathsf{\Delta }{\underline{U}}_{f,n}\left(t\right)& =max\{{\underline{U}}^{RBC}-U_{f,n}\left(t\right),0\},\hfill \\ \hfill \mathsf{\Delta }{\overline{U}}_{f,n}\left(t\right)& =max\{U_{f,n}\left(t\right)-{\overline{U}}^{RBC},0\},\hfill \\ \hfill \mathsf{\Delta }{\overline{I}}_{f,l}\left(t\right)& =max\{I_{f,l}\left(t\right)-{\overline{I}}^{RBC},0\}.\hfill \end{array}$$

(21)

Then, RBC applies a uniform curtailment action to the $\eta$ upstream buses of the violation location (here it is considered at bus n or line l) and all downstream buses, which is computed as follows. First, the following auxiliary curtailment multipliers are computed:

$$\begin{array}{cc}\hfill c_{f,n}^{\underline{U}}\left(t\right)& =1-M^{\underline{U}}·{\displaystyle \frac{\mathsf{\Delta }{\underline{U}}_{f,n}(t-1)}{N_f-max\{n-\eta ,0\}+1}},\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill c_{f,n}^{\overline{U}}\left(t\right)& =1-M^{\overline{U}}·{\displaystyle \frac{\mathsf{\Delta }{\overline{U}}_{f,n}(t-1)}{N_f-max\{n-\eta ,0\}+1}},\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill c_{f,l}^{\overline{I}}\left(t\right)& =1-M^{\overline{I}}·{\displaystyle \frac{\mathsf{\Delta }{\overline{I}}_{f,l}(t-1)}{N_f-max\{n-\eta ,0\}+1}},\hfill \end{array}$$

(24)

where $M^{\underline{U}},M^{\overline{U}}$, and $M^{\overline{I}}$ are the sensitivity coefficients for undervoltage, overvoltage, and overcurrent violations, respectively, which are computed experimentally. Then, the auxiliary curtailment multipliers are normalized by the ratio of the allowed power at the previous time step to the expected power at the current time step, i.e.,

$$\begin{array}{c}\hfill {\pi }_{f,n}^X(t,c)=\left\{\begin{array}{cc}min\left\{{\displaystyle \frac{P_{f,n}^X(t-1)·c}{P_{f,n}^{X,p}\left(t\right)}},1\right\},\hfill & \mathrm{if}{P}_{f,n}^{X,p}\left(t\right)\ne 0,\hfill \\ c,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

(25)

where $X\in \{EV,PV\}$ and c is one of the coefficients in (22)–(24). Intuitively, when the upcoming power injection is expected to be lower than the previous realization, a decreased curtailment action can be adequate; otherwise, the suggested curtailment amount is increased to prevent constraint violations.

If no violations occur in the entire feeder, RBC still applies a curtailment action that, compared to the curtailment action of the previous time step, increases proportionally to the relative expected power generation/consumption drop from the previous time step. This is expressed as follows:

$$\begin{array}{cc}\hfill & {\psi }_{f,n}^X\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{P_{f,n}^{X,d}(t-1)-P_{f,n}^{X,p}\left(t\right)}{P_{f,n}^{X,d}(t-1)}}+a_{f,n}^X(t-1),\hfill & \mathrm{if}0<\left|P_{f,n}^{X,p}\left(t\right)\right|<\left|P_{f,n}^{X,d}(t-1)\right|,\hfill \\ 1,\hfill & \mathrm{else}\mathrm{if}{P}_{f,n}^{X,p}\left(t\right)=0,\hfill \\ 0,\hfill & \mathrm{else}\mathrm{if}{a}_{f,n}^X(t-1)=0,\hfill \\ a_{f,n}^X(t-1),\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

(26)

Note that when multiple curtailment actions are suggested to the same bus because of constraints violations at different locations, the controller applies the maximum of them.

The steps of the RBC controller are summarized below:

• For BESSs set $a_{f,n}^{BESS}\left(t\right)\leftarrow {\tilde{a}}_f^{BESS}\left(t\right)$, $\forall n\in {\mathcal{N}}_f^{BESS}$.
• Set $a_{f,n}^{EV}\left(t\right)\leftarrow 1$, $\forall n\in {\mathcal{N}}_f^{EV}$ and $a_{f,n}^{PV}\left(t\right)\leftarrow 1$, $\forall n\in {\mathcal{N}}_f^{PV}$.
• $Y\leftarrow \left\{\begin{array}{c}EV,\mathrm{if}\mathrm{net}\mathrm{consumption}\mathrm{over}\mathrm{the}\mathrm{feeder},\hfill \\ PV,\mathrm{otherwise}.\hfill \end{array}\right.$
• Compute $c_{f,n}^{\underline{U}}\left(t\right),c_{f,n}^{\overline{U}}\left(t\right),c_{f,l}^{\overline{I}}\left(t\right),\forall n\in {\mathcal{N}}_f,\forall l\in {\mathcal{L}}_f$ according to (22)–(24).
• For every n where $c_{f,n}^{\underline{U}}\left(t\right)>0$ do $a_{f,j}^{EV}\left(t\right)\leftarrow min\{a_{f,j}^{EV}\left(t\right),{\pi }_{f,n}^{EV}(t,c_{f,n}^{\underline{U}}\left(t\right))\},$$\forall j\in \{n-\eta ,\dots ,N_f\}\cap {\mathcal{N}}_f^{EV}$.
• For every n where $c_{f,n}^{\overline{U}}\left(t\right)>0$ do $a_{f,j}^{PV}\left(t\right)\leftarrow min\{a_{f,j}^{PV}\left(t\right),{\pi }_{f,n}^{PV}(t,c_{f,n}^{\overline{U}}\left(t\right))\},$$\forall j\in \{n-\eta ,\dots ,N_f\}\cap {\mathcal{N}}_f^{PV}$.
• For every n where $c_{f,n}^{\overline{I}}\left(t\right)>0$ do $a_{f,j}^Y\left(t\right)\leftarrow min\{a_{f,j}^Y\left(t\right),{\pi }_{f,n}^Y(t,c_{f,n}^{\overline{I}}\left(t\right))\},$ $\forall j\in \{n-\eta ,\dots ,N_f\}\cap {\mathcal{N}}_f^Y$.
• If No Violations then $a_{f,n}^Y\left(t\right)\leftarrow min\{{\psi }_{f,n}^Y\left(t\right),1\},\forall n\in \{1,\dots ,N_f\}\cap {\mathcal{N}}_f^Y$.

5. Results

5.1. Simulation Setup and Sketch of Experiments

We consider a dual-feeder radial low-voltage grid consisting of 17 households per feeder and the PCC. The considered total number of buses is realistic, since it may represent real distribution grids such as the one used in [32]. However, in Section 5.4, we also consider larger grids. The grid parameters are obtained from the SimBench dataset [33]. Specifically, the voltage bounds are set to $\underline{U}=0.9$ p.u. and $\overline{U}=1.1$ p.u. with a base voltage equal to $0.4$ kV, and the ampacity limit is set to $\overline{I}=0.27$ kA. We assume that there is an EV connected to all buses, whereas PVs are connected to half of the buses, and specifically, those with indices n in the set $\{1,3,5,\dots ,17\}$ for each feeder. BESSs are connected to buses with indices n within the set $\{1,5,\dots ,17\}$ for each feeder, and their parameters are obtained from [34], i.e., the SoC capacity is set to $E_{f,n}^{max}=20$ kWh, the maximum power injection is equal to ${\overline{P}}_{f,n}^{BESS}\left(t\right)=10$ kW, and the charging/discharging efficiencies are ${\eta }_{f,n}^{ch}={\eta }_{f,n}^{dis}=0.91$, for each bus $(f,n)\in {\mathcal{N}}_f^{BESS},\forall f\in \mathcal{F}$. The open-source Python library PandaPower 2.13.1 [35] is incorporated to model the grid.

The household demand, EV demand and PV generation data are obtained from SimBench [33]. The measurements took place in a time horizon of 366 days with a time resolution of 15 min. Thus, the duration of the time step is set to $\mathsf{\Delta }t=15$ min as well. Reactive power is considered only for the household demand, whereas, PVs and EVs generate and consume, respectively, only active power. Similarly with [7], $90\%$ of the days are used for training, $5\%$ for hyperparameter tuning, and $5\%$ as the test set.

RL agents are trained using the open-source implementation of the SAC algorithm in Stable-Baselines3 2.1.0 [36]. The hyperparameter values are set as in [7]: the learning rate is set equal to $3\times {10}^{-4}$, the minibatch size is set to 100, and the replay buffer size is set to ${10}^6$. The actor and critic networks have identical architecture, consisting of two layers with 256 neurons each. Regarding the discount factor $\gamma$, it is set to 0 when there are no BESSs. However, due to the temporal dependency introduced by BESSs, a positive value for $\gamma$ is applied when BESSs are present. After experimentation, this value is set to $\gamma =0.5$. Training is performed for six epochs where an epoch corresponds to training over the whole dataset once, and this is sufficient for convergence. Regarding the RL agent trained to control BESSs along with RBC, the learning rate is set to ${10}^{-4}$ and the discount factor to $\gamma =0.9$. A total of four epochs is sufficient for convergence of the training process in this case. The remaining parameters of the optimization problem and the controllers are listed in Table 1.

Table 1. Optimization and controller/disaggregator parameters.

Parameter	Value
$w_1$	$1.093$
$w_2$	$1.633$
$w_3$	$0.560$
$w_4$	$0.008$
$w_5$	$0.008$
h	2
$m_s^{PV}$	$-0.1$
$m_s^{EV}$	$-0.1$
T	96
$\mathsf{\Delta }t$	15 min
$ϵ$	$0.35$
${\underline{U}}^{RBC}$	$0.92$ p.u.
${\overline{U}}^{RBC}$	$1.08$ p.u.
${\overline{I}}^{RBC}$	$0.24$ kA
$M^{\underline{U}}$	250
$M^{\overline{U}}$	175
$M^{\overline{I}}$	$87.5$

We perform four sets of experiments to evaluate the proposed two-step solution approach. The first does not include BESSs and aims to assess the performance of the disaggregators in terms of reducing constraint violations and power curtailment as well as achieve fairness. The performance of the disaggregators is compared to linearized OPF solutions, which are explained in more detail in [8]. The NLOPF is used to estimate the optimal performance values. In particular, NLOPF minimizes the objective function (8) independently for each time step, which is equivalent to minimizing the aggregated objective, as there is no time dependency when BESSs are excluded. The constraint (9) is replaced by a linearized approximation of power flow equations based on a sensitivity study to improve computational efficiency. The voltage and current operating limits are tightened to $[0.905,1.095]$ and $[0,0.265]$, respectively, to account for approximation errors. We assume that the NLOPF method has access to exact predictions to achieve optimal performance. The second baseline is referred to as ULOPF and is similar to NLOPF but applies a uniform curtailment action per feeder, analogous to AA. As the uniform actions enforce the fairness conditions at each time step, this approach can be considered as a fairness-aware OPF formulation. Next, we perform more detailed sensitivity analysis to demonstrate which parameters can be properly adjusted to tune the observed performance–fairness trade-off. The second set of experiments includes BESSs to examine the performance and fairness improvements attributed to them. In addition, we perform a third set of experiments to examine the training needs for more challenging scenarios of higher load and larger grids. Finally, we study the generalization capabilities of the proposed solution approach including BESSs by evaluating its performance in different grid topologies and loads compared with those used to train the AA. Unless otherwise specified, the reported results are derived by averaging the performance of five trained AAs. In all cases, persistent forecasting is applied for the PBD, CPBD, EPBD, and RBC controllers, i.e., we use, as forecast of the PV generation and EV demand of the next time slot, their currently observed values.

5.2. Evaluation Metrics

The first two metrics are defined to assess the two-step solution performance. The first metric used is the APC percentage, which is calculated as

$$\begin{array}{c}\text{APC percentage}\hfill \\ =\left(1-{\displaystyle \frac{{\sum }_{t\in \mathcal{T}}{\sum }_{f\in \mathcal{F}}\left({\sum }_{n\in {\mathcal{N}}_f^{EV}}{a}_{f,n}^{EV}\left(t\right)·P_{f,n}^{EV,d}\left(t\right)-{\sum }_{n\in {\mathcal{N}}_f^{PV}}{a}_{f,n}^{PV}\left(t\right)·P_{f,n}^{PV,d}\left(t\right)\right)}{{\sum }_{t\in \mathcal{T}}{\sum }_{f\in \mathcal{F}}\left({\sum }_{n\in {\mathcal{N}}_f^{EV}}{P}_{f,n}^{EV,d}\left(t\right)-{\sum }_{n\in {\mathcal{N}}_f^{PV}}{P}_{f,n}^{PV,d}\left(t\right)\right)}}\right)·100\%.\hfill \end{array}$$

(27)

The second metric is the ratio of violations occurring in the test set to the number of violations occurring when no control is performed.

The remaining metrics quantify fairness properties of the diverse disaggregators in the two-step solution approach. Fairness is assessed for PVs and EVs curtailment. Let us first define the following auxiliary variables:

$$\begin{array}{c}\hfill y_{f,n}^{PV}={\displaystyle \frac{{\sum }_{t\in \mathcal{T}}\left(P_{f,n}^{PV,d}\left(t\right)-a_{f,n}^{PV}\left(t\right)·P_{f,n}^{PV,d}\left(t\right)\right)}{{\sum }_{t\in \mathcal{T}}{P}_{f,n}^{PV,d}\left(t\right)}},\end{array}$$

(28)

$$\begin{array}{c}\hfill y_{f,n}^{EV}={\displaystyle \frac{{\sum }_{t\in \mathcal{T}}\left(P_{f,n}^{EV,d}\left(t\right)-a_{f,n}^{EV}\left(t\right)·P_{f,n}^{EV,d}\left(t\right)\right)}{{\sum }_{t\in \mathcal{T}}{P}_{f,n}^{EV,d}\left(t\right)}}.\end{array}$$

(29)

The first considered fairness metric is the Min–Max Ratio (MMR), defined as follows:

$$MM{R}_f^X={\displaystyle \frac{{min}_{(f,n)\in {\mathcal{N}}_f^X}{y}_{f,n}^X}{{max}_{(f,n)\in {\mathcal{N}}_f^X}{y}_{f,n}^X}}·100\%,X\in \{EV,PV\}.$$

(30)

The second fairness metric is the Jain’s Fairness Index (JFI), defined as follows:

$$JF{I}_f^X={\displaystyle \frac{{\left({\sum }_{(f,n)\in {\mathcal{N}}_f^X}{y}_{f,n}^X\right)}^2}{|{\mathcal{N}}_f^X|{\sum }_{(f,n)\in {\mathcal{N}}_f^X}{\left(y_{f,n}^X\right)}^2}}·100\%,X\in \{EV,PV\}.$$

(31)

MMR assesses fairness based on extreme cases, whereas JFI considers all buses of the feeder. In the results that follow, for each fairness metric, we present its minimum value along all the feeders, which corresponds to the worst case in terms of fairness.

Another metric related to fairness that is evaluated in this work is the Minimum Utilization. We define utilization as the percentage of allowed power to the power when no curtailment is applied, which is expressed for a particular bus n as

$$u{t}_{f,n}^X={\displaystyle \frac{{\sum }_{t\in \mathcal{T}}{a}_{f,n}^X\left(t\right)·P_{f,n}^{X,d}\left(t\right)}{{\sum }_{t\in \mathcal{T}}{P}_{f,n}^{X,d}\left(t\right)}}·100\%,X\in \{EV,PV\}.$$

(32)

The minimum utilization value along all buses of the grid corresponds to the evaluated metric. The utilization metric is critical, especially for PVs, as low values may discourage possible investment.

5.3. Evaluation of the Proposed Disaggregators Without BESSs

Figure 3a depicts the performance metrics, i.e., the APC percentage, and the remaining violations for the AA, the two-step solution including the different disaggregators and the OPF solutions. All disaggregators present improved performance compared to the AA agent in terms of APC. For RBC, this comes at the expense of a slight increase in violations count. This comparison unveils the benefits of the tailored per-bus curtailments compared to the uniform per-feeder decisions. All disaggregators mitigate $99\%$ or more violations compared to the uncontrolled case that corresponds to fewer than $0.049$ violations per time step observed on average. The lowest number of violations is achieved by EPBD, while RBC achieves the lowest APC percentages. Especially, when the parameter $\eta$ is set equal to 0, i.e., no upstream buses are affected, RBC achieves an APC percentage equal to $40.28\%$, which is much lower than the one of the second-best-performing disaggregator, i.e., $50.44\%$ for EPBD. PBD has similar performance to EPBD. CPBD and LD exhibit equivalent performance, which is better than AA, but not as good as PBD and EPBD.

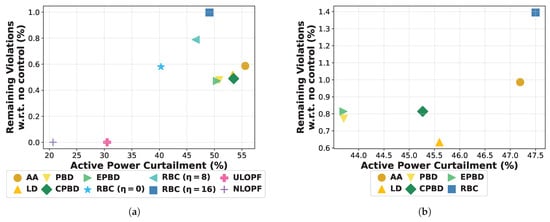
Figure 3. Performance evaluation of the controllers in terms of ratio of violations and APC percentage (a) without BESSs; (b) with BESSs.

Regarding the RBC controller, we examine three different values for the parameter $\eta$, namely, $\eta =0,8,16$. RBC with $\eta =0$ does not apply violation penalties to upstream buses from the violation location, whereas all buses (all upstream and all downstream buses) share the violation penalty for $\eta =16$. The evaluation results indicate that lower values of $\eta$ improve the performance as RBC with $\eta =0$ achieves an APC percentage that is $6.3$ degrees lower, accompanied by at least $35\%$ fewer violations than RBC with $\eta =8$. RBC with $\eta =16$ still curtails less power than EPBD, but the number of violations is doubled, i.e., it is less efficient.

OPF approaches give the near-optimal solutions and thus, as expected, they achieve much better performance than the two-step solution approach. However, they are not suitable for real-time decision making as they are computationally intensive, requiring a full grid model and accurate forecasts. Computational complexity worsens when BESSs are included (e.g., in Figure 3b where OPF solutions are meaningless for real-time and, thus, not included in the comparisons) due to the introduced time dependencies that demand for multi-period optimization in this case.

Next, we discuss the fairness properties of the AA, the disaggregators, and the OPF-based solutions. Figure 4 presents the MMR and JFI values for the curtailment of PVs and EVs from different buses. As expected, AA is the most fair controller. Indeed, it achieves almost $100\%$ in both metrics on PV curtailment, while it also significantly outperforms the remaining controllers in terms of fair EV curtailment. It achieves a lower value in the MMR metric for the EVs because there exist buses whose EV demand is compensated by PV generation, leading to reduced EV curtailment needs (which impacts the numerator of MMR); however, it performs even better than ULOPF, verifying its fair design. With respect to the OPF baselines, although NLOPF is the best-performing in terms of violations and APC, it has the worst performance in terms of fairness (note that fairness is not accounted for in its objective). On the contrary, ULOPF, by determining a uniform per-feeder action, achieves high fairness, which for PVs is close to the AA fairness, but at the expense of APC performance. Next, we focus on PV curtailment by the proposed disaggregators to assess the fairness of our schemes, which allows for more accurate conclusions, as in this simulation, the grid is PV-dominated.

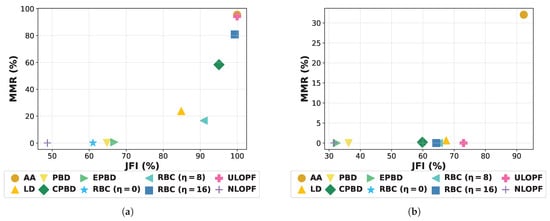
Figure 4. Fairness evaluation of the controllers in the absence of BESSs. (a) PV curtailment. (b) EV curtailment.

For RBC, the evaluation indicates that higher values of $\eta$ yield fairer strategies. In particular, RBC with $\eta =16$ is the most competitive alternative to AA in the PV curtailment, whereas RBC with $\eta =0$ is the least fair one. Thus, by properly setting the value of $\eta$, RBC’s trade-off between fairness in curtailment and performance can be properly tuned. In next subsection, we elaborate further on this tuning. PBD seems much less efficient in providing fair solutions, especially with respect to MMR, which is expected as it hardly penalizes buses far from the PCC. With respect to its enhancements, CPBD performs much better than EPBD in terms of both fairness metrics, indicating that although the additional constraint of Equation (19) induces a small performance drop compared to PBD and EPBD, it improves fairness among buses.

Lastly, in Figure 5, we observe the minimum utilization of PVs and EVs for the suggested controllers and the OPF baselines. RBC with $\eta =16$ obtains the maximum minimum utilization for both PVs and EVs. In general, RBC with any value of $\eta$ achieves higher minimum utilization of EVs compared to other controllers, but lower values of $\eta$ underperform with respect to the minimum utilization of PVs compared to other disaggregators or RBC with higher values of $\eta$. Specifically, for RBC with $\eta =0$, the minimum utilization of PVs is equal to $8.23\%$, whereas RBC with $\eta =16$ allows at least $38\%$ of the generated PV power to all buses. Moreover, the AA performs close to RBC, achieving approximately a value of $32\%$ for the minimum PV utilization. CPBD follows, presenting around $23.6\%$ minimum PV utilization and $50.2\%$ minimum EV utilization, whereas for the remaining disaggregators, there is at least one bus where less than $10\%$ of the PV generation is permitted. Regarding the OPF-based methods, ULOPF achieves optimal utilization for both PVs and EVs, which makes evident the impact of fairness. In contrast, the NLOPF presents competitive performance in terms of minimum PV utilization compared to fairness-aware controllers due to its significantly lower curtailment requirements. In general, we conclude that methods that achieve higher fairness in terms of MMR and JFI metrics, i.e., the AA, RBC with high $\eta$, and CPBD, also achieve high values of minimum PV and EV utilization, which underlines the correlation between minimum utilization and fairness.

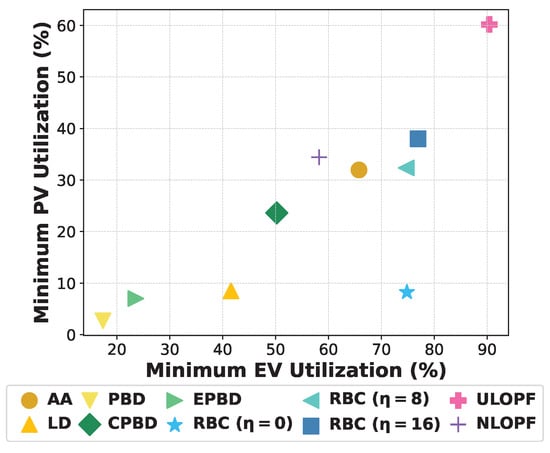
Figure 5. Minimum utilization metric for all controllers: x-axis represents the minimum EV utilization and y-axis the minimum PV utilization.

5.4. Sensitivity Analysis of the Performance–Fairness Trade-off to Controller Parameters

In this section, we explain which parameters can be adjusted to tune the trade-off between fairness and performance and we perform a sensitivity analysis to assess their impact.

Regarding the LD controller, the parameters $m_s^{PV}$ and $m_s^{EV}$ are significant in balancing fairness and performance. In the previous section, we have shown that LD achieves better performance but reduced fairness compared to AA when the parameters $m_s^{PV}$ and $m_s^{EV}$ are set to $-0.1$. Notably, LD becomes identical to AA when $m_s^{PV}=m_s^{EV}=0$. Next, we set $m_s^{PV}=m_s^{EV}=m_s$ and simulate the controller for $m_s$ values ranging from $-0.5$ to 0 with a step of $0.05$. We do not study values lower than $-0.5$ because in our setting, the cardinalities of ${\mathcal{N}}_f^{EV}$ and ${\mathcal{N}}_f^{PV}$ are odd and, thus, values of $m_s$ lower than $-0.5$ do not affect disaggregation. The corresponding results are illustrated in Figure 6.

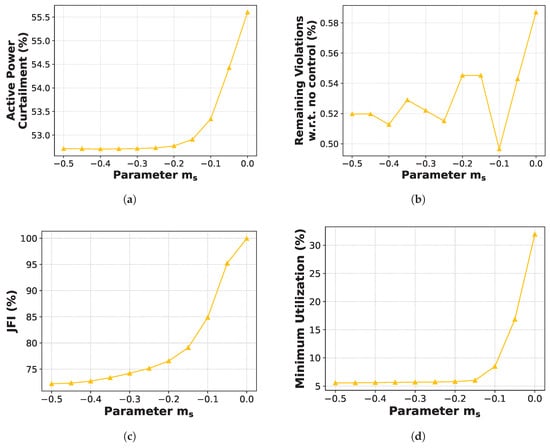
Figure 6. Sensitivity of the LD-obtained metric values with respect to the parameter $m_S$. (a) Active Power Curtailment. (b) Remaining violations. (c) JFI of PVs. (d) Minimum PV utilization.

As observed in Figure 6a, higher $m_s$ values result in higher curtailment, while for $m_s<-0.2$, the improvement in curtailment becomes marginal. In terms of violation mitigation, lower $m_s$ values generally lead to fewer violations, with the minimum observed for $m_s=-0.1$. Figure 6c demonstrates that increasing $m_s$ improves the fairness of PV curtailment. Similar trends are observed for EVs and for the MMR metric. Furthermore, values of $m_s$ close to 0 are beneficial to the minimum utilization metric.

Regarding the CPBD controller, the parameter $ϵ$ distinguishes it from PBD and enhances fairness. We simulate the controller for $ϵ$ values ranging from 0 to 1, and the results are presented in Figure 7. The sensitivity analysis indicates that lower $ϵ$ values lead to improvements in fairness-related metrics, whereas higher values are more favorable in terms of performance. However, $ϵ$ values that are too high may increase the number of violations. Regarding the fairness metrics, similar results are obtained for JFI of EVs and MMR of both PVs and EVs.

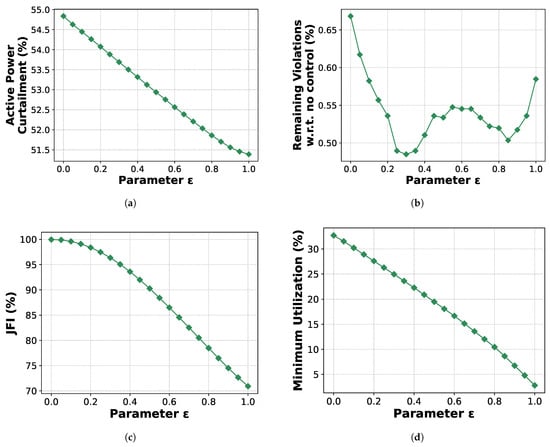
Figure 7. Sensitivity of the CPBD-obtained metric values with respect to the parameter $ϵ$. (a) Active Power Curtailment. (b) Remaining violations. (c) JFI of PVs. (d) Minimum PV utilization.

The last controller with adjustable parameters affecting the fairness–performance trade-off is the RBC. In the previous section, representative values of $\eta$ were selected to demonstrate that RBC is sensitive to this parameter. In this section, we analyze the behavior of RBC by examining all possible values of $\eta$ for the dual-feeder grid with 17 buses per feeder, i.e., $\eta \in \{0,1,\dots ,16\}$. As illustrated in Figure 8, we observe that higher values of $\eta$ enhance fairness-related metrics but the performance deteriorates. Moreover, RBC demonstrates the highest sensitivity. In particular, the increase from the best to the worst APC value is approximately 20%, whereas the corresponding increase is below 10% for LD and CPBD.

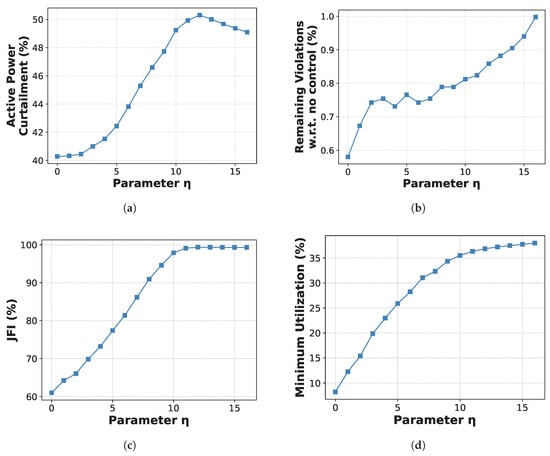
Figure 8. Sensitivity of the RBC-obtained metric values with respect to the parameter $\eta$. (a) Active Power Curtailment. (b) Remaining violations. (c) JFI of PVs. (d) Minimum PV utilization.

5.5. Evaluation of the Proposed Disaggregators with BESSs

The results of the previous section highlight the emerging trade-off between fairness and performance: the best-performing controllers do not entail fair solutions, resulting in suboptimal utilization of PVs or high curtailments of EV demands in specific buses, which may render the investment for the installation of PVs or charging stations in those buses unattractive. Thus, we include BESSs in the grid to examine their potential benefits towards increasing fairness in PV use and EV charging while maintaining high performance levels.

Figure 3b presents the APC percentage and the ratio of violations achieved for the AA and different disaggregators in the presence of BESSs. With BESSs, the AA controller shows a significant decrease in APC percentage (from $55.60$% to $47.20$%) compared to the case without BESSs with a slight penalty in the ratio of violations (from $0.59$% to $0.99$%). Similar behavior is obtained for the LD, PBD, CPBD, and EPBD disaggregators for which the APC percentage is reduced by around 15%, while the number of violations still remains below 1%. In particular, LD is the best-performing controller in terms of violations mitigation, allowing only $0.03$ violations per time step on average. In the experiments with BESSs, RBC is evaluated only with $\eta =16$, as this choice has led to the highest fairness without BESSs. For this RBC version, BESSs bring a modest decrease in the APC percentage (by 2 units) and a slight increase in the ratio of violations, which becomes around $1.4\%$. Therefore, when BESSs are included, the EPBD disaggregator demonstrates the best performance in reducing curtailment requiriments, with PBD achieving comparable results.

Regarding the fairness metrics, which are illustrated in Figure 9, the relative ordering of controllers remains unchanged as in Figure 4. The AA maintains its performance in terms of JFI, but with BESSs, it achieves a lower MMR value than without BESSs. This observation can be explained by the formula of MMR in Equation (30). In more detail, focusing on a single-feeder, the denominator of the MMR metric is equal to $1-{min}_{(f,n)\in {\mathcal{N}}_f^X}\left\{u{t}_{f,n}^X\right\}$; thus, an increase in the mininum utilization value implies a decrease in the denominator of the MMR metric. Similarly, the numerator is given by $1-{max}_{(f,n)\in {\mathcal{N}}_f^X}\left\{u{t}_{f,n}^X\right\}$. If we denote by $\delta$ the absolute increase in ${min}_{(f,n)\in {\mathcal{N}}_f^X}\left\{u{t}_{f,n}^X\right\}$, ${\delta }^{\prime }$ the absolute increase in ${max}_{(f,n)\in {\mathcal{N}}_f^X}\left\{u{t}_{f,n}^X\right\}$, and ${\widehat{MMR}}_f^X$ the initial MMR ratio, the derived MMR value is lower if the relation ${\displaystyle \frac{{\delta }^{\prime }}{\delta }}>{\widehat{MMR}}_f^X$ holds as can be proven by trivial calculations. Considering the uniform actions of AA and the reduced curtailment needs, the values of $\delta$ and ${\delta }^{\prime }$ are expected to be similar and positive, but ${\widehat{MMR}}_f^X$ is lower or equal to 1; hence, the drop of MMR value is justified. Furthermore, RBC and CPBD are again the most fair disaggregators, even though the corresponding JFI and MMR fairness metric values have slightly dropped compared to the case without BESSs. Worth mentioning are the improvements noticed in the fairness metrics for PVs of the PBD and EPBD controllers and in the JFI metric for EVs of EPBD and RBC.

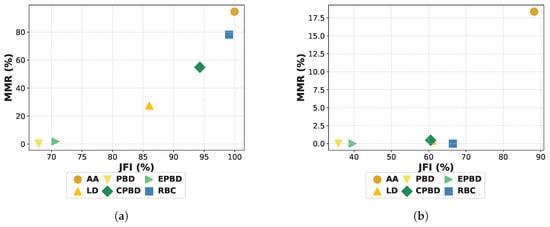
Figure 9. Fairness evaluation of the controllers after the integration of BESSs. (a) PV curtailment. (b) EV curtailment.

Figure 10 depicts the minimum utilization values for all controllers. We observe that BESSs contribute significantly into increasing the values of this metric allowing for more efficient PV utilization and higher EV demand satisfaction. AA and RBC controllers achieve optimal performance. The former has a slight advantage on PVs, while the latter is better at fulfilling EV demand. In Figure 11, the relative improvement in the minimum utilization metric, when BESSs are included, to the minimum utilization without BESSs is plotted. All methods except RBC present an average improvement more than $35\%$ on minimum PV utilization. The improvement achieved for RBC is only about $1\%$. Considering that RBC is the most effective controller concerning the minimum utilization, this improvement is satisfactory. The two-step solution combined with BESSs control shows also an improvement on average in minimum EV utilization.

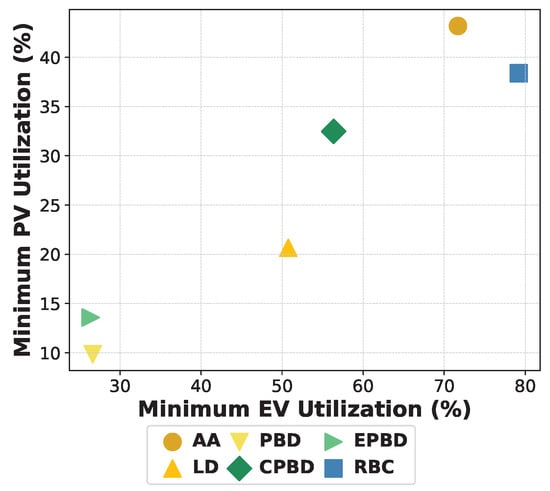
Figure 10. Minimum utilization metric for all controllers after the adoption of BESSs: x-axis is the minimum EV utilization and y-axis the minimum PV utilization.

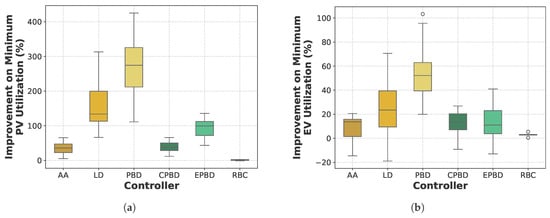
Figure 11. Improvement in the minimum utilization metric due to the integration of BESSs. (a) Minimum PV utilization. (b) Minimum EV utilization.

5.6. Study on the Scalability of the Proposed Controllers

In this section, we examine the scaling properties of the AA, when BESSs are included, by varying the peak load and grid topology. Scalability is mostly related to training, since after obtaining the trained AA agent, decision making is quite fast. The AA agent infers a decision instantly whereas disaggregators are also very fast, scaling in the worst case linearly with the maximum number of buses over all feeders. Regarding the LD method, if each bus is aware its relative order on the feeder, there is an efficient implementation, where each bus computes locally the disaggregated action. However, training is offline and does not affect the decision time during deployment of the controllers, which is also studied at the end of the section.

For each configuration we train three agents for the same number of epochs as in the reference case, i.e., six epochs for AA and four epochs for RBC. The results are averages over the three trained agents. The first experiment increases the peak PV generation and EV demand by 50%, thereby expecting it to be a more challenging scenario in terms of training effort. However, we maintain the training effort similar to the reference case and observe the quality of the obtained AA. In Figure 12, we observe that controllers remain effective in this setting. In particular, the LD controller mitigates $99.7$% of the violations observed in the uncontrolled case, i.e., only $0.024$ violation per time step occur on average. As expected, the required curtailment increases due to the higher generation and demand levels. The RBC achieves the best APC performance at the expense of the number of violations that is approximately four times higher than that of LD. In terms of fairness, the observed trends are consistent with the lower load case. Notably, the JFI metric is improved for the AA-based disaggregators. Specifically, the CPBD presents better fairness properties than RBC in this scenario. Overall, although we applied the same training effort to obtain the AA, the two-step solution retains its good performance even in higher load conditions.

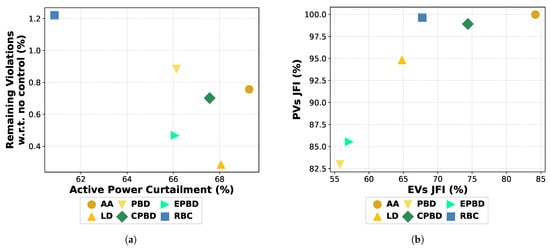
Figure 12. Evaluation of the controllers for a higher load scenario. (a) Performance metrics. (b) Fairness metrics.

In the next experiment, we train the AA and evaluate the proposed methods on a larger grid consisting of four feeders with 17 households each. For reference, training for six epochs lasts $3.5$ h in this case, while the corresponding training time for the dual-feeder grid was 2 h. As shown in Figure 13, the performance is similar to dual-feeder case. A notable improvement is observed for the RBC controller, which achieves the lowest APC percentage. However, RBC allows $0.17$ constraints violation per time step on average, which is significantly higher compared to corresponding violations observed for PBD, CPBD, and LD controllers. Regarding fairness, the observed trends are consistent with those in the dual-feeder grid scenario. Again, although we applied the same training effort to obtain the AA, the proposed approach maintains its performance for larger grids.

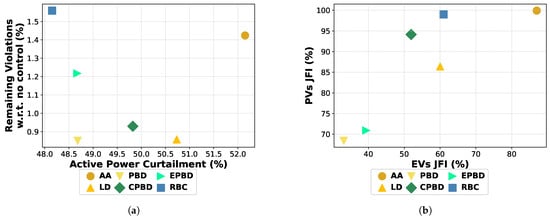
Figure 13. Evaluation of the controllers on a grid with 4 feeders. (a) Performance metrics. (b) Fairness metrics.

Finally, we assess the scalability of the controllers in terms of action inference time during deployment. Figure 14 presents the average calculation time per time step for varying number of households and feeders. In all cases, the controllers achieve inference times below 9 ms, demonstrating their applicability for real-time control applications. Note that the reported times correspond to a setup where the AA is executed centrally, followed by parallel disaggregation calculations per feeder, except for the RBC where the centralized BESS action inference runs in parallel with the RBC-based PV and EV curtailment computations. The highest computation time is observed for the LD disaggregator. However, this can be significantly reduced by implementing an alternative approach, in which each bus performs the disaggregation locally, considering its index within the feeder is known. This modification would yield computation times similar to those of the AA controller.

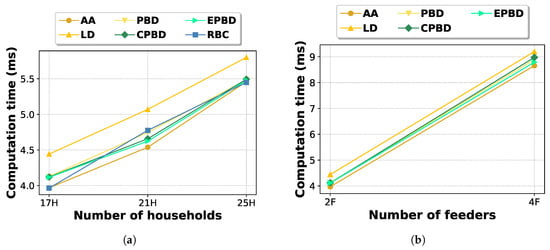
Figure 14. Inference time of controllers. (a) Varying number of buses per feeder. (b) Varying number of feeders.

5.7. Generalization Potential of AA with BESSs

In absence of BESSs, the AA can be effectively applied to similar but not identical networks [7]. By aggregating its state and action spaces per feeder, the AA can be applied to grids with varying numbers of buses, provided that the number of feeders remains the same as in the training setup, due to the fixed dimensions of its input and output vectors. In this section, we examine whether the AA can be applied in unseen grid topologies and loads with satisfactory performance even when BESSs are included. In particular, we applied the AA agent trained for the previous experiments to unseen dual-feeder radial grids with the same PV, EV, and BESS adoption rate but with a different number of households. Specifically, a grid with 13 households per feeder and a grid with 21 households per feeder are tested.

In the grid consisting of 13 households per feeder, AA mitigates $99.7\%$ of the violations, while curtailing only $41.65\%$ of the active power. Observing the more challenging case of the grid with 21 households per feeder, $96\%$ of the violations are avoided, while the APC percentage is about $52.1\%$. The trend is similar to the case without BESSs as demonstrated in Figure 15, leading to the conclusion that the integration of BESSs does not affect the generalization properties of the AA. Finally, these experiments highlight once more the effect of including BESSs in achieving a significant decrease in the APC percentage of around $15\%$, with the penalty of a small increase in the number of violations even under unseen grid topologies and loads.

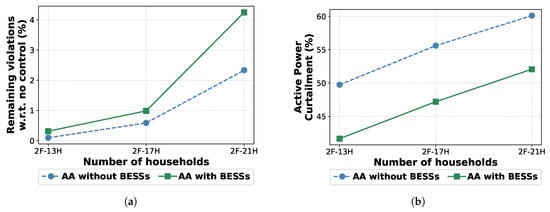
Figure 15. Evaluation of the AA with and without BESSs on multiple grids: (a) Remaining violations compared to no control case. (b) Active Power Curtailment percentage.

6. Conclusions

In this work, we studied the problem of APC in radial grids with PVs, EVs, and BESSs by proposing a fast solution approach that enhances fairness among buses in the determined curtailments. Fairness is not imposed as a hard constraint but encouraged via intelligently designing the disaggregators that determine the tailored per-bus curtailments based on the RL-based uniform per-feeder actions. BESSs control is also incorporated in the proposed fairness-encouraging APC strategy and further enhances the fairness–performance trade-off with respect to the considered metrics. In detail, BESSs help to significantly reduce the APC percentages and increase the minimum utilization metric for all controllers without impacting the controllers’ ordering with respect to JFI and MMR fairness metrics. The most outstanding advantage of BESSs is the significant increase in the minimum PV utilization, which is beneficial for increasing the adoption of PV systems in the grid. Lastly, we have shown via simulations that the AA can be applied with satisfactory performance in unseen grids even in the presence of BESSs and that integrating BESSs is beneficial for reducing APC levels even under unseen settings.

In our future work, we plan to investigate optimal BESSs placement to optimize APC performance and fairness. Moreover, properly tuning the initial and terminal BESSs SoC levels is a promising direction for further improving the fairness–performance trade-off. In addition, we plan to study the integration of Vehicle-to-Grid (V2G) in our generalizable two-step solution approach. V2G can function as a cost-efficient alternative to BESSs by avoiding installation costs while not limiting energy storage capabilities.