Simulation Modeling and Working Fluid Usage Reduction for Small-Scale Low-Temperature Organic Rankine Cycle (ORC) Plate Heat Exchangers
Abstract
1. Introduction
2. Modeling
3. Experimental Equipment
4. Results and Discussion
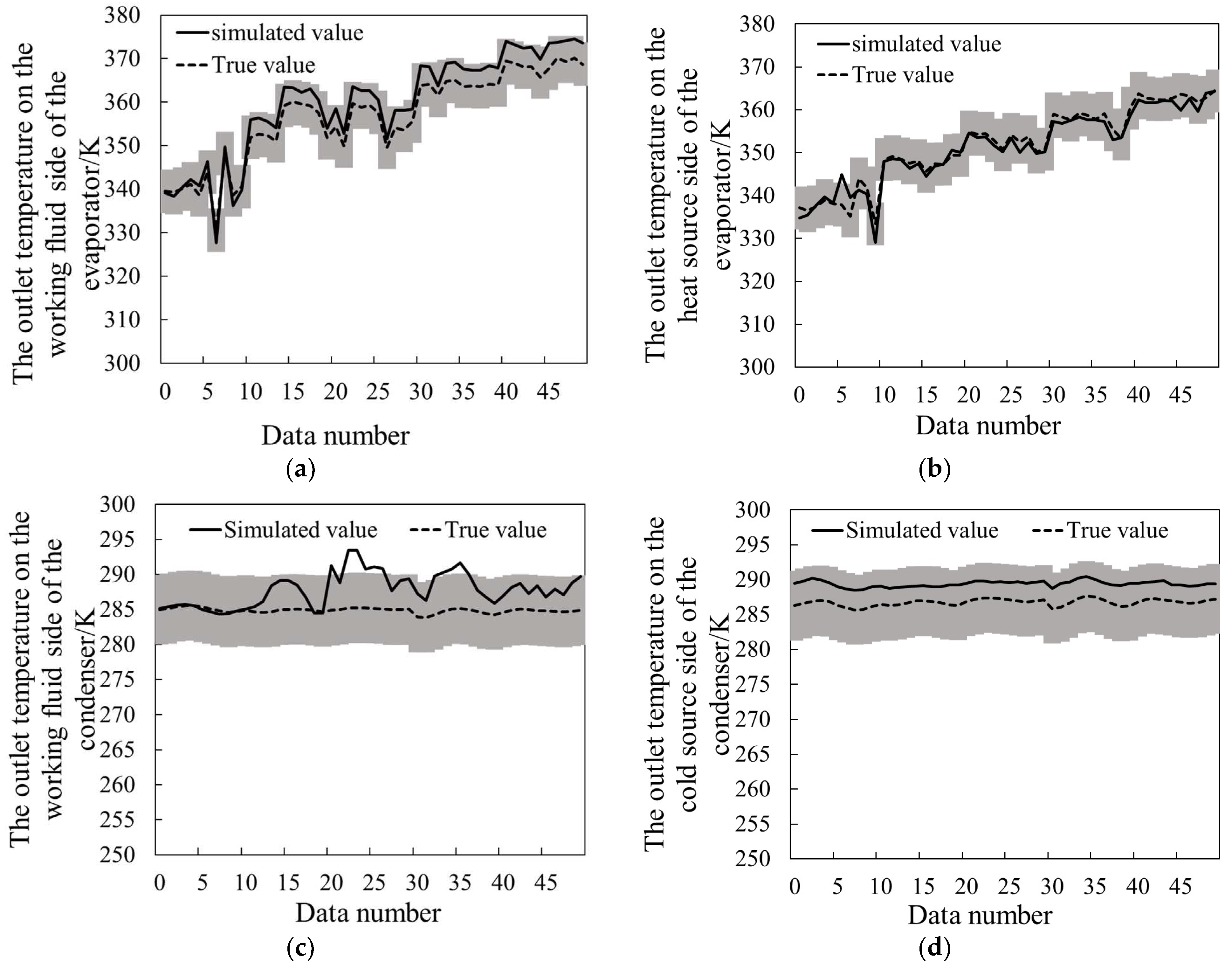
4.1. Model Validation
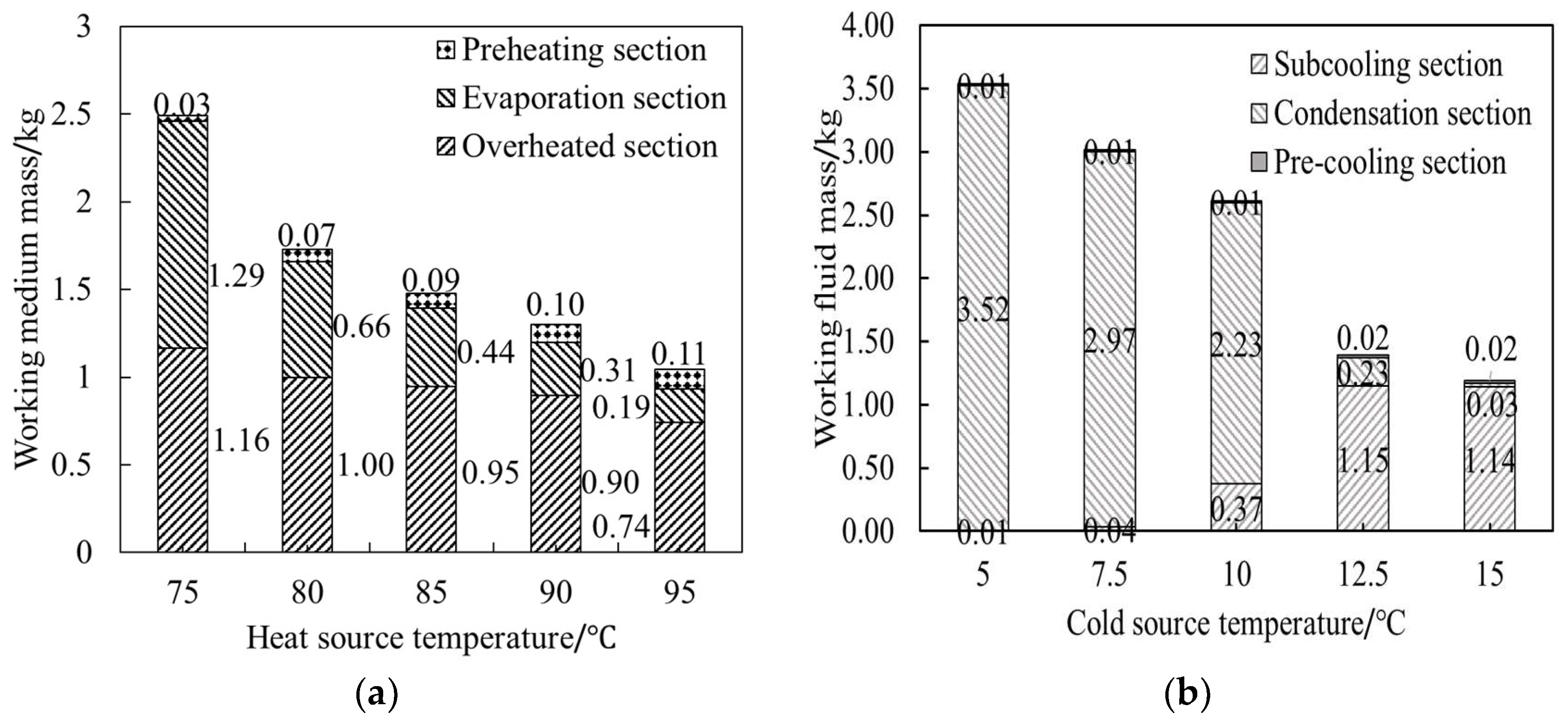
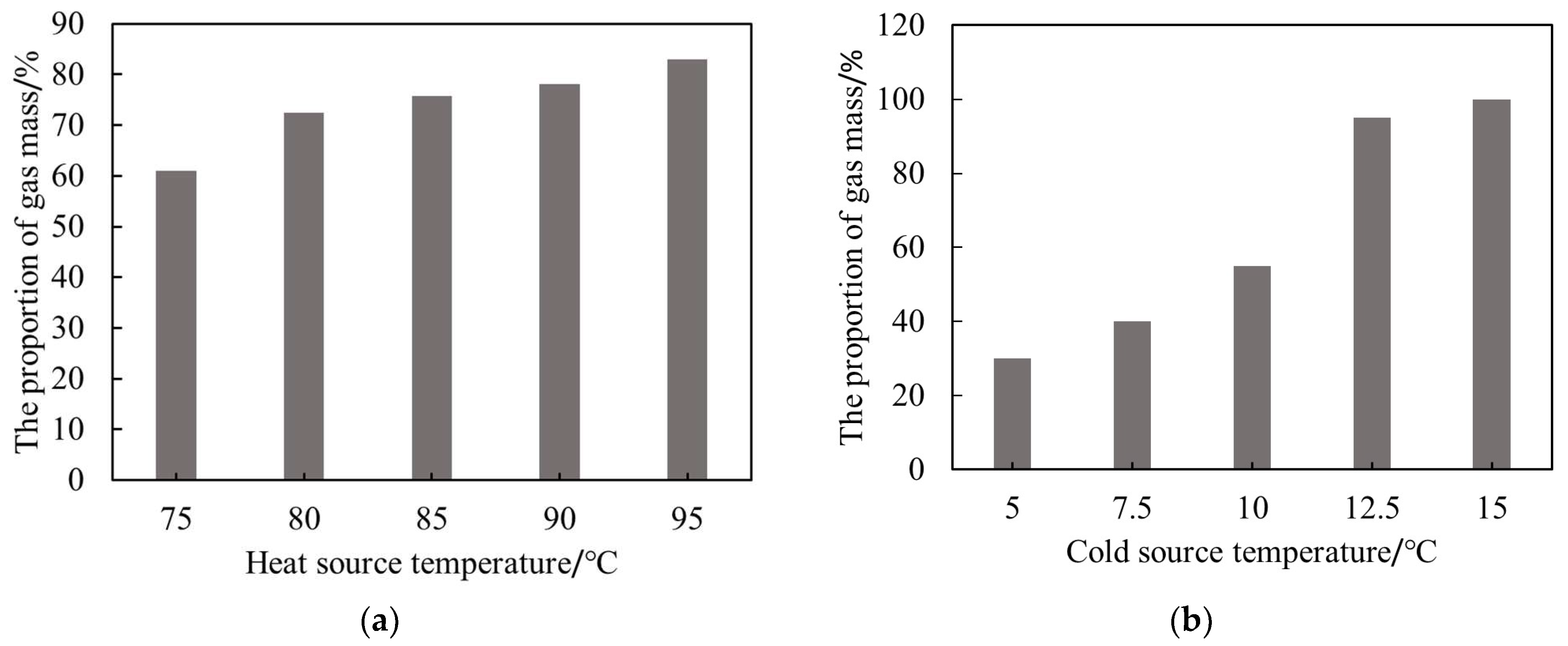
4.2. Simulation Analysis of Heat Transfer Characteristics and Working Fluid Mass
5. Plate Configuration and Flow Rate Effect Simulation
5.1. Plate Configuration Effects
5.2. Flow Rate Analysis
5.3. Economic Analysis
6. Conclusions
- A new mathematical model for the plate evaporator and condenser was developed, and its accuracy was validated by comparing the predicted data with experimental data. The limitations of this model were also discussed. The results showed that the temperature prediction error of the model was less than 5 K. However, the model ignored the pressure drop of the working fluid, and its simulation accuracy decreased under conditions with excessive liquid in the heat exchanger.
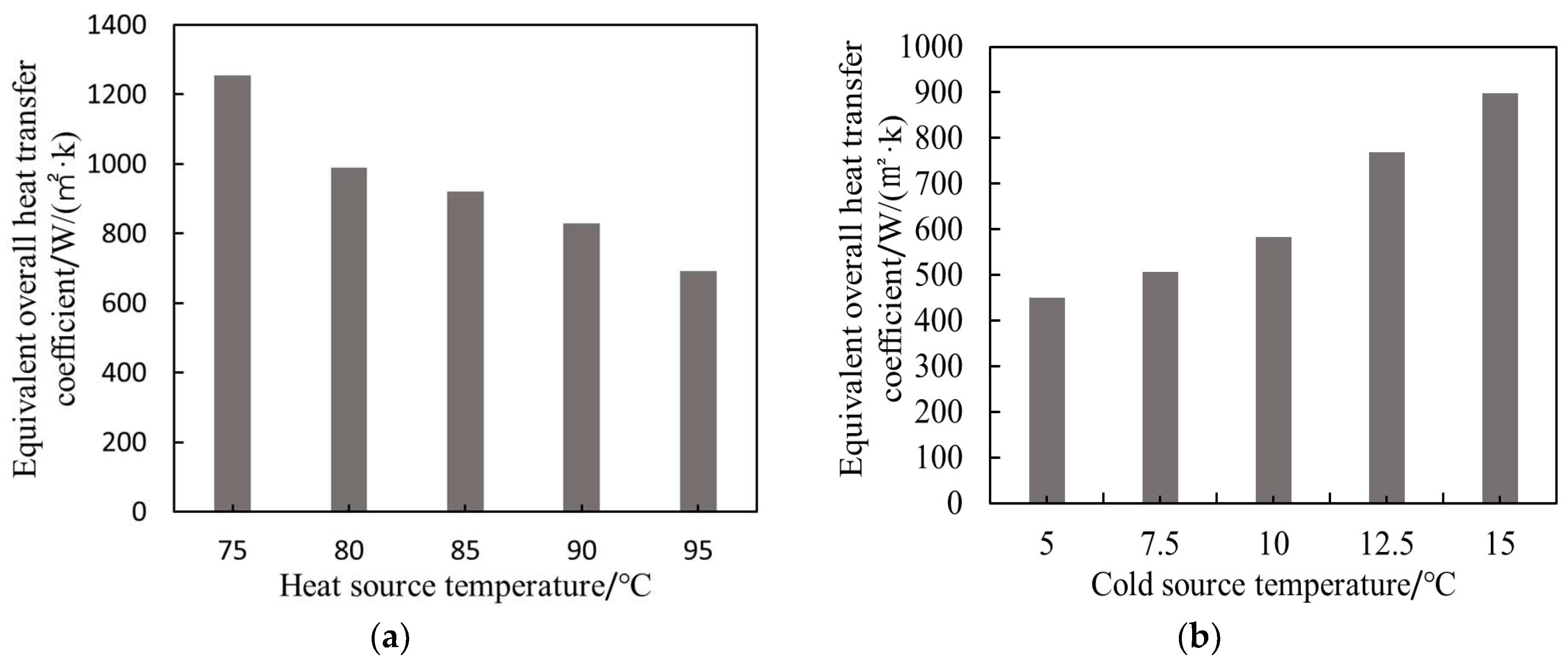
- The mass of the working fluid in the condenser and evaporator must be optimized in coordination with the hot and cold source temperatures. For example, when the cold source temperature increased from 5 °C to 15 °C, the working fluid mass in the condenser decreased by approximately 66.4%. When the heat source temperature increased from 75 °C to 90 °C, the working fluid mass in the evaporator decreased by approximately 58.0%.
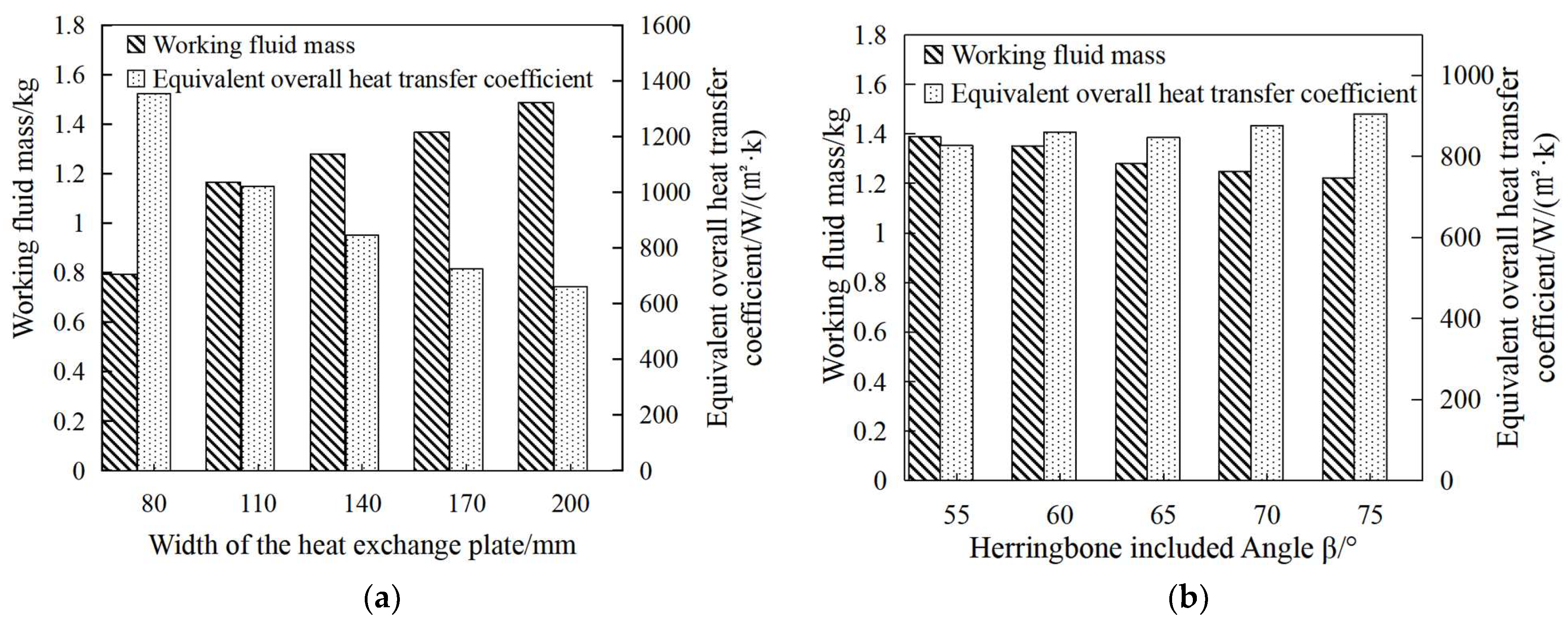
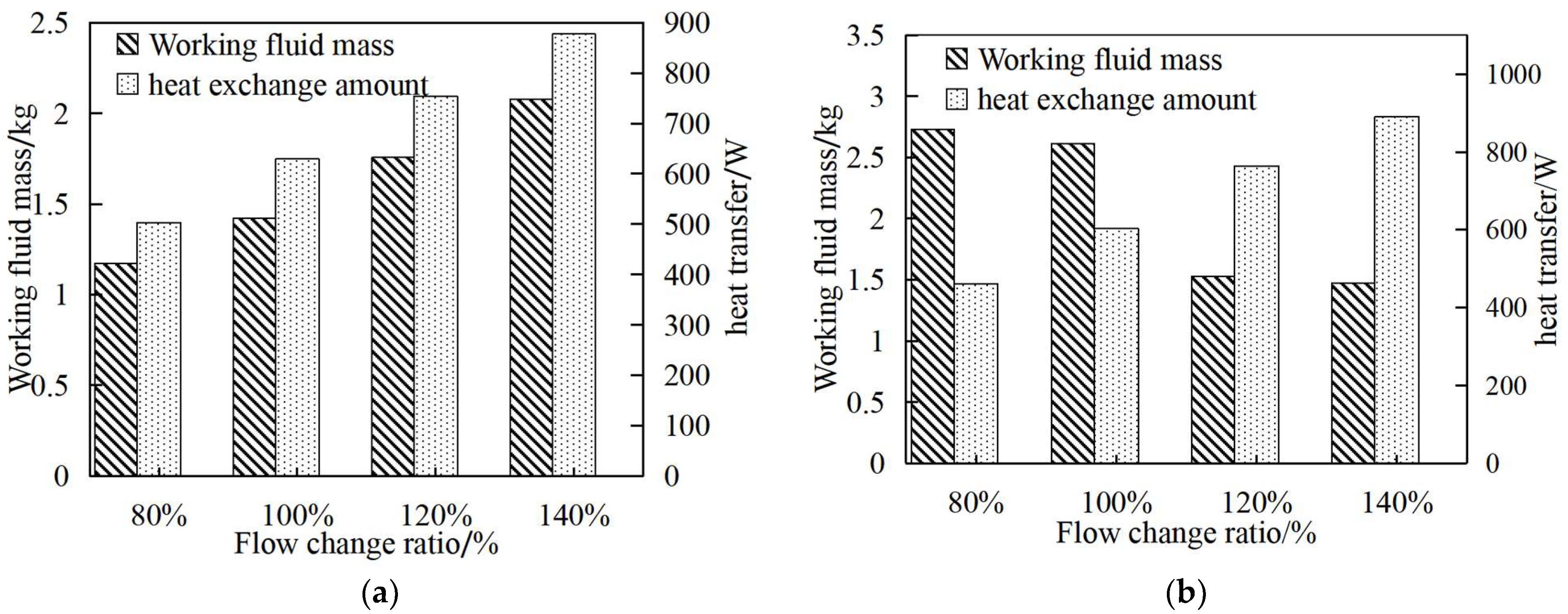
- The working fluid mass in the condenser and evaporator can be reduced by adjusting the plate width and flow rate, with suitable parameter combinations identified through sensitivity analysis, but β angle has a slight effect on the working fluid mass. For example, when the plate width was reduced from 140 mm to 80 mm, the mass of the working fluid in the evaporator and condenser decreased by 37.9% and 33.1%, respectively. When β increased from 55° to 75°, the working fluid mass in the evaporator and condenser decreased by 11.9% and 1.5%, respectively. The working fluid flow rate exhibited different influence trends on the working fluid mass in the evaporator and condenser. When the flow rate increased to 120% of the 80%, the mass of the total working fluid decreased from 3.9 kg to 3.3 kg.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation List
| Notation | Meaning | Subscripts | Meaning |
| A | Area, m2 | a | Actual value |
| b | Plate spacing, m | as | Assumed value |
| D | Density, kg m−3 | cal | Calculated value |
| dp | Plate thickness, m | con | Condenser |
| dh | Hydraulic diameter, m | eva | Evaporator |
| Pressure drop coefficient | eq | Equivalent | |
| G | Mass flux, kg·m−2·s | c | Cold side |
| H | Heat transfer coefficient, W·m−2·K−1 | h | Hot side |
| h | Enthalpy, kJ/kg | in | Inlet |
| K | Thermal conductivity, W·m−1·K−1 | max | Maximum value |
| L1, L2 | Chevron plate length; length between heat exchanger interfaces, mm | min | Minimum value |
| M | Mass, kg | r | Working fluid side |
| m | Volumetric flow rate, m3·h−1 | out | Outlet |
| N | Number of working fluid flow channels in the heat exchanger, – | st | Saturated state |
| P | Pressure, kPa | sup | Superheated |
| Q | Heat transfer amount, W | sub | Subcooled |
| R | Thermal resistance, m2·K·W−1 | wall | Wall surface |
| r | Area error, % | ||
| s | Number of iterations | ||
| T | Temperature, K | ||
| t | Step size of vapor mass fraction | ||
| U | Heat transfer coefficient, W·m−2·K−1 | ||
| V | Flow velocity, m·s−1 | ||
| W1, W2 | Chevron plate width; distance between heat exchanger inlet and outlet, mm | ||
| x | Vapor mass fraction/dryness, % | ||
| Δ | Difference/change | ||
| β | Chevron angle, ° | ||
| μ | Dynamic viscosity, Pa·s | ||
| φ | Amplification factor | ||
| ω | Relative error |
References
- IEA. CO2 Emissions in 2023; IEA: Paris, France, 2024; Available online: https://www.iea.org/reports/co2-emissions-in-2023 (accessed on 12 May 2025).
- Jiménez-García, J.C.; Ruiz, A.; Pacheco-Reyes, A.; Rivera, W. A Comprehensive Review of Organic Rankine Cycles. Processes 2023, 11, 1982. [Google Scholar] [CrossRef]
- Wang, X.; Cai, Y.; Yu, X.; Li, Q. Study on organic Rankine cycle system for low-temperature waste heat power generation. In Proceedings of the Third International Conference on Mechanical, Electronics, and Electrical and Automation Control (METMS 2023), Online, 17 February 2023; SPIE: Washington, DC, USA, 2023; Volume 12722, pp. 132–149. [Google Scholar]
- Xia, L.; Liu, R.; Zeng, Y.; Zhou, P.; Liu, J.; Cao, X.; Xiang, S. A review of low-temperature heat recovery technologies for industry processes. Chin. J. Chem. Eng. 2019, 27, 2227–2237. [Google Scholar] [CrossRef]
- Zhihong, W.; Xiaoming, D.; Ming’ou, W.U. Application of organic Rankine cycle in multi-grade waste heat power generation. Chem. Ind. Eng. Prog. 2019, 38, 2189–2196. [Google Scholar]
- Altun, A.; Kilic, M. Thermodynamic performance evaluation of a geothermal ORC power plant. Renew. Energy 2020, 148, 261–274. [Google Scholar] [CrossRef]
- Fiaschi, D.; Lifshitz, A.; Manfrida, G.; Tempesti, D. An innovative ORC power plant layout for heat and power generation from medium-to low-temperature geothermal resources. Energy Convers. Manag. 2014, 88, 883–893. [Google Scholar] [CrossRef]
- Mahlia, T.M.I.; Syaheed, H.; Abas, A.E.P.; Kusumo, F.; Shamsuddin, A.H.; Ong, H.C.; Bilad, M.R. Organic Rankine Cycle (ORC) System Applications for Solar Energy: Recent Technological Advances. Energies 2019, 12, 2930. [Google Scholar] [CrossRef]
- Ramos, A.; Chatzopoulou, M.A.; Freeman, J.; Markides, C.N. Optimisation of a high-efficiency solar-driven organic Rankine cycle for applications in the built environment. Appl. Energy 2018, 228, 755–765. [Google Scholar] [CrossRef]
- Świerzewski, M.; Kalina, J. Optimisation of biomass-fired cogeneration plants using ORC technology. Renew. Energy 2020, 159, 195–214. [Google Scholar] [CrossRef]
- Zhu, J.; Cao, X.; Chen, Z.; Zhu, Q. Progress in Low-grade Thermal Energy Organic Rankine Cycle Power Generation Technology. Low Temp. Supercond. 2021, 49, 73–80. [Google Scholar] [CrossRef]
- Hu, K. Research on the Heat Exchange Characteristics of the Evaporator and the Influence of Superheat on the Stability of the ORC System. Ph.D. Thesis, Tianjin University, Tianjin, China, 2017. [Google Scholar]
- Chen, Q.; Xu, J.; Chen, H. A new design method for Organic Rankine Cycles with constraint of inlet and outlet heat carrier fluid temperatures coupling with the heat source. Appl. Energy 2012, 98, 562–573. [Google Scholar] [CrossRef]
- Lecompte, S.; Huisseune, H.; van den Broek, M.; De Schampheleire, S.; De Paepe, M. Part load based thermo-economic optimization of the Organic Rankine Cycle (ORC) applied to a combined heat and power (CHP) system. Appl. Energy 2013, 111, 871–881. [Google Scholar] [CrossRef]
- Lee, Y.-R.; Kuo, C.-R.; Liu, C.-H.; Fu, B.-R.; Hsieh, J.-C.; Wang, C.-C. Dynamic Response of a 50 kW Organic Rankine Cycle System in Association with Evaporators. Energies 2014, 7, 2436–2448. [Google Scholar] [CrossRef]
- Zheng, X.; Luo, X.; Luo, J.; Chen, J.; Liang, Y.; Yang, Z.; Chen, Y.; Wang, H. Experimental investigation of operation behavior of plate heat exchangers and their influences on organic Rankine cycle performance. Energy Convers. Manag. 2020, 207, 112528. [Google Scholar] [CrossRef]
- Nematollahi, O.; Abadi, B.G.; Kim, Y.D.; Kim, K. Experimental study of the effect of brazed compact metal-foam evaporator in an organic Rankine cycle performance: Toward a compact ORC. Energy Convers. Manag. 2018, 173, 37–45. [Google Scholar] [CrossRef]
- Luo, X.; Yi, Z.; Zhang, B.; Mo, S.; Wang, C.; Song, M.; Chen, Y. Mathematical modelling and optimization of the liquid separation condenser used in organic Rankine cycle. Appl. Energy 2015, 185, 1309–1323. [Google Scholar] [CrossRef]
- Bull, J.; Buick, M.J.; Radulovic, J. Heat Exchanger Sizing for Organic Rankine Cycle. Energies 2020, 13, 3615. [Google Scholar] [CrossRef]
- Du, W.; Zhao, J.; Zhang, L.; Wang, Z.; Ji, W. Review and Prospect of Heat Exchanger Structure Development. J. Shandong Univ. (Eng. Sci. Ed.) 2021, 51, 76–83. [Google Scholar]
- Yang, J.; Ye, Z.; Yu, B.; Ouyang, H.; Chen, J. Simultaneous experimental comparison of low-GWP refrigerants as drop-in replacements to R245fa for Organic Rankine cycle application: R1234ze(Z), R1233zd(E), and R1336mzz(E). Energy 2019, 173, 721–731. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, L.; Wang, X. A comparative study of pure and zeotropic mixtures in low-temperature solar Rankine cycle. Appl. Energy 2010, 87, 3366–3373. [Google Scholar] [CrossRef]
- García-Cascales, J.; Vera-García, F.; Corberán-Salvador, J.; Gonzálvez-Maciá, J. Assessment of boiling and condensation heat transfer correlations in the modelling of plate heat exchangers. Int. J. Refrig. 2007, 30, 1029–1041. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, C.; Wang, S.; Xu, X.; Li, Q. Thermo-economic comparison of subcritical organic Rankine cycle based on different heat exchanger configurations. Energy 2017, 123, 728–741. [Google Scholar] [CrossRef]
- Zhang, C. Comprehensive Performance Evaluation and Experimental Study of Low-Grade Waste Heat Organic Rankine Cycle. Ph.D. Thesis, Chongqing University, Chongqing, China, 2018. [Google Scholar]
- Amalfi, L.R.; Vakili-farahani, F.; Thome, R.J. Flow boiling and frictional pressure gradients in plate heat exchangers. Part 1: Review and experimental database. Int. J. Refrig. 2016, 61, 166–184.3. [Google Scholar] [CrossRef]
- Jafari, A.; Sadeghianjahromi, A.; Wang, C.C. Experimental and numerical investigation of brazed plate heat exchangers—A new approach. Appl. Therm. Eng. 2022, 200, 117694. [Google Scholar] [CrossRef]
- Kim, B.M.; Park, Y.C. An experimental study on single phase convection heat transfer and pressure drop in two brazed plate heat exchangers with different chevron shapes and hydraulic diameters. J. Mech. Sci. Technol. 2017, 31, 2559–2571. [Google Scholar] [CrossRef]
- Sha, H.; Yu, H.; Ma, Q.; Yang, Y.; Feng, Y.; Luo, S. Investigation of lifelong learning methods with elastic weight consolidation (EWC) for low-temperature ORC scroll expander modeling. Appl. Therm. Eng. 2025, 278, 127359. [Google Scholar] [CrossRef]
- Peris, B.; Navarro-Esbrí, J.; Molés, F.; Mota-Babiloni, A. Experimental study of an ORC (organic Rankine cycle) for low grade waste heat recovery in a ceramic industry. Energy 2015, 85, 534–542. [Google Scholar] [CrossRef]
- Bianchi, M.; Branchini, L.; De Pascale, A.; Orlandini, V.; Ottaviano, S.; Peretto, A.E.; Melino, F.; Pinelli, M.; Spina, P.R.; Suman, A. Experimental investigation with steady-state detection in a micro-ORC test bench. Energy Procedia 2017, 126, 469–476. [Google Scholar] [CrossRef]
- Luo, J.; Lu, P.; Chen, K.; Luo, X.; Chen, J.; Liang, Y.; Yang, Z.; Chen, Y. Experimental and simulation investigation on the heat exchangers in an ORC under various heat source/sink conditions. Energy 2023, 264, 126189. [Google Scholar] [CrossRef]
- Shanghai Haomai Energy Co. R245fa Refrigerant. Available online: https://detail.1688.com/offer/899707422332.html (accessed on 1 October 2025).
- Made-in-China.com. R245fa Refrigerant. Available online: https://zjjushen.en.made-in-china.com/product/ynZpKucOwCVW/China-99-9-High-Purity-Refrigerant-Gas-R245fa-with-Comprtitive-Prices.html (accessed on 1 October 2025).


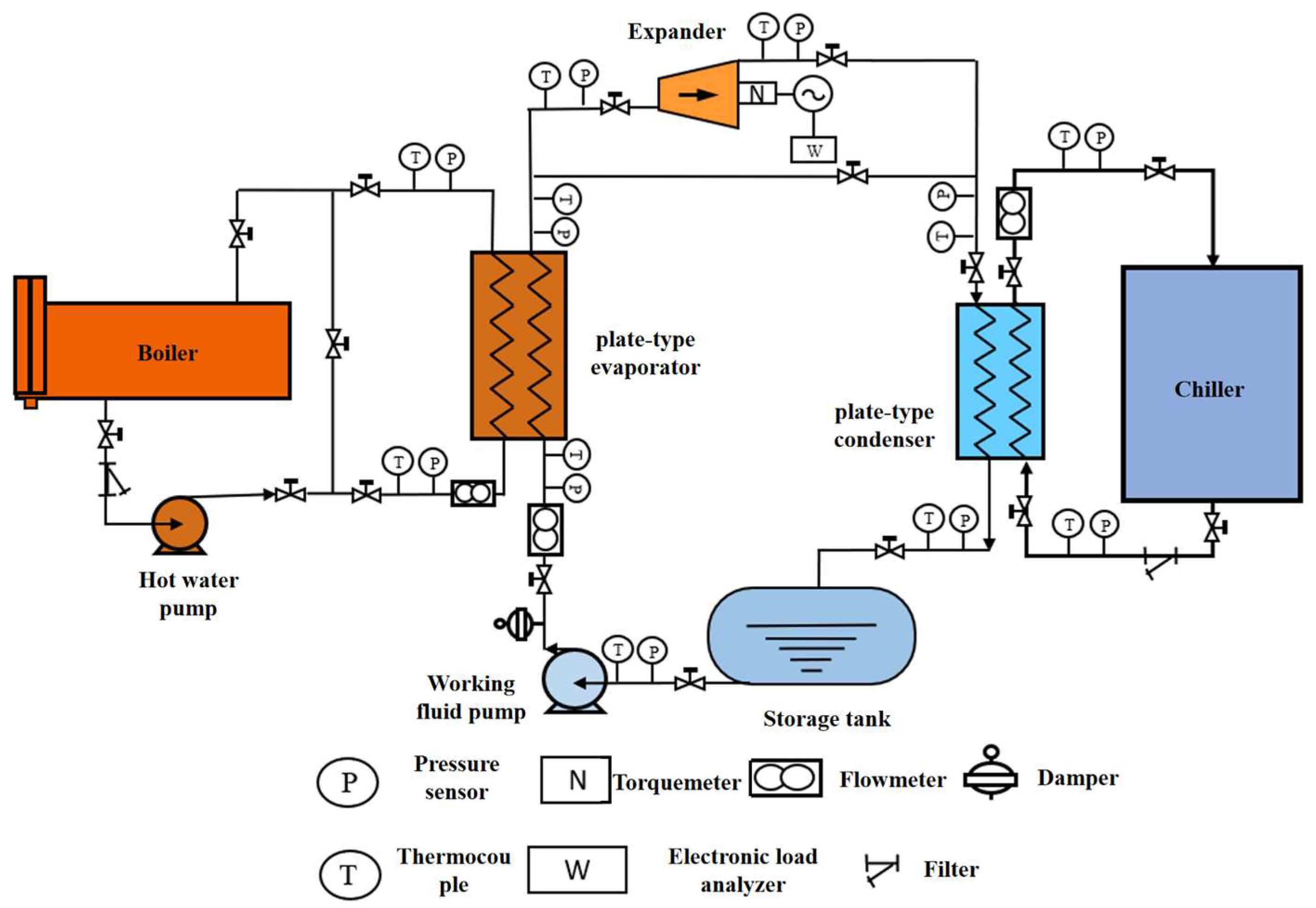

| Parameter | Symbol | Value |
|---|---|---|
| Plate length (mm) | L1 | 476 |
| Length between the centers of two ports (mm) | L2 | 410 |
| Plate width (mm) | W1 | 140 |
| Distance between the centers of two ports (mm) | W2 | 74 |
| Hydraulic diameter (mm) | dh | 5 |
| Plate thickness (mm) | dp | 0.4 |
| Plate spacing (mm) | b | 2.55 |
| Chevron angle (°) | β | 65 |
| Enlargement factor (–) | 1.2 | |
| Thermal conductivity of plate wall (W m−1 K−1) | Kwall | 16.3 |
| Source | Heat Transfer Correlation |
|---|---|
| Liquid-phase region of evaporator and condenser [22,23] | Nu = |
| Vapor-phase region of evaporator and condenser [24,25] | Nu = |
| Two-phase region of the working fluid in the evaporator [26] | Re = G [(1-x) + x·()0.5]·D·V Nu = 2.7· |
| Two-phase region of the working fluid in condenser [27] | Nu = 0.145·· |
| Hot water heat transfer correlation [24] | Re = V·D· Nu = |
| Cold water heat transfer correlation [27,28] | Nu = 0.145·· |
| Equipment | Measurement Range and Error |
|---|---|
| Temperature Sensor | 0–1370 °C, ±0.5% of rdg. + 1.0 °C |
| Pressure Sensor | 0–4 Mpa, ±0.25% |
| Working Fluid Flow Meter | >0.05 m3/h, ±2% |
| Cold and Hot Source Flow Meter | 1.5–15 m3/h, accuracy class 1.0 (±0.135) |
| Heat Exchanger | Parameter | Value |
|---|---|---|
| Evaporator | Heat source temperature (°C) | 75, 80, 85, 90, 95 |
| Working fluid inlet temperature (°C) | 12 °C | |
| Heat source flow rate (m3/h) | 2.2 | |
| Working fluid flow rate (m3/h) | 0.22 | |
| Total number of flow channels | 65 | |
| Condenser | Cold source temperature (°C) | 5, 7.5, 10, 12.5, 15 |
| Working fluid inlet temperature (°C) | 55 | |
| Cold source flow rate (m3/h) | 3.38 | |
| Working fluid flow rate (m3/h) | 0.22 | |
| Total number of flow channels | 65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Q.; Lv, Y.; Sha, H.; Yu, H.; Luo, S. Simulation Modeling and Working Fluid Usage Reduction for Small-Scale Low-Temperature Organic Rankine Cycle (ORC) Plate Heat Exchangers. Energies 2025, 18, 5549. https://doi.org/10.3390/en18205549
Ma Q, Lv Y, Sha H, Yu H, Luo S. Simulation Modeling and Working Fluid Usage Reduction for Small-Scale Low-Temperature Organic Rankine Cycle (ORC) Plate Heat Exchangers. Energies. 2025; 18(20):5549. https://doi.org/10.3390/en18205549
Chicago/Turabian StyleMa, Qingxu, Yupei Lv, Haohan Sha, Haiming Yu, and Siyi Luo. 2025. "Simulation Modeling and Working Fluid Usage Reduction for Small-Scale Low-Temperature Organic Rankine Cycle (ORC) Plate Heat Exchangers" Energies 18, no. 20: 5549. https://doi.org/10.3390/en18205549
APA StyleMa, Q., Lv, Y., Sha, H., Yu, H., & Luo, S. (2025). Simulation Modeling and Working Fluid Usage Reduction for Small-Scale Low-Temperature Organic Rankine Cycle (ORC) Plate Heat Exchangers. Energies, 18(20), 5549. https://doi.org/10.3390/en18205549





