Research on Energy-Saving Optimization of Mushroom Growing Control Room Based on Neural Network Model Predictive Control
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection and Processing
2.2. Principal Component Analysis (PCA) and Information Entropy Method
- (1)
- Let the temperature data matrix collected by the sensor be represented as shown in Equation (2).where is the length of the time series, is the number of sensors, and is the temperature value of the th sensor at time .
- (2)
- Obtain matrix through standardized processing, calculate its covariance matrix as shown in Equation (3), and perform eigenvalue decomposition using Equation (4).where denotes the th eigenvalue, denotes the corresponding eigenvector.
- (3)
- Calculate the loadings of the sensor on each principal component as shown in Equation (5), then compute the variance contribution rate of the selected sensor using Equation (7).where represents the load of the th sensor on the th principal component, denotes the component of the th eigenvector in the th sensor dimension, indicates the absolute variance contribution of the th sensor, signifies the number of selected principal components, and represents the selected sensors.
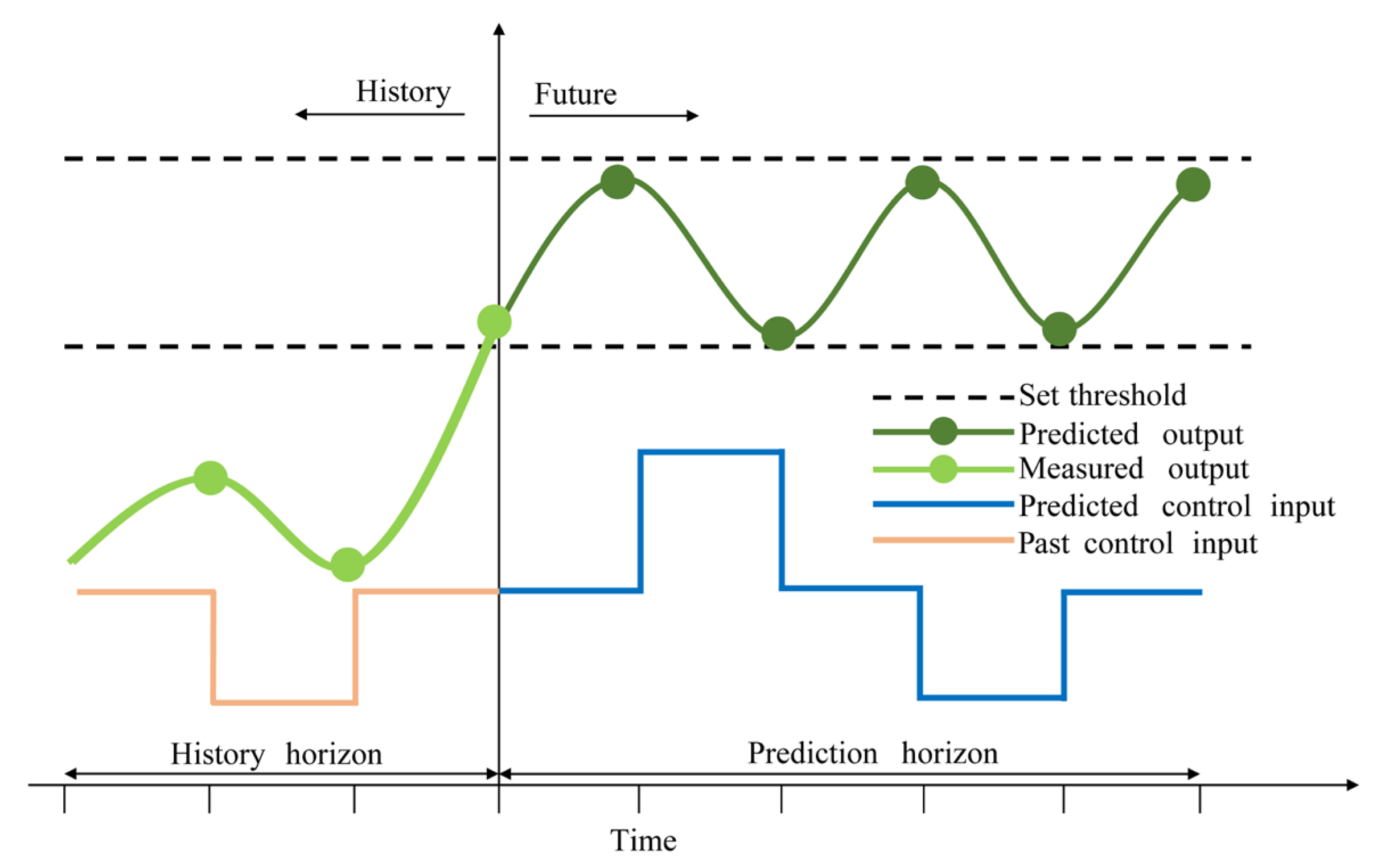
2.3. Principles of Model Predictive Control (MPC)
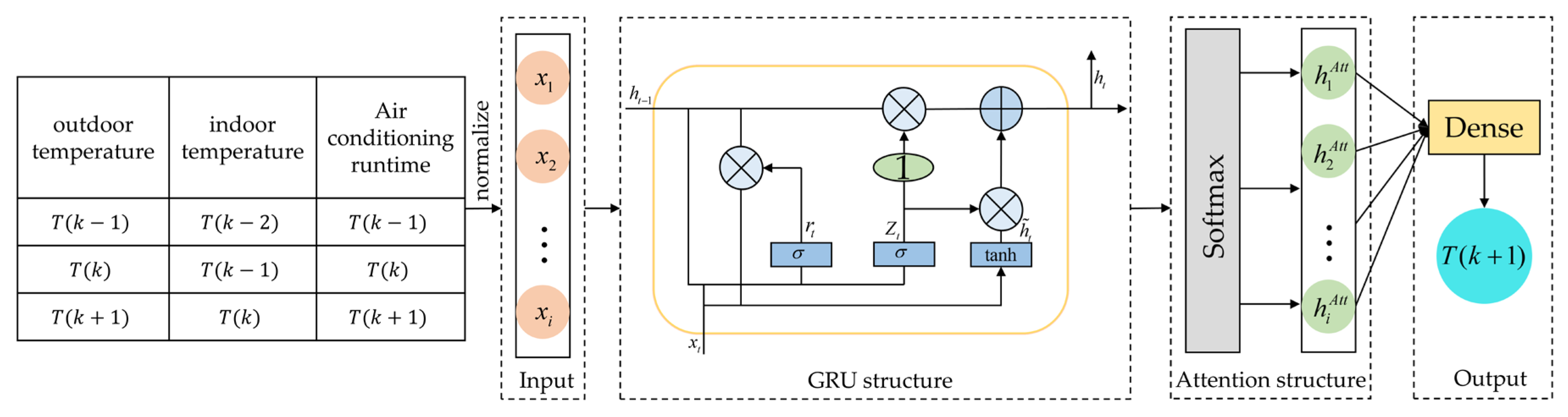
2.4. Predictive Model
- (1)
- Outdoor temperature, indoor temperature, and air conditioning runtime were normalized as input data and fed into the prediction model.
- (2)
- The normalized data were passed into the GRU, where a preliminary temperature prediction was generated.
- (3)
- The weights of the data features obtained from the GRU module were recalculated and reassigned through the Attention mechanism, thereby enhancing the focus on important information.
- (4)
- The processed data were fed into the fully connected layer to output the prediction results. After the prediction was completed, the data were inverse normalized, and the predicted values were compared with the actual values.
| Algorithm 1: Pseudocode for hyperparameter optimization of GRU-Attention model using Optuna |
| Input: Training data x, Labels y, Number of trials T, Search space of the hyperparameter set H for the GRU-Attention model Output: Optimal hyperparameter combination H* for the GRU-Attention model after optimization
|
2.5. Rolling Optimization
- (1)
- Initialization stage
- (2)
- Define temperature and food intake
- (3)
- Summer resort stage
- (4)
- Competition stage
- (5)
- Foraging stage
2.6. Feedback Correction
2.7. Assessment Indicators
3. Results
3.1. Sensor Number Selection and Results Analysis
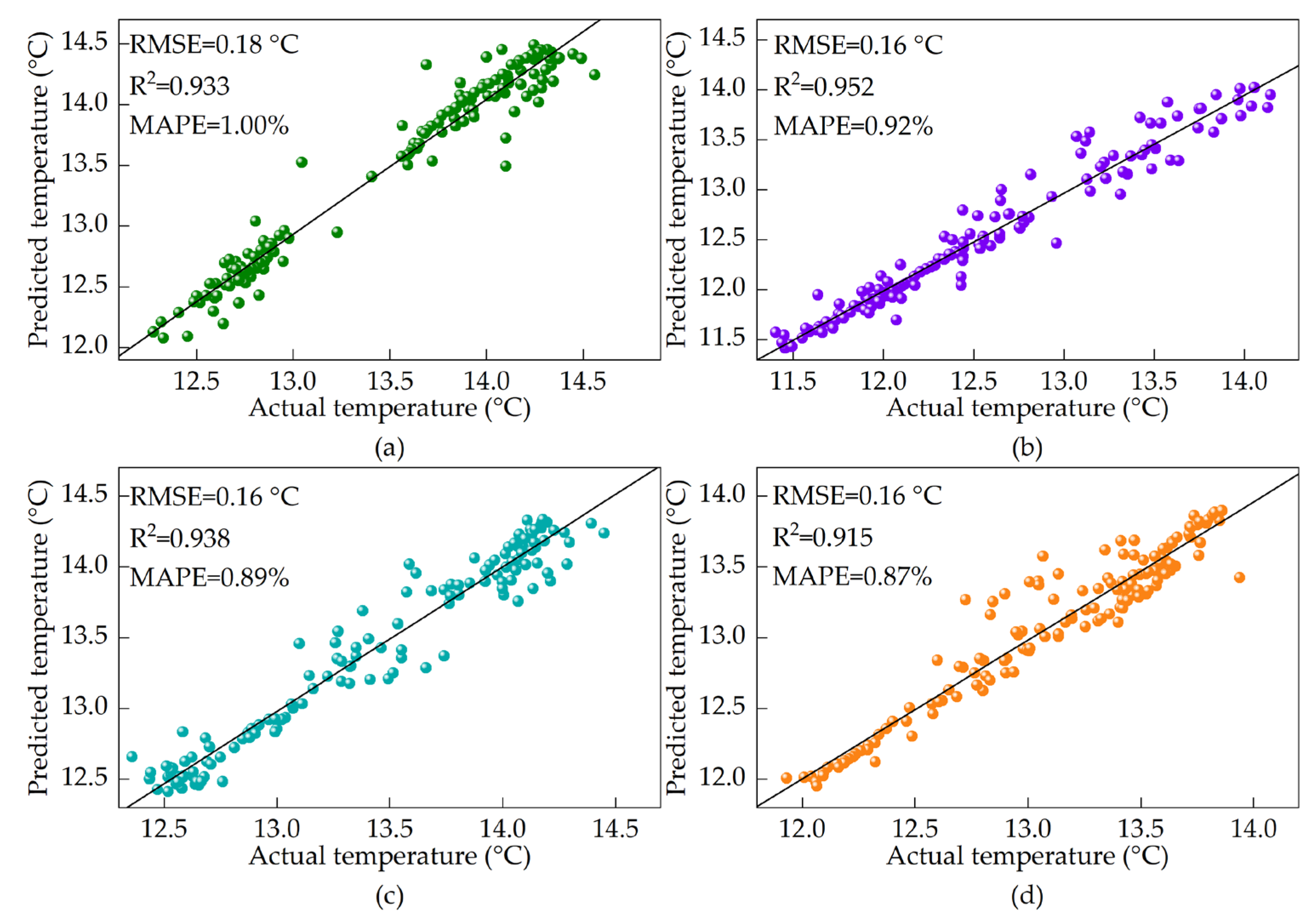
3.2. Predictive Model Analysis
3.3. Optimization Algorithm Analysis
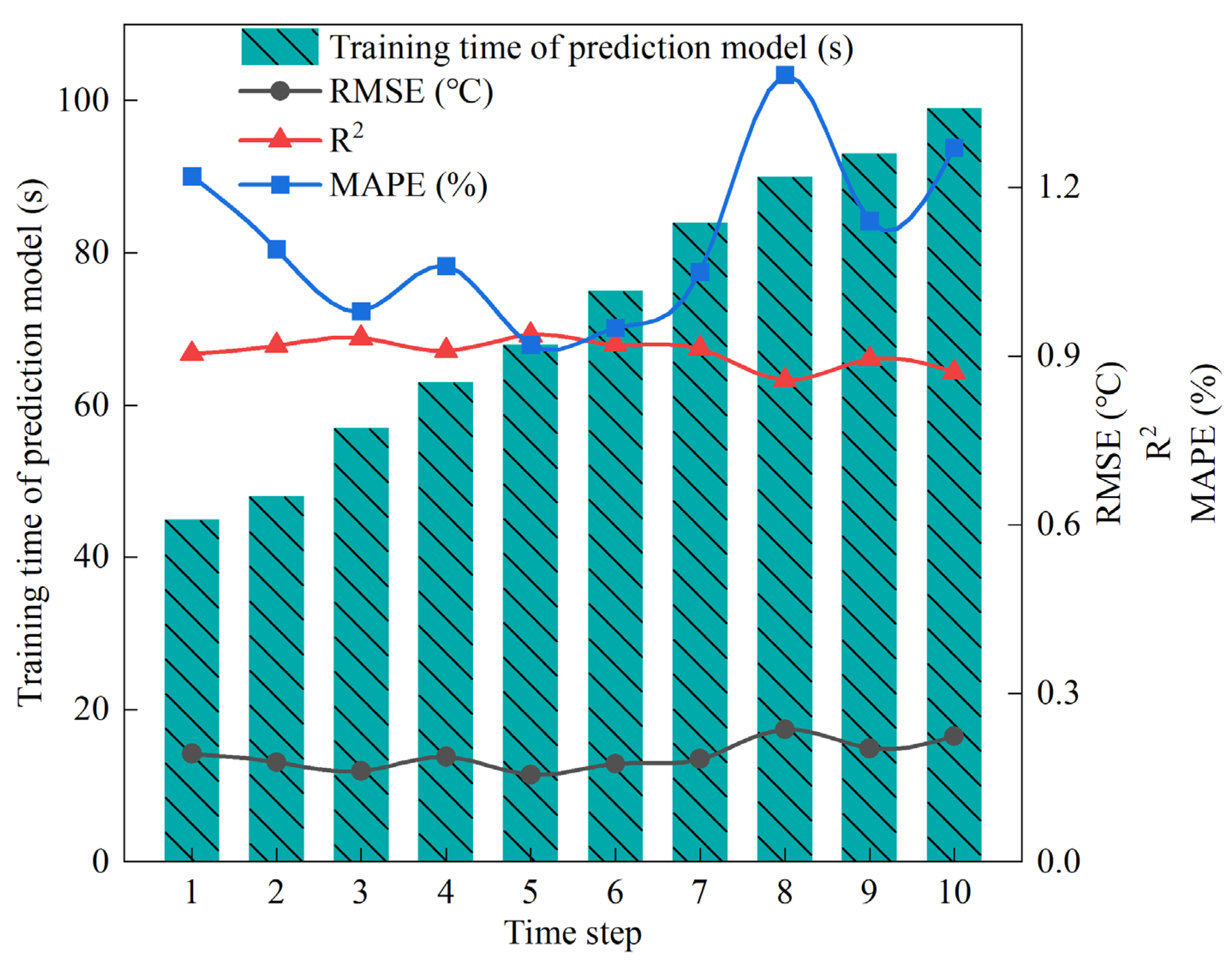
3.4. Predictive Time Step Analysis
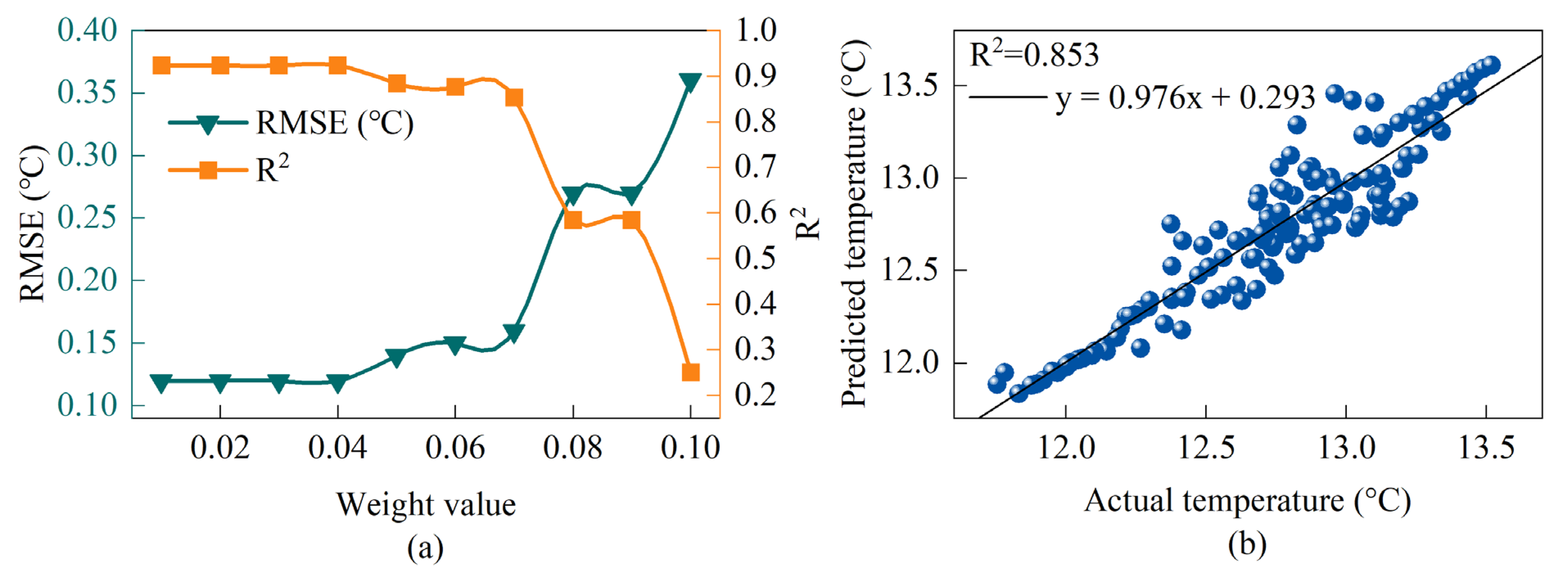
3.5. Objective Function Weight Analysis
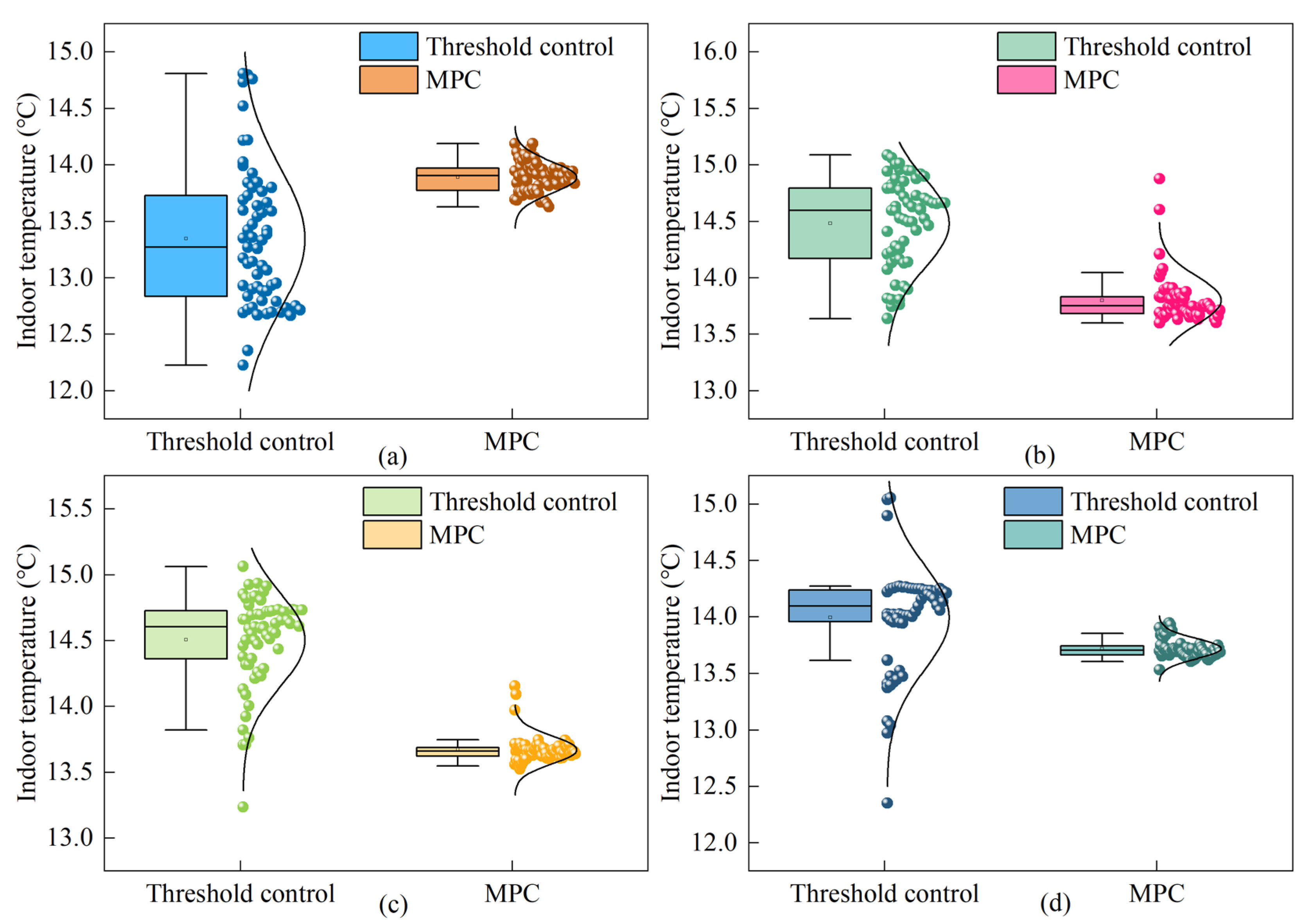
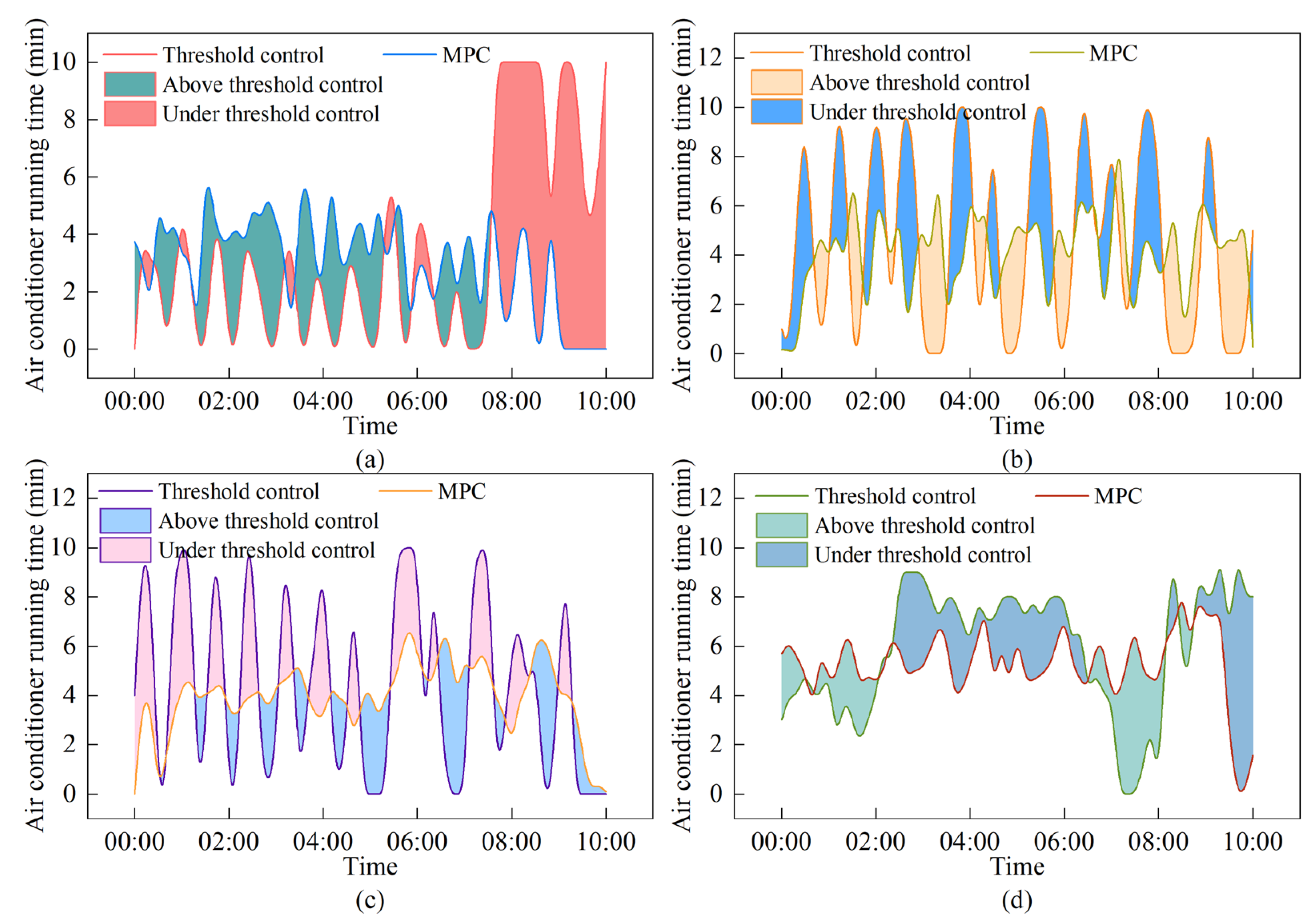
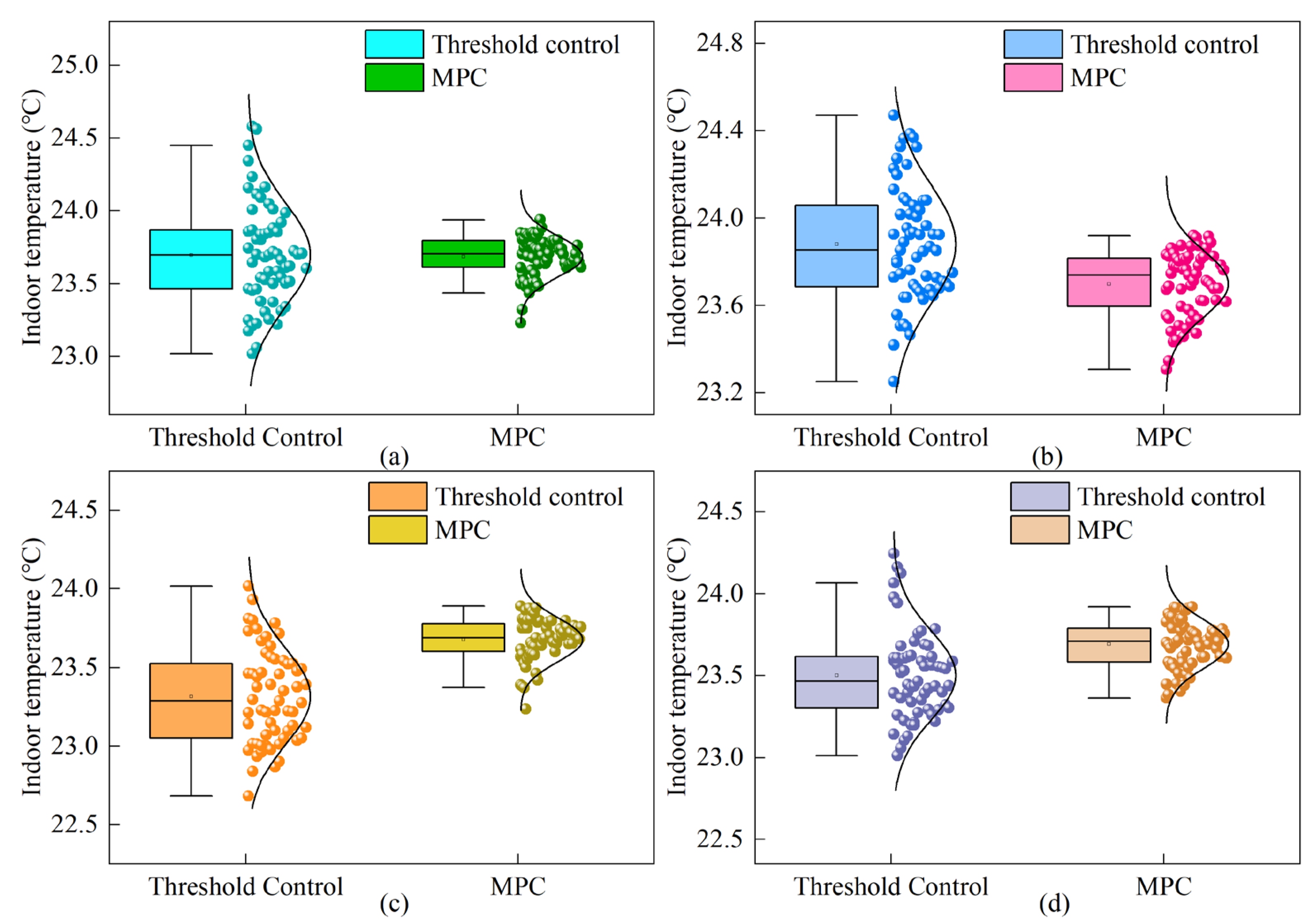
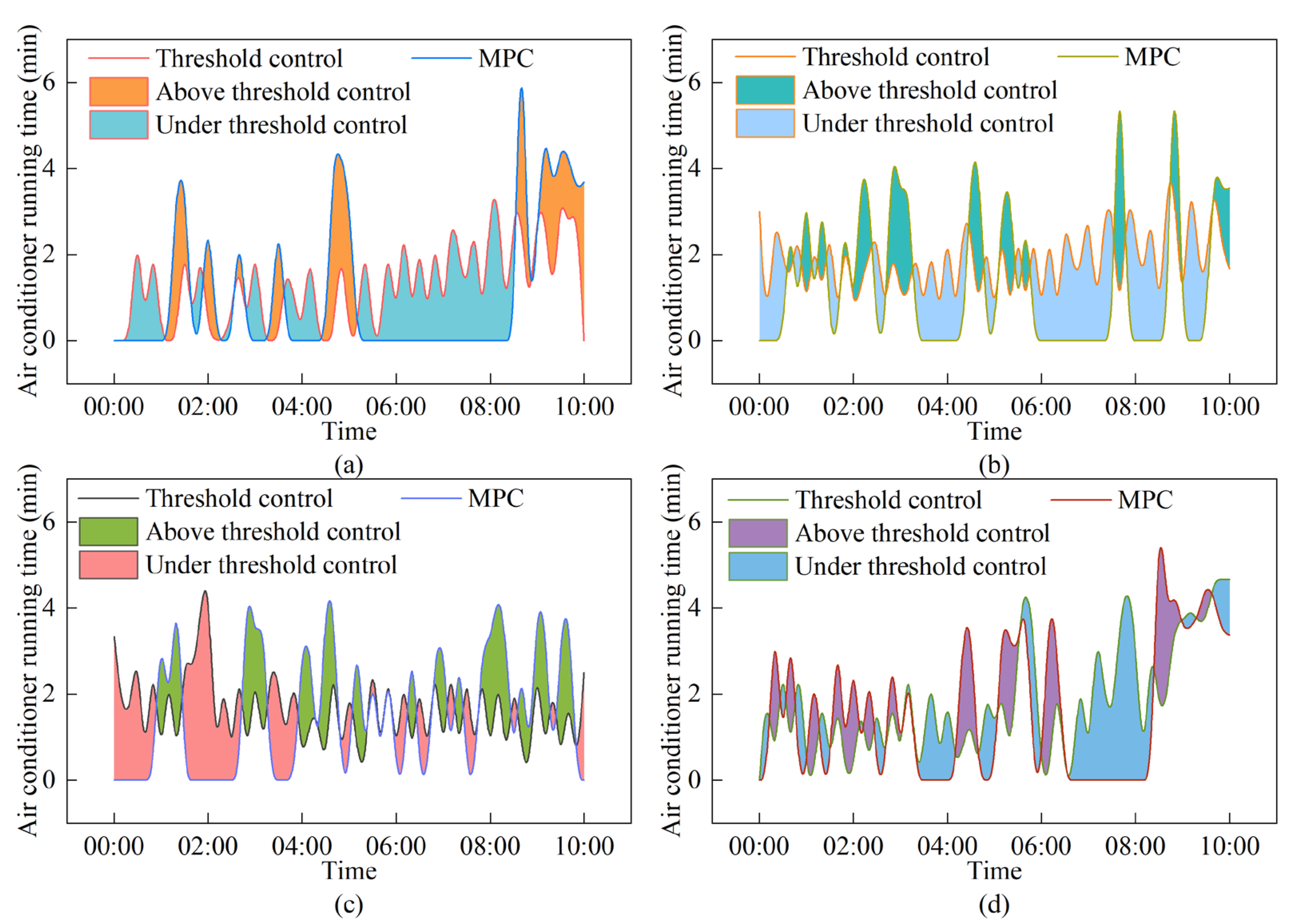
3.6. Assessment of MPC Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sganzerla, W.G.; Todorov, S.D.; da Silva, A.P. Research Trends in the Study of Edible Mushrooms: Nutritional Properties and Health Benefits. Int. J. Med. Mushrooms 2022, 24, 1–18. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, D.; Chen, Y.; Liu, T.; Zhang, S.; Fan, H.; Liu, H.; Li, Y. Healthy Function and High Valued Utilization of Edible Fungi. Food Sci. Hum. Wellness 2021, 10, 408–420. [Google Scholar] [CrossRef]
- Liu, J.; Sun, J.; He, R.; Xia, J.; He, P. The situation of counterfeited and mislabeled commercialized edible mushrooms in China and the development of possible controls. Foods 2024, 13, 3097. [Google Scholar] [CrossRef]
- Ali, B.M.; Akkaş, M. The green cooling factor: Eco-innovative heating, ventilation, and air conditioning solutions in building design. Appl. Sci. 2023, 14, 195. [Google Scholar] [CrossRef]
- Adesanya, M.A.; Obasekore, H.; Rabiu, A.; Na, M.H.; Ogunlowo, Q.O.; Akpenpuun, T.D.; Kim, M.H.; Kim, H.T.; Kang, B.Y.; Lee, H.W. Deep reinforcement learning for PID parameter tuning in greenhouse HVAC system energy Optimization: A TRNSYS-Python cosimulation approach. Expert Syst. Appl. 2024, 252, 124126. [Google Scholar] [CrossRef]
- Killian, M.; Kozek, M. Ten questions concerning model predictive control for energy efficient buildings. Build. Environ. 2016, 105, 403–412. [Google Scholar] [CrossRef]
- Zhuang, J.; Chen, Y.; Chen, X. A new simplified modeling method for model predictive control in a medium-sized commercial building: A case study. Build. Environ. 2018, 127, 1–12. [Google Scholar] [CrossRef]
- Salem, F.M.; Mosaad, M.I.; Awadallah, M.A. A comparative study of MPC and optimised PID control. Int. J. Ind. Electron. Drives 2015, 2, 242–250. [Google Scholar] [CrossRef]
- Wang, M.; Zheng, W.; Zhao, C.; Zhang, X.; Kong, X.; Shan, F.; Zhao, Q. Energy-saving control method for factory mushroom room air conditioning based on MPC. Energies 2023, 16, 7623. [Google Scholar] [CrossRef]
- Wang, D.; Chen, Y.; Wang, W.; Gao, C.; Wang, Z. Field test of Model Predictive Control in residential buildings for utility cost savings. Energy Build. 2023, 288, 113026. [Google Scholar] [CrossRef]
- Jeon, B.K.; Kim, E.J. LSTM-Based Model Predictive Control for Optimal Temperature Set-Point Planning. Sustainability 2021, 13, 894. [Google Scholar] [CrossRef]
- Yao, Y.; Shekhar, D.K. State of the art review on model predictive control (MPC) in Heating Ventilation and Air-conditioning (HVAC) field. Build. Environ. 2021, 200, 107952. [Google Scholar] [CrossRef]
- Wang, H.; Bo, S.; Zhu, C.; Hua, P.; Xie, Z.; Xu, C.; Wang, T.; Li, X.; Wang, H.; Lahdelma, R. A zoned group control of indoor temperature based on MPC for a space heating building. Energy Convers. Manag. 2023, 290, 117196. [Google Scholar] [CrossRef]
- Drgoňa, J.; Arroyo, J.; Figueroa, I.C.; Blum, D.; Helsen, L. All you need to know about model predictive control for buildings. Annu. Rev. Control 2020, 50, 190–232. [Google Scholar] [CrossRef]
- Afroz, Z.; Shafiullah, G.; Urmee, T.; Higgins, G. Modeling techniques used in building HVAC control systems: A review. Renew. Sustain. Energy Rev. 2018, 83, 64–84. [Google Scholar] [CrossRef]
- Kumar, P.; Rawlings, J.B.; Wenzel, M.J.; Risbeck, M.J. Grey-box model and neural network disturbance predictor identification for economic MPC in building energy systems. Energy Build. 2023, 286, 112936. [Google Scholar] [CrossRef]
- Tol, H.İ.; Madessa, H.B. Development of a white-box dynamic building thermal model integrated with a heating system. J. Build. Eng. 2023, 68, 106038. [Google Scholar] [CrossRef]
- Hu, Y.; Qin, L.; Li, S.; Li, X.; Zhou, R.; Li, Y.; Sheng, W. Adaptive corrected parameters algorithm applied in cooling load prediction based on black-box model: A case study for subway station. Energy Build. 2023, 297, 113429. [Google Scholar] [CrossRef]
- Zhang, L.; Jin, G.; Liu, T.; Zhang, R. Generalized hierarchical expected improvement method based on black-box functions of adaptive search strategy. Appl. Math. Model. 2022, 106, 30–44. [Google Scholar] [CrossRef]
- Wang, M.; Kong, X.; Shan, F.; Zheng, W.; Ren, P.; Wang, J.; Chen, C.; Zhang, X.; Zhao, C. Temperature Prediction of Mushrooms Based on a Data—Physics Hybrid Approach. Agriculture 2024, 14, 145. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Review of modeling methods for HVAC systems. Appl. Therm. Eng. 2014, 67, 507–519. [Google Scholar] [CrossRef]
- Mtibaa, F.; Nguyen, K.K.; Azam, M.; Papachristou, A.; Venne, J.S.; Cheriet, M. LSTM-based indoor air temperature prediction framework for HVAC systems in smart buildings. Neural Comput. Appl. 2020, 32, 17569–17585. [Google Scholar] [CrossRef]
- Mtibaa, F.; Nguyen, K.K.; Dermardiros, V.; Cheriet, M. Context-aware model predictive control framework for multi-zone buildings. J. Build. Eng. 2021, 42, 102340. [Google Scholar] [CrossRef]
- Zhang, J.; Poon, K.H.; Kwok, H.H.; Hou, F.; Cheng, J.C. Predictive control of HVAC by multiple output GRU-CFD integration approach to manage multiple IAQ for commercial heritage building preservation. Build. Environ. 2023, 245, 110802. [Google Scholar] [CrossRef]
- Fujimori, K.; Goto, Y.; Liu, Y.; Taniguchi, M. Sparse principal component analysis for high-dimensional stationary time series. Scand. J. Stat. 2023, 50, 1953–1983. [Google Scholar] [CrossRef]
- Merrikh-Bayat, F. The runner-root algorithm: A metaheuristic for solving unimodal and multimodal optimization problems inspired by runners and roots of plants in nature. Appl. Soft Comput. 2015, 33, 292–303. [Google Scholar] [CrossRef]
- Jia, H.; Rao, H.; Wen, C.; Mirjalili, S. Crayfish optimization algorithm. Artif. Intell. Rev. 2023, 56 (Suppl. S2), 1919–1979. [Google Scholar] [CrossRef]
- Chen, J.; Xu, G.; Zhou, Z. Data-driven learning-based Model Predictive Control for energy-intensive systems. Adv. Eng. Inform. 2023, 58, 102208. [Google Scholar] [CrossRef]
- Zarzycki, K.; Ławryńczuk, M. Advanced predictive control for GRU and LSTM networks. Inf. Sci. 2022, 616, 229–254. [Google Scholar] [CrossRef]
- Li, F.; Meng, X.; Zhu, K.; Yan, J.; Liu, L.; Liu, P. Research on Ginger Price Prediction Model Based on Deep Learning. Agriculture 2025, 15, 596. [Google Scholar] [CrossRef]
- Li, Y.; Cao, Y.; Yang, J.; Wu, M.; Yang, A.; Li, J. Optuna-DFNN: An Optuna framework driven deep fuzzy neural network for predicting sintering performance in big data. Alex. Eng. J. 2024, 97, 100–113. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, Y.; Pan, R.; Zhou, X.; Wei, Z. Prediction of the critical temperature of superconductors based on two-layer feature selection and the optuna-stacking ensemble learning model. ACS Omega 2023, 8, 3078–3090. [Google Scholar] [CrossRef]
- Beheshti, Z.; Shamsuddin, S.M.; Hasan, S. Memetic binary particle swarm optimization for discrete optimization problems. Inform. Sci. 2015, 299, 58–84. [Google Scholar] [CrossRef]



| Device Name | Manufacturer | Model | Range |
|---|---|---|---|
| Temperature Sensor | Onset Computer Corporation (Bourne, MA, USA) | U23-001A | −40~70 °C |
| AC Current Sensor | Onset Computer Corporation (Bourne, MA, USA) | CTV-C | 0~100 A |
| Value | Selected Sensor Number | Variance Contribution Rate | Information Capture Rate |
|---|---|---|---|
| 0.01~0.04 | all sensors | 100% | 100% |
| 0.05 | 1, 3, 4, 5, 6, 7, 8, 9, 10, 12, 15, 16 | 82.71% | 98.87% |
| 0.06 | 4, 6, 7, 12, 15 | 45.71% | 96.46% |
| 0.07 | 7, 12, 15 | 33.56% | 95.77% |
| 0.08~0.09 | 7, 12 | 26.43% | 87.63% |
| 0.1 | 12 | 7.13% | 64.05% |
| Predictive Model | Hyperparameters Name | Search Space | Best Hyperparameters |
|---|---|---|---|
| CNN | Number of convolutional layers | [1, 2, 3] | 1 |
| Number of filters 1 | [16, 32, 64, 128] | 64 | |
| FC units 2 | [16, 32, 64, 128] | 128 | |
| Learning rate | [1 × 10−4~1 × 10−2] | 0.00390567294 | |
| Batch size | [8, 16, 32, 64] | 8 | |
| Epochs | [30~100] | 57 | |
| CNN-Attention | Number of convolutional layers | [1, 2, 3] | 1 |
| Number of filters 1 | [16, 32, 64, 128] | 64 | |
| Attention layer dimension | [16, 32, 64, 128] | 128 | |
| FC units 2 | [16, 32, 64, 128] | 16 | |
| Learning rate | [1 × 10−4~1 × 10−2] | 0.0028632374 | |
| Batch size | [8, 16, 32, 64] | 8 | |
| Epochs | [30~100] | 77 | |
| GRU | Number of GRUs | [16, 32, 64, 128] | 16 |
| FC units 2 | [16, 32, 64, 128] | 64 | |
| Learning rate | [1 × 10−4~1 × 10−2] | 0.0045723438 | |
| Batch size | [8, 16, 32, 64] | 8 | |
| Epochs | [30~100] | 56 | |
| GRU-Attention | Number of GRU layer units | [16, 32, 64, 128] | 64 |
| Attention layer dimension | [16, 32, 64, 128] | 32 | |
| FC units 2 | [16, 32, 64, 128] | 32 | |
| Learning rate | [1 × 10−4~1 × 10−2] | 0.0016217518 | |
| Batch size | [8, 16, 32, 64] | 8 | |
| Epochs | [30~100] | 72 |
| Predictive Model | RMSE (°C) | R2 | MAPE (%) | Computation Time (s) |
|---|---|---|---|---|
| CNN | 0.20 | 0.899 | 1.29 | 37 |
| CNN-Attention | 0.19 | 0.909 | 1.17 | 76 |
| GRU | 0.21 | 0.884 | 1.22 | 35 |
| GRU-Attention | 0.17 | 0.926 | 0.99 | 42 |
| Optimization Algorithm | Population Size | Fitness Value j(k) |
|---|---|---|
| GA | 30 | 107.66 |
| SA | 120.51 | |
| PSO | 30 | 74.36 |
| SSA | 30 | 62.45 |
| COA | 30 | 49.36 |
| ICOA | 30 | 24.19 |
| No. | Fitness Value j(k) | No. | Fitness Value j(k) |
|---|---|---|---|
| 1 | 24.19 | 6 | 26.05 |
| 2 | 24.35 | 7 | 23.52 |
| 3 | 27.42 | 8 | 23.72 |
| 4 | 22.50 | 9 | 22.14 |
| 5 | 24.62 | 10 | 23.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Zheng, W.; Guo, G.; Wang, M.; Luo, C.; Chen, C.; Li, Z. Research on Energy-Saving Optimization of Mushroom Growing Control Room Based on Neural Network Model Predictive Control. Energies 2025, 18, 5550. https://doi.org/10.3390/en18205550
Song Y, Zheng W, Guo G, Wang M, Luo C, Chen C, Li Z. Research on Energy-Saving Optimization of Mushroom Growing Control Room Based on Neural Network Model Predictive Control. Energies. 2025; 18(20):5550. https://doi.org/10.3390/en18205550
Chicago/Turabian StyleSong, Yifan, Wengang Zheng, Guoqiang Guo, Mingfei Wang, Changshou Luo, Cheng Chen, and Zuolin Li. 2025. "Research on Energy-Saving Optimization of Mushroom Growing Control Room Based on Neural Network Model Predictive Control" Energies 18, no. 20: 5550. https://doi.org/10.3390/en18205550
APA StyleSong, Y., Zheng, W., Guo, G., Wang, M., Luo, C., Chen, C., & Li, Z. (2025). Research on Energy-Saving Optimization of Mushroom Growing Control Room Based on Neural Network Model Predictive Control. Energies, 18(20), 5550. https://doi.org/10.3390/en18205550






