Abstract
This research aims to assess the integration of different fuel cell (FC) options with battery and waste heat recovery systems through a mathematical modelling process to determine the most feasible retrofit solutions for a marine electricity generation plant. This paper distinguishes itself from existing literature by incorporating future cost projection scenarios involving variables such as carbon tax, fuel, and equipment prices. It assesses the environmental impact by including upstream emissions integrated with the Energy Efficiency Existing Ship Index (EEXI) and the Carbon Intensity Indicator (CII) calculations. Real-time data have been collected from a Kamsarmax vessel to build a hybrid marine power distribution plant model for simulating six system designs. A Multi-Criteria Decision Making (MCDM) methodology ranks the scenarios depending on environmental benefits, economic performance, and system space requirements. The findings demonstrate that the hybrid configurations, including solid oxide (SOFC) and proton exchange (PEMFC) FCs, achieve a deduction in equivalent CO2 of the plant up to 91.79% and decrease the EEXI and the average CII by 10.24% and 6.53%, respectively. Although SOFC-included configurations show slightly better economic performance and require less fuel capacity, the overall performance of PEMFC designs are ranked higher in MCDM analysis due to the higher power density.
1. Introduction
Global warming due to rising levels of greenhouse gases (GHG) in the atmosphere is one of the most pressing international issues facing humanity [1,2]. The increased extreme weather conditions have made the topic more attention-grabbing in recent years [3]. Although shipping is the most efficient way of transporting goods because of its high utilisation capacity, its contribution to air pollution and global warming is undeniable due to the usage of heavy marine fuels [4,5,6]. Maritime transport is responsible for 3% of the world’s GHG, which is primarily due to compounds such as carbon dioxide (CO2), nitrous oxide (N2O), and methane (CH4) [7,8]. In addition to GHG, shipping activities also produce particulate matter (PM), volatile organic compounds (VOCs), sulphur oxides (SOx), and nitrogen oxides (NOx) [9,10]. In addition to global warming, other pressing challenges must be resolved immediately, such as potential health risks from waterborne air pollution released near coastal areas [11].
To reduce the environmental impact of marine vessels, the International Maritime Organization (IMO) adopted novel objectives and revised them in 2023 [12]. The revised decarbonisation targets are to reduce emissions by 20% by 2030 and 70% by 2040 over 2008 levels and reach net zero emissions by 2050 [13,14]. The Energy Efficiency Existing Index (EEXI) and Carbon Intensity Indicator (CII) have been introduced to transform and guide the global merchant ship fleet [15]. To comply with the requirements of these two metrics, several adaptations can be made onboard the ship. These can involve applications on conventional systems like engine power limitation, hull cleaning, air lubrication, energy-saving devices, and route or speed optimisation to enhance energy efficiency. Incorporating batteries or waste heat recovery systems (WHRS) into existing configurations or retrofitting with alternative fuels and systems to replace or improve internal combustion engines (ICEs) offers a viable pathway to achieve higher emission reductions aligned with the 2040 and 2050 targets [16].
Those system designs that target the marine power distribution system are especially relevant to large maritime vessels since its power demand is smaller and more stable than the propulsion plant. Prominent implementations to assist or replace auxiliary engines (A/Es) include batteries [17], WHRS [18], and fuel cells (FCs) [19,20,21]. Hybrid FC configurations have proven effective in reducing waterborne emissions and are compatible with various alternative fuels, including liquefied natural gas (LNG), ammonia, and hydrogen (H2). These benefits include high modularity, high efficiency, minimal air and noise emissions, no moving components, and fewer maintenance requirements [22,23]. The FC technologies that are currently available for commercial use include proton exchange membrane FCs (PEMFCs), alkaline fuel cells, direct methanol FCs, phosphoric acid fuel cells (PAFCs), molten carbonate FCs (MCFCs), and solid oxide FCs (SOFCs). PEMFCs are now one of the most prominent FC types because of their excellent electrical efficiency and advanced technology [24]. Their application in transportation is facilitated by their shorter start-up time compared to FCs operating at high temperatures, particularly SOFCs and MCFCs [25]. On the other hand, they require high-purity H2, making the operation more complicated onboard the ship [26].
1.1. Literature Review
Various research papers have been published in the last decade investigating the emission reduction potential and economic performance of FCs in ship power generation systems. For example, Wu and Bucknall [27] optimised a PEMFC/Battery-based propulsion system for a coastal ferry. The system reduced 65% of the life cycle GHG of the vessel.
Ghenai, et al. [28] designed a Photovoltaic (PV)/PEMFC/Diesel Generator system to meet the electrical load of a cruise vessel and presented the system’s economic feasibility and environmental benefits. This system reduced PM emissions by 9.84% compared to the conventional setup.
Sapra, et al. [29] performed an analysis to combine SOFCs with marine diesel generators (D/Gs) to meet the electrical requirements of a ship. LNG was used to reform H2, which was then used as a pilot fuel for the generators in the study. The 67–33% power share between the internal combustion engines and the SOFCs gave the best results and reduced CO2 by 12%, implying a 1.7-fold increase in weight.
Meca, et al. [30] developed a PEMFC/battery hybrid system tailored to a small container vessel’s electrical and propulsion requirements operating within emission control areas. Over a 14-h operational period, the system avoided the emission of 10 tonnes of CO2, 195 kg of NOx, and 9 kg of SOx, demonstrating its potential for significant environmental benefits.
Perčić, et al. [31] evaluated the feasibility of different FC types for integration into power systems used in short-sea shipping operations. Life cycle analysis (LCA) was conducted and upstream emissions from production to usage were calculated. Blue and green ammonia usage ensured the CO2 equivalent (CO2-eq) reduction at 84%, and blue ammonia provided the second-highest economic performance after the diesel engine.
Chen and Lam [32] conducted an LCA study on tugboats powered by H2 PEMFCs and SOFCs, benchmarking their performance against conventional propulsion systems. The H2 FCs provided up to 85% GHG reduction, mitigating approximately 48.55 metric tons of CO2-eq emissions.
Seyam, et al. [33] proposed innovative propulsion systems, incorporating steam Rankine cycles, gas Brayton cycles, and SOFCs as alternatives to conventional two-stroke marine engines. The study evaluated the integration of these systems with WHRS and assessed the performance of alternative environmentally friendly marine fuels. The proposed configurations demonstrated a maximum CO2 emission reduction of 53%, highlighting their potential for significant environmental benefits in maritime applications.
Yuksel [34] modelled dual-fuel (DF) engines as the main engine (M/E) using LNG and SOFCs as A/Es and using H2 or LNG on a crude oil tanker. The study involved eight scenarios varying LNG percentage in DF, WHRS usage, and SOFC fuel type. Economic, environmental, and regulatory aspects were examined. The most considerable CO2 emission reductions, 47.95% operationally and 48.47% upstream (well-to-tank), were achieved with LNG as the primary fuel and H2-powered SOFCs.
Duong, et al. [35] conducted a thermodynamic analysis of a novel system, including a combined system of LNG-SOFCs, PEMFCs, WHRS, a carbon capture system, and a gas turbine. The proposed system is predicted to achieve an energy efficiency of 68.76% and an exergy efficiency of 33.58%, showcasing its potential for high performance in energy conversion processes.
Seyfi, et al. [36] used a multi-criteria decision-making (MCDM) approach to determine which type of FC was the best for onboard implementation. The potential H2 carriers, tank capacities, economic performances, and emission reduction potential of the selected fuel cell to replace D/Gs on a very large crude oil carrier were analysed. The PEMFC was the most environmentally benign, and in a hypothetical cruise from the Persian Gulf to China, it could prevent a total of 3.14 tonnes of CO2-eq.
Lee, et al. [37] proposed two SOFC hybrid systems with power outputs of 2.5 MW and 5.0 MW, integrated with dual-fuel (DF) engines for the electrification of a crude oil tanker. The 2.5 MW system achieved a 5.4% reduction in CO2 emissions, while the 5.0 MW system delivered an 8.8% decrease.
Hwang, et al. [38] conducted a comprehensive Life Cycle Cost Analysis (LCCA) for ferries operating in Scotland, assessing PEMFC/Battery hybrid propulsion and PV/Battery-based electrification systems. H2 FC propulsion systems emerged as financially advantageous for short-distance ferries, offering greater cost efficiency than ammonia PEMFCs and batteries.
Korkmaz, et al. [39] benchmarked molten carbonate (MCFC) and phosphoric acid fuel cells (PAFC) with various batteries under different conditions on an oil/chemical tanker’s electric distribution system. The study modelled FCs and battery charge/discharge events, incorporating battery ageing effects, and evaluated systems through environmental and economic analyses. Using an MCDM approach, the best configuration involving MCFCs achieved a 49.5% CO2 reduction.
De Lorenzo, et al. [40] evaluated a bio-methane-powered SOFC system integrated with a WHRS for the propulsion and electrification of a cruise vessel. This innovative energy system achieved reductions of 12.74% in primary energy consumption and 40.23% in CO2 emissions compared to traditional energy systems.
Ammar, et al. [41] analysed and compared LNG DF diesel-electric propulsion with different power limitations (25%, 15%, and 0%) and FCs on the propulsion system of an LNG carrier regarding economic and IMO-EEXI requirements. Results revealed that liquefied-H2 systems offered economically competitive costs of USD 2.1 and USD 2.5 per kilogram for hybrid options 1 and 2, respectively, compared to the dual-fuel diesel-electric system.
Inal, et al. [19] evaluated H2 PEMFC utilisation instead of D/Gs on a general cargo vessel. The impact of the conceptual retrofitting on the operational emissions was demonstrated in the study. The proposed system achieved a CO2 reduction of 37.5%, with comparable reductions observed for NOx, SOx, and PM emissions. The economic performance and volumetric requirements related to H2 storage were discussed.
Iqbal, et al. [42] investigated three hybrid marine power system configurations for a passenger ship using HOMER Pro: PV/Wind/Battery (Case 1), PV/Wind/Battery/Diesel Generator (Case 2), and PV/Wind/Fuel Cell/Battery (Case 3), with separate assessments for lead-acid and lithium-ion batteries. Case 2 with lead-acid batteries was the most cost-effective, while Case 1 with lithium-ion batteries had the lowest net present cost and highest economic feasibility. Regarding power generation, Case 1 (lithium-ion) and Case 3 (lead-acid) excelled, with lithium-ion systems producing lower emissions overall.
Wang, et al. [43] evaluated various FC types for ship power systems. The results indicate that LNG FCs, direct methanol FCs, and low-temperature PEMFCs had superior performance when compared to other FCs, achieving Energy Efficiency Design Index (EEDI) values of 11.62, 12.72, and 10.05, respectively. This highlights their advantages in energy efficiency and carbon emission reduction.
This literature review has involved studies concerning hybrid systems, including FC utilisation, on marine vessels to reduce GHG emissions. The results have shown that researchers have evaluated PV systems, various types of FCs, and batteries in recent years. The most utilised FC types are MCFC and SOFC due to their high-power outputs, while PEMFC has been investigated considerably because of its high efficiency. A few studies have examined PAFCs as an option due to their commercial availability. The addition of WHRS and DF engines using various alternative fuels has also been investigated. The marine power distribution systems have been targeted mainly, but some studies have presented system designs for propulsion and electric distribution units. LCA studies or separate environmental and economic evaluations have been conducted in the examined research findings.
1.2. Research Gap and Motivation
The comparison of various FC types in marine power distribution plants, including batteries and WHRS options for 2024, 2030, and 2050 projections, has been detected as a gap in the literature. This paper aims to develop a simulation framework that includes SOFC, PEMFC, and PAFC as FC options and battery and WHRS-support configurations to evaluate retrofit options for the onboard electricity generation plant. In recent years, PAFCs have been selected as a promising solution for emission reduction due to their use of LNG. Conversely, scenarios involving SOFCs and PEMFCs considered running on H2 aim for more aggressive emission reductions. SOFCs operate on various fuel types; however, in this analysis, SOFCs are considered using pure H2 as fuel to emphasise their full potential for emission reduction. Similarly, PEMFCs require H2 as their primary fuel to function effectively. However, their practical application remains to be determined due to the lack of technological maturity of ships’ onboard H2 storage and transfer systems. This research is motivated by the need to provide a tool for the decision-making process through a detailed analysis that includes environmental, economic, and regulatory issues to determine the most promising FC configuration for the auxiliary power units of large merchant ships.
This research differentiates itself from the literature by implementing future cost projection scenarios, including carbon tax, fuel, and equipment prices, and examining the environmental impact of upstream emissions of different FC systems combined with the EEXI and CII calculation infrastructure. Data collection from a bulk carrier has been ensured to conduct the analysis. The modelling of a hybrid marine power distribution plant has been coded in Python. The simulation has evaluated six different hybrid case scenarios. An MCDM approach has determined the rank of each scenario by considering the results of environmental and economic calculations.
The developed simulation framework is designed with flexibility, allowing it to be adapted and applied to other types of ships beyond bulk carriers. This adaptability ensures that the methodology can be extended to various vessel types, providing a comprehensive decision-making tool for optimising onboard power generation across diverse maritime applications.
2. Materials and Methods
Hybrid system configurations have been evaluated using the case study bulk carrier data, as shown in Figure 1.
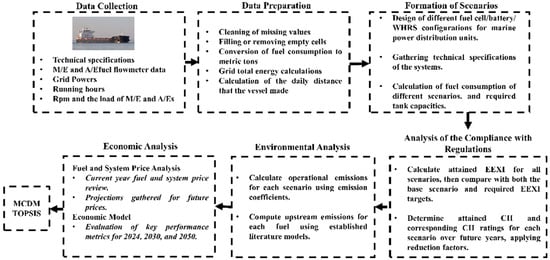
Figure 1.
The methodology flowchart.
A hardware system featuring advanced smart collectors is integrated into the vessel’s infrastructure for data collection. These devices capture synchronised and highly reliable data from onboard sensors, instruments, and control systems. Operating within a robust wireless network, this system ensures efficient and uninterrupted data collection, supporting precise monitoring and analysis [44]. The devices utilised for data collection are certified by the Bureau Veritas classification society and comply with the European Declaration of Conformity standards, ensuring adherence to stringent quality and safety regulations.
The system incorporates three key components, the Quax 8S Node, G Node, and S Node, each designed for specialised data collection. The Quax 8S Node gathers voyage-specific data, including ship speed, longitude, and other navigational metrics. The Quax G Node focuses on the main and auxiliary engines, collecting critical performance data such as turbocharger RPM and power output. Meanwhile, the Quax S Node captures flow and RPM data, enhancing the system’s comprehensive monitoring capabilities.
Data collection was conducted between 1 February 2021, and 10 February 2023, yielding 1,064,161 data points recorded at one-minute intervals. After preprocessing, the dataset comprises 1,003,490 data points, representing approximately 1.96 years of continuous operation. The collected parameters include power, fuel flow, temperature, and density for generators, electrical load analysis of ship consumers, main engine exhaust, power output, load, speed, and fuel properties. Data on fuel cells, battery performance curves, converter voltage, and conversion efficiencies have been sourced from relevant literature and commercially available manuals for hybrid systems. Figure 2 illustrates a sample of the collected data, showcasing the power outputs of the diesel generators (D/Gs).
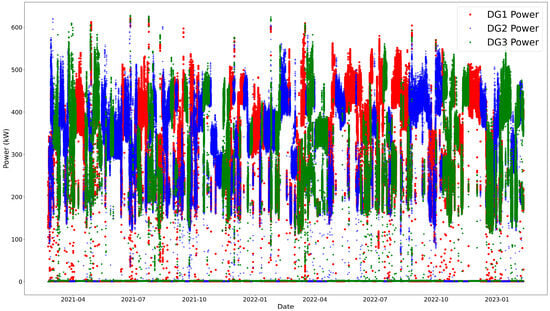
Figure 2.
Sample data: Power output distribution of D/Gs.
After data collection, the sensory data, collected at one-minute intervals, were pre-processed. Removal of empty values and grid power calculation have been conducted. The formation of scenarios, including FCs, batteries, and WHRS, has been arranged. The hybrid grid simulation has calculated the total fuel consumption of the marine power distribution plant units. The EEXI, CII, and operational and upstream emissions have been computed after the fuel consumption calculation. A cost-benefit analysis has been performed by computing installation and fuel costs. Finally, an MCDM analysis using the Technique for Order of Preference by Similarity to the Ideal Solution (TOPSIS) has been conducted to determine the preferred configuration, including the system design’s size, environmental performance, and economic efficiency.
2.1. Case Study Description
The case study vessel is a Kamsarmax bulk carrier owned and managed by the project partner LASKARIDIS SHIPPING CO., LTD (based in Athens, Greece). Table 1 illustrates the ship particulars.

Table 1.
Ship particulars.
The conventional marine power distribution system comprises three D/Gs working in parallel. The vessel’s electricity demand dictates the generated power, while its magnitude allows for flexibility in selecting the number of simultaneous D/Gs in operation, which is integral to the optimisation process [45]. Figure 3 illustrates the simplified system scheme of the conventional system and the assessed hybrid power distribution systems.
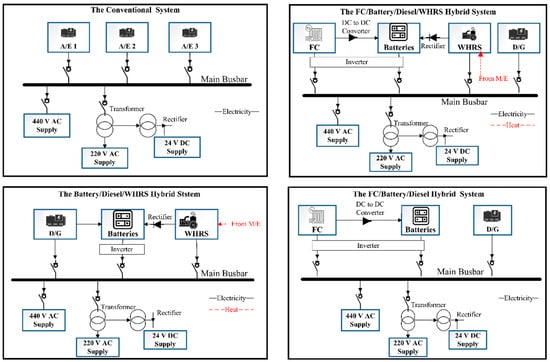
Figure 3.
The conventional and investigated hybrid design for marine power distribution unit.
The study separately evaluated the implementation of various FCs (i.e., SOFC, PEMFC, and PAFC), batteries, and WHRS. Their suitability, sizing, and usage scenarios were analysed based on environmental impact, economic feasibility, volume, weight, and availability for maritime applications. The utilisation of the D/G and its power capacity share was analysed across various scenarios involving FC/Battery/WHRS combinations, considering the vessel’s entire electrical demand and partial load sharing between the D/G and alternative systems. The waste heat sources for the WHRS were the exhaust gases from the M/E following the exhaust gas boiler. The battery system was modelled, with optimal charging and discharging voltages determined using a grid search algorithm that accounted for the state of charge (SoC), state of health (SoH), capacity, and voltage drop. Table 2 presents the system configurations for load-sharing scenarios involving marine diesel engines (MDEs) and various (FC) types, along with the corresponding equipment weights and volumes.

Table 2.
System specifications of the combinations considering various FC types.
The FCs utilised in this study, as shown in Table 2, are all commercially available products widely applied in various industrial settings. SOFCs and PAFCs have been selected for suitability in marine applications due to their resilience to impurities in H2. SOFCs have been assumed to operate on H2, targeting ambitious decarbonisation goals for the future, while PAFCs have been evaluated with LNG to assess their feasibility for earlier implementation.
MCFCs, although highly suitable for marine propulsion applications [46], have been excluded from this study due to their large-scale power outputs starting at 1.4 MW and significant spatial requirements, which are unsuitable for the electrification plant in the case study vessel. PEMFCs, on the other hand, are noted for their high power density and rapid start-up times. However, their sensitivity to H2 purity poses a limitation. Despite this, PEMFCs are emerging as commercially viable solutions for marine applications, making them the third product in the analysis.
Alkaline fuel cells (AFCs) also offer good power density, albeit lower than PEMFCs, and share similar disadvantages regarding H2 purity. Consequently, recent marine applications have prioritised PEMFCs over AFCs [46], a rationale also reflected in this study. Additionally, AFCs have been excluded due to the lack of a robust dataset on commercially available products.
The determination of FC and Battery capacities is based on achieving equivalence to one or two D/Gs, depending on the available waste heat power. Hybrid 1 and 3 configurations have FC/Battery capacities adjusted to meet one D/G’s power, while Hybrid 2 and 4 systems correspond to two D/Gs. WHRS supports Hybrid 3 and 4 configurations, whereas Hybrid 1 and 2 do not. This approach ensures that the D/Gs are not operating at very low loads, which is considered in the design process by analysing the load data.
In Table 2, the weights and volumes of PEMFCs are remarkably lower than solely D/Gs and configurations of D/Gs and other types of FCs. Since the fuel-reforming modules of the FCs are integrated with the rest of the system, SOFC and PAFC weigh more and occupy more space. On the other hand, the H2 production system for PEMFC must be implemented externally for the examined product.
In Hybrid 1 and Hybrid 3 configurations, the FC/Battery system has been designed to meet the power of one D/G. On the other hand, Hybrid 2 and Hybrid 4 FC/Battery configurations have replaced two D/Gs. Table 3 demonstrates the technical specifications of the D/Gs on the case study ship.

Table 3.
Technical properties of ICE used in the analysis.
Table 3 shows the conventional marine diesel engine on the case study vessel. Figure 4 illustrates its specific fuel consumption (SFC) and power curves with varying engine loads.
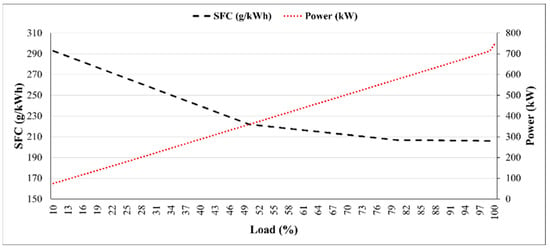
Figure 4.
The specific fuel consumption curve of the marine diesel engine.
Regarding fuel requirement, SFC refers to the fuel consumed per unit of time necessary to generate a specified engine output [47]. Curves presented in Figure 4 have been utilised to calculate the fuel consumption of a conventional MDE operating HFO. The variable load of the D/Gs has been determined through simulation, and the corresponding SFC and power values were interpolated from the curve.
Two different fuel configurations have been evaluated for the FC setups. The PAFC system includes an integrated steam methane reformer to produce H2 by reforming LNG. The SOFC system can operate with an integrated LNG decomposer or pure H2 from another source. The H2 bunkering scenario has been assessed exclusively for SOFCs. PEMFCs require high-purity H2, and its supply from an external facility has been considered in this study. For volume calculations, the dimensions of the SOFC reformer system were used. Table 4 depicts the technical specifications of the assessed FC models.

Table 4.
Technical specifications of FCs used in the analysis.
The power values for each FC are provided for a single module. While PEMFC operates exclusively on highly purified H2, SOFC and PAFC can also utilise LNG, resulting in significantly larger module sizes than PEMFC. PAFCs incorporate an integrated H2 production unit from LNG within their system architecture. Conversely, in the case of PEMFC, determining system dimensions and weight necessitates a separate calculation owing to the absence of an inherent H2 production unit within the cell design. Table 5 shows the properties of a commercial battery cell [52] used to form the stack.

Table 5.
Technical specifications of the battery cell.
The properties listed in Table 5 pertain to a single battery cell. Based on the required battery capacity and assuming a 440 V line voltage for the ship’s grid, battery packs have been assembled from these individual cells. The constant current constant voltage (CC-CV) charging protocol has been used as the charging method, and the modelling of the battery pack has been ensured by considering this protocol. The battery voltage drop was simulated using the SoC versus Voltage curves from the manufacturer’s datasheet [52].
The SoH curves have also been obtained from the manufacturer data sheet, and the curve slope varies depending on the C-rate (charge/discharge rate). The algorithm logic for using SoH equations is shown in the modelling section. On the other hand, the WHRS uses an organic Rankine Cycle (ORC) to produce electricity from exhaust waste heat. Table 6 shows the exhaust mass flow rates () and the inlet temperature of the exhaust to the WHRS after the exhaust boiler () taken from the manufacturer’s datasheet.

Table 6.
The load, power, SFC, and exhaust gas data of the M/E.
The M/E power, speed, and load were collected from the case study vessel, and the exhaust gas amount and temperatures were interpolated from the data. The ORC model was taken from the models developed by Konur, et al. [53]. The total volume and required area for the FC battery configurations were calculated by considering the distance of 1.8 m between each piece of equipment [54].
2.2. Simulation Logic
An energy management strategy (EMS) algorithm and simulation designed by the authors has provided the determination processes of load-sharing, the number of generators or FCs, and battery charging/discharging conditions. The simulation was developed in Python, and the powertrain options for the hybrid marine power distribution plant were conducted using the same code infrastructure. At the beginning of the simulation, the user can adjust the FC, battery, and WHRS implementations and their capacities. Figure 5 illustrates the simplified algorithm scheme of the simulation and EMS.
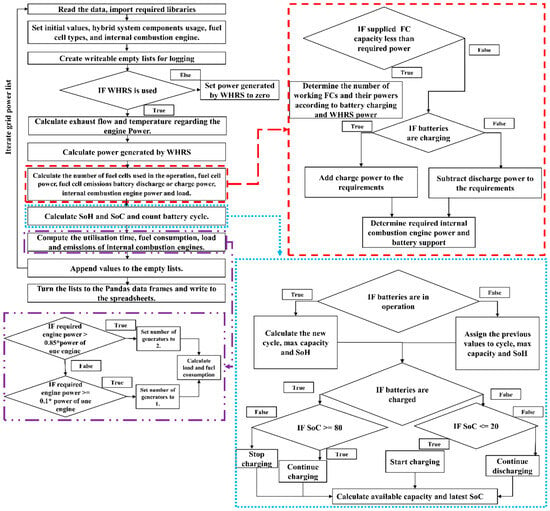
Figure 5.
The algorithm scheme of the model and EMS (The red, blue, and purple dashed boxes delineate the modelling frameworks for the load sharing of FC, battery, and ICE respectively).
The algorithm starts with importing data and necessary libraries while setting the initial values and empty lists for the iteration. The iteration is conducted based on the size of the grid power data; the program then verifies whether WHRS is selected as a support option by the user and calculates the power produced by the system based on the ME power.
After the WHRS determination, the function decides the number of operating FCs, battery charge/discharge power, and engine load. The capacity of FCs and battery changes are determined according to the hybrid scenario and FC type, while the WHRS power availability affects the parameters’ determination. The sizes of FCs and batteries have been selected to ensure that MDEs operate outside the low-load zones. Considering the battery charging/discharging state and power, the EMS manages the battery performance. The SoC has been kept between 20% and 80% to extend the battery life.
The collected operational data includes instantaneous load increases, such as those caused by thruster usage. The algorithm determines the ship’s operation mode based on changes in the power of the M/E and A/E. The EMS evaluates the slope of power increases in the A/Es. Under near-constant operation, the FCs and WHRS, if available, are prioritised in the hierarchy. The availability of WHRS, if present in the configuration, is determined based on the operation mode and a M/E load exceeding 50%. If the slope of demand increases rapidly or the power demand surpasses the capabilities of the FCs and WHRS, the batteries are incorporated into the operation. Finally, if these measures are insufficient, the MDE is activated.
In scenarios utilising FCs, the FC charges the batteries, with the SoC-voltage curves provided earlier are used to calculate voltage drop and determine the battery’s available power. The SoH is calculated simultaneously. In the subsequent step, the required engine power is assessed to determine the number of operational D/Gs, and the HFO consumption has been estimated using the curve shown in Figure 4.
The computed parameters within the loop are appended to pre-initialized empty lists at the start of the algorithm. At the end of each iteration, these lists are exported to MS Excel for further analysis and cleared for the next iteration. Once the total fuel consumption for the hybrid scenarios is calculated, additional evaluations are performed, including fuel tank capacity design, upstream emissions computation, EEXI/CII rating evaluation, and economic performance assessment.
2.3. Mathematical Background
This section contains the mathematical equations used in the FC, battery, WHRS, and ICE calculations. The coefficients and methods used in the environmental and economic analysis have also been indicated. In addition, the EEXI and CII computation process and the stages of the MCDM approach have been described.
2.3.1. Fuel Cell Calculations
This section demonstrates and explains the equations used in the mathematical model. Equation (1) has been employed to calculate the H2 consumption of SOFC and PAFC.
The operation time is denoted as t in h, and the power of one FC is represented by in kW, Lower heating value ( for the H2 has been taken at 120,000 kJ/kg [55], and the efficiency of fuel ( cells have been computed by applying a 0.5% degradation per 1000 h [56]. The calculation of the tank capacities concerning the H2-utilized scenarios has been ensured by assuming that it has been stored at the compressed state, having a density of 75 kg/m3 [57,58].
The efficiency and fuel consumption values have been interpolated using the curves provided by the manufacturer [50] for the PEMFC. Emissions of FCs ( have been calculated by using Equation (2) and the LNG consumption of PAFC has been computed by employing Equation (3) [34].
where represents the emission coefficient given in Table 4, and the number of operating FCs is . LNG consumption has been calculated by using the t of PAFC, the coefficient of LNG consumption () depicted in Table 4, and 0.007 is the conversion coefficient from Nm3 to metric tons [59].
2.3.2. Waste Heat Recovery Model
Equation (4) computes the generated power by the WHRS () by using the data illustrated in Table 6.
where is in kg/s and is in °C, as shown in Table 6. is the outlet temperature from ORC, which is taken at 100 °C, and is the amount of thermal energy that, when pressure stays stable, a mass of exhaust emits or absorbs with an alteration in temperature and is taken at 1.089 kJ/kg.K [60]. The efficiency of ORC () is taken at 13.2% from the thermodynamic model of Konur, et al. [53].
2.3.3. Battery Model
The voltage of the battery stack has been computed by fitting the curves provided by the battery manufacturer [52]. The EMS decides the operational state of the batteries by using the SoC, which is the rate of available battery capacity, while calculating the voltage from curves. The time-dependent SoC has been calculated with the traditional Coulomb counting method depicted in Equation (5) [61,62].
SoC (0) refers to the initial SoC at the beginning of the iteration, while SoC(t) represents the updated SoC at time t. The EMS maintains the battery’s SoC between 20% and 80% to minimise internal resistance, thereby preserving battery health and longevity [61]. The coulombic efficiency has been assumed at 1 (, the charging or discharging current is denoted as I(t), and the available battery capacity in Ah is represented by in the formula. CC-CV charging protocol and CC discharge have been implemented to control the charging and discharging of the batteries.
The capacity reduction because of the battery degradation has been implemented in the battery model by employing the SoH curves from the battery cell manufacturer [52]. The capacity decrease of the battery is calculated iteratively during operation, with adjustments made based on the C-rate. The SoH has been found by employing Equation (6), which is the ratio between actual battery capacity () after degradation and capacity at the beginning () of the operation [63].
Due to lacking memory impact and having higher specific energy, lithium-ion batteries have been utilised in hybrid operation scenarios [62]. The conversion of DC battery current to AC for grid use is assumed to utilise the SMA Sunny_SCS2900 model inverter, with an efficiency of 0.984 (at 800 V DC to 450 V AC).
2.3.4. Internal Combustion Engine Calculations
The algorithm determines the required engine power and the number of working generators () in each time interval (t = 1 min). The load and power of each generator were calculated in the simulation, and their SFC was obtained by interpolating the curves shown in Figure 4 . The load sharing has been determined by using the model presented in the study of Yuksel and Koseoglu [45]. The load-sharing mechanism operates based on an algorithm that monitors the frequency and power of the generator; if the required power exceeds 85% of the generator’s load capacity, an additional generator is automatically started to share the load, balancing it according to their respective frequencies and power factors. The fuel consumption of ICEs () in t in each iteration has been calculated by using Equation (7) [39].
2.3.5. Environmental Analysis
The operational emissions from the engines () has been determined by utilising the operational emission coefficients (OEC) for HFO presented in Table 7. The upstream emissions of fuels used in ICEs and FCs have been computed using the upstream emission coefficient (UEC) in Table 7.

Table 7.
OEC and UEC values.
Operational (tank-to-wake) emissions for ICEs have been calculated by multiplying the HFO consumption with the OEC provided in Table 7. For FCs, manufacturer-provided coefficients and total energy production derived from the mathematical model have been used. The process is described in Section 2.3.1. Upstream (well-to-tank) emissions have been computed by applying the UEC to operational emissions or total energy production, depending on the units specified in Table 7.
The equivalent CO2 () indicating 100 years of global warming potential (GWP100) has been calculated for consideration of both operational and upstream GHGs by using Equation (8) [7].
The units in are tons. The coefficients for GWP100 provided in the IMO’s LCA guidelines [7] have been used to calculate the warming potential of N2O and CH4 in terms of , as their warming potentials are approximately 260 to 273 times and 27 to 30 times higher than CO2, respectively.
The operational and upstream emissions have been calculated for each configuration’s fuel consumption and operational duration to evaluate the overall life cycle environmental impact. By employing a streamlined approach, this methodology simplifies the assessment process, enhancing the comprehensibility of these parameters for maritime stakeholders.
Additionally, the operational CO2 emissions have been used to compute recent energy efficiency metrics, highlighting the role of presented hybrid electrification systems in achieving regulatory compliance, which is expected to become more stringent in the coming years.
2.3.6. Energy Efficiency Metrics
Equation (9) is the concept formula to compute the attained EEXI, which is the ratio of operational carbon emission to the multiplication of capacity and reference speed () [67].
The capacity is DWT for the bulk carriers [68] and is 14.3 knots for the case study ship. CO2 emissions were calculated by multiplying the operational CO2 coefficient provided in Table 7 with the HFO consumption determined through mathematical simulation. The operational data also include details on the duration of operation, expressed in hours. The attained EEXI of the base case has been compared with various hybrid scenarios to identify the configuration that achieves the most significant reduction. The required EEXI has been calculated by employing Equation (10), which is the product of the reduction factor (X) and reference EEDI line for the reference bulk carrier [67].
X is 20% for the bulk carriers, and the coefficients in Equation (10) are also specific to the bulk carriers [68]. The required EEXI has been calculated as an upper limit and benchmark to compare with the attained EEXI, assessing whether the vessel, under various configurations, complies with the latest technical requirements established by the IMO.
The CII is an operational measure established by the IMO, whereas the EEXI is a technical measure. Attained CII has been calculated by using Equation (11) [69].
where the travelled distance is denoted by and the capacity is the operational DWT depending on the loading condition of the vessel [67]. CO2 emissions have been calculated annually based on the yearly HFO consumption and the operational CO2 coefficient provided in Table 7. The attained CII of the base scenario has been compared with zero-carbon hybrid configurations to identify the hybrid system with the most significant potential reduction. The required CII has been calculated using the reference CII line for bulk carriers and Equation (12).
The CII reference line is for 2019. The required CII is calculated by applying the reduction factor (Z), starting at 5% for 2023 and increasing by 2% annually until 2026 [69]. The required CII has been calculated to establish threshold values for ratings and to facilitate the comparison of zero-carbon configurations with the base scenario.
The CII ratings of the configurations have been determined by using the dd vectors for the reference bulk carrier taken from IMO [70]. The ratings have been calculated by multiplying the dd vectors with the required CII after the Z has been applied according to each year [70].
Energy efficiency metrics have been calculated to demonstrate the impact of regulatory compliance provided by hybrid electrification systems. While the environmental analysis emphasises operational CO2 emissions, the results from this analysis were utilised to calculate the EEXI and CII metrics. These metrics offer a structured approach for the maritime industry to evaluate energy efficiency, ensuring alignment with the framework established by the IMO.
2.3.7. Economic Analysis
The economic performance of the scenarios has been measured by the levelized cost of energy (LCOE) and electricity production cost (EPC). LCOE is the principal tool of choice for assessing the unit costs at the plant level of different baseload technologies throughout their operational lives [71]. Equation (13) demonstrates the calculation of the LCOE [72].
where the installation costs are depicted as , fuel costs are denoted as , and represents the operation and maintenance spending. Generated total power ) and total t of the plant have been computed using the collected data. Discount rate (r) has been assumed at 10%, and plant lifetime (LT) has been taken at 20 years [71,73]. The calculation of the LCOE has been performed by accounting for annual expenses, including and , over the plant’s LT with a fixed r value The total of these recurring expenses, combined as , has been divided by the cumulative energy production over the system LT to determine the LCOE. Table 8 shows the LT, , and of the equipment.

Table 8.
, , and LT of scenarios.
has been calculated by multiplying the ratios provided in Table 8 with the . The analysis has been conducted using United States Dollars (USD). The exchange rate between Euro (EUR) to USD has been taken at 1.07. The prices taken from previous years have been corrected by employing the rate of the related data year and recent Chemical Engineering Plant Cost Index (CEPCI). The latest CEPCI has been announced as 800.3 for February 2024. The CEPCI values for previous years, as well as the most recent data, have been taken from Maxwell [81].
Future projection rates for cost changes have been obtained from the literature for each specific type of equipment. For FCs, the price reduction trends of PEMFCs over time have also been assumed to apply to other types. In cases where future cost projections for specific equipment are unavailable in the literature, the costs have been considered to remain constant throughout the analysis period.
The expected LT values for FCs have been established as 40,000 h for PEMFC and PAFC and 60,000 h for SOFC. If these FCs are not projected to reach their expected lifetimes, it is assumed that they will need to be replaced within 10 years. The LT of batteries is contingent upon their hybrid configuration and is calculated based on SoH curves. In scenarios where battery usage is minimal and the calculated lifetime exceeds 10 years, it is assumed that batteries will be replaced every ten years in the analysis.
Equation (14) calculates the EPC, which is the fuel cost per kWh produced [73]. EPC is chosen as a metric because it practically evaluates the price spent on fuel per kWh, offering a simpler and more practical alternative to the more complex LCOE. Table 9 demonstrates the current , the projection ratios of future fuel prices, and carbon tax costs.

Table 9.
Carbon prices, , for 2024, and the future change ratios according to low, medium, and high scenarios.
The EPC calculation focuses on and carbon taxes, with cost projection scenarios outlined in Table 9. for 2024 has been obtained from ShipandBunker [82] on 18 June 2024. The values of in Table 9 indicate the projected annual rates of change, which the economic model uses to evaluate the scenarios for 2030 and 2050. Projection cases are classified as low, medium, and high, reflecting different trends in fuel price dynamics. The low case assumes slow increases or steep decreases in fuel prices, the medium case represents a moderate rate of price growth, and the high case anticipates rapid price increases or slower decreases. For example, in the LNG low scenario, a 2.04% annual reduction has been applied, and the values for 2030 and 2050 have been calculated.
This framework is similarly applied to carbon prices, aligning them with the corresponding fuel price scenarios based on data from the literature. Various carbon tax scenarios and projections exist in the literature, reflecting uncertainty in the direction of future prices. The analysis classifies carbon prices according to the scenarios and expectations established in the literature to encompass the diverse carbon pricing pathways.
The described economic modelling approach has been applied to account for the variability in fuel price dynamics and uncertainty of carbon taxes, enabling a comprehensive evaluation of future economic scenarios under different conditions and policy environments.
2.3.8. Technique for Order of Preference by Similarity to Ideal Solution
Using TOPSIS, a popular MCDM technique in academic research, the hybrid and conventional setups have been ranked based on various criteria. The methodology generates optimal solutions and highly understandable results by employing a straightforward approach [87].
The selected criteria have been determined based on three primary aspects: environmental performance, economic feasibility, and space requirements. Two specific parameters represent each criterion. For environmental performance, these are total hourly CO2-eq: emissions and the sum of other hourly emissions. Economic feasibility is assessed through the LCOE and EPC metrics, depending on the financial projection scenario and year. Space requirements are evaluated using parameters such as required tank capacities, mass, and equipment volume.
All six criteria are non-beneficial, and their relative weights have been assigned using the equal weighting method (16.66% for six criteria), an objective weighting approach commonly employed in general evaluation scenarios such as this application.
The TOPSIS application in this study is specifically employed to compare many hybrid configurations, facilitating ease of understanding and interpretation. This methodology is beneficial for demonstrating variations across different economic scenarios and with increasing carbon prices. It is important to note that the weights and resulting rankings may vary depending on the decision-maker’s preferences. The TOPSIS method’s applicability and the ranking system’s clarity offer significant advantages, especially in fostering collaboration with industry partners in the maritime sector.
In the method, the best rankings are determined by finding the closest range to the positive ideal solution () or the furthest extent to the negative ideal solution (). The benefits are maximised by while the costs are scaled up by the . The methodology starts with the creation of the decision matrix and applying the normalisation process shown in Equation (15) to the matrix [88].
The normalised matrix element is denoted by , and is the member of the decision matrix. The normalised decision matrix is multiplied by the criteria weights in the next step. The determination of and , depending on whether the criterion is beneficial or non-beneficial, is the following stage. For the non-beneficial or cost-type criterion, is the minimum and is the maximum value in the decision matrix, while the beneficial parameter is the opposite. The Euclidean distance between each weighted normalised matrix member () and is , and similarly is between each member and . and are calculated by applying Equations (16) and (17) [87,88].
The rank of each configuration is determined by sorting the relative closeness coefficient () computed by Equation (18) [87,89].
2.3.9. Uncertainty Analysis
Uncertainty quantifies the reliability of a result and is essential for evaluating the data’s suitability for informed decision-making in areas such as health, safety, commerce, and scientific research [90]. Among statistical methods, uncertainty analysis effectively identifies scenarios influenced by uncertainties and enhances data accuracy [91]. Different uncertainty levels are combined using Equation (19) [92].
In Equation (19), U values denote the fractional uncertainties of individual independent variables (x1, x2,…xn), UR presents the uncertainty of the combined computation, while R corresponds to the result or utilised value for each independent parameter [93].
An uncertainty analysis of the mathematical model used to calculate fuel consumption, as described in Section 2.2, has been performed to evaluate the reliability of the computations. Two primary sources of uncertainty are identified in the simulation. First, the ICE fuel consumption is derived from SFC curves provided by the manufacturer for hybrid configurations. When the model is applied to these curves for the base case, the error rate between experimental data and modelling results is 5.63%. Second, as specified in the data sheets, the FC efficiencies have an associated error rate of 2%. Using Equation (19), the mathematical model demonstrates a combined uncertainty of 5.98%.
3. Results
3.1. Fuel Consumption and Tank Capacity Results
Six different hybrid marine power distribution plant configurations have been analysed through a simulation, utilising the combinations of the presented alternative energy systems. Various alternative systems have been employed to reduce marine diesel engine usage. Some configurations have involved batteries in the operation, and others have implemented them as the backup energy storage unit. Figure 6 shows the distribution of utilisation hours for power generation and storage equipment throughout the scenario, covering a total data collection period of 17,167.48 h (equivalent to 1.96 years) after data preprocessing.
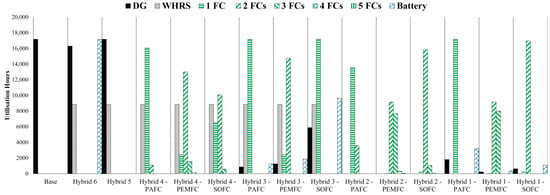
Figure 6.
Usage hour distribution of equipment.
For 1.96 years, the ME has been utilised for 9,488.15 h in the base scenario, and 8,849.93 h have been suitable to generate power through WHRS. A/Es have worked for 17,167.48 h; hybrid system configurations have split the operation time. In Hybrid 2 and Hybrid 4 power configurations, the battery packs have been used as spare power units to respond to instant fluctuations in demand. Depending on the maximum FC power outcome, the battery usage time has been varied in the other system design cases.
Hybrid 1 scenario involved battery usage during the oper2ation; however, they were not used frequently. Hybrid 1-PAFC has used batteries for 3238.93 h, yielding the SoH at 95.5%. In the same design, PEMFC and SOFC configurations have involved the batteries 363.87 h and 1106.17 h, respectively, leading to the SoH being at 99.51% and 98.54%. These outcomes showed that the battery life spans with this type of usage will last over the ship’s lifetime for the PEMFC and SOFC. The PAFC design is going to require battery pack renewal every 9.12 years.
Hybrid 3 also included the active integration of batteries to meet the operational load, and SOFCs were incorporated with batteries for 9622.18 h, yielding a final SoH of 87.31 after 1.96 years. This usage sequence will require new battery packs every 3.09 years. On the other hand, PAFC and PEMFC designs did not require battery integration during operation as frequently as the SOFC. The final SoHs for these designs were 98.35% and 97.54%, respectively, leading to 23.71 and 15.91 years of projected battery life spans regarding the SoH curves.
Hybrid 6 scenario assessed the sole usage of batteries and WHRS. In this design, battery packs were used continuously throughout the operation, and the final SoH was calculated at 79.84% after 1.96 years of operation. Considering this outcome, the Hybrid 6 scenario will require battery renewal every 1.94 years. Table 10 indicates FC lifespan, total usage times, and the number of expected renewals during the system lifetime for scenarios.

Table 10.
Lifespan, usage time and number of required renewals of FC and batteries.
In Figure 6, the general usage time of FCs has been demonstrated, while Table 10 indicates the total FC time calculated by the running hour distribution with the number of working FCs. In Table 10, if the estimated lifespan based on usage time behaviour exceeds ten years, it has been standardised to a maximum of ten years. In other words, even if the battery’s lifespan exceeds ten years, it is assumed to be replaced in the tenth year in the economic analysis. Figure 7 illustrates the fuel consumption distribution of the scenarios throughout the 1.96-year operation period. The total FC usage time involves the parallel running times and is calculated by multiplying the number of FCs by their utilisation hours. Figure 7 illustrates the fuel consumption distribution of the scenarios.
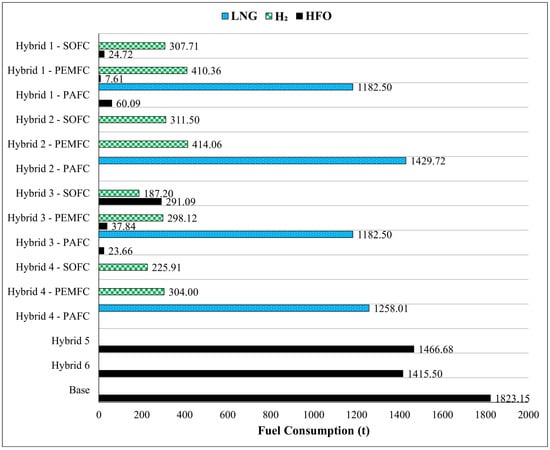
Figure 7.
Fuel consumption distribution of scenarios.
Fossil fuel usage can be close to zero in PEMFC and SOFC scenarios. The sole utilisation of WHRS (Hybrid 5) has decreased the HFO consumption of the plant by 19.55%, while the addition of battery packs (Hybrid 6) has increased this reduction to 22.36%. The SOFCs provided a lower H2 consumption compared to PEMFCs. The tank capacity for the HFO tanks has been 50.14% of the annual total consumption, according to the M/E and A/E data. Considering the same principle, HFO tanks for A/Es have been adjusted. The H2 and LNG capacities have been determined for 60 days of bunkering. Table 11 depicts the calculated tank capacities of the hybrid cases.

Table 11.
Tank capacities of the configurations.
In the base case scenario, the D/G fuel tank capacity is 467.68 m3. For each configuration, the D/G fuel tank capacity has been adjusted downward by the fuel-saving ratios on HFO. The additional LNG and H2 tanks have been designed to meet the plant’s sixty-day fuel demand, replacing the need for HFO capacity. The volumes of the H2 tanks have been calculated based on the compressed state of the H2. The PAFC-utilized cases have required less volume since there has been no requirement for H2 tanks. The volume reductions can be added to the HFO, LNG or H2 depending on the vessel’s demand, equipment type, or bunkering options.
An onboard H2 production facility could reduce H2 storage capacities in H2-FC combinations. This would extend the intervals between bunkering, enabling more reliable operation. However, for this study, sixty-day bunkering capacities to meet the minimum navigation requirements of the vessel have been utilised in the economic analyses. In other words, the capacities have been calculated based on all fuels being bunkered through external facilities.
On the other hand, within this frequent bunkering interval, existing ships can be retrofitted to accommodate these systems, considering weight and volume requirements. Table 11 shows reductions left as safety margins in tank capacities, which can be utilised as additional tank capacity to extend bunkering intervals or meet FCs’ additional space requirements.
3.2. Environmental Outcomes
Figure 8 indicates the upstream and operational GHGs and yielding CO2-eq of the system configurations for the operation time of 1.96 years.
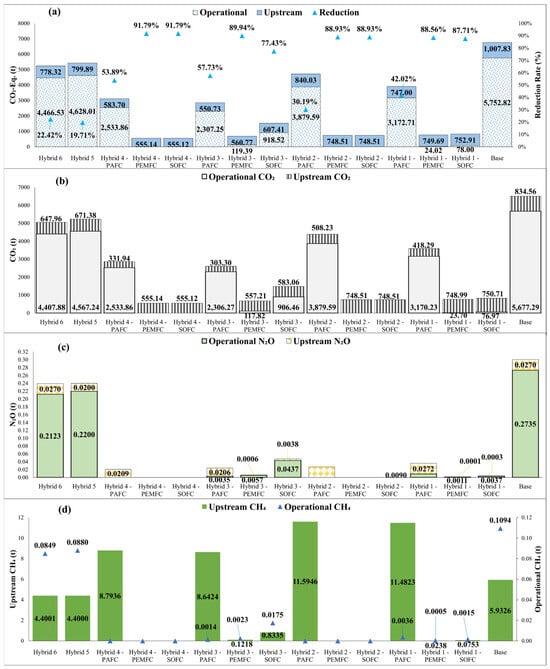
Figure 8.
The operational and upstream (a) CO2-eq, (b) CO2, (c) N2O, and (d) CH4 emissions of the scenarios.
Figure 8a illustrates the upstream and operational CO2-eq emissions for each scenario and the total reduction rates compared to the base case. The left vertical axis represents the CO2-eq amounts, while the right vertical axis indicates the reduction ratio. For example, the Hybrid 5 scenario shows operational and upstream CO2-eq values of 4628.01 and 799.99 tonnes, respectively, resulting in a total CO2-eq reduction of 19.71%. The GHG emissions used to calculate the CO2-eq are presented in the subfigures of Figure 8. Upstream and operational CO2 emissions of the configurations have been illustrated in Figure 8b. For instance, Hybrid 1, including PEMFC (Hybrid 1-PEMFC), has emitted 23.70 t operational and 748.99 t upstream CO2. In Figure 8c, operational and upstream N2O emissions for the same case have been reported as 0.0011 and 0.0001, respectively. Figure 8d presents the operational and upstream CH4 emissions on separate axes due to the difference in their quantities. The triangle markers denote the operational CH4 emissions, which can be read from the right vertical axis, while the column chart represents the upstream emissions, viewable on the left vertical axis. For example, the Hybrid 3 scenario involving SOFCs (Hybrid 3-SOFC) generated 0.02 tonnes of operational CH4 and 0.83 tonnes of upstream CH4.
PAFC scenarios generated higher CH4 emissions due to the LNG usage on the plant. Hybrid 2 and 4 scenarios involving PEMFC and SOFC (Hybrid 2-PEMFC, Hybrid 2-SOFC, Hybrid 4-PEMFC, Hybrid 4-SOFC) produced zero CH4 and N2O emissions and provided the most significant reduction in CO2 emissions due to eliminating diesel engines. These configurations have achieved the most significant decrease in total CO2-eq at 91.79% and 88.93%, respectively. Hybrid 4 scenario, including PEMFC and SOFC, has decreased overall CO2-eq, including M/E emissions, by 15.53%. Hybrid 3 design with PAFCs has achieved the most significant reduction in marine electricity generation plant CO2-eq, at 57.73%, among other PAFC scenarios, which equals 9.76% of the vessel’s CO2-eq. Figure 9 indicates the other emissions of the scenarios and reduction ratios compared to the base case for the total operation time.
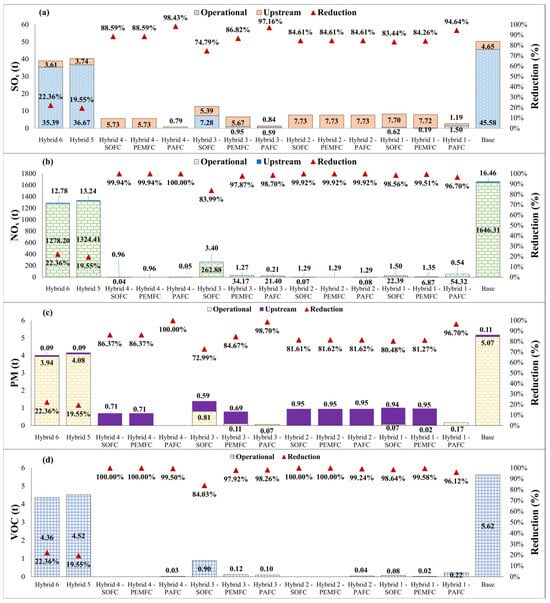
Figure 9.
The operational and upstream (a) SOx, (b) NOx, (c) PM, and (d) VOC emissions of the scenarios.
In Figure 9, the triangles indicate the total emission reduction ratios, the solid bars represent upstream emissions, and the textured bars depict operational emissions. The left y-axis shows the emissions in tones, and the right vertical axis indicates the reduction ratios compared to the base case.
Figure 9a indicates the SOx emissions of designs. The highest elimination rate (97.16%) has been achieved by Hybrid 3 configurations involving PAFC (Hybrid 3-PAFC) with the upstream and operational SOx at 0.84 and 0.59 t, respectively. Figure 9b shows the plant’s NOx emissions, which Hybrid 4-PAFC has eliminated. SOFC and PEMFC plants have effectively prevented NOx emissions as well. For example, Hybrid 4-SOFC eliminated 99.94% of NOx, with upstream and operational emissions totalling just 0.96 and 0.04 tonnes, respectively. Figure 9c shows that PM emissions have been eliminated by Hybrid 4-PAFC, while Hybrid 1 and 3-PAFC configurations achieved near-complete prevention.
The remaining configurations achieved emission reductions ranging from 80.48% to 86.37%. Hybrid 3-SOFC performed the worst among the FC configurations, primarily due to increased D/G usage, resulting in a 72.99% reduction in PM, with upstream and operational PM emissions at 0.59 and 0.81 tonnes, respectively. Figure 9d depicts the VOC emissions, excluding upstream emissions from this calculation. Hybrid 2 and 4 configurations of SOFC and PEMFC eliminated operational VOC emissions, while other FC designs achieved reduction rates exceeding 96%. Like PM, Hybrid 3-SOFC configuration demonstrated the lowest performance among the FC scenarios, with a reduction rate of 84.03% and VOC emissions at 0.90 tonnes.
3.3. Energy Efficiency Metrics Results
Figure 10 illustrates the attained EEXI values and the corresponding reductions for the analysed configurations.
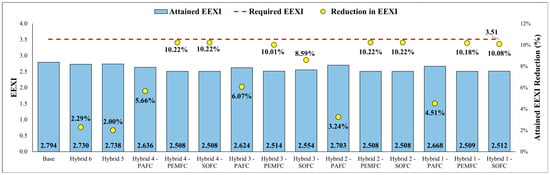
Figure 10.
Attained EEXI values of combinations.
The required EEXI for the case study bulk carrier, represented by the dashed line in Figure 10, has been calculated at 3.51 using Equation (10). The base case meets the current EEXI requirements because the vessel, built in 2019, must comply with Phase 1 EEDI standards. The attained EEXI values have been shown as bars in Figure 10 for each case and can be read from the left-vertical axis. The deduction rates of EEXI compared to the base case have been depicted as circle markers and can be viewed on the right y-axis of the chart.
The zero-carbon emitter cases have achieved the most significant reductions, specifically Hybrid 2 and 4 configurations running on SOFC and PEMFC, with an attained EEXI of 2.508 and a 10.22% reduction from the base case. PAFC-utilized cases have performed worse than other FC types due to the use of LNG. The Hybrid 3-PAFC configuration has achieved the most significant reduction in EEXI among PAFC cases, with a 6.07% decrease and an attained EEXI of 2.703. Hybrid 6 and 5 cases ensured 2.29% and 2% decreases in the attained EEXI, respectively. Figure 11 shows the attained CII of base and zero-carbon A/E scenarios.
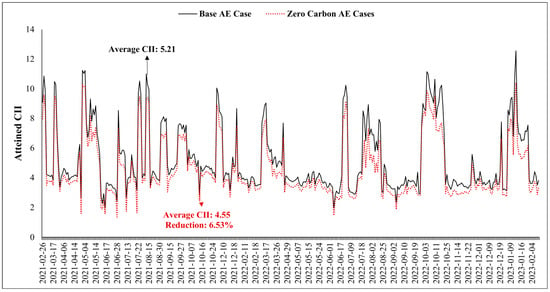
Figure 11.
The CII variation of base and zero-carbon cases was attained.
The operational data from close to two years have been used to calculate the attained CII values for the base and zero-carbon cases for comparison. The average CII value has been reduced by 6.53% by eliminating the A/E-sourced CO2. This reduction elevates the CII rating of the vessel by one level.
3.4. Economic Model Results
Figure 12 illustrates the economic performance of scenarios according to year and low, medium, or high projection ratios shown in Table 9. The in the LCOE calculation shown in Equation (13) has been computed by multiplying the annual rates with the 2024 prices.
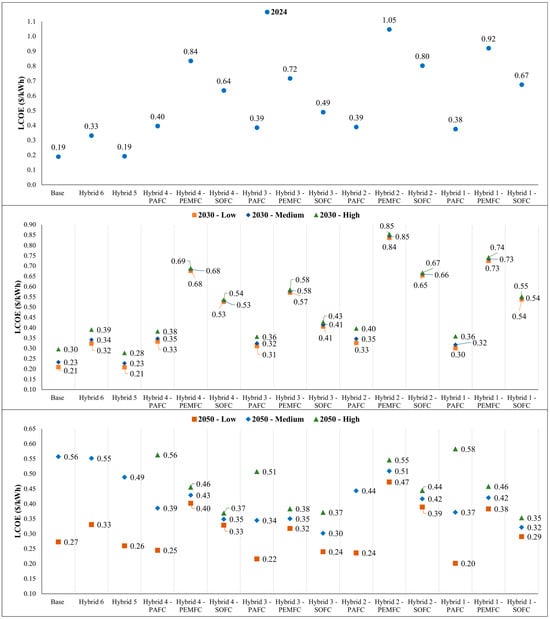
Figure 12.
LCOE of hybrid scenarios considering the economic projection cases and year.
In 2024, the lowest LCOE was achieved by the base case at 0.19 USD/kWh, while the largest was by Hybrid 2-PEMFC at 1.05 USD/kWh. Among the FC-used scenarios, Hybrid 1-PAFC is closest to the base case at 0.38 USD/kWh. In 2030, depending on the economic projection scenario, Hybrid 3-PAFC and Hybrid 1-PAFC configurations are projected to perform similarly to the base case, with estimated LCOEs between USD 0.30 and USD 0.36 per kWh. By 2050, due to the widening disparities in carbon prices under high economic projection scenarios, both the base case and PAFC configurations have emerged as the poorest performers. However, under the low economic projections for 2050, the Hybrid 3-PAFC configuration has achieved the lowest LCOE at 0.22 USD/kWh, nearly matching the base case LCOE from 2024. In the medium and high projected scenarios in 2050, Hybrid 3-SOFC at 0.30 USD/kWh and Hybrid 1-SOFC at 0.32 USD/kWh have shown the best performances.
The base scenario has been the most economical option regarding the whole scenario; however, the gap between hybrid scenarios and conventional systems will be reduced starting from 2030 due to the increased carbon tax. Hybrid systems, including PAFCs, have performed best in economics because they lack expensive H2 equipment and fuel. Hybrid 3-SOFC and Hybrid 1-SOFC have been the most successful among H2-utilized cases. PEMFCs have shown an LCOE close to the SOFC scenarios. The sole WHRS or WHRS-battery addition has increased the LCOE slightly compared to the base case. The renewal costs of batteries and FCs have decreased the economic performance of the scenarios. The H2 storage, pressurisation, and transfer (P/T) have primarily impacted the financial performance since their portion has significantly increased the . For the distribution of , the system’s configuration is illustrated for 2024, 2030, and 2050 in Table 12.

Table 12.
Rates of equipment regarding the total investment costs of evaluated configurations for the 2024, 2030, and 2050 scenarios.
Table 12 presents the cost ratios for each equipment type across different years and configurations. For instance, in 2030, the of Hybrid 3-PEMFC configuration has been calculated at USD 18,445,127 and equipment price distributions are as follows: FC at USD 3,489,439 (18.92%), Battery at USD 195,350 (1.06%), H2 Storage at USD 10,702,593 (58.02%), P/T Equipment at USD 2,088,640 (11.32%), WHRS at USD 1,348,578.56 (7.31%), MDE at USD 605,996.64 (3.29%), and HFO Storage at USD 14,530 (0.08%). The of each configuration have been demonstrated in Appendix A.
Even though it is predicted to decrease in 2050, the H2 storage tanks have been the most significant portion of the , followed by the P/T equipment. values of FCs are the third most expensive item. Figure 13 indicates the EPC of each configuration for 2024, 2030, and 2050.
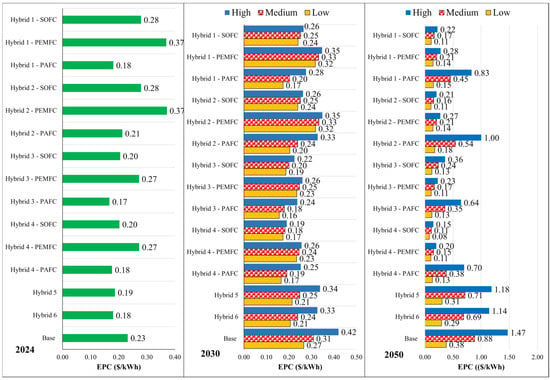
Figure 13.
EPC of hybrid scenarios considering the economic projection cases and year.
Considering the fuel prices and estimated carbon taxes, the EPC of the base scenario has increased remarkably over the years. Adding batteries and WHRS decreases the EPC significantly compared to the base scenario. They have a lower EPC compared to the base scenario in 2024. The PAFCs have exceeded all cases due to the cost-friendly LNG usage on the plant. They are the most feasible among all hybrid cases in 2024. Hybrid 3-SOFC and Hybrid 4-SOFC scenarios have reduced the EPC below the conventional system in 2024. The 2030 4th hybrid scenario has become the configuration with the lowest H2-used scenario EPC, followed by the 4th PEMFC design. PAFC scenarios regarding EPC in the upcoming years have not been as feasible as in 2024 due to the LNG utilisation resulting in increased CO2.
3.5. TOPSIS Outcomes
Table 13 demonstrates the overall ranking of configurations assigned by the MCDM using the TOPSIS methodology.

Table 13.
values and rank of each configuration regarding TOPSIS.
The values for each configuration in the projected economic scenarios are presented alongside their corresponding ranks in Table 13. A higher value yields a higher rank. The detailed calculation process is provided in Appendix B. The TOPSIS approach has provided an overall demonstration based on the different analyses applied in the study.
4. Discussion
By considering the economic and environmental benefits in addition to the dimensions of equipment equally, the highest-ranked configuration is Hybrid 3-PEMFC for all projection scenarios. Hybrid 4-PEMFC is the second preferred option, while the SOFC scenarios follow them. In fact, for 2050 high-case economic projection, it is detected as the most suitable system. The financial and environmental performances of PEMFC and SOFC have been close to each other. The changemaker aspect in the MCDM has been the dimension and weight of the equipment. PEMFCs analysed in the study provide much better power density than the PAFC scenarios. Although PAFC scenarios will be economically successful in 2024, CO2 reduction will not be enough for these designs in the coming years. The WHRS and battery additions have improved the performance, but it is not enough to meet the 2050 decarbonisation targets.
The study findings comply with the literature findings that the PEMFC is the highest-ranked option. Sohani, et al. [24] stated that the PEMFCs have emerged as the preferred FC type because of their research’s electrical efficiency and technological development. Seyfi, et al. [36] selected the PEMFC as the most prominent choice for marine applications in their MCDM analysis while Inal, et al. [19] demonstrated the benefits of PEMFCs on the marine electricity generation plant. Compared to studies examining MCFC and PAFC, they have provided a more significant reduction in GHG emissions [4,39]. In terms of environmental and economic benefits, SOFCs have been equal or, in some cases, superior to PEMFCs since they have the potential to provide zero-carbon operations. [34,65]. Their main disadvantage is the power density yielding higher space requirements on board ships [76]. The startup times and temperatures of PEMFCs have been advantageous compared to SOFCs and PAFCs [94,95].
PAFC configurations have not provided CO2-eq deductions like PEMFCs and SOFCs; however, they have provided a satisfactory reduction in some configurations. Especially considering the technological maturity of H2 bunkering on marine vessels, they are running on LNG, which is ready-to-use fuel for the current applications. They have performed successfully in the economic analysis due to the lack of H2 usage and the price of LNG and carbon in 2024. The bunkering networks of LNG are much more active and usable compared to H2 right now; therefore, running on H2 solely cannot be achieved or can limit the working area of the vessel in 2024 conditions [96].
The implementation of WHRS in the systems, in general, increases emission reduction, and it is an economically viable option [18]. The scenarios involving constant battery usage require frequent changes over a lifetime, decreasing the economic performance of these cases. Balanced usage by employing the EMS and selecting the correct capacity for FCs and WHRS can be ensured and increases the economic feasibility as well as the battery waste management [17].
Hybrid configurations have thus far been evaluated primarily for ship electrification systems, achieving up to a 15.53% reduction in total CO2-eq emissions for the vessel. Integrating zero-carbon electrification with LNG-fuelled DF engines can amplify this reduction to approximately 50% [34]. DF engines operating on LNG within a diesel-electric propulsion system offer the potential to reduce CO2-eq emissions by up to 20% [97], while ensuring compliance with the EEXI and CII requirements [41]. Gas and steam turbines, for example, exhibit significant potential for carbon reduction; in particular, analyses have demonstrated superior environmental performance compared to DF engines [98]. The decrease in emissions can be further augmented by integrating carbon-free fuels such as ammonia or H2, which are increasingly recognised for their role in sustainable energy transitions [99].
However, the emission reductions achieved by these systems using currently available alternative fuels remain insufficient to meet the ambitious decarbonisation targets set for 2050. To address this gap, these systems must be supplemented with advanced alternative energy systems and transitioned to operate on carbon-neutral fuels [5,97]. Among the complementary solutions, FCs have emerged as promising future energy systems to enhance the performance of both turbines and DF engines. Furthermore, H2 is widely regarded as the most viable alternative fuel for the shipping industry, given its potential to enable substantial emissions reductions and facilitate long-term sustainability [94].
5. Conclusions
The study evaluated several hybrid configurations, including various power settings for batteries, WHRS, and commercially reachable FC types for marine vessels on marine electricity generation plants of the reference bulk carrier.
Findings revealed that active battery usage in Hybrid 3-SOFC and Hybrid 5 designs significantly reduces battery lifespan, necessitating frequent replacements that diminish economic performance significantly when renewals exceed three during the system’s lifetime. Similarly, low-powered FC configurations experienced reduced lifespans due to consistently utilising the same unit.
The minimum FC plant power was determined to be 400 kW based on the electricity demand of the case study vessel. Incorporating WHRS power enhanced both economic and environmental performance. Among FC scenarios, LNG-utilized PAFC configurations provided short-term benefits regarding tank capacities and financial performance. SOFC-included designs were slightly more favourable economically among H2-based cases, while PEMFC configurations excelled in meeting equipment space and volume requirements.
Green-H2 utilised FCs achieve the most significant CO2-eq reductions in Hybrid 2 and 4 configurations (15.53% of total vessel emissions), with near-zero non-GHG emissions from the electrification unit observed in all FC-utilized scenarios. These technologies also deliver the lowest EEXI and CII in these designs.
For 2030 targets, LNG-PAFCs exhibited a significant reduction in GHG emissions (9.76% of total vessel emissions) with an LCOE of 0.38 USD/kWh projected for 2024, decreasing to 0.30 USD/kWh under 2030 scenarios. These values, particularly under 2030 conditions, approach those of fossil fuel usage even under minimal carbon penalty schemes. Consequently, LNG-PAFCs emerge as a viable option for meeting 2030 and 2040 targets, balancing economic feasibility with fuel management considerations.
Based on MCDM analysis, PEMFCs in Hybrid 3 ranked highest overall across most economic scenarios, followed by the PEMFC-based Hybrid 4 configuration. Looking further toward 2050 targets, H2-utilized FCs are essential. The challenges posed by storage costs and capacity limitations can be addressed by incorporating onboard H2 production facilities, paving the way for a more sustainable and scalable solution.
Limitations of the analyses used in the study can be listed as follows:
- In the economic analysis, the equipment costs unavailable for future projections have been taken as constant.
- The bunkering interval for hybrid configurations has been set to 60 days.
- The energy consumption and grid load data have been utilised to compute the H2 and LNG (if used) utilisation of FCs.
- Scrap prices for batteries and FCs have not been included.
This study contributed to the literature by presenting a detailed assessment of retrofit options on marine electricity generation plants to achieve the decarbonisation targets set by IMO using the simulation framework developed by the authors. The findings are helpful for academics interested in maritime decarbonisation, marine system innovators, ship power system designers, and battery, FC, or WHRS manufacturers willing to develop systems for the maritime industry.
Future studies will focus on designing an onboard H2 production unit tailored to the needs of the system design proposed in this paper. The life-cycle environmental impact and economic performance of various H2 carriers, including ammonia, dimethyl ether, and CH4, may be evaluated. Incorporating a decomposition system could further exOnur tend the 60-day bunkering interval.
Another research direction would be implementing the simulation and decision support framework on vessels of different types and sizes to gather data and build an application with a more customisable interface to evaluate retrofit options for A/Es depending on the user’s needs. An advanced EMS, supported by machine learning or deep learning algorithms to detect load demand increments more accurately, could also be a potential direction for future research.
Author Contributions
Conceptualization, O.Y., E.B.-D. and M.A.; methodology, O.Y., E.B.-D., J.W. and V.S.; software, O.Y.; validation, O.Y. and N.T.; formal analysis, O.Y., E.B.-D., M.A., V.S., M.C.D.P. and M.P.; investigation, O.Y., E.B.-D., A.S., D.H. and V.S.; resources, E.B.-D., J.W., N.T., M.C.D.P. and M.P.; data curation, N.T., O.Y., M.C.D.P. and M.P.; writing—original draft preparation, O.Y., E.B.-D., A.S., D.H., V.S. and J.W.; review and editing, O.Y., E.B.-D., A.S., D.H., V.S., M.C.D.P., M.P. and J.W.; visualisation, O.Y., E.B.-D., A.S., D.H., V.S., M.C.D.P. and J.W.; supervision, J.W., E.B.-D., M.C.D.P. and M.P.; project administration, E.B.-D., A.S. and M.P.; funding acquisition, E.B.-D., A.S., M.A., N.T. and M.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Retrofit Solutions to Achieve 55% GHG Reduction by 2030, grant number 10064483 from UKRI and from EU (grant number: Horizon Europe 101096068).
Data Availability Statement
The dataset is available upon request from the authors.
Conflicts of Interest
Author Nikolaos Tsoulakos was employed by the company Laskaridis Shipping Co., Ltd. Milad Armin was the owner of the company Enki Marine Technology Consultancy. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
| Abbreviation | Explanation | Unit |
| A/Es | Auxiliary engines | - |
| AFC | Alkaline fuel cell | - |
| Actual battery capacity | Ah | |
| Available battery capacity after usage | Ah | |
| Emission coefficient for fuel cells | - | |
| Relative closeness coefficient | - | |
| Initial battery capacity | Ah | |
| Operation and maintenance cost | USD | |
| Specific heat rate of the exhaust | kJ/kg·K | |
| Capital cost of systems. | USD | |
| Fuel prices | USD | |
| CC-CV | Constant current, constant voltage | - |
| CEPCI | Chemical Engineering Plant Cost Index | - |
| CH4 | Methane | - |
| CII | Carbon intensity indicator | - |
| CO2 | Carbon dioxide | - |
| CO2-eq | Carbon dioxide equivalent | - |
| Decision matrix member | - | |
| D/G | Marine diesel generator | |
| Distance Travelled | nm | |
| DF | Dual fuel | |
| DWT | Deadweight | t |
| EEXI | Energy efficiency existing index | |
| EMS | Energy management strategy | - |
| EPC | Energy Pro | |
| ICE fuel consumption | t | |
| FC | Fuel cell | |
| FCe | Emissions of fuel cells | t |
| GHG | Greenhouse gases | - |
| H2 | Hydrogen | - |
| HFO | Heavy fuel oil | - |
| I | Current | A |
| ICE | Internal combustion engine | - |
| M/E | Main engine | - |
| MCDM | Multi-criteria decision making | - |
| MCFC | Molten carbonate fuel cell | - |
| LCA | Life cycle assessment | - |
| LCOE | Levelized cost of energy | - |
| LHV | Lower heating value | kJ/kg |
| LNG | Liquefied natural gas | - |
| PAFC LNG consumption coefficient | Nm3/kWh | |
| LT | Lifetime | years or h |
| Exhaust mass flow rate | kg/s | |
| Number of fuel cells | - | |
| Number of ICEs | - | |
| NOx | Nitrogen oxides | - |
| N2O | Nitrogen dioxide | - |
| OEC | Operational emission coefficient | - |
| ORC | Organic Rankine cycle | - |
| P/T | Pressurisation and transfer | - |
| PFC | Fuel cell power | kW |
| Generated total plant power | kW | |
| PAFC | Phosphoric acid fuel cell | - |
| PEMFC | Proton exchange membrane fuel cell | - |
| PM | Particulate matter | - |
| PV | Photovoltaic | - |
| r | Discount (interest) rate | - |
| Normalised matrix element | - | |
| The Euclidean distance between each weighted and | - | |
| The Euclidean distance between each weighted and . | ||
| SFC | Specific fuel consumption | - |
| Specific fuel consumption of ICE | - | |
| SOx | Sulphur oxides | - |
| SoC | State of charge | - |
| SoH | State of health | |
| SOFC | Solid oxide fuel cell | - |
| t | Operation time | h, min, or year |
| The inlet temperature of the exhaust (after the exhaust boiler) | K | |
| Outlet temperature from ORC | K | |
| TOPSIS | Technique for order of preference by similarity to the ideal solution | - |
| UEC | Upstream emission coefficient | - |
| WHRS power outcome | kW | |
| WHRS | Waste heat recovery system | |
| Positive ideal solution | - | |
| Weighted normalised matrix member | - | |
| Negative ideal solution | - | |
| Reference speed | kn | |
| VOCs | Volatile organic compounds | |
| X | Reduction factor for EEXI | - |
| Z | Reduction factor for CII | - |
| Greek Symbols | ||
| Columbic efficiency | - | |
| Efficiency of fuel cell | - | |
| Organic Rankine cycle efficiency | - | |
Appendix A

Table A1.
The installation costs of configurations.
Table A1.
The installation costs of configurations.
| Configuration | Installation Cost (USD) | ||
|---|---|---|---|
| 2024 | 2030 | 2050 | |
| Base | 2,518,147 | 2,518,147 | 2,518,147 |
| Hybrid 6 | 9,953,031 | 8,916,245 | 7,079,778 |
| Hybrid 5 | 3,710,175 | 3,710,175 | 3,710,175 |
| Hybrid 4-PAFC | 12,143,370 | 9,741,555 | 6,817,156 |
| Hybrid 4-PEMFC | 28,436,738 | 22,535,778 | 13,785,657 |
| Hybrid 4-SOFC | 21,629,919 | 17,594,686 | 11,361,953 |
| Hybrid 3-PAFC | 12,034,529 | 9,155,989 | 5,903,566 |
| Hybrid 3-PEMFC | 23,853,036 | 18,445,127 | 10,506,343 |
| Hybrid 3-SOFC | 15,891,316 | 12,710,261 | 6,987,796 |
| Hybrid 2-PAFC | 11,165,203 | 8,701,677 | 5,568,274 |
| Hybrid 2-PEMFC | 34,996,877 | 27,224,854 | 15,717,850 |
| Hybrid 2-SOFC | 26,725,645 | 21,283,587 | 12,997,095 |
| Hybrid 1-PAFC | 11,335,142 | 8,350,778 | 4,668,677 |
| Hybrid 1-PEMFC | 30,113,218 | 22,936,068 | 12,335,835 |
| Hybrid 1-SOFC | 21,837,489 | 16,851,597 | 9,251,150 |
Appendix B

Table A2.
The decision, normalized and weighted normalized matrices, positive and negative ideal solutions.
Table A2.
The decision, normalized and weighted normalized matrices, positive and negative ideal solutions.
| Configuration | Tank Capacity | CO2,eq (t/h) | Other Emissions (t/h) | Weight | Volume | LCOE | 2030 | 2050 | EPC | 2030 | 2050 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2024 | Low | Medium | High | Low | Medium | High | 2024 | Low | Medium | High | Low | Medium | High | ||||||
| Base | 2738.30 | 0.39 | 0.1004 | 25.25 | 49.96 | 0.19 | 0.19 | 0.21 | 0.23 | 0.30 | 0.27 | 0.56 | 0.89 | 0.23 | 0.27 | 0.31 | 0.42 | 0.38 | 0.88 |
| Hybrid 6 | 2646.86 | 0.31 | 0.0780 | 11.9 | 17.45 | 0.33 | 0.33 | 0.32 | 0.34 | 0.39 | 0.33 | 0.55 | 0.81 | 0.18 | 0.21 | 0.24 | 0.33 | 0.29 | 0.69 |
| Hybrid 5 | 2633.73 | 0.32 | 0.0808 | 8.416 | 16.65 | 0.19 | 0.19 | 0.21 | 0.23 | 0.28 | 0.26 | 0.49 | 0.75 | 0.19 | 0.21 | 0.25 | 0.34 | 0.31 | 0.71 |
| Hybrid 4-PAFC | 2548.70 | 0.18 | 0.0001 | 57.18 | 65.24 | 0.40 | 0.40 | 0.33 | 0.35 | 0.38 | 0.25 | 0.39 | 0.56 | 0.18 | 0.17 | 0.19 | 0.25 | 0.13 | 0.38 |
| Hybrid 4-PEMFC | 2670.61 | 0.03 | 0.0004 | 15.27 | 21.52 | 0.84 | 0.84 | 0.68 | 0.68 | 0.69 | 0.40 | 0.43 | 0.46 | 0.27 | 0.23 | 0.24 | 0.26 | 0.11 | 0.15 |
| Hybrid 4-SOFC | 2567.87 | 0.03 | 0.0004 | 41.88 | 47.9 | 0.64 | 0.64 | 0.53 | 0.53 | 0.54 | 0.33 | 0.35 | 0.37 | 0.20 | 0.17 | 0.18 | 0.19 | 0.08 | 0.11 |
| Hybrid 3-PAFC | 2538.08 | 0.17 | 0.0014 | 45.98 | 62.08 | 0.39 | 0.39 | 0.31 | 0.32 | 0.36 | 0.22 | 0.34 | 0.51 | 0.17 | 0.16 | 0.18 | 0.24 | 0.13 | 0.35 |
| Hybrid 3-PEMFC | 2672.58 | 0.04 | 0.0025 | 19.69 | 35.61 | 0.72 | 0.72 | 0.57 | 0.58 | 0.58 | 0.32 | 0.35 | 0.38 | 0.27 | 0.23 | 0.25 | 0.26 | 0.11 | 0.17 |
| Hybrid 3-SOFC | 2591.60 | 0.09 | 0.0164 | 28.62 | 43.87 | 0.49 | 0.49 | 0.41 | 0.41 | 0.43 | 0.24 | 0.30 | 0.37 | 0.20 | 0.19 | 0.20 | 0.22 | 0.13 | 0.24 |
| Hybrid 2-PAFC | 2586.66 | 0.27 | 0.0001 | 68.99 | 74.72 | 0.39 | 0.39 | 0.33 | 0.35 | 0.40 | 0.24 | 0.44 | 0.70 | 0.21 | 0.20 | 0.24 | 0.33 | 0.18 | 0.54 |
| Hybrid 2-PEMFC | 2815.43 | 0.04 | 0.0006 | 16.32 | 22.58 | 1.05 | 1.05 | 0.84 | 0.85 | 0.85 | 0.47 | 0.51 | 0.55 | 0.37 | 0.32 | 0.33 | 0.35 | 0.14 | 0.21 |
| Hybrid 2-SOFC | 2680.49 | 0.04 | 0.0006 | 51.77 | 58.03 | 0.80 | 0.80 | 0.65 | 0.66 | 0.67 | 0.39 | 0.42 | 0.44 | 0.28 | 0.24 | 0.25 | 0.26 | 0.11 | 0.16 |
| Hybrid 1-PAFC | 2547.43 | 0.23 | 0.0034 | 47.12 | 62.34 | 0.38 | 0.38 | 0.30 | 0.32 | 0.36 | 0.20 | 0.37 | 0.58 | 0.18 | 0.17 | 0.20 | 0.28 | 0.15 | 0.45 |
| Hybrid 1-PEMFC | 2812.52 | 0.05 | 0.0010 | 20.74 | 36.67 | 0.92 | 0.92 | 0.73 | 0.73 | 0.74 | 0.38 | 0.42 | 0.46 | 0.37 | 0.32 | 0.33 | 0.35 | 0.14 | 0.21 |
| Hybrid 1-SOFC | 2681.84 | 0.05 | 0.0019 | 38.51 | 54 | 0.67 | 0.67 | 0.54 | 0.54 | 0.55 | 0.29 | 0.32 | 0.35 | 0.28 | 0.24 | 0.25 | 0.26 | 0.11 | 0.17 |
| Normalized Matrix | |||||||||||||||||||
| Base | 0.27 | 0.53 | 0.66 | 0.17 | 0.27 | 0.08 | 0.08 | 0.11 | 0.12 | 0.14 | 0.22 | 0.34 | 0.40 | 0.24 | 0.30 | 0.32 | 0.37 | 0.53 | 0.53 |
| Hybrid 6 | 0.26 | 0.41 | 0.51 | 0.08 | 0.09 | 0.14 | 0.14 | 0.17 | 0.17 | 0.19 | 0.27 | 0.34 | 0.37 | 0.19 | 0.23 | 0.25 | 0.29 | 0.41 | 0.41 |
| Hybrid 5 | 0.26 | 0.42 | 0.53 | 0.06 | 0.09 | 0.08 | 0.08 | 0.11 | 0.12 | 0.14 | 0.21 | 0.30 | 0.34 | 0.19 | 0.24 | 0.26 | 0.30 | 0.42 | 0.43 |
| Hybrid 4-PAFC | 0.25 | 0.24 | 0.00 | 0.39 | 0.35 | 0.17 | 0.17 | 0.17 | 0.18 | 0.19 | 0.20 | 0.24 | 0.26 | 0.18 | 0.19 | 0.20 | 0.22 | 0.18 | 0.23 |
| Hybrid 4-PEMFC | 0.26 | 0.04 | 0.00 | 0.10 | 0.12 | 0.35 | 0.35 | 0.35 | 0.35 | 0.34 | 0.33 | 0.26 | 0.21 | 0.28 | 0.27 | 0.25 | 0.22 | 0.15 | 0.09 |
| Hybrid 4-SOFC | 0.25 | 0.04 | 0.00 | 0.29 | 0.26 | 0.27 | 0.27 | 0.27 | 0.27 | 0.26 | 0.27 | 0.21 | 0.17 | 0.21 | 0.20 | 0.19 | 0.17 | 0.11 | 0.07 |
| Hybrid 3-PAFC | 0.25 | 0.22 | 0.01 | 0.32 | 0.33 | 0.16 | 0.16 | 0.16 | 0.16 | 0.17 | 0.18 | 0.21 | 0.23 | 0.17 | 0.18 | 0.19 | 0.21 | 0.17 | 0.21 |
| Hybrid 3-PEMFC | 0.26 | 0.05 | 0.02 | 0.14 | 0.19 | 0.30 | 0.30 | 0.29 | 0.29 | 0.29 | 0.26 | 0.21 | 0.17 | 0.28 | 0.27 | 0.26 | 0.23 | 0.15 | 0.10 |
| Hybrid 3-SOFC | 0.25 | 0.12 | 0.11 | 0.20 | 0.24 | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | 0.20 | 0.18 | 0.17 | 0.21 | 0.21 | 0.21 | 0.20 | 0.17 | 0.14 |
| Hybrid 2-PAFC | 0.25 | 0.37 | 0.00 | 0.47 | 0.40 | 0.16 | 0.16 | 0.17 | 0.18 | 0.19 | 0.19 | 0.27 | 0.32 | 0.22 | 0.23 | 0.25 | 0.29 | 0.24 | 0.33 |
| Hybrid 2-PEMFC | 0.27 | 0.06 | 0.00 | 0.11 | 0.12 | 0.44 | 0.44 | 0.43 | 0.43 | 0.42 | 0.39 | 0.31 | 0.25 | 0.39 | 0.36 | 0.35 | 0.31 | 0.20 | 0.12 |
| Hybrid 2-SOFC | 0.26 | 0.06 | 0.00 | 0.35 | 0.31 | 0.34 | 0.34 | 0.34 | 0.33 | 0.33 | 0.32 | 0.25 | 0.20 | 0.29 | 0.27 | 0.26 | 0.23 | 0.15 | 0.09 |
| Hybrid 1-PAFC | 0.25 | 0.31 | 0.02 | 0.32 | 0.33 | 0.16 | 0.16 | 0.16 | 0.16 | 0.18 | 0.17 | 0.23 | 0.26 | 0.19 | 0.20 | 0.21 | 0.24 | 0.21 | 0.27 |
| Hybrid 1-PEMFC | 0.27 | 0.06 | 0.01 | 0.14 | 0.20 | 0.39 | 0.39 | 0.37 | 0.37 | 0.36 | 0.31 | 0.26 | 0.21 | 0.38 | 0.36 | 0.35 | 0.30 | 0.20 | 0.13 |
| Hybrid 1-SOFC | 0.26 | 0.06 | 0.01 | 0.26 | 0.29 | 0.28 | 0.28 | 0.28 | 0.28 | 0.27 | 0.24 | 0.20 | 0.16 | 0.29 | 0.27 | 0.26 | 0.23 | 0.15 | 0.10 |
| Weighted Normalized Matrix | |||||||||||||||||||
| Base | 0.04 | 0.08 | 0.09 | 0.02 | 0.04 | 0.01 | 0.01 | 0.02 | 0.02 | 0.02 | 0.03 | 0.05 | 0.06 | 0.03 | 0.04 | 0.05 | 0.05 | 0.08 | 0.08 |
| Hybrid 6 | 0.04 | 0.06 | 0.07 | 0.01 | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 | 0.03 | 0.04 | 0.05 | 0.05 | 0.03 | 0.03 | 0.04 | 0.04 | 0.06 | 0.06 |
| Hybrid 5 | 0.04 | 0.06 | 0.08 | 0.01 | 0.01 | 0.01 | 0.01 | 0.02 | 0.02 | 0.02 | 0.03 | 0.04 | 0.05 | 0.03 | 0.03 | 0.04 | 0.04 | 0.06 | 0.06 |
| Hybrid 4-PAFC | 0.04 | 0.03 | 0.00 | 0.06 | 0.05 | 0.02 | 0.02 | 0.02 | 0.03 | 0.03 | 0.03 | 0.03 | 0.04 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 |
| Hybrid 4-PEMFC | 0.04 | 0.01 | 0.00 | 0.01 | 0.02 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.04 | 0.03 | 0.04 | 0.04 | 0.04 | 0.03 | 0.02 | 0.01 |
| Hybrid 4-SOFC | 0.04 | 0.01 | 0.00 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.03 | 0.02 | 0.03 | 0.03 | 0.03 | 0.02 | 0.02 | 0.01 |
| Hybrid 3-PAFC | 0.04 | 0.03 | 0.00 | 0.05 | 0.05 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.03 | 0.03 | 0.03 | 0.02 | 0.03 | 0.03 | 0.03 | 0.02 | 0.03 |
| Hybrid 3-PEMFC | 0.04 | 0.01 | 0.00 | 0.02 | 0.03 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.03 | 0.02 | 0.04 | 0.04 | 0.04 | 0.03 | 0.02 | 0.01 |
| Hybrid 3-SOFC | 0.04 | 0.02 | 0.02 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.02 | 0.03 | 0.03 | 0.03 | 0.03 | 0.02 | 0.02 |
| Hybrid 2-PAFC | 0.04 | 0.05 | 0.00 | 0.07 | 0.06 | 0.02 | 0.02 | 0.02 | 0.03 | 0.03 | 0.03 | 0.04 | 0.05 | 0.03 | 0.03 | 0.04 | 0.04 | 0.03 | 0.05 |
| Hybrid 2-PEMFC | 0.04 | 0.01 | 0.00 | 0.02 | 0.02 | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | 0.04 | 0.04 | 0.06 | 0.05 | 0.05 | 0.04 | 0.03 | 0.02 |
| Hybrid 2-SOFC | 0.04 | 0.01 | 0.00 | 0.05 | 0.04 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.04 | 0.03 | 0.04 | 0.04 | 0.04 | 0.03 | 0.02 | 0.01 |
| Hybrid 1-PAFC | 0.04 | 0.04 | 0.00 | 0.05 | 0.05 | 0.02 | 0.02 | 0.02 | 0.02 | 0.03 | 0.02 | 0.03 | 0.04 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.04 |
| Hybrid 1-PEMFC | 0.04 | 0.01 | 0.00 | 0.02 | 0.03 | 0.06 | 0.06 | 0.05 | 0.05 | 0.05 | 0.04 | 0.04 | 0.03 | 0.05 | 0.05 | 0.05 | 0.04 | 0.03 | 0.02 |
| Hybrid 1-SOFC | 0.04 | 0.01 | 0.00 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.03 | 0.03 | 0.02 | 0.04 | 0.04 | 0.04 | 0.03 | 0.02 | 0.01 |
| 0.04 | 0.01 | 0.00 | 0.01 | 0.01 | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 | 0.03 | 0.02 | 0.02 | 0.03 | 0.03 | 0.02 | 0.02 | 0.01 | 0.01 | |
| 0.04 | 0.08 | 0.09 | 0.07 | 0.06 | 0.06 | 0.06 | 0.06 | 0.06 | 0.05 | 0.05 | 0.06 | 0.06 | 0.05 | 0.05 | 0.05 | 0.08 | 0.08 | 0.07 | |

Table A3.
and values of the configurations in TOPSIS.
Table A3.
and values of the configurations in TOPSIS.
| Si* | 2024 | 2030 | 2050 | Si- | 2024 | 2030 | 2050 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case | Low | Medium | High | Low | Medium | High | Case | Low | Medium | High | Low | Medium | High | ||
| Base | 0.015 | 0.015 | 0.015 | 0.015 | 0.018 | 0.019 | 0.020 | Base | 0.005 | 0.005 | 0.004 | 0.004 | 0.004 | 0.003 | 0.002 |
| Hybrid 6 | 0.008 | 0.008 | 0.008 | 0.009 | 0.010 | 0.011 | 0.011 | Hybrid 6 | 0.008 | 0.008 | 0.007 | 0.007 | 0.007 | 0.006 | 0.006 |
| Hybrid 5 | 0.009 | 0.009 | 0.009 | 0.009 | 0.011 | 0.011 | 0.012 | Hybrid 5 | 0.009 | 0.009 | 0.008 | 0.008 | 0.008 | 0.007 | 0.006 |
| Hybrid 4-PAFC | 0.005 | 0.005 | 0.005 | 0.005 | 0.005 | 0.005 | 0.005 | Hybrid 4-PAFC | 0.013 | 0.013 | 0.013 | 0.013 | 0.014 | 0.013 | 0.013 |
| Hybrid 4-PEMFC | 0.002 | 0.002 | 0.001 | 0.001 | 0.001 | 0.001 | 0.000 | Hybrid 4-PEMFC | 0.018 | 0.018 | 0.018 | 0.019 | 0.021 | 0.022 | 0.022 |
| Hybrid 4-SOFC | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | Hybrid 4-SOFC | 0.016 | 0.016 | 0.016 | 0.016 | 0.019 | 0.019 | 0.020 |
| Hybrid 3-PAFC | 0.003 | 0.003 | 0.003 | 0.003 | 0.003 | 0.004 | 0.004 | Hybrid 3-PAFC | 0.014 | 0.013 | 0.013 | 0.013 | 0.015 | 0.014 | 0.013 |
| Hybrid 3-PEMFC | 0.002 | 0.002 | 0.001 | 0.001 | 0.001 | 0.001 | 0.000 | Hybrid 3-PEMFC | 0.017 | 0.017 | 0.017 | 0.017 | 0.020 | 0.020 | 0.021 |
| Hybrid 3-SOFC | 0.002 | 0.002 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | Hybrid 3-SOFC | 0.014 | 0.013 | 0.013 | 0.013 | 0.015 | 0.016 | 0.015 |
| Hybrid 2-PAFC | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.009 | 0.010 | Hybrid 2-PAFC | 0.012 | 0.011 | 0.011 | 0.011 | 0.012 | 0.011 | 0.010 |
| Hybrid 2-PEMFC | 0.004 | 0.003 | 0.003 | 0.002 | 0.002 | 0.001 | 0.000 | Hybrid 2-PEMFC | 0.018 | 0.018 | 0.018 | 0.018 | 0.020 | 0.021 | 0.021 |
| Hybrid 2-SOFC | 0.004 | 0.004 | 0.004 | 0.004 | 0.004 | 0.003 | 0.003 | Hybrid 2-SOFC | 0.014 | 0.014 | 0.014 | 0.014 | 0.017 | 0.018 | 0.018 |
| Hybrid 1-PAFC | 0.004 | 0.004 | 0.004 | 0.004 | 0.004 | 0.005 | 0.005 | Hybrid 1-PAFC | 0.012 | 0.012 | 0.012 | 0.012 | 0.013 | 0.012 | 0.011 |
| Hybrid 1-PEMFC | 0.003 | 0.003 | 0.002 | 0.002 | 0.002 | 0.001 | 0.001 | Hybrid 1-PEMFC | 0.016 | 0.016 | 0.016 | 0.016 | 0.019 | 0.020 | 0.020 |
| Hybrid 1-SOFC | 0.003 | 0.003 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | Hybrid 1-SOFC | 0.015 | 0.015 | 0.015 | 0.015 | 0.017 | 0.018 | 0.019 |
References
- Kamran, M.; Yan, Z.; Ahmad, I.; Jia, Q.; Ghani, M.U.; Chen, X.; Chang, S.; Li, T.; Siddique, K.H.M.; Fahad, S.; et al. Assessment of greenhouse gases emissions, global warming potential and net ecosystem economic benefits from wheat field with reduced irrigation and nitrogen management in an arid region of China. Agric. Ecosyst. Environ. 2023, 341, 108197. [Google Scholar] [CrossRef]
- Zhong, Y.; Li, J.; Xiong, H. Effect of deficit irrigation on soil CO2 and N2O emissions and winter wheat yield. J. Clean. Prod. 2021, 279, 123718. [Google Scholar] [CrossRef]
- Mikhaylov, A.; Moiseev, N.; Aleshin, K.; Burkhardt, T. Global climate change and greenhouse effect. Entrep. Sustain. Issues 2020, 7, 2897–2913. [Google Scholar] [CrossRef] [PubMed]
- İnal, Ö.B.; Deniz, C. Emission Analysis of LNG Fuelled Molten Carbonate Fuel Cell System for a Chemical Tanker Ship: A Case Study. Mar. Sci. Technol. Bull. 2021, 10, 118–133. [Google Scholar] [CrossRef]
- Ammar, N.R.; Seddiek, I.S. Hybrid/dual fuel propulsion systems towards decarbonization: Case study container ship. Ocean Eng. 2023, 281, 114962. [Google Scholar] [CrossRef]
- Bacalja Bašić, B.; Krčum, M.; Jurić, Z. Propeller Optimization in Marine Power Systems: Exploring Its Contribution and Correlation with Renewable Energy Solutions. J. Mar. Sci. Eng. 2024, 12, 843. [Google Scholar] [CrossRef]
- IMO. 2024 Guidelines on Life Cycle GHG Intensity of Marine Fuels (2024 LCA Guidelines). Available online: https://wwwcdn.imo.org/localresources/en/KnowledgeCentre/IndexofIMOResolutions/MEPCDocuments/MEPC.391(81).pdf (accessed on 13 November 2024).
- UNCTAD. Review of Maritime Transport 2023. Towards a Green and Just Transition. Available online: https://unctad.org/publication/review-maritime-transport-2023 (accessed on 3 May 2024).
- Bach, H.; Hansen, T. IMO off course for decarbonisation of shipping? Three challenges for stricter policy. Mar. Policy 2023, 147, 105379. [Google Scholar] [CrossRef]
- Skoko, I.; Stanivuk, T.; Franic, B.; Bozic, D. Comparative Analysis of CO2 Emissions, Fuel Consumption, and Fuel Costs of Diesel and Hybrid Dredger Ship Engines. J. Mar. Sci. Eng. 2024, 12, 999. [Google Scholar] [CrossRef]
- Styhre, L.; Winnes, H.; Black, J.; Lee, J.; Le-Griffin, H. Greenhouse gas emissions from ships in ports—Case studies in four continents. Transp. Res. Part D Transp. Environ. 2017, 54, 212–224. [Google Scholar] [CrossRef]
- Tu, H.; Liu, Z.; Zhang, Y. Study on Cost-Effective Performance of Alternative Fuels and Energy Efficiency Measures for Shipping Decarbonization. J. Mar. Sci. Eng. 2024, 12, 743. [Google Scholar] [CrossRef]
- Ejder, E.; Dinçer, S.; Arslanoglu, Y. Decarbonization strategies in the maritime industry: An analysis of dual-fuel engine performance and the carbon intensity indicator. Renew. Sustain. Energy Rev. 2024, 200, 114587. [Google Scholar] [CrossRef]
- IMO. 2023 IMO Strategy on Reduction of GHG Emissions from Ships. Available online: https://www.imo.org/en/OurWork/Environment/Pages/2023-IMO-Strategy-on-Reduction-of-GHG-Emissions-from-Ships.aspx (accessed on 24 April 2024).
- Ivanova, G. Analysis of the Specifics in Calculating the Index of Existing Marine Energy Efficiency EEXI in Force since 2023. In Proceedings of the 2021 13th Electrical Engineering Faculty Conference (BulEF), Varna, Bulgaria, 8–11 September 2021; pp. 1–4. [Google Scholar]
- Tadros, M.; Ventura, M.; Guedes Soares, C. Review of the Decision Support Methods Used in Optimizing Ship Hulls towards Improving Energy Efficiency. J. Mar. Sci. Eng. 2023, 11, 835. [Google Scholar] [CrossRef]
- Peralta , P.C.O.; Vieira , G.T.T.; Meunier , S.; Vale, R.J.; Salles , M.B.C.; Carmo , B.S. Evaluation of the CO2 Emissions Reduction Potential of Li-ion Batteries in Ship Power Systems. Energies 2019, 12, 375. [Google Scholar] [CrossRef]
- Mondal, S.; Datta, S.; De, S. Auxiliary power through marine waste heat recovery using a CO2-organic cascading cycle. Clean Technol. Environ. Policy 2020, 22, 893–906. [Google Scholar] [CrossRef]
- Inal, O.B.; Zincir, B.; Dere, C.; Charpentier, J.-F. Hydrogen Fuel Cell as an Electric Generator: A Case Study for a General Cargo Ship. J. Mar. Sci. Eng. 2024, 12, 432. [Google Scholar] [CrossRef]
- Van Rheenen, E.S.; Padding, J.T.; Slootweg, J.C.; Visser, K. Hydrogen carriers for zero-emission ship propulsion using PEM fuel cells: An evaluation. J. Mar. Eng. Technol. 2024, 23, 166–183. [Google Scholar] [CrossRef]
- Luna, M.; La Tona, G.; Accetta, A.; Pucci, M.; Pietra, A.; Di Piazza, M.C. Optimal Management of Battery and Fuel Cell-Based Decentralized Generation in DC Shipboard Microgrids. Energies 2023, 16, 1682. [Google Scholar] [CrossRef]
- Markowski, J.; Pielecha, I. The potential of fuel cells as a drive source of maritime transport. IOP Conf. Ser. Earth Environ. Sci. 2019, 214, 012019. [Google Scholar] [CrossRef]
- Animah, I.; Adjei, P.; Djamesi, E.K. Techno-economic feasibility assessment model for integrating hybrid renewable energy systems into power systems of existing ships: A case study of a patrol boat. J. Mar. Eng. Technol. 2023, 22, 22–37. [Google Scholar] [CrossRef]
- Sohani, A.; Naderi, S.; Torabi, F.; Sayyaadi, H.; Golizadeh Akhlaghi, Y.; Zhao, X.; Talukdar, K.; Said, Z. Application based multi-objective performance optimization of a proton exchange membrane fuel cell. J. Clean. Prod. 2020, 252, 119567. [Google Scholar] [CrossRef]
- HFTO. Comparison of Fuel Cell Technologies. Available online: https://www.energy.gov/eere/fuelcells/comparison-fuel-cell-technologies (accessed on 2 July 2024).
- McNicol, B.D.; Rand, D.A.J.; Williams, K.R. Fuel cells for road transportation purposes—Yes or no? J. Power Sources 2001, 100, 47–59. [Google Scholar] [CrossRef]
- Wu, P.; Bucknall, R. Hybrid fuel cell and battery propulsion system modelling and multi-objective optimisation for a coastal ferry. Int. J. Hydrogen Energy 2020, 45, 3193–3208. [Google Scholar] [CrossRef]
- Ghenai, C.; Bettayeb, M.; Brdjanin, B.; Hamid, A.K. Hybrid solar PV/PEM fuel Cell/Diesel Generator power system for cruise ship: A case study in Stockholm, Sweden. Case Stud. Therm. Eng. 2019, 14, 100497. [Google Scholar] [CrossRef]
- Sapra, H.; Stam, J.; Reurings, J.; van Biert, L.; van Sluijs, W.; de Vos, P.; Visser, K.; Vellayani, A.P.; Hopman, H. Integration of solid oxide fuel cell and internal combustion engine for maritime applications. Appl. Energy 2021, 281, 115854. [Google Scholar] [CrossRef]
- Meca, V.L.; Villalba-Herreros, A.; d’Amore-Domenech, R.; Leo, T.J. Zero emissions wellboat powered by hydrogen fuel cells hybridised with batteries. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2021, 236, 525–536. [Google Scholar] [CrossRef]
- Perčić, M.; Vladimir, N.; Jovanović, I.; Koričan, M. Application of fuel cells with zero-carbon fuels in short-sea shipping. Appl. Energy 2022, 309, 118463. [Google Scholar] [CrossRef]
- Chen, Z.S.; Lam, J.S.L. Life cycle assessment of diesel and hydrogen power systems in tugboats. Transp. Res. Part D Transp. Environ. 2022, 103, 103192. [Google Scholar] [CrossRef]
- Seyam, S.; Dincer, I.; Agelin-Chaab, M. Investigation of a hybridized combined cycle engine with SOFC system for marine applications. J. Therm. Anal. Calorim. 2022, 148, 8323–8344. [Google Scholar] [CrossRef]
- Yuksel, O. A comprehensive feasibility analysis of dual-fuel engines and solid oxide fuel cells on a tanker ship considering environmental, economic, and regulation aspects. Sustain. Prod. Consum. 2023, 42, 106–124. [Google Scholar] [CrossRef]
- Duong, P.A.; Ryu, B.R.; Kyu, S.S.; Jeon, H.; Kang, H. Performance analysis of a fuel cells integrated system utilizing Liquified Natural Gas as fuel for a green shipping target. Int. J. Nav. Archit. Ocean Eng. 2023, 15, 100543. [Google Scholar] [CrossRef]
- Seyfi, H.; Hitchmough, D.; Armin, M.; Blanco-Davis, E. A Study on the Viability of Fuel Cells as an Alternative to Diesel Fuel Generators on Ships. J. Mar. Sci. Eng. 2023, 11, 1489. [Google Scholar] [CrossRef]
- Lee, J.I.; Yoon, B.Y.; Cha, S.W. Analysis of solid oxide fuel cell hybrid power system in marine application for CO2 reduction. Energy Rep. 2023, 9, 3072–3081. [Google Scholar] [CrossRef]
- Hwang, I.; Park, C.; Jeong, B. Life Cycle Cost Analysis for Scotland Short-Sea Ferries. J. Mar. Sci. Eng. 2023, 11, 424. [Google Scholar] [CrossRef]
- Korkmaz, S.A.; Erginer, K.E.; Yuksel, O.; Konur, O.; Colpan, C.O. Environmental and economic analyses of fuel cell and battery-based hybrid systems utilized as auxiliary power units on a chemical tanker vessel. Int. J. Hydrogen Energy 2023, 48, 23279–23295. [Google Scholar] [CrossRef]
- De Lorenzo, G.; Ruffo, R.M.; Fragiacomo, P. Preliminary Design of the Fuel Cells Based Energy Systems for a Cruise Ship. World Electr. Veh. J. 2023, 14, 263. [Google Scholar] [CrossRef]
- Ammar, N.R.; Almas, M.; Nahas, Q. Economic Analysis and the EEXI Reduction Potential of Parallel Hybrid Dual-Fuel Engine–Fuel Cell Propulsion Systems for LNG Carriers. Pol. Marit. Res. 2023, 30, 59–70. [Google Scholar] [CrossRef]
- Iqbal, R.; Liu, Y.; Zeng, Y.; Zhang, Q.; Zeeshan, M. Comparative study based on techno-economics analysis of different shipboard microgrid systems comprising PV/wind/fuel cell/battery/diesel generator with two battery technologies: A step toward green maritime transportation. Renew. Energy 2024, 221, 119670. [Google Scholar] [CrossRef]
- Wang, Z.; Dong, B.; Wang, Y.; Li, M.; Liu, H.; Han, F. Analysis and evaluation of fuel cell technologies for sustainable ship power: Energy efficiency and environmental impact. Energy Convers. Manag. X 2024, 21, 100482. [Google Scholar] [CrossRef]
- LAROS. How Laros Works? Available online: https://www.laros.gr/ (accessed on 20 December 2024).
- Yuksel, O.; Koseoglu, B. Numerical simulation of the hybrid ship power distribution system and an analysis of its emission reduction potential. Ships Offshore Struct. 2023, 18, 78–94. [Google Scholar] [CrossRef]
- Inal, O.B.; Deniz, C. Assessment of fuel cell types for ships: Based on multi-criteria decision analysis. J. Clean. Prod. 2020, 265, 121734. [Google Scholar] [CrossRef]
- Gültekin, N.; Ciniviz, M. Examination of the effect of combustion chamber geometry and mixing ratio on engine performance and emissions in a hydrogen-diesel dual-fuel compression-ignition engine. Int. J. Hydrogen Energy 2023, 48, 2801–2820. [Google Scholar] [CrossRef]
- FuelCellEnergy. Solid Oxide Fuel Cell 250 kW. Available online: https://go.fuelcellenergy.com/hubfs/Solid%20Oxide%20Fuel%20Cell%20Spec%20Sheet.pdf (accessed on 1 May 2024).
- Doosan. PureCell Model 400. Available online: https://www.doosanfuelcellpower.com/download/pdf/catalog/pafc-400kw_en.pdf (accessed on 1 May 2021).
- PowerCellGroup. Marine System 200. Available online: https://powercellgroup.com/product/marine-system-200/ (accessed on 1 May 2024).
- ISO 14687:2019; Hydrogen Fuel Quality—Product Specification. ISO: Geneva, Switzerland, 2019. Available online: https://www.iso.org/standard/69539.html (accessed on 30 December 2024).
- Panasonic. Specifications for NCR18650GA. Available online: https://www.orbtronic.com/content/Datasheet-specs-Sanyo-Panasonic-NCR18650GA-3500mah.pdf (accessed on 1 May 2024).
- Konur, O.; Yuksel, O.; Aykut Korkmaz, S.; Ozgur Colpan, C.; Saatcioglu, O.Y.; Koseoglu, B. Operation-dependent exergetic sustainability assessment and environmental analysis on a large tanker ship utilizing Organic Rankine cycle system. Energy 2023, 262, 125477. [Google Scholar] [CrossRef]
- MAN. L16/24 Project Guide—Marine Four-stroke GenSet Compliant with IMO Tier II. Available online: https://man-es.com/applications/projectguides/4stroke/manualcontent/PG_M-II_L1624.pdf (accessed on 29 April 2024).
- Abdin, Z.; Zafaranloo, A.; Rafiee, A.; Mérida, W.; Lipiński, W.; Khalilpour, K.R. Hydrogen as an energy vector. Renew. Sustain. Energy Rev. 2020, 120, 109620. [Google Scholar] [CrossRef]
- Zarabi Golkhatmi, S.; Asghar, M.I.; Lund, P.D. A review on solid oxide fuel cell durability: Latest progress, mechanisms, and study tools. Renew. Sustain. Energy Rev. 2022, 161, 112339. [Google Scholar] [CrossRef]
- Rambert, O.; Febvre, L. The challenges of Hydrogen Storage on a Large Scale. Available online: https://hysafe.info/uploads/papers/2021/189.pdf (accessed on 21 June 2024).
- Raucci, C.; Calleya, J.; Suarez De La Fuente, S.; Pawling, R. Hydrogen on Board Ship: A First Analysis of Key Parameters and Implications. Available online: https://decarbonisingfreight.co.uk/wp-content/uploads/2023/05/Raucci-et-al-2015-Hydrogen-on-board-ship.pdf (accessed on 21 June 2024).
- Eagle. LNG Calculator. Available online: https://www.eaglelng.com/lng-calculator (accessed on 23 May 2024).
- Lyu, L.; Kan, A.; Chen, W.; Zhang, Y.; Fu, B. Energy, Exergy and Environmental Analysis of ORC Waste Heat Recovery from Container Ship Exhaust Gases Based on Voyage Cycle. J. Mar. Sci. Eng. 2023, 11, 2029. [Google Scholar] [CrossRef]
- Saxena, S.; Hendricks, C.; Pecht, M. Cycle life testing and modeling of graphite/LiCoO2 cells under different state of charge ranges. J. Power Sources 2016, 327, 394–400. [Google Scholar] [CrossRef]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. Inline state of health estimation of lithium-ion batteries using state of charge calculation. J. Power Sources 2015, 299, 246–254. [Google Scholar] [CrossRef]
- Omar, N.; Monem, M.A.; Firouz, Y.; Salminen, J.; Smekens, J.; Hegazy, O.; Gaulous, H.; Mulder, G.; Van den Bossche, P.; Coosemans, T.; et al. Lithium iron phosphate based battery—Assessment of the aging parameters and development of cycle life model. Appl. Energy 2014, 113, 1575–1585. [Google Scholar] [CrossRef]
- Kuzu, S.L.; Bilgili, L.; Kiliç, A. Estimation and dispersion analysis of shipping emissions in Bandirma Port, Turkey. Environ. Dev. Sustain. 2021, 23, 10288–10308. [Google Scholar] [CrossRef]
- Gilbert, P.; Walsh, C.; Traut, M.; Kesieme, U.; Pazouki, K.; Murphy, A. Assessment of full life-cycle air emissions of alternative shipping fuels. J. Clean. Prod. 2018, 172, 855–866. [Google Scholar] [CrossRef]
- Pavlenko, N.; Comer, B.; Zhou, Y.; Clark, N.; Rutherford, D. The Climate Implications of Using LNG as a Marine Fuel; Swedish Environmental Protection Agency: Stockholm, Sweden, 2020. [Google Scholar]
- IMO. 2021 Guidelines on the Method of Calculation of the Attained Energy Efficiency Existing Ship Index (EEXI). Available online: https://wwwcdn.imo.org/localresources/en/KnowledgeCentre/IndexofIMOResolutions/MEPCDocuments/MEPC.333(76).pdf (accessed on 24 May 2024).
- ClassNK. Outlines of EEXI Regulation. Available online: https://www.classnk.or.jp/hp/pdf/activities/statutory/eexi/eexi_rev3e.pdf (accessed on 24 May 2024).
- ClassNK. CII (Carbon Intensity Indicator). Available online: https://www.classnk.or.jp/hp/pdf/activities/statutory/seemp/CII_en.pdf (accessed on 24 May 2024).
- IMO. 2021 Guidelines on the Operational Carbon Intesnity Rating of Ships (CII Rating Guidelines, G4). Available online: https://wwwcdn.imo.org/localresources/en/OurWork/Environment/Documents/Air%20pollution/MEPC.339(76).pdf (accessed on 25 May 2024).
- IEA. Projected Costs of Generating Electricity. Available online: https://www.oecd-nea.org/upload/docs/application/pdf/2020-12/egc-2020_2020-12-09_18-26-46_781.pdf (accessed on 27 June 2024).
- Hansen, K. Decision-making based on energy costs: Comparing levelized cost of energy and energy system costs. Energy Strategy Rev. 2019, 24, 68–82. [Google Scholar] [CrossRef]
- Shu, G.; Liu, P.; Tian, H.; Wang, X.; Jing, D. Operational profile based thermal-economic analysis on an Organic Rankine cycle using for harvesting marine engine’s exhaust waste heat. Energy Convers. Manag. 2017, 146, 107–123. [Google Scholar] [CrossRef]
- Behling, N.H. Chapter 4—History of Phosphoric Acid Fuel Cells. In Fuel Cells; Behling, N.H., Ed.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 53–135. [Google Scholar]
- Wang, Y.; Pang, Y.; Xu, H.; Martinez, A.; Chen, K.S. PEM Fuel cell and electrolysis cell technologies and hydrogen infrastructure development—A review. Energy Environ. Sci. 2022, 15, 2288–2328. [Google Scholar] [CrossRef]
- Gianni, M.; Pietra, A.; Taccani, R. Outlook of future implementation of PEMFC and SOFC onboard cruise ships. E3S Web Conf. 2021, 238, 04004. [Google Scholar] [CrossRef]
- Whiston, M.M.; Azevedo, I.M.L.; Litster, S.; Samaras, C.; Whitefoot, K.S.; Whitacre, J.F. Meeting U.S. Solid Oxide Fuel Cell Targets. Joule 2019, 3, 2060–2065. [Google Scholar] [CrossRef]
- Bayraktar, M.; Nuran, M. Economic Analysis of A Vessel In Service Equipped with an LNG Fueled Ship Engine. In Proceedings of the 12th International Conference on Marine Navigation and Safety of Sea Transportation (TransNav 2017), Gdynia, Poland, 21–23 June 2017; pp. 337–344. [Google Scholar]
- Seo, S.; Chu, B.; Noh, Y.; Jang, W.; Lee, S.; Seo, Y.; Chang, D. An economic evaluation of operating expenditures for LNG fuel gas supply systems onboard ocean-going ships considering availability. Ships Offshore Struct. 2016, 11, 213–223. [Google Scholar] [CrossRef]
- Terlouw, T.; Bauer, C.; McKenna, R.; Mazzotti, M. Large-scale hydrogen production via water electrolysis: A techno-economic and environmental assessment. Energy Environ. Sci. 2022, 15, 3583–3602. [Google Scholar] [CrossRef]
- Maxwell, C. Cost Indices. Available online: https://toweringskills.com/financial-analysis/cost-indices/ (accessed on 25 June 2024).
- ShipandBunker. World Bunker Prices. Available online: https://shipandbunker.com/prices (accessed on 25 June 2024).
- Helgason, R.; Cook, D.; Davíðsdóttir, B. An evaluation of the cost-competitiveness of maritime fuels—A comparison of heavy fuel oil and methanol (renewable and natural gas) in Iceland. Sustain. Prod. Consum. 2020, 23, 236–248. [Google Scholar] [CrossRef]
- Zou, J.; Yang, B. Evaluation of alternative marine fuels from dual perspectives considering multiple vessel sizes. Transp. Res. Part D Transp. Environ. 2023, 115, 103583. [Google Scholar] [CrossRef]
- ShipandBunker. EU-ETS Understanding the EU’s Emissions Trading System for Shipping. Available online: https://shipandbunker.com/eu-ets (accessed on 25 June 2024).
- Bayraktar, M. Investigation of alternative fuelled marine diesel engines and waste heat recovery system utilization on the oil tanker for upcoming regulations and carbon tax. Ocean Eng. 2023, 287, 115831. [Google Scholar] [CrossRef]
- Pandey, V.; Komal; Dincer, H. A review on TOPSIS method and its extensions for different applications with recent development. Soft Comput. 2023, 27, 18011–18039. [Google Scholar] [CrossRef]
- Li, X.; Zhou, S.; Zhao, Y.; Wan, G. A CRITIC-TOPSIS and optimized nonlinear grey prediction model: A comparative convergence analysis of marine economic resilience. Expert Syst. Appl. 2024, 236, 121356. [Google Scholar] [CrossRef]
- Balin, A.; Demirel, H.; Alarcin, F. A novel hybrid MCDM model based on fuzzy AHP and fuzzy TOPSIS for the most affected gas turbine component selection by the failures. J. Mar. Eng. Technol. 2016, 15, 69–78. [Google Scholar] [CrossRef]
- Esen, H.; Inalli, M.; Esen, M.; Pihtili, K. Energy and exergy analysis of a ground-coupled heat pump system with two horizontal ground heat exchangers. Build. Environ. 2007, 42, 3606–3615. [Google Scholar] [CrossRef]
- Taner, T.; Sivrioglu, M. Energy–exergy analysis and optimisation of a model sugar factory in Turkey. Energy 2015, 93, 641–654. [Google Scholar] [CrossRef]
- Taner, T. Optimisation processes of energy efficiency for a drying plant: A case of study for Turkey. Appl. Therm. Eng. 2015, 80, 247–260. [Google Scholar] [CrossRef]
- Akpinar, E.K. Mathematical modelling of thin layer drying process under open sun of some aromatic plants. J. Food Eng. 2006, 77, 864–870. [Google Scholar] [CrossRef]
- Liu, Y.; Juckel, M.; Menzler, N.H.; Weber, A. Ni/GDC Fuel Electrode for Low-Temperature SOFC and its Aging Behavior Under Accelerated Stress. J. Electrochem. Soc. 2024, 171, 054514. [Google Scholar] [CrossRef]
- Wang, M.; Ruan, J.; Zhang, J.; Jiang, Y.; Gao, F.; Zhang, X.; Rahman, E.; Guo, J. Modeling, thermodynamic performance analysis, and parameter optimization of a hybrid power generation system coupling thermogalvanic cells with alkaline fuel cells. Energy 2024, 292, 130557. [Google Scholar] [CrossRef]
- Qu, J.; Feng, Y.; Zhu, Y.; Wu, B.; Wu, Y.; Xiao, Z.; Zheng, S. Assessment of a methanol-fueled integrated hybrid power system of solid oxide fuel cell and low-speed two-stroke engine for maritime application. Appl. Therm. Eng. 2023, 230, 120735. [Google Scholar] [CrossRef]
- Issa, M.; Ilinca, A.; Martini, F. Ship Energy Efficiency and Maritime Sector Initiatives to Reduce Carbon Emissions. Energies 2022, 15, 7910. [Google Scholar] [CrossRef]
- Budiyanto, M.A.; Putra, G.L.; Riadi, A.; Andika, R.; Zidane, S.A.; Muhammad, A.H.; Theotokatos, G. Techno-Economic Analysis of Combined Gas and Steam Propulsion System of Liquefied Natural Gas Carrier. Energies 2024, 17, 1415. [Google Scholar] [CrossRef]
- Alzayedi, A.M.T.; Alkhaledi, A.N.F.N.R.; Sampath, S.; Pilidis, P. TERA of Gas Turbine Propulsion Systems for RORO Ships. Energies 2023, 16, 5875. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).