Calculation of the Optimal Magnetic Duty Cycle for a Graded Coaxial Magnet of a Rotary Type Magnetic Refrigerator †
Abstract
1. Introduction
2. Materials and Design of the Regenerator Material System
3. The Setting of Simulation
4. Results and Discussion
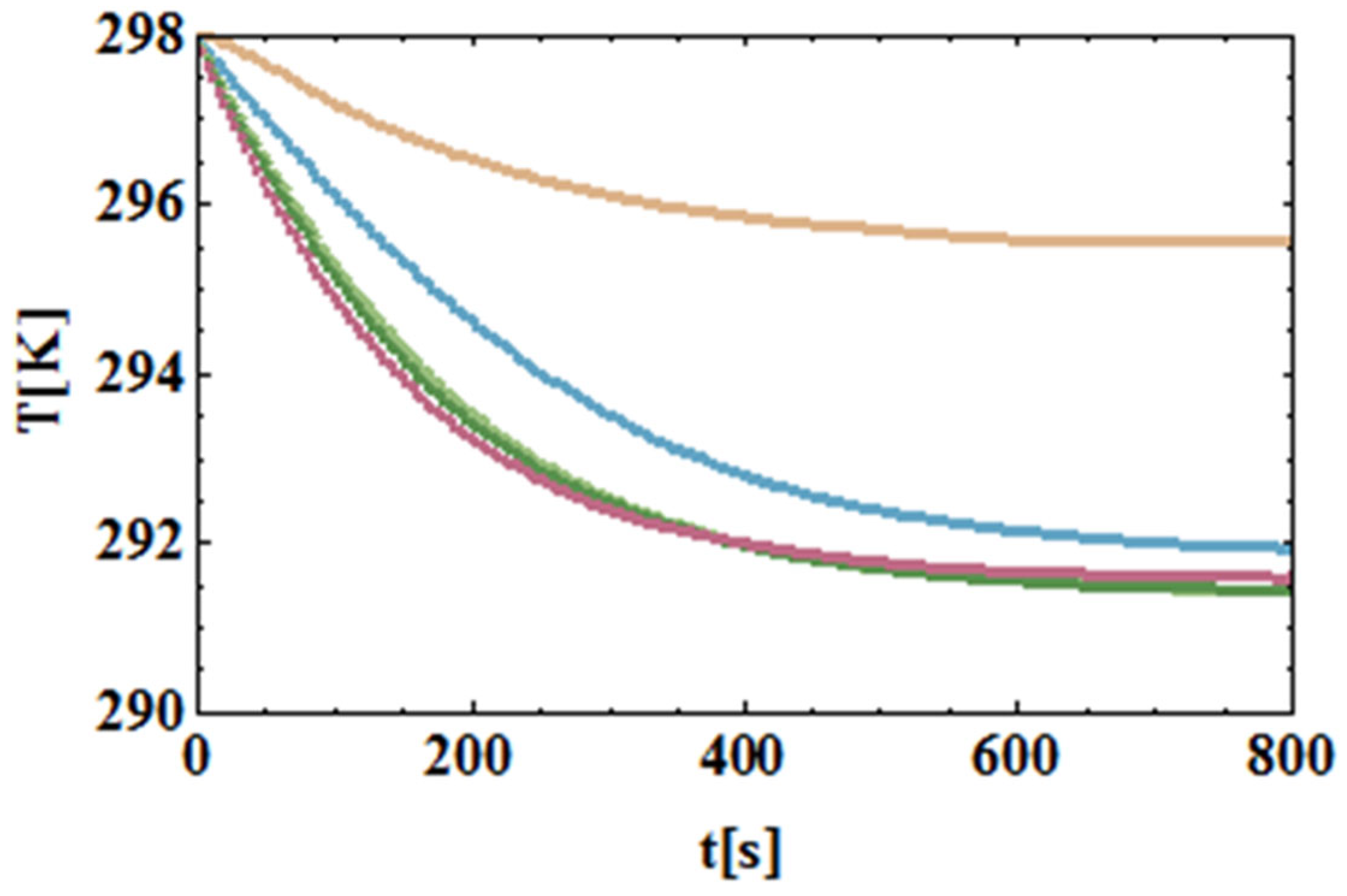
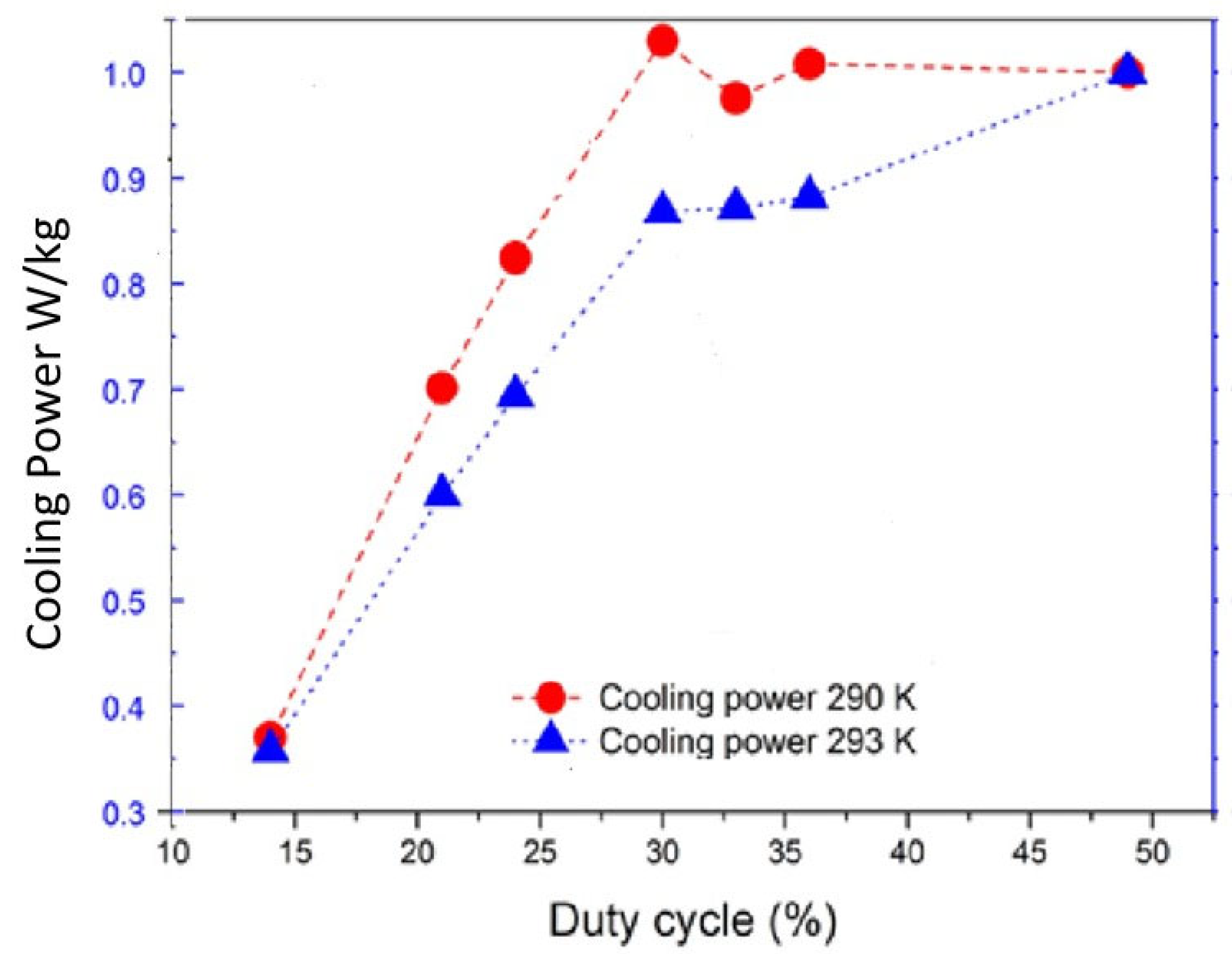
4.1. Optimize the Magnetic Duty Cycle
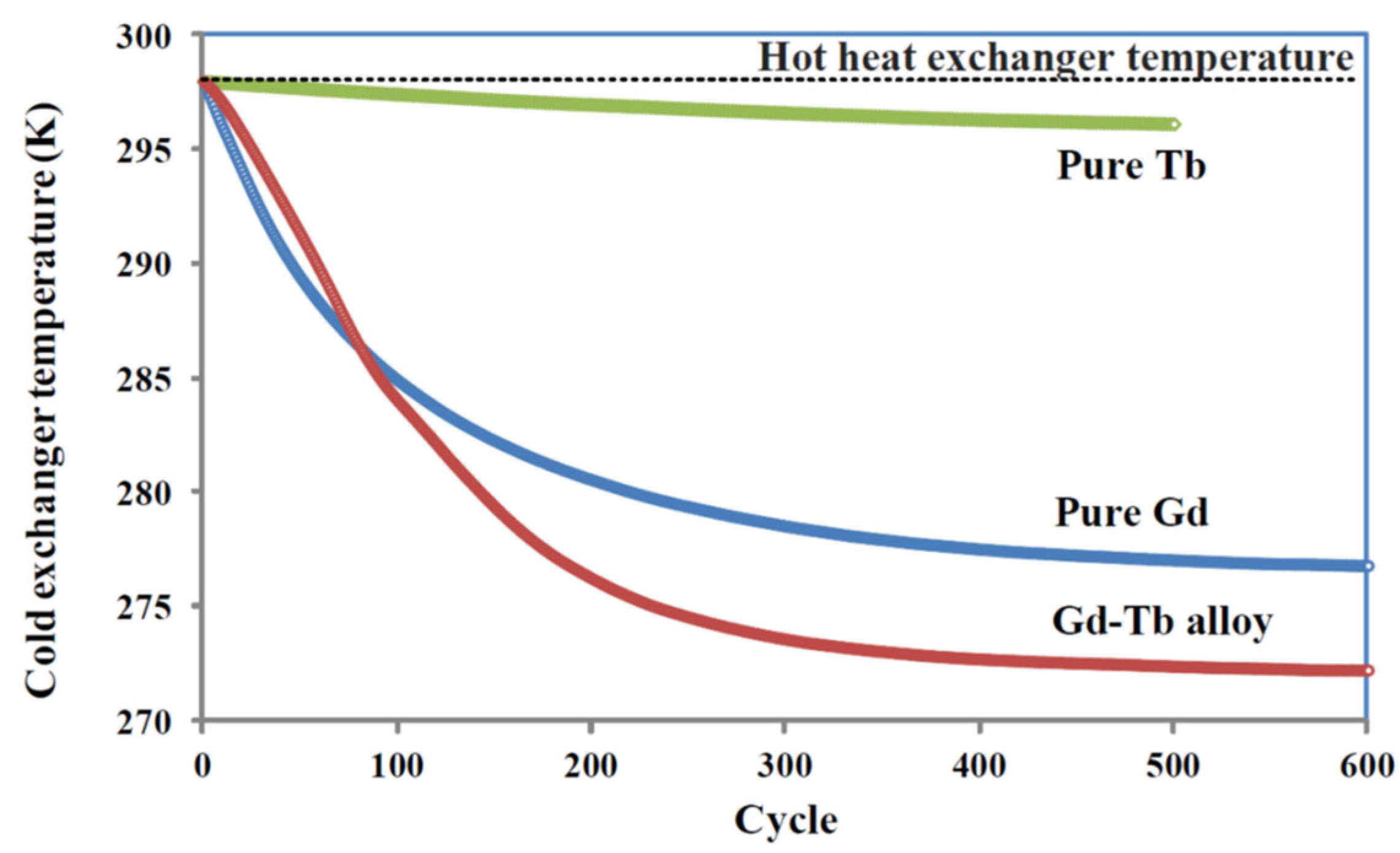
4.2. The Graded AMR Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bjork, R.; Bahl, C.R.H.; Smith, A.; Pryds, N. Review and comparison of magnet designs for magnetic refrigeration. Int. J. Refrig. 2010, 33, 437–448. [Google Scholar] [CrossRef]
- Alahmer, A.; Al-Amayreh, M.; Mostafa, A.O.; Al-Dabbas, M.; Rezk, H. Magnetic Refrigeration Design Technologies: State of the Art and General Perspectives. Energies 2021, 14, 4662–4687. [Google Scholar] [CrossRef]
- Bocanegra, J.A.; Scarpa, F.; Fanghella, P.; Marchitto, A.; Tagliafco, L.A. Optimization and development of a new rotary magnetic refrigerator. In Clean Technologies and Environmental Policy; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar] [CrossRef]
- Zheng, Z.G.; Yu, H.Y.; Zhong, X.C.; Zeng, D.C.; Liu, Z.W. Design and Performance Study of the Active Magnetic Refrigerator for Room-Temperature Application. Int. J. Refrig. 2009, 32, 78–86. [Google Scholar] [CrossRef]
- Yu, B.F.; Gao, Q.; Zhang, B.; Meng, X.Z.; Chen, Z. Review on research of room temperature magnetic refrigeration. Int. J. Refrig. 2003, 26, 622–636. [Google Scholar] [CrossRef]
- Hsieh, C.M.; Su, Y.C.; Lee, C.H.; Cheng, P.H.; Leou, K.C. Modeling of graded active magnetic regenerator for room-temperature, energy-efficient refrigeration. IEEE Trans. Magn. 2014, 50, 4002904. [Google Scholar] [CrossRef]
- Ayas, A.O.; Akça, G.O.; Akyol, M.; Ekicibil, A. Magnetic refrigeration: Current progress in magnetocaloric properties of perovskite manganite materials. Mater. Today Comm. 2023, 35, 105988. [Google Scholar] [CrossRef]
- Yu, B.; Liu, M.; Egolf, P.W.; Kitanovski, A. A review of magnetic refrigerator and heat pump prototypes built before the year 2010. Int. J. Refrig. 2010, 33, 1029–1060. [Google Scholar] [CrossRef]
- Bahl, C.R.H.; Engelbrecht, K.; Bjork, R.; Eriksen, D.; Smith, A.; Pryds, N. Design concepts for a continuously rotating active magnetic regenerator. In Proceedings of the International Conference on Magnetic Refrigeration at Room Temperature, Baotou, China, 23–28 August 2010; pp. 1–7. [Google Scholar]
- Xia, D.; Xia, L. A novel permanent magnet system for magnetic refrigerator and its magnetic field analysis. In Proceedings of the International Conference on Electrical and Control Engineering, Wuhan, China, 25–27 June 2010; pp. 4928–4931. [Google Scholar]
- Bjork, R.; Bahl, C.R.H.; Smith, A.; Christensen, D.V.; Pryds, N. An optimized magnet for magnetic refrigeration. J. Magn. Magn. Mater. 2010, 322, 3324–3328. [Google Scholar] [CrossRef]
- Okamura, T. Improvement of 100 W Class Room Temperature Magnetic Refrigerator. In Proceedings of the 2nd International Conference on Magnetic Refrigeration at Room Temperature, Portoroz, Slovenia, 11–13 April 2007; pp. 377–382. [Google Scholar]
- Beltrán-López, J.F.; Palacios, E.; Velázquez, D.; Burriel, R. Design and optimization of a magnet for magnetocaloric refrigeration. J. Appl. Phys. 2019, 126, 164502. [Google Scholar] [CrossRef]
- Eriksen, D.; Engelbrecht, K.; Bahl, C.R.H.; Bjørk, R.; Nielsen, K.K.; Insinga, A.R.; Pryds, N. Design and experimental tests of a rotary active magnetic regenerator prototype. Int. J. Refrig. 2015, 58, 14–21. [Google Scholar] [CrossRef]
- Karpenkov, A.; Tukmakova, A.; Dunaeva, G.; Dergachev, P.; Karpenkov, D. Simulation of an operation of nested Halbach cylinder arrays in regenerative magnetic cooling cycles: The way to maximum thermal span. Int. J. Refrig. 2024, 168, 29–39. [Google Scholar] [CrossRef]
- Lee, C.H.; Cheng, P.H.; Leou, K.C.; Hsieh, C.M.; Su, Y.C. Study the Optimal Duty Cycle of a Coaxial Magnet for a Rotary Type Magnetic Refrigerator. In Proceedings of the Intermag 2023, Sendai, Japan, 15–19 May 2023. [Google Scholar] [CrossRef]
- Rowe, A.; Tura, A. Experimental investigation of a three-material layered active magnetic regenerator. Int. J. Refrig. 2006, 29, 1286–1293. [Google Scholar] [CrossRef]
- Nielsen, K.K.; Tusek, J.; Engelbrecht, K.; Schopfer, S.; Kitanovski, A.; Bahl, C.R.H.; Smith, A.; Pryds, N.; Poredos, A. Review on numerical modeling of active magnetic regenerators for room temperature applications. Int. J. Refrig. 2011, 34, 603–616. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A. A numerical analysis of an active magnetic regenerative cascade system. Int. J. Energy Res. 2011, 35, 177–188. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A. The use of the first and of the second order phase magnetic transition alloys for an AMR refrigerator at room temperature: A numerical analysis of the energy performances. Energy Convers. Manag. 2013, 70, 40–55. [Google Scholar] [CrossRef]
- COMSOL. A Multi-Physics Program, Version 4.4. Available online: https://www.comsol.com/ (accessed on 27 November 2013).
- Petersen, T.F.; Pryds, N.; Smith, A.; Hattel, J.; Schmidt, H.; Knudsen, H.-J.H. Two-dimensional mathematical model of a reciprocating room-temperature active magnetic regenerator. Int. J. Refrig. 2008, 31, 432–443. [Google Scholar] [CrossRef]
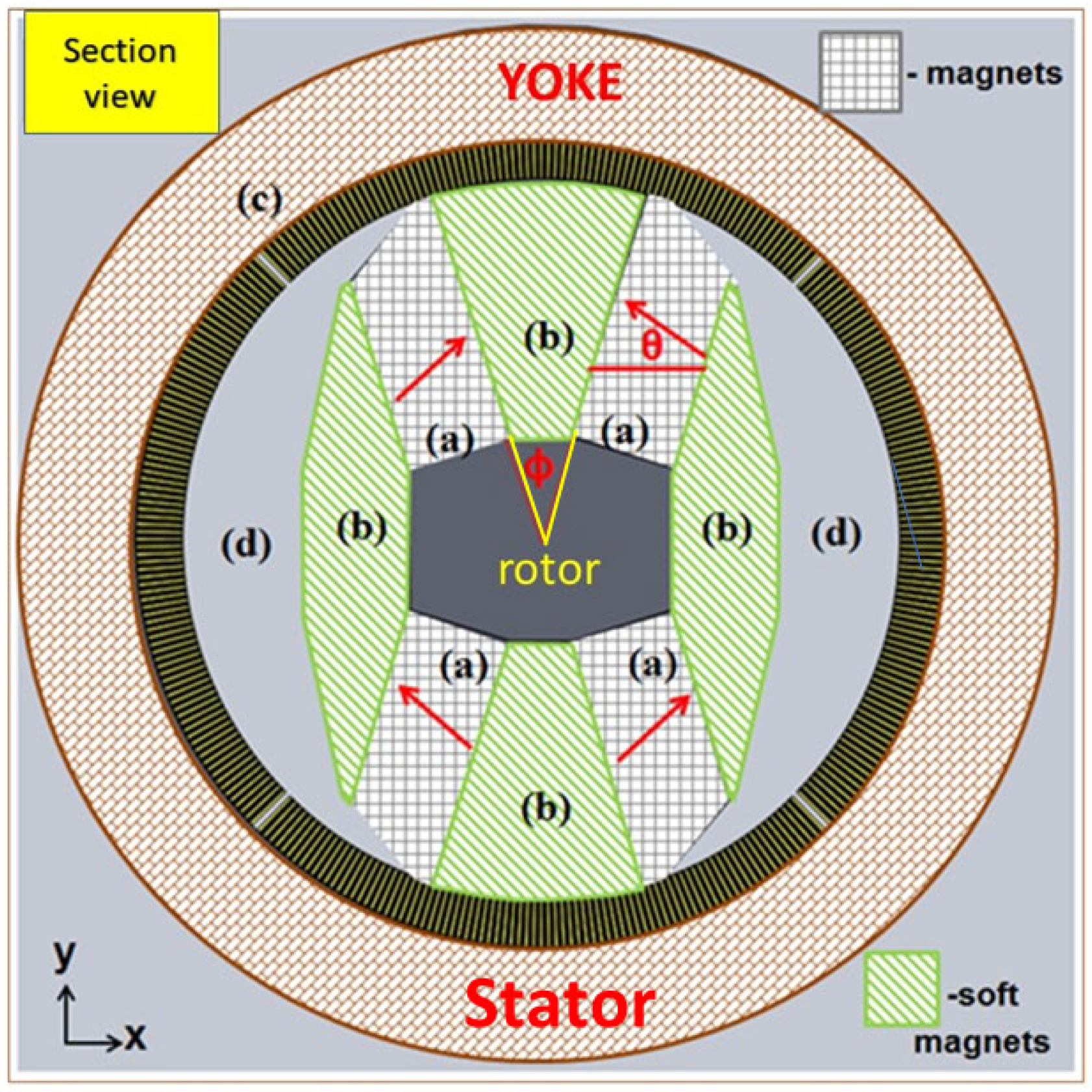
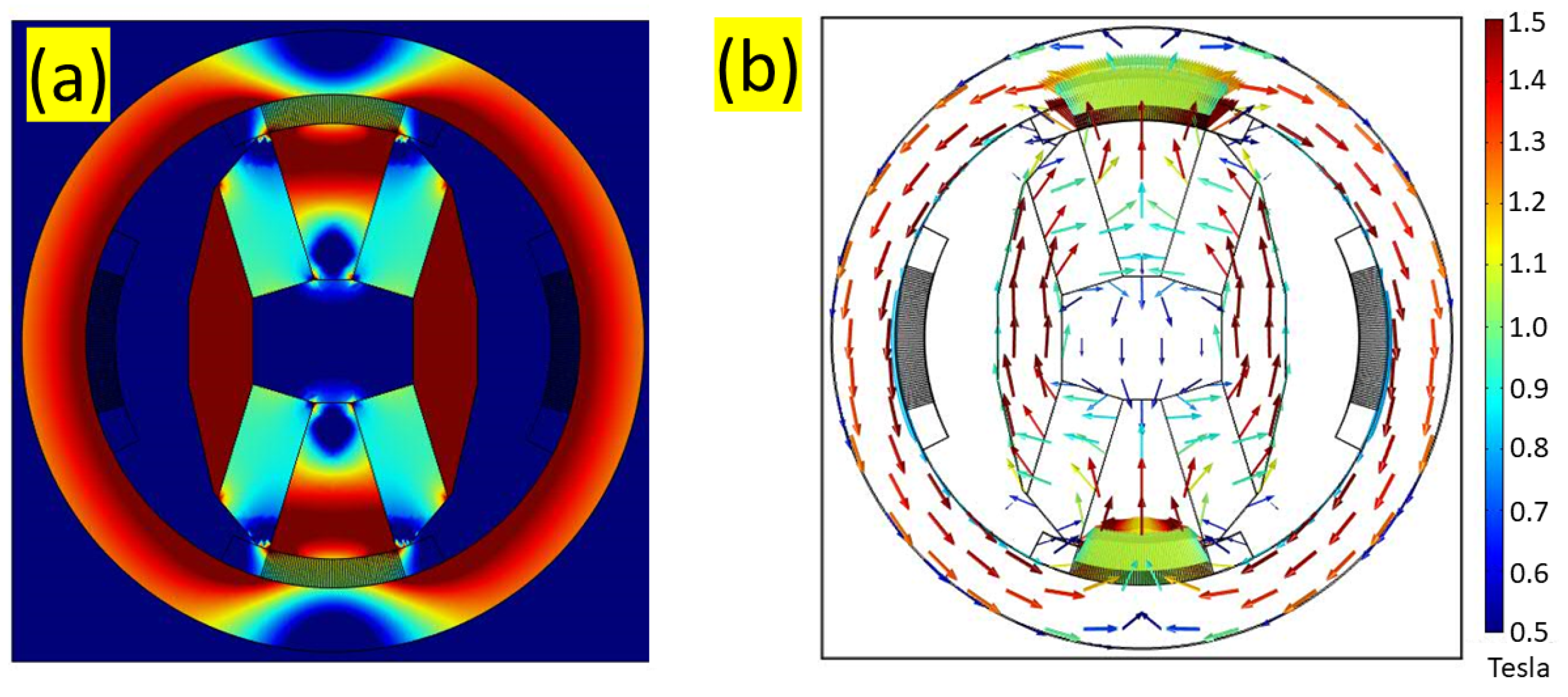
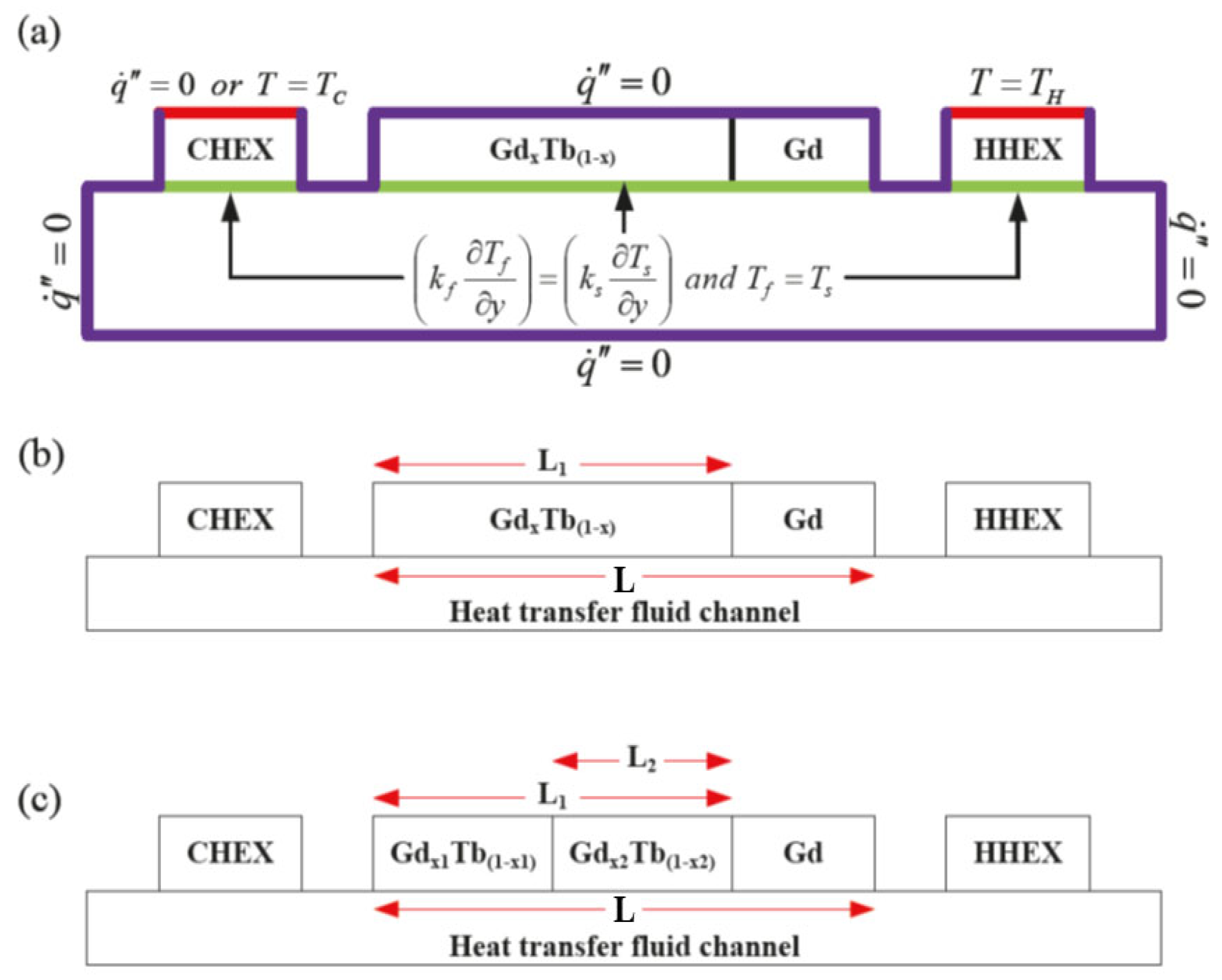
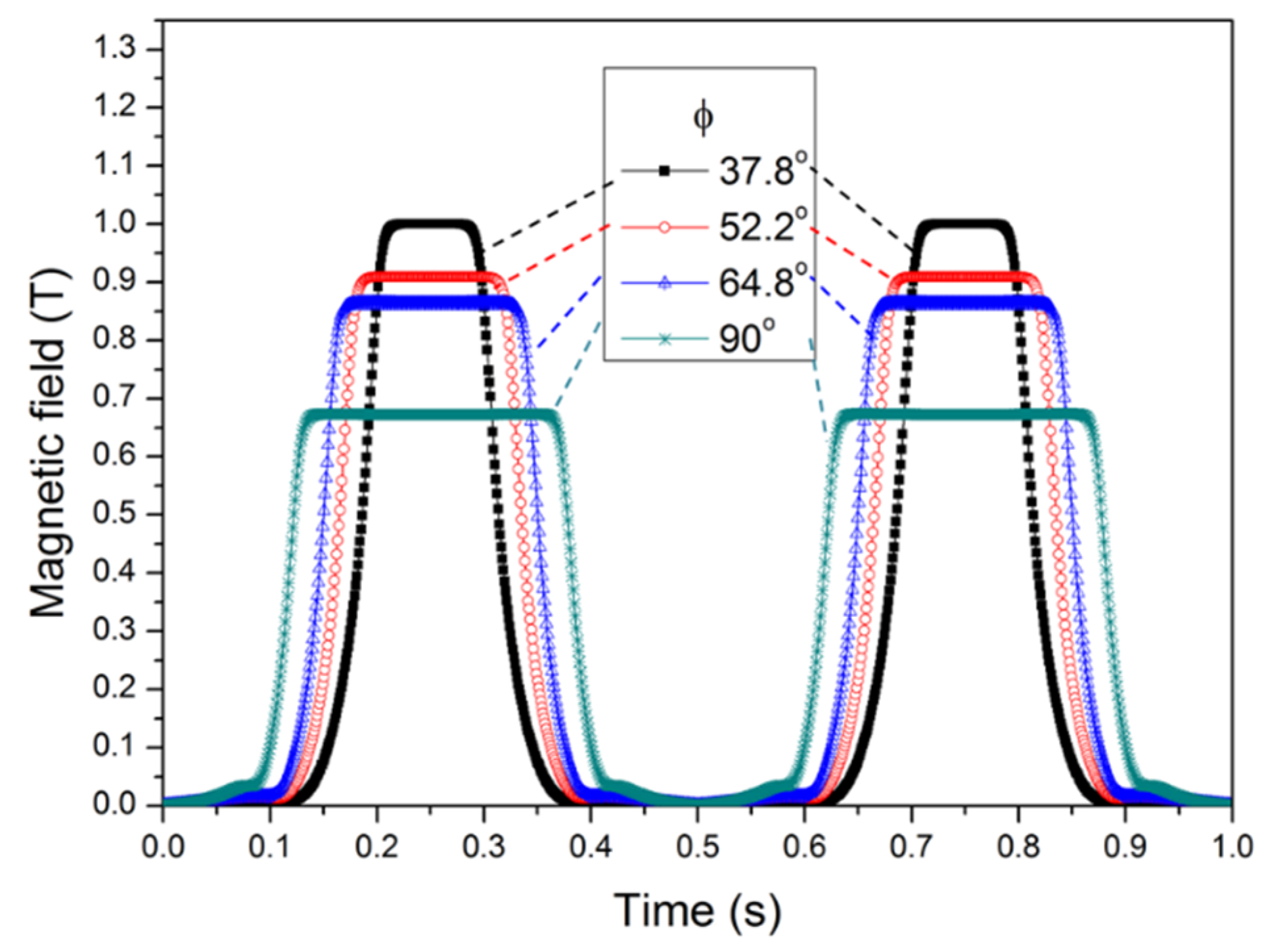
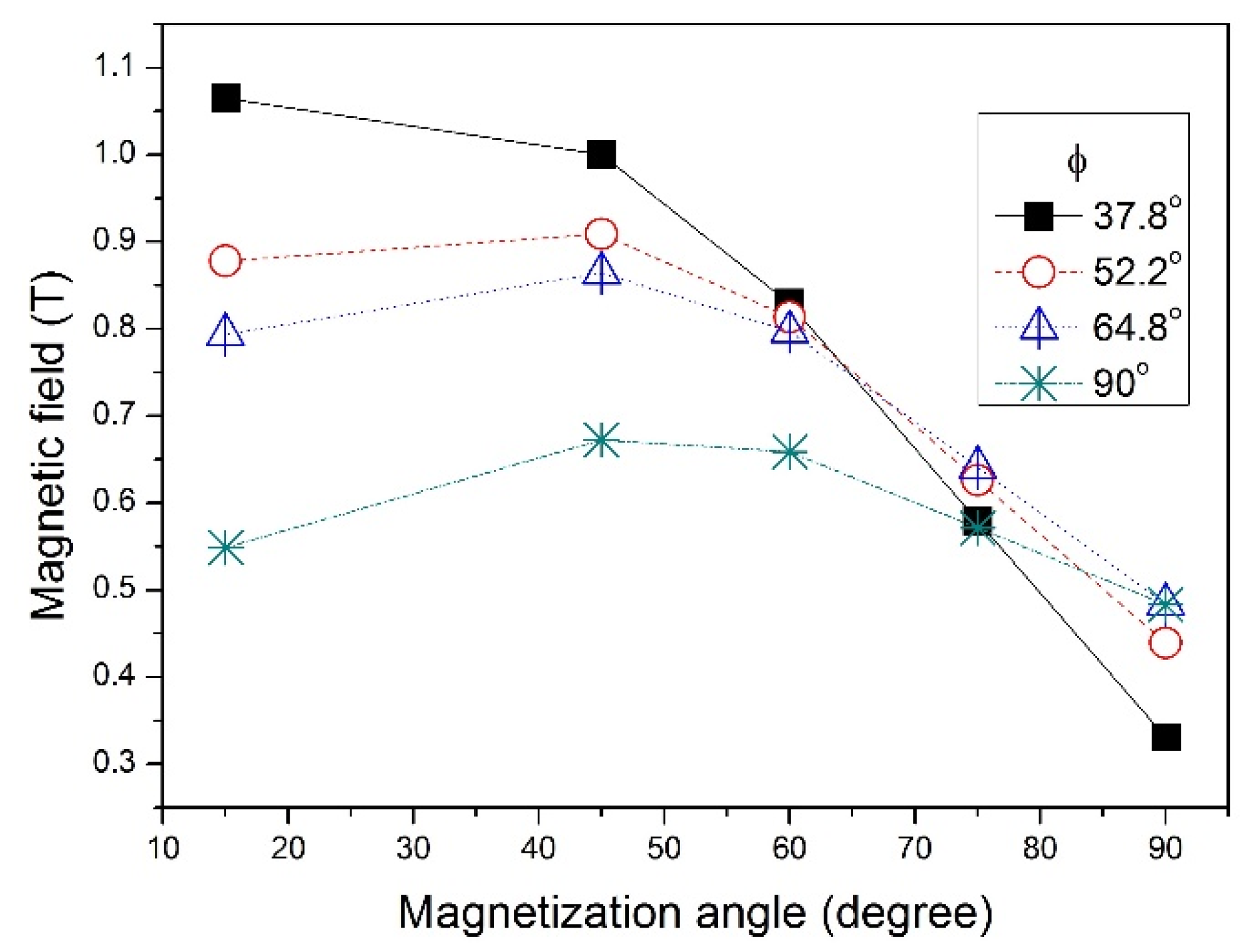
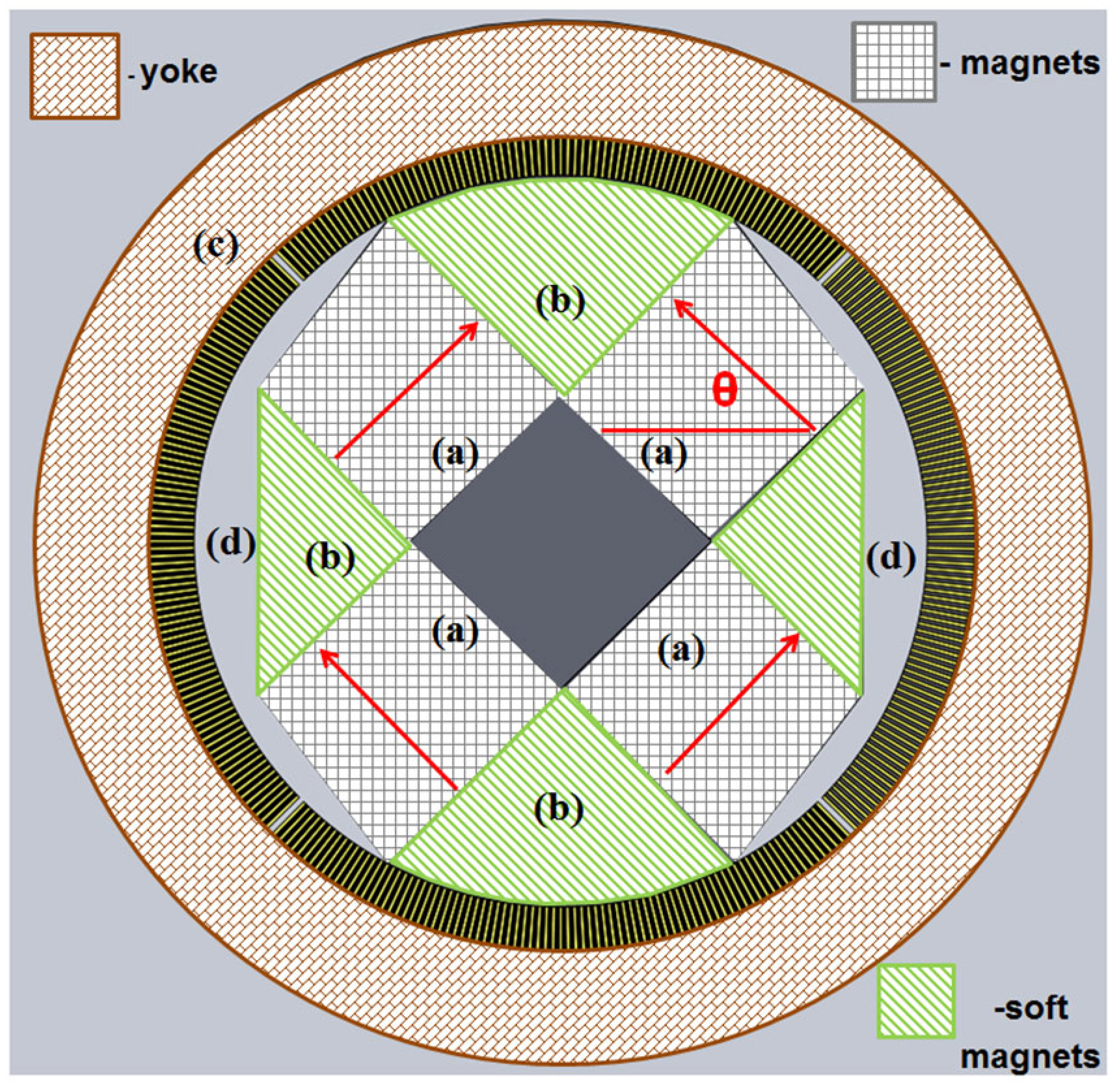
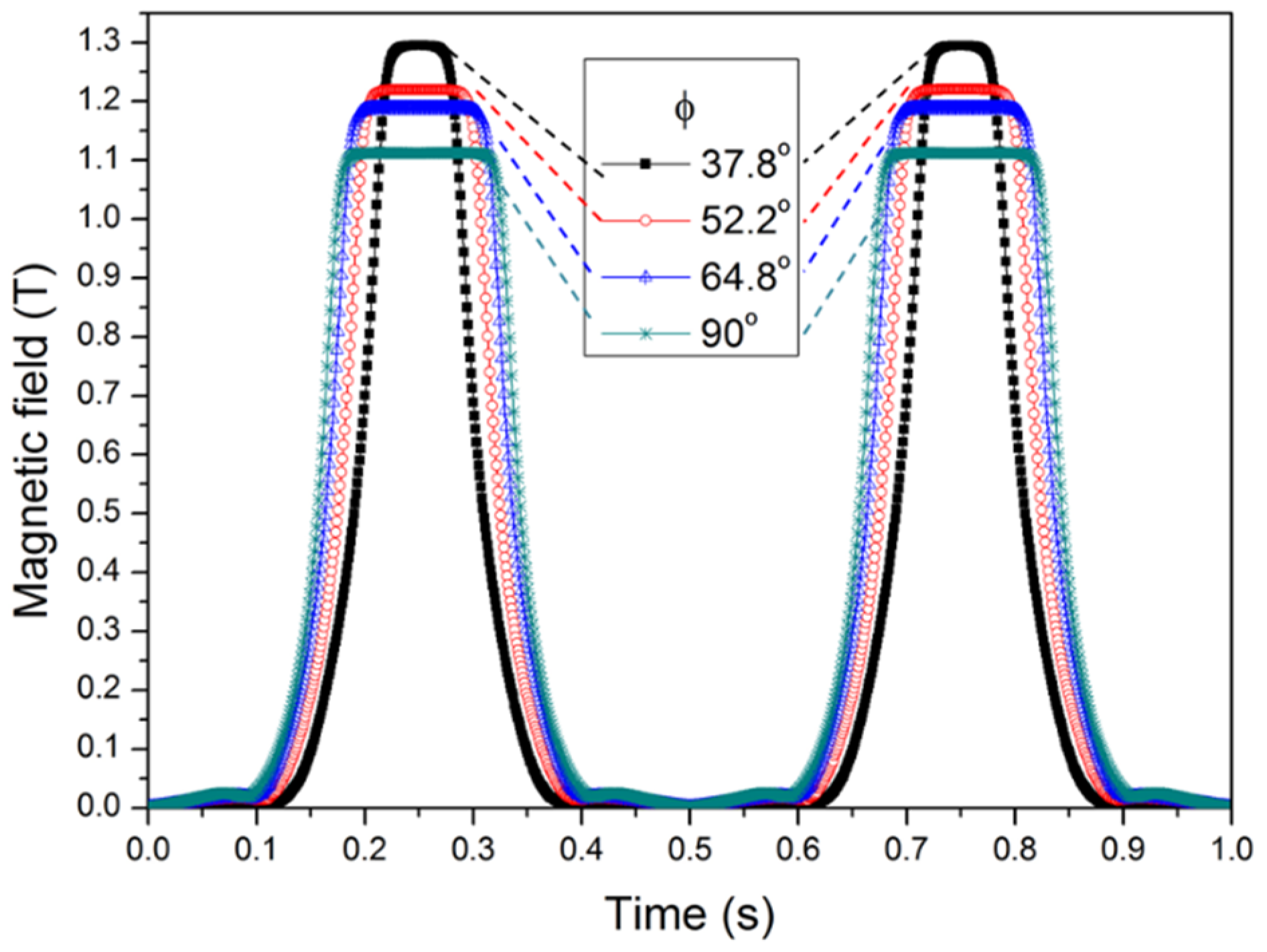
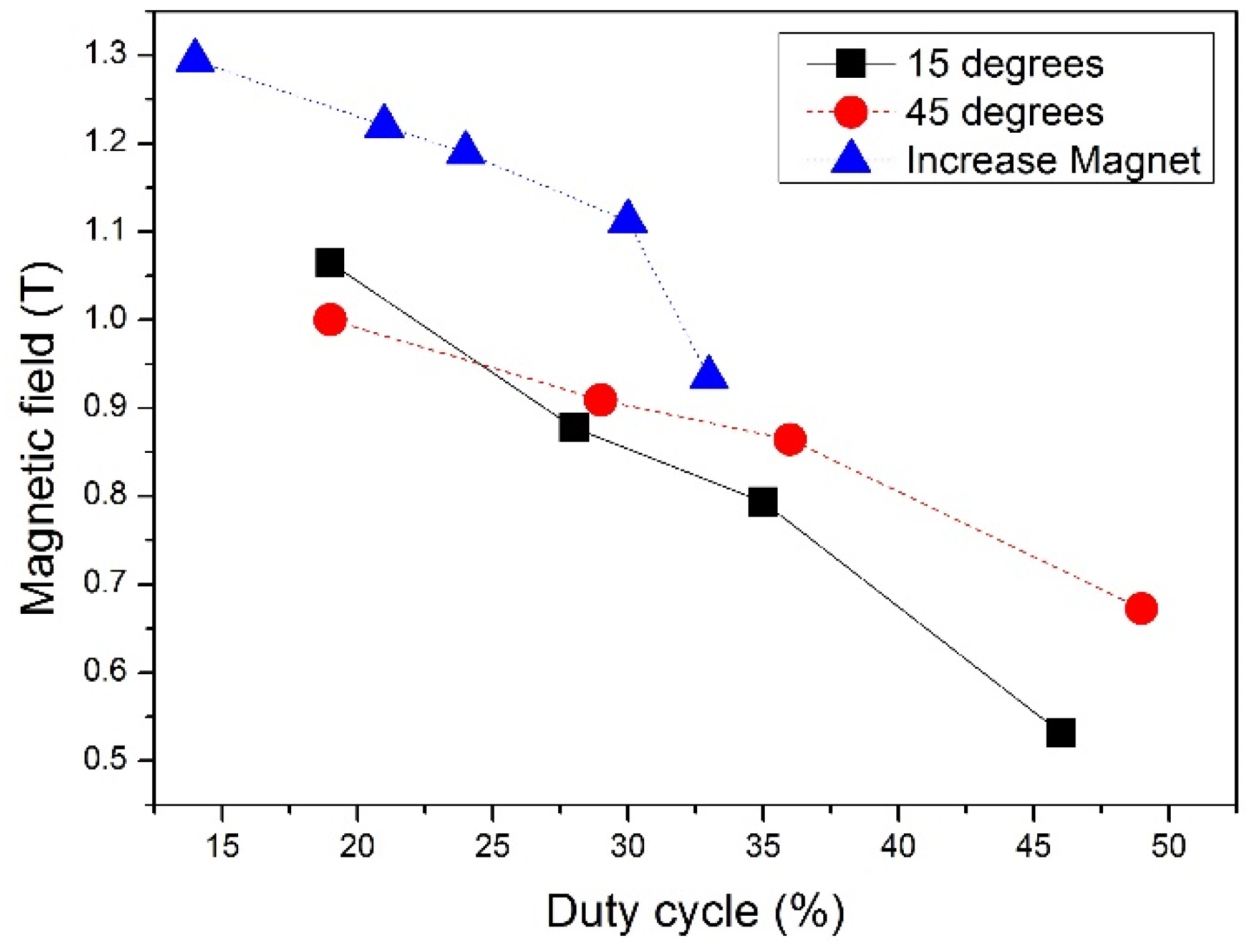



| Relative Amount of Nd-Fe-B | θ (Degrees) | ϕ (Degrees) | Bmax (T) | Duty Cycle (%) |
|---|---|---|---|---|
| 100 | 15 | 32.78 | 1.07 | 19 |
| 100 | 15 | 52.2 | 0.88 | 28 |
| 100 | 15 | 64.8 | 0.79 | 35 |
| 100 | 15 | 90.0 | 0.53 | 46 |
| 100 | 45 | 32.78 | 1.00 | 19 |
| 100 | 45 | 52.2 | 0.91 | 29 |
| 100 | 45 | 64.8 | 0.86 | 36 |
| 100 | 45 | 90.0 | 0.67 | 49 |
| 129 | 45 | 32.78 | 1.29 | 14 |
| 164 | 45 | 52.2 | 1.22 | 21 |
| 189 | 45 | 64.8 | 1.19 | 24 |
| 223 | 45 | 90.0 | 1.11 | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-H.; Cheng, P.-H.; Leou, K.-C.; Hsieh, C.-M.; Su, Y.-C. Calculation of the Optimal Magnetic Duty Cycle for a Graded Coaxial Magnet of a Rotary Type Magnetic Refrigerator. Energies 2025, 18, 289. https://doi.org/10.3390/en18020289
Lee C-H, Cheng P-H, Leou K-C, Hsieh C-M, Su Y-C. Calculation of the Optimal Magnetic Duty Cycle for a Graded Coaxial Magnet of a Rotary Type Magnetic Refrigerator. Energies. 2025; 18(2):289. https://doi.org/10.3390/en18020289
Chicago/Turabian StyleLee, Chih-Hao, Pai-Hsiang Cheng, Keh-Chyang Leou, Chih-Ming Hsieh, and Yu-Chuan Su. 2025. "Calculation of the Optimal Magnetic Duty Cycle for a Graded Coaxial Magnet of a Rotary Type Magnetic Refrigerator" Energies 18, no. 2: 289. https://doi.org/10.3390/en18020289
APA StyleLee, C.-H., Cheng, P.-H., Leou, K.-C., Hsieh, C.-M., & Su, Y.-C. (2025). Calculation of the Optimal Magnetic Duty Cycle for a Graded Coaxial Magnet of a Rotary Type Magnetic Refrigerator. Energies, 18(2), 289. https://doi.org/10.3390/en18020289







