Abstract
With countries around the world required to change their energy systems to mitigate climate change, offshore wind power has become one of the most important renewable energy sources. This study aims to analyze the potential for offshore wind power generation based on the water depth and annual average wind speed in the Akita region, Japan. A geographical information system was used not only for a conventional square mesh but also for a rectangular mesh when there is a prevailing wind, and a greater water depth was also considered. The results obtained indicate that the use of a rectangular mesh reduces the potential for implantable offshore wind turbines compared to a square mesh. It was also found that the potential for offshore wind power generation is significant up to a water depth of 500 m.
1. Introduction
The escalating climate crisis demands a rapid and profound transformation of the global energy system towards decarbonization. Transitioning to renewable energy sources is paramount, not only for mitigating climate change but also for enhancing energy security and fostering sustainable development [1]. Among the portfolio of renewable technologies, offshore wind power (OWP) has emerged as a particularly promising solution due to its significant potential for large-scale electricity generation. Compared to its onshore counterpart, OWP often benefits from stronger and more consistent wind resources, reduced land-use constraints, and potentially lower visual and noise impacts [2,3]. Recent years have witnessed remarkable technological advancements, including the development of larger, more efficient turbines and the maturation of floating foundation technologies, which unlock access to deep-water resources [4,5]. Concurrently, costs for OWP have seen significant reductions, making it increasingly competitive with conventional energy sources [6]. Consequently, numerous countries across the world have set ambitious OWP deployment targets and have implemented supportive policy frameworks to accelerate its growth [7].
The global installed capacity of OWP has reached 83 GW, with an additional 48 GW currently under construction, indicating rapid growth [8]. In 2024, new installations totaled 8 GW, with China accounting for 50%, Europe (including the UK) for 33.7%, Taiwan for 11.6%, and Japan for 1.25%. Cumulatively, China holds 50.3% of the installed capacity, followed by Europe at 45.2%. Other countries and regions, including Japan, are just beginning to expand their offshore wind infrastructure.
As of 2025, Japan’s cumulative installed capacity stands at 253.5 MW, with only three operational offshore wind farms comprising multiple turbines. Despite this nascent stage, Japan aims to significantly increase its offshore wind capacity to 10 GW by 2030 and 30–45 GW by 2040. Under the Act on Promoting Utilisation of Sea Areas for Renewable Energy Generation, eight sea areas have been designated for offshore wind power development, totaling 3.55 GW. Furthermore, operators are currently being selected for an additional two sea areas with a combined capacity of 1 GW. While most of these projects are bottom-fixed offshore wind farms, the enactment of legislation in 2025 permitting installations within Japan’s exclusive economic zone is expected to accelerate the adoption of floating offshore wind power in the coming years.
Achieving large-scale integration of renewable energy (RE) in Japan faces several challenges. The International Energy Agency highlights the necessity of resolving grid connection constraints for RE [9]. While Wakiyama et al. suggest that the Japanese government’s 2030 RE deployment targets are achievable even with current grid limitations, they also emphasize the need for systematic consideration of future grid development plans to avoid creating “hotspots” of grid instability due to the integration of variable renewable energy (VRE) sources like solar and wind power [10]. It is important to note that the 2018 study by the Renewable Energy Institute did not account for large-scale offshore wind power deployment, as it predates its significant introduction in Japan. More recent research has begun to address this. For instance, Kuriyama et al. analyzed a 100% RE scenario, including offshore wind, and proposed minimal transmission grid reinforcement by integrating hydrogen production systems as an alternative [11]. Conversely, Bogdanov et al. demonstrated that a RE-based system would require substantial grid reinforcement to facilitate large-scale energy transfer from resource-rich eastern regions to densely populated central and western regions [12]. These varying conclusions underscore that grid reinforcement and development strategies are highly dependent on the specific types and locations of RE sources deployed. Therefore, understanding the spatial distribution of RE potential is crucial for optimizing future grid planning.
The accurate and comprehensive assessment of OWP potential is fundamental for informed decision-making by policymakers, grid operators, project developers, and investors. Such assessments underpin the setting of realistic deployment goals, effective maritime spatial planning (zoning), infrastructure investment planning, and de-risking project development. While numerous studies have assessed OWP potential at various scales [13,14,15,16,17], the potential assessment studies have generally used a square mesh, e.g., measuring . Bardenhagen and Nakata presented an approalch for estimating the OWP potential of Japan [17]. They assessed the potential using the bathymetry data that is 1 km mesh, and showed the potential of the floating and fixed-bottom OWP of each area if Japan were divided into 9 areas. This is suitable for wind turbine installations that receive wind from all directions. If wind turbines are to be installed to receive wind from a specific direction, it is not appropriate to separate them into square meshes because the spacing of the wind turbines would need to vary for each direction.
Therefore, the primary objective of this study is to conduct a comprehensive and updated assessment of the potential for OWP in Akita, Japan, considering different types of mesh and deeper water depths. Specifically, this research seeks to answer the following key questions:
- What is the theoretical maximum OWP resource available within the defined study area based purely on wind resource and water depth criteria?
- How is this potential reduced when applying a comprehensive set of social constraints?
- What is the estimated technical potential for both fixed-bottom and floating OWP technologies, considering current technological limitations?
- To what extent does the shape of the mesh affect the potential of OWP?
The scope of this analysis is geographically focused on Akita in Japan and considers annual average wind speed and the Rayleigh distribution. The assessment evaluates average wind speed, water depth, and fishing rights as the social constraint for both fixed-bottom and floating offshore wind technologies, utilizing a geographical information system (GIS). The accuracy of the potential assessment is contingent upon the resolution and reliability of the input data.
Akita Prefecture is a frontrunner in offshore wind power development within Japan. Of the ten offshore wind promotion zones designated under Japan’s Act on Promoting the Utilization of Sea Areas for the Development of Marine Renewable Energy Power Generation Facilities, four are located off the coast of Akita. Selection as a promotion zone under this Act requires the consent of local residents, including fishing communities, which highlights the advanced social acceptance of offshore wind in Akita. While Hokkaido and northern Kyushu have larger areas with water depths less than 200 m [18], Akita’s offshore areas boast excellent wind conditions [19]. Specifically, its coastal areas with depths less than 50 m—ideal for fixed-bottom installations—exhibit superior average wind speeds, comparable to western Hokkaido and northwestern Aomori Prefecture. Furthermore, environmental constraints, such as the risk of the collision risk between seabirds and offshore wind turbines, are relatively lower in Akita compared to regions like Hokkaido. For these reasons, Akita is expected to continue to be a driving region for the introduction of offshore wind power in Japan.
The following contributions of this study to offshore wind power are noteworthy:
- Clarifying the impact of rectangular mesh analysis considering prevailing winds on potential assessment.
- Quantitatively demonstrating the power generation potential of both fixed-bottom and floating offshore wind, thereby contributing to necessary infrastructure development and policies such as future grid enhancement plans.
- Evaluating the potential in deep-sea areas with water depths exceeding 200 m, providing guidance for future technological development of floating offshore wind power.
2. Methodology
The OWP potential was estimated according to the following steps:
- The wind turbine standards were set.
- We created mesh data representative of the size of one wind turbine that was being considered for installation in one mesh. The average wind speed and water depth data were assigned to the mesh data.
- The annual power generation potential off the coast of the target area was obtained by summing the amount of electricity generated by each mesh. The amount of power generation for each mesh was estimated from the average wind speed and the occurrence rate of wind speed, which were obtained from the Rayleigh distribution.
Figure 1 shows a flow diagram summarizing the methodological steps.
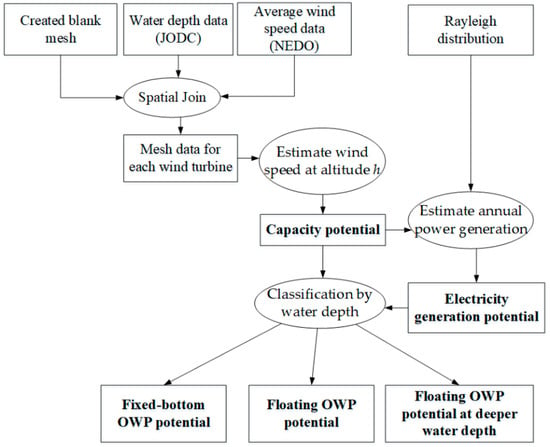
Figure 1.
Flow diagram summarizing the methodological steps.
2.1. Wind Turbine Standards
The unit capacity of wind turbines used in a previous study conducted by the Ministry of Environment was 5 MW until 2018, which changed to 10 MW in 2019. We assumed three types of wind turbine, as shown in Table 1. The rotor diameter is related to the mesh size, and the hub height is related to the wind speed.

Table 1.
Wind turbine standards in this study [20].
2.2. Mesh Data Creation
We set the mesh size so that only one wind turbine could be installed in the mesh. The two types of mesh were created as shown in Figure 2. One is the mesh designed for the case of no prevailing wind, and the other mesh is designed for cases considering prevailing wind. We considered the cases whereby the total target area was divided using mesh type (a) in Figure 2, or that the total target area was divided using mesh type (b). The mesh of the target area was created using the following procedure:
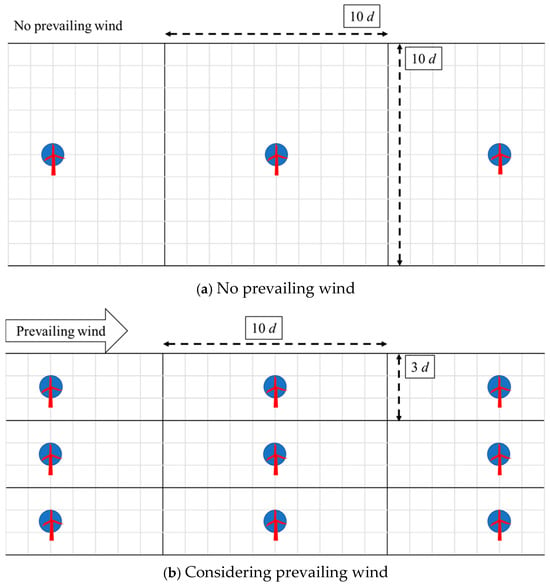
Figure 2.
Created mesh size and shape in the case of (a) no prevailing wind and (b) prevailing wind. Blue circles denote wind turbines with diameter d.
- ➀
- A wide area including the target area was divided by a mesh on the GIS.
- ➁
- A mesh was selected whose distance from the center of the mesh to the coast was more than 1.5L km and less than 30 km. Here, L denotes the length of the long side of the mesh. The reason why we used 1.5L km instead of L km is that a part of the mesh will be on land if the distance is L km. Since the onshore areas along the coast may be cliffs or onshore wind farms, we chose 1.5L km so that the entire mesh would be in the sea.
- ➂
- The wind speed and water depth data were assigned to the created mesh. The average wind speed and water depth data were available in the form of mesh data [18,19]; however, the mesh size of the obtained data was different from the mesh size used in this study. The average wind speed data [19] is 500 m grid mesh data, representing the average values over a 20-year period from 1995 to 2014. Similarly, the water depth data [18] is also 500 m grid mesh data, consistent with the wind speed data. Therefore, the average wind speed and water depth data were converted to point data, and the point data were assigned to the created mesh on the GIS platform through a spatial join. If there were multiple point data in one mesh, the average value for wind speed and the maximum value for water depth were assigned, respectively. If no point data existed within a mesh, the nearest point data from the mesh’s centroid was assigned.
It was assumed that the fixed-bottom structure installed in the mesh was at a water depth of less than 50 m, and that the floating structure is installed in the mesh at a water depth of more than 50 m and less than 200 m in the conventional system. It was assumed that the floating structure would be able to be installed in the mesh at a water depth of more than 200 m during the analysis of the potential at deeper water depths.
Average wind speed data were available for 60 m, 80 m, 100 m, 120 m, and 140 m altitude; however, the hub heights for 5 MW and 8 MW wind turbine were 90 m and 110 m. The average wind speed vh [m/s] at altitude h [m] was estimated as follows.
where v0 [m/s] denotes the average wind speed at base altitude h0 [m], and 1/n [-] denotes an exponent of the exponential rule. We calculated 1/n using the wind speed at 60 m for v0 and 120 m for vh, and estimated the average wind speed for altitudes of 90 m and 110 m. The resulting n values ranged from 5 to 60. No correlation was observed between these values and either offshore distance or water depth. This range, while broad, is considered reasonable, encompassing the previously reported value of 1/n = 0.11 [21]. The proportion of meshes where n < 10 and n > 50 is very small, each less than 1% of the total. In most meshes, n falls within the 10–30 range, and since the wind speed difference between n = 10 and n = 30 is only about 3–5%, its impact on power output estimation is limited.
The Ministry of Environment in Japan analyzed the OWP potential under the assumption that the 2 MW wind turbine was installed in a mesh measuring 500 m per side [22]. Bardenhagen and Nakata also analyzed the OWP in Japan, assuming that the 10.6 MW wind turbine was installed in a mesh measuring 1 km per side [17]. These previous studies used square meshes for analyzing OWP potential considering the presence of prevailing wind. However, as shown in Figure 2, the area required for the installation of a single offshore wind turbine is rectangular [23]. The wake effects behind wind turbines are not considered because there is enough distance between wind turbines for prevailing winds. In order to evaluate the effect of the mesh shape, this study also analyzed the OWP potential using conventional 1 km2 square meshes for a 10 MW wind turbine, comparing the results with those using rectangular meshes.
Note that this mesh design is optimized for east–west winds, meaning the influence of north–south winds was not considered. Even if the prevailing wind is primarily east–west, there are times when winds blow from the north or south. During these periods, wake effects are expected to reduce the power output of downstream wind turbines. While the reduction amount depends on the wind direction angle and wind speed, this study calculated power output based on the annual occurrence rate of each wind speed derived from the Rayleigh distribution, which does not allow for the consideration of wind direction. A quantitative analysis for wake effects would require considering the temporal variation in both wind direction and wind speed.
2.3. Annual Power Generation Potential
The annual power generated Ewind,m by a wind turbine in mesh m [GWh/year] was estimated as follows [24]:
where fi,m(vi) [-] denotes the occurrence rate of wind speed vi according to the Rayleigh distribution in the mesh m; pi(vi) [GWh] denotes the generated power for wind speed vi [GWh]; [m/s] denotes the average wind speed; denotes the air density [kg/m3]; A [m2] denotes the disk area of a wind turbine; and ηwind [-] denotes the conversion efficiency of a wind turbine, which is calculated using a rated wind speed and a rated power output. The Rayleigh distribution corresponds to a Weibull distribution with a shape parameter k = 2. Although the Weibull distribution coefficients for the study area are unknown, and the estimation accuracy of the Rayleigh distribution is lower than that of the Weibull distribution, prior studies suggest it is sufficiently accurate [25]. Also, Rezaei and Nejad observed the fair performance of Rayleigh distribution in offshore wind site [26]. Therefore, we opted to use the Rayleigh distribution in this study. Based on the air density analysis using data from Japanese meteorological observatories [27] and the average atmospheric pressure and average temperature in Akita City during winter, when wind speeds are high, the air density is approximately 1.225 kg/m3. Note that the generated power pi(vi) is zero when the wind speed is less than the cut-in velocity and larger than the cut-off velocity, as shown in Table 1.
The annual power generation potential off the coast of the target area Ewind [GWh/year] was obtained by summing Ewind,m as follows:
2.4. Case Setting
We considered three cases—the base case considering no constraint, the natural case considering natural constraint, and the social case considering social constraint. In the base case, the target area was within a distance of 30 km from the shoreline. In the natural case, the constraint of wind speed and water depth was considered. Meshes with average wind speeds of less than 6.5 m/s or a water depth of more than 200 m were excluded from the analysis. In the social case, the nature constraint and the fishing rights were considered because Japanese coastal fishermen have legally guaranteed equitable access to and “ownership” of the living aquatic resources of coastal waters [28]. Meshes of the area within the fishing rights were excluded from the analysis. The area of other major social constraints such as marine parks, habitats of natural monuments, and Self-Defense Force-related facilities are included in the area of fishing rights [19].
The constraints in each case are shown in Table 2.

Table 2.
The constraints for excluding meshes in each case.
The target area is Akita Prefecture, Japan, which is expected to be suitable for the introduction of OWP generation [29]. Figure 3 shows the target sea area in the base case. Since the target area is within 30 km of the coastline of Akita Prefecture, some of the sea areas extend into Aomori Prefecture in the north and Yamagata Prefecture in the south. Regarding constraints related to maintenance access and grid connection, it was suggested that port capacity and transmission line connectivity are already reaching their limits, even with the ongoing development of 2 GW of bottom-fixed offshore wind power. Shiraki et al. indicated that grid connection limitations influence wind power potential [30], and Onodera et al. propose a new power network for designing a 100% renewable energy system [31]. Consequently, the utilization of alternative ports and the expansion of transmission lines are being planned. Therefore, this study does not consider these constraints but instead assesses the offshore wind potential off Akita Prefecture to indicate the scale of future port and transmission capacity requirements. Also, while research on the impact of offshore wind farms on marine ecosystems is well-advanced in Europe [32], Japan has limited empirical studies due to the scarcity of offshore wind installations outside of port areas. Obane et al. investigated the impact of offshore wind farm construction on seabirds in Hokkaido [33], and Mikami et al. estimated the collision risk between two gull species and offshore wind turbines in Hokkaido [34]. However, based on a seabird colony database that identifies the habitats of 48 seabird species [35], Akita Prefecture only hosts one seabird species in a single inland location; thus, we did not consider seabird impact in this study.
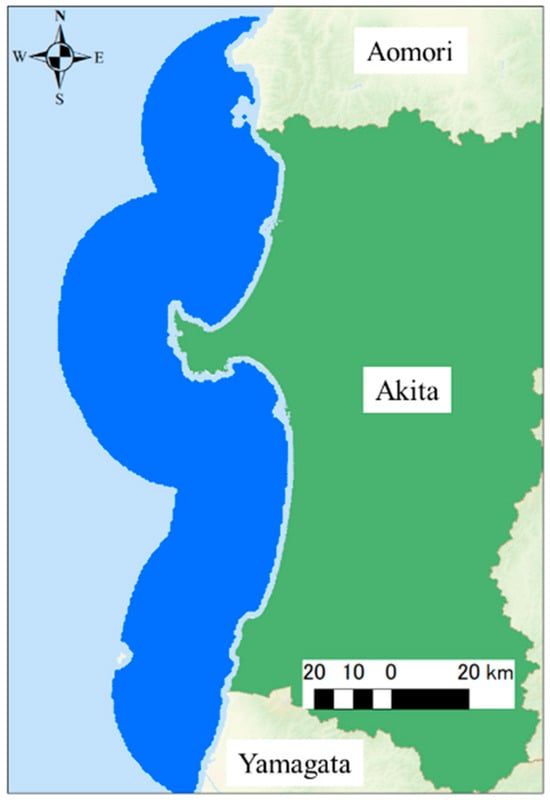
Figure 3.
Target area in this study. Blue area shows target sea; green area shows Akita Prefecture.
2.5. Potential at Deeper Water Depths
In above, it was assumed that the water depth range for offshore wind was less than 50 m for fixed-bottom structures and less than 200 m for floating structures. Previous studies analyzed offshore wind in deeper sea areas. For example, Campanile et al. analyzed the relevant installation and maintenance costs of offshore wind for water depths ranging from 200 to 350 m [36]. Lin et al. investigated the effect of water depth on the global performance of a floating wind turbine, considering water depths between 200 and 300 m [37]. Lin also discussed future wind turbines being operated at depths of more than 500 m. In order to achieve a zero-carbon society in the future, it is important to discuss the potential of OWP in the future as well as in the current situation.
3. Results and Discussion
3.1. Created Mesh and Capacity Potential
Figure 4 shows (a) the water depth and (b) the average wind speed at height 120 m [19] in the target area. It was found that the sea area within 30 km from the coast includes almost all areas where the water depth is less than 200 m and the average wind speed is greater than 6.5 m/s. Table 3 and Table 4 show the number of created meshes in each case, both with and without prevailing wind. In this study, it was assumed that one wind turbine is installed in a mesh. Figure 5 shows the installation capacity of OWP based on the number of created meshes in each case.
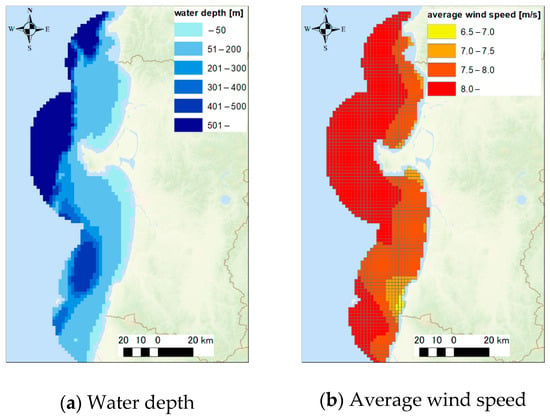
Figure 4.
Natural conditions in the target area.

Table 3.
Number of created meshes in each case for no prevailing wind.

Table 4.
Number of created meshes in each case for prevailing wind.
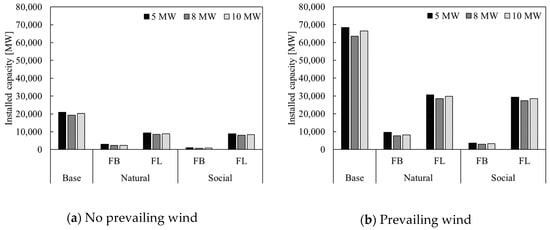
Figure 5.
Installation capacity of OWP in each case. FB—fixed-bottom; FL—floating.
Comparing the capacity of the wind turbines, it can be seen that the number of meshes is almost inversely proportional to the equipment’s capacity. This is because the capacity per unit and the area required for installation per unit are both proportional to the square of the rotor diameter. In the case of fixed-bottom offshore wind turbines, the number of meshes decreased to 40–45% when the installation capacity doubled. The area of the sea that is less than 50 m deep, which is the target area for the installation of fixed-bottom wind turbines, is small, and the number of possible installations was strongly influenced by the boundary, which, in turn, limited the number of possible installations of larger wind turbines. The largest capacity in each case was obtained in relation to the installation of 5 MW wind turbines, as shown in Figure 5. Conversely, the smallest capacity was obtained in relation to the installation of 8 MW wind turbines. The installation capacities of floating structures were 92–93% for 8 MW wind turbines and 94–97% for 10 MW wind turbines, compared to 5 MW turbines; for fixed-bottom structures, these values were 75–83% for 8 MW and 79–89% for 10 MW wind turbines. When wind turbine capacities increase further, for instance to 26 MW or 35 MW [8], the required installation area will grow due to the larger rotor diameters. For bottom-fixed turbines, this is expected to further reduce the installable capacity compared to 10 MW turbines. However, floating offshore turbines are anticipated to be less affected by this increase in size.
Comparing each case, the total number of created meshes in the natural and social cases was almost half that of the base case because almost half of the target sea area is more than 200 m deep, as shown in Figure 4a. In the social case, the number of created meshes decreased by considering the social constraint and fishing rights. In particular, the number of fixed-bottom structures decreased to less than 40%. The decrease in the number of floating systems is only about 5%. Since most of the fishing rights are set in shallow waters near the coast, this has a large impact on the fixed-bottom type, but only a small impact on the floating type. The share of fixed-bottom structures in relation to the total installation capacity was 21–24% in the natural case, but decreased to 9–10% in the social case.
Comparing the presence or absence of prevailing winds, the number of created meshes increased by more than three times due to the consideration of prevailing wind because the required area to install one wind turbine considering prevailing wind is 33% of the required area for the installation not considering prevailing wind. In particular, the number of fixed-bottom structures in the social case considering prevailing wind increased to four times that of the case with no prevailing wind because of the area boundary mentioned above.
In the case of no prevailing wind, the total installation capacities were 56–59% in the natural case and 45–47% in the social case compared with the base case.
It is important to note here that Akita Prefecture lacks 500 kV transmission lines, and the only coastal area with access to 275 kV transmission lines is Noshiro City, located in the northern part of the prefecture. While plans are underway to improve the 275 kV transmission lines and construct new substations and 500 kV transmission lines for the full-scale operation of fixed-bottom offshore wind farms from 2028 onwards, these developments primarily target inland areas. Therefore, it is anticipated that new transmission lines will need to be constructed separately from the offshore wind farms to the onshore substations. This presents a regulatory risk concerning transmission line connections, potentially affecting deployment schedules and prioritization.
3.2. Comparison with Conventional 1 km2 Square Mesh
We compared the offshore wind turbine potential using rectangular meshes with that using square meshes. The capacity of a wind turbine was 10 MW for both mesh shapes. The constraints for conventional square meshes were the same as in the natural case. Table 5 shows the results of the number of created meshes and the power generation potential.

Table 5.
Number of created meshes and power potential for rectangular and square meshes.
The number of meshes and the power generation potential using square mesh were similar to those using rectangular mesh for floating structures; this difference was significant in shallow waters. This is because the closest distance between the center of each mesh and the coast is 1.5 km for square meshes, while it is 2.6 km for rectangular meshes. As a result, the area of the sea where square meshes can be installed is larger than the area where rectangular meshes can be installed, which is thought to have resulted in a larger number of meshes and a larger amount of power generation. Figure 6 shows the rectangular meshes and the center of square meshes nearest the coast. Bardenhagen and Nakata estimated the OWP potential for Tohoku region where includes Akita prefecture [17]. The share of floating structure in total potential number of wind turbines was 74%, and that of fixed-bottom structure was 26%. These shares are almost the same as those obtained using square meshes in this study. Therefore, it is expected that the share of the fixed-bottom structure will similarly decrease, and the share of the floating structure will increase if a rectangular mesh is used.
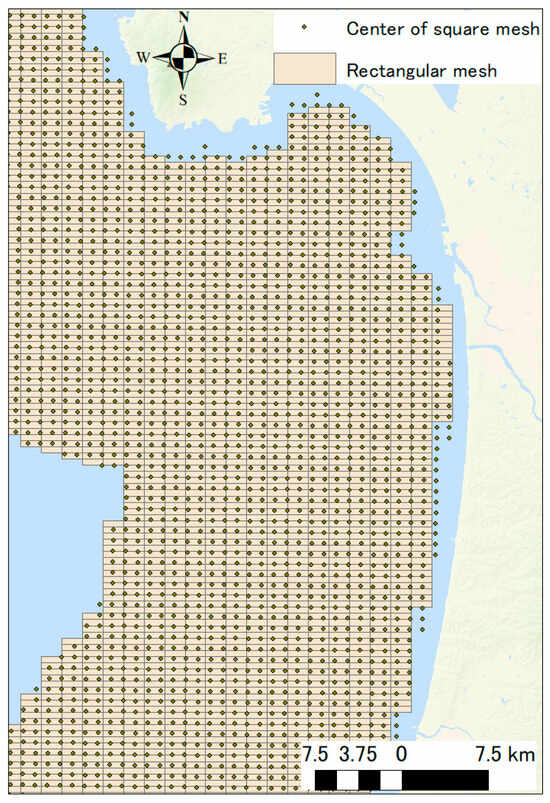
Figure 6.
Example of the rectangular meshes and the center of the square meshes.
This result is expected to be similar not only in the target area of this study but also in other ocean areas. It is also expected that the smaller the shallow sea area, the more pronounced the difference between the square and rectangular meshes will be. Therefore, for a more accurate potential analysis, a rectangular mesh should be used that takes into account the prevailing wind.
However, it is difficult to analyze the entire sea area of Japan using a rectangular mesh that takes into account the presence or absence of prevailing winds. Therefore, it is important to select promising areas for OWP generation based on the studies by the Ministry of the Environment [22] and Bardenhagen and Nakata [17] as well as to conduct detailed analyses that consider the presence or absence of prevailing winds in the target areas.
3.3. Electricity Generation Potential
Figure 7 shows the electricity generation potential of offshore wind both in the presence and absence of prevailing wind. The electricity demands in the target area—Akita Prefecture—and in the seven prefectures of the Tohoku region [38] are also shown.
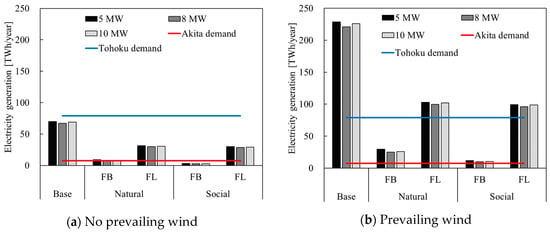
Figure 7.
Electricity generation potential of offshore wind in different cases. FB—fixed-bottom; FL—floating. The red line shows the electricity demand in Akita Prefecture, while the blue line shows the electricity demand in the seven prefectures of the Tohoku region, including Akita Prefecture.
In the case of no prevailing wind, the electricity generation by the fixed-bottom structures just met the electricity demand of 7.3 TWh/year in Akita Prefecture in the natural case but was insufficient in the social case. The electricity generation by the floating structures was more than four times the electricity demand in Akita Prefecture, but less than half of the electricity demand (79.1 TWh/year) in the Tohoku region. Even the electricity generation in the base case was not able to meet the electricity demand in the Tohoku region.
In the case of prevailing wind, the electricity generation by the fixed-bottom structure was larger than the electricity demand in Akita Prefecture, and that by the floating structure was larger than the electricity demand in the Tohoku region, even in the social case. The surplus electricity after the total electricity generation met the electricity demand in the Tohoku region was 45.6–53.7 TWh/year in the natural cases and 27.0–31.8 TWh/year in the social cases. The surplus electricity in the base case was 142–149 TWh/year, which is sufficient to meet the electricity demand in urban areas, e.g., 78.2 TWh/year in Tokyo. These results cannot be compared to measured offshore wind data or output data from operational wind farms due to the lack of them. However, our results show reasonable capacity factors 35.6–37.3% for fixed-bottom wind turbines when compared to planned fixed-bottom offshore wind farms: the Yurihonjo offshore wind farm, scheduled to begin operation in 2030, has a projected capacity factor of 36.2%, and the Noshiro-Oga-Mitane project, scheduled to begin operation in 2028, has a projected capacity factor of 33.4%. This suggests that our estimation achieves a similar level of accuracy to project plans. Nevertheless, a limitation of this study is that wind direction was not considered. The meshes are designed to optimally capture wind from the east and west. Therefore, when winds originate from the north or south, power generation is expected to decrease due to wake effects.
Bardenhagen and Nakata [17] also showed that the electricity generation potential of OWP in Tohoku region was more than 10 times larger than the electricity demand in Tohoku region. Using a rectangular mesh in their study methodology as well, it is expected that the share of the fixed-bottom structure in the electricity generation potential decreases and that of floating structure increases.
In this study, the air density is assumed to be constant 1.225 kg/m3. However, the air density can exceed 1.25 kg/m3 when temperatures drop below 0 °C between November and April, and can fall below 1.2 kg/m3 when atmospheric pressure decreases between May and October [27], which could potentially impact power generation. If seasonal variations in air density are considered, the potential for wind power generation is estimated to change within a range of plus or minus 2–3%. Furthermore, as the Rayleigh distribution used in this study is noted to be influenced by terrain, there are limitations to the accuracy of power output estimations for fixed-bottom offshore wind farms located close to coastal areas.
3.4. Potential at Deeper Water Depths
We analyzed the OWP potential for each 100 m depth after 200 m; the results are shown in Table 6 in the absence of prevailing wind and in Table 7 in the presence of prevailing wind. Common across all cases, the largest potential (43–45% of the total potential) was obtained at water depths from 50 m to 200 m. In total, 6–10% of the total potential was obtained at water depths from 200 m to 300 m, from 300 m to 400 m, and from 400 m to 500 m. After depths from 500 m to 1000 m, the potential of each depth of 100 m was less than 2% of the total potential. The total share of depths prior to 500 m was more than 75% for all cases, and that of depths subsequent to 1000 m was more than 13%. Therefore, enough evidence was provided to develop depths prior to 500 m in this area. If more than 90% of the total potential is required to be installed, an innovative offshore wind turbine that is able to be installed at depths of more than 1000 m is needed.

Table 6.
OWP potential for each depth of 100 m in the absence of prevailing wind.

Table 7.
OWP potential for each depth of 100 m in the presence of prevailing wind.
In the natural cases, the second largest potential was obtained at water depths of less than 50 m; however, in the social cases, which consider fishing rights, the second largest potential was obtained at depths from 200 m to 300 m. At water depths deeper than 300 m, there is no difference between the natural case and the social case because there are no fishing rights.
For comparing the effect of wind turbine capacity, as shown in Section 3.1 and Section 3.3, the potentials using 5 MW/unit were the largest at water depths less than 50 m and depths ranging from 50 m to 200 m. However, after 200 m, the potentials using the 10 MW/unit were the largest or almost the same as the other capacities. Therefore, the 5 MW offshore wind turbine should be installed in the sea at depths of less than 50 m, while the 10 MW offshore wind turbine should be installed in deeper sea areas. Note that we focused only on the potential and did not consider the cost. The number of offshore wind turbine units of 5 MW would be twice that of 10 MW units, and the capital cost, as well as the operation and maintenance costs, is expected to be more expensive. For sustainable operation, the cost of offshore wind turbines with different capacities should be analyzed.
Farr et al. [39] evaluated six categories of potential effects: changes to atmospheric and oceanic dynamics due to energy removal and modifications, electromagnetic field effects on marine species from power cables, habitat alterations to benthic and pelagic fish and invertebrate communities, underwater noise effects on marine species, structural impediments to wildlife, and changes to water quality. They suggested that the effects associated with electromagnetic fields, noise, habitat alterations, and changes to water quality are likely to have minor impacts on marine organisms if mitigation strategies and best-practice protocols are properly adopted. It was also suggested that preventative initiatives such as the careful siting of deepwater, floating offshore wind farms outside of important habitats, may reduce otherwise moderate impacts of displacement, avian collision, and marine mammal collision and entanglement. Watson et al. [40] also pointed out that prior to 2022 January, there were no studies investigating the potentially negative effects of invasive species that might attach on deep-water floating offshore wind farms, identifying this as a crucial future research area. Therefore, investigating marine organism habitats in deep-sea environments and invasive species that may attach to floating offshore wind farms is crucial.
3.5. Livilized Cost of Electricity (LCOE)
Although this study did not aim to estimate the LCOE of the OWP in Japan, it is important to discuss the effects of larger turbine and deeper installation on the LCOE. Regarding the cost of bottom-fixed offshore wind power generation in Japan, the Agency for Natural Resources and Energy estimates it at 30.9 JPY/kWh [41], while IRENA reports 0.211 USD/kWh (equivalent to 29.8 JPY/kWh) that is much more expensive than those of China and Europe [6]. Capital cost and O&M cost constitute approximately 40% and 28%, respectively, of the total generation cost, and these expenses are influenced by the scale of the turbines. While the cost per turbine increases with larger turbines, the total construction cost for a wind farm of the same capacity may decrease due to a reduced number of installed turbines. In Japan, there are currently only three commercial-scale offshore wind farms, making the cost implications of larger turbines unclear. The cost breakdown of renewable energy in Japan differs from that in Europe. According to IRENA [42], although hardware costs, such as module prices for solar photovoltaic (PV), are comparable, installation costs in Japan are relatively higher. If a similar trend holds for offshore wind power, larger turbines could potentially lead to a reduction in installation cost per unit capacity.
Currently, there are no commercially operating floating offshore wind farms in Japan, and the construction costs have not been validated, making it impossible to quantitatively assess the impact of increased water depth. The Agency for Natural Resources and Energy only provides projected prices for 2040 [41], with 2023 values remaining undisclosed. Satymov et al. indicates that costs increase with greater offshore distance [43], and Benabadji et al. suggest that CAPEX increases linearly with water depth [44]. Therefore, for the sea areas considered in this study, it is anticipated that costs will rise as offshore distances increase and water depths deepen.
Table 8 shows the LCOEs of each renewable power in Japan [41]. Currently, utility-scale solar PV is the least expensive, with onshore wind power being comparable to geothermal power. Offshore wind power is relatively more expensive and lacks strong cost competitiveness. By 2040, when cost reductions are anticipated, fixed-bottom offshore wind power is projected to become as inexpensive as onshore wind power at JPY 14/kWh. However, floating offshore wind power remains more costly compared to both geothermal and onshore wind. Furthermore, offshore wind power construction and O&M costs vary with distance from port and water depth; thus, costs are expected to be even higher in the deep-water areas analyzed in this study. Nevertheless, offshore wind power is also anticipated to generate local economic ripple effects through construction and maintenance [45], suggesting it may still be promoted despite its higher generation costs.

Table 8.
LCOE of each renewable power [JPY/kWh] [41].
4. Conclusions
This study analyzed the offshore wind power (OWP) potential within 30 km from the coast in Akita Prefecture, Japan, considering mesh shape and water depths that are deeper than conventional depths. The results showed that the OWP potential using fixed-bottom structures in Akita Prefecture was almost equal to the electricity demand in the target area and that the OWP potential using the floating structure was larger than the electricity demand of the seven prefectures in the Tohoku region, including Akita. Therefore, the development of OWP using floating structures is important to achieving a zero-carbon society.
A rectangular mesh in the case of prevailing wind showed a smaller potential of the fixed-bottom structure than the conventional 1 km2 square mesh. This result depends on the geographic and weather conditions, and different results may be obtained in other regions. To estimate offshore wind potential, it is suggested that wider areas, potentially on a national scale, should first be analyzed using a 1 km2 square mesh before higher potential areas are analyzed using rectangular mesh in the case of prevailing wind. In particular, when planning for an implantable offshore wind farm, it is important to analyze the potential of the project considering the prevailing wind direction and mesh shape of the target area. There is huge OWP potential at water depths of less than 200 m. While transmission lines and substations are being upgraded to support the planned 2 GW of bottom-fixed offshore wind capacity, this study estimated the OWP potential reveals a much larger need. Even in the most conservative social case, fixed-bottom OWP potential ranged from 3.2 to 3.5 GW, and floating OWP was as high as 28 GW. This clearly indicates that significantly larger-scale grid reinforcement will be necessary to accommodate floating offshore wind development.
The OWP potential at water depths from 200 m to 500 m is large, and there was only a small potential at water depths above 500 m. It is suggested that wind turbines that can be installed at water depths of up to 500 m be developed if OWP generation is to expand beyond the current target water depths of less than 200 m. This suggestion also depends on geographic conditions; different results will be obtained in other regions. Thus, it is important to analyze the OWP potential at deeper water depths in each region.
For future work, it will be necessary to analyze the grid reinforcement plan for the Tohoku region, based on an offshore wind power potential analysis of the area using the methodology employed in this study. Our study’s “Natural case” results show a potential of 7.6–9.4 GW for fixed-bottom and 30 GW for floating offshore wind in Akita Prefecture. While the use of rectangular meshes in our methodology resulted in a reduced fixed-bottom potential compared to conventional approaches, Akita Prefecture alone demonstrates the capacity to meet the Tohoku region’s targets of 4.0–5.3 GW by 2030 and 5.9–9.0 GW by 2040. Additionally, these values are close to Japan’s installation targets of 10 GW by 2030 and 30–45 GW by 2040. However, the existing grid in Tohoku region including Akita prefecture lacks the capacity to accommodate such a large scale of offshore wind, necessitating significant grid reinforcement. Furthermore, other parts of the Tohoku region are also planning or considering offshore wind development. Therefore, proposing a comprehensive development schedule for zero carbon society will require analyzing deployment plans and potential in these other regions, followed by a corresponding grid reinforcement plan for the entire Tohoku region. After analyzing the grid reinforcement plan, a multi-criteria analysis (MCA) that integrates technical, economic, social, and environmental factors to prioritize zones within the Tohoku area will be developed.
Another challenge lies in extending the current GIS methodology to enable real-time or dynamic evaluations. A key limitation of this study is its inability to account for wind direction; addressing this would require analysis using hourly wind speed and direction data. Wind condition data from sources like ERA5 or GSM have large grid mesh sizes (20–30 km), which are too coarse compared to the mesh size analyzed in this study. This discrepancy could lead to results that do not accurately reflect actual wind conditions. It is expected that a more refined analysis incorporating temporal variations in wind direction and speed could be achieved by either using data with finer grid mesh sizes or by utilizing the same average wind speed data as in this study while only employing the nearest ERA5 or GSM data for the time-varying ratios of wind direction and speed.
Author Contributions
Conceptualization: T.F. and K.T.; methodology: T.F. and K.T.; software: K.T.; validation: T.F.; formal analysis: T.F. and K.T.; investigation: T.F. and K.T.; resources: K.T.; data curation: K.T.; writing—original draft preparation: T.F.; writing—review and editing: T.F.; visualization: T.F. and K.T.; supervision: T.F.; project administration: T.F.; funding acquisition: T.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by JSPS KAKENHI Grant Number JP24K15386.
Data Availability Statement
All datasets used in this research are publicly available.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Intergovernmental Panel on Climate Change. Summary for Policymakers of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2023. [Google Scholar]
- Díaz, H.; Guedes Soares, C. Review of the current status, technology and future trends of offshore wind farms. Ocean Eng. 2020, 209, 107381. [Google Scholar] [CrossRef]
- Li, J.; Wang, G.; Li, Z.; Yang, S.; Chong, W.T.; Xiang, X. A review on development of offshore wind energy conversion system. Int. J. Energy Res. 2020, 44, 9283–9297. [Google Scholar] [CrossRef]
- Pham, T.D.; Dinh, M.C.; Kim, H.M.; Nguyen, T.T. Simplified floating wind turbine for real-time simulation of large-scale floating offshore wind farms. Energies 2021, 14, 4571. [Google Scholar] [CrossRef]
- Edwards, E.C.; Holcombe, A.; Brown, S.; Ransley, E.; Hann, M.; Greaves, D. Evolution of floating offshore wind platforms: A review of at-sea devices. Renew. Sustain. Energy Rev. 2023, 183, 113416. [Google Scholar] [CrossRef]
- International Renewable Energy Agency. Renewable Generation Costs in 2022; IRENA: Abu Dhabi, United Arab Emirates, 2022; ISBN 9789292605445. [Google Scholar]
- Williams, R.; Zhao, F.; Backwell, B.; Lee, J.; Patel, A.; Hutchinson, M.; Qiao, L.; Nguyen, T.; Lathigara, A.; Liang, W.; et al. Global Offshore Wind Report 2024; Global Wind Energy Council (GWEC): Lisbon, Portugal, 2024. [Google Scholar]
- Global Wind Energy Council. Global Offshore Wind Report 2025; Global Wind Energy Council (GWEC): Lisbon, Portugal, 2025. [Google Scholar]
- International Energy Agency. Japan 2021 Energy Policy Review; International Energy Agency: Paris, France, 2021. [Google Scholar]
- Wakiyama, T.; Kuriyama, A. Assessment of renewable energy expansion potential and its implications on reforming Japan’s electricity system. Energy Policy 2018, 115, 302–316. [Google Scholar] [CrossRef]
- Kuriyama, A.; Liu, X.; Naito, K.; Tsukui, A.; Tanaka, Y. Importance of Long-Term Flexibility in a 100% Renewable Energy Scenario for Japan. Sustain. Sci. 2024, 19, 165–187. [Google Scholar] [CrossRef]
- Bogdanov, D.; Oyewo, A.S.; Mensah, T.N.O.; Nishida, Y.; Saito, T.; Aikawa, T.; Kimura, S.; Gagnebin, M.; Pescia, D.; Shimoyama, T.; et al. Energy transition for Japan: Pathways towards a 100% renewable energy system in 2050. IET Renew. Power Gener. 2023, 17, 3298–3324. [Google Scholar] [CrossRef]
- Karamanski, S.; Erfort, G. Wind Energy Supply Profiling and Offshore Potential in South Africa. Energies 2023, 16, 3668. [Google Scholar] [CrossRef]
- Bonthu, S.; Purvaja, R.; Singh, K.S.; Ganguly, D.; Muruganandam, R.; Paul, T.; Ramesh, R. Offshore wind energy potential along the Indian Coast considering ecological safeguards. Ocean Coast. Manag. 2024, 249, 107017. [Google Scholar] [CrossRef]
- Przewoźniak, M.; Wyrwa, A.; Zyśk, J.; Raczyński, M.; Pluta, M. Conducting a Geographical Information System-Based Multi-Criteria Analysis to Assess the Potential and Location for Offshore Wind Farms in Poland. Energies 2024, 17, 283. [Google Scholar] [CrossRef]
- Vinhoza, A.; Schaeffer, R. Brazil’s offshore wind energy potential assessment based on a Spatial Multi-Criteria Decision Analysis. Renew. Sustain. Energy Rev. 2021, 146, 111185. [Google Scholar] [CrossRef]
- Bardenhagen, Y.; Nakata, T. Regional Spatial Analysis of the O ff shore Wind. Energies 2020, 13, 6303. [Google Scholar] [CrossRef]
- Japan Oceanographic Data Center Water Depth Data of 500 m Mesh. Available online: https://jdoss1.jodc.go.jp/vpage/depth500_file_j.html (accessed on 8 September 2023).
- NEDO. NeoWins. Available online: https://appwdc1.infoc.nedo.go.jp/Nedo_Webgis/index.html (accessed on 8 September 2023).
- Desmond, C.; Murphy, J.; Blonk, L.; Haans, W. Description of an 8 MW reference wind turbine. J. Phys. Conf. Ser. 2016, 753, 092013. [Google Scholar] [CrossRef]
- Emeis, S. Wind Energy Meteorology. In Atmospheric Physics for Wind Power Generation; Springer: Cham, Switzerland, 2018; ISBN 978-3-319-72859-9. [Google Scholar]
- Ministry of Environment Renewable Energy Potential System. Available online: https://repos.env.go.jp/web/ (accessed on 3 August 2025).
- Gupta, N. A review on the inclusion of wind generation in power system studies. Renew. Sustain. Energy Rev. 2016, 59, 530–543. [Google Scholar] [CrossRef]
- Andrews, J.; Jelly, N. Energy Science, 3rd ed.; Oxford University Press: Oxford, UK, 2017; ISBN 978-0-19-875581-4. [Google Scholar]
- Bidaoui, H.; El Abbassi, I.; El Bouardi, A.; Darcherif, A. Wind Speed Data Analysis Using Weibull and Rayleigh Distribution Functions, Case Study: Five Cities Northern Morocco. Procedia Manuf. 2019, 32, 786–793. [Google Scholar] [CrossRef]
- Rezaei, A.; Nejad, A.R. Effect of wind speed distribution and site assessment on pitch bearing loads and life. J. Phys. Conf. Ser. 2023, 2507, 012021. [Google Scholar] [CrossRef]
- Nishimura, H.; Asami, Y.; Murakami, T. Statistical investigation on the air density near ground in severs storms. J. Wind Eng. 2000, 84, 71–77. [Google Scholar] [CrossRef]
- Ruddle, K. Administration and conflict management in Japanese coastal fisheries. FAO Fish. Tech. Rep. 1992, 273, 93. [Google Scholar]
- Ministry of Economy, Trade and Industry. Act on Promoting the Utilization of Sea Areas for the Development of Marine Renewable Energy Power Generation Facilities. Available online: https://www.japaneselawtranslation.go.jp/en/laws/view/3580/en (accessed on 8 September 2023).
- Shiraki, H.; Sugiyama, M.; Matsuo, Y.; Komiyama, R.; Fujimori, S.; Kato, E.; Oshiro, K.; Silva, D.H. The role of renewables in the Japanese power sector: Implications from the EMF35 JMIP. Sustain. Sci. 2021, 16, 375–392. [Google Scholar] [CrossRef]
- Onodera, H.; Delage, R.; Nakata, T. The role of regional renewable energy integration in electricity decarbonization—A case study of Japan. Appl. Energy 2024, 363, 123118. [Google Scholar] [CrossRef]
- Vaissière, A.C.; Levrel, H.; Pioch, S.; Carlier, A. Biodiversity offsets for offshore wind farm projects: The current situation in Europe. Mar. Policy 2014, 48, 172–183. [Google Scholar] [CrossRef]
- Obane, H.; Kazama, K.; Hashimoto, H.; Nagai, Y.; Asano, K. Assessing areas suitable for offshore wind energy considering potential risk to breeding seabirds in northern Japan. Mar. Policy 2024, 160, 105982. [Google Scholar] [CrossRef]
- Mikami, K.; Kazama, K.; Kazama, M.T.; Watanuki, Y. Mapping the collision risk between two gull species and offshore wind turbines: Modelling and validation. J. Environ. Manag. 2022, 316, 115220. [Google Scholar] [CrossRef]
- Biodiversity Center of Japan Seabird Colony Database. Available online: https://www.sizenken.biodic.go.jp/seabirds/ (accessed on 3 August 2025).
- Campanile, A.; Piscopo, V.; Scamardella, A. Mooring design and selection for floating offshore wind turbines on intermediate and deep water depths. Ocean Eng. 2018, 148, 349–360. [Google Scholar] [CrossRef]
- Lin, Z.; Liu, X.; Lotfian, S. Impacts of water depth increase on offshore floating wind turbine dynamics. Ocean Eng. 2021, 224, 108697. [Google Scholar] [CrossRef]
- Agency of National Resources and Energy. Handbook of Electric Power Industry; Research Institute of Economy, Trade and Industry; Agency of National Resources and Energy: Tokyo, Japan, 2019; ISBN 978-4-8065-3025-1.
- Farr, H.; Ruttenberg, B.; Walter, R.K.; Wang, Y.H.; White, C. Potential environmental effects of deepwater floating offshore wind energy facilities. Ocean Coast. Manag. 2021, 207, 105611. [Google Scholar] [CrossRef]
- Watson, S.C.L.; Somerfield, P.J.; Lemasson, A.J.; Knights, A.M.; Edwards-Jones, A.; Nunes, J.; Pascoe, C.; McNeill, C.L.; Schratzberger, M.; Thompson, M.S.A.; et al. The global impact of offshore wind farms on ecosystem services. Ocean Coast. Manag. 2024, 249, 107023. [Google Scholar] [CrossRef]
- Agency of National Resources and Energy. Advisory Committee for Natural Resources and Energy. Available online: https://www.enecho.meti.go.jp/committee/council/basic_policy_subcommittee/index.html#cost_wg (accessed on 3 August 2025).
- International Renewable Energy Agency. Renewable Cost Database Renewable Power Generation Costs in 2020; IRENA: Abu Dhabi, United Arab Emirates, 2020; ISBN 978-92-9260-244-4. [Google Scholar]
- Satymov, R.; Bogdanov, D.; Breyer, C. Techno-economics of offshore wind power in global resolution. Appl. Energy 2025, 393, 125980. [Google Scholar] [CrossRef]
- Benabadji, A.S.; Rahmoun, K.; Bahar, F.A.; Dahani, A.; Martinez, A.; Iglesias, G. Geospatial LCOE analysis for floating offshore wind energy in SW Mediterranean Sea. Renew. Energy 2025, 245, 122797. [Google Scholar] [CrossRef]
- ERM Japan Ltd. Offshore Wind Development and Its Local Socio-Economic Impact in Akita Prefecture; ERM Japan Ltd.: Yokohama, Japan, 2025; Available online: https://www.erm.com/contentassets/667d29fe38cd446ab818e9f27464d272/0751034---oep---akita-offshore-wind-gva-report_rev-6.pdf (accessed on 3 August 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).