Abstract
Building energy baseline models, particularly machine learning-based models, are a core aspect in the evaluation of building energy performance to identify inefficient energy consumption behavior. In smart city design, energy planners and decision makers require comprehensive information on energy consumption across diverse building types as well as comparisons between different types of buildings. However, there is no comprehensive study of baseline modeling across the main building types to help identify factors that influence the performance of different machine learning algorithms for baseline modeling. Therefore, the goal of this paper is to review and analyze energy consumption behavior and evaluate the prediction performance and interpretability of machine learning-based baseline modeling techniques across major building types. The results have shown that the Extreme Gradient Boosting Machine (XGBoost) model is the most accurate baseline modeling method for all building types. Time-related factors, especially the week of the year and the day of the week, have the most impact on energy consumption across all building types. This study is presented as a useful resource for smart city energy managers to help in choosing and setting up appropriate methodologies for better operational effectiveness and efficiencies when designing and planning smart energy systems.
1. Introduction
The building sector consumes 39% and 40% of energy consumption in the U.S. and Europe, leading to 39% and 40% of CO2 emissions, respectively [1]. Building energy consumption management and control are critical to improve the decision making towards energy saving and CO2 emission reduction. In recent years, the importance of energy efficiency in buildings has been emphasized through newly released policies [2,3]. For example, the Australian government initiated a national plan aiming to achieve zero-energy and carbon-ready commercial and residential buildings, to address Australia’s 40% energy productivity improvement target by 2030 [3]. To estimate the effectiveness of energy efficiency projects, measurement and verification (M&V) are introduced to predict energy baselines and assess saving by measuring the difference between building energy consumption before and after retrofitting.
Energy baseline models characterize building energy consumption according to the key variables. Baseline model accuracy is critical to energy saving assessment, which can impact the investment strategies and operations of the building retrofit market. Techniques for building energy modeling (e.g., for energy prediction) are applied to predict the baseline of building energy consumption [4]. The data-driven approach, learning from historical data by employing machine learning models without the use of the on-site physical information of buildings, has been more commonly applied in recent studies because the complex building information that is required in the physical modeling approach can lead to high computational cost and low running speed [5]. Recent review studies [5,6] have shown that artificial neural networks (ANNs) [7,8] support vector machine (SVM) [9,10], statistical regression [11,12], and decision tree-based models (DT) [13] are the most popular data-driven methods for building energy baseline modeling. However, the literature lacks a comprehensive comparative analysis across all major types of buildings. This comparison study is especially valuable for energy planners and smart city designers. Such a comparison study can be especially valuable for smart city design and planning where diverse building types come under the management of single entities, so energy planners and decision makers can identify factors that influence the performance of different machine learning algorithms for baseline modeling among different types of buildings. Thus, we are motivated to provide a holistic review and a critical assessment of baseline modeling methods and a guideline for future studies on building energy consumption baseline modeling.
There are four main contributions in this study. First, this study compares the effectiveness of existing data-driven building energy consumption baseline modeling techniques across major building types, including residential buildings, commercial buildings, industrial buildings, and academic buildings, based on different time frequencies. The advantages and limitations of each technique are critically analyzed according to different building types. Second, by using interpretable techniques, important factors that influence the performance of energy baseline modeling for different buildings are identified. Third, building profiles of different types are investigated and compared in this study which further explain the different results in baseline modeling for the major types of buildings. Last but not least, it provides a guideline for energy consumption baseline modeling for the major building types with detailed baseline modeling procedures described in this paper.
The rest of this paper is organized as follows. Related background work is presented in Section 2 and Section 3, describing the selected case studies across the building types and the data preprocessing requirements. Section 4 provides details of exploratory analysis conducted before baseline modeling and Section 5 presents the baseline modeling process and outcomes. Section 6 presents an explanatory analysis that helps in understanding the potential causality of the modeling. Finally, in Section 7, we conclude the reported research.
2. Background
2.1. Related Work
Traditionally, building energy models have been constructed through calibrated physics-based simulation modeling. These methods required building engineering expertise and custom calculations for different buildings. To reduce the time and cost of energy modeling for building baselines, M&V 2.0 [14] emphasizes the importance of M&V automation, which can be achieved by using machine learning techniques.
Based on several review studies [1,5,6], the most widely used methods are statistical regression models such as multiple linear regression and Lasso regression, and tree-based models such as gradient boosting models (GBMs), artificial neural networks (ANNs), and support vector machine (SVM). Cho et al. [11] and Ma et al. [15] used the regression algorithm to build energy consumption prediction models under different time frequencies, such as 1 day, 1 week, 1 month, and 3 month. Comparative analysis of the results showed that the length of the measurement period strongly influences the model performance [11]. Jain et al. [12] applied Lasso to predict the energy consumption in a residential building setting at both 30 min and 1 h time intervals. Their study proved that Lasso can select the most important features for a residential energy baseline model. Touzani et al. [13] used GBM on commercial buildings and proved the advantages of this model when compared with linear regression and random forest models. González and Zamarreño [8] predicted short-term electricity load with a special neural network that feeds back part of its outputs. This special neural network showed the best prediction performance when compared with statistical regression, Bayesian regression, and feed-forward neural networks. Later on, Azadeh et al. [16] and Wong et al. [17] developed and applied more complex feed-forward networks to industrial buildings and commercial buildings, respectively. Comparisons with the conventional regression model [16] and Energy Plus [17] showed that neural networks generated more accurate energy predictions, especially when energy consumption shows high fluctuation. Dong et al. [9] and Li et al. [10] validated the effectiveness of the SVM models in predicting energy consumption in commercial buildings and showed a better performance than the conventional back-propagation neural networks.
Several studies compared different algorithms in building energy consumption and analyzed the difference in performance between different models. For example, SVM is found to be more effective in energy consumption in commercial office buildings and university office buildings, when compared with Backpropagation Neural Networks [10], Radial basis function neural networks [18], Lasso regression [12], and Multilinear regression [19]. However, the autoregressive model performed better than SVM [20], ANNs, and Bayesian Networks [21] in some other building types, such as academic buildings and commercial research buildings. In terms of residential buildings, SVM achieved the best performance in hourly energy prediction, when compared with ANNs; SVM; two tree-based models, namely CART (Classification and regression tree) and CHAID (Chi-squared automatic interaction detector); and GLR (General linear regression) [22].
However, these past studies compared prediction results with different models on one or two types of buildings, but there has been no comprehensive study comparing and contrasting baseline modeling across all the key building types, which can assist the understanding of how different models perform across different building types and what features and factors impact such variation in performance.
2.2. Interpretability of Machine Learning Techniques for Energy Baseline Models
Interpretability is the degree to which a model can be understood by users and analysts [23]. Interpretability from a baseline model is very important, from which we can understand what governs the performance of the baseline model, and what features or behavioral patterns can influence the baseline model. Therefore, adjustments can be made to control energy usage.
Among the machine learning techniques, decision tree and linear regression models are recognized as model-specific interpretable models, since we can look at this model’s tree structure or the parameters to understand how a prediction is made [23].
However, if a model becomes complicated with more complex structures and parameters (e.g., ANN), it is difficult to interpret the predictions. Therefore, some model-agnostic techniques have been proposed and applied to understand how these models make predictions. For example, researchers can use a proxy-interpretable model to explain the black-box model, e.g., via measuring variable importance. Among these techniques, LIME [24] is one of the most popular methods for understanding the contribution of each variable in individual prediction, whereas SHAP [25] is another popular method for understanding both the local and global contributions of each variable.
2.3. Evaluation Measures for Energy Baseline Models
Advised by ASHRAE Guideline 14 [26], FEMP [27], and IPMVP [28], the predictive capability of the energy baseline models was evaluated using three evaluation metrics: cross-validation-based R squared (), coefficient of variation of root-mean-squared error (), and mean absolute percentage error ().
Over-fitting is a major concern in many machine learning predictive algorithms, when the model fits the training data too well at the cost of predictive generalization, resulting in poor prediction performance with testing data. Cross-validation (CV), and especially the k-fold-CV, were used to help assess the over-fitting without the use of large training datasets.
CV(RMSE) measures the variability in the errors between measured and predicted values. A good hourly prediction model is expected to have a value of less than 30 required by FEMP [27] and ASHRAE Guideline 14 [26] or less than 20 by IPMVP [28]. is used to measure the closeness between the predicted values and the regression line of the measured values. The value is between 0 and 1, where 1 indicates a perfect match between the predicted values and the measured values, and 0 indicates no match between them. ASHRAE Handbook [29] and IPVMP [28] recommend that a good model should have an value of more than 0.75. The MAPE metric is conceptually very similar to the and is useful to compare prediction performance between signals of different mean magnitudes. When applying the k-fold-CV in baseline modeling, the average testing of each fold is calculated as , similarly for and .
3. Case Studies and Data Preparation
This section first introduces the key building types included in this research and describes the related data sources used for the analysis of each building type. The data sets were selected to make it possible to compare and contrast the energy consumption patterns across these building types as well as the construction of baseline models. The second part of this section briefly describes the data preparation carried out as post-processing for the analysis and baseline construction.
3.1. Building Types
Buildings can be classified into two main categories based on functionality and purpose: residential buildings and non-residential buildings. The non-residential building consists of commercial buildings, industrial buildings, and other non-residential building types, including academic buildings, entertainment and recreation buildings, hospitals, etc. [30]. A recent review study [1] has shown that 19% of past research has focused on residential buildings, while the majority of the remaining 81% focuses on commercial and academic buildings. Only a few studies have targeted energy consumption analysis and prediction for industrial buildings.
As the aim of this study is to conduct a comparative analysis of energy modeling in major building types, one or two representative datasets for each building type, namely residential, commercial, industrial, and other non-residential buildings, were selected. Since other non-residential buildings consist of many sub-building types, we included the academic buildings, which were found to consume the most energy than other non-residential buildings. Detailed information on the datasets used in this study for different building types is shown in Table 1, and this information can be the integration of different data sources, for example, the combination of energy usage, as well as weather data.

Table 1.
Detailed information for the dataset used in different building types.
3.1.1. Residential Buildings
A public dataset SustData [31] was used to analyze the energy consumption behavior of residential buildings. We only included houses as individual residential buildings in our study, since the energy consumption data at the whole building level for apartment buildings are not provided in the dataset. Apart from power usage information, wind, temperature, humidity, and pressure information was also included in our study.
3.1.2. Commercial Buildings
EnerNOC, an open-source dataset [32], with 100 anonymized buildings for the year 2012 throughout the USA, was used for commercial building energy consumption analysis. There are a total of 25 commercial buildings in this dataset with different commercial uses.
3.1.3. Industrial Buildings
The EnerNOC dataset includes 25 industrial buildings and we used this subset to analyze the energy consumption behavior of industrial buildings.
3.1.4. Academic Buildings
Two datasets were used for the analysis of academic buildings. One is from the La Trobe University Energy Analytics Platform (LEAP), the main project of the La Trobe Net Zero program [33] for reducing energy consumption on campus. There are 76 buildings available in the dataset with 32 academic buildings.
The second academic data source is a public temporal dataset from the United World College of South East Asia (UWC-SEA) Tampines Campus in Singapore [34]. Since we identified some gaps in the dataset timeline, only data from February 2012 to March 2012 were applied in our study.
3.2. Data Preparation
The scope of building energy consumption prediction can be classified into four types based on time frequencies: long-term prediction model (years ahead), medium-term prediction model (months ahead), short-term prediction model (hours to weeks ahead), and very short-term prediction model (seconds to minutes ahead) [5].
Traditionally, medium-term frequency is most commonly applied in baseline modeling because of the absence of finer granular energy consumption data [35]. The development of smart meters and devices in recent years has enabled short-term and very short-term baseline modeling, providing great potential in the analysis of the relationship between energy consumption and its impact factors at a much finer time granularity with higher predicting time frequency [35]. These more frequent energy predictions can help make faster reactions when policies change and are more desirable in terms of practicality. Thus, our study focuses on these finer granularities, at different time frequencies.
3.2.1. Variables
Previous studies [1,4,36] found that time, weather, indoor conditions, building characteristics, and occupancy have a significant impact on the quality of predictive models for building energy consumption. Daut et al. [36] advise that among all these factors, the weather conditions, including ambient temperature, humidity, and solar radiation, are the major forecasting factor that may impact indoor conditions and activities and lead to the change in building electrical energy consumption. Liang et al. [2] showed that the combined use of time and weather can help efficiently capture the energy use behavior, and even with the occupancy-related information added, not much improvement can be found in the modeling performance. Thus, our study mostly focused on the impact factors of time and temperature. However, due to the absence of weather information in some data sources, only time-related information has been included in the analysis of some building types. The detailed variables applied to the energy consumption baseline modeling in different datasets for different buildings at different time frequencies are shown in Table 2.

Table 2.
Variables applied for different baseline models for buildings.
3.2.2. Missing Value Handling
Due to possible errors involved in reading energy data, there is always a certain extent of data loss in the collected data. By investigating the datasets, only less than 0.1% of missing values were found. Therefore, we applied two rules to deal with missing values: if the missing values were at the beginning or end of the evaluation period, we removed the data sample; else, if the missing values were in between two close observations, we imputed it with the previously observed value.
3.2.3. Outliers
The presence of outliers in the datasets can impact the energy model performance. Therefore, in this study, we applied a common method, the quartile method [37], to identify and remove the outliers. With this method, a normal energy consumption range is first identified with Equation (1), where is the first quartile of energy consumption, is the third quartile, is the interquartile range, and is a constant to determine the upper fence and lower fence of normal energy consumption values. Energy values out of the normal range are then identified as outliers. To properly define the value, we trialed different with descriptive analysis and visualization of the outcome. We found that only the UWC-SEA dataset has outliers, and these outliers and a of 6 generated the best model performance.
4. Exploratory Analysis
This section describes the exploratory analysis carried out before the baseline modeling, including correlation analysis, descriptive analysis, and profile analysis.
4.1. Descriptive Analysis
After aggregating all the datasets at a time frequency of 30 min, we conducted a descriptive analysis. The results are shown in Supplementary S2. Most of the datasets contain more than 17,000 observations at the 30 min interval. Only some buildings in the UWC-SEA datasets contain fewer than 4000 observations. Only the LEAP dataset used kWh in the energy consumption measure; the rest of the datasets applied a measure of kW. Although we noticed the difference between kWh (a measure of energy) and kW (a measure of power), it does not have a significant impact on the prediction capability of a baseline model, as long as the measure is consistent at the whole building level. Temperature and humidity vary from dataset to dataset, but this does not affect the quality of a baseline model, since each building has a unique baseline model.
4.2. Correlation Analysis
Before building baseline models, correlation analyses were applied to understand the relationship between the selected variables and the energy consumption using two common correlation analysis methods, namely Spearman and Pearson. The range of both Pearson and Spearman correlation coefficients is between −1 and +1, where +1 indicates a perfect positive relationship between two variables and −1 indicates a perfect negative relationship between them. A value of close to 0 means no clear relationship. Since Pearson benchmarks linear relationships, we applied it to measure the relationship in continuous variables, such as temperature, humidity, and wind speed. Spearman benchmarks monotonic relationships, so we applied it to the ordinal variables, such as day of the month, week of the year, and hour of the day. The (or probability) value is commonly used to measure the significance of the correlation. In our study, a -value smaller than 0.05 is considered a significant correlation.
As shown in Table 3, whether the day is a weekend is significantly correlated with energy consumption at all three time frequencies of 30 min, 1 h, and 1 day, for most building types except residential buildings. Although only the datasets for residential buildings and academic buildings include weather information, relative humidity always showed a significant correlation with energy consumption at all time frequencies for these building types. Day of the week is significantly correlated with energy consumption for most commercial and industrial buildings at all time frequencies, whereas week of the year is significantly correlated with energy consumption for residential and academic buildings. Hour of the day showed a significant correlation with energy consumption at 30 min and 1 h prediction frequencies for most building types except light industrial buildings. Month of the year showed a significant impact on residential and academic buildings. Although HDD and CDD are only available in the LEAP academic building dataset, it shows a significant influence on energy consumption.

Table 3.
Significant influential variables of building energy consumption in correlation analysis.
4.3. Profile Analysis
Profile analysis can provide a basic understanding of energy consumption behavior and detect the existence of any general usage patterns across building types. This profiling also provides insights into the potential causality of the performance of different machine learning algorithms.
There are a few interesting findings in comparing the profiles between different building types (all energy profiles including annual, monthly, and daily profiles including weekdays and weekends for all building types are available in Supplementary S3). As shown in Figure 1, two typical monthly profiles are found across all building types. Except for residential buildings in Figure 1a, which do not show any clear pattern in the monthly profile, all other building types present weekly periodical patterns in the monthly profile as shown in Figure 1b.
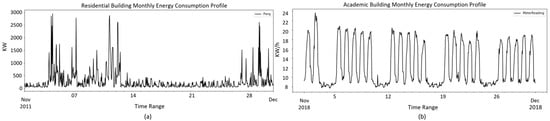
Figure 1.
Two types of typical monthly energy consumption profiles for all types of buildings. (a) presents the monthly energy consumption profile for a residential building in November 2011. (b) shows the monthly energy consumption profile for an academic building in November 2018.
Three typical daily profiles are found across all types of buildings as shown in Figure 2. Figure 2a,b show the typical weekday and weekend energy profiles for the residential buildings, with no clear difference between the weekday and weekend energy consumption. Figure 2c,d are the typical weekday and weekend energy profiles for the academic buildings based on two data sources, where weekday energy profiles are significantly different from weekend profiles. Energy consumption increases from 6 a.m. and decreases after 6 p.m. during weekdays, while there is no significant energy use on weekends. Similar daily profiles are found in industrial buildings and most commercial buildings, but industrial buildings show more energy fluctuations. An interesting daily energy consumption pattern is found in bank/financial service buildings, as shown in Figure 2e,f. Similar to the weekday profiles of academic buildings, the energy consumption of these buildings increases during the daytime on weekdays, especially during working hours from 9 a.m. to 5 p.m., but decreases during the daytime at weekends. We argue that this may result from the activation of electronic higher-level security systems for the banks at night time.
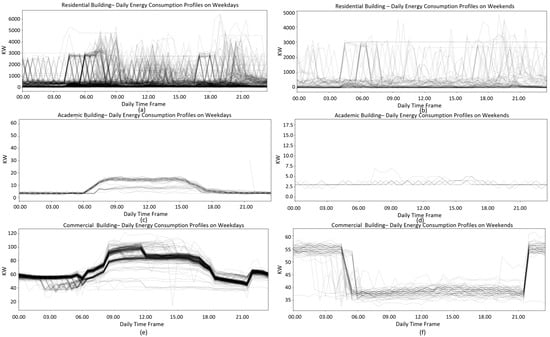
Figure 2.
Three types of typical daily energy consumption profiles for all building types. Profiles on the left-hand side are weekday profiles and the profiles on the right-hand side are their correspondent weekend profiles. (a,b) shows the typical energy consumption profiles for weekdays and weekends for residential buildings. (c,d) shows the typical energy consumption profiles for weekdays and weekends for academic buildings. (e,f) shows the typical energy consumption profiles for weekdays and weekends for commercial buildings.
Based on the profile analysis of the four major building types, commercial buildings and academic buildings show more regular energy usage patterns. Therefore, we argue that the baseline modeling on these two building types can capture the consumption behavior more accurately compared to the other two building types. Residential buildings do not show regular energy usage patterns, which could be due to individual household usage behaviors. In commercial and academic buildings, energy usage is mostly governed by building usage regulations, opening hours, and work patterns, with less impact from individual behavior.
5. Baseline Modeling
In this section, eight different machine learning methods, including multiple linear regression (MLR), ridge regression, Lasso regression, Bayesian ridge regression, support vector machine (SVM), gradient boosting machine (GBM), extreme gradient boosting machine (XGBoost), and multilayer perceptron (MLP), were applied to the five data sources. The method that can produce the best performance with the best parameter settings was automatically selected as the baseline model for a building, as shown in Figure 3. All models were trained and refined using the scikit-learn package with an exhaustive search over various parameter settings. Detailed descriptions of each method can be found in Supplementary S1 and parameter settings for models can be found in Supplementary S5. It is worth noting that although, by definition, the lowest R squared is zero, the implementation of R squared in the scikit learn package can have a negative value when the predicted regression line is not better than using the mean.
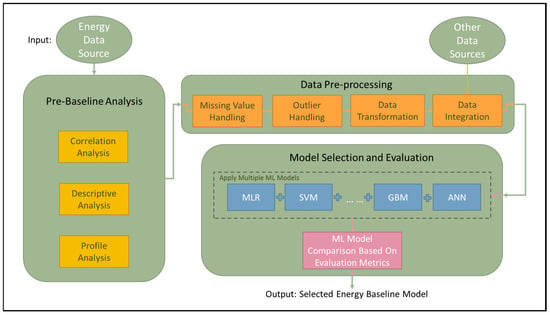
Figure 3.
Baseline modeling process.
The baseline model predictive performance is evaluated by the three metrics via the 10-fold cross-validation process: R squared (), coefficient of variation of root-mean-squared error (), and mean absolute percentage error (). Since many buildings are included in the dataset, the three measures are the mean value for all the buildings. All the detailed modeling results can be found in Supplementary S4.
The baseline prediction results do not show good performance in residential buildings, while tree-based models demonstrate better performance, as shown in Figure 4. We believe that the varying consumption behaviors with no clear energy consumption pattern identified from profile analysis in Section 4.3 could be a reason for this outcome.

Figure 4.
Average baseline model performance comparisons on residential buildings based on , , and .
5.1. Commercial Buildings
Figure 5 shows the average baseline modeling performance for commercial buildings in the EnerNOC dataset. XGBoost demonstrates the best performance in all the three time frequencies across all sub-building types of commercial buildings, while GBM and SVR also show relatively good performances. It is noticeable that the performances of linear models such as MLR, Ridge, Bayesian Ridge, and Lasso are very poor at the 30 min interval, but performance improves at the 1-day interval. For the non-linear models, performance decreases from 30 min to 1 day. In addition, among all the sub-building types of commercial buildings, it is most difficult to build baseline models for shopping malls. This may result from the complex and varying behaviors of customers (diversity of occupants in a shopping mall).
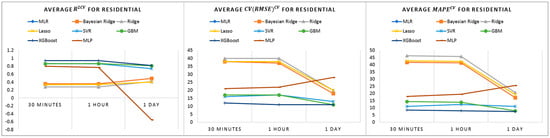
Figure 5.
Average baseline model performance comparisons on commercial buildings based on , , and .
5.2. Industrial Buildings
Figure 6 shows the average baseline modeling performance of industrial buildings in the EnerNOC dataset. Similar to the findings in commercial buildings, XGBoost is still the highest-performing model, followed by GBM and SVR. All linear models do perform well, particularly for the MLP model at the 1-day interval.
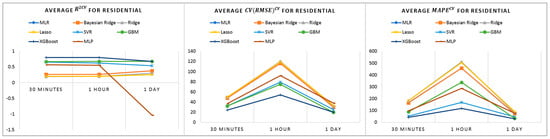
Figure 6.
Average baseline model performance comparisons on industrial buildings based on , , and .
5.3. Academic Buildings
Figure 7 shows the average baseline modeling performance for the academic buildings in the LEAP dataset. XGBoost is the best baseline modeling algorithm among all the methods. MLP shows its limitation in 1-day baseline modeling, while linear models maintain a poor level of performance at all time frequencies.

Figure 7.
Average baseline model performance comparisons on academic buildings of the LEAP dataset based on , , and .
Figure 8 shows the average baseline modeling performance for the academic buildings in the UWC-SEA dataset. Although XGBoost remains the best method, it does not show a significant advantage over GBM. In addition, all models perform poorly at the 1-day-level baseline modeling. The best baseline performance in this dataset can be found at the 1 h interval with a of 28. Since this value is still higher than the IPMVP requirement on with less than 20, none of the models could be considered acceptable for prediction. By comparing with the LEAP data features, we argue that the unavailability of sufficient data features could be the reason for this. This is further verified with the explanatory analysis in Section 6.

Figure 8.
Average baseline model performance comparisons on academic buildings of the UWC-SEA dataset based on , , and .
5.4. Discussion
From the results presented in this section, XGBoost shows the best baseline performance for all building types and all time intervals. Linear models can perform better at a lower time frequency, such as at the 1-day interval. Therefore, when interpretability matters in building energy modeling at low temporal frequencies, linear models which are easier to interpret can be applied.
Residential buildings, in particular houses, are difficult to model, since their energy usage behaviors vary due to residents’ behavior and lifestyle. In the analysis of daily profiles, no clear patterns could be found, resulting in low performance in very short-term modeling. Some patterns can be seen in the monthly and yearly profile, for example, between 14 November and 26 November; thus, the prediction performance of baseline improves in the residential building baseline models, at a lower time frequency.
For industrial buildings, the value is relatively high for the prediction at a 30 min interval, but and values are also high. When referring to the profile analysis result in Section 4.3, it is found that this is due to the unstable daily energy consumption profiles of industrial buildings with frequent changes during the day. The consumption behavioral curve becomes more stable at a lower time frequency, so and decrease at the 1 h and the 1-day time intervals.
Commercial buildings in the EnerNOC dataset and academic buildings in the LEAP dataset show better baseline modeling performance, because these buildings have clearer energy usage patterns based on the profile analysis in Section 4.3. However, it is interesting to find that even though the academic buildings in the UWC-SEA do have clear energy usage patterns, none of the models show very good predicting performance. We argue that this can be due to the absence of information from HDD, CDD, and whether the day is a holiday, since when compared with the LEAP dataset which has better modeling performance, this information is available in the dataset.
6. Further Analysis for Interpretability
In this section, further analysis was conducted on all model results and the best performing models were explained with a commonly applied interpretation approach.
We plotted the prediction model against the measured energy consumption, as shown in Figure 9. From this figure, we can identify that XGBoost is the best fit to the measured energy consumption throughout time, whereas MLP tends to underestimate the consumption.
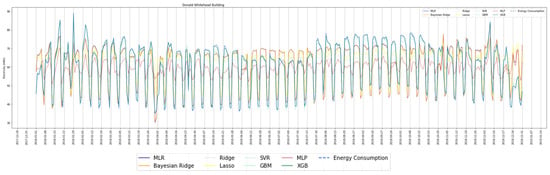
Figure 9.
Modeling results with different methods against the measured energy consumption.
We took a further analysis based on the best-performing model, the XGBoost model, to understand how each feature influences energy consumption. This can be implemented by using a unified interpretation framework, SHapley Additive exPlanations (SHAP) [25]. Figure 10 shows the SHAP values for the important variables for a residential building. The blue bar is the actual energy consumption based on the sensor measurements, and the orange bar is the predicted energy consumption using the XGBoost model. The grey bar represents the base value, which is the value that would be predicted if none of the features used in the modeling are applied. Each feature more or less contributes to pushing the model output from the base value (the grey bar) to the final model prediction (the orange bar), either positively (in green) or negatively (in red). The SHAP plots for the rest of the buildings can be found in Supplementary S5 and the results are summarized in Table 4.
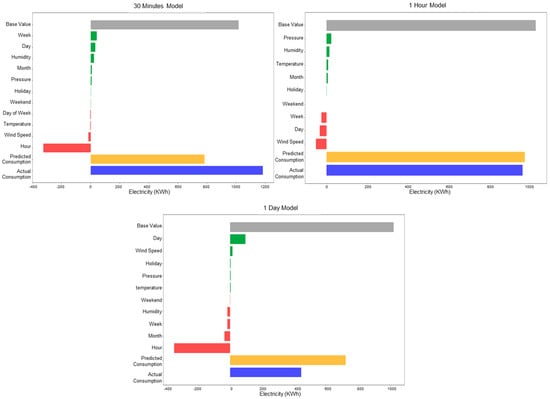
Figure 10.
Important variables at 3 different time intervals for residential buildings at a random time.

Table 4.
Top 2 contributed variables of energy consumption of baseline model in explanatory analysis based on SHAP values.
As shown in Table 4, the most important variables for predicted energy consumption of residential buildings at the 30 min interval are hour of the day and week of the year. At the 1 h interval, hour of the day and day of the week are the most important, while at the 1-day interval, wind speed and relative pressure are the most important.
The most important variables for energy consumption of shopping centers, corporate offices, business service buildings, and bank/financial services at the 30 min interval are hour of the day and day of the week. For commercial real estate, week of the year, instead of day of the week, is the second-most important variable. At the 1 h interval, hour of the day and day of the week remain the most important for most of the sub-building types, except corporate offices, for which week of the year is the second-most important. At the 1-day interval, hour of the day and week of the year are the most important for shopping malls and bank or financial services buildings. And for corporate offices, business services, and commercial real estate buildings, instead of week of the year, whether the day is weekend is one of the most important. It is also identified that most of the buildings tend to use more energy in the afternoon.
In terms of industrial buildings, day of the week, week of the year, and hour of the day are most important at the 30 min and 1 h intervals, while day of the week and week of the year are the most important at the 1-day interval. It is also interesting to find that all industrial buildings tend to use more energy at the beginning of the week, as well as at the beginning of the year.
Hour of the day influences most at both the 30 min and 1 h intervals for academic buildings. At the 1-day interval, it is noticeable that weekends show a negative impact on energy consumption in academic buildings. From the LEAP dataset, we identify that holidays have a significant impact on energy consumption. Thus, it is suggested that another academic building dataset, UWC-SEA, not achieving good baseline performances may result from the absence of holiday-related information in the data.
In summary, week of the year, day of the week, and hour of the day are the most important variables that impact energy consumption in all building types. And this finding is consistent with the finding from the correlation analysis in Section 4.2.
7. Conclusions
This paper provided a comparative analysis of baseline modeling performance for four major building types based on a wide range of machine learning methods. This can provide a useful reference for not only researchers in the area but energy managers and smart city designers who are interested in better and more efficient energy consumption modeling across multiple building types. With this audience in mind, we have provided step-by-step details of the overall process which include the selection of datasets and variables, data preprocessing steps, exploratory analysis, building profiling and machine learning algorithmic details, and the baseline modeling process. The final section on explanatory analysis when associated with the exploratory and profile analysis helps to provide a better understanding of the potential causality for the baseline model outcomes (which are mostly considered as black box models).
Across all four major building types, XGBoost shows the best baseline performance. Linear models can perform better at a longer time interval, such as at the 1-day interval, while non-linear models perform better at shorter time intervals. Among non-linear models, MLP showed the lowest performance in most of the cases, especially in 1-day energy consumption prediction.
Residential buildings in our study were difficult to model, since their energy usage behaviors vary due to the resident behavior and lifestyle. This is especially significant in the daily profile, where no clear patterns could be captured, resulting in low performance in short-term or very short-term modeling. Prediction performance of the baseline model improves, at longer time intervals, when some seasonal patterns can be found in the monthly and yearly profiles.
Commercial buildings, industrial buildings, and academic buildings all show clearer usage patterns, compared to residential buildings. For industrial buildings, we found that their daily profiles are quite unstable, and this leads to the high and values, although the value is relatively high for the prediction at the 30 min interval. The consumption behavioral curve becomes more stable at longer time intervals, thus leading to a decrease in and . Commercial buildings and academic buildings from LEAP both have clearer usage patterns than other buildings, thus showing better baseline modeling performance. However, for academic buildings in the UWC-SEA dataset, it is interesting to find that even though the buildings do have clear energy usage patterns, none of the models show very good performance. We argue that this outcome is due to the absence of information from HDD, CDD, and whether the day is a holiday, since when compared with another academic dataset—the LEAP dataset, which has better modeling performance—this information is available in the dataset.
In conclusion, the main contributions of our paper are as follows: First, this study compares the effectiveness of existing data-driven building energy baseline modeling techniques based on different time frequencies and across four major building types. This study has been extended with a critical analysis of the advantages and limitations of each modeling technique. Second, with the use of interpretable techniques, this study identifies the most important factors that influence the performance of energy baseline modeling for different buildings. In addition, building profiles of different types were investigated and compared to further explain the different results in baseline modeling across building types. Third, it provides a guideline for energy consumption baseline modeling for the major building types with detailed baseline modeling procedures described in this paper.
In the future, extended work will be conducted to compare the roughness and transferability of these models on other buildings with the same type or with different types. In addition, more experiments will be taken to include more recent energy modeling methods and attention-based ANNs [38,39,40] in the review and comparison analysis.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/en17061285/s1. Table S1. Variables selected for different baseline models for residential buildings from SustData. Table S2. Variables selected for different baseline models for commercial buildings from EnerNOC. Table S3. Variables selected for different baseline models for industrial buildings from EnerNOC. Table S4. Variables selected for different baseline models for academic buildings from UWC-SEA. Table S5. Variables selected for different baseline models for academic buildings from LEAP. Table S6. Average baseline model performance comparisons for residential buildings. Table S7. Average baseline model performance comparisons for commercial buildings. Table S8. Average baseline model performance comparisons for industrial buildings. Table S9. Average baseline model performance comparisons on academic buildings for leap dataset. Table S10. Average baseline model performance comparisons on academic buildings for the UWC-SEA dataset. Table S11. Parameter settings for different models applied in the paper. Figure S1. Energy consumption behavior in the year 2011 for building #1 in SustData. 1(a) shows the energy behavior across the year 2011, and 1(b) depicts energy consumption in November 2011. 1(c) shows the daily energy profile, while 1(d) and 1(e) are the energy profiles for weekdays and weekends respectively. Figure S2. Energy consumption behavior in the year 2012 for a typical commercial building (bank and financial service building) in EnerNOC. 2(a) shows the energy usage across the year 2012 and 2(b) depicts energy usage in January 2012. 2(c) shows the daily energy usage profile for this building, while 2(d) and 2(e) are the energy profiles for weekdays and weekends respectively. Figure S3. Energy consumption behavior in the year 2012 for a typical industrial building (food processing building) in EnerNOC. 3(a) shows the energy behavior across the year 2012, and 3(b) depicts energy usage in January 2012. 3(c) is the daily energy profile for this building, while 3(d) and 3(e) show the daily energy profile for weekdays and weekends respectively. Figure S4. Energy consumption behavior in the year 2012–2013 for a typical academic building in the UWC-SEA dataset. 4(a) shows the energy behavior from February 2012 to February 2013, and 4(b) depicts the energy usage plot in November 2012. 4(c) is the daily energy profile for this building, while 4(d) and 4(e) are daily profiles for weekdays and weekends, respectively. Figure S5. Energy consumption behavior in the year 2018 for a typical academic building in the LEAP dataset. 5(a) shows its energy consumption behavior across the year 2018, and 5(b) depicts its energy usage in November 2018. 5(c) is the daily energy profile for this building, while 5(d) and 5(e) are daily energy profiles for weekdays and weekends, respectively. Figure S6. Important variables at 3 different time intervals for commercial buildings at a random time (left: 30 min, middle: 1 h, right: 1 day). The first row (a) is the performance results for shopping centres. The second row (b) is the performance results for corporate offices, followed by business services buildings (c), commercial real estate buildings (d) and bank/financial services buildings (e). Figure S7. Important variables at 3 different time intervals for industrial buildings at a random time (left: 30 min, middle: 1 h, right: 1 day). The first row is the performance results for food processing buildings. The second row is the variable contributions for manufacturing buildings and the last row is for other light industrial buildings. Figure S8. Important variables at 3 different time intervals for academic buildings (LEAP) at a random time (left: 30 min, middle: 1 h, right: 1 day). Figure S9. Important variables at 3 different time intervals for academic buildings (UWC-SEA) at a random time (left: 30 min, middle: 1 h, right: 1 day).
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Liang, X.; Hong, T.; Shen, G.Q. Improving the accuracy of energy baseline models for commercial buildings with occupancy data. Appl. Energy 2016, 179, 247–260. [Google Scholar] [CrossRef]
- Australian Government. National Energy Productivity Plan 2015–2030. 2015. Available online: https://apo.org.au/node/66621 (accessed on 10 August 2022).
- Batlle, E.A.O.; Palacio, J.C.E.; Lora, E.E.S.; Reyes, A.M.M.; Moreno, M.M.; Morejón, M.B. A methodology to estimate baseline energy use and quantify savings in electrical energy consumption in higher education institution buildings: Case study, Federal University of Itajubá (UNIFEI). J. Clean. Prod. 2020, 244, 118551. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, X.; Shi, Y.; Xia, L.; Pan, S.; Wu, J.; Han, M.; Zhao, X. A review of data-driven approaches for prediction and classification of building energy consumption. Renew. Sustain. Energy Rev. 2018, 82, 1027–1047. [Google Scholar] [CrossRef]
- Bourdeau, M.; Zhai, X.Q.; Nefzaoui, E.; Guo, X.; Chatellier, P. Modeling and forecasting building energy consumption: A review of data-driven techniques. Sustain. Cities Soc. 2019, 48, 101533. [Google Scholar] [CrossRef]
- Nizami, S.J.; Al-Garni, A.Z. Forecasting electric energy consumption using neural networks. Energy Policy 1995, 23, 1097–1104. [Google Scholar] [CrossRef]
- González, P.A.; Zamarreño, J.M. Prediction of hourly energy consumption in buildings based on a feedback artificial neural network. Energy Build. 2005, 37, 595–601. [Google Scholar] [CrossRef]
- Dong, B.; Cao, C.; Lee, S.E. Applying support vector machines to predict building energy consumption in tropical region. Energy Build. 2005, 37, 545–553. [Google Scholar] [CrossRef]
- Li, Q.; Meng, Q.; Cai, J.; Yoshino, H.; Mochida, A. Applying support vector machine to predict hourly cooling load in the building. Appl. Energy 2009, 86, 2249–2256. [Google Scholar] [CrossRef]
- Cho, S.-H.; Kim, W.-T.; Tae, C.-S.; Zaheeruddin, M. Effect of length of measurement period on accuracy of predicted annual heating energy consumption of buildings. Energy Convers. Manag. 2004, 45, 2867–2878. [Google Scholar] [CrossRef]
- Jain, R.K.; Damoulas, T.; Kontokosta, C.E. Towards data-driven energy consumption forecasting of multi-family residential buildings: Feature selection via the Lasso. In Computing in Civil and Building Engineering, Proceedings of the 2014 International Conference on Computing in Civil and Building Engineering, Orlando, FL, USA, 23–25 June 2014; ASCE Press: Reston, VA, USA, 2014; pp. 1675–1682. [Google Scholar] [CrossRef]
- Touzani, S.; Granderson, J.; Fernandes, S. Gradient boosting machine for modeling the energy consumption of commercial buildings. Energy Build. 2018, 158, 1533–1543. [Google Scholar] [CrossRef]
- Kupser, J.; Francois, S.; Rego, J.; Steele-Mosey, P.; Galvin, T.; McDonald, C.; Navigant. M&V 2.0: Hype vs. Reality. 2016. Available online: https://www.aceee.org/files/proceedings/2016/data/papers/2_868.pdf (accessed on 19 June 2022).
- Ma, Y.; Yu, J.-Q.; Yang, C.-Y.; Wang, L. Study on power energy consumption model for large-scale public building. In Proceedings of the 2010 2nd International Workshop on Intelligent Systems and Applications, ISA 2010, Wuhan, China, 22–23 May 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Azadeh, A.; Ghaderi, S.; Sohrabkhani, S. Annual electricity consumption forecasting by neural network in high energy consuming industrial sectors. Energy Convers. Manag. 2008, 49, 2272–2278. [Google Scholar] [CrossRef]
- Wong, S.; Wan, K.K.; Lam, T.N. Artificial neural networks for energy analysis of office buildings with daylighting. Appl. Energy 2010, 87, 551–557. [Google Scholar] [CrossRef]
- Liu, D.; Chen, Q. Prediction of building lighting energy consumption based on support vector regression. In Proceedings of the 2013 9th Asian Control Conference, ASCC 2013, Istanbul, Turkey, 23–26 June 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Massana, J.; Pous, C.; Burgas, L.; Melendez, J.; Colomer, J. Short-term load forecasting in a non-residential building contrasting models and attributes. Energy Build. 2015, 92, 322–330. [Google Scholar] [CrossRef]
- Borges, C.E.; Penya, Y.K.; Fernández, I.; Prieto, J.; Bretos, O. Assessing Tolerance-Based Robust Short-Term Load Forecasting in Buildings. Energies 2013, 6, 2110–2129. [Google Scholar] [CrossRef]
- Penya, Y.K.; Borges, C.E.; Agote, D.; Fernandez, I. Short-term load forecasting in air-conditioned non-residential Buildings. In Proceedings of the ISIE 2011: 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 1359–1364. [Google Scholar] [CrossRef]
- Chou, J.-S.; Bui, D.-K. Modeling heating and cooling loads by artificial intelligence for energy-efficient building design. Energy Build. 2014, 82, 437–446. [Google Scholar] [CrossRef]
- Gilpin, L.H.; Bau, D.; Yuan, B.Z.; Bajwa, A.; Specter, M.; Kagal, L. Explaining explanations: An overview of interpretability of machine learning. In Proceedings of the 2018 IEEE 5th International Conference on Data Science and Advanced Analytics, DSAA 2018, Turin, Italy, 1–3 October 2018; pp. 80–89. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Model-Agnostic Interpretability of Machine Learning. In Proceedings of the 2016 ICML Workshop on Human Interpretability in Machine Learning (WHI 2016), New York, NY, USA, 23 June 2016; pp. 91–95. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 2017-Decem, pp. 4766–4775. [Google Scholar] [CrossRef]
- American Society of Heating Refrigerating and Air-Conditioning Engineers. ASHRAE Guideline 14-2014 Measurement of Energy and Demand Savings. Ashrae. 2014. Available online: https://upgreengrade.ir/admin_panel/assets/images/books/ASHRAE%20Guideline%2014-2014.pdf (accessed on 18 June 2022).
- Schiller Associates. M&V Guidelines: Measurement and Verification for Federal Energy Projects Version 2.2. Washington, DC, USA. 2000. Available online: http://www.ipmvp.org/ (accessed on 19 June 2022).
- IPMVP Committee. International Performance Measurement and Verification Protocol: Concepts and Options for Determining Energy and Water Savings, Volume I. Washington, DC, USA. 2001. Available online: www.ipmvp.org (accessed on 19 June 2022).
- ASHRAE. 2013 ASHRAE Handbook—HVAC Fundamentals, No. 404; ASHRAE: Peachtree Corners, GA, USA, 2019. [Google Scholar]
- Council of Australian Governments. Baseline Energy Consumption and Greenhouse Gas Emissions in Commercial Buildings in Australia Part 1—Report Council of Australian Governments (COAG) National Strategy on Energy Efficiency; Department of Climate Change and Energy Efficiency: Canberra, Australia, 2012; pp. 1–10. Available online: www.climatechange.gov.au (accessed on 19 June 2022).
- Pereira, L.; Quintal, F.; Gonçalves, R.; Nunes, N.J. SustData: A public dataset for ICT4S electric energy research. In Proceedings of the ICT for Sustainability 2014, ICT4S 2014, Stockholm, Sweden, 24–27 August 2014; pp. 359–368. [Google Scholar] [CrossRef]
- Batra, N.; Parson, O.; Berges, M.; Singh, A.; Rogers, A. A comparison of non-intrusive load monitoring methods for commercial and residential buildings. arXiv 2014. [Google Scholar] [CrossRef]
- Net Zero, Sustainability, La Trobe University. Available online: https://www.latrobe.edu.au/sustainability/net-zero (accessed on 19 June 2022).
- Miller, C.; Nagy, Z.; Schlueter, A. A seed dataset for a public, temporal data repository for energy informatics research on commercial building performance. In Proceedings of the 3rd Conference on Future Energy Business & Energy Informatics, Rotterdam, The Netherlands, 20 June 2014; pp. 1–2. [Google Scholar] [CrossRef]
- Granderson, J.; Price, P.N.; Jump, D.; Addy, N.; Sohn, M.D. Automated measurement and verification: Performance of public domain whole-building electric baseline models. Appl. Energy 2015, 144, 106–113. [Google Scholar] [CrossRef]
- Daut, M.A.M.; Hassan, M.Y.; Abdullah, H.; Rahman, H.A.; Abdullah, P.; Hussin, F. Building electrical energy consumption forecasting analysis using conventional and artificial intelligence methods: A review. Renew. Sustain. Energy Rev. 2017, 70, 1108–1118. [Google Scholar] [CrossRef]
- Do, H.; Cetin, K.S. Evaluation of the causes and impact of outliers on residential building energy use prediction using inverse modeling. Build. Environ. 2018, 138, 194–206. [Google Scholar] [CrossRef]
- Jia, L.; Liu, J.; Chong, A.; Dai, X. Deep learning and physics-based modeling for the optimization of ice-based thermal energy systems in cooling plants. Appl. Energy 2022, 322, 119443. [Google Scholar] [CrossRef]
- Peng, J.; Kimmig, A.; Wang, J.; Liu, X.; Niu, Z.; Ovtcharova, J. Dual-stage attention-based long-short-term memory neural networks for energy demand prediction. Energy Build. 2021, 249, 111211. [Google Scholar] [CrossRef]
- Li, A.; Xiao, F.; Zhang, C.; Fan, C. Attention-based interpretable neural network for building cooling load prediction. Appl. Energy 2021, 299, 117238. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





