Abstract
The purpose of this work is to present a convenient design approach for metal hydride reactors that meet the specific requirements for hydrogen storage. Three methods from the literature, the time scale, the acceptable envelope, and the reaction front, are used to estimate the maximum thickness of the bed allowing for sufficient heat transfer. Further heat transfer calculations are performed within the framework of standardized heat exchanger via the homemade design software, to generate the complete geometry and dimensions of the reactor. LaNi5 material packed in tubular units based on conventional shell-and-tube heat exchanger is selected for analysis for an expected charging time of 500 s, 1000 s, and 1500 s. Apparently, the smaller the expected charging time, the smaller the bed thickness and hence the diameter of the tubular units. After comparison, the method of reaction front was adopted to output standard tube diameters and calculate the weight of the reactor. Significant weight differences were found to result from the varying wall thickness and number of tubes. In general, the shorter the expected charging time, the more tubular units with a small diameter will be built and the heavier the reactor. Fluent 2022 R2 was used to solve the reactor model with a tube diameter of 50 mm supposed to fulfill a charging time of 1500 s. The simulation results revealed that the reaction fraction reaches its maximum and the hydrogen storage process is completed at 500 s. However, because the calculation is conducted on meeting the heat exchange requirements, the average temperature of the bed layer is close to the initial temperature of 290 K and stops changing at 1500 s. The applicability of the method to the design of metal hydride reactors is thus confirmed by the temperature and reaction fraction judgment criteria.
1. Introduction
The need for energy is growing as human society develops. Traditional fossil fuel reserves are finite and non-renewable, and their production and utilization processes result in pollution [1,2,3] and intensify global warming. To mitigate such negative effects, scientists are working to develop clean, sustainable alternatives to fossil fuels [4,5]. The most promising candidate is hydrogen, a clean energy source with high calorific value, plentiful reserves, and non-polluting products. However, the safe and efficient storage and transport of hydrogen energy is a crucial technological barrier for the growth of hydrogen energy [6,7,8]. Common techniques for this purpose include solid-state hydrogen storage, low-temperature liquid hydrogen storage, and high-pressure gaseous hydrogen storage. High-pressure gaseous hydrogen storage and low-temperature liquid hydrogen storage are difficult to apply on a large scale due to the constraints of high cost and low safety [9,10,11,12,13,14]. On the other hand, solid-state hydrogen storage using metal hydrides has the advantages of high energy density, small volume, and safe and stable compounds generated, and is thought of as one of the promising technologies of the future.
Metal hydride-based hydrogen storage involves complex heat and mass transfer processes. If the reaction heat is not managed effectively, the reaction can slow down or even halt [15,16,17,18]. Because metal hydride materials have low thermal conductivity, more efficient heat transfer can be realized by expanding their heat transfer area or raising their heat transfer coefficient. In recent years, numerous studies on the reactor are focused on the structure of shell-and-tube heat exchanger, the number of heat exchanger tubes increases, and the shape of the heat exchanger tube is also continuously optimized [19,20,21]. To improve the heat transfer of hydride materials, various heat-conducting matrices like fins, aluminum foam, and natural graphite can be added. Then, their parameters can be further optimized [19,22,23,24]. Bai et al. [22] studied a tree-finned reactor using genetic algorithms, which reduced the hydrogen absorption time by 20.7% compared to radial fins. Hafsa et al. [24] numerically investigated a cylindrical reactor fitted with a phase change material, and found the hydrogen storage rate was more influenced by the latent heat of phase transition than by the metal hydride bed’s thermal conductivity. The efficiency of heat transfer can be significantly increased and the rate of hydrogen storage accelerated by adding fins, metal foam, modifying the geometry of the heat exchanger tubes, and increasing their number. However, there is no unified method to implement such heat transfer enhancement techniques, and a more complicated reactor structure and a weight penalty often arise.
As shown in Figure 1, heat exchanger, filter, and hydrogen storage alloy are typically included in reactor designs. A standardized reactor design facilitates large-scale production quickly [23,25]. Based on ASME standards, Raju et al. [26] constructed an embedded cooling tube reactor, described the reactor design process that serves as a guide for large-scale reactor design, and used simulation to confirm the methodology’s viability. Mazzucco et al. [27] conducted sensitivity analysis on the development of three types of shell-and-tube heat exchangers through heat transfer efficiency, where the baffle space of the heat exchanger is the most sensitive parameter, providing a valuable reference for reactor design. Wang et al. [28] investigated a metal hydride reactor for a forklift system, with three different baffles compared for flow field and reaction time; the diagonal baffle showed a higher flow rate than the other two with the best heat transfer performance. Prasad et al. [29] developed the modular design methodology of a reactor for large-scale hydrogen storage, where the heat transfer fluid was oil and three configurations of annular reactors were analyzed. The configuration with a finned structure had the best performance for hydrogen absorption, and the hydrogen charging time was faster than that of embedded cooling tube reactors. The aforementioned design techniques quicken the rate at which hydrogen is stored, but they do not provide clear guidance for choosing the standardized size of reactor, not to mention making a connection between the standard tube diameter and the rate at which hydrogen is stored. As a result, it is necessary to propose guidelines for standardized reactor design.
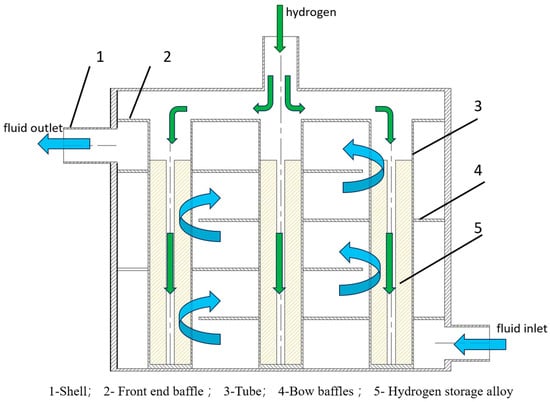
Figure 1.
Reactor model diagram.
In light of this, this study is dedicated to generating the full geometry and dimension of “standardized” metal hydride reactors according to given requirements on hydrogen storage, e.g., hydrogen storage capacity and charging time. The main contents are organized as follows. Firstly, a design framework conforming to national standards for heat exchangers, which is based on an estimate of bed thickness and fundamental heat transfer calculations, is described in Section 2. The procedure was programmed in a homemade software, whose output is exemplified for a typical shell-and-tube heat exchanger. Next, a detailed analysis on the weight composition of the reactor for varying charging time is presented, and a numerical simulation on the charging process of a reactor prototype is performed to confirm the viability of the design procedure in Section 3. Finally, concluding remarks are drawn in Section 4. The design framework can be helpful in efficiently developing metal hydride reactors to meet diverse requirements, hence promoting the utilization of solid hydrogen storage technology.
2. Metal Hydride Reactor Design Method
A metal hydride reactor is designed with an emphasis on standardizing the size of hydrogen storage tubes. In general, the first step is to identify the hydrogen storage alloy and analyze the heat generated during the hydrogen storage process. Next, the design and analysis are carried out adopting the standard diameter of the hydrogen storage tubes and the shell diameter of the heat exchanger. Finally, the feasibility of the design scheme of reactor is verified using simulations and experiments. This design method, if conducted manually, is slow and not effective. When integrated with heat exchanger design standards and the public Metal Hydride Toolbox [30], design software can significantly reduce design costs. Figure 2 illustrates the calculation procedure.
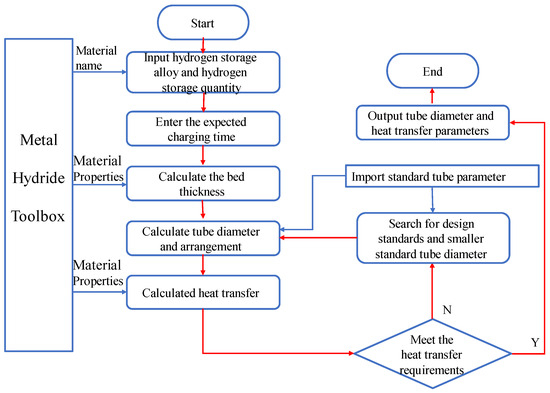
Figure 2.
Reactor design flow chart.
The reactor’s shell and tube parameters can be computed by using the flow chart above, which has been implemented in a homemade program. The program mainly consists of the Metal Hydride Toolbox, a heat transfer computing platform, and a standardized tube diameter database. The equilibrium temperature and pressure are provided by the Toolbox. The choice of tube diameter is relatively simple: the standard diameter of seamless tube following national standards for heat exchanger [31] is found as the round-down value of the sum of the calculated bed thickness and the filter diameter. When the heat exchange requirements are satisfied, the heat exchange parameters will output; if not, incrementally reduced standard tube diameters are employed until the heat exchange requirements are satisfied. Standard reactor sizes can be quickly designed using this design process in accordance with user requirements.
2.1. Reaction Heat Flow during Hydrogen Storage
When the appropriate alloy material is chosen, the alloy mass is calculated based on the required capacity for hydrogen storage. The reaction heat flow (RHF), or the amount of heat released, can be determined using the expected charging time, as shown in Equation (1) [24].
where wt% is the weight fraction of hydrogen when the reaction reaches saturation, ms is the mass of the hydrogen storage alloy, tc is the expected charging time, and ΔH and Mg are the reaction enthalpy and molar mass of hydrogen, respectively. These equations can provide a reference for the design of the heat exchange capacity of the reactor.
2.2. Bed Thickness Calculation
Due to the low thermal conductivity of the hydrogen storage alloy powders, which makes it difficult to dissipate the heat during the reaction process, a maximum bed thickness exists for a given charging time without altering the thermal conductivity of the bed. In this case, the thickness of the bed largely determines the reactor size.
Wang et al. [32] developed time scale (TS) equations for a reactor by analyzing the scaling of the energy equations and making the assumption that the hydrogen storage process features fast heat generation and slow cooling:
and
where t is the bed cooling time (ignoring the reaction heat generation time, which is the reaction completion time), L is the bed thickness, λeff and (ρc)eff are the effective thermal conductivity and specific heat, ε is the porosity, (ρcp)g is the heat capacity of hydrogen gas, and (ρc)s is the heat capacity of the solid metal phase.
Marty et al. [33] investigated the thickness and time equation of an axisymmetric reactor and a 1D reactor, as well as the relationship between reaction front (RF) and charging time in magnesium hydride.
In the axisymmetric reactor:
and
where Teq is the equilibrium temperature at which the corresponding equilibrium pressure is equal to hydrogen charging pressure; Twall is the wall temperature; and ρs is the density of the hydrogen storage alloy.
Cludio et al. [34] developed the acceptable envelope (AE) scoping method, which makes the modeling of hydrogen storage systems very flexible. The following equation was proposed for determining the bed thickness in two dimensions:
where ms is the mass of the alloy and Δmg is the mass of hydrogen absorbed. Among the three methods, the determination of bed thickness from the charging time in TS is only related to the physical parameters of the alloy, while the other two are also related to the reaction equilibrium, i.e., the equilibrium pressure determined by the Van’t Hoff equation. [35]:
where Peq is the equilibrium pressure of hydrogen at temperature T, Pref is the reference pressure, R is the ideal gas constant, and ∆S is entropy. On the other hand, the temperature Teq can be calculated by setting Peq as the exerted hydrogen pressure.
These three methods can all be applied to bed thickness calculations. The influence of other parameters is disregarded in TS, and the bed thickness is exclusively connected to thermal conductivity and volume specific heat. On the other hand, thermal conductivity, temperature change, and enthalpy all have an impact on bed thickness in AE and RF calculations. Moreover, porosity is taken into account in RF. Because LaNi5 has excellent kinetic properties, it was chosen for discussion to determine the optimal bed design strategy. The bed thicknesses calculated using the three methods are shown in Figure 3.
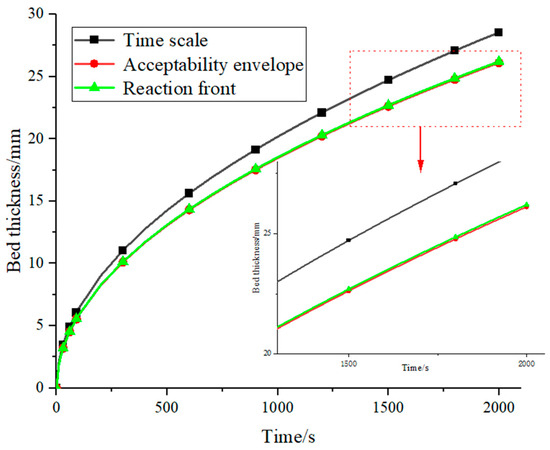
Figure 3.
Theoretical and actual bed thickness.
The TS design has the maximum thickness for the LaNi5, while the AE and RF designs are nearly equal in thickness. Since the results are comparable for different methods, and rigorous consideration on various factors is made for RF, the following discussion will be performed in terms of the RF design technique.
Figure 4a shows the bed thickness at different pressures, which increases accordingly as the pressure increases. Generally speaking, the reaction rate accelerates with increasing hydrogen storage pressure, necessitating an increase in bed thickness in proportion. In the RF calculation, as the hydrogen storage pressure increases, the corresponding equilibrium temperature Teq increases, which makes the temperature gradient increase. With the other parameters remaining constant, the bed thickness from Equations (6) and (7) is increased with increasing pressure.
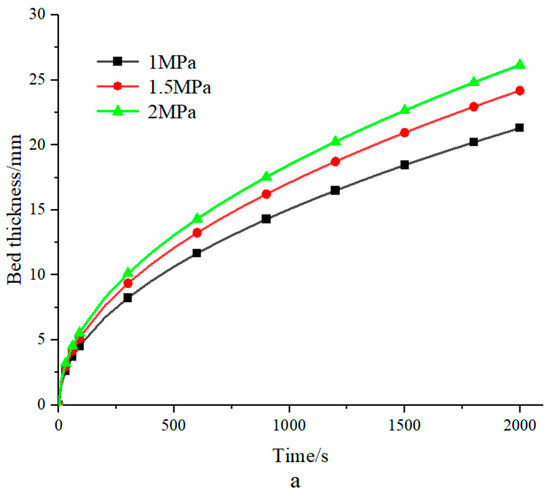
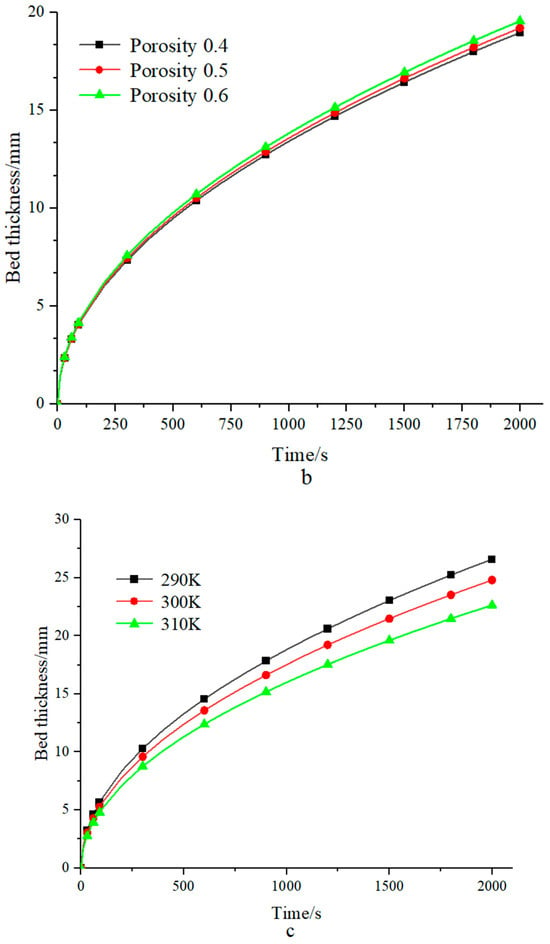
Figure 4.
(a) Bed thickness under different pressures; (b) the bed thickness of different porosities was calculated using the RF technique; (c) bed thickness at different heat transfer fluid temperatures.
The bed thickness is displayed under various porosities in Figure 4b, and it increases as porosity increases. From Equation (7), it can be found that as porosity increases, the amount of heat produced per unit volume will be lowered. On the other hand, the effective thermal conductivity is also reduced according to the linear weighted formula (Equation (4)). The overall effect leads to a rise in the ratio of λeff to (1 − ε), which in turn causes the calculated bed thickness to increase.
The bed thickness with various fluid temperatures is shown in Figure 4c. The bed thickness reduces as the temperature of the heat transfer fluid rises, primarily due to a decrease in the temperature differential between the fluid and the bed; see Equation (7). A low-temperature heat transfer fluid is chosen in the reactor design process.
2.3. Determining Heat Transfer Parameters
In the design process, the heat transfer fluid velocity lies in the range of 1~2.5 m/s [11]. The total thermal resistance includes the thermal resistance of the hydrogen storage alloy, the thermal resistance of the tube wall, and that for convective heat transfer.
Heat exchange:
where U is the total heat transfer coefficient, A is the reactor heat transfer area, ∆T is the average temperature difference, and Q is the design heat flow (DHF).
The total heat transfer coefficient is calculated as [36]:
where Ld is the thickness of the tube, Ls is the thickness of the alloy, and so on. λd is the thermal conductivity of the tube wall.
The heat transfer coefficient between fluid and tube wall can be set as [37]:
where des is the equivalent diameter of the shell, and Nu is the Nussel number. For the baffle notch in the heat exchanger being 25% [37], 2 × 103 < Re < 1 × 106, Nu can be expressed as:
where Re is the Reynolds number, Pr is the Prandtl constant, and μ and μw are the viscosity at the mean temperature of the shell fluid and the viscosity at the temperature of the tube wall.
By implementing the program, the standard diameter of the tube can be found. Figure 5 shows the tube determined using RF and the rounded result towards standard value.
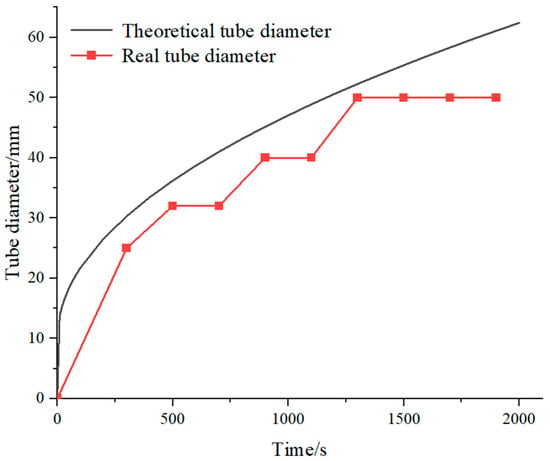
Figure 5.
Theoretical and real tube diameter.
In the output, equal tube diameters are observed for some cases with different calculated thickness. One reason is that it is difficult to obtain different tube sizes due to the non-uniformity of the spanning of standard tube diameter. Another reason is that in the iteration process, the thickness of the determined tube diameter by the expected charging time does not meet the heat transfer requirements. In this case, the iteration continues to a smaller tube diameter.
3. Results and Discussion
3.1. Calculation of Shell Parameters
LaNi5 is chosen as the hydrogen storage material in this paper. The hydrogen storage capacity is 5 Nm3, and the hydrogen charging pressure is 2 MPa. Table 1 displays the output parameters under various charging times. The hydrogen storage tube material is 316 L stainless steel [38], and the relevant parameters are shown in Table 2.

Table 1.
Tube parameters and shell parameters.

Table 2.
Hydrogen storage tube-related parameters.
The shell parameters calculated for a charging time of 500, 1000, and 1500 s are shown in Table 1. The range of the standard tube diameter affects the output results.
Figure 6 shows the comparison of the RHF for the expected charging time of 500–1500 s with the DHF calculated using RF. With increasing time, the RHF decreases, the bed thickness increases, and the calculated DHF decreases. The DHF is in the range of 1.26–1.39 of RHF for the expected charging time.
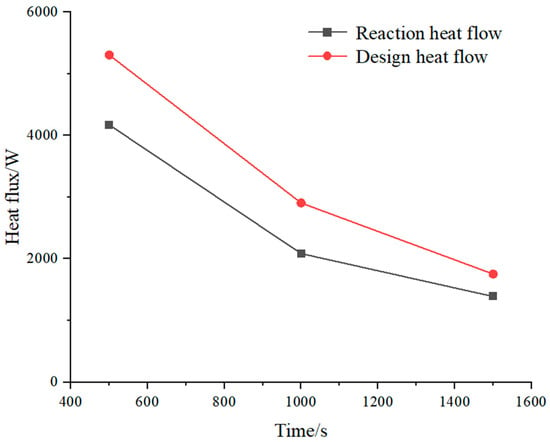
Figure 6.
Expected time response heat flow and calculated heat flow.
3.2. Reactor Weight
Large-scale applications of metal hydride reactors are challenging to actualize, in part because of the reactor’s enormous weight, which makes it difficult to use in mobile scenarios but appropriate for stationary ones [39]. The weight of the reactor is primarily made up of the weight of the hydrogen storage alloy, the hydrogen storage tube, the baffle plate, and the shell. Since the weight of the alloy is the same for the given hydrogen capacity, only the other three parts have an impact on the reactor weight. The alloy’s percentage of the total should also be taken into consideration, and its calculation is shown in Equation (14):
where mV is the mass of the hydrogen storage tube, the baffle plate, and the shell, and w is the weight ratio of the alloy to the whole. The larger the weight ratio, the smaller the reactor proportion.
The reactor weight values under the RF design method are shown in Figure 7. The reactor weight is maximum for a charging time of 500 s and almost the same for 1000 s and 1500 s. Table 1 shows that the shell diameter remains constant and that the main factor causing the variations in reactor weights is the tube parameter. The maximum number of reactor tubes is found at 500 s, and the increase in the weight of the tubes leads to an increase in the total weight of the reactor. For reactor designs fulfilling charging in 1000 s and 1500 s, the number of tubes is different, but the wall thickness of the hydrogen storage tubes affects the weight results, and the thickness of the reactor is taken according to the standard and is not treated uniformly, resulting in a small difference in volume between the two.
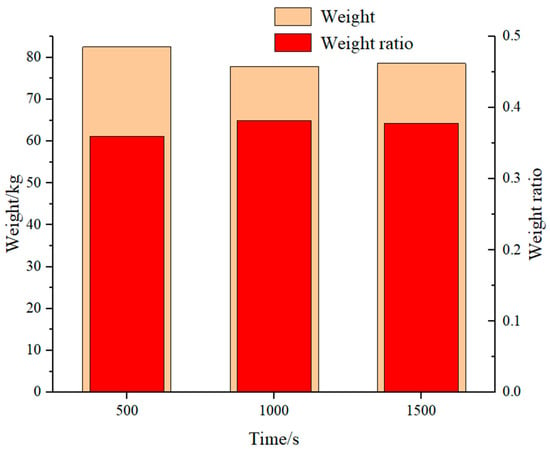
Figure 7.
Reactor weight to alloy weight ratio.
The weight ratio is defined to evaluate the design of the reactor from the perspective of weight efficiency. Since the mass of the alloy remains constant for a given hydrogen storage capacity, the weight of the hydrogen storage tubes, baffle plates, and shells has the great impact on the weight ratio of the alloy. The weight ratios are 0.36, 0.38, and 0.39 for the above method. Sreeraj [40] designed a tubular reactor structure similar to this study, and the calculation of different schemes results in a weight ratio of 0.301–0.405. The scheme of embedded cooling tubes was proposed by Nithin [26]. The weight ratio of the alloy to the vessel was calculated, and the ratio of alloy to the overall weight was determined to be between 0.515 and 0.602. Since the embedded cooling tubes can be surrounded by a large percentage of alloy storage, the weight ratio of the alloy is higher. In a word, the rationality of the reactor design can be indirectly confirmed from the above comparison.
3.3. Simulation Verification
3.3.1. Physical Modeling
As shown in Figure 1, the metal hydride reactor is similar to a shell-and-tube heat ex-changer, with heat exchange fluid (water) on the shell side and hydrogen storage alloy LaNi5 on the tube side; the physical properties are shown in Table 3. The 1500 s results were chosen for the 50 mm inner diameter of the tube, and other relevant parameters are shown in Table 1 and Table 2. The volume expansion of the material during hydrogen absorption is taken into account, and 20% void space is reserved. The alloy bed is a porous medium model. Due to the complexity of the reaction process, the following assumptions are made in this paper for ease of calculation [41,42]:

Table 3.
Thermophysical properties of materials [43].
- The alloy material is the same;
- Radiative heat transfer is ignored throughout;
- The heat loss in the heat transfer process is ignored;
- The ambient temperature is 290 K and the ambient pressure is 1 standard atmospheric pressure;
- The change in alloy volume during the reaction process is ignored;
- At each location, there is a local thermal balance between the bed and the gas.
3.3.2. Mathematical Model and Numerical Procedure
The mass conservation equation for hydrogen is as follows [43]:
The mass conservation equation of the hydrogen storage alloy is as follows:
where is the hydrogen absorption rate per unit volume, which can be obtained by the reaction kinetic equation of LaNi5:
The apparent velocity of hydrogen in the bed is as follows:
The energy conservation equation of the metal hydride in the reactor is as follows [38,43]:
Initial and boundary conditions:
When t = 0, the metal hydride bed temperature is assumed to be the ambient temperature and has a uniform density:
The inlet temperature of the heat transfer fluid is constant:
It is assumed that the hydrogen absorption reaction begins under hydrogen supply pressure:
The convective boundary condition of tube surfaces are expressed as:
In the shell, adiabatic boundary conditions are assumed:
The reaction fraction X is defined as the mass of absorbed hydrogen divided by the hydrogen storage capacity [22]:
3.3.3. Simulation Methodology and Model Validation
The reactor is an axisymmetric model. To improve the production rate of the mesh, Fluent Meshing in Fluent 2020 R2 is used for generating Poly-Hexcore body mesh, which can be divided into polyhedral mesh and hexahedral mesh in different regions to adapt to the computational needs [44]. The governing equations with the aforementioned boundary conditions are solved using the SIMPLE algorithm. The energy convergence threshold is 10−6, and the time step is set to 1 s. The maximum skewness of the grid is less than 0.65, and the minimum orthogonal quality is 0.37. Figure 8 displays the grid independence results. Considering computational accuracy and cost, this paper uses a 2 million mesh to perform the calculations.
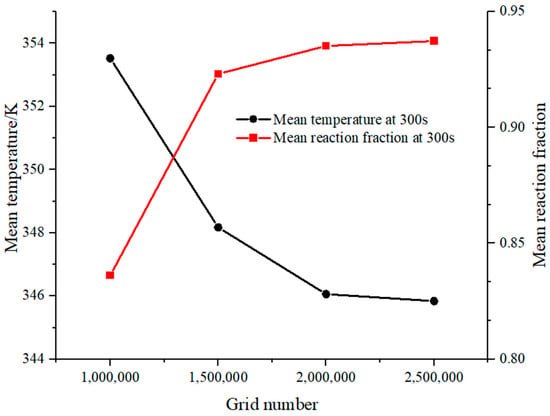
Figure 8.
Grid independence verification.
As shown in Figure 9, the simulation results are verified with the experimental results of Jemni et al. [45]. The experimental results show the results of the bed temperature under the hydrogen supply pressure of 0.8 MPa when the temperature of the heat exchanger fluid is 293 K and 313 K, respectively. The maximum deviation between the simulated and numerical results does not exceed 3%, proving the accuracy of the model.
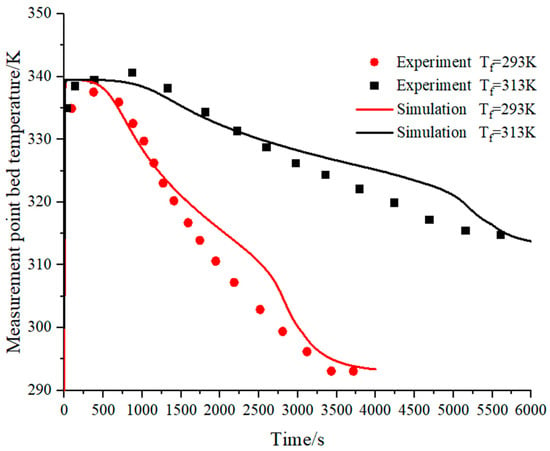
Figure 9.
The validation of the mathematic mode.
3.3.4. Simulation of Hydrogen Storage Process
Figure 10 shows the results of the average bed temperature and reaction fraction at the hydrogen supply pressure of 2 MPa and the heat exchange fluid temperature of 290 K. In the initial stage of the reaction, the reaction fraction increases dramatically and the bed temperature peaks rapidly at 100 s. Thereafter, the reaction proceeds slowly, and the bed temperature drops. However, the heat released by the hydrogen storage process still does not dissipate, and the heat transfer process continue. At 1500 s, the reactor temperature returns back to a temperature of 290 K.
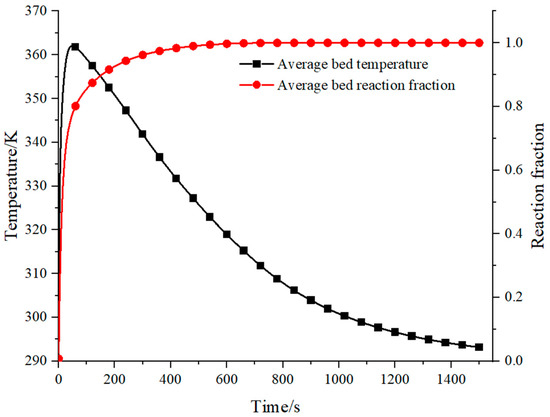
Figure 10.
Average reactor bed temperature and reaction fraction.
According to the design scheme, hydrogen storage is expected to be completed in 1500 s. From the predicted result using numerical simulation, the hydrogen storage process can be completed in only 500 s and the reaction fraction reaches the maximum. From the comparison, it can be found that the reaction completion time is faster than the expected reaction time. There are some reasons for this phenomenon. As analyzed, the MH reaction process can be divided into two stages. In the first stage, the reaction is not limited by heat transfer, but only depends on the initial bed temperature and inlet pressure. In the second stage, the reaction area advances from the heat transfer wall towards the adiabatic wall due to the limitation of heat transfer. The first stage of the reaction is ignored in current theoretical models, resulting in the actual reaction process ending earlier than the theoretical prediction time. In the second stage of the reaction, the temperature of the reaction area is near the equilibrium temperature. When the reaction is complete, the temperature in the vast majority of areas is between equilibrium temperature and wall temperature. Therefore, the reaction completion time is earlier than the heat transfer completion time (i.e., bed cooling time).
Figure 11 shows the temperature distribution in a cross-section of the reactor (150 mm vertical height). At 100 s, the hydrogen storage process is at the rapid reaction stage and releases a significant quantity of heat. The heat taken away by the heat transfer fluid is insufficient to lower the temperature of the bed. After the hydrogen storage process is finished at 500 s, heat is no longer released and it is gradually removed by the fluid, and the temperature of the bed drops. The heat exchange process is close to completion at 1000 s, when the fluid takes away nearly all of the heat in the bed and the temperature of the bed is approaching 300 K.
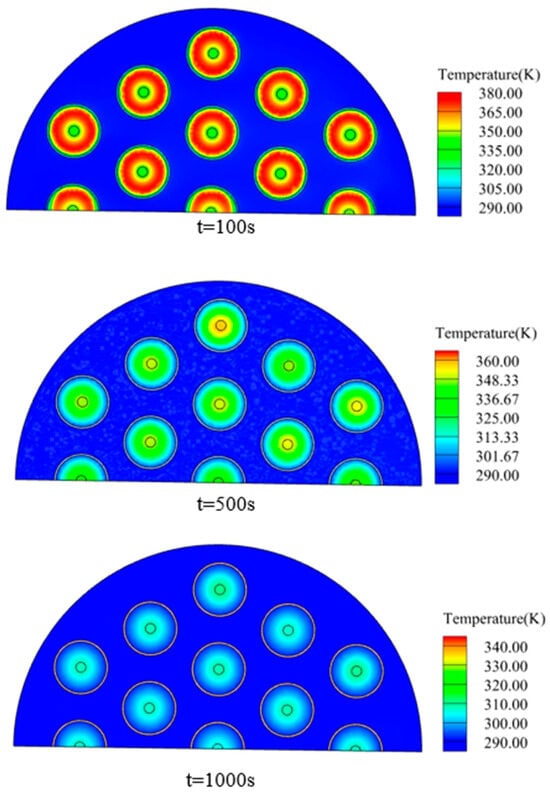
Figure 11.
Temperature cloud map at different times.
Heat transfer is commonly used as an indicator for the reactor to finish the reaction in the design process, as can be found in the expressions of the TS, RF, and AE methods. The fulfillment of the heat transfer conditions determines when the hydrogen storage reaction is considered complete. From the simulation results, the average temperature of the bed tends to the temperature of 290 K at 1500 s, and the reactor heat transfer ends. From the perspective of heat transfer, the software design method is reasonable, and the heat transfer completion time is almost the same as predicted. Therefore, the software can be used to estimate the thickness of the bed from the expected charging time. However, for reactors in large-scale use, heat and mass transfer have great changes, and the calculation of the transient heat of the reaction process as the steady state in the methods of TS, RF, and AE will cause a deviation from the practical hydrogen storage process. However, from the simulation results for the RF reactor scheme, hydrogen storage can be completed in the expected charging time of 1500 s, while under the other two schemes, the bed thickness and hence other key dimensions of the reactors are comparable, and the hydrogen storage process can also be completed within the corresponding expected time.
4. Conclusions
In this research, standardized reactor dimensions were obtained using programming based on relevant hydrogen storage requirements. LaNi5 material was chosen to analyze the design methodology and weight results. The maximum results of the tube diameter were also simulated and verified. The key conclusions are as follows:
- (1)
- The calculated bed thicknesses using TS, RF, and AE are comparable, and RF is chosen for use because of the higher number of physical factors considered. According to the results of the RF calculation, the bed thickness will increase as pressure and porosity increase, while it will reduce as the temperature of the heat transfer fluid rises.
- (2)
- The diameter of the hydrogen storage tubes grows and the number of tubes reduces with increasing bed thickness. Therefore, a large number of tubes contribute to a large reactor weight for a relatively short charging time of 500 s. The alloy weight ratios determined in this study are found to be close to the results reported in the literature.
- (3)
- From the simulation results, the reaction fraction of the reactor designed for a charging time of 1500 s reaches its maximum at 500 s. Since the reactor model is the outcome of the heat exchange calculation, where complete heat dissipation back to the initial temperature is assumed in the theoretical tool, such contradiction suggests that a more accurate tool for estimating bed thickness needs to be developed.
Author Contributions
Conceptualization, R.R., F.Y. and R.I.; Methodology, R.R.; Software, R.R. and J.W.; Validation, R.R., F.Y. and R.I.; Formal analysis, R.R.; Investigation, R.R.; Resources, R.R.; Data curation, R.R. and J.W.; Writing—original draft, R.R.; Visualization, R.R.; Supervision, J.W., F.Y. and R.I.; Project administration, F.Y. and R.I. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support from National Natural Scientific Foundation of China under grant NO. 52076178 is greatly acknowledged.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | Area, m2 |
| AE | Acceptability Envelope |
| cp | Specific heat, J/(kg·K) |
| d | Tube diameter, mm |
| D | Shell diameter, mm |
| DHF | Design heat flow |
| H | Enthalpy |
| K | Permeability, m2 |
| L | Thicknesses |
| M | Molecular weight, kg/mol |
| Normal vector | |
| Np | Baffle plates number |
| Nu | Nussel number |
| Pt | Pitch of the tubes, mm |
| q | Reaction heat flow, W |
| Q | Design heat flow, W |
| Re | Reynolds number |
| RF | Reaction front |
| RHF | Reaction heat flow |
| S | Entropy |
| t | Time, s |
| T | Temperature |
| TS | Time scale |
| U | Heat transfer coefficient |
| w | Weight ratio |
| Greek Symbols | |
| ε | Porosity |
| ρ | Density, kg/m3 |
| λ | Thermal conductivity, W/(m·K) |
| μ | Dynamic viscosity, kg/(m·s) |
| Subscripts | |
| 0 | Initial value |
| d | Tube |
| D | Shell |
| es | Equivalent diameter |
| eq | Equilibrium |
| eff | Effective value |
| f | Cooling water |
| in | Inner |
| g | Hydrogen |
| o | Out |
| ref | Reference |
| s | Metal hydride |
| sat | Saturation value |
| v | Vessel |
| w | Tube |
References
- Xu, G.; Chen, W.; Fang, Z. Research progress of supercritical water hydrogen production from biomass. Trans. Chin. Soc. Agric. Eng. 2023, 39, 24–35. [Google Scholar] [CrossRef]
- Sazali, N. Emerging technologies by hydrogen: A review. Int. J. Hydrogen Energy 2020, 45, 18753–18771. [Google Scholar] [CrossRef]
- Dawood, F.; Anda, M.; Shafiullah, G.M. Hydrogen production for energy: An overview. Int. J. Hydrogen Energy 2020, 45, 3847–3869. [Google Scholar] [CrossRef]
- Yue, M.; Lambert, H.; Pahon, E.; Roche, R.; Jemei, S.; Hissrl, D. Hydrogen energy systems: A critical review of technologies, applications, trends and challenges. Renew. Sustain. Energy Rev. 2021, 146, 111180. [Google Scholar] [CrossRef]
- Thomas, J.M.; Edwards, P.P.; Dobson, P.J.; Owen, G.P. Decarbonising energy: The developing international activity in hydrogen technologies and fuel cells. J. Energy Chem. 2020, 51, 405–415. [Google Scholar] [CrossRef]
- Kovač, A.; Paranos, M.; Marciuš, D. Hydrogen in energy transition: A review. Int. J. Hydrogen Energy 2021, 46, 10016–10035. [Google Scholar] [CrossRef]
- Acar, C.; Dincer, I. Review and evaluation of hydrogen production options for better environment. J. Clean. Prod. 2019, 218, 835–849. [Google Scholar] [CrossRef]
- Lebrouhi, B.E.; Djoupo, J.J.; Lamrani, B.; Benabdelaziz, K.; Kousksou, T. Global hydrogen development-A technological and geopolitical overview. Int. J. Hydrogen Energy 2022, 47, 7016–7048. [Google Scholar] [CrossRef]
- Cevahir, T.; Ali, M.Ç. A study on hydrogen, the clean energy of the future: Hydrogen storage methods. J. Energy Storage 2021, 40, 102676. [Google Scholar] [CrossRef]
- Singh, G.; Ramadass, K.; DasiReddy, V.D.; Yuan, X.; Ok, Y.S.; Bolan, N.; Xue, X.; Tianyi, M.; Ajay, K.; Yi, J.; et al. Material-based generation, storage, and utilisation of hydrogen. Prog. Mater. Sci. 2023, 135, 101104. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, W.; Kang, J.; Yuan, T. The Necessity and Feasibility of Hydrogen Storage for Large-Scale, Long-Term Energy Storage in the New Power System in China. Energies 2023, 16, 4837. [Google Scholar] [CrossRef]
- Liu, C.; Pei, Y.; Han, H.; Zhou, H.; Zhang, R.; Li, Y.; Zhu, J.; Wang, C.; Kong, Y. Research status and development trend of hydrogen energy industry chain and the storage and transportation technologies. Oil Gas Storage Transp. 2022, 41, 498–514. [Google Scholar] [CrossRef]
- Huang, J.; Tian, Z.; Lei, L.; Wang, C.; Shu, R.; Luo, X.; Liu, J. Advances and Development Trends of Hydrogen Storage and Refueling Industry. Adv. New Renew. Energy 2023, 11, 162–173. [Google Scholar] [CrossRef]
- Yao, J.; Zhu, P.; Ren, J.; Wu, Z. Simulation on hydrogen absorption process of metal hydride-based hydrogen storage reactor coupled with phase change thermal storage. Chin. J. Process Eng. 2018, 18, 1093–1101. [Google Scholar] [CrossRef]
- Afzal, M.; Mane, R.; Sharma, P. Heat transfer techniques in metal hydride hydrogen storage: A review. Int. J. Hydrogen Energy 2017, 42, 30661–30682. [Google Scholar] [CrossRef]
- Yang, F.S.; Wang, G.X.; Zhang, Z.X.; Meng, X.Y.; Rudolph, V. Design of the metal hydride reactors—A review on the key technical issues. Int. J. Hydrogen Energy 2010, 35, 3832–3840. [Google Scholar] [CrossRef]
- Krane, P.; Nash, A.L.; Ziviani, D.; Braun, J.E.; Marconnet, A.M.; Jain, N. Dynamic modeling and control of a two-reactor metal hydride energy storage system. Appl. Energy 2022, 325, 119836. [Google Scholar] [CrossRef]
- Liu, Y.; Ayub, I.; Khan, M.; Yang, F.; Wu, Z.; Zhang, Z. Numerical investigation of metal hydride heat storage reactor with two types multiple heat transfer tubes structures. Energy 2022, 253, 124142. [Google Scholar] [CrossRef]
- Kudiiarov, V.; Elman, R.; Pushilina, N.; Kurdyumov, N. State of the Art in Development of Heat Exchanger Geometry Optimization and Different Storage Bed Designs of a Metal Hydride Reactor. Materials 2023, 16, 4891. [Google Scholar] [CrossRef] [PubMed]
- Tong, L.; Xiao, J.; Bénard, P.; Chahine, R. Thermal management of metal hydride hydrogen storage reservoir using phase change materials. Int. J. Hydrogen Energy 2019, 44, 21055–21066. [Google Scholar] [CrossRef]
- Kumar, A.; Raju, N.N.; Muthukumar, P.; Selvan, P.V. Experimental studies on industrial scale metal hydride based hydrogen storage system with embedded cooling tubes. Int. J. Hydrogen Energy 2019, 44, 13549–13560. [Google Scholar] [CrossRef]
- Bai, X.S.; Yang, W.W.; Tang, X.Y.; Yang, F.S.; Jiao, Y.H.; Yang, Y. Optimization of tree-shaped fin structures towards enhanced absorption performance of metal hydride hydrogen storage device: A numerical study. Energy 2021, 220, 119738. [Google Scholar] [CrossRef]
- Sreeraj, R.; Aadhithiyan, A.K.; Anbarasu, S. Integration of thermal augmentation methods in hydride beds for metal hydride based hydrogen storage systems: Review and recommendation. J. Energy Storage 2022, 52, 105039. [Google Scholar] [CrossRef]
- El Mghari, H.; Huot, J.; Xiao, J. Analysis of hydrogen storage performance of metal hydride reactor with phase change materials. Int. J. Hydrogen Energy 2019, 44, 28893–28908. [Google Scholar] [CrossRef]
- Shafiee, S.; McCay, M.H. Different reactor and heat exchanger configurations for metal hydride hydrogen storage systems–A review. Int. J. Hydrogen Energy 2016, 41, 9462–9470. [Google Scholar] [CrossRef]
- Raju, N.N.; Muthukumar, P.; Selvan, V.P.; Malleswararao, K. Design methodology and thermal modelling of industrial scale reactor for solid state hydrogen storage. Int. J. Hydrogen Energy 2019, 44, 20278–20292. [Google Scholar] [CrossRef]
- Mazzucco, A.; Voskuilen, G.T.; Waters, L.E.; Pourpoint, L.T.; Rokni, M. Heat exchanger selection and design analyses for metal hydride heat pump systems. Int. J. Hydrogen Energy 2016, 41, 4198–4213. [Google Scholar] [CrossRef]
- Wang, H.; Du, M.; Wang, Q.; Li, Z.; Wang, S.; Gao, Z.; Derksen, J.J. Enhancement of hydrogen storage performance in shell and tube metal hydride tank for fuel cell electric forklift. Int. J. Hydrogen Energy 2023, 48, 23568–23580. [Google Scholar] [CrossRef]
- Prasad, J.S.; Muthukumar, P. Design and performance analysis of an annular metal hydride reactor for large-scale hydrogen storage applications. Renew. Energy 2022, 181, 1155–1166. [Google Scholar] [CrossRef]
- Purdue Metal Hydride Toolbox. Available online: https://github.com/PurdueH2Lab/MetalHydrideToolbox (accessed on 13 January 2022).
- GB/T 177395-2008; Dimensions, Shapes, Masses and Tolerances of Seamless Steel Tubes. China Standard Press: Beijing, China, 2008.
- Wang, C.S.; Brinkerhoff, J. Is there a general time scale for hydrogen storage with metal hydrides or activated carbon? Int. J. Hydrogen Energy 2021, 46, 12031–12034. [Google Scholar] [CrossRef]
- Marty, P.; de Rango, P.; Delhomme, B.; Garrier, S. Various tools for optimizing large scale magnesium hydride storage. J. Alloys Compd. 2013, 580, S324–S328. [Google Scholar] [CrossRef]
- Claudio, C.; Bruce, J.H.; David, A.T.; Stephen, L.G.; Donald, L.A. Acceptability envelope for metal hydride-based hydrogen storage systems. Int. J. Hydrogen Energy 2011, 37, 2812–2824. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, H.; Liu, Y.; Shi, Q. Metal hydride thermal energy storage and its research progress. Mater. Sci. Eng. Powder Metall. 2019, 24, 391–399. [Google Scholar] [CrossRef]
- Wu, Z.; Yang, F.; Zhang, Z.; Bao, Z. Magnesium based metal hydride reactor incorporating helical coil heat exchanger: Simulation study and optimal design. Appl. Energy 2014, 130, 712–722. [Google Scholar] [CrossRef]
- Qiu, S.; Qian, B. Principle, Structure and Design of Heat Exchanger; Shanghai Jiao Tong University Press: Shanghai, China, 1990; pp. 43–146. [Google Scholar]
- Sun, C.; Ai, S.; Liu, Y. Numerical simulation plate side flow heat transfer new plate-shell heat exchanger with considering physical property changes and shell heat transfer. Chem. Ind. Eng. Prog. 2024, 1–18. [Google Scholar] [CrossRef]
- Dong, Z.; Wang, Y.; Wu, H.; Zhang, X.; Sun, Y.; Li, Y.; Chang, J.; He, Z.; Hong, J. A design methodology of large-scale metal hydride reactor based on schematization for hydrogen storage. J. Energy Storage 2022, 49, 104047. [Google Scholar] [CrossRef]
- Sreeraj, R.; Aadhithiyan, A.K.; Anbarasu, S. Comparison, advancement, and performance evaluation of heat exchanger assembly in solid-state hydrogen storage device. Renew. Energy 2022, 198, 667–678. [Google Scholar] [CrossRef]
- Bao, Z.; Wu, Z.; Nyamsi, S.N.; Yang, F.; Zhang, Z. Three-dimensional modeling and sensitivity analysis of multi-tubular metal hydride reactors. Appl. Therm. Eng. 2013, 52, 97–108. [Google Scholar] [CrossRef]
- Pandey, V.; Krishna, K.V.; Maiya, M.P. Numerical modelling and heat transfer optimization of large-scale multi-tubular metal hydride reactors. Int. J. Hydrogen Energy 2023, 48, 16020–16036. [Google Scholar] [CrossRef]
- Bai, X.S.; Yang, W.W.; Tang, X.Y.; Dai, Z.Q.; Yang, F.S. Parametric optimization of coupled fin-metal foam metal hydride bed towards enhanced hydrogen absorption performance of metal hydride hydrogen storage device. Energy 2022, 243, 123044. [Google Scholar] [CrossRef]
- Li, K.; Wang, Z.; Zhan, J.; He, Q.; Li, Y. Parameter optimization of J -type heat exchanger baffles based on numerical simulation. Cryog. Supercond. 2023, 51, 43–48. [Google Scholar] [CrossRef]
- Jemni, A.; Nasrallah, S.B.; Lamloumi, J. Experimental and theoretical study of ametal–hydrogen reactor. Int. J. Hydrogen Energy 1999, 24, 631–644. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).