Abstract
The growing demand to reduce emissions of pollutants and CO2 from internal combustion engines has led to a critical need for the development of ultra-lean burn engines that can maintain combustion stability while mitigating the risk of knock. One of the most effective techniques is the pre-chamber spark-ignition (PCSI) system, where the primary combustion within the cylinder is initiated by high-energy reactive gas jets generated by pilot combustion in the pre-chamber. Due to the complex physical and chemical processes involved in PCSI systems, performing 3D CFD simulations is crucial for in-depth analysis and achieving optimal design parameters. Moreover, combining a detailed CFDs model with a calibrated 0D/1D model is expected to provide a wealth of new insights that are difficult to gather through experimental methods alone, making it an indispensable tool for improving the understanding and optimization of these advanced engine systems. In this context, numerous previous studies have utilized CFD models to optimize key design parameters, including the geometric configuration of the pre-chamber, and to study combustion characteristics under various operating conditions in PCSI engines. Recent studies indicate that several advanced models designed for conventional spark-ignition (SI) engines may not accurately predict performance under the demanding conditions of Turbulent Jet Ignition (TJI) systems, particularly when operating in lean mixtures and environments with strong turbulence–chemistry interactions. This review highlights the pivotal role of Computational Fluid Dynamics (CFDs) in optimizing the design of pre-chamber spark-ignition (PCSI) engines. It explores key case studies and examines both the advantages and challenges of utilizing CFDs, not only as a predictive tool but also as a critical component in the design process for improving PCSI engine performance.
1. Introduction
Given the current global energy demand and shortages, developing technological solutions that enhance fuel conversion efficiency in internal combustion engines is imperative. Two prominent strategies are lean burn combustion and stoichiometric combustion with exhaust gas recirculation (EGR), each offering distinct advantages and challenges.
Leaner combustion strategies are recognized for their potential to boost thermal efficiency and reduce pumping losses [1,2]. Studies have demonstrated that lean fuel–air mixtures significantly reduce fuel consumption and NOx emissions while improving thermal efficiency [1,2]. However, applying lean burn strategies to gasoline engines presents several challenges. One major limitation is the incompatibility with three-way catalytic converters, which are essential for reducing emissions in gasoline engines. Additionally, to meet current NOx emission regulations, λ levels must be increased to 1.8–2.0 [2], surpassing the lean stability limit (λ ~ 1.4). Moreover, leaner air–fuel mixtures can lead to serious issues such as combustion stability degradation, increased cycle-by-cycle variation, reduced thermal efficiency, and elevated unburned hydrocarbon (UHC) emissions.
In contrast, maintaining a stoichiometric air-to-fuel ratio (λ = 1) while reducing oxygen concentration through EGR offers another viable approach to improving SI engine efficiency [3,4]. This method allows using three-way catalytic converters, which are highly effective in reducing NOx emissions [4]. Additionally, as a diluent, EGR reduces the knock tendency at low-speed, high-load conditions and enhances fuel economy by eliminating the need for fuel enrichment [5]. However, this approach is also associated with challenges such as increased cycle-to-cycle variability, reduced flame propagation speed, and the risk of misfires, challenges typically seen in lean combustion without EGR.
Previous literature [6,7] has identified that the primary obstacles in lean burn operations, whether using air or EGR as diluents, are the increased energy required to initiate combustion and the low flame propagation velocity. Therefore, the most significant challenge in implementing lean combustion technology is developing an ignition system capable of reliably igniting a lean fuel–air mixture. Lean-burn internal combustion engines, which aim to reduce nitrogen oxide (NOx) emissions, require substantial ignition power and widespread ignition sources charge to ignite and burn the lean premixed charge effectively. This strategy is crucial for enhancing efficiency and reducing residual hydrocarbon emissions.
To address this limitation, researchers have proposed and thoroughly examined alternative ignition approaches such as laser-induced plasma ignition [8,9], diesel pilot injection [10], and pre-chamber ignition systems. Despite extensive research efforts, only a few of these methods have transitioned into commercial applications. Laser-induced plasma ignition technology offers precise control over ignition timing and high-energy ignition potential. However, challenges such as high costs, complexity in implementation, and sensitivity to environmental conditions have limited its widespread commercial adoption, keeping the technology mainly in the research phase. Diesel pilot injection also has drawbacks, including increased engine complexity due to the additional fuel source and the reliance on auto-ignition of diesel, which requires high in-cylinder temperatures and offers less precise control. Consequently, the advantages of pilot injection may be limited under specific operating conditions.
All Turbulent Jet Ignition (TIJ) systems are equipped with a spark plug, a compact pre-chamber (<3% of clearance volume), and one or more orifices through which the pre-chamber’s reacting contents are injected into the main chamber. The spark plug ignites the mixture in the pre-chamber, creating a pressure differential that drives the flame through the nozzle. This results in a jet of intermediate combustion products containing active radicals and high-temperature burned materials, which rapidly ignite the charge in the main chamber, initiating fast and turbulent combustion.
Recently, pre-chamber spark-ignition (PCSI) technology has been actively implemented as an ignition method not only in highly downsized TGI engines [11,12] and heavy-duty gas engines [13,14] but also in hybrid vehicle engines [15]. The PCSI systems have recently been applied to carbon-neutral fueled passenger car engines for automotive applications.
Summarizing the research results of the PCSI system above, it can be observed that by supplying a higher amount of energy in the main chamber at the start of combustion, stable combustion can be achieved under very lean conditions (λ > 2.5) for gasoline-fueled engines [16,17] and λ of up to 2.6 for heavy-duty natural gas engines with near zero NOx emission [18]. Recently, a pre-chamber was applied to a gasoline-fueled PFI engine, achieving 52.5% indicated thermal efficiency and stable ultra-lean burn combustion at a lambda of 2.4 [19]. These make PCSI a more practical and economical lean combustion technique than lean combustion methods.
1.1. Pre-Chamber Ignition Concept
The first pre-chamber combustion engine is often attributed to the Ricardo Dolphin engine, developed in the early 20th century [20]. Sir Harry Ricardo, a pioneering British engineer, designed this engine to improve combustion efficiency and reduce knock in gasoline engines.
Pre-chamber combustion technology later advanced into the jet igniter system [2,4,21,22], characterized by a significantly smaller orifice that connects the main combustion chamber to the pre-chamber cavities. The reduced orifice size accelerates the flow of the burning mixture, effectively quenching the flame while allowing reactive radical species to ignite farther from the pre-chamber. Jet ignition technology was first conceptualized in the late 1950s by Nikolai Semenov, renowned for his contributions to the general theory of chemical chain reactions. In 1981, the LAG system was integrated into the Volga vehicle’s powertrain, using a cam-driven injector to introduce a rich mixture (λ = 0.5) into the pre-chamber, which then ignited an ultra-lean mixture (λ = 2) in the main cylinder [22,23].
The detailed development process and characteristics of the PCSI system are thoroughly described in previously published review papers [22,23]; therefore, this paper will omit those details for brevity. The most successful representative example of a modern PCSI engine with a divided chamber (pre-chamber) is Honda’s Compound Vortex Controlled Combustion (CVCC) system, developed between 1968 and 1972 [24] and first introduced in the 1975 Honda Civic. This technology was innovative at the time as it met the suddenly stringent emission regulations of the California Air Resources Board without the need for a catalytic converter.
However, the CVCC system was not continuously applied to Honda cars for several reasons, such as advancements in emission control technology, cost and complexity, and the shift to direct fuel injection. As emission regulations became stricter, newer and more effective technologies were developed. Catalytic converters and advanced electronic fuel injection systems became standard, offering better performance, efficiency, and lower emissions compared to the CVCC system. Direct fuel injection systems provided better control over the combustion process, improving fuel efficiency and lower emissions. These systems became more prevalent in the automotive industry, replacing older technologies like CVCC. Additionally, emission standards continued to evolve, requiring more sophisticated and integrated approaches to meet the new requirements. The CVCC system, while effective in its time, could not keep up with the increasingly stringent regulations without significant modifications.
Pre-chamber combustion techniques have recently gained renewed attention as a critical technology for environmentally friendly, next-generation engine-based vehicles. This can be attributed to advancements in machining, production technologies, air/fuel ratio control techniques, and improvements in turbulence flow control both inside and outside the pre-chamber. These improvements have enhanced combustion stability under lean burn conditions and advanced knock control techniques. Furthermore, the development of combustion visualization techniques and chemiluminescence using Rapid Compression Expansion Machines (RCEMs), along with advancements in CFD analysis techniques, has significantly contributed to more detailed analysis and understanding of turbulent jet flame development and combustion characteristics.
This section presents a concise overview of the combustion strategies and principles employed in the PCSI engine, which has recently attracted significant interest.
This ignition strategy can be implemented in two main ways: active [25,26] (or scavenged) and passive (or unscavenged) systems [27,28,29]. Figure 1 schematically compares the operating principles of active and passive pre-chambers with those of a conventional SI engine.
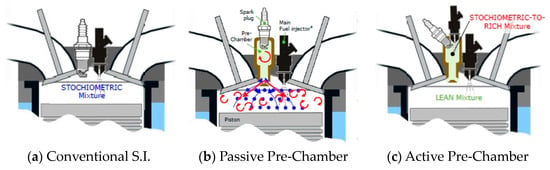
Figure 1.
The basics of pre-chamber combustion engine [30].
The active system features a dedicated fuel injector or a miniature check valve within the pre-chamber that does not allow the backflow of pressurized gases and combustion products from the pre-chamber to the fuel line, ensuring the air-to-fuel mixture remains optimal for combustion near stoichiometric conditions [31]. Hence, in an active, fueled PCSI system, an auxiliary fueling event occurs in the pre-chamber via an injector or check valve, forming a stoichiometric or fuel-rich mixture near the spark plug. In contrast, the passive system simplifies the design by excluding this secondary fuel injector, which lowers assembly and packaging costs, making it a viable option for passenger vehicles. Thus, fuel injection is performed solely in the main chamber, utilizing either port fuel injection (PFI) or direct injection (DI), ensuring an identical air/fuel ratio in both combustion chambers. The air–fuel mixture then flows into the pre-chamber through interconnection orifices. Consequently, the geometry of the pre-chamber and connecting pipelines plays a crucial role in the combustion process. Numerous studies have confirmed the importance of this ignition system over the past decade. Several studies examined the fundamental aspects of jet ignition using both experimental and simulation methods [32] and the effects of pre-chamber configuration on jet dynamics and combustion physics [33,34].
Recently, Benajes et al. [35,36] have assessed the synergies between pre-chamber ignition and other strategies aimed at enhancing engine thermal efficiency, such as lean burn and CO2-free fuel use, as well as hydrogen [37,38,39] and ammonia [36].
Furthermore, numerous studies have been conducted to optimize the geometry of the pre-chamber to maximize the effects of the turbulence–chemistry interaction caused by the shear stress of the flow through the holes. Numerous previous studies [14,39,40,41] investigated how nozzle diameter and pre-chamber volume influence combustion performance for this goal.
1.2. Review Objectives
Review papers on the performance enhancement and emission reduction effects of PCSI combustion engines, as well as EGR and lean burn limits, have been consistently published from 2010 to 2023 [2,22,42,43,44]. This indicates ongoing research and technological advancements in this field. Numerous studies have focused on improving the accuracy of CFD analysis techniques to numerically model the complex physical phenomena of PCSI engines more accurately.
Pre-chamber combustion techniques have recently gained renewed attention as a key technology for environmentally friendly, next-generation engine-based vehicles [42,44]. However, PCSI engines are strongly influenced by turbulence–chemistry interactions between the turbulent flame jet generated in the pre-chamber and the turbulent characteristics such as swirl and tumble within the main chamber [2,44]. Therefore, the optimal design of PCSI engines requires a thorough analysis and prediction of complex physical phenomena, including multi-mode combustion, optimization of the nozzle diameter and number, orifice length, shape, and volume of the pre-chamber, the stretching and quenching of the turbulent jet torch, the rapid changes in turbulence length scales, and the thermal mixing between the turbulent jet and lean mixture in the main chamber [2,43]. For this purpose, the utilization of three-dimensional computational fluid dynamics (CFDs) capable of simulating physicochemical processes in PCSI systems is essential. This study aims to review and analyze the technical achievements and limitations of CFD analysis techniques in PCSI engine research over the past 20 years and to discuss the prospects for future advancements in CFD technology.
This paper reviews the evolution and application of CFDs in PCSI engines, with a detailed look at the numerical modeling of the complex physicochemical processes involved in the PCSI ignition system and the contemporary issues regarding the limitations of commercial CFD codes. Finally, the prospects for future advancements in CFD technology are discussed. We explored the relevant literature in-depth using the Web of Science Core Collection, SAE Mobilus, and Google Scholar.
This paper is organized as follows: Section 2 presents the major achievements of CFD applications on PCSI engine design, focusing on optimizing geometric configurations and combustion characteristics within the pre-chamber. Section 3 provides an in-depth analysis of the CFD modeling techniques employed in PCSI engines, including the turbulence and combustion models used in the simulations. Section 4 discusses the interaction between turbulence and chemistry, emphasizing its impact on ignition, flame propagation, and overall combustion performance. Finally, Section 5 concludes this paper by summarizing key findings and suggesting prospects for future advancements in CFD technology for PCSI engines. Each section is thoroughly analyzed to provide a comprehensive understanding of the topics covered.
2. Major Achievements of CFD Applications on PCSI Engine Design
Since the early 2000s, research on PCSI using CFD simulation has primarily focused on optimizing the geometric configuration of the pre-chamber, including the nozzle diameter and number, orifice length, shape, and volume. Recently, these research themes have continued with the application of upgraded and more accurate numerical models. Figure 2 schematically illustrates these research topics utilizing CFDs. The research topics using CFDs can be summarized into two categories.
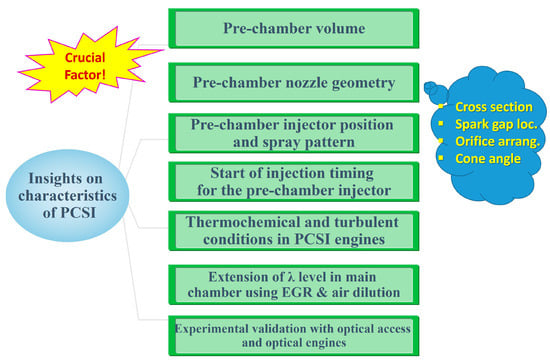
Figure 2.
Major topics previous and current literature for optimizing PCSI engines.
First, some articles [45,46] study the influence of pre-chamber volume and nozzle diameter on the resultant ignition characteristics using CFD simulation. The impact of the pre-chamber’s nozzle orifice diameter and, thereby, the total cross-sectional area of the nozzle orifices has been investigated several times. The effect of the orientation and number of nozzle orifices connecting the pre-chamber and the main combustion chamber, as well as the pre-chamber’s internal volume and shape, is evaluated.
Silva et al. [47] developed a CFDs model based on the Reynolds-Averaged Navier–Stokes (RANS) approach for a methane-fueled engine, incorporating a well-stirred reactor combustion model [30,31] along with a detailed methane oxidation mechanism. They investigated the effects of various geometric parameters of the passive pre-chamber, such as the throat diameter, nozzle length, and nozzle diameter, on the overall combustion characteristics. Model validation was performed by comparing pressure profiles in both the main chamber and pre-chamber under motoring conditions at 1200 rpm. The findings revealed that the throat diameter plays a crucial role in influencing pressure accumulation and residence time within the pre-chamber, while the nozzle diameter impacts both the peak pressure and residence time.
Distaso et al. [48] performed 3D CFD simulations on an active pre-chamber ignition system in a lean-burn methane engine, analyzing six phases of scavenging and combustion: filling & scavenging, mixing, flame propagation, ejection, reburning, and expulsion & extraction. Thelen et al. [49,50,51] conducted extensive CFD modeling of the TJI process. Their 3D CFD simulations, incorporating detailed combustion chemistry, investigated the effects of various orifice diameters (1.0 mm, 1.5 mm, 2.0 mm, and 3.0 mm). The findings indicated that a 1.5 mm orifice diameter provides the quickest ignition and overall combustion, based on pressure data, while a 1.0 mm orifice diameter results in higher jet velocity but a longer burn duration compared to larger diameters.
Secondly, using 3D CFD simulation, research has been conducted on the combustion characteristics within the pre-chamber, which cannot be measured experimentally, and the effects of the turbulent jet generated from the nozzle on the combustion characteristics and NOx emissions in the main chamber. Through these studies, various parametric studies have reported on the optimal geometry of the pre-chamber that can extend the lean limit of the main chamber. Recently, research has been published analyzing the turbulence–flame interaction caused by the hot turbulent jet and the turbulence (swirl and tumble) within the main chamber, along with the predictive limitations of related combustion models used in commercial CFD softwares. In addition, research utilizing optically accessible engines and engine-like geometries is focused on capturing the turbulence and mixture characteristics of hot turbulent jets from pre-chambers while replicating engine-relevant thermodynamic conditions [33,51]. Experiments conducted with rapid compression machines [52,53,54] equipped with generic pre-chamber geometries have provided valuable insights into combustion dynamics and the influence of nozzle size. The benefit of optical data compared to pressure-only data from traditional metal engines is that it offers additional validation opportunities for model development. By comparing key metrics such as jet exit timing, jet penetration velocity, and cyclic variations, simulations can be validated, enhancing our understanding of the phenomena occurring in the engine under similar conditions [32,55]. From a simulation standpoint, this involves using 0D models [11,56,57] to represent turbulence generation/dissipation, heat transfer, and combustion; 3D RANS calculations with level-set combustion models for industrial CFDs and design optimization [12,13,58,59,60,61,62,63,64,65,66]; Large Eddy Simulation (LES) for detailed analysis of mixing and combustion behavior [54,67]; and 2D/3D Direct Numerical Simulation (DNS) tools [32,54], which provide highly accurate data for studying fundamental phenomena and refining models. However, a physically accurate analytical model for PCSI combustion has not yet been developed [42,44,68]. So, uncertainties remain in understanding the combustion phenomena, as well as in the accuracy of turbulence and combustion models, especially concerning turbulence–flame interactions [44,68]. These aspects will be discussed in detail in the following sections. Recently, an experimental study has been conducted to optimize all previously researched pre-chamber shapes using Taguchi’s method, followed by redesigning to enhance performance [69].
3. CFD Modeling PCSI Engines
3.1. CFD Software
Developing user-friendly and feature-rich CFD software has greatly expanded its usage across different research fields. This section provides an overview of the significant achievements of CFDs in the PCSI engine over the past 30 years to assess the reasons for the increased usage of CFDs in recent years.
I reviewed various CFD software used for modeling the PCSI engines and the RCEM, as shown in Figure 3. Out of 61 studies [1,11,12,13,16,29,32,33,38,47,48,51,52,53,54,55,56,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100], one did not specify the CFD software employed by the researchers. Most of the remaining articles used the commercial software CONVERGE™ [70] for simulations. Other programs like STAR-CD™ [71], FIRE™ [72], and VECTICS [73] were used much less frequently. CFD codes that appeared in only one study were grouped into an ‘Others’ category, which includes two programs such as KIVA-V3 [74]. Some studies used open-source software and custom-built codes; three used OpenFOAM [75].
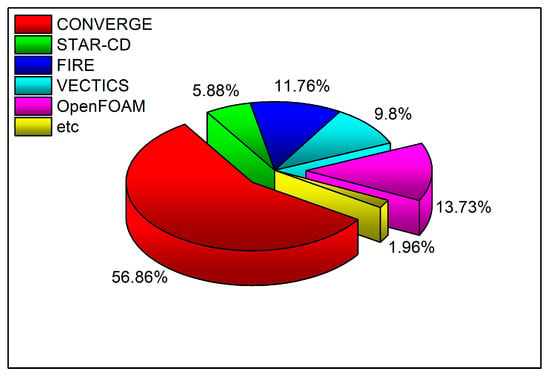
Figure 3.
Categorical distribution of the type of CFD software for simulating PCSI engines.
The selection of CFD software is primarily influenced by its capabilities, accessibility, and user preferences. Typically updated annually with enhanced features, commercial programs are adept at handling a broad spectrum of simulation tasks, as illustrated in Figure 3. Their user-friendly interfaces further improve their popularity by simplifying the simulation workflow. However, the substantial cost of licenses and limited customization options have driven some users towards open-source alternatives or the development of custom CFD codes. While utilizing these software tools has enhanced the accessibility of CFDs across more comprehensive users, it is imperative to acknowledge that mere accessibility is insufficient in addressing the challenges outlined in PCSI engines, as detailed earlier. The following sections discuss four critical focal points investigated to overcome these challenges. These include the distinctive features and comparative analysis of LES and Reynolds-averaged Navier–Stokes (RANS) models, the establishment of appropriate inflow and outflow boundary conditions, multi-mode combustion models, wall heat transfer, turbulence–chemistry interaction, rigorous verification and validation processes, and development of best practice guidelines in the field.
3.2. Turbulence Models
In computational fluid dynamics (CFDs), turbulence modeling can generally be divided into direct numerical simulation (DNS) [101], LES [102,103], and the Reynolds-averaged Navier–Stokes (RANS) model. Due to the challenges of applying DNS to real-world engineering problems, especially in automotive engineering, LES and the RANS model are more frequently utilized.
Turbulence models, especially simpler ones like RANS models, often struggle to accurately predict not only flow separation and reattachment, which are critical in engine intake and exhaust processes, but also the turbulence length scale, which is crucial for determining not only the rate of energy dissipation and mixing efficiency in engine flows but also combustion processes.
Moreover, the flow fields encountered in PCSI engines are highly complex, involving phenomena such as impinging flows, jet-like flow, flow separation, strong swirl, large variable turbulent length scale, and vortex shedding (refer to Section 2). Accurately and universally modeling all these turbulent flow characteristics remains a formidable challenge.
As shown in Figure 4, in the analysis of 52 publications reviewed, 52.8% of studies relied solely on the RNG k-ε turbulence model [103,104,105,106], while 11.91% of studies opted for LES alone. Moreover, 7.14% of studies integrated both LES and RANS models in their research. Common RANS turbulence models cited were standard k-ε, renormalization group (RNG) k-ε, and shear stress transport (SST) k-ω [106,107]. Sub-grid scale models for LES included Smagorinsky [107,108] only.
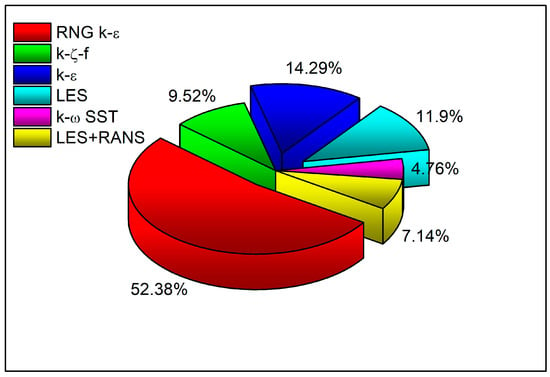
Figure 4.
Categorical distribution of type of turbulence for simulating PCSI engines.
3.2.1. RANS Turbulence Models
The RANS-type turbulence models are simple, computationally inexpensive, and economical [102,107].
Hence, given its simplicity and shorter computation time, the RANS-based model, which represents the average behavior of essential, is typically chosen over the LES model. However, the RANS-type k- ε turbulence models are based on Boussinesq’s isotropic eddy viscosity assumptions, and it is well known that they have several problems with deteriorated prediction performance in cases of swirling flow, separation, and reattached flow and flows with large rapid extra strains. Therefore, numerous k-ε model variants have been researched and reported and are currently used to overcome these challenges [104,105]. Numerous k-ε model variants exist due to the ε equation with 3–4 model coefficients, which are empirically derived or determined through ad-hoc methods based on various turbulent flow patterns [103,105,106,109]. Additionally, turbulent flows can vary significantly in their characteristics depending on the geometry, flow velocity, pressure gradients, and other factors. To accurately capture these diverse turbulent flow patterns, modifications to the standard k-epsilon model, particularly in the ε equation, are necessary [104,105]. Each variant attempts to address specific deficiencies of the standard model in certain flow regimes, such as free shear flows, boundary layers, or rotating flows. Consequently, a universally accurate RANS-type turbulence model has not yet been achieved. Therefore, engineers face the challenge of selecting a turbulence model that is appropriate for the specific turbulent flow characteristics of the geometry of interest.
The RNG (Re-Normalization Group) k-ε model [103], which is the most frequently adopted in previous studies for PCSI systems for various engine types [104,105,106], is one of the variations of the standard k-ε model used for turbulence modeling in various kinds of CFD simulations. It incorporates additional terms that account for the interaction between turbulence and mean strain rate, which is not present in the standard k-ε model, and modifications to the standard k-ε model to improve accuracy for certain flow conditions, particularly for swirling and highly strained flows. To achieve this goal, this model contains a strain-dependent correction term in the constant C1ε of the production term in the RNG k-ε model’s dissipation rate (ε) equation [103,104,105]. The RNG k-ε model is beneficial for simulations involving complex flow features such as swirling flows, recirculating flows, and flows with high strain rates, making it suitable for jet-like flows and complex industrial applications in which the velocity gradients are significant, causing intense mixing and variations in velocity [70,104,105]. In PCSI internal combustion engines, the scavenging processes in the pre-chamber, along with turbulent flame jets and combustion, create regions of high strain rates. Turbulent jets from pre-chamber nozzles are typical examples of flows with high strain rates. Therefore, for these reasons, applying the RNG k-ε model to PCSI engines extensively is considered practical for engine simulation, as it provides a good balance between accuracy and computational efficiency. However, a noteworthy demerit of the RNG k-ε model is the fact that near-wall treatment of this model can struggle with accurately predicting flows close to walls, particularly in cases involving adverse pressure gradients or separation [70,104,105,109,110,111]. Hence, one should be careful to use the k-ε model if the turbulent jet interacts significantly with cylinder walls or piston head surface. Additionally, it is clear that the RNG k-ε model is less accurate for detailed structures and does not capture the detailed eddy structures as well as LES [101,103,104,105].
After the RNG model, the k-ζ-f turbulence model [109,110,111] is the second most commonly used turbulence model in PCSI engine CFDs simulation. The k-ζ-f model is an extension of the eddy-viscosity concept. It includes three transport equations for turbulence quantities, namely turbulent kinetic energy (k), Turbulence Frequency (ζ), and Dissipation Rate (f). This is the turbulence model in previous studies due to its high accuracy and convergence stability. This model, optimized from Durbin’s near-wall turbulence closure model [112,113], is a variant of RSM (Reynolds Stress Model) turbulence models [112,113,114]. The k-ζ-f model benefits complex flow simulations with significant near-wall effects and flow separation [105,109]. It enhances the standard k-ε turbulence model by introducing the wall-normal velocity fluctuation v2 and its source term f, which incorporate near-wall turbulence anisotropy and non-local pressure-strain effects. The careful introduction of these relaxation terms eliminates the need for damping functions. Additionally, this model improves numerical stability over the original v2-f model by solving a transport equation for the velocity scale ratio ζ = v2/k instead of the velocity scale v2. Moreover, this model demonstrates superior predictive accuracy in heat transfer, surface friction at low Reynolds numbers, adverse pressure gradients, and recirculation regions compared to traditional k-ε turbulence models [115,116]. While it shares characteristics with low-Reynolds-number models, it uniquely eliminates the need for wall functions by being applicable near the wall. It introduces a transport mechanism for turbulent energy from the wall, effectively representing near-wall viscous damping effects through an elliptic relaxation equation [109,110,111]. Hence, this model may offer superior performance in capturing the detailed flow features and interactions in the intake and exhaust processes and the scavenging process inside the pre-chamber, which is crucial for predicting flame propagation, heat transfer, and emissions. Its improved near-wall treatment is advantageous for accurately predicting heat transfer inside orifices of pre-chamber and flow separation around valves and ports.
3.2.2. LES Turbulence Model
Due to the substantial turbulent energy and significant influence on momentum transfer and turbulent mixing carried by large eddies, LES methodologies offer superior accuracy compared to RANS turbulence models [117]. LES captures flow structures from the domain scale down to the filter scale, necessitating the significant resolution of high-frequency turbulent fluctuations. This requires using high-order numerical methods or acceptable grid resolution when employing lower-order numerical techniques. Therefore, implementing LES methods in automotive and mechanical engineering necessitates finely resolved grids with grid points positioned close to the boundary layers. This results in significantly heightened computational costs compared to Reynolds-Averaged Navier–Stokes (RANS) methods [118]. Consequently, previous studies have reported only a limited number of simulations utilizing LES, with the majority being conducted on Rapid Compression Machines (RCEMs) [33,54] rather than on full-scale metal engines [67].
Recently, 3D CFD analysis using LES turbulence models was performed to investigate the engine characteristics of active and passive PCSI engines fueled by natural gas for large ships under a single operating condition, both at stoichiometric and lean conditions (λ = 2). Additionally, the heat release rate curves obtained from the analysis were compared with experimental results [67]. However, to perform accurate CFD simulations of PCSI engines using the LES turbulence model, it is necessary to understand the limitations and characteristics of various sub-models.
The most crucial noteworthy point is that the accuracy of LES heavily relies on the Sub-grid Scale (SGS) models used to represent the unresolved scales. This is because the computational grid limits the size of eddies that can be physically expressed. Despite their presence in the flow field, these eddies cannot be resolved because the CFD mesh lacks the resolution to capture and depict them accurately in CFD simulations. We are mainly concerned with the eddies larger than the mesh size in LES. These eddies are too large to be broken down by molecular viscosity; therefore, we need to find a way to model and remove these eddies from the grid. The turbulent kinetic energy predicted in our LES will be too high if we do not. These eddies are removed by applying an additional stress term to the Navier–Stokes equations, known as the sub-grid scale (SGS) stress. While various SGS models such as the Smagorinsky model [107], dynamic Smagorinsky model [71,72], WALE model [119], and others are available, none are universally applicable to all types of flows, leading to potential inaccuracies in specific scenarios. Different SGS models provide various methods for calculating the sub-grid kinematic viscosity, . The sub-grid kinematic viscosity is calculated using Equation (1) provided below:
where, Sij is the strain rate of the resolved eddies on the CFD mesh and Δ is the length scale or grid filter width.
One of the shortcomings of the Smagorinsky Sub-grid Scale model, which is the most frequently adopted in CFD simulations of PCSI combustion, is that it includes model constant Cs called the Smagorinsky coefficient that is not universal and depends on the local flow conditions and the fraction of the cell size that gives the sub-grid length scale. Cs for homogeneous isotropic turbulence is around 0.17. This value is crucial for accurate simulation and comes from an analytical mathematical derivation based on homogeneous isotropic turbulence. It is noted that modern CFD codes use different values of Cs. In STAR-CD [71], Fire [72], Fluent [120], Cs = 0.1, whereas in PHOENICS [121], Cs = 0.17. However, no matter what Cs’ values are, this is not true in the case of rotation or near the wall because of too much dissipation near the wall. Additionally, in the Smagorinsky model, sub-grid stress is not damped close to the wall. Hence, some modification to the model is needed. Therefore, various types of sub-grid scale models have been developed. The most frequently used near-wall treatment of the Smagorinsky model is the Van Driest damping function, which is a damping function for proper results in wall-bounded flows [71,72,120]. Figure 5 illustrates the necessary adjustments to the Smagorinsky model for accurate near-wall treatment. To address this, the sub-grid scale stress should ideally approach zero as the wall is approached. This can be achieved through various methods. One option is to implement a different model, such as one based on sub-grid scale kinetic energy, replacing the traditional Smagorinsky model. Alternatively, we can modify the length scale near the wall, reducing it to zero to account for sub-grid scale eddies. Another approach is to adjust the velocity scale, making it less dependent on strain rate. The primary goal of these adjustments is to decrease the sub-grid kinematic viscosity near the wall, reducing the sub-grid scale stress and effectively simulating the damping effects on the eddies.
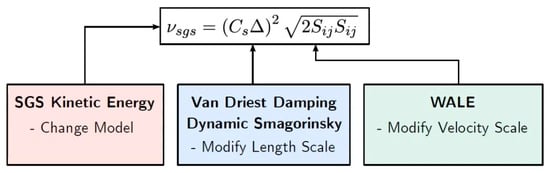
Figure 5.
Schematic diagram of different options for correcting νsgs near the wall [108].
Instead of single user-defined constant Cs, modern CFD codes like Fire and STAR-CD implemented the Dynamic Smagorinsky Sub-grid Scale model [122,123]. This model computes a local time-varying Cs value by test-filtering the flow field at a length scale greater than the grid length scale, which allows it to compute the correct result for wall-bounded flows without the use of damping functions.
The Wall-Adapting Local-Eddy Viscosity (WALE) Sub-grid Scale model [124] is a more advanced sub-grid-scale approach that incorporates an innovative form of the velocity gradient tensor in its formulation and is widely utilized in CFD platforms such as STAR-CCM+ and OpenFOAM [75,125]. Like the Smagorinsky Sub-grid Scale model, it faces the limitation that the model coefficient Cw is not a universal constant. However, it has been observed that the WALE model is generally less sensitive to variations in this coefficient compared to the Smagorinsky model. Another key advantage of the WALE model is that it does not require additional near-wall damping, as it inherently provides accurate scaling near wall boundaries [124].
Figure 5 schematically shows various options for correcting sub-grid scale kinematic viscosity near the wall. Here, Sij is the strain rate of the resolved eddies on the CFD mesh.
Additionally, a Coherent Structure Model (CSM) as a sub-grid-scale model is applied [59,67] and adopted in the Fire Code [72]. It is reported that the CSM gives good predictions and performs almost the same as the dynamic Smagorinsky model for various complex geometries [119].
Additionally, applying appropriate boundary conditions for LES is complex. Inflow boundary conditions, in particular, must accurately represent turbulent fluctuations, which is challenging to achieve in practice. Due to the factors above, achieving dependable LES simulations necessitates more expertise and experience than the requirements for utilizing the RANS model [125].
Bolla et al. [52,54] executed numerical studies of RANS-LES comparison using an RCEM to analyze an automotive-sized scavenged pre-chamber, aiming to compare the two turbulence models’ ability to predict turbulence and fuel-air mixing. This study used a Smagorinsky-type sub-grid scale model [126] to compute the unresolved turbulent scales for the LES turbulence model. In contrast, the RANS turbulence model employed the time scale Bounded k-ε Turbulence Model in VECTIS, an enhanced version of the standard k-ε model for high strain rates or strong adverse pressure gradients [73]. The outcomes indicated that the RANS-based model could effectively reproduce the key ensemble-averaged flow patterns seen in LES for two pre-chamber setups. However, RANS often falls short in accurately capturing the radial fuel-air mixing compared to LES.
3.3. Physical Phenomena and Combustion Models of PCSI Engines
The most commonly used combustion models for engine simulations are based on the flamelet combustion regime, particularly for spark-ignition (S.I.) engines. In this regime, turbulence can distort and increase the surface area of the flame front while maintaining its inner laminar structure and flame speed. This condition is characterized by a Damköhler number (Da) greater than 1 and a Karlovitz number (Ka) less than 1.
Numerous previous studies [17,25,29,44,124,127,128,129,130,131,132] have investigated the operating mechanisms of TJI in PCSI engines, which are schematically illustrated in Figure 6. The characteristics of TJI can be categorized into enrichment, thermal effects, and chemical effects. As shown in Figure 6a, fundamental heat transfer phenomena during flame propagation include thermal quenching, which occurs due to rapid heat transfer to solid surfaces as the flame passes through the nozzle, and hydrodynamic quenching, which happens when the flame mixes with the cool, lean mixture as it enters the main chamber. For a detailed explanation of TJI, please refer to the referenced literature [44]. Recent studies [93,124,128,129,130,131,132] have validated that the two-stage combustion process in the main chamber is comprised of a jet-dominant phase and controlled mixing, which is influenced by the combustion intensity within the pre-chamber, and a flame propagation phase, which depends on the reactivity of the mixture in the main chamber driven by the in-cylinder bulk flow and the associated turbulence.
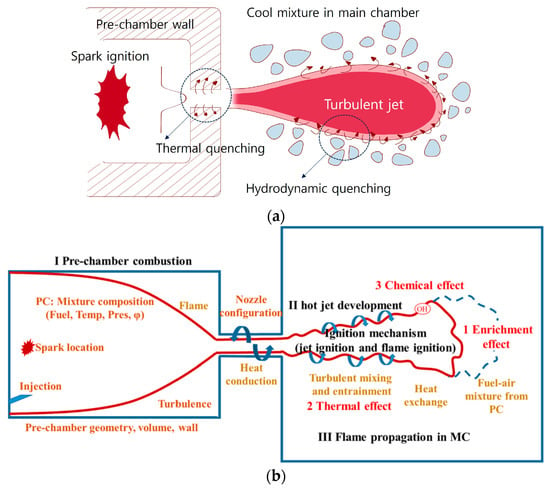
Figure 6.
Schematic diagram of (a) quenching and (b) overview of turbulent jet ignition process [44].
As described above, capturing the flame dynamics across the pre-chamber nozzles is a significant challenge due to the complexity of flame propagation through the orifices [133]. Most previous premixed combustion models were based on the corrugated flame zone; however, recent studies have demonstrated that PCSI engines operate at highly diluted conditions, which approach the thickened flame regime. Consequently, flamelet-based combustion models, conventionally used for SI engine combustion analysis, are unsuitable for application in PCSI engines operating under these ultra-lean conditions. These models fail to capture the combustion behavior of flame quenching and stretching through the orifices, potentially shortening ignition delays in the main chamber [105].
In the studies conducted thus far on 3D CFD combustion analysis of PCSI engines, the combustion models applied have been flamelet-based premixed combustion models originally used for premixed combustion in homogeneously operated spark-ignition engines. However, the PCSI engines operate under very lean conditions (λ > 2) and in high Karlovitz number (Ka > 1) regimes due to the presence of turbulent jets and turbocharging, which result in extremely high turbulence intensities. Therefore, to accurately predict the combustion characteristics of PCSI engines, a combustion model must effectively capture multiple and distributed ignition points within the main chamber, covering both premixed and partially premixed combustion regimes. Furthermore, under the typical operating conditions of TJI systems, characterized by lean mixtures and highly turbulent flow fields, the foundational assumptions of flamelet-based models may no longer be applicable [64]. Therefore, recent studies have raised questions about the predictive performance of flamelet-based combustion models and have made significant efforts to find countermeasures. In this section, we discuss the application cases, comparative predictive performance, and limitations of combustion models that have been applied to the combustion analysis of PCSI engines. Additionally, we review various methods to enhance predictive performance and overcome the limitations of flamelet-based models.
3.3.1. Flamelet Assumption
As mentioned above, combustion models for PCSI engines are often based on the so-called flamelet assumption [70,71,72,73,132,134], which has frequently been adopted for premixed combustion in homogeneously operated spark-ignition engines [134]. The combustion models based on flamelet assumption simplify the complex interactions between turbulence and chemical reactions by assuming that the flame can be represented as an ensemble of thin, locally laminar flame structures, or “flamelets”, embedded within the turbulent flow. They assume a clear separation of scales between the turbulent eddies and the flame thickness. This allows the detailed chemical reactions to be precomputed and stored in a database, which can be accessed during the simulation. The chemical reactions are solved in a laminar flame configuration under temperature, pressure, and mixture composition conditions. The results are stored in flamelet libraries, which provide information about species concentrations, temperatures, and reaction rates as functions of mixture fraction and scalar dissipation rate.
In summary, flamelet models balance accuracy and computational cost, making them suitable for capturing the essential features of premixed combustion in S.I. engines. However, it is necessary to recognize their limitations, especially when dealing with non-premixed or partially premixed combustion regimes. Researchers continue to refine these models and explore more detailed approaches to improve engine combustion simulations.
3.3.2. G-Equation Model
A flamelet-based combustion model, the G-equation, is one of the widely adopted combustion models for simulating the combustion processes of PCSI engines in CFD simulations within the engine modeling community. This approach utilizes a level-set method, representing moving interfaces or boundaries on a fixed computational mesh. It is beneficial for problems where the computational domain is divided into two regions separated by an interface. The level-set modeling technique allows the fluid–fluid interface to move within any given velocity field [1,135,136]. Extensive details on the G-equation model are available in the literature [38,52,53,54,58,60,63,65,82,89,91,95], with only a brief summary provided here. To ensure consistency with the commonly used Favre averaging method in premixed turbulent combustion, the G function and the velocity vector v are decomposed into Favre-averaged components and their corresponding fluctuations. By applying several closure assumptions as outlined by Peters [4], the governing equations are derived, as both the Favre-averaged G function and its variance are defined [137]. To solve the equation, a model for turbulent flame speed is required. The turbulent flame speed is a crucial parameter typically modeled as a function of the laminar flame speed and turbulence characteristics such as turbulent intensity and length scales. This allows the model to incorporate the effects of turbulence on flame propagation without directly solving the detailed turbulence–chemistry interactions.
Within the context of the G-equation, several correlations for turbulent burning velocity from the literature [4,72] have been presented and evaluated in previous studies [138]. Among the most popular is Peters’s correlation [139], shown in Equation (2), valid for both large-scale and small-scale turbulence.
where SL is laminar flame speed, u’ is the fluctuating turbulent component, δL is the laminar flame thickness, is the integral length scale, b1 and b3 are the model constants corresponding to large and small-scale turbulence enhancement, respectively, and Da is the Damkohler number, which is a ratio between the flow time scale ( over the chemical time scale (
The laminar flame speed, SL, depends upon the local pressure, the fresh gas temperature, the local unburned fuel/air equivalence ratio using the Metghalchi and Keck correlation [95,96], and the chemical time arising due to the flame stretching [72,136,138,139,140]. These common correlations for SL are equations derived from fitting forms based on combustion experiments conducted over various temperature and pressure ranges. Therefore, outside the range of these correlations, the SL is calculated using extrapolation methods, which inherently introduce relevant input errors into any combustion model.
Another way to get SL is to use tabulated values, which were created based on the 30-species skeletal mechanism developed by Lu and Law [91].
The laminar flame thickness is determined by analyzing the temperature gradient along the flame front’s normal direction and by using the chemical time. The chemical time is derived from the characteristic time of the laminar flame, which is calculated using the Zeldovich Number, a parameter that depends on the activation energy of the fuel oxidation process.
3.3.3. The Extended Coherent Flame Model (ECFM)
The Extended Coherent Flame Model (ECFM) [72,136] builds upon the basic principles of the Coherent Flame Model (CFM) by incorporating additional features to handle more complex combustion scenarios, which focus on turbulence and flame interaction and includes detailed modeling of how turbulent eddies affect flame stretch and flamelet behavior. This involves correcting for the effects of turbulence on flame stretch, considering the turbulence intensity, and adjusting for the curvature and thermal expansion of flamelets [141]. Thus, the flame stretch is influenced by turbulence and the ratios of turbulent to laminar flame velocities and lengths. It is adjusted for curvature and thermal expansion effects caused by laminar combustion in flamelets based on the assumption of isotropic flame distribution [72].
The model calculates the rate of fuel consumption based on the flame surface density (FSD) and the reaction rate per unit flame surface area.
In the case of the coherent flame model, flame surface area per unit volume is defined as follows:
Using flamelet assumption, the mean turbulent reaction rate is computed as the product of the flame surface density Σ and the laminar burning velocity SL as follows:
In this, ωL is the mean laminar fuel consumption rate per unit surface along the flame front, ρfu,fr the partial fuel density of the fresh gas, ρ is the density of the fresh gas, and yfu,fr is the fuel mass fraction in the fresh gas.
When combustion starts, several new terms have to be computed. Among them are source terms and two quantities for Equation (2): Σ and SL.
The first term of the left-hand side is the time-dependent component, and the second term is the convective transport of the FSD. The first term of the right-hand side is the source term, which represents the production of flame surface density that comes essentially from the turbulent net flame stretch; the second term is the sink term, which represents the quenching effect referring to the local extinction or reduction of the flame surface density due to unfavorable conditions, such as excessive strain, heat loss, or insufficient reactants. Hence, the FSD transport equation incorporates these effects into a combined source term, SΣ, which includes both the creation and destruction mechanisms:
where Sother represents additional source terms that might be relevant depending on the specific combustion scenario.
SΣ = Sproduction − Sdestruction = Sstretch + Squenching + Sother
This approach allows for detailed tracking of how turbulence affects the flame surface and, consequently, the combustion process.
Recently, the ECFM-3Z model has been extensively adopted for 3D CFD analysis of PCSI engines using AVL’s Fire CFD code [72]. The ECFM-3Z model is an extension of the ECFM combustion model based on the FSD transport equation and mixing model that can describe premixed inhomogeneous turbulence and diffusion combustion and operates within three distinct zones or regions: fuel, air, and the air–fuel mixture. In this model, the fuel can be represented as a mixture of various components. Both the burnt and unburnt gases are categorized into these three zones.
The extent of mixing among these zones is determined using a characteristic time scale, which is computed based on the k-zeta-f turbulence model [1,58,79,80]. The ECFM-3Z model assumes that the composition of unburnt gases, including air and Exhaust Gas Recirculation (EGR), remains consistent across mixed and unmixed zones. The properties of the burnt gases are calculated based on the reaction progress variable.
In conclusion, this combustion model focuses on flame propagation and the interaction between turbulent flow and flame while utilizing simplified global kinetics for chemical kinetics.
3.3.4. The Multizone Well-Stirred Reactor (MZ-WSR) Model
A homogeneous reactor-type combustion model, MZ-WSR [88], operates on the premise that sharp gradients in temperature and density are unlikely to occur within a cell and models combustion as an ignition-based phenomenon. This model divides the reactor into several well-mixed zones, each assumed to be perfectly mixed with a uniform composition. Additionally, chemical reactions are thought to occur instantaneously within each zone. The governing equation of the MZ-WSR combustion model can be represented as follows:
where γ is the multiplier, Yi is the mass fraction of species i, the reaction rate of species i, is the mass flow rate, and is the mass fraction of species i in the inflow.
The MZ-WSR model, coupled with detailed kinetic calculations, is particularly suitable for modeling the jet ignition process. Therefore, most of the studies [13,38,47,61,62,63,64,66,90,91] investigating the PCSI system using WSR models have considered detailed chemical mechanisms derived from GRI Mech 3.0 by Lu and Law [142] by utilizing the integrated chemistry solver known as SAGE [13,88,143], which is included in the commercial code CONVERGE [70]. However, the use of the SAGE model for combustion involves considerable simplification. In the simulations, turbulence models are not applied to the mean chemical production terms in the governing equations. This means the potential impacts of turbulent fluctuations on these terms are not accounted for in the simulations. It should be noted that the influence of turbulence, as modeled using the RANS k-ɛ turbulence approach discussed earlier, is applied exclusively to the transport equations of mass, energy, and momentum in the averaged equations. Prior numerical investigation into the jet ignition process [143] demonstrated that the WSR assumption could produce cooler temperatures in cells with thin flamelets. This issue can become more pronounced in ultra-lean mixtures. Recently, several papers [63,64] have evaluated the prediction performance of this model by comparing it with the G-equation model for the combustion processes in passive [64] and active PCSI engines [63] fueled by natural gas. This literature showed that the MZ-WSR model predicts faster combustion rates in the main chamber than the G-equation model, which fails to match the pre-chamber combustion phase correctly. However, this model’s prediction of the combustion rate in the main chamber matched well with the experimental results. The MZ-WSR model requires that each cell be treated as an individual well-stirred reactor. For this to be accurate, the characteristic time of the turbulence in the cell must be significantly smaller than the characteristic time of the combustion chemistry. In other words, the Damköhler number must be much less than 1 to assume a well-stirred reaction. Therefore, in the case of PCSI combustion, where lean and highly heterogeneous turbulent flows exist, this model can result in significant errors.
Despite its limitations, this model has been extensively used to analyze the combustion processes of PCSI engines within the RANS framework up to the present [26,27]. This is because the MZ-WSR model excels in providing a detailed and chemically accurate representation of combustion processes and allows for more flexibility in adjusting the model to account for different fuels such as natural gas [27,28] and gasoline [26] and dual-fuel combustion conditions [16,31,37] due to its detailed chemical kinetics. This makes it particularly useful for research and development where precise emission predictions and understanding of combustion chemistry are crucial. The experimental validation of this model was conducted using in-cylinder pressure and heat release profiles, and it demonstrated good predictive accuracy for both pressure and the combustion process within the range of 1.6 < λ < 2. [13,88,143].
Recently, when the G-equation has been utilized, the MZ-WSR model is integrated before, during, and after the flame front to calculate the intermediate and post-reaction species instead of using simplified global kinetics [64,65,91]. However, its effects have not been quantitatively proven.
3.4. Turbulence–Chemistry Interaction
The interaction between turbulence and chemistry-related quantities is crucial in determining the combustion characteristics of PCSI applications, such as ignition, flame propagation speed in both the pre-chamber and main chamber and burn rate trends. Namely, combustion and turbulent flow are affected by each other within the turbulent reactive flow. Compared to traditional SI engines, the turbulent flow field in PCSI systems is highly inhomogeneous, exhibits large spatial gradients at the jet boundaries, and undergoes rapid temporal evolution. One of the key factors distinguishing the flame evolution in PCSI systems from conventional SI engines is the high level of turbulent fluctuation near the spark plug, driven by jet-to-jet interaction during the scavenging process. This is because this high level of turbulence level makes the flame behavior clearly not isotropic [144]. As the flame front moves through a turbulent flow, it is influenced by both large and small eddies. The larger eddies, which are much bigger than the thickness of a laminar flame, primarily cause the flame to wrinkle and distort. Meanwhile, the smaller eddies are capable of penetrating the flame front, allowing them to directly interact with the combustion chemistry. This interaction enhances turbulent mixing and amplifies diffusive processes within the flame. However, from a macroscopic point of view, the main effect of turbulence on the flame is to increase the propagation speed [145].
Previous literature utilized the source terms of combustion models developed for pre-mixed or non-premixed conventional gasoline S.I. engines to simulate these complex turbulence–chemistry interactions, such as the ECFM-3Z and G-equation models. These models differ in their approaches to representing turbulence–chemistry interactions, leading to variations in calculated laminar flame speeds, turbulence intensities, and spatiotemporal scales. As a result, they produce different turbulent flame speeds, which significantly impact engine output, fuel consumption, and pollutant formation. The predictive accuracy of these models hinges on their ability to accurately calculate turbulent flame speed.
The G-equation model calculates turbulent flame speed using explicit correlations, while the ECFM-3Z model derives it from the Flame Surface Density (FSD) equation. Differences in the velocity scale ratio ( and length scale ratio ( during combustion, as illustrated in the Borghi–Peters diagram, highlight the distinct approaches these models take in handling the flame brush, particularly in terms of the spatial distribution of the reaction volume. These differences are primarily due to varying turbulence intensities and scales, which affect mean turbulence–flame interaction.
Figure 7 analyzes the behavior of the velocity scale ratio and length scale ratio on the Borghi–Peters diagram for the two combustion models previously discussed under the operating conditions of a GDI engine at 2000 rpm and stoichiometric conditions [132]. As shown in the figure, the ECFM-3Z model indicates that, except for the initial combustion phase, the combustion predominantly falls within the corrugated flamelet regime. In contrast, for the G-equation model using four different turbulent flame speed correlations, most of the combustion is observed to occur within the stirred reaction regime and thin reaction regime. The variation in combustion traces between these models is attributed to the different treatments of the flame brush by each model. This result underscores the significance of turbulence–flame interaction as a critical factor in determining the combustion characteristics in engine analysis. Furthermore, it suggests that the current flamelet-based combustion models may introduce significant errors in the analysis of PCSI engines.
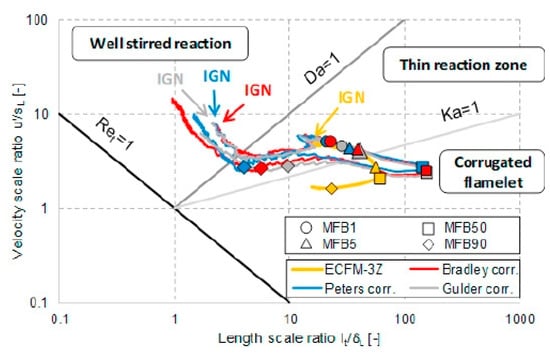
Figure 7.
Flame evolution on the Borghi–Peters diagram using ECFM-3Z and G-equation with three different turbulent flame speed correlations [132].
As shown in Figure 7, the flamelet-based combustion models exhibit significant differences in turbulence–flame interactions during the combustion process. However, when compared to experimental ensemble-averaged in-cylinder pressure and burn rate traces, these differences are not substantial. Figure 8 illustrates a comparison between pressure traces (left) and heat release rate curves (right) from experiments and various combustion models under the same engine and operating conditions as Figure 7. From an engineering perspective, the results demonstrate overall good agreement with the experimental ensemble averages.
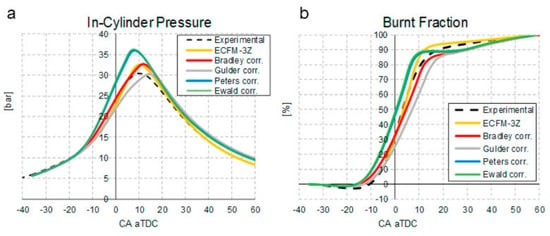
Figure 8.
Experimental validation of (a) averaged pressure trace and (b) burn rate trend [132].
The FSD transport equation includes source and sink terms accounting for stretching and quenching effects, which are crucial for accurately modeling the dynamic behavior of the flame front in both laminar and turbulent combustion conditions. By incorporating these effects, the FSD equation comprehensively describes flame surface evolution, which is essential for predicting combustion performance and stability. As illustrated in Equation (6), the stretching effect accounts for the deformation of the flame surface due to the flow field, influenced by both laminar and turbulent strain rates. In turbulent flows, this term can be complex, involving contributions from large-scale and small-scale turbulent eddies stretching.
To simulate stretching and quenching conditions in term SΣ of Equation (7), the intermittent turbulent net flame stretches (ITNFS) model [141] is utilized. The ITNFS model characterizes the interaction between a single vortex and the flame front, extrapolating this interaction to represent the complete turbulent flow. It assumes that each turbulence scale influences the flame independently, with no interaction between different turbulence scales, allowing for the overall effects of turbulent fluctuations to be predicted from the behavior of individual scales in the unburned gas mixture, as shown in Figure 9.
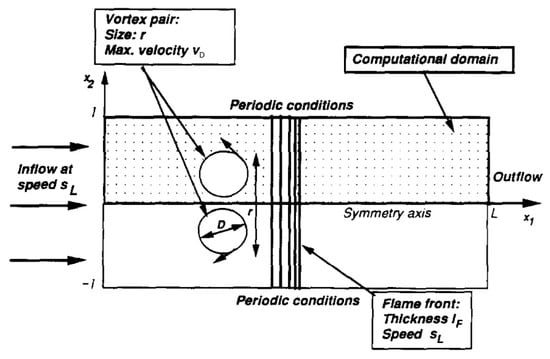
Figure 9.
Configuration of flame vortex interaction [141,145].
By applying this model to a complete turbulent flow, it is assumed that the cumulative effect of all turbulent fluctuations can be inferred from the behavior of each scale. The limitation of this model is that it cannot account for vortex interactions. It is clear that this model has limitations when applied to PCSI engines, where strong turbulence intensity is distributed near the flame front of the hot turbulent jet and highly inhomogeneous turbulence exists. The production of flame surface density primarily results from the net flame stretch due to turbulence. This flame stretch is expressed as the large-scale characteristic strain (ε/k), adjusted by a function Ct, which considers the size of turbulence scales and viscous and transient effects [146]. Ct depends on turbulence parameters and the properties of the laminar flame. Hence, the right-hand side of Equation (4) can be expressed as follows:
Here,
Kt is a critical property since it influences the source term for the flame surface and, therefore, the mean turbulent reaction rate. The coefficient α is the stretching factor, and β in Equation (8) is the arbitrary tuning constant used in ECFM.
However, it is important to better understand the contexts in which the ITNFS model can be effectively applied and where additional considerations or alternative models may be necessary. This is particularly due to the lack of consideration for nonlinear effects in the interaction of turbulence scales with the flame front, flame-generated turbulence, and the reignition of fresh gases crossing a locally quenched flame front [141].
Several previous studies [11,12,135,145,147] have reported the average turbulence–flame interaction experienced by engine flames in PCSI engines and recently developed highly downsized engines on the Borghi–Peters diagram, confirming the occurrence of multiple regimes during S.I. combustion. The results of these studies emphasize the necessity for combustion models to be predictive across all potential combustion regimes [135,141,147]. The high turbulence levels generated by the pre-chamber (PC), combined with the reduction in laminar flame speed due to dilution, significantly impact the combustion regime of PC-initiated combustion systems. These interactions are illustrated in the schematic Borghi diagram in Figure 10 and Figure 11, where the Karlovitz (Ka) and Damköhler (Da) numbers are used to compare relevant timescales of turbulent combustion to determine the combustion regime. Consequently, the PC-initiated jet ignition combustion regime shifts into the thin reaction zone, bringing it closer to the stability limits.
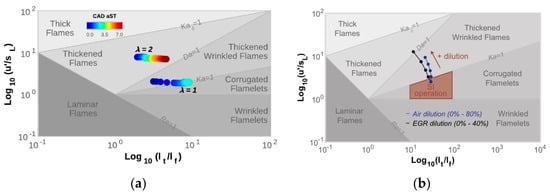
Figure 10.
Evolution of the flame regime for (a) various air-fuel ratios and (b) dilution ratios as the pre-chamber combustion progresses [11,12].
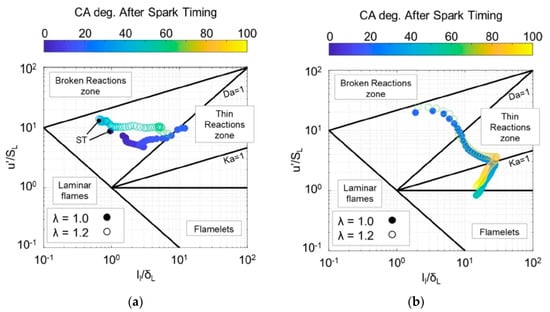
Figure 11.
Evolution of the flame regions during pre-chamber (a) and main chamber (b) from spark timing to the hot gas ejection in the main chamber (a); from the start of main chamber combustion to MFB90 (b) [61].
The two figures below are based on the same passive PCSI engine with a port fuel injection system in a gasoline engine. Figure 10a shows the progression of the combustion region at 2000 rpm on the Borghi–Peters diagram for λ = 1 and λ = 2 cases [12]. Figure 10b illustrates the change in the flame structure during the combustion period at 4500 rpm by increasing the air/fuel ratio using air and EGR [11]. From these results, it is clear that lean combustion shifts the combustion characteristics to the thickened flame regime. As is well known, this occurs because the eddies become smaller than the flame thickness, allowing some eddies to penetrate the pre-heat zone of the flame. Another vital piece of information evident from Figure 10b is that EGR dilution exhibits higher sensitivity than air dilution [11,12].
Recently, the gasoline-fueled, passive, pre-chamber engine has been numerically modeled using the RNG k-ε turbulence model and MZ-WSR with the SAGE combustion model, and the combustion characteristics for λ = 1.0 and 1.2 at 4000 rpm have been investigated [61]. Figure 11 shows the evolution of the turbulent regimes in the pre-chamber and main chamber for two operating conditions on the Borghi–Peters diagram. A noteworthy feature of this figure is that almost all pre-chamber combustion, even in lean cases, evolves in a thin reaction regime due to the high turbulence intensity produced by strong jet-to-jet interaction during compression stroke. As shown in Figure 11a, during the initial stages of combustion, the velocity scale ratio decreases due to the weakening of the initial turbulence intensity. Subsequently, it recovers as the residual gas decreases. The length scale ratio shows that the integral length scale (ll) remains constant, and the laminar flame thickness (δL) gradually decreases and stabilizes. Under lean conditions, the laminar flame thickness increases, and the laminar flame speed decreases, causing the curve to shift upward. From these results, it can be deduced that the MZ-WSR model is suitable for pre-chamber combustion. Figure 11b shows that compared to pre-chamber combustion, main chamber combustion occupies a broader area on the Borghi–Peters diagram, starting from the border of the broken reaction zone, passing through the thin reaction zone, and moving into the wrinkled flame zone. This occurs because the high turbulence intensity is distributed across the flame front when the hot turbulent jet is ejected. As the intensity of the jet and turbulence decreases, the combustion quickly transitions through the thin reaction zone and linearly moves into the corrugated reaction zone. Therefore, combustion in the main chamber experiences three combustion regimes due to the rapid changes in velocity and length scale ratios, indicating the presence of complex turbulence–flame interactions. This figure suggests that for PCSI engines, a multi-mode combustion model that can cover a wide range of the Borghi–Peters diagram needs to be developed. It is important to note that Figure 10 and Figure 11 are based on the RANS type k-epsilon turbulence model using Boussinesq’s isotropic eddy viscosity assumptions and flamelet-based combustion models, which may introduce some errors.
3.5. The Well-Tuned Versions of Combustion Models
As previously explained, to accurately predict the combustion in a PCSI engine, developing a model capable of calculating multi-mode combustion is essential. Currently, utilizing a flamelet-based combustion model is a practical alternative. Therefore, recent research has focused on tuning the model coefficients b1 and b3 in Equation (2), which represent the large and small-scale turbulence enhancements in the G-equation model described by Equation (2) [64,65,91]. This tuning process is performed ad hoc.
In the case of combustion models using Flame Surface Density (FSD) or MZ-WSR, efforts have been made to adjust the flame stretch factor, α in Equation (8) for FSD and multiplier, γ in Equation (7) ad hoc to align with experimentally obtained in-cylinder pressure traces and heat release rate profiles [148]. However, these treatments could not be adequate to achieve a precise correlation between simulations and experimental results in both the pre-chamber and the main combustion chamber [64,65,148]. As described above, such studies attempt to address the limitations of telling the turbulence–flame interaction using RANS-type turbulence models and flamelet-based combustion models by calibrating the model coefficients included in the equations that represent combustion speed or burn rate.
Kim et al. [64] tuned the multiplier of the MZ-WSR model within the range of 1.0 to 1.4. Additionally, they adjusted the coefficients b1 and b3 for the G-equation model between 1.0 and 2.5. for two air/fuel ratios at 1200 rpm. The engine used in this study is a 1.86-L passive PCSI PFI engine fueled by natural gas. They validated the improvement in prediction accuracy by comparing the in-cylinder pressure traces and heat release rate profiles with experimental data. Figure 5 compares the cylinder pressure and heat release rate obtained from experimental data and the simulation results using the tuned models. The experimental data includes results from 300 cycles (represented by light gray lines) and the averaged pressure (depicted by a bold black line). Figure 12 and Figure 13 compare the simulation results to the corresponding experimental results without tuning the model coefficients. The results show that without tuning the model coefficients, it is impossible to predict the combustion characteristics of the PCSI engine accurately. Additionally, the discrepancies are more pronounced in the lean region, likely due to the inability to account for the transition to the thin reaction zone as the flame thickness increases and the laminar burning velocity decreases.
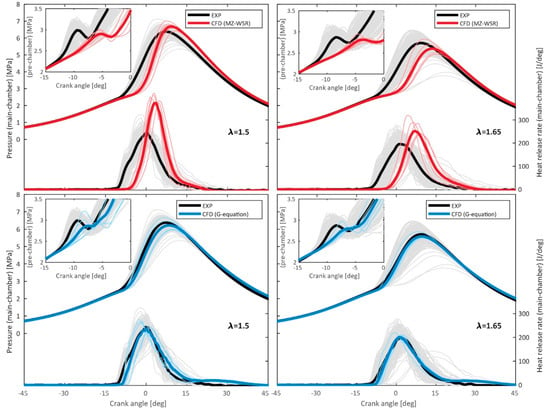
Figure 12.
Comparison of pressure traces and heat release rate curves between experimental data and tuned simulation results for MZ-SWR and G-equation [64].
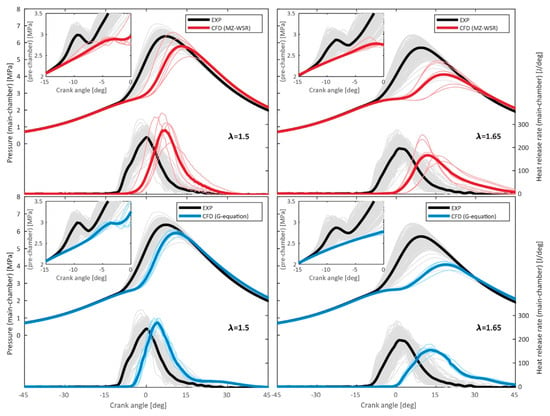
Figure 13.
Comparison of Pressure traces and heat release rate curves between experimental data and untuned simulation results for MZ-SWR and G-equation [64].
The tuning of model coefficients significantly improves the predictive accuracy of the G-equation model. However, the MZ-WSR model fails to enhance predictive accuracy with coefficient tuning, as it does not account for the effects of small-scale turbulence on the reaction rates.
Silva M et al. [65] conducted a detailed analysis on a 2.1-L active pre-chamber engine using natural gas as fuel, focusing on the impact of turbulent jets ejected from the pre-chamber on the burn rate in the main chamber. This study utilized the G-equation combustion and RANS-type turbulence models for two different orifice diameters. In this work, the turbulent flame speed equation was tuned with coefficients b1 and b3 set to 0.78 and 2.0, respectively. Figure 14 compares the pre-chamber, and central chamber pressure traces at 1200 rpm for the two orifice diameters between the calculated and experimental results. As observed, there is excellent agreement between the experimental and predicted data.
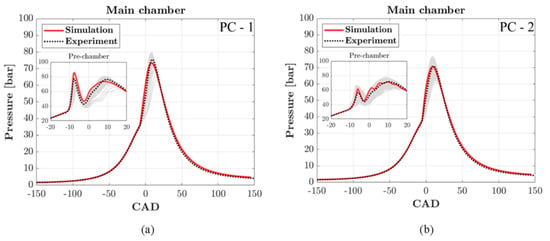
Figure 14.
Experimental validation of pressure curves for throat diameters of (a) 3.5 mm and (b) 5.5 mm [65].
In this computation, a highly sophisticated 0D/1D wave model [11,65] was employed to obtain initial conditions and temperatures at the walls, as well as temperature and pressure values at the inflow and outflow boundaries for the 3D CFD analysis. However, this model requires input conditions such as lift curves of intake and exhaust valves, pressure pulsations in the intake and exhaust pipes, and fuel lines. Additionally, experimentally obtained pressure traces are needed to analyze pre-chamber and main-chamber combustion phenomena.
Therefore, performing precise 3D CFD analysis of the PCSI engine without preceding experiments is challenging. Moreover, tuning model constants in the combustion model based on experimental values is necessary, which varies depending on the engine displacement, fuel used, pre-chamber geometry, and fuel supply system.
To the authors’ knowledge, only a few studies have utilized well-calibrated combustion models [45,76]. Although the physical phenomena of TJI combustion are not yet fully understood, model constants in the correlation or source term for various combustion models are adjusted to correct the laminar flame speed and align with experimental pressure traces [41,47,48]. However, the ability to accurately predict all phenomena involved in TJI combustion remains uncertain [45].
Figure 15 shows the recent share of (a) combustion models and fuels for PCSI simulations. The majority, 45.9% of studies, relied on the MZ-WSR model, while 32.4% opted for the G-equation model. Subsequently, the frequency of usage for the ECFM(3Z) model accounted for 16.2%, while less frequently used combustion models, such as the Weller model, were grouped as ‘etc’. Additionally, the fuels used in the CFD simulation for the PCSI engine were categorized and shown in Figure 15b. As illustrated in the figure, 50% of PCSI engine studies utilized natural gas fuel, followed by gasoline fuel. Recently, research has emerged on using carbon-free fuels such as ammonia and hydrogen in PCSI engines [36,44,86]. These studies employ a dual fueling strategy, utilizing natural gas [84] and diesel fuel for the initial combustion stage, and have been grouped under dual fuel.
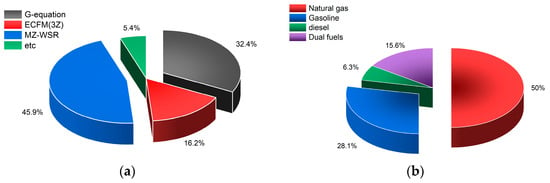
Figure 15.
Categorical distribution of type of (a) combustion model and (b) used fuel for simulating PCSI engines.
3.6. Numerical Grid of Pre-Chamber Engine
The process of subdividing a physical domain into smaller subdomains is known as grid generation or spatial discretization, which divides the spatial domain into a mesh or grid. Each grid point, cell, or control volume represents a discrete location in the domain. In this context, meshing is crucial in defining the discrete elements where physical laws are applied. These meshes establish the cells or elements over which flow calculations are conducted. The primary goal of the simulation is to generate numerical values for critical variables, such as velocity, pressure, and temperature, at specific points within the mesh. As the grid size decreases, the solution to the discretized problem converges to the solution of the continuous problem. Thus, the grid significantly influences both the rate of convergence and the accuracy of the solution. Therefore, the grid generation step is a critical component of the simulation process [137], and generating a sufficiently fine and uniform grid for complex geometries is both challenging and time-intensive. It is difficult to ensure that the grid adequately captures all relevant scales of turbulence while keeping the computational requirements manageable.
3.6.1. Mesh Generation for LES Turbulence Model
In the LES turbulent model, the mesh limits the size of the eddy that we can physically represent on the mesh [54,102]. LES resolves scales from the domain size L down to the filter size Δ, requiring substantial resolution of high wave number turbulent fluctuations. This necessitates high-order numerical schemes or acceptable grid resolution if low-order numerical schemes are employed [102,103,107]. Δ is the length scale or grid filter width and is determined as follows:
where the integral length scale, , the size of the eddy, is directly related to the computational cell volume, V.
It is known that good LES should resolve at least 80% of the turbulent kinetic energy, which is dependent on mesh size [108]. As mentioned above, the remaining kinetic energy is modeled in the sub-grid model. Finally, the finer the mesh, the more turbulent kinetic energy is resolved. As shown in Figure 5, the sub-grid scale viscosity is also a function of the mesh size. Hence, we are solving different equations on each level of refined mesh. Consequently, a traditional mesh independence study, which aims to ensure that simulation results are not influenced by mesh density, becomes impractical. Instead, alternative validation techniques must be employed to ensure the reliability of LES results.
Accordingly, the LES turbulence model requires representing the integral length scale of each eddy with at least five grid cells, which demands an enormous number of grids. Additionally, it is not easy to ensure that Equation (10) conditions are satisfied meticulously. Due to the computational burden resulting from a large number of computational grids, studies using LES (Large Eddy Simulation) [32,52] have primarily focused on geometrically and computationally simple cases, such as engine-like structures like the RCEM or constant volume chambers with single-hole nozzles and low-pressure air [57]. However, recent studies [59,67] have conducted three-dimensional CFD analyses using LES models to understand the complex thermo-fluid dynamic processes throughout the entire working cycle of the engine. This trend is clearly illustrated in Figure 4.
3.6.2. Mesh Generation for URANS Turbulence Model
It is well-known that huge grid sizes in RANS simulations can lead to under-resolved mean fields. This discrepancy significantly differs between the actual RANS and computationally resolved fields. Such under-resolution substantially impacts the accuracy of chemical simulations, often more so than the direct effects of turbulent fluctuations on the chemistry, which turbulent combustion interaction models are typically designed to account for [145]. Consequently, in scenarios of poor resolution, typical turbulent combustion models must compensate for under-resolution to maintain accuracy, even though they were not initially intended for this purpose. Therefore, increasing the resolution in under-resolved areas of the simulation can minimize the errors the unresolved field has on the chemistry. Once the resolution-related errors are mitigated, it can be observed that the remaining effects of turbulent interactions on combustion chemistry are of the same order of magnitude as the accuracy of the detailed kinetic mechanism being used. Additionally, it should be noted that in the case of an under-resolved flame front, the second derivative in the species conservation equation (representing diffusion) and the second derivative in the energy equation (representing conduction) would be under-estimated. This underestimation reduces the mixing, resulting in a lower calculated laminar flame speed.
All commercial CFD software provides grid generation tools in their pre-processors. When using the Converge CFD code, which is most commonly used for CFD analysis of PCSI engines, as shown in Figure 3, the Adaptive Mesh Refinement (AMR) algorithm is employed to increase the grid refinement level only in regions characterized by high velocities and large temperature gradients (e.g., flame fronts), without excessively slowing down the simulation with the uniformly refined grid. The mesh was re-generated at each iteration and dynamically refined. This approach resulted in the total number of cells in the computational domain ranging from 300,000 to 700,000 during the compression stroke to 1.23~3 [61] million to 9 million [88] at the end of the combustion phase. Studies using the Converge CFD code have set the base grid size in the pre-chamber to 1 mm [48,63,64]~4 mm [13,88] and, through a series of localized mesh refinements, achieved a minimum cell size of 0.125 [48,61,63]~0.5 [13,63,64] mm. By varying the grid size in the pre-chamber, the y+ value is monitored to ensure that the simulation results fall either within the recommended range (30 < y+ < 100) or within a range (20 < y+ < 30) that can be handled by a wall function [64]. Additional fixed mesh refinement is applied locally around the spark plug gap to capture the ignition phase [13,47,61,63,64] accurately. Additionally, the pre-chamber area, including the nozzles and the regions traversed by turbulent jets entering the main chamber, is locally refined to a resolution of 0.125 [13,47]~0.25 mm [64,88]. Figure 16 and Figure 17 display the complete engine geometry and the computational grid layout along a plane intersecting the center of the pre-chamber. A cut-cell method using a Cartesian grid was applied to model the two different complex geometries with moving boundaries. As shown in Figure 17, the AMR algorithm can be used to optimize the grid distribution during the flame propagation phase in order to minimize computational errors caused by grid under-resolution in the ejection phase, where there are steep gradients in velocity, pressure, temperature, and concentration due to turbulent jets.
Figure 16.
Cross section of computational grid configuration [63].
Figure 17.
Local refinements and AMR strategy employed in PCSI Engine during the ejection phase [48].
3.6.3. Differencing Process
A differencing scheme is a specific method to approximate the derivatives in the discretized equations. These schemes define how the values at the discrete points in the grid approximate the derivatives of the flow variables. There are several differencing schemes for convection and diffusion terms. One frequently adopted for PCSI engine CFD simulation is the upwind differencing scheme [149], which uses values from upstream points to approximate the derivatives. It introduces numerical false diffusion [149] but is more stable for convection-dominated problems. There are several variations, such as first-order upwind and higher-order upwind schemes. Although higher-order differencing schemes such as the Quadratic Upwind Interpolation for Convective Kinematics (QUICK) scheme and Total Variation Diminishing (TVD) scheme [150] can achieve high-accuracy solutions, they often compromise solution stability. As a result, for the CFD analysis of PCSI engines, which requires the simultaneous resolution of complex multi-mode combustion coupled with strong turbulence and conjugate heat transfer, most studies do not employ differencing schemes with accuracy higher than second order. Finally, it is always a big challenge for CFD engineers to choose an appropriate differencing scheme that better balances between accuracy and stability. In automotive and mechanical engineering, the sensitivity of discretization schemes for convection terms in LES has been thoroughly explored, as documented [151].
The primary function of a Sub-Grid Scale (SGS) model in LES is to dissipate resolved turbulent fluctuations effectively. The SGS model is specifically designed to provide the appropriate level of dissipation. Therefore, in LES, we should employ central differencing schemes, as they do not introduce any numerical dissipation due to their symmetric treatment of fluxes, ensuring that no artificial viscosity is introduced into the system. Central differencing schemes are second-order accurate, balancing accuracy and computational cost well. However, they can be less stable than upwind schemes.
Central Differencing Scheme: Uses the average of values at surrounding points to approximate derivatives. It is second-order accurate but may introduce numerical dispersion and can be unstable in convection-dominated flows. Opting for the central difference scheme is generally favored to mitigate numerical inaccuracies; nonetheless, a common practice involves blending the outcomes of upwind schemes with those of the central scheme to enhance computational stability.
3.7. Time Discretization
To obtain a numerical solution, partial differential equations must be discretized in both spatial and temporal domains. Partial differential equations must be discretized in spatial and temporal domains to obtain a numerical solution. Time-dependent variables, also known as transient terms, are mathematically represented as derivatives concerning time. However, from a physical standpoint, these terms require special handling. Transient terms describe the variation of a specific variable over time within an infinitesimally small control volume, adhering to conservation principles while preserving generality. When addressing the discrete treatment of transient factors, it is generally preferable to seek a time-varying solution, as this approach directly influences the accuracy of the numerical results. For predominantly steady flows, it is advisable first to determine a time-dependent approximation and transition to a steady-state approximation. Selecting the appropriate time step is crucial in simulating turbulent jet ignition and spark-ignition combustion in PCSI combustion (IC) engines. Accurately capturing pressure fluctuations due to deflagration within the cylinder or other phenomena in two divided chamber IC engines depends heavily on the time step resolution used in the simulation. A variable time-step approach, utilizing the Courant–Friedrichs–Lewy (CFL) number, has been implemented in almost all previous literature [28,29,30,31,32,33,48,63,148]. The maximum CFL number differed across various domain regions, spanning from 1 to 5, and the time step was automatically adjusted within a range of 0.001 to 1 CAD [48] or 2.5 × 10−5 to 1× 10−8 s [88].
3.8. Appropriate Initial and Boundary Conditions
The most straightforward method for obtaining initial conditions (such as intake and exhaust temperatures, pressures, injection quantity, and ignition timing) and boundary conditions is to utilize experimental data. However, this approach cannot be employed until a prototype engine is constructed, so it is only applied in a few specialized research studies [29]. In addition, one of the primary difficulties in 3D CFD simulating PCSI combustion systems is the scarce availability of boundary and initial conditions within the main chamber and the pre-chamber. Typically, installing measurement instruments in the confined space of a pre-chamber is extremely difficult. Therefore, in most previous studies related to 3D CFD simulation, initial values of all required thermodynamic parameters (including composition) were directly transferred from the 0D/1D model(s). This section describes the 0D/1D simulations that provide the necessary initial and boundary conditions for the 3D CFD simulation of the PCSI engine based on the findings of previous studies.
3.8.1. Inflow and Outflow Boundary Conditions of Intake and Exhaust
In the CFD analysis of a PCSI engine using RANS models, the most influential boundary conditions are the inflow and outflow conditions. It is necessary to obtain time-dependent variations in velocity, pressure, temperature, and chemical composition at the cross-sections of the engine’s intake and exhaust pipes. The value of CFD simulations lies in their ability to provide precise foundational design data before the prototype is created. Therefore, an additional simulation is required to obtain the aforementioned boundary conditions before the prototype engine is built. Thus, time-varying pressure, temperature, and chemical composition profiles derived from a 0D/1D model built using commercially available 1D gas dynamic codes, such as GT-SUITE [152], GT-POWER [11,12,16,82,83,84,85,86,87,88], and WAVE [58], validated with experimental data, were implemented as the inflow and outflow boundary conditions. These same 1D CFD models were utilized to specify the chemical composition.
These one-dimensional gas dynamic commercial programs thermodynamically model the components comprising the engine and consider the intake and exhaust pipes, which connect each element, as one-dimensional reacting compressible. They utilize the Method of Characteristics (MOCs) [153] to calculate the pulsating flow characteristics during the intake, compression, combustion, and exhaust processes. This approach allows for fast and accurate calculations of these characteristics at the system level of the entire engine. The gas dynamic simulation consists of intake, exhaust system, and cylinder units. Geometrical data, flow losses, and heat transfer between the pipe wall and the gas are considered. The pre-chamber combustion engine model incorporates two different thermodynamic descriptions of the main chamber and pre-chamber operating cycle, integrated with the gas exchange processes through the intake and exhaust valves and orifices in the pre-chamber. The main chamber, pre-chamber, and intake and exhaust pipes are treated as a control volume, ensuring that energy and mass balances are maintained during the intake and exhaust phases, which utilize two distinct systems, each containing two thermodynamic zones, to independently model the combustion processes within the pre-chamber and main chamber. These systems are interconnected through nozzles, facilitating the exchange of mass and enthalpy between them. During the compression, combustion, and expansion phases of both chambers, the energy balance of the combustion and heat release rate is obtained from either experimental information [11] or a two-zone model-like approach [154,155], which requires the 3D-derived turbulent intensity profiles in both chambers because preliminary 3D CFD analyses or experiments should be carried out in motored conditions to tune the constants of the turbulence sub-model included in this model [8,9]. Another straightforward way of modeling the combustion of the pre-chamber is using the Wiebe function [11,153], which was obtained from the heat release rate from the experimental pressure trace [11].
A very recent, very delicate 1D model based on GT-Power is used to further refine initial and boundary conditions of pressure and temperature to the 3D CFDs model [11,12,16,29,60,61,82,83,84,85,86,87,88]. However, this 1D model requires intake and exhaust valve profile curves, intake, exhaust, fuel lines, pre-chamber, and main chamber pressure traces. Combustions in the pre- and main chambers are expressed by heat release-based calibration (HRBC), where the heat release rates are computed from the measured pressure traces. The discharge coefficient through the pre-chamber nozzle is also calibrated to accurately replicate the pre-chamber pressure rise observed in the experimental data [45,65].
Figure 18 illustrates the single-cylinder active pre-chamber engine modeled using GT-POWER. This figure is a representative schematic diagram of an active PCSI engine modeled using a one-dimensional thermodynamic numerical analysis method (0D/1D model). As shown in the figure, the pre-chamber is modeled as a constant volume chamber, a check valve, and a nozzle. To obtain a more refined 1D model, calibration must be performed using experimentally obtained pressure traces from both the pre-chamber and main chamber to get accurate flow coefficients of the nozzle and check valve [45,65].
Figure 18.
The 1D model is based on GT-Power for single-cylinder active PCSI engines [45].
Applying appropriate boundary conditions for LES is complex, especially since inflow conditions must accurately represent turbulent fluctuations. This is critical because LES requires supplying a dynamic velocity field that fluctuates across both temporal and spatial dimensions. However, studies using LES [32,33,59] do not provide detailed information regarding the boundary conditions.
3.8.2. Wall Heat Transfer Modeling
Given the challenges in experimentally measuring instantaneous gas-to-wall heat fluxes, 3D CFD simulations of in-cylinder processes have become indispensable. These simulations are crucial for assessing the overall heat transfer to the combustion chamber walls, its spatial distribution, and the heat losses through the boundaries of the computational domain. A conjugate heat transfer model is indispensable for precisely simulating the uneven temperature profiles in both the pre-chamber and principal chamber and effectively capturing their effects on the turbulent jet quenching and stretching phenomena. While numerous studies have emphasized the importance and necessity of developing models suitable for PCSI engines, no related research results have been reported to date.
In the 3D CFD simulation of IC engines, the heat flux to the walls significantly impacts the temperature inside the combustion chamber, thus greatly influencing the accuracy of predicting emissions such as NOx [156]. Therefore, numerous heat transfer models and wall heat flux correlations exist in the literature [157,158,159,160,161], many of which were developed and validated through experiments conducted in research laboratories over the past decades, typically under low-load and low-speed engine conditions. Due to engine downsizing, operating conditions in the low-speed high-load range have become increasingly important, resulting in a significant increase in the thermal loads on engine components facing the combustion chamber. Under high-load, low-speed operating conditions, the suppression and control of NOx emissions and knocking are critical design factors. As a result, extensive research has been actively conducted on the development and validation of wall heat transfer models with high predictive accuracy. Recent studies [156] have revealed that existing wall heat transfer models (Angelberger’s [160] and Han and Reitz’s [161]) tend to overestimate wall heat transfer, as evidenced by experimental engine thermal surveys and temperature measurements conducted on four currently produced engines. Consequently, existing heat transfer models require a new calibration. Recent studies have proposed alternative heat transfer models for optimizing wall heat transfer in highly downsized spark-ignition engines [156,162] and for engines using carbon-free fuels like hydrogen [163].
As inferred from previous research findings, all these commonly used wall heat transfer models are sufficient under certain conditions. However, their adequacy for PCSI engines has yet to be evaluated and remains uncertain. For PCSI engines, the validation and calibration of wall heat transfer models are crucial. The conjugate heat transfer between the pre-chamber surface and the gas greatly affects flame quenching, significantly impacting the flame speed prediction. The importance of developing wall heat transfer models suitable for PCSI engine modeling has been highlighted in previous research. Chinnathambi et al. [88] underscored that a specialized wall heat transfer treatment would be necessary for the pre-chamber wall and the nozzles to address the uneven temperature distribution and the quenching effects accurately.
The wall heat transfer model by O’Rourke and Amsden [74] and Angelberger [12,160] is the most frequently adopted wall heat transfer model for PCSI engines. This model is one of the most widely used for both isothermal and non-isothermal wall heat transfer. The O’Rourke and Amsden model assumes constant near-wall flow temperature and density, as well as a fixed Prandtl number in the boundary layer. In contrast, Angelberger’s model allows for variations in near-wall flow temperature and density within the specified modeling range [164]. Surface temperatures are determined using a simplified predictive FEM model based on simulations that incorporate calibrated 0D/1D models [67].
Furthermore, utilizing the lumped model based on a thermal resistor network [153] with the experiments can yield the wall temperatures for the piston, liner, and cylinder head within the 3D CFDs model [29,165].
In the thermal resistor network model, the film coefficient, necessary to calculate heat loss between the gas and the wall, is obtained from empirical correlations such as Woschni’s or Annand’s correlations [153,163]. Recent research [166] suggested using a modified Woschni’s correlation for pre-chamber heat transfer analysis to simulate PCSI combustion’s characteristics precisely. It is important to note that the two heat transfer empirical formulas require calibration of constants, including the correlations, to accurately describe the conjugate heat transfer between the cylinder wall and in-cylinder gases based on factors such as fuel type, combustion method, bore, stroke, and turbocharging type [163,167]. However, a specific heat transfer model for pre-chamber walls is currently unavailable [166], and calibrating these empirical formulas for PSCI engines is time-consuming. Consequently, the uncertainties related to this aspect cannot be eliminated. Figure 18 illustrates a schematic diagram of the single-cylinder pre-chamber system modeled using a 0D/1D approach [59].
4. Experimental Validation
Experimental validation plays a vital role in CFD modeling as it determines the accuracy of a model in representing real-world scenarios for specific engineering applications. Conducting validation involves comparing CFD simulation outcomes with experimental data to ensure precision in engineering analyses. For PCSI engines, most numerical studies have used the in-cylinder pressure traces and heat release rate curves in the main chamber as validation data. As shown in Figure 19, multi-cycle LES calculations with the ECFM-3Z combustion model show different combustion paths with cycle variation on the in-cylinder pressure traces [67]. This trend is also observed in the heat release rate curves. This is because the HRR is derived from the pressure signal in the main chamber. It’s important to recognize that the experimental HRR provides a simplified estimation of the energy released during combustion. Therefore, only the ignition onset, peak combustion rate, and duration should be rigorously considered for validation.
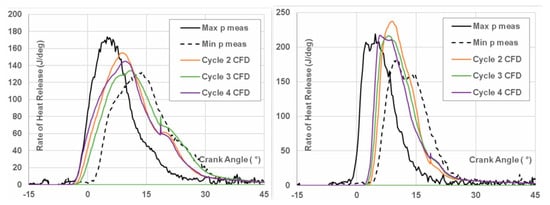
Figure 19.
Comparison of in-cylinder heat release rate for small and big active PCSI engines between CFDs based on LES and Experiment [67].
Additionally, as seen in Figure 12 and Figure 13, in the case of the G-equation, it was found that the model constants related to large and small-scale turbulence enhancement, which represent flame propagation speed, can significantly impact the pressure and heat release rate behavior inside the cylinder of a PCSI engine. However, this does not necessarily guarantee an accurate representation of turbulence–chemistry interaction. Therefore, before fine-tuning the physical models used in predictive PCSI engine modeling, it is crucial to identify and understand the primary sources of uncertainties. Many researchers have pointed out various uncertainties, including the lambda value inside the pre-chamber, excessively rich air/fuel ratios [168], and the correct calculation of laminar flame speed under ultra-lean conditions [91].
Syrovatka et al. [67] performed multi-cycle simulations on a single-cylinder active PCSI engine fueled by natural gas using the high-fidelity turbulence model LES and the ECFM-3Z combustion model. The results were compared to experimentally obtained heat release rate curves, as shown in the figure below. The operating conditions were set at a speed of 1800 rpm with an air excess ratio of 1.05. To analyze the cycle-by-cycle variation (CCV) effect, heat release rate curves for three cycles, excluding the first cycle calculated from the CFDs model, were displayed for two engines with different pre-chamber volumes. The maximum and minimum heat release rate curves obtained from the experimentally measured pressure traces over 120 cycles were shown for experimental validation. Figure 19 indicates that the LES modeling approach effectively captures the cycle-by-cycle variation of the PCSI engine, with all CFD traces falling within the limits of the experimental data. The figure also highlights the significant CCV in heat release rate curves due to lean combustion in the main chamber.
These results show that it is evident that analyzing model uncertainty by validating pressure and heat release rate curves averaged over 300 cycles using RANS-type turbulence models is very challenging. These findings suggest that the development of high-fidelity turbulence models capable of accounting for vortex-to-vortex interaction and non-uniform distribution of vortices, along with combustion models that can simulate multi-mode combustion, will be pivotal in establishing CFD analysis technology as a vital process in design engineering.
5. Critical Issues of CFD Simulation of a PCSI Engine
This study demonstrated that the ignition process in a pre-chamber spark-ignition (PCSI) engine is a complex phenomenon driven by the intricate thermo–chemical interactions governed by both chemical kinetics and fluid dynamics. The interaction between the pre-chamber jets and the main chamber charge plays a pivotal role in this process. Therefore, a thorough understanding of these kinetic and dynamic factors is crucial for a complete comprehension of pre-chamber behavior. To date, most of the fluid dynamic and chemical kinetics models employed in research have not been specifically developed for pre-chamber spark-ignition (PCSI) engines but rather have been predominantly designed for use in conventional spark-ignition (SI) engines. This indicates that, despite extensive research into the jet formation process and subsequent combustion in PCSI engines through three-dimensional CFD analysis, numerous issues remain that have yet to be fully understood. Figure 20 schematically illustrates the types of numerical models and their interrelationships used to represent the multi-physics nature occurring in a PCSI engine through CFDs. The figure provides an integrated overview of how these models are employed to simulate the complex interactions within the engine.
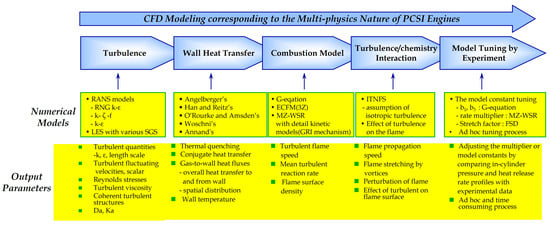
Figure 20.
Schematical diagram of CFD modeling corresponding to the multi-physics nature of PCSI engine.
This study also provides a thorough and concise explanation of the limitations associated with various numerical models that have been widely applied to CFD modeling of PCSI engines. In this section, Figure 21 presents a schematic illustration aimed at clarifying the current predictive limitations and uncertainties of CFD models for PCSI engines. As depicted in the figure, uncertainties inherent in turbulence models propagate through to combustion processes, turbulence–flame interactions, and turbulent jet–wall interactions. A significant challenge in current CFD simulations are the uncertainty in predicting the anisotropic behavior of turbulent flames, which stems from the assumption of isotropic turbulence in widely used RANS-averaged turbulence models. Addressing this issue is critical for advancing the accuracy of CFD simulations.
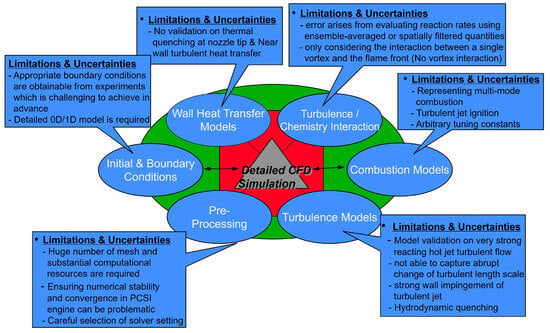
Figure 21.
Schematic diagram of limitations and uncertainties of CFD models for the PCSI engine.
Additionally, the development of a multi-mode combustion model capable of accurately simulating turbulent premixed flames at medium and high Karlovitz numbers, particularly in PCSI engine combustion, is essential for enhancing the reliability of future CFD analyses. Furthermore, as discussed in Section 3.3, improving the ITNFS model, which currently simulates flame–vortex interactions independently without accounting for vortex-to-vortex interactions, is an urgent priority. Developing a model that incorporates flame interactions with multiple vortices could lead to more precise predictions of combustion rates and flame propagation speeds.
Another noteworthy limitation that should be highlighted is that when the mean field generated in a RANS simulation is insufficiently resolved, often due to the use of overly coarse grid sizes, a significant disparity can arise between the actual RANS field and the one represented on the computational grid. This under-resolution poses a major challenge to accurately simulating the chemical processes, with its negative impact likely surpassing the direct influence of turbulent fluctuations on the chemistry. When the flame front is insufficiently resolved, the second derivative terms in both the species conservation equation (pertaining to diffusion) and the energy equation (pertaining to conduction) are likely to be underestimated. This underestimation leads to diminished mixing, which, in turn, results in a lower calculated laminar flame speed. Finally, recent advancements in hardware and computational models have enhanced the quality of numerical analysis and made these tools more accessible to a broader range of researchers. However, as previously mentioned, 3D CFD simulations for PCSI engines remain highly time-consuming due to the large number of grids required, especially when compared to other simulation methods. Additionally, these simulations require boundary conditions that are often only obtainable through experimental methods or repetitive calculations using 0D/1D models, which represents a significant drawback to numerical simulations.
6. Conclusions and Future Research Directions
This paper comprehensively reviews how CFD technology has been applied and developed over the past 20 years, particularly in the context of emerging PCSI technology. It thoroughly analyzes the models used for 3D CFD simulations, highlighting their interactions and examining the limitations and errors associated with these complex physics-based numerical models. The paper also discusses the challenges faced in using CFD as a design tool, including difficulties in obtaining initial and boundary conditions, which currently hinder CFD’s effectiveness in the initial design phase. Moreover, it explains why relying solely on 0D/1D analysis cannot fulfill the role of a predictive tool.
Despite its extensive use in industrial and academic research, as well as in optimizing pre-chamber designs, CFDs still exhibit significant limitations in their predictive capabilities. These challenges are particularly evident in turbulence modeling, affecting mixing and combustion, wall heat transfer modeling, and accurately depicting combustion processes. In the specific context of pre-chamber spark ignition, unresolved challenges remain, including flame and jet–wall interactions, ignition and combustion dynamics within the main chamber, and the ability of simplified combustion models in commercial CFD tools to accurately represent these complex processes.
To fully realize the potential of CFDs as more than just a predictive tool and develop it into an advanced design instrument, it is essential to enhance CFDs with precisely tailored, physics-based numerical models. Ultimately, for high-fidelity CFD modeling of pre-chamber combustion engines, the primary sources of uncertainty must be identified and corrected before proposing fine-tuning and improvements related to various turbulence and combustion models.
Funding
This work was supported by the Material and Parts Technology Development Project of the Korea Evaluation Institute of Industrial Technology, funded by the Korean government (Grant No. 20004900).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study, in the collection, analyses, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
References
- Baumgartner, L.S.; Wohlgemuth, S.; Zirngibl, S.; Wachtmeister, G. Investigation of a Methane Scavenged Prechamber for Increased Efficiency of a Lean-Burn Natural Gas Engine for Automotive Applications; SAE Technical Paper 2015-01-0866; SAE International: Warrendale, PA, USA, 2015. [Google Scholar]
- Zhu, S.; Akehurst, S.; Lewis, A.; Yuan, H. A review of the pre-chamber ignition system applied on future low-carbon spark ignition engines. Renew. Sustain. Energy Rev. 2022, 154, 111872. [Google Scholar] [CrossRef]
- Novella, R.; Gomez-Soriano, J.; Martinez-Hernandiz, P.J.; Libert, C.; Rampanarivo, F. Improving the performance of the passive pre-chamber ignition concept for spark-ignition engines fueled with natural gas. Fuel 2021, 290, 119971. [Google Scholar] [CrossRef]
- Wei, H.; Zhu, T.; Shu, G.; Tan, L.; Wang, Y. Gasoline engine exhaust gas recirculation—A review. Appl. Energy 2012, 99, 534–544. [Google Scholar] [CrossRef]
- Bravo, Y.; Larrosa, C.; Lujan, J.; Climent, H.; Rivas, M. Evaluation of EGR System Implementation in a GTDI Engine with Different Configurations: Assessment on Fouling and Corrosion Issues; SAE Technical Paper 2016-01-1016; SAE International: Warrendale, PA, USA, 2016. [Google Scholar] [CrossRef]
- Uyehara, O.A. Prechamber for Lean Burn for Low Nox; SAE Technical Paper; SAE International: Warrendale, PA, USA, 1995. [Google Scholar]
- Toulson, E.; Watson, H.C.; Attard, W.P. The Effects of Hot and Cool EGR with Hydrogen Assisted Jet Ignition; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2007. [Google Scholar]
- Ronney, P.D. Laser versus conventional ignition of flames. Opt. Eng. 1994, 33, 510–521. [Google Scholar] [CrossRef]
- Böker, D.; Brüggemann, D. Advancing lean combustion of hydrogen–air mixtures by laser-induced spark ignition. Int. J. Hydrogen Energy 2011, 36, 14759–14767. [Google Scholar] [CrossRef]
- Getzlaff, J.; Pape, J.; Gruenig, C.; Kuhnert, D.; Latsch, R. Investigations on Pre-Chamber Spark Plug with Pilot Injection; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2007. [Google Scholar]
- Benajesa, J.; Novellaa, R.; Gomez-Sorianoa, J.; Martinez-Hernandiza, P.J.; Libertb, C.; Dabirib, M. Evaluation of the passive pre-chamber ignition concept for future high compression ratio turbocharged spark-ignition engines. Appl. Energy 2019, 248, 576–588. [Google Scholar] [CrossRef]
- Benajesa, J.; Novellaa, R.; Gomez-Sorianoa, J.; Barberya, I.; Libertb, C.; Rampanarivob, F.; Dabiri, M. Computational assessment towards understanding the energy conversion and combustion process of lean mixtures in passive pre-chamber ignited engines. Appl. Therm. Eng. 2020, 178, 115501. [Google Scholar] [CrossRef]
- Wang, M.; Leng, X.; He, Z.; Wei, S.; Chen, L.; Jin, Y. A Numerical Study on the Effects of the Orifice Geometry between Pre- and Main Chamber for a Natural Gas Engine; SAE Technical Paper 2017-01-2195; SAE International: Warrendale, PA, USA, 2017. [Google Scholar]
- Onofrio, G.; Napolitano, P.; Tunestål, P.; Beatrice, C. Combustion sensitivity to the nozzle hole size in an active prechamber ultra-lean heavy-duty natural gas engine. Energy 2021, 235, 121298. [Google Scholar] [CrossRef]
- Bozza, F.; De Bellis, V.; Malfi, E.; Teodosio, L.; Tufano, D. Optimal Calibration Strategy of a Hybrid Electric Vehicle Equipped with an Ultra-Lean Pre-Chamber SI Engine for the Minimization of CO2 and Pollutant Emissions. Energies 2020, 13, 4008. [Google Scholar] [CrossRef]
- Assanis, D.; Engineer, N.; Neuman, P.; Wooldridge, M. Computational Development of a Dual Pre-Chamber Engine Concept for Lean Burn Combustion; SAE Technical Paper 2016-01-2242; SAE International: Warrendale, PA, USA, 2016. [Google Scholar] [CrossRef]
- Attard, W.P.; Toulson, E.; Huisjen, A.; Chen, X.; Zhu, G.; Schock, H. Spark Ignition and Pre-Chamber Turbulent Jet Ignition Combustion Visualization; SAE Technical Paper 2012-01-0823; SAE International: Warrendale, PA, USA, 2012. [Google Scholar]
- Shah, A.; Tunestal, P.; Johansson, B. Effect of Relative Mixture Strength on Performance of Divided Chamber ‘Avalanche Activated Combustion’ Ignition Technique in a Heavy Duty Natural Gas Engine; SAE Technical Paper 2014-01-1327; SAE International: Warrendale, PA, USA, 2014. [Google Scholar]
- Chao, Y.; Hu, K.; Wei, H.; Li, S.; Hu, Y.; Yu, J.; Scholten, I. Geely Jet Ignition System for 52.5% Indicated Thermal Efficiency. In Proceedings of the 43rd International Vienna Motor Symposium, Vienna, Austria, 27–29 April 2022. [Google Scholar]
- Turkish, M.C. 3-Valve Stratified Charge Engines: Evolvement, Analysis and Progression; SAE Technical Paper 741163; SAE International: Warrendale, PA, USA, 1974. [Google Scholar] [CrossRef]
- Dale, J.D.; Oppenheim, A.K. Enhanced Ignition for I.C. Engines with Premixed Gases. SAE Trans. 1981, 90, 810146. [Google Scholar]
- Toulson, E.; Schock, H.J.; Attard, W.P. A Review of Pre-Chamber Initiated Jet Ignition Combustion Systems; SAE Technical Paper 2010-01-2263; SAE International: Warrendale, PA, USA, 2010. [Google Scholar]
- Oppenheim, A.K. Combustion in Piston Engines: Technology, Evolution, Diagnosis and Control; Springer: New York, NY, USA, 2004. [Google Scholar]
- Date, T.; Yagi, S.; Ishizuya, A.; Fujii, I. Research and Development of the Honda CVCC Engine; SAE Technical Paper; SAE International: Warrendale, PA, USA, 1974. [Google Scholar]
- Gentz, G.; Gholamisheeri, M.; Toulson, E. A study of a turbulent jet ignition system fueled with iso-octane: Pressure trace analysis and combustion visualization. Appl. Energy 2017, 189, 385–394. [Google Scholar] [CrossRef]
- Toulson, E.; Huisjen, A.; Chen, X.; Squibb, C.; Zhu, G.; Schock, H. Visualization of propane and natural gas spark ignition and turbulent jet ignition combustion. SAE Int. J. Engines 2012, 5, 1821–1835. [Google Scholar] [CrossRef]
- Di Sabatino, F.; Martinez-Hernandiz, P.J.; Novella, R.; Ekoto, I. Investigation of the effects of passive pre-chamber nozzle pattern and ignition system on engine performance and emissions. Int. J. Engine Res. 2023, 24, 2592–2613. [Google Scholar] [CrossRef]
- Xu, G.; Wright, Y.M.; Schiliro, M.; Boulouchos, K. Characterization of combustion in a gas engine ignited using a small un-scavenged pre-chamber. Int. J. Engine Res. 2020, 21, 1085–1106. [Google Scholar] [CrossRef]
- Novella, R.; Gomez-Soriano, J.; Barbery, I.; Libert, C. Numerical analysis of the passive pre-chamber ignition concept for light-duty applications. Appl. Therm. Eng. 2022, 213, 118610. [Google Scholar] [CrossRef]
- Wanker, R. Simulation Methods Covering Recent Technologies for GDI Engines. In Proceedings of the AVL International Simulation Conference, Graz, Austria, 22–24 October 2019. [Google Scholar]
- Vedula, R.T.; Song, R.; Stuecken, T.; Zhu, G.G.; Schock, H. Thermal efficiency of a dual-mode turbulent jet ignition engine under lean and near-stoichiometric operation. Int. J. Engine Res. 2017, 18, 1055–1066. [Google Scholar] [CrossRef]
- Mastorakos, E.; Allison, P.; Giusti, A.; De Oliveira, P.; Benekos, S.; Wright, Y.; Frouzakis, C.; Boulouchos, K. Fundamental aspects of jet ignition for natural gas engines. SAE Int. J. Engines 2017, 10, 2429–2438. [Google Scholar] [CrossRef]
- Allison, P.; de Oliveira, M.; Giusti, A.; Mastorakos, E. Pre-chamber ignition mechanism: Experiments and simulations on turbulent jet flame structure. Fuel 2018, 230, 274–281. [Google Scholar] [CrossRef]
- Bunce, M.; Blaxill, H. Methodology for combustion analysis of a spark ignition engine incorporating a pre-chamber combustor. In Proceedings of the SAE 2014 International Powertrain, Fuels & Lubricants Meeting, Birmingham, UK, 20–23 October 2014; SAE International: Warrendale, PA, USA, 2014. [Google Scholar]
- Benajes, J.; Novella, R.; Gomez-Soriano, J.; Barbery, I.; Libert, C. Advantages of hydrogen addition in a passive pre-chamber ignited SI engine for passenger car applications. Int. J. Energy Res. 2021, 45, 13219–13237. [Google Scholar] [CrossRef]
- Dong, D.; Wei, M.; Zhang, Z.; Wei, F.; Long, W.; Dong, P.; Tian, J.; Lu, M.; Wang, R.; Xiao, G. Enhanced ignition possibilities of ammonia by the prechamber fueled methanol: Rich, stoichiometric and lean combustion evaluations. Sustain. Energy Technol. Assess. 2024, 64, 103723. [Google Scholar] [CrossRef]
- Liu, X.; Aljabri, H.; Panthi, N.; AlRamadan, A.S.; Cenker, E.; Alshammari, A.T.; Magnotti, G.; Im, H.G. Computational study of hydrogen engine combustion strategies: Dual-Fuel compression ignition with Port- and Direct-Injection, Pre-Chamber Combustion, and Spark-Ignition. Fuel 2023, 350, 128801. [Google Scholar] [CrossRef]
- Liu, X.; Aljabri, H.; Panthi, N.; AlRamadan, A.S.; Cenker, E.; Alshammari, A.T.; Magnotti, G.; Im, H.G. Hydrogen pre-chamber combustion at lean-burn conditions on a heavy-duty diesel engine: A computational study. Fuel 2023, 335, 127042. [Google Scholar] [CrossRef]
- Biswas, S.; Qiao, L. Ignition of ultra-lean premixed H2/air using multiple hot turbulent jets generated by pre-chamber combustion. Appl. Therm. Eng. 2018, 132, 102–114. [Google Scholar] [CrossRef]
- Thelen, B.C.; Toulson, E. A computational study on the effect of the orifice size on the performance of a turbulent jet ignition system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 231, 536–554. [Google Scholar] [CrossRef]
- Biswas, S.; Qiao, L. Ignition of ultra-lean premixed hydrogen/air by an impinging hot jet. Appl. Energy 2018, 228, 954–964. [Google Scholar] [CrossRef]
- Trombley, G.; Toulson, E. A fuel-focused review of pre-chamber initiated combustion. Energy Convers. Manag. 2023, 298, 117765. [Google Scholar] [CrossRef]
- Alvarez, C.E.C.; Couto, G.E.; Roso, V.R.; Thiriet, A.B.; Valle, R.M. A review of prechamber ignition systems as lean combustion technology for SI engines. Appl. Therm. Eng. 2018, 128, 107–120. [Google Scholar] [CrossRef]
- Zhou, L.; Zhong, L.; Liu, Z.; Wei, H. Toward highly-efficient combustion of ammonia–hydrogen engine: Prechamber turbulent jet ignition. Fuel 2023, 352, 129009. [Google Scholar] [CrossRef]
- Hlaing, P.; Echeverri Marquez, M.; Cenker, E.; Im, H.G.; Johansson, B.; Turner, J.W.G. CFD-based methodology for the characterization pre-chamber combustion engines. Fuel 2022, 313, 123029. [Google Scholar] [CrossRef]
- Shah, A.; Tunestal, P.; Johansson, B. Effect of Pre-Chamber Volume and Nozzle Diameter on Pre-Chamber Ignition in Heavy Duty Natural Gas Engines; SAE Technical Paper 2015-01-0867; SAE International: Warrendale, PA, USA, 2015. [Google Scholar]
- Silva, M.; Sanal, S.; Hlaing, P.; Cenker, E.; Johansson, B.; Im, H.G. Effects of Geometry on Passive Pre-Chamber Combustion Characteristics; SAE Technical Paper 2020-01-0821; SAE International: Warrendale, PA, USA, 2020. [Google Scholar]
- Distaso, E.; Amirante, R.; Cassone, E.; De Palma, P.; Sementa, P.; Tamburrano, P.; Vaglieco, B.M. Analysis of the combustion process in a lean-burning turbulent jet ignition engine fueled with methane. Energy Convers. Manag. 2020, 223, 113257. [Google Scholar] [CrossRef]
- Gholamisheeri, M.; Thelen, B.; Toulson, E. CFD Modeling and Experimental Analysis of a Homogeneously Charged Turbulent Jet Ignition System in a Rapid Compression Machine; SAE Technical Paper 2017-01-0557; SAE International: Warrendale, PA, USA, 2017. [Google Scholar]
- Thelen, B.C.; Gentz, G.; Toulson, E. Computational Study of a Turbulent Jet Ignition System for Lean Burn Operation in a Rapid Compression Machine; SAE Technical Paper 2015-01-0396; SAE International: Warrendale, PA, USA, 2015. [Google Scholar]
- Gentz, G.; Thelen, B.; Litke, P.; Hoke, J.; Toulson, E. Combustion visualization, performance, and CFD modeling of a pre-chamber turbulent jet ignition system in a rapid compression machine. SAE Int. J. Engines 2015, 8, 538–546. [Google Scholar] [CrossRef]
- Bolla, M.; Shapiro, E.; Tiney, N.; Kyrtatos, P.; Kotzagianni, M.; Boulouchos, K. Numerical Simulations of Pre-Chamber Combustion in an Optically Accessible RCEM; SAE Technical Paper 2019-01-0224; SAE International: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Shapiro, E.; Ahmed, I.; Tiney, N. Advanced ignition modelling for pre-chamber combustion in lean burn gas engines. In Proceedings of the Ignition Systems for Gasoline Engines: Internationale Tagung Zündsysteme für Ottomotoren, Berlin, Germany, 6–7 December 2018; p. 104. [Google Scholar]
- Bolla, M.; Shapiro, E.; Tiney, N.; Kyrtatos, P.; Kotzagianni, M.; Boulouchos, K. Numerical Study of Turbulence and Fuel-Air Mixing within a Scavenged Pre-Chamber Using RANS and LES; SAE Technical Paper 2019-01-0198; SAE International: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Fei, Q.; Shah, A.; Zhi-wei, H.; Li-na, P.; Tunestal, P.; Xue-Song, B. Detailed numerical simulation of transient mixing and combustion of premixed methane/air mixtures in a pre-chamber/main-chamber system relevant to internal combustion engines. Combust. Flame 2018, 188, 357–366. [Google Scholar]
- Sforza, L.; Lucchini, T.; Gianetti, G.; D’Errico, G.; Onofrio, G.; Beatrice, C.; Tunestal, P. A 3D-CFD Methodology for Combustion Modeling in Active Prechamber SI Engines Operating with Natural Gas; SAE Technical Paper 2022-01-0470; SAE International: Warrendale, PA, USA, 2022. [Google Scholar] [CrossRef]
- Yin, Y.; Lei, Y.; Shen, H.; Yi, Y.; Zhao, T.; Qiu, T. Modeling Investigation on Transient Behaviors of Gaseous Ammonia Jet Flow with Direct Injection. Fuel 2024, 358, 129997–130011. [Google Scholar] [CrossRef]
- Shapiro, E.; Tiney, N.; Kyrtatos, P.; Kotzagianni, M.; Bolla, M.; Boulouchos, K.; Tallu, G.; Lucas, G.; Weissner, M. Experimental and Numerical Analysis of Pre-Chamber Combustion Systems for Lean Burn Gas Engines; SAE Technical Paper 2019-01-0260; SAE International: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Vavra, J.; Syrovatka, Z.; Vitek, O.; Macek, J.; Takats, M. Development of a Pre-Chamber Ignition System for Light Duty Truck Engine; SAE Technical Paper 2018-01-1147; SAE International: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Zhou, H.; Meng, S.; Han, Z. Combustion characteristics and misfire mechanism of a passive pre-chamber direct-injection gasoline engine. Fuel 2023, 352, 129067. [Google Scholar] [CrossRef]
- Piano, A.; Scalambro, A.; Millo, F.; Catapano, F.; Sementa, P.; Di Iorio, S.; Bianco, A. CFD-based methodology for the characterization of the combustion process of a passive pre-chamber gasoline engine. Transp. Eng. 2023, 13, 100200. [Google Scholar] [CrossRef]
- Peethambaram, M.R.; Zhou, Q.; Waters, B.; Pendlebury, K.; Fu, H.; Haines, A.; Hale, D.; Hu, T.; Zhang, J.; Wu, X.; et al. Combustion Analysis of Active Pre-Chamber Design for Ultra-Lean Engine Operation. SAE Int. J. Engines 2024, 17, 705–720. [Google Scholar] [CrossRef]
- Kim, J.; Scarcelli, R.; Som, S.; Shah, A.; Biruduganti, M.S.; Longman, D.E. Numerical Investigation of a Fueled Pre-Chamber Spark-Ignition Natural Gas Engine. Int. J. Engine Res. 2021, 23, 1475–1494. [Google Scholar] [CrossRef]
- Kim, J.; Scarcelli, R.; Som, S.; Shah, A.; Biruduganti, M.S.; Longman, D.E. Assessment of turbulent combustion models for simulating prechamber ignition in a natural gas engine. J. Eng. Gas Turbines Power 2021, 143, 091004. [Google Scholar] [CrossRef]
- Silva, M.; Liu, X.; Hlaing, P.; Sanal, S.; Cenker, E.; Chang, J.; Johansson, B.; Im, H.G. Computational assessment of effects of throat diameter on combustion and turbulence characteristics in a pre-chamber engine. Appl. Therm. Eng. 2022, 212, 118595. [Google Scholar] [CrossRef]
- Zhao, P.; Ge, H.; Parameswaran, S. CFD-guided development of a pre-chamber ignition system for internal combustion engines. Int. J. Powertrains 2021, 10, 79–103. [Google Scholar] [CrossRef]
- Syrovatka, Z.; Vitek, O.; Vavra, J.; Takats, M. Scavenged Pre-Chamber Volume Effect on Gas Engine Performance and Emissions; SAE Technical Paper 2019-01-0258; SAE International: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Kyrtatos, P.; Bolla, M.; Benekos, S.; Bardis, K.; Xu, G.; Kotzagianni, M.; Wright, Y.M.; Giannakopoulos, G.; Frouzakis, C.E.; Boulouchos, K. Advanced Methods for Gas-Prechamber Combustion Research and Model Development. In Proceedings of the 16th Conference, The Working Process of the Internal Combustion Engine, Graz, Austria, 28–29 September 2017; pp. 167–183. [Google Scholar]
- Wang, B.; Xie, F.; Hong, W.; Du, J.; Chen, H.; Su, Y. The effect of structural parameters of pre-chamber with turbulent jet ignition system on combustion characteristics of methanol-air pre-mixture. Energy Convers. Manag. 2022, 274, 116473. [Google Scholar] [CrossRef]
- Convergent Science Inc. Converge 2.3 Theory Manual; Convergent Science Inc.: Madison, WI, USA, 2017. [Google Scholar]
- Siemens PLM. STAR-CD 12.02, Simcenter, Userguide; Simens: Plano, TX, USA, 2020. [Google Scholar]
- AVL. AVL FIRE, Software Documentation, Version 2021 R2; AVL: Graz, Austria, 2021. [Google Scholar]
- Ricardo Software Ltd. VECTIS CFD Release 2017.1 Theory Manual; Ricardo PLC: London, UK, 2017. [Google Scholar]
- Amsden, A.A. KIVA-3V, Release2 A Block-Structured KIVA Program for Engines with Vertical or Canted Valve; LA-UR-97-689; Los Alamos National Laboratory: Los Alamos, NM, USA, 1997. [Google Scholar]
- The OpenFOAM Foundation. OpenFOAM v2206; The OpenFOAM Foundation: London, UK, 2022. [Google Scholar]
- Xu, G.; Wright, Y.M.; Kyrtatos, P.; Bardis, K.; Schiliro, M.; Boulouchos, K. Experimental and Numerical Investigation of the Engine Operational Conditions’ Influences on a Small Un-Scavenged Pre-Chamber’s Behavior. SAE Int. J. Engines 2017, 10, 2414–2428. [Google Scholar] [CrossRef]
- Wu, X.; Feng, Y.; Gao, Y.; Xia, C.; Zhu, Y.; Shreka, M.; Ming, P. Numerical simulation of lean premixed combustion characteristics and emissions of natural gas-ammonia dual-fuel marine engine with the pre-chamber ignition system. Fuel 2023, 343, 127990. [Google Scholar] [CrossRef]
- Silva, M.; Mohan, B.; Badra, J.; Zhang, A.; Hlaing, P.; Cenker, E.; AlRamadan, A.S.; Im, H.G. DoE-ML guided optimization of an active pre-chamber geometry using CFD. Int. J. Engine Res. 2022, 24, 2936–2948. [Google Scholar] [CrossRef]
- Krajnović, J.; Sjerić, M.; Tomić, R.; Kozarac, D. A novel concept of active pre-chamber engine with a single injector—The passive main chamber approach. Appl. Therm. Eng. 2024, 250, 123509. [Google Scholar] [CrossRef]
- Kammel, G.; Mair, F.; Zelenka, J.; Lackner, M.; Wimmer, A.; Kogler, G.; Bärow, E. Simulation Based Predesign and Experimental Validation of a Prechamber Ignited HPDI Gas Combustion Concept; SAE Technical Paper 2019-01-0259; SAE International: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Beran, R.; Wimmer, A. Application of 3D-CFD Methods to Optimize a Gaseous Fuelled Engine with Respect to Charge Motion, Combustion and Knocking; SAE Technical Paper 2000-01-0277; SAE International: Warrendale, PA, USA, 2000. [Google Scholar]
- Shin, J.; Choi, J.; Seo, J.; Park, S. Pre-chamber combustion system for heavy-duty engines for operating dual fuel and diesel modes. Energy Convers. Manag. 2022, 255, 115365. [Google Scholar] [CrossRef]
- Wang, H.; Wang, T.; Feng, Y.; Lu, Z.; Sun, K. Synergistic effect of swirl flow and prechamber jet on the combustion of a natural gas-diesel dual-fuel marine engine. Fuel 2022, 325, 124935. [Google Scholar] [CrossRef]
- Wu, X.; Feng, Y.; Xu, G.; Zhu, Y.; Ming, P.; Dai, L. Numerical investigations on charge motion and combustion of natural gas-enhanced ammonia in marine pre-chamber lean-burn engine with dual-fuel combustion system. Int. J. Hydrogen Energy 2023, 48, 11476–11492. [Google Scholar] [CrossRef]
- Dempsey, A.B.; Zeman, J.; Wall, M. A System to Enable Mixing Controlled Combustion with High Octane Fuels Using a Prechamber and High-Pressure Direct Injector. Front. Mech. Eng. 2021, 7, 637665. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, R.; Lin, H.; Jin, Z.; Qian, Y.; Zhou, D.; Yin, Y.; Li, Z.; Lu, X. Computational insights into flame development and emission formation in an ammonia engine with hydrogen-assisted pre-chamber turbulent jet ignition. Energy Convers. Manag. 2024, 314, 118706. [Google Scholar] [CrossRef]
- Oliveira, W.P.; Mendonça, M.S.; Chavda, N.B.; Rodrigues Filho, F.A.; Baeta, J.G.C. Numerical and experimental analysis of the combustion in a Single-Cylinder research engine with passive TJI pre-chamber operating with hydrated ethanol. Energy Convers. Manag. 2024, 310, 118459. [Google Scholar] [CrossRef]
- Chinnathambi, P.; Bunce, M.; Cruff, L. RANS Based Multidimensional Modeling of an Ultra-Lean Burn PreChamber Combustion System with Auxiliary Liquid Gasoline Injection; SAE Technical Paper 2015-01-0386; SAE International: Warrendale, PA, USA, 2015. [Google Scholar] [CrossRef]
- Xu, L.; Li, G.; Yao, M.; Zheng, Z.; Wang, H. Numerical Investigation on the Jet Characteristics and Combustion Process of an Active Prechamber Combustion System Fueled with Natural Gas. Energies 2022, 15, 5356. [Google Scholar] [CrossRef]
- Gholamisheeri, M.; Wichman, I.S.; Toulson, E. A study of the turbulent jet flow field in a methane fueled turbulent jet ignition (TJI) system. Combust. Flame 2017, 183, 194–206. [Google Scholar] [CrossRef]
- Silva, M.; Liu, X.; Hlaing, P.; Cenker, E.; Turner, J.; Im, H.G. A Computational Assessment of Combustion Submodels for Predictive Simulations of Pre-Chamber Combustion Engines. In Proceedings of the ASME 2022 ICE Forward Conference, Indianapolis, IN, USA, 16–19 October 2022. [Google Scholar]
- Thelen, B.; Toulson, E. A Computational Study of the Effects of Spark Location on the Performance of a Turbulent Jet Ignition System; SAE Technical Paper 2016-01-0608; SAE International: Warrendale, PA, USA, 2016. [Google Scholar] [CrossRef]
- Jamrozik, A.; Tutak, W.; Kociszewski, A.; Sosnowski, M. Numerical simulation of two-stage combustion in SI engine with prechamber. Appl. Math. Model. 2013, 37, 2961–2982. [Google Scholar] [CrossRef]
- Borghi, F.T.; Moreira, T.A.A.; Whanco, R.; Barros, J.E.M.; Valle, R.M. Aerodynamic In-Cylinder Flow Simulation in an Internal Combustion Engine with Torch Ignition System; SAE Technical Paper 2014-36-0298; SAE International: Warrendale, PA, USA, 2022. [Google Scholar]
- Hernández, I.; Shapiro, E.; Tiney, N.; Kotzagianni, M.; Kyrtatos, P.; Boulouchos, K. Flame-wall interaction modelling for pre-chamber combustion in lean burn gas engines. In Proceedings of the 35th International CAE Conference and Exhibition (CAE 2018), Vicenza, Italy, 8–9 October 2018. [Google Scholar] [CrossRef]
- Miccichè, S. Comparison of Optimization Methods for Prechamber Spark Plug Operations in Natural Gas Engines Using CFD-Simulation. Master’s Thesis, Mechanical Engineering, Institut für Kolbenmaschinen (IFKM), Karlsruhe, Germany, 2019. [Google Scholar]
- Nodi, A.; Sforza, L.; Lucchini, T.; Onorati, A.; Buttitta, M.; Marmorini, L. CFD Modeling of Conventional and Pre-Chamber Ignition of a High-Performance Naturally Aspirated Engine; SAE Technical Paper 2024-01-2102; SAE International: Warrendale, PA, USA, 2024. [Google Scholar] [CrossRef]
- Addabbo, A. A CFD Methodology for the Design of Active Prechambers in SI Engines. Master’s Thesis, Mechanical Engineering, Politecnico, Italy, 2023. [Google Scholar]
- Posch, S.; Gößnitzer, C.; Rohrhofer, F.M.; Geiger, B.; Wimmer, A. Finding the Optimum Design of Large Gas Engines Prechambers using CFD and Bayesian Optimization. In Scientific Computing 2023: Conference Proceedings; Granigg, W., Ed.; Verlag der FH JOANNEUM Gesellschaft mbH: Graz, Austria, 2023; pp. 160–168. [Google Scholar]
- Krajnovic, J.; Dilber, V.; Tomic, R.; Sjeric, M.; Ilincic, P.; Kozarac, D. Numerical Simulations of Pre-Chamber Induced HCCI Combustion (PC-HCCI); SAE Technical Paper 2023-01-0274; SAE International: Warrendale, PA, USA, 2023. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cornell University: New York, NY, USA, 2000; ISBN 9780521598866. [Google Scholar]
- Hanjalic, K. Will RANS survive LES? A view of perspectives. J. Fluid Eng. 2005, 127, 831–839. [Google Scholar] [CrossRef]
- Davidson, L. Fluid Mechanics, Turbulent Flow and Turbulence Modeling; Chalmers University of Technology: Goteborg, Sweden, 2024. [Google Scholar]
- Chen, C.-J.; Jaw, S.-Y. Fundamentals of Turbulence Modeling; Taylor & Francis: New York, NY, USA, 1998; ISBN 1-56032-405-8. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 2nd ed.; DCW Industries Inc.: La Canada, CA, USA, 1994. [Google Scholar]
- Yakhot, V.; Orszag, S.A.; Thangam, S.; Gatski, T.B.; Speziale, C.G. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids A 1992, 4, 1510–1520. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics-the Finite Volume Method, 2nd ed.; Pearson Education: Tamil Nadu, India, 2007. [Google Scholar]
- The Smagorinsky Turbulence Model (Part 2). Fluid Mechanics 101, YouTube Channel. Available online: https://www.youtube.com/watch?v=GdXLyfRK188&t=992s (accessed on 1 June 2024).
- Durbin, P.A.; Pettersson Reif, B.A. Statistical Theory and Modeling for Turbulent Flows; Wiley: Hoboken, NJ, USA, 2001; ISBN 0471497363. [Google Scholar]
- Nzebuka, G.G.; Waheed, M.A. Thermal evolution in the direct chill casting of an Al-4 pct Cu alloy using the low-Reynolds number turbulence model. Int. J. Therm. Sci. 2020, 147, 106152. [Google Scholar] [CrossRef]
- Hanjalić, K.; Popovac, M.; Hadžiabdić, M. A robust near-wall elliptic-relaxation eddy-viscosity turbulence model for CFD. Int. J. Heat Fluid Flow 2004, 25, 1047–1051. [Google Scholar] [CrossRef]
- Durbin, P.A. Near-wall turbulence closure modeling without “damping functions”. Theor. Comput. Fluid Dyn. 1991, 3, 1–13. [Google Scholar] [CrossRef]
- Durbin, P.A. A Reynolds Stress Model for Near-wall Turbulence. J. Fluid Mech. 1993, 249, 465–498. [Google Scholar] [CrossRef]
- Sunden, B.; Faghri, M. Modelling and Simulation of Turbulent Heat Transfer; WIT Press: Southampton, UK, 2005; ISBN 978-1-85312-956-8. [Google Scholar]
- Wu, X.; Durbin, P.A. Numerical simulation of heat transfer in a transitional boundary layer with passing wakes. J. Heat Transf. 1999, 122, 248–257. [Google Scholar] [CrossRef]
- Spall, R.E. An Assessment of k-w and v2-f Turbulence Models for Strongly Heated Internal Gas Flows. Numer. Heat Transf. Part A 2004, 46, 831–849. [Google Scholar] [CrossRef]
- Argyropoulos, C.D.; Markatos, N.C. Recent advances on the numerical modelling of turbulent flows. Appl. Math. Model. 2015, 39, 693–732. [Google Scholar] [CrossRef]
- Smyth, T.A.G. A review of computational fluid dynamics (CFD) airflow modelling over aeolian landforms. Aeolian Res. 2016, 22, 153–164. [Google Scholar] [CrossRef]
- Kobayashi, H.; Hama, F.; Wu, X. Application of a Local SGS Model Based on Coherent Structures to Complex Geometries. Int. J. Heat Fluid Flow 2008, 29, 640–653. [Google Scholar] [CrossRef]
- Ansys, Inc. Fluent 18.0 User’s Guide; Ansys, Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- CHAM, PHOENICS v.1.0 User’s Guide, October 2022. Available online: https://www.cham.co.uk/phoenics/d_polis/d_docs/tr316/tr316.pdf (accessed on 1 February 2024).
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A Dynamic Subgrid-Scale Eddy Viscosity Model. Phys. Fluids A 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics: An Advanced Introduction with OpenFOAM® and Matlab; Springer: Berlin/Heidelberg, Germany, 2015; ISBN 978-3319168739. [Google Scholar]
- Yoshizawa, A. Statistical Theory for Compressible Turbulent Shear Flows, with the Application to Subgrid Modeling. Phys. Fluids 1986, 29, 2152–2164. [Google Scholar] [CrossRef]
- Kyrtatos, P.; Bardis, K.; Bolla, M.; Denisov, A.; Wright, Y.; Herrmann, K.; Boulouchos, K. Transferability of Insights from Fundamental Investigations into Practical Applications of Prechamber Combustion Systems. In Proceedings of the Ignition Systems for Gasoline Engines: Internationale Tagung Zündsysteme für Ottomotoren, Berlin, Germany, 6–7 December 2018; p. 442. [Google Scholar]
- Zhou, L.; Liu, P.; Zhong, L.; Feng, Z.; Wei, H. Experimental observation of lean flammability limits using turbulent jet ignition with auxiliary hydrogen and methane in pre-chamber. Fuel 2021, 305, 121570. [Google Scholar] [CrossRef]
- Xu, G.; Kotzagianni, M.; Kyrtatos, P.; Wright, Y.M.; Boulouchos, K. Experimental and numerical investigations of the unscavenged prechamber combustion in a rapid compression and expansion machine under engine-like conditions. Combust. Flame 2019, 204, 68–84. [Google Scholar] [CrossRef]
- Rajasegar, R.; Niki, Y.; Garcia-Oliver, J.M.; Li, Z.; Musculus, M.P.B. Fundamental insights on ignition and combustion of natural gas in an active fueled prechamber spark-ignition system. Combust. Flame 2021, 232, 111561. [Google Scholar] [CrossRef]
- Atis, C.; Chowdhury, S.S.; Ayele, Y.; Stuecken, T.; Schock, H.; Voice, A.K. Ultra-Lean and High EGR Operation of Dual Mode, Turbulent Jet Ignition (DM-TJI) Engine with Active Pre-Chamber Scavenging; SAE Technical Paper 2020-01-1117; SAE International: Warrendale, PA, USA, 2020. [Google Scholar]
- Iacovano, C.; d’Adamo, A.; Cantore, G. Analysis and Simulation of Non-Flamelet Turbulent Combustion in a Research Optical Engine. Energy Procedia 2018, 148, 463–470. [Google Scholar] [CrossRef]
- Dekena, M.; Peters, N. Combustion Modeling with the G-Equation. Oil Gas Sci. Technol. 1999, 54, 265–270. [Google Scholar]
- Stiesch, G. Modeling Engine Spray and Combustion Processes; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Peters, N. Turbulent Combustion. Cambridge Monographs on Mechanics, 4th ed.; Cambridge University Press: Cambridge, UK, 2006; ISBN 9780521660822. [Google Scholar]
- Chinnan, J.A. Simulation and Validation of In-Cylinder Combustion for a Heavy-Duty Otto Gas Engine Using 3D-CFD Technique. Master’s Thesis, KTH Industrial Engineering and Management Machine Design, Stockholm, Sweden, 2018. [Google Scholar]
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Ewald, J.; Peters, N. On unsteady premixed turbulent burning velocity prediction in internal combustion engines. Proc. Combust. Inst. 2007, 31, 3051–3058. [Google Scholar] [CrossRef]
- Gulder, O.L. Turbulent Premixed Flame Propagation Models for Different Combustion Regimes; The Combustion Institute: Pittsburgh, PA, USA, 1990; pp. 743–750. [Google Scholar]
- Bradley, D.; Lau, A.K.C.; Lawes, M. Flame stretch rate as a determinant of turbulent burning velocity. Philos. Trans. R. Soc. Lond. 1992, 338, 359–387. [Google Scholar] [CrossRef]
- Meneveau, C.; Poinsot, T. Stretching and quenching of flamelets in Premixed turbulent combustion. Combust. Flame 1991, 86, 311–332. [Google Scholar] [CrossRef]
- Lu, T.; Law, C.K. A Criterion Based on Computational Singular Perturbation for the Identification of Quasi Steady State Species: A Reduced Mechanism for Methane Oxidation with NO Chemistry. Combust. Flame 2008, 154, 761–774. [Google Scholar] [CrossRef]
- Toulson, E. Applying Alternative Fuels in Place of Hydrogen to the Jet Ignition Process. Ph.D. Thesis, Department of Mechanical Engineering, The University of Melbourne, Parkville, VIC, Australia, 2009. [Google Scholar]
- Veynante, D.; Vervisch, L. Turbulent Combustion Modeling. Prog. Energy Combust. Sci. 2002, 28, 193–266. [Google Scholar] [CrossRef]
- Suillaud, E. Modelling of High Karlovitz Combustion in Spark-Ignition Engines. Ph.D. Thesis, Chemical and Process Engineering, Université Paris-Saclay, Gif-sur-Yvette, France, 2021. [Google Scholar]
- Meneveau, C.; Sreenivasan, K.R. The Multifractal Nature of Turbulent Energy Dissipation. J. Fluid Mech. 1991, 224, 429–484. [Google Scholar] [CrossRef]
- Salerno, F.; Bargende, M.; Kulzer, A.; Grill, M.; Burkardt, P.; Günther, M.; Pischinger, S.; Villforth, J. A Quasi-Dimensional Burn Rate Model for Pre-Chamber-Initiated Jet Ignition Combustion. SAE Int. J. Adv. Curr. Pract. Mobil. 2023, 5, 2258–2277. [Google Scholar] [CrossRef]
- Kim, J.; Scarcelli, R.; Som, S.; Shah, A.; Biruduganti, M.S.; Longman, D.E. Evaluation of Combustion Models for CFD Simulation of Pre-Chamber Ignition in a Natural Gas Engine. In Proceedings of the 11th U.S. National Combustion Meeting, Pasadena, CA, USA, 24–27 March 2019. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-25202-3. [Google Scholar]
- Ikegaya, N.; Okaze, T.; Kikumoto, H.; Imano, M.; Ono, H.; Tominaga, Y. Effect of the numerical viscosity on reproduction of mean and turbulent flow fields in the case of a 1:1:2 single block model. J. Wind Eng. Ind. Aerodyn. 2019, 191, 279–296. [Google Scholar] [CrossRef]
- GAMMA Technologies. GT-SUITE. 2024. Available online: https://www.gtisoft.com/gt-suite/ (accessed on 1 June 2024).
- Benson, R.S.; Horlock, J.H.; Winterbone, D.E. The Thermodynamics and Gas Dynamics of Internal-Combustion Engines; Clarendon Press: Oxford, UK, 1982. [Google Scholar]
- Bozza, F.; De Bellis, V.; Tufano, D.; Malfi, E.; Müller, C.; Habermann, K. A Quasi-Dimensional Model of Pre-Chamber Spark-Ignition Engines; SAE Technical Paper 2019-01-0470; SAE International: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- De Bellis, V.; Bozza, F.; Fontanesi, S.; Severi, E.; Berni, F. Development of a Phenomenological Turbulence Model through a Hierarchical 1D/3D Approach Applied to a VVA Turbocharged Engine. SAE Int. J. Engines 2016, 9, 506–519. [Google Scholar] [CrossRef]
- Berni, F.; Cicalese, G.; Fontanesi, S. A modified thermal wall function for the estimation of gas-to-wall heat fluxes in CFD in-cylinder simulations of high performance spark-ignition engines. Appl. Therm. Eng. 2017, 115, 1045–1062. [Google Scholar] [CrossRef]
- Reitz, R. Assessment of Wall Heat Transfer Models for Premixed-Charge Engine Combustion Computations; SAE Technical Paper 910267; SAE International: Warrendale, PA, USA, 1991. [Google Scholar] [CrossRef]
- Jayatilleke, C.L.V. The influence of Prandtl number and surface roughness on the resistance of the laminar sublayer to momentum and heat transfer. In Progress in Heat and Mass Transfer; Pergamon Press: Oxford, UK, 1969; Volume 1. [Google Scholar]
- Kays, W.M.; Crawford, M.E. Convective Heat and Mass Transfer, 3rd ed.; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Angelberger, C.; Poinsot, T.; Delhay, B. Improving Near-Wall Combustion and Wall Heat Transfer Modeling in SI Engine Computations; SAE Technical Paper 972881; SAE International: Warrendale, PA, USA, 1997. [Google Scholar] [CrossRef]
- Han, Z.; Reitz, R.D. A temperature wall function formulation for variable density turbulent flows with application to engine convective heat transfer modeling. Int. J. Heat Mass Transf. 1997, 40, 613–625. [Google Scholar] [CrossRef]
- Dou, X.; Yosri, M.; Talei, M.; Yang, Y. Impact of wall heat transfer modelling in large-eddy simulation of hydrogen knocking combustion. Int. J. Hydrogen Energy 2024, 62, 405–417. [Google Scholar] [CrossRef]
- Heywood, J.B. Internal Combustion Engine Fundamentals, 2nd ed.; McGraw-Hill: New York, NY, USA, 2018. [Google Scholar]
- Rakopoulos, C.D.; Kosmadakis, G.M.; Pariotis, E.G. Critical evaluation of current Heat transfer models used in CFD in-cylinder engine simulations and establishment of a comprehensive wall-function formulation. Appl. Energy 2010, 87, 1612–1630. [Google Scholar] [CrossRef]
- Torregrosa, A.J.; Broatch, A.; Gil, A.; Gomez-Soriano, J. Numerical approach for assessing combustion noise in compression-ignited Diesel engines. Appl. Acoust. 2018, 135, 91–100. [Google Scholar] [CrossRef]
- Hiraoka, K.; Nomura, K.; Yuuki, A.; Oda, Y.; Kameyama, T. Phenomenological 0 Dimensional Combustion Model for Spark-Ignition Natural Gas Engine Equipped with Pre-Chamber; SAE Technical Paper 2016-01-0556; SAE International: Warrendale, PA, USA, 2016. [Google Scholar]
- Le Guen, S.; Maiboom, A.; Bougrine, S.; Tauzia, X. Analysis of Systematic Calibration of Heat Transfer Models on a Turbocharged GDI Engine Operating Map; SAE Technical Paper 2018-01-0787; SAE International: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Silva, M.; Sanal, S.; Hlaing, P.; Cenker, E.; Bengt, J.; Hong, G.I. A Computational Investigation of Fuel Enrichment in the Pre-Chamber on the Ignition of the Main Chamber Charge; SAE Technical Paper 2021-01-0523; SAE International: Warrendale, PA, USA, 2021. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).