Equalized Distributed Control Strategy for AC Microgrid Energy Storage SOCs

Abstract

Most of the previous SOC equalization methods for microgrid energy storage target DC microgrids and use centralized control structures, while in recent years many researchers have begun to focus on a decentralized, communication-based implementation of distributed control structures. In this paper, based on the existing research, we use the multi-agent system (MAS) structure and dynamic consistency algorithm (DCA) to realize the estimation of the SOC mean value of microgrid energy storage obtained by each agent in the system. For the problems of the iterative convergence that exists in the distributed control, such as being too slow, too frequent communication, stability, etc., we optimally select the parameters of the consistency iterative summation to improve convergence. In addition, we use the event-driven method to further reduce the unnecessary communication frequency. Finally, a numerical simulation model of the AC microgrid is established by Matlab to verify the effectiveness of the method, which reduces the communication volume by about 50% while maintaining the effect of the control strategy.

1. Introduction

Microgrids are gaining more and more attention in recent years as a new kind of miniature power system to cope with the shortage of fossil fuels and environmental pollution [1,2,3]. However, due to the stochasticity and uncertainty of renewable energy output, which can easily bring many negative impacts to microgrids [4,5,6], microgrids are usually equipped with corresponding energy storage systems to work together [7]. A Battery Energy Storage Device (BESD) is a common energy storage method for microgrids due to its high reliability, mature technology, and other advantages [8,9], but with the continuous operation of the system, the State of Charge (SOC) of the batteries will be different, which may cause some BESDs to be over-charged or to exit the operation prematurely due to the low battery level, thus causing the rest of the storage to bear an excessive load, further deteriorating the microgrid operation state and affecting the battery life [9,10,11]. Therefore, if the SOC balancing strategy can be introduced to optimize the power allocation of microgrid energy storage when smoothing out the frequency fluctuation, it is of great significance to make full use of the capacity of energy storage and improve the security and stability of the microgrid [8,9,10,11].

The current equalization methods for energy storage SOCs in microgrids can be classified into centralized and distributed control strategies according to the presence or absence of a central controller that communicates with each energy storage unit.

In [8], the authors propose a fuzzy control-based method to equalize the battery SOC and maintaine the stability of the system output voltage. In [10], the authors use improved sag control to incorporate the battery SOC into the frequency sag equation, thus correcting the energy storage local sag control parameters to realize the energy storage charging and discharging power control. In [12], the authors propose a hierarchical operation control strategy for multiple energy storage units based on SOC, which can avoid the over-discharging or over-charging of energy storage units and realize the SOC equalization of multiple energy storage units, but there is no communication between the energy storage systems in this method, which may lead to a greatly reduced control effect due to the collection of bad data. In [13,14,15,16,17], the authors investigate relatively independent energy storage battery packs, mainly using mutual charging and discharging between energy storage cells as a means of the SOC equalization control. In [8,10,12,13,14,15,16,17], the authors use all centralized control strategies, and these control strategies impose extremely high requirements on the reliability of the control center, and the failure of a single point may cause the whole system to fail to work properly. Moreover, most of the traditional methods consider DC microgrids [18]. In AC microgrids, there are frequency and phase attributes as well as three-phase line characteristics, and the methods for DC microgrids are usually unable to deal with the reactive power distribution and frequency of sag problems in AC microgrids [19]. In recent years, decentralized distributed control structures have gained popularity among researchers for their higher reliability, scalability, and flexibility [20]. In [11], the authors introduce the SOC equalization factor in sag control to achieve the SOC equalization of distributed energy storage units (DESUs) with different power ratings, but the energy storage is not involved in the frequency or voltage control of the microgrid. The authors of [18,21] address the frequency sag problem in AC microgrids based on a multi-agent structure and improved sag control, where the agent gives its own estimate of the overall SOC average through consistent iteration and uses this as a criterion to regulate the power output, although the method does not consider that the energy storage system may have different power ratings. In [21], the authors adopt a distributed structure and propose a two-tier SOC equalization control strategy based on a dynamic consistency algorithm, in which each individual estimates the overall SOC mean and calculates the deviation from its own SOC, and the difference is controlled by PI to form a virtual impedance correction quantity, which then regulates the output power of each energy storage.

In addition, the authors of [22,23] propose a distributed control strategy using distributed consensus based on ADMM to manage batteries’ integrations considering different sources of uncertainties. However, these authors did not consider the impact of communication volume on control, as frequent data requests in control algorithms and rapid changes in loads may lead to a significant increase in communication volume between devices. It can cause communication congestion, communication delay, and packet loss. This will result in inaccurate raw data, reduced SOC calculation accuracy, increased calculation iterations, and higher requirements for agent devices and communication networks.

In [24] the authors consider the difference between different storage capacities and use improved sag control and storage local information to achieve SOC equalization independent of communication. In [25], an event-driven control structure combined with a consistency algorithm is used to realize power allocation among inverter sources of islanded AC microgrids to achieve a consistent power loading rate, which effectively reduces the frequency of communication between agents, but does not take into account the difference in capacity between individuals.

The main purpose of this paper is to propose a distributed control strategy that can realize microgrid power balance and SOC equalization. To be specific, the contributions of this paper are as follows:

1. Introducing event-driven control to reduce the amount of communication between the MAS agents in the process of achieving SOC equalization, while ensuring the proper SOC equalization control;

2. Accelerating the linear iterative process of agents using consistent parameter optimization methods in distributed control and convergence analysis;

3. Based on the existing distributed microgrid SOC equalization control, and considering the rated capacity of energy storage and the initial SOC, a distributed control strategy that can realize microgrid power balance and SOC equalization is proposed.

The main contents of the subsequent sections of this paper are as follows: Section 2 establishes the power model of the energy storage system, distributed power sources, and loads within the AC microgrid. Section 3 gives the definition of the agent, describes the communication network in a graph-theoretic way through which it establishes a multi-agent control system, and then conducts the convergence analysis of the system and proposes the distributed power calculation method that can realize the SOC equalization and the power balancing. Section 4, based on this foundation, defines the indexes to quantitatively measure the communication volume, introduces the optimization of the parameters of the consistency algorithm, and also introduces the event-driven mechanism to form the SOC balanced distributed control strategy for energy storage in microgrids. Section 5 conducts simulation experiments through Matlab R2018b to verify the effectiveness of the control strategy proposed in this paper and the optimization effect on the communication volume. Section 6 concludes the whole paper.

2. The Model for AC Microgrid

2.1. Energy Storage Model Considering SOCs

Based on the definitions of electricity and electrical energy, the classical SOC estimation method can be obtained [26]

$$SOC={\displaystyle \frac{Q_0-{\displaystyle \underset{0}{\overset{t}{\int }}\eta I\left(\tau \right)d\tau }}{Q_N}},$$

(1)

where $Q_0$ denotes the initial power of the battery; $Q_N$ denotes the rated power of the battery; $\eta$ denotes the charging/discharging efficiency; and $I\left(\tau \right)$ denotes the battery charging/discharging current at the moment τ. In the microgrid, the energy storage output during the time between two neighboring power commands can be regarded as unchanged, and the discrete energy storage model considering SOC can be obtained.

$$SOC\left(t+1\right)=SOC\left(t\right)+{\displaystyle \frac{P\left(t\right)}{C}}\mathrm{\Delta }t,$$

(2)

where $P\left(t\right)$ denotes the power of energy storage in time period t, because the power dissipated by IGBT is usually not large, and this paper approximates the AC side power for SOC calculation; $C$ denotes the change in SOC that will be caused by the unit power in time period Δt and the specific expression can be written as

$$C={\displaystyle \frac{Q_{N}V}{\eta }}.$$

(3)

This parameter is proportional to the rated power of the storage and the DC side voltage V. Each storage takes a different value and can be approximated as not changing with time; $\mathrm{\Delta }t$ indicates the time interval between two power changes.

Batteries are usually connected to the AC microgrid through an energy storage converter (ESC), and the two common existing ESC control methods are the PQ control strategy and V/f control strategy [27].

The system flow of the PQ control for energy storage is shown in Figure 1. Under the PQ control strategy, the system realizes the tracking control of the given power Pref and Qref through the power control loop and current inner-loop control, at which time the inverter power supply can be regarded as a constant power supply.

In this paper, each energy storage system is regarded as an agent (agent) in a multi-agent system (MAS) with the ability to communicate with neighboring agents and with the PQ control, which can operate according to a given power command and is regarded as a constant power source during normal operation.

2.2. Distributed Power and Load Modeling

In microgrids, photovoltaic (PV) power systems are the main form of distributed generation, and in this paper, only PV is included in the consideration of distributed power sources. In order to maximize the utilization of light, a PV power generation system usually adopts maximum power point tracking (MPPT) [28]. Figure 2 shows the structure of a common two-stage inverter grid-connected system; the first stage DC/DC converter usually adopts a boost circuit to realize boost and MPPT control, and the second stage is a DC/AC converter with constant power control.

Under this control method, the PV power generation system usually behaves as a constant power source in the microgrid, and its output is only determined by external conditions such as light intensity and temperature, which is highly stochastic.

The microgrid load also has a certain degree of randomness; in some cases, when the load rises and photovoltaic power is not enough to meet the load demand, the frequency of the microgrid bus will fall. In order to stabilize the frequency of the system within the allowable range, the microgrid energy storage system has to increase the power.

3. Energy Storage SOC Equalization Control Strategy

3.1. Definition of Agent Internal Data

In order to achieve a balanced SOC among parallel storage systems, the power should be allocated according to its own SOC while the total power of the storage system satisfies the loads and distributed power sources, which requires each agent to obtain an approximate estimation of the average value of the SOC of all the energy storage within the microgrid.

A single energy storage system is regarded as an individual with communication and computation capabilities, called an agent.Each agent needs to record within itself its own numbered ID, the current overall SOC mean value $SO{C}_{i,mean}$, the increment of the SOC mean value $SO{C}_{i,mean}$, and the above information of its neighbors that are able to communicate. The current SOC can be obtained by sampling according to the SOC estimation algorithm Equation (2), while the current SOC mean value needs to be obtained through communication with neighbors.Therefore each agent has the estimation of the overall mean value from itself and each neighbor.

When the agent obtains the above information through communication, it can calculate the required output of the energy storage system at the current moment based on this information, and realize the equalization of each energy storage SOC under the premise of satisfying the power balance of the microgrid.

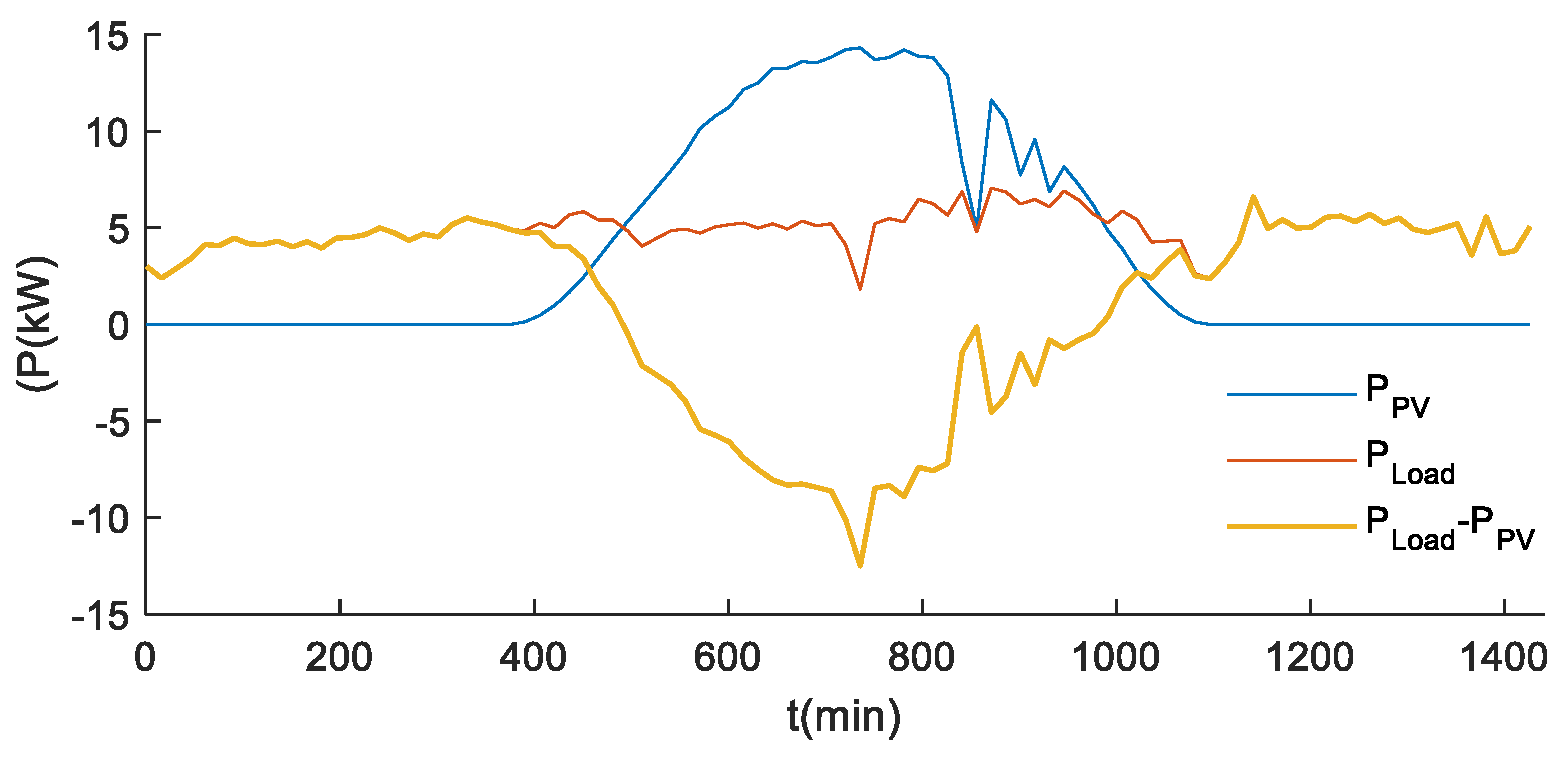
Figure 3 illustrates the communication connectivity relationships and the information stored locally by each agent in an AC microgrid containing six energy storage systems. While PDG denotes the sum of the outputs of the distributed power sources, PL denotes the total load within the microgrid, Pi (i = 1, …, 6) denotes the output of the ith energy storage system, DESUi, which is the energy storage system in the communication network, is represented by the agent i, and A and D denote the correlation matrix and degree matrix of the communication network, respectively. When Agent 1 needs to communicate with Agent 2, then Agent 1 sends its ID, its estimate of the overall SOC mean, and the SOC increment to Agent 2, which saves the received data locally according to the ID and updates the existing record x₂₁ where x₂₁ denotes the estimate of the overall SOC mean recorded by Agent 2 by Agent 1. In turn, Agent 2 sends the state quantity to Agent 1, which saves it locally and updates the local information in the same way.

3.2. Graph-Theoretic Representation of Communication Networks

In this paper, it is assumed that the energy storage systems under study can communicate with each other in both directions with the help of a communication network, and all such communication relationships can be described by an undirected graph containing the connection relationships between agents, denoted as $\mathit{G}=\left\{\mathit{N},\mathit{E}\right\}$. Where $\mathit{N}=\left\{v_1,v_2,\dots ,v_n\right\}$ denotes the set of all agents in the communication network, and $\mathit{E}=\left\{{\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_m\right\}$ denotes the set consisting of all communication connections in the communication network, where the group communication connection is an unordered set of two agents.

A communication relationship is said to exist between intelligence i and intelligence j if $\left\{v_i,v_j\right\}\in \mathit{E}$, and the set of all neighbors of intelligence i is denoted as ${\mathit{N}}_i=\left\{v_j|\left\{v_i,v_j\right\}\in \mathit{E}\begin{array}{cc};& j=1,\dots ,n\end{array}\right\}$.

For an undirected graph G, notate A to denote the association matrix of graph G. The association matrix of graph G is denoted as where $\mathit{A}={\left(a_{ij}\right)}_{n\times n}$, if $\left\{v_i,v_j\right\}\in E$ then $a_{ij}=1$, otherwise $a_{ij}=0$. $\mathit{D}=diag\left(d_1,\dots ,d_n\right)$. Denote the degree matrix of the graph, where $d_i$ is the number of edges connected to node i. Then, the Laplace matrix of G is $\mathit{L}=\mathit{D}-\mathit{A}$. The Laplace matrix L is a semipositive definite matrix capable of reflecting the connectivity of the graph, and the number of zeros in the L eigenvectors denotes the number of connected components in graph G, and its next smallest eigenvalue denotes the closeness of the communication network connection. In this paper, it is assumed that the communication network formed between the energy storage of the microgrid is connected, i.e., the L eigenvector contains only one zero.

3.3. Multi-Agent SOC Equalization Control System Model

Consider a communication-based MAS, and let the MAS contain n agents and the state of intelligence i be denoted by $x_i$. It is assumed that its state equation is described by Equation (4).

$${\dot{x}}_i=u_i,i=1,\dots ,n,$$

(4)

where $u_i$ denotes the input control signal of the agent i.

Using the graph theory described in Section 4.2 to describe the agents and their communication relationships in MAS, the following can be seen: (1) Each node represents an intelligence in the system, and all the agents constitute the set of nodes $N=\left\{v_1,v_2,\dots ,v_n\right\}$. (2) If there exists a direct communication between agents i and j, the two are connected by an edge, and all the communication relationships in the system constitute the set of edges $E=\left\{{\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_m\right\}$. (3) Agents that have a direct communication with intelligence i are neighbors of node i in the graph. The neighbors of node i are denoted by the set $N_i=\left\{v_j|\left\{v_i,v_j\right\}\in E\begin{array}{cc};& j=1,\dots ,n\end{array}\right\}$.

The agents communicate with each other and eventually the overall state is consistent, and according to the consistency algorithm [28], the control signal can be expressed as Equation (5):

$$u_i=-{\displaystyle \sum _{j\in N_i}\left(x_i-x_j\right)}.$$

(5)

In order to ensure the convergence of the iterations of the discrete consistency algorithm, the coefficient α [29] is introduced to obtain the state update Formula (6) for the discrete consistency algorithm:

$$x_i\left(t+1\right)=x_i\left(t\right)+\alpha u_i.$$

(6)

3.4. Convergence Analysis

In the microgrid system depicted in Figure 3 of Section 3.1, the agent state variable $x_i=SO{C}_{i,mean}$ is selected. Representing the consistency in matrix form, iterating Equation (5) yields

$$\mathit{u}=-\mathit{L}\mathit{x}.$$

(7)

Describe the consistency iteration formula as a matrix and write

$$\mathit{W}=\mathit{I}-\alpha \mathit{L},$$

(8)

where $\mathit{I}$ is the unit diagonal array. Then, the system state update method can be expressed as

$$\mathit{x}\left(t+1\right)=\mathit{W}\mathit{x}\left(t\right).$$

(9)

Theorem 1.

[30]. Under the iterative formulation described in Equation (9), the matrix $\mathit{W}$ satisfies the following three conditions if and only if:

(1) 

${\mathbf{1}}^T\mathit{W}={\mathbf{1}}^T$

(2) 

$\mathit{W}\mathbf{1}=\mathbf{1}$

(3) 

$\rho \left(\mathit{W}-{\displaystyle \frac{1}{n}}{\mathbf{11}}^T\right)<1$

The state quantity of each intelligence $x_i$ can eventually converge to the average value of the initial state quantity $x_i\left(0\right)$ through iteration. Where $\mathbf{1}$ is the unit column vector, $\rho (·)$ denotes the matrix spectral radius.

Noting that the communication network in the MAS is connected and the communication between the energy storage systems considered in this paper is bidirectional, the Laplace matrix L satisfies

$${\mathbf{1}}^T\mathit{L}={\mathbf{0}}^T,$$

(10)

$$\mathit{L}\mathbf{1}=\mathbf{0},$$

(11)

where $\mathbf{0}$ is a zero-column vector. Thus, it is not difficult to show that both conditions (1) and (2) of Theorem 1 are satisfied.

The spectral radius of $\mathit{W}-{\displaystyle \frac{1}{n}}{\mathbf{11}}^T$ can be written as

$$\rho \left(\mathit{W}-{\displaystyle \frac{1}{n}}{\mathbf{11}}^T\right)=\max \left\{{\lambda }_2\left(\mathit{W}\right)\begin{array}{cc},& -{\lambda }_n\left(\mathit{W}\right)\end{array}\right\},$$

(12)

where ${\lambda }_k(·)$ denotes the kth largest eigenvalue of the matrix. From (8), the eigenvalues of matrix W and matrix L satisfy the relationship between them according to their size

$${\lambda }_k\left(\mathit{W}\right)=1-\alpha {\lambda }_{n-k+1}\left(\mathit{L}\right).$$

(13)

Bringing (13) into Equation (12) yields

$$\rho \left(\mathit{W}-{\displaystyle \frac{1}{n}}{\mathbf{11}}^T\right)=\max \left\{1-\alpha {\lambda }_{n-1}\left(\mathit{L}\right)\begin{array}{cc},& \alpha {\lambda }_1\left(\mathit{L}\right)-1\end{array}\right\}.$$

(14)

Since the communication network of the energy storage system is connected and contains only one connected component, the Laplace matrix L of the graph is semipositive definite, and there are ${\lambda }_n\left(\mathit{L}\right)=0\begin{array}{cc},& {\lambda }_{n-1}\left(\mathit{L}\right)>0\end{array}$. Thus, Equation (14) only needs to ensure that $\alpha {\lambda }_1\left(\mathit{L}\right)-1<1$ satisfies the conditions of Theorem 1, i.e.,

$$\alpha <{\displaystyle \frac{2}{{\lambda }_1\left(\mathit{L}\right)}}.$$

(15)

To summarize, in the case where Equation (15) is satisfied, it can be ensured that the state of the multi-agent system converges to the mean of the initial values after consistency iterations. Therefore, each agent in the MAS can obtain the overall SOC mean value via communication.

3.5. Agent Power Calculation Method

Following the MAS framework described in Section 3.3, each energy storage system in the microgrid is treated as an intelligence in the system, and the state variable is the current intelligence’s estimate of the overall SOC, with control signals generated by communication with neighbors.

Before the start of each instruction cycle, the state variable $x_i$ is initialized to its own current SOC

$$x_i\left(0\right)=SO{C}_i.$$

(16)

After completing the update of its own state, the agent notifies all neighbors of the change in its own state and sends the updated amount of state to the neighbors, and when the neighbor j receives the state update information from the agent i, the state information of the agent i recorded by the agent j is updated

$$x_{ji}=x_i\left(0\right)j\in N_i,$$

(17)

where $x_{ji}$ denotes the state of agent i as recorded by agent j. When an agent notifies a neighbor of a status update, it is treated as if a communication has taken place.

At the beginning of the iteration, each intelligence calculates the increment of its own estimate of the overall SOC according to its own recorded information

$$u_i=-{\displaystyle \sum _{j\in N_i}\left(x_i-x_{ij}\right)}.$$

(18)

After calculating the increment, the agent’s own state is updated according to Equation (19)

$$x_i\left(k+1\right)=x_i\left(k\right)+\alpha u_i.$$

(19)

Here, k denotes the number of iterations performed in one instruction cycle. From the consistency algorithm and reasoning described in Section 4.4, it is clear that Equations (17)–(19) are able to converge the state variables recorded by each intelligence to the average value of the overall SOC.

It is assumed that the microgrid power deficit is obtained from the difference between the distributed power output and the load, and when the distributed power output is lower than the load, the microgrid frequency will drop. The droop-controlled islanded microgrid bus frequency satisfies the equation:

$${\omega }_B={\omega }_0+K_d\left(P_{DG}-P_L\right).$$

(20)

where ${\omega }_B$ denotes the microgrid bus frequency; ${\omega }_0$ denotes the standard frequency; $K_d$ denotes the sag control coefficient; $P_{DG}$ denotes the total power of the distributed power sources in the microgrid; and $P_L$ denotes the total power of loads.

After the agent consistency iteration is carried out, the bus frequency is detected ${\omega }_B$, and the agent power is calculated using its own SOC, SOC mean, and capacity-related parameters, and the power is calculated by Equation (21).

$$P_i={\displaystyle \frac{{\omega }_0-{\omega }_B}{K_d}}[C_i/{\displaystyle \sum _{j=1}^n{C}_j}+\mathrm{sgn}\left({\omega }_0-{\omega }_B\right)K_{soc}\left(SO{C}_i-SO{C}_{i,mean}\right)],$$

(21)

where $C_i$ denotes the storage capacity-related parameter, which generally does not change over time, so it can be informed to all the agents and recorded in the initialization phase of MAS; $SO{C}_i$ denotes the current moment SOC of storage; $SO{C}_{i,mean}$ denotes the estimated value of storage on the average value of SOC; sgn denotes the sign function; and $K_{soc}$ denotes the SOC equilibrium coefficient of storage, and the larger the value is, the larger the difference of the power produced by the difference of SOC, and the faster the SOC convergence is, but the smaller the value is, the slower the SOC convergence is. The larger the value, the larger the power difference due to the SOC difference, the faster the SOC convergence, but also the more likely that the storage power exceeds the upper limit, and the smaller the value, the slower the SOC convergence.

If the consistency iteration reaches convergence, then the estimation of the overall SOC mean by all the stored energy converges to the SOC mean at the beginning of the iteration, i.e.,

$$SO{C}_{i,mean}=SO{C}_{j,mean}=\cdots ={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^{n}SO{C}_i}.$$

(22)

However, the estimated and actual values are not necessarily equal in practice, and the gap is determined by the number of iterations and convergence conditions.

By bringing Equation (22) into Equation (21), the sum of all the stored energy powers is

$${\displaystyle \sum _{i=1}^n{P}_i}={\displaystyle \frac{{\omega }_0-{\omega }_B}{K_d}}=P_L-P_{DG}.$$

(23)

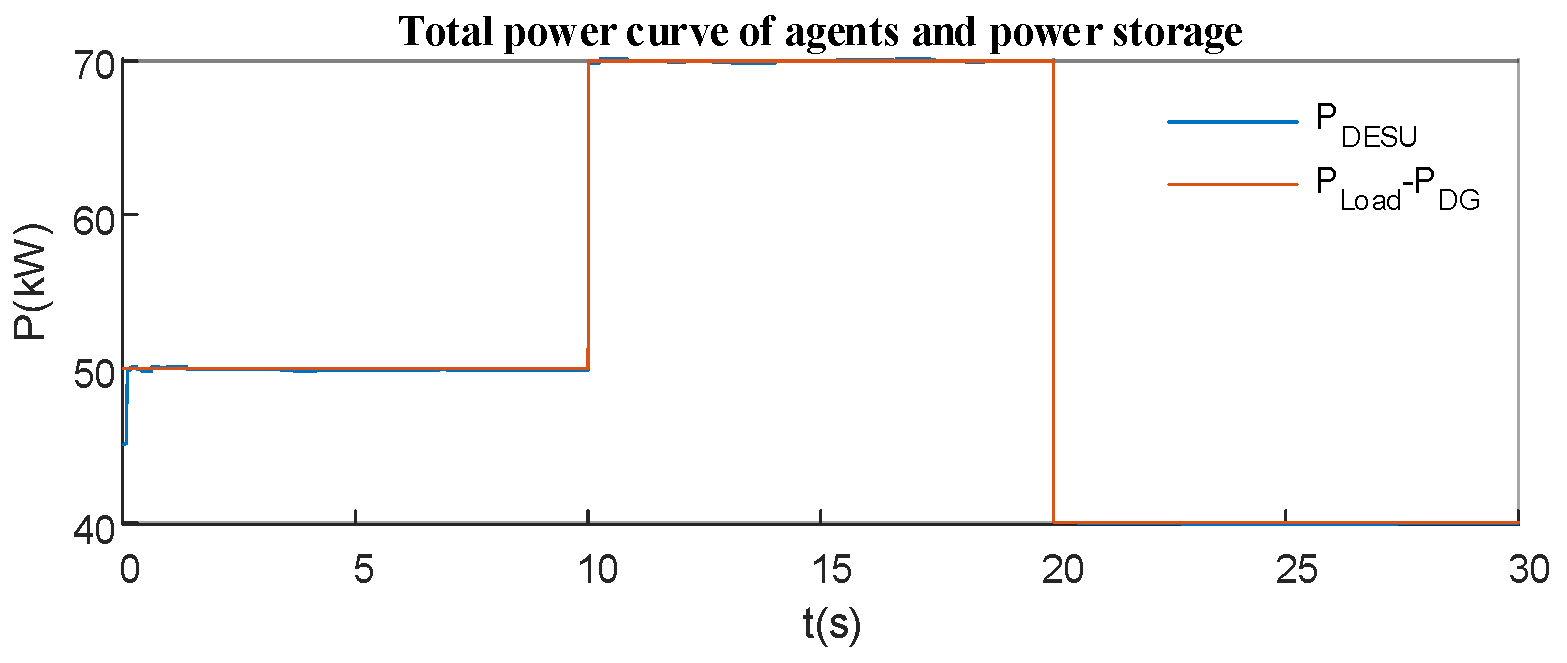
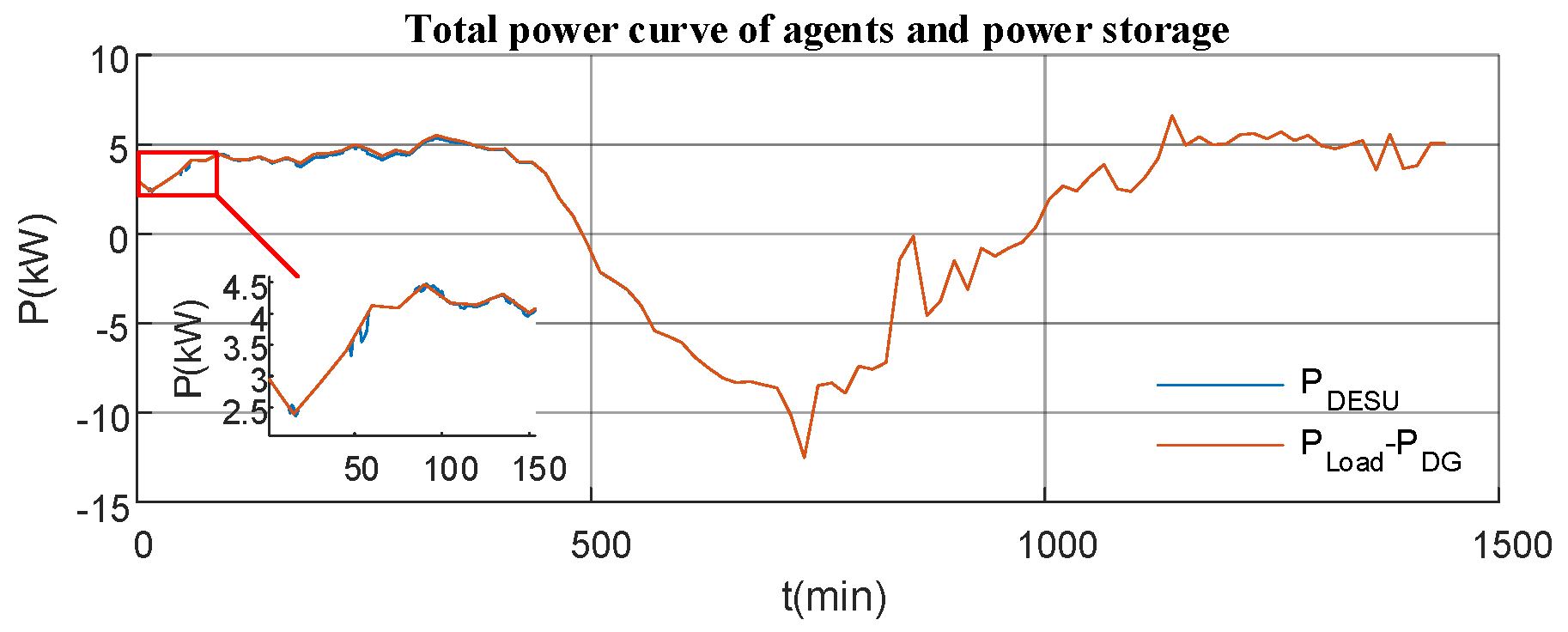
Equation (23) illustrates that the control strategy is able to make the sum of the total power of all the energy storage equal to the difference between the load and the distributed power output.

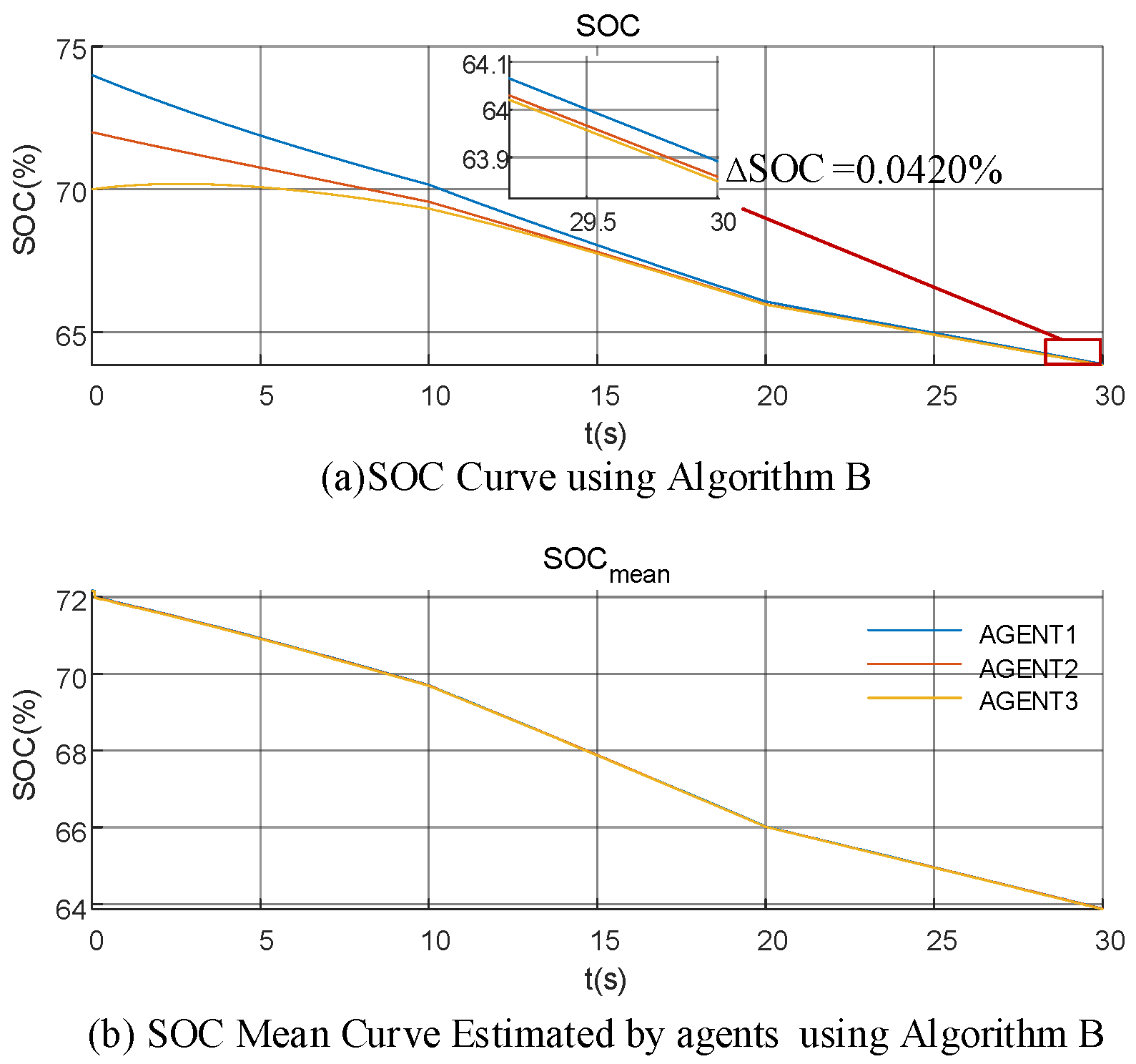
When the SOC of each intelligence is equalized after running for a period of time, there are

$$SO{C}_{i,mean}=SO{C}_i i=1,\cdots ,n.$$

(24)

Bringing Equation (24) into Equation (21), for any two different agents i and intelligence j, one obtains

$${\displaystyle \frac{P_i}{P_j}}={\displaystyle \frac{C_i}{C_j}} i\ne j.$$

(25)

Combined with Equation (2), we can see that

$$\mathrm{\Delta }SO{C}_i=\mathrm{\Delta }SO{C}_j i\ne j.$$

(26)

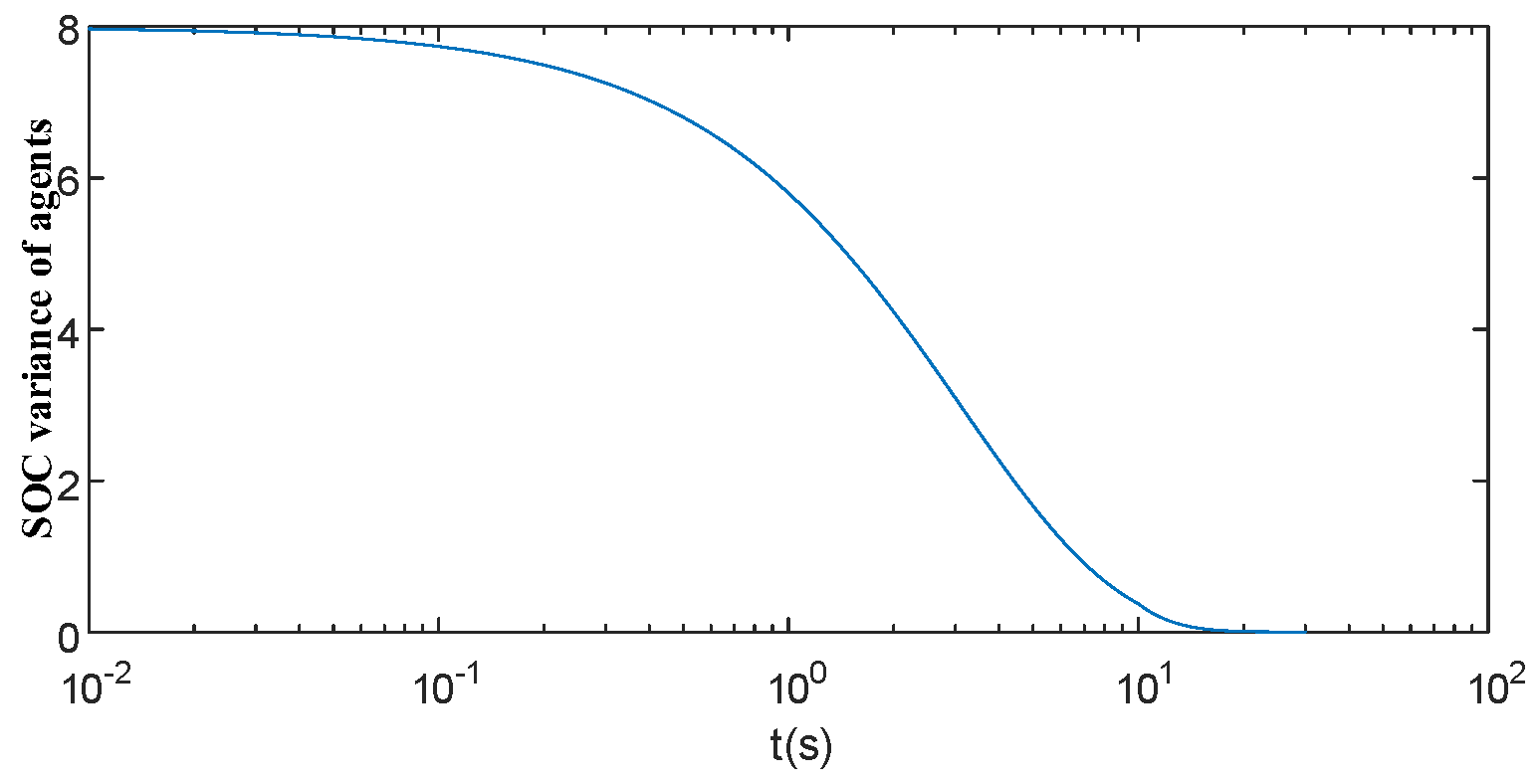
Equation (26) shows that when the system reaches stability, the SOC increment of each intelligence is consistent in one control cycle, so the control algorithm can keep the SOC stable equilibrium after equilibrium.

4. Communication Volume Analysis and Control Strategy Optimization

4.1. Number of Iterations and Communication Statistics

From the MAS control model in Section 3.3, it is known that the system communicates to make the overall SOC average available to all agents. Whenever an agent updates its own state, it has to notify all its neighbors of the state change, so the amount of communication in the system is directly related to the number of times an agent updates its own SOC. So, on the one hand, it is possible to use Formula (27) for judgment in the consistency control to reduce the redundant communication carried out after the energy storage SOC reaches consistency.

$$\left|\alpha u_i\right|\ge \epsilon \left|x_i\right|,$$

(27)

where $\epsilon$ is a positive real number indicating precision.

On the other hand, it is known from Section 4.3 that the value of α directly affects the convergence of the SOC estimation effect of the agents and the number of iterations required to reach convergence, and a reasonable value of α can reduce the number of iterations to reach agreement, which in turn reduces the number of communications.

When (27) is satisfied, it means that there is still a gap between the neighbor’s estimation of SOC and the intelligence’s own estimation, and the consistency iteration has not yet converged, and a state update is needed. If (27) is not satisfied, the intelligence maintains its state unchanged and does not notify the neighbors in this calculation, and in this mechanism, the values of α and $\epsilon$ are directly related to the size of the communication, and a reasonable selection of α and $\epsilon$ can effectively reduce unnecessary communication during the control. The reasonable selection of α can effectively reduce the unnecessary communication in the control process.

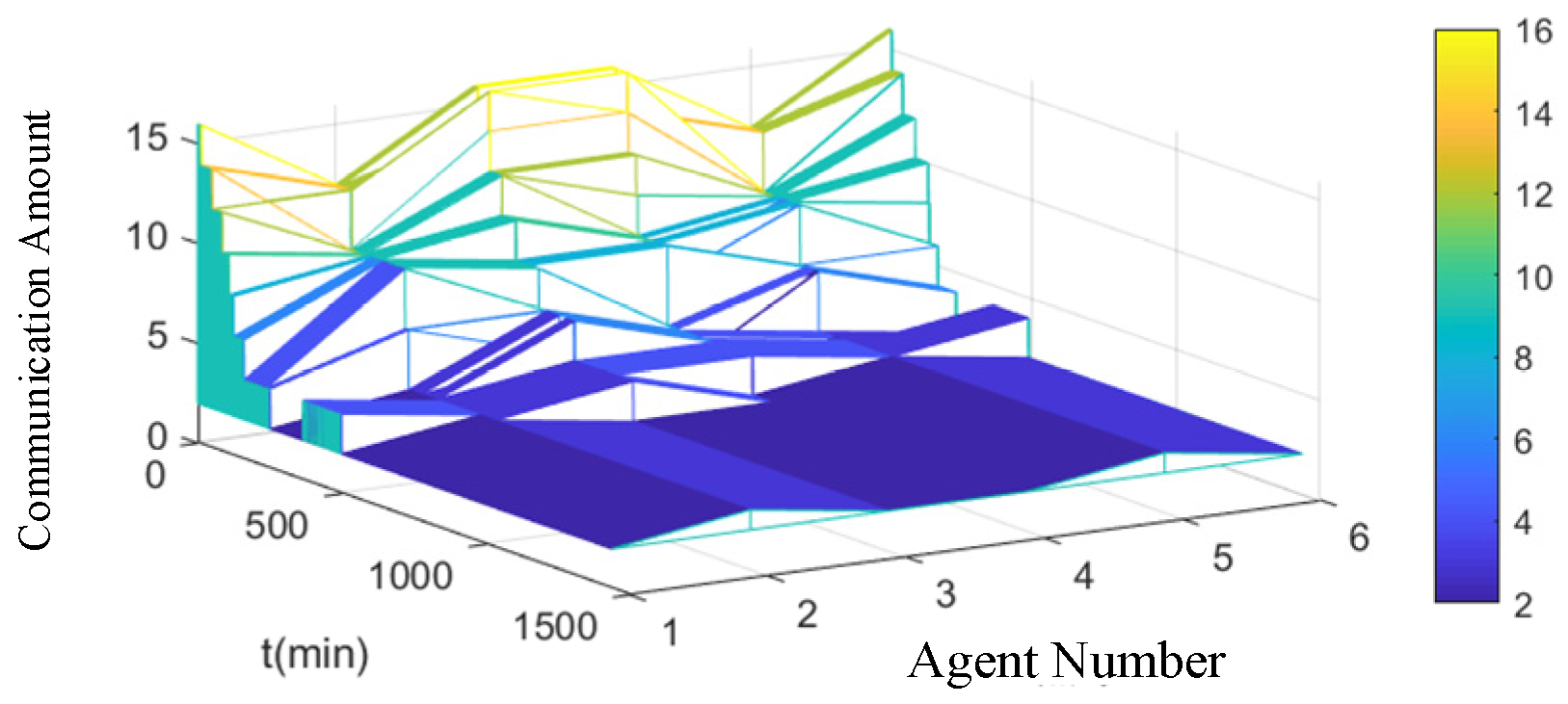
Considering that the number of communications is related to the topology of the communication network and the maximum number of iterations allowed in the same instruction cycle of a single agent, in order to compare the effect of the control strategy on the amount of communication, the ratio of the total communication to the maximum communication is defined as $\sigma$.

$$\sigma ={\displaystyle \frac{N_{com}}{2\left|E\right|\left(K_{\max }+1\right)T}},$$

(28)

where $T$ denotes the total number of instruction cycles; $N_{com}$ denotes the total number of communications of the system in $T$ instruction cycle time; $\left|E\right|$ denotes the number of edges in the communication network; and $K_{\max }$ denotes the maximum number of iterations allowed for a single agent in MAS in one instruction cycle.

4.2. Optimization of Parameter Selection

The value of α in the iteration formula described in Equation (6) is directly related to the convergence of the consistency iteration, a reasonable α can reduce the number of iterations performed by the system while ensuring the convergence of the iteration, and the number of iterations in the MAS is directly related to the amount of communication in the control process, so optimally selecting the value of α is of great significance. From Equation (9) and Theorem 1, It can be obtained:

$$\underset{t\to \infty }{\lim }{\mathit{W}}^t={\displaystyle \frac{1}{n}}{\mathbf{11}}^T$$

Therefore, fast consistency convergence can be achieved by minimizing the value of $\Vert {\mathit{W}}^t-{\displaystyle \frac{1}{n}}{\mathbf{11}}^T\Vert$ by selecting the optimization variable $\mathit{W}$. It can be obtained through the conditions of Theorem 1:

$${\mathit{W}}^t-{\displaystyle \frac{1}{n}}{\mathbf{11}}^T=\mathit{W}-{\displaystyle \frac{1}{n}}{\mathbf{11}}^T$$

Then, the optimization problem turns to minimize $\Vert \mathit{W}-{\displaystyle \frac{1}{n}}{\mathbf{11}}^T\Vert$. Since the optimization problem is a convex optimization problem, its global optimal solution [30] can be obtained. The value of optimal α can be obtained from $\mathit{W}=\mathit{I}-\alpha \mathit{L}$:

$$\alpha ={\displaystyle \frac{2}{{\lambda }_1\left(\mathit{L}\right)+{\lambda }_{n-1}\left(\mathit{L}\right)}},$$

(29)

4.3. Event-Driven Iterative Mechanism

In the traditional energy storage SOC balanced distributed control strategy, a large number of communications between agents are often required, and even with the communication conditions limited by Equation (27) and the parameter optimization method described in Section 4.2, many redundant communications still occur, because Equation (27) judges whether convergence is achieved by the relative increment of the agents’ own states. If an event-driven condition can be proposed based on the neighbor information recorded locally by the energy storage and its own SOC estimation, the agents can judge whether the states agree or not according to the data, and the energy storage is able to update its state when the condition is triggered, or otherwise maintain its state at the time of the last triggering, and the amount of required communication can be further reduced.

Record the average value of SOC of agent i recorded at the neighbor of agent i as $x_i\left(t_k^i\right)$. For the current state of agent i $SO{C}_{i,mean}$, if the state is updated, the result of the update is $x_i\left(t\right)$, denote $e_i\left(t\right)=x_i\left(t_k^i\right)-x_i\left(t\right)$. Then, bringing in Equation (7), we have

$$\dot{\mathit{x}}=-\mathit{L}\mathit{x}\left(t_k^i\right)=-\mathit{L}\left(\mathit{x}+e\right),$$

(30)

define $\mathit{z}=\mathit{L}\mathit{x}$, i.e.,

$$z_i={\displaystyle \sum _{j\in N_i}\left[x_i\left(t\right)-x_{ji}\left(t\right)\right]}, i=1,\cdots ,n.$$

For the control system described by Equations (5) and (7), let its Lyapunov function be

$$V={\displaystyle \frac{1}{2}}{\mathit{x}}^T\mathit{L}\mathit{x}$$

From Equation (30), we can obtain

$$\dot{V}={\mathit{x}}^T\mathit{L}\dot{\mathit{x}}=-{\mathit{x}}^T\mathit{L}\left(\mathit{L}\mathit{x}+\mathit{L}\mathit{e}\right)=-{\mathit{z}}^T\mathit{z}-{\mathit{z}}^T\mathit{L}\mathit{e}.$$

(31)

Writing the vector expression in the form of a real number yields

$$\dot{V}=-{\mathit{z}}^T\mathit{z}-{\mathit{z}}^T\mathit{L}\mathit{e}=-{\displaystyle \sum _{i=1}^n{z}_i^2}-{\displaystyle \sum _{i=1}^{n}n{z}_i{e}_i}+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\in N_i}{z}_i{e}_j}}.$$

(32)

Introducing the positive constant a and deflating $z_i{e}_j$ in the final summation part of Equation (32) using the arithmetic-geometric mean inequality yields

$$\dot{V}=-{\displaystyle \sum _{i=1}^n{z}_i^2}-{\displaystyle \sum _{i=1}^{n}n{z}_i{e}_i}+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\in N_i}{z}_i{e}_j}}\le -{\displaystyle \sum _{i=1}^n{z}_i^2}+{\displaystyle \sum _{i=1}^{n}an{z}_i^2}+{\displaystyle \sum _{i=1}^n\frac{1}{2a}n{e}_i^2}+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\in N_i}\frac{1}{2a}{e}_j^2}}.$$

(33)

Note that in the last summation in the above equation, since all communications are bidirectional in the communication model studied in this paper, if $j\in N_i$, then there must be $i\in N_j$. This yields

$${\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\in N_i}\frac{1}{2a}{e}_j^2}}={\displaystyle \sum _{i=1}^n\frac{n}{2a}{e}_i^2}.$$

(34)

Bringing Equation (34) into Equation (33) yields

$$\dot{V}\le -{\displaystyle \sum _{i=1}^n\left(1-an\right)z_i^2}+{\displaystyle \sum _{i=1}^n\frac{1}{a}n{e}_i^2}.$$

(35)

When the system is in a steady state at $\dot{V}\le -{\displaystyle \sum _{i=1}^n\left(1-an\right)z_i^2}+{\displaystyle \sum _{i=1}^n\frac{1}{a}n{e}_i^2}\le 0$, the sufficient condition that enables the above equation to be satisfied is, for each intelligence, the following $-\left(1-an\right)z_i^2+{\displaystyle \frac{1}{a}}n{e}_i^2\le 0$ $i=1,\cdots ,n$

i.e.,

$$e_i^2\le {\displaystyle \frac{{\sigma }_{i}a\left(1-an\right)}{n}}{z}_i^2,$$

(36)

where the parameter ${\sigma }_i\in \left(0,1\right)$, the coefficient introduced by the inequality $a\in \left(0,1/n\right)$ is usually taken as $a=1/2n$ to maximize the coefficient. Equation (36) is the common event-driven condition for the consistency control of multi-agent systems [29], and when Equation (36) is satisfied, the system is stable in Lyapunov’s sense, and when the above Equation is not satisfied, after updating the state of the agent so $e_i=0$, the system still satisfies the stability criterion $\dot{V}\le 0$.

It should be noted that the expression of the original $z_i$ is not a good representation of the difference between the state of agent i and its neighbors, because the difference between the state of agent i and its neighbors may be positive or negative, and the addition leads to the offset of the state difference. The calculation of the $z_i$ value is on the low side, which leads to the low threshold of the event triggering condition of Equation (36), and the event is easily triggered in some cases, which increases the unnecessary communication. Therefore, in this paper, the $z_i$ value is calculated by Equation (37) in the strategy.

$$z_i={\displaystyle \sum _{j\in N_i}\left|x_i\left(t\right)-x_{ji}\left(t\right)\right|}.$$

(37)

In the control strategy proposed in this paper, the agent performs a self-state update using only the neighbor state information that has been updated in the current command cycle, and there is no chance that the state of the agent will be consistent to a value that deviates from the mean value because the neighbor event has not been triggered under this strategy.

In the control strategy of this paper, the current state of i recorded by neighbor j of agent I $SO{C}_{i,mean}$ is used as the result of updating after the most recent event trigger $x\left(t_k^i\right)$, and the current result of agent i computed by Equation (19) is used as the actual amount of the state of agent i at the current moment $x\left(t\right)$. When Equation (36) is satisfied in the iteration, the agent updates its own state according to Equation (19) and broadcasts it to its neighbors. Otherwise, the agent maintains its own state and enters into the next round of iteration, which reduces the occurrence of unnecessary communication in the control by this event-driven approach.

4.4. SOC Equalization Policy Flow

On the basis of the distributed balanced control strategy for the microgrid energy storage SOC described in Section 4, the method of a balanced control strategy for the energy storage SOC described in this paper is obtained by combining the consistency parameter optimization and event-driven control structure described in Section 4.2 and Section 4.3, and the flow of the control strategy is shown in Figure 4.

The control flow of the SOC equalization strategy described in this paper is as follows:

(1) Initialization of the system, determining the consistency of the calculated parameters between the MAS agents, and checking the status of the communication network;

(2) After the energy storage system detects the frequency change, the control strategy starts to execute. At the beginning of each process, i.e., before the strategy starts running at time t, each agent samples the current state, i.e., calculates the current SOC of the energy storage system according to Equation (2), and uses it to update the locally stored state quantity. According to the communication network, it sends its own SOC information to all its neighbors, and at the same time, receives SOC information from its neighbors and updates the locally recorded data;

(3) Each agent performs an iterative computation according to the information of the local record in accordance with Equations (18) and (19) to determine whether the local state quantity needs to be updated. There may be some un-updated data in the local record, and the agent will skip the local records that have not been updated by its neighbors when performing a single computation. The judgment condition here is Equation (27), and also the event-driven condition derived in Section 4.3 is a prerequisite for communication to take place; the agent updates and initiates communication when, and only when, both mechanisms simultaneously believe that the state needs to be updated;

(4) If the local state quantity of the agent is updated, i.e., Equation (27) and the event-driven condition are satisfied, the updated state quantity is sent to all the neighbors, and the neighbors who receive the message record the state locally;

(5) After all the agents that need to communicate have completed this communication, go back to step (3) until the maximum number of iterations is reached or the convergence condition is reached;

(6) Completing a round of consistency calculation, each agent checks itself. If the agent does not initiate any communication other than initialization during the command cycle, it indicates that the current SOC has reached a level close to the mean. The agent updates its own SOC mean with local information to maintain the difference between the current SOC and the overall SOC mean. Each agent obtains the overall SOC mean value locally, and each agent calculates the power locally using Equation (21);

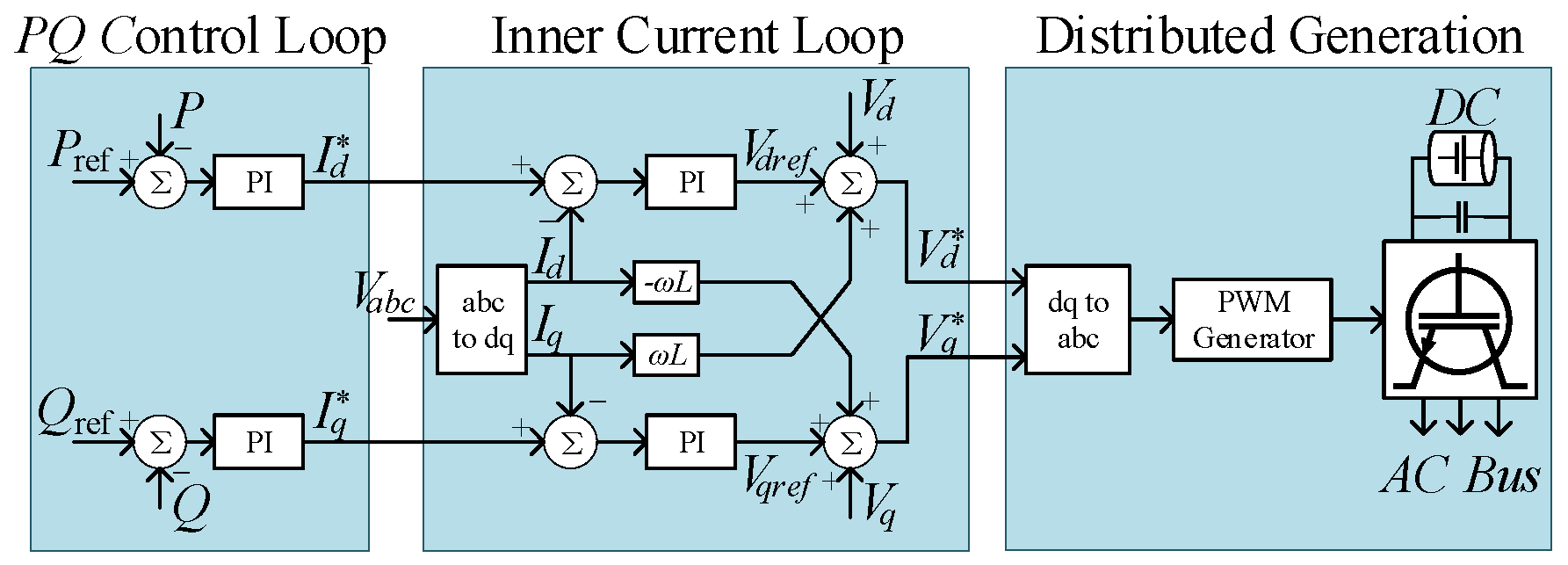
(7) The locally calculated power is sent down to the energy storage PQ control input loop as the power reference value, and the converter quickly follows the power command to realize the control target.

In the above control process, except for what is obtained by the agent when communicating with its neighbors, the rest of the required data come from local sources, which do not need to be regulated by a central controller, achieving distributed control and realizing energy storage SOC equalization under the condition of satisfying the distributed power and load power constraints.

5. Simulation Verification

5.1. Calculation Example 1: SOC Equalization for Small-Capacity AC Microgrids

A SOC balancing strategy based on a multi-agent system is proposed in the literature [31], which employs PI control and droop control structures to regulate the energy storage power. In addition, the literature [31] builds a numerical simulation model of a three-storage microgrid as a platform for strategy validation. According to the parameters of the literature, the numerical simulation system in this paper is built, as shown in Figure 5, with three agents which form a bidirectional communication network using the minimum spanning tree of the graph with a total of two communication connections.

Appendix B 

Table A1. Parameter of AC microgrid 1.

Sports Event	Notation	Numerical Value
Battery 1 capacity	$C_{1\_bt}$	50 Ah
Battery 2 capacity	$C_{2\_bt}$	25 Ah
Battery 3 capacity	$C_{3\_bt}$	25 Ah
SOC initial value	$SO{C}_i$	[74 72 70]%
SOC correction factor	$K_{SOC}$	3.5 × 10−2
Maximum number of iterations	$k_{\max }$	20
Convergence accuracy	$\epsilon$	5× 10−3
Consistency iteration factor	α	0.5

shows the parameters of this microgrid system, energy storage, and control algorithm. According to the communication network here, α is not difficult to be calculated from Equation (29):

$$\alpha ={\displaystyle \frac{2}{{\lambda }_1\left(\mathit{L}\right)+{\lambda }_{n-1}\left(\mathit{L}\right)}}={\displaystyle \frac{1}{2}}$$

The simulation time is 30 s, and the storage command period is 1 ms. The variation curve of each storage SOC obtained after executing the algorithm in the literature [31], which is named algorithm A, is shown in Figure 6. In contrast, the curve obtained after executing the algorithm in this paper, which is named algorithm B, is shown in Figure 6 and Figure 7. The variation curve of each storage power, the total power and the microgrid power deficit, and the variation curve of the storage SOC variance during the simulation using algorithm B are shown in Figure A1, Figure A2 and Figure A3 in the Appendix A.

By comparing Figure 6 and Figure 7, it can be seen that agent 2 and agent 3 achieve a SOC balancing at 10 s in Figure 7, which is better than it is in Figure 6, and the time for three agents to achieve a SOC balancing in Figure 7 is similar to Figure 6. It can demonstrate that the algorithm proposed in this article has the higher convergence speed.

As shown in Figure 7a, the strategy given in this paper reduces the maximum difference between the SOC of each cell to 0.0420% at 30 s, and when compared with the control method in the literature [31], the system has a difference of 0.4% between the SOC of each cell at 30 s [31], and this paper ultimately achieves a better SOC equalization. Figure 7b demonstrates the variation of the estimation of the SOC mean value by each intelligence during the control process, and each intelligence accurately obtains the overall SOC mean value and maintains it consistently in each command cycle.

Appendix A Figure A1 shows the power change of each storage energy during the SOC equalization process. Appendix A Figure A2 shows the change curve of the difference between the total storage power, load, and distributed power output. It can be seen that the algorithm in this paper meets the microgrid power balancing requirements through the accurate estimation of the overall SOC by each agent and the proposed power calculation formula. Appendix A Figure A3 demonstrates the variation curve of the actual SOC variance of each energy storage in 30 s, and the SOC variance is approximated to decrease at an exponential rate under the control strategy of this paper.

5.2. Calculation Example 2: Large-Capacity Optical Storage Microgrid Power Balance

5.2.1. Parameters of High-Capacity Optical Storage Microgrids

In order to further validate the effectiveness of the algorithm in the complex and variable AC microgrid environment, especially to verify the SOC equalization effect when the load power and distributed power output change frequently, the islanded microgrid model containing six energy storage systems and the communication network topology shown in Figure 3 are established in the Matlab environment.

The microgrid parameters and control parameters are shown in Appendix B Table A1, where the energy storage rating $C_i$ is expressed in the form of Equation (3), which is a parameter obtained by synthesizing the energy storage rating itself, charging and discharging efficiency, and DC terminal voltage.

5.2.2. Impact of Parameters in Consistency on Communication Volume

In order to verify the effectiveness of the parameter optimization method given by Section 3.2, simulation experiments are considered by taking different values of α and comparing the number of communications during the simulation. From Figure 3, the Laplace matrix of the communication topology graph is given by

$$\mathit{L}=\mathit{D}-\mathit{A}=\left[\begin{array}{cccc}\begin{array}{c}2\\ -1\\ \\ \begin{array}{c}\\ \\ -1\end{array}\end{array}& \begin{array}{c}-1\\ 3\\ 1\\ \begin{array}{c}\\ -1\\ \end{array}\end{array}& \begin{array}{c}\\ -1\\ 2\\ \begin{array}{c}-1\\ \\ \end{array}\end{array}& \begin{array}{ccc}\begin{array}{c}\\ \\ -1\\ \begin{array}{c}2\\ -1\\ \end{array}\end{array}& \begin{array}{c}\\ -1\\ \\ \begin{array}{c}-1\\ 3\\ -1\end{array}\end{array}& \begin{array}{c}-1\\ \\ \\ \begin{array}{c}\\ -1\\ 2\end{array}\end{array}\end{array}\end{array}\right]$$

Calculate its maximum and minimum positive eigenvalues to obtain

$${\lambda }_{n-1}\left(\mathit{L}\right)=5{\lambda }_1\left(\mathit{L}\right)=1$$

The computed eigenvalues are brought into Equation (29) to obtain

$$\alpha ={\displaystyle \frac{2}{{\lambda }_1\left(\mathit{L}\right)+{\lambda }_{n-1}\left(\mathit{L}\right)}}={\displaystyle \frac{1}{3}}$$

In order to compare the effect of different values of α on the communication volume and control stability, given a command power of 5 kW in this microgrid, the SOC equalization and communication volume changes are observed under different values of α as shown in Figure 7, while the values of the total communication volume corresponding to σ are recorded in

Table 1. Communication amount with different α.

α	σ	Instruction Cycles Required for SOC Consistency
1/2	99.873%	go out of control
1/2.6	85.561%	137
1/3	29.733%	138
1/4	29.461%	139
1/5	33.302%	139

, and the following total power is shown in Figure 8.

Figure 8 demonstrates the effect of different values of α on the amount of communication. Due to the value of α being too large, the system cannot be stabilized in Figure 8a, and the system is unable to reach a SOC that is consistent at the set accuracy in Figure 8b. In contrast, by comparing Figure 8c with Figure 8d,e, it can be seen that when the value of α is too small, the agents have to make the SOCs consistent through repeated communication, which is reflected in the fact that the amount of communication is more than 150 times for the first 100 instruction cycles the amount of communication in Figure 8d,e. In addition, in Figure 8c, when α takes the optimal value, it is able to stay around 150 times during this period.

From Equations (15) and (29), the stability threshold and optimal value of α are 1/2 and 1/3, respectively. Table 1 demonstrates the σ values corresponding to different α values and the number of instruction cycles required to reach the SOC equilibrium. With α set near the optimal value, σ decreases by about 30%, and when α continues to decrease, although the SOC is able to track the SOC mean more accurately in the iterative process due to the decrease in the iteration’s step size, from Figure 8d,e, it can be seen that this will lead to a significant rise in the number of iterations and a sharp increase in the communication volume at the beginning of the control, which may bring great pressure to the communication network in a short time, while the communication volume change curve for the optimal α value is relatively smoother. In addition, the smaller α is more likely to make Equation (27) not hold after reaching SOC convergence, leading to more offset total power constraints after the system is stabilized, as shown in Figure 9b,c.

In terms of combining the communication volume and the need for accuracy in meeting the total power constraint, the choice of the value of α determined by Equation (29) has a better performance in realizing the SOC equalization control for energy storage.

5.2.3. Verification of Simulation Examples

As seen in Figure 3, the microgrid system contains six distributed energy storage units, as well as distributed power sources and loads, with the PV generation data in one day at a certain location as the output curve of distributed power sources, and the local load variation data as the load curve in the microgrid, as shown in Figure A4 in the Appendix A. The starting SOC and capacity of energy storage are shown in

Table A2. Parameter of AC microgrid 2.

Sports Event	Notation	Numerical Value
Frequency of sag factor	$K_d$	1× 10−4 rads/W
Energy storage rating	$C_i$	[200 200 200 140 120 100]
SOC initial value	$SO{C}_i$	[50 50 25 40 70 75]%
SOC correction factor	$K_{SOC}$	3.5× 10−2
Maximum number of iterations	$k_{\max }$	20
Convergence accuracy	$\epsilon$	5× 10−3
Event-driven factor	${\sigma }_i$	[5× 10−4 5× 10−4 5× 10−4 5× 10−4 5× 10−4 5× 10−4]
The inequality introduces the parameter	$a$	1/12

in the Appendix A. The simulation results are shown in Figure 9 and Figure 10 and Figure A5, Figure A6 and Figure A7 in the Appendix A.

Figure 10 shows the change curves of SOC and state quantity in each energy storage system. It can be seen that each storage SOC can quickly achieve equalization. After 340 min of simulation, the difference between the maximum and minimum values of storage SOC in the microgrid is reduced to 1.2836%, and it can be assumed that the SOC reaches consistency. In addition, the consistency iteration enables each energy storage to obtain a more accurate overall SOC average and dynamically follow the SOC average during operation.

Figure 11 shows the variation in the number of communications of each agent during the whole process. It can be found that since AGENT2 and AGENT5 have three neighbors, the total number of communications of these two and three is about 1.5 times more than that of each of the remaining agents.

From Figure 11, it can be seen that before the overall energy storage SOC is equalized, frequent communications are required to achieve an accurate estimation of the SOC mean, while after the SOC variance is reduced, the number of communications decreases significantly. In fact, 58.04% of the communications throughout the whole process occur in the first 500 min, suggesting that the triggering mechanism expressed by Equations (27) and (36) is able to significantly reduce the unnecessary communications without affecting the agent’s effectiveness in estimating the overall SOC.

The results in Appendix A Figure A5, Figure A6 and Figure A7 surface that the control strategy described in this paper is able to achieve fast SOC equalization while satisfying the power balance within the microgrid.

Appendix A Figure A5 shows the power variation curves of six different capacities of energy storage under the control strategy described in this paper, and the storage output power is proportional to the rated power parameter of the energy storage after reaching SOC equalization.

Appendix A Figure A6 shows the variation curves of the difference between the power of loads and distributed power sources within the microgrid $P_L-P_{DG}$ and the sum of the power of all the stored energies $P_{DESU}={\displaystyle \sum _{i=1}^n{P}_i}$. The total power of each stored energy achieves a stable following of the microgrid power demand within a small number of command cycles and automatically maintains the power balance within the microgrid.

Appendix A Figure A7 demonstrates the variance change of each energy storage SOC, and the variance decreases approximately exponentially. As can be seen from Appendix A Figure A7, the SOC variance has been reduced to stable after 500 min, and the SOC equalization effect has been basically achieved. Since the agent local SOC is very close to the overall SOC mean value, the communication is only for the agent to update its own real-time SOC to its neighbors, and the estimate SOC mean is obtained with almost no iterative computation.

The simulation is performed during $t\in \left(500,900\right)$ when the PV output is higher than the load within the microgrid, and from Equation (21), it can be seen that at this time the energy storage SOC produces a negative contribution to the proportion of power distribution, so the higher the SOC is, the lower the value of power absorbed by the storage, which is in line with the actual demand.

Figure 12 demonstrates the effect of the event-driven mechanism described in Section 4.3 on the communication volume. When there is a difference between the actual SOCs of the energy storage, event-driven and non-event-driven have significant differences in the communication volume. However, when the actual SOCs of the energy storage have been basically made consistent, event-driven and non-event-driven mechanisms have the same communication volume, which is only the broadcasted communication of the actual SOCs of the agent itself before the start of each instruction cycle. According to the method described in the previous section, the proportion of communication using event-driven and non-event-driven methods in this example was calculated using Equation (28). The value of σ in the event-driven approach is 7.4709% and the value of σ in the non-event-driven approach is 15.241%, which shows that the event-driven structure is able to further minimize the communication pressure of the multi-agent control system.

6. Conclusions

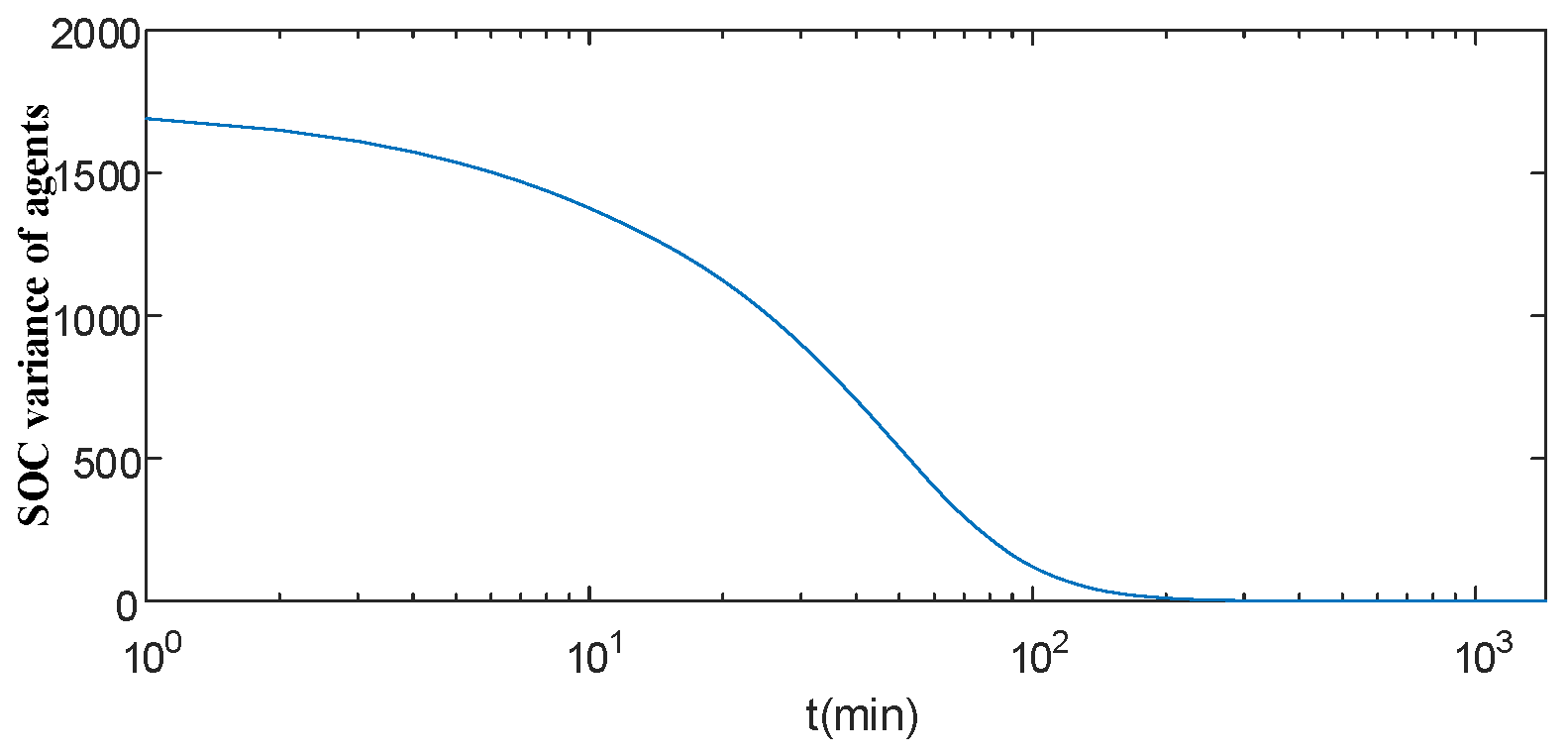
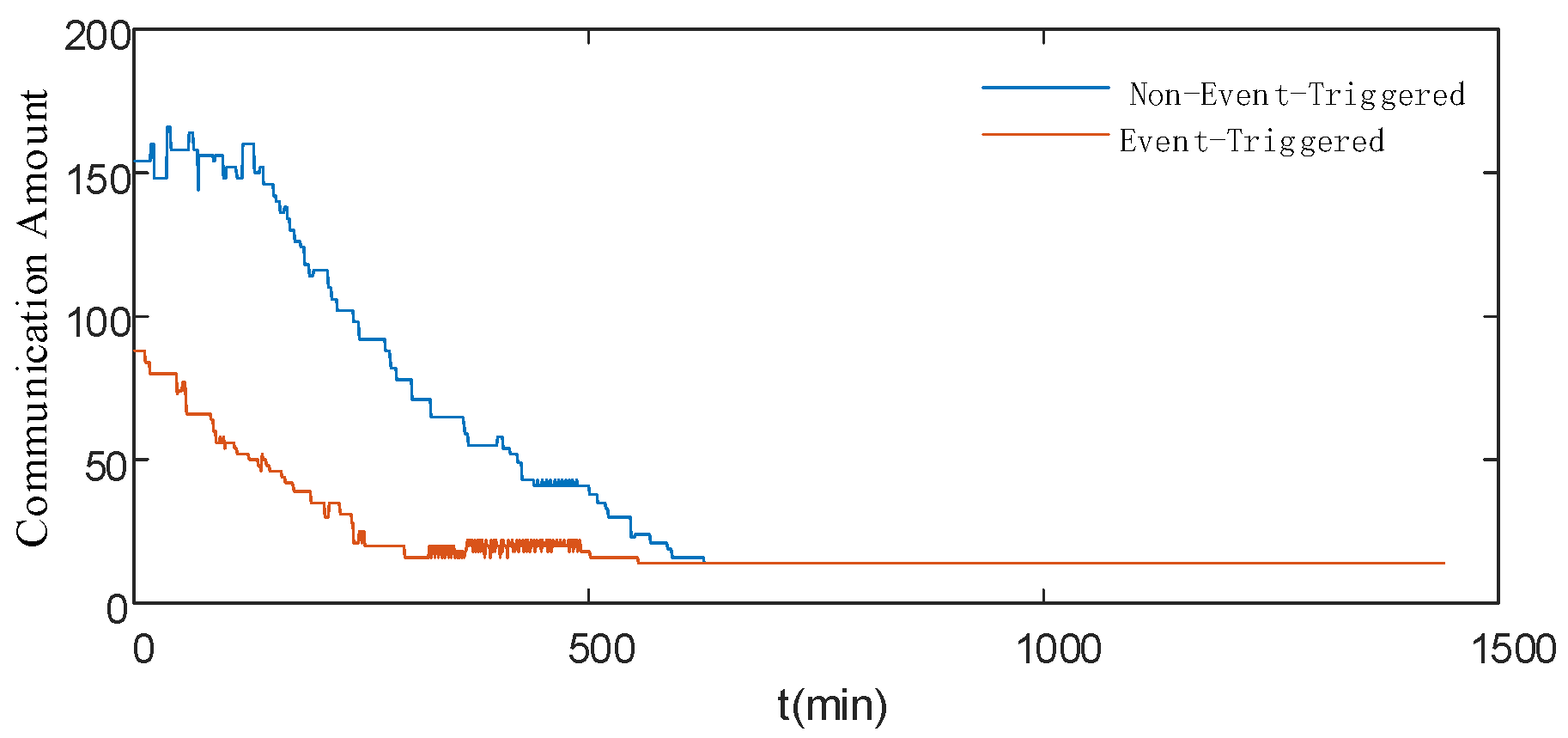
Considering that in the future, large-scale microgrids may have energy storage systems provided by different manufacturers, long distances, and other factors, the centralized control structure cannot solve the problem of the coordinated control of each energy storage system. This paper is based on the multi-intelligence body distributed control strategy, adopts the consistency algorithm to realize the overall SOC equalization, and accelerates the convergence of iterations by appropriately selecting the coefficients in the consistency iterative summation and adopts the event-driven condition in the form of event-triggered communication when communicating. In the form of event-driven triggering in communication, the communication volume during iteration is reduced, and in the simulation results carried out in this paper, the communication volume can be reduced by about 50% while maintaining the effect of the control strategy.

In the energy storage SOC equalization control strategy described in this paper, the existence of different power ratings and different SOC initial value factors for energy storage is considered, and it has the characteristics of a distributed structure, high robustness, and suitability for scenarios with limited communication resources, etc. It is able to achieve frequency restoration in AC microgrids with droop control and satisfy the power balance conditions while maintaining the SOCs of each storage in a relatively balanced state, and has a certain prospect of application in the future. When the efficiency of the centralized energy storage control structure decreases due to the further expansion of the microgrid scale, it has certain application prospects.