Benchmarking Electrolytes for the Solid Oxide Electrolyzer Using a Finite Element Model

Abstract

The demand for green hydrogen is increasing, as it is estimated to reduce ten percent of total global green-house-gas emissions from fossil fuel. The solid oxide electrolysis cell (SOEC) is an electrochemical energy-conversion device (EECD) that produces green hydrogen via steam electrolysis. It is preferred to other EECDs for clean hydrogen production owing to its high efficiency, robust kinetics, and lack of precious-metal requirements for cell construction. Herein, we report a Multiphysics model describing the transport phenomena in the SOEC. The governing equations used in the model include a thorough description of the electrode kinetics and of the behavior of the three electrode–electrolyte interfaces in the cell. For the first time, the effect of the scandium-doped zirconia (SCGZ), yttrium-stabilized zirconia (YSZ), and gadolinium-doped ceria (GDC) electrolytes was modeled at different temperatures and pressures. By linking the convection and diffusion equations with the Butler–Volmer at shorter scales, a true representation of the cell operation was simulated. Our models show a R² value of over 0.996 in predicting the cell-polarization curves and electrochemical properties at the given operating conditions. The impedance of the SCGZ was 0.0240 Ohm.cm². This value was two- and four-fold lower than the values of the YSZ and GDC, respectively. Furthermore, our theoretical findings of both the polarization data and the impedance were in good agreement with the experimental data.

1. Introduction

Global energy demands and the need to reduce reliance on fossil fuels have led to a search for an alternative source of energy that is clean, sustainable, reliable, and accessible globally [1]. Green hydrogen is emerging as an option that satisfies all these requirements. It is produced through the electrolysis of water using electricity produced from renewable sources of energy. Hydrogen produced globally through electrolysis is projected to rise to 14 MT by 2030 (a 55% increase from 2021) [2]. The solid oxide electrolysis cell (SOEC) is a promising technology that is being developed as an electrochemical energy-conversion device (EECD) for H₂ production. These SOECs are utilized for large-scale electrolysis operations instead of other EECDs, such as proton-exchange-membrane electrolysis cells, alkaline electrolysis, etc., due to thee fast kinetics of their electrolysis reactions. Additionally, SOECs have a high efficiency, of over 75%, and no precious metals, like platinum, are required for their construction. They also provide flexibility of operation in various feeds, such as CO₂. The operation of SOECs in fuel-cell mode can be used to power electricity grids, whereas this option for reversible operations is not present in other EECDs. The cell consists of a ceramic electrolyte sandwiched between porous cathode and anode layers, which acts as catalyst for electrolysis reactions. The assembly is enclosed between interconnections, which provides a flow channel for the supply of feed and the exit of the products, as shown in Figure 1a, which also illustrates the overall cell reaction and operation. The cell utilizes high-temperature steam, which is supplied through the manifold electrodes to the flow channel. The steam diffuses into the cathode as depicted in Figure 2a, and it is reduced to hydrogen gas and oxide ions. The hydrogen diffuses back through the electrode and into the gas channel, and the oxide ions are conducted through the electrolyte into the anode, as illustrated in Figure 2b. At the anode, the oxide ions react to form oxygen gas. The oxygen gas is taken out of the cell through a carrier gas, as depicted in Figure 2c.

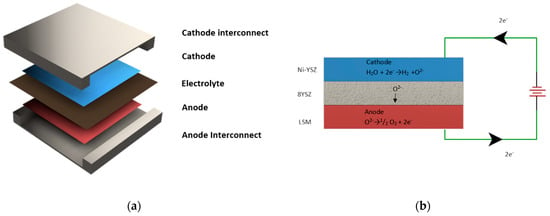
Figure 1. (a) Components of SOEC. (b) SOEC’s working principle.

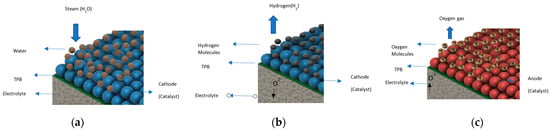
Figure 2. (a) Diffusion of steam into cathode. (b) Hydrogen-evolution reaction in cathode t and oxide-ion conduction. (c) Oxygen-evolution reaction in anode.

Multiphysics modeling is a key approach to understanding the macroscopic functioning of the SOEC. It takes account of multiple physical phenomena occurring within cells, such as mass transfer, fluid dynamics, electrochemical reaction kinetics, etc. The incorporation of these phenomena into a single model helps to provide a better understanding of the interdependence of these phenomena and to accurately predict cell performance. This approach is critical for optimizing the design of the cell and the operating conditions. Many studies of SOECs have been performed to assess the temperature distribution, Nernst potential distribution, current-density distribution, hydrogen-concentration distribution across electrolytes, triple-phase boundary (TPB) [3], overpotential [4], area-specific resistance (ASR) [5], impact of the flow configuration [6], and effect of delamination [7,8] using 0D and 1D equations. The details of the cell design, the experimental findings, and the empirical model’s results are listed in Table 1.

Table 1. Review of literature available on multiphysics modeling of a SOEC.

Sl No	Cathode (Material–Thickness–Porosity)	Anode (Material–Thickness–Porosity)	Electrolyte (Material–Thickness)	Steam-Feed Rate	Feed Composition	Temperature K	Parameters Studied	Ref.
1	Ni-YSZ-25 μm-0.37	LSM-25 μm-0.37	YSZ-140 μm	4.33 × 10−6 kgs−1.	N2:H2:H2O-0.51:0.0074:0.483	1073	Temperature, Nernst potential, current density, hydrogen-concentration distribution across electrolyte	[2]
2	Ni-YSZ-240 μm-0.3	LSM-20 μm-0.3	YSZ-7 μm	1.25 ms−1	N2: H2O-0.3:0.7 (molar)	1073	Overpotential across cell, steam distribution across hydrogen electrode, temperature profile across flow channels	[3]
3	Ni-YSZ-25 μm-0.37	LSM-25 μm-0.37	YSZ-140 μm SSZ-140 μm	4 × 10−6 kgs−1.	N2:H2:H2O-0.5:0.006098:0.493902	1073	Effect of cell active area, ASR, effect of flow rates	[4]
4	Ni-YSZ-10 μm-0.4	LSM-20 μm-0.4	YSZ-10 μm	0.217 Lmin−1	H2: H2O-0.1:0.9	1073	Multi-channel cell-flow configuration, distribution of hydrogen concentration, water concentration, temperature profile, activation overpotential across electrodes	[5]
5	Ni-YSZ-510 μm-0.5	LSM-60 μm-0.5	YSZ-100 μm	1.61 × 10−5 kgs−1.	H2: H2O-0:1	1073	Distribution of current and concentrations across TPB layer for various condition	[6]
6	Ni-YSZ-500 μm-0.5	LSM-30 μm-0.5	YSZ-15 μm	0.040 Lmin−1.	H2: H2O-0.1:0.9	1073	Modeling of delamination in SOEC and effect of delamination size and location	[7]

The performance of the SOEC components is characterized using cell-polarization data and impedance data [3,4]. The polarization curve gives the relationship between the current density applied and the potential difference measured across the cell, and it can provide a fundamental understanding of the overall losses measured across range of the applied current. The polarization curve is divided into three regions based on the types of loss experienced in particular regions. The low-current region (0–0.2 A-cm⁻²) is primarily dominated by activation losses. Activation loss occurs due to the demand for higher potential to overcome the activation-energy barrier of the reaction. The intermediate current region (0.3–1 A-cm⁻²) suffers from primarily ohmic losses. Ohmic losses are caused by the electrical and ionic resistance in the cell components. The high-current region (over 1 A-cm⁻²) is dominated by mass-transport losses. Mass-transport losses result from slow mass-transfer rates of species from and to electrodes.

Impedance plots, such as Bode and Nyquist plots, help to understanding fundamental aspects of cell kinetics and transport phenomenon [9]. Additionally, impedance plots help to characterize the contribution of each type of loss (activation, ohmic, and mass-transport), which is not possible in a polarization curve, thus aiding greatly in material characterization and diagnosing failure modes. Jensen et al. [9] modelled impedance spectra in SOEC using equivalent circuit fitting to study the impact of the degradation of cells on cell performance. No multiphysics models of the role of transport phenomena of SOEC in simulating impedance were found in the literature. However, such a model was reported by Yixiang Shi et al. [10] for a solid oxide fuel cell (SOFC). They reported a model to simulate the transient impedance response of a SOFC by coupling the electrochemical equations with the convection, reaction, and diffusion terms in the mass-balance equation.

The authors of the available research on modeling report their results in terms of polarization data. There is an inadequate amount of research that reports models of both polarization and impedance data for evaluating and characterizing SOEC performance. No research has been published on utilizing polarization and impedance modelling to benchmark the performances of the materials used in the SOEC components. Therefore, the objectives of the present work are as follows:

• To develop a theoretical model to assess polarization and impedance for three different SOECs based on the following criteria: the model shall evaluate the performances of three electrolyte materials, namely yttrium-stabilized zirconia (YSZ), gadolinium-doped ceria (GDC), and scandium-, cerium-, and gadolinium-doped zirconia (SCGZ).
• To ensure that the model reveals how operating conditions such as temperature and pressure affect the performance of cell.

For the first time, the effects of temperature and pressure on three electrolytes, SCGZ, YSZ, and GDC, is theoretically modeled and validated for an operating cell.

2. Materials and Methods

2.1. Multiphysics Modeling

Simplified block diagram of the model workflow used in the present study is provided in Figure 3.

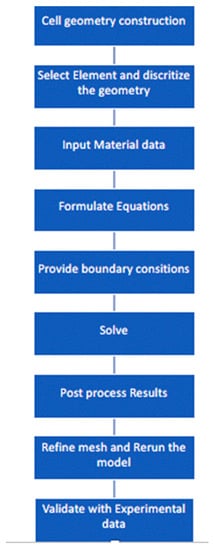
Figure 3. Model-workflow diagram.

2.1.1. Model Description

Model dimensionality of a finite element model refers to the spatial dimensions of the geometry in the model. Models with lower dimensionality allow incorporation of more complex physics at the expense of spatial fidelity [11]. A zero-dimensional model can help in understanding interdependence of system variables, such as cell potential, current density, temperature, pressure, and gas-flow rate, thus helping in determining kinetic and net ohmic losses [12]. A one-dimensional model can help in accounting for physical phenomena across lines in cells. A 1-D approach is used either to model electrochemical reactions and gas-species transport across the thicknesses of cell layers (flow channels, electrodes, and electrolytes) [13] or to model feed depletion across gas channels. Internal boundary conditions are defined at interfaces to distinguish processes at each layer. A two-dimension model uses the 1-D model’s dimension and an additional direction (either across or along the channel). A 2-D model can provide insights into impact of flow configuration and distribution of species and temperature across a plane [14]. However, the present work requires an understanding of distribution of electric potentials and species concentrations in three-dimensional space. Thus, a 3D geometry was used to model the kinetics and the transport phenomena. The following equations were selected for the model”

(i)

Continuity equation.

(ii)

Momentum-conservation equation (Brinkman equation—modified Navier–Stokes).

(iii)

Species conservation (mass balance).

(iv)

Charge balance and electrochemical kinetics (Butler–Volmer equation and Nernst equation).

These equations were solved at a steady state for obtaining polarization data and in variable frequency domain in order to obtain impedance data through a commercial finite-element-method solver (COMSOL 5.6). The application files and user manual provided for SOEC modeling were used as template [15,16]. The FEM utilizes numerical methods to solve the governing partial differential equation of the system. In FEM, the geometrical domain is discretized into smaller parts, called finite elements. The discretization is achieved by construction of a mesh. The solution is approximated within each element using a set of basis functions. The resulting system of equations is solved using numerical methods to obtain the solution for the entire system. The model is valid under following assumptions:

(1)

The kinetics and the mass transfer occurring the cell are in steady state.

(2)

Model is operated only in low- and intermediate-current regions and, thus, the mass-transport loss is assumed be negligible and ignored.

(3)

The gas species involved in the reaction follows ideal gas law.

(4)

The species are assumed to follow Newton’s law of viscosity.

(5)

All flows are assumed to be laminar due to the low velocity of gas species.

2.1.2. Governing Equations

The model couples the transport equations in the flow channel and electrode with the electrochemical equations to obtain polarization and impedance data. The equations used for the model are discussed in this section.

• Transport in Gas Channel

Mass continuity for gas-flow channel is given by

$$\frac{\partial \rho }{\partial t}+\nabla ·\left(\rho u\right)=0$$

(1)

where $\rho$ is the density of the fluid in kg.cm⁻³ and $u$ is the velocity of the fluid in m.s⁻¹.

Momentum conservation for the gas mixture in the channel is given by

$$\frac{\partial \left(\rho u\right)}{\partial t}+\nabla ·\left(\rho u\right)u-\nabla ·\left(\mu \nabla u\right)=\nabla ·\left[\mu {\left(\nabla u\right)}^T-\frac{2}{3}\mu Tr\left[{(\nabla u)}^T\right]I\right]-\nabla p$$

(2)

where $p$ is the pressure in Pa, $\mu$ is the dynamic viscosity in Pa.s, $I$ represents an identity matrix, and Tr represents a trace operation.

Species conservation in the channel is given by

$$\frac{\partial \left(\rho {\omega }_i\right)}{\partial t}+\nabla ·j_i+\rho \left(\nabla ·u\right){\omega }_i=Q_{m,i}$$

(3)

where ${\omega }_i$ is the mass fraction of species i, $j_i$ is the diffusive mass flux of species in mol.m⁻².s⁻¹, and $Q_{m,i}$ is the mass source or sink in mol.m⁻³.s⁻¹ for species i.

Diffusive mass flux is given by

$$j_i=-\rho {\omega }_i{{\displaystyle \sum }}_k{D}_{i,eff} .d_i$$

(4)

where $D_{i,eff}$ is the diffusion coefficient of component i in m².s and $d_i$ is the diffusion’s driving force in m⁻¹.

The diffusion’s driving force is given by

$$d_k=\nabla x_k+\frac{1}{p_A}\left[\left(x_k-{\omega }_k\right)\nabla p_A\right]$$

(5)

where $x_k$ is the mole fraction of component k and $\nabla p_A$ is the pressure gradient measured across.

• Transport in Electrode

Mass continuity for the electrodes is given by

$$\frac{\partial \left({ϵ}_p\rho \right)}{\partial t}+\nabla ·\left(\rho u\right)=Q_m$$

(6)

where ${ϵ}_p$ is the porosity of the electrode and $Q_m$ is the mass source term.

Momentum conservation for the gas mixture in the electrodes is given by

$$\frac{\rho }{{ϵ}_p}\left(\frac{\partial u}{\partial t}+\left(\nabla ·u\right)\frac{u}{{ϵ}_p}\right)=-\nabla p+\nabla ·\left[\frac{1}{{ϵ}_p}\left\{\mu \left(\nabla u+{\left(\nabla u\right)}^T\right)-\frac{2}{3}\mu \left(\nabla ·u\right)I\right\}\right]-\left({\kappa }^{-1}\mu +\frac{Q_m}{{ϵ}_p{}^2}\right)u+F$$

(7)

where $\kappa$ is the permeability of the porous medium in m² and $F$ is used to account for influence of other forces, like gravity, in N.

Species conservation in the electrode is given by

$$\frac{\partial \left({ϵ}_p\rho {\omega }_i\right)}{\partial t}+\nabla ·j_i+\rho \left(\nabla ·u\right){\omega }_i=Q_{m,i}$$

(8)

• Electrochemical Equations and Charge Balance

The Nernst equation is given by

$$E_{eq}=E^0-\frac{RT}{nF}\ln \left({{\displaystyle \prod }}_i{\left(\frac{p_i}{p_{i,ref}}\right)}^{{\upsilon }_i}\right)$$

(9)

where $E_{eq}$ is the equilibrium potential in V, $E^0$ is the standard potential in V, R is the universal gas constant in J.mol⁻¹.K⁻¹, T is the temperature in K, n is the number of electrons in the reaction, F is the Faraday constant in C.mol⁻¹, $p_i$ is the partial pressure of species i in Pa, $p_{i,ref}$ is the reference pressure of component i, and ${\upsilon }_i$ is the stoichiometric coefficient of species i in the reaction.

The Butler–Volmer equation for the anode and cathode is given by

$$i_a=i_{0,a}\left(\exp \left(\frac{{\alpha }_{b,a}F{\eta }_a}{RT}\right)-\exp \left(\frac{{\alpha }_{f,a}F{\eta }_a}{RT}\right)\right)$$

(10)

$$i_c=i_{0,c}\left(\exp \left(\frac{{\alpha }_{b,c}F{\eta }_c}{RT}\right)-\exp \left(\frac{{\alpha }_{f,c}F{\eta }_c}{RT}\right)\right)$$

(11)

The exchange-current density is given by

$$i_0=i_{0,ref}({{\displaystyle \prod }}_i^{ }{\left(\frac{p_i}{p_{i,ref}}\right)}^{{\gamma }_i}$$

(12)

The cell overpotential is given by

$$\eta =E-E_{eq}$$

(13)

where $i$ is the current density in A.m⁻², $i_0$ is the exchange-current density A.m⁻², ${\alpha }_f$ and ${\alpha }_b$ are the forward and backward charge-transfer coefficients, respectively, and $\eta$ is the activation overpotential in V. The $i_{0,ref}$ is the reference exchange-current density in A.m⁻², at a given temperature and ${\gamma }_i$ is the pressure dependence of species i. The ${\varphi }_s$ and ${\varphi }_l$ are the electrode and electrolyte potential in V, respectively.

The charge balance in the electrode and electrolyte is given by

$$\nabla ·\left({\sigma }_s.\nabla {\varphi }_s\right)=-i_{v,total}$$

(14)

$$\nabla ·\left({\sigma }_l.\nabla {\varphi }_l\right)=-i_{v,total}$$

(15)

where ${\sigma }_s$ and ${\sigma }_l$ and are the electrode and electrolyte conductivities in S.m⁻¹, respectively, ${\varphi }_s$ and ${\varphi }_l$ are the electrode and electrolyte potential in V, respectively, and $i_{v,total}$ is the volumetric current density consumed by the electrochemical reactions in A.m⁻³.

• Impedance Equations

The current supplied to the cell during impedance modeling contains a stationary component and a frequency-domain perturbation, and it is given by

$$i_{cell}=i_{st}+i_p\exp \left(j\omega t\right)$$

(16)

$$\omega =2\Pi f$$

(17)

where $i_{cell}$ is the overall current supplied in A.m⁻², $i_{st}$ is the stationary component of the current, $i_p$ is the magnitude of the perturbation current, $j$ is imaginary number iota, $\omega$ is the angular frequency in Hz, $f$ is the frequency in Hz, and t is the time period in sec.

The potential response measured is given by

$$V_{cell}=V_{st}+V_p\exp \left(j\omega t+\varphi \right)$$

(18)

where $V_{cell}$ is the overall voltage response from the cell in V, $V_{st}$ voltage response to the stationary component of the current in V, i.e., the DC component, $V_p$ is the magnitude of voltage response to the perturbation current, and $\varphi$ is the phase difference in degrees between current and voltage. The impedance is given by

$$\mathrm{Z}=\frac{V_p\exp \left(j\left(\omega t+\varphi \right)\right)}{I_p\exp \left(j\omega t\right)}={\mathrm{Z}}_{\mathrm{p}}\exp \left(j\varphi \right)={\mathrm{Z}}_{\mathrm{p}}\cos \left(\varphi \right)+j.{\mathrm{Z}}_{\mathrm{p}}\sin \left(\varphi \right)={\mathrm{Z}}_{\mathrm{real}}+{\mathrm{Z}}_{\mathrm{img}}$$

(19)

where ${\mathrm{Z}}_{\mathrm{p}}$ is the magnitude of impedance in Ohm.m², ${\mathrm{Z}}_{\mathrm{real}}$ is the real component in impedance, and ${\mathrm{Z}}_{\mathrm{img}}$ is the imaginary component in impedance.

2.1.3. Numerical Details

The proposed model is of a simplified planar SOEC with anode, electrolyte, and cathode with a steam-flow channel. The geometry is discretized using the default meshing tool available in COMSOL 5.6. The material properties, such as electrical and ionic conductivities, were sourced from [17]. The experimental work of Temluxame et al. [18] was adapted to define operating conditions for the model (flow rates, composition, temperature, and pressure). The cell dimensions and operating conditions used in the model are reported in Table 2. Electrochemical parameters for the cathode and anode, such as reference exchange-current density, charge-transfer coefficients, and pressure dependence and porosity of the electrode and electrolyte were fitted to validate the experimental polarization results (i-V curve) from [18]. The material properties of the components and the fitted electrochemical parameters are reported in Table 3. The impedance was calculated for the frequency range of 1 Hz to 107 Hz for a perturbation amplitude of 0.005 A.m⁻² at a stationary current of 1 A.cm⁻²

Table 2. Dimensions and operating condition of the cells.

Dimensions of the Cell
Cell length	1.25	cm
Cell width	0.6	cm
Cathode thickness	80	μm
Anode thickness	400	μm
Electrolyte thickness	20	μm
Number of ribs in gas channel	3
Length of rib	1	cm
Width of rib	0.15	cm
Thickness of rib	0.05	cm
Operating Condition
Temperature	800	°C
Pressure	1	atm
Feed composition (H2O:H2)	0.7:0.3
Feed-flow rate	8.5 × 10−8	kgs−1

Table 3. Material properties and electrochemical parameters for the model.

Material Properties
Electrolyte porosity	0.225
Electrode porosity	0.4
Electrolyte conductivity	$\mathrm{SCGZ}=6.92\times {10}^4{e}^{\frac{-9681}{T}}$ $\mathrm{GDC}=\frac{100}{T}\times {10}^{\left(6.66071-\frac{5322.92}{T}\right)}$ $\mathrm{YSZ}=3.34\times {10}^4{e}^{\frac{-10300}{T}}$	Sm−1
Electrochemical Parameters
Cathode reference exchange-current density $i_{0,ref}$	1500	A.m−2
Cathode charge-transfer coefficient ${\alpha }_f$/${\alpha }_b$	0.5/0.5
Cathode pressure dependence ${\gamma }_{H_{2}O}/{\gamma }_{H_2}$	1/1
Anode reference exchange-current density $i_0$	2000	A.m−2
Anode charge-transfer coefficient ${\alpha }_f$/${\alpha }_b$	0.5/0.5
Anode pressure dependence ${\gamma }_{O_2}$	0.25

2.1.4. Validation Criteria

The model’s validation was performed using polarization data and the coefficient of determination, or R² value, was utilized to evaluate the validity of the model against experimental data. The R² value was used as the criterion for measuring the fit, as it provided a standardized metric to evaluate the efficacy of the model (values ranged from 0 to 1), whereas other common criteria, such as MSE, MAE, and RMSE, are dependent on the scale of the response variable, thus making the interpretation complex. A high R² value implies the good fit of the model.

For a dataset with n datapoints,

$$R^2=1-\frac{{{\displaystyle \sum }}_i^n{\left(y_i-f\left(x_i\right)\right)}^2}{{{\displaystyle \sum }}_i^n{\left(y_i-\overline{y}\right)}^2}$$

(20)

where $R^2$ is the coefficient of determination, $y_i$ is the observed value, $f\left(x_i\right)$ is the calculated value, and $\overline{y}$ is the mean of all the observed values.

3. Results and Discussion

3.1. Validity of the Model

The validity of the polarization and the impedance model were confirmed using the polarization data reported in Figure 3. The model evaluated the performance of the cell for three electrolytes, namely YSZ, GDC, and SCGZ, at a temperature of 1073 K, 1 atm of pressure, and a steam:hydrogen ratio of 70:30. The results were then compared with the experimental data. The R² values for the models of the cells with YSZ, GDC, and SCGZ as the electrolytes were found to be 0.99627, 0.99848, and 0.99895, respectively, thus demonstrating that the model provided an excellent fit with the experimental data. Mass-transport losses are very low in SOECs due to their high-temperature operations.

3.2. Comparison of the Electrolytes

The polarization plot and Nyquist plot in Figure 4 and Figure 5, respectively, were used to determine the best-performing electrolyte. The SCGZ demonstrated the best performance of the three electrolytes, as it had the lowest losses recorded for the entire range of operating current, as shown by the polarization curve, and it had the lowest polarization resistance, of 0.0240 Ohm.cm²; the YSZ and GDC had polarization resistances of 0.0885 Ohm.cm² and 0.0428 Ohm.cm² respectively. By taking YSZ as the benchmark, we can report that GDC has 51.63% less polarization resistance and SCGZ has 72.88% less polarization resistance at 1073 K. The reduction in the ohmic losses and resistance can be attributed to the fact that the SCGZ had higher ionic conductivity at the given temperatures than the YSZ and GDC. The variance in conductivities was due to the structural differences between the three electrolytes. The zirconia- and ceria-based electrolytes formed a fluorite structure (MO₂), in which the tetravalent cations (Zr⁴⁺, Ce⁴⁺) assumed a face-centered cubic arrangement and the oxide ions occupied the tetrahedral interstitial sites [19]. The structure leaves a large number of octahedral interstitial voids to allow the conduction of oxide ions. Zirconia can only form fluorites at temperatures above 2370 °C [20]; thus, it requires dopants like Y³⁺ or Sc³⁺ to be stabilized into a fluorite structure at lower temperatures. Although ceria does not require dopants to stabilize it into a fluorite structure at low temperatures, it is usually doped with rare-earth sesquioxides, like gadolinium sesquioxide or samarium sesquioxide, to improve conductivity, as ceria displays extensive solid solutions with these sesquioxides.

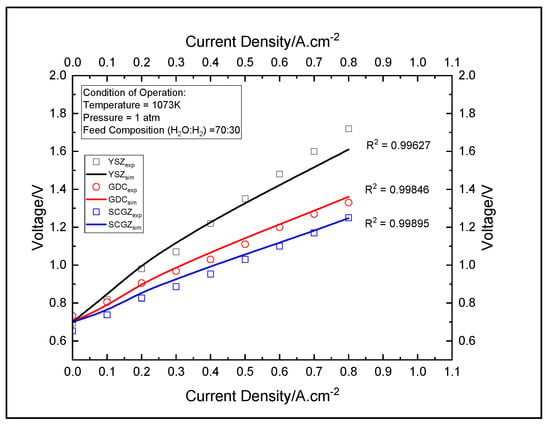
Figure 4. Polarization curve for establishing.

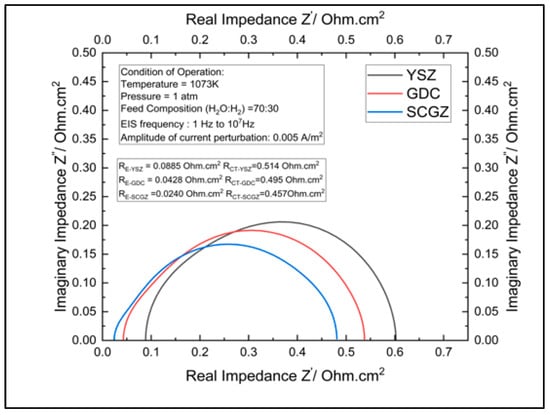
Figure 5. Impedance curves for YSZ-, GDC-, and SCGZ--based validity of the model.

The present work recognizes ionic conductivity of the material as the most critical factor affecting the performances of electrolytes. The SCGZ was identified as the best electrolyte out of the three electrolytes studied due to its high ionic conductivity. However, in practical applications, more criteria, such as electrical conductivity, durability, mechanical strength, and cost are also evaluated. The most commonly used electrolyte for solid oxide cells is YSZ (8% yttria doping), but with attempts to shift to lower operating temperatures (600–800 °C), other zirconia- and ceria-based electrolytes with dopants, like scandia and gadolinia are being are being explored. In particular, ScSZ (10% scandia doping) has received wide attention due to its high conductivity in the 600–800 °C range [21]. However, ScSZ shows significant degradation in long operations at high temperatures (1000 °C for 1000 h). The co-doping of ScSZ with CeO₂ (10 mol%Sc₂O₃⁻¹%CeO₂) has been adapted to counter ageing and improve stability and conductivity. In addition to conductivity and stability, SCGZ also demonstrates high mechanical strength and toughness, which are desirable properties for an electrolyte. These factors make SCGZ a promising material for adaption into commercial SOECs.

3.3. Effects of Operating Conditions on Cell Performance

The impact of operating conditions such as temperature and pressure has been studied using polarization and impedance data. For an operating condition to positively affect cell performance, it needs to lower the losses computed in the polarization curve and to reduce the resistances computed in the Nyquist plot.

3.3.1. Impact of Temperature on Cell Performance

Figure 6 and Figure 7 report the polarization and impedance of a cell with SCGZ as the electrolyte at 973 K, 1073 K, and 1173 K. By using 0.1 A.cm⁻² and 0.6 A.cm⁻² as reference points for the activation and ohmic regions in the polarization curves and taking a voltage simulated at 973 K as the baseline, reductions in potential of 5.2% and 10.2% at 1073 K and of 7.6% and 16.29% at 1173 K were observed for the activation and ohmic reference points, respectively. The impedances simulated at the specified temperature are reported in Table 4. Taking operation at 973 K as the baseline, drops in polarization and charge-transfer resistance of 60.39% and 11.89%, respectively, at 1073 K, and reductions of 81.68% and 23.65%, respectively, at 1173 K, were observed.

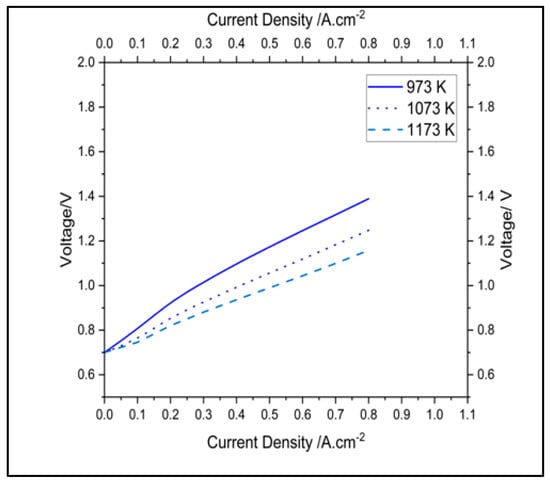
Figure 6. Impact of temperature on polarization of the cell.

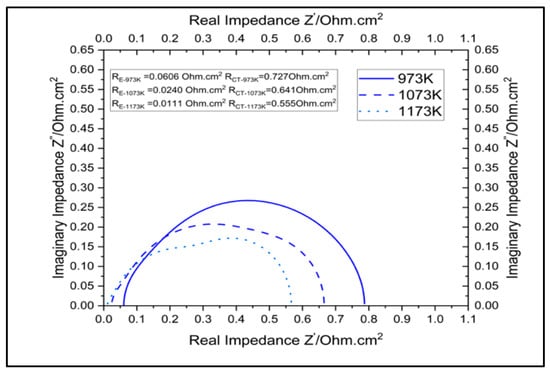
Figure 7. Impact of temperature on impedance of the cell.

Table 4. Impedance computed at various operating conditions.

Parameter		RE Ohm.cm2	RCT Ohm.cm2
Temperature	973 K	0.0606	0.727
	1073 K	0.024	0.641
	1173 K	0.0111	0.555
Pressure	0.5 atm	0.02395	0.660
	1 atm	0.02395	0.641
	10 atm	0.02395	0.58535

The reductions in the activation and ohmic losses and in the resistance were due to the improved kinetics and conductivity in the cell. The increase in temperature led to an increase in the Tafel slope, which in turn led to an increase in kinetic losses. However, the increase in temperature exponentially increased the exchange-current density, which compensated for the Tafel-slope increase and significantly reduced the kinetic and ohmic losses computed in the cell [22]. In addition, operation at higher temperatures also increase the conductivities of all the cell components, leading to reductions in contact losses and resistance. The impact of high-temperature operations on the long-term stability of the cell is not addressed in the present model. Longer exposures to high temperatures cause thee sintering of the microstructure in electrodes, which leads to the agglomeration of the fine-grained particles in electrodes (hydrogen electrodes in particular). This agglomeration leads to the loss of active sites in electrodes, which decreases cell performance. Rises in the operating temperature increase the rate of this degradation mechanism [23,24,25,26,27]. Thus, it can be inferred that higher-temperature operations improve cell performance, as identified in the model. However, for longer operations, the operating temperature needs to be optimized to balance the performance and the long-time durability of the cell.

3.3.2. Impact of Pressure on Cell Performance

The plots in Figure 8 and Figure 9 show the effects of pressure on the polarization and impedance of a cell in the SCGZ case at 0.5, 1, and 10 atm. When taking 0.1 A.cm⁻² as a reference in the activation region, the cell voltages modeled for the three pressures (values) were 0.751 V, 0.765 V, and 0.812 V, respectively. When taking 0.5 atm as the baseline, increases in potential of 1.8% at 1 atm and 8.12% at 10 atm were identified. These increases in cell potential can be attributed to increases in the Nernst potential, particularly in the anode. However, in the ohmic region, the differences in voltage for the three pressures seemed to diminish. The impedances for the three pressures are reported in Table 4. It was identified that increases in pressure reduced the charge transfer resistance. At 1 atm of pressure, there was a 2.94% reduction and at 10 atm of pressure, there was a 11.39% reduction in charge-transfer resistance compared to the baseline operation at 0.5 atm. However, the pressure did not have an observable impact on the polarization resistance of the cell. The improvement in charge-transfer resistance with increases can be attributed to the impact of the pressure on the exchange-current density. Exchange-current density is proportional to surface concentration, which is in turn directly proportional to pressure [22]. The increase in the exchange-current density improved the current density in the cell and lowered the charge-transfer resistance at the bias current, for which the impedance was computed from both the model and the experiments. There was no observable impact of the pressure on the ohmic region or on the polarization resistance, as pressure does not have an impact on intrinsic properties like the conductivity of cell materials.

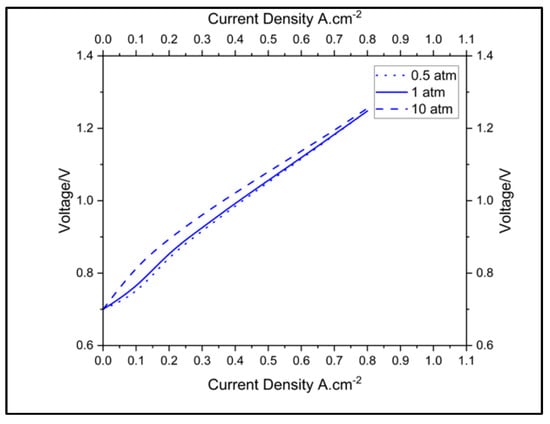
Figure 8. Impact of pressure on polarization of the cell.

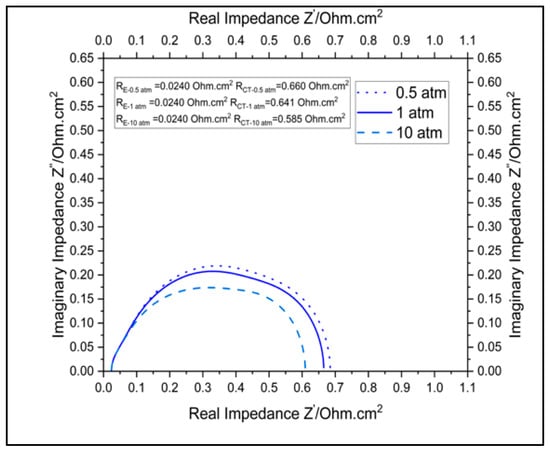
Figure 9. Impact of pressure on impedance of the cell.

4. Conclusions

The present work reported the use of a finite-element model to assess the performances of YSZ-, GDC-, and SCGZ-based SOECs. The performances of the cells were evaluated using modeled polarization and impedance data at three different temperatures and pressures. All the modeled datasets were validated with experimental data for the electrolytes. The R² values for the models of the cells with YSZ, GDC, and SCGZ as the electrolytes were found to be 0.99627, 0.99848, and 0.99895, respectively. Higher ionic conductivity in the electrolyte reduces both polarization and charge-transfer resistances significantly, leading to better performance. It was observed that the SCGZ provided the best performance of the three electrolytes studied. The SCGZ had the lowest polarization resistance computed, of 0.0240 Ohm.cm²; by comparison, the YSZ and GDC had polarization resistances of 0.0885 Ohm.cm² and 0.0428 Ohm.cm² respectively. An increment of 200 K over the baseline operation of 973 K was found to reduce the voltage simulated in the activation and ohmic regions by 7.6% and 16.29%, respectively. At 1173 K, the polarization and charge-transfer resistance simulated were also found to decrease, by 81.68% and 23.65%, respectively, compared to the baseline operation. An elevated operation pressure (10 atm) compared to the baseline operating pressure (0.5 atm) was found to increase the voltage measured in the activation region by 8.12%, but this difference in voltage diminished in the ohmic region of the polarization curve. At 10 atm, the simulated charge-transfer resistance was found to decrease by 11.39% compared to the operation at 0.5 atm. However, the elevated pressure did not have an observable impact on the polarization resistance of the cell. By contrast, the SCGZ-based SOEC operated at 1173 K at 10 atm.