Abstract
Wind direction and speed are the most important factors that determine the degree of damage caused by a jet fire. In this study, the metal hose used to extract/supply fuel was identified as the component with the highest risk for a jet fire occurring at an aerospace facility. A risk assessment was performed to evaluate the individual risk of a jet fire from the metal hose according to the wind direction and speed. HSE failure data was applied for calculating the jet fire probability including metal hose failure, ignition frequency, and jet fire frequency. Which was 3.0 × 10−4. The individual risk of different fatality probabilities was calculated according to the wind rose data for the aerospace facility. The individual risk from jet fire in the aerospace facility was calculated with a maximum risk of 3.35 × 10−5 and a minimum risk of 1.49 × 10−6. The individual risk satisfied HSE ALARP criteria. In addition, firewalls, extinguishing systems, and an emergency shut off system were enhanced, and it was thought that the risk from jet fire could satisfy acceptable criteria.
1. Introduction
Fire risk is the likelihood of a fire or explosion to occur, which is affected by any unique feature or potential hazard. Increases in indoor combustibles, diverse high-rise buildings, and population density have led to increased fire risks. Fire risk assessment is necessary for maintaining the safety of buildings and designing fire safety measures. Insufficient measures can result in massive casualties and damage to property. Risk assessment considers the structure of the building, its contents, layout, wind speed, and escape routes in the event of a fire.
Fire risk assessment can be of two types: quantitative and qualitative. Quantitative assessment methods are based on frequency analysis of entities that may cause fire and explosion and a consequence analysis of the potential damage of an accident to humans or property [1,2,3]. Examples of quantitative assessment methods include fault tree analysis (FTA), event tree analysis (ETA), cause–consequence analysis (CCA), layer of protection analysis, risk matrix, and the frequency–number of fatalities (F–N) curve. On the contrary, qualitative assessment methods comprehensively collect the opinions of many experts and include what-if analysis, hazard and operability, and process hazard review. In Korea, fire risk assessments are generally qualitative; a quantitative assessment method has not yet been universally accepted. Quantitative fire risk assessments are needed for liquefied natural gas plants, aerospace facilities, and other facilities with major fire hazards [4,5]. Fire risk assessment for existing nuclear plants and safety-critical systems can widely vary in approaches and outcomes [6].
Recently, in order to promote national economic growth and national interest, not only government space activities, but also commercial space activities of private companies are considered as one of the key areas of activity [7]. According to the establishment and operation of space launch sites increases through the active space activities, various risks may occur in the aerospace facility, such as damage to structure and human life due to complexity and risk factors of aerospace systems. As such, a quantitative risk assessment of all parts, procedures, and operations of the aerospace facility is required [8,9,10]. Aerospace facilities perform various operations that pose a fire risk, such as rocket transfer and assembly, fuel and oxidant charging, and maintenance of electronics and general machinery. If a launch is rescheduled, the charged kerosene should be immediately extracted and then recharged. Due to the large amount of kerosene involved in the extraction and charging processes, as even a small leak can pose a fire risk. Jet and pool fires can be caused by fuel and oxidant leakage, tank failure, and catastrophic tank rupture. The potential of an explosion and secondary damage increases with the size of the leak. Thus, a quantitative fire risk assessment should be conducted to minimize the primary and secondary fire damage that could occur in aerospace facilities, with a special focus on the metal hose that is connected to the tank inside the rocket for supplying and extracting fuel [11,12]. Due to the metal hose posing a high risk in the event of a fuel leak, quantitative risk assessment should be performed for metal hose.
In this study, UK Health and Safety Executive (HSE) probability data was used to analyze metal hose failure and ignition frequency, and a consequence analysis was performed to analyze the fatality of jet fire. Wind rose was used to analyze the effect of wind direction and speed, which are the most important factors in the case of a jet fire. Finally, the individual risk assessment to the aerospace facility from metal hose jet fire was performed, considering the probability of failure and ignition, consequence of jet fire, wind direction and speed through comparison with the HSE risk standard.
2. Methodology
Validation for quantitative risk assessment can have several meanings that are disputable. As such, quantitative risk assessment of validation aspects, considering the objectives, expected results may be necessary [13,14]. Specifically, sampling proper data and its methods are most important to conduct quantitative risk assessment exactly. Therefore, in this study, through the validation approaches, a quantitative risk assessment was performed.
2.1. Validation Approach
Quantitative risk assessment is expressed as multiplying the frequency by consequence of a hazard factor leading to an injury or disease. In the case of frequency, it is the probability of occurrence of accidents and diseases for hazardous and dangerous work. In the case of consequence, it is the degree of exposure to human and material damage. As such, the quantitative fire risk assessment risk is a method of predicting the degree of risk for multiplying the frequency by consequence values of fire, according to the accident scenario, which are dependent on various parameters. Finally, after the quantitative risk assessment, it establishes mitigation to solve the workplace risk factors, such as installing emergency warning devices and securing a minimum safety distance [2,4,15]. Quantitative fire risk assessment consists of five methods, as shown in Figure 1 [16]. This section is introduced based on quantitative fire risk assessment to perform this research.
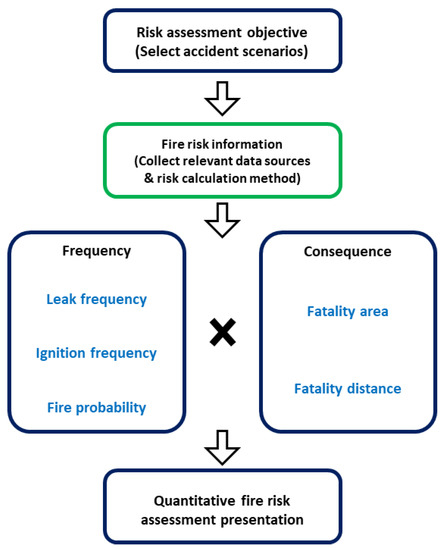
Figure 1.
Quantitative fire risk assessment procedure.
2.1.1. Part 1. Risk Assessment Objective (Select Accident Scenarios)
This part means to identify hazardous source and accident scenarios that match installation specific interests. In some cases, relevant guidelines and standards could be applied for this part. Selecting proper accident scenarios is important. When a risk is calculated by considering an accident with a very low frequencies and low impact, it takes a lot of time and money to control the risk. To select the proper hazardous source, a P&ID (Piping and Instrument Diagram) and aerospace facility drawing were analyzed, and a metal hose was selected as the most dangerous source.
2.1.2. Part 2. Fire Risk Information (Collect Relevant Data Sources and Risk Calculation Method)
This part is necessary to conduct quantitative risk assessment adequately. A frequency data, which is needed to calculate fire occurrence probability, could be collected to analyze accident data from HSE, OGP (Oil and Gas Producers), NFPA (National Fire Protection Association), and HIAD (Hydrogen Incident Accident Database) [4,5]. A consequence could be calculated from various empirical equations or differential equations. Since solving differential equations is very difficult and complex, empirical equations based on various experiments are used to calculate the consequence and risk analysis. A fatality of jet fire and consequences are calculated based on the TNO Green book [17] and Han and Weng [18], considering mass release rate and probit function. An individual risk is calculated from fatality, frequency of jet fire, and weather conditions, which is made from HSE; a simplified approach to estimating individual risk [19]. A jet breakup length that is corresponded to velocity, density, surface tension, and viscosity, where the empirical equation was validated from Miesse [20]. Considering weather conditions in the Republic of Korea, wind rose data from Korea Meteorological Administration (KMA) was used.
2.1.3. Part 3. Frequency (Selecting Proper Database and Applying)
As a result of the accident probability database analysis, the specific accident probability data for a metal hose does not exist. As such HSE probability database applicable to general leak situations were selected.
In this part, the metal hose fire probability was calculated from metal hose failure and ignition probability values using the HSE and cox et al. database [21,22].
2.1.4. Part 4. Consequence
The consequence of accidents can be analyzed through fatality of overpressure, radiation intensity, and toxic gas concentration. In the case of jet fire, fatality is caused by the radiation of the flame. In this study, the fatality area and distance were calculated using the Han and Weng [18] equation based on mass release rate and probit function.
2.1.5. Part 5. Quantitative Fire Risk Assessment Presentation
Quantitative fire risk assessment can derive the final individual risk using frequency and consequence analysis. In this study, wind rose data was applied to HSE’s individual risk equation [19] to consider both wind direction and speed.
2.2. Scenario and Boundary Definitions (Metal Hose)
The target scenario was set in the space launch facility at Goheung, Republic of Korea, which was operated by the Korea Aerospace Research Institute. The risk assessment focused on the metal hose, which was highly likely to cause a jet fire due to leakage, failure to switch off, cracking, or excessive flow rate. The risk of a jet fire was calculated by considering the size of the metal hose, internal temperature and pressure, flow rate, and location. Since the metal hose charges and discharges fuel, it was always exposed to danger in the event of a fire or accident. If the metal hose and rocket were separated, a larger fire may occur. Figure 2 shows the schematic of the metal hose used at the Goheung rocket launch facility, respectively. Table 1 presents the properties of kerosene [23,24]. As shown in Figure 2, the metal hose could be divided into three stages. A jet fire may occur at any stage. However, jet fires at higher stages will not result in injury to humans; thus, the fire risk assessment focused on the lowest stage (i.e., metal hose 1), since this part was most likely to cause injuries to humans.
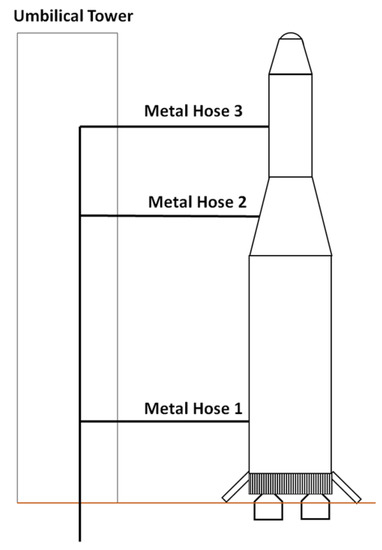
Figure 2.
Schematic of metal hoses connecting the rocket to the umbilical tower.

Table 1.
Properties of kerosene [23,24].
2.3. Individual Risk
Individual risk (IR) refers to the probability of personal injury in hazardous facilities when a fire occurs near an ignition source [19,25]. It can be expressed in two ways. The first is by plotting risk contours to designate the range around a hazardous facility for the same risk level. The second is a two-dimensional profile that indicates the risk level according to distance from the hazardous facility. IR can be calculated as follows [19]:
where is IR of population group k; is the overall fraction of time that population group k is in the area; is the probability that population group k is at location i; is the frequency of fatalities at location i [19,26].
can be calculated as follows [19]:
where is the frequency of event outcome j; and are the probabilities of fatality and weather conditions produced by event outcome j (from meteorological data, 1 for weather independent event outcomes), respectively; is the probability of the direction required to produce event outcome i (related to the wind rose and cloud width for gas dispersion events, one for omnidirectional events). For the sake of simplicity, the following assumptions are used to calculate the individual risk [19,27,28]:
- The wind distribution is constant, and accidents can occur in all directions.
- Only one wind speed and climate stability degree are used.
- Mitigation factors, such as evacuation, are not considered.
- Leakage sources are uniformly distributed; thus, accidents can occur at any point.
2.4. Jet Fire Fatality
The fatality of a jet fire is calculated from the thermal radiation. In the case of the jet fire fatality probability function, the Equation (3) considering the thermal radiation exposure time to the target and the thermal radiation flux is used [17,29,30].
where t is the time that the target is exposed to radiation. The exposure time is generally assumed as 30 s in urban settings. is the thermal radiation flux [30].
Second, if you replace the thermal radiation flux, you can use the Equation (4) using the leakage flow rate and the distance between the target and the center of the flame zone.
where is the mass flow rate of leakage; is the distance between the target and the center of the flame zone [30].
In the study, the probabilities of 99%, 50%, and 1% fatality can be calculated according to the radiation, while the areas and distance for these fatalities, due to a metal hose failure, can be calculated using Equation (5) with the probability values of 7.33, 5, and 2.67, respectively [17,30].
The average fatality probability in each area can be calculated as follows [29,30].
Figure 3 shows a schematic of the three fatality areas around a jet fire.
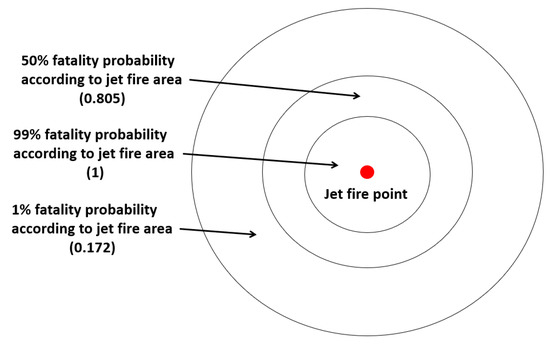
Figure 3.
Schematic of fatality probability according to areas around a jet fire point.
2.5. Kerosene Atomization
During the charging process, fuel flows through the metal hose at a velocity of 4–100 m/s and a pressure of 1.5–10 bar. If the metal hose ruptures, the high velocity of the leaking fuel can cause a jet fire, where the fuel is atomized or evaporated as it combusts. At room temperature (15–20 °C), liquid propellants evaporate more slowly than liquefied propellants; thus, a pool fire is more likely to occur [31,32,33,34]. However, a jet fire can occur under high velocity and pressure conditions. Khan et al. [35] reported the combustion characteristics of kerosene droplet. Due to the research data, a kerosene droplet under the 125 μm, was immediately burned by ignitor. Therefore, atomized kerosene was sufficiently burned by ignitor, and jet fires can be generated. The size and shape of the atomization depend on and of the leaking fuel. Liquid fuel frequently atomizes when the velocity was over 100 m/s [35,36,37]. An atomization characteristic was correlated with leakage velocity, and when the leakage velocity was increased over 100 m/s, mostly liquid fuels, which were passed atomization length (jet breakup length), were atomized and immediately vaporized, but liquefied fuels were atomized and evaporated under 100 m/s easily [31,32].
As shown in Figure 4, the atomization of the leak jet occurred at a constant breakup length. Miesse [20] had and established Equation (7) for calculating the atomization length. The Equation (7) was suitable for the density range 300 to 1500 kg/m3, and viscosity range 0.01 to 10 cp conditions. The position where kerosene atomizes can be calculated as follows [32]:
where is the breakup length, is the diameter, is the Weber number, and is the Reynolds number. Table 2 presents the parameters of the metal hose according to its diameter. With the metal hose, it was impossible to meet the high-pressure conditions for kerosene atomization. Preferentially, a breakup length is calculated to consider fatality areas accurately, since the jet fire occurred after the breakup length. As show in Table 2, the minimum breakup length was 3.2 m. In this study, the accurate fatality area was described in Section 3, using the breakup length value.
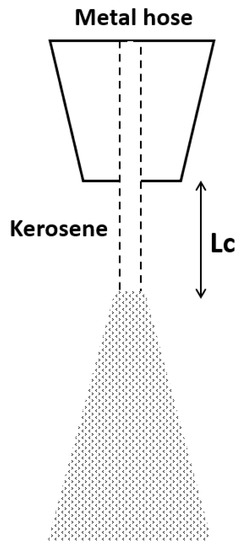
Figure 4.
Kerosene atomization.

Table 2.
Parameters of the metal hose.
2.6. Metal Hose Ignition Probability and Wind Rose Data
Frequency analysis is a hierarchical method for calculating the probability of a fire or explosion occurring in a given structure. It can be used to identify equipment failure, faults, operating conditions, environmental conditions, and human error that contribute to fire and explosion accidents. FTA and ETA were used to calculate the failure and ignition probabilities to determine the probabilities of a pool fire, fireball, and jet fire for one year.
For FTA, the ignition probability of various flammable materials in the event of a metal hose leak was taken from the literature [38,39,40]. Table 3 presents the probability of a fire occurring for different release rates. The frequency analysis results for metal hoses are detailed in Section 3. Data from the UK Health and Safety Executive (HSE) were referenced to determine the failure probability of the metal hose, which was set to 1.0 × 10−2 [21,38].

Table 3.
Ignition probability of a liquid according to the release rate.
A wind rose graphs the frequencies of the wind direction and speed at an observation point. It can be used to show the long-term average wind direction and speed [41,42], which are important factors that affect the location and extent of damage caused by a jet fire [42,43,44]. In this study, the wind direction was expressed as a probability, and it was combined with the frequency analysis for the fire risk assessment. Twelve wind directions were selected, and their probabilities were set according to the wind data from Goheung, which is where the aerospace facility is located. The software WPLOT [45] was used to analyze the wind rose data. Figure 5 shows the wind rose for Goheung. Table 4 presents wind data sourced from KMA from 2009 to 2018 in 12 directions according to frequency. Wind rose data is the probability data about wind direction and speed. For example, in Table 4, when the wind direction is 345 to 15 degrees, the probability of blowing with a wind speed of 0 to 1 m/s can be expressed as 26.6538%.
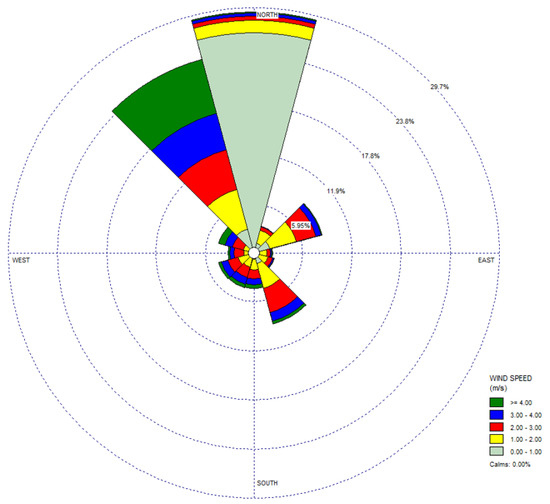
Figure 5.
Wind direction and speed at the aerospace facility in Goheung (Korea Meteorological Administration).

Table 4.
Probability of jet fire, according to wind direction and speed.
Wind speeds >5 m/s accounted for less than 1% of the 10 years of data and thus, were excluded from the analysis. Although a higher wind speed can lead to greater damage, the frequency was so low that the risk was negligible. The remaining wind speed data were used to quantify the probability of a jet fire in each wind direction. The total probability of a jet fire was determined by summing the probabilities in each wind direction. According to the wind rose data for this aerospace facility, the highest probability of a jet fire was at 345–15° for a wind speed of 0–1 m/s and at 315–345° for wind speeds of 1–2, 2–3, 3–4, and >4 m/s.
3. Consequence Analysis
For the consequence analysis, a kerosene jet fire was assumed to occur under the following conditions:
- Kerosene leaks from the metal hose at a high speed.
- Metal hose has a hole diameter of 13 mm.
- Kerosene atomizes to form a jet fire when Lc = 3.20 m.
- Radii from the jet fire for 99%, 50%, and 1% fatality can be determined.
- Frequency of a jet fire can be determined for four directions, and the frequencies in each direction can be summed to obtain the total frequency.
Table 5 presents the fire probability for a metal hose with a hole diameter of 13 mm and release rate of 10.93 kg/s, while Table 6 presents the radii for 99%, 50%, and 1% fatality when a jet fire occurs with a leakage flow rate of 10.93 kg/s. According to Equations (5) and (6), the 99%, 50%, and 1% fatality areas and radii were 493.87 m2 and 3.20~12.94 m, 518.01 m2 and 12.94~18.23 m, and 1027.71 m2 and 18.23~25.68 m, respectively. When the analysis of the results was performed, it was confirmed that the lower the fatality, the lower the degree of damage, but the wider the damage range.

Table 5.
Metal hose fire probability.

Table 6.
Fatality area and distance from jet fire point according to metal hose release rate.
4. Risk Analysis
IR was obtained from the results of the frequency analysis and consequence analysis, which is calculated as follows:
where is the overall fraction of time that a person is in a given area, is the probability that the person is at a location, is the fire probability of the metal hose, is the fatality probability of a jet fire, and is the probability that the jet fire will be in one of the windrose (obtained through WPLOT).
For the risk analysis, a kerosene jet fire individual risk was assumed to occur under the following conditions:
- is set to 0.33 since Korean labour standards are applied to work 8 h out of 24 h.
- The was set as follows, since the person working at the space launch facility was among those working at the Korea Aerospace Research Institute located in Goheung was 0.88.
In this study, Equation (10) was created based on Equation (2). Although Equation (2) assumed to have a constant velocity distribution in all wind directions, Equation (10) used in this study that considered both wind direction and speed to calculate the individual risk result value.
Table 7 presents the values of the terms in Equation (10). Figure 5 lists the IR ranges by applying different colors to visually express the IR result values derived through Equation (10). The colors in Figure 6 are used in Figure 7, Figure 8 and Figure 9 to visualize IR according to the wind speed and direction for each fatality probability. Figure 7, Figure 8 and Figure 9 show the results for 99%, 50%, 1% IR. For Table 7, all probability values of the wind rose are omitted since they are listed in Section 2.5.

Table 7.
Calculation of IR for different fatality probabilities.
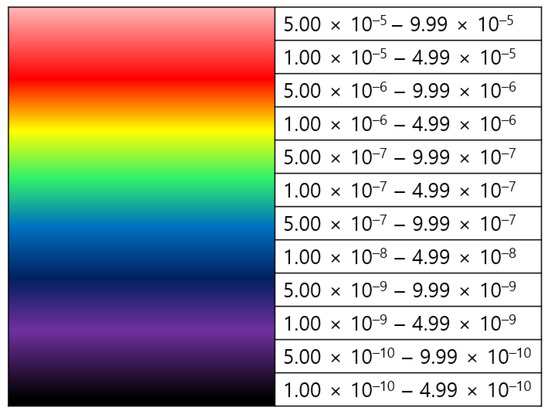
Figure 6.
IR contours.
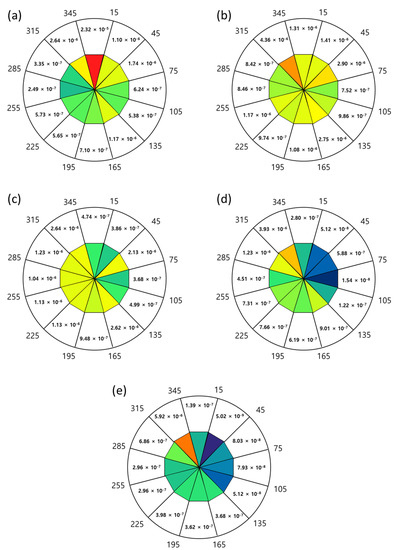
Figure 7.
IR of 99% fatality at different wind directions and speeds: (a) 0–1 m/s, (b) 1–2 m/s, (c) 2–3 m/s, (d) 3–4 m/s, and (e) >4 m/s.
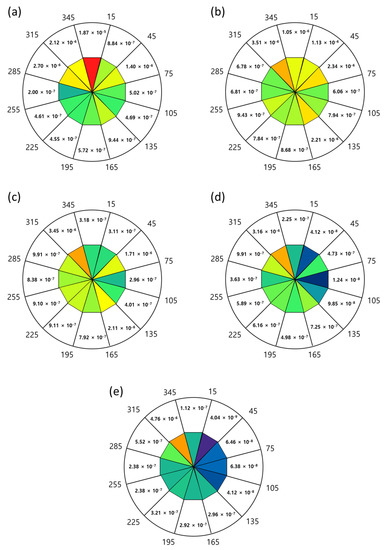
Figure 8.
IR of 50% fatality at different wind directions and speeds: (a) 0–1 m/s, (b) 1–2 m/s, (c) 2–3 m/s, (d) 3–4 m/s, and (e) >4 m/s.
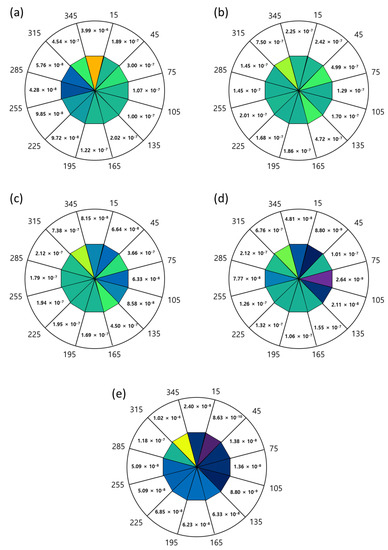
Figure 9.
IR of 1% fatality at different wind directions and speeds: (a) 0–1 m/s, (b) 1–2 m/s, (c) 2–3 m/s, (d) 3–4 m/s, and (e) >4 m/s.
The IR results were calculated for the areas corresponding to 99%, 50%, and 1% fatality in each wind direction. The total IR was calculated for each wind speed. For the case of 99% fatality, the highest IR was at 345°–15° for a wind speed of 0–1 m/s and at 315°–345° for wind speeds >1 m/s. The lowest IR was at 255°–285° for a wind speed of 0–1 m/s, 75°–105° for wind speeds of 1–4 m/s, and 15°–45° for wind speeds >4 m/s. For the case of 50% fatality, the highest IR was at 345°–15° for a wind speed of 0–1 m/s and 315°–345° for wind speeds >1 m/s. The lowest IR was at 255°–285° for a wind speed of 0–1 m/s, 75°–105° for wind speeds of 1–4 m/s, and 15°–45° for a wind speed >4 m/s. For the case of 1% fatality, the highest IR was at 345°–15° for a wind speed of 0–1 m/s and 315°–345° for wind speeds >1 m/s. The lowest IR was at 255°–285° for a wind speed of 0–1 m/s, 75°–105° for wind speeds of 1–4 m/s, and 15°–45° for a wind speed >4 m/s. The IR showed the same tendencies at 99%, 50%, and 1% fatality. The total IR was high at 0–1 m/s, which was the most frequent wind speed; this indicates a high probability of IR when a jet fire occurs.
5. Results and Discussion
In Section 4, individual risk results were calculated by considering the 99%, 50%, and 1% fatality ranges and wind direction and speed. Furthermore, in the case of Section 4, individual risks for all wind directions, speeds, and fatality ranges were, respectively, calculated and presented. In Section 5, the total individual risk considering wind speed and fatality ranges is calculated, and the safety of the aerospace facility is confirmed when metal hose jet fire occurred through comparison with the HSE risk standard. The HSE risk standard is a criteria created to ensure plant safety from unexpected accident that does not generate damage to workers, the environment, or assets [46,47].
HSE risk standard follows the ALARP (As Low as Reasonably Practicable) standard. As shown in Figure 10, ALARP is set for the safe operation of chemical facilities and plants, and there is a difference between the risk standard for workers and for the public [48,49,50].
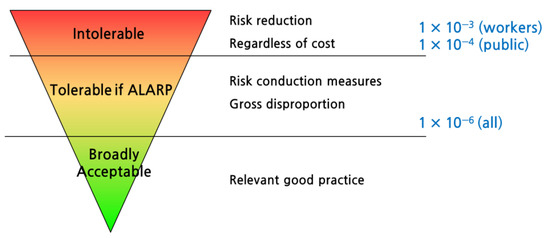
Figure 10.
HSE ALARP standard.
As a result, the total individual risk result value considering fatality and wind speed was shown in Figure 11, and it was found that the individual risk decreased as the wind speed increased and the fatality decreased. In the case of wind speed, due to the probability decreasing as the wind speed was increased, the of Equation (10) was decreased and, consequently, the individual risk was lowered. Similarly, in the case of fatality, due to the fatality decreasing as the of Equation (10) was decreased, consequently, the individual risk was lowered. Finally, when compared with the ALARP standard, all individual risks were included in the ALARP standard regardless of wind speed and fatality. The individual risk from jet fire in an aerospace facility was calculated that maximum risk is 3.35 × 10−5, minimum is 1.49 × 10−6. According to this study’s results, when a jet fire occurred from a metal hose, the risk satisfied tolerable criteria. Therefore, enhanced firewalls, extinguishing systems, and emergency shut off systems are needed to prevent jet fire accidents and to satisfy acceptable criteria. If the same accident occurs in another area, a jet fire risk assessment can be performed by implementing the same method using the wind data of the area where the rocket launch facility is located.
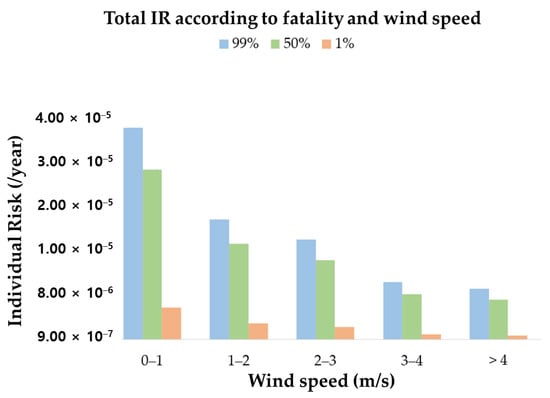
Figure 11.
Total IR values according to fatality and wind speed.
In this study, the quantitative risk assessment according to the wind rose of the aerospace facility where a jet fire in a metal hose occurs was performed. Further studies should be conducted including the social risk, which is the probability of injury to the entire population in hazardous facilities when a fire occurs near an ignition source.
6. Sensitivity Analysis
Sensitivity analysis is an evaluation method that changes how the individual parameters affect the optimal solution. Sensitivity analysis was performed using as a parameter. As a special and high-risk facility, the aerospace facility is not required for many working people, and it was an important factor in calculating individual risk results for metal hose jet fires in aerospace facilities, as well as fire and explosion scenarios that may occur in aerospace equipment. Therefore, in this study, sensitivity analysis was calculated by considering among the various parameters used in the individual risk equation of metal hose jet fire according to wind direction and speed. In addition, the value of was the average standard of a working person in the aerospace facility, and as such sensitivity analysis was performed by selecting for higher and lower values than the average standard that was 0.88.
For the sensitivity analysis, according to the total individual risk it was assumed to occur under the following conditions:
- The high value is set to 1, assuming that the working person is the maximum in the aerospace facility.
- The high and low values are 1 and 0.5.
- Sensitivity analysis was compared based on 99% fatality.
- In the results and discussion, 99% fatality was selected, due to the high individual risk and sensitivity analysis was performed.
As a result, Figure 12 shows the sensitivity analysis considering the value. In the case of the value is higher than the average standard, when the maximum risk is 3.81 × 10−5 and the minimum is 9.71 × 10−6. When the value is lower than the average standard, the maximum risk is 1.90 × 10−5 and the minimum is 4.86 × 10−6. Finally, this study confirmed that individual risk satisfied the tolerable criteria even if the value was maximum.
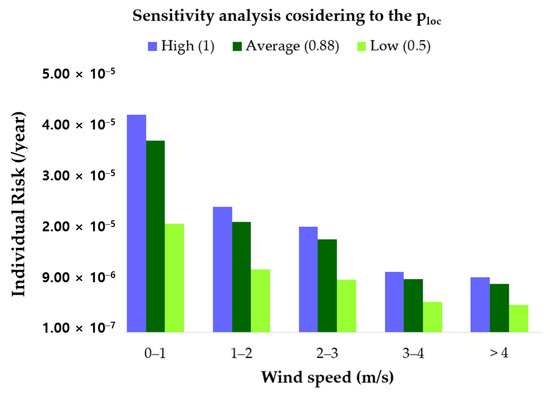
Figure 12.
Sensitivity analysis considering to the .
7. Conclusions
In this study, a risk assessment was performed on a jet fire at an aerospace facility considering the wind direction and speed. A consequence analysis was performed based on the properties of the metal hose, kerosene, and jet fire. Next, the IR was calculated for the wind rose when a jet fire occurred in a metal hose. The following conclusions can be drawn:
- The fire probability of a metal hose with a hole diameter of 13 mm and release rate of 10.93 kg/s is 3.0 × 10−4.
- In a case of jet fire occurring from a metal hose, the 99% fatality area and distance are 493.87 m2 and 3.20~12.94 m, the 50% fatality area and distance are 518.01 m2 and 12.94~18.23 m, and 1% fatality area and distance are 1027.71 m2 and 18.23~25.68 m, respectively.
- The highest IR was at 345°–15° for a wind speed of 0–1 m/s and at 315°–345° for wind speeds >1 m/s. The lowest IR was at 255°–285° for a wind speed of 0–1 m/s, 75°–105° for wind speeds of 1–4 m/s, and 15°–45° for wind speeds >4 m/s. The IR showed similar tendencies at different fatality probabilities.
- The individual risk from jet fire in an aerospace facility was calculated that maximum risk is 3.35 × 10−5, minimum is 1.49 × 10−6. The highest IR of 3.35 × 10−5 is within the tolerable range according to the risk assessment criteria set by HSE ALARP standard. Furthermore, all individual risks were satisfied with the ALARP standard, regardless of wind speed and fatality. Therefore, the risk of metal hose jet fire was tolerable.
- As a result of sensitivity analysis according to , which is an important factor in considering individual risk results for metal hose jet fire, this study appeared that all individual risks satisfy the tolerable criteria, even if the value is maximum.
To summarize the results of this study, the major risk component is the metal hose, and the maximum IR in aerospace facility satisfies HSE ALARP standard. Further, using these results, it is possible to strengthen safety by applying additional firewalls, extinguishing systems, and emergency shut off systems.
Author Contributions
Conceptualization: I.S.Y. and E.S.J.; methodology: H.J.K. and K.M.J.; formal analysis: H.J.K.; data curation: H.J.K. and K.M.J.; writing-original draft preparation: H.J.K., K.M.J. and E.S.J.; writing-review and editing: H.Y.O. and S.I.K.; visualization: H.J.K.; supervision: E.S.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Acknowledgments
This work was supported by the Korea Space Launch Vehicle (KSLV-II) funded by the Ministry of Science and ICT (MSIT, Republic of Korea).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| IR of population group k (1/year) | |
| Overall fraction of time that population group k is in the area (-) | |
| Probability that population group k is at location i (-) | |
| Frequency of fatalities at location i (-) | |
| Frequency of event outcome j (1/year) | |
| Probabilities of fatality produced by event outcome j (-) | |
| Probabilities of weather conditions produced by event outcome j (-) | |
| Probability of the direction required to produce event outcome i (-) | |
| Time that the target is exposed to radiation (s) | |
| Thermal radiation flux (W/m2) | |
| Mass flow rate of leakage (kg/s) | |
| Distance between the target and the center of the flame zone (m) | |
| Jet breakup length (m) | |
| Weber number | |
| Reynolds number | |
| Density (kg/m3) | |
| Jet velocity (m/s) | |
| Diameter of nozzle or hole (m) | |
| Surface tension (N/m) | |
| Viscosity (kg/m/s) | |
| Overall fraction of time that a person is in a given area (-) | |
| Probability that the person is at a location (-) | |
| Fire probability of the metal hose (1/year) | |
| The fatality probability of a jet fire (-) | |
| Probability that the jet fire will be in one of the wind rose (-) |
References
- West Yorkshire Fire & Rescue Service (WYFRA). Methods of Fire Risk Assessment (Fire Safety Training), West Yorkshire Fire & Rescue Service Procedure & Guidance Fire Safety, UK. 2011. Available online: https://www.westyorksfire.gov.uk/your-safety/work/fire-risk-assessments/ (accessed on 15 June 2020).
- Burt, B.A. Definitions of Risk. J. Dent. Educ. 2001, 65, 1007–1008. [Google Scholar] [CrossRef] [PubMed]
- Alp, E.; Eng, P.; Atkinson, D.; Beatty, R.; De Gagne, D.; Gagner, V.; Gulbinas, E.; Hilber, M.; Hyatt, N.; Kelly, B.; et al. Risk Assessment—Recommended Practices for Municipalities and Industry; Canadian Society for Chemical Engineering: Ottawa, ON, Canada, 2004; Available online: https://www.cheminst.ca/about/about-csche/ (accessed on 7 September 2018).
- Uijt de Haag, P.A.M.; Ale, B.J.M. Guidelines for quantitative risk assessment, CPR 18E. In TNO Purple Book; Netherlands Or-ganisation for Applied Scientific Research: The Hague, The Netherlands, 2005. [Google Scholar]
- CCPS (Center for Chemical Process Safety). Event Probability and Failure Frequency Analysis. In Guidelines for Chemical Process Quantitative Risk Analysis, 2nd ed.; American Institute of Chemical Engineers: New York, NY, USA, 2010. [Google Scholar]
- Cummings, M.L. Factors that Influence the Acceptance of New Aerospace Risk Assessment Techniques. AIAA Scitech Forum 2020. [Google Scholar] [CrossRef]
- Gonzales, E.; Murray, D. FAA’s Approaches to Ground and NAS Separation Distances for Commercial Rocket Launches. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; pp. 1–12. [Google Scholar]
- Altavilla, A.; Garbellini, L. Risk assessment in the aerospace industry. Saf. Sci. 2002, 40, 271–298. [Google Scholar] [CrossRef]
- Padiha, D.; Butt, C.; Tisato, J.; Wilson, S. The Australian approach to ground population modelling and risk assessment. In Proceedings of the 4th IAASS Workshop on Launch and Re-entry Safety, Chincoteague, VA, USA, 18 September 2012; pp. 1–6. [Google Scholar]
- Lariviere, M.; Kezirian, M.T. Preliminary safety assessment of the DLR SpaceLiner vehicle. J. Space Saf. Eng. 2019, 6, 15–23. [Google Scholar] [CrossRef]
- Coccorullo, I.; Russo, P. Jet fire consequence modeling for high-pressure gas pipelines. AIP Conf. Proc. 2016, 1790, 110007. [Google Scholar] [CrossRef]
- Jo, Y.-D.; Ahn, B.J. A method of quantitative risk assessment for transmission pipeline carrying natural gas. J. Hazard. Mater. 2005, 123, 34. [Google Scholar] [CrossRef]
- Lee, S.; Landucci, G.; Reniers, G.; Paltrinieri, N. Validation of Dynamic Risk Analysis Supporting Integrated Operations Across Systems. Sustainability 2019, 11, 6745. [Google Scholar] [CrossRef] [Green Version]
- Goerlandt, F.; Khakzad, N.; Reniers, G. Validity and validation of safety-related quantitative risk analysis: A review. Saf. Sci. 2017, 99, 127–139. [Google Scholar] [CrossRef]
- Tixier, J.; Dusserre, G.; Salvi, O.; Gaston, D. Review of 62 risk analysis methodologies of industrial plants. J. Loss Prev. Process. Ind. 2002, 15, 291–303. [Google Scholar] [CrossRef] [Green Version]
- Lee, S. Quantitative risk assessment of fire & explosion for regasification process of an LNG-FSRU. Ocean Eng. 2020, 197, 106825. [Google Scholar] [CrossRef]
- Roos, A.J. Methods for the Determination of Possible Damage, CPR 16E. In TNO Green Book; Netherlands Organisation for Applied Scientific Research: The Hague, The Netherlands, 1992. [Google Scholar]
- Han, Z.; Weng, W. An integrated quantitative risk analysis method for natural gas pipeline network. J. Loss Prev. Process. Ind. 2010, 23, 428–436. [Google Scholar] [CrossRef]
- Franks, A. A Simplified Approach to Estimating Individual Risk, Health & Safety Executive, UK. 2017. Available online: https://www.hse.gov.uk/research/misc/vectra300-2017-r03.pdf (accessed on 23 June 2019).
- Miesse, C.C. Correlation of Experimental Data on the Disintegration of Liquid Jets. Ind. Eng. Chem. 1955, 47, 1690–1701. [Google Scholar] [CrossRef]
- Washington, J. Failure Rate and Event Data for Use within Risk Assessments. Health & Safety Executive, UK. 2012. Available online: https://wwwhsegovuk/landuseplanning/failure-ratespdf (accessed on 6 February 2018).
- Cox, A.W.; Lees, F.P.; Ang, M.L. Classification of Hazardous Locations; IChemE: London, UK, 1990; pp. 56–61. [Google Scholar]
- Magee, J.W.; Bruno, T.J.; Friend, D.G.; Huber, M.L.; Laesecke, A.; Lemmon, E.W.; McLinden, M.O.; Perkins, R.A.; Baranski, J.; Widegren, J.A. Thermophysical Properties Measurements and Models for Rocket Propellant RP-1: Phase I, National Institute of Standards and Technology (NIST), USA. 2007. Available online: https://nvlpubs.nist.gov/nistpubs/Legacy/IR/nistir6646.pdf/ (accessed on 10 December 2021).
- Vukadinovic, V.; Habisreuther, P.; Zarzalis, N. Influence of pressure and temperature on laminar burning velocity and markstein number of kerosene jet A-1: Experimental and numerical study. Fuel 2013, 111, 401–410. [Google Scholar] [CrossRef]
- Franks, A.; Maddison, T. A Simplified Method for the Estimation of Individual Risk. Process. Saf. Environ. Prot. 2006, 84, 101–108. [Google Scholar] [CrossRef]
- Shao, H.; Duan, G. Risk Quantitative Calculation and ALOHA Simulation on the Leakage Accident of Natural Gas Power Plant. Procedia Eng. 2012, 45, 352–359. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.B.; Kim, Y.H.; Lee, C.; Um, S.I.; Ko, J.W.; Baek, J.B. A study on the individual and societal risk estimation for the use and storage facility with toxic materials. J. Korean Soc. Saf. 1997, 12, 51–59. Available online: https://www.koreascience.or.kr/article/JAKO199711922390725.page (accessed on 23 May 2021).
- Renjith, V.R.; Madhu, G. Individual and societal risk analysis and mapping of human vulnerability to chemical accidents in the vicinity of an industrial area. Int. J. Appl. Eng. Res. 2010, 1, 135–148. Available online: https://www.semanticscholar.org/paper/Individual-and-societal-risk-analysis-and-mapping-RenjithV-Madhu/af09801ce0302f54fd67740704a1b36c1486d654 (accessed on 19 October 2021).
- Skřínský, J.; Sluka, V.; Senčík, J.; Pražáková, M.; Maly, S. Application of emergency planning criteria for the control of major accident hazards—Calculation of the consequences of fire accidents. Saf. Reliab. Risk Anal. 2013, 2013, 135–142. [Google Scholar] [CrossRef]
- Ma, L.; Li, Y.; Liang, L.; Li, M.; Cheng, L. A novel method of quantitative risk assessment based on grid difference of pipe-line sections. Saf. Sci. 2013, 59, 219–226. [Google Scholar] [CrossRef]
- Bayvel, L.; Orzechowski, Z. Liquid Atomization, 1st ed.; Taylor & Francis: Milton Park, FL, USA, 1993. [Google Scholar]
- Lefebvre, H.; McDonell, V.G. Atomization and Sprays, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Bremond, N.; Clanet, C.; Villermaux, E. Atomization of undulating liquid sheets. J. Fluid Mech. 2007, 585, 421–456. [Google Scholar] [CrossRef]
- Chen, X.; Ma, D.-J.; Yang, V.; Popinet, S. High-fidelity simulations of impinging jet atomization. At. Sprays 2013, 23, 1079–1101. [Google Scholar] [CrossRef] [Green Version]
- Khan, O.S.; Baek, S.W.; Hojat, G. On the autoignition and combustion characteristics of kerosene droplets at elevated pressure and temperature. Combust. Sci. Technol. 2007, 179, 2437–2451. [Google Scholar]
- Inoue, C.; Watanabe, T.; Himeno, T. Numerical Analysis on Dynamics and Inner Structures of Liquid Jet in Pinch-Off. In Proceedings of the 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati, OH, USA, 8–11 July 2007. [Google Scholar]
- Wang, T.-S. Thermophysics Characterization of Kerosene Combustion. J. Thermophys. Heat Transf. 2001, 15, 140–147. [Google Scholar] [CrossRef] [Green Version]
- Daycock, J.H.; Rew, P.J. Development of a Method for the Determination of On-Site Ignition Probabilities; Health & Safety Executive: Bootle, UK, 2004. Available online: https://www.hse.gov.uk/research/rrhtm/rr226.htm (accessed on 22 May 2019).
- Zhu, C.; Jiang, J.; Yuan, X. Study on Ignition Probability of Flammable Materials after Leakage Accidents. Procedia Eng. 2012, 45, 435–441. [Google Scholar] [CrossRef] [Green Version]
- Rew, P.J.; Spencer, H. A framework for ignition probability of flammable gas clouds. Icheme. Symp. Ser. 2005, 141, 151–162. Available online: https://wwwsemanticscholarorg/paper/A-FRAMEWORK-FOR-IGNITION-PROBABILITY-OF-FLAMMABLE-Rew-Spencer/3c0e49153a49710d3e448ef62af2aaa371406153 (accessed on 23 August 2018).
- Applequist, S. Wind Rose Bias Correction. J. Appl. Meteorol. Clim. 2012, 51, 1305–1309. [Google Scholar] [CrossRef]
- Slusser, W. Wind Rose Maps of the United States. Weather 1965, 18, 260–263. [Google Scholar] [CrossRef]
- Varma, S.A.K.; Srimurali, M.; Varma, S.V. Evolution of wind rose diagrams for RTPP. Kadapa, AP, India. Int. J. Innovat. Res. Dev. 2013, 2, 2278. Available online: https://wwwsemanticscholarorg/paper/Evolution-of-Wind-Rose-Diagrams-for-RTPP%2C-KADAPA%2C-Varma-Srimurali/652d3848683cd8f43fe46f0b2df85915b1db1752 (accessed on 13 January 2021).
- Bharani, R.; Sivaprakasam, A. Meteorosoft: A excel function for wind data processing and rose diagram. Earth Sci. Inform. 2019, 13, 965–971. [Google Scholar] [CrossRef]
- Thé, J.L.; Thé, C.L.; Johnson, M.A. WRPLOT View Release Notes; Lakes Environmental: Waterloo, ON, Canada, 2018. [Google Scholar]
- Amir-Heidari, P.; Maknoon, R.; Taheri, B.; Bazyari, M. Identification of strategies to reduce accidents and losses in drilling industry by comprehensive HSE risk assessment—A case study in Iranian drilling industry. J. Loss Prev. Process. Ind. 2016, 44, 405–413. [Google Scholar] [CrossRef]
- Brookes, K.; Limbert, C.; Deacy, C.; O’Reilly, A.; Scott, S.; Thirlaway, K. Systematic review: Work-related stress and the HSE Management Standards. Occup. Med. 2013, 63, 463–472. [Google Scholar] [CrossRef] [Green Version]
- Baybutt, P. The ALARP principle in process safety. Process. Saf. Prog. 2014, 33, 36–40. [Google Scholar] [CrossRef]
- Melchers, R. On the ALARP approach to risk management. Reliab. Eng. Syst. Saf. 2001, 71, 201–208. [Google Scholar] [CrossRef]
- Maselli, G.; Macchiaroli, M.; Nesticò, A. ALARP Criteria to Estimate Acceptability and Tolerability Thresholds of the Investment Risk. Appl. Sci. 2021, 11, 9086. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).