Abstract
Asynchronous motors are widely used in industry and agriculture because of their simple structure, low cost, and easy maintenance. However, due to the coupling and uncertain factors of the actual operation of the motor, a traditional controller cannot achieve a satisfactory control effect. A linear active disturbance rejection controller (LADRC), featuring good robustness and adaptability, was proposed to improve the control efficiency of a nonlinear, uncertain plant. A linear extended state observer (LESO) is the core part of a L. The accuracy of the observation of state variables and unknown disturbances is related to the control effect of the controller. The performance of a traditional LESO is not high enough, and thus an error differential is introduced by analyzing the principle of LESO to improve its observation performance. The improved LADRC applies to the vector speed control of the induction motor. Additionally, low-speed and high-speed no-load starting, sudden load, electromagnetic torque, and three-phase stator current of the induction motor was simulated using MATLAB (Developed by MathWorks in Natick, MA, USA, and dealt by MathWorks Software (Beijing) Co., Ltd. in Beijing, China). Theoretical analysis and simulation results show that the ADRC based on the improved linear expansion observer was better than the traditional linear ADRC in terms of the dynamic and static performance and robustness.
1. Introduction
Three-phase asynchronous motors are commonly used in industrial and agricultural production due to their advantages of simple structure, ruggedness, and low price [1,2,3,4]. The emergence of vector control allows the AC speed regulation system to have good speed regulation performance, just like a DC speed regulation system [5]. However, vector control has disadvantages, such as dependence on accurate mathematical models, poor adaptability to instruction changes, and sensitivity to changes in the system parameters. Even if the motor parameters and rotor flux linkage are known accurately, decoupling can be achieved under steady-state conditions, and there are still couplings during the field-weakening speed regulation. The nonlinearity of the magnetization curve of the ferromagnetic material in the motor [6] leads to the nonlinearity of the motor inductance, and the change of the inductance parameter reduces the speed control effect of the vector control. The AC control system has the characteristics of non-linearity [1,4], strong couplings, and having multiple variables, which means the traditional control method based on a precise mathematical model faces severe challenges.
The active disturbance rejection control (ADRC) theory was proposed for the control of nonlinear uncertain systems. The system is linearized by compensating for the observed total disturbance. The compensated system can be converted into an integrator series independent of whether the object is deterministic, linear, or nonlinear, or whether it is time-varying or time-invariant. At present, the ADRC theory has been applied to a six-rotor aircraft [7], a permanent magnet synchronous motor [8], DC–DC boost converter [9], and other fields. Abdul-Adheem et al. [10] applied the improved ADRC to the decoupling control of multivariable systems. The coupling is divided into two parts: static coupling (control input of the system) and dynamic coupling (parts other than the control input to the system). All ADRC pass a reversible static matrix (approximately reversible also applies) that is used for decoupling. Compared with the traditional decentralized control method (an automatic disturbance rejection controller designed independently for each part of the system), the improved ADRC decoupling algorithm uses part of the system model information, easing the burden of the extended state observer (ESO) such that the decoupling effect is better. Although both numerical simulations and physical verification show that the ADRC controller has a good control effect, the large number of modeled non-linear links between the ADRC require high system hardware requirements and increases the difficulty of real-time control. The second-order auto-disturbance rejection controller has 15 parameters that need to be adjusted, and the direction of the parameter adjustment is difficult to determine, which brings certain difficulties in the practical application of the controller. In short, many factors limit the popularity and engineering application of ADRC.
American scholar Gao Zhiqiang explored the connotation and meaning of the idea of auto-disturbance control. He was inspired by the concept of “time scale” [11] proposed by Han Jingqing researchers and proposed the concept of “frequency scale.” The parameter setting is carried out through the pole configuration in the frequency domain, and the parameters to be set are reduced to three, which greatly promotes the development and application of the auto-disturbance control theory. Since then, the linear auto-rejection controller has been used in fault detection [12], a wind energy conversion system [13], maximum power point tracking [14], and other fields. Li et al. [15] adopted the concept of “relative order” to determine the order of the linear ADRC (LADRC) controller and designed a second-order LADRC controller to suppress the harmonics to the grid in the AC microgrid. Laghridat et al. [13] applied LADRC to the control of generators and grid-side converters. Compared with the ADRC, an LADRC has the advantages of a fixed structure, an independent object model, clear physical meaning, easy theoretical analysis [13,16], and easy engineering application. However, in practical applications, it is found that the anti-interference performance of LADRC decreases rapidly with the increase of interference and input frequency, which is related to the insufficient performance of a traditional ESO [17].
This study took the three-phase cage asynchronous motor as the control object, established a mathematical model for it according to the rotor flux linkage orientation, and introduced the structure of the ADRC controller and the role of each component. First, the structure and function of each part of the ADRC controller are introduced. Then, based on the basic principle of deviation control, the adjustment process of each state variable of traditional LESO is discussed and improved. Through theoretical analysis, the stability proof and precision analysis of an improved LESO are given. From the frequency domain, the convergence, tracking, and immunity of the improved linear auto-disturbance controller are analyzed. In the time domain, a large deviation band of the initial value of the internal state variable of the observer is seen and the corresponding value of the system’s overshooting is compared. Finally, the control effects of the two controllers are compared based on results from Matlab/Simulink digital simulation software (Developed by MathWorks in Natick, MA, USA, and dealt by MathWorks Software (Beijing) Co., Ltd. in Beijing, China).
2. Mathematical Modeling of an Asynchronous Motor and Introduction to Classic LADRC
2.1. Mathematical Modeling of the Rotor Flux Orientation of Induction Motor
To facilitate the research, it was necessary to treat the motor as an ideal motor; therefore, it was necessary to make the following assumptions [18]:
- The stator and rotor three-phase windings of the motor are completely symmetrical.
- The surfaces of the stator and rotor are smooth without any cogging effect, and the air gap magnetic potential of each phase of the stator and rotor exhibits a sinusoidal distribution in space.
- The influences of the core eddy current, saturation, and hysteresis loss are ignored, and the skin effect of the conductor is ignored. (Note: the parameters of the rotor side have been converted to those of the stator side.)
The three-phase winding voltage balance equation in the three-phase stationary coordinate system is shown in Figure 1:
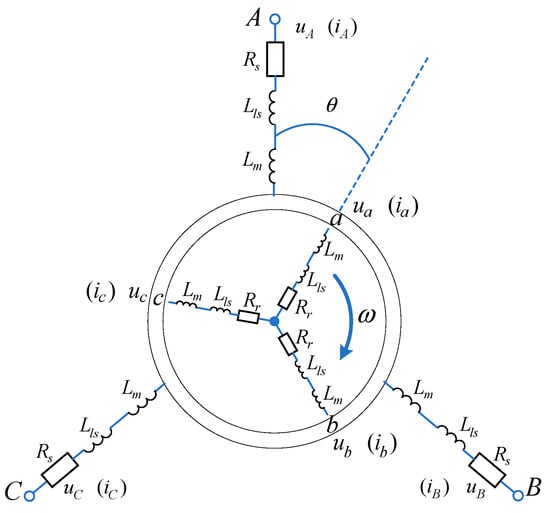
Figure 1.
Physical model of an asynchronous motor.
The three-phase winding voltage balance equation in the three-phase stationary coordinate system is shown in Equation (1):
where ,,,, and are the instantaneous values of the stator (A, B, C) and rotor phase (a, b, c) voltages; ,,, , , and are the instantaneous values of the stator (A, B, C) and rotor (a, b, c) phase currents; and ,,,,, are the full flux of each phase winding. and are the resistances of the stator and rotor windings, respectively.
The flux of each winding of an asynchronous motor is the sum of its own self induction flux and the mutual inductance flux of other windings. Therefore, the flux of the six windings can be expressed as follows:
where ,,, and .
The stator inductance matrix is:
The rotor inductance matrix is:
The mutual inductance matrix of the stator and rotor is:
The voltage equation of the asynchronous motor in the rotating orthogonal coordinate system can be obtained from a Park transform:
where , , , and are the components of the voltage of the stator and rotor sides along the d and q axes; , , , are the components of the current of the stator and rotor sides along the d and q axes; , , , and are the components of the magnetic flux of the stator and rotor sides along the d and q axes; and and are the synchronous angular velocity and the rotor angular velocity, respectively.
The flux equation of the asynchronous motor in the synchronous rotation orthogonal coordinates system is:
where , , and are stator inductance, rotor inductance, and mutual inductance between the stator and rotor, respectively. when the rotor flux is oriented as in Figure 2.
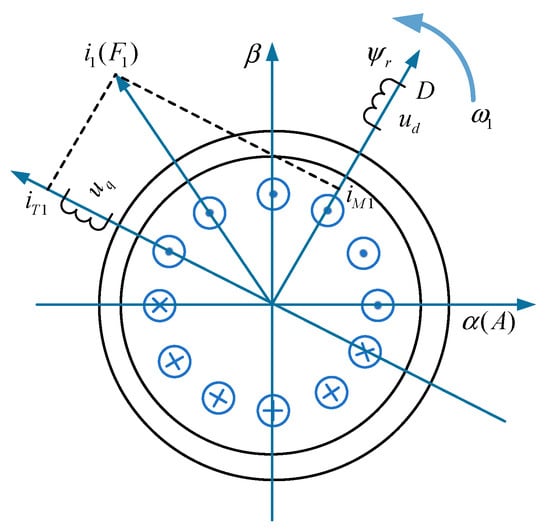
Figure 2.
Rotor flux orientation.
Selecting the stator currents and rotor flux as the state variables, and the stator voltages as the control variables, a fourth-order simplified nonlinear differential equation can be given as follows:
In the above state equations, , , and represent the number of pole pairs of the motor, the load torque, and the rotor time constant, respectively. The coupling between the state variables in Equation (8) causes the nonlinearity of the system [4,10]. The vector control block diagram of the asynchronous motor is shown in Figure 3, in which automatic speed regulator (), the automatic current torque regulator (), and the automatic current magnetic regulator () are the controllers of the vector speed regulation system.
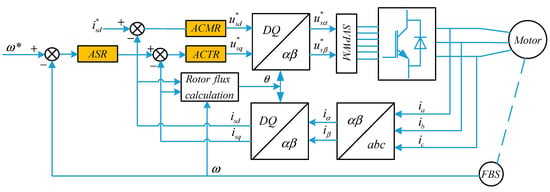
Figure 3.
Vector control structure of an asynchronous motor. ASR: automatic speed regulator, ACTR: Automatic torque current regulator, ACMR: Automatic magnetic field current regulator SVPWM: Space Vector Pulse Width Modulation.
In Equation (8), there is a cross-coupling term in the state equation of the asynchronous motor, thus resulting in the mutual effect of control of the torque component and the excitation component of the stator current, which further affects the dynamic and static performance of the system. The graphical representation of the coupling term is shown in Figure 4. Decoupling can be achieved if the coupling terms are observed and compensated for [19].
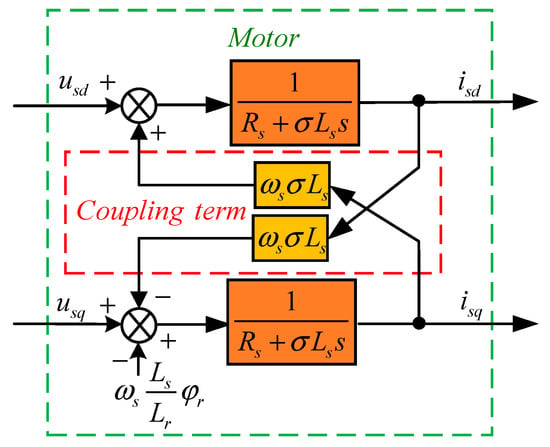
Figure 4.
Coupling structure of an asynchronous motor.
2.2. LADRC Introduction and First-Order LADRC Design
The ADRC consists of a tracking differentiator (TD) [20,21], an extended state observer (ESO) [22,23], and a nonlinear states error feedback control laws (NLSEF) . Among them, the TD can arrange the transition process for the given input, reduce the “impact” of the original error on the system caused by the given mutation, and realize the differential signal extraction; ESO can observe the state variables and total disturbances (unmodeled dynamics and external disturbances) of the controlled object in a real-time manner; and the NLSEF is used to improve the dynamic characteristics of the closed-loop system. The linear ADRC only replaces the nonlinear part of the original controller with the linear part, where the structure of the controller is shown in Figure 5.
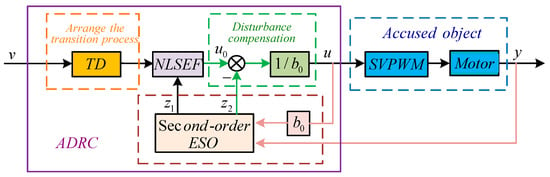
Figure 5.
Structure of an active disturbance rejection controller (TD: tracking differentiator, NLSEF: nonlinear state error feedback, ESO: extended state observer).
Consider the first-order system [24]:
where is the output of the controller, is the system output, is the external disturbance, is the system parameter, is the controller gain that satisfies ; the parameters and are unknown. Let and , where represents the system output and represents the total disturbance of the system. Assuming that is derivable and satisfies , the state variables and are selected to establish the continuous extended state equation s shown in Equation (10):
The corresponding continuous expansion state observer can be established as:
In Equation (11), and are the state variables of the linear extended state observer, which can be adjusted using the difference between the state variables and the system output . By selecting the appropriate observer gain coefficients and , the observer state variables can be used to observe the system output and the total disturbance .
Estimate the total disturbance of the system through the expanded state variables, and compensate for the input side of the system:
If the estimation error of to is excluded, Equation (9) is simplified to a pure integral link:
The linear feedback control law uses proportional links:
In Equation (14), is the controller bandwidth and is the given reference input. Pole assignment of the parameters of the observer and controller is performed using the bandwidth method [10]:
where is the controller gain and is the observer gain. The bandwidth of the observer is about 3 to 5 times that of the controller .
3. Design and Performance Analysis of ADRC
3.1. Design and Stability Proof of the Improved State Observer
The traditional observer estimates the internal state variables of the system using the difference between the estimated value of the system output and the output of the system. In Sun [25], it is pointed out that the observer should first track the output of the system with , and then track the output with . Before the tracking of the estimated value to the system output is completed, other state variables of the observer cannot complete the tracking of the corresponding state variables of the system. However, when the observation variable can better track the output of the system, the smaller error makes it difficult to adjust other observation variables; therefore, we have to use a larger coefficient to speed up the tracking of the observation variables to the real value. Meanwhile, to ensure the stability of the system, the value of cannot be too large. In general, the gain coefficient of the observer increases by an order of magnitude, which is more serious in the higher-order ADRC. Yang et al. [26] mentioned that the extended observer could be improved by introducing the differential of the observation error, but the parameters of the controller were doubled and the parameters of the observer needed to be configured; therefore, it had to be further simplified.
From Equation (11), we can get:
The following equation can be obtained by sorting Equation (16):
It can be seen from Equation (17) that the error between and is , and adjusting by using it as a correction amount can speed up the convergence without significantly increasing the observer gain. Therefore, the classic LESO can be modified as follows:
Equations (12), (14), and (18) form the improved Linear Active Disturbance Rejection Controller of Equation (8), whose structure is shown in Figure 6.
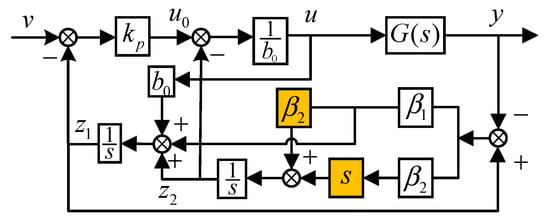
Figure 6.
Structure of the improved controller.
3.1.1. Improved Stability Proof of LESO
Let and . From Equations (10) and (18), we obtain:
Let and to obtain the error equation of the LESO system:
The characteristic equation of Equation (20) is:
The necessary and sufficient conditions for the stability of the second-order system are and . The zero solution (, ) of the second-order constant-coefficient differential equation shown in Equation (20) is globally asymptotically stable because and are stable.
When considering the disturbance , the system has a steady-state error. Specify when . When the system reaches a steady-state, then:
The steady-state error is calculated according to Equation (19):
3.1.2. Observation Errors of the Classical First-Order LESO
Stability and error analyses are performed on the traditional first-order LESO represented by Equation (11). Let and be used to obtain the equation of the traditional LESO error system:
The characteristic equation of Equation (24) is given as follows:
Using the Hurwitz theorem, the necessary and sufficient conditions for the stability of the second-order system are and . The zero solution (, ) of the second-order constant-coefficient differential equation shown in Equation (24) is globally asymptotically stable because and are stable.
When considering the disturbance , the system has a steady-state error. Specify when . When the system reaches a steady-state, then:
The steady-state error of the observer can be expressed as:
According to the above analysis, the modified LESO shown in Equation (18) can exhibit a better dynamic regulation performance and a smaller steady-state observation error than the traditional LESO when the parameters and are the same. Compared with Equations (23) and (27), the improved LESO exhibits a higher observation accuracy than the traditional LESO when the observer and controller bandwidths are the same.
3.2. Performance Index Analysis of the Improved Linear ADRC
3.2.1. Convergence and Estimation Error of the Improved LESO
The Laplace transform of Equation (18) can be used to obtain the transfer function of the observer:
Taking and into account for analyzing a typical , and as the amplitude step signal, then the steady-state error of LESO is given as:
Equation (29) shows that the improved LESO has a good convergence performance for realizing the invariant estimation of the system state variables and generalized disturbances. Further analyzing its dynamic process, the response of under the step signal when is as follows:
The time-domain response of under the action of a step signal can be obtained using an inverse Laplace transform:
In Equation (30), for , the derivative of and taking can produce the extreme point of :
The extreme value of is obtained by substituting the extreme value into Equation (30):
The trajectory of with the observer bandwidth value can be obtained via digital simulation. According to Figure 7, when , the tracking overshoot of observer to is the largest. At this time, the system overshoot is equal to the traditional LESO overshoot. The traditional LESO has a 13.5% overshoot at and the amount of overshoot is independent of the value of the observer bandwidth .
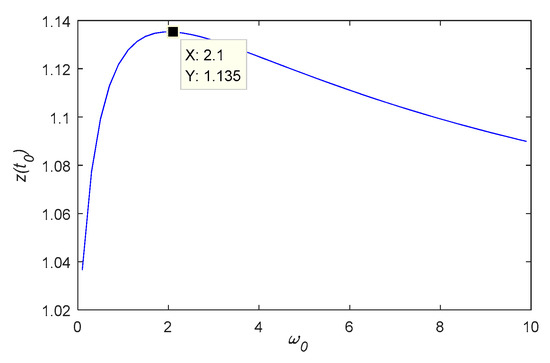
Figure 7.
Relation curve between the system overshoot and observer bandwidth.
The overshoot of the improved LESO varies with the observer bandwidth . The maximum overshoot of the observer state variable is equal to that of the traditional observer. The corresponding speed of the system can be increased and the amount of overshoot is reduced by selecting a larger observer bandwidth . Although the observer bandwidth is larger and the tracking speed is faster, it will lead to noise amplification. The ability of LESO to suppress noise needs to be analyzed.
3.2.2. Improved Disturbance Immunity Analysis of LESO
The closed-loop transfer function of the improved LADRC can be obtained by combining Equations (12), (14), and (18):
The transfer functions of and in Equation (34) are as follows:
According to Equation (34), the diagram of the system structure shown in Figure 8 is obtained [24]:
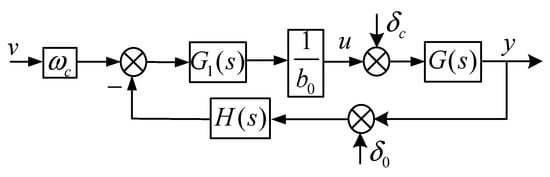
Figure 8.
Equivalent system structure diagram.
Now the effect of the observation noise at the output of the system and the disturbance at the output of the controller for the improved LESO will be discussed. Based on Equation (28), the transfer function of the improved LADRC is:
Similarly, the transfer function of of the traditional LESO’s observation noise can be obtained as follows:
The transfer function of the disturbance at the output of the LESO controller can be improved according to:
The transfer function of the disturbance at the output of a traditional LESO controller is:
Figure 9 shows the characteristic amplitude and phase–frequency curves for the improved and traditional LESOs. The bandwidth of the improved LESO was higher than that of the traditional LESO, and the phase lag of the intermediate frequency segment was improved. Unlike Figure 9, the improved LESO with the same observer bandwidth in Figure 10 is basically the same as the traditional LESO in the high frequency band, but it has better noise immunity in the low frequency band compared with the traditional LESO, and can more effectively suppress the interference at the input end.
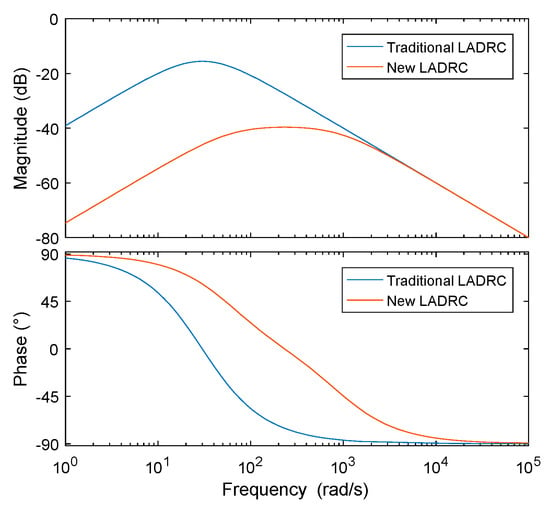
Figure 9.
Frequency-doman characteristic curves of the observed noise.
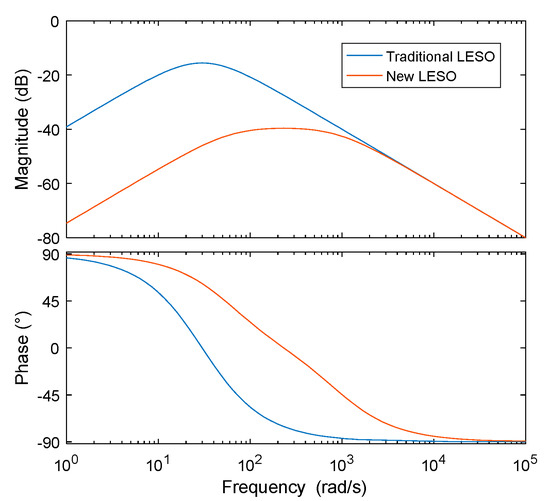
Figure 10.
Frequency-domain characteristic curves of the input disturbance.
3.2.3. Immunity Analysis of the Improved Self-Disturbance Rejection Controller
According to Equation (10), the control object can be written as:
Combined with Figure 8, the closed-loop transfer function of the system is as follows:
The closed-loop transfer function of the system includes the tracking term and the disturbance term. If the state variable of the observer can be used to accurately estimate the total disturbance of the system, the closed-loop transfer function of the system is simplified to the first-order inertial link. At this time, it relates the corresponding speed of the system to the bandwidth of the controller, and the larger the bandwidth, the faster the system.
It can be seen from the closed-loop transfer function that the disturbance term impacts the observer and controller bandwidths. The same observer and controller bandwidths were selected for comparing the improved LESO with the traditional LESO. It can be seen from Figure 11 that under the same bandwidth, the immunity of the improved LESO in the middle- and low-frequency bands were better than that of the traditional LESO, and it improved the phase lag of the middle-frequency band.
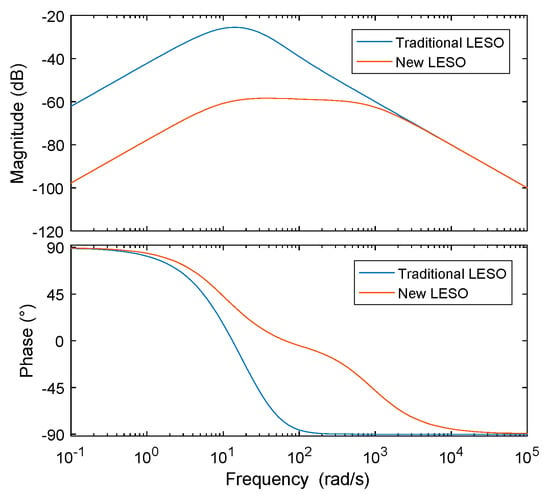
Figure 11.
Logarithmic phase–frequency characteristic curves of the disturbance term.
In particular, if the disturbance is taken as the unit step signal, we can obtain the output response using Equation (41):
The time domain for the anti-Laplace transformation to obtain system output can be expressed as:
It is easy to find , i.e., the steady-state output of the system is zero under the external step disturbance.
(a) Controller Stability with an Unknown Input Gain
Considering only the influence of the input gain on the stability of the system, i.e., if , then Equation (40) can be simplified to:
The following equation can be obtained by combining Equations (26) and (30):
In Equation (46), the coefficients are as follows: ,, , and . As and are greater than zero, it is easy to see that ,, and are all positive numbers. The necessary and sufficient condition for the stability of the Leonard qipat stability criterion (Equation (46)) is that all odd or even Hurwitz determinants are positive.
Since , , and are all positive numbers, is true, i.e., the improved LADRC can be stable for any parameter greater than zero.
(b) Stability of the Controller when the System Parameters are Unknown
Set the controlled object as the following:
where in Equation (48) is an unknown system parameter, and the closed-loop transfer function of the system is obtained by combining with Figure 8:
The necessary and sufficient conditions for the stability of Equation (49) are:
If the roots of Equation (51) are , , and (), the conditions of system stability are or .
According to the digital simulation results, the equation had a pair of conjugate complex roots and a real root. Figure 12 shows the boundary curve for ensuring the system stability when and , and Figure 13 shows the boundary curve for ensuring the system stability when and . From Figure 12 and Figure 13, it can be seen that the stability region of the system increased with an increase of the observer bandwidth and the controller bandwidth
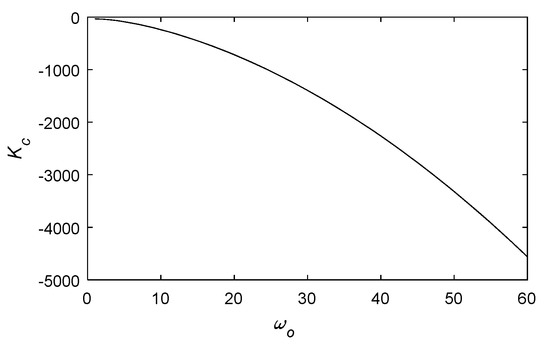
Figure 12.
System stability region under different observer bandwidths .
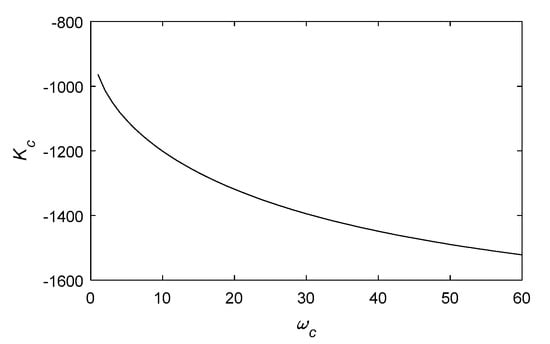
Figure 13.
System stability region under different controller bandwidth .
4. Simulation Study
To verify the actual control effect of the improved LADRC , a vector control model of a three-phase asynchronous motor based on rotor flux linkage orientation was established based on MATLAB and Simulink simulation software (Development by MathWorks, Natick, MA, USA, and agent of MathWorks Software (Beijing) Co., Ltd.). The motor parameters are shown in Table A1. The current loop controller adopted the improved LADRC control, and the outer loop adopted Proportional integral controller (PI) control. The control effect of the controller was verified by simulating the motor speed, the three-phase stator current, the electromagnetic torque, and the sudden load when the motor was started without load at different speeds.
4.1. Dynamic Performance of the Controller for an Induction Motor at Different Given Speeds
4.1.1. Dynamic Performance of the Controller Given a Low Speed of the Motor
Figure 14a shows the simulation diagram of the no-load starting process of the asynchronous motor with a given reference speed of 200 rev/min. The red curve represents the improved LADRC, while the blue curve represents the traditional LADRC. It can be seen from Figure 14 that the traditional LADRC could reach the given value near the motor speed at 0.1 s, while the improved LADRC could reach the given value near the motor speed at 0.07 s. Therefore, the controller effect of the improved LADRC was better than that of the traditional LADRC.
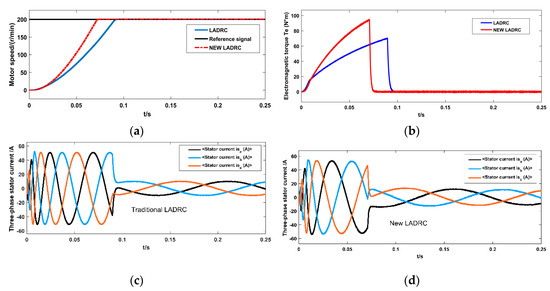
Figure 14.
Low-speed simulation of an asynchronous motor. LADRC: Linear ADRC.
Figure 14b is a simulation diagram of the electromagnetic torque of the induction motor during no-load starting. The corresponding speed of the electromagnetic torque of the motor was greater when the improved LADRC was adopted. The electromagnetic torque of the motor when the improved LADRC was adopted was larger than that when the traditional LADRC was adopted at the same time point; therefore, the electromagnetic torque of the motor could be restored to zero in a shorter time.
Figure 14c is the simulation diagram of the three-phase stator current when the asynchronous motor started up without a load under the action of the traditional LADRC. After the improved LADRC was adopted, the three-phase stator current reached the steady-state again near 0.09 s, and the motor speed reached the given value. Figure 14d is the simulation diagram of the three-phase stator when the asynchronous motor started up without a load under the action of the improved LADRC. After the improved LADRC was adopted, the three-phase stator current reached the steady-state again near 0.07 s. It can be seen from the simulation diagram of the three-phase stator under the action of two controllers that the dynamic performance of the improved linear observer was better.
The improved linear expansion observer can better estimate the total disturbance in the system and realize the decoupling between the excitation subsystem and the torque subsystem. Therefore, the motor controlled by the improved Linear Active Disturbance Rejection Controller at the same time in Figure 14b can obtain a greater electromagnetic torque. The key to motor speed regulation is the adjustment of electromagnetic torque. At the same time in Figure 14b, the electromagnetic torque obtained by the motor under the improved linear auto-disturbance control is larger than that under the traditional linear auto-disturbance controller, so the improvement in Figure 14a Under the Linear Active Disturbance Rejection Controller, the motor speed can reach the given value of a shorter time.
The load in the equivalent circuit of the motor is purely resistive and the magnitude of the equivalent resistance is related to the slip rate. The slip rate is 1 when the motor is started without load. At this time, the total impedance of the system is small and the current on the stator side is large. When the motor reaches a given speed, the slip ratio is less than 1 and the total impedance of the system becomes larger. Therefore, the three-phase stator currents in Figure 14c,d become smaller when the motor speed reaches a given value.
4.1.2. Dynamic Performance of the Controller Given a High Speed of the Motor
Figure 15a is the speed simulation diagram of the asynchronous motor at a given reference speed of 800 rev/min, in which the blue curve is the simulation diagram under the action of the traditional LADRC, and the red curve is that under the action of the improved LADRC. It can be seen from the figure that the traditional LADRC reached the given value near the motor speed at 0.23 s, while the improved LADRC reaches the given value near the motor speed at 0.18 s, and exhibited a better control effect than the traditional LADRC.
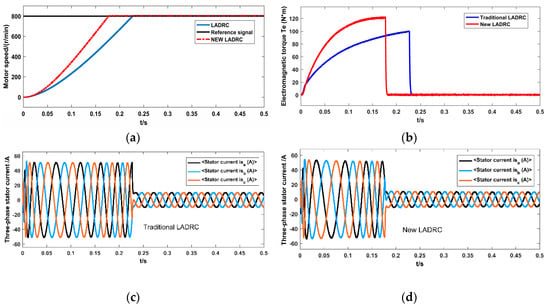
Figure 15.
High-speed simulation of the asynchronous motor.
Figure 15c is the simulation diagram of the three-phase stator when the asynchronous motor started up without a load under the action of the traditional LADRC. After the improved LADRC was adopted, the three-phase stator current reached the steady-state again near 0.17 s, when the motor speed reached the given value. Figure 15d is the simulation diagram of the three-phase stator when the asynchronous motor started up without a load under the action of the improved LADRC. After the improved LADRC was adopted, the three-phase stator current reached the steady-state again near 0.16 s. According to Figure 15c,d, the dynamic performance of the improved linear observer was better.
4.2. Steady State Error of Asynchronous Motor Controller at Different Given Speeds
Figure 16a is the local amplification of Figure 15a. Although the steady-state error of the system under the action of the traditional Linear Active Disturbance Rejection Controller is not large at a given reference speed of 200 r/min, the steady-state error of the asynchronous motor under the action of the improved Linear Active Disturbance Rejection Controller is smaller. Figure 16b is the local amplification of Figure 16a. Compared with the given reference speed of 200 r/min, the steady-state error of the asynchronous motor under the action of the improved Linear Active Disturbance Rejection Control is still better than the traditional Linear Active Disturbance Rejection Controller, which, although, becomes larger under the given reference speed of 200 r/min.
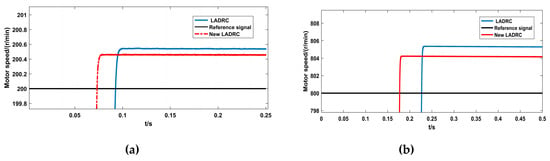
Figure 16.
Steady-state error of the system at different speeds.
PI control uses error feedback to eliminate the error. When the system output is equal to the given input, the controller output is zero. At this time, the motor cannot maintain the current speed and deviates from the given value, resulting in the steady-state error of motor speed. The coupling between the excitation subsystem and the torque subsystem increases with the increase of the speed, resulting in the steady-state error of the speed of the motor in Figure 16b at high speed higher than that in Figure 16a at low speed.
4.3. Immunity Performance of the Asynchronous Motor Controller at Different Given Speeds
Figure 17a is a simulation diagram of the motor speed during the process of a sudden increase in the mechanical torque by 10 N·m in 0.35 s and a subsequent sudden decrease in the mechanical torque by 10 N·m in 0.4 s at a given speed of 200 rev/min (returning to the state before the system loading). Figure 17b is a simulation diagram of the motor speed during the process of a sudden increase in the mechanical torque by 10 N·m in 0.35 s and subsequent sudden decrease in the mechanical torque by 10 N·m in 0.4 s (returning to the state before the system loading) at a given speed of 800 rev/min. From Figure 17a,b, it can be seen that the motor speed controlled by the traditional LADRC fluctuated more after the mechanical load of the motor suddenly increased; therefore, the immunity of the improved LADRC was better than that of the traditional LADRC.
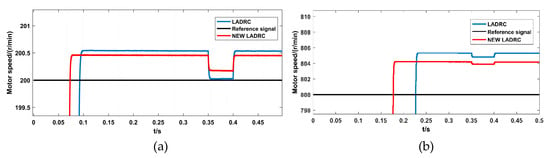
Figure 17.
Sudden load increase and decrease of the motor at different speeds.
The coupling between the excitation subsystem and the torque subsystem increases to the increase in speed, resulting in the steady-state error of the motor in Figure 17b at a high speed greater than that in Figure 17a at low speed. The improved linear expansion observer can estimate the total disturbance more accurately, reduce the coupling between the two subsystems to a certain extent, and improve the control of electromagnetic torque. Since the improved Linear Active Disturbance Rejection Controller is applied to the current inner loop decoupling and the outer loop still adopts PI control, the improvement of load torque and the steady-state error is not obvious.
5. Conclusions
The key to the performance of an ADRC is whether the extended state observer can accurately estimate the state variables of the system. There is a cross-coupling term in the state equation of the asynchronous motor in the synchronous rotating coordinate system. The control of the torque component and the excitation component of the motor stator current will affect each other, thus further affecting the dynamic and static performances of the system.
Actual systems always have unknown dynamic characteristics, i.e., the uncertainty of the model. In the control system, there are often various external disturbances, such as the control quantity disturbance or the measurement noise. LESOo regards the coupling of the dynamic model of the asynchronous motor system as a part of the total disturbance of the system. The disturbance is added to the input of the system model using feedforward compensation. After compensation, the model of the controlled asynchronous motor is transformed into the integrator series type.
The key to the motor speed regulation lies in the regulation of the electromagnetic torque. The improved LESOo had a higher observation accuracy, the estimated value of total disturbance was closer to the real value, the coupling degree between the torque component and excitation component was smaller after compensation, and the improved LESOo could control the torque component more independently; therefore, the control effect of the motor speed was better. Theoretical analysis and simulation results showed that the control effect of the improved LADRC was better than that of the traditional LADRC.
Author Contributions
C.W. was responsible for the theoretical analysis and simulation, and wrote the first draft of the paper. X.Z. and Y.M. provided theoretical guidance and content revision. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China (no. 51877152) and the Natural Science Foundation of Tianjin of China (no. 18JCZDJC97300).
Acknowledgments
Thanks to X.Z. and Y.M. for their theoretical guidance during the writing of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Acronym | Definition |
| LESO | Linear extended state observer |
| LSEF | Linear state error feedback |
| LTD | Linear tracking differentiator |
| LADRC | Linear active disturbance rejection control |
Appendix A

Table A1.
Three-phase cage asynchronous motor parameters.
Table A1.
Three-phase cage asynchronous motor parameters.
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Rated Capacity | 3730 | ||
| Rated voltage | 220 | ||
| Rated frequency | 50 | ||
| Stator resistance | 0.435 | ||
| Rotor resistance | 0.069 | ||
| Stator inductance | 0.079 | ||
| Rotor inductance | 0.071 | ||
| Stator and rotor mutual inductance | 0.069 | ||
| Pole pairs of asynchronous motor | 2 |
References
- Fedor, P.; Perdukova, D.; Kyslan, K.; Fedak, V. Stable and Robust Controller for Induction Motor Drive; IEEE: Piscataway, NY, USA, 2018; pp. 764–769. [Google Scholar]
- Hannan, M.A.; Ali, J.A.; Mohamed, A.; Hussain, A. Optimization techniques to enhance the performance of induction motor drives: A review. Renew. Sustain. Energy Rev. 2018, 81, 1611–1626. [Google Scholar] [CrossRef]
- Happyanto, D.C.; Fauzi, R.; Hair, J. Backstepping Development as Controller in Fast Response Three Phase Induction Motor Based on Indirect Field Oriented Control; IEEE: Piscataway, NY, USA, 2016; pp. 25–30. [Google Scholar]
- Mehazzem, F.; Nemmour, A.L.; Reama, A. Real time implementation of backstepping-multiscalar control to induction motor fed by voltage source inverter. Int. J. Hydrogen Energy 2017, 42, 17965–17975. [Google Scholar] [CrossRef]
- Feng, G.; Liu, Y.F.; Huang, L.P. A new robust algorithm to improve the dynamic performance on the speed control of induction motor drive. IEEE Trans. Power Electron. 2004, 19, 1614–1627. [Google Scholar] [CrossRef]
- Ansari, M.N.; Dalal, A.; Kumar, P. A Method for Determining Nonlinear Inductances of Electrical Equivalent Circuit for Three-Phase Induction Motor. Electr. Power Compon. Syst. 2018, 46, 379–390. [Google Scholar] [CrossRef]
- Aydemir, M.; Arikan, K.B. Evaluation of the Disturbance Rejection Performance of an Aerial Manipulator. J. Intell. Robot. Syst. 2020, 97, 451–469. [Google Scholar] [CrossRef]
- Sira-Ramirez, H.; Linares-Flores, J.; Garcia-Rodriguez, C.; Antonio Contreras-Ordaz, M. On the Control of the Permanent Magnet Synchronous Motor: An Active Disturbance Rejection Control Approach. IEEE Trans. Control Syst. Technol. 2014, 22, 2056–2063. [Google Scholar] [CrossRef]
- Ahmad, S.; Ali, A. Active disturbance rejection control of DC-DC boost converter: A review with modifications for improved performance. IET Power Electron. 2019, 12, 2095–2107. [Google Scholar] [CrossRef]
- Abdul-Adheem, W.R.; Ibraheem, I.K. Decoupled control scheme for output tracking of a general industrial nonlinear MIMO system using improved active disturbance rejection scheme. Alex. Eng. J. 2019, 58, 1145–1156. [Google Scholar] [CrossRef]
- Han, J.Q.; Wang, X.J. Time scale and nonlinear PID controller of the system. In Proceedings of the 1994 China Control Conference, Taiyuan, Shanxi, China, 1 August 1994; p. 8. [Google Scholar]
- Hua, X.X.; Huang, D.; Guo, S.H. Extended State Observer Based on ADRC of Linear System with Incipient Fault. Int. J. Control Autom. Syst. 2019. [Google Scholar] [CrossRef]
- Laghridat, H.; Essadki, A.; Nasser, T. Comparative Analysis between PI and Linear-ADRC Control of a Grid Connected Variable Speed Wind Energy Conversion System Based on a Squirrel Cage Induction Generator. Math. Probl. Eng. 2019. [Google Scholar] [CrossRef]
- Lin, X.; Xiahou, K.S.; Liu, Y.; Zhang, Y.B.; Wu, Q.H. Maximum Power Point Tracking of DFIG-WT Using Feedback Linearization Control Based Current Regulators; IEEE: Piscataway, NY, USA, 2016; pp. 718–723. [Google Scholar]
- Li, H.; Li, S.; Lu, J.; Qu, Y.; Guo, C. A Novel Strategy Based on Linear Active Disturbance Rejection Control for Harmonic Detection and Compensation in Low Voltage AC Microgrid. Energies 2019, 12, 3982. [Google Scholar] [CrossRef]
- Bose, S.; Hote, Y.V.; Siddhartha, V. Analysis and Application of Linear ADRC for the Control of DC-DC Converters; IEEE: Piscataway, NY, USA, 2019; pp. 436–441. [Google Scholar]
- Gu, J.; AI, Y.; Shan, X.; Wang, Z.; Liu, M.; Xiong, Z. Improvement of linear extended state observer and its application in coarse tracking of space optical communication. Infrared Laser Eng. 2016, 45. [Google Scholar] [CrossRef]
- He, H.C.; Sun, L.; Zhang, Y.; Zhu, Q. Active disturbance rejection control of induction motor based on vector control. J. Electr. Mach. Control 2019, 23, 120–125. [Google Scholar]
- Zhou, Y.S. A survey of decoupling control strategy for asynchronous motor. Small Medium Mot. 2005, 2, 56, 60–64. [Google Scholar]
- Ren, Y.; Zhao, G.H.; Liu, H. Design of fast arctangent tracking differentiator. Control Eng. 2019, 26, 412–416. [Google Scholar]
- Tan, S.L.; Lei, H.m.; Wang, P.F. Inverse control of hypersonic vehicle with tracking differentiator. Acta Astronaut. 2019, 40, 673–683. [Google Scholar]
- Shen, Z.P.; Cao, X.M. An extended observer based output feedback control for trajectory tracking dynamic surface of an input constrained four rotor vehicle. Syst. Eng. Electron. Technol. 2018, 40, 2766–2774. [Google Scholar]
- Yu, B.; Liu, Y.L.; Gao, Z.J.; Kong, X. Dong Position disturbance rejection control of hydraulic drive unit based on extended observer. Hydraul. Pneum. 2018, 6, 1–8. [Google Scholar]
- Zhou, X.S.; Tian, C.W.; Ma, Y.J.; Liu, S.J.; Zhao, J.; Liu, J. SHAPF model and current tracking control strategy based on LADRC. Power Autom. Equip. 2013, 33, 49–54. [Google Scholar]
- Sun, D.S. SRM control system based on time-varying parameter Active disturbance rejection. Electr. Drive 2018, 48, 19–22. [Google Scholar]
- Yang, L.; Zeng, J.; Ma, W.J.; Huang, Z.L. Voltage control of micro grid inverter based on improved second-order linear auto disturbance rejection technology. Power Syst. Autom. 2019, 43, 146–158. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).