Abstract
Wind Diesel Power Systems (WDPS) are isolated microgrids which combine Wind Turbine Generators (WTGs) with Diesel Generators (DGs). The WDPS modelled in this article is composed of a DG, a WTG, consumer load, Dump Load (DL) and a Flywheel Energy Storage System (FESS). In the Wind-Diesel (WD) mode both the DG and WTG supply power to the consumers. The WDPS is simulated in the WD mode in the case that the WTG produced power exceeds the load consumption. This WTG excess power case is simulated in the subcases of DL and FESS turned off, only-DL and only-FESS. Simulations for the DL and FESS-off case show that the WTG excess power leads to a continuous system frequency increase, so that the tripping of the WTG Circuit Breaker (CB) is required to guarantee the WDPS power supply continuity. Simulations for the only-DL/only-FESS cases show that commanding the DL/FESS to consume controlled power, so that the required DG power to balance the system active power is positive, enables the DE speed governor to regulate the system frequency. Furthermore, the frequency and voltage variations in the DL/FESS cases are moderate and there is no need to trip the WTG-CB, so that the WDPS reliability and power quality are greatly improved. Additionally, the only-FESS case obtains better WDPS relative stability than the only-DL case.
1. Introduction
Wind diesel power systems (WDPS) are isolated microgrids which combine wind turbine generators (WTGs) with diesel generators (DGs) to supply electrical power to remote consumers. All WDPSs have two modes of operation [1]: Diesel-Only (DO) mode, where the DGs supply all the power (active and reactive) to the isolated consumers, and Wind-Diesel (WD) mode, where both the WTGs and the DGs supply active power. In both DO and WD modes, the system frequency regulation is performed by speed governors included in each diesel engine (DE) and system voltage regulation is performed by automatic voltage regulators (AVR) included in each synchronous machine (SM). High penetration WDPSs can also work in Wind-Only (WO) mode, where the WTGs are the only active power suppliers and the DGs do not run.
WDPSs are low inertia isolated power systems, where the balance between power generation and consumption is difficult to achieve due to the uncontrolled WTGs power production and consumer loading. As a result, the WDPS frequency and voltage can have significant deviations. The WDPS stability and power quality have been dealt with in literature mostly by the dynamic simulation of different WDPS architectures. Ref. [2] shows how the variations in load and WTG power affects the power quality of a no-storage WDPS. In the no-storage WDPS of ref. [3], a static reactive compensator and a synchronous machine voltage regulator are coordinated to control the system voltage. In the WDPS of [4], distributed resistive loads are controlled to support the speed governor of the diesel engine in the regulation of frequency. When a short-term Energy Storage System (ESS) is added to a WDPS, several benefits such as voltage and frequency support and increasing stability [5] are obtained. Previous benefits are greater in WDPS than in large power systems that have much bigger inertia. The WDPS frequency in [6] is stabilized by an ultra-capacitor based ESS. In [7] a battery-based ESS (BESS) in a WDPS supplies the active power needed to prevent temporarily a DG overloaded situation, so that load shedding is avoided and the WDPS reliability is increased. In [8] the simulations in WD mode of a WDPS with a flywheel based ESS (FESS) show that the WDPS power quality is improved by the addition of the FESS.
WDPS are isolated microgrids and the following microgrid studies are related to WDPS: [9] shows a BESS providing frequency support to a microgrid with high penetration of renewable energy sources, and the BESS in [9] is also used as an uninterrupted power supply for critical loads, a working mode that can be used in the ESS employed in a WDPS; in [10], a BESS supports voltage regulation by counteracting the voltage variations resulting from power fluctuations of renewable power sources; ref. [11] shows how a BESS included in a DGs-based isolated ship power plant smooths the active power variation, so that this study can be applied to the DO mode of a WDPS; ref. [12] shows, with simulation results, the coordination between a supercapacitor and a battery ESSs to balance the active power in an isolated microgrid with only a WTG as a generator. The simulations in [12] can be applied to the WO mode of a WDPS. The “El Hierro” island Diesel-Hydro-Wind power system includes hydropower pumped-storage and has been simulated with the DGs shut-off (Wind-Hydro mode) in the following publications: ref [13] shows the system frequency regulation by using the variable and fixed speed pumps integrated into the hydropower pumped-storage; ref [14] shows, among other frequency control schemes, how the frequency regulation is improved by adding a FESS to the system.
The first part of this article presents the modelling of the WDPS shown in Figure 1, which can work in DO and WD modes. In addition to a DG, WTG and consumer load, the WDPS includes a dump load (DL) and a flywheel ESS (FESS). The second part and main goal of this article aims to present solutions for the WD mode of the WDPS of Figure 1 in the case where the WTG produced power PT exceeds the load consumption PL, a situation that makes the WDPS unstable. The WTG power excess situation (PT > PL) is simulated in WD mode in three cases, namely DL and FESS-off (DL and FESS are turned off), only-DL (DL actuates but FESS is turned off) and only-FESS (FESS actuates but DL is turned off). In the DL and FESS-off simulation case, it is shown that to prevent the isolated power system collapse that the WTG power excess provokes, the solution is to trip the WTG circuit breaker (IT in Figure 1). In both the only-DL and only-FESS simulation cases, it is shown how the DL/FESS are commanded to consume controlled power, avoiding the WTG circuit breaker trip necessary in the DL and FESS-off case so that the WDPS absolute stability is increased. A previous paper [15] deals with simulations in WO mode of a system that comprises a WTG, a grid forming SM, load and a FESS. Ref [15] does not include a diesel engine, therefore this article’s isolated power system architecture is different. In a previous paper [8], the simulated WDPS includes a FESS, but no DL is considered. Furthermore, the WTG power levels in [8] are below the load consumption (PT < PL) in all the simulations, so [8] does not deal with the WTG power excess situation. In addition, [8] focuses on the control of the FESS power converter. Previous papers [5] and [7] use a battery ESS instead of a flywheel ESS, so the used power converter and ESS variables shown in the simulations are different. Additionally, [5] and [7] do not use the DL. The WD mode simulations in [7] do not consider the WTG power excess situation dealt in this paper. Ref. [5] deals with a high penetration WDPS and its main simulations are in WO mode.
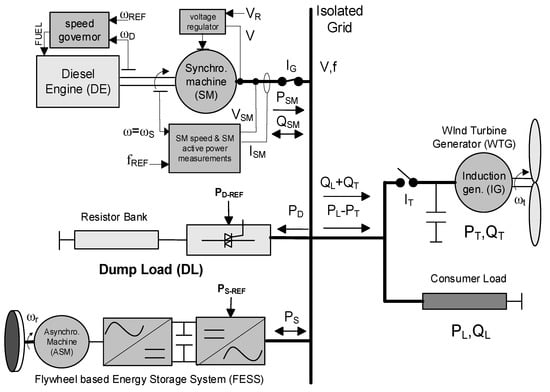
Figure 1.
Layout of the Wind Diesel Power System (WDPS) with Dump Load (DL) and Flywheel Energy Storage.
After this introduction, this article contains the following sections: Section 2 presents the modelling of the WDPS components: DG, WTG, DL and FESS. The WTG power excess situation is analysed and simulated in Section 3 for the DL and FESS-off case and in Section 4 for the only-DL and only-FESS cases. Section 4 also compares its simulation results with the ones in Section 3 and makes a comparison between the only-DL and only-FESS cases. The last section contains conclusions, summarizing the benefits in terms of greater stability and reliability of using the DL/FESS.
2. Isolated WDPS Modelling
Figure 1 shows the WDPS presented in this paper. All the parameters of the presented WDPS are shown in Appendix A. The DG supplies controlled active and reactive power and the WTG supplies uncontrolled active power. The consumer load consumes uncontrolled active power and the DL consumes controlled active power. The FESS consumes/generates controlled active power. The state opened/closed of the WTG circuit breaker IT defines the DO/WD operation mode of the WDPS.
The MATLAB–Simulink framework was used to model and simulate the WDPS, and Figure 2 shows the WPDS Simulink schematic. The next subsections describe the modelling of the WDPS components.
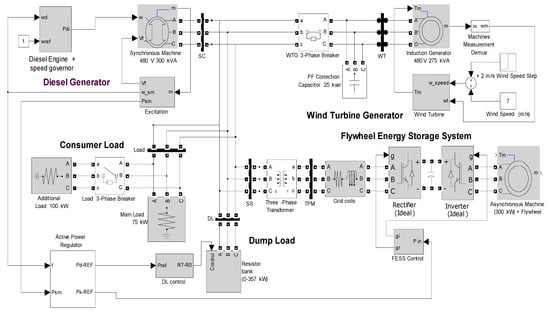
Figure 2.
Simulink-SimPowerSystem of the WPDS with Dump Load and Flywheel Energy Storage.
2.1. The Diesel Generator Model.
The DG consists of a Diesel Engine (DE) and a Synchronous machine (SM), and its rated power is 300 kVA. The DE converts the fuel energy into the shaft mechanical power PD and the SM converts the DE mechanical power into electrical power. The SM provides the isolated grid sinusoidal voltage waveform. By following the command of its automatic voltage regulator, the SM provides reactive power to the WDPS, which is necessary to keep the system voltage module V within the allowable limits. The relationship between the voltage waveform frequency f (Hz) and the shaft speed of the DE/SM ω (rad/s) is:
where p is the SM number of pole pairs.
ω =2πf/p
To control the system frequency, a speed governor controls the speed of the DE. The speed governor comprises a speed regulator and an actuator. In this article, the speed regulator applies a Proportional Integral derivative (PID) type algorithm to the DE speed error (ωref – ωd in Figure 2, where ωref is the DE reference speed and ωd the actual speed ω) so the DE speed control is isochronous, that is, in steady state the DE speed is rated one (therefore rated system frequency) provided that the electrical load is within 0–300 kW range. The actuator converts the output of the speed regulator into a proper signal to control a fuel valve. In this way, the incoming fuel rate to the DE is adjusted to control the DE produced mechanical power to the needed value to achieve the rated speed in the DE.
In this article, the SM electrical part is modelled by a sixth-order model and the SM automatic voltage regulator model is the IEEE type 1. The SymPowerSystem blockset [16] provides both models.
The models for the DE and its speed regulator described in [17] are followed. The DE model consists of a gain which relates the DE mechanical power with the rate of fuel consumed and a transport lag to model the firing delay between pistons. A second order system models the actuator. The DG inertia constant HDG is 1.75 s.
2.2. The Wind Turbine Generator Model
The 275 kW WTG comprises a fixed pitch Wind Turbine (WT) driving through a gearbox a Squirrel Cage Induction Generator (SCIG). The WT converts the wind power into shaft mechanical power and the SCIG converts the WT mechanical power into electrical power. The fixed pitch WT model follows the one in ref. [18] and is included in the Wind Turbine block of Figure 2. The model consists of the wind turbine power curves that relate the mechanical shaft power produced by the WT PT-MEC with the wind speed (v_speed) and the WT shaft speed ωt. The output of the Wind Turbine block is the torque applied to the SCIG (Tm= PT-MEC/ωt)
For generator operation, the SCIG speed range is very limited, within a narrow range between 1 and 1.02 of the synchronous speed [19], and for this reason, this WT-SCIG type is called constant speed WTG. Therefore this WT-SCIG type does not allow to adjust its rotational speed to maximize the capture of wind energy [20]. Other types of WTGs used in WDPS [21,22,23,24] allow variable speed operation to maximize the capture of wind energy by performing a maximum power point tracking technique. In [12,21,22,23], the WTG equips a synchronous generator and an AC-DC-AC electronic power converter, which connects the synchronous generator to the grid. In [24], the WTG equips a double fed IG with its stator connected to the grid and its rotor connected to an AC-DC-AC converter through a slip ring. Additionally, as the used WT is a fixed pitch blade type, PT-MEC is mainly a function of the cube of the wind speed [25]. The wind speed is quasi-random, so that the WT-SCIG behaves as an uncontrolled active power supplier. In spite of the previously commented disadvantages, the WT-SCIG fixed pitch constant speed type used in this article has remarkable features for the remote locations of WDPS, such as robust construction, simple maintenance and low cost. The used WT-SCIG type is more robust than [12,21,22,23,24] as it does not equip an electronic power converter and has less maintenance than [24], as the SCIG does not have slip rings.
The WT-SCIG has two additional positive features. First, as the SCIG stator is directly connected to the isolated grid, the WTG inertia also participates in the moderation of the WDPS frequency changes. This property is not available in [12,21,22,23] as the double power converter uncouples the WTG- electrical generator from the grid. Second, as in the WTG-SCIG working speed range the SCIG torque is proportional to its slip (ωt – ω in per unit values) [25], the WTG-SCIG improves the system frequency by providing a damped response [26].
The 25 kVA capacitor bank of Figure 2 provides reactive power to improve the WTG-SCIG power factor. The SymPowerSystem blockset [16] provides the SCIG model. The SCIG electrical model is a fourth-order one. Typical WTG inertia constants HW range between 2–6 s [27] for low–high power WTGs. The used WTG is a low power one, so that HW = 2 s is set for this parameter.
2.3. The Dump Load Model
The DL in a WDPS is actuated when a WTG power excess exists. In the WD mode, the WDPS control commands the DL to dump the power needed to ensure a DG minimum positive load, avoiding a DG reverse power. In the WO mode, the WDPS control commands the DL to consume the WTG power excess (PT-PL) to regulate system frequency [23,28]. The Figure 2 DL consists of eight three-phase resistors connected in series with solid-state switches, which connect/disconnect the resistors at the zero crossing in order to prevent harmonic injection. The values of the resistors follow a binary progression, with values R, R/2, R/22…R/27. If P0 is the rated power of the resistor of value R (P0 = Vn2/R, where Vn is the rated system voltage), the eight resistor’s rated powers are P0, 2·P0, 22·P0, …, 27·P0. Being IJ the state closed(1)/opened(0) of the three phase switch associated with the resistor of power 2J·P0, the power consumed by the DL PD if the system voltage is the rated value, can be expressed as:
PD = (I0 + I1·21 + … + I7·27)·P0
According to Equation (2), PD can be varied discretely in steps of P0 from 0 to 255· P0. P0 was chosen to be 1.4 kW, so the DL rated power PD-NOM is 357 kW (1.4·255). The DL control block of Figure 2 determines which resistors have to be connected to consume the assigned PD-REF. The details of the DL implementation in Simulink can be found in [18].
2.4. The Flywheel Energy StorageSystem Model
A low speed (LS) FESS type [15] was included as a short term ESS in the WDPS. The LS-FESS consists of a steel flywheel driven by an electrical asynchronous machine (ASM). Features such as high power/torque, robust construction, low cost and wide availability are determinant to select an ASM for WDPS. The simple manufacturing and low cost are determinant to select a steel flywheel [29]. The rotating flywheel stores kinetic energy. The ASM converts the kinetic energy into electrical energy and the electrical energy into kinetic energy when it works as a generator/motor respectively. The flywheel has the moment of inertia I, and its speed range is from a minimum ωr-min to a maximum ωr-max rotating speed, so the maximum available kinetic energy, Ec-max is:
As Figure 2 shows, the FESS includes two electronic power converters that share a common DC-link built with a bank of capacitors to connect the ASM to the isolated grid. The machine-side converter of Figure 2 controls the ASM in order to keep a constant DC-voltage in the capacitor bank. Therefore, if the capacitor bank voltage rises/falls, this converter discharges/charges the capacitor bank by commanding motor/brake torque to the ASM, so that the flywheel accelerates/decelerates. The rated DC-link voltage and capacitor bank capacitance are 800 V and 4.7 mF, respectively. The grid-side converter of Figure 2 connects the constant voltage DC-link to the isolated grid and is controlled to exchange the necessary active and reactive powers with the grid by setting the corresponding current references. In the present application, this converter works with the power factor equal to unity, so its reactive power reference is zero. As Figure 2 shows, the grid-side converter uses an inductance L-filter to limit the harmonic injection and an isolation transformer is used for coupling with the isolated grid.
The ASM dynamic control is achieved by using Field Oriented Control (FOC). The FOC decouples the control of flux and torque of the ASM [30] and uses a dq-reference frame where the d axis is aligned with the rotor flux vector Ψr. The rotor flux is:
where imr and Lm are the magnetizing current and inductance respectively. The relation between imr and the stator direct current isd is given by:
where Tr is the rotor time constant and Tr = Lr/Rr, where Rr and Lr are the rotor resistance and inductance respectively. Therefore, isd produces the rotor flux Ψr, but with slow dynamics due to the high value of Tr. The ASM electromagnetic torque Tel is proportional to the product of the rotor flux and the stator quadrature current isq [31]:
where 3/2 constant considers the 2–3 axes scaling. The FOC keeps the rotor flux constant (imr = isd = constant) at its optimal value and the required Tel is obtained by setting the corresponding quadrature current isq according to Equation (6). If all the ASM losses are neglected (stator and rotor resistance and stator iron losses), the exchanged ASM active power can be approximated to the product of the electromagnetic torque Tel and the ASM rotor speed ωr. Also neglecting the FESS double power converter losses, the exchanged FESS active power PS is approximately:
Ψr = Lmimr
PS ≈ Tel ωr
The high flywheel inertia allows considering ωr speed constant when it is compared to the electric dynamics. Hence, the FESS exchanged power is controlled by setting the needed isq.
The LS-FESS was sized to store a maximum available energy of 18,000 kJ, to supply the 150 kW FESS rated power (PS-NOM) during 2 min and with the flywheel operating speed range ωr-min–ωr-max within 1500–3300 rpm [8], so Equation (3) gives 380 kg·m2 for the flywheel moment of inertia I. The selected ASM is a standard 50 Hz one, with a single pole pair and 300 kW of rated power [8]. The model of the 300 kW ASM-FESS uses the block included in the SimPowerSystems blockset for Simulink [16] and its electrical model is a fourth-order one. The flywheel 380 kg m2 inertia is included in the inertia parameter of the FESS-ASM SimPowerSystems model to simulate the flywheel.
3. The WTG Power Excess Situation and the DL and FESS-off Case Simulation
In the WD mode of the Figure 1 WDPS, the active power produced by the WTG can exceed the load consumption (PT > PL). If there is no ESS and no DL in the WDPS to consume additional power, the DE should consume the active excess power to balance active powers in the system and thus to control system frequency. However, the DE speed governor cannot command the DE to consume power. In the extreme case of no fuel injection into the DE cylinders, the DE power will be negative (PDE < 0) and will consist of losses from compression in the cylinders, shaft, etc., but the DE losses are not controllable. Therefore, if the WTG power excess surpasses the DE losses, the system frequency will rise without control. This frequency increasing is better observed by analyzing the equation which relates the active powers of the DE (PDE), WTG (PT) and load (PL) with the DG speed (ω)/frequency (f):
In Equation (8), the power exchanged by the generators (PDE and PT) are positive when produced and the consumer load power PL positive when consumed, J is the DG moment of inertia and the losses are neglected. Since the left side of Equation (8) is positive in the WTG power excess case and J and ω are positive, this implies dω/dt > 0 and a continuous uncontrolled frequency increase.
All DGs have some shut-down alarms, that is, alarms that, when activated, trip the SM circuit breaker (CB) (IG in Figure 1) and shut down the DE by cutting the fuel supply to the DE cylinders. Among these alarms is the overspeed alarm, which avoids the uncontrolled acceleration of the DG and therefore excessive centrifugal forces that could damage the rotating parts of the DG. The overspeed alarm is activated when the DG speed is greater than the overspeed setpoint, which is normally 1.1 the DG rated speed. Additionally, all DG have some SM-CB trip alarms, among them the reverse power alarm. This alarm is activated when the DG is connected in parallel with other generators and the DG output power is negative (the SM is behaving as a motor) during a certain time interval. During a DG reverse power activation, the system frequency is supported in the rated value by the other supplying generators.
When there is a WTG power excess (PT > PL), the DG output power is negative and at the same time the system frequency increases, so that this situation could be confused with an overspeed alarm if the overspeed set point is reached and therefore the protection control will shut down the DG. The WTG power excess case could also be confused with the reverse power alarm if the conditions to active this trip alarm occur. In both cases, the SM-CB will be open and there will not be supply for the consumer load. However, to prevent the discontinuation in the power supply in the WTG power excess case, the solution is to open the WTG CB (IT in Figure 1) and allow the DG to continue supplying the loads.
The above solution is shown in Figure 3, Figure 4 and Figure 5, where the Figure 2 WDPS, with both the DL and FESS turned off, is simulated from an initial state where the DG produces 25 kW, the WTG produces 50 kW for a 7 m/s wind speed and the load consumes 75 kW. Figure 3 and Figure 4 show the system frequency and RMS voltage both in pu. Figure 5 shows the active powers in kW for the WTG, DG and load and these active powers are plotted positive/negative when produced/consumed, so that the active powers sum is null at steady state. At t = 0.2 s a wind speed step of +2 m/s is applied and consequently the WTG produced power increases. Soon, the WTG power surpasses the load consumption, the DG power becomes negative, the system frequency increases permanently and the WDPS becomes unstable. As Figure 3 shows, when the frequency reaches 1.08 pu (before the 1.1 pu overspeed alarm set point) at t = 2.935 s, the control system orders a trip of the WTG 3-phase breaker (3PB) of Figure 2, disconnecting the WTG to protect the WDPS and ensure the power supply continuity. Figure 4 shows increasing voltage oscillations before t = 2.935, which corresponds to an unstable system, and presents a strong peak after the tripping of the WTG-3PB. After the WTG disconnection, Figure 3 shows that the system frequency recovers the rated value due to the action of the DE speed governor and Figure 5 shows that in the steady state the DG supplies all the active power (75 kW) to the load.
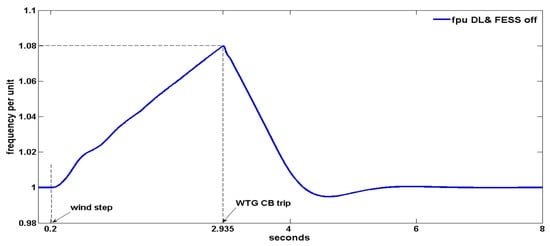
Figure 3.
WDPS frequency per unit for the DL and Flywheel Energy Storage System (FESS)-off case.
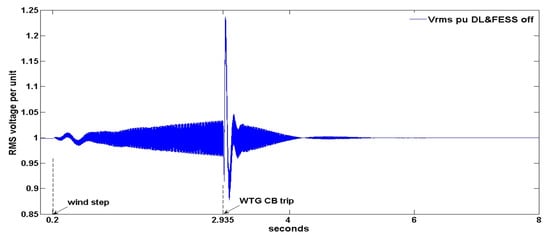
Figure 4.
Root Mean Square (RMS) Voltage per unit for the DL and FESS-off case.
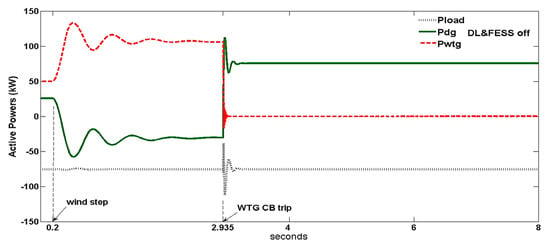
Figure 5.
Wind turbine generator (WTG), diesel generator (DG) and load active powers (kW) for the DL and FESS-off case.
4. The WTG Power Excess Situation in the Only-DL/Only-FESS Cases
4.1. The DL and FESS Control
To avoid the DE reverse power and the WDPS frequency increasing that causes the WTG power excess, the WDPS control must command the FESS or DL or both to consume controlled power so that the required DG power to balance the WDPS active power is positive. With a positive DE power, the set speed governor + DE can regulate the WDPS frequency.
In the DL-only case, Equation (8) in steady state (dω/dt = 0) converts into:
where PDL is the DL consumed power and using for PDL the same consumer load sign criteria. As the DL rated power (357 kW) is greater than the WTG rated power (275 kW), Equation (9) indicates that it is possible, by controlling the DL consumed power, to obtain a positive PDE in steady state, even with null load (PL = 0). In this article, the DL dumped power follows the PINV output shown in Figure 6 (PD-REF = PINV). The Figure 6 control is an integral one, and its aim is to keep the DG active power (PSM) in the reference range 15–21 kW (5–7% PDG-NOM) in steady state when a WTG active power excess exists. The control output PINV increases when the DG power PSM is less than 15 kW and decreases its value when PSM is greater than 21 kW. In Figure 6, the integral control is limited to the DL power limits [0, PD-NOM]. The integral constant KI of Figure 6 was tuned taking into account the used DL discrete nature. To follow PINV, the DL control must order the DL resistors to switch on and off, and this switching produces system voltage variations, as the following simulations graphics show. Therefore, excessive switching must be avoided.
PDE = PL + PDL − PT
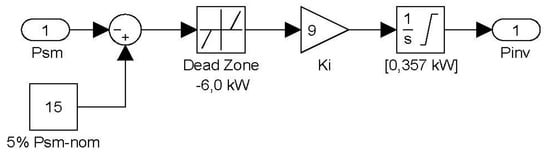
Figure 6.
DL/FESS integral control schematic.
In the only-FESS case, Equation (9) also applies if PDL is substituted by the power exchanged by the FESS PS. As the FESS rated power is 150 kW, the FESS cannot guarantee a positive PDE in steady state if the WTG power excess surpasses 150 kW. In the only-FESS case, the reference power PS-REF to be consumed by the FESS is given by the following equation:
where a PD regulator with the frequency error ef as input (ef = f − fNOM, where f/fNOM are the current/rated WDPS frequency) is added to the formerly explained term PINV. KP and KD are the PD proportional and derivate constants. The integral control limits of PINV are [0, PS-NOM] in this only-FESS case. The PD regulator supports frequency regulation, improving the transients of the WDPS and it is compatible with the PID regulator inside the DE speed governor. KP and KD were adjusted to moderate the system frequency over/under shooting. Equation (10) makes use of the fast-acting power electronic converter with PWM unlike the DL, which uses the zero-crossing connection of the resistors and this results in slower actuation. Moreover, the DL power is in discrete steps and it may lead to excessive voltage variations as explained previously.
4.2. The Simulation Tests for the Only-DL and Only-FESS Cases
The WDPS initial state for this section’s simulations is the same as the previous Section 3. The simulation results are presented in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. The plots of Figure 7 and Figure 8 show the system frequency and RMS voltage in per unit. Graphs that show the active powers in kW are Figure 9 for the DG and WTG and Figure 10 for DL, consumer load and FESS. The same sign criterion of Section 3 is applied to the active powers. The WDPS response is plotted with dot line for the only-DL case and in solid line for the only-FESS case.
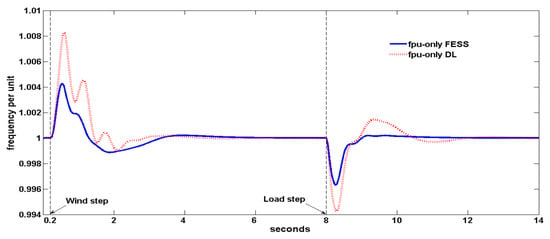
Figure 7.
System frequency per unit for the only-FESS and only-DL cases.
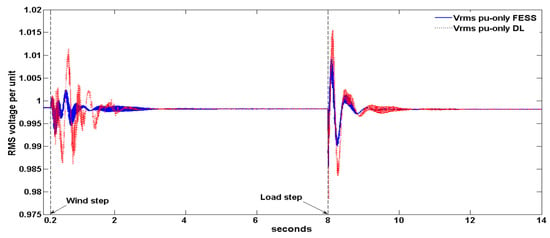
Figure 8.
RMS Voltage per unit for the only-FESS and only-DL cases.
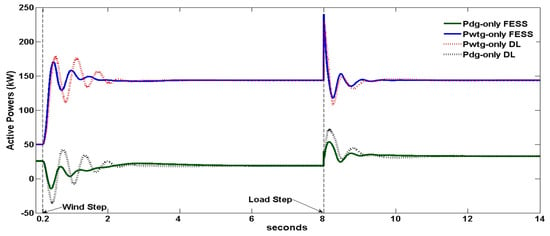
Figure 9.
WTG and DG active powers (kW) for the only-FESS and only-DL cases.
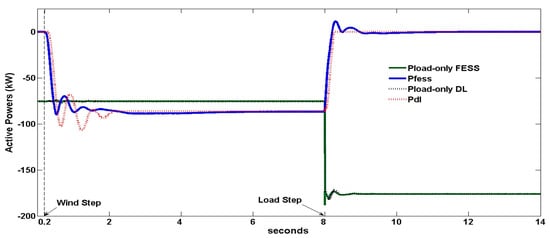
Figure 10.
DL, FESS and load active powers (kW) for the only-FESS and only-DL cases.
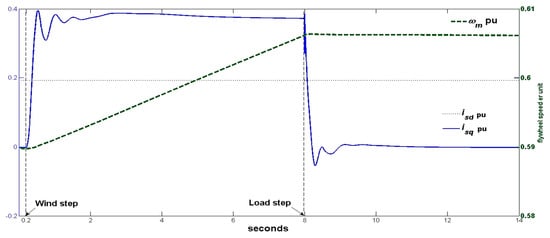
Figure 11.
Per unit asynchronous machine (ASM) speed and direct and quadrature currents.
As in the previous section, a +2 m/s wind speed step is applied at t = 0.2 s, and the WTG produced power increases. The DG decreases its power commanded by the speed governor, and when it is under the minimum 15 kW level, the Figure 6 integral control commands the DL/FESS to start increasing its power consumption. The DL/FESS increases its power so that the DG power keeps positive and, therefore, the set speed governor +DE can regulate the system frequency. In the steady state, the WTG produces 143 kW, the load consumes 75 kW, the DG produced power is 18.5/19 kW for the DL/FESS cases (a value inside the 15–21 kW set interval) and the DL/ FESS consumes 87.5/87 kW (minimum DG load plus WTG power excess). The initial active power excess leads the frequency to increase and, later on, the frequency undershoots. The fpu minimum–maximum are 0.999–1.0083 pu and 0.9989–1.0042 pu for the DL and FESS cases, respectively. The fpu oscillations are higher in the DL case than in the FESS case. The voltage also oscillates, its minimum–maximum are 0.9859–1.0116 and 0.9944–1.0042 pu for the DL and FESS cases, respectively. The voltage oscillations are bigger in the DL case. The FESS case also obtains less oscillation (better relative stability) in the active powers of the WTG and DG. This a consequence of using fast PWM with high resolution in the FESS converter. In both cases, the frequency maximum is much less than 1.08 pu, so the Figure 2 WTG-3PB is not tripped and the voltage variations are also much smaller than the ones shown in the DL and FESS-off case.
At t = 8 s, the load is increased by 100 kW as Figure 10 shows. The speed governor orders the DG to increase its power production above 21 kW, and the integral control of Figure 6 commands DL/FESS to decrease its consumed power. In DL case, the decreasing consumption of power stops when its power reaches zero and remains at that value, so that the WDPS frequency is regulated solely by the DE speed governor. In the FESS case, the FESS power has small positive peaks due to the PD regulator, which means that FESS supplies power during a brief interval until it reaches zero after the transient, so the FESS briefly supports the DE speed governor. In steady state, the DG supplies 32 kW, the WTG remains supplying the same 143 kW (for the 9 m/s wind speed), the load consumes 175 kW, and the DL/FESS consumption is 0 kW. During the +100 kW transient, the frequency decreases due to the deficit of active power, with a minimum–maximum of 0.9943–1.0014 and 0.9963–1.0002 pu for the DL and FESS cases respectively, being the frequency transient better in the FESS case. The WTG positive peak after the +100 kW of Figure 9 is due to an instantaneous increase in the SCIG slip as the system frequency falls faster than the WTG-SCIG speed. This WTG positive peak counteracts partly the active power shortage, so the WTG-SCIG provides damping to the system. The voltage minimum–maximum are 0.9754–1.0157 and 0.9874–1.011 pu for the DL and FESS cases respectively, so the FESS frequency support also results in a better voltage transient. The FESS case also provides less oscillatory waveforms and, therefore, better relative stability for the WTG and DG active powers.
Table 1 summarizes the voltage and frequency variations in percentage for the presented simulations in the three considered cases.

Table 1.
Frequency and voltage variations in percentage in the three considered subcases.
4.3. The Flywheel Variables
The direct isd and quadrature isq stator currents of the ASM, relative to the 360 A ASM base current and the flywheel shaft speed, relative to the 3000 r.p.m ASM base speed are shown for the FESS test in Figure 11. The direct current creates the ASM magnetic flux, and its sign is always positive. The quadrature current sets the ASM torque and its sign is positive/negative for motor/brake torque (sign criteria usually employed with servos), increasing/decreasing the flywheel speed, and with the FESS consuming/supplying power from/to the isolated grid. There is no PWM current ripple in quadrature and direct currents, since the FESS power converters use average models for faster simulation. The ASM (flywheel) speed indicates how the FESS changes its stored energy, as FESS SOC is proportional to the square of the flywheel speed. Figure 11 left scale is for currents pu and right scale is for speed pu.
Following the ASM-FOC, the direct current value is +0.1923 pu, which is the optimum magnetizing current for maximum power factor at rated power. As explained in Section 2.4, the FESS exchanged power is controlled by adjusting the ASM quadrature current as the ASM-flywheel speed can be considered fairly constant, due to the flywheel high inertia and the short length of the simulations. The initial FESS power and quadrature current are null. After the wind speed step, the 87 kW FESS consumed power is the sum of the WTG power excess (143–75 kW) and the minimum loading of the DG (19 kW), the quadrature current maximum is 0.3951 pu at t = 0.5354 s, and its steady state value is 0.3724 pu. During the +100 kW load step transient, the quadrature current has small negative peaks, which corresponds to the FESS supplying power. After the transient, the FESS power is null, and so the quadrature current returns to null value.
Initially, the FESS speed is 0.5898 pu. After the wind speed step, the FESS speed increases almost linearly as the FESS absorbed power is constant after the transient. After the load step transient, the FESS power is null and the FESS speed remains constant in 0.6061 pu, as FESS losses are not considered.
5. Conclusions
An isolated WDPS with a DL and a LS-FESS was modelled using the Matlab–Simulink framework in Section 2. Section 3 presented, analysed (using Equation (8)) and simulated the WTG power excess scenario in the DL and FESS-off case giving a solution which guarantees power supply continuity with a practical engineering view. Section 4.1 analysed (using Equation (9)) how to guarantee the WDPS absolute stability by using the DL/FESS, and Equation (10) made use of the power supply capability of the FESS to additionally perform frequency support. Section 4.2 presented the simulations for the only-DL and only-FESS cases, showing that both DL and FESS cases prevent the DE reverse power and system frequency increase and therefore it is not necessary to trip the WTG CB unlike the DL and FESS-off case. Table 1 summarized that both DL and FESS cases improve the WDPS power quality by avoiding the strong frequency and voltage perturbations existing in the DL and FESS-off case. Additionally, Figure 7, Figure 8, Figure 9 and Figure 10 and Table 1 show that the frequency support of the only-FESS case results in lower variations and oscillations in the WDPS frequency and voltage amplitude than the only-DL case. The reason for the better performance of the FESS is the use of its fast action PWM converter with high bandwidth and high resolution instead of the connection of the discrete value resistors at the zero crossing performed by the DL with limited bandwidth.
Further research will include simplifying the dump load by making use of the higher energy density of the last generation FESS [32].
Author Contributions
Conceptualization, R.S.; methodology, R.S., R.P.-A.; software, R.P.-A.; validation, R.S.; investigation, R.S., R.P.-A.; writing—original draft preparation, R.S.; writing—review and editing, R.S., R.P.-A.; visualization, R.S.; supervision, R.S.; project administration, R.S.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding
Conflicts of Interest
The authors declare no conflict of interest.
List of Abbreviations
| ASM: asynchronous machine |
| CB: Circuit Breaker |
| DE: Diesel Engine |
| ESS: Energy storage system; BESS: battery ESS |
| SCIG: squirrel cage Induction Generator |
| SM: synchronous machine |
| WDPS operation modes: Diesel Only (DO), Wind Diesel (WD), Wind Only (WO) |
| WT: Wind Turbine |
Appendix A. Wind Diesel Power System (WDPS) Parameters
| WDPS rated frequency and voltage = 60 Hz and 440 V |
| Diesel Generator (DG) rated power and inertia constant = 300 kVA and 1.75 s. |
| Wind Turbine Generator (WTG) rated power and inertia constant = 275 kW and 2 s. |
| Dump Load (DL) rated power = 357 kW |
| DL integral control KI = 9 s−1 |
| Flywheel Energy Storage System (FESS); LS-FESS: low speed FESS |
| FESS rated power, PS-MOM = 150 kW |
| FESS maximum available energy = 18,000 kJ |
| FESS Direct Current (DC) -link voltage = 800 V |
| FESS capacitor bank capacitance = 4.7 mF |
| FESS inductance (L) filter = 2.5 mH |
| FESS Proportional and Derivative (PD) constants: kP = 151 kW/Hz, KD = 7 kWs/Hz |
References
- Bhuvaneswari, G.; Balasubramanian, R. 6—Hybrid wind-diesel energy systems. In Stand-Alone and Hybrid Wind Energy Systems; Kaldellis, J.K., Ed.; Woodhead Publishing: Sawston, UK, 2010; pp. 191–215. ISBN 9781845695279. [Google Scholar]
- Muljadi, E.; McKenna, H.E. Power quality issues in a hybrid power system. IEEE Trans. Ind. Appl. 2002, 38, 803–809. [Google Scholar] [CrossRef]
- Kassem, A.M.; Abdelaziz, A.Y. Functional Predictive Control for Voltage Stability Improvements of Autonomous Hybrid Wind–Diesel Power System. Electr. Power Comp. Syst. 2014, 42, 831–844. [Google Scholar] [CrossRef]
- Janssen, N.T.; Wies, R.W.; Peterson, R.A. Frequency Regulation by Distributed Secondary Loads on Islanded Wind-Powered Microgrids. IEEE Trans. Sustain. Energy 2016, 7. [Google Scholar] [CrossRef]
- Sebastián, R. Battery energy storage for increasing stability and reliability of an isolated Wind Diesel power system. IET Renew. Power Gener. 2017, 11, 296–303. [Google Scholar] [CrossRef]
- Tarkeshwar, M.; Mukherjee, V. Quasi-oppositional harmony search algorithm and fuzzy logic controller for load frequency stabilisation of an isolated hybrid power system. IET Gener. Trans. Distrib. 2015, 9, 427–444. [Google Scholar] [CrossRef]
- Sebastián, R. Application of a battery energy storage for frequency regulation and peak shaving in a wind diesel power system. IET Gener. Trans. Distrib. 2016, 10, 764–770. [Google Scholar] [CrossRef]
- Sebastián, R.; Peña-Alzola, R. Control and simulation of a flywheel energy storage for a wind diesel power system. Int. J. Electr. Power Energy Syst. 2015, 64, 1049–1056. [Google Scholar] [CrossRef]
- Serban, I.; Marinescu, C. Control Strategy of Three-Phase Battery Energy Storage Systems for Frequency Support in Microgrids and with Uninterrupted Supply of Local Loads. IEEE Trans. Power Electr. 2014, 29, 5010–5020. [Google Scholar] [CrossRef]
- Krata, J.; Saha, T.K. Real-Time Coordinated Voltage Support with Battery Energy Storage in a Distribution Grid Equipped with Medium-Scale PV Generation. IEEE Trans. Smart Grid 2019. [Google Scholar] [CrossRef]
- Bø, T.I.; Johansen, T.A. Battery Power Smoothing Control in a Marine Electric Power Plant Using Nonlinear Model Predictive Control. IEEE Trans. Control Syst. Technol. 2017, 25, 1449–1456. [Google Scholar] [CrossRef]
- Mendis, N.; Muttaqi, K.M.; Perera, S. Management of Battery-Supercapacitor Hybrid Energy Storage and Synchronous Condenser for Isolated Operation of PMSG Based Variable-Speed Wind Turbine Generating Systems. IEEE Trans. Smart Grid 2014, 5, 944–953. [Google Scholar] [CrossRef]
- Sarasúa, J.; Martínez-Lucas, G.; Platero, C.; Sánchez-Fernández, J. Dual Frequency Regulation in Pumping Mode in a Wind–Hydro Isolated System. Energies 2018, 11, 2865. [Google Scholar] [CrossRef]
- Sarasúa, J.I.; Martínez-Lucas, G.; Lafoz, M. Analysis of alternative frequency control schemes for increasing renewable energy penetration in El Hierro Island power system. Int. J. Electr. Power Energy Syst. 2019, 113, 807–823. [Google Scholar] [CrossRef]
- Sebastián, R.; Alzola, R.P. Flywheel energy storage systems: Review and simulation for an isolated wind power system. Renew. Sustain. Energy Rev. 2012, 16, 6803–6813. [Google Scholar] [CrossRef]
- The MathWorks. SimPowerSystems, Simulink, Block Library Online Documentation. Available online: https://www.mathworks.com/help/physmod/sps/specialized-power-systems.html (accessed on 15 April 2020).
- Yeager, K.E.; Willis, J.R. Modelling of emergency diesel generators in an 800 Megawatt nuclear power plant. IEEE Trans. Energy Convers. 1993, 8, 433–441. [Google Scholar] [CrossRef]
- Gagnon, R.; Saulnier, B.; Sybille, G.; Giroux, P. Modelling of a Generic High-Penetration No-Storage Wind-Diesel System Using Matlab/Power System Blockset. In Proceedings of the 2002 Global Windpower Conference, Paris, France, 2–5 April 2002. [Google Scholar]
- Hansen, A.; Jauch, C.; Sørensen, P.; Iov, F.; Blaabjerg, F. Dynamic Wind Turbine Models in Power System Simulation Tool DIgSILENT; Technical Report No. Risø-R-1400(EN); Risø National Laboratory: Roskilde, Denmark, 2003. [Google Scholar]
- Li, H.; Chen, Z. Overview of different wind generator systems and their comparisons. IET Renew. Power Gener. 2008, 2, 123–138. [Google Scholar] [CrossRef]
- Kamal, E.; Koutb, M.; Sobaih, A.A.; Abozalam, B. An intelligent maximum power extraction algorithm for hybrid wind-diesel- storage system. Int. J. Electr. Power Energy Syst. 2010, 32, 170–177. [Google Scholar] [CrossRef]
- Haruni, A.M.O.; Gargoom, A.; Haque, M.E.; Negnevitsky, M. Dynamic operation and control of a hybrid wind-diesel stand alone power systems. In Proceedings of the 2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, CA, USA, 21–25 February 2010; pp. 162–169. [Google Scholar]
- Lukasievicz, T.; Oliveira, R.; Torrico, C. A Control Approach and Supplementary Controllers for a Stand-Alone System with Predominance of Wind Generation. Energies 2018, 11, 411. [Google Scholar] [CrossRef]
- Tiwari, S.K.; Singh, B.; Goel, P.K. Control of wind diesel hybrid system with bess for optimal operation. In Proceedings of the 2016 IEEE 7th Power India International Conference (PIICON), Bikaner, India, 25–27 November 2016; pp. 1–6. [Google Scholar]
- Amenedo, J.L.R.; Diaz, J.C.B.; Gomez, S.A. Sistemas Eólicos de Producción de Energía Eléctrica; Editorial Rueda, S.L.: Madrid, Spain, 2003; ISBN 9788472071391. [Google Scholar]
- Margaris, I.D.; Papathanassiou, S.A.; Hatziargyriou, N.D.; Hansen, A.D.; Sorensen, P. Frequency Control in Autonomous Power Systems with High Wind Power Penetration. IEEE Trans. Sustain. Energy 2012, 3, 189–199. [Google Scholar] [CrossRef]
- Knudsen, H.; Nielsen, J.N. Introduction to the modeling of wind turbines. In Wind Power in Power Systems; Chapter, 24, Ackermann, T., Eds.; Wiley: Chichester, UK, 2005; pp. 525–554. [Google Scholar]
- Sebastian, R. Simulation of the transition from wind only mode to wind diesel mode in a no-storage Wind Diesel System. Latinoam. Trans. IEEE 2009, 7, 539–544. [Google Scholar] [CrossRef]
- Hamsic, N.; Schmelter, A.; Mohd, A.; Ortjohann, E.; Schultze, E.; Tuckey, A.; Zimmermann, J. Stabilising the grid voltage and frequency in isolated power systems using a flywheel energy storage system. In Proceedings of the Great Wall World Renewable Energy Forum (GWREF), Beijing, China, 24–27 October 2006. [Google Scholar]
- Boldea, I.; Nasar, S.A. Vector Control of AC Drives; CRC Press: Boca Raton, Florida, USA, 1992. [Google Scholar]
- Cardenas, R.; Pena, R.; Asher, G.M.; Clare, J.; Blasco-Gimenez, R. Control strategies for power smoothing using a flywheel driven by a sensorless vector-controlled induction machine operating in a wide speed range. IEEE Trans. Ind. Electr. 2004, 51, 603–614. [Google Scholar] [CrossRef]
- Lee, B.; Pina, F.; Hope, L.T.; Oglesby, R. Low-Cost Flywheel Energy Storage Demonstration; Technical Report No. CEC-500-2015-089; Amber Kinetics: Union City, CA, USA, 2015. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).