Disturbance-State Modeling and Oscillation Analysis of Modular Multilevel Converters under P/Q Control Mode

Abstract

To investigate the oscillation problems in power systems with modular multilevel converters (MMCs), a disturbance-state model of the MMC under P/Q control mode is established based on the harmonic state-space (HSS) method. Firstly, the basic structure of the MMC with P/Q control is presented, including the circuit structure and the controller structure. Next, the dynamic characteristics of each module in the MMC are described with the time-domain state-space model or the s-domain transfer function. The complete controller structure is considered, including the P/Q outer-loop controller, the inner-loop control, the phase-locked loop (PLL), the circulating current suppression control (CCSC) and the control delay. On the basis, the disturbance-state HSS model of the MMC and its corresponding steady-state condition are established by the HSS method. Lastly, the case studies are performed to verify the accuracy of the proposed model, based on an MMC based test system in PSCAD/EMTDC. Moreover, one oscillation phenomenon in test system is illustrated by analyzing the AC-side impedance characteristics based on the proposed model. The results indicate that the MMC system under P/Q control mode has certain oscillation risk due to its negative resistance effect and the proposed model could be applied to its oscillation analysis.

1. Introduction

The modular multi-level converter (MMC) has become one of the most promising topologies of high voltage direct current (HVDC) systems, due to its more flexible control scheme and lower manufacturing difficulty [1,2]. However, it also brings some oscillation problems in power systems, similar to the oscillation problems in the renewable energy power system [3,4]. As reported, some oscillation phenomena have appeared in the asynchronous interconnection system and the offshore wind farm, where MMC-HVDC system is integrated [5,6,7]. Theoretically, the oscillation phenomena could be analyzed by time-domain simulation or analytical model. However, the time-domain simulation is computationally demanding and time consuming, which is feasible for actual applications due to the large number of possible operation conditions. Therefore, it is necessary to establish one analytical model describing the disturbance response characteristics of the MMC to clarify the oscillation mechanism.

Nowadays, lots of literatures focus on the oscillation problems caused by two-level voltage source converters (VSCs), while only a few researches pay attention to the MMCs. In [8], the oscillation problem in the doubly-fed induction generator (DFIG)-based wind farm with MMC-HVDC is analyzed. In [9], the mitigation strategies of the oscillation problem in the DFIG-based wind farm with the MMC-HVDC is proposed. In [10], the influence of the MMC for wind farm integration on the oscillation stability is analyzed. In [11], the resonance stability of different wind farms transmitted by the MMC-HVDC is studied. In [12,13], the oscillation problem in the asynchronous systems connected by MMC-HVDC is investigated. In these literatures, the frequency-domain impedance model is widely adopted to represent the MMC. Till now, there are three methods to derive the frequency-domain impedance model of the MMC, i.e., the small-signal linearization (SSL) method [12], the multi-harmonic linearization (MHL) method [14,15] and the harmonic state-space (HSS) method [16]. Theoretically, all three methods are equivalent in describing the disturbance response characteristics of the MMC [17,18]. However, the mathematical model describing the influence of sub-module (SM) capacitors and the complete controller structure with the SSL method is very complex, and its derived frequency-domain impedance model is usually over-simplified [12]. Essentially, the MHL method and the HHS method are identical [16], and they could describe the relationship between disturbance components more clearly, especially the frequency coupling effect [19,20]. Furthermore, the HSS method has been widely used in the steady-state harmonic analysis for the linear periodical time-variant systems [21,22]. With the HSS method, the SM capacitors and the controller of the MMC could be considered conveniently. Even so, there still exists a little inadequacy in the existed research. Firstly, the mid-point voltage of the DC side is usually ignored in the circuit structure of the MMC [23]. It has an important influence on the disturbance components with zero-sequence characteristics [24]. In the controller structure of the MMC, the outer-loop controller and the control delay is rarely involved in the existed research, and the inner-loop controller of the MMC in the existed research is inconsistent with the commonly used vector current controller. Moreover, the existed literatures mostly focus on analyzing the MMC used in offshore wind farm integration, i.e., the MMC with V/F control. Therefore, the influence of the phase-locked loop (PLL) is also rarely considered.

To overcome the aforementioned shortcomings, one analytical model describing the disturbance response characteristics of the MMC under P/Q control mode is established in this paper. In the analysis, the complete controller structure is considered, including the P/Q outer-loop controller, the circulating current suppression control (CCSC), the PLL and the control delay. In addition, taking the DC-side mid-point voltage into account, the three-phase of the MMC are all modeled. Based on the disturbance-state model, the AC-side impedance characteristics could be analyzed to investigate the oscillation phenomenon in MMC-based power system.

This remainder of this paper is organized as follows: In Section 2, the common structure of the MMC under P/Q control mode is introduced in details, including its circuit structure and controller structure. In Section 3, the dynamic characteristics of each module in the MMC are described with time-domain state-space method or s-domain transfer-function. On the basis, the relationship among disturbance components in each module are analyzed, and the disturbance-state HSS model of the MMC and its steady-state condition are established in Section 4. In Section 5, the proposed model is verified by the time-domain simulation in PSCAD/EMTDC [25]. In addition, one oscillation phenomenon occurred in test system is illustrated by analyzing the AC-side impedance of the MMC, based on the proposed model. Finally, Section 6 is the conclusion section.

2. Basic Structure of the MMC under P/Q Control Mode

The structure schematic diagram of the MMC under P/Q control mode is shown as Figure 1. It consists of three parts, namely the converter itself, the converter transformer and the control system. Both the converter itself and the converter transformer belong to the circuit structure, which are used in power transmission; the control system belongs to the controller structure, which is used in signal control.

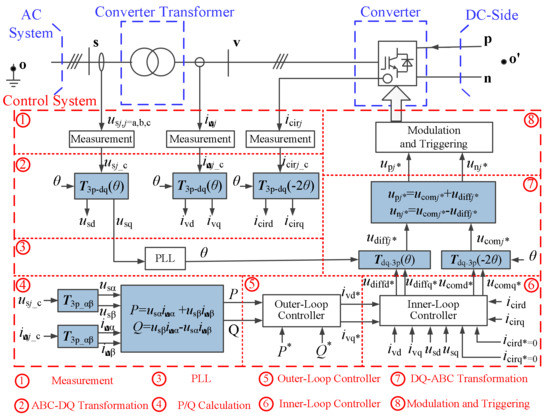
Figure 1. Structure schematic diagram of the modular multilevel converters (MMC) under P/Q control mode.

2.1. Circuit Structure

The converter transformer is similar to the commonly used AC transformer, which could be represented by the ideal transformer with a series-connected equivalent inductor. The converter itself consists of three phase units, and each phase unit consists of the upper arm and the lower arm. Each arm is made up of N series-connected SMs and an arm reactor, as shown in Figure 2.

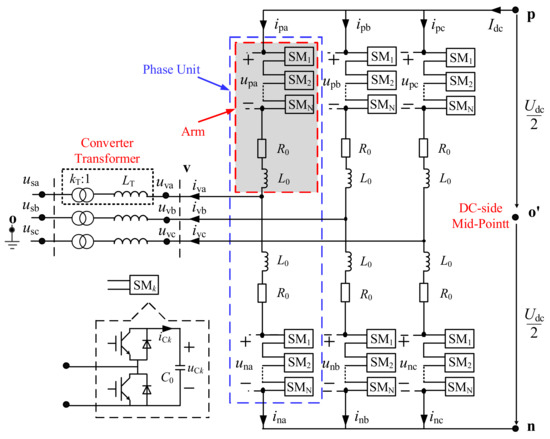
Figure 2. Circuit structure of the MMC.

2.2. Controller Structure

As shown in Figure 1, the controller system of the MMC under P/Q control mode consists of eight modules, including the measurement module, the ABC-DQ transformation, the PLL, the P/Q calculation, the outer-loop controller, the inner-loop controller, the DQ-ABC transformation and the modulation and triggering module, respectively. The ABC-DQ transformation, the P/Q calculation and the DQ-ABC transformation are only involved with algebraic operation, which are shown in Figure 1. The other five modules are discussed in the following paragraphs.

2.2.1. Measurement Module

The measurement module of the MMC contains two parts: the standardization and the low-pass filter. The control block diagram of the measurement module is shown as Figure 3.

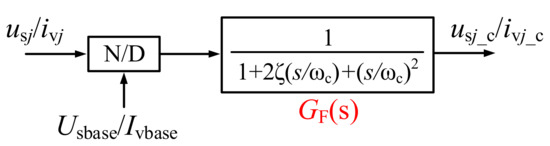
Figure 3. Control block diagram of the measurement module.

2.2.2. Phase-Locked Loop (PLL)

Under P/Q control mode, the phase-locked loop (PLL) is adopted to keep the MMC synchronized with AC system, which is very important for the stable operation. The synchronous reference frame phase-locked loop (SRF-PLL) [26] is analyzed in this paper, as shown in Figure 4.

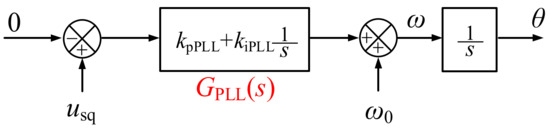
Figure 4. Control block diagram of the synchronous reference frame phase-locked loop (SRF-PLL).

2.2.3. Outer-Loop Controller

The active power and reactive power control is adopted in the outer-loop controller of the MMC under P/Q control mode. The control block diagram of active power and reactive power control is shown as Figure 5.

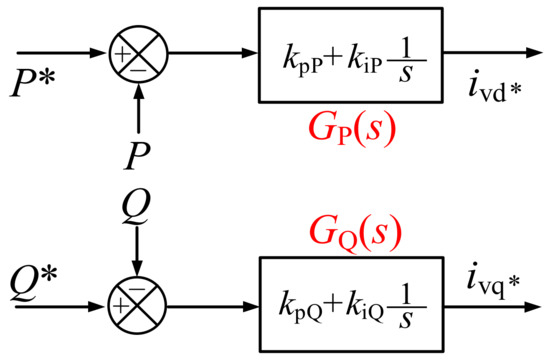
Figure 5. Control block diagram of the P/Q outer-loop controller.

2.2.4. Inner-Loop Controller

Generally, the inner-loop controller of the MMC consists of two parts, i.e., the output current tracking control (OCTC) and the circulating current suppression control (CCSC). The OCTC controls the output current tracking its reference to satisfy the output power requirement. The CCSC suppresses the circulating current of twice the fundamental frequency to reduce the MMC power losses. Both the OCTC and the CCSC are plotted in Figure 6, together with the control delay G_delay(s).

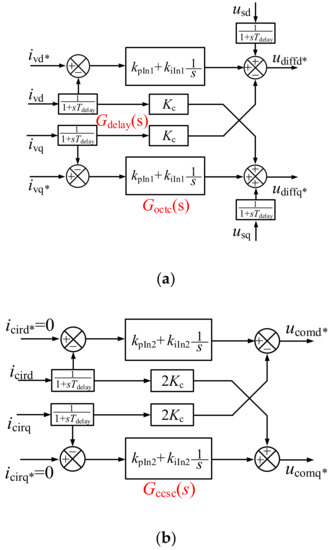
Figure 6. Control block diagram of the inner-loop controller. (a) Output current tracking control (OCTC). (b) Circulating current suppression control (CCSC).

2.2.5. Modulation and Triggering Module

Usually, the nearest level modulation (NLM) strategy is adopted in the modulation module, and the triggering module controls the insertion or bypass of SMs based on the output signal of the modulation module. Considering larger number of series connected SMs in each arm, the switching dynamics of the SMs could be ignored [23].

3. Dynamic Characteristics Analysis of Each Module in the MMC

In this Section, the dynamic characteristics of each module are described with the time-domain state-space model or the s-domain transfer-function.

3.1. Converter Itself

The dynamic characteristics of the converter itself are mainly involved with the SM capacitor and the arm reactor.

Due to the SM capacitor voltage balance control, the SM capacitor voltages in the same arm are always approximately identical. As a simplification, all SMs in the same arm could be equivalent to one averaged module, as shown in Figure 7.

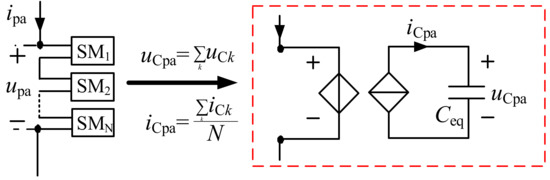
Figure 7. Equivalent averaged module of all sub-modules (SMs) in one arm (e.g., upper arm of phase a).

Subsequently, the dynamic characteristics of all SM capacitors in the upper arm and the lower arm of phase a could be described as in Equation (1).

$$\begin{array}{c}{C}_{eq}\frac{d}{dt}{u}_{Cra}=i_{Cra},r=\mathrm{p},\mathrm{n}\\ \left\{\begin{array}{c}{u}_{ra}=S_{ra}{u}_{Cra},i_{Cra}=S_{ra}{i}_{ra}\\ S_{ra}=N_{ra}/N,C_{eq}=C_0/N\end{array}\right.\end{array}$$

(1)

Considering the DC-side mid-point voltage, the dynamic characteristics of the arm reactor in the phase unit of phase a could be described as in Equation (2).

$$\begin{array}{l}{u}_{\mathrm{va}}=-R_0{i}_{\mathrm{pa}}-L_0\frac{\mathrm{d}}{\mathrm{d}t}{i}_{\mathrm{pa}}-u_{\mathrm{pa}}+\frac{U_{\mathrm{dc}}}{2}+u_{\mathrm{o}’\mathrm{o}}\\ u_{\mathrm{va}}=R_0{i}_{\mathrm{na}}+L_0\frac{\mathrm{d}}{\mathrm{d}t}{i}_{\mathrm{na}}+u_{\mathrm{na}}-\frac{U_{\mathrm{dc}}}{2}+u_{\mathrm{o}’\mathrm{o}}\end{array}$$

(2)

With the help of the output current and the circulating current, Equation (2) could be rewritten as Equation (3).

$$\begin{array}{c}2u_{\mathrm{va}}=-R_0{i}_{\mathrm{va}}-L_0\frac{\mathrm{d}}{\mathrm{d}t}{i}_{\mathrm{va}}-2u_{\mathrm{diffa}}+2u_{\mathrm{o}’\mathrm{o}}\\ 0=2R_0{i}_{\mathrm{cira}}+2L_0\frac{\mathrm{d}}{\mathrm{d}t}{i}_{\mathrm{cira}}+2u_{\mathrm{coma}}-U_{\mathrm{dc}}\\ \left\{\begin{array}{c}{i}_{\mathrm{va}}=i_{\mathrm{pa}}-i_{\mathrm{na}},u_{\mathrm{diffa}}=\left(u_{\mathrm{pa}}-u_{\mathrm{na}}\right)/2\\ i_{\mathrm{cira}}=\left(i_{\mathrm{pa}}+i_{\mathrm{na}}\right)/2,u_{\mathrm{coma}}=\left(u_{\mathrm{pa}}+u_{\mathrm{na}}\right)/2\end{array}\right.\end{array}$$

(3)

After combining Equations (1) and (3), the time-domain state-space model of phase a could be established as Equation (4).

$$\frac{\mathrm{d}}{\mathrm{d}t}\underset{{\mathit{x}}_a}{\underbrace{\left[\begin{array}{c}{i}_{\mathrm{va}}\\ i_{\mathrm{cira}}\\ u_{\mathrm{Cpa}}\\ u_{\mathrm{Cna}}\end{array}\right]}}=\underset{A_a}{\underbrace{\left[\begin{array}{cccc}-\frac{R_0}{L_0}& 0& -\frac{S_{\mathrm{pa}}}{L_0}& \frac{S_{\mathrm{na}}}{L_0}\\ 0& -\frac{R_0}{L_0}& -\frac{S_{\mathrm{pa}}}{{2L}_0}& -\frac{S_{\mathrm{na}}}{{2L}_0}\\ \frac{S_{\mathrm{pa}}}{{2C}_{\mathrm{eq}}}& \frac{S_{\mathrm{pa}}}{C_{\mathrm{eq}}}& 0& 0\\ -\frac{S_{\mathrm{na}}}{{2C}_{\mathrm{eq}}}& \frac{S_{\mathrm{na}}}{C_{\mathrm{eq}}}& 0& 0\end{array}\right]}}\left[\begin{array}{c}{i}_{\mathrm{va}}\\ i_{\mathrm{cira}}\\ u_{\mathrm{Cpa}}\\ u_{\mathrm{Cna}}\end{array}\right]+\underset{B_a}{\underbrace{\left[\begin{array}{ccc}-\frac{2}{L_0}& 0& \frac{2}{L_0}\\ 0& \frac{1}{{2L}_0}& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]}}\underset{u_a}{\underbrace{\left[\begin{array}{c}{u}_{\mathrm{va}}\\ U_{\mathrm{dc}}\\ u_{0’0}\end{array}\right]}}$$

(4)

Similarly, the time-domain state-space model of phase b and phase c in the converter itself could be derived. In conclusion, the three-phase time-domain state-space model of the converter itself could be generalized as Equation (5).

$$\frac{\mathrm{d}}{\mathrm{d}t}\underset{{\mathit{x}}_{\mathrm{abc}}}{\underbrace{\left[\begin{array}{c}{\mathit{x}}_{\mathrm{a}}\\ {\mathit{x}}_{\mathrm{b}}\\ {\mathit{x}}_{\mathrm{c}}\end{array}\right]}}=\underset{{\mathit{A}}_{\mathrm{abc}}}{\underbrace{\left[\begin{array}{ccc}{\mathit{A}}_{\mathrm{a}}& 0& 0\\ 0& {\mathit{A}}_{\mathrm{b}}& 0\\ 0& 0& {\mathit{A}}_{\mathrm{c}}\end{array}\right]}}\left[\begin{array}{c}{\mathit{x}}_{\mathrm{a}}\\ {\mathit{x}}_{\mathrm{b}}\\ {\mathit{x}}_{\mathrm{c}}\end{array}\right]+\underset{{\mathit{B}}_{\mathrm{abc}}}{\underbrace{\left[\begin{array}{ccc}{\mathit{B}}_{\mathrm{a}}& 0& 0\\ 0& {\mathit{B}}_{\mathrm{b}}& 0\\ 0& 0& {\mathit{B}}_{\mathrm{c}}\end{array}\right]}}\underset{{\mathit{u}}_{\mathrm{abc}}}{\underbrace{\left[\begin{array}{c}{\mathit{u}}_{\mathrm{a}}\\ {\mathit{u}}_{\mathrm{b}}\\ {\mathit{u}}_{\mathrm{c}}\end{array}\right]}}$$

(5)

3.2. Converter Transformer

As mentioned above, the converter transformer is represented as the ideal transformer with a series-connected equivalent inductor. Therefore, its dynamic characteristics could be described as Equation (6).

$$\frac{\mathrm{d}}{\mathrm{d}t}\underset{{\mathit{i}}_{\mathrm{vabc}}}{\underbrace{\left[\begin{array}{c}{i}_{\mathrm{va}}\\ i_{\mathrm{vb}}\\ i_{\mathrm{vc}}\end{array}\right]}}=\underset{{\mathit{A}}_{\mathrm{T}}}{\underbrace{\left[\begin{array}{ccc}1/L_{\mathrm{T}}& 0& 0\\ 0& 1/L_{\mathrm{T}}& 0\\ 0& 0& 1/L_{\mathrm{T}}\end{array}\right]}}\left(\underset{{\mathit{u}}_{\mathrm{vabc}}}{\underbrace{\left[\begin{array}{c}{u}_{\mathrm{va}}\\ u_{\mathrm{vb}}\\ u_{\mathrm{vc}}\end{array}\right]}}-\frac{1}{k_{\mathrm{T}}}\underset{{\mathit{u}}_{\mathrm{sabc}}}{\underbrace{\left[\begin{array}{c}{u}_{\mathrm{sa}}\\ u_{\mathrm{sb}}\\ u_{\mathrm{sc}}\end{array}\right]}}\right)$$

(6)

3.3. Measurement Module

Based on the control block diagram in Figure 3, the dynamic characteristics of the AC system voltage measurement module could be described with s-domain transfer function as in Equation (7).

$$\underset{{\mathit{u}}_{\mathrm{sabc}\_\mathrm{c}}}{\underbrace{\left[\begin{array}{c}{u}_{\mathrm{sa}\_\mathrm{c}}\\ u_{\mathrm{sb}\_\mathrm{c}}\\ u_{\mathrm{sc}\_\mathrm{c}}\end{array}\right]}}=\frac{1}{U_{\mathrm{sbase}}}\underset{{\mathit{A}}_{\mathrm{F}}\left(s\right)}{\underbrace{\left[\begin{array}{ccc}{G}_{\mathrm{F}}\left(s\right)& 0& 0\\ 0& G_{\mathrm{F}}\left(s\right)& 0\\ 0& 0& G_{\mathrm{F}}\left(s\right)\end{array}\right]}}\left[\begin{array}{c}{u}_{\mathrm{sa}}\\ u_{\mathrm{sb}}\\ u_{\mathrm{sc}}\end{array}\right]$$

(7)

In addition, the dynamic characteristics of the valve-side current measurement module and the circulating current measurement module are similar to that of the AC system voltage measurement module.

3.4. ABC-DQ Transformation

The ABC-DQ transformation is only involved with the algebraic operation, whose transformation matrix is shown as Equation (8).

$${\mathit{T}}_{3\mathrm{p}-\mathrm{dq}}\left(\theta \right)=\frac{2}{3}\left[\begin{array}{ccc}\cos \left(\theta \right)& \cos \left(\theta -\frac{2\mathsf{\pi }}{3}\right)& \cos \left(\theta +\frac{2\mathsf{\pi }}{3}\right)\\ -\sin \left(\theta \right)& -\sin \left(\theta -\frac{2\mathsf{\pi }}{3}\right)& -\sin \left(\theta +\frac{2\mathsf{\pi }}{3}\right)\end{array}\right]$$

(8)

3.5. Phase-Locked Loop (PLL)

According to the control block diagram in Figure 4, the dynamic characteristics of the PLL could be described with s-domain transfer function as in Equation (9).

$$s\theta =\underset{{\mathit{A}}_{\mathrm{PLL}}\left(s\right)}{\underbrace{\left[\begin{array}{cc}0& G_{\mathrm{PLL}}\left(s\right)\end{array}\right]}}\underset{{\mathit{u}}_{\mathrm{sdq}}}{\underbrace{\left[\begin{array}{c}{u}_{\mathrm{sd}}\\ u_{\mathrm{sq}}\end{array}\right]}}+{\omega }_0$$

(9)

3.6. P/Q Calculation

The P/Q calculation module consists of two parts, i.e., the ABC-αβ frame transformation and the power calculation, whose mathematical descriptions are shown as in Equations (10) and (11).

$${\mathit{T}}_{3\mathrm{p}-\mathsf{\alpha }\mathsf{\beta }}=\frac{2}{3}\left[\begin{array}{ccc}1& -1/2& -1/2\\ 0& \sqrt{3}/2& -\sqrt{3}/2\end{array}\right]$$

(10)

$$\underset{\mathit{p}}{\underbrace{\left[\begin{array}{c}P\\ Q\end{array}\right]}}=\underset{{\mathit{U}}_{\mathrm{s}\mathsf{\alpha }\mathsf{\beta }}}{\underbrace{\left[\begin{array}{cc}{u}_{\mathrm{s}\mathsf{\alpha }}& u_{\mathrm{s}\mathsf{\beta }}\\ u_{\mathrm{s}\mathsf{\beta }}& -u_{\mathrm{s}\mathsf{\alpha }}\end{array}\right]}}\underset{{\mathit{i}}_{\mathrm{v}\mathsf{\alpha }\mathsf{\beta }}}{\underbrace{\left[\begin{array}{c}{i}_{\mathrm{v}\mathsf{\alpha }}\\ i_{\mathrm{v}\mathsf{\beta }}\end{array}\right]}}$$

(11)

3.7. P/Q Outer-Loop Controller

Based on the control block diagram in Figure 5, the dynamic characteristics of the P/Q outer-loop controller could be described with s-domain transfer function as in Equation (12).

$$\underset{{\mathit{i}}_{\mathrm{vdq}*}}{\underbrace{\left[\begin{array}{c}{i}_{\mathrm{vd}*}\\ i_{\mathrm{vq}*}\end{array}\right]}}=\underset{{\mathit{A}}_{\mathrm{PQ}}\left(s\right)}{\underbrace{\left[\begin{array}{cc}{G}_{\mathrm{P}}\left(s\right)& 0\\ 0& G_{\mathrm{Q}}\left(s\right)\end{array}\right]}}\left(\underset{\mathit{p}*}{\underbrace{\left[\begin{array}{c}{P}^{*}\\ Q^{*}\end{array}\right]}}-\left[\begin{array}{c}P\\ Q\end{array}\right]\right)$$

(12)

3.8. Inner-Loop Controller

Based on the control block diagram in Figure 6, considering the control delay, the dynamic characteristics of the OCTC and the CCSC could also be described with s-domain transfer function as in Equations (13) and (14).

$$\begin{array}{ll}\underset{{\mathit{u}}_{\mathrm{diffdq}*}}{\underbrace{\left[\begin{array}{c}{u}_{\mathrm{diffd}*}\\ u_{\mathrm{diffq}*}\end{array}\right]}}& =\underset{{\mathit{A}}_{\mathrm{octc}}\left(s\right)}{\underbrace{\left[\begin{array}{cc}{G}_{\mathrm{octc}}\left(s\right)& 0\\ 0& G_{\mathrm{octc}}\left(s\right)\end{array}\right]}}\left(\left[\begin{array}{c}{i}_{\mathrm{vd}*}\\ i_{\mathrm{vq}*}\end{array}\right]-\underset{{\mathit{A}}_{\mathrm{delay}}\left(s\right)}{\underbrace{\left[\begin{array}{cc}{G}_{\mathrm{delay}}\left(s\right)& 0\\ 0& G_{\mathrm{delay}}\left(s\right)\end{array}\right]}}\underset{{\mathit{i}}_{\mathrm{vdq}}}{\underbrace{\left[\begin{array}{c}{i}_{\mathrm{vd}}\\ i_{\mathrm{vq}}\end{array}\right]}}\right)\\ & +\underset{{\mathit{A}}_{\mathrm{c}}}{\underbrace{\left[\begin{array}{cc}0& -K_{\mathrm{c}}\\ K_{\mathrm{c}}& 0\end{array}\right]}}\left[\begin{array}{cc}{G}_{\mathrm{delay}}\left(s\right)& 0\\ 0& G_{\mathrm{delay}}\left(s\right)\end{array}\right]\left[\begin{array}{c}{i}_{\mathrm{vd}}\\ i_{\mathrm{vq}}\end{array}\right]+\left[\begin{array}{cc}{G}_{\mathrm{delay}}\left(s\right)& 0\\ 0& G_{\mathrm{delay}}\left(s\right)\end{array}\right]\left[\begin{array}{c}{u}_{\mathrm{sd}}\\ u_{\mathrm{sq}}\end{array}\right]\end{array}$$

(13)

$$\underset{{\mathit{U}}_{\mathrm{comdq}*}}{\underbrace{\left[\begin{array}{c}{u}_{\mathrm{comd}*}\\ u_{\mathrm{comq}*}\end{array}\right]}}=-\underset{{\mathit{A}}_{\mathrm{c}\csc }\left(s\right)}{\underbrace{\left[\begin{array}{cc}{G}_{\mathrm{c}\csc }\left(s\right)& -2K_{\mathrm{c}}\\ 2K_{\mathrm{c}}& G_{\mathrm{c}\csc }\left(s\right)\end{array}\right]}}\left[\begin{array}{cc}{G}_{\mathrm{delay}}\left(s\right)& 0\\ 0& G_{\mathrm{delay}}\left(s\right)\end{array}\right]\underset{{\mathit{i}}_{\mathrm{cirdq}}}{\underbrace{\left[\begin{array}{c}{i}_{\mathrm{cird}}\\ i_{\mathrm{cirq}}\end{array}\right]}}$$

(14)

3.9. DQ-ABC Transformation

The DQ-ABC transformation is the inverse process of the ABC-DQ transformation, whose transformation matrix is shown as Equation (15).

$${\mathit{T}}_{\mathrm{dq}-3\mathrm{p}}\left(\theta \right)=\left[\begin{array}{cc}\cos \left(\theta \right)& -\sin \left(\theta \right)\\ \cos \left(\theta -\frac{2\mathsf{\pi }}{3}\right)& -\sin \left(\theta -\frac{2\mathsf{\pi }}{3}\right)\\ \cos \left(\theta +\frac{2\mathsf{\pi }}{3}\right)& -\sin \left(\theta +\frac{2\mathsf{\pi }}{3}\right)\end{array}\right]$$

(15)

3.10. Modulation and Triggering Module

Adopting the NLM strategy and ignoring the switching dynamics of SMs, the mathematical description of the modulation and triggering module could be described as Equation (16).

$$\underset{{\mathit{N}}_{r\mathrm{abc}}}{\underbrace{\left[\begin{array}{c}{N}_{r\mathrm{a}}\\ N_{r\mathrm{b}}\\ N_{r\mathrm{c}}\end{array}\right]}}=\mathrm{Int}\left(N\cdot K_m\underset{{\mathit{u}}_{r\mathrm{abc}*}}{\underbrace{\left[\begin{array}{c}{u}_{r\mathrm{a}*}\\ u_{r\mathrm{b}*}\\ u_{r\mathrm{c}*}\end{array}\right]}}\right)+\frac{N}{2}\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right],r=\mathrm{p},\mathrm{n}$$

(16)

where in Equation (16), function ‘Int(x)’ means rounding towards the nearest integer about x.

4. Disturbance-State HSS Modeling of the MMC

On the basis of the above dynamic characteristics analysis, the disturbance-state HSS model and the steady-state condition of the MMC could be established by the HSS method.

The HSS method [21,22] has been widely used in the stead-state harmonic analysis for the linear periodical time-variant system, whose core is the Fourier transform. For any periodical time-variant variables in steady state, they could be transformed to that in harmonic-domain by the Fourier transform as in Equation (17).

$$z\left(t\right)={\displaystyle \sum _{k=-\infty }^{\infty }z\left(k{\omega }_0\right){\mathrm{e}}^{\mathrm{j}k{\omega }_{0}t}}$$

(17)

where z represents one periodical time-variant variable.

Correspondingly, the operation rule in time-domain could be transformed to that in the harmonic-domain by the Fourier transform, as shown in Equation (18).

$$\left\{\begin{array}{l}y\left(t\right)=a_1{z}_1\left(t\right)+a_2{z}_2\left(t\right)\\ y\left(t\right)=a{z}_1\left(t\right)z_2\left(t\right)\end{array}\right.\Rightarrow \left\{\begin{array}{l}y\left(h{\omega }_0\right)=a_1{z}_1\left(h{\omega }_0\right)+a_2{z}_2\left(h{\omega }_0\right)\\ y\left(h{\omega }_0\right)=a{\displaystyle \sum _k{z}_1\left(k{\omega }_0\right)z_2\left(\left(h-k\right){\omega }_0\right)}\end{array}\right.$$

(18)

where y represents the periodical time-variant output variable; z₁ and z₂ represent the periodical time-variant input variable; a, a₁ and a₂ are the coefficients of y, z₁ and z₂; variables with (t) represent the time-domain variable; variables with (hω₀) and ((h-k)ω₀) represents the harmonic-domain variable

In addition, for the operation rules in s-domain, they could also be transformed to the harmonic-domain, as shown in Equation (19).

$$y=G\left(s\right)z\Rightarrow y\left(h{\omega }_0\right)=G\left(\mathrm{j}h{\omega }_0\right)z\left(h{\omega }_0\right))$$

(19)

where G(s) and G(jhω₀) represents the s-domain and the harmonic-domain transfer function. Then, the steady-state condition of the MMC could be analyzed based on Equations (18) and (19).

When a disturbance component of frequency ω_p appears in the input variables, it will derivate a series of disturbance components with frequencies of ω_p ± hω₀. For the disturbance components, Equations (18) and (19) could be rewritten as Equations (20) and (21).

$$\begin{array}{c}\left\{\begin{array}{l}y\left(t\right)=a_1{z}_1\left(t\right)+a_2{z}_2\left(t\right)\\ y\left(t\right)=a{z}_1\left(t\right)z_2\left(t\right)\end{array}\right.\\ \Rightarrow \left\{\begin{array}{c}y\left({\omega }_{\mathrm{p}}\pm h{\omega }_0\right)=a_1{z}_1\left({\omega }_{\mathrm{p}}\pm h{\omega }_0\right)+a_2{z}_2\left({\omega }_{\mathrm{p}}\pm h{\omega }_0\right)\\ y\left({\omega }_{\mathrm{p}}\pm h{\omega }_0\right)=a\left\{{\displaystyle \sum _k{z}_1\left(k{\omega }_0\right)z_2\left(\left({\omega }_{\mathrm{p}}\pm h{\omega }_0\right)-k{\omega }_0\right)}+{\displaystyle \sum _k{z}_1\left(\left({\omega }_{\mathrm{p}}\pm h{\omega }_0\right)-k{\omega }_0\right)z_2\left(k{\omega }_0\right)}\right\}\end{array}\right.\end{array}$$

(20)

$$y=G\left(s\right)z\Rightarrow y\left({\omega }_{\mathrm{p}}\pm h{\omega }_0\right)=G\left(\mathrm{j}\left({\omega }_{\mathrm{p}}\pm h{\omega }_0\right)\right)z\left({\omega }_{\mathrm{p}}\pm h{\omega }_0\right)$$

(21)

Subsequently, the relationship among disturbance components in all modules of the MMC could be established based on Equations (20) and (21), which constitutes the disturbance-state HSS model of the MMC.

4.1. Disturbance Components Analysis in Each Module

4.1.1. Converter Itself

Due to the influence of the controller, there will exist the disturbance components in the insertion index. For emphasizing their influence, the first term in the right of Equation (5) could be rewritten as Equation (22).

$$\begin{array}{c}{\mathit{A}}_{\mathrm{abc}}{\mathit{x}}_{\mathrm{abc}}={\mathit{A}}_{\mathrm{abc}1}{\mathit{x}}_{\mathrm{abc}}+{\mathit{C}}_{\mathrm{abc}}{\mathit{s}}_{\mathrm{abc}}\\ \left\{\begin{array}{c}{\mathit{A}}_{\mathrm{abc}1}=\mathsf{\Lambda }\left(\left[\begin{array}{ccc}{\mathit{A}}_{\mathrm{a}1}& {\mathit{A}}_{\mathrm{b}1}& {\mathit{A}}_{\mathrm{c}1}\end{array}\right]\right),{\mathit{C}}_{\mathrm{abc}}=\mathsf{\Lambda }\left(\left[\begin{array}{ccc}{\mathit{C}}_{\mathrm{a}}& {\mathit{C}}_{\mathrm{b}}& {\mathit{C}}_{\mathrm{c}}\end{array}\right]\right),{\mathit{s}}_{\mathrm{abc}}={\left[\begin{array}{ccc}{{\mathit{s}}_{\mathrm{a}}}^{\mathrm{T}}& {{\mathit{s}}_{\mathrm{b}}}^{\mathrm{T}}& {{\mathit{s}}_{\mathrm{c}}}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}\\ {\mathit{A}}_{j1}=\left[\begin{array}{cccc}-\frac{R_0}{L_0}& 0& 0& 0\\ 0& -\frac{R_0}{L_0}& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right],{\mathit{C}}_j=\left[\begin{array}{cc}-\frac{u_{\mathrm{Cp}j}}{L_0}& \frac{u_{\mathrm{Cn}j}}{L_0}\\ -\frac{u_{\mathrm{Cp}j}}{2L_0}& -\frac{u_{\mathrm{Cn}j}}{2L_0}\\ \frac{i_{\mathrm{v}j}+2i_{\mathrm{cir}j}}{2C_{\mathrm{eq}}}& 0\\ 0& \frac{-i_{\mathrm{v}j}+2i_{\mathrm{cir}j}}{2C_{\mathrm{eq}}}\end{array}\right],{\mathit{s}}_j=\left[\begin{array}{c}{S}_{\mathrm{p}j}\\ S_{\mathrm{n}j}\end{array}\right],j=\mathrm{a},\mathrm{b},\mathrm{c}\end{array}\right.\end{array}$$

(22)

where label ‘Λ ([x₁ x₂ x₃])’ represents the diagonal matrix whose diagonal elements are x₁, x₂ and x₃, and superscript ‘T’ represents the transposition of a matrix.

According to Equations (5), (22) and (20), the relationship among the disturbance components in the converter itself could be described as Equation (23).

$$\begin{array}{c}{\Lambda }_0{\mathit{x}}_{\mathrm{abcp}}={\mathit{A}}_{\mathrm{abc}0}{\mathit{x}}_{\mathrm{abcp}}+{\mathit{B}}_{\mathrm{abc}0}{\mathit{u}}_{\mathrm{abcp}}+{\mathit{C}}_{\mathrm{abc}0}{\mathit{s}}_{\mathrm{abcp}}\\ \left\{\begin{array}{cc}\hfill & {\Lambda }_0=\mathsf{\Lambda }\left(\left[\begin{array}{ccccc}\mathrm{j}\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)& \cdots & \mathrm{j}{\omega }_{\mathrm{p}}& \cdots & \mathrm{j}\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)\end{array}\right]\right)\hfill \\ \hfill & {\mathit{H}}_0=\left[\begin{array}{ccccc}\mathit{H}\left(0\right)& \cdots & \mathit{H}\left(\mathrm{n}{\omega }_0\right)& \cdots & 0\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ \mathit{H}\left(-\mathrm{n}{\omega }_0\right)& \cdots & \mathit{H}\left(0\right)& \cdots & \mathit{H}\left(\mathrm{n}{\omega }_0\right)\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ 0& \cdots & \mathit{H}\left(-\mathrm{n}{\omega }_0\right)& \cdots & \mathit{X}\left(0\right)\end{array}\right],\mathit{H}={\mathit{A}}_{\mathrm{abc}},{\mathit{B}}_{\mathrm{abc}},{\mathit{C}}_{\mathrm{abc}}\hfill \\ \hfill & {\mathit{h}}_{\mathrm{p}}={\left[\begin{array}{ccccc}\mathit{h}{\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}},\mathit{h}={\mathit{x}}_{\mathrm{abc}},{\mathit{u}}_{\mathrm{abc}},{\mathit{s}}_{\mathrm{abc}}\hfill \end{array}\right.\end{array}$$

(23)

4.1.2. Converter Transformer

Similarly, according to Equations (6) and (20), the relationship among the disturbance components in the converter transformer could be described as Equation (24).

$$\begin{array}{c}{\mathit{\Lambda }}_0{\mathit{i}}_{\mathrm{vabcp}}={\mathit{A}}_{\mathrm{T}0}{\mathit{u}}_{\mathrm{vabcp}}-\frac{1}{k_{\mathrm{T}}}{\mathit{A}}_{\mathrm{T}0}{\mathit{u}}_{\mathrm{sabcp}}\\ \left\{\begin{array}{l}{\mathit{A}}_{\mathrm{T}0}=\left[\begin{array}{ccc}{\mathit{A}}_{\mathrm{T}}& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathit{A}}_{\mathrm{T}}\end{array}\right]\\ {\mathit{h}}_{\mathrm{p}}={\left[\begin{array}{ccccc}\mathit{h}{\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}},\mathit{h}={\mathit{i}}_{\mathrm{vabc}},{\mathit{u}}_{\mathrm{vabc}},{\mathit{u}}_{\mathrm{sabc}}\end{array}\right.\end{array}$$

(24)

4.1.3. Measurement Module

According to Equations (7) and (21), the relationship among disturbance the components in the AC system voltage measurement module could be described as Equation (25).

$$\begin{array}{c}{\mathit{u}}_{\mathrm{sabcp}\_\mathrm{c}}=\frac{1}{U_{\mathrm{sbase}}}{\mathit{A}}_{\mathrm{F}0}{\mathit{u}}_{\mathrm{sabcp}}\\ \left\{\begin{array}{l}{\mathit{A}}_{\mathrm{F}0}=\left[\begin{array}{ccc}{\mathit{A}}_{\mathrm{F}}\left(\mathrm{j}\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)\right)& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathit{A}}_{\mathrm{F}}\left(\mathrm{j}\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)\right)\end{array}\right]\\ {\mathit{h}}_{\mathrm{p}}={\left[\begin{array}{ccccc}\mathit{h}{\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}},\mathit{h}={\mathit{u}}_{\mathrm{sabc}\_\mathrm{c}},{\mathit{u}}_{\mathrm{sabc}}\end{array}\right.\end{array}$$

(25)

The relationship among disturbance components in the valve-side current measurement module and the circulating current measurement module are similar to that in AC system voltage measurement module.

4.1.4. ABC-DQ Transformation

Considering the influence of the disturbance components in the PLL, the transformation matrix could be rewritten as Equation (26).

$$\begin{array}{c}{\mathit{T}}_{3\mathrm{p}-\mathrm{dq}}\left(\theta \right)={\mathit{T}}_{3\mathrm{p}-\mathrm{dq}}\left({\theta }_0+\mathrm{d}\theta \right)\approx {\mathit{T}}_{3\mathrm{p}-\mathrm{dq}}\left({\theta }_0\right)+\mathit{T}{’}_{3\mathrm{p}-\mathrm{dq}}\left({\theta }_0\right)\mathrm{d}\theta \\ \mathit{T}{’}_{3\mathrm{p}-\mathrm{dq}}\left(\theta \right)=\frac{2}{3}\left[\begin{array}{ccc}-\sin \left(\theta \right)& -\sin \left(\theta -\frac{2\mathsf{\pi }}{3}\right)& -\sin \left(\theta +\frac{2\mathsf{\pi }}{3}\right)\\ \cos \left(\theta \right)& \cos \left(\theta -\frac{2\mathsf{\pi }}{3}\right)& \cos \left(\theta +\frac{2\mathsf{\pi }}{3}\right)\end{array}\right]\end{array}$$

(26)

Taking the ABC-DQ transformation of the AC system voltage as an example, the relationship among its disturbance components could be derived from Equations (26) and (20), as described in Equation (27).

$$\begin{array}{c}{\mathit{u}}_{\mathrm{sdqp}}={\mathit{T}}_{3\mathit{p}-\mathrm{dq}0}{\mathit{u}}_{\mathrm{sabcp}\_\mathrm{c}}+\mathit{T}{{}^{\prime }}_{3\mathrm{p}-\mathrm{dq}0}{\mathit{u}}_{\mathrm{sabc}0\_\mathrm{c}}{\theta }_{\mathrm{p}}\\ \left\{\begin{array}{cc}\hfill & {\mathit{h}}_0={\left[\begin{array}{ccccc}\mathit{h}{\left(\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left(0\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left(-\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}},\mathit{h}={\mathit{u}}_{\mathrm{sabc}\_\mathrm{c}}\hfill \\ \hfill & {\mathit{H}}_0=\left[\begin{array}{ccccc}\mathit{H}\left(0\right)& \cdots & \mathit{H}\left(\mathrm{n}{\omega }_0\right)& \cdots & 0\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ \mathit{H}\left(-\mathrm{n}{\omega }_0\right)& \cdots & \mathit{H}\left(0\right)& \cdots & \mathit{H}\left(\mathrm{n}{\omega }_0\right)\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ 0& \cdots & \mathit{H}\left(-\mathrm{n}{\omega }_0\right)& \cdots & \mathit{X}\left(0\right)\end{array}\right],\mathit{H}={\mathit{T}}_{3\mathrm{p}-\mathrm{dq}},\mathit{T}{{}^{\prime }}_{3\mathrm{p}-\mathrm{dq}}\hfill \\ \hfill & {\mathit{h}}_{\mathrm{p}}={\left[\begin{array}{ccccc}\mathit{h}{\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}},\mathit{h}={\mathit{u}}_{\mathrm{sdq}},\theta \hfill \end{array}\right.\end{array}$$

(27)

Moreover, the relationship among disturbance components in the ABC-DQ transformation of the valve-side current and circulating current are similar to Equation (27). It should be pointed out that the reference phase used in the ABC-DQ transformation for the circulating current is twice the output phase angle of the PLL.

4.1.5. Phase-Locked Loop (PLL)

According to Equations (9) and (21), the relationship among disturbance components in the PLL could be described as Equation (28).

$$\begin{array}{c}{\Lambda }_0{\theta }_{\mathrm{p}}={\mathit{A}}_{\mathrm{PLL}0}{\mathit{u}}_{\mathrm{sdqp}}\\ \left\{\begin{array}{cc}\hfill & {\mathit{A}}_{\mathrm{PLL}0}=\left[\begin{array}{ccc}{\mathit{A}}_{\mathrm{PLL}}\left(\mathrm{j}\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)\right)& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathit{A}}_{\mathrm{PLL}}\left(\mathrm{j}\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)\right)\end{array}\right]\hfill \\ \hfill & {\mathit{h}}_{\mathrm{p}}={\left[\begin{array}{ccccc}\mathit{h}{\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}},\mathit{h}=\theta ,{\mathit{u}}_{\mathrm{sdq}}\hfill \end{array}\right.\end{array}$$

(28)

4.1.6. P/Q Calculation

To emphasize the disturbance components in the AC system voltage, Equation (11) could be rewritten as Equation (29).

$$\left[\begin{array}{c}P\\ Q\end{array}\right]=\underset{{\mathit{I}}_{\mathrm{v}\mathsf{\alpha }\mathsf{\beta }}}{\underbrace{\left[\begin{array}{cc}{i}_{\mathrm{v}\mathsf{\alpha }}& i_{\mathrm{v}\mathsf{\beta }}\\ -i_{\mathrm{v}\mathsf{\beta }}& i_{\mathrm{v}\mathsf{\alpha }}\end{array}\right]}}\underset{{\mathit{u}}_{\mathrm{s}\mathsf{\alpha }\mathsf{\beta }}}{\underbrace{\left[\begin{array}{c}{u}_{\mathrm{s}\mathsf{\alpha }}\\ u_{\mathrm{s}\mathsf{\beta }}\end{array}\right]}}$$

(29)

According to Equations (11), (29) and (20), the relationship among disturbance components in the P/Q calculation could be described as Equation (30).

$$\begin{array}{c}{\mathit{p}}_{\mathrm{p}}={\mathit{U}}_{\mathrm{s}\mathsf{\alpha }\mathsf{\beta }0}{\mathit{i}}_{\mathrm{v}\mathsf{\alpha }\mathsf{\beta }\mathrm{p}}+{\mathit{I}}_{\mathrm{v}\mathsf{\alpha }\mathsf{\beta }0}{\mathit{u}}_{\mathrm{s}\mathsf{\alpha }\mathsf{\beta }\mathrm{p}}\\ \left\{\begin{array}{cc}\hfill & {\mathit{H}}_0=\left[\begin{array}{ccccc}\mathbf{H}\left(0\right)& \cdots & \mathit{H}\left(\mathrm{n}{\omega }_0\right)& \cdots & 0\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ \mathit{H}\left(-\mathrm{n}{\omega }_0\right)& \cdots & \mathit{H}\left(0\right)& \cdots & \mathit{H}\left(\mathrm{n}{\omega }_0\right)\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ 0& \cdots & \mathit{H}\left(-\mathrm{n}{\omega }_0\right)& \cdots & \mathit{X}\left(0\right)\end{array}\right],\mathit{H}={\mathit{U}}_{\mathrm{s}\mathsf{\alpha }\mathsf{\beta }},{\mathit{I}}_{\mathrm{v}\mathsf{\alpha }\mathsf{\beta }}\hfill \\ \hfill & {\mathit{h}}_{\mathrm{p}}={\left[\begin{array}{ccccc}\mathit{h}{\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}},\mathit{h}=\mathit{p},{\mathit{i}}_{\mathrm{v}\mathsf{\alpha }\mathsf{\beta }},{\mathit{u}}_{\mathrm{s}\mathsf{\alpha }\mathsf{\beta }}\hfill \end{array}\right.\end{array}$$

(30)

4.1.7. P/Q Outer-Loop Controller

According to Equations (12) and (21), the relationship among disturbance components in the P/Q outer-loop controller could be described as Equation (31).

$$\begin{array}{c}{\mathit{i}}_{\mathrm{vdqp}*}={\mathit{A}}_{\mathrm{PQ}0}{\mathit{p}}_{\mathrm{p}}*-{\mathit{A}}_{\mathrm{PQ}0}{\mathit{p}}_{\mathrm{p}}\\ \left\{\begin{array}{l}{\mathit{A}}_{\mathrm{PQ}0}=\left[\begin{array}{ccc}{\mathit{A}}_{\mathrm{PQ}}\left(\mathrm{j}\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)\right)& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathit{A}}_{\mathrm{PQ}}\left(\mathrm{j}\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)\right)\end{array}\right]\\ {\mathit{h}}_{\mathrm{p}}={\left[\begin{array}{ccccc}\mathit{h}{\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}},\mathit{h}={\mathit{i}}_{\mathrm{vdq}*},\mathit{p}*,\mathit{p}\end{array}\right.\end{array}$$

(31)

4.1.8. Inner-Loop Controller

According to Equations (13) and (21), the relationship among disturbance components in the OCTC could be described as Equation (32).

$$\begin{array}{c}{\mathit{u}}_{\mathrm{diffdqp}*}={\mathit{A}}_{\mathrm{octc}0}{\mathit{i}}_{\mathrm{vdqp}*}-{\mathit{A}}_{\mathrm{octc}0}{\mathit{A}}_{\mathrm{delay}0}{\mathit{i}}_{\mathrm{vdqp}}+{\mathit{A}}_{\mathrm{c}0}{\mathit{A}}_{\mathrm{delay}0}{\mathit{i}}_{\mathrm{vdqp}}+{\mathit{A}}_{\mathrm{delay}0}{\mathit{u}}_{\mathrm{sdqp}}\\ \left\{\begin{array}{cc}\hfill & {\mathit{A}}_{\mathrm{octc}0}=\left[\begin{array}{ccc}{\mathit{A}}_{\mathrm{octc}}\left(\mathrm{j}\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)\right)& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathit{A}}_{\mathrm{octc}}\left(\mathrm{j}\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)\right)\end{array}\right]\hfill \\ \hfill & {\mathit{A}}_{\mathrm{delay}0}=\left[\begin{array}{ccc}{\mathit{A}}_{\mathrm{delay}}\left(\mathrm{j}\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)\right)& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathit{A}}_{\mathrm{delay}}\left(\mathrm{j}\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)\right)\end{array}\right],{\mathit{A}}_{\mathrm{c}0}=\left[\begin{array}{ccc}{\mathit{A}}_{\mathrm{c}}& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathit{A}}_{\mathrm{c}}\end{array}\right]\hfill \\ \hfill & {\mathit{h}}_{\mathrm{p}}={\left[\begin{array}{ccccc}\mathit{h}{\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}},\mathit{h}={\mathit{u}}_{\mathrm{diffdq}*},{\mathit{i}}_{\mathrm{vdq}*},{\mathit{i}}_{\mathrm{vdq}},{\mathit{u}}_{\mathrm{sdq}}\hfill \end{array}\right.\end{array}$$

(32)

According to Equations (14) and (21), the relationship among disturbance components in the CCSC could be described as Equation (33).

$$\begin{array}{c}{\mathit{u}}_{\mathrm{comdqp}*}=-{\mathit{A}}_{\mathrm{c}csc0}{\mathit{A}}_{\mathrm{delay}0}{\mathit{i}}_{\mathrm{cirdqp}}\\ \left\{\begin{array}{cc}\hfill & {\mathit{A}}_{\mathrm{c}csc0}=\left[\begin{array}{ccc}{\mathit{A}}_{\mathrm{c}csc}\left(\mathrm{j}\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)\right)& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathit{A}}_{\mathrm{c}csc}\left(\mathrm{j}\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)\right)\end{array}\right]\hfill \\ \hfill & {\mathit{h}}_{\mathrm{p}}={\left[\begin{array}{ccccc}\mathit{h}{\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}},\mathit{h}={\mathit{u}}_{\mathrm{comdq}*},{\mathit{i}}_{\mathrm{cirdq}}\hfill \end{array}\right.\end{array}$$

(33)

4.1.9. DQ-ABC Transformation

Considering the influence of the disturbance components in the PLL, the transformation matrix could be described as Equation (34), which is similar to the ABC-DQ transformation.

$$\begin{array}{c}{\mathit{T}}_{\mathrm{dq}-3\mathrm{p}}\left(\theta \right)={\mathit{T}}_{\mathrm{dq}-3\mathrm{p}}\left({\theta }_0+\mathrm{d}\theta \right)\approx {\mathit{T}}_{\mathrm{dq}-3\mathrm{p}}\left({\theta }_0\right)+\mathit{T}{’}_{\mathrm{dq}-3\mathrm{p}}\left({\theta }_0\right)\mathrm{d}\theta \\ \mathit{T}{’}_{\mathrm{dq}-3\mathrm{p}}\left(\theta \right)=\left[\begin{array}{cc}-\sin \left(\theta \right)& -\cos \left(\theta \right)\\ -\sin \left(\theta -\frac{2\mathsf{\pi }}{3}\right)& -\cos \left(\theta -\frac{2\mathsf{\pi }}{3}\right)\\ -\sin \left(\theta +\frac{2\mathsf{\pi }}{3}\right)& -\cos \left(\theta +\frac{2\mathsf{\pi }}{3}\right)\end{array}\right]\end{array}$$

(34)

Taking the DQ-ABC transformation of the reference value of the differential mode voltage as an example, the relationship among its disturbance components could be derived from Equations (34) and (20), as described in Equation (35).

$$\begin{array}{c}{\mathit{u}}_{\mathrm{diffabcp}*}={\mathit{T}}_{\mathrm{dq}-3\mathrm{p}0}{\mathit{u}}_{\mathrm{diffdqp}*}+\mathit{T}{{}^{\prime }}_{\mathrm{dq}-3\mathrm{p}0}{\mathit{u}}_{\mathrm{diffdq}0*}{\theta }_{\mathrm{p}}\\ \left\{\begin{array}{cc}\hfill & {\mathit{h}}_0={\left[\begin{array}{ccccc}\mathit{h}{\left(\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left(0\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left(-\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}},\mathit{h}={\mathit{u}}_{\mathrm{diffdq}*}\hfill \\ \hfill & {\mathit{H}}_0=\left[\begin{array}{ccccc}\mathit{H}\left(0\right)& \cdots & \mathit{H}\left(\mathrm{n}{\omega }_0\right)& \cdots & 0\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ \mathit{H}\left(-\mathrm{n}{\omega }_0\right)& \cdots & \mathit{H}\left(0\right)& \cdots & \mathit{H}\left(\mathrm{n}{\omega }_0\right)\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ 0& \cdots & \mathit{H}\left(-\mathrm{n}{\omega }_0\right)& \cdots & \mathit{X}\left(0\right)\end{array}\right],\mathit{H}={\mathit{T}}_{\mathrm{dq}-3\mathrm{p}},\mathit{T}{{}^{\prime }}_{\mathrm{dq}-3\mathrm{p}}\hfill \\ \hfill & {\mathit{h}}_{\mathrm{p}}={\left[\begin{array}{ccccc}\mathit{h}{\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}},\mathit{h}={\mathit{u}}_{\mathrm{diffabc}*},{\mathit{u}}_{\mathrm{diffdq}*},\theta \hfill \end{array}\right.\end{array}$$

(35)

Furthermore, the relationship among disturbance components in the DQ-ABC transformation about the reference value of the common mode voltage is similar to that in the DQ-ABC transformation for the reference value of the differential mode voltage. Note that the reference phase angle used in the DQ-ABC transformation about the common mode voltage is twice the output phase angle of the PLL.

4.1.10. Modulation and Triggering Module

Due to the larger number of series connected SMs in each arm, the influence of the rounding function on the disturbance components could be ignored. The relationship among disturbance components in the modulation and triggering module could be described as Equation (36), based on Equations (16) and (20).

$$\begin{array}{c}{\mathit{N}}_{r\mathrm{abcp}}=N\cdot K_m{\mathit{u}}_{r\mathrm{abcp}*}\\ \left\{{\mathit{h}}_{\mathrm{p}}={\left[\begin{array}{ccccc}\mathit{h}{\left({\omega }_{\mathrm{p}}+\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}\right)}^{\mathrm{T}}& \cdots & \mathit{h}{\left({\omega }_{\mathrm{p}}-\mathrm{n}{\omega }_0\right)}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}},\mathit{h}={\mathit{N}}_{r\mathrm{abc}},{\mathit{u}}_{r\mathrm{abc}*}\right.\end{array}$$

(36)

In all, Equations (22)–(25), (27), (28), (30)–(33), (35) and (36) are the relationship equations about disturbance components in all modules, which constitute the disturbance-state HSS model of the MMC with P/Q control. It is one linear structural equation system with the style of matrix.

4.2. Steady-State Condition of the MMC under P/Q Control Mode

It is noted that the disturbance-state HSS model of the MMC is related with its steady-state condition. Therefore, this paper further analyses the steady-state condition of the MMC under P/Q control mode.

In steady state, the harmonic-domain AC system voltage, the harmonic-domain DC-side voltage, the reference value of the active power and reactive power are known. Additionally, the steady-state output phase of the PLL, which is also the steady-state phase angle of the AC system voltage in phase a, could be calculated.

Next, it is known that the steady-state valve-side current only has the ω₀ frequency component, and it is symmetrical in three-phase. Thus, it could be obtained based on the power equation as in Equation (37).

$$\begin{array}{c}{P}^{*}{+\mathrm{jQ}}^{*}=\frac{3}{k_{\mathrm{T}}{S}_{\mathrm{base}}}\left[u_{\mathrm{sa}}\left({\omega }_0\right)i_{\mathrm{va}}\left(-{\omega }_0\right)+u_{\mathrm{sa}}\left(-{\omega }_0\right)i_{\mathrm{va}}\left({\omega }_0\right)\right]\\ u_{\mathrm{sa}}\left(-{\omega }_0\right)=u_{\mathrm{sa}}{\left({\omega }_0\right)}^{^},i_{\mathrm{va}}\left(-{\omega }_0\right)=i_{\mathrm{va}}{\left({\omega }_0\right)}^{^}\end{array}$$

(37)

where superscript ‘^’ represents the conjugate of a complex value.

There should exist two frequency components in the steady-state circulating current, i.e., the DC component and the 2ω₀ frequency component. The DC components in three-phase are equal, which is one third of the DC-side current. The 2ω₀ frequency component is zero, considering the effect of the CCSC.

Thus, taking the circulating current in phase a as an example, its frequency components could be described as Equation (38).

$$\begin{array}{c}{i}_{\mathrm{cira}}\left(0\right)=\frac{I_{\mathrm{dc}}}{3}\\ i_{\mathrm{cira}}\left(2{\omega }_0\right)=i_{\mathrm{cird}*}+\mathrm{j}{i}_{\mathrm{cirq}*}=0,i_{\mathrm{cira}}\left(-2{\omega }_0\right)=i_{\mathrm{cira}}{\left(2{\omega }_0\right)}^{^}\end{array}$$

(38)

By analyzing the steady-state harmonic components in phase a of the converter itself, the frequency components in the steady-state capacitor voltage of arm equivalent module and the frequency components in the steady-state insertion index could be obtained as Equation (39).

$$\begin{array}{c}{i}_{\mathrm{va}}\left({\omega }_0\right)=\frac{-2u_{\mathrm{va}}\left({\omega }_0\right)-2u_{\mathrm{pa}}\left({\omega }_0\right)}{R_0+\mathrm{j}{\omega }_0{L}_0},i_{\mathrm{va}}\left(-{\omega }_0\right)=\frac{-2u_{\mathrm{va}}\left(-{\omega }_0\right)-2u_{\mathrm{pa}}\left(-{\omega }_0\right)}{R_0-\mathrm{j}{\omega }_0{L}_0}\\ i_{\mathrm{cira}}\left(0\right)=\frac{U_{\mathrm{dc}}-2u_{\mathrm{pa}}\left(0\right)}{2R_0},i_{\mathrm{cira}}\left(2{\omega }_0\right)=\frac{0-2u_{\mathrm{pa}}\left(2{\omega }_0\right)}{2\left(R_0+\mathrm{j}2{\omega }_0{L}_0\right)},i_{\mathrm{cira}}\left(-2{\omega }_0\right)=\frac{0-2u_{\mathrm{pa}}\left(-2{\omega }_0\right)}{2\left(R_0-\mathrm{j}2{\omega }_0{L}_0\right)}\\ 0=i_{\mathrm{Cpa}}\left(0\right),u_{\mathrm{Cpa}}\left({\omega }_0\right)=\frac{i_{\mathrm{Cpa}}\left({\omega }_0\right)}{2\mathrm{j}{\omega }_0{C}_{\mathrm{eq}}},u_{\mathrm{Cpa}}\left(-{\omega }_0\right)=\frac{i_{\mathrm{Cpa}}\left(-{\omega }_0\right)}{-2\mathrm{j}{\omega }_0{C}_{\mathrm{eq}}},u_{\mathrm{Cpa}}\left(2{\omega }_0\right)=\frac{i_{\mathrm{Cpa}}\left(2{\omega }_0\right)}{4\mathrm{j}{\omega }_0{C}_{\mathrm{eq}}},u_{\mathrm{Cpa}}\left(-2{\omega }_0\right)=\frac{i_{\mathrm{Cpa}}\left(-2{\omega }_0\right)}{-4\mathrm{j}{\omega }_0{C}_{\mathrm{eq}}}\\ \left[\begin{array}{l}{u}_{\mathrm{pa}}\left(2{\omega }_0\right)\\ u_{\mathrm{pa}}\left({\omega }_0\right)\\ u_{\mathrm{pa}}\left(0\right)\\ u_{\mathrm{pa}}\left(-{\omega }_0\right)\\ u_{\mathrm{pa}}\left(-2{\omega }_0\right)\end{array}\right]=\left[\begin{array}{lllll}{S}_{\mathrm{pa}}\left(0\right)& S_{\mathrm{pa}}\left({\omega }_0\right)& S_{\mathrm{pa}}\left(2{\omega }_0\right)& 0& 0\\ S_{\mathrm{pa}}\left(-{\omega }_0\right)& S_{\mathrm{pa}}\left(0\right)& S_{\mathrm{pa}}\left({\omega }_0\right)& S_{\mathrm{pa}}\left(2{\omega }_0\right)& 0\\ S_{\mathrm{pa}}\left(-2{\omega }_0\right)& S_{\mathrm{pa}}\left(-{\omega }_0\right)& S_{\mathrm{pa}}\left(0\right)& S_{\mathrm{pa}}\left({\omega }_0\right)& S_{\mathrm{pa}}\left(2{\omega }_0\right)\\ 0& S_{\mathrm{pa}}\left(-2{\omega }_0\right)& S_{\mathrm{pa}}\left(-{\omega }_0\right)& S_{\mathrm{pa}}\left(0\right)& S_{\mathrm{pa}}\left({\omega }_0\right)\\ 0& 0& S_{\mathrm{pa}}\left(-2{\omega }_0\right)& S_{\mathrm{pa}}\left(-{\omega }_0\right)& S_{\mathrm{pa}}\left(0\right)\end{array}\right]\left[\begin{array}{l}{u}_{\mathrm{Cpa}}\left(2{\omega }_0\right)\\ u_{\mathrm{Cpa}}\left({\omega }_0\right)\\ u_{\mathrm{Cpa}}\left(0\right)\\ u_{\mathrm{Cpa}}\left(-{\omega }_0\right)\\ u_{\mathrm{Cpa}}\left(-2{\omega }_0\right)\end{array}\right]\\ \left[\begin{array}{l}{i}_{\mathrm{Cpa}}\left(2{\omega }_0\right)\\ i_{\mathrm{Cpa}}\left({\omega }_0\right)\\ i_{\mathrm{Cpa}}\left(0\right)\\ i_{\mathrm{Cpa}}\left(-{\omega }_0\right)\\ i_{\mathrm{Cpa}}\left(-2{\omega }_0\right)\end{array}\right]=\left[\begin{array}{lllll}{i}_{\mathrm{cira}}\left(0\right)& i_{\mathrm{va}}\left({\omega }_0\right)/2& i_{\mathrm{cira}}\left(2{\omega }_0\right)& 0& 0\\ i_{\mathrm{va}}\left(-{\omega }_0\right)/2& i_{\mathrm{cira}}\left(0\right)& i_{\mathrm{va}}\left({\omega }_0\right)/2& i_{\mathrm{cira}}\left(2{\omega }_0\right)& 0\\ i_{\mathrm{cira}}\left(-2{\omega }_0\right)& i_{\mathrm{va}}\left(-{\omega }_0\right)/2& i_{\mathrm{cira}}\left(0\right)& i_{\mathrm{va}}\left({\omega }_0\right)/2& i_{\mathrm{cira}}\left(2{\omega }_0\right)\\ 0& i_{\mathrm{cira}}\left(-2{\omega }_0\right)& i_{\mathrm{va}}\left(-{\omega }_0\right)/2& i_{\mathrm{cira}}\left(0\right)& i_{\mathrm{va}}\left({\omega }_0\right)/2\\ 0& 0& i_{\mathrm{cira}}\left(-2{\omega }_0\right)& i_{\mathrm{va}}\left(-{\omega }_0\right)/2& i_{\mathrm{cira}}\left(0\right)\end{array}\right]\left[\begin{array}{l}{S}_{\mathrm{pa}}\left(2{\omega }_0\right)\\ S_{\mathrm{pa}}\left({\omega }_0\right)\\ S_{\mathrm{pa}}\left(0\right)\\ S_{\mathrm{pa}}\left(-{\omega }_0\right)\\ S_{\mathrm{pa}}\left(-2{\omega }_0\right)\end{array}\right]\end{array}$$

(39)

From Equation (39), it is known that there are twenty independent equations and twenty unknown variables. Therefore, they could be solved by the iteration method (e.g., the Newton–Raphson iteration method).

In all, Equations (37)–(39) describe the relationship among variables of the MMC in steady state, and constitute the steady-state condition equations of the MMC under P/Q control mode.

5. Case Study

5.1. System Parameters

To verify the proposed disturbance-state model, the case studies are carried on one test system with MMC in PSCAD/EMTDC [25]. PSCAD/EMTDC is a professional and commonly used time-domain electromagnetic transient simulation software for power system transient analysis, especially the transient behavior of the power electronics. The structure of the test system is shown as Figure 8 and its main parameters are listed in Table 1 and Table 2.

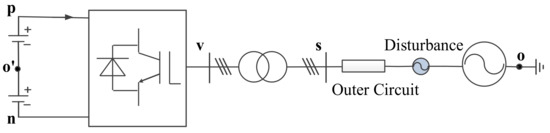
Figure 8. Single-line diagram of the test system.

Table 1. Main parameters of the test system.

Item	Values
AC system rated voltage	145 kV
AC system rated frequency	50 Hz
Transformer ratio	145 kV/220 kV
Transformer rated capacity	800 MVA
Transformer leakage inductance	0.18 pu
Rated DC voltage	400 kV
MMC rated capacity	800 MVA
MMC arm inductance	29 mH
MMC arm resistance	1.5 Ω
Number of SMs per arm	150
MMC SM capacitor	7500 μF
Active power reference	0.8 pu
Reactive power reference	0.0 pu
Modulation ratio	0.9
Control delay	0.0045 s
Damping coefficient of filter	0.707
Characteristics frequency of filter	2000 Hz

Table 2. Parameters of PI controllers in the test system.

Parameters of PI Controller	Proportional Coefficient	Integral Coefficient
OCTC	1.1	2
CCSC	1.5	2.5
PLL	100	222.2
Active power controller	0.64	60.61
Reactive power controller	0.21	34.48

5.2. Model Verification

Firstly, the MMC steady-state condition equations of Equations (37)–(39) are verified. The disturbance voltage source in Figure 8 is set as zero. The simulation results by PSCAD/EMTDC and the analytical results based on the steady-state condition equations are shown in Table 3.

Table 3. Simulation result and analytical result of steady-state condition.

Variable	Frequency	Simulation Result		Analytical Result
		Magnitude	Phase Angle	Magnitude	Phase Angle
iva	DC	0	--	0	--
	ω0	2.4053 kA	−112.2549°	2.3610 kA	−101.2879°
	2ω0	0	0	0	0
icira	DC	0.5413 kA	--	0.5333 kA	--
	ω0	0	0	0	0
	2ω0	0	0	0	0
uCpa	DC	2.6335 kV	--	2.6334 kV	--
	ω0	0.1543 kV	148.1338°	0.1551 kV	148.7124°
	2ω0	0.0584 kV	−122.6353°	0.0582 kV	−123.2604°
Spa	DC	0.5000	--	0.5000	--
	ω0	0.4571	77.9301°	0.4586	78.3345°
	2ω0	0.0244	51.0754°	0.0176	49.3115°

It could be noted from Table 3 that the analytical results based on the steady-state condition equations are consistent with the simulation results in PSCAD/EMTDC, which verifies the accuracy of the steady-state condition equations.

Then, this paper sets the disturbance voltage source with frequency of f_p (f_p = ω_p/2π) to verify the disturbance-state HSS model of the MMC. The magnitude of the disturbance voltage is about 5% of the AC system rated voltage, and the frequency of the disturbance voltage varies from 1 Hz to 100 Hz. The simulation results from PSCAD/EMTDC and the analytical results from the disturbance-state HSS model are shown in Figure 9. In addition, the analytical results without the P/Q outer-loop controller, the PLL or the control delay are also plotted in Figure 9.

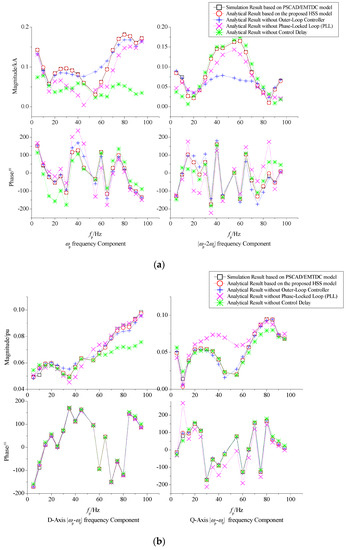
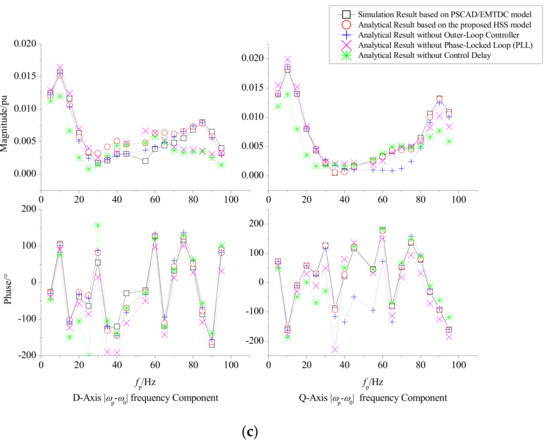
Figure 9. Simulation result and analytical result of disturbance components. (a) Valve-side current. (b) Output of the OCTC in inner-loop controller. (c) Output of the CCSC in inner-loop controller.

It could be concluded from Figure 9 that the analytical results based on the complete control structure is consistent with the simulation result in PSCAD/EMTDC. The P/Q outer-loop controller, the PLL and the control delay all play an important role in the accuracy of the analytical results. It indicates that it is necessary to consider the influence of the P/Q outer-loop controller, the PLL and the control delay when analyzing the disturbance response characteristics of the MMC.

In addition, it is noted that when the AC-side voltage of the MMC has one disturbance component of single frequency, there will appear two main disturbance components in its output current, whose frequencies are complementary with twice the fundamental frequency. It indicates that there exists frequency coupling effect among disturbance components, but the cause of frequency coupling effect needs to be further analyzed.

5.3. Oscillation Analysis

There would appear an unstable oscillation phenomenon in the output power of the MMC, when the outer circuit in test system is adjusted, as shown in Figure 10.

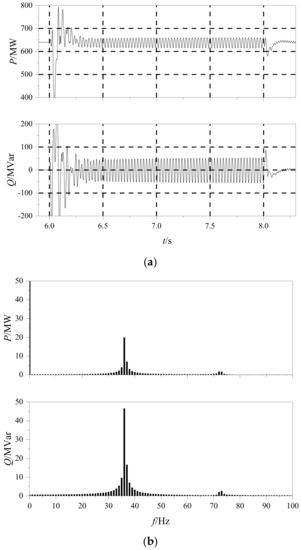
Figure 10. Oscillation phenomenon in output power. (a) Time-domain waveform. (b) Frequency spectrum.

As plotted Figure 10, there exists one oscillation mode in test system, whose oscillation frequency is about 36 Hz.

To investigate the cause of the unstable oscillation, the AC-side impedance characteristics of the MMC are analyzed, based on the proposed disturbance-state HSS model. The AC-side impedance characteristics are plotted in Figure 11.

Figure 11. AC-side impedance characteristics of the MMC (Z_MMC) and the outer circuit (Z_SYS).

As shown in Figure 11, there exists obvious negative resistance effect in the AC-side impedance of the MMC, which is in the frequency range of 7 Hz–13 Hz and 27 Hz–75 Hz. Moreover, the MMC has one resonance frequency point of 13 Hz with the outer circuit, which is close to the complementary frequency of the oscillation frequency of output power. When the positive resistance of the electrical network is lower than the negative resistance of power electronic equipment in a certain frequency range, there would appear unstable oscillation phenomena if the resonance frequency lies in this frequency range [27]. Therefore, the resonance of the MMC with its outer circuit is the main cause of this oscillation phenomenon, and the negative resistance effect causes the instability of this oscillation phenomenon.

6. Conclusions

Considering the complete control structure, the disturbance-state HSS model of the MMC are established based on the HSS method. On its basis, the AC-side impedance characteristics of the MMC could be analyzed, and the cause of the unstable oscillation could be investigated. Finally, the main conclusions of this paper are listed as follows:

(1)

By the time-domain simulation with PSCAD/ EMTDC, the analytical disturbance-state HSS model of the MMC proposed in this paper is verified. Moreover, the oscillation analysis results indicate that the proposed model could be applied to analyzing the oscillation risk of power system with the MMC.

(2)

Under P/Q control mode, the AC-side impedance of the MMC has certain negative resistance effect in the 1 Hz-100 Hz frequency range. It would cause the instability of resonance mode. Therefore, the negative resistance effect of the MMC should be taken much attention in the grid-connection planning stage.

(3)

When the AC-side voltage of the MMC has one disturbance component of single frequency, there will appear two main disturbance components in its output current, whose frequencies are complementary on twice the fundamental frequency. It indicates that there exists frequency coupling effect among disturbance components, but the cause of frequency coupling effect needs to be further analyzed in the future work.