The Sensitivity of an Electro-Thermal Photovoltaic DC–DC Converter Model to the Temperature Dependence of the Electrical Variables for Reliability Analyses
Abstract
1. Introduction
2. Electro-Thermal Model of the Photovoltaic DC/DC Converter
2.1. Electrical
2.2. Thermal
2.3. ElectroThermal Coupling
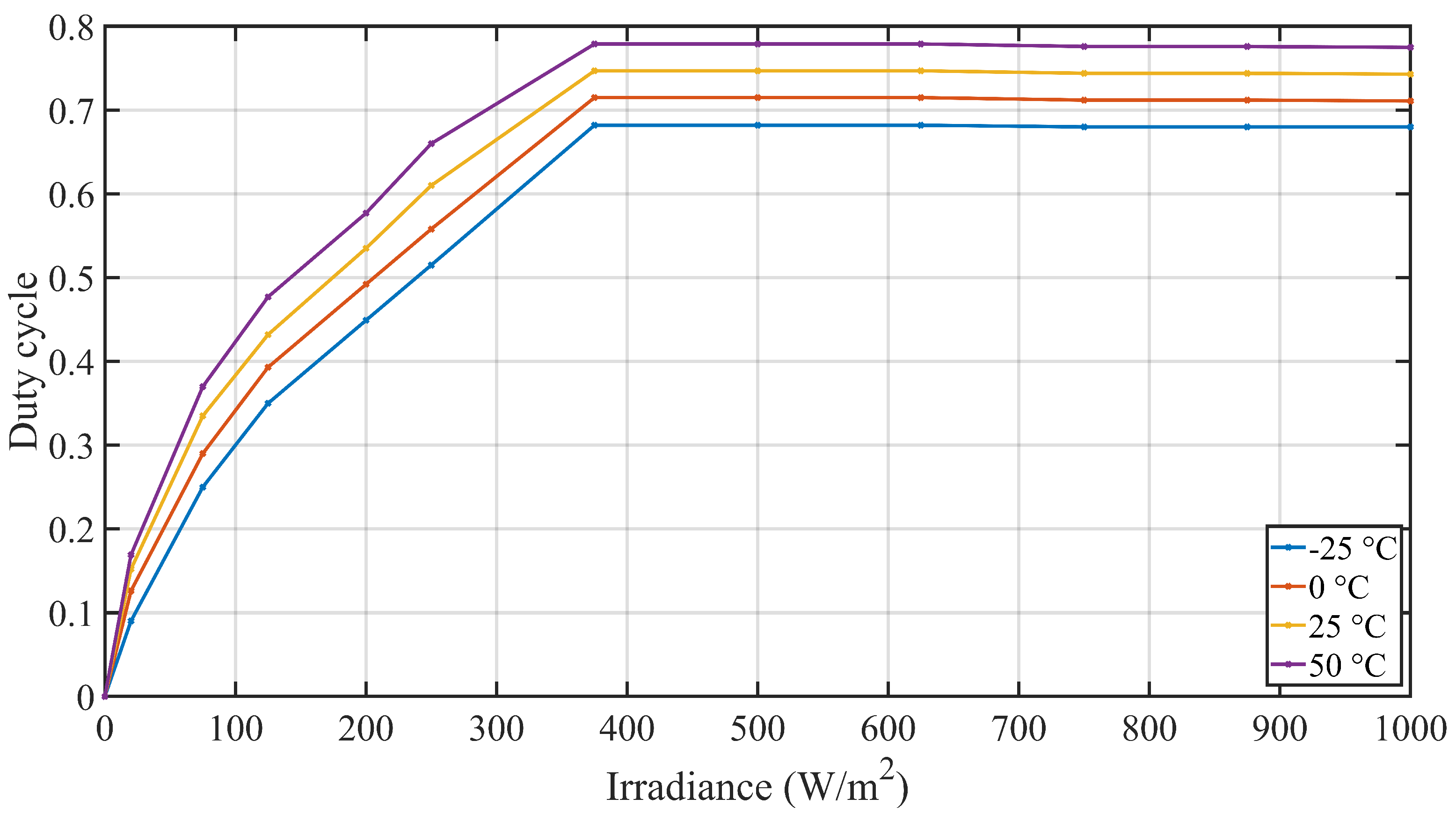
2.4. Maximum Power Point Tracking
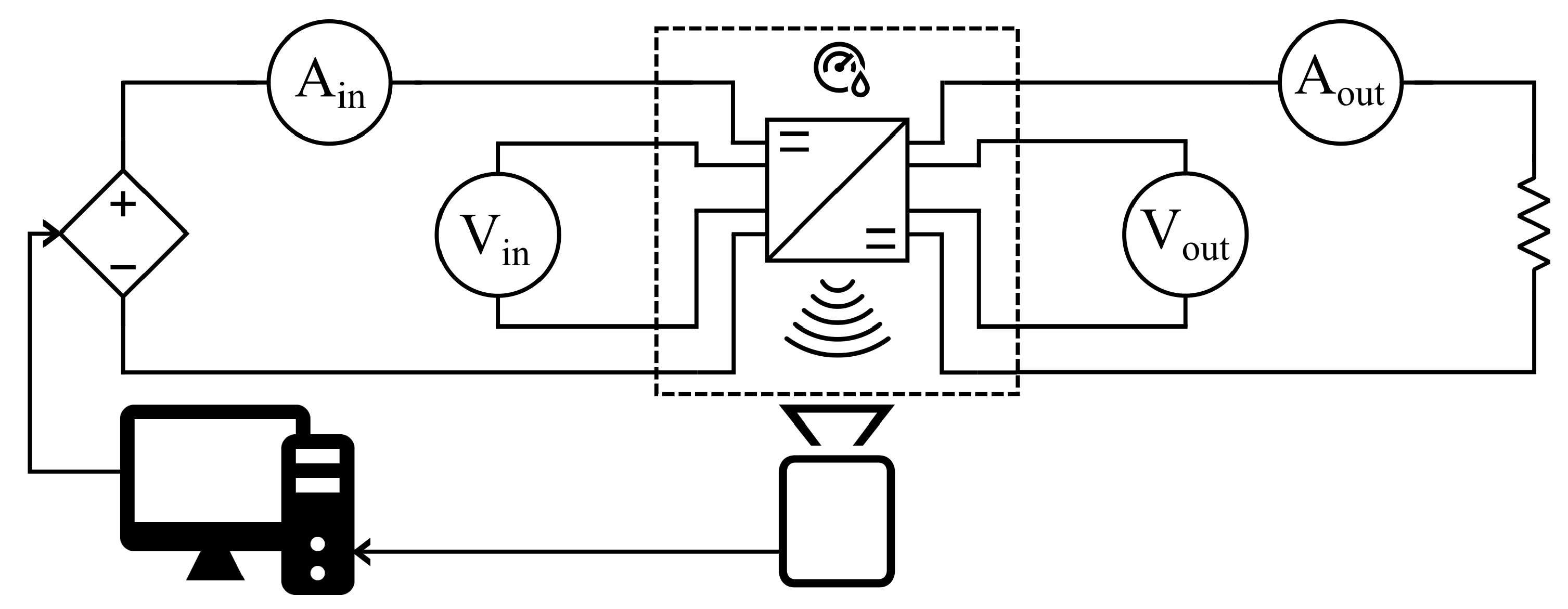
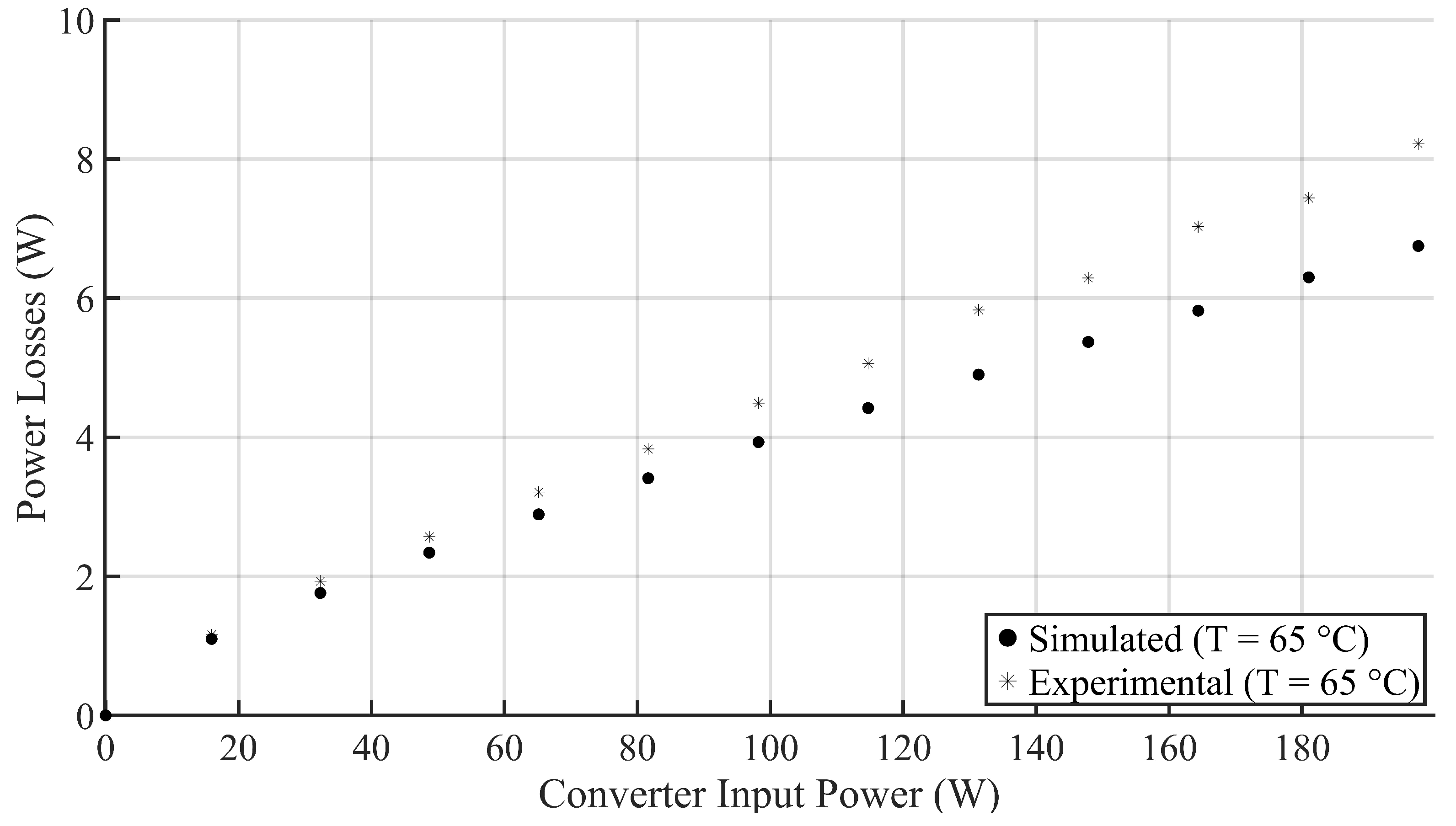
3. Experimental Fine-Tuning and Validation of the Electro-Thermal Model
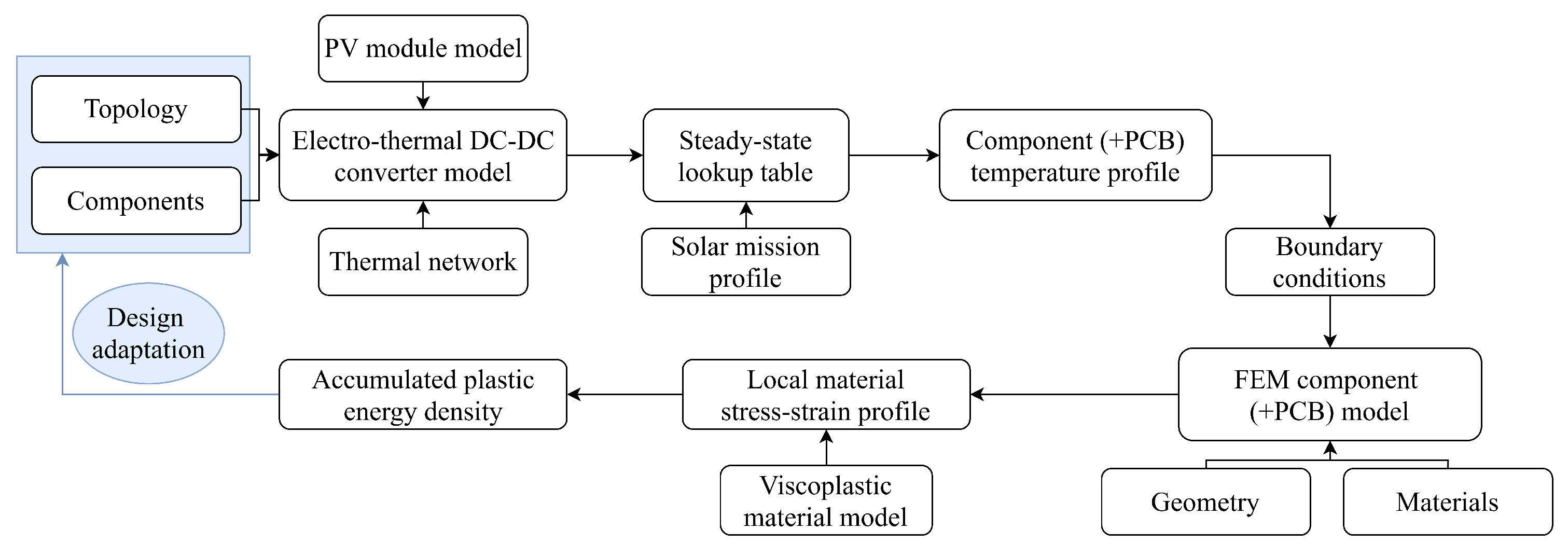
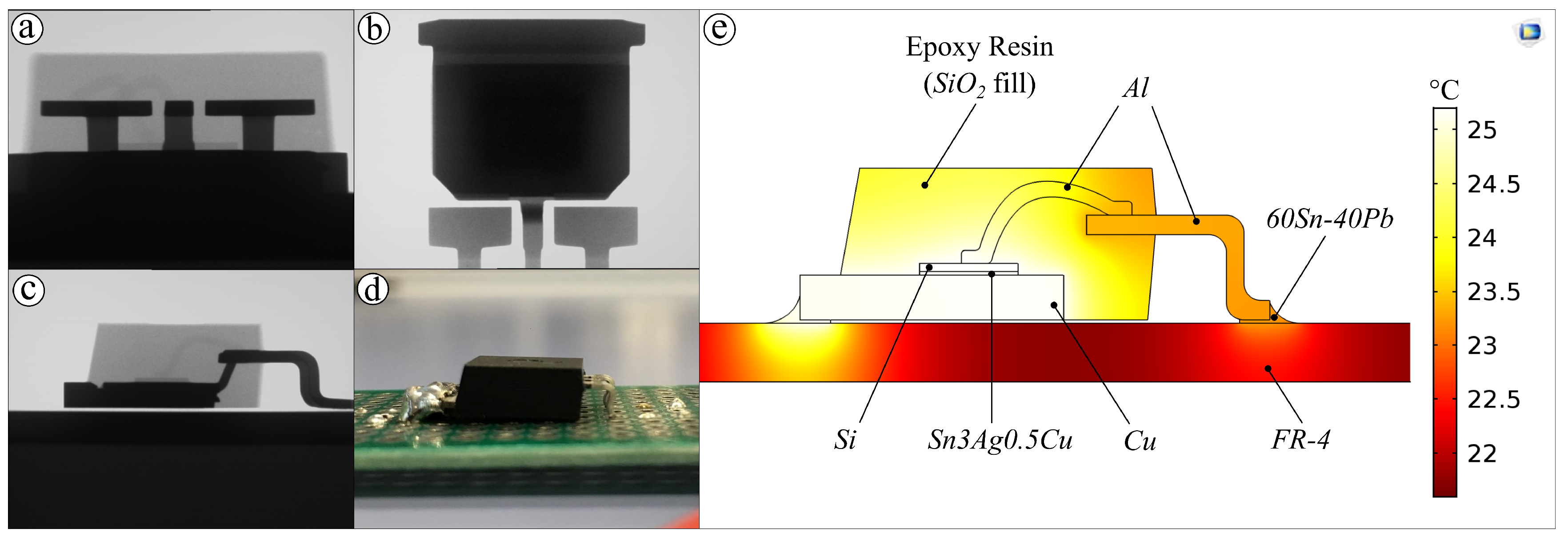
4. Constructing A FEM MOSFET Model
5. Sensitivity Analysis of the Electro-Thermal Model to the Temperature Dependent Electrical Variables
5.1. Capacitor
5.2. Photovoltaic Module
5.3. Inductor
5.4. MOSFET
5.5. Diode
5.6. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International Energy Agency. 2019 Snapshot of Global PV Markets. Available online: https://www.researchgate.net/publication/332606669_2019_-_Snapshot_of_Global_Photovoltaic_Markets (accessed on 18 February 2020).
- Jäger-Waldau, A. PV Status Report 2019; Publications Office of the European Union: Brussels, Belgium, 2019. Available online: https://publications.jrc.ec.europa.eu/repository/handle/JRC118058 (accessed on 26 February 2020).
- The International Renewable Energy Agency. Renewable Energy Market Analysis: GCC 2019; International Renewable Energy Agency (IRENA): Abu Dhabi, UAE, 2019; Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2019/Jan/IRENA_Market_Analysis_GCC_2019.pdf (accessed on 22 February 2020).
- The International Renewable Energy Agency. Renewable Power Generation Costs in 2017; International Renewable Energy Agency (IRENA): Abu Dhabi, UAE; Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2019/Jan/IRENA_Market_Analysis_GCC_2019.pdf (accessed on 1 March 2020).
- Moore, L.; Post, H. Five years of operating experience at a large, utility-scale photovoltaic generating plant. Prog. Photovolt. Res. Appl. 2008, 16, 249–259. [Google Scholar] [CrossRef]
- Reigosa, P.D.; Wang, H.; Yang, Y.; Blaabjerg, F. Prediction of bond wire fatigue of IGBTs in a PV inverter under long-term operation. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 3052–3059. [Google Scholar] [CrossRef]
- Wang, N.; Cotton, I.; Evans, K. Impact of Thermal Cycling in Humid Environments on Power Electronic Modules. IEEE Trans. Compon. Packag. Manuf. Technol. 2012, 2, 1085–1091. [Google Scholar] [CrossRef]
- GopiReddy, L.; Tolbert, L.; Ozpineci, B. Power Cycle Testing of Power Switches: A Literature Survey. IEEE Trans. Power Electron. 2015, 30, 2465–2473. [Google Scholar] [CrossRef]
- Smet, V.; Forest, F.; Huselstein, J.; Richardeau, F.; Khatir, Z.; Lefebvre, S.; Berkani, M. Ageing and Failure Modes of IGBT Modules in High-Temperature Power Cycling. IEEE Trans. Ind. Electron. 2011, 58, 4931–4941. [Google Scholar] [CrossRef]
- Khazaka, R.; Mendizabal, L.; Henry, D.; Hanna, R. Survey of High-Temperature Reliability of Power Electronics Packaging Components. IEEE Trans. Power Electron. 2015, 30, 2456–2464. [Google Scholar] [CrossRef]
- Liu, Y. Power Electronic Packaging: Design, Assembly Process, Reliability, and Modeling; Springer: New York, NY, USA, 2012. [Google Scholar]
- Yang, S.; Xiang, D.; Bryant, A.; Mawby, P.; Ran, L.; Tavner, P. Condition Monitoring for Device Reliability in Power Electronic Converters: A Review. IEEE Trans. Power Electron. 2010, 25, 2734–2752. [Google Scholar] [CrossRef]
- Ye, X.; Chen, C.; Wang, Y.; Zhai, G.; Vachtsevanos, G.J. Online Condition Monitoring of Power MOSFET Gate Oxide Degradation Based on Miller Platform Voltage. IEEE Trans. Power Electron. 2017, 32, 4776–4784. [Google Scholar] [CrossRef]
- Kozak, J.P.; Ngo, K.D.; DeVoto, D.J.; Major, J.J. Impact of Accelerated Stress-Tests on SiC MOSFET Precursor Parameters. In Proceedings of the 2018 Second International Symposium on 3D Power Electronics Integration and Manufacturing (3D-PEIM), College Park, MD, USA, 25–27 June 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Bormanis, O.; Ribickis, L. Accelerated Life Testing in Reliability Evaluation of Power Electronics Assemblies. In Proceedings of the 2018 IEEE 59th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 12–13 November 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Zhou, D.; Sangwongwanich, A.; Wang, H. Design for reliability in renewable energy systems. In Proceedings of the 2017 International Symposium on Power Electronics (Ee), Novi Sad, Serbia, 19–21 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Van De Sande, W.; Ravyts, S.; Sangwongwanich, A.; Manganiello, P.; Yang, Y.; Blaabjerg, F.; Driesen, J.; Daenen, M. A mission profile-based reliability analysis framework for photovoltaic DC-DC converters. Microelectron. Reliab. 2019, 100, 113383. [Google Scholar] [CrossRef]
- Ye, H.; Lin, M.; Basaran, C. Failure modes and FEM analysis of power electronic packaging. Finite Elem. Anal. Des. 2002, 38, 601–612. [Google Scholar] [CrossRef]
- Yang, Y.; Sangwongwanich, A.; Blaabjerg, F. Design for Reliability of Power Electronics for Grid-Connected Photovoltaic Systems. CPSS Trans. Power Electron. Appl. 2016, 1, 92–103. [Google Scholar] [CrossRef]
- Menozzi, R.; Cova, P.; Delmonte, N.; Giuliani, F.; Sozzi, G. Thermal and electro-thermal modeling of components and systems: A review of the research at the University of Parma. Facta Univ. Ser. Electron. Energetics 2015, 28, 325–344. [Google Scholar] [CrossRef]
- Shahjalal, M.; Lu, H.; Bailey, C. A review of the computer based simulation of electro-thermal design of power electronics devices. In Proceedings of the 20th International Workshop on Thermal Investigations of ICs and Systems, Greenwich, London, UK, 24–26 September 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Albarbar, A.; Batunlu, C. Thermal Analysis of Power Electronics: Review. In Thermal Analysis of Power Electronic Devices Used in Renewable Energy Systems; Springer International Publishing: Cham, Switzerland, 2018; pp. 19–47. [Google Scholar] [CrossRef]
- Li, F.; Hao, R.; Lei, H.; Zhang, X.; You, X. The Influence of Parasitic Components on LLC Resonant Converter. Energies 2019, 12, 4305. [Google Scholar] [CrossRef]
- Rekioua, D.; Matagne, E. Optimization of Photovoltaic Power Systems: Modelization, Simulation and Control; Green Energy and Technology; Springer: London, UK; New York, NY, USA, 2012; OCLC: ocn756595412. [Google Scholar]
- Batunlu, C.; Musallam, M. 3D thermal model of power electronic conversion systems for wind energy applications. In Proceedings of the IEEE Global Humanitarian Technology Conference (GHTC), San Jose, CA, USA, 10–13 October 2014; pp. 369–376. [Google Scholar] [CrossRef]
- Infineon. Transient Thermal Measurements and Thermal Equivalent Circuit Models; Application Report AN 2015-10; Infineon Technologies AG: Neubiberg, Germany, 2018. [Google Scholar]
- Ravyts, S.; Vecchia, M.D.; Zwysen, J.; van den Broeck, G.; Driesen, J. Study on a cascaded DC-DC converter for use in building-integrated photovoltaics. In Proceedings of the 2018 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 8–9 February 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Künzi, R. Thermal design of power electronic circuits. In CERN Accelerator School: Power Converters; INSPIRE: Baden, Switzerland, 2014; pp. 311–327. [Google Scholar] [CrossRef]
- Texas Instruments. AN-1520 A Guide to Board Layout for Best Thermal Resistance for Exposed Packages; Application Report SNVA183B; Texas Instruments Incorporated: Dallas, TX, USA; Available online: http://www.ti.com/lit/an/snva183b/snva183b.pdf?ts=1591212046276 (accessed on 7 March 2020).
- Graovac, D.; Pürschel, M.; Kiep, A. MOSFET Power Losses Calculation Using the Data-Sheet Parameters. Available online: https://application-notes.digchip.com/070/70-41484.pdf (accessed on 10 March 2020).
- Texas Instruments. AN-2020 Thermal Design By Insight, Not Hindsight. Application Report SNVA419C. Available online: http://www.ti.com/lit/an/snva419c/snva419c.pdf?ts=1591212214437 (accessed on 17 March 2020).
- Rezk, H.; Eltamaly, A.M. A comprehensive comparison of different MPPT techniques for photovoltaic systems. Sol. Energy 2015, 112, 1–11. [Google Scholar] [CrossRef]
- Stoyanov, S.; Bailey, C.; Desmulliez, M. Optimisation modelling for thermal fatigue reliability of lead-free interconnects in fine-pitch flip-chip packaging. Solder. Surf. Mt. Technol. 2009, 21, 11–24. [Google Scholar] [CrossRef]
- Anderson, J.M.; Cox, R.W. On-line condition monitoring for MOSFET and IGBT switches in digitally controlled drives. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 3920–3927. [Google Scholar] [CrossRef]
- Ruffilli, R.; Berkani, M.; Dupuy, P.; Lefebvre, S.; Weber, Y.; Legros, M. In-depth investigation of metallization aging in power MOSFETs. Microelectron. Reliab. 2015, 55, 1966–1970. [Google Scholar] [CrossRef][Green Version]
- Khong, B.; Legros, M.; Tounsi, P.; Dupuy, P.; Chauffleur, X.; Levade, C.; Vanderschaeve, G.; Scheid, E. Characterization and modelling of ageing failures on power MOSFET devices. Microelectron. Reliab. 2007, 47, 1735–1740. [Google Scholar] [CrossRef]
- Ruffilli, R.; Berkani, M.; Dupuy, P.; Lefebvre, S.; Weber, Y.; Warot-Fonrose, B.; Marcelot, C.; Legros, M. Aluminum metallization and wire bonding aging in power MOSFET modules. Mater. Today Proc. 2018, 5, 14641–14651. [Google Scholar] [CrossRef]
- Siow, K.S. (Ed.) Die-Attach Materials for High Temperature Applications in Microelectronics Packaging: Materials, Processes, Equipment, and Reliability; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Li, T.; Zhao, B.; Lu, X.; Xu, H.; Zou, D. A Comparative Study on Johnson Cook, Modified Zerilli–Armstrong, and Arrhenius-Type Constitutive Models to Predict Compression Flow Behavior of SnSbCu Alloy. Materials 2019, 12, 1726. [Google Scholar] [CrossRef]
- Zein, H.; Irfan, O. Surface Roughness Investigation and Stress Modeling by Finite Element on Orthogonal Cutting of Copper. Metals 2018, 8, 418. [Google Scholar] [CrossRef]
- Qin, F.; An, T.; Chen, N. Strain rate effect and Johnson-Cook models of lead-free solder alloys. In Proceedings of the 2008 International Conference on Electronic Packaging Technology & High Density Packaging, Shanghai, China, 28–31 July 2008; pp. 1–7. [Google Scholar] [CrossRef]
- Bressan, J.D.; Lopez, K. New constitutive equation for plasticity in high speed torsion tests of metals. Int. J. Mater. Form. 2008, 1, 213–216. [Google Scholar] [CrossRef]







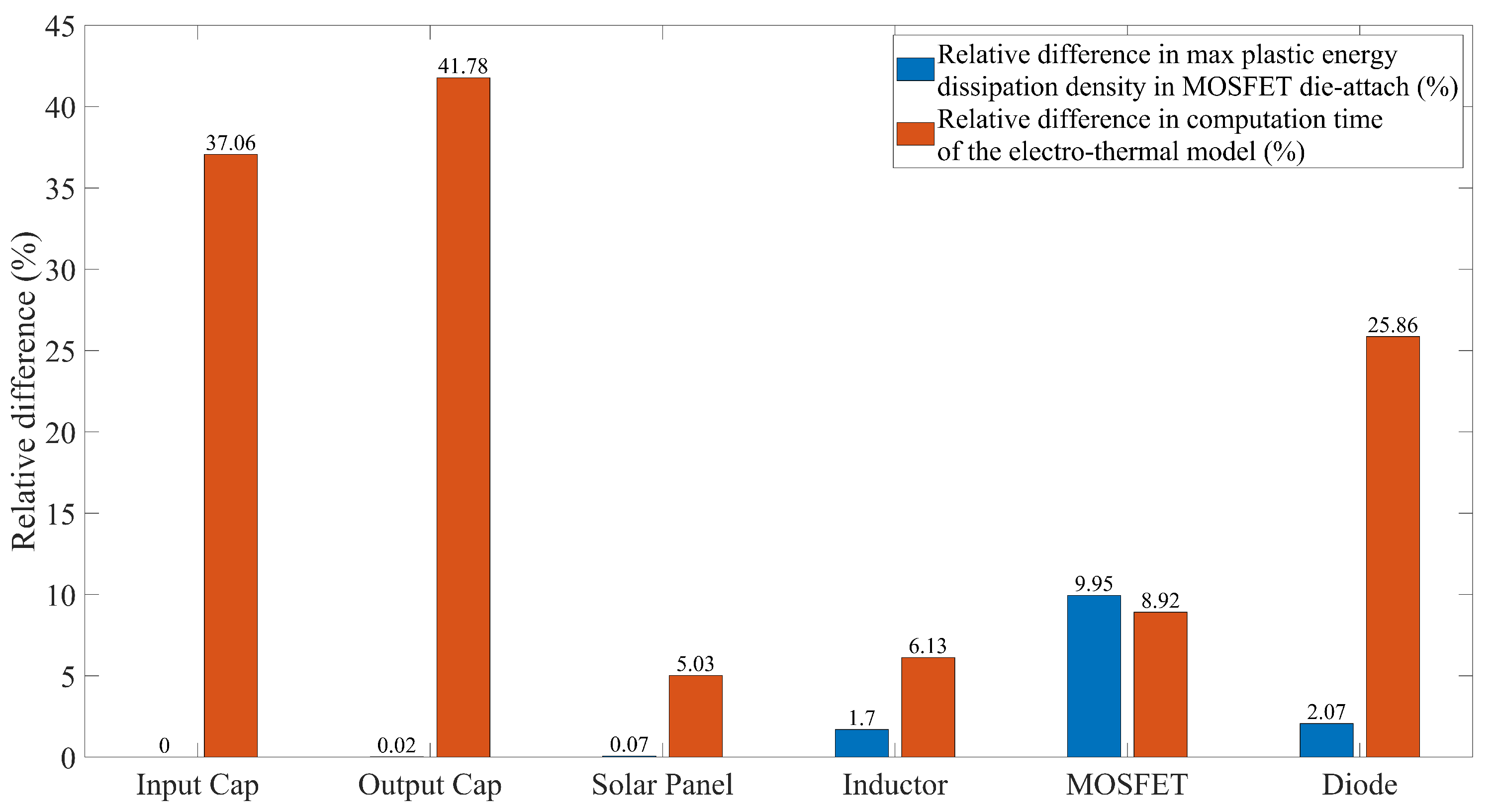
| Component | Type | Value | Series Resistance |
|---|---|---|---|
| Solar panel PV | Kyocera Solar | ||
| KC200GT | |||
| Input Capacitor Cin () | AVX MLCC | ||
| 12061C225KAT2A | |||
| Inductor L1, L2, L3 | Bourns | ||
| SRP1770TA-101M | |||
| MOSFET S1, S2, S3 | Infineon | ||
| IPB320N20N3 | |||
| Diode D1, D2, D3 | Vishay | ||
| VS-10CSH02HM3 | |||
| Output Capacitor Cout () | KEMET MLCC | ||
| C1206C154K2RACTU |
| Thermal Resistance | Value (K/W) | Thermal Resistance | Value (K/W) | Thermal Resistance | Value (K/W) |
|---|---|---|---|---|---|
| Inductor core to case | Inductor case to PCB | Inductor case to air | |||
| Diode junction to case | Diode case to PCB | Diode case to air | |||
| Input capacitor hotspot to case | Input capacitor case to PCB | Input capacitor case to air | |||
| Output capacitor hotspot to case | output capacitor case to PCB | Output capacitor case to air | |||
| MOSFET junction to case | MOSFET case to ambient | PCB to air |
| Ambient Temperature | MOSFET Max. | Diode Max. | Input Capacitor | Output Capacitor | Inductor Max. |
|---|---|---|---|---|---|
| (C) | Error (C) | Error (C) | Max. Error (C) | Max. Error (C) | Error (C) |
| 15 | |||||
| 35 | |||||
| 65 |
| Material | Young’s Modulus | Poisson’s | Thermal Conductivity | Coefficient of Thermal |
|---|---|---|---|---|
| (GPa) | Ratio | (W/mK) | Expansion (10−6/K) | |
| Epoxy resin ( fill) | 13 | |||
| 170 | ||||
| 70 | ||||
| 55 | ||||
| 110 | ||||
| 22 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van De Sande, W.; Ravyts, S.; Alavi, O.; Nivelle, P.; Driesen, J.; Daenen, M. The Sensitivity of an Electro-Thermal Photovoltaic DC–DC Converter Model to the Temperature Dependence of the Electrical Variables for Reliability Analyses. Energies 2020, 13, 2865. https://doi.org/10.3390/en13112865
Van De Sande W, Ravyts S, Alavi O, Nivelle P, Driesen J, Daenen M. The Sensitivity of an Electro-Thermal Photovoltaic DC–DC Converter Model to the Temperature Dependence of the Electrical Variables for Reliability Analyses. Energies. 2020; 13(11):2865. https://doi.org/10.3390/en13112865
Chicago/Turabian StyleVan De Sande, Wieland, Simon Ravyts, Omid Alavi, Philippe Nivelle, Johan Driesen, and Michaël Daenen. 2020. "The Sensitivity of an Electro-Thermal Photovoltaic DC–DC Converter Model to the Temperature Dependence of the Electrical Variables for Reliability Analyses" Energies 13, no. 11: 2865. https://doi.org/10.3390/en13112865
APA StyleVan De Sande, W., Ravyts, S., Alavi, O., Nivelle, P., Driesen, J., & Daenen, M. (2020). The Sensitivity of an Electro-Thermal Photovoltaic DC–DC Converter Model to the Temperature Dependence of the Electrical Variables for Reliability Analyses. Energies, 13(11), 2865. https://doi.org/10.3390/en13112865





