Abstract
Dredge pumps are usually operated at part-load conditions, in which the low-solidity centrifugal impeller could experience large internal energy dissipation, related to flow separation and vortices. In this study, SST k-ω and SAS-SST turbulence models were used, in steady and unsteady simulations, for a low-head centrifugal pump with a three-bladed impeller. The main focus of the present work was to investigate the internal energy dissipation in rotating an impeller at part-load operating conditions, related to flow separation and stall. The unsteady nature of these operating conditions was investigated. Performance experiments and transient wall pressure measurements were conducted for validation. A methodology for internal energy dissipation analysis has been proposed; and the unsteady pressure fluctuations were analyzed in the rotating impeller. The internal power losses in the volute and the impeller were mostly found in the centrifugal pump. The rotating stall phenomenon occurred with flow separation and detachment at the part-load operating condition, leading to a dissipation of the internal energy in the impeller. The rotating impeller experienced pressure fluctuations with low frequencies, at part-load operating conditions, while in the design operating condition only experienced rotating frequency.
1. Introduction
Low-head centrifugal pumps are widely used in small-scale dredging equipment, for delivering slurry. For the slurry transportation, the centrifugal impellers usually feature three to six blades with a large expansion ratio of the flow passages. Most studies on slurry pumps were conducted on pumps with four to six impeller blades [1]. The asymmetric impeller structure with fewer blades had an important influence on the performance and pressure fluctuation of the pumps. For single-bladed sewage pump, Nishi et al. [2] performed numerical simulations and experiments and detected the asymmetric pressure and velocity distribution. Pei et al. [3] investigated the uneven distribution of pressure fluctuation intensity in the single-bladed impeller and volute, using the CFD method. Melzer et al. [4] studied the transient pressure in the volute, numerically and experimentally. The pressure indicated a significant periodicity with the rotation of the impeller. In regards to the three-bladed dredge pumps, current research has mainly focused on the wear characteristics of solid and liquid flow [5,6]. Therefore, it is still necessary to investigate the performance and energy loss of dredge pumps, for geometry and operating parameter modifications in the design and optimization process.
The energy loss in the centrifugal pump could be divided into flow dissipation, disk friction, and discharge leakage loss. Kara Omar et al. [7] calculated the losses through empirical and semi-empirical models, and verified them with experimental results. El-Naggar [8] conducted an experimental one-dimensional flow analysis and predicted the pump performance in a dimensionless form. Klas et al. [9] performed simulations on a centrifugal pump and investigated the energy loss in different flow components, to detect the influence of the component geometry. These studies focused on the whole energy transformation in flow components, without a detailed loss analysis.
The inner flow characteristic was investigated as the energy loss reasons for centrifugal pumps. Posa et al. [10] investigated the streamline distribution on the impeller blade surface and found that a stall phenomenon developed near the impeller shroud. Zhang et al. [11] applied velocity vector distribution to detect the flow pattern near the volute tongue, and to discuss its effects on the efficiency fluctuation of a centrifugal pump. Barrio et al. [12] detected a counter-rotating vortex near the interface between the impeller and the volute, through velocity distribution. Pacot et al. [13] used the pressure distribution to explore the stall propagation mechanism. Asim et al. [14] applied the Q-criterion to illustrate that a secondary flow generated near the volute tongue, with an impact on the pump head. Miorini et al. [15] and Zhou et al. [16] adopted a vorticity study to investigate tip leakage flow and rotating stall, respectively, to describe the development of these unsteady flow phenomena and to prove their effects on pump performance. These methods are able to make apparent specific flow structures inside the centrifugal pump, and could assist the design and optimization of centrifugal pumps [17,18,19].
The quantity of energy loss related to these particular flow structures, needs to be investigated in details, at different operating conditions. Zheng et al. [20] applied an energy gradient function to describe the energy change rate, along streamlines, and argued that this function represented the turbulence intensity. More researchers were concentrated on the specific turbulent kinetic energy. Keller et al. [21] proposed a method of normalized turbulent kinetic energy, and argued that a high value of normalized turbulent kinetic energy corresponded to the flow detachment. Additionally, turbulent kinetic energy was used to make apparent flow separation [22], reversed flow [23] and impeller wake [24] inside the centrifugal pumps, and was linked directly to the energy loss [25]. Meanwhile, the reduction of specific turbulent kinetic energy has been proposed as a corroborative evidence to prove that the optimized pumps featured a better performance [26,27] and [28]. In fact, the production of specific turbulent kinetic energy has been linked to the energy transfer from the mean flow to the turbulent flow. However, the quantity of specific turbulent kinetic energy cannot directly represent the energy loss [29,30]. Therefore, an accurate method for the quantification of energy dissipation in centrifugal pumps, still needs to be investigated.
The specific speed NQE and the number of blades of the studied centrifugal pumps from the above-mentioned studies are summarized in Table 1. The discharge factor, specific energy factor and specific speed for the design operating condition, are defined by Equations (1)–(3).

Table 1.
Specific speed and number of blades of the study cases in the cited literature.
Pei et al. [3] studied a single-bladed pump with a high specific speed. Additionally, References [8,25] investigated the low-solidity centrifugal pump, however, both pumps had a low specific speed. In this study, a high-specific-speed dredge pump with a low-solidity centrifugal impeller was used. In the impeller, the blades were curved with a large ratio between the outlet and the inlet flow section. Low solidity pumps experience a complex unsteady flow phenomena inside the impeller at off-design operating conditions [31,32], such as, flow separation, rotating stall, and secondary flow. These phenomena have a negative impact on the efficiency and could generate pressure fluctuations and vibrations.
The internal energy dissipation at part-load operating conditions was the focus of this study. The causes for internal energy dissipation at part-load operating conditions were analyzed for their flow separation and stall phenomena in the three-bladed centrifugal impeller. Pressure fluctuation time and dominant frequency were further investigated to establish what comprised the unsteady characteristics of the pump.
This paper has been structured as follows: in Section 2, the case study has been presented; in Section 3, the numerical simulation setup, the experimental setup, as well as the internal energy dissipation methodology have been described; in Section 4, numerical simulating results have been validated with the help of the available experimental data, analysis on internal power loss in the simulating domains have been performed, and the results of the internal energy dissipation and pressure fluctuation have been presented; in Section 5, the analysis on numerical simulating results have been expressed; and finally, in Section 6, the conclusions of the present work have been provided.
2. Case Study
The studied case was an industrial pump and the impeller outlet diameter was 310 mm. The discharge and specific energy factors at the design operating conditions ( and ) were 0.16 and 4.15, respectively. The specific speed (NQE) of the pump was 0.14. The assembly drawing and computing domains of the centrifugal pump of the dredge pump are shown in Figure 1. The calculation domains included the suction pipe, the centrifugal impeller, front gap, pump-out vanes, the back gap, and the volute.
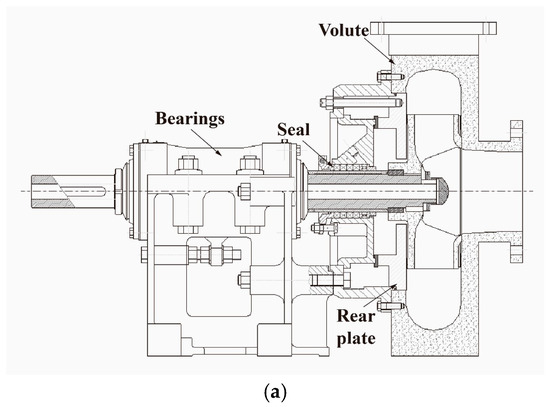
Figure 1.
Assembly drawing and computing domains of the centrifugal pump. (a) Cross-sectional assembly drawing of the centrifugal pump; (b) computing domains; and (c) meridional view of the computing domains.
3. Methodology
3.1. Governing Equations and Numerical Setup
The continuity equation:
The momentum equation:
The specific energy equation:
In which, C, Dij, h, htot, p, t, μ, ρ, and λt are velocity, strain rate tensor, specific enthalpy, specific total enthalpy, pressure, time, dynamic viscosity, density, and thermal conductivity, respectively. The physical property of water was regarded as a constant in numerical simulations.
The SST turbulence model [33] was used for the steady simulations, in which a switching function was used to combine the k-ω model with the k-ε model. The SST turbulence model was widely used in numerical simulations of pumps, with satisfying results [34,35,36]. The SAS–SST turbulence model [37] was used in the unsteady simulations, which included the von Karman length-scale in the turbulence eddy frequency equation. The SAS–SST model was proved to satisfactorily describe the unsteady flow patterns, especially with the complex flow phenomena at the off-design operating conditions [38,39,40]. To accommodate the streamline curvature and the rotating feature in the centrifugal impeller, curvature correction [41] was added as an advanced turbulence control [42].
Mesh sensitivity checks were conducted with five different meshes. The influence of the mesh amount on the head and efficiency at the design operating condition is shown in Figure 2.
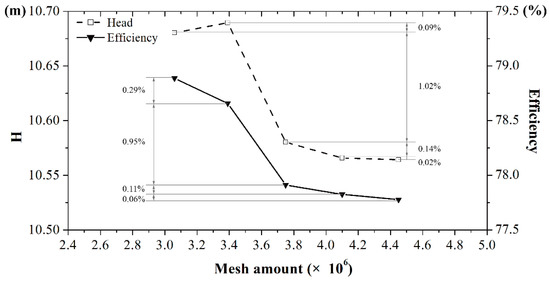
Figure 2.
Influence of mesh amount on the head and efficiency.
As the differences in head and efficiency in the last three meshes were less than 1%, the mesh set with 3.75 × 106 elements was utilized in the simulations, considering both the precision and the cost of calculation. The definitions of head H, power P, and efficiency η are as follows:
where Q is the discharge; Tt is the torque; Ain and Aout represent the inlet and outlet boundary, respectively. All of mesh elements were structural meshes, except for the impeller computing domain. The averaged y+ value in each domain was less than 130.
The mass flow rate boundary condition was set at the pipe inlet at an initial temperature of 25 °C. The inlet turbulence intensity was set as 5%. The outlet boundary at the volute outlet was set as the static pressure. The domains of the impeller and nine pump-out vanes were set as the rotating parts with the same rotation speed, while others were stationary. The wall boundary was set as smooth wall, no-slip, and adiabatic. The interface between the rotating and stationary domains corresponded to frozen rotor in steady simulations and to transient frozen rotor in unsteady simulations. The steady results were set as the initial flow field of unsteady simulations. The time step in unsteady simulations was 2 × 10−4 s, which was 1/300 of a rotating period.
Pressure signal was recorded in unsteady simulations. Monitor point arrangements in numerical simulations are shown in Table 2. The monitor points in the impeller were distributed at the pressure and suction sides of a flow passage. The cylindrical coordinates of the monitor points are shown in Figure 3.

Table 2.
Cylindrical coordinates of the monitor points.
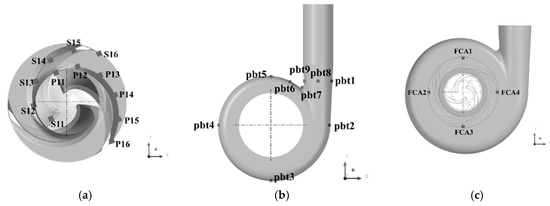
Figure 3.
Monitor point arrangements in the numerical simulations. (a) Impeller; (b) volute; and (c) front chamber.
3.2. Experimental Setup
The experimental setup for the centrifugal pump is shown in Figure 4. In the test bed, the mass flow rate was measured by a magnetic flowmeter (LDG-500S, Shanghai Guanghua Instrument Co., Ltd., Shanghai, China). The measurement uncertainty of the mass flow rate was ±0.2%. The flowmeter was installed between the two tanks, which is not shown in the picture. The torque was measured with a torque meter (JCZL2-500, Powerlink, Instrument Co., Ltd, Changsha, China) and the measurement uncertainty of the torque was ±0.5%. The pressure transmitter was V15712-HD1A1D7D (Newsruipu Instrument Co., Ltd, Zhengzhou, China) and the maximum error of the head was 1% of the measurement range. The pressure fluctuation sensor was CGYL-201 (Hefei Dekong Instruments Co., Ltd., Hefei, China) with a sampling frequency 4096 Hz. The monitor point set in the volute and the front gap was the same as that in numerical simulations. The shaft power was calculated by the torque difference between the torque measured by a torque meter and resistance torque from bearings, which was measured when the impeller was not installed on the shaft.
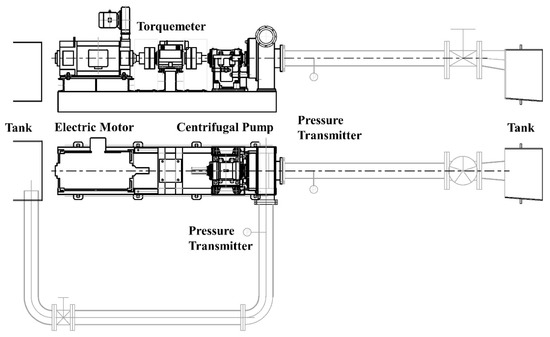
Figure 4.
Experimental setup of the centrifugal pump.
3.3. Energy Analysis Method
From the first law of thermodynamics, the total specific energy balance for the pump system yielded Equation (10). The gravitational potential energy change and the thermal radiation were ignored.
where e represents the specific internal energy; is the heat flux; and is the total stress tensor.
The local equation of the specific kinetic energy balance for the incompressible fluid could be derived from the momentum balance equation, as:
Substituting Equations (10) and (12), the time change rate of the specific internal energy could be expressed as:
According to the URANS method, time averaging was performed on Equation (13), in which, the time scale was larger than the turbulent time scale, but was much smaller than the time scale of mean flow 37. Equation (13) read as follows:
where T is the temperature; and λt is the thermal conductivity of the fluid. The items on the right side of Equation (14) describes the viscous dissipation, turbulent production, turbulent dissipation, and dissipation from heat transfer, respectively. Since the turbulent fluctuating flow parameters and T′ could not be obtained directly from the URANS simulations, the internal energy dissipation in the turbulent fluctuating flow needed to be expressed by mean flow components. Expressions and approximations from the previous research, based on the eddy viscosity model [43], were adopted.
Viscous dissipation rate:
Turbulent production rate:
Turbulent dissipation rate:
Dissipation rate from heat transfer:
where μt is the eddy viscosity; ε is the turbulence dissipation rate; and λeff is the effective thermal conductivity.
The internal energy dissipation rate was expressed as follows:
The distribution of the dissipated internal energy could explain the local energy transformation and could be related to the flow structures. The volumetric integration on the left hand of Equation (19), represents the internal power loss in the whole domain.
Since the internal energy dissipation near the wall could not be calculated accurately from the above-mentioned method, when y+ value was larger than 50 [44], an approximation for the internal power loss near the wall, was defined as Equation (20).
where τi is the wall shear stress vector component. The internal power loss could be expressed as:
For the purpose of comparing the internal power loss with the hydraulic power loss, the definition of the hydraulic power loss is described as Equation (22).
4. Results
4.1. Validation of Numerical Simulating Results
Since the centrifugal impeller was composed of three blades, steady simulations were conducted at three different clocking positions, between the impeller and the volute. The influence of the clocking positions between the three-bladed impeller and the volute on the head and power, varied at different operating conditions, see Figure 5. The result was consistent with the previous research on centrifugal pump [39]. The averaged results were regarded as the final results in the steady simulations. A comparison of the head and efficiency between the steady numerical simulations and the experimental results, are shown in Figure 6. There was a good quantitative agreement for the operating conditions near the design operating condition, while the difference was larger at the part and overload conditions. The maximum relative errors were less than 5% for the 13 operating conditions.
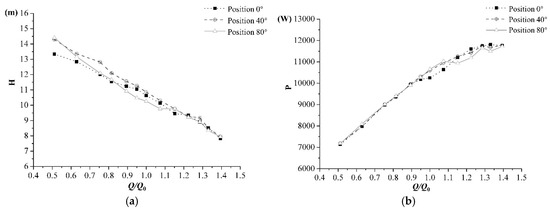
Figure 5.
The influence of clocking positions on the head and power at different operating conditions—(a) head; and (b) power.
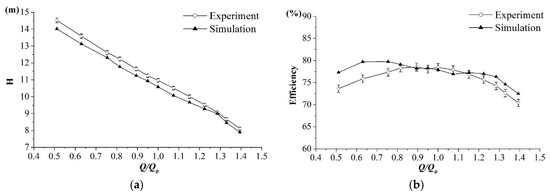
Figure 6.
Comparison of the head and efficiency, between the numerical simulations and experimental results—(a) head; and (b) efficiency.
The numerical simulation and experimental results of the pressure signal in the stationary volute and front gap were compared to verify the reliability of the unsteady simulations. The fast Fourier transform (FFT) method was applied to analyze the pressure signals. The pressure normalization cp was defined as Equation (23), in which the U2 is the rotating velocity at the impeller outlet [45]. Both, the time history and frequency domain of the monitor points pbt5 and FCA1, from the numerical and experimental results, at 1.0 × Q0 and 0.8 × Q0 operating conditions, are shown in Figure 7, where n represents the rotating frequency. In Figure 7a,c,e,g, it can be seen that there were three oscillations during one impeller revolution. In Figure 7b,d,f,h, the dominant frequency was the blade passing frequency as 3 × n. The pressure analysis from unsteady numerical simulation results can basically describe the periodical change of pressure fluctuations, while there exists differences in the pressure amplitudes.
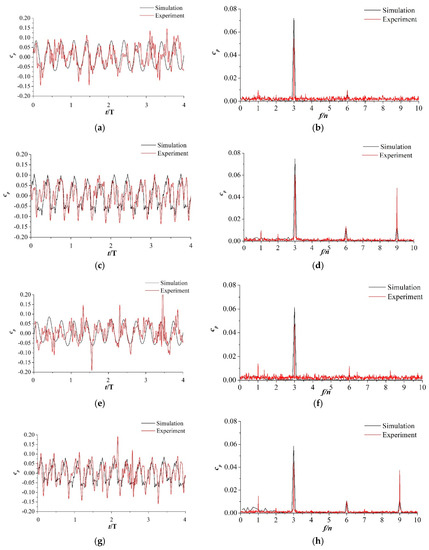
Figure 7.
Time history and frequency domain of the monitor points pbt5 and FCA1 from the numerical and experimental results (a) Time history (pbt5, 1.0 × Q0); (b) frequency domain (pbt5, 1.0 × Q0); (c) time history (FCA1, 1.0 × Q0); (d) frequency domain (FCA1, 1.0 × Q0); (e) time history (pbt5, 0.8 × Q0); (f) frequency domain (pbt5, 0.8 × Q0); (g) time history (FCA1, 0.8 × Q0); and (h) frequency domain (FCA1, 0.8 × Q0).
4.2. Internal Power Loss
The influence of the discharge on both the internal and hydraulic power losses, see Equations (21) and (22), are shown in Figure 8. With an increase in discharge, both, internal and hydraulic power losses increased. The internal power loss was in accordance with the hydraulic power loss. Near the design point, the difference between the internal power loss and the hydraulic power loss was small, while the difference was larger at the part and overload operating conditions. In general, the methodology mentioned above could be used to describe the internal energy dissipation inside the centrifugal pump.
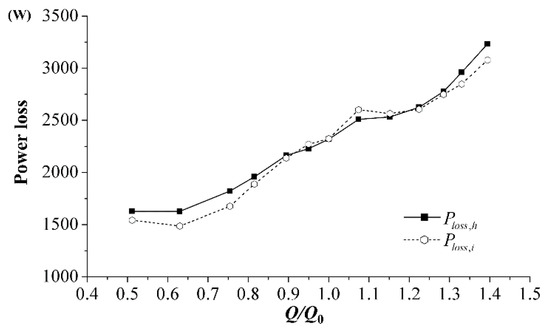
Figure 8.
Influence of the discharge on both the internal and hydraulic power losses.
Influence of the discharge on the internal power loss, in each flow component for the centrifugal pump is shown in Figure 9. The pump-out vanes and the impeller were regarded as a whole flow component. The internal power losses inside the volute and the impeller accounted for the most power loss in the pump, at all operating conditions, and increased with discharge. The internal power losses inside the other flow components were similar at different operating conditions.
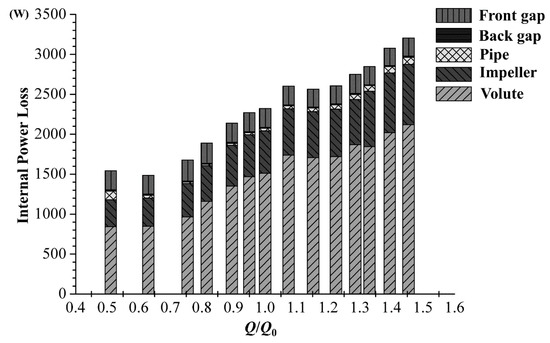
Figure 9.
Influence of the discharge on the internal power loss in each component for the centrifugal pump.
4.3. Local Internal Energy Dissipation in the Impeller
Relative flow velocity vectors on the cross-section A, near the impeller shroud (Z = 0.03 m) in the impeller, at the design and part-load operating conditions are shown in Figure 10. At the design operating condition, see Figure 10b, the flow in the impeller was smooth, without obvious flow separation or vortices. With a reduction in discharge, the vortex flow developed near the blade suction side. At 0.9 × Q0 operating condition, see Figure 10c, the vortex with low velocity was observed near the trailing edge of the blade suction side, in one flow passage. At 0.8 × Q0 and 0.7 × Q0 operating conditions, see Figure 10d,e, the vortex flow existed in two flow passages. At 0.6 × Q0 and 0.5 × Q0 operating conditions, see Figure 10f,g, the low-velocity vortices were apparent in all the three flow passages.
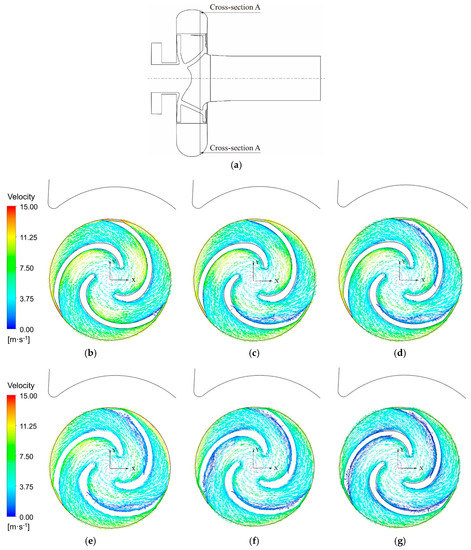
Figure 10.
Relative flow velocity vector on the cross-section A at the design and part-load operating conditions, (a) cross-section A; (b) 1.0 × Q0; (c) 0.9 × Q0; (d) 0.8 × Q0; (e) 0.7 × Q0; (f) 0.6 × Q0; and (g) 0.5 × Q0.
Unsteady results at the 1.0 × Q0, 0.8 × Q0, and 0.5 × Q0 operating conditions were applied to analyze the variation of internal energy dissipation rate distribution, in the rotating impeller. The distribution of internal energy dissipation rate on the cross-section A at six different instances of the 0.8 × Q0 operating condition, is shown in Figure 11. In each flow passage, the internal energy dissipation rate near the blade suction side was larger than that near the pressure side. The internal energy dissipation rate was the most significant near the blade suction side of Blade 2. The large internal energy dissipation region existed with an invariable relative position during the rotating period. However, the strength of the internal energy dissipation rate changed with the impeller rotation. The region with large internal energy dissipation rate also existed near the outlet of impeller, especially at the trailing edge of three impeller blades, as shown with the triangle marked in Figure 11b,d,f.
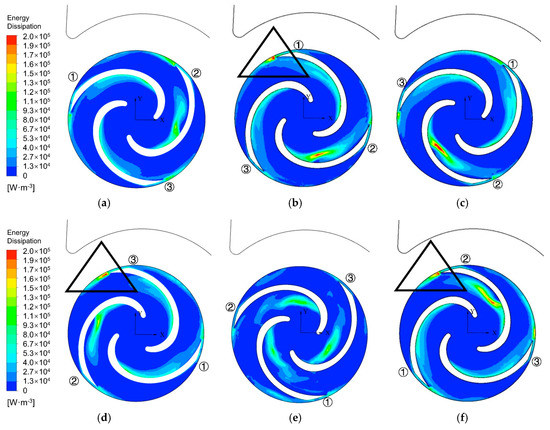
Figure 11.
Internal energy dissipation rate on the cross-section A at six different moments at 0.8 × Q0 operating condition (a) t = 0.84 s (0°); (b) t = 0.85 s (60°); (c) t = 0.86 s (120°); (d) t = 0.87 s (180°); (e) t = 0.88 s (240°); and (f) t = 0.89 s (300°).
The internal energy dissipation rate on the cross-section A at six different moments at 0.5 × Q0 operating condition is shown in Figure 12. In all flow passages, there were regions with large internal energy dissipation rate. The strength of the internal energy dissipation rate in each passage, varied with time. It is similar to the flow characteristic at the 0.8 × Q0 operating condition. Taking the flow structure between Blade 1 and Blade 3 as an example, when the impeller rotated from 0° to 60°, the internal energy dissipation strengthened. At the relative position of 120°, the flow separation and detachment developed with a large internal energy dissipation. With the impeller rotating, the detached flow propagated downstream to the trailing edge of the blade suction side and the internal energy dissipation rate decreased. Vortex flow with high internal energy dissipation rate occupied a large area of the flow passage, causing flow blockage. Compared with the 0.8 × Q0 operating condition, the internal energy dissipation near the impeller outlet was not significant.
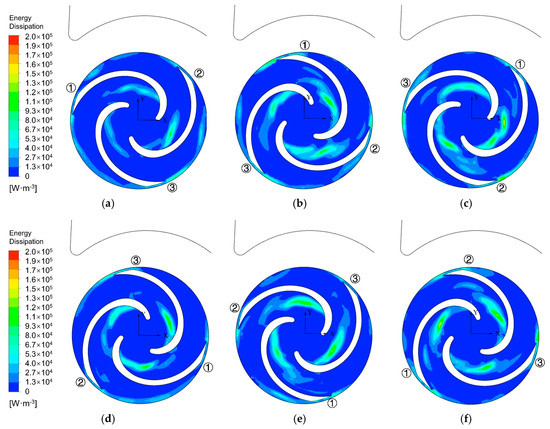
Figure 12.
Internal energy dissipation rate on the cross-section A at six different moments at 0.5 × Q0 operating condition. (a) t = 0.84 s (0°); (b) t = 0.85 s (60°); (c) t = 0.86 s (120°); (d) t = 0.87 s (180°); (e) t = 0.88 s (240°); (f) t = 0.89 s (300°).
When analyzing the contour of each source term in the internal energy dissipation rate, it was found that the distribution of each term was similar. The turbulent production and turbulent dissipation were the main causes for internal energy dissipation, in the centrifugal pump. It was in accordance with the characteristic of a high Reynold number flow [46].
4.4. Pressure Fluctuations in the Impeller
The pressure fluctuation in the rotating impeller was analyzed by the FFT method. The characteristic frequencies and amplitudes of pressure fluctuations at 1.0 × Q0, 0.8 × Q0, and 0.5 × Q0 operating conditions are listed in Table 3.

Table 3.
Characteristic frequencies and amplitudes of pressure fluctuations at 1.0 × Q0, 0.8 × Q0, and 0.5 × Q0 operating conditions.
The dominant frequency in the rotating impeller was n under 1.0 × Q0 and 0.8 × Q0 operating conditions, and the amplitudes decreased with a smaller discharge. In addition, a low-frequency like 0.5 × n was found with a relatively small amplitude at the 0.8 × Q0 operating condition.
At 0.5 × Q0 operating condition, the dominant frequency was 3 × n with the maximum amplitudes at the blade leading edge. The low-frequency component was more significant with a frequency of 0.7 × n. Its amplitude reached 40% of the amplitude of 3 × n, at monitor point P11 and was 38% of the amplitude of 3 × n at the monitor point S13.
The inverse fast Fourier transform (IFFT) method was applied to decompose the pressure signal of the monitor points P11 and S13 at the 0.5 × Q0 operating condition. Time history of the pressure signal and pressure components of frequencies, like 3 × n and 0.7 × n, at 0.5 × Q0 operating condition is shown in Figure 13. It was found that the pressure signal was mainly affected by the two pressure components of 3 × n and 0.7 × n. The pressure signal in monitor point P11 was more complex than the superposition of the two waves.
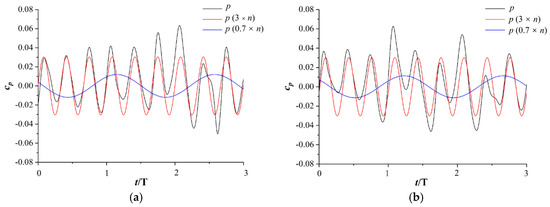
Figure 13.
Time history of pressure signal and pressure components of frequencies as 3 × n and 0.7 × n at 0.5 × Q0 operating condition. (a) Monitor point P11; and (b) monitor Point S13.
5. Discussion
In numerical simulations, the disk friction loss between the impeller hub and the back gap was not taken into account, since the back gap was regarded as a stationary flow domain. The wall friction loss and the discharge leaked through the seal were not considered. These factors led to the difference between the numerical and experimental results on performance. In experiments, the recording time of pressure signal was longer and the sampling time was shorter than that in numerical simulations, which had an impact on the difference of unsteady pressure fluctuations, between the numerical and experimental data.
When analyzing the integral internal energy dissipation, the flow irregularity at the off-design operating conditions had an influence on the error between the internal and hydraulic power losses, since the approximation was applied in the near-wall region. The internal energy dissipation inside the volute accounted for the most among the flow components. The section area in the volute of the centrifugal dredge pump was designed to be larger than that of other centrifugal pumps, to reduce the impact and friction from the slurry to the volute wall. There could be non-uniform flow structures inside the volute, causing internal energy dissipation.
With the discharge decreasing, the angle between the relative velocity and tangential velocity decreased and the angle of attack increased at the impeller inlet. The impeller experienced flow separation, near the blade suction. The vortices were more evident at the part-load operating conditions, with smaller discharge.
At 0.8 × Q0 operating condition, the internal energy dissipation rate of the vortex inside one flow passage changed with the rotating impeller. The vortex flow was related to the internal energy dissipation in the impeller and had an unsteady feature. This flow structure brought about a pressure fluctuation with a low-frequency, which is 50% of the rotating frequency. The amplitude was not obvious because the separating vortex flow only existed in one impeller passage and occupied a small part of the passage.
In addition, the internal energy dissipation was obvious near the trailing edge of the impeller blades. It was due to the rotor–stator interaction between the impeller and the volute. The wake flow of the rotating blades impacted the flow field downstream and led to an energy loss involving the viscous effect [47,48]. The rotor–stator interaction caused a pressure fluctuation with the rotating frequency n and the maximum amplitudes were found at the blade trailing edge.
At 0.5 × Q0 operating condition, the vortex detachment and propagation generated the internal energy dissipation and enhanced the unsteady characteristic. The periodical change of internal energy dissipation strength showed that the vortex structure was a form of rotating stall. The periodical separation and detachment made the low-frequency components more complicated, with higher amplitudes. The characteristic frequency was 70% of the rotating frequency, which corresponded with the feature of the rotating stall phenomenon, inside the impeller [49,50,51,52].
The stall blocked the impeller passage and reduced the flow interference downstream. The internal energy dissipation near the blade trailing edge was not evident. The rotating frequency was not significant in the pressure fluctuation spectra. The dominant frequency was the blade passing frequency, with the maximum amplitudes at the blade leading edge, which was caused by the rotor–stator interaction between the suction pipe and the impeller. Flow pattern on the midsection of the suction pipe at 0.5 × Q0 operating condition is shown in Figure 14. The reverse flow developed at the suction pipe outlet, which had an influence on the flow and the pressure fluctuations, downstream of the impeller. Therefore, the pressure fluctuation at the blade leading edge contained more complex frequency components.
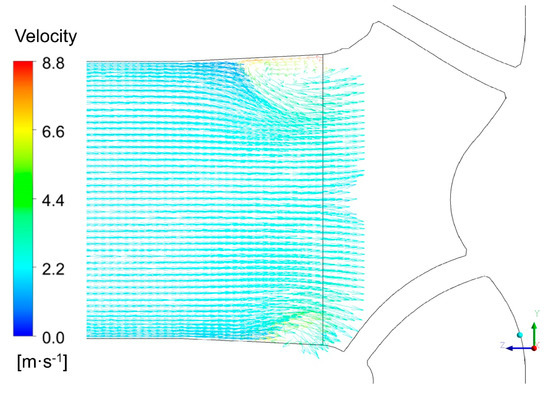
Figure 14.
Flow pattern on the midsection of the suction pipe at 0.5 × Q0 operating condition.
6. Conclusions
In this study, an investigation of the internal energy dissipation at part-load operating conditions has been presented for a low-head pump. This pump was a high-specific-speed dredge pump, with a low-solidity centrifugal impeller.
The numerical simulation domains included a suction pipe, a three-bladed centrifugal impeller, pump-out vanes, a volute, as well as the front and back side gaps. The flow was solved by steady and unsteady numerical simulations with consideration of the total energy balance equation. SST k-ω and SAS–SST turbulence models with curvature correction, were applied.
The performance and pressure fluctuations were compared between the numerical simulation results and the experimental results, to validate the simulations. The internal power losses were in accordance with the hydraulic power loss, at the design and off-design operating conditions. The internal power losses in the impeller and the volute account for the most among all flow components. For the volute, the large section area of the volute in the dredge pump, weakened the control of the volute on the flow.
The causes for the internal energy dissipation inside the impeller at the part-load operating conditions were the flow separation and the rotating stall. When discharge decreased from the design operating condition, flow separation generated near the impeller shroud and led to a periodical change of internal energy dissipation rate. At 0.5 × Q0 operating condition, the impeller experienced an unsteady rotating stall. The pressure fluctuation analysis made the unsteady characteristic of these flow phenomena apparent. At the 0.5 × Q0 operating condition, there was an obvious low-frequency of pressure fluctuation, like 0.7 × n in the impeller, which was related to the rotating stall phenomenon. The reverse flow near the interface between the suction pipe and the impeller had an influence on the flow patterns, downstream. The cause for the complicated pressure components at the blade leading edge was explained as the reverse flow at the pipe outlet.
Rotor–stator interaction between the impeller and the volute tongue caused internal energy dissipation rate near the blade trailing edge and brings about pressure fluctuation with rotating frequency. Since the stall occupied a large area in the flow passage at 0.5 × Q0 operating condition, the internal energy dissipation due to the rotor–stator interaction and pressure amplitudes of rotating frequency were not obvious. The blade passing frequency was the dominant frequency at the impeller inlet, due to the flow interaction between the pipe and the impeller.
Author Contributions
Conceptualization, X.Z., Y.L., Z.W., Y.X., and F.A.; methodology, X.Z., Z.W., and F.A.; formal analysis, X.Z., Z.W., and Y.X.; funding acquisition, Z.W.; investigation, X.Z., Y.L., and Z.W.; writing–original draft, X.Z.; writing–review & editing, X.Z., Y.L., Z.W., Y.X., and F.A.
Funding
This research was funded by the State Key Program of National Science of China, Grant Numbers 51876099 and 51439002; the National Natural Science Foundation of China, Grant Number 51279083; National Key Research and Development Program of China, Grant Number 2017YFC0404200; the Key Laboratory of Fluid and Power Machinery (Xihua University) Ministry of Education, Grant Number SZJJ-2018-125; and the Research Fund Program of State key Laboratory of Hydroscience and Engineering (sklhse-2019-E-01).
Acknowledgments
The support provided by the Chinese Scholarship Council (CSC) and Ecole polytechnique fédérale de Lausanne (EPFL) during the visit of Xiaoran Zhao at the EPFL Laboratory for Hydraulic Machines is acknowledged.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Nomenclature
| A | Area (m2) |
| Ain | Inlet boundary area (m2) |
| Aout | Outlet boundary area (m2) |
| cp | Pressure normalization (-) |
| Flow velocity (m·s−1) | |
| D | Impeller diameter (m) |
| Strain rate tensor (s−1) | |
| e | Specific internal energy (J·kg−1) |
| Specific energy factor at design operating condition (-) | |
| g | Gravitational acceleration (m·s−2) |
| h | Specific enthalpy (J·kg−1) |
| htot | Specific total enthalpy (J·kg−1) |
| H | Head (m) |
| H0 | Rated head (m) |
| Unit tensor (-) | |
| n | Rotating speed (s−1) |
| NQE | Specific speed (-) |
| p | Pressure (Pa) |
| P | Power (W) |
| Total stress tensor (Pa) | |
| Ploss,A | Internal power loss near wall (W) |
| Ploss,h | Hydraulic power loss (W) |
| Ploss,i | Internal power loss (W) |
| Heat flux (W·m−2) | |
| Q | Discharge (m3·s−1) |
| Q0 | Design discharge (m3·s−1) |
| Discharge factor at design operating condition (-) | |
| R | Radial coordinate (m) |
| t | Time (s) |
| T | Temperature (K) |
| Tt | Torque (N·m) |
| U2 | Circumferential velocity at the impeller outlet (m·s−1) |
| V | Volume (m3) |
| y+ | Dimensionless wall distance (-) |
| Z | Height coordinate (m) |
| Turbulence dissipation rate (m2·s−3) | |
| Effective thermal conductivity (W·K−1·m−1) | |
| Thermal conductivity (W·K−1·m−1) | |
| Efficiency (-) | |
| Dynamic viscosity (kg·m−1·s−1) | |
| Eddy viscosity (kg·m−1·s−1) | |
| Density (kg·m−3) | |
| Wall shear stress (Pa) | |
| Angular coordinate (°) |
References
- Tarodiya, R.; Gandhi, B. Hydraulic performance and erosive wear of centrifugal slurry pumps—A review. Powder Technol. 2017, 305, 27–38. [Google Scholar] [CrossRef]
- Nishi, Y.; Matsuo, N.; Fukutomi, J. A study on internal flow in a new type of sewage pump. J. Fluid Sci. Technol. 2009, 4, 648–660. [Google Scholar] [CrossRef]
- Pei, J.; Yuan, S.; Wang, W. Numerical analysis of pressure fluctuation intensity for a low-speed sewage centrifugal pump. Adv. Mech. Eng. 2014, 2014, 929672. [Google Scholar] [CrossRef]
- Steffen, M.; Tim, M.; Stephan, S.; Tobias, K.; Romuald, S. Experimental and numerical investigation of the transient characteristics and volute casing wall pressure fluctuations of a single-blade pump. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2018, 233, 280–291. [Google Scholar] [CrossRef]
- Munts, E.; Dasselaar, S.; Bugdayci, H.; Goeree, J.; Rhee, C. Numerical investigation of sand-water mixture behavior in a centrifugal dredge pump. In Proceedings of the 19th International Conference on Hydrotransport 2014, Golden, CO, USA, 24–26 September 2014; pp. 29–41. [Google Scholar]
- Peng, G.; Luo, Y.; Wang, Z. Research on wear properties of centrifugal dredge pump based on liquid-solid two-phase fluid simulations. IOP Conf. Ser. Mater. Sci. Eng. 2015, 72, 042048. [Google Scholar] [CrossRef]
- Kara Omar, A.; Khaldi, A.; Ladouani, A. Prediction of centrifugal pump performance using energy loss analysis. Aust. J. Mech. Eng. 2017, 15, 210–221. [Google Scholar] [CrossRef]
- El-Naggar, M.A. A one-dimensional flow analysis for the prediction of centrifugal pump performance characteristics. Int. J. Rotating Mach. 2013, 2013, 473512. [Google Scholar] [CrossRef]
- Klas, R.; Pochylý, F.; Rudolf, P. Analysis of novel low specific speed pump designs. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 012010. [Google Scholar]
- Posa, A.; Lippolis, A.; Balaras, E. Investigation of Separation Phenomena in a Radial Pump at Reduced Flow Rate by Large-Eddy Simulation. ASME J. Fluids Eng. 2016, 138, 121101. [Google Scholar] [CrossRef]
- Zhang, H.; Deng, S.; Qu, Y. Numerical investigation of periodic fluctuations in energy efficiency in centrifugal pumps at different working points. Energies 2017, 10, 342. [Google Scholar] [CrossRef]
- Barrio, R.; Parrondo, J.; Blanco, E. Numerical analysis of the unsteady flow in the near-tongue region in a volute-type centrifugal pump for different operating points. Comput. Fluids 2010, 39, 859–870. [Google Scholar] [CrossRef]
- Pacot, O.; Kato, C.; Guo, Y.; Yamade, Y.; Avellan, F. Large eddy simulation of the rotating stall in a pump-turbine operated in pumping mode at a part-load condition. ASME J. Fluids Eng. 2016, 138, 111102. [Google Scholar] [CrossRef]
- Asim, T.; Mishra, R. Large-Eddy-Simulation-based analysis of complex flow structures within the volute of a vaneless centrifugal pump. Sādhanā 2017, 42, 505–516. [Google Scholar]
- Miorini, R.L.; Wu, H.; Katz, J. The internal structure of the tip leakage vortex within the rotor of an axial waterjet pump. J. Turbomach. 2012, 134, 031018. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, F.; Yang, Z.; Mou, G. Investigation of rotating stall for a centrifugal pump impeller using various SGS models. J. Hydrodyn. Ser. B 2017, 29, 235–242. [Google Scholar] [CrossRef]
- Paul, G.; Rezaienia, A.; Avital, E.; Korakianitis, T. Machinability and optimization of shrouded centrifugal impellers for implantable blood pumps. J. Med. Devices 2017, 11, 021005. [Google Scholar] [CrossRef]
- Shigemitsu, T.; Fukutomi, J.; Wada, T.; Shinohara, H. Performance analysis of mini centrifugal pump with splitter blades. J. Therm. Sci. 2013, 22, 573–579. [Google Scholar] [CrossRef]
- Grigoriev, S.; Mayorov, S.; Polyakov, R. Centrifugal pump’s impeller optimization using methods of calculation hydrodynamics. IOP Conf. Ser. Mat. Sci. Eng. 2017, 233, 012009. [Google Scholar] [CrossRef]
- Zheng, L.; Dou, H.; Jiang, W.; Chen, X.; Zhu, Z.; Cui, B. Influence of rotor-stator interaction on flow stability in centrifugal pump based on energy gradient method. Int. J. Turbo Jet Eng. 2016, 33, 413–419. [Google Scholar] [CrossRef]
- Keller, J.; Blanco, E.; Barrio, R.; Parrondo, J. PIV measurements of the unsteady flow structures in a volute centrifugal pump at a high flow rate. Exp. Fluids 2014, 55, 1820. [Google Scholar] [CrossRef]
- Hou, H.; Zhang, Y.; Xu, C.; Zhang, J.; Li, Z. Effects of radial diffuser hydraulic design on a double-suction centrifugal pump. IOP Conf. Ser. Mat. Sci. Eng. 2006, 129, 012017. [Google Scholar] [CrossRef]
- Kocaaslan, O.; Ozgoren, M.; Babayigit, O.; Aksoy, M.H. Numerical investigation of the effect of number of blades on centrifugal pump performance. AIP Conf. Proc. 2017, 1863, 030028. [Google Scholar]
- Posa, A.; Lippolis, A.; Balaras, E. Large-eddy simulation of a mixed-flow pump at off-design conditions. ASME J. Fluids Eng. 2015, 137, 101302. [Google Scholar] [CrossRef]
- Chen, R.; Zeng, Y.; Liu, X. Research on Effects of Blade Thickness on the Low-specific-speed Centrifugal Pump Performance. Mach. Mater. Sci. Energy Eng. 2015, 207–214. [Google Scholar] [CrossRef]
- Heo, M.; Ma, S.; Shim, H.; Kim, K. High-efficiency design optimization of a centrifugal pump. J. Mech. Sci. Technol. 2016, 30, 3917–3927. [Google Scholar] [CrossRef]
- Kocaaslan, O.; Ozgoren, M.; Aksoy, M.H.; Babayigit, O. Experimental and Numerical Investigation of Coating Effect on Pump Impeller and Volute. J. Appl. Fluid Mech. 2016, 9, 2475–2487. [Google Scholar] [CrossRef]
- Yuan, Y.; Yuan, S. Analyzing the effects of splitter blade on the performance characteristics for a high-speed centrifugal pump. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef]
- Roberts, P.; Webster, D. Turbulent Diffusion; ASCE Press: Reston, VA, USA, 2002. [Google Scholar]
- Pope, S. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Staff Fluid Machinery Group. Centrifugal Pumps: State of the Art and New Opportunities; Ta Engineering Civil Engineering: London, UK, 2004. [Google Scholar]
- Lobanoff, V.; Ross, R. Centrifugal Pumps: Design and Application; Gulf Publishing Company: Houston, TX, USA, 1992. [Google Scholar]
- Menter, F. A comparison of some recent eddy-viscosity turbulence models. ASME J. Fluids Eng. 1996, 118, 514–519. [Google Scholar] [CrossRef]
- Suh, S.; Kim, K.; Kim, H.; Yoon, I.; Cho, M. A study on energy saving rate for variable speed condition of multistage centrifugal pump. J. Therm. Sci. 2015, 24, 566–573. [Google Scholar] [CrossRef]
- Tao, R.; Xiao, R.; Wang, Z. Influence of blade leading-edge shape on cavitation in a centrifugal pump impeller. Energies 2018, 11, 2588. [Google Scholar] [CrossRef]
- Braun, O.; Avellan, F.; Dupont, P. Unsteady numerical simulations of the flow related to the unstable energy-discharge characteristic of a medium specific speed double suction pump. In Proceedings of the Fluids Engineering Division Summer Meeting, San Diego, CA, USA, 30 July–2 August 2007; Volume 2, pp. 971–977. [Google Scholar]
- Menter, F.R.; Egorov, Y. The scale-adaptive simulation method for unsteady turbulent flow predictions. Part 1: Theory and model description. Flow Turbul. Combust. 2010, 85, 113–138. [Google Scholar] [CrossRef]
- Lucius, A.; Brenner, G. Unsteady CFD simulations of a pump in part load conditions using scale-adaptive simulation. Int. J. Heat Fluid Flow 2010, 31, 1113–1118. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.; Gandhi, B. Investigation of a high head Francis turbine at runaway operating conditions. Energies 2016, 9, 149. [Google Scholar] [CrossRef]
- Si, Q.; Yuan, J.; Yuan, S.; Wang, W.; Zhu, L.; Bois, G. Numerical investigation of pressure fluctuation in centrifugal pump volute based on SAS model and experimental validation. Adv. Mech. Eng. 2014, 6, 972081. [Google Scholar] [CrossRef]
- Spalart, P.R.; Shur, M. On the sensitization of turbulence models to rotation and curvature. Aerosp. Sci. Technol. 1997, 1, 297–302. [Google Scholar] [CrossRef]
- Tao, R.; Xiao, R.; Yang, W.; Wang, F. A comparative assessment of Spalart-Shur rotation/curvature correction in RANS simulations in a centrifugal pump impeller. Math. Probl. Eng. 2014, 2014, 342905. [Google Scholar] [CrossRef]
- Sun, J.; Kuhn, D.; Naterer, G. Eddy viscosity and Reynolds stress models of entropy generation in turbulent channel flows. ASME J. Fluids Eng. 2017, 139, 034501. [Google Scholar] [CrossRef]
- Li, D.; Wang, H.; Qin, Y.; Han, L.; Qin, D. Entropy production analysis of hysteresis characteristic of a pump-turbine model. Energy Convers. Manag. 2017, 149, 175–191. [Google Scholar] [CrossRef]
- Berten, S.; Dupont, P.; Fabre, L.; Kayal, M.; Avellan, F.; Farhat, M. Experimental investigation of flow instabilities and rotating stall in a high-energy centrifugal pump stage. In Proceedings of the ASME 2009 Fluids Engineering Division Summer Meeting, Vail, CO, USA, 2–6 August 2009; pp. 505–513. [Google Scholar]
- Leguizamón, S.; Ségoufin, C.; Hai-Trieu, P.; Avellan, F. On the Efficiency Alteration Mechanisms Due to Cavitation in Kaplan Turbines. ASME J. Fluids Eng. 2017, 139, 061301. [Google Scholar] [CrossRef]
- Ubaldi, M.; Zunino, P.; Barigozzi, G.; Cattanei, A. An experimental investigation of stator induced unsteadiness on centrifugal impeller outflow. J. Turbomach. 1996, 118, 41–51. [Google Scholar] [CrossRef]
- Shuai, Z.; Jiang, C.; Wang, D.; Zhou, Z.; Li, F. Numerical simulation of dynamic flow characteristics in a centrifugal water pump with three-vaned diffuser. Adv. Mech. Eng. 2015, 7. [Google Scholar] [CrossRef]
- Krause, N.; Zähringer, K.; Pap, E. Time-Resolved Particle Imaging Velocimetry for the Investigation of Rotating Stall in a Radial Pump. Exp. Fluids 2005, 39, 192–201. [Google Scholar] [CrossRef]
- Zhao, X.; Xiao, Y.; Wang, Z.; Luo, Y.; Cao, L. Unsteady Flow and Pressure Pulsation Characteristics Analysis of Rotating Stall in Centrifugal Pumps Under Off-Design Conditions. ASME J. Fluids Eng. 2017, 140, 021105. [Google Scholar] [CrossRef]
- Hasmatuchi, V.; Farhat, M.; Roth, S.; Botero, F.; Avellan, F. Experimental evidence of rotating stall in a pump-turbine at off-design conditions in generating mode. ASME J. Fluids Eng. 2011, 133, 051104. [Google Scholar] [CrossRef]
- Shibata, A.; Hiramatsu, H.; Komaki, S.; Miyagawa, K.; Maeda, M.; Kamei, S.; Hazama, R.; Sano, T.; Iino, M. Study of Flow Instability in Off Design Operation of a Multistage Centrifugal Pump. J. Mech. Sci. Technol. 2016, 30, 493–498. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).