Abstract
As the core component and main power source for aircrafts, the reliability of an aero engine is vital for the security operation of aircrafts. Degradation tendency measurement on an engine can not only improve its safety, but effectively reduce the maintenance costs. In this paper, a hybrid method using multi-sensor data based on fast ensemble empirical mode decomposition permutation entropy (FEEMD-PE) and regularized extreme learning machine (RELM), systematically blending the signal processing technology and trend prediction approach, is proposed for aircraft engine degradation tendency measurement. Firstly, a synthesized degradation index was designed utilizing multi-sensor data and a data fusion technique to evaluate the degradation level of the engine unit. Secondly, in order to eliminate the irregular data fluctuation, FEEMD was employed to efficiently decompose the constructed degradation index series. Subsequently, considering the complexity of intrinsic mode functions (IMFs) obtained through sequence decomposition, a permutation entropy-based reconstruction strategy was innovatively developed to generate the refactored IMFs (RIMFs), which have stronger ability for describing the degradation states and contribute to improving the prediction accuracy. Finally, RIMFs were used as the inputs of the RELM model to measure the degradation tendency. The proposed method was applied to the degradation tendency measurement of aircraft engines. The results confirm the effectiveness and superiority of the proposed method, and it is more suitable for actual applications compared with other existing approaches.
1. Introduction
With the growing complexity of mechanical systems, such as aircraft engines, electricity-producing devices, and high-speed vehicles, the increasing requirements of online health monitoring based on distributed sensor networks have become a focal point for the purpose of stable and reliable operation [1,2,3,4]. As the core component and power source of aircrafts, the operational reliability of an aero engine has significant impact on the personal safety and maintenance costs [5,6,7,8]. Recently, with the development of condition-based maintenance (CBM), the fault response pattern experienced a transformation from passive reply to active prevention [9,10]. CBM can effectively avoid unnecessary maintenance tasks and became one of the most commonly used maintenance strategies [11]. In particular, degradation tendency measurement is an important step for CBM, which can help discover abnormal operation conditions before faults occur, and is also crucial for reducing failure rate and maintenance costs [12,13,14,15].
Due to the development of sensor technology and simulation techniques, the operation condition of complex aircraft engine systems can be continuously monitored, and various sensor data from different positions can be collected in real time [16,17,18]. How to evaluate the extent of degradation of an aircraft engine using these sensor data is the primary problem facing degradation tendency measurement. Based on this, some efforts on establishing an appropriate index to accurately reflect the deterioration levels of equipment were carried out by many researchers. For instance, Volponi first pointed out that the health condition of gas turbines can be characterized by the fuel flow rate [19]. Gebraeel evaluated the rolling bearing on the basis of collected vibration signals [20]. Kral utilized the oil status to analyze the operation state of vehicle cooling systems [21]. However, these analyses are mostly based on single signals, and some important sensor data containing degradation information may be ignored, which means that there are many restrictions in practical applications. In addition, because of the high degree of equipment integration, it is difficult to find a single signal from a mass of sensory signals that can effectively indicate the degradation condition. Thus, the construction of an appropriate degradation index utilizing multi-sensor data of aircraft engine is a difficulty in the process of degradation trend measurement.
Degradation tendency measurement aims at forecasting the evolution of deterioration in the future and providing sufficient data support for decision-making. Generally, the existing models for predicting the degradation trend can be classified into three types: physics-based models, knowledge-based models, and data-driven approaches. Specifically, because of the difficulties in building an excellent physical model and acquiring domain knowledge, the implementation of the former two models realistically results in many restrictions. Data-driven models, which fully utilize the monitored operation data, can efficiently forecast the degradation trend using historical data without physical models and prior knowledge. Zhou used a prognostic model based on gray model (GM) to forecast the degradation of energy conversion equipment [22]. Fu presented the application of a support vector regression (SVR) model in the state trend prediction for a hydro-turbine generating unit [23]. Peng adopted the hybrid Gaussian process function regression (HGPFR) to predict the health state and remaining useful lifetime (RUL) of a lithium-ion battery [24]. Extreme learning machine (ELM) is one such model which is widely applied in forecasting because of its faster convergence speed and lower artificial inference in comparison with other models. Wang forecasted wind speed utilizing an ELM model optimized by the cuckoo algorithm [25]. The results indicated that the proposed method had satisfactory performance. In Reference [26], an extreme deep learning approach combining stacked autoencoders with the ELM was developed to realize accurate prediction of the building energy consumption. The results suggested the method had the best prediction performance in different cases. Until now, the merits of ELM over other prediction models was validated, and the uncertainties of forecasting were also quantified by the bootstrapping approach. Due to lots of advantages such as low time cost, high prediction accuracy, and no manual tuning, ELM can achieve optimal solutions. However, there are still some limitations in the application of ELM. Firstly, ELM is established on the empirical risk minimization principle; thus it inevitably has an over-fitting problem. Secondly, because of the stochastic volatility and inherent complexity of multi-sensor data, the accurate prediction of degradation trend with only a single ELM becomes difficult. In an effort to achieve better forecasting results, it is necessary to analyze the original data features. Therefore, the multi-scale decomposition of the original degradation data is helpful in improving the forecasting accuracy. Common data processing approaches, such as empirical mode decomposition (EMD) [27,28] and wavelet transform (WT) [29,30], are used to decompose the degradation data series and eliminate irregular fluctuation. Compared with the methods mentioned above, a new decomposing algorithm named fast ensemble empirical mode decomposition (FEEMD) is increasingly used in data preprocessing because of its high computational performance and strong predicting ability for jumping data samples [31]. Liu proposed a reliable forecasting approach by combining FEEMD, a genetic algorithm, and an artificial neural network (ANN) [32]. The author demonstrated that FEEMD could deal with the data fluctuation efficiently. Consequently, this provides a path for further research on improving prediction accuracy to combine the advantages of FEEMD and ELM.
The main contributions of this paper can be summarized as follows: (1) in order to get rid of the limitations of single prediction model, a hybrid measurement method is proposed to accurately forecast the degradation tendency of aircraft engines; (2) to quantitatively evaluate the degradation level, a synthesized degradation index (SDI) is constructed with multi-sensor data; (3) to eliminate the series fluctuation and reduce the components’ complexity, an intrinsic mode function (IMF) reconstruction strategy is developed with FEEMD and permutation entropy (PE) theory; (4) to prevent over-fitting, regularized ELM (RELM) is adopted to efficiently predict the degradation trend. The general implementation of the proposed method can be divided into four steps, i.e., SDI construction, series decomposition, IMF reconstruction, and trend prediction. Firstly, an SDI for the aircraft engine degradation status was constructed utilizing multi-sensor signals and a data fusion approach, which is a remarkable improvement compared with the traditional single-signal representation adopted in References [19,20,21]. Secondly, in order to reduce the potential impact of stochastic volatility, the FEEMD algorithm was employed to efficiently decompose the constructed SDI series. Compared with the decomposition approaches used in References [27,28,29,30], the application of FEEMD contributes to forecast the jumping points with high computation efficiency. Subsequently, a PE-based reconstruction strategy was innovatively developed to reduce the complexity of IMF components, i.e., to decrease the number of IMFs. With the idea of entropy similarity, refactored IMFs (RIMFs) have stronger ability for describing the degradation states, and further improve the prediction accuracy. Finally, RIMFs served as the inputs of the RELM prediction model to measure the degradation tendency. Based on the consideration of structural and empirical risk minimization, the over-fitting problems which occurred in References [25,26] can be effectively solved. The proposed method was applied to the degradation tendency measurement of aircraft engines, where the sensor data were measured from engine units equipped with embedded sensor networks. The results validate the effectiveness and superiority of the proposed method, and it is more suitable for actual applications compared with other existing approaches.
The rest of this paper is organized as follows: in Section 2, the essential background knowledge about FEEMD, ELM, and RELM is reviewed. The proposed method is presented in Section 3. In Section 4, the proposed method is applied to the degradation tendency measuring of aircraft engines, and the experimental results are analyzed and discussed in detail. Finally, general conclusions are given in Section 5.
2. Methodology
2.1. Fast Ensemble Empirical Mode Decomposition
In order to improve the computational speed of EEMD, an FEEMD method was investigated by Wang in 2014 [31]. Essentially, FEEMD has the same fundamentals as EEMD, and it was verified that FEEMD is a computationally efficient algorithm [33]. More details about FEEMD can be found in Reference [31]. The general procedures of FEEMD are shown below.
- (1)
- Initialize the number of replicated times M, the amplitude of added white noises, and m = 1.
- (2)
- Add a random Gaussian white noise sequence into the original time series to generate a noise-added signal ,
- (3)
- Decompose the noise-added signal into a series of intrinsic mode functions (IMFs) and a residue using the EMD method,where is the i-th IMF of the m-th trial, is the residue of the m-th trial, and n is the number of IMFs.
- (4)
- If m < M, then repeat step (2) to step (3) with m = m + 1, and add different white noise sequences each time.
- (5)
- Calculate the ensemble mean of the M trials for each IMF and the residue as the final results,where is the i-th IMF component obtained using FEEMD method, and is the final residue.
2.2. Extreme Learning Machine
Extreme learning machine (ELM) is a novel and efficient learning algorithm based on the traditional single-hidden-layer feed-forward networks (SLFNs) [34]. The significant advantage of ELM is that the weights and thresholds between the input layer and the hidden layer are randomly assigned and do not need to be adjusted during the learning process; thus, the training process can be executed quickly [35].
The structure of an ELM network is shown in Figure 1, and the calculation process is given below.
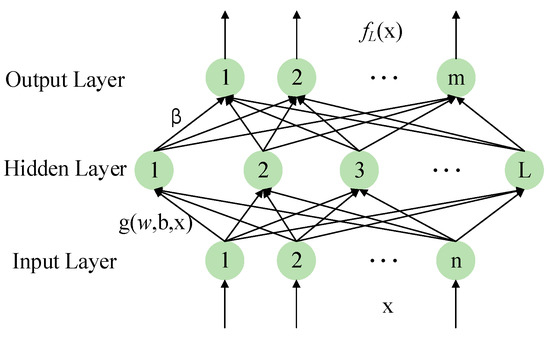
Figure 1.
The structure of an extreme learning machine (ELM) network [35].
- (1)
- For a given training set , set the activation function containing L hidden layer nodes as .
- (2)
- The network output of ELM can be expressed aswhere is the weight vector connecting the input vector and the i-th hidden layer node, is the weight vector connecting the i-th hidden node and the output vector, is the bias of the i-th hidden node, is the i-th training sample, and is output vector.
Equation (5) can be written in the following form:
where
- (3)
- The objective function of ELM can be formulated as
In fact, the training process of ELM is essentially to find a least-squares solution of optimal parameter ,
- (4)
- The output weight matrix can be obtained by the following formula:where represents the generalized inverse matrix of hidden layer output matrix .
2.3. Regularized Extreme Learning Machine
Although ELM has many advantages mentioned above, it does not consider structural risk and is prone to over-fitting [36]. In an effort to address these shortcomings, empirical risk minimization and structural risk minimization should be considered simultaneously when building a prediction model. Therefore, a regularized ELM (RELM) model was developed, which effectively enhances the stability and generalization performance of ELM.
The defining objective function of RELM can be expressed as
where is the regularization coefficient, and represent the empirical risk and structural risk, respectively, and is the network output error corresponding to training sample . According to Karush–Kuhn–Tucker conditions, the Lagrangian function can be defined as follows:
where the nonnegative (i = 1, 2, …, N) is the Lagrange multiplier. We take the derivative with respect to each variable in Equation (13) as
Substituting Equations (14) and (15) into Equation (16), we get
The output weight matrix can be calculated as follows:
where is the solution of . Thus, the predicting results of RELM can be obtained by
3. Proposed Degradation Tendency Measurement Method
In this paper, a hybrid method using multi-sensor data based on FEEMD-PE and RELM is proposed for the degradation tendency measurement of aircraft engines. This section includes three parts: the construction of a synthesized degradation index using multi-sensor data, the reconstruction of intrinsic mode functions based on PE theory, and the general procedure of the proposed method.
3.1. Construction of Synthesized Degradation Index Using Multi-Sensor Data
In order to effectively characterize the state of degradation, an appropriate degradation indicator should be constructed. This task considers a mass of sensory signals from different positions of aircraft engines. Based on that, a synthesized degradation index (SDI) is proposed in this paper using a linear transformation from a multi-dimensional sensory signal domain to a one-dimensional index domain.
Suppose of matrix and of matrix, which represent the faulty and healthy conditions of engines, respectively, are two groups of a multi-dimensional sensory dataset. and are the numbers of the dataset for faulty and healthy conditions, and is the dimension of the sensor dataset. With these two matrices, a transformation matrix can be calculated to transform the multi-dimensional sensory data into the one-dimensional SDI as
where, , , is a zero vector, and is a unit vector. With transformation matrix and the historical sensory dataset , the SDI denoted by can be defined as
It is worth noting that the SDI varies between 0 and 1, and “0” represents a healthy condition and “1” represents a faulty condition. In essence, the construction of SDI is a process of multi-sensor data fusion, and it provides an effective approach for quantifying the degradation status of aircraft engines.
3.2. Reconstruction of Intrinsic Mode Functions Based on Permutation Entropy Theory
Because of the influence of background noise and environmental factors, the decomposition results from FEEMD consist of many IMFs, which will cause a heavy computation burden and a decline in forecasting accuracy. In order to solve the problem of IMF complexity, an IMF reconstruction strategy based on the permutation entropy (PE) theory is firstly developed in this paper. The refactor principle is described below.
For an obtained IMF series , according to the Takens–Maine theorem, its phase space reconstruction vector can be acquired as
where m represents the embedded dimension and is the time delay. For the reconstructed vector , the elements can be arranged by m number of real values in ascending order as
Based on Equation (23), the reconstructed vector can be mapped to a set of symbols,
where , and , is one of the permutations. The probability for each symbol, denoted as , can be calculated, and then the PE of IMF series can be obtained as
where is the regularization coefficient, and . According to the definition, the PE can be used to measure the randomness of the series. Therefore, with an idea of proximity-based aggregation, the refactored IMFs (RIMFs) can be calculated based on the PE values of IMF sequences (n is the number of IMFs).
With the proposed reconstruction strategy, the IMFs decomposed from the same series will be divided into several groups adaptively, and the PE values of each group are closer together. The generated RIMFs retain the complete information in the IMFs and significantly reduce the IMF complexity. In this way, the RIMFs can serve as the inputs of the forecasting model to predict the degradation trend of engines.
3.3. Procedure of the Proposed Method
As mentioned above, the decomposition algorithm is often utilized to improve the prediction accuracy, and the IMF reconstruction contributes to the improvement of forecasting efficiency. Therefore, in this paper, FEEMD and the PE-based IMF refactor strategy are put forward to further enhance the performance of prediction model. The flowchart of the proposed degradation tendency measurement method is shown in Figure 2, and the general procedures are summarized below.
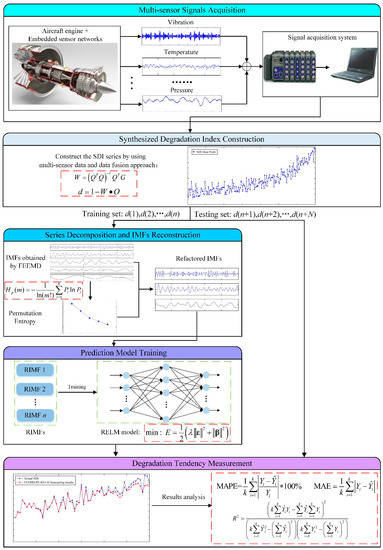
Figure 2.
The flowchart of the proposed degradation tendency measurement method.
Step 1: The different sensory signals during the entire lifecycle are collected by the sensor networks equipped on the aircraft engines.
Step 2: The SDI sequences are constructed with the collected multi-sensor data to assess the degradation conditions of engines.
Step 3: The constructed SDI sequences are randomly divided into a training set and testing set.
Step 4: For the training set, the SDI sequences can be decomposed into a series of IMFs using the FEEMD algorithm.
Step 5: All the IMFs are refactored with the proposed PE-based aggregation strategy to obtain the RIMFs.
Step 6: RIMFs serve as the inputs of RELM to train the forecasting model, and the optimal RELM is used to predict the future SDI series.
Step 7: The testing set is utilized to demonstrate the effectiveness and superiority of the proposed tendency measurement method.
4. Experimental Results and Discussion
In this section, the proposed method is applied to measure the degradation trend of aircraft engines. The “Prognostic Data Challenge Problem 2008” datasets are introduced for model validation, which contain multivariate sensory signals from different components of an aircraft engine [37]. The simplified schematic illustration of the engine model is shown in Figure 3, which mainly includes two compressors, two turbines, a fan, a combustor, and a nozzle [37]. The data for each cycle consist of the unit identifier (ID), cycle index, three independent operation setting parameters, and 21 sensor monitoring parameters [37]. According to different operating modes, the monitored data can be approximately classified into six clusters [38], as listed in Table 1. Because of the diversity and fluctuation of raw data, it is difficult to measure the degradation condition and predict the degradation trend using these raw sensory data directly. The objective of this paper is to construct a new indicator to effectively characterize the degradation performance of the engine, and accurately forecast the evolution trend of the indicator in the future.
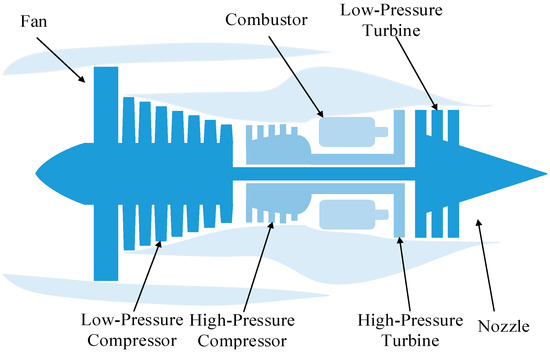
Figure 3.
The simplified schematic illustration of the aircraft engine model [37].

Table 1.
Six different operation modes (steady state of engine operation).
4.1. Model Performance Evaluation
In order to effectively evaluate the performance of the degradation trend prediction model, three generally adopted error criteria are presented to evaluate the forecasting accuracy, including mean absolute percentage error (MAPE), mean absolute error (MAE), and coefficient of determination [39]. MAPE is a measurement of average prediction ability of the model at each data point, and MAE can represent the deviation of the actual value and predicted value. , within the range [0, 1], is usually used as an indicator for the assessment of fitting performance. Definitions of the above indexes are formulated below.
where k is the number of testing samples, and and represent the i-th actual value and forecasting value, respectively.
Additionally, to highlight the higher calculation efficiency of RELM, the computational time of RELM and other different prediction models are contrasted in this paper. It is worth noting that all the experiments were conducted with MATLAB 2014 and run on the same personal computer (PC) with a central processing unit (CPU) of 2.3 GHz and 4 GB random-access memory (RAM).
4.2. SDI Series Construction
Among the 21 sensor monitoring parameters shown in Reference [37], some parameters contain no or little degradation information of engine units, whereas others do. This study intends to select some parameters that show obvious changing trends with time for the construction of the SDI. Finally, seven monitoring parameters shown in Table 2 were chosen in this study. More detailed information about the parameter selection can be found in Reference [38].

Table 2.
Description of the selected sensor monitoring parameters for the construction of the synthesized degradation index (SDI).
Based on these parameters, the SDI series can be built to represent the engine degradation states. Different transformation matrices (i = 1, 2, …, 6) should be established using Equation (20) for six different operation modes. For this, and matrices must be constructed firstly for operation modes. In this paper, is created with the sensor data under faulty conditions, in which the residual lifecycle (, where is the operational cycle of an engine unit and is the whole cycle of an engine unit) is between −3 and 0. Similarly, is built with the sensor data under healthy conditions, in which the residual lifecycle is smaller than −200. With the six transformation matrices and sensory datasets, a one-dimensional SDI series can be obtained, as shown in Figure 4. We can observe from the figure that the constructed SDI sequence shows an evident health degradation process with the evolution of cycle index. As a result, the one-dimensional SDI transformed from the multi-dimensional sensor signals is suitable for the degradation performance measurement of aircraft engines.
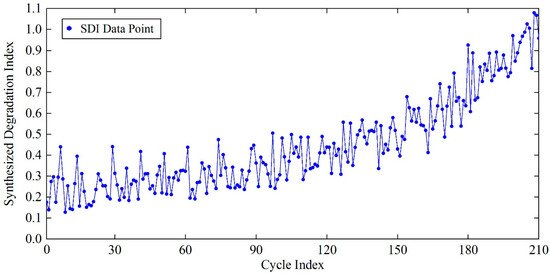
Figure 4.
The constructed synthesized degradation index (SDI) series based on the multi-dimensional sensor data.
Furthermore, for the model training and validation, the SDIs of the first 150 cycles () are selected as the training set, and remaining data () are used as the testing set.
4.3. SDI Series Decomposition and IMF Reconstruction
Figure 4 shows that the constructed SDI sequence fluctuates severely. From the figure, there is no obvious regularity of SDI series. Therefore, FEEMD was employed to decompose the original SDI series to decrease the non-stationary characteristic. The results are depicted in Figure 5, in which the SDI series is decomposed into eight independent IMFs and one residue.
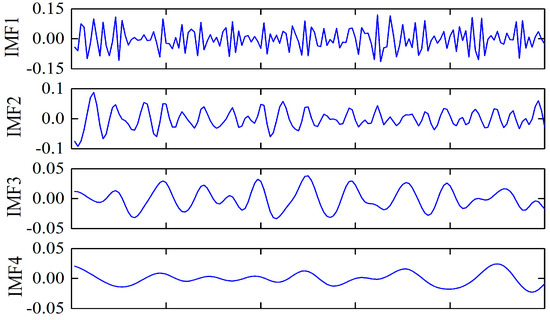
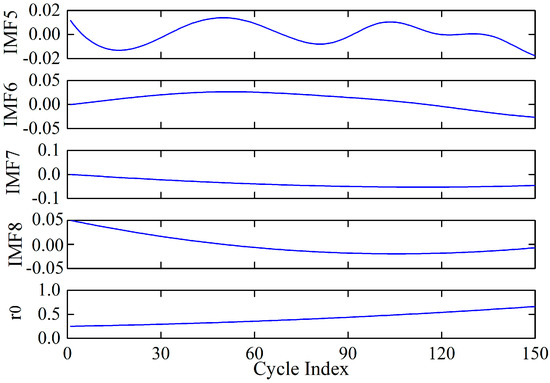
Figure 5.
The decomposed results of the original SDI series.
Because of the tremendous influence of IMF complexity on computation efficiency and prediction accuracy, a PE-based IMF reconstruction method was developed to establish a new RIMF system. Figure 6 presents the PE distribution of the obtained eight IMFs and one residue, and Table 3 lists the detailed PE values of these IMFs. From Figure 6, it can be found that the PE values of IMFs present a gradual decreasing trend in the decomposition process. The phenomenon indicates that the complexities of obtained IMF sequences are lowering gradually. According to the refactor principle illustrated in Section 3.2, the interval value of PE for the reconstruction of IMFs, i.e., , was set to 0.200. Based on Equation (26), the constructed RIMFs after IMF refactoring are presented in Table 4. As shown in the table, IMF3, IMF4, and IMF5 were selected to construct the RIMF3 based on the proximity of PE values. A similar principle was applied to generate other RIMFs, including RIMF1, RIMF2, and RIMF4. Figure 7 shows the obtained RIMF1 to RIMF4, which were reconstructed using the FEEMD decomposition results. It is obvious that the four RIMFs have significantly different characteristics. More specifically, RIMF1 has the highest frequency and strongest non-stationarity, while RIMF4 is almost stable across the entire lifecycle. Therefore, because of their distinct features and relatively few components, the reconstructed RIMFs can be used as the input of the prediction model to further improve the forecasting accuracy and efficiency.
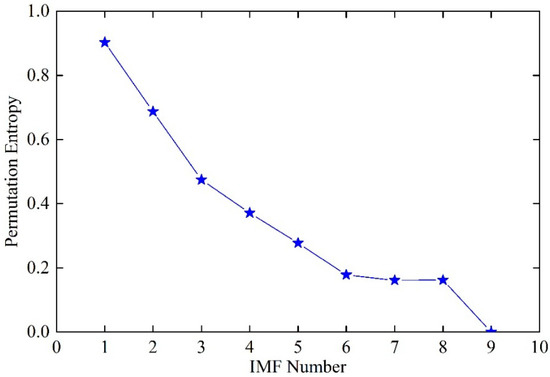
Figure 6.
The permutation entropy (PE) distribution of the intrinsic mode functions (IMFs).

Table 3.
Permutation entropy (PE) values of intrinsic mode functions (IMFs) decomposed by fast ensemble empirical mode decomposition (FEEMD) algorithm.

Table 4.
Analysis of IMF reconstruction results after FEEMD. RIMF—refactored IMF.
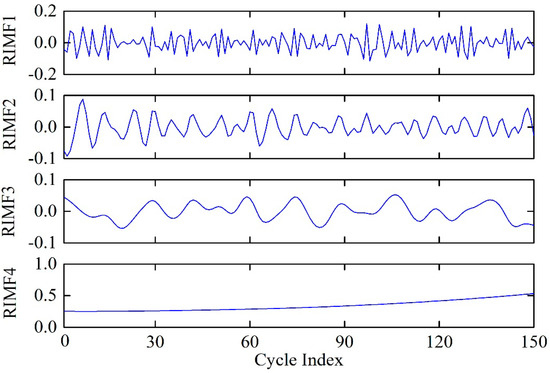
Figure 7.
Refactored IMFS (RIMFs) from fast ensemble empirical mode decomposition (FEEMD) decomposition results.
4.4. Degradation Tendency Measurement of Aircraft Engines
Based on RIMFs and RELM, the degradation tendency measuring results of the proposed FEEMD-PE/RELM method for aircraft engines can be obtained using the steps given in Figure 2. For comparison, seven other models, including EMD-PE/RELM, FEEMD/RELM, single RELM, single ELM, single support vector regression (SVR) model, single autoregressive integrated moving average (ARIMA) model, and single back propagation neural network (BPNN), were also adopted for degradation tendency measurement in comparison with the proposed method based on three error criteria. As Figure 8 shows, the comparisons can be divided into three parts. The first was conducted to verify the superiority of FEEMD, the second investigated the feasibility of the PE-based reconstruction strategy, and the last validated the efficiency of RELM in degradation trend measuring. In addition, the contrast between the three parts can further show that the ideas of decomposition and reconstruction contribute to the improvement of forecasting accuracy.
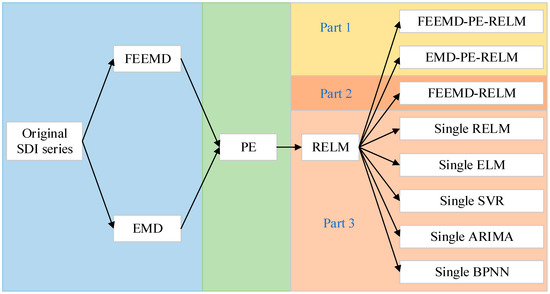
Figure 8.
Framework of the model comparisons.
Figure 9 presents the degradation trend measuring curves of aircraft engines achieved using eight models. We can observe from the figure that (1) compared with the other seven models, the proposed FEEMD-PE/RELM method realizes the highest degree of fitting between the forecasting value and the actual SDI value, while ARIMA shows the lowest degree; (2) the hybrid models have better predicted results than the corresponding single format, which indicates that the combination of signal decomposition and trend prediction contributes to the improvement of the prediction performance of single models; (3) with the PE-based reconstruction strategy, the forecasting precision was significantly improved during the whole prediction period; (4) at some jumping points of SDI, the prediction ability of RELM is better than that of ELM, which illustrates that the sensitivity of RELM was enhanced by the regularization improvement. However, it is worth noting that the proposed method suffers the same dilemma as other methods, i.e., a higher error with the evolution of cycle index. The reason is that the number of training samples and the method of single-step prediction limit the time scale of the forecast period. This paper aims to develop a novel measurement method that can predict the degradation trend with higher accuracy compared with other existing approaches. Consequently, there is less attention focused on the time scale of the prediction period. Despite this, it can be found from Figure 9 that the proposed FEEMD-PE/RELM method still shows higher accuracy as cycle index increases compared with the other seven models.
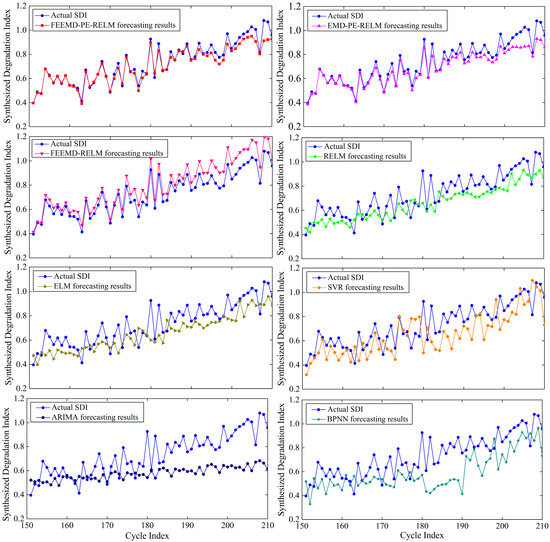
Figure 9.
The results of the eight models in the degradation tendency measurement.
The evaluated results of the eight models are shown in Figure 10, and the detailed comparisons of the three criteria are given in Table 5. It can be concluded from the results that FEEMD-PE/RELM shows the best forecasting performance, while BPNN has the worst. The main reason is that the number of hidden layer nodes of BPNN is mainly determined by trial and error and the optimal network structure is difficult to obtain. Additionally, the performance of hybrid models is superior to that of single models, for example, the MAPEs of FEEMD-PE/RELM, EMD-PE/RELM, and FEEMD/RELM are 3.552%, 5.134%, and 9.847%, respectively, which is lower than that of RELM. This is because the decomposition by FEEMD and EMD is helpful to capture the dynamic behavior of SDI series. Moreover, the MAPE of the FEEMD-based measuring model is lower than that of the EMD-based model. The reason is that the addition of Gaussian white noise in FEEMD can effectively overcome the mode mixing problem existing in EMD. Furthermore, the MAPE, MAE, and of FEEMD-PE/RELM are superior to those of FEEMD/RELM. It illustrates that the proposed PE-based IMF reconstruction method can obviously improve the performance of the prediction model, which significantly reduces the complexity of IMFs and simplifies the input of forecasting model. Finally, compared with other single models, RELM has the most preferable performance. It inherits the great generalization ability of ELM, and, at the same time, the over-fitting of ELM is reduced due to the adoption of regularization.
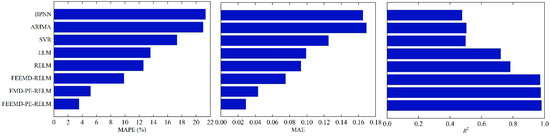
Figure 10.
Analysis of degradation tendency measuring results in terms of mean absolute percentage error (MAPE), mean absolute error (MAE), and coefficient of determination (R2).

Table 5.
Forecasting accuracy comparison of the eight models. RELM—regularized extreme learning machine; MAPE—mean absolute percentage error; MAE—mean absolute error; R2—coefficient of determination.
The computing time of RELM, ELM, SVR, ARIMA, and BPNN in degradation tendency measurements is shown in Table 6. Based on the computing time shown in this table, the times of RELM and ELM are far lower than those of the other three models, which indicates that ELM-based forecasting models have high computation speed. The main reason is that the model parameters are selected randomly and never need to be updated during the whole training process. Furthermore, it is worth noting that the time of RELM is 0.17 s longer than that of ELM, which illustrates that the application of regularization has a slight effect on the computational speed of ELM. In conclusion, RELM not only retains the characteristic of high speed, but improves the forecasting accuracy of ELM.

Table 6.
Computing time of RELM, ELM, SVR, ARIMA, and BPNN in degradation tendency measurement.
5. Conclusions
In this paper, a hybrid measurement method using multi-sensor data based on a permutation entropy reconstruction scheme and a regularized extreme learning machine (RELM) prediction model was proposed to forecast the degradation tendency of aircraft engines. The proposed method has three unique advantages. Firstly, a one-dimensional synthesized degradation index based on multi-dimensional sensor data was constructed to accurately indicate the extent of degradation. Secondly, because of the volatility of the degradation index, FEEMD was used to decompose the original index series, and a permutation entropy-based intrinsic mode function (IMF) reconstruction strategy was developed to reduce the complexity of components. Finally, the refactored IMFs were employed as the inputs of RELM to predict the degradation trend in the future.
A well-known multi-sensor dataset of aircraft engines was used to validate the effectiveness and superiority of the proposed measurement method. The experimental results confirm that the proposed method can accurately and rapidly predict the degradation trend of engine units, and is much more effective than and superior to other existing methods for volatility fitting.
Author Contributions
W.J. and Y.X. supervised the work, developed the innovative method, and prepared this manuscript. Y.S. helped conduct some experiments. H.L. contributed to the analysis of data.
Funding
This research was funded by the National Natural Science Foundation of China (NSFC) (Nos. 51809099).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, D.; Tsui, K.L. Brownian motion with adaptive drift for remaining useful life prediction: Revisited. Mech. Syst. Signal Process. 2018, 99, 691–701. [Google Scholar] [CrossRef]
- Zhu, S.P.; Huang, H.Z.; Li, Y.; Liu, Y.; Yang, Y. Probabilistic modeling of damage accumulation for time-dependent fatigue reliability analysis of railway axle steels. Proc. Inst. Mech. Eng. Part F 2015, 229, 23–33. [Google Scholar] [CrossRef]
- Witos, M.; Wachlaczenko, M. Structural health monitoring of compressor and turbine blades with the use of variable reluctance sensor and tip timing method. In Proceedings of the 19th WCNDT World Conference on Non-Destructive Testing, Munich, Germany, 13–17 June 2016. [Google Scholar] [CrossRef]
- Bouckaert, J.F. Tip Timing and Tip Clearance Problem in Turbomachines; VKI Lecture Series 2007-03; von Karman Institute for Fluid Dynamics: Sint-Genesius-Rode, Belgium, 2007. [Google Scholar]
- Zhu, S.P.; Huang, H.Z.; Peng, W.; Wang, H.; Mahadevan, S. Probabilistic physics of failure-based framework for fatigue life prediction of aircraft gas turbine discs under uncertainty. Reliab. Eng. Syst. Saf. 2016, 146, 1–12. [Google Scholar] [CrossRef]
- Yu, Z.Y.; Zhu, S.P.; Liu, Q.; Liu, Y. A new energy—Critical plane damage parameter for multiaxial fatigue life prediction of turbine blades. Materials 2017, 10, 513. [Google Scholar] [CrossRef] [PubMed]
- Beaudoin, M.A.; Behdinan, K. Analytical lump model for the nonlinear dynamic response of bolted flanges in aero-engine casings. Mech. Syst. Signal Process. 2019, 115, 14–28. [Google Scholar] [CrossRef]
- Nie, Z.W.; Lin, Y.Y.; Tong, Q.B. Numerical simulations of two-phase flow in open-cell metal foams with application to aero-engine separators. Int. J. Heat Mass Transf. 2018, 127, 917–932. [Google Scholar] [CrossRef]
- Jardine, A.K.S.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Fu, W.L.; Tan, J.W.; Li, C.S.; Zou, Z.B. A hybrid fault diagnosis approach for rotating machinery with the fusion of entropy-based feature extraction and SVM optimized by a chaos quantum sine cosine algorithm. Entropy 2018, 20, 626. [Google Scholar] [CrossRef]
- Asgarpour, M.; Sørensen, J.D. Bayesian based diagnostic model for condition based maintenance of offshore wind farms. Energies 2018, 11, 300. [Google Scholar] [CrossRef]
- Li, Y.F.; Liu, H.L.; Ma, Z.J. Trend extraction of rail corrugation measured dynamically based on the relevant low-frequency principal components reconstruction. Meas. Sci. Technol. 2016, 27, 105005. [Google Scholar] [CrossRef]
- Heng, A.; Zhang, S.; Tan, A.C.C.; Mathew, J. Rotating machinery prognostics: State of the art, challenges and opportunities. Mech. Syst. Signal Process. 2009, 23, 724–739. [Google Scholar] [CrossRef]
- Witos, M. Increasing the durability of turbine engines through active diagnostic and control. Res. Works Air Force Inst. Technol. 2011. [CrossRef]
- Xu, Y.H.; Zheng, Y.; Du, Y.; Yang, W.; Peng, X.Y.; Li, C.S. Adaptive condition predictive-fuzzy PID optimal control of start-up process for pumped storage unit at low head area. Energy Convers. Manag. 2018, 177, 592–604. [Google Scholar] [CrossRef]
- Provost, M.J. The Use of Optimal Estimation Techniques in the Analysis of Gas Turbines. Ph.D. Thesis, Crandfield University, Bedford, UK, 1994. [Google Scholar]
- Sharpe, J. Active Control of Engine Dynamics, RTO AVT/VKI Special Course; von Karman Institute for Fluid Dynamics: Sint-Genesius-Rode, Belgium, 2001. [Google Scholar]
- Matioudakis, K. Neural Network in Gas Turbine Fault Diagnostics [in:] Gas Turbine Condition Monitoring & Fault Diagnosis; Lecture Series 2003-01; von Karman Institute for Fluid Dynamics: Sint-Genesius-Rode, Belgium, 2003. [Google Scholar]
- Volponi, A.J.; Alonso, F.J. Gas turbine engine health management: Past, present, and future trends. J. Eng. Gas Turbines Power 2014, 136, 051201. [Google Scholar] [CrossRef]
- Gebraeel, N.Z.; Lawley, M.A.; Li, R.; Ryan, J.K. Residual-life distributions from component degradation signals: A Bayesian approach. IIE Trans. 2005, 37, 543–557. [Google Scholar] [CrossRef]
- Kral, J.; Konecny, B.; Kral, J.; Madac, K.; Fedorko, G.; Molnar, V. Degradation and chemical change of longlife oils following intensive use in automobile engines. Measurement 2014, 50, 34–42. [Google Scholar] [CrossRef]
- Zhou, D.J.; Yu, Z.Q.; Zhang, H.S.; Weng, S.L. A novel grey prognostic model based on Markov process and grey incidence analysis for energy conversion equipment degradation. Energy 2016, 109, 420–429. [Google Scholar] [CrossRef]
- Fu, W.L.; Zhou, J.Z.; Zhang, Y.C.; Zhu, W.L.; Xue, X.M.; Xu, Y.H. A state tendency measurement for a hydro-turbine generating unit based on aggregated EEMD and SVR. Meas. Sci. Technol. 2015, 26, 125008. [Google Scholar] [CrossRef]
- Peng, Y.; Hou, Y.D.; Song, Y.C.; Pang, J.Y.; Liu, D.T. Lithium-ion battery prognostics with hybrid Gaussian process function regression. Energies 2018, 11, 1420. [Google Scholar] [CrossRef]
- Wang, R.; Li, J.R.; Wang, J.Z.; Gao, C.Z. Research and application of a hybrid wind energy forecasting system based on data processing and an optimized extreme learning machine. Energies 2018, 11, 1712. [Google Scholar] [CrossRef]
- Li, C.D.; Ding, Z.X.; Zhao, D.B.; Yi, J.Q.; Zhang, G.Q. Building energy consumption prediction: An extreme deep learning approach. Energies 2017, 10, 1525. [Google Scholar] [CrossRef]
- An, N.; Zhao, W.G.; Wang, J.Z.; Shang, D.; Zhao, E.D. Using multi-output feedforward neural network with empirical mode decomposition based signal filtering for electricity demand forecasting. Energy 2013, 49, 279–288. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P.N.; Srikanth, N. A comparative study of empirical mode decomposition-based short-term wind speed forecasting methods. IEEE Trans. Sustain. Energy 2015, 6, 236–244. [Google Scholar] [CrossRef]
- Chitsaz, H.; Amjady, N.; Zareipour, H. Wind power forecast using wavelet neural network trained by improved Clonal selection algorithm. Energy Convers. Manag. 2015, 89, 588–598. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Congedo, P.M.; Malvoni, M.; Laforgia, D. Error analysis of hybrid photovoltaic power forecasting models: A case study of mediterranean climate. Energy Convers. Manag. 2015, 100, 117–130. [Google Scholar] [CrossRef]
- Wang, Y.H.; Yeh, C.H.; Young, H.W.V.; Hu, K.; Lo, M.T. On the computational complexity of the empirical mode decomposition algorithm. Physica A 2014, 400, 159–167. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Liang, X.F.; Li, Y.F. New wind speed forecasting approaches using fast ensemble empirical mode decomposition, genetic algorithm, mind evolutionary algorithm and artificial neural networks. Renew. Energy 2015, 83, 1066–1075. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Li, Y.F. Comparison of new hybrid FEEMD-MLP, FEEMD-ANFIS, wavelet packet-MLP and wavelet packet-ANFIS for wind speed predictions. Energy Convers. Manag. 2015, 89, 1–11. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; pp. 985–990. [Google Scholar]
- Salcedo-Sanz, S.; Muñoz-Bulnes, J.; Portilla-Figueras, J.; Del Ser, J. One-year-ahead energy demand estimation from macroeconomic variables using computational intelligence algorithm. Energy Convers. Manag. 2015, 99, 62–71. [Google Scholar] [CrossRef]
- Lombardi, A.M. Some reasoning on the RELM-CSEP likelihood-based tests. Earth Planets Space 2014, 66, 4. [Google Scholar] [CrossRef]
- Saxena, A.; Gobel, K. Damage propagation modeling for aircraft engine run-to-failure simulation. In Proceedings of the IEEE International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008. [Google Scholar]
- Wang, T.; Yu, J.; Siegel, D.; Lee, J. A similarity-based prognostics approach for remaining useful life estimation of engineered systems. In Proceedings of the IEEE International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008. [Google Scholar]
- Xu, Y.H.; Li, C.S.; Wang, Z.B.; Zhang, N.; Peng, B. Load frequency control of a novel renewable energy integrated micro-grid containing pumped hydro power energy storage. IEEE Access 2018, 6, 29067–29077. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).