Optimization of Battery Capacity Decay for Semi-Active Hybrid Energy Storage System Equipped on Electric City Bus

Abstract

In view of severe changes in temperature during different seasons in cold areas of northern China, the decay of battery capacity of electric vehicles poses a problem. This paper uses an electric bus power system with semi-active hybrid energy storage system (HESS) as the research object and proposes a convex power distribution strategy to optimize the battery current that represents degradation of battery capacity based on the analysis of semi-empirical LiFePO₄ battery life decline model. Simulation results show that, at a room temperature of 25 °C, during a daily trip organized by the Harbin City Driving Cycle including four cycle lines and four charging phases, the percentage of battery degradation was 9.6 × 10⁻³%. According to the average temperature of different months in Harbin, the percentage of battery degradation of the power distribution strategy proposed in this paper is 3.15% in one year; the electric bus can operate for 6.4 years until its capacity reduces to 80% of its initial value, and it can operate for 0.51 year more than the rule-based power distribution strategy.

1. Introduction

As the sole power source in a traditional electric vehicle, a battery needs to satisfy the power and energy demands of a bus under different operating conditions. When the battery is repeatedly over-charged and over-discharged in the long-term operating, the battery degradation will be accelerated. Furthermore, when the battery is operated at low temperature, its capacity degradation is more significant. The hybrid energy storage system (HESS) is composed of a battery and super capacity (SC); the battery provides the required energy and the SC satisfies the instantaneous power requirements, can effectively inhibit the battery charge and discharge current changes, and optimizes the working conditions of the energy system [1].

Currently, experts and scholars in the field of electric vehicle hybrid energy storage research are focused on the modeling and performance of the system components, system parameters matching, power distribution, etc. In terms of system component modeling and experimentation, Luo et al. [2] derived and verified a driving cycle life prediction model for LiFePO₄ battery based on the experimental verification of the existing capacity decay model for LiFePO₄ under a constant current charge/discharge condition. Abeywardana et al. [3] proposed a new type of inverter combined with boost circuits used in HESS, which eliminates the high current injected into the drive motor as compared to conventional controllers that eliminate the equivalent series resistance of the inverter. Henson et al. [4] conducted a comparative study of the battery/SC with different depths of discharge (DODs) for minimizing the cost of the HESS. Xiong et al. [5,6] used different algorithms to estimate the relationship of the voltage to the state-of-charge (SOC) and capacity of lithium ion battery, and they also validated the accuracy of the method through hardware-in-the-loop experiments. In terms of system parameter matching and power distribution, Mid-Eum et al. [7] used the convex optimization method to optimize the power loss and battery power fluctuations considering the real-time dynamic load to propose a method for calculating the SC reference voltage. Song et al. [8,9] proposed a new semi-active topology; the operation cost of the HESS, including the battery degradation cost and electricity cost, is minimized by using the dynamic programming (DP) approach. Further, they studied four topologies and proposed a rule-based power distribution strategy with four kinds of topologies based on the optimization results. Hu et al. [10] conducted energy efficiency analysis and component selection of the plug-in hybrid power system using convex optimization.

In summary, there have been studies related to the parameter matching and system control of HESS facing battery degradation. However, to the best of our knowledge, there are no published papers that combine the climatic conditions in northern China and the corresponding urban driving cycle operating conditions to optimize the functioning of the HESS. In order to attain the full potential of the HESS to enhance the battery life of electric buses under local conditions, in this study, we considered the electric bus operating in Harbin, China as an example, and proposed a method to optimize charge/discharge current of battery through convex optimization considering the average monthly temperature change in one year.

This paper is organized as follows. In Section 2, we analyze the configuration and working modes of the HESS. In Section 3, we introduce the models of LiFePO₄ batteries, SCs, and vehicle. Section 4 presents a convex optimization power distribution strategy based on the semi-empirical model of battery degradation. In Section 5, the simulation results and operating years were analyzed and the results are compared with those of the rule-based strategy.

2. Analysis of Configuration and Working Modes of Hybrid Energy Storage System

As the main energy source of electric vehicles, energy-based batteries have the disadvantages of low power density and high capacity degradation [11]. In order to satisfy the peak power demand, the power density of batteries should be sufficiently high; further, considering a battery that is the only power source of a traditional electric car, in principle, the only way to increase the power density of the batteries is to increase the number of batteries. Thus, it will result in high cost and high battery degradation. However, the SCs have characteristics of high power density and low capacity degradation. A combination of the battery and SC satisfies power and energy requirements, as well as the different performance requirements of the vehicles.

According to the different connections between the battery, SC, and DC/DC converter, the HESS can be classified into three major types, namely, fully active, passive, and semi-active, as shown in Figure 1. In the fully active HESSs, both the battery and SC are connected to the DC bus via a DC/DC converter; two DC/DC converters can simultaneously control the output power of the battery and the SC. Further, it has good control margins. However, a fully active HESS has low system efficiency and a complicated system structure owing to the existence of the two converters; it also increases the system cost owing to the additional cost of the DC/DC converter. Therefore, the fully active topology can achieve a good control effect, but at the expense of system efficiency, complexity, and cost [12]. In the passive topology, the battery and SC are directly connected to the DC bus and the system structure is simple. Owing to the absence of a converter, the system efficiency of the passive topology is the highest, whereas it is uncontrollable of the energy flowing [13]. In the semi-active topology, either the battery or the SC is connected to the DC/DC converter through a unique converter to control the distribution of the output power of the two energy sources. Since the DC bus is connected to one of the battery and SC directly, a fast DC/DC converter is required to maintain DC voltage when the load is changed. However, compared to the fully active and passive topologies, the semi-active topology solved the problems of low efficiency, high cost, uncontrollability, etc. [14].

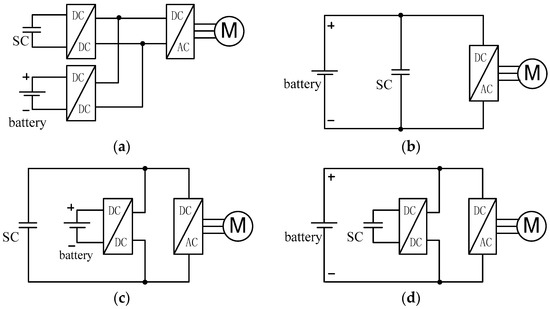
Figure 1. The topology of the electric vehicle HESS: (a) fully active topology; (b) passive parallel topology; (c) semi-active topology 1; and (d) semi-active topology 2.

The topology adopted in this study is shown in Figure 1d. Semi-active topology 2 employs a DC/DC converter to decouple the SC from the battery/DC bus. Furthermore, the DC bus voltage is equal to the battery voltage as they are directly connected. Compared to the other three topologies, the use of SC is more flexible [15], and its working mode is shown in Figure 2. In the driving mode, both the battery and SC provide power to the motor, and the SC satisfies the instantaneous high power requirements. In the braking mode, the energy charging for the SC first through the converter, then the braking energy charging for the battery when the SC is full. For the power conversion between SC and DC bus, a fast three-leg bidirectional DC/DC converter is used. It can be operated in the interleaved manner and has the merit of being commercially available [16,17]. The degradation of the SC is very small and its working life can accommodate millions of charge/discharge cycles. The power demand from the vehicle will be volatile during rapid acceleration and braking; hence, the SC plays the role of power and energy buffer when it is connected between the battery and driving motor through the DC/DC converter.

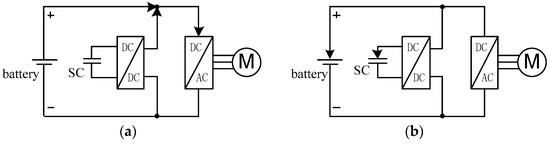
Figure 2. The different modes of operation of semi-active topology: (a) power flow based on driving mode; and (b) power flow based on braking mode.

3. Power System Modeling Based on HESS

3.1. Battery Model

Compared to the Nickel Metal Hydride (Ni-MH) power battery, lead-acid power battery, and the other driving batteries utilized in electric vehicles, the LiFePO₄ battery has the characteristic of good battery service life and high energy density. However, its low temperature performance is not outstanding [18]. The parameters of the LiFePO₄ cell used in this study are shown in Table 1.

Table 1. Basic parameters of the LiFePO₄ battery cell.

Item	Value
Vbat_norm, nominal voltage (V)	3.2
Qbat, capacity (Ah)	180
mbat_cell, cell mass (kg)	5.6
Ibat_max,min, max dis/charge current (A)	±540

The Rint model shown in Figure 3 was adopted to represent the battery behavior, where U_bat is the battery terminal voltage and R_bat is the resistance of the battery. Since the voltage and SOC are strongly correlated [19] in Equation (1), and in order to adopt the subsequent power distribution strategy, the one-time curve fitting is used to find the functional relationship between the battery open circuit voltage V_bat and its SOC, as shown in Figure 4.

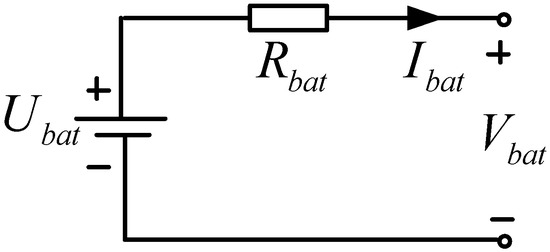
Figure 3. Rint model of the LiFePO₄ battery.

Figure 4. The relationship between V_bat and SOC.

$${\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}}=({\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}1}-{\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}0})\mathrm{S}\mathrm{O}{\mathrm{C}}_{\mathrm{b}\mathrm{a}\mathrm{t}}+{\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}0}$$

(1)

where V_bat1 is the open circuit voltage corresponding to SOC_bat = 100% and V_bat0 is the open circuit voltage when SOC_bat = 0. The storage energy E_bat of the battery pack can be calculated as

$${\mathrm{E}}_{\mathrm{b}\mathrm{a}\mathrm{t}}=\frac{1}{2}{\mathrm{n}}_{\mathrm{b}\mathrm{a}\mathrm{t}}{\mathrm{Q}}_{\mathrm{b}\mathrm{a}\mathrm{t}}({{\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}}}^2-{{\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}0}}^2)$$

(2)

where n_bat is the number of battery cells and Q_bat is the cell capacity. The battery pack output power P_bat can be calculated by Equation (3).

$${\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}}=-\frac{\mathrm{d}{\mathrm{E}}_{\mathrm{b}\mathrm{a}\mathrm{t}}}{\mathrm{d}\mathrm{t}}$$

(3)

The power consumption on battery internal resistance P_{bat_loss} can be calculated by the following equation, where I_bat is the current flowing through the battery cell. The charge resistance and discharge resistance of the cell are measured under different SOCs at a room temperature of 25 °C, as shown in Figure 5.

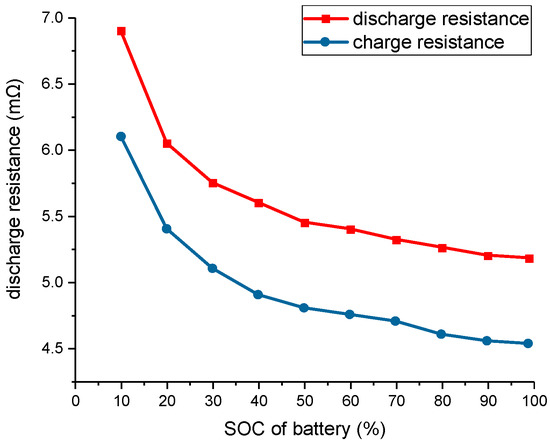
Figure 5. Charge and discharge resistances of the LiFePO₄ cell at room temperature of 25 °C.

$${\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}={\mathrm{n}}_{\mathrm{b}\mathrm{a}\mathrm{t}}{{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}}}^2{\mathrm{R}}_{\mathrm{b}\mathrm{a}\mathrm{t}}$$

(4)

3.2. Super Capacitor Model

The main purpose of using the SC is to protect the battery more effectively; it has the characteristics of high charge and discharge efficiency, long service life, and better low temperature performance. The SC equivalent circuit model is shown in Figure 6, where R_cap is the equivalent series resistance, I_cap is the current flowing through the SC cell, C_cap is the capacitance of the SC cell, and V_cap is the Open Circuit Voltage (OCV) of the SC cell. In this study, we use The Maxwell Technologies^® company’s super capacity and the parameters of the SC cell are listed in Table 2. Since the SC can achieve millions of charge/discharge cycles, this article ignores the capacity degradation of the SC in the entire process [20]. The open circuit voltage method is used to express the relationship between its open circuit voltage V_cap and SOC_cap.

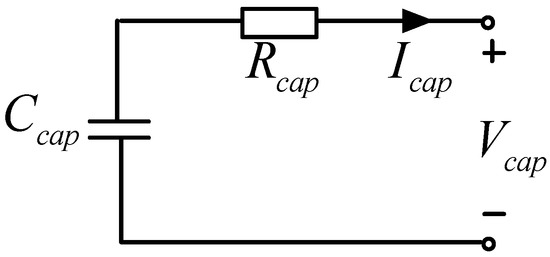
Figure 6. Equivalent circuit modelof the SC.

Table 2. Basic parameters of the SC cell.

Item	Value
Vcap_norm, nominal voltage (V)	2.7
Ccap, capacity (F)	2 × 103
Rcap, resistance (Ω)	3.5 × 10−4
mcap_cell, cell mass (kg)	0.36
Icap_max,min, max dis/charge current (A)	±1.6 × 103

$${\mathrm{V}}_{\mathrm{c}\mathrm{a}\mathrm{p}}={\mathrm{V}}_{\mathrm{c}\mathrm{a}\mathrm{p}1}\mathrm{S}\mathrm{O}{\mathrm{C}}_{\mathrm{c}\mathrm{a}\mathrm{p}}$$

(5)

where V_cap1 is the open circuit voltage corresponding to SOC_cap = 100%. As shown in Equation (6), E_cap is the energy released when the SC is discharged from the fully-charged state to SOC_cap.

$${\mathrm{E}}_{\mathrm{c}\mathrm{a}\mathrm{p}}=\frac{1}{2}{\mathrm{n}}_{\mathrm{c}\mathrm{a}\mathrm{p}}{\mathrm{C}}_{\mathrm{c}\mathrm{a}\mathrm{p}}{{\mathrm{V}}_{\mathrm{c}\mathrm{a}\mathrm{p}1}}^2(1-\mathrm{S}\mathrm{O}{\mathrm{C}}_{\mathrm{c}\mathrm{a}\mathrm{p}})$$

(6)

where n_cap is the number of SC cells. The output power of the SCs P_cap is the first derivative of its release time, as shown in Equation (7).

$${\mathrm{P}}_{\mathrm{c}\mathrm{a}\mathrm{p}}=-\frac{\mathrm{d}{\mathrm{E}}_{\mathrm{c}\mathrm{a}\mathrm{p}}}{\mathrm{d}\mathrm{t}}$$

(7)

The power consumption on SCs internal resistance P_{cap_loss} can be calculated by Equation (8), where I_cap is the current flowing through the SC cell.

$${\mathrm{P}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}={\mathrm{n}}_{\mathrm{c}\mathrm{a}\mathrm{p}}{{\mathrm{I}}_{\mathrm{c}\mathrm{a}\mathrm{p}}}^2{\mathrm{R}}_{\mathrm{c}\mathrm{a}\mathrm{p}}$$

(8)

3.3. Battery Degradation Model

The high cost of lithium-ion battery is one of the main factors restricting the development of electric vehicles. The conversion cost of electric vehicles can be reduced by extending the lifespan of lithium-ion battery. In recent years, researchers have made significant efforts to calculate and predict the degradation of the battery [21,22,23]. In Ref. [21], the authors conducted a series of charge/discharge experiments through constant current-constant voltage (CC-CV) and used a scanning electron microscope (SEM) to characterize the structure of cathode, anode, and separator in Li-ion batteries. The results have shown that the capacity fading of batteries can be attributed primarily to the loss of active Li⁺ and the losses of cathode and anode active materials. In Ref. [22], a large number of charge and discharge experiments were carried out on LiFePO₄ batteries, and the semi-empirical formula of battery decay percentage and ambient temperature, charge/discharge rate, and cycling time were obtained. In Ref. [23], the effect of parameters such as the end of charge voltage, DOD, film resistance, exchange current density, and over voltage of the parasitic reaction on the capacity fading and battery performance were studied. However, in summary, it is very difficult to calibrate and parameterize the degree of battery degradation in an electric vehicle during actual operation. Therefore, we considered many factors that affect battery degradation and adopted the semi-empirical model used in Ref. [24]. The semi-empirical formula is as shown in Equation (9).

$${\mathrm{Q}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}=\mathrm{B}\cdot {\mathrm{e}}^{-\left(\frac{\mathrm{E}+\mathrm{a}\cdot \mathrm{n}}{\mathrm{R}\mathrm{T}}\right)}{({\mathrm{A}}_{\mathrm{h}})}^{\mathrm{x}}$$

(9)

where Q_loss is the percentage of battery degradation, E is the activation energy, R is the gas constant, T is the absolute temperature, A_h is the A_h-throughput, and B, a, and x are constants. The percentage of discrete battery degradation at different temperatures can be calculated using Equation (10).

$${\mathrm{Q}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}\_\mathrm{k}+1}-{\mathrm{Q}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}\_\mathrm{k}}=9.78\times {10}^{-4}{\mathrm{e}}^{-\left(\frac{15162-1516\cdot \mathrm{n}}{0.849\mathrm{R}(\left|285.75-\mathrm{T}\right|+265)}\right)}\cdot \Delta {\mathrm{A}}_{\mathrm{h}}\cdot {{\mathrm{Q}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}\_\mathrm{k}}}^{-0.1779}$$

(10)

where Q_{loss_k} and Q_{loss_k+1} are the percentages of battery capacity decay degradation for the steps k and k + 1, respectively. ΔA_h is the A_h-throughput from t_k to t_k+1, and it satisfies Equation (11), where ∆t is the sampling time.

$$\Delta {\mathrm{A}}_{\mathrm{h}}=\frac{1}{3600}\cdot \left|{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}}\right|\cdot \Delta \mathrm{t}$$

(11)

3.4. Vehicle Model

The vehicle power system model can be used to obtain the power demand of the vehicle at different times during the operation. The power demand of a vehicle should be the output power of the driving wheel for an electric bus with semi-active HESS. The output power of the driving wheel is the product of the demand torque and the required angular velocity, as shown in Equation (12).

$${\mathrm{P}}_{\mathrm{d}\mathrm{e}\mathrm{m}}={\mathrm{T}}_{\mathrm{d}\mathrm{e}\mathrm{m}}{\mathsf{\omega }}_{\mathrm{d}\mathrm{e}\mathrm{m}}{{\mathsf{\eta }}_{\mathrm{T}}}^{-\mathrm{k}}$$

(12)

where η_T is transmission system efficiency; and k is the power factor: k = 1 when the bus is in the driving state and k = −1 when the bus is in the braking state. T_dem and ω_dem are the demand torque and the demand angular velocity, respectively, which can be calculated as shown in Equation (13). The basic parameters involved in Equation (13) are listed in Table 3. In Table 3, a_ω is angular acceleration, and the total mass m_bus is equal to the sum of the body quality, passenger quality, batteries, and SCs mass (15% additional mass).

Table 3. Basic parameters of the vehicle.

Item	Value
mveh, body quality	1.3 × 104
mp, passenger quality (F)	3 × 103
cr, rolling resistance coefficient	0.007
ρ, air density (kg/m3)	1.18
J, total inertia (kgm2)	143.41
A, frontal area (m2)	7.83
cd, aerodynamic drag coefficient	0.75
Rw, wheel radius (m)	0.51
gfinal ,final gear ratio	6.2
ηDC, DC/DC converter efficiency	0.9
ηT, powertrain efficiency	0.9

$$\{\begin{array}{l}{\mathrm{T}}_{\mathrm{d}\mathrm{e}\mathrm{m}}=\left[\left({\mathrm{m}}_{\mathrm{b}\mathrm{u}\mathrm{s}}\mathrm{g}{\mathrm{c}}_{\mathrm{r}}\cos (\mathsf{\theta })+{\mathrm{m}}_{\mathrm{b}\mathrm{u}\mathrm{s}}\mathrm{a}+{\mathrm{m}}_{\mathrm{b}\mathrm{u}\mathrm{s}}\mathrm{g}\sin (\mathsf{\theta })\right)+(\frac{\mathrm{J}{\mathrm{a}}_{\mathsf{\omega }}}{{\mathrm{R}}_{\mathrm{w}}}+\frac{1}{2}\mathsf{\rho }\mathrm{A}{\mathrm{c}}_{\mathrm{d}}{\mathrm{v}}^2)\right]\cdot \frac{{\mathrm{R}}_{\mathrm{w}}}{{\mathrm{g}}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}}\\ {\mathsf{\omega }}_{\mathrm{d}\mathrm{e}\mathrm{m}}=\frac{\mathrm{v}\cdot {\mathrm{g}}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}}{{\mathrm{R}}_{\mathrm{w}}}\\ \mathrm{A}\mathrm{m}\mathrm{o}\mathrm{n}\mathrm{g}:\\ {\mathrm{m}}_{\mathrm{b}\mathrm{u}\mathrm{s}}={\mathrm{m}}_{\mathrm{v}\mathrm{e}\mathrm{h}}+{\mathrm{m}}_{\mathrm{p}}+1.15({\mathrm{n}}_{\mathrm{b}\mathrm{a}\mathrm{t}}{\mathrm{m}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}+{\mathrm{n}}_{\mathrm{c}\mathrm{a}\mathrm{p}}{\mathrm{m}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}})\\ \mathrm{a}=\frac{\mathrm{d}\mathrm{v}}{\mathrm{d}\mathrm{t}};{\mathrm{a}}_{\omega }=\frac{\mathrm{a}}{{\mathrm{R}}_{\mathrm{w}}}\end{array}$$

(13)

In the optimization process, the minimal mileage L of more than 50 km should be considered, obtained at a constant cruising speed v₀ (50 km/h) on a flat road [25]. Accordingly, we can deduce the following inequality constraints.

$${\mathrm{n}}_{\mathrm{b}\mathrm{a}\mathrm{t}}\ge \left(\frac{1}{2}\mathsf{\rho }\mathrm{A}{\mathrm{c}}_{\mathrm{d}}{{\mathrm{v}}_0}^2+{\mathrm{m}}_{\mathrm{b}\mathrm{u}\mathrm{s}}\mathrm{g}{\mathrm{c}}_{\mathrm{r}}\right)\frac{\mathrm{L}}{{\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}}{\mathrm{Q}}_{\mathrm{b}\mathrm{a}\mathrm{t}}{\mathsf{\eta }}_{\mathrm{T}}}$$

(14)

We assume that the maximum required power in the drive mode and brake mode is provided by the SCs (SCs output power in driving mode, and SCs absorb power in braking mode). The following inequality constraints should be satisfied when selecting the number of SCs.

$${\mathrm{n}}_{\mathrm{c}\mathrm{a}\mathrm{p}}\ge \frac{\max \left\{\left|{\mathrm{P}}_{\mathrm{d}\mathrm{e}\mathrm{m}}\right|\right\}}{\left|{\mathrm{I}}_{\mathrm{cap}\_\max }\right|{\mathrm{V}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}}}$$

(15)

4. Convex Optimal Control Strategy Based on the Battery Degradation

Through the driving cycle, we can calculate the power demand of the bus at every step. In the driving mode, the required power P_dem should be the output power of the drive motor on its output shaft. The electrical power output on the DC bus is equal to the motor output power plus the motor power loss, which is obtained by the fitting. The electrical power output on the DC bus at this time is the total power to be satisfied by the batteries and the SCs (considering the efficiency of DC/DC converter).

Assuming that the SCs are in the same energy storage state at the beginning and end of the driving cycle, the degradation percentage Q_{loss_sum} of the battery is calculated using the following equation.

$${\mathrm{Q}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}\_\mathrm{s}\mathrm{u}\mathrm{m}}={\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{N}}{\mathrm{Q}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}(\mathrm{k})}$$

(16)

In order to reduce the computation time in the convex optimization, as shown in Figure 7, the relationship between the battery current I_bat and the battery degradation percentage Q_loss is determined at room temperature 25 °C based on Equation (9). Irrespective of the braking or driving modes, Q_loss always increases as the charge or discharge current I_bat increases. Hence, the optimization of the entire driving cycle of battery degradation can be equivalent to optimizing the entire driving cycle of the battery current in the absolute value. There is the following relationship:

$$\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}\left\{{\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{N}}{\mathrm{Q}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}(\mathrm{k})}\right\}\iff \mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}\left\{{\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{N}}\left|{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}}(\mathrm{k})\right|}\right\}$$

(17)

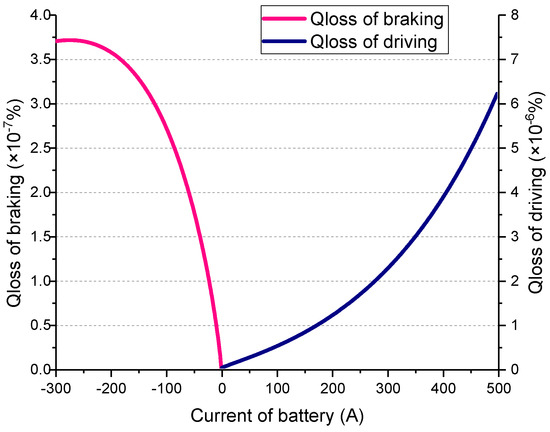
Figure 7. The relationship between battery charge/discharge current I_bat and battery degradation percentage Q_loss.

Therefore, as shown in Equation (18), the equivalent optimization target for the purpose of optimizing the battery degradation could be obtained. According to the constraints of the optimization target in the convex optimization [26], Equation (18) satisfies the requirement that the convex optimization must be a convex function or an affine function for the objective function.

$$\mathrm{J}=\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}\left\{{\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{N}}\left|{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}}(\mathrm{k})\right|}\right\}$$

(18)

The implementation process of the convex optimization strategy used in this study is shown in Figure 8. In order to satisfy the constraints on the number of battery cells and SC cells in Equations (14) and (15), the number of selected battery and SC cells is n_bat = 120 and n_cap = 240, respectively. The battery pack and SC pack in the HESS are all grouped by n series and one parallel connection, and the unbalance between the cells is ignored [27]. As the energy source of the vehicle, the LiFePO₄ battery pack is not only for the drive motor to provide energy, but also for the super capacitor when SOC_cap is low. The SC pack is between the LiFePO₄ battery pack and the drive motor, acting as an energy and power buffer, and absorbing the braking energy from the drive motor during braking.

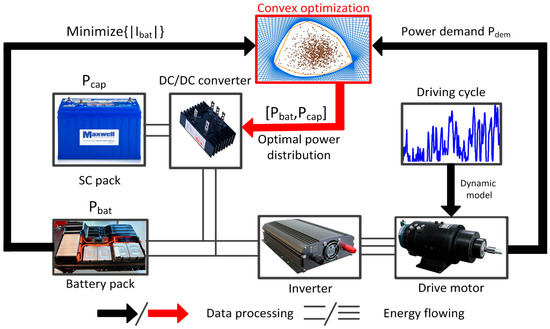
Figure 8. The implementation process of the convex optimization strategy.

According to the output voltage changes of the battery and the SC cell, we can constrain the output energy range of the battery pack and capacitor group,

$$\{\begin{array}{l}{\mathrm{E}}_{\mathrm{b}\mathrm{a}\mathrm{t}}(\mathrm{k})\in \frac{{\mathrm{n}}_{\mathrm{b}\mathrm{a}\mathrm{t}}{\mathrm{Q}}_{\mathrm{b}\mathrm{a}\mathrm{t}}}{2}([{{\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\min }}^2,{{\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\max }}^2]-{{\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}0}}^2)\\ {\mathrm{E}}_{\mathrm{c}\mathrm{a}\mathrm{p}}(\mathrm{k})\in \frac{{\mathrm{n}}_{\mathrm{c}\mathrm{a}\mathrm{p}}{\mathrm{C}}_{\mathrm{c}\mathrm{a}\mathrm{p}}}{2}([{{\mathrm{V}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\min }}^2,{{\mathrm{V}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\max }}^2]-{{\mathrm{V}}_{\mathrm{c}\mathrm{a}\mathrm{p}0}}^2)\end{array}$$

(19)

where V_{bat_min}, V_{bat_max,} V_{cap_min}, and V_{cap_max} are the maximum and minimum voltages corresponding to the battery and the SOC of the SC, given by Equation (20).

$$\{\begin{array}{l}{\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\min ,\mathrm{m}\mathrm{a}\mathrm{x}}=\mathrm{S}\mathrm{O}{\mathrm{C}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\min ,\max }({\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}1}-{\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}0})+{\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}0}\\ {\mathrm{V}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\min ,\mathrm{m}\mathrm{a}\mathrm{x}}=\mathrm{S}\mathrm{O}{\mathrm{C}}_{\mathrm{S}\mathrm{C}\_\min ,\max }{\mathrm{V}}_{\mathrm{S}\mathrm{C}1}\end{array}$$

(20)

The range of the output power of the battery and SC pack can be limited according to the maximum charge/discharge current of the battery and SC cell.

$$\{\begin{array}{l}{\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}}\in [{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\min },{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\max }]{\mathrm{n}}_{\mathrm{b}\mathrm{a}\mathrm{t}}{\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}}\\ {\mathrm{P}}_{\mathrm{c}\mathrm{a}\mathrm{p}}\in [{\mathrm{I}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\min },{\mathrm{I}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\max }]{\mathrm{n}}_{\mathrm{c}\mathrm{a}\mathrm{p}}{\mathrm{V}}_{\mathrm{c}\mathrm{a}\mathrm{p}}\end{array}$$

(21)

The power consumed on the battery pack and the SC pack internal resistance can be calculated from Equation (22).

$$\{\begin{array}{l}{\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}={\mathrm{n}}_{\mathrm{b}\mathrm{a}\mathrm{t}}{{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}}}^2{\mathrm{R}}_{\mathrm{b}\mathrm{a}\mathrm{t}}\\ {\mathrm{P}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}={\mathrm{n}}_{\mathrm{c}\mathrm{a}\mathrm{p}}{{\mathrm{I}}_{\mathrm{c}\mathrm{a}\mathrm{p}}}^2{\mathrm{R}}_{\mathrm{c}\mathrm{a}\mathrm{p}}\end{array}$$

(22)

where I_bat and I_cap are the currents flowing through the battery and the SC cell, respectively. Both I_bat and I_cap have the following constraints.

$$\{\begin{array}{l}{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}}\in [{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\min },{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\max }]\\ {\mathrm{I}}_{\mathrm{c}\mathrm{a}\mathrm{p}}\in [{\mathrm{I}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\min },{\mathrm{I}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\max }]\end{array}$$

(23)

For the battery pack and the SC pack, it is necessary to satisfy the total power demand in different cases, by satisfying the following equation constraints.

$$\{\begin{array}{cc}{\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{open}}+{\mathrm{P}}_{\mathrm{c}\mathrm{a}\mathrm{p}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{n}}{\mathsf{\eta }}_{\mathrm{D}\mathrm{C}}={\mathrm{P}}_{\mathrm{e}\mathrm{m}\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}+{\mathrm{P}}_{\mathrm{d}\mathrm{e}\mathrm{m}}/{\eta }_{\mathrm{T}}& {\mathrm{P}}_{\mathrm{d}\mathrm{e}\mathrm{m}}\ge 0\\ {\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{open}}+{\mathrm{P}}_{\mathrm{c}\mathrm{a}\mathrm{p}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{n}}/{\mathsf{\eta }}_{\mathrm{D}\mathrm{C}}={\mathrm{P}}_{\mathrm{e}\mathrm{m}\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}+{\mathrm{P}}_{\mathrm{d}\mathrm{e}\mathrm{m}}{\eta }_{\mathrm{T}}& {\mathrm{P}}_{\mathrm{d}\mathrm{e}\mathrm{m}}<0\end{array}$$

(24)

where P_batopen and P_capopen are the output powers of the battery pack and SC pack, respectively. P_emloss is the motor power loss and can be interpolated by the motor power loss curve.

In this study, we use Equation (18) as an optimization target, and the battery pack energy E_b, SC pack energy E_cap, battery pack port output power P_batopen, and SC pack port output power P_capopen as the convex optimization variables. The battery pack power P_bat, SC pack power P_cap, battery pack power loss P_{bat_loss}, and SC pack power loss P_{cap_loss} are used as the equation constraints of the convex optimization. The overall optimization function is given in Table 4.

Table 4. Convex optimization function of hybrid energy storage system

Variables	${\mathrm{E}}_{\mathrm{b}\mathrm{a}\mathrm{t}}(\mathrm{N}+1),{\mathrm{E}}_{\mathrm{c}\mathrm{a}\mathrm{p}}(\mathrm{N}+1),{\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{n}}(\mathrm{N}),{\mathrm{P}}_{\mathrm{c}\mathrm{a}\mathrm{p}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{n}}(\mathrm{N})$
Minimize	${\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{N}}\left|{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}}(\mathrm{k})\right|}$
Subject to	$\begin{array}{l}\{\begin{array}{l}{\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{open}}(\mathrm{k})+{\mathrm{P}}_{\mathrm{c}\mathrm{a}\mathrm{p}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{n}}(\mathrm{k}){\mathsf{\eta }}_{\mathrm{D}\mathrm{C}}={\mathrm{P}}_{\mathrm{e}\mathrm{m}\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}(\mathrm{k})+{\mathrm{P}}_{\mathrm{d}\mathrm{e}\mathrm{m}}(\mathrm{k})/{\mathsf{\eta }}_{\mathrm{T}}{\mathrm{P}}_{\mathrm{d}\mathrm{e}\mathrm{m}}(\mathrm{k})\ge 0\\ {\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{open}}(\mathrm{k})+{\mathrm{P}}_{\mathrm{c}\mathrm{a}\mathrm{p}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{n}}(\mathrm{k})/{\mathsf{\eta }}_{\mathrm{D}\mathrm{C}}={\mathrm{P}}_{\mathrm{e}\mathrm{m}\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}(\mathrm{k})+{\mathrm{P}}_{\mathrm{d}\mathrm{e}\mathrm{m}}(\mathrm{k}){\mathsf{\eta }}_{\mathrm{T}}{\mathrm{P}}_{\mathrm{d}\mathrm{e}\mathrm{m}}(\mathrm{k})\ge 0\end{array}\\ {\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}(\mathrm{k})={\mathrm{n}}_{\mathrm{b}\mathrm{a}\mathrm{t}}{{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}0}}^{(\mathrm{k})2}{\mathrm{R}}_{\mathrm{b}\mathrm{a}\mathrm{t}};{\mathrm{P}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}={\mathrm{n}}_{\mathrm{c}\mathrm{a}\mathrm{p}}{\mathrm{I}}_{\mathrm{c}\mathrm{a}\mathrm{p}0}{(\mathrm{k})}^2{\mathrm{R}}_{\mathrm{c}\mathrm{a}\mathrm{p}}\\ {\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}}(\mathrm{k})=-\Delta {\mathrm{E}}_{\mathrm{b}\mathrm{a}\mathrm{t}}(\mathrm{k});{\mathrm{P}}_{\mathrm{c}\mathrm{a}\mathrm{p}}(\mathrm{k})=-\Delta {\mathrm{E}}_{\mathrm{c}\mathrm{a}\mathrm{p}}(\mathrm{k})\\ {\mathrm{E}}_{\mathrm{b}\mathrm{a}\mathrm{t}}(\mathrm{k})\in ([{{\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\min }}^2,{{\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\max }}^2]-{{\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}0}}^2){\mathrm{n}}_{\mathrm{b}\mathrm{a}\mathrm{t}}{\mathrm{Q}}_{\mathrm{b}\mathrm{a}\mathrm{t}}/2\\ {\mathrm{E}}_{\mathrm{c}\mathrm{a}\mathrm{p}}(\mathrm{k})\in ([{{\mathrm{V}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\min }}^2,{{\mathrm{V}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\max }}^2]-{{\mathrm{V}}_{\mathrm{c}\mathrm{a}\mathrm{p}0}}^2){\mathrm{n}}_{\mathrm{c}\mathrm{a}\mathrm{p}}{\mathrm{C}}_{\mathrm{c}\mathrm{a}\mathrm{p}}/2\\ {\mathrm{P}}_{\mathrm{b}\mathrm{a}\mathrm{t}}(\mathrm{k})\in [{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\min },{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\mathrm{m}\mathrm{a}\mathrm{x}}]{\mathrm{n}}_{\mathrm{b}\mathrm{a}\mathrm{t}}{\mathrm{V}}_{\mathrm{b}\mathrm{a}\mathrm{t}}(\mathrm{k})\\ {\mathrm{P}}_{\mathrm{c}\mathrm{a}\mathrm{p}}(\mathrm{k})\in [{\mathrm{I}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\min },{\mathrm{I}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\mathrm{m}\mathrm{a}\mathrm{x}}]{\mathrm{n}}_{\mathrm{c}\mathrm{a}\mathrm{p}}{\mathrm{V}}_{\mathrm{c}\mathrm{a}\mathrm{p}}(\mathrm{k})\\ {\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}}\in [{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\min },{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{t}\_\max }];{\mathrm{I}}_{\mathrm{c}\mathrm{a}\mathrm{p}}\in [{\mathrm{I}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\min },{\mathrm{I}}_{\mathrm{c}\mathrm{a}\mathrm{p}\_\max }]\end{array}$
	$\forall \mathrm{k}\in \left\{0,\dots ,\mathrm{N}\right\}$

According to the description of the convex optimization problem in Ref. [26], the constraint conditions in Table 4 are convex or affine functions; the entire convex optimization problem satisfies the convex optimization requirement, and the convex optimization implementation flow is shown in Figure 9.

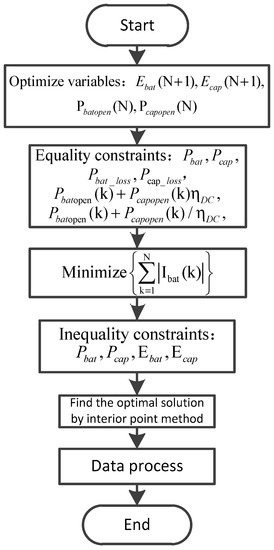
Figure 9. Convex optimization implementation flow.

5. Simulation and Results Analysis

In order to verify the effectiveness of the HESS optimization proposed in this study, we compared its performance with that of the rule-based power distribution strategy under the Harbin city driving cycle [28]. The Harbin city driving cycle and the power demand is shown in Figure 10. The convex optimization result is shown in Figure 11. It can be observed that the battery only provides a small range of demand for power fluctuations, whereas the SC satisfies instantaneous high power requirements. When the required power is greater than a certain threshold, the SC and the battery pack together provide the power required. However, owing to the presence of DC/DC converter efficiency and powertrain efficiency, the sum of the power of the battery pack and the SC pack is much greater than the power demand. Furthermore, the same as the result of two efficiency effects, in the braking mode, the SC cannot recover all the braking energy. In addition, as shown in Figure 11b, the battery only provides a small demand for power and the SC satisfies instantaneous high power requirements; this can be reflected in the relationship between power demand and SC power. When the power demand fluctuates in the range of 0 kW to 20 kW, the SC does not output power. This part of the power is borne by the battery and when the power demand fluctuates in the range of 20 kW to the highest power demand, the SC satisfies the power demand. Owing to the efficiency of DC/DC converter and the efficiency of the powertrain, the slope of the fitted line k is slightly greater than 1 when the demand power is greater than 20 kW. When the power demand fluctuates in the negative range, the SC absorbs the braking energy, and the slope of the fitting line k is less than 1 owing to the DC/DC converter efficiency and the efficiency of the powertrain. The entire convex optimization process consumes 1.33 × 10⁷ J, i.e., approximately 3.70 kWh. Since the optimization target is absolute value of the battery current, while the terminal voltage drop of the battery pack is very small in one driving cycle. Therefore, the optimization goal also has a significant role in optimizing the battery energy consumption.

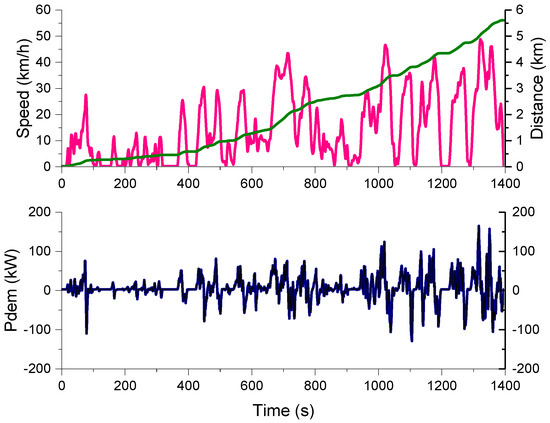
Figure 10. Harbin city driving cycle and the power demand.

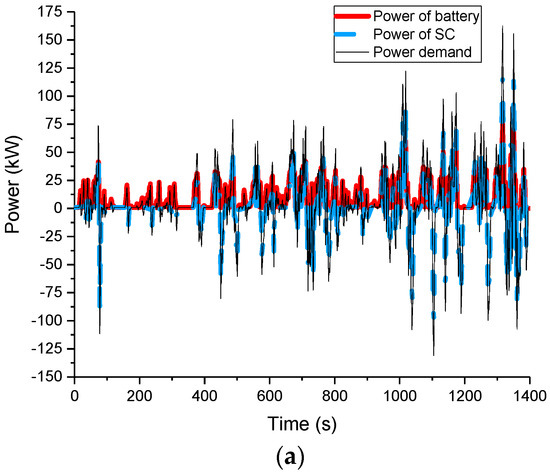
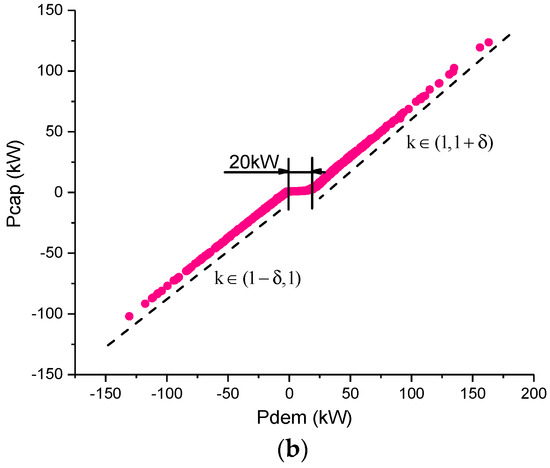
Figure 11. Convex optimization results: (a) power distribution results based on convex optimization; and (b) the relationship between power demand and SC power.

Figure 12 shows the battery current and battery degradation percent at a room temperature of 25 °C based on convex optimization. In the latter part of the driving cycle, the acceleration/deceleration of the vehicle is violent; hence, the battery current undergoes greater fluctuations. However, the maximum value of the battery current does not exceed 200 A. The battery runs within 1C discharge magnification rate altogether. In addition, according to the relationship between the battery charge/discharge current I_bat and the battery degradation percentage Q_loss in Figure 7, it can be observed that the battery current has approximately an exponential relationship with the battery degradation percentage Q_loss when the battery current is greater than zero. Therefore, Q_loss obtained in Figure 12 is more intense than the battery current fluctuation. At room temperature of 25 °C, the battery degradation percent in one driving cycle is 2.16 × 10⁻⁴%.

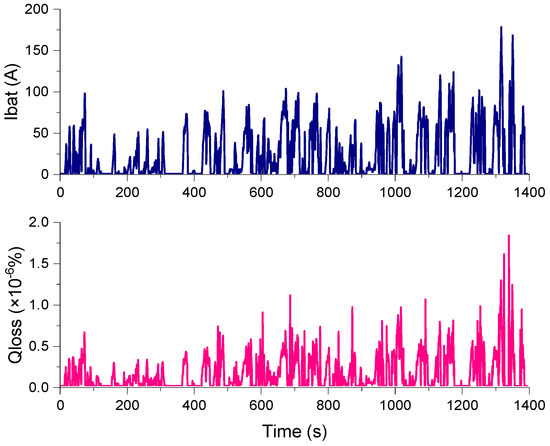
Figure 12. Battery current and battery degradation percentage at room temperature of 25 °C based on convex optimization.

In order to verify the effectiveness of the proposed optimization method in this paper for the electric bus equipped with semi-active HESS, it is compared with the rule-based strategy in Harbin driving cycle. The rule-based strategy is shown in Figure 13 [9,29]. When the power demand P_dem ≥ 0, the battery only provides the threshold power P_thr, and when P_dem > P_thr, the battery will provide the part of power demand exceed according to the SOC_cap. When the power demand P_dem < 0, it is also need to charge for SC according to the charge of state of the SC, when the SC pack is fully charged and then to the battery pack for energy braking. According to the characteristics of the SC power and the power demand relationship obtained from the convex optimization, the threshold power P_thr in the rule-based strategy is set to 20 kW, and the same power system model and initial parameters are used to calculate the power distribution based on the rules strategy, as shown in Figure 14.

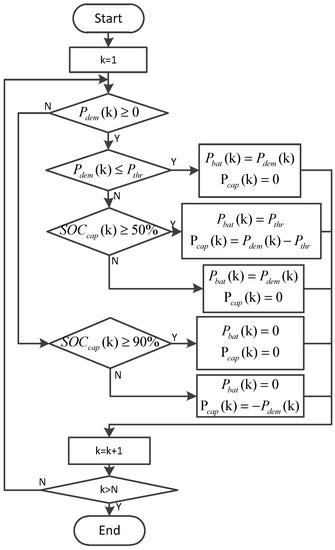
Figure 13. The implementation process of rule-based strategy.

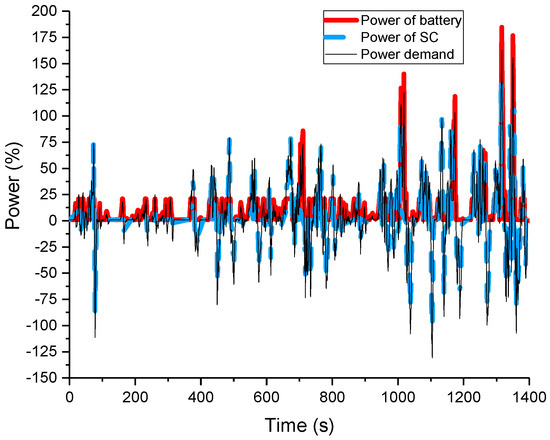
Figure 14. Power distribution results based on the rule-based strategy.

Figure 15 shows the battery current and battery degradation percent at 25 °C based on the rule strategy. In the latter part of the driving cycle, it can be seen that the SC obtained the energy from braking cannot satisfy the power demand; this part of the power demand difference can only be borne by the battery. Therefore, the battery experiences a large output power fluctuation. The battery current and battery decay percentages have several significant peaks in the later stages based on the rule strategy. However, in contrast, the SC satisfies the instantaneous high power ripple and the battery outputs a smaller power fluctuation in the convex optimization. According to the energy management strategy evaluation method in Ref. [30], the standard deviation of the battery current in two strategies has been calculated, as shown in Equation (25), where the I_{b_avg} is the average of battery current, s is the standard deviation of battery current.

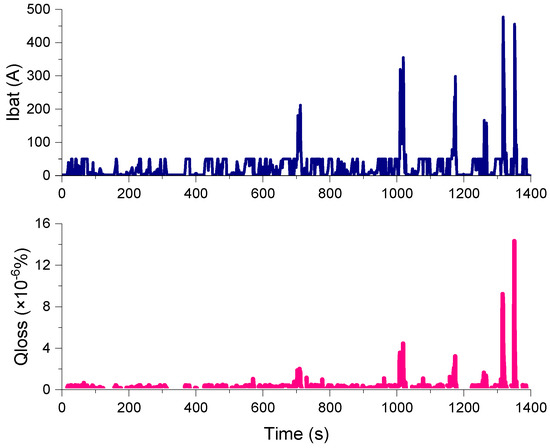
Figure 15. Battery current and battery degradation percentage at room temperature of 25 °C based on the rule strategy.

$$\mathrm{s}=\sqrt{\frac{{\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{N}}{({\mathrm{I}}_{\mathrm{b}}(\mathrm{k})-{\mathrm{I}}_{\mathrm{b}\_\mathrm{a}\mathrm{v}\mathrm{g}})}^2}}{\mathrm{N}}}$$

(25)

The standard deviation of the battery current based on the convex optimization strategy and rule-based strategy is 31.03 and 43.99, respectively, the battery current fluctuation based on the convex optimization strategy is smaller than rule-based strategy. Figure 16 shows the battery capacity degradation curve based on convex optimization and rule-based strategy. At approximately t = 1050 s, t = 1320 s, and t = 1360 s, the battery degradation percent based on the rule strategy has three significant rising intervals, which correspond to three battery current pulses based on the rules strategy; further, it can be reflected from the battery current and battery degradation percentage result of the rule-based strategy shown in Figure 15. In contrast, the battery power fluctuation is smoother when based on the convex optimization strategy, thus protecting the battery better. The rule-based strategy consumes 1.35 × 10⁷ J in one driving cycle, i.e., approximately 3.75 kWh, and the percentage of battery degradation is 2.31 × 10⁻⁴%.

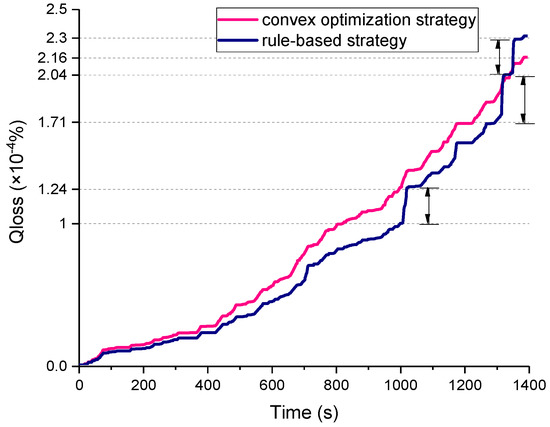
Figure 16. The percentage of battery degradation under two strategies.

In order to further reflect the real situation of a bus running on Harbin city roads in a day, and quantitatively analyze the potential of convex optimization relative to the rule-based strategy to improve battery life, we use nine Harbin city driving cycles (total 50.4 km) to simulate a cycle line: a bus from the bus terminal, followed by a cycle line, and subsequently back to the bus terminal. When the bus arrives at the terminal again, the CC-CV is used to recharge the battery. When the battery pack is recharged, the SOC_bat returns to 0.9. Table 5 shows the indicators of the battery pack when the bus drives in one cycle line based on the two strategies.

Table 5. The indicators of two strategies under one cycle line.

Strategy	Total Length	Initial SOC	Final SOC	ΔSOC	Recharge Time
Based on convex	50.4 km	0.9	0.4223	0.4777	1561 s
Based on rules	50.4 km	0.9	0.4112	0.4888	1598 s

For the LiFePO₄ battery pack with 120 cells in series and one in parallel, the SOC of the battery varies from SOC_bat = 0.9 to SOC_bat = 0.4223 through one cycle line under convex optimization, and the SOC of the battery varies from SOC_bat = 0.9 to SOC_bat = 0.4112 through one cycle line under rule-based strategy. In the process of the recharge phase, the recharge magnification is set to 1C. The entire recharge state continues for 1561 s in convex optimization and 1598 s in rule-based strategy. After the recharge, the battery SOC of the convex optimization strategy and the rule-based strategy are returned from SOC_bat = 0.4223 and SOC_bat = 0.4112 to SOC_bat = 0.9, respectively. According to the actual operation, the electric bus run four line cycles (approximately 200 km) in one day, and the electric bus needs to recharge the battery four times. Assuming that the battery is fully charged (SOC_bat = 0.9) in the first trip every day, the battery SOC change curve based on the convex optimization strategy and rule-based strategy can be obtained as shown in Figure 17.

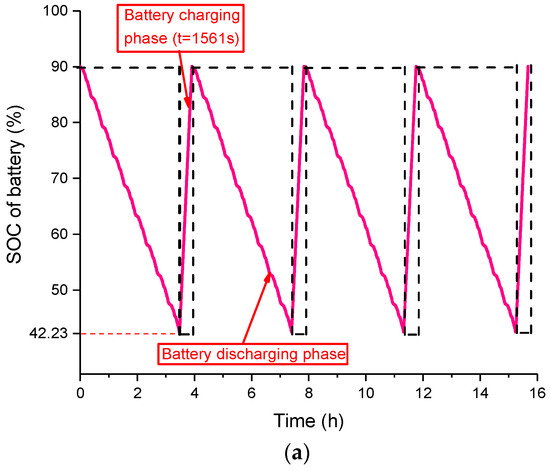
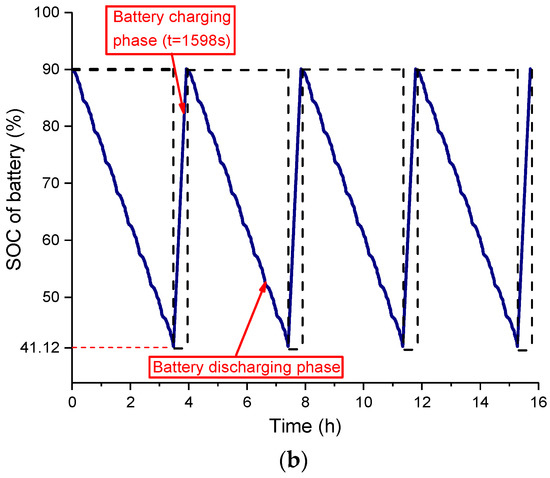
Figure 17. The battery SOC change based on different power distribution strategies in one day: (a) the battery SOC based on the optimization strategy described in this paper; and (b) the battery SOC based on the rules of the power distribution strategy.

The battery capacity degradation will occur during the entire charge/discharge process. Therefore, we can obtain the battery degradation percentage curve of the battery pack using the semi-empirical model in one day according to the battery charge/discharge situation. At room temperature of 25 °C, Q_loss base on the convex optimization strategy and the rules strategy are shown in Figure 18. After a day of operation (four cycle lines and four charging phases), Q_loss based on convex optimization is 9.6 × 10⁻³%, and the battery pack can be used for approximately 2.08 × 10³ days when the battery degradation is attenuated to 80% of its initial capacity, whereas Q_loss based on rules strategy is 10.3 × 10⁻³%, and the battery pack can be used for approximately 1.94 × 10³ days when the battery is attenuated to 80% of its initial capacity.

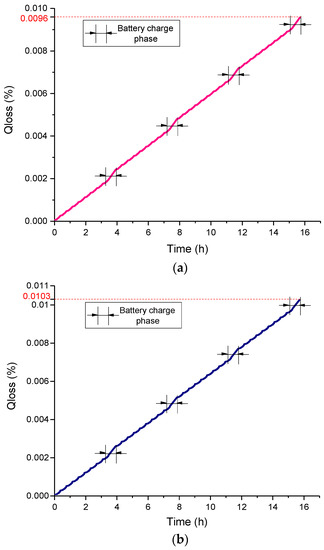
Figure 18. Q_loss based on the two strategies in one day: (a) battery degradation percentage based on convex optimization strategy; and (b) battery degradation percentage based on rules strategy.

Notably, there are two main causes of the greater battery degradation under rule-based strategy: (1) The battery current I_bat based on the convex optimization is more stable; hence, this results in a smaller Q_loss than the rule-based strategy, and this is reflected in the comparison of battery degradation under the two strategies shown in Figure 16; (2) Since the rule-based strategy consumes more energy in one day, the battery discharges deeper during operation (SOC_bat $\in$ [0.4223, 0.9] during one cycle line based on convex optimization and SOC_bat $\in$ [0.4112, 0.9] during one cycle line based on rules). Similarly, in order to return the battery back to the initial SOC, the rule-based strategy must be charging deeper than the convex optimized strategy (charging time t = 1561 s based on the convex optimization and t = 1598 s based on the rules). Consequently, the rule-based strategy increases the SOC operating range of the battery used in the same road cycle as compared to the strategy based on the convex optimization, which also increases the percentage of battery capacity degradation.

The battery usage time based on the two strategies is approximately 15 h in one day, but the usage time of the rule-based strategy is slightly longer because the charging time is longer. In Figure 18, Q_loss slope of the battery charging phase is larger than Q_loss at the time of traveling on the road; hence, the battery degradation caused by charging the battery at a charging magnification of 1C is greater than that caused by running on the road.

In order to obtain further analysis of Q_loss for one year in Harbin, we assume that the Harbin city bus will run for cycle lines in one day, and the bus operates for 30 days in a month. Therefore, the bus will operate for 360 days in a year. According to the average temperature of different months in Harbin, the daily value of Q_loss for every month can be calculated. It is assumed that the vehicle in each month is running at the monthly average temperature value and ignores the self-heating effect of the battery [31]. The semi-empirical model is also used to calculate the battery degradation. The average monthly temperature in Harbin is given in Table 6 [32], i.e., the temperature range of T $\in$ [−18.3 °C, 23.0 °C].

Table 6. The average temperature of the city in Harbin.

Month	Jan	Feb	Mar	Apr	May	Jun
Temp (°C)	−18.3	−13.6	−3.4	7.1	14.7	20.4
Month	Jul	Aug	Sep	Oct	Nov	Dec
Temp (°C)	23.0	21.1	14.5	5.6	−5.3	−14.8

According to the different average temperatures in different months, we can calculate the electric bus battery degradation percentage in one day for different months, as shown in Figure 19.

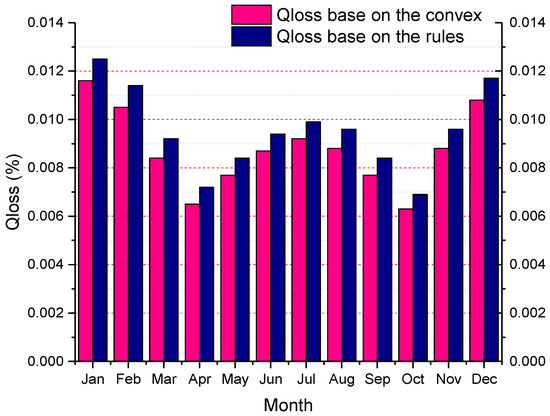
Figure 19. Percentage of battery degradation Q_loss in one day for different months.

As evident in Figure 19, Q_loss in different months based on the rules strategy is larger than that based on the convex optimization strategy. It can also be observed that, when the temperature is within ±10 °C during spring and autumn, Q_loss is minimal, whereas Q_loss is large in summer and winter with higher or lower temperatures. Especially in the winter months of December, January, and February, the two strategies under daily operation of the battery degradation reached ≥ 0.01%. This directly reflects the problem of large degradation of LiFePO₄ battery at low temperatures. The total battery degradation percentage of the year is shown in Table 7.

Table 7. The total battery degradation percentage in different month of the year.

Month	Jan	Feb	Mar	Apr	May	Jun
Qloss base on the convex/rules (%)	0.348/0.375	0.315/0.342	0.252/0.276	0.195/0.216	0.231/0.252	0.261/0.282
Month	Jul	Aug	Sep	Oct	Nov	Dec
Qloss base on the convex/rules (%)	0.276/0.297	0.264/0.288	0.231/0.252	0.189/0.207	0.264/0.288	0.324/0.351

In Table 7, Q_loss in one year based on the convex optimization strategy is 3.15%, and Q_loss based on the rules strategy is 3.43%. A quantitative analysis of battery life extension is addressed in this paper, assuming that the battery cannot be used when its capacity reduces to 80% of the initial value. Subsequently, the year of usage of the battery can be calculated using Equation (26).

$${\mathrm{Y}}_{\mathrm{o}\mathrm{p}\mathrm{e}}=20/{\displaystyle \sum _{\mathrm{m}=1}^{12}{\mathrm{Q}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}\_\mathrm{m}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{h}}(\mathrm{m})}$$

(26)

where Y_ope is the year of usage of battery and Q_{loss_month} is the percentage of Q_loss per month. It can be calculated that the bus equipped with HESS can operate for 6.35 years based on the convex optimization strategy. However, the bus equipped with HESS can operate for 5.84 years based on the rules strategy. The superiority of the convex optimization strategy is reflected, further illustrating the effectiveness of the use of convex optimization.

6. Conclusions

This paper used the electric bus power system with semi-active HESS as the research object, in the Harbin city driving cycle and proposed a convex optimization power distribution strategy target to optimize the battery current that represents battery degradation. According to the average temperature of different months of the year in the northern city of Harbin, the percentage of battery degradation of the electric bus with the HESS is analyzed and calculated. Simulation results show that using the convex optimization strategy proposed in this paper, at a room temperature of 25 °C, in a daily trip composed of the Harbin City Driving Cycle—including four cycle lines and four charging stages—the percentage of the battery degradation is 9.6 × 10⁻³%, whereas the battery degradation is 10.3 × 10⁻³% based on the rules under the same conditions. Assuming the daily mileage of an electric bus is approximately 200 km, and it will operate for 360 days in a year, the percentage of battery degradation is 3.15% in one year in Harbin. Before the battery capacity reduces to 80% of the initial value, the electric bus can run for 6.35 years based on the strategy proposed in this paper. However, the battery degrades 3.43% per year in Harbin using the rule-based strategy, and the bus can run for 5.84 years. Thus, the convex-based optimization strategy can operate for 0.51 year more than the rule-based strategy.