Sensible Heat Transfer during Droplet Cooling: Experimental and Numerical Analysis
Abstract
:1. Introduction
1.1. Objectives
1.2. Motives
1.3. Research Importance
1.4. Research Questions
- Is it possible to reproduce high spatial-temporal resolution experiments numerically? If yes, which are the limitations?
- Can the numerical results describe properly the sensible heat transfer in droplet cooling?
- How is the flow field within the droplet connected with the heat removed?
- Gap in knowledge 1: Validation of a numerical solver has never been conducted comparing high resolution, transient, experimental and numerical results for the entire temperature field that is developed in the solid region during the droplet impact.
- Gap in knowledge 2: The relation between the flow field within the droplet and the heat removed during droplet spreading has not been accurately described yet.
1.5. Literature Review
1.6. State of the Art
2. Materials and Methods
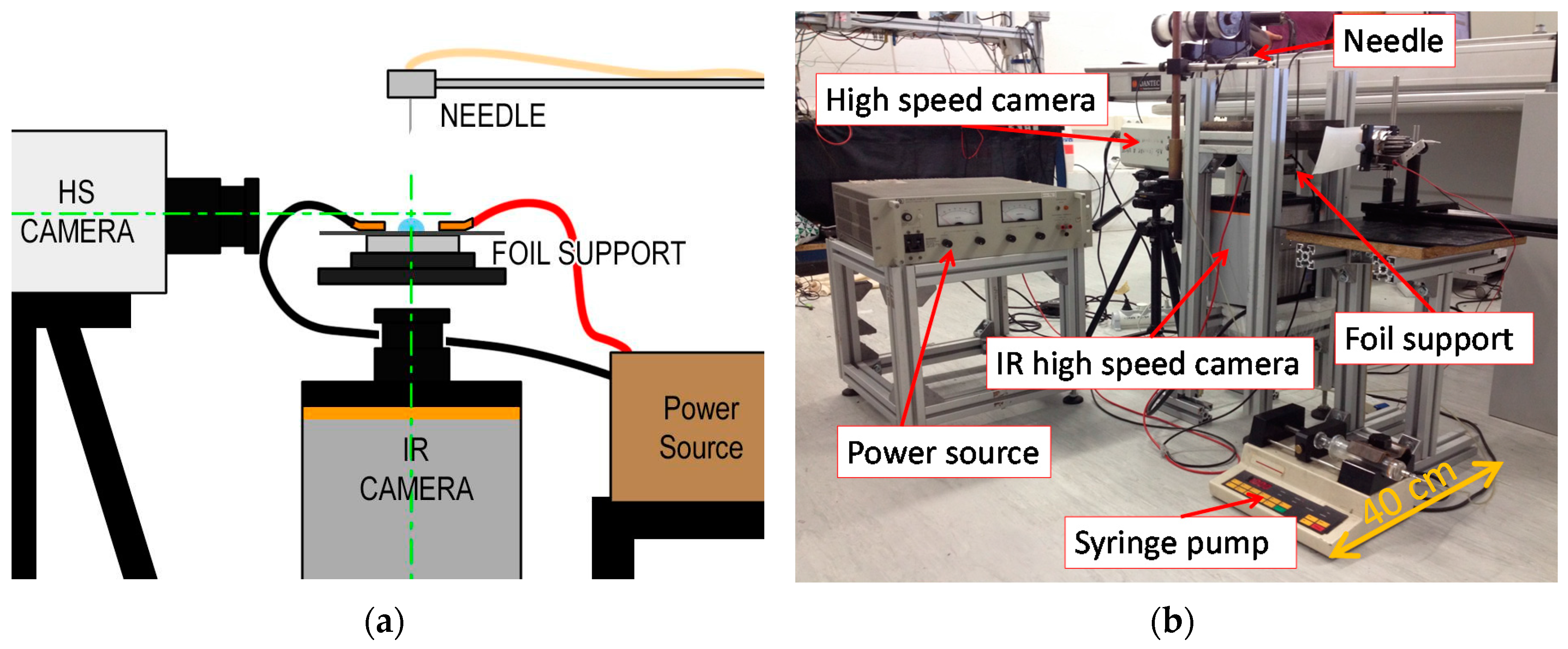
2.1. IR Thermography—High Speed Visualization Set-Up
2.2. Experimental Methods
2.3. Measurement Uncertainties
2.4. Numerical Methodology
2.5. Numerical Set Up
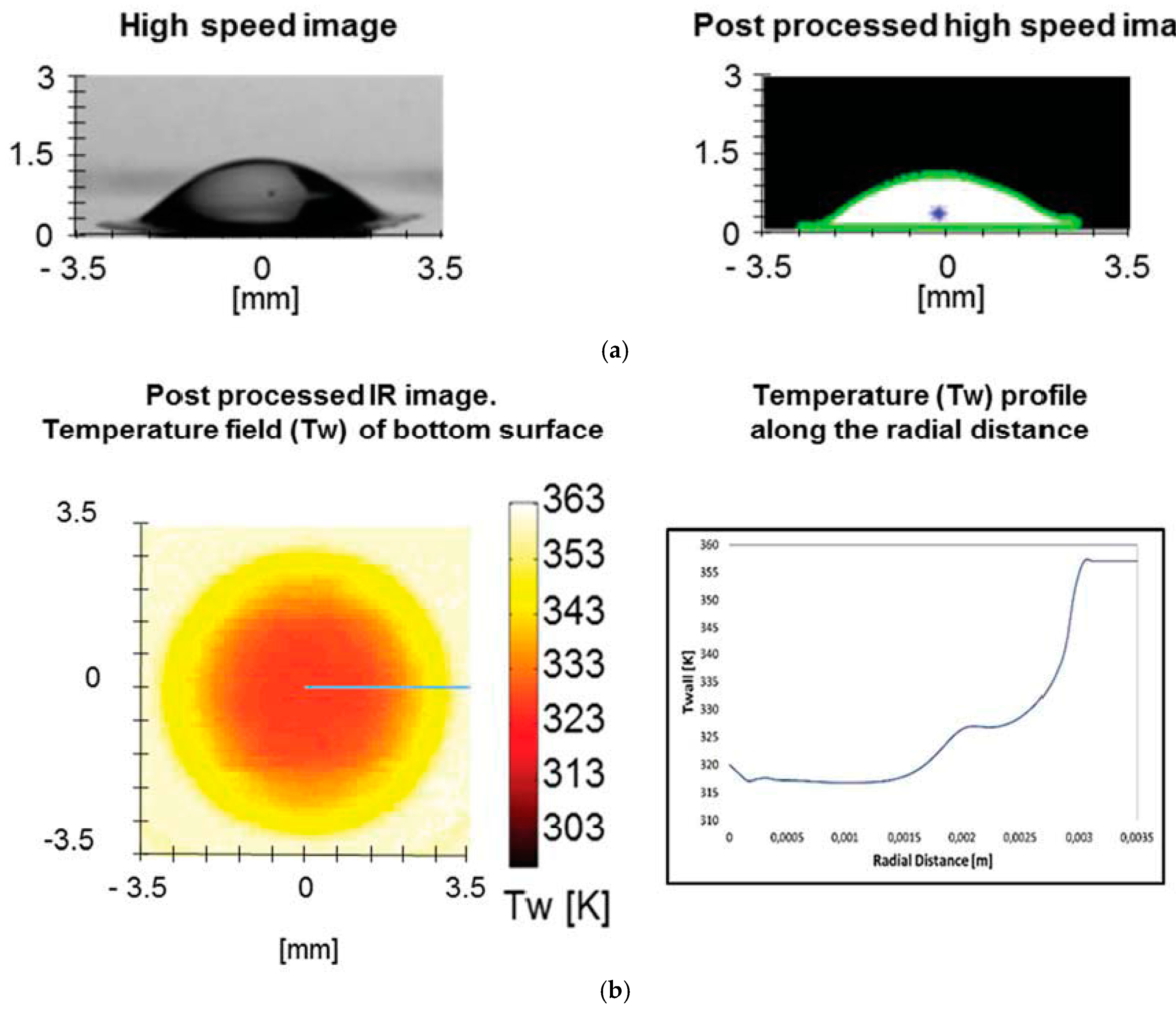
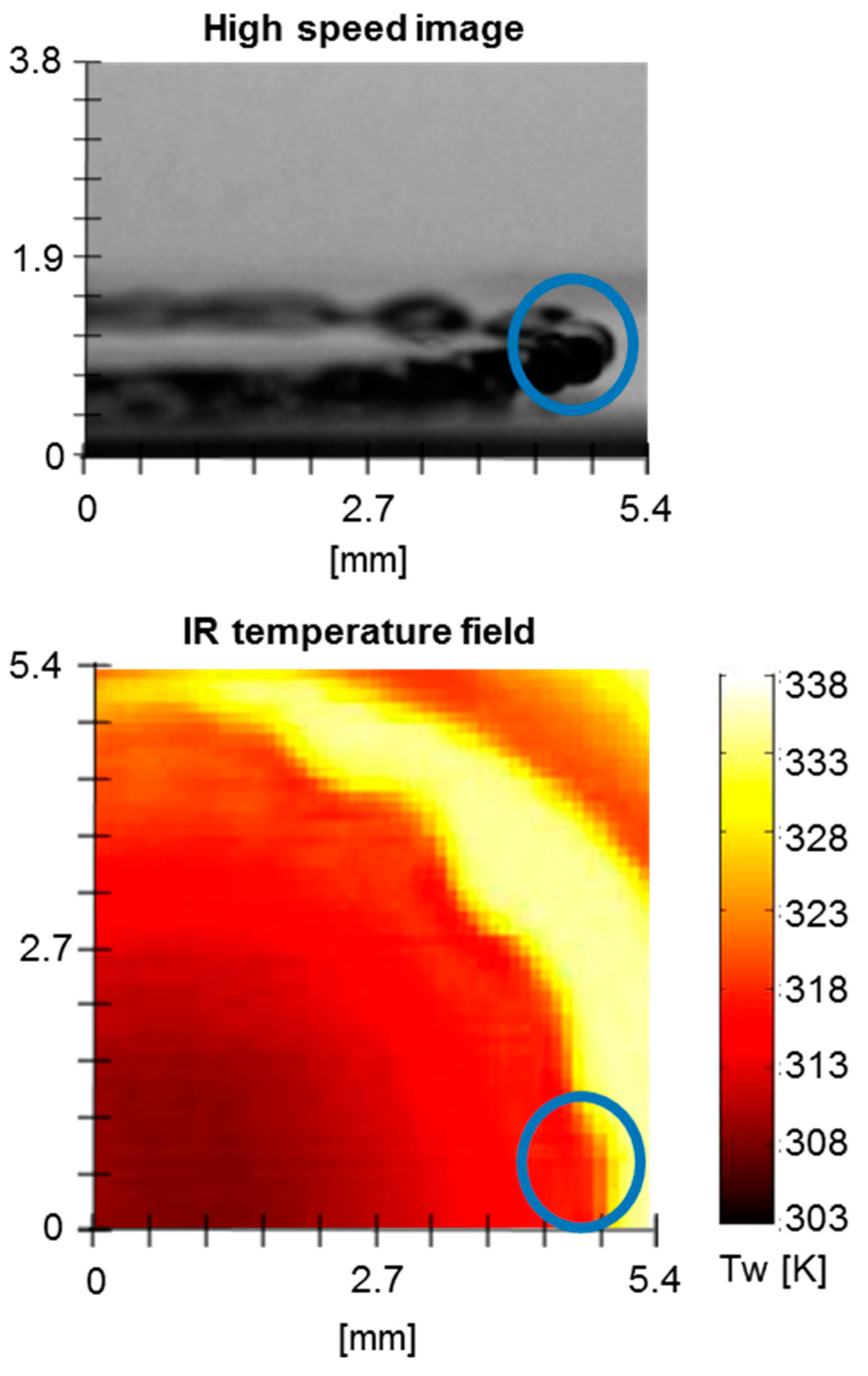
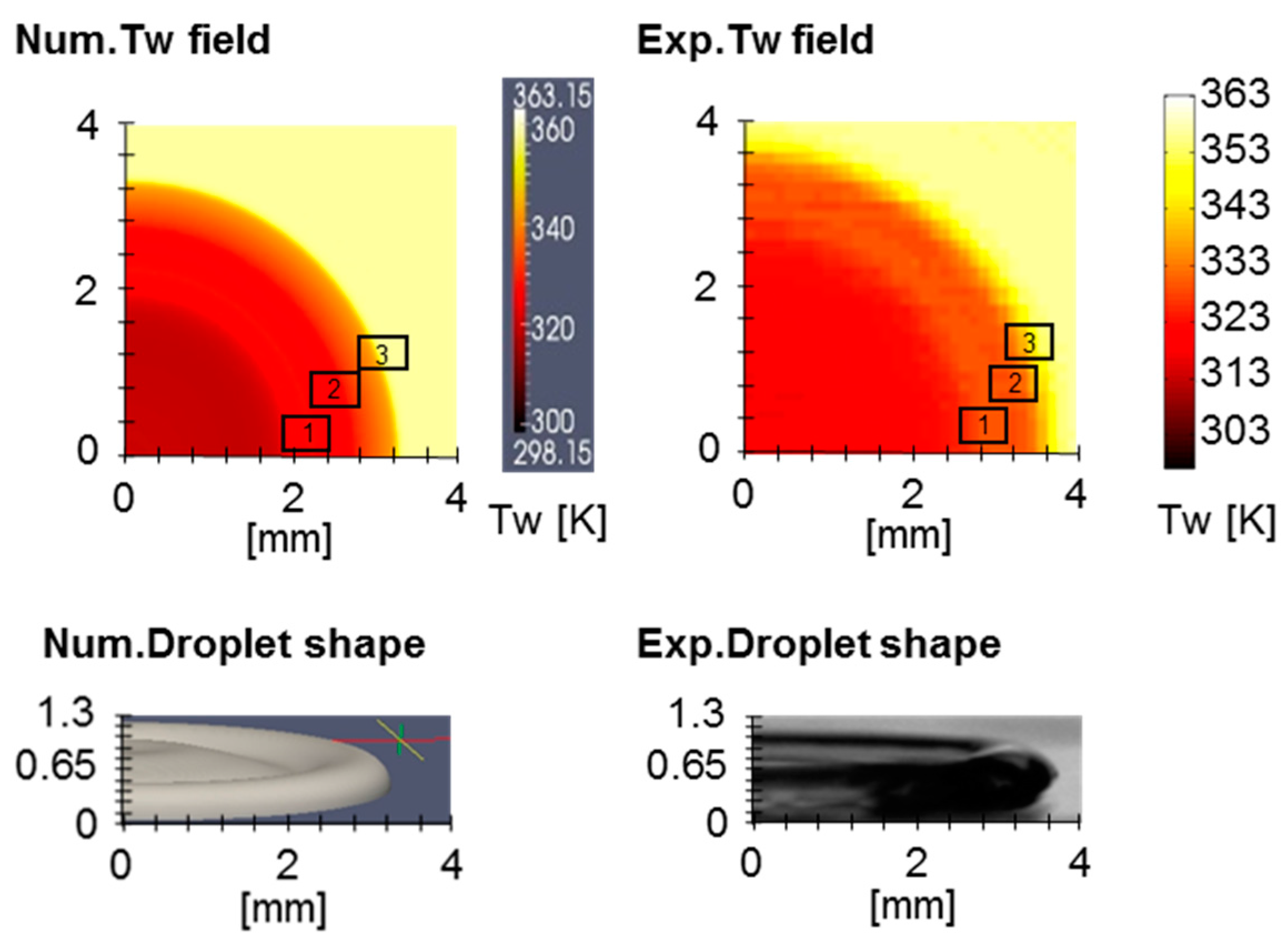
3. Results
3.1. Comparison Between Experimental and Numerical Results
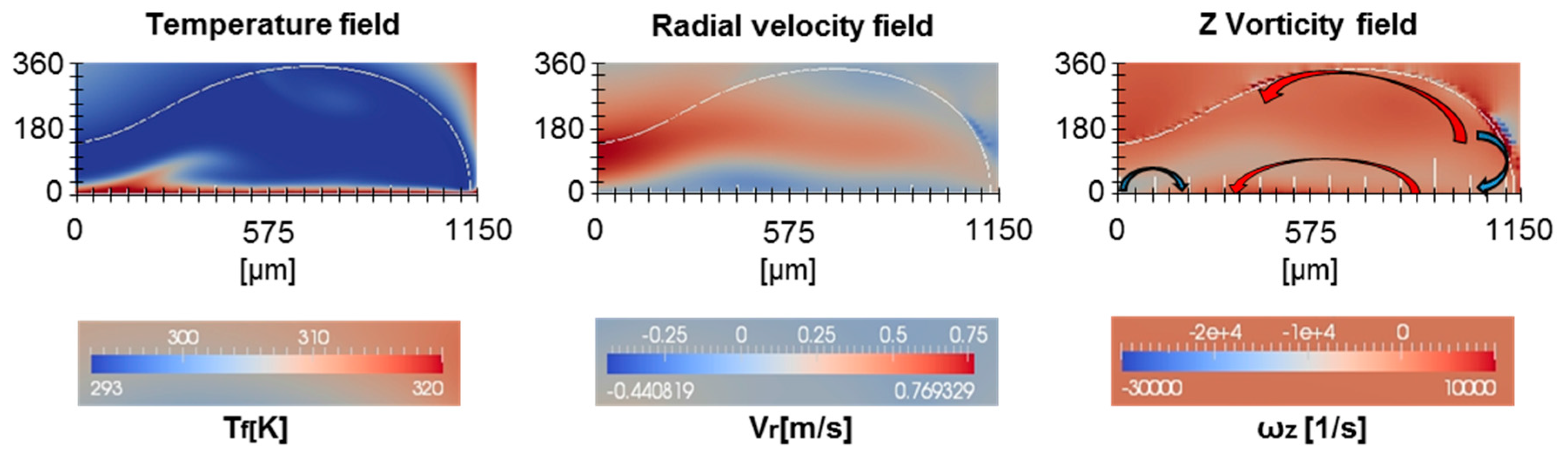
3.2. Relation Between Heat Tranfer and Droplet Dynamics
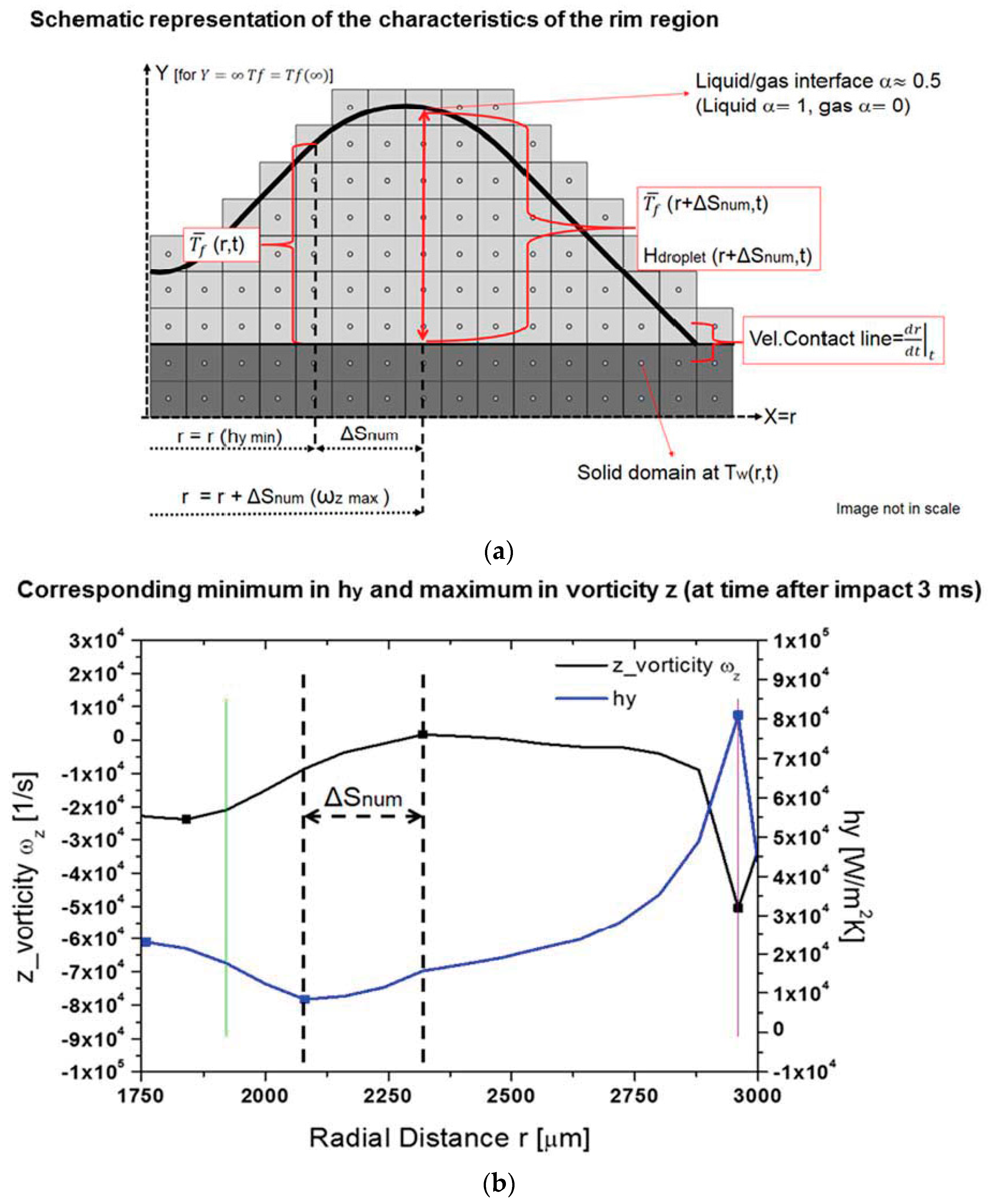
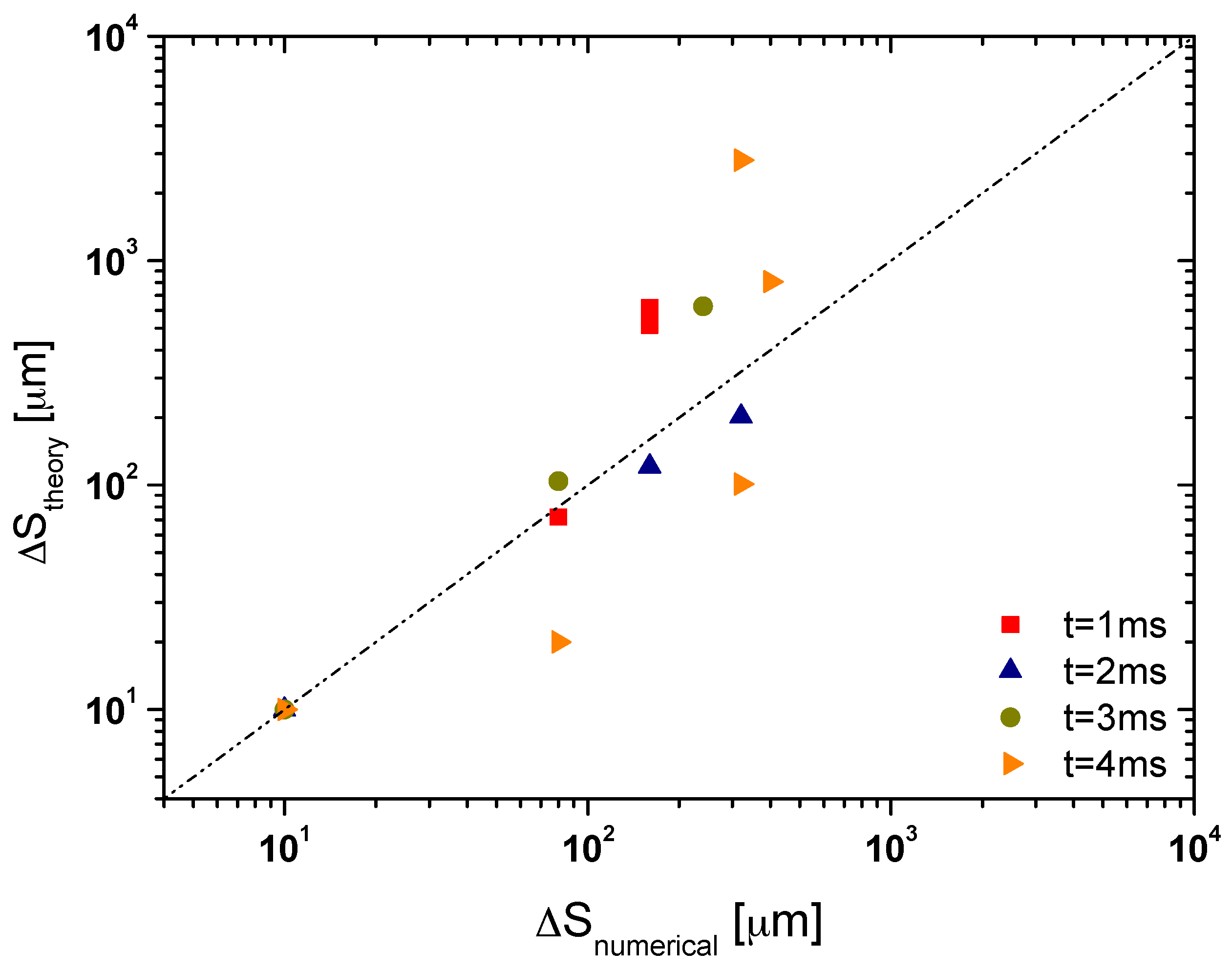
3.3. Theoretical Analysis of Heat and Mass Tranfer in the Rim Region
- A characteristic dimension for the vorticity field is the height of the droplet measured at the position of the minima or maxima of the vorticity, . The height of the droplet corresponds to the maximum value of the Y coordinate, measured for a volume fraction of . Therefore, the height of the droplet coincides with the vertical position of the liquid-air interface. substitutes the distance in Equation (17).
- The shifts relate to phenomena occurring in the bulk of the rim. Hence, the variation of the average temperature of the fluid measured along the shift dimension, should be accounted as . Here is the average temperature where the local minima or maxima of the heat transfer coefficient are, while is the average temperature at the corresponding local maxima or minima of the vorticity. The average temperature of the fluid is obtained as the average of the calculated temperatures in the vertical direction of the droplet for . replaces in the initially proposed formulation (Equation (17)).
- A characteristic velocity of the droplet can be defined as measured in time by the forward finite difference method, from the previously obtained spreading factors. This has been chosen since the minima or maxima for the vorticity and heat transfer coefficient in the region of the contact line, move together with the contact line and consequently with a velocity similar to . The proposed velocity also accounts for the bulk conditions of the droplet. This characteristic velocity substitutes in Equation (17).
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kim, J. Spray cooling heat transfer: The state of the art. Int. J. Heat Fluid Flow 2007, 28, 753–767. [Google Scholar] [CrossRef]
- Karwa, N.; Kale, S.R.; Subbarao, P.M.V. Experimental study of non-boiling heat transfer from a horizontal surface by water sprays. Exp. Therm. Fluid Sci. 2007, 32, 571–579. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, M.; Liu, D.; Xu, K. Heat flux correlation for spray cooling in the nonboiling regime. Heat Transf. Eng. 2011, 32, 1075–1081. [Google Scholar] [CrossRef]
- Rein, M. Phenomena of liquid drop impact on solid and liquid surfaces. Fluid Dyn. Res. 1993, 12, 61–93. [Google Scholar] [CrossRef]
- Yarin, A.L. Drop impact dynamics: Splashing, spreading, receding, bouncing. Annu. Rev. Fluid Mech. 2005, 38, 159–192. [Google Scholar] [CrossRef]
- Josserand, C.; Thoroddsen, S.T. Drop impact on a solid surface. Annu. Rev. Fluid Mech. 2016, 48, 365–391. [Google Scholar] [CrossRef]
- Moreira, A.L.N.; Moita, A.S.; Panão, M.R. Advances and challenges in explaining fuel spray impingement: How much of single droplet impact research is useful? Prog. Energy Combust. Sci. 2010, 36, 554–580. [Google Scholar] [CrossRef]
- Chandra, S.; Avedisian, C.T. On the collision of a droplet with a solid surface. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1991, 432, 1525. [Google Scholar] [CrossRef]
- Antonini, C.; Innocenti, M.; Horn, T.; Marengo, M.; Amirfazli, A. Understanding the effect of superhydrophobic coatings on energy reduction in anti-icing systems. Cold Reg. Sci. Technol. 2011, 67, 58–67. [Google Scholar] [CrossRef]
- Moita, A.S.; Moreira, A.L.N. Drop impacts onto cold and heated rigid surfaces: Morphological comparisons, disintegration limits and secondary atomization. Int. J. Heat Fluid Flow 2007, 28, 735–752. [Google Scholar] [CrossRef]
- Rioboo, R.; Marengo, M.; Tropea, C. Time evolution of liquid drop impact onto solid, dry surfaces. Exp. Fluids 2002, 33, 112–124. [Google Scholar] [CrossRef]
- Moita, A.S.; Moreira, A.L. Experimental study on fuel drop impacts onto rigid surfaces: Morphological comparisons, disintegration limits and secondary atomization. Proc. Combust. Inst. 2007, 31, 2175–2183. [Google Scholar] [CrossRef]
- Liang, G.; Mudawar, I. Review of drop impact on heated walls. Int. J. Heat Mass Transf. 2017, 106, 103–126. [Google Scholar] [CrossRef]
- Lee, J.; Kim, J.; Kiger, K.T. Time- and space-resolved heat transfer characteristics of single droplet cooling using microscale heater arrays. Int. J. Heat Fluid Flow 2001, 22, 188–200. [Google Scholar] [CrossRef]
- Paik, S.W.; Kihm, K.D.; Lee, S.P.; Pratt, D.M. Spatially and temporally resolved temperature measurements for slow evaporating sessile drops heated by a microfabricated heater array. J. Heat Transf. 2006, 129, 966–976. [Google Scholar] [CrossRef]
- Sodtke, C.; Ajaev, V.S.; Stephan, P. Evaporation of thin liquid droplets on heated surfaces. Heat Mass Transf. 2007, 43, 649–657. [Google Scholar] [CrossRef]
- Chen, Q.; Li, Y.; Longtin, J.P. Real-time laser-based measurement of interface temperature during droplet impingement on a cold surface. Int. J. Heat Mass Transf. 2003, 46, 879–888. [Google Scholar] [CrossRef]
- Bhardwaj, R.; Longtin, J.P.; Attinger, D. Interfacial temperature measurements, high-speed visualization and finite-element simulations of droplet impact and evaporation on a solid surface. Int. J. Heat Mass Transf. 2010, 53, 3733–3744. [Google Scholar] [CrossRef]
- Girard, F.; Antoni, M.; Sefiane, K. Infrared thermography investigation of an evaporating sessile water droplet on heated substrates. Langmuir 2010, 26, 4576–4580. [Google Scholar] [CrossRef] [PubMed]
- Tartarini, P.; Corticelli, M.A.; Tarozzi, L. Dropwise cooling: Experimental tests by infrared thermography and numerical simulations. Appl. Therm. Eng. 2009, 29, 1391–1397. [Google Scholar] [CrossRef]
- Jackson, R.G.; Kahani, M.; Karwa, N.; Wu, A.; Lamb, R.; Taylor, R.; Rosengarten, G. Effect of surface wettability on carbon nanotube water-based nanofluid droplet impingement heat transfer. J. Phys. Conf. Ser. 2014, 525, 12024. [Google Scholar] [CrossRef]
- Gradeck, M.; Seiler, N.; Ruyer, P.; Maillet, D. Heat transfer for Leidenfrost drops bouncing onto a hot surface. Exp. Therm. Fluid Sci. 2013, 47, 14–25. [Google Scholar] [CrossRef]
- Gambaryan-Roisman, T.; Budakli, M.; Roisman, I.V.; Stephan, P. Heat transfer during drop impact onto wetted heated smooth and structured substrates: Experimental and theoretical study. Prooceedings of the 14th International Heat Transfer Conference, Washington, DC, USA, 8–13 August 2010; pp. 755–761. [Google Scholar]
- Harlow, F.H.; Shannon, J.P. The splash of a liquid drop. J. Appl. Phys. 1967, 38, 3855–3866. [Google Scholar] [CrossRef]
- Tsurutani, K.; Yao, M.; Senda, J.; Fujimoto, H. Numerical analysis of the deformation process of a droplet impinging upon a wall. JSME Int. J. Ser. 2 Fluids Eng. Heat Transf. Power Combust. Thermophys. Prop. 1990, 33, 555–561. [Google Scholar] [CrossRef]
- Watanabe, T.; Kuribayashi, I.; Honda, T.; Kanzawa, A. Deformation and solidification of a droplet on a cold substrate. Chem. Eng. Sci. 1992, 47, 3059–3065. [Google Scholar] [CrossRef]
- Zhao, Z.; Poulikakos, D.; Fukai, J. Heat transfer and fluid dynamics during the collision of a liquid droplet on a substrate—I. Modeling. Int. J. Heat Mass Transf. 1996, 39, 2771–2789. [Google Scholar] [CrossRef]
- Francois, M.; Shyy, W. Computations of drop dynamics with the immersed boundary method, part 1: Numerical algorithm and buoyancy-induced effect. Numer. Heat Transf. Part B Fundam. 2003, 44, 101–118. [Google Scholar] [CrossRef]
- Francois, M.; Shyy, W. Computations of drop dynamics with the immersed boundary method, part 2: Drop impact and heat transfer. Numer. Heat Transf. Part B Fundam. 2003, 44, 119–143. [Google Scholar] [CrossRef]
- Healy, W.M.; Hartley, J.G.; Abdel-Khalik, S.I. On the validity of the adiabatic spreading assumption in droplet impact cooling. Int. J. Heat Mass Transf. 2001, 44, 3869–3881. [Google Scholar] [CrossRef]
- Rueda Villegas, L.; Tanguy, S.; Castanet, G.; Caballina, O.; Lemoine, F. Direct numerical simulation of the impact of a droplet onto a hot surface above the Leidenfrost temperature. Int. J. Heat Mass Transf. 2017, 104, 1090–1109. [Google Scholar] [CrossRef]
- Attané, P.; Girard, F.; Morin, V. An energy balance approach of the dynamics of drop impact on a solid surface. Phys. Fluids 2007, 19, 12101. [Google Scholar] [CrossRef]
- Roisman, I.V.; Rioboo, R.; Tropea, C. Normal impact of a liquid drop on a dry surface: Model for spreading and receding. Proc. R. Soc. A Math. Phys. Eng. Sci. 2002, 458, 1411–1430. [Google Scholar] [CrossRef]
- Pasandideh-Fard, M.; Aziz, S.D.; Chandra, S.; Mostaghimi, J. Cooling effectiveness of a water drop impinging on a hot surface. Int. J. Heat Fluid Flow 2001, 22, 201–210. [Google Scholar] [CrossRef]
- Strotos, G.; Aleksis, G.; Gavaises, M.; Nikas, K.-S.; Nikolopoulos, N.; Theodorakakos, A. Non-dimensionalisation parameters for predicting the cooling effectiveness of droplets impinging on moderate temperature solid surfaces. Int. J. Therm. Sci. 2011, 50, 698–711. [Google Scholar] [CrossRef]
- Pasandideh-Fard, M.Y.M.; Qiao, Y.M.; Chandra, S.; Mostaghimi, J. Capillary effects during droplet impact on a solid surface. Phys. Fluids 1996, 8, 650–659. [Google Scholar] [CrossRef]
- Vignes-Adler, M. Physico-chemical aspects of forced wetting. In Drop-Surface Interactions; Rein, M., Ed.; Springer: Vienna, Austria, 2002; pp. 103–157. [Google Scholar]
- Marmur, A. Measures of wettability of solid surfaces. Eur. Phys. J. Spec. Top. 2011, 197, 193. [Google Scholar] [CrossRef]
- Rioboo, R. Impactes De Gouttes Sur Surfaces Solides et Sèches. Ph.D. Thesis, Université de Paris VI, Paris, France, 2001. (In French). [Google Scholar]
- Teodori, E.; Valente, T.; Malavasi, I.; Moita, A.S.; Marengo, M.; Moreira, A.L.N. Effect of extreme wetting scenarios on pool boiling conditions. Appl. Therm. Eng. 2016, 115, 1424–1437. [Google Scholar] [CrossRef]
- Georgoulas, A.; Koukouvinis, P.; Gavaises, M.; Marengo, M. Numerical investigation of quasi-static bubble growth and detachment from submerged orifices in isothermal liquid pools: The effect of varying fluid properties and gravity levels. Int. J. Multiph. Flow 2015, 74, 59–78. [Google Scholar] [CrossRef]
- Hoang, D.A.; van Steijn, V.; Portela, L.M.; Kreutzer, M.T.; Kleijn, C.R. Benchmark numerical simulations of segmented two-phase flows in microchannels using the Volume of Fluid method. Comput. Fluids 2013, 86, 28–36. [Google Scholar] [CrossRef]
- Deshpande, S.S.; Anumolu, L.; Trujillo, M.F. Evaluating the performance of the two-phase flow solver interFoam. Comput. Sci. Discov. 2012, 5, 14016. [Google Scholar] [CrossRef]
- OpenFOAM, the Open Source CFD Toolbox, User Guide. Available online: http://www.openfoam.com/documentation/user-guide/ (accessed on 5 June 2017).
- Brackbill, J.; Kothe, D.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Kunkelmann, C. Numerical Modeling and Investigation of Boiling Phenomena. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2011. [Google Scholar]
- Healy, W.M.; Hartley, J.G.; Abdel-Khalik, S.I. Comparison between theoretical models and experimental data for the spreading of liquid droplets impacting a solid surface. Int. J. Heat Mass Transf. 1996, 39, 3079–3082. [Google Scholar] [CrossRef]







| Parameter | Uncertainties (rel. or abs) | Evaluation Method |
|---|---|---|
| Temperature T (K) | for is the one given by manufacturer. for is calculated after black body recalibration of the Infrared Camera. No standard deviation was accounted. | |
| Temperature difference ΔT (K) | ; ; | ; |
| Non-dimensional temperature T* (-) | ; ; | ; |
| Imposed volumetric heat rate | ||
| Radial distance r (mm) (infrared) | is evaluated according to the resolution in the arrangement used in the study |
| Parameter | Uncertainties (rel. or abs) | Evaluation Method |
|---|---|---|
| Contact Diameter Droplet diameter before impact | The uncertainty of post processed and was given as the maximum uncertainty of the image post processing in the definition of the interface of the droplet. | |
| Spreading ratio (-) | ||
| Impact velocity | In which is the measured value of velocity considering a vertical displacement of the droplet in the time interval between three consecutive frames i.e., 1.5 ms. is the velocity that would result from a displacement equal to in the same interval between three consecutive frames. is considered to be ±1 pixel (40 µm) in the optical arrangement used. | |
| Weber number We (-) |
| Material Properties | (kg/m3) | (J/kg·K) | (W/m·K) | ν (m2/s) | σ (N/m) |
|---|---|---|---|---|---|
| Air | 1 | 1006.4 | 0.025874 | 0.0000148 | - |
| Water | 1000 | 4184 | 0.59844 | 0.000001 | 0.007 |
| Stainless steel | 7880 | 477 | 18 | - | - |
| (W/m3) | Tw(in) (K) | We (-) |
|---|---|---|
| 98.6 × 106 | 353.15 | 24 |
| 65.4 × 106 | 333.15 | 151 |
| 122.8 × 106 | 373.15 | 151 |
| Time after Impact = 1 ms | ||||
| 160 | 516 | 238 | 1.3 | 0.67 |
| 160 | 616 | 179 | 2 | 0.67 |
| 80 | 72 | 89 | 1.5 | 0.67 |
| Time after Impact = 2 ms | ||||
| 160 | 121 | 240 | 0.2 | 0.45 |
| 320 | 202 | 298 | 0.3 | 0.45 |
| 0 | 0 | 29 | 0 | 0.45 |
| Time after Impact = 3 ms | ||||
| 80 | 104 | 209 | 0.3 | 0.26 |
| 240 | 626 | 327 | 0.5 | 0.26 |
| 0 | 0 | ≈0 | 0 | 0.26 |
| Time after Impact = 4 ms | ||||
| 80 | 20 | 149 | 0.2 | 0.08 |
| 320 | 2811 | 327 | 3 | 0.08 |
| 400 | 806 | 358 | 3.2 | 0.08 |
| 320 | 101 | 120 | 1.2 | 0.08 |
| 0 | 0 | 0 | 0 | 0.08 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teodori, E.; Pontes, P.; Moita, A.; Georgoulas, A.; Marengo, M.; Moreira, A. Sensible Heat Transfer during Droplet Cooling: Experimental and Numerical Analysis. Energies 2017, 10, 790. https://doi.org/10.3390/en10060790
Teodori E, Pontes P, Moita A, Georgoulas A, Marengo M, Moreira A. Sensible Heat Transfer during Droplet Cooling: Experimental and Numerical Analysis. Energies. 2017; 10(6):790. https://doi.org/10.3390/en10060790
Chicago/Turabian StyleTeodori, Emanuele, Pedro Pontes, Ana Moita, Anastasios Georgoulas, Marco Marengo, and Antonio Moreira. 2017. "Sensible Heat Transfer during Droplet Cooling: Experimental and Numerical Analysis" Energies 10, no. 6: 790. https://doi.org/10.3390/en10060790
APA StyleTeodori, E., Pontes, P., Moita, A., Georgoulas, A., Marengo, M., & Moreira, A. (2017). Sensible Heat Transfer during Droplet Cooling: Experimental and Numerical Analysis. Energies, 10(6), 790. https://doi.org/10.3390/en10060790










