Abstract
This study presents a fairness-aware framework for modeling the Probability of Default (PD) in individual credit scoring, explicitly addressing the trade-off between predictive accuracy and fairness. As machine learning (ML) models become increasingly prevalent in financial decision-making, concerns around bias and transparency have grown, particularly when improvements in fairness are achieved at the expense of predictive performance. To mitigate these issues, we propose a model-agnostic, post-processing threshold optimization framework that adjusts classification cut-offs using a tunable parameter, enabling institutions to balance fairness and performance objectives. This approach does not require model retraining and supports a scalarized optimization of fairness–performance trade-offs. We conduct extensive experiments with logistic regression, random forests, and XGBoost, evaluating predictive accuracy using Balanced Accuracy alongside fairness metrics such as Statistical Parity Difference and Equal Opportunity Difference. Results demonstrate that the proposed framework can substantially improve fairness outcomes with minimal impact on predictive reliability. In addition, we analyze model-specific trade-off behaviors and introduce diagnostic tools, including quadrant-based and ratio-based analyses, to guide threshold selection under varying institutional priorities. Overall, the framework offers a scalable, interpretable, and regulation-aligned solution for deploying responsible credit risk models, contributing to the broader goal of ethical and equitable financial decision-making.
1. Introduction
The financial sector is undergoing a significant transformation, driven by technological advancements such as Data Science (Dhar, 2013; Donoho, 2017; Han et al., 2011) and ML (Bishop, 2006; Mitchell, 1997; Vapnik, 1995), alongside an increasing emphasis on risk management. These developments enable institutions to optimize decision-making processes, particularly in credit risk assessment, which is crucial for managing loan defaults and complying with regulatory frameworks.
PD modeling plays a central role in credit risk management by estimating the likelihood that a borrower will fail to meet their financial obligations. Accurate PD models help institutions minimize financial risk, allocate capital efficiently, and enhance transparency in decision-making.
While traditional approaches (Gietzen, 2017; Hanea et al., 2021; Izzi et al., 2012) and statistical methods (Cox, 2018) are interpretable and well-established, they often struggle to capture complex patterns in data, making them less suitable for dynamic and high-dimensional environments. In contrast, ML models offer greater flexibility and predictive power to address these challenges. However, their adoption raises critical concerns regarding fairness, transparency, and bias (Pagano et al., 2022; Rabonato & Berton, 2025).
Bias in ML models can arise from various sources (de Vargas et al., 2022; Hort et al., 2024; Jafarigol & Trafalis, 2023; Jiang & Nachum, 2020; Robinson et al., 2024; Y. Zhang et al., 2024). For example, underrepresented groups in training data may experience disproportionately high error rates, leading to discriminatory outcomes (Borza et al., 2024; Duan et al., 2022; Langbridge et al., 2024). Addressing such biases requires robust methodologies to evaluate fairness and mitigate inequities without compromising model performance. This is particularly important in financial applications, where fairness violations can have legal, ethical, and reputational consequences.
Thus, fairness is a critical requirement in PD modeling because PD estimates directly influence credit allocation decisions. Unfair or biased PD models may systematically disadvantage certain socio-demographic groups, reinforcing structural inequalities and exposing institutions to regulatory, legal, and reputational risks. ML models may unintentionally replicate past discrimination unless fairness is explicitly measured and monitored. Therefore, incorporating fairness metrics into PD modeling is essential to ensuring equitable access to credit and compliance with modern regulatory frameworks.
In this context, we propose a fairness-aware framework for modeling the PD of individual borrowers by explicitly addressing the trade-off between predictive accuracy and fairness. While traditional scoring systems have primarily emphasized predictive accuracy, growing evidence shows that these models may inadvertently introduce or amplify biases, systematically disadvantaging certain groups of applicants. These biases raise ethical and regulatory concerns and risk undermining public trust in financial institutions. As ML methods become more prevalent, the pursuit of higher predictive performance must be balanced against fairness considerations. To this end, we introduce a threshold optimization framework (see Section 5) that adjusts the decision boundary of classification models using a tunable parameter, offering a practical and interpretable mechanism for managing fairness–performance trade-offs without retraining the underlying model. This approach enables institutions to implement credit scoring systems that are not only effective but also socially responsible.
The remainder of this paper is structured as follows. After highlighting the key contributions, Section 3 introduces both traditional and ML techniques for PD modeling. Section 4 explores different types of biases and fairness notions in credit risk assessment, along with corresponding mitigation strategies. Section 5 presents an optimization framework for selecting an appropriate threshold for PD classification, balancing model performance and fairness. Section 6 describes the dataset and variable selection process. Experimental results, including model performance, bias analysis, and the decision boundary adjustment framework, are presented in Section 7. Legal and ethical considerations are discussed in Section 8. Section 9 outlines the limitations of this study and suggests directions for future research. Finally, Section 10 summarizes the main findings and discusses their practical implications.
2. Key Contributions
This study contributes a threshold optimization framework for credit risk modeling, with a specific emphasis on post-processing decision boundaries in probabilistic classifiers. The approach is particularly tailored to credit scoring applications, when predictive accuracy and fairness conflict and must be transparently managed. Our key contributions are as follows:
First, we examine the intrinsic tension between predictive accuracy and algorithmic fairness in PD modeling across several machine learning classifiers. Our analysis incorporates established fairness metrics (see Section 4.2), and reveals model-specific behaviors under fairness constraints. This sheds light on how post-processing interventions can meaningfully influence the fairness–performance balance in credit scoring scenarios. Hence, this work contributes to the development of responsible credit risk models by providing a transparent and auditable post-processing method to control group-level disparities, aligning fairness adjustments with major regulatory frameworks, enabling interpretable fairness–performance trade-offs consistent with supervisory expectations, and promoting more inclusive credit access by mitigating disparate impacts in PD estimation.
Second, we propose a post-processing threshold optimization strategy based on a scalarized objective function that jointly considers fairness and performance losses. A single, interpretable parameter (Equation (9)) governs this trade-off, enabling continuous control without modifying the underlying models or requiring retraining. This design supports transparent and flexible deployment in regulated financial environments.
Third, to better understand the effect of optimized thresholds (Equation (15)), we introduce a dual-reference comparison strategy relative to both the default threshold and the minimax-optimal threshold (Equation (13)). We further develop a diagnostic ratio-based visualization () (Equations (16)–(18)) in quadrant form to evaluate fairness–performance gains, providing intuitive support for threshold selection in operational settings.
Last, we conduct comprehensive experiments on both synthetic data and the German Credit dataset, applying the framework to multiple classifiers. We analyze the sensitivity of the optimized thresholds to different fairness–performance preferences, evaluate generalization to real data, and quantify trade-offs across settings. These results provide insights for institutions seeking to implement fairness-aware decision rules with minimal loss in predictive power.
3. Modeling the Probability of Default
The modeling of PD has been extensively studied, with techniques evolving from traditional approaches to more advanced ML methods. On the one hand, the traditional methods for estimating PD include both qualitative and quantitative approaches. For example, expert judgment-based techniques (Gietzen, 2017; Hanea et al., 2021; Izzi et al., 2012) rely mainly on the intuition and experience of credit officers to assess the likelihood of default. While flexible, these methods often suffer from subjectivity and inconsistency, making them less reliable in modern regulatory contexts. On the other hand, the advent of ML introduced a paradigm shift in credit risk modeling. For example, algorithms such as Logistic Regression (LR) (Cox, 2018), Random Forests (RF) (Breiman, 2001), or XGBoost (T. Chen & Guestrin, 2016) enable the modeling of complex, non-linear relationships and are well-suited for high-dimensional data, offering greater predictive accuracy and robustness.
Advancements in fairness-aware ML aim to mitigate bias in financial decision-making. Despite their predictive strength, ML models can unintentionally reinforce systemic discrimination, especially when trained on biased datasets. To address this issue, a range of fairness-aware techniques has been developed. Bias mitigation typically occurs across three stages:
Pre-processing refers to techniques applied to the data before training a ML model. The aim is to reduce or eliminate bias present in the dataset, which often stems from historical or societal inequalities. During this phase, one can normalize and balance the dataset to remove biases before training. Methods such as reweighting (Harris, 2020; Stevens et al., 2020; Y. Zhang & Ramesh, 2020), optimized pre-processing (Calmon et al., 2017), or modifying features to reduce disparate impact, or resampling (Puyol-Antón et al., 2021; Y. Zhang & Sang, 2020) could be suitable. The later includes generating synthetic data, to augment underrepresented class (oversampling) (Koziarski, 2021; Puyol-Antón et al., 2021; Rajabi & Garibay, 2021; Vairetti et al., 2024), or to reduce the number of samples from the majority class to balance it with the minority class (undersampling) (Koziarski, 2021; Sharma et al., 2020; Smith & Ricanek, 2020; Vairetti et al., 2024). These approaches at at this stage are model-agnostic, meaning they can be used regardless of the algorithm chosen, and they tackle bias at its root, within the data itself.
Subsequently, in-processing involves modifying the learning algorithm during the model training phase to incorporate fairness constraints or objectives. During the training stage, this can be performed by adding regularization terms that penalize unfair outcomes (Harris, 2020; Zheng et al., 2021) or using adversarial training to remove information about protected attributes (Abbasi-Sureshjani et al., 2020; B. H. Zhang et al., 2018). For example, methods such as Fairness Through Unawareness ensures that protected attributes are excluded during model training to avoid discriminatory predictions; however, this approach may be ineffective if proxies for sensitive attributes remain within the dataset (Dwork et al., 2012). Causal Inference-based methods provide a more nuanced solution by identifying and addressing indirect biases arising from latent relationships between variables (Kilbertus et al., 2017).
Finally, the post-processing techniques are applied after a model has been trained. These methods adjust the model’s predictions to ensure fairer outcomes without altering the model or the training data. Examples of this situation include the evaluation of the equalized odds or reject option classification (Alam, 2020; Harris, 2020; Stevens et al., 2020; Y. Zhang & Ramesh, 2020). The other approach includes adjusting the decision threshold, rather than relying on the standard threshold . For example, the advanced three-way decision frameworks for credit risk prediction addresses the limitations of traditional binary (default, or non-default) classification models (Li et al., 2024; Li & Sha, 2024; Pang et al., 2024). By introducing an additional uncertain or deferment category, these methods allow for deferred decisions, optimizing decision thresholds and improving decision accuracy by incorporating more information before classifying borrowers (Pang et al., 2024). Each approach optimizes decision thresholds, often using techniques like particle swarm optimization (Li & Sha, 2024) or support vector data descriptions (Li et al., 2024), and applies these methods to real-world datasets.
Recent studies have increasingly focused on fairness and performance trade-offs for financial applications, particularly in credit risk modeling. Among others, Das et al. (2021) provides a comprehensive overview of fairness metrics and legal considerations, highlighting threshold adjustment as a post-processing technique. Hardt et al. (2016) introduced the concept of equalized odds, proposing post-processing methods to adjust predictors for fairness. Building on this, Woodworth et al. (2017) analyzed the statistical and computational aspects of learning predictors that satisfy equalized odds, suggesting relaxations to address computational intractability. Diana et al. (2021) proposed a minimax group-fairness framework, aiming to minimize the maximum loss across groups, thereby directly addressing the worst-case group performance. Lahoti et al. (2020) tackled fairness without access to demographic data by introducing adversarially reweighted learning, optimizing for Rawlsian max–min fairness. In the realm of natural language processing, Resck et al. (2024) explored the trade-off between model performance and explanation plausibility, employing multi-objective optimization to balance these aspects. Similarly, Bui and Von Der Wense (2024) examined the interplay between performance, efficiency, and fairness in adapter modules for text classification, underscoring the complexity of achieving fairness alongside other objectives.
In contrast to all such prior works, our approach, as introduced in Section 5, presents a mathematically grounded, model-agnostic framework for optimizing decision thresholds through a weighted trade-off between fairness and performance. We introduce a formal objective function with a tunable parameter that allows institutions to navigate this trade-off, offering a practical tool for aligning predictive accuracy with regulatory and ethical fairness standards. By analyzing how the optimal threshold shifts across different weight values, our contribution complements previous works, and our method advances from conceptual fairness guidance to insights into implementation in credit risk modeling where balancing fairness and performance are important.
4. Biases and Fairness in PD Modeling
Bias can emerge in ML modeling even when the data used is considered entirely accurate and with many different sources. In this section we describe the types of bias often encountered in PD modeling.
4.1. Types of Biases and Fairness
Firstly, we comment on examples of biases expected in the modeling process. Exhaustive reviews on bias can be found in (Ferrara, 2023; Hort et al., 2024; Mehrabi et al., 2021; Mikołajczyk-Bareła & Grochowski, 2023).
- Representation Bias: It arises when the training dataset does not adequately represent all groups in the population (Borza et al., 2024; Duan et al., 2022; Langbridge et al., 2024). In credit default risk modeling, it can occur because historical loan datasets contain a disproportionately high number of non-defaulting applicants, which can negatively affect model performance (Y. Chen et al., 2024; Namvar et al., 2018; Sun et al., 2024; S. Zhang et al., 2024). Techniques such as resampling, balanced metrics or decision threshold adjustments can help reduce the impact of imbalanced data.
- Label Bias: This bias arises when the labels used for training a model reflect existing discriminatory practices, potentially perpetuating biases, an example of when past loan approvals were influenced by discriminatory practices. This issue can be addressed, for example, through re-labeling, debiasing algorithms to correct skewed labeling patterns (Diao et al., 2024; Guo et al., 2025; Xia et al., 2024), or re-weighting data points without altering labels (Jiang & Nachum, 2020). Other example of techniques include post-processing steps to adjust model outputs (Doherty et al., 2012; Feldman, 2015; Hardt et al., 2016).
- Algorithmic Bias: This type arises from the design of ML algorithms, often leading to disproportionate misclassifications of certain groups. This can occur due to overfitting to majority groups, where models trained on imbalanced datasets fail to generalize to minority groups. To mitigate these biases, bias-conscious algorithms can optimize fairness metrics (Langbridge et al., 2024), or hyperparameter tuning can help balance accuracy and fairness (Weerts et al., 2020; Yu & Zhu, 2020).
- Selection and Evaluation Bias: Selection bias arises when the training data are not representative of the target population, such as when credit models only analyze approved loans, ignoring rejected applicants. This can be mitigated by incorporating denied loan applications or using synthetic data generation. Evaluation bias, on the other hand, occurs when model performance metrics fail to consider fairness across different groups. To address this, fairness metrics like disparate impact ratio, equal opportunity, and group-specific precision and recall should be included alongside traditional evaluation metrics to ensure equitable performance.
Types of Fairness include:
- Demographic Parity: This ensures that the model’s predictions are independent of sensitive attributes, such as gender, race, or age (Dwork et al., 2012; Kusner et al., 2017). For example, the proportion of approved loans should be similar across all demographic groups. Among the possible mitigation strategies, one could modify the decision threshold or re-weight the training data to achieve parity in predictions or applying post-processing techniques to adjust outcomes to align with fairness criteria.
- Equal Opportunity: This criterion (Hardt et al., 2016) ensures that true positive rates are equal across all groups (default and non default). In credit risk, it means that applicants who are genuinely creditworthy have an equal chance of being approved, regardless of group membership. Using fairness constraints during model training to balance true positive rates or applying adversarial debiasing techniques (Grari et al., 2023; B. H. Zhang et al., 2018) could reduce disparities.
- Individual Fairness: This requires that individuals with similar characteristics receive similar predictions. In credit risk modeling, two applicants with comparable financial profiles should have similar default probabilities. Possible mitigation technics could include the implementation of distance-based fairness regularization (Gouk et al., 2021) during training to ensure similar inputs produce consistent outputs.
- Fairness Through Awareness: This approach explicitly incorporates sensitive attributes to correct biases, rather than ignoring them (Dwork et al., 2012). In this case, using sensitive attributes during pre-processing to reweigh or adjusting data distributions, ensuring fairer outcomes for historically disadvantaged groups could help.
It is worth commenting that the bias and fairness mitigation methods are not limited to the ones mentioned in this paper, and also that they can be applied alone or in combination with others to improve the performance.
4.2. Metrics for Evaluating Performance, Biases and Fairness
Mitigating bias and ensuring fairness in ML-based modeling of the PD requires a multifaceted approach, combining technical adjustments with ethical considerations. This requires us to evaluate both predictive performance and fairness to achieve equitable and reliable outcomes in credit risk assessment. In this work, we use several metrics to evaluate the biases and fairness discussed in Section 4.1.
Firstly, the performance of the models will be accessed via the Balanced Accuracy (BA) metric (Brodersen et al., 2010). BA is particularly useful for imbalanced classification problems. Unlike standard accuracy, which can misrepresent performance when one class dominates, and is calculated as the average of sensitivity and specificity. The sensitivity represents the true positive rate, that is the percentage of positive cases the model is able to detect, and the specificity, the true negative rate, measures the proportion of correctly identified negatives over the total negative predictions made by the model. This metric ensures a fairer assessment across both majority and minority classes. By definition, , with a high BA indicating effective model performance across all classes, while a low BA highlighting difficulties in correctly identifying positive or negative cases, signaling potential issues such as high false positive or false negative rates. Thus, its ideal value is .
Secondly, concerning the biases, we focus on a set of metrics to assess fairness and bias in ML models. These metrics, denoted as m, along with their corresponding ideal values , are as follows:
- -
- Average Odds Difference (AOD) (Hardt et al., 2016) measures the difference between the sensitivity and specificity of privileged and non-privileged groups. It balances true and false positive rates to avoid unfair denials and risky loans. Thus, the ideal value is . Positive or negative values indicate biases favoring one group or the other.
- -
- Disparate Impact (DI) (Feldman et al., 2015) compares favorable outcome rates between protected groups. It detects indirect discrimination in credit scoring models. A value of indicates perfect fairness, while values below or above 1 suggest bias.
- -
- Statistical Parity Difference (SPD) (Corbett-Davies et al., 2017) assesses the difference in favorable outcomes between groups. It helps identify imbalances in loan approval rates across demographics. A score of indicates equal benefit, while positive or negative values highlight disparities.
- -
- Equal Opportunity Difference (EOD) (Hardt et al., 2016; Pleiss et al., 2017) examines sensitivity differences between groups, ensuring equally creditworthy individuals are treated fairly. A score of means equal opportunity, while positive or negative values indicate bias.
- -
- Theil Index (TI) (Speicher et al., 2018), also known as the entropy index, measures fairness at individual and group levels. Lower values indicate equitable outcomes (), while higher values signal disparities, accounting for prediction errors and their distribution across decisions.
5. Threshold Adjustment Framework
In conventional PD modeling, the decision threshold used to classify observations as default or non-default is typically fixed at a default value, denoted by . A common choice is , corresponding to the point where the predicted PD exceeds 50%. This convention implicitly assumes symmetric mis-classification costs and balanced class distributions, conditions that rarely hold in real-world credit risk applications, where default events are relatively rare. As a result, may not provide an optimal balance between model performance and fairness. Moreover, biases across protected groups can further exacerbate disparities, as a fixed threshold may disproportionately affect certain subpopulations.
To address these limitations, this section introduces a threshold-adjustment framework, applied as a post-processing step for bias and fairness mitigation. The approach generalizes the standard practice by treating the threshold T as an optimization variable rather than a fixed constant. For a given balance between performance and fairness preferences, an optimal threshold (Equation (15)) is determined to achieve the best trade-off between the two objectives. When the relative importance of performance and fairness is uncertain, or when a robust and weight-independent decision rule is preferred, a single threshold (Equation (11)) can be identified to ensure stability across all possible weighting scenarios. Together, these thresholds provide a flexible and principled way to adjust model decisions, balancing predictive accuracy with fairness considerations while extending the conventional fixed-threshold paradigm. The performance and bias/fairness metrics considered in this work are discussed in Section 4.2.
Concerning the strategy, we will assess the performance using BA, and analyze disparities between protected groups (see Section 6.2) using group fairness metrics introduced in Section 4.2. For this, we employ the AIF360 library (Bellamy et al., 2018; Blow et al., 2023), which offers robust tools for quantifying group-based bias. It uses a weighted resampling procedure, a pre-processing technique that adjusts the relative influence of samples without modifying their labels, to examine fairness in model outcomes.
5.1. Definition and Normalization of Metrics Functions
The first step involves defining and normalizing the metric functions, each of which depends on the decision threshold value T. The normalization ensures that all metrics are expressed on a comparable scale, facilitating their combined optimization. The goal is to construct a scalarized objective function combines both performance and fairness metrics, which naturally operate on heterogeneous numerical scales. To ensure commensurability, each metric will be normalized with respect to theoretically or empirically bounded intervals. These bounded intervals provide stable reference points that align with the interpretability requirements of financial risk governance.
Let denote the function corresponding to a given metric m, and its ideal value. The normalized metric function, denoted , maps values into the interval according to:
where and are the minimum and maximum observed values of across the admissible range of T. The goal is to bring all metric values to a common scale, allowing meaningful aggregation of performance and fairness measures that may originally have different units or ranges.
The normalization process requires determining the lower and upper bounds and for each metric . These bounds are defined empirically as:
where represents the range of threshold values considered in this study. The values are typically obtained by computing each metric over a discrete grid of thresholds.
It is worth noting that we adopted the empirical min–max normalization approach because it is simple, model-agnostic, and directly grounded in the operational threshold space used by practitioners. Unlike dataset-dependent standardization methods, this approach yields normalized metrics that remain interpretable for credit risk committees and consistent with threshold-based decision rules. Since the normalization depends solely on the achievable range of metric values under threshold variation, it avoids injecting subjective assumptions or model-specific scaling factors.
5.2. Definition of the Objective Function
Once normalized, the metrics are combined into a single objective function using a weighted Tchebycheff scalarization approach (Dächert et al., 2012; Helfrich et al., 2023; Hwang et al., 1980; Silva et al., 2022). This approach enables balancing trade-offs among multiple objectives while allowing different priorities through weighting. The aggregated objective function is given by:
where is the weight assigned to metric m, and . Here, represents the normalized reference or ideal value of metric m, as discussed subsequently in Section 5.3.
This formulation minimizes the weighted deviation in each normalized metric from its ideal value. The term measures how far each metric lies from its desired target, and the weights control the influence of each metric in the optimization.
5.3. Reference Value Adjustment
In practical post-processing applications, the adjustment of the decision threshold does not modify the underlying predictive distribution of the model. Consequently, the theoretical ideal value of a metric may not be empirically attainable. To ensure numerical stability and interpretability, it is therefore reasonable to define the reference value as the best observed (empirical) value of the metric over the threshold domain . Specifically, one may set for maximization-oriented metrics and for minimization-oriented ones, leading, respectively, to or . For instance, assigning and yields and . This choice guarantees that the ideal point is attainable within the observed range and contributes to stabilizing the optimization process.
Nevertheless, to maintain consistency between the normalized metric functions and their corresponding reference (ideal) values in Equation (3), each can also be normalized using the same transformation:
This ensures that both the metric functions and their ideal targets are expressed on the same scale. For example, if a fairness metric has and an empirical range , the normalized reference value becomes , which remains consistent with the desired direction of improvement (lower values correspond to better fairness).
When assessing the quality of normalization, the position of the normalized reference value relative to the normalized interval provides an indication of the consistency between the empirical and theoretical scales. Ideally, , meaning that the empirical and adequately capture the attainable domain of the metric. When lies outside this range, it implies that the theoretical ideal cannot be reached within the observed data distribution. To quantify this discrepancy, we define the deviation magnitude:
The quantity measures how far the normalized ideal lies beyond the empirical normalized range, providing a direct indicator of potential normalization-induced bias.
Previous studies (e.g., Wang et al., 2017) have shown that the choice of normalization scheme significantly affects the stability of multi-objective optimization and the convergence of scalarization-based methods. Although there is no universal consensus on strict numerical tolerances for , we adopt heuristic bounds based on the magnitude of deviation relative to the normalized interval :
- : negligible deviation; the empirical range sufficiently captures the theoretical target.
- : moderate deviation; partial misalignment; but the normalization remains acceptable for optimization purposes.
- : substantial deviation; the theoretical ideal lies significantly outside the attainable domain, and the normalization may bias the optimization process. In such cases, the reference should be adjusted to the empirical bound ( or ) to ensure numerical stability, implying or .
These tolerance levels provide a pragmatic guideline for assessing normalization reliability and ensuring robustness of the optimization process.
5.4. Decomposing the Objective Function and Trade-Off Parameter
To better understand and control the trade-off between predictive performance and fairness, the total objective function, defined in Equation (3), can be decomposed into two components:
The first term, , captures model accuracy, while the second, , aggregates fairness and bias-related metrics. They are expressed as:
where denotes the weight assigned to performance, and are the individual weights for the fairness metrics .
This step is important since it allows us to efficiently weight the performance and bias in the objective function. In other words, it permits to access the trade-off between performance and bias via a proper assignment of weights.
Assuming for simplicity that the bias metrics weights are all equal to in this work, that is,
the relationship between the weights for the bias metrics and is given by:
The parameter is the number of bias and fairness metrics contributing to the objective function. Notice that in this work. The parameter determines the trade-off between performance and fairness.
By adjusting , the objective function becomes a function of two parameters: the threshold T and the performance weight . For example, means an equal contribution of both performance and bias, however less (more) than would mean the importance of the fairness (performance) over the performance (fairness) in the objective function. Notice that the choice of would depend on business objectives, whether the performance of the models is more, less, or equally important than the bias. Thus, by tuning , practitioners can emphasize either predictive accuracy or fairness mitigation, depending on application needs and ethical requirements.
5.5. Threshold Optimization
The goal is to identify the threshold that minimizes F, while ensuring that the result is robust to variations in . The optimal threshold balances performance and fairness, aligning with the desired objectives of the loan decision-making process. As such, they are indicative of how each model balances the trade-off between predictive accuracy and fairness in the context of the loan decision-making process. The approach described in this section is effective in achieving the goal of simultaneously minimizing the maximum weighted deviation in the metrics functions from their ideal values.
In our formulation, the objective function depends on a threshold parameter T and a weight parameter . Assuming Equation (9), the expression of Equation (5) can be written as:
where captures one aspect of the system we wish to align with a reference value , and are a set of metric functions (Equation (1)) we aim to align with target values for each index j. The parameter thus modulates the trade-off between optimizing for and the collective alignment of the .
It could be worth examining the behavior of as the threshold T approaches 0 or 1, across different values of the performance weight :
- Case (bias only): As , the objective function converges to , where . This reflects the importance of the DI, as all other normalized bias metrics vanish in this limit. For , the function converges to , where , since TI would be maximal.
- Case (performance only): As , the function converges to , since BA is minimized, making the normalized performance metric to vanish, . Same limit as , that is , since the performance metric continues to reflect low classification quality under extreme thresholds, as expected for a performance-centric objective.
- Case (mixed bias and performance): In this intermediate regime, as (or ), the function converges to (or ). This reflects a weighted trade-off between fairness and performance penalties in the extreme threshold limits.
It is important to comment that because fairness metrics are often correlated, there is a legitimate concern that one indicator could dominate the optimization. Empirically, however, correlations are only moderate, and the optimization does not collapse onto a single fairness dimension. This is because the framework aggregates normalized deviations from parity rather than raw metric values, ensuring that each metric contributes proportionally within its predefined range. Furthermore, the trade-off parameter explicitly controls the relative influence of performance versus fairness, preventing fairness metrics from overwhelming the objective and vice versa.
Also, the numerical stability of the scalarized objective can be argued from the boundedness of all normalized metrics. Since thresholds vary in and fairness metrics change smoothly with respect to threshold shifts, the resulting optimization surface remains well-behaved. Empirically, the optimization does not exhibit explosive gradients or oscillations, and multiple initialization points would converge to consistent minima. Hence, the normalization strategy we used balances interpretability, regulatory alignment, and optimization stability, ensuring that the scalarized objective remains meaningful and robust.
5.5.1. Independent Threshold
At first, we wish is to find the suitable threshold, , independently of . Thus, we frame the problem as a minimax optimization (see Du & Pardalos, 1995; Razaviyayn et al., 2020 and references therein). The goal is to minimize the objective function with respect to one variable, and to maximize the objective function with respect to another. In this case, we seek a value of T that performs well regardless of the specific weighting:
Since is a convex combination (Ref. Rockafellar, 1997) of two absolute-value terms and linear in , the inner maximum over occurs at one of the endpoints of the interval. Therefore, the worst-case scenario for a given T can be rewritten as:
The parameter thus minimizes the worst deviation between and its target value 1, and and its target value . The optimization problem simplifies to:
This formulation identifies the value of T that remains robust to variations in , rather than optimizing for a specific weighting configuration by minimizing the worst-case value of the objective function over all possible within . In this sense, can be interpreted as a robust or weight-independent solution, ensuring stable performance across different weighting preferences. In practice, this ensures that neither component dominates the error disproportionately and is particularly suited for applications requiring robustness against imbalanced weighting.
It is important to distinguish between the threshold defined in Equation (13) and the equilibrium threshold obtained when the deviations between performance and fairness are equal, that is,
The threshold corresponds to the point where the normalized deviations in performance and fairness metrics are balanced in magnitude, representing an equal-deviation condition. As such it can be interpreted as the point at which the optimization landscape transitions from being dominated by one objective to a balanced regime, where further improvements in one dimension necessarily entail trade-offs in the other. In contrast, minimizes the maximum of these deviations, yielding the smallest possible worst-case imbalance between performance and fairness objectives. While may coincide with in monotonic or well-behaved cases, in general provides a more robust solution by explicitly controlling the dominant deviation rather than merely equalizing them.
5.5.2. Influence of : Threshold
While is chosen to be independent of , it is still interesting to examine how different values of affect the behavior of , especially when a particular application might favor one objective over the other.
Recall that the parameter explicitly controls the emphasis placed on minimizing the error in versus : when , the objective prioritizes minimizing , potentially at the cost of a larger deviation in . Alternatively, when , the focus shifts towards minimizing . The intermediate values of provide a tunable trade-off between the two objectives.
This flexibility may be beneficial in settings where domain knowledge or context dictates a preference toward one function over the other. In such cases, the parameter can be selected to reflect that preference and T may be optimized accordingly:
where is given by Equation (10). The Equation (15) defines the optimal decision threshold as the value of T that minimizes the composite objective function for a given performance weight . This formulation reflects the balance between model performance and fairness objectives: a higher value of emphasizes performance-oriented metrics, whereas a lower value prioritizes bias and fairness mitigation. Accordingly, represents the optimal trade-off threshold corresponding to a specific choice of weight configuration. By varying within the range , one can explore the sensitivity of the optimal threshold to the relative importance assigned to performance and fairness, thereby characterizing the full trade-off curve between these competing objectives.
In sum, while captures the best trade-off for a chosen set of priorities, identifies a threshold that performs consistently even when the exact balance between performance and fairness is uncertain or difficult to specify.
Practical Guidance for Choosing the Trade-Off Parameter
A central component of the proposed framework is the trade-off parameter , which controls the relative influence of performance and fairness in the scalarized objective function. We acknowledge that practitioners may require more explicit guidance on its selection. In practice, should be interpreted as a policy-driven knob rather than a purely statistical hyperparameter. When the institutional objective prioritizes predictive accuracy, such as in environments with strict risk-based capital constraints, values of close to 1 will favor thresholds that maximize the performance while still accounting for fairness. Conversely, when regulatory, ethical, or reputational considerations place fairness at the forefront, choosing close to 0 yields thresholds that minimize disparities across protected groups, even at the expense of some predictive performance. Intermediate values (e.g., ) provide a controlled compromise and are appropriate when institutions aim to balance both objectives rather than optimize one exclusively.
To support practitioners, our experiments illustrate the empirical effects of varying through ratio-based plots and quadrant analyses, as discussed in Section 5.5.3, that make fairness–performance trade-offs visually interpretable. We therefore recommend a calibration procedure in which institutions (i) define acceptable tolerance ranges for both fairness and performance metrics, (ii) compute the corresponding values of across a grid of values, and (iii) select the smallest that satisfies performance constraints or the largest that satisfies fairness constraints, depending on the institutional priority. This policy-aligned calibration strategy allows the choice of to be transparent, documented, and compatible with internal model governance processes.
5.5.3. Insights into the Selection of Threshold
In the following, we give intuitive insights into the effects of threshold selection, and discuss practical decisions about when and how to adjust classification thresholds. To summarize, we distinguish:
- is the standard threshold used in binary classification, assuming calibrated probabilities and no explicit fairness correction. It’s simple and interpretable, but may perpetuate existing biases in the data.
- (defined in Equation (13)) is a fixed, model-specific threshold computed independently of the fairness–performance weight . It minimizes the maximum deviation between ideal performance and average fairness deviations.
- (given in Equation (15)) is dynamic threshold optimized to minimize the objective function that combines performance and fairness losses based on a tunable weight . This could allow institutions to explicitly tune the trade-off depending on policy priorities or regulatory requirements.
Each threshold offers different strengths. is operationally simple; would provide a robust, model-specific compromise; and allows for a tuning, context-sensitive optimization aligned with institutional priorities.
To complement the theoretical distinctions presented earlier, we now analyze threshold selection empirically through ratio-based comparisons of the objective functions. These comparisons are visualized in Figure 1, where each point corresponds to a specific value of the parameter .
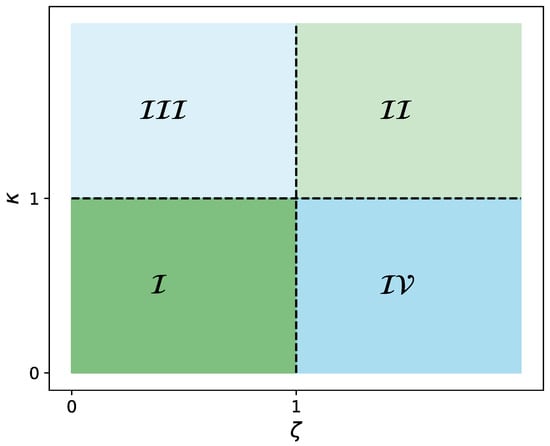
Figure 1.
Visualization-based interpretation of threshold comparisons. Each point represents a comparison between thresholds, either vs. , vs. , or vs. . The x-axis denotes the fairness objective ratio, and the y-axis denotes the performance objective ratio, where values below 1 indicate improvement. Points in the bottom-left quadrant (Region I) signify that enhances both fairness and performance. The top-right quadrant (Region II) indicates deterioration in both. Region IV (bottom-right) reflects performance gains at the expense of fairness, while Region III (top-left) shows improved fairness with reduced performance. This visualization serves as a practical diagnostic tool for informed threshold selection beyond abstract optimization metrics.
To evaluate the performance of the optimized threshold relative to the default threshold , we consider the following ratios:
Points falling in the lower-left quadrant (region I) of Figure 1, where both ratios are below 1, indicate that improves both performance and fairness compared to the default threshold. Conversely, points in the upper-right quadrant (region II) suggest that remains preferable due to its simplicity or stability.
To assess whether the dynamically optimized yields benefits beyond the static fairness-optimal threshold , we define:
Here, points with both ratios below 1 again indicate simultaneous improvements. If instead they fall in region II, it implies limited added value from optimizing beyond .
For completeness, we also report the relative advantage of over the default threshold:
which are independent of and provide baseline context for interpreting the relative utility of thresholding strategies.
More generally, points in the bottom-right quadrant (region IV) signify improved performance at the cost of fairness, which may be acceptable in risk-sensitive applications. In contrast, the top-left quadrant (region III) reflects gains in fairness with a loss in predictive accuracy, a trade-off often relevant in regulated or equity-focused settings.
Finally, while this framework centers on balancing a scalarized fairness–performance trade-off, it is worth noting that competing fairness metrics may themselves be in tension. Exploring such multi-metric trade-offs is a promising direction for future research.
5.6. Positioning of the Proposed Framework Within Fairness Mitigation Strategies
We emphasize that the framework introduced above operates solely at the post-processing stage, and the threshold adjustment is model-agnostic, computationally efficient, and compatible with institutional settings where models cannot be retrained or modified once validated. However, post-processing acts only on the final model outputs and therefore cannot correct deeper structural biases arising from imbalanced data, label biases, or model design choices. For this reason, the proposed method should be viewed as a complementary tool within the broader family of fairness mitigation strategies. In settings where structural or data-driven biases are present, post-processing can be combined with pre-processing approaches and with in-processing methods that introduce fairness constraints directly during model training.
It is worth noting that incorporating fairness metrics does not increase the complexity of the underlying ML model. The proposed fairness-aware threshold optimization operates entirely at the decision layer, leaving the model’s structure intact. Rather than reducing interpretability, the approach enhances it by providing transparent, measurable indicators of fairness, as well as diagnostic tools, such as ratio curves and quadrant plots, that help practitioners understand and justify fairness–performance trade-offs.
5.7. Choice of Machine Learning Models
In this study, we illustrate this framework using some commonly used ML models. The selection of these models was guided by their complementary methodological strengths, and their balance between interpretability and predictive power. LR (Cox, 2018) is included due to its long-standing role in credit risk modeling, ease of implementation, and transparency, which make it well suited for regulatory compliance. RF (Breiman, 2001) were selected as a representative ensemble method capable of capturing non-linear feature interactions and providing robustness against noise and overfitting. XGBoost (T. Chen & Guestrin, 2016), a gradient-boosting technique, was chosen for its state-of-the-art performance on structured tabular data and its interest in financial risk management (Feng et al., 2025; Qin, 2022). Together, these three models span a spectrum from traditional interpretable methods to advanced ensemble approaches, allowing for a comprehensive evaluation of our threshold optimization framework across different levels of model complexity. Importantly, this diversity enables us to analyze how fairness–performance trade-offs manifest differently between linear and non-linear classifiers.
Other models and classes of models were not considered in order to maintain clarity and focus. For example, Support Vector Machine (Cortes & Vapnik, 1995) can be computationally expensive on large datasets. More complex deep learning architectures (Mowbray, 2025), such as neural networks, were also not employed because the dataset is static and tabular, where gradient boosting and ensemble methods typically outperform. Similarly, unsupervised (Tyagi et al., 2022) or semi-supervised (Chapelle et al., 2006) approaches were not explored, since this study focuses explicitly on supervised classification with known default outcomes. By restricting the analysis to three representative and practically relevant models, we ensure that our evaluation remains methodologically rigorous, computationally tractable, and aligned with industry practices in credit risk assessment. Expanding the analysis to include these families of models constitutes a promising direction for future work, particularly for exploring whether the fairness–performance trade-offs identified in this study generalize to more complex learning systems.
5.8. Operational Deployment in Financial Institutions
Although the proposed threshold optimization framework is model-agnostic and relatively lightweight to implement, practical adoption in a financial institution requires a clear operational roadmap. This subsection outlines the key steps and governance mechanisms needed for deployment.
- Threshold Calibration Procedure: Institutions may calibrate the decision threshold using three reference values: (i) the baseline threshold , (ii) the minimax fairness-oriented threshold , and (iii) the scalarized threshold that balances performance and fairness. Calibration can be performed on a validation dataset, and thresholds be selected based on institution-specific criteria such as minimizing disparities, maximizing balanced accuracy, or meeting regulatory constraints. The choice of could be documented in model governance files in a manner similar to hyperparameter selection.
- Governance of Fairness–Performance Trade-offs: Financial institutions typically rely on established governance structures to approve model design choices. The trade-off parameter provides a clear and interpretable mechanism for documenting the tolerance for fairness versus performance deviations. Governance bodies can define acceptable fairness ranges or maximum disparities, and recalibrate the threshold periodically through back-testing, monitoring, or stress-testing exercises. This aligns naturally with existing model governance requirements, for example under Basel II/III (Basel Committee on Banking Supervision, 2004, 2009, 2011, 2017), or the EU AI Act (Kelly et al., 2024; EU AI Act, 2024).
- Integration into Existing Credit-Scoring Systems: Because the proposed approach operates exclusively at the post-processing stage, it can be integrated without modifying the underlying model or retraining pipelines. The threshold adjustment can be embedded into batch scoring systems (e.g., IFRS9 staging), real-time credit decision engines, or web-based advisory tools. Furthermore, the fairness and performance metrics can be monitored through dashboards, enabling continuous supervision and documentation for compliance and audit purposes.
- Operational Considerations: The interpretability of threshold adjustment facilitates communication with loan officers and allows for human-in-the-loop decision-making. Overrides, manual reviews, and escalation mechanisms can coexist with the optimized threshold, preserving transparency and explainability. Finally, because the method affects only the final decision rule, it remains compatible with data privacy and non-discrimination requirements under GDPR (Parliament of the European Union, 2016).
Overall, this operational roadmap demonstrates that the framework is not only theoretically sound but also readily deployable within modern credit risk governance infrastructures.
6. Dataset
This study initially employs a synthetic dataset from the Kaggle platform (Kaggle, 2020), which simulates historical loan application records, and contains 32,581 observations. Although not derived from real bank data, the dataset was specifically constructed to reflect realistic credit risk scenarios. It includes a wide range of features commonly found in actual lending contexts, such as income, loan amount, interest rate, and credit history. Crucially, it reproduces structural properties often observed in production environments: class imbalance, inter-feature correlations, and the presence of proxy-sensitive attributes. These characteristics make it a suitable and controlled environment for systematically evaluating the behavior of fairness-aware decision thresholds under imbalanced and biased conditions. Given that the proposed framework is model-agnostic, post hoc, and interpretable, the synthetic data allows for insights into fairness–performance balance across different classifiers.
To further assess real-world applicability, we complement this analysis in Section 7.4 with experiments on the German Credit dataset. This serves to validate the framework’s robustness and generalizability in realistic settings. This dataset contains 1000 observations with balanced protected attributes (gender and foreign status). The list of variables is provided in Table A1.
6.1. Exploratory Analysis
The synthetic dataset includes both applicant-specific and loan-specific features, as summarized in Table 1. Variables range from demographic and financial characteristics (e.g., age, income, home ownership) to loan attributes (e.g., amount, purpose, interest rate, grade). The target variable, Loan Status, indicates whether the applicant eventually defaulted (value 1) or not (value 0).

Table 1.
Features and target variables in the synthetic dataset.
The dataset exhibits significant class imbalance, with approximately 78% of instances representing non-default cases, while only 22% correspond to defaults. To reduce the impact of this imbalance, stratified splitting and cross-validation were used during model development. Oversampling methods such as SMOTE (Chawla et al., 2002) were also tested, but yielded minimal improvements. Therefore, evaluations were based on metrics robust to imbalance, including accuracy, recall, f1-score, and AUC-ROC. Note that pre-processing steps were applied to ensure data quality and compatibility with ML models. For example, missing values in employment length were imputed with zero, and median imputation was used for missing interest rates. Numerical features were normalized to the range, and categorical features were encoded with label encoding.
A correlation analysis revealed strong linear relationships between certain features. For example, default history and age were highly correlated (), suggesting potential redundancy. Similarly, credit score and interest rate showed a correlation of , highlighting the impact of creditworthiness on loan conditions. A moderate positive correlation () was observed between interest rate and default history, indicating that applicants with past defaults tend to receive higher interest rates. On the other hand, correlations between loan amount and interest rate were weak (), implying that factors other than amount influence rate determination.
Correlations between most features and the target variable (loan status) were modest, with the highest being between credit score and default status (). Additionally, mutual information scores were low for several categorical features, such as loan purpose and home ownership, suggesting limited predictive utility. These features were retained in this study for completeness but could be excluded in a real-world optimization pipeline.
Note that although strong correlations between certain features (for example, credit score and interest rate) suggest that one of each highly correlated pair could be excluded without significantly affecting classification performance, all features are retained in this study to enable a more comprehensive and controlled comparison across models and thresholds. This choice prioritizes experimental completeness over model parsimony, recognizing that variable selection strategies may differ in production environments where interpretability and efficiency are critical.
6.2. Protected and Proxy Attributes
Distinguishing between protected and proxy attributes is a fundamental step in addressing fairness and bias. On one hand, protected variables represent attributes where discrimination is legally or ethically unacceptable, such as age. Models that rely directly or indirectly on protected variables risk perpetuating discriminatory practices if these features influence predictions in an unjust manner. Proxy, on the other hand, are attributes that are not explicitly sensitive but may correlate with protected variables. The use of proxy in predictive models can lead to unintended bias, as they may inadvertently capture patterns of historical or structural discrimination. Identifying these proxies is essential to ensure that models remain fair and unbiased.
Concerning the dataset we considered in this study, age could be a primary choice for a protected variable. Discrimination in lending practices, such as offering unfavorable terms or denying credit based on age, raises significant concerns about fairness.
Also, while features like income, property ownership and interest rate are not inherently sensitive, they can act as proxies for other sensitive or protected characteristics. Income could act as a proxy for factors such as socio-economic background, property ownership may correlate with demographic characteristics, indirectly reflecting sensitive traits such as age. Regarding the interest rate on a loan, it may be influenced by a combination of borrower-specific factors, economic conditions, and lender policies. Key borrower attributes may include loan grade, income stability, loan amount, and purpose, with for example stable incomes generally leading to lower rates.
However, correlation analysis indicates on the one hand that the target variable is moderately correlated, with interest rate () and income (), while being very low with age (). On the other hand, the default history is moderately correlated, with interest rate while very low with income about and ∼−0.003, respectively.
Therefore, as the approach in this study, we will focus on the interest rate as the protected attribute, and leave the other scenarios or combinations of scenarios for future works.
6.3. Definition of Protected Groups
The data suggests that higher interest rates are associated with historical default status, with a critical threshold around (see Figure 2). Applicants receiving rates above this level are more likely to face rejection, possibly due to their higher risk profiles. This trend raises questions about potential systemic biases in loan approvals. If historical trends influence interest rate assignments, some groups may be disproportionately disadvantaged. Thus, there are two groups of the protected attribute: privileged which consists of applicants with an interest rate below , and the otherwise underprivileged. The proportions of these groups in the dataset can be found in Figure 3.
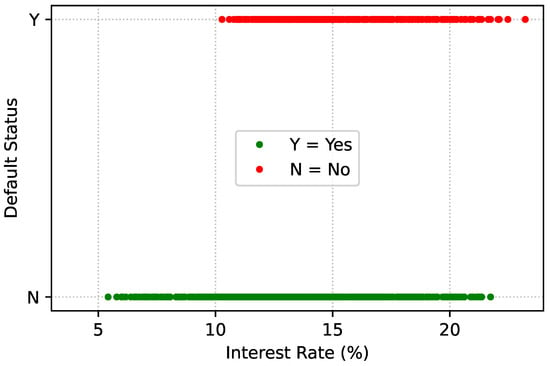
Figure 2.
Historical default status versus Interest rates.
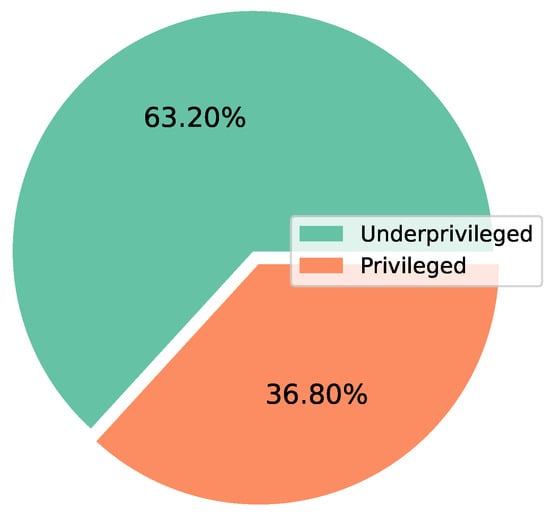
Figure 3.
Proportions of two groups of the sensitive variable used to access bias and fairness. Privileged (underprivileged) corresponds to group of applicants with an interest rate lower (higher) than .
7. Experimental Results
7.1. Performance of the Models
Table 2 presents the standard performance metrics for the ML models we considered. All models achieve strong overall accuracy, with RF performing best at 88.95%, followed by XGBoost at 85.58% and LR at 83.53%.

Table 2.
Performance of models. The classes 0 and 1 corresponds to non-defaults and default, respectively.
More informative than raw accuracy, the ROC-AUC scores provide insight into the models’ ability to discriminate between default and non-default cases. XGBoost achieves the highest ROC-AUC at 89.13%, closely followed by RF at 88.98%, while LR records a respectable 84.32%. These results suggest that tree-based models (RF and XGBoost) exhibit stronger discriminatory power relative to the linear baseline. Recall and F1-score values for each class reveal how models handle class imbalance. All models perform well in detecting non-defaults (class 0), with recall values above 0.95. However, performance drops sharply for defaults (class 1), which are the minority class. RF stands out with the highest recall (0.59) and F1-score (0.72) for class 1, suggesting it offers the best balance between sensitivity and precision for identifying high-risk applicants. In contrast, LR and XGBoost exhibit lower recall for class 1 (0.41 and 0.34, respectively), indicating under-detection of defaults.
The disparity in class discrimination could come from differences in features reliance. As shown in Figure 4, LR relies most heavily on loan-to-income percent, followed by loan amount, employment length, and interest rate. Due to its linear structure, LR applies uniform penalties to high-risk indicators and lacks the nuance to account for mitigating factors such as extended work history or smaller loan sizes. This rigidity likely contributes to its limited effectiveness in detecting defaulters. In contrast, the RF demonstrates a more distributed reliance on input variables. Key drivers include Loan to Income Percent, interest rate, home ownership, loan intent, and loan amount. Thanks to its tree-based design, RF can capture nonlinear relationships and assess the conditional influence of features like Interest Rate, enhancing predictive accuracy while reducing dependence on sensitive attributes. XGBoost similarly prioritizes loan-to-income percent, with additional emphasis on home ownership, interest rate, default on file, and loan intent. Although its performance in identifying defaults is somewhat lower, its more restrained use of interest rate supports stronger fairness outcomes, as elaborated in Section 7.2.
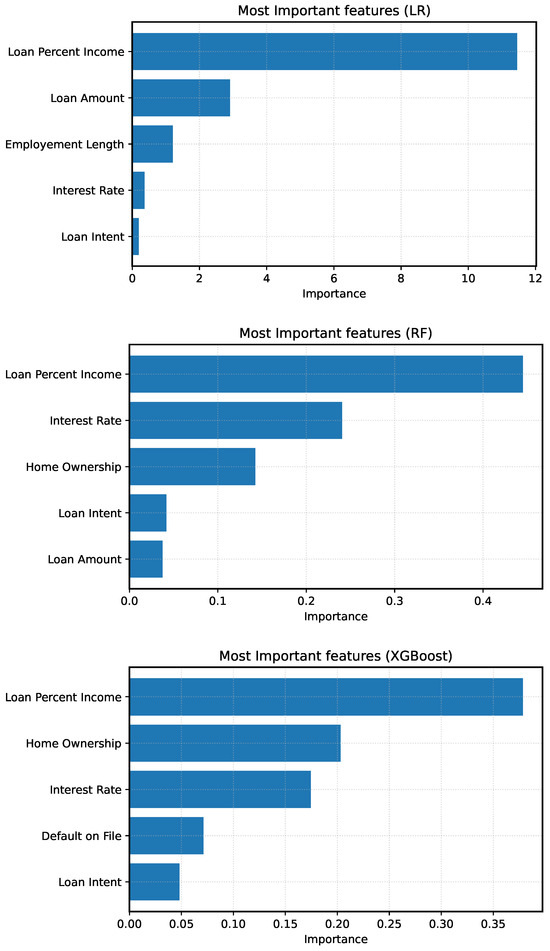
Figure 4.
Feature importance plots for LR, RF, and XGBoost. Feature contributions highlight model reliance patterns, which may influence bias levels, especially when dominant features correlate with protected attributes.
The BA reported in Table 3, supports this interpretation. While all models achieve a BA above 0.5, suggesting meaningful prediction beyond majority class guessing, only RF scores near 0.79. LR and XGBoost trail at 0.68 and 0.67, further reflecting their weaker class discrimination performance.

Table 3.
Performance (BA) and bias & fairness (SPD, AOD, EOD, DI, TI) metrics evaluated at decision default threshold , with respect to the protected attribute interest rate. All the models considered are displayed.
7.2. Evaluation of Fairness and Bias
While model performance metrics highlight how well each classifier distinguishes between defaults and non-defaults, a fairness evaluation at decision default threshold reveals substantial disparities in how these predictions are distributed across protected and unprotected groups. Using interest rate as the protected attribute to define fairness groups (see Section 6.3), we observe substantial disparities in how the models treat underprivileged versus privileged individuals (Figure 5, Table 3).
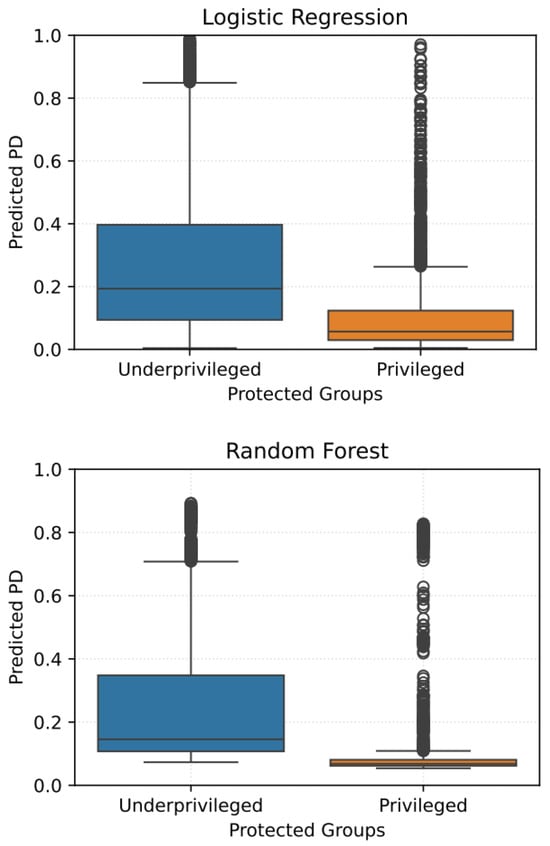
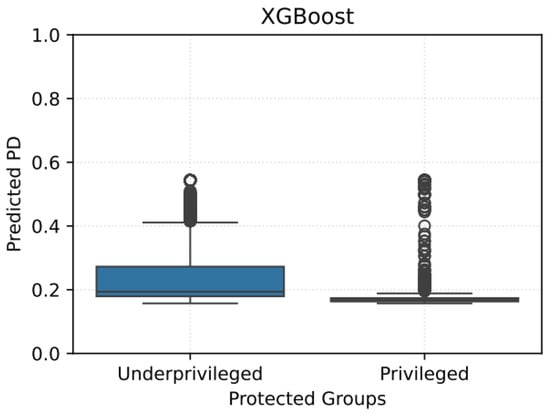
Figure 5.
Distribution of predicted loan approval probabilities across protected groups (privileged vs. underprivileged). Illustrates disparities in classification rates that drive fairness metrics such as SPD and EOD.
RF exhibits stronger fairness overall. With an SPD of −0.1297, AOD of 0.0525, EOD of −0.0251, and DI of 0.8565, RF demonstrates more consistent outcomes across groups. Its low TI of 0.04057 reflects equitable probability distributions and supports its position as a reliable compromise between performance and fairness. The probability plots (Figure 5) show that RF produces relatively less severe separation between privileged and underprivileged groups compared to LR.
XGBoost remains the fairest model, with the most favorable fairness metrics: SPD = −0.02269, AOD = 0.12135, EOD = 0.0, DI = 0.975, and TI = 0.040. The almost perfect parity in positive classifications and true positive rates across groups stems from its controlled use of interest rate and heavier reliance on home ownership and default history instead. The predicted probability plot (Figure 5) shows well-overlapped distributions between privileged and underprivileged groups, indicating a lack of systemic preference toward one group over the other.
LR, on the other hand, performs poorly on fairness dimensions. It yields SPD = −0.141, AOD = 0.1286, EOD = −0.0637, DI = 0.851, and TI = 0.073. Its reliance on highly weighted features like loan to income percent and the lack of nuanced interaction of feature results in significant disadvantages for underprivileged individuals. As shown in the predicted probability graph (top left plot of Figure 5), LR separates groups, resulting in disproportionately negative outcomes for those with high interest rates.
It is worth commenting that some metrics, shown in Table 3, such as SPD, AOD, and EOD, exhibit negative values for certain models. They indicate the direction of bias rather than its magnitude. For example, a negative SPD value means that the protected group has a lower positive classification rate compared to the unprotected group. Similarly, negative AOD suggests that false positive and true positive rates are lower for the protected group. Negative values highlight that bias can disproportionately disadvantage the protected group, a critical consideration when evaluating the fairness of the model.
These results show that the selected models exhibit distinct bias profiles before any adjustment: LR displays smooth score distributions but tends to amplify disparities in SPD and EOD, while RF and XGBoost reduce some disparities yet introduce others due to their non-linear decision boundaries. When such biases are present, relying solely on the raw PD estimates can lead to systematic differences in approval rates or error rates across protected groups. The proposed threshold optimization framework directly addresses this issue by providing an interpretable and model-agnostic mechanism for mitigating disparities at the decision stage. By tuning the scalarization trade-off parameter and adjusting the decision threshold, institutions can explicitly reduce unfair group-level differences while controlling the loss in BA. This offers a practical and transparent corrective measure when baseline model outputs are biased.
7.3. Optimization of the PD Threshold
7.3.1. Performance-Based Threshold
The BA of the models is analyzed across different classification thresholds for the predicted PD. For each model, the respective threshold () that maximizes performance (denoted as ) was identified, as illustrated in Figure 6. Notice that is same as setting in Equation (15).
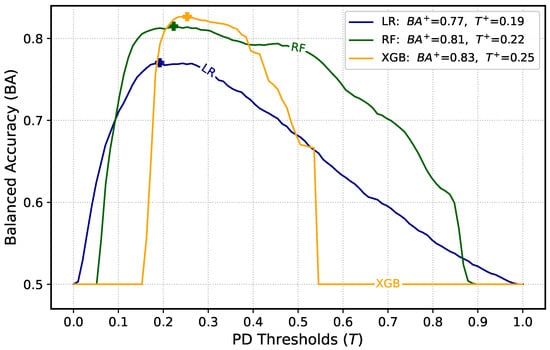
Figure 6.
Performance of the models versus the PD decision threshold. Different colors correspond to different models. The stars indicate the points where the maximum balanced accuracy (BA+) with its corresponding threshold () are attained.
At its highest BA, LR achieved an threshold of , with moderate BA compared to the other models. RF demonstrated good performance, with a threshold of and consistently higher BA in a wide range of thresholds. Its BA curve remained stable, highlighting the model’s robustness and relative balanced classification ability for both majority and minority classes. XGBoost performed comparably to RF, with a threshold of . Its BA curve closely followed RF’s, maintaining high values across various thresholds. Despite having the largest , the shape of the curve reflects the less effectiveness of XGBoost in identifying the minority class in the dataset.
Notice that the thresholds corresponding to maximum performance for all models are below the standard . This is not surprising, since there is a class imbalance in the dataset, where the defaults cases are significantly underrepresented compared to the non-defaults cases. In this case, models are naturally biased toward predicting the majority class, often resulting in higher predicted probabilities for non-defaults class. To counter this bias and improve classification of the minority class, a lower threshold is required to increase sensitivity (recall) for defaults. The need to lower thresholds can also be explained by the objective of maximizing BA. Since it equally weighs sensitivity and specificity, it encourages a trade-off where both classes are fairly represented in the classification. By setting the threshold below , models improve recall for the minority class while maintaining reasonable specificity for the majority class.
7.3.2. Trade-Offs Between BA and Fairness
We investigated the trade-off between fairness and performance across the classification models considered, by analyzing how performance BA varies with the decision threshold, and how bias & fairness metrics behave across this spectrum. For example Figure 7 presents this relationship, where BA is plotted against threshold, and SPD is encoded using a sequential color map. Lighter tones indicate SPD values closer to zero (i.e., fairer predictions), while darker tones indicate more negative SPD (greater disparity between protected groups). A black dot marks the default threshold , and a blue cross indicates the threshold that yields the maximum BA for each model.
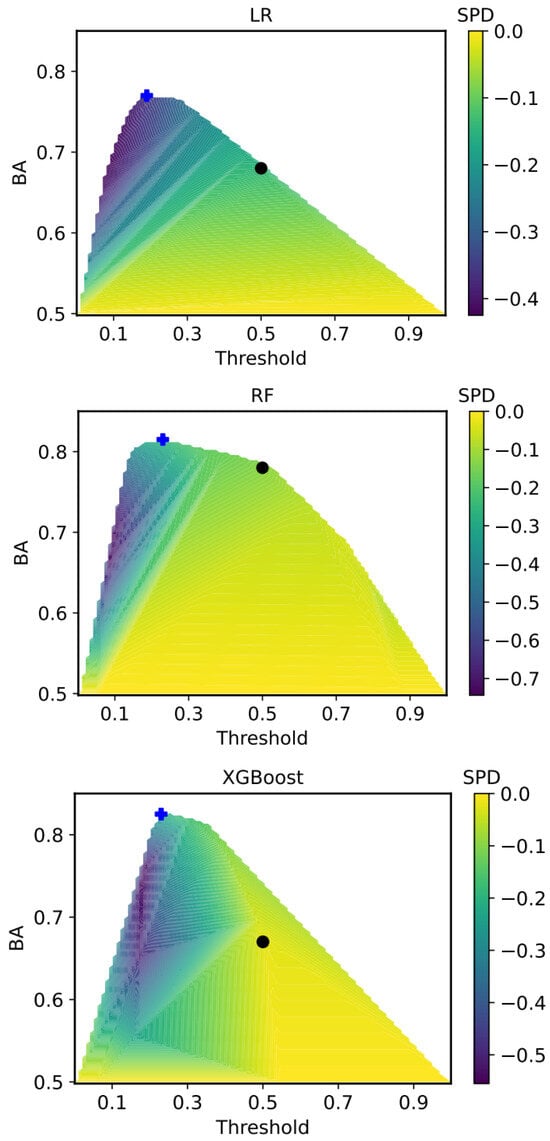
Figure 7.
BA versus classification threshold across all models. The background color scale represents SPD, using the color map. Lighter tones (yellow-green) indicate lower disparity (SPD closer to 0), and darker tones (purple) indicate greater disparity (more negative SPD). The dot (•) indicates the default threshold ; the cross (+) denotes the threshold at which BA is maximized.
As the threshold varies from 0 to 1, we observe that BA generally improves as the threshold moves away from the default value , particularly toward lower values. This shift reflects the class imbalance present in the dataset, where the defaults class is underrepresented. Lowering the threshold increases the sensitivity toward this minority class, enhancing overall BA. However, this improvement in performance is often accompanied by increased group disparity, as indicated by rising SPD values. For example, in LR, maximum BA of 0.77 is achieved at , but with a corresponding increase in SPD.
Each model displays a distinct trade-off landscape. LR demonstrates a sharp trade-off. As the threshold decreases and the BA increases, SPD becomes significantly more negative. This suggests that fairness deteriorates rapidly as the model optimizes for performance. RF displays a smoother transition. It achieved its maximum BA of 0.81 at with moderate fairness degradation. Its contour surface suggests a stable region of operation balancing accuracy and equity. XGBoost stands out by achieving both high performance and fairness. Its maximum BA of 0.83 at is achieved within a region of relatively light coloration, indicating lower SPD and minimal fairness loss. This makes XGBoost particularly well-suited for applications requiring a fair yet accurate model.
This implies that enhancing fairness can sometimes come at the expense of accuracy, making it necessary to strike a careful balance between the two. For any given model, it’s important not to consider accuracy or fairness in isolation, but rather to examine how both objectives evolve as thresholds are adjusted.
7.3.3. Optimal Threshold
We define as the model-specific threshold that minimizes the maximum deviation between ideal performance and fairness. It corresponds to the minimax solution of the fairness objective and is formally introduced in Equation (13).
To illustrate the independence of from the trade-off parameter , we analyze the behavior of the objective function for three representative values: (performance only), (fairness only), and (equal weighting). These scenarios are shown in Figure 8 with green, blue, and orange curves, respectively. For , the objective reflects pure performance, aligning with the analysis in Section 7.3. In contrast, focuses exclusively on reducing fairness disparities, while the intermediate case reflects a balanced compromise between both objectives.
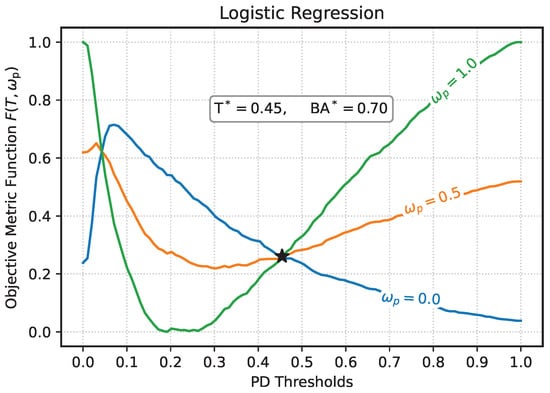
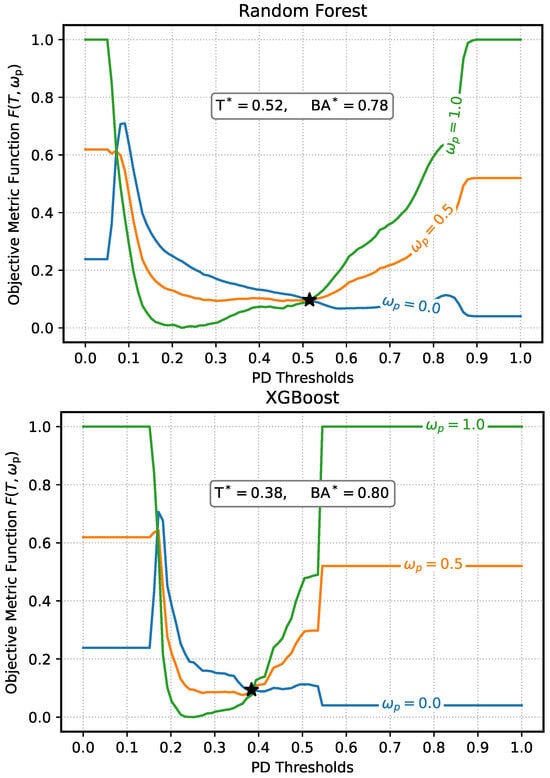
Figure 8.
Objective metric function as function of the PD threshold values for the models considered, for different values of . The parameter is given by Equation (5), and stands for the weight of performance in the objective metric function. The star (★) mark represents the point where is achieved. Recall that stands for optimal threshold determined by Equation (13), with the corresponding balance accuracy BA*.
Figure 8 compares these objective curves across models. For LR, the optimal threshold is , yielding a . This central threshold is consistent with the well-calibrated probability outputs typical of LR models. For RF, with , indicating a conservative yet stable decision boundary. XGBoost achieves the lowest threshold () and highest performance (), reflecting its strong optimization capacity and more aggressive decision boundaries.
It is also instructive to consider the limiting behavior of the objective function as or . As discussed in Section 5.5, when (fairness only) and , the objective approaches , dominated by DI term. In contrast, as , the normalized TI term dominates, pushing the objective to . For , which prioritizes performance, the function converges to the same value at both extremes: , since balanced accuracy is minimized at extreme thresholds. For intermediate trade-offs like , the limits reflect convex combinations: and , indicating gradual shifts in the trade-off as fairness and performance weights are balanced.
It is worth noting that, in each plot of Figure 8, in addition to , there exists a threshold value at which the objective function becomes independent of the performance weight . This invariance indicates that the trade-off between performance and fairness has reached a point of balance across the different metrics. Such a threshold corresponds to the equilibrium threshold defined in Equation (14), where the deviations of performance and fairness from their respective reference values are equal in magnitude. Empirically, these equilibrium points occur around , , and for the LR, RF, and XGBoost models, respectively. A closer examination reveals, however, that the value of the objective function at the equilibrium threshold, , is noticeably larger than at the optimal threshold . This observation supports the interpretation that while represents a balance point where performance and fairness deviations are equal, it does not necessarily minimize the overall objective function. In other words, corresponds to a condition of equilibrium rather than optimality. The difference between and therefore quantifies how far the balanced trade-off lies from the true optimum, offering insight into the degree of compromise required to achieve fairness–performance parity across models.
7.3.4. Effectiveness of Minimax Optimization
We examine how the optimal threshold affects both fairness and performance objectives. Table 4 displays, for each model, the relative improvement in the fairness and performance objectives when using compared to the default threshold . Recall that ratios below 1 indicate an improvement (i.e., a reduction in the corresponding objective function), while ratios above 1 indicate a deterioration. Ideally, both fairness and performance ratios should be below 1, meaning the optimized threshold improves both objectives.

Table 4.
Ratios of fairness and performance objective values at the optimized threshold , relative to the default threshold . The parameters , and are defined in Equation (18). Ratios below 1 indicate improvement in the corresponding objective function.
Concerning the model-specific results as displayed in Table 4, for the LR, the performance improves significantly by 25% (ratio = 0.75), while fairness worsens by 12.4% (ratio = 1.124). The optimization favors predictive accuracy at the cost of increased bias. For RF, the fairness improves slightly (ratio = 0.968) by approximately 3.2%, but performance worsens slightly by 8.9% (ratio = 1.089), reflecting a mild trade-off. XGBoost delivers strong gains on both fronts, with fairness ratio = 0.823 by 17.7%, and performance ratio about 0.16 by a substantial 84%. This indicates that the cut-off adjustment substantially reduces both bias and performance-related loss, making it the best dual-gain model among those tested.
This somehow highlights the model-dependent nature of post-processing threshold tuning strategy proposed in this work. While some models exhibit trade-offs between fairness and performance, others like XGBoost benefit significantly on both dimensions.
It is important to note that the minimax threshold can lie either below or above the default threshold . When , the model benefits from a more lenient decision boundary, classifying a larger share of applicants as positive. This shift increases sensitivity, as more true positives from the non-default class are correctly identified. Conversely, when , the model adopts a stricter decision rule, reducing the overall rate of positive classifications across groups. Such a reduction may contribute to narrowing disparities in fairness metrics such as SPD, AOD, or EOD.
The divergent outcomes observed for LR and XGBoost when (see Table 4) illustrate how model capacity influences these dynamics. LR, as a linear model, generates relatively smooth and overlapping score distributions between default and non-default classes. Lowering the threshold thus enhances sensitivity and yields a performance gain, but simultaneously exacerbates disparities, resulting in a degradation in fairness. By contrast, XGBoost leverages its non-linear ensemble structure to construct sharper decision boundaries that better separate the two classes. As a result, reducing the threshold produces gains on both fronts: an improvement in performance and in fairness.
7.3.5. Sensitivity of Threshold to the Weight
An important aspect of our fairness-aware modeling framework is the choice of the performance weight parameter , which governs the trade-off between predictive accuracy and fairness. To investigate its impact, we analyze how the optimal decision threshold (see Equation (15)) varies as a function of , for each model considered. The results are illustrated in Figure 9.
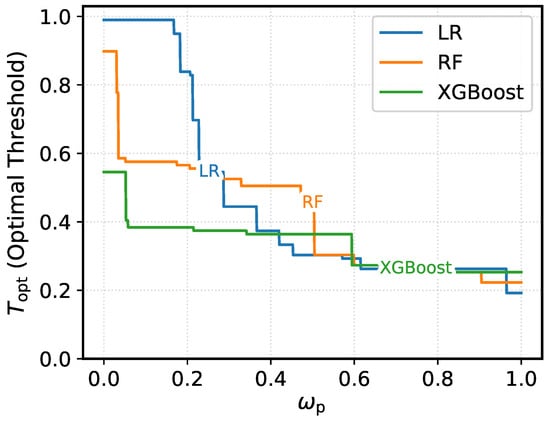
Figure 9.
Optimal threshold , defined by Equation (15), as a function of the performance weight for the models.
LR exhibits a sharp decrease in as increases. When fairness is fully prioritized (), the optimal threshold is high (), limiting positive classifications to minimize disparate impact. As approaches 1, favoring performance, drops to approximately 0.2, increasing recall at the cost of fairness. This sensitivity highlights LR’s flexibility but also its instability under shifting priorities. RF maintains a relatively stable threshold across the full range of , with fluctuating between 0.45 and 0.55. This indicates RF’s robustness and natural balance between accuracy and fairness, making it a practical choice when model behavior should remain predictable under different policy scenarios. XGBoost demonstrates a moderate and smooth variation in , starting from around 0.25 when performance is prioritized, and rising to approximately 0.5 as fairness becomes dominant. This suggests that XGBoost adapts well to the trade-off, without being overly sensitive.
Notice as discussed in the previous sections, at , the objective function minimizes fairness-related metrics only. Consequently, most models raise to suppress biased positive classifications, particularly in LR. At , performance is prioritized exclusively, and all models adopt lower thresholds to improve sensitivity for the minority class (defaults), often at the cost of fairness.
In sum, the selection of would be guided by institutional objectives and regulatory context. For institutions with strong fairness or compliance mandates, a value of is advisable. In contrast, risk-driven environments may prefer to emphasize accuracy. A balanced setting () ensures equal weighting and provides a compromise solution, suitable for institutions seeking to meet both performance and ethical benchmarks.
7.3.6. Navigating Between , and
To support practical threshold selection, we analyze the effectiveness of the optimized threshold relative to both the standard threshold and the model-specific compromise minimax threshold . Figure 10 presents a comparative analysis of fairness and performance trade-offs obtained by the optimized threshold , relative to two baselines: the default threshold and the minimax-optimal threshold . Each point corresponds to a scalarization weight and is color-coded accordingly. The plotted quantities, namely fairness ratio and performance ratio , evaluate the degree to which improves (values below 1) or degrades (values above 1) the respective objectives relative to the baseline. Each model exhibits a distinct structure in the resulting trade-off space.
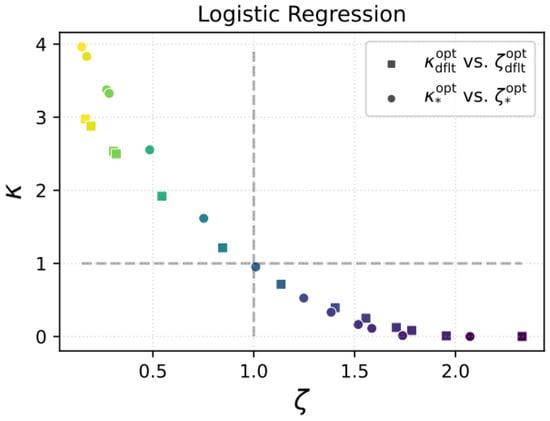
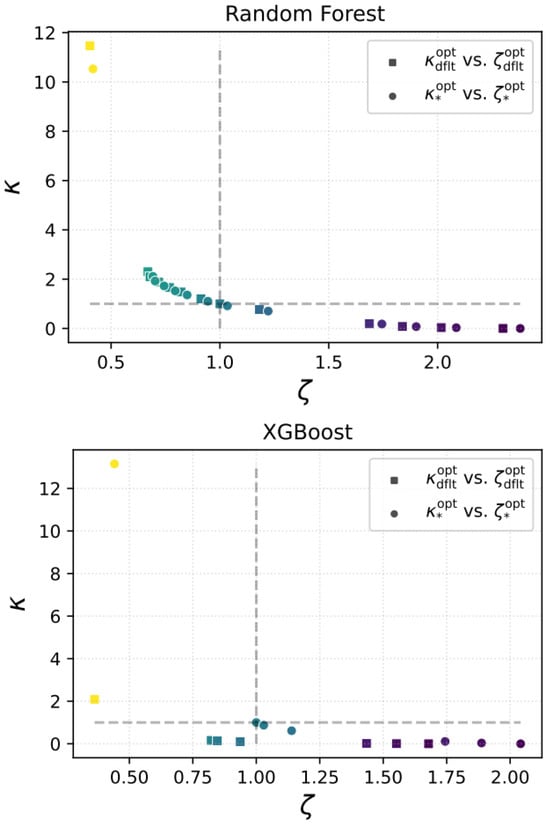
Figure 10.
Quadrant-based comparison of fairness–performance trade-offs for optimized thresholds , evaluated against two baselines: the default threshold (shown as squares) and the minimax-optimal threshold (shown as dots). The x-axis shows the fairness ratio , and the y-axis shows the performance ratio , where the denominator is either or depending on the marker, as defined in Equations (16) and (17). Points are color-coded by the scalarization parameter . Values in the lower-left quadrant indicate simultaneous improvement in both fairness and performance.
For LR, the fairness and performance ratios relative to both baselines highlight a steep trade-off surface. At very low (e.g., 0.01), we observe significant fairness gains versus both baselines: , , but at the expense of large performance degradation: , . As increases, both fairness ratios exceed 1, indicating that degrades fairness compared to both baselines. This shift confirms that the scalarization parameter offers fine control but also exposes the model’s limited flexibility.
For RF, the model exhibits more favorable behavior across both comparisons. At moderate , the ratios remain below 1: , ; and similarly, , . This suggests that can outperform both and simultaneously in many regions of the scalarization space. However, as , performance gains saturate while fairness ratios increase, indicating a convergence toward performance-maximizing but less equitable thresholds.
In the case of XGBoost, the trade-off surface is particularly smooth and controlled. At , achieves nearly balanced trade-offs against both baselines: , ; and , . Even at high fairness weights (e.g., ), it delivers significant fairness gains compared to both and , with acceptable performance trade-offs. This confirms that threshold tuning in XGBoost is not only effective but also stable across a wide range of preferences.
In sum, the joint analysis relative to both and reveals several aspects. often dominates in fairness, especially at low . Also, when focuses on fairness, provides a performance recovery mechanism via scalarization. Further, the three models differ in sensitivity, LR displays sharp transitions; RF allows smoother adjustment; and XGBoost offers the most robust trade-offs. These results support the use of as a principled way to navigate between fixed and fairness-optimized thresholds, with serving as an interpretable dial for stakeholder priorities.
7.4. Robustness and Generalization
To assess the generalizability of the proposed threshold optimization framework beyond synthetic data, we conducted additional experiments using German Credit Dataset (Hofmann, 1994). It contains 1000 loan application records described by 20 variables, including demographic, financial and credit history features. The binary target variable classifies applicants as good or bad credit risks. Table A1 summarizes these variables.
Among the dataset’s sensitive attributes, such as sex, age, and foreign worker status, we selected sex as the protected attribute for this study. Applicants were divided into privileged (male) and underprivileged (female) groups, aligning with common fairness auditing conventions in credit risk research (Alves et al., 2023; Coraglia et al., 2024; Kozodoi et al., 2022; Szepannek & Lübke, 2021; Trivedi, 2020).
The pre-processing followed a pipeline similar to that in the synthetic dataset, and then we evaluated the performance of each model under the default classification threshold and the minimax optimized threshold .
Table 5 reports and presents the corresponding performance and fairness objective ratios with respect to the . LR shows mixed results: some points lie in the lower-left quadrant, suggesting potential for improvement, but the performance ratio indicates substantial loss in predictive quality when transitioning to , despite a modest gain in fairness. RF achieves a more favorable balance, with both ratios under 1 (, ), demonstrating that decision cut-off optimization improves both objectives simultaneously. XGBoost provides the most consistent and robust behavior: the fairness ratio drops significantly to 0.653 while the performance ratio remains close to 1, indicating a clear fairness gain with minimal cost to predictive power.

Table 5.
Ratios of fairness and performance objective values at the optimized threshold , relative to the default threshold , for the German Credit dataset. Ratios below 1 indicate improvement.
Figure 11 provides a visualization-based diagnostic of the fairness–performance trade-offs achieved by the optimized thresholds , compared to both the default threshold and the minimax-optimal threshold , similar to Figure 10 in the case of synthetic data. Each point represents a particular value of the scalarization parameter , with dots indicating comparisons to and squares indicating comparisons to . Colors encode the corresponding values. The plotted ratios, and , indicate whether the optimized threshold improves or degrades the respective objectives.
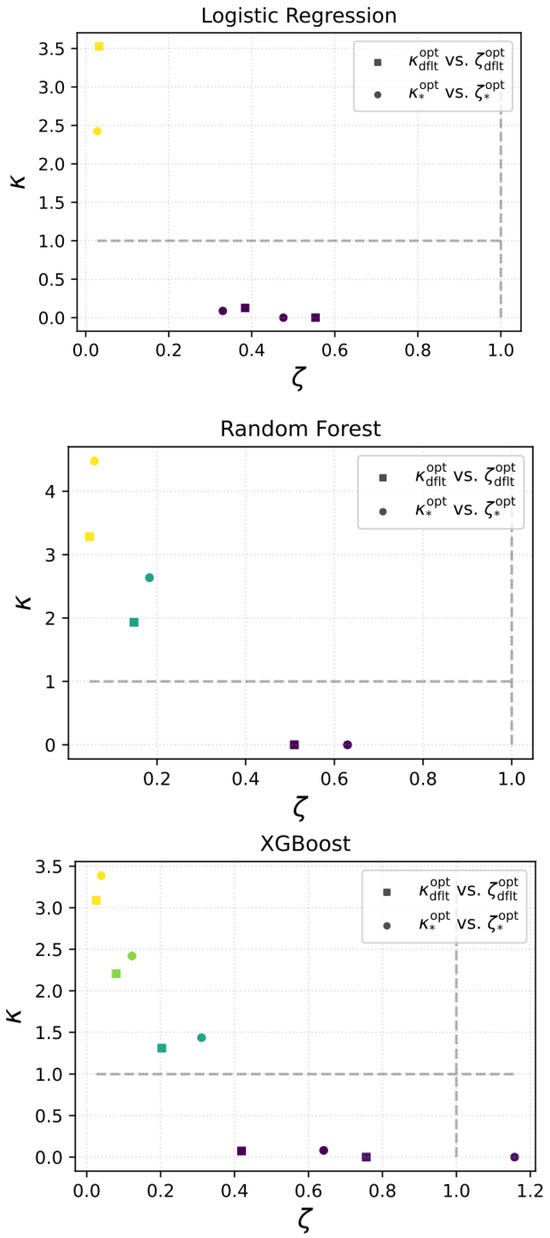
Figure 11.
Same as Figure 10, but using the German Credit dataset. Each point represents an optimized threshold obtained under a specific weight parameter , compared against (squares) or (dots). Axes show the ratios and for fairness and performance, respectively. Points in the lower-left quadrant indicate Pareto improvements over the reference threshold. Color gradient encodes the value of , with darker tones representing higher weights on performance.
For LR, the behavior of reveals a trade-off pattern consistent with the model’s linear nature. For instance, at low , we observe strong fairness gains versus both references (, ), but accompanied by substantial performance loss (, ). At higher scalarization (e.g., ), fairness and performance both degrade compared to , indicating that converges toward a performance-oriented but fairness-averse regime.
RF demonstrates more favorable and symmetric behavior. At moderate , we observe simultaneous improvement across both baselines: , , and , . Even at , the performance ratio drops to zero, indicating preservation of classification outcomes while maintaining notable fairness gains. This reflects RF’s flexibility in leveraging post-threshold adjustments without sacrificing predictive utility.
The optimized thresholds consistently yield strong fairness improvements with minimal or no loss in performance, in the case of XGBoost. At , for example, we observe , , while also outperforming the default with , . At very low fairness weight (e.g., ), the performance degradation is still controlled (), while fairness gain remains substantial (). This consistent sub-unity behavior in both axes confirms that XGBoost’s calibrated scores make it highly responsive to scalarized threshold optimization.
Across all models, the optimized threshold shows an ability to interpolate between fairness- and performance-driven solutions. While LR exhibits more extreme trade-offs, RF and XGBoost deliver ratio-based improving thresholds under many scalarization settings. The joint comparison against both and validates the robustness of the optimization strategy, and provides an interpretable, continuous mechanism for balancing fairness and accuracy based on policy or institutional priorities.
7.5. Impact of Incorporating the Fairness Framework
To evaluate the effect of incorporating fairness metrics into the decision rule, we compare baseline model outcomes at the default threshold with those obtained after optimization using the scalarized objective that jointly accounts for BA and multiple group fairness criteria (SPD, AOD, EOD, DI, TI). For example, the ratios reported in Table 5 could allow us to quantify the relative change in fairness and performance when moving from to the optimized threshold . For the German Credit dataset, RF exhibits substantial simultaneous improvements: fairness violations decrease by while BA improves by . XGBoost shows a similar pattern, achieving an reduction in fairness disparities together with a strong gain in predictive performance. These results highlight that flexible nonlinear models can benefit meaningfully from fairness-aware thresholding, uncovering latent efficiency gains without retraining. LR behaves differently: fairness worsens by and performance declines by . This is consistent with its more linear and overlapping score distributions, which limit the extent to which group-level disparities can be mitigated through post-processing alone. These contrasting behaviors confirm that fairness–performance dynamics are intrinsically model-dependent.
Across both datasets, post-processing threshold optimization consistently reduces group disparities for RF and XGBoost relative to the baseline , especially for SPD, AOD, and EOD. Under the default threshold, models often produce unequal approval or true-positive rates between protected groups. By contrast, systematically mitigates these disparities, and provides additional controlled improvement depending on institutional priorities. These results demonstrate that fairness does not arise automatically from predictive accuracy: explicit fairness-aware decision rules are required.
Overall, the comparison between baseline decisions and fairness-adjusted thresholds confirms that the proposed framework produces materially different, more ethically aligned, and more regulatorily compliant credit decisions. Without fairness intervention, results are driven purely by score distributions and may preserve inequities embedded in historical data. With the fairness framework, institutions gain transparent and tunable control over fairness–performance trade-offs without retraining the underlying model, supporting more responsible PD estimation practices.
8. Ethical and Legal Considerations
The use of ML in credit risk modeling introduces important ethical, legal, and governance responsibilities due to the direct impact of automated decisions on individuals’ access to financial services. As credit-scoring systems influence loan approvals, denials, and pricing, it is essential to ensure that these models do not reproduce or exacerbate structural biases embedded in historical data. Our threshold-optimization framework responds to this challenge by providing an interpretable mechanism to adjust model decisions while explicitly balancing predictive performance and fairness.
A central ethical concern in ML-based credit scoring is the risk of unfair discrimination. Models trained on historical data may inadvertently reflect past inequities, disproportionately disadvantaging certain demographic or socio-economic groups. Beyond predictive accuracy and explainability, fairness must therefore be actively assessed and governed. The proposed framework contributes to this aim by introducing a tunable post-processing adjustment that enables transparent control over fairness–performance trade-offs, rather than implicitly favoring accuracy at the expense of equitable outcomes. In this sense, the approach promotes more responsible and socially aligned decision-making in credit assessment. Moreover, biased PD models can have long-term societal implications: systematic denial of credit to specific groups may reinforce economic disparities, limit social mobility, and reduce trust in financial institutions. By reducing disparate outcomes in a controlled and interpretable manner, the framework supports more inclusive lending practices and contributes to sustaining institutional legitimacy.
Credit scoring is increasingly regulated under frameworks that prioritize fairness, transparency, and accountability. In the European Union, the General Data Protection Regulation (GDPR) (Parliament of the European Union, 2016) mandates non-discrimination in automated processing and grants individuals the right to a meaningful explanation of algorithmically generated decisions, and restricts the use of sensitive data without consent. Additionally, GDPR Recital 71 explicitly warns against profiling that results in unfair discrimination. Because the threshold optimization operates at the decision stage, without altering the internal model, it enables institutions to mitigate disparate impacts while maintaining interpretability and compliance with these provisions.
The EU Artificial Intelligence Act (Kelly et al., 2024; EU AI Act, 2024) classifies creditworthiness assessment as a high-risk AI system, imposing stringent requirements on risk management, monitoring of discriminatory outcomes, documentation, and auditability. The proposed post-processing mechanism constitutes an interpretable and auditable lever for adjusting outcomes, supporting continuous monitoring and governance obligations without requiring model retraining.
In the United States, the Equal Credit Opportunity Act (ECOA) and Fair Lending laws (Congress, 1974, 1977) prohibit discrimination based on protected attributes and require institutions to ensure that credit models do not generate disparate impacts. Integrating fairness metrics directly into the threshold-adjustment process provides a means to detect and mitigate such disparities, thereby enhancing compliance with fair lending expectations.
Banking-specific regulatory frameworks, including the Basel II/III standards (Basel Committee on Banking Supervision, 2004, 2009, 2011, 2017) and European Banking Authority (EBA) guidelines (European Banking Authority, 2021, 2025), emphasize requirements for model stability, explainability, validation, and governance. Threshold optimization, being model-agnostic and external to the training pipeline, integrates seamlessly into existing oversight processes such as back-testing and monitoring. While our study does not include an explicit benchmarking against supervisory frameworks, the proposed approach can be incorporated within established validation and model risk management procedures.
Although the framework is technically simple and computationally light, its practical integration requires appropriate governance. Institutions must define procedures for calibrating thresholds, documenting rationale for fairness–performance trade-offs, and monitoring their stability over time. Because the approach produces interpretable ratios and objective functions, it facilitates communication with risk committees, compliance units, and regulators. Furthermore, adopting such a framework can encourage institutions to systematically evaluate the fairness of their credit decisions, thereby strengthening transparency and accountability. Threshold optimization provides a pragmatic control mechanism that aligns with operational practices, enabling responsible deployment of ML models in lending contexts.
9. Limitations and Perspectives
Despite its contributions, this study has several limitations that point to valuable avenues for future research and application.
First, the analysis centers on a single protected or proxy attribute (e.g., interest rate or sex, depending on the dataset), selected for its observable disparities and relevance to credit risk assessment. However, real-world fairness concerns are often intersectional, involving simultaneous effects of multiple demographic and socio-economic characteristics such as gender, age combinations, income, or foreign status. Our current formulation evaluates fairness exclusively at the group level and aggregates several fairness criteria into a scalar objective, assuming equal weights across metrics (see Equation (8)). This may mask conflicts between fairness definitions and does not capture fairness at the individual level (e.g., counterfactual fairness) or the dynamic, temporal propagation of disparities over time. Future work could extend the framework to multi-attribute and intersectional fairness settings, incorporate individual-level fairness notions, and explore multi-objective optimization strategies that explicitly represent the trade-offs between potentially competing fairness metrics such as SPD and EOD.
Second, another limitation of the proposed approach lies in its dependence on the normalization scheme applied to the metric functions. Since the optimization operates in a normalized objective space, the bounds directly influences the relative weighting and scaling of each metric. If the observed range of a metric is narrow or strongly asymmetric, small perturbations in these bounds can lead to disproportionate changes in the normalized values and in the normalized reference points . As a result, the solution (or ) may become unstable, particularly when lies far outside the normalized interval . This instability reflects a well-known issue in multi-objective optimization, where improper normalization can distort the toward certain objectives (Wang et al., 2017). Hence, the stability of the final solution depends not only on the weighting scheme but also on the empirical quality of the normalization process. In practice, we recommend verifying the robustness of the results by perturbing the normalization bounds, assessing the sensitivity of to these changes, and ensuring that deviations of from the [0, 1] range remain moderate.
We also acknowledge that aggregating multiple fairness metrics into a single scalar objective can introduce simplification. While the bounded normalization used here reduces scale-driven dominance, it cannot entirely eliminate interactions among correlated fairness indicators. Future work may therefore explore other normalization schemes, for example those that offer dataset-independent scaling guarantees, or avoid scalarization bias and make fairness–performance trade-offs explicit.
Third, we assumed that predicted probabilities are well-calibrated, i.e., that the output scores from the classifiers meaningfully reflect true likelihoods of default. This assumption is particularly relevant because fairness metrics, such as SPD or EOD, are sensitive to the distributional shape of predicted scores, and the thresholding operation directly affects group-level outcomes. Poor calibration can distort both performance and fairness assessments, leading to misaligned decision threshold adjustment. Although we did not explicitly calibrate the classifiers in this study, future work could incorporate calibration diagnostics and correction steps prior to threshold adjustment. This would ensure that the ethical and predictive balance reflect true underlying risks and improve the interpretability and regulatory reliability of the decision thresholds.
Fourth, the current evaluation is based on static, single-period datasets, both synthetic and the German Credit dataset. These do not reflect evolving borrower behavior, macroeconomic shifts, or feedback loops introduced by model deployment. Extending the framework to support temporal validation, drift detection, and longitudinal fairness would enhance its operational realism and regulatory alignment, especially in banking environments where model performance must be monitored over time.
Additionally, the proposed framework focuses exclusively on post-processing threshold adjustment, which offers the advantage of being model-agnostic, computationally efficient, and compatible with existing credit scoring systems that may be costly or impractical to retrain. However, this post hoc intervention cannot correct structural sources of bias arising from data imbalance, label bias, or model design. As a result, the method addresses disparities in model outputs but does not resolve deeper forms of unfairness embedded in the training process. A comprehensive fairness strategy would combine post-processing with pre-processing techniques (such as reweighting or data debiasing) and in-processing approaches (such as fairness-aware regularization or adversarial training). Developing an integrated framework that unifies these three levels of mitigation constitutes an important avenue for future work.
Also, the empirical analysis focuses on LR, RF, and XGBoost, which remain among the most widely deployed algorithms for credit scoring due to their interpretability, stability, and strong regulatory acceptance. However, this model selection does not encompass more complex architectures such as neural networks, support vector machines, or hybrid ensemble methods increasingly used in the literature, as highlithed in the text. Because the proposed threshold optimization method is model-agnostic, future research could extend the experiments to these additional families to assess whether the fairness–performance trade-off patterns observed here persist under more expressive learning architectures.
Moreover, even though the framework supports post hoc threshold tuning, legal and regulatory standards on fairness in automated decision-making remain evolving. Different fairness definitions may yield different legal interpretations. Future work could map fairness metrics to specific regulatory frameworks (e.g., the EU AI Act, ECOA, or GDPR), and assess how institutions can align threshold choices with policy objectives or legal constraints. This includes investigating threshold policies that are auditable, documentable, and aligned with model governance procedures.
Furthermore, although the proposed threshold optimization framework focuses on statistical fairness and predictive performance, credit risk modeling inherently involves asymmetric economic costs associated with misclassification. In practice, false negatives (i.e., approving applicants who later default) generate expected financial losses quantified through the regulatory triplet , while false positives (i.e., rejecting creditworthy applicants) correspond to forgone revenue, diminished client relationships, and potential regulatory scrutiny regarding equal access to credit. Therefore, economic considerations play a central role in threshold calibration for lending decisions. The present work intentionally isolates the fairness–performance trade-off without embedding cost-sensitive terms in the objective function. This design ensures model-agnostic applicability and avoids dependence on institution-specific loss preferences, which vary considerably across portfolios, risk appetites, and regulatory environments. However, the framework is fully compatible with cost-sensitive extensions. In particular, misclassification losses could be integrated by associating distinct penalties to false positives and false negatives, or by replacing balanced accuracy with a profit-based or expected-loss-based objective function. Such extensions would allow the joint optimization of fairness, predictive reliability, and financial impact. In future work, cost-sensitive calibration could be implemented by embedding expected-loss terms directly into the scalarized objective, or by imposing economic constraints (e.g., maximum allowable expected loss) alongside fairness constraints. This integration would enhance the managerial interpretability of the framework and align threshold decisions more closely with real-world credit risk management practices.
Finally, public, large-scale datasets are extremely scarce, as credit risk data are confidential and protected by strict regulatory and privacy constraints. For this reason, our empirical analysis relies on the German Credit dataset and a synthetic benchmark, which are among the few publicly accessible resources commonly used in credit-scoring research. Access to real large-scale institutional datasets, often containing millions of records, was not possible due to confidentiality restrictions. Future work could aim to validate the framework on larger proprietary datasets through collaborations with financial institutions.
10. Conclusions
This study introduces a fairness-aware post hoc threshold refinement framework for PD modeling, designed to improve the equity of credit scoring decisions without retraining underlying ML models. It aligns with the growing concerns for ethical, transparent, and efficient decision-making in the financial sector. While traditional metrics such as accuracy and ROC-AUC offer insights into model performance, they can overlook the complex challenges posed by bias and disparate treatment. The approach is model-agnostic and post-processing in nature, allowing financial institutions to flexibly adjust decision boundaries via a scalarization parameter that balances predictive performance and group fairness objectives.
Our empirical analysis, conducted on both synthetic and real-world datasets, shows that the optimized threshold can outperform both the default threshold and the minimax fairness-optimal threshold , depending on institutional priorities. The results confirm that fairness improvements, measured through metrics such as Statistical Parity Difference and Equal Opportunity Difference, can be achieved with minimal or acceptable trade-offs in performance metrics such as balanced accuracy.
Across models, RF and XGBoost show particularly robust responses to threshold optimization. RF balances fairness and performance over a wide range of scalarization weights, while XGBoost often yields fairness gains with very little degradation in performance. LR, by contrast, is more sensitive to threshold shifts, often requiring sharper trade-offs to improve fairness. These differences reflect not only model expressiveness but also the shape of the score distributions from which thresholds are selected.
A key contribution of this work is the formalization and evaluation of a scalarized threshold selection procedure that provides interpretable, controllable access to fairness–performance balance. The inclusion of quadrant-based diagnostics and ratio-based comparisons enables practitioners to understand and visualize how optimized thresholds behave relative to both fairness-driven and accuracy-driven baselines. Notably, we observed instances, particularly in XGBoost and RF, where achieved improvements over both baselines.
The generalization study using the German Credit dataset further reinforces the practical relevance of this framework. Even under different data distributions, model families, and protected attributes, threshold optimization remains a reliable tool for aligning classification outputs with ethical and regulatory expectations. When the scalarized objective exhibits non-uniqueness, the resulting solution set provides valuable flexibility for integrating operational or legal constraints into threshold selection.
More broadly, this work contributes to the growing body of research on responsible AI in finance. It underscores the role of post-processing techniques as viable, low-cost strategies for reducing algorithmic bias. Future research directions include extending this framework to support group-specific thresholds, incorporating temporal fairness constraints, and integrating threshold selection with regulatory audit requirements under frameworks such as the EU AI Act or U.S. Fair Lending laws.
By embedding fairness considerations into threshold selection, this work contributes to more transparent, accountable, and equitable lending decisions in ML-driven credit risk assessment.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
We conducted our experiments using two publicly available datasets: the German Credit Dataset, accessible at https://doi.org/10.24432/C5NC77, and the Credit Risk Dataset, available at www.kaggle.com/datasets/laotse/credit-risk-dataset (accessed on 21 October 2025).
Conflicts of Interest
The author declares no conflicts of interest. The employer acted as a sponsor in the study’s design, data collection, analysis, interpretation, manuscript preparation, and the decision to publish the findings. Nevertheless, the employer did not influence the nature, representation, or interpretation of the research results.
Appendix A. List of Variables in the German Credit Dataset
The German Credit Data contains data on 20 variables and the classification whether an applicant is considered a Good or a Bad credit risk for 1000 loan applicants. Table A1 summarizes these variables. See (Hofmann, 1994) for an exhaustive description of variables.

Table A1.
Features and target variable in the German Credit dataset.
Table A1.
Features and target variable in the German Credit dataset.
| Type | Name and Description |
|---|---|
| Features (inputs) | Checking Account Status |
| Duration in Months | |
| Credit History | |
| Purpose of Credit | |
| Credit Amount | |
| Savings Account/Bonds | |
| Present Employment | |
| Installment Rate (% of Income) | |
| Personal Status and Sex | |
| Other Debtors/Guarantors | |
| Present Residence Since | |
| Property | |
| Age | |
| Other Installment Plans | |
| Housing | |
| Number of Existing Credits | |
| Job Category | |
| Number of People Liable | |
| Telephone Availability | |
| Foreign Worker Status | |
| Target (output) | Loan Status (Good/Bad Credit) |
References
- Abbasi-Sureshjani, S., Raumanns, R., Michels, B. E., Schouten, G., & Cheplygina, V. (2020, October 4–8). Risk of training diagnostic algorithms on data with demographic bias. In Interpretable and annotation-efficient learning for medical image computing: Third international workshop, iMIMIC 2020, second international workshop, MIL3ID 2020, and 5th international workshop, LABELS 2020, held in conjunction with MICCAI 2020, Lima, Peru (pp. 183–192). Springer. [Google Scholar]
- Alam, M. A. U. (2020, December 7–9). Ai-fairness towards activity recognition of older adults. MobiQuitous 2020-17th EAI International Conference on Mobile and Ubiquitous Systems: Computing, Networking and Services (pp. 108–117), Darmstadt, Germany. [Google Scholar]
- Alves, G., Bernier, F., Couceiro, M., Makhlouf, K., Palamidessi, C., & Zhioua, S. (2023). Survey on fairness notions and related tensions. EURO Journal on Decision Processes, 11, 100033. [Google Scholar] [CrossRef]
- Basel Committee on Banking Supervision. (2004). International convergence of capital measurement and capital standards: A revised framework (Tech. Rep.). Bank for International Settlements. Available online: https://www.bis.org/publ/bcbs128.pdf (accessed on 30 June 2025).
- Basel Committee on Banking Supervision. (2009). Enhancements to the basel II framework (Tech. Rep.). Bank for International Settlements. Available online: https://www.bis.org/publ/bcbs157.pdf (accessed on 13 July 2025).
- Basel Committee on Banking Supervision. (2011). Basel III: A global regulatory framework for more resilient banks and banking systems (Tech. Rep.). Bank for International Settlements. Available online: https://www.bis.org/publ/bcbs189.pdf (accessed on 1 June 2025).
- Basel Committee on Banking Supervision. (2017). Basel III: Finalising post-crisis reforms (Tech. Rep.). Bank for International Settlements. Available online: https://www.bis.org/bcbs/publ/d424.pdf (accessed on 7 May 2025).
- Bellamy, R. K. E., Dey, K., Hind, M., Hoffman, S. C., Houde, S., Kannan, K., Lohia, P., Martino, J., Mehta, S., Mojsilovic, A., Nagar, S., Ramamurthy, K. N., Richards, J., Saha, D., Sattigeri, P., Singh, M., Varshney, K. R., & Zhang, Y. (2018, October). AI fairness 360: An extensible toolkit for detecting, understanding, and mitigating unwanted algorithmic bias. arXiv. [Google Scholar] [CrossRef]
- Bishop, C. M. (2006). Pattern recognition and machine learning (information science and statistics). Springer. [Google Scholar]
- Blow, C. H., Qian, L., Gibson, C., Obiomon, P., & Dong, X. (2023). Comprehensive validation on reweighting samples for bias mitigation via AIF360. arXiv. [Google Scholar] [CrossRef]
- Borza, V., Estornell, A., Ho, C.-J., Malin, B., & Vorobeychik, Y. (2024). Dataset representativeness and downstream task fairness. arXiv. [Google Scholar] [CrossRef]
- Breiman, L. (2001). Random forests. Machine Learning, 45(1), 5–32. [Google Scholar] [CrossRef]
- Brodersen, K. H., Ong, C. S., Stephan, K. E., & Buhmann, J. M. (2010, August 23–26). The balanced accuracy and its posterior distribution. 2010 20th International Conference on Pattern Recognition (pp. 3121–3124), Istanbul, Turkey. [Google Scholar]
- Bui, M. D., & Von Der Wense, K. (2024). The trade-off between performance, efficiency, and fairness in adapter modules for text classification. arXiv. [Google Scholar] [CrossRef]
- Calmon, F., Wei, D., Vinzamuri, B., Natesan Ramamurthy, K., & Varshney, K. R. (2017, December 4–9). Optimized pre-processing for discrimination prevention. 31st International Conference on Neural Information Processing Systems (Vol. 30), Long Beach, CA, USA. [Google Scholar]
- Chapelle, O., Schölkopf, B., & Zien, A. (2006). Semi-supervised learning (adaptive computation and machine learning). The MIT Press. [Google Scholar]
- Chawla, N. V., Bowyer, K. W., Hall, L. O., & Kegelmeyer, W. P. (2002). SMOTE: Synthetic minority over-sampling technique. Journal of Artificial Intelligence Research, 16, 321–357. [Google Scholar] [CrossRef]
- Chen, T., & Guestrin, C. (2016, August 13–17). XGBoost: A scalable tree boosting system. 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (pp. 785–794), San Francisco, CA, USA. [Google Scholar]
- Chen, Y., Calabrese, R., & Martin-Barragan, B. (2024). Interpretable machine learning for imbalanced credit scoring datasets. European Journal of Operational Research, 312(1), 357–372. [Google Scholar] [CrossRef]
- Coraglia, G., Genco, F. A., Piantadosi, P., Bagli, E., Giuffrida, P., Posillipo, D., & Primiero, G. (2024). Evaluating AI fairness in credit scoring with the brio tool. arXiv. [Google Scholar] [CrossRef]
- Corbett-Davies, S., Pierson, E., Feller, A., Goel, S., & Huq, A. (2017). Algorithmic decision making and the cost of fairness. arXiv. [Google Scholar] [CrossRef]
- Cortes, C., & Vapnik, V. (1995). Support-vector networks. Machine Learning, 20(3), 273–297. [Google Scholar] [CrossRef]
- Cox, D. R. (2018). The regression analysis of binary sequences. Journal of the Royal Statistical Society: Series B (Methodological), 20(2), 215–232. [Google Scholar] [CrossRef]
- Das, S., Donini, M., Gelman, J., Haas, K., Hardt, M., Katzman, J., Kenthapadi, K., Larroy, P., Yilmaz, P., & Zafar, B. (2021). Fairness measures for machine learning in finance. The Journal of Financial Data Science, 3(4), 33–64. [Google Scholar] [CrossRef]
- Dächert, K., Gorski, J., & Klamroth, K. (2012). An augmented weighted Tchebycheff method with adaptively chosen parameters for discrete bicriteria optimization problems. Computers & Operations Research, 39(12), 2929–2943. [Google Scholar] [CrossRef]
- de Vargas, V. W., Aranda, J. A. S., dos Santos Costa, R., da Silva Pereira, P. R., & Barbosa, J. L. V. (2022). Imbalanced data preprocessing techniques for machine learning: A systematic mapping study. Knowledge and Information Systems, 65(1), 31–57. [Google Scholar] [CrossRef]
- Dhar, V. (2013). Data science and prediction. Communications of the ACM, 56(12), 64–73. [Google Scholar] [CrossRef]
- Diana, E., Gill, W., Kearns, M., Kenthapadi, K., & Roth, A. (2021, May 19–21). Minimax group fairness: Algorithms and experiments. 2021 AAAI/ACM Conference on AI, Ethics, and Society (pp. 66–76), Virtual Event. [Google Scholar]
- Diao, Y., Li, Q., & He, B. (2024, February 20–27). Exploiting label skews in federated learning with model concatenation. AAAI Conference on Artificial Intelligence (Vol. 38, pp. 11784–11792), Vancouver, BC, Canada. [Google Scholar]
- Doherty, N. A., Kartasheva, A. V., & Phillips, R. D. (2012). Information effect of entry into credit ratings market: The case of insurers’ ratings. Journal of Financial Economics, 106(2), 308–330. [Google Scholar] [CrossRef]
- Donoho, D. (2017). 50 years of data science. Journal of Computational and Graphical Statistics, 26, 745–766. [Google Scholar] [CrossRef]
- Du, D.-Z., & Pardalos, P. M. (Eds.). (1995). Minimax and applications. Springer. [Google Scholar]
- Duan, H., Zhao, Y., Chen, K., Xiong, Y., & Lin, D. (2022, October 23–27). Mitigating representation bias in action recognition: Algorithms and benchmarks. European Conference on Computer Vision (pp. 557–575), Tel Aviv, Israel. [Google Scholar]
- Dwork, C., Hardt, M., Pitassi, T., Reingold, O., & Zemel, R. (2012, January 8–10). Fairness through awareness. 3rd Innovations in Theoretical Computer Science Conference (pp. 214–226), Cambridge, MA, USA. [Google Scholar]
- European Banking Authority. (2021). Guidelines on internal governance under crd. Available online: https://www.eba.europa.eu/activities/single-rulebook/regulatory-activities/internal-governance/guidelines-internal-governance-under-crd (accessed on 17 March 2025).
- European Banking Authority. (2025). Final draft implementing technical standards on the joint decision process for internal model authorisation. Available online: https://www.eba.europa.eu/publications-and-media/press-releases/eba-updates-technical-standards-joint-decision-process-internal-model-authorisation (accessed on 17 March 2025).
- Feldman, M. (2015). Computational fairness: Preventing machine-learned discrimination. Available online: https://api.semanticscholar.org/CorpusID:196099523 (accessed on 8 May 2015).
- Feldman, M., Friedler, S. A., Moeller, J., Scheidegger, C., & Venkatasubramanian, S. (2015, August 10–13). Certifying and removing disparate impact. 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (pp. 259–268), Sydney, Australia. [Google Scholar]
- Feng, J., Zhu, Y., Pan, H., & Mou, Y. (2025, March 28–30). Research on financial data risk prediction models based on XGBoost algorithm. 2nd Guangdong-Hong Kong-Macao Greater Bay Area International Conference on Digital Economy and Artificial Intelligence (pp. 686–690), Dongguan, China. [Google Scholar]
- Ferrara, E. (2023). Fairness and bias in artificial intelligence: A brief survey of sources, impacts, and mitigation strategies. Journal of Computational Social Science, 6(1), 3. [Google Scholar] [CrossRef]
- Gietzen, T. (2017, June). Credit scoring vs. expert judgment—A randomized controlled trial (Working Papers on Finance No. 1709). University of St. Gallen, School of Finance. Available online: https://ideas.repec.org/p/usg/sfwpfi/201709.html (accessed on 15 June 2025).
- Gouk, H., Hospedales, T., & Pontil, M. (2021, May 4). Distance-based regularisation of deep networks for fine-tuning. International Conference on Learning Representations, Vienna, Austria. Available online: https://openreview.net/forum?id=IFqrg1p5Bc (accessed on 25 March 2025).
- Grari, V., Laugel, T., Hashimoto, T., Lamprier, S., & Detyniecki, M. (2023). On the fairness road: Robust optimization for adversarial debiasing. arXiv. [Google Scholar] [CrossRef]
- Guo, K., Ding, Y., Liang, J., Wang, Z., He, R., & Tan, T. (2025, February 27–March 4). Exploring vacant classes in label-skewed federated learning. AAAI Conference on Artificial Intelligence (Vol. 39, pp. 16960–16968), Philadelphia, PA, USA. [Google Scholar]
- Han, J., Kamber, M., & Pei, J. (2011). Data mining: Concepts and techniques (3rd ed.). Morgan Kaufmann Publishers Inc. [Google Scholar]
- Hanea, A. M., Nane, G. F., Bedford, T., & French, S. (Eds.). (2021). Expert judgement in risk and decision analysis (No. 978-3-030-46474-5). Springer. [Google Scholar] [CrossRef]
- Hardt, M., Price, E., & Srebro, N. (2016, December 5–10). Equality of opportunity in supervised learning. 30th International Conference on Neural Information Processing Systems (Vol. 29), Barcelona, Spain. [Google Scholar]
- Harris, C. (2020, April 20–24). Mitigating cognitive biases in machine learning algorithms for decision making. Companion Proceedings of the Web Conference 2020 (pp. 775–781), Taipei, Taiwan. [Google Scholar]
- Helfrich, S., Perini, T., Halffmann, P., Boland, N., & Ruzika, S. (2023). Analysis of the weighted Tchebycheff weight set decomposition for multiobjective discrete optimization problems. Journal of Global Optimization, 86(2), 417–440. [Google Scholar] [CrossRef]
- Hofmann, H. (1994). Statlog (German credit data). UCI Machine Learning Repository. [Google Scholar] [CrossRef]
- Hort, M., Chen, Z., Zhang, J. M., Harman, M., & Sarro, F. (2024). Bias mitigation for machine learning classifiers: A comprehensive survey. ACM Journal on Responsible Computing, 1(2), 11. [Google Scholar] [CrossRef]
- Hwang, C., Paidy, S., Yoon, K., & Masud, A. (1980). Mathematical programming with multiple objectives: A tutorial. Computers & Operations Research, 7(1), 5–31. [Google Scholar] [CrossRef]
- Izzi, L., Oricchio, G., & Vitale, L. (2012). Expert judgment-based rating assignment process. In Basel III credit rating systems: An applied guide to quantitative and qualitative models (pp. 155–181). Palgrave Macmillan UK. [Google Scholar] [CrossRef]
- Jafarigol, E., & Trafalis, T. (2023). A review of machine learning techniques in imbalanced data and future trends. arXiv. [Google Scholar] [CrossRef]
- Jiang, H., & Nachum, O. (2020, August 26–28). Identifying and correcting label bias in machine learning. In S. Chiappa, & R. Calandra (Eds.), Proceedings of the twenty third international conference on artificial intelligence and statistics (Vol. 108, pp. 702–712). PMLR. [Google Scholar]
- Kaggle. (2020). Credit risk dataset. Available online: https://www.kaggle.com/datasets/laotse/credit-risk-dataset (accessed on 6 February 2025).
- Kelly, J., Zafar, S. A., Heidemann, L., Zacchi, J.-V., Espinoza, D., & Mata, N. (2024, June 25–27). Navigating the EU AI act: A methodological approach to compliance for safety-critical products. 2024 IEEE Conference on Artificial Intelligence (CAI) (pp. 979–984), Singapore. [Google Scholar]
- Kilbertus, N., Rojas-Carulla, M., Parascandolo, G., Hardt, M., Janzing, D., & Schölkopf, B. (2017, December 4–9). Avoiding discrimination through causal reasoning. 31st International Conference on Neural Information Processing Systems (pp. 656–666), Long Beach, CA, USA. [Google Scholar]
- Koziarski, M. (2021, July 18–22). CSMOUTE: Combined synthetic oversampling and undersampling technique for imbalanced data classification. 2021 International Joint Conference on Neural Networks (IJCNN) (pp. 1–8), Shenzhen, China. [Google Scholar]
- Kozodoi, N., Jacob, J., & Lessmann, S. (2022). Fairness in credit scoring: Assessment, implementation and profit implications. European Journal of Operational Research, 297(3), 1083–1094. [Google Scholar] [CrossRef]
- Kusner, M. J., Loftus, J., Russell, C., & Silva, R. (2017). Counterfactual fairness. Advances in Neural Information Processing Systems, 30, 4066–4076. [Google Scholar]
- Lahoti, P., Beutel, A., Chen, J., Lee, K., Prost, F., Thain, N., Wang, X., & Chi, E. (2020). Fairness without demographics through adversarially reweighted learning. Advances in Neural Information Processing Systems, 33, 728–740. [Google Scholar]
- Langbridge, A., Quinn, A., & Shorten, R. (2024). Overcoming representation bias in fairness-aware data repair using optimal transport. arXiv. [Google Scholar] [CrossRef]
- Li, Y., Gao, F., Sha, M., & Shao, X. (2024). Sequential three-way decision with automatic threshold learning for credit risk prediction. Applied Soft Computing, 165, 112127. [Google Scholar] [CrossRef]
- Li, Y., & Sha, M. (2024). Two-stage credit risk prediction framework based on three-way decisions with automatic threshold learning. Journal of Forecasting, 43(5), 1263–1277. [Google Scholar] [CrossRef]
- Mehrabi, N., Morstatter, F., Saxena, N., Lerman, K., & Galstyan, A. (2021). A survey on bias and fairness in machine learning. ACM Computing Surveys, 54(6), 115. [Google Scholar] [CrossRef]
- Mikołajczyk-Bareła, A., & Grochowski, M. (2023). A survey on bias in machine learning research. arXiv. [Google Scholar] [CrossRef]
- Mitchell, T. M. (1997). Machine learning (1st ed.). McGraw-Hill, Inc. [Google Scholar]
- Mowbray, T. (2025). A survey of deep learning architectures in modern machine learning systems: From CNNs to transformers. Journal of Computer Technology and Software, 4(8). [Google Scholar] [CrossRef]
- Namvar, A., Siami, M., Rabhi, F., & Naderpour, M. (2018). Credit risk prediction in an imbalanced social lending environment. International Journal of Computational Intelligence Systems, 11(1), 925–935. [Google Scholar] [CrossRef]
- Pagano, T. P., Loureiro, R. B., Lisboa, F. V. N., Cruz, G. O. R., Peixoto, R. M., de Sousa Guimarães, G. A., dos Santos, L. L., Araujo, M. M., Cruz, M., de Oliveira, E. L. S., Winkler, I., & Nascimento, E. G. S. (2022). Bias and unfairness in machine learning models: A systematic literature review. arXiv. [Google Scholar] [CrossRef]
- Pang, M., Wang, F., & Li, Z. (2024). Credit risk prediction based on an interpretable three-way decision method: Evidence from Chinese SMEs. Applied Soft Computing, 157, 111538. [Google Scholar] [CrossRef]
- Parliament of the European Union. (2016). Regulation (EU) 2016/679 of the european parliament and of the council of 27 April 2016 on the protection of natural persons with regard to the processing of personal data and on the free movement of such data (general data protection regulation) (Vol. L119). Available online: https://eur-lex.europa.eu/eli/reg/2016/679/oj (accessed on 27 April 2025).
- Pleiss, G., Raghavan, M., Wu, F., Kleinberg, J., & Weinberger, K. Q. (2017). On fairness and calibration. In I. Guyon, U. Von Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, & R. Garnett (Eds.), Advances in neural information processing systems (Vol. 30, pp. 5680–5689). Curran Associates, Inc. [Google Scholar]
- Puyol-Antón, E., Ruijsink, B., Piechnik, S. K., Neubauer, S., Petersen, S. E., Razavi, R., & King, A. P. (2021, September 27–October 1). Fairness in cardiac MR image analysis: An investigation of bias due to data imbalance in deep learning based segmentation. Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Proceedings, Part III 24 (pp. 413–423), Strasbourg, France. [Google Scholar]
- Qin, R. (2022). The construction of corporate financial management risk model based on XGBoost algorithm. Journal of Mathematics, 2022(1), 2043369. [Google Scholar] [CrossRef]
- Rabonato, R., & Berton, L. (2025). A systematic review of fairness in machine learning. AI and Ethics, 5, 1943–1954. [Google Scholar] [CrossRef]
- Rajabi, A., & Garibay, O. O. (2021, July 24–29). Towards fairness in AI: Addressing bias in data using gans. HCI International 2021-Late Breaking Papers: Multimodality, eXtended Reality, and Artificial Intelligence: 23rd HCI International Conference, HCII 2021, Proceedings 23 (pp. 509–518), Virtual Event. [Google Scholar]
- Razaviyayn, M., Huang, T., Lu, S., Nouiehed, M., Sanjabi, M., & Hong, M. (2020). Nonconvex min-max optimization: Applications, challenges, and recent theoretical advances. IEEE Signal Processing Magazine, 37(5), 55–66. [Google Scholar] [CrossRef]
- Regulation (eu) 2024/1689 of the european parliament and of the council of 13 June 2024 laying down harmonised rules on artificial intelligence and amending certain union legislative acts (artificial intelligence act). (2024, July) (OJ L 2024/1689, 12.7.2024). Available online: https://eur-lex.europa.eu/eli/reg/2024/1689/oj (accessed on 30 July 2025).
- Resck, L., Raimundo, M. M., & Poco, J. (2024, June 16–21). Exploring the trade-off between model performance and explanation plausibility of text classifiers using human rationales. Findings of the Association for Computational Linguistics: NAACL 2024 (pp. 4190–4216), Mexico City, Mexico. [Google Scholar]
- Robinson, T. S., Tax, N., Mudd, R., & Guy, I. (2024). Active learning with biased non-response to label requests. Data Mining and Knowledge Discovery, 38(4), 2117–2140. [Google Scholar] [CrossRef]
- Rockafellar, R. T. (1997). Convex analysis (Vol. 28). Princeton University Press. [Google Scholar]
- Sharma, S., Zhang, Y., Ríos Aliaga, J. M., Bouneffouf, D., Muthusamy, V., & Varshney, K. R. (2020, February 7–9). Data augmentation for discrimination prevention and bias disambiguation. AAAI/ACM Conference on AI, Ethics, and Society (pp. 358–364), New York, NY, USA. [Google Scholar]
- Silva, E. J., Karas, E. W., & Santos, L. B. (2022). Integral global optimality conditions and an algorithm for multiobjective problems. Numerical Functional Analysis and Optimization, 43(10), 1265–1288. [Google Scholar] [CrossRef]
- Smith, P., & Ricanek, K. (2020, March 1–5). Mitigating algorithmic bias: Evolving an augmentation policy that is non-biasing. IEEE/CVF Winter Conference on Applications of Computer Vision Workshops (pp. 90–97), Snowmass Village, CO, USA. [Google Scholar]
- Speicher, T., Heidari, H., Grgic-Hlaca, N., Gummadi, K. P., Singla, A., Weller, A., & Zafar, M. B. (2018, August 19–23). A unified approach to quantifying algorithmic unfairness: Measuring individual & group unfairness via inequality indices. 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (pp. 2239–2248), London, UK. [Google Scholar]
- Stevens, A., Deruyck, P., Van Veldhoven, Z., & Vanthienen, J. (2020, December 1–4). Explainability and fairness in machine learning: Improve fair end-to-end lending for kiva. 2020 IEEE Symposium Series on Computational Intelligence (SSCI) (pp. 1241–1248), Canberra, Australia. [Google Scholar]
- Sun, X., Qin, Z., Zhang, S., Wang, Y., & Huang, L. (2024). Enhancing data quality through self-learning on imbalanced financial risk data. arXiv. [Google Scholar] [CrossRef]
- Szepannek, G., & Lübke, K. (2021). Facing the challenges of developing fair risk scoring models. Frontiers in Artificial Intelligence, 4, 681915. [Google Scholar] [CrossRef] [PubMed]
- Trivedi, S. K. (2020). A study on credit scoring modeling with different feature selection and machine learning approaches. Technology in Society, 63, 101413. [Google Scholar] [CrossRef]
- Tyagi, K., Rane, C., Sriram, R., & Manry, M. (2022). Chapter 3—Unsupervised learning. In R. Pandey, S. K. Khatri, N. kumar Singh, & P. Verma (Eds.), Artificial intelligence and machine learning for edge computing (pp. 33–52). Academic Press. [Google Scholar] [CrossRef]
- U.S. Congress. (1974). Equal credit opportunity act. Available online: https://www.govinfo.gov/content/pkg/USCODE-2011-title15/html/USCODE-2011-title15-chap41-subchapIV.htm (accessed on 15 May 2025).
- U.S. Congress. (1977). Fair lending act. Available online: https://www.govinfo.gov/content/pkg/STATUTE-91/pdf/STATUTE-91-Pg1111.pdf (accessed on 5 May 2025).
- Vairetti, C., Assadi, J. L., & Maldonado, S. (2024). Efficient hybrid oversampling and intelligent undersampling for imbalanced big data classification. Expert Systems with Applications, 246, 123149. [Google Scholar] [CrossRef]
- Vapnik, V. N. (1995). The nature of statistical learning theory. Springer-Verlag New York, Inc. [Google Scholar]
- Wang, R., Xiong, J., Ishibuchi, H., Wu, G., & Zhang, T. (2017). On the effect of reference point in MOEA/D for multi-objective optimization. Applied Soft Computing, 58, 25–34. [Google Scholar] [CrossRef]
- Weerts, H. J. P., Mueller, A. C., & Vanschoren, J. (2020). Importance of tuning hyperparameters of machine learning algorithms. arXiv. [Google Scholar] [CrossRef]
- Woodworth, B., Gunasekar, S., Ohannessian, M. I., & Srebro, N. (2017, July 7–10). Learning non-discriminatory predictors. Conference on Learning Theory (pp. 1920–1953), Amsterdam, The Netherlands. [Google Scholar]
- Xia, T., Ghosh, A., Qiu, X., & Mascolo, C. (2024, August 25–29). FLea: Addressing data scarcity and label skew in federated learning via privacy-preserving feature augmentation. 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (pp. 3484–3494), Barcelona, Spain. [Google Scholar]
- Yu, T., & Zhu, H. (2020). Hyper-parameter optimization: A review of algorithms and applications. arXiv. [Google Scholar] [CrossRef]
- Zhang, B. H., Lemoine, B., & Mitchell, M. (2018, February 2–3). Mitigating unwanted biases with adversarial learning. 2018 AAAI/ACM Conference on AI, Ethics, and Society (pp. 335–340), New Orleans, LA, USA. [Google Scholar]
- Zhang, S., Tay, J., & Baiz, P. (2024). The effects of data imbalance under a federated learning approach for credit risk forecasting. arXiv. [Google Scholar] [CrossRef]
- Zhang, Y., Li, B., Ling, Z., & Zhou, F. (2024, February 20–27). Mitigating label bias in machine learning: Fairness through confident learning. Thirty-Eighth AAAI Conference on Artificial Intelligence and Thirty-Sixth Conference on Innovative Applications of Artificial Intelligence and Fourteenth Symposium on Educational Advances in Artificial Intelligence, Vancouver, BC, Canada. [Google Scholar]
- Zhang, Y., & Ramesh, A. (2020). Learning fairness-aware relational structures. arXiv. [Google Scholar] [CrossRef]
- Zhang, Y., & Sang, J. (2020, October 12–16). Towards accuracy-fairness paradox: Adversarial example-based data augmentation for visual debiasing. 28th ACM International Conference on Multimedia (pp. 4346–4354), Seattle, WA, USA. [Google Scholar]
- Zheng, Y., Wang, S., & Zhao, J. (2021). Equality of opportunity in travel behavior prediction with deep neural networks and discrete choice models. Transportation Research Part C: Emerging Technologies, 132, 103410. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).