The Co-Movement of JSE Size-Based Indices: Evidence from a Time–Frequency Domain

Abstract

This research examines the time–frequency co-movement patterns among the Johannesburg Stock Exchange (JSE) size-based indices, utilizing daily data covering the period from November 2016 to December 2024. To conduct the analysis, three sophisticated wavelet techniques are applied: the Maximal Overlap Discrete Wavelet Transform (MODWT), the Continuous Wavelet Transform (WTC), and the Wavelet Phase Angle (WPA) model. Subsequently, the Multivariate Generalized Autoregressive Conditional Heteroscedasticity–Asymmetric Dynamic Conditional Correlation (MGARCH-DCC) model is employed to evaluate the robustness of the findings. The results reveal that the co-movement among the JSE size-based indices is influenced by investment holding periods and prevailing market conditions. Notably, a lead–lag relationship is identified, indicating that a single size-based index often drives the co-movement of the others. These findings carry important implications for investors, policymakers, and portfolio managers. Investors should account for optimal holding periods to avoid increased correlation and reduced diversification benefits. Policymakers are advised to mitigate financial market uncertainty, particularly during bearish phases, to manage excessive index co-movement. Portfolio managers must integrate both holding periods and market conditions into their investment strategies. This research offers a novel contribution to the South African investment landscape by providing practical and risk-mitigating insights into the role of JSE size-based indices within diversified portfolios—a topic that has received limited attention despite its growing relevance.

1. Introduction

The establishment of the Johannesburg Stock exchange (JSE) in South Africa can be traced back to 1983, when financial market authorities established the JSE to assist with managing the gold rush (De Beer et al., 2015). Since then, the JSE has evolved to cater to the diverse needs of investors both locally and globally. These needs include establishing a variety of asset markets to assist investors with mitigating risk. Presently, the JSE includes asset markets such as equity, property, bond, foreign exchange, and commodity markets, all of which are important determinants of investors’ portfolio composition. Despite this, the equity market has attracted interests as it is the most liquid among emerging African markets. The liquidity characteristics can be traced back to the development of the JSE headline indices, also known as the JSE size-based indices.

The JSE size-based indices track the performance of listed companies on the JSE (Lawrence et al., 2024). They include the JSE All-Share, Top-40, Large-Cap, Large-Mid Cap, Mid-Cap, Small-Cap, and Fledgling indices (JSE, 2025). These indices represent the JSE’s total market capitalization: the All-Share captures 99%, Top-40 covers the 40 most investable companies, Large-Cap captures 85%, Large-Mid Cap and Mid-Cap 85–96%, Small-Cap 97–99%, and Fledgling 1% (JSE, 2025). Together, they provide a performance benchmark for JSE-listed companies and attract passive investors.

A passive investor is an individual that has a long-term investment strategy that entails buying and holding securities that track a specific index (Haddad et al., 2025). The aim of passive investors is not to beat the market, rather they want to achieve average market returns by mirroring the performance of the specific index. Consequently, the JSE size-based indices assist with enhancing information matrices for passive investors as it provides a gage of the performance of companies listed under each index. Although these gages assist investors in maintaining an average return with limited risk exposure, they are not without limitations.

During market uncertainty such as the COVID-19 pandemic, many investors used JSE size-based indices to reduce portfolio volatility. However, this strategy failed as all indices were negatively affected, with declining returns and increased volatility due to excessive co-movement (Lawrence et al., 2024). As a result, investors faced significant losses, revealing that these indices did not provide diversification benefits during financial turmoil. Portfolio values fell sharply, and many fund managers lost their jobs for failing to rebalance portfolios effectively during the crisis.

To understand the poor performance of JSE size-based indices during the COVID-19 pandemic, researchers examined their volatility and found that heightened volatility drove negative returns (Naidoo et al., 2025). However, this alone does not explain why combining these indices failed to enhance diversification or reduce portfolio volatility, despite their low-risk nature. To address this gap, this study examines the correlation of JSE size-based indices in the time–frequency domain—an area largely unexplored in the existing literature. The study’s main objective is to analyze the time–frequency co-movement of selected JSE size-based indices, with two secondary aims: (1) to compare correlations among different index pairs across investment and time periods, and (2) to determine whether lead–lag relationships exist between them.

Achieving these objectives makes significant contributions to emerging market literature. Practically, the study assesses the effectiveness of JSE size-based indices in promoting portfolio diversification by analyzing their co-movement over time, particularly during volatile periods. The findings help investors identify optimal holding periods before diversification benefits diminish and guide portfolio rebalancing during market uncertainty. This supports more effective portfolio management by enhancing diversification, reducing volatility, and limiting losses. Academically, the study shifts the focus from the determinants of JSE index returns to their dynamic co-movement, offering new insights. Methodologically, it introduces advanced econometric analysis through wavelet modeling—the first of its kind in South Africa—providing a more robust measure of co-movement than traditional models.

The remainder of this paper is structured as follows. Section 2 provides the literature review, outlining the theoretical framework underpinning this study and summarizing relevant empirical research. Section 3 details the methodology, including the data description and the specification of the empirical models. Section 4 presents the empirical findings, divided into preliminary analyses and model estimation results. Section 5 provides the robustness checks in the form of the MGARCH-ADCC model. Section 6 presents the discussion of results. Finally, Section 7 discusses the implications of the study and concludes the paper.

2. Literature Review

2.1. Theoretical Conceptualization

The theoretical basis guiding this study is the Fractal Market Hypothesis (FMH), originally developed by Mandelbrot (1966). The FMH emphasizes the significance of incorporating information flow and investment horizons when analyzing investor behavior. By doing so, it simplifies the complexities of asset price movements by proposing that financial markets are heterogeneous, reflecting the diverse preferences and behaviors of market participants, or investors. These differences arise from varying levels of risk tolerance and differing perceptions of institutional constraints on information access. Consequently, investors are distinguished by their investment horizons, which can be categorized as short-term, medium-term, or long-term (Bredin et al., 2015).

Across these investment periods, investors routinely rebalance their portfolios to ensure alignment with their risk preferences, thereby achieving heterogeneous returns and improving portfolio diversification. This diversification is often pursued by investing across various JSE size-based indices to optimize returns. However, in recent years, the effectiveness of such diversification has come into question, as JSE size-based indices have shown weaker performance during periods of financial turbulence and uncertainty. As a result, the diversification advantage traditionally associated with these indices has diminished, with the duration of holding periods now playing a more critical role in determining optimal portfolio diversification.

2.2. Empirical Review

The growing number of studies in South Africa that attempt to examine the co-movement of equity market returns are isolated to sectoral indices and cross border analysis. For example, Boako and Alagidede (2017) investigated the co-movement of African equity markets across different time and frequency domains. The study employed several wavelet coherence techniques, including the Maximal Overlap Discrete Wavelet Transform (MODWT), Continuous Wavelet Transform (CWT), and Wavelet Phase Angle (WPA), covering the period from 2003 to 2014. The results indicated that the South African equity market express elevated co-movement levels with African regional country equity markets. More specifically, the co-movement during the COVID-19 pandemic is persistent and increasing in the long-run time horizon as opposed to other holding periods. Moreover, the South Africa equity market has a lead–lag relationship with other equity markets. The findings underscore the importance of portfolio rebalancing in the long horizon, when faced with market uncertainty to ensure added diversification. Similarly, Anyikwa and Le Roux (2020) also examined the co-movement of African stock markets, but the analysis did not extend into the time–frequency domain, but rather developed markets. Contrary to Boako and Alagidede (2017), the Dynamic Conditional Correlation (DCC)-GARCH model revealed limited evidence of co-movement between the South African equity market and other African equity markets during COVID-19. However, the South African equity market expressed heighten co-movement with developed equity markets during the COVID-19 pandemic.

Kalu et al. (2024) applied the Generalized Autoregressive Conditional Heteroskedasticity (GARCH) family of models to analyze the co-movement between the South African and Nigerian equity markets during both stable and volatile periods. Their findings revealed that the degree of co-movement between the two markets intensified during episodes of heightened volatility, such as the COVID-19 pandemic, whereas during periods of relative market stability, the co-movement remained close to zero. The findings further demonstrate the persistence of equity market co-movement during market uncertainty. These findings were in line with a study conducted by Yonis (2011) on the South African and United States (US) equity markets.

Maiti et al. (2022) broadened their investigation beyond the African continent by examining the equity markets of Brazil, Russia, India, China, and South Africa (BRICS). Using daily data spanning from 1999 to 2019, the authors employed MODWT, CWT, and WPA approaches to analyze the time–frequency co-movement among the BRICS equity markets. Their findings indicated evidence of contagion across these markets, with co-movement being more persistent over the long-term investment horizon. In contrast, short-term horizons offered greater diversification opportunities, as the co-movement was generally weak or negative. Furthermore, during the COVID-19 pandemic, a pronounced increase in co-movement was observed in the long-term horizon. Coherent with this, Sayed and Charteris (2024) also focused on the BRICS countries equity market. However, the analysis covered the period 2004–2024. Despite the deviation in the sample period, the findings also demonstrated that the co-movement between BRICS countries’ equity market is not persistent in the short-run and medium-run, suggesting that the long-term investment horizon will not yield adequate diversification benefits. Moreover, the WPA model demonstrate no evidence of a lead–lag relationship among the surveyed equity markets. This highlights the relative independence of each equity market in influencing the co-movement dynamics. Likewise, during the COVID-19 pandemic, the co-movement between equity market pairs intensified, particularly over the long-term investment horizon.

Given the above information, this study hypothesizes the following:

H1: 

The co-movement among JSE size-based indices increases during the medium-term and the long-term investment horizons.

H2: 

The co-movement among JSE size-based indices intensifies during the COVID-19 pandemic, particularly over the long-term investment horizon.

H3: 

The returns of the JSE Large-Cap, JSE Mid-Cap, and JSE Fledgling indices drive the lead–lag relationship among the indices.

If one turns to the JSE size-based indices literature, it is evident that it is still centered on the determinants of JSE size-based indices returns as opposed to examining their co-movement at a time–frequency domain in South Africa. For example, Muzindutsi et al. (2023) examined the effect of country-specific risk on JSE size-based index returns. The sample period included monthly data for the period July 2002 to December 2018. The dependent variable comprised of the JSE Large-Cap index, JSE Mid-Cap index, JSE Small-Cap index and JSE Fledgling index. However, the independent variable consisted of economic, political, and financial risks. The results from the Markov regime-switching model indicated that political and economic risks significantly impact the returns of the JSE mid-cap and small-cap indices during a bull market regime. In contrast, financial risk exhibits a weak but statistically significant effect on all JSE size-based indices during a bear market regime. The observations demonstrate adaptive behavior of the JSE size-based indices returns as highlighted by Lo (2004), suggesting that stable and volatile market conditions make the effect time-varying.

Similarly, Kunjal (2025) also used the Markov regime-switching model, but the academic examined the effect of geopolitical risk on JSE size-based indices returns. The dependent variable comprised of the JSE Top-40 index, JSE All-Share index, JSE Mid-Cap index and JSE Small-Cap index. The study utilized the geopolitical risk index developed by Caldara and Iacoviello (2022) to proxy for geopolitical risk in South Africa. The results indicated that domestic geopolitical risk has a significant positive impact on all JSE size-based indices during a bull market regime, while its effect is not significant in a bear market regime. However global geopolitical risk has a negative effect on JSE size-based indices returns in a bear regime. The findings further support Muzindutsi et al.’s (2023) evidence of adaptive behavior as the effect is time-varying and alternate with market conditions.

Naidoo et al. (2025) examined the effect of investor sentiment on the volatility of JSE size-based indices returns in South Africa. The study used daily returns for the period January 2000 to December 2023. The academics developed an investor sentiment index using market-wide proxies whereas the JSE size-based indices comprised of the JSE Large-Cap, JSE Mid-Cap and JSE Small-Cap indices. The study employed the Generalized Autoregressive Conditional Heteroskedasticity–Mixed Data Sampling (GARCH-MIDAS) model to separate the impact of investor sentiment on JSE size-based volatility across short-term and long-term horizons. The results show that investor sentiment significantly influences volatility in the short term, whereas in the long term, macroeconomic factors such as inflation and exchange rates are the primary drivers of JSE size-based volatility.

Although many of the studies examine the determinants of JSE size-based indices returns, there exists a single study that looked at the connectedness of the JSE size-based indices during COVID-19. However, Lawrence et al. (2024) failed to examine the lead–lag relationship and the co-movement at different investment periods. The study made use of daily data from January 2017 to 30 June 2023, whereas four indices were considered, namely the JSE Large-Cap index, JSE Mid-Cap index, JSE Small-Cap index and JSE Fledgling index. The results from the time-varying parameter vector autoregressive (TVP-VAR) model indicated that the correlation among JSE size-based indices strengthened during the COVID-19 pandemic, leading to heightened co-movement. Moreover, the academics extended their analysis to determine the drivers of the co-movement of the JSE size-based indices. The Markov regime-switching model revealed that macroeconomic variables such as inflation, money supply, interest rate and gross domestic product have an alternating effect on JSE size-based indices returns during bull and bear periods.

The review of the literature reveals various shortcomings. Firstly, there exist limited literature surrounding JSE size-based indices in South Africa. Secondly, the majority of the studies that do consider JSE size-based indices look at the determinants such as country risk, geopolitical risk, and macroeconomics. Thirdly, where the co-movement was considered, it isolates such periods before, during and post the COVID-19 pandemic and then tests how macroeconomic variables influence the co-movement of JSE size-based indices. This analysis fails to shed light on how such a co-movement varies at investment periods during the COVID-19 pandemic and if such a co-movement is driven by a certain JSE size-based index, exposing investors to adverse portfolio volatility. Consequently, this study rectifies this gap by looking at the co-movement of JSE size-based indices at a time–frequency domain, contributing significantly to emerging market literature.

3. Data and Methodology

3.1. Data

The following study uses daily data for the period October 2016 to December 2024 to examine the time–frequency co-movement of JSE size-based indices. The choice of the sample is dictated by the availability of data, such that the JSE Large-Cap historical data is only available from October 2016. Nevertheless, the sample period is robust for the analysis as it incorporates the COVID-19 pandemic. The choice of daily data follows that of Zhu et al. (2024) who advocate for the use of high frequency data when implementing Wavelet-based models as this generates robust output. The data used in the study considers four JSE sized-based indices, which include the JSE Large-Cap index, JSE Mid-Cap index, JSE Small-Cap index and the JSE Fledgling index. The sample is isolated to these sets of size-based indices as data availability on the other size-based indices is non-existent. These indices comprise companies that are listed on the JSE and are grouped according to their market capitalization rates (JSE, 2025). Table 1 below provides an overview of the said data.

Table 1. Description of data.

Variable	Abbreviation	Start Date	Full Market Capitalization
JSE Large-Cap index	LARGE	2016	85%
JSE Mid-Cap index	MID	1995	86% to 96%
JSE Small-Cap index	SMALL	1995	97–99%
JSE Fledgling index	FLEDLGING	2002	1%

Note: Source: author’s own depiction (2025).

3.2. Methodology

This study applies the wavelet approach to investigate the co-movement of returns among JSE size-based indices over time and across different investment horizons. The methodology builds on the frameworks of Karim and Masih (2019), Niu et al. (2023), and Sayed and Charteris (2024). A key strength of the wavelet technique lies in its ability to analyze correlations between two time series simultaneously across both time and frequency domains (In & Kim, 2013). By decomposing these correlations into multiple time–frequency components, the approach reveals how relationships evolve over various investment periods (Gençay et al., 2002). Moreover, it can identify which series leads the other, offering insights into directional dynamics. The procedure involves selecting the relevant series, decomposing them into time–frequency intervals, and producing visual outputs that illustrate correlation structures, which serve as the foundation for evaluating co-movement behavior. The specific wavelet models employed are described in the following section.

3.2.1. The Maximal Overlap Discrete Wavelet Transform

The Maximal Overlap Discrete Wavelet Transform (MODWT) is employed in this study to analyze the performance of JSE size-based indices across various time–frequency domains. MODWT is particularly suitable for this type of analysis because it accommodates data sets of any size and does not require the sample length to be a power of two or for the data to be stationary (Percival & Walden, 2000). An additional advantage of MODWT is that it retains all coefficients without down sampling (Cornish et al., 2006), meaning the number of wavelet coefficients remains equal to the number of original observations at each level of transformation. The wavelet correlation and covariance between two time series, X and Y, at a given scale j are calculated using specific MODWT-based formulas outlined below.

$${\widehat{V}}_{Xy}^2\left(T_i\right)={\displaystyle \frac{1}{M}}{\sum }_{{T-l}_j}^{N=1}{\overline{d}}_{j,t}^{\left(X\right)}{\overline{d}}_{j,t}^{\left(Y\right)}$$

(1)

$$\widehat{\rho }X,Y\left(T_j\right)={\displaystyle \frac{\widehat{V}X,Y{(}^{tj})}{\widehat{V}X,Y{(}^{tj})\widehat{V,}{Y(}^{tj})}}$$

(2)

where $⌊\widehat{\rho }X,Y\left(T_j\right)⌋\le 1$ indicates the wavelet correlation is analogous to its Fourier equivalent, the complex coherency (see Gençay et al., 2002). This analysis adopts the time scale framework outlined by Zhu et al. (2024), as detailed in Table 2 below. The MODWT method will be used to decompose the multi-asset time series data. Following the decomposition, wavelet correlations derived from MODWT will be calculated and analyzed across different investment horizons for comparative purposes.

Table 2. Decomposed time scales.

Wavelet Decomposed Series	Time-Frequencies	Investment Periods
R(1)	2–4 days (intraweek)	Short-term
R(2)	4–8 days(weekly)	Short-term
R(3)	8–16 days (fortnightly)	Medium-term
R(4)	16–32 days (monthly)	Medium-term
R(5)	32–64 days (quarterly)	Long-term
S(5)	64 days beyond	Long-term

Note: Source: author’s own depiction (2025).

3.2.2. Continuous Wavelet Transform

The Continuous Wavelet Transform (CWT) is used to decompose the sample period. In contrast to MODWT, CWT allows for a more detailed analysis by extending the time–frequency representation down to specific trading days. The CWT, ($W_{x(K,B)}$), is computed by applying a mother wavelet ($\psi$) to the time series ($x\left(t\right)ϵI^2\left(R\right)$) under investigation, as defined by the following:

$$W_{x(K,B)}={\int }_{-\propto }^{\propto }X(t){\displaystyle \frac{1}{\sqrt{B}}}\psi \left({\displaystyle \frac{t-K}{B}}\right)dt$$

(3)

Here, K represents the time domain, and B represents the frequency domain, following Torrence and Webster (1999). The wavelet coherence between the two-time series is then estimated as follows:

$$R_n^2\left(B\right)={\displaystyle \frac{IB\left(b^{-1}{W}_n^{xy}\left(B\right)\right)I^2}{S(b^{-1}{IW}_n^x\left(B\right)I^2.B(b^{-1}{IW}_n^x\left(B\right))I^2}}$$

(4)

Here, B represents the smoothing operator, b denotes the wavelet scale, and $W_n^x\left(B\right)$ is the CWT of the time series X. Similarly, $W_n^x\left(B\right)$ is the CWT of the time series Y, and $Y^{xy}\left(B\right)$ represents the cross-wavelet transform of X and Y, as described by In and Kim (2013).

3.2.3. Wavelet Phase Angle

This study investigates the lead–lag relationships among JSE size-based index returns. To do so, the Wavelet Phase Angle (WPA) difference is employed, following the approach of Bloomfield et al. (2004). The WPA difference between X(t) and Y(t) is defined as follows:

$${\mathrm{\varnothing }}_{xy}=ta{n}^{-1}\left({\displaystyle \frac{\mathfrak{I}\left\{S\left(s^{-1}{W}_{xy}\left(u,s\right)\right)\right\}}{\mathfrak{N}\left\{S\left(s^{-1}{W}_{xy}\left(u,s\right)\right)\right\}}}\right)\left(xi\right) with {\phi }_{xy}ϵ\left|-\pi ,\pi \right|$$

(5)

To determine the lead–lag relationships among JSE size-based indices, this study utilizes the wavelet coherence map. The direction of the arrows on the map provides insights into both correlation and causality. Arrows pointing to the right indicate a positive correlation between X(t) and Y(t), while those pointing to the left suggest a negative correlation. The direction of the arrows also reveals the causality or lead–lag dynamic. Specifically, arrows pointing right and downward or left and upward imply that X(t) lags behind Y(t), whereas arrows pointing right and upward or left and downward suggest Y(t) follows that X(t) (Karim & Masih, 2019).

3.2.4. Multivariant GARCH Model

The MGARCH-ADCC model is used to confirm the robustness of the wavelet models. The model was selected as it can capture the time-varying co-movement of JSE size-based indices, which is performed by the above wavelet models. Consequently, the MGARCH-ADCC model will serve as a confirmation factor to that of the Wavelet model results.

The estimation of the MGARCH-ADCC model follows the approach of Moodley et al. (2024) and employs a two-step procedure. The first step involves standardizing the residuals:

$$N_{it=}{\displaystyle \frac{{\epsilon }_{i,t}}{\sqrt{h_{ii,t}}}}$$

(6)

Here, $N_{it}$ represents the standardized residuals, and $h_{ii,t}$ denotes the conditional variances obtained from the estimated univariate GARCH model. In the second step, these standardized residuals are used to estimate time-varying conditional covariances, which constitute an extension of Engle’s (2002) MGARCH-CCC model.

$$H_t=D_t{C}_t{D}_t$$

(7)

where $D_t$ = $diag(\sqrt{h_{ii,t}},\dots \dots \sqrt{h_{NN,t}})$, $h_{ii,t}$ is the conditional variances from the estimated univariate GARCH model, and $C_{ij}={\rho }_{ij}$ is a positive symmetric matrix with ones on the diagonal. The off-diagonal entries are the conditional correlations in the C-matrix above and are assumed to be time-varying. The following equation then gives the dynamic conditional correlation structure:

$$Q_{io,t}=\left(1-{\theta }_1{-\theta }_2\right)\overline{(Q})+{\theta }_1\left({\epsilon }_{i,t-1}{\epsilon }_{0,t-1}^{’}\right)+{\theta }_2\left(Q_{io,t-1}\right)$$

(8)

The unconditional covariance between asset returns i and o is denoted as $Q_{io,t}$, where $\overline{Q}$ represents the unconditional covariance estimated in the first step using univariate GARCH models. The scalar coefficients ${\theta }_1$ and ${\theta }_2$ are estimated via the likelihood function. Using these estimates, the dynamic conditional correlation matrix, $C_t$, between the two asset returns i and o is then derived:

$$C_t=\left(Q_{io,t}^{\mathrm{*}}{)}^{-1}\right(Q_{io,t}\left)\right(Q_{io,t}^{\mathrm{*}}{)}^{-1}$$

(9)

$Q_{io,t}^{*}$ is the diagonal matrix with the square root of the diagonal elements of $Q_{io,t}$ as its entries. Hence, $Q_{io,t}^{*}=Diag(Q_t{)}^{{\displaystyle \frac{1}{2}}}$. The entries in the bivariant framework are as follows:

$${\rho }_{ij}={\displaystyle \frac{q_{io,t}}{\sqrt{\left(q_{ii,t}\right){(q}_{oo,t})}}}={\displaystyle \frac{\left(1-{\theta }_1{-\theta }_2\right)\overline{(q})+{\theta }_1\left({\epsilon }_{i,t-1}{\epsilon }_{0,t-1}^{’}\right)+{\theta }_2\left(q_{io,t-1}\right)}{\left((1-{\theta }_1{-\theta }_2\right)\overline{(q_i})+{\theta }_1\left({\epsilon }_{i,t-1}^2\right)+{\theta }_2(q_{ii,t-1}\left)\right)(\left(1-{\theta }_1{-\theta }_2\right)\overline{(q_o})+{\theta }_1\left({\epsilon }_{0,t-1}^2\right)+{\theta }_2\left(q_{oo,t-1}\right))}}$$

(10)

The MGARCH-DCC model can be extended to include asymmetry in the conditional correlations. The MGARCH-ADCC model of Cappiello et al. (2006) is given by the following:

$$Q_{io,t}=\left(1-{\theta }_1{-\theta }_2\right)\overline{(Q}-g)({\overline{\mathsf{\Psi }}}_t)+{\theta }_1\left({\epsilon }_{i,t-1}{ϵ}_{0,t-1^{’}}\right)+{\theta }_2\left(Q_{io,t-1}\right)+({\theta }_3)({\epsilon }_{t-1}{ϵ}_{t-1^{’}})$$

(11)

${\overline{\mathsf{\Psi }}}_{\mathrm{t}}=\mathrm{E}\left|\overline{{\mathsf{\epsilon }}_{\mathrm{i},\mathrm{t}}{\mathsf{ϵ}}_{0,{\mathrm{t}}^{’}}}\right|21$, and $\overline{{\epsilon }_{I,t}}=\left(I⌊\overline{{\epsilon }_{i,t}}<0⌋o\overline{{\epsilon }_{i,t}}\right)$; the element-wise Hadamard product of the residuals is considered only when the asset market shocks are adverse; otherwise, $\overline{{\mathsf{\epsilon }}_{\mathrm{t}}}=0$.

4. Results and Discussion

4.1. Preliminary Tests

In the following sub-section, the graphical plots, descriptive statistics, and stationarity results of the JSE sized-based indices returns are presented and interpreted.

4.1.1. JSE Size-Based Plots

Figure 1 presents the plots associated with the JSE size-based indices returns, namely the JSE Large-Cap, JSE Mid-Cap, JSE Small-Cap and JSE Fledgling are depicted. It can be visualized for all the return variance of the JSE size-based indices that it fluctuates over time, displaying an autoregressive pattern that is indicative of volatility clustering. Despite this, graphical analysis confirms that all JSE size-based index returns exhibit stationarity, as shown by relatively stable mean values throughout the sample period. However, the plots also reveal distinct periods marked by sharp return spikes, indicating deviations from the mean and higher volatility during those intervals. Notably, the most volatile period across all indices aligns with the onset of the COVID-19 global pandemic in 2019.

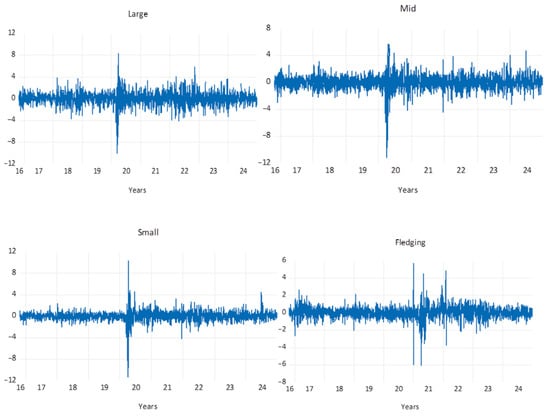
Figure 1. JSE size-based indices returns. Source: author’s own estimation (2025).

Among the indices, the JSE Fledgling index appears to be the most volatile, characterized by a higher frequency of return spikes. Interestingly, these spikes predominantly occur after 2020, whereas the other indices begin showing heightened volatility around 2019—coinciding with the emergence of the COVID-19 crisis. This suggests that the JSE Fledgling index was initially more resilient to the early stages of market turbulence. Nevertheless, it experienced increased volatility during 2021 and 2022, as reflected by larger deviations from its mean returns. These findings carry meaningful implications for index-tracking investors. The JSE Fledgling index may offer a buffer during the early phases of market instability, allowing investors time to adjust their portfolios before volatility intensifies. As such, this index could serve as a strategic component in portfolio construction, particularly in anticipation of extended volatile market conditions.

4.1.2. Descriptive Statistics

In Table 3, the descriptive statistics, stationarity, and unit root tests are provided for the JSE sized-based indices returns. In Panel A, it is noted that the JSE Large-Cap index attains the highest average return, whereas the JSE Fledging index attains the lowest average return. These findings suggest that on average, the JSE Large-Cap will provide more favorable returns if incorporated in a portfolio as compared to the JSE Fledgling index. However, the risk-return proposition that higher returns yield higher risk is evident herein. Although the JSE Large-Cap index attains the highest average return, it is the most volatile as it attains the highest standard deviation value. On the contrary, the JSE Fledgling index attains the lowest standard deviation figure, suggesting it is the least risky among the JSE size-based indices, providing the lowest average return.

Table 3. Descriptive statistics and unitroot test results.

	LARGE	MID	SMALL	FLEDGLING
Panel A: Descriptive Statistics
Mean	0.025530	0.009321	0.019863	0.007201
Median	0.030611	0.025209	0.021838	0.013693
Maximum	8.285119	5.649510	10.29176	5.602304
Minimum	−10.08809	−11.21429	−11.29942	−6.070189
Std. Dev.	1.217714	1.117906	0.927825	0.710083
Skewness	−0.354270	−1.282014	−1.125886	−0.400180
Kurtosis	9.384159	16.63764	32.78999	13.69863
Jarque–Bera	3517.374	16,415.69	76,086.80	9812.389
Probability	0.000000	0.000000	0.000000	0.000000
Sum	52.23443	19.07159	40.63996	14.73301
Sum Sq. Dev.	3032.382	2555.665	1760.458	1031.125
Observations	2046	2046	2046	2046
Panel B: Unit Root and Stationarity Tests
ADF	−45.78315 ***	−43.17247 ***	−17.84580 ***	−23.65352 ***
KPSS	0.019022	0.120849	0.472772	0.238610
ADF-Break	−46.71941 ***	−44.30006 ***	−43.46352 ***	−48.12083 ***
Break Period	3/12/2020	3/27/2020	11/25/2020	4/06/2021

Notes: 1. *** indicate a 1% statistically significant level. 2. The critical values associated with the KPSS tests at a 1%, 5% and 10% significance level are 0.739000, 0.463000 and 0.347000, respectively. 3. Source: author’s own estimation (2025).

The kurtosis values for all JSE size-based indices exceed or equal 3, indicating that their return distributions exhibit heavier tails and sharper peaks compared to a normal distribution. This implies that returns tend to experience larger deviations from their mean more frequently than would be expected under normality. Consistent with this, the skewness of the indices is negative over the sample period, suggesting a higher occurrence of extreme negative returns, with the mean positioned to the left of the mode. These patterns are further supported by the Jarque–Bera test, which rejects the null hypothesis of normality, confirming that the JSE size-based indices’ returns do not follow a normal distribution. Such characteristics are not unexpected, as emerging markets like South Africa typically experience greater financial market volatility, which has a pronounced impact on equity returns.

Panel B presents the results of unit root and stationarity tests, including the Augmented Dickey–Fuller (ADF) test, the Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test, and the ADF breakpoint test. The ADF test statistics for all JSE size-based indices are more negative than their respective critical values, leading to the rejection of the null hypothesis that the returns contain a unit root. This indicates that the returns of the JSE size-based indices are stationary at all significance levels. These results are corroborated by the KPSS test, where the test statistics are lower than the critical values across all significance levels, resulting in a failure to reject the null hypothesis of stationarity.

The ADF-breakpoint test was also employed to assess the stationarity of JSE size-based indices returns in the presence of structural breaks. The test statistics for all indices are more negative than the corresponding critical values at all significance levels, leading to the rejection of the null hypothesis that the returns contain a unit root when structural breaks are considered. Therefore, it can be concluded that the returns of all JSE size-based indices are stationary both at levels and in the presence of structural breaks. These results are consistent with the findings from Section 4.1.1, which indicate that the identified structural breaks correspond to the COVID-19 pandemic period, with the JSE Fledgling index exhibiting notable changes post-2020.

4.2. Empirical Model Results

4.2.1. MODWT Results

The first component of the study’s secondary objective is to analyze the correlations among JSE size-based indices returns across different time–frequencies, corresponding to various investment horizons. Following the approach of Zhu et al. (2024), the study employs the MODWT to decompose the time series into distinct investment periods. Given the heterogeneity of market participants, with short-term, medium-term, and long-term investment horizons, decomposing the time series in this manner is crucial, as these horizons collectively shape market outcomes (Karim et al., 2022).

Figure 2 presents the wavelet-based correlations between the JSE size-based indices returns. The X-axis represents the decomposed investment periods (2, 4, 8, 16, 32, 64, 128, and 256 days), while the Y-axis indicates the correlation at each period. Observing the correlation between the Large-Mid cap index and the Large-Small cap index, the short-term correlations (2–4 days and 4–8 days) tend to increase but remain close to zero. In contrast, medium-term investment periods (8–16 days and 16–32 days) show correlations falling below zero. For the long-term periods (32–64 days and beyond 64 days), correlations rise above zero and approach one. These patterns suggest that medium-term combinations of the JSE Large-Cap with the Mid-Cap and Small-Cap indices offer the greatest diversification benefits, whereas short-term and long-term periods provide relatively less diversification.

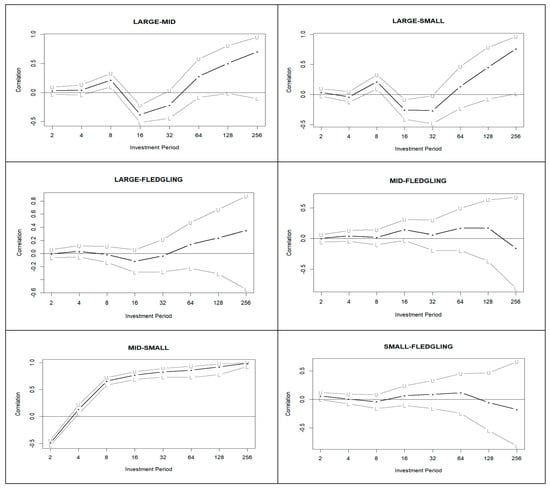
Figure 2. MODWT-based correlations of JSE size-based indices returns at different investment periods. Notes: 1. The black line represents the standard correlations, while the letters “U” and “L” indicate the upper and lower bound correlations, respectively. The asterisk (*) denotes the investment periods. Source: author’s own estimations (2025).

Similarly, for the correlation associated with the Large-Fledgling index, it is seen that in the short-term, the correlations are relatively stable and close to 0. During the medium-term, the correlations fall below 0 and remain there throughout the medium-term. However, in the long-term, the correlations start to increase to levels above 0 reaching values close to 1. Consequently, one can then conclude that incorporating a combination of the JSE Large-Cap and JSE Fledgling index returns in a portfolio for the long-term will yield no diversification benefits as the correlation tends to increase and reach perfect positive correlations. This suggests that in the long-term, the two indices return will move together, increasing portfolio volatility and the possibility of extensive losses. On the contrary, the best investment horizon to hold these two indices is in the short-term and medium-term as the correlations are close to 0 and decrease below 0.

The Mid-Fledgling and Small-Fledgling index correlations are stable and close to 0 throughout the different investment horizons (short-term, medium-term and long-term). These observations provide insightful conclusions, such that holding a combination of the JSE Mid-Cap index and JSE Fledgling index as well as the JSE Small-Cap index and JSE Fledgling index in a portfolio will yield constant diversification. That being said, investment horizons do not influence the co-movement of these indices overtime which enhances portfolio diversification and increases prospect returns.

Contrary to this, the Mid-Small index correlations increase over the different investment periods. However, in the short-term (2–4 days), it is below 0, suggesting that there is negative correlation between the JSE Mid-Cap index and JSE Small-Cap index returns which provides added diversification benefits. However, moving into the medium-term and long-term investment periods, the correlation increases above 0 reaching values close to 1. Hence, holding a combination of the JSE Mid-Cap and JSE Small-Cap index in a portfolio during these periods will yield no diversification benefits.

4.2.2. WCT and WPA Results

The second part of the first secondary objective entails examining the JSE size-based indices correlations at different periods within the sample, whereas the second secondary objective entails examining the lead–lag relationship between JSE size-based indices. To this extent, the study incorporates the CWT model to assist with achieving the second part of the first primary objective whereas the WPA is included to assist with answering the second secondary objective. In Figure 3, the vertical axis represents the investment periods, while the horizontal axis shows time in trading days, spanning from 2016 to 2024. The curved line indicates the 5% significance level, estimated using Monte Carlo simulations. Areas outside this line are considered statistically insignificant at the 95% confidence level. It is evident from the wavelet coherence plots of each JSE size-based index pair that there exist red areas at the top, bottom, right-hand side and left-hand side of the plots. These areas indicate heightened correlations at the start and end of each time period as well as at different investment periods.

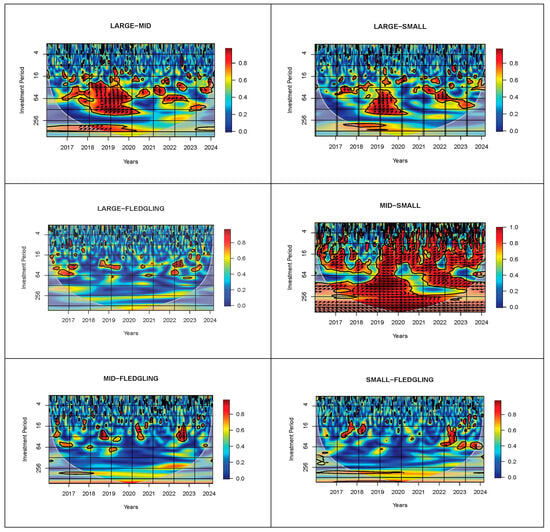
Figure 3. CWT results. Notes: 1. Source: author’s own estimation (2024).

The Large-Mid index correlations are seen to be sporadic as suggested by the red and yellow areas throughout the wavelet coherence plots. However, the majority of these sporadic areas exist during the COVID-19 pandemic. The interdependency during the COVID-19 pandemic was higher in the medium term (16–32 days) and long-term (32–64 days and 64 days beyond). These findings suggest that including the JSE Large-Cap and JSE Mid-Cap in a portfolio during the medium-term and long-term in a volatile market condition like the COVID-19 pandemic will not yield any diversification, rather they should be held for the short-term as it provides the greatest diversification. Similarly, correlations between the Large-Cap and Small-Cap indices were sporadic during the COVID-19 pandemic, with stronger interdependencies observed primarily in the long term. Therefore, investors may achieve the greatest diversification benefits under volatile market conditions by including both the JSE Large-Cap and Small-Cap indices in their portfolios during short- and medium-term horizons. It is worth noting that the high interdependency existed for periods before the COVID-19 pandemic, suggesting that these indices will tend to co-move prior to volatile market conditions. Hence, investors should use these observations as a signal of negative market conditions persisting in the near future and conduct portfolio rebalancing.

The interdependency between the Mid-Cap and Small-Cap indices remains high throughout the entire sample period and across short-term, medium-term, and long-term investment horizons. This indicates that including both indices in a portfolio would result in elevated correlations, reducing diversification benefits and increasing portfolio volatility. Therefore, investors seeking well-diversified holdings and improved risk-adjusted returns are advised against combining the JSE Mid-Cap and Small-Cap indices in the same portfolio. Furthermore, the interdependency tends to be high before, during and after the COVID-19 pandemic, suggesting that JSE Mid-Cap and Small-Cap co-moves at stable and volatile market conditions making it an unsatisfactory index to include in a portfolio. If one turns their focus to the wavelet coherence plots of the Large-Fledgling, Mid-Fledgling and Small-Fledgling index pairs it is evident there exist blue areas throughout the sample period and at all investment periods. This suggests that the said indices do not co-move overtime, especially in volatile market conditions like the COVID-19 pandemic. Thus, the inclusion of the combination of any JSE size-based index with the JSE Fledgling index will yield heightened levels of diversification and protect a portfolio against unstable market conditions.

Figure 3’s wavelet coherence plots illustrate the WPA, showing the directional relationships between JSE size-based index pairs. The arrows point both left and right, indicating positive and negative correlations, consistent with the MODWT findings. This suggests that correlations among JSE size-based index pairs are heterogeneous across time and investment horizons. For instance, the Large–Mid Cap pair shows left-pointing arrows (negative correlation) in the medium-term during 2018, but right-pointing arrows (positive correlation) in the long-term during 2019. These results confirm that correlations are dynamic and time-varying, influenced by market conditions and investment periods. The color changes in the shaded areas further support this, showing shifts in interdependence before, during, and after the COVID-19 pandemic.

In addition to using the arrows in the wavelet coherence plot to determine the direction of the co-movement, one can also derive the lead–lag relationship from the same set of arrows. The Large-Mid, Large-Small and Mid-Small index pair arrows point right and up suggesting that these JSE size-based pairs move in phase. However, the JSE Large-Cap index returns lead the JSE Mid-Cap index returns and the JSE Small-Cap index returns, but the JSE Mid-Cap index returns lead the JSE Small-Cap index returns. These findings suggest that the relationship between the JSE Large-Cap index returns, JSE Mid-Cap index returns and JSE Small-Cap index returns are driven by the JSE Large-Cap index returns. However, the relationship between the JSE Mid-Cap index returns and JSE Small-Cap index returns are driven by the JSE Mid-Cap index returns. Conversely, the arrows associated with the Mid-Fledgling index pairs and Small-Fledgling index pairs point down and right, suggesting that the JSE Mid-Cap index returns and JSE Small-Cap index returns follow the JSE Fledgling index returns. These results suggest that the relationship between the JSE Mid-Cap, Small-Cap, and Fledgling index returns is driven by the Fledgling index itself. Accordingly, the study concludes that the JSE Large-Cap, Mid-Cap, and Fledgling indices can serve as effective tools for investors to mitigate portfolio risk during adverse market conditions, such as the COVID-19 pandemic, when returns are declining, as these indices tend to lead the co-movement in returns.

5. Robustness Tests

In order to confirm the robustness of the findings of the wavelet model results the study undertook to run a MGARCH-ADCC model to confirm the dynamic nature of the co-movement between JSE size-based indices pairs. The results associated with the estimation of the MGARCH-ADCC model are presented in this section.

5.1. Univariant GARCH Specification

Before estimating the MGARCH-ADCC model, preliminary tests were conducted to detect Autoregressive Conditional Heteroskedasticity (ARCH) effects in the JSE size-based index returns and to identify appropriate univariate GARCH specifications. Panel A of Table 4 shows that the ARCH-LM test confirms the presence of ARCH effects across all indices, as the F-statistics are significant at all levels, leading to the rejection of the null hypothesis of no ARCH effects.

Table 4. ARCH-LM and univariant GARCH model specification.

Panel A: ARCH-LM Test
JSE Large cap	49.89612 ***
JSE Mid-cap	34.06005 ***
JSE Small cap	203.5878 ***
JSE Fledgling	105.4491 ***
Panel B: Univariant GARCH Results
	GARCH		GJR GARCH		EGARCH
Variables	Normal	Student T	Normal	Student T	Normal	Student T
JSE Large cap	3.038386	3.013679	3.018423	2.999912	3.015851	2.997680
JSE Mid-cap	2.795550	2.767149	2.789174	2.763422	2.797625	2.767205
JSE Small cap	2.235977	2.189697	2.231781	2.187683	2.232626	2.190691
JSE Fledgling	1.937624	1.873130	1.939644	1.876596	1.944442	1.873302

Notes: 1. *** indicate a 1% statistically significant level. 2. The F-statistic associated with the ARCH-LM test was used to test ARCH effects. 3. The bold figures illustrate the suitable model. 4. Source: author’s own estimation (2025).

Given these results, univariate GARCH models were specified, as their residuals are required for MGARCH-ADCC estimation. The optimal models were selected based on the lowest SIC values. As shown in Panel B of Table 4, the best-fitting models are EGARCH(1,1) for the JSE Large-Cap Index, GJR-GARCH(1,1) for the JSE Mid-Cap and Small-Cap indices, and GARCH(1,1) for the JSE Fledgling index.

5.2. MGARCH-ADCC Results

The results of the MGARCH-ADCC model are presented in Table 5. The parameter θ₁ captures the impact of past shocks on current dynamic conditional correlations, while θ₂ represents the effect of past and current dynamic conditional correlations. Notably, θ₁ is statistically significant for the Large-Small Cap, Large-Fledgling, and Mid-Fledgling index pairs. This indicates that both past and current market volatility influence the co-movement among these indices, resulting in time-varying correlations. The findings align with the lead–lag relationship identified by the WPA as it was found that the JSE Large-Cap, JSE Mid-Cap and JSE Fledgling index cause risk transmission. Similarly, ${\theta }_2$ coefficients attained to all JSE size-based index pairs are significant. This indicates that past dynamic conditional correlations influence current dynamic conditional correlations. Accordingly, the co-movement among JSE size-based indices pairs is dynamic, suggesting it varies overtime. Again, these findings align with the CWT, as the graphical descriptions demonstrates varying correlations over the sample period and at different investment periods.

Table 5. MGARCH-ADCC results.

MGARCH-ADCC
	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{\theta }}_3$	ρi,j (min)	ρi,j (max)	ρi,j (σ)
Large-Mid	0.010782 (0.462873)	0.713210 *** (4.457261)	−0.071128 (−1.573314)	−0.371487	0.084342	0.042047
Large-Small	−0.020323 *** (−20.29546)	0.676119 *** (2.795003)	0.033091 (1.379061)	−0.602008	0.187703	0.027752
Large-Fledgling	−0.007732 *** (−7.995101)	0.837378 *** (6.775756)	−0.024971 (−1.043880)	−0.245873	0.069988	0.030574
Mid-Small	−0.009484 (−0.886693)	0.686468 ** (2.153044)	0.000813 (0.044908)	−0.082260	0.312961	0.015202
Mid-Fledgling	−0.009090 *** (−4.42 × 109)	0.826384 *** (9908.892)	−0.004026 *** (−26.46234)	−0.089452	1.682405	0.041441
Small-Fledgling	−0.006691 (0.2983)	0.877240 *** (0.0000)	0.012873 (0.4473)	−0.059651	0.142695	0.014304

Notes: 1. *** and ** indicate a 1% and 5% statistically significant level, respectively. 2. The z-statistic is provided in parenthesis. 3. Source: author’s own estimation (2025).

The asymmetry coefficient, θ₃, is significant only for the Mid-Fledgling index pair, indicating the presence of leverage effects. This suggests that negative market movements amplify the co-movement between the JSE size-based indices more than positive movements of the same magnitude (Moodley et al., 2024). Additionally, the stationarity condition, θ₁ + θ₂ < 1, is satisfied for all index pairs, further confirming the model’s appropriateness.

Collectively, the findings of the MGARCH-ADCC model confirm the robustness of the wavelet model results as the findings are identical.

6. Discussion of Results

6.1. MODWT

The MODWT analysis shows that the co-movement among JSE size-based index pairs varies across different investment horizons, including short-term, medium-term, and long-term periods. To this extent, void of financial market volatility, the optimal periods for holding a combination of the JSE Large-Cap and JSE Fledgling in a portfolio is the short-term and medium term. However, for the JSE Large-Mid index pairs and JSE Large-Small index pairs, the optimal holding period is the medium-term. Similarly, for the JSE Mid-Small index pair, the optimal period is the short-term. These findings align with the FMH, which posits that the co-movement of JSE size-based indices will vary at investment periods, which require portfolio rebalancing to ensure diversification benefits.

If such portfolio rebalancing is not conducted, it will have severe economic consequences for investors. For example, if investors hold the JSE Large-Fledging index pair in a portfolio during the long-term, JSE Mid-Small asset pair (JSE Large-Mid index pair and JSE Large-Small index pair) in the medium-term and long-term (in the short-term and long-term), then they will be exposed to excessive portfolio losses. This is owing to elevated correlation between the said JSE size-based index pairs during the identified investment periods, which enhances portfolio volatility, reduces portfolio diversification, causing investors to return a deficit. Consequently, passive investors who consider JSE size-based index returns in their portfolio must correctly time their entry and exit points into the JSE size-based indices market, if they thus wish to enhance their return.

It is worth noting that the JSE Mid-Fledgling and Small-Fledgling index pair co-movement is not aligned to investment periods as the co-movement is stable across the short-term, medium-term and long-term. Although these findings contradict the FMH, it does not come as a shock. That being said, the AMH suggests that stock markets index returns, like the JSE size-based indices, will attribute varying performance levels when compared to other stock market index returns. To this extent, the variation in the co-movement of JSE size-based index pairs will not be the same at each investment period for each index pair. Thus, it is see that the optimal holding period varies among each JSE size-based index pair, with the JSE mid-fledging optimal holding period being at all investment periods.

6.2. CWT

If one turns to the CWT results, it is clearly evident that extreme market events like the COVID-19 pandemic have a significant impact on the co-movement of JSE size-based index pairs. The most common finding herein is that during the COVID-19 pandemic, the co-movement of JSE size-based index pairs increased during the long-term investment period. These findings align with studies conducted by Boako and Alagidede (2017); Maiti et al. (2022); Sayed and Charteris (2024) who also find the long-term investment period as the least attractive for holding equity market securities in a portfolio during extreme market volatility. Again, these findings do not come as a shock because the longer the time-period, the longer the JSE size-based index pair co-movement can change. Consequently, when a volatile period is added to the longer time-period, the correlations will fluctuate more often, which leads to an increase overtime as volatile conditions tend to enhance correlations.

The economic consequences of this are easily derived. If investors wish to enhance their return perspective during volatile market conditions by investing in a variety of JSE size-based indices, they need to only do so in the short-term and medium-term. If such is not considered, then investors will be exposed to portfolio volatility and heighten losses in relation to monetary value.

6.3. WPA

The findings of the WPA reveal that the JSE Large-Cap, JSE Mid-Cap and JSE Fledgling index returns tends to drive the lead–lag relationship among JSE size-based index returns. This means that the said JSE size-based index returns are net transmitters of volatility to other JSE size-based indices, which align with a study conducted by Lawrence et al. (2024). These findings suggest that risk transmission exists among JSE size-based indices, as such, investors must take into consideration the market performance of the JSE Large-Cap, JSE Mid-Cap and JSE Fledgling index returns before determining to include JSE size-based indices in their portfolio.

For example, if it is seen that the performance of the three JSE size-based indices returns are volatile and not stable, then such volatility will be transmitted to other JSE size-based indices, which will expose investors to losses if they incorporate JSE size-based indices in their portfolio. Consequently, examining the performance of the JSE Large-Cap, JSE Mid-Cap and JSE Fledgling indices, would assist investors in adequately determining the future performance of JSE size-based indices, which may assist investors in mitigating risk in their portfolio.

Collectively, these findings do not come as a shock as the companies that form part of the three indices tend to be the large companies listed on the JSE as it captures a large portion of the overall market capitalization of the JSE. Consequently, it is not uncommon to find these JSE size-based indices to lead risk transmission because they capture a large portion of the market share.

6.4. Macroeconomic Drivers

The fundamental base theory posits those macroeconomic factors such as interest rates, exchange rates and inflation play an important role when observing co-movement. That being said, elevated interest rates within a country negatively effects JSE indices as it makes fixed-income assets more feasible than equities, which drives volatility and enhances co-movement. These findings align with this study as it is evident that JSE size-based co-movement tended to increase substantially during the COVID-19 pandemic. This does not come as a shock as interest rates were increased during the pandemic to reduce inflation and ensure stability. Similarly, during the COVID-19 pandemic, the rand depreciated significantly in relation to the US dollar, which made cost of borrowing more expensive. Consequently, the pricing of companies listed among the JSE size-based indices was negatively affected. This resulted in many investors selling off their ownership, which caused excess volatility and enhanced co-movement. Collectively, macroeconomic drivers like the above mentioned played an important role in the current observations of JSE size-based indices co-movement. Hence, it is important to understand how policy adjustments such as inflation and interest rate targeting, among others, drive co-movement.

7. Conclusions and Implications

The primary objective of this study was to examine the time–frequency co-movement of JSE size-based indices. To achieve this, two secondary objectives were established: (1) to compare the correlations of various JSE size-based index pairs across different investment horizons and time periods, and (2) to assess whether lead–lag relationships exist among these index pairs. The study focused on four JSE size-based indices—Large-Cap, Mid-Cap, Small-Cap, and Fledgling—and employed three empirical methods: MODWT, CWT, and WPA.

The findings indicate that the co-movement among JSE size-based index pairs varies across different investment horizons, highlighting that the holding period is a key factor for achieving portfolio diversification. Consequently, simply including all JSE size-based indices in a portfolio does not automatically ensure diversification; rather, strategically timing the inclusion or exclusion of these indices can maximize diversification, as co-movement patterns differ between short-term, medium-term, and long-term periods. Moreover, the co-movement of these index pairs is influenced not only by investment horizons but also by prevailing conditions in the South African market.

That being, during the COVID-19 pandemic, the co-movement of the Large-Mid, Large-Small and Mid-Small were at heightened levels. This implies that including a combination of the said JSE size-based indices in a portfolio during a volatile condition will increase portfolio correlation. Similarly, a lead–lag relationship exists between JSE size-based indices pairs, where JSE Large-Cap index, JSE Mid-Cap index and JSE Fledging index lead the co-movement within the sample.

The findings of the study have meaningful implications for investors, policymakers and portfolio managers. Investors must consider the optimal holding period for companies that form part of the size-based indices, as holding it for either the short-term, medium-term, or long-term may increase the correlation in a portfolio and reduce diversification benefits. Policymakers must control the co-movement of these size-based indices by mitigating financial market uncertainty as co-movements are driven by periods of bearish conditions. Lastly, portfolio fund managers must consider holding periods and the state of the financial market when formulating portfolios for investors as these determinants are key for investors’ return. Collectively, the study provides a novel contribution to the South African investment landscape as it provides evidence on appropriate risk mitigating strategies when considering JSE size-based indices in a portfolio, which has not been considered before, despite the growing prominence of incorporating JSE sized-based companies in a portfolio.

The achievement of the desired objective is not without certain limitations. Acknowledging these limitations helps provide a more balanced conclusion and guides the direction of future research. In this study, the sample period is specifically limited to the COVID-19 pandemic, rather than encompassing other historical market conditions. This focus was chosen because the COVID-19 pandemic represents the most recent major historical event, and analyzing it enhances the novelty of the study. Future research is encouraged to extend the sample period to include additional historical market events, such as the 2007–2008 global financial crisis. Moreover, the study isolates the observation to South Africa to answer the desired objective. However, future research can extend the analysis to emerging markets and provide a comparative analysis to determine which countries’ size-based indices are more robust to market conditions and investment periods. This way, investors can limit investing in emerging market countries’ size-based indices that co-move during market volatility and at investment periods, thereby enhancing portfolio diversification and reducing portfolio volatility.