RWKV-VIO: An Efficient and Low-Drift Visual–Inertial Odometry Using an End-to-End Deep Network
Abstract
1. Introduction
- A temporal modeling method based on the RWKV architecture is proposed. It captures long-term and short-term dependencies in visual and inertial data efficiently. Its lightweight design reduces computational complexity.
- A novel IMU encoder, Res-Encoder, integrates convolutional layers with residual connections to enhance the extraction of inertial features. It effectively preserves historical information, enhancing the depth and stability of feature representations.
- A parallel IMU encoder structure is introduced to extract diverse features from inertial data, enhancing the expressiveness of inertial features and improving the fusion of multi-modal data.
2. Related Work
2.1. Visual Odometry
2.2. Visual-Inertial Odometry
2.3. Temporal Modeling
3. Materials and Methods
3.1. End-to-End Deep Learning-Based Visual–Inertial Odometry
3.2. Feature Encoder
3.2.1. Visual Encoder
3.2.2. IMU Encoder
3.3. Decoder
3.3.1. Positional Encoding
3.3.2. Time-Mixing Block
3.3.3. Channel-Mixing Block
3.3.4. Pose Regression Module
3.4. Loss Function
4. Results
4.1. Experiment Setup
4.1.1. Dataset
4.1.2. Implementation Details
4.2. Main Results
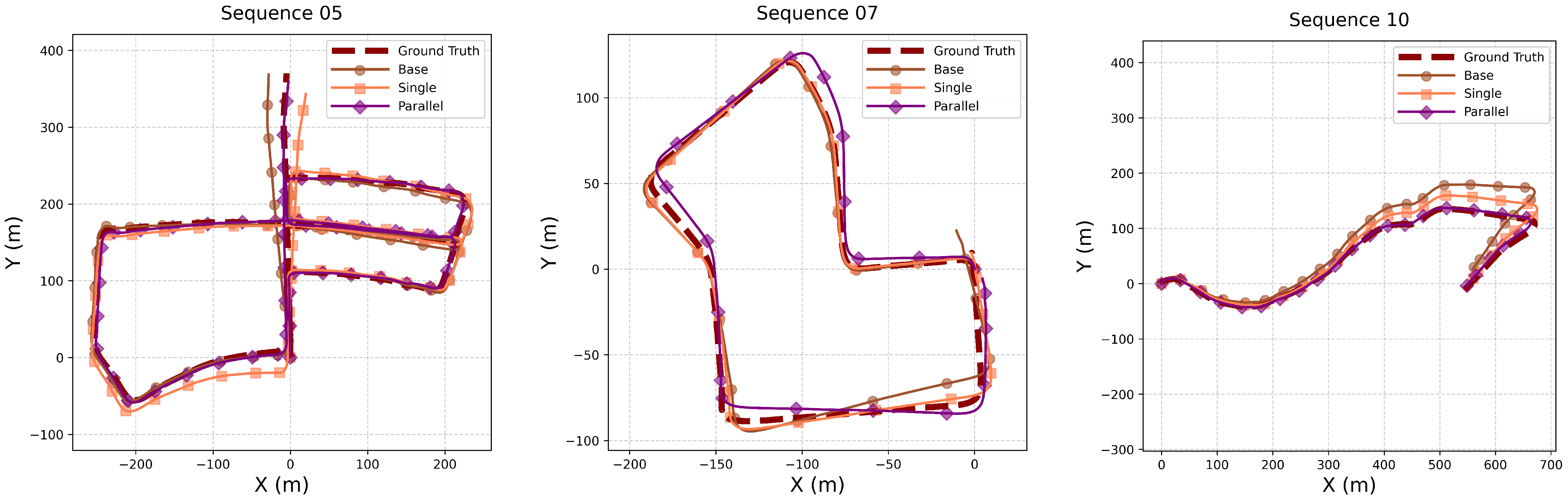
4.3. Ablation Study
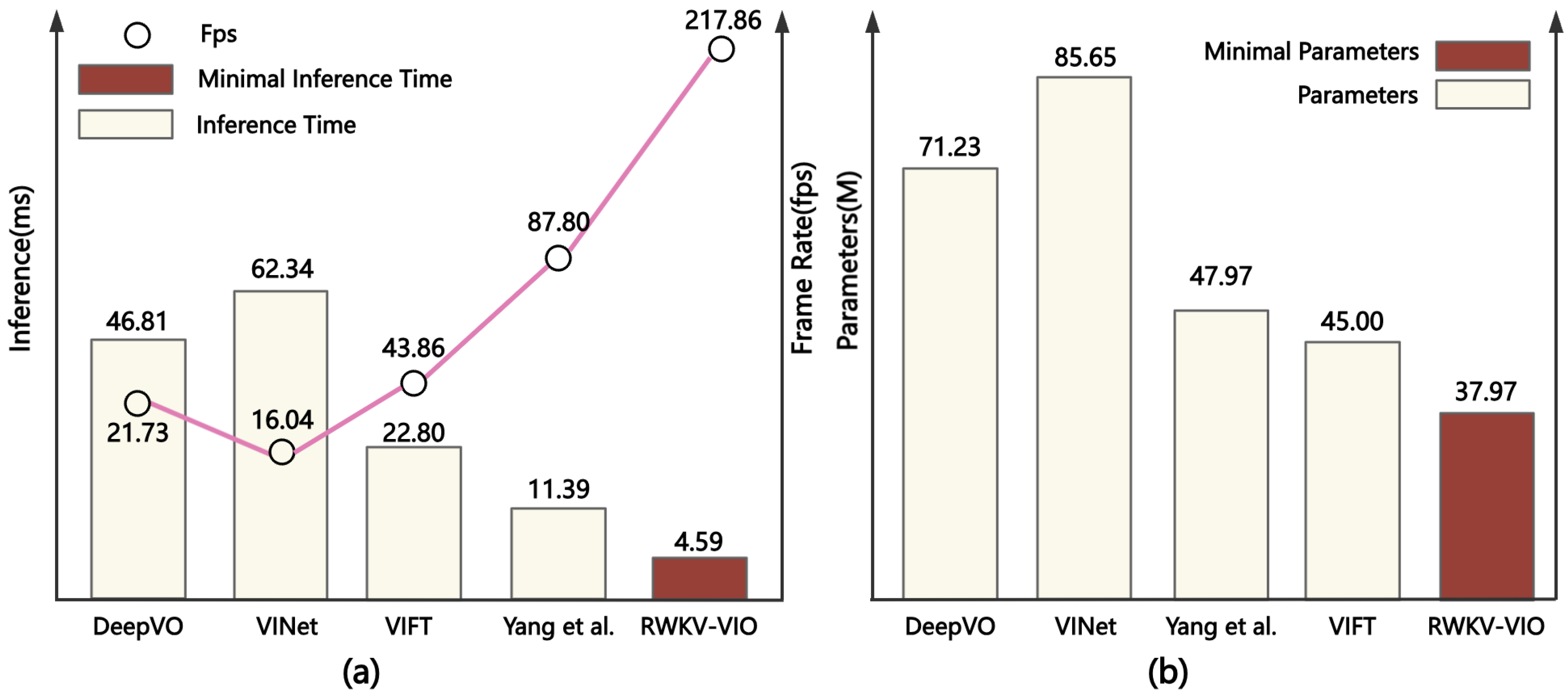
4.4. Efficiency Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, F.; Shi, J.; Wu, L.; Dai, K.; Zhong, S. Consistent Monocular Ackermann Visual–Inertial Odometry for Intelligent and Connected Vehicle Localization. Sensors 2020, 20, 5757. [Google Scholar] [CrossRef]
- Cao, H.; Yang, T.; Yiu, K.-F.C. A Method Integrating the Matching Field Algorithm for the Three-Dimensional Positioning and Search of Underwater Wrecked Targets. Sensors 2025, 25, 4762. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Q.; Hu, Y.; Gallay, M.; Zheng, W.; Guo, J. Recent Advances in SLAM for Degraded Environments A Review. IEEE Sens. J. 2025, 25, 27898–27921. [Google Scholar] [CrossRef]
- Song, J.; Jo, H.; Jin, Y.; Lee, S.J. Uncertainty-Aware Depth Network for Visual Inertial Odometry of Mobile Robots. Sensors 2024, 24, 6665. [Google Scholar] [CrossRef]
- Xu, Z.; Xi, B.; Yi, G.; Ahn, C.K. High-precision control scheme for hemispherical resonator gyroscopes with application to aerospace navigation systems. Aerosp. Sci. Technol. 2021, 119, 107168. [Google Scholar] [CrossRef]
- Lee, J.-C.; Chen, C.-C.; Shen, C.-T.; Lai, Y.-C. Landmark-Based Scale Estimation and Correction of Visual Inertial Odometry for VTOL UAVs in a GPS-Denied Environment. Sensors 2022, 22, 9654. [Google Scholar] [CrossRef]
- Nan, F.; Gao, Z.; Xu, R.; Wu, H.; Yu, Z.; Zhang, Y. Stiffness Tuning of Hemispherical Shell Resonator Based on Electrostatic Force Applied to Discrete Electrodes. IEEE Trans. Instrum. Meas. 2024, 73, 8505810. [Google Scholar] [CrossRef]
- Cao, H.; Zhang, Y.; Han, Z.; Shao, X.; Gao, J.; Huang, K.; Shi, Y.; Tang, J.; Shen, C.; Liu, J. Pole-Zero Temperature Compensation Circuit Design and Experiment for Dual-Mass MEMS Gyroscope Bandwidth Expansion. IEEE/ASME Trans. Mechatronics 2019, 24, 677–688. [Google Scholar] [CrossRef]
- Yang, C.; Cheng, Z.; Jia, X.; Zhang, L.; Li, L.; Zhao, D. A Novel Deep Learning Approach to 5G CSI/Geomagnetism/VIO Fused Indoor Localization. Sensors 2023, 23, 1311. [Google Scholar] [CrossRef]
- Zhang, Y.; Chu, L.; Mao, Y.; Yu, X.; Wang, J.; Guo, C. A Vision/Inertial Navigation/Global Navigation Satellite Integrated System for Relative and Absolute Localization in Land Vehicles. Sensors 2024, 24, 3079. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Wang, B.; Lu, C.X.; Trigoni, N.; Markham, A. Deep Learning for Visual Localization and Mapping: A Survey. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 17000–17020. [Google Scholar] [CrossRef] [PubMed]
- Luo, R.C.; Yih, C.-C.; Su, K.L. Multisensor fusion and integration: Approaches, applications, and future research directions. IEEE Sens. J. 2002, 2, 107–119. [Google Scholar] [CrossRef]
- Zhu, H.; Qiu, Y.; Li, Y.; Mihaylova, L.; Leung, H. An Adaptive Multisensor Fusion for Intelligent Vehicle Localization. IEEE Sens. J. 2024, 24, 8798–8806. [Google Scholar] [CrossRef]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, Present, and Future of Simultaneous Localization and Mapping: Toward the Robust-Perception Age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef]
- Engel, J.; Koltun, V.; Cremers, D. Direct Sparse Odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 611–625. [Google Scholar] [CrossRef]
- Forster, C.; Pizzoli, M.; Scaramuzza, D. SVO: Fast semi-direct monocular visual odometry. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 15–22. [Google Scholar] [CrossRef]
- Sun, Q.; Tang, Y.; Zhang, C.; Zhao, C.; Qian, F.; Kurths, J. Unsupervised Estimation of Monocular Depth and VO in Dynamic Environments via Hybrid Masks. IEEE Trans. Neural Networks Learn. Syst. 2022, 33, 2023–2033. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.; Tardós, J.D. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual–Inertial, and Multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Bloesch, M.; Omari, S.; Hutter, M.; Siegwart, R. Robust visual inertial odometry using a direct EKF-based approach. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 298–304. [Google Scholar] [CrossRef]
- Chen, C.; Rosa, S.; Miao, Y.; Lu, C.X.; Wu, W.; Markham, A.; Trigoni, N. Selective Sensor Fusion for Neural Visual-Inertial Odometry. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10534–10543. [Google Scholar] [CrossRef]
- Yang, M.; Chen, Y.; Kim, H.S. Efficient deep visual and inertial odometry with adaptive visual modality selection. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer Nature: Cham, Switzerland, 2022; pp. 233–250. [Google Scholar]
- Tu, Z.; Chen, C.; Pan, X.; Liu, R.; Cui, J.; Mao, J. EMA-VIO: Deep Visual–Inertial Odometry With External Memory Attention. IEEE Sens. J. 2022, 22, 20877–20885. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gülçehre, Ç.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation. In Proceedings of the Conference Empirical Methods in Natural Language Processing, Doha, Qatar, 25–29 October 2014. Available online: https://api.semanticscholar.org/CorpusID:5590763 (accessed on 9 September 2025).
- Antonello, R.; Vaidya, A.; Huth, A. Scaling laws for language encoding models in fMRI. Adv. Neural Inf. Process. Syst. 2023, 36, 21895–21907. [Google Scholar]
- Zou, Y.; Ji, P.; Tran, Q.H.; Huang, J.B.; Chandraker, M. Learning monocular visual odometry via self-supervised long-term modeling. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 710–727. [Google Scholar]
- Peng, B.; Alcaide, E.; Anthony, Q.; Anthony, Q.; Albalak, A.; Arcadinho, S.; Biderman, S. RWKV: Reinventing RNNs for the Transformer Era. arXiv 2023, arXiv:2305.13048. [Google Scholar] [CrossRef]
- Clark, R.; Wang, S.; Wen, H.; Markham, A.; Trigoni, N. VINet: Visual-Inertial Odometry as a Sequence-to-Sequence Learning Problem. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar] [CrossRef]
- Wang, S.; Clark, R.; Wen, H.; Trigoni, N. DeepVO: Towards end-to-end visual odometry with deep recurrent convolutional neural networks. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 24 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2043–2050. [Google Scholar]
- Shamwell, E.J.; Leung, S.; Nothwang, W.D. Vision-Aided Absolute Trajectory Estimation Using an Unsupervised Deep Network with Online Error Correction. In Proceedings of the 2018 IEEE/RSJ international conference on intelligent robots and systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2524–2531. [Google Scholar]
- Chen, C.; Rosa, S.; Lu, C.X.; Wang, B.; Trigoni, N.; Markham, A. Learning Selective Sensor Fusion for State Estimation. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 4103–4117. [Google Scholar] [CrossRef]
- Han, L.; Lin, Y.; Du, G.; Lian, S. DeepVIO: Self-supervised Deep Learning of Monocular Visual Inertial Odometry using 3D Geometric Constraints. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 4–8 November 2019; pp. 6906–6913. [Google Scholar] [CrossRef]
- Godard, C.; Aodha, O.M.; Firman, M.; Brostow, G. Digging Into Self-Supervised Monocular Depth Estimation. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3827–3837. [Google Scholar] [CrossRef]
- Xue, F.; Wang, X.; Li, S.; Wang, Q.; Wang, J.; Zha, H. Beyond Tracking: Selecting Memory and Refining Poses for Deep Visual Odometry. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8567–8575. [Google Scholar]
- Liu, L.; Li, G.; Li, T.H. ATVIO: Attention Guided Visual-Inertial Odometry. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 4125–4129. [Google Scholar] [CrossRef]
- Xue, F.; Wang, Q.; Wang, X.; Dong, W.; Wang, J.; Zha, H. Guided feature selection for deep visual odometry. In Asian Conference on Computer Vision; Springer International Publishing: Cham, Switzerland, 2018; pp. 293–308. [Google Scholar]
- Kurt, Y.B.; Akman, A.O.; Alatan, A.A. Causal Transformer for Fusion and Pose Estimation in Deep Visual Inertial Odometry. arXiv 2024, arXiv:2409.08769. [Google Scholar] [CrossRef]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.X.; Yan, X. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Liu, S.; Yu, H.; Liao, C.; Li, J.; Lin, W.; Liu, A.X.; Dustdar, S. Pyraformer: Low-Complexity Pyramidal Attention for Long-Range Time Series Modeling and Forecasting. In Proceedings of the Tenth International Conference on Learning Representations (ICLR 2022), Virtual Event, 25–29 April 2022. [Google Scholar]
- Wang, H.; Peng, J.; Huang, F.; Wang, J.; Chen, J.; Xiao, Y. MICN: Multi-scale local and global context modeling for long-term series forecasting. In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Liu, M.; Zeng, A.; Chen, M.; Xu, Z.; Lai, Q.; Ma, L.; Xu, Q. SciNet: Time series modeling and forecasting with sample convolution and interaction. Adv. Neural Inf. Process. Syst. 2022, 35, 5816–5828. [Google Scholar]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are transformers effective for time series forecasting? In Proceedings of the AAAI Conference on Artificial Intelligence 2023, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 11121–11128. [Google Scholar]
- Hou, H.; Yu, F.R. RWKV-TS: Beyond Traditional Recurrent Neural Network for Time Series Tasks. arXiv 2024, arXiv:2401.09093. [Google Scholar] [CrossRef]
- Ilg, E.; Mayer, N.; Saikia, T.; Keuper, M.; Dosovitskiy, A.; Brox, T. FlowNet 2.0: Evolution of Optical Flow Estimation with Deep Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1647–1655. [Google Scholar] [CrossRef]
- Yang, J.; Zeng, X.; Zhong, S.; Wu, S. Effective Neural Network Ensemble Approach for Improving Generalization Performance. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 878–887. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Wu, Y.; He, K. Group Normalization. arXiv 2018, arXiv:1803.08494. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Fischer, P.; Ilg, E.; Hausser, P.; Hazirbas, C.; Golkov, V.; Van Der Smagt, P.; Cremers, D.; Brox, T. FlowNet: Learning Optical Flow with Convolutional Networks. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 13–16 December 2015; pp. 2758–2766. [Google Scholar] [CrossRef]




| Method Category | Model | Year | Sensor | Keywords |
|---|---|---|---|---|
| Geometry-based | ORB-SLAM2 [19] | 2021 | Mono/RGB-D/Stereo | ORB feature tracking; nonlinear optimization |
| VINS-Mono [18] | 2018 | Mono + IMU | Tight mono-IMU coupling; EKF-based estimation | |
| ROVIO [20] | 2015 | Mono + IMU | Direct EKF; robust inertial fusion | |
| Deep Learning-based | VINet [29] | 2017 | Mono + IMU | End-to-end seq2seq; LSTM fusion |
| DeepVO [30] | 2017 | Mono | DRCNNs; end-to-end VO | |
| VIOLearner [31] | 2018 | Mono + IMU | Unsupervised learning; online trajectory correction | |
| Chen et al. [32] | 2019 | Mono + IMU | Selective sensor fusion; neural network | |
| DeepVIO [33] | 2019 | Mono + IMU | Self-supervised learning | |
| Monodepth2 [34] | 2019 | Mono | Self-supervised depth | |
| BeyondTracking [35] | 2019 | Mono | Memory selection; pose refinement | |
| Zou et al. [27] | 2020 | Mono | Self-supervised long-term; CNN-RNN hybrid | |
| Deep Learning-based | ATVIO [36] | 2021 | Mono + IMU | Attention fusion; adaptive loss |
| GFS-VO [37] | 2018 | Mono | Guided feature selection | |
| Tu et al. (EMA-VIO) [23] | 2022 | Mono + IMU | External memory attention | |
| Yang et al. [22] | 2022 | Mono + IMU | Adaptive visual modality; LSTM modeling | |
| VIFT [38] | 2024 | Mono + IMU | Causal Transformer | |
| Fusion [32] | 2025 | Mono + IMU | Selective fusion |
| Method | Model | Type | Seq. 05 | Seq. 07 | Seq. 10 | avg | avg | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Geometry | ORB-SLAM2 [19] | VO | 9.12 | 0.2 | 10.34 | 0.3 | 4.04 | 0.3 | 7.8 | 0.27 |
| VINS-Mono [18] | VIO | 11.6 | 1.26 | 10.0 | 1.72 | 16.5 | 2.34 | 12.7 | 1.77 | |
| ROVIO [20] | VIO | 3.21 | 1.22 | 2.97 | 1.38 | 3.20 | 1.33 | 3.13 | 1.31 | |
| Learning | Monodepth2 [34] | VO | 4.66 | 1.7 | 4.58 | 2.6 | 7.73 | 3.4 | 5.65 | 2.56 |
| Zou et al. [27] | VO | 2.63 | 0.5 | 6.43 | 2.1 | 5.81 | 1.8 | 4.95 | 1.46 | |
| VIOLearner [31] | VIO | 3.00 | 1.40 | 3.60 | 2.06 | 2.04 | 1.37 | 2.88 | 1.61 | |
| DeepVIO [33] | VO | 2.86 | 2.32 | 2.71 | 1.66 | 0.85 | 1.03 | 2.14 | 1.67 | |
| GFS-VO [37] | VO | 3.27 | 1.6 | 3.37 | 2.2 | 6.32 | 2.3 | 4.32 | 2.03 | |
| DeepVO [30] | VO | 2.62 | 3.61 | 3.91 | 4.60 | 8.11 | 8.83 | 4.88 | 5.58 | |
| BeyondTracking [35] | VO | 2.59 | 1.2 | 3.07 | 1.8 | 3.94 | 1.7 | 3.2 | 1.56 | |
| ATVIO [36] | VIO | 4.93 | 2.4 | 3.78 | 2.59 | 5.71 | 2.96 | 4.8 | 2.65 | |
| Fusion [32] | VIO | 4.44 | 1.69 | 2.95 | 1.32 | 3.41 | 1.41 | 3.02 | 1.42 | |
| Yang et al. [22] | VIO | 2.61 | 1.06 | 1.83 | 1.35 | 3.11 | 1.12 | 2.55 | 1.17 | |
| VIFT [38] | VIO | 2.02 | 0.53 | 1.75 | 0.47 | 2.57 | 0.54 | 2.01 | 0.71 | |
| (Ours) RWKV-VIO | VIO | 2.03 | 1.0 | 2.73 | 1.79 | 2.1 | 0.99 | 2.29 | 1.26 | |
| Method | Seq. 05 | Seq. 07 | Seq. 10 | avg | avg | |||
|---|---|---|---|---|---|---|---|---|
| base | 3.38 | 1.25 | 2.65 | 1.70 | 4.04 | 1.85 | 3.36 | 1.58 |
| +new imu encoder | 2.76 | 1.13 | 2.99 | 1.81 | 3.13 | 1.56 | 2.96 | 1.50 |
| +parallel imu encoder | 2.03 | 1.00 | 2.73 | 1.79 | 2.13 | 0.99 | 2.29 | 1.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Xu, X.; Xu, Z.; Wu, Z.; Chu, W. RWKV-VIO: An Efficient and Low-Drift Visual–Inertial Odometry Using an End-to-End Deep Network. Sensors 2025, 25, 5737. https://doi.org/10.3390/s25185737
Yang J, Xu X, Xu Z, Wu Z, Chu W. RWKV-VIO: An Efficient and Low-Drift Visual–Inertial Odometry Using an End-to-End Deep Network. Sensors. 2025; 25(18):5737. https://doi.org/10.3390/s25185737
Chicago/Turabian StyleYang, Jiaxi, Xiaoming Xu, Zeyuan Xu, Zhigang Wu, and Weimeng Chu. 2025. "RWKV-VIO: An Efficient and Low-Drift Visual–Inertial Odometry Using an End-to-End Deep Network" Sensors 25, no. 18: 5737. https://doi.org/10.3390/s25185737
APA StyleYang, J., Xu, X., Xu, Z., Wu, Z., & Chu, W. (2025). RWKV-VIO: An Efficient and Low-Drift Visual–Inertial Odometry Using an End-to-End Deep Network. Sensors, 25(18), 5737. https://doi.org/10.3390/s25185737






