Abstract
The optical force exerted on a dipole particle can be divided into gradient force, scattering force, and spin–curl force, all of which can be derived from Maxwell’s stress tensor with the dipole approximation. Here, we identify an additional spin–curl force for arbitrary objects beyond the dipole approximation, which is named the generalized spin–curl force in this paper. The generalized spin–curl force originates from the Minkowski force density and depends on the imaginary parts of the permittivity, permeability, and chirality of the object. However, it remains imperceptible in conventional optical force calculations due to its exact cancellation by a compensatory surface force during MST surface integration. The study of the generalized spin–curl force provides critical insights into elucidating the mechanisms underlying optical momentum transfer and internal force distribution within complex media. Furthermore, the generalized spin–curl force offers a novel mechanism for enhancing optical sensors, enabling highly sensitive detection of absorptive or chiral perturbations in systems such as microcavities and metasurfaces. Its ability to manipulate internal force distributions also provides new pathways for advancing optical force probes and chirality-selective sensing at the nanoscale.
1. Introduction
Optical forces play a pivotal role in modern science and technology [1,2,3], including optical manipulation [4,5,6], chirality sorting [7,8], optical spanners and stretchers [9], thermally limited force sensing [10], and biological systems [11,12,13]. In all this research, the optical force calculation is prominent and is primarily achieved through the integration of Maxwell’s stress tensor, which is derived from the Lorentz force densities and Maxwell’s equations [14,15,16]. When media are introduced, several different formulations of force density have been proposed, with the most renowned ones by Einstein–Laub, Ampère–Lorentz, Minkowski, and Abraham [14,17,18,19]. From a physical perspective, Ampère and Lorentz posited that the electric and magnetic fields exert forces on the densities of total charges and currents [14], based on which the Ampère–Lorentz force density was proposed. Interestingly, several studies have questioned the accuracy of the Ampère–Lorentz force density in recent years, but subsequent investigations have refuted these claims [20,21,22,23,24].
Corresponding to the force densities, various stress tensors have also been proposed, with the Minkowski stress tensor (MST) being the most commonly used in optical force calculations [21]. By employing the MST and dipole approximation, an additional scattering force from the curl of the spin angular momentum of a light field has been identified and studied [25,26]. Up to now, it is regarded that the optical force calculated from the surface integration of MST is the total optical force. It certainly contains all the contributions of the gradient force, scattering force, and the spin–curl force in the case of dipole approximation.
The identification of the generalized spin–curl force (GSCF) enriches the understanding of light–matter interactions in complex media, which is essential for designing highprecision optical force sensors. The GSCF, though canceled in net force measurements, may play a critical role in redistributing internal forces within sensor structures such as photonic crystal cavities or metasurfaces, potentially enhancing light–matter interactions and enabling new sensing modalities [10,27]. In optical sensors, GSCF-driven internal force redistribution may enable new detection paradigms: for instance, in whispering-gallerymode biosensors, absorption-induced GSCF perturbations could amplify single-molecule binding signals; in terahertz chiral sensors, spin–curl interactions might enhance the discrimination of enantiomers via momentum transfer [28]. Additionally, the ability to probe internal force distributions non-invasively could lead to novel sensor designs for biomedical applications, such as intracellular force mapping or nanomechanical property characterization, and the chirality-sensitive nature of GSCF may be harnessed in label-free biosensors for discriminating biomolecular handedness [29].
In this work, we checked the MST in the most general case of medium and cautiously identified an additional term in force density beyond the MST, which consequently contributes an additional term in the optical force. The new term arises from the spin angular momentum of the total field and depends on the imaginary parts of the permittivity, permeability, and chirality of the object. However, the additional force is imperceptible, due to its cancellation by a surface force. The properties and potential applications of the addition force are discussed, with particular emphasis on its implications for and critical role in advanced optical sensing technologies.
2. Theory
The Lorentz force exerted on charged matter is given by
where and are the electric field and the magnetic induction, respectively; and are the densities of the charge and current, respectively. Employing the Maxwell’s equations in matter, the force density becomes
where is the Minkowski stress tensor of
In order to calculate the averaged optical force, a time-average operation should be performed to neglect the effect of fast oscillation of the optical fields, and the last term in Equation (3) is zero. Without loss of generality, we assume that the time-varying fields are time-harmonic monochromatic plane waves,
Then, the time-averaged Minkowski force density is given by
with the time-averaged Minkowski stress tensor of
Then, the total optical force can be obtained through the integration of the Minkowski force density
where V is the volume of the object, and is the normal vector of its surface S. This is the widely known procedure to derive the optical force and the stress tensor, which can be found in electrodynamics-related textbooks [30,31,32].
Here, we argue that, in the most general cases, there should be another item in the total optical force calculation. As we know, it is quite vague in the derivation from Equation (2) to Equation (3) [32]. The degenerate form of the Minkowski stress tensor under vacuum conditions can be derived by using the formula [30]
In the derivation from Equation (2) to Equation (3), the following formula could be used, which is
However, this formula only holds for homogeneous, isotropic, and lossless medium. Mathematically, the general relation for a complex medium is [33]
For a simple medium, Equations (10) and (11) become exactly the same. In a general complex medium, however, they may give different results.
Employing the more general Equation (11), we reexamine the Minkowski force density for the time-harmonic fields and obtain
The last two items are not necessarily zero in general cases. The forms of the two nonzero items indicate that they are related to the angular momentum of the electric field and magnetic field. Consequently, the optical force for the generalized case can be calculated as
where
is the surface force with the inner and outer surfaces and , respectively. The additional body force is given by
Since and are related to the angular momentum density of the electric field and the magnetic field [34,35], respectively, the additional force can be interpreted as the generalized spin–curl force (GSCF). It is emphasized that the GSCF described in Equation (15) is distinct from the spin–curl force discussed in Refs. [25,26], which arises solely from the spin angular momentum of the electric field. More importantly, the GSCF is not included in the integration of MST. It should be noted that the sum of the surface force and the GSCF is zero, i.e., . As a result, the generalized optical force in Equation (13) is reduced to , i.e.,
Without loss of generality, we consider a chiral particle with complex permittivity and permeability, i.e.,
where is the chiral parameter. Then, the additional force becomes
with
Using the identity for vectors, a further simplification yields
In Equation (21), the first two terms are related to the spins of the electromagnetic field, and the last term depends on the chirality. Since and are pure imaginary, the first two terms are nonzero in the case of and with nonzero imaginary parts. Similarly, the last term is nonzero if the imaginary part of is nonzero.
3. Numerical Results and Discussion
In this section, we focus on and study the properties of the GSCF. We numerically calculate the optical response of a dielectric sphere illuminated by a laser beam with wavelength nm, as shown in Figure 1. The dielectric particle (such as silicon) has a real part of permittivity of and a manually tunable imaginary part of permittivity of or (for the comparison of the additional force item of the GSCF). The dielectric sphere is levitated in water with refractive index , and the light is linearly polarized and propagates along the +z-axis. For simplicity, we introduce the normalized size parameter with the radius of the sphere r and the wave number of the light . In the following discussion, we manually modify the parameters of the sphere, such as the imaginary part of and the chirality , in order to show the contribution of the GSCF. Figure 1b shows the scattering cross section of the sphere as a function of the size parameter . The results show that, when the imaginary part of the permittivity is taken into account, the scattering of the spheres at the resonance becomes pronounced, resulting in a stronger optical force [Figure 1c, where we focus on the optical force along the z-axis only]. Figure 1d shows the GSCF as a function of . When the dielectric material is lossless, both the and the are zero, indicating that the generalized spin–curling force is imperceptible in traditional optical force calculations. When the imaginary part of the dielectric function is considered, the remains zero because the magnetic permeability of the dielectric sphere is 1 at optical frequency, while the exhibits a significant additional optical force in the z direction, which varies significantly with . This can be attributed to the imaginary part of in Equation (19), which generates an additional total optical force when the permittivity has a nonzero imaginary part. Mathematically speaking, this is because and are pure imaginary.
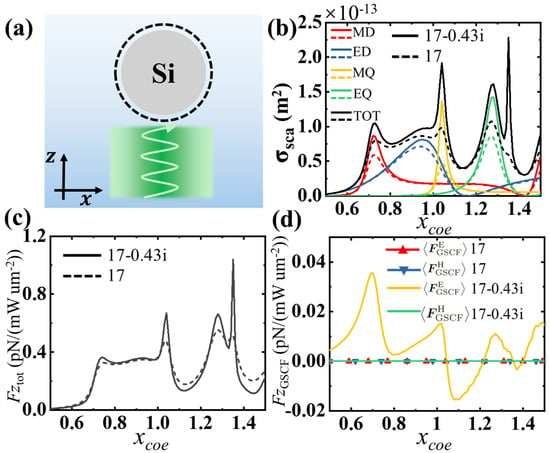
Figure 1.
(a) Schematic of structure. A homogeneous dielectric sphere, such as silicon, with a manually tunable imaginary permittivity is immersed in water. The incident light is a linearly polarized green light with the wavelength of 532 nm. (b) Scattering cross section and multipolar decomposition spectra of the spheres with permittivity of (dashed curves) and (solid curves), respectively. The red, blue, yellow, and green lines correspond to the scattering of magnetic dipoles (MD), electric dipoles (ED), magnetic quadrupoles (MQ), and electric quadrupoles (EQ), respectively. (c) The z-component of the total optical force (Equation (13)) corresponds to the spheres with and , respectively. (d) The GSCF associated with the spin angular momentum of the electric and magnetic fields with and , respectively.
Next, we consider the effect of chirality on the GSCF, i.e., . Figure 2 illustrates the GSCF on a chiral silicon sphere at Mie resonance (ED, MD, EQ, MQ) for a real chirality parameter. It is observed that when a non-absorbing silicon sphere is illuminated by linearly polarized (LP) and left/right-handed circularly polarized (LCP/RCP) light [see Figure 2a–c], the electric and magnetic fields produce additional forces that contribute significantly to the total optical force. However, these forces cancel each other out because and have opposite signs, resulting in a net value of zero for the additional spin–curl force. Yet, when an absorbing silicon sphere () is illuminated by linearly and circularly polarized light [see Figure 2d–f], the additional forces generated by the electric and magnetic fields do not completely cancel each other out. Therefore, the net GSCF can be observed [see Figure 2d–f], and the GSCF at the Mie resonance changes significantly with the change in the real number , which is consistent with the third term of Equation (21), further verifying the theoretical results.
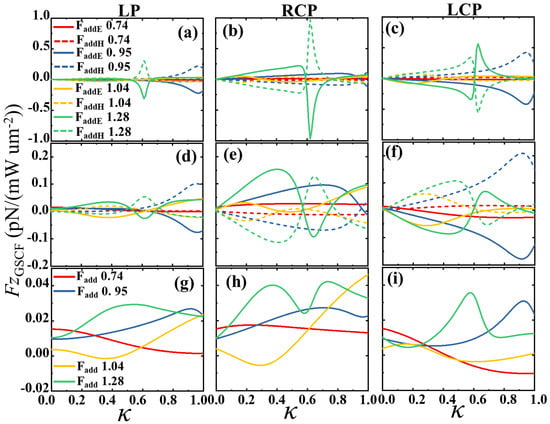
Figure 2.
The GSCF forces on (a–c) non-absorbing chiral spheres () and (d–f) on absorbing chiral spheres () under the linearly polarized (LP) and left/right-handed circularly polarized (LCP/RCP) light. The normalized radius of , , , and are selected, which correspond to the magnetic dipoles (MD), electric dipoles (ED), magnetic quadrupoles (MQ), and electric quadrupoles (EQ), respectively (See Figure 1b). (g–i) The sum of forces corresponding to the spin angular momentum of the electric and magnetic in (d–f). The imaginary part of the chiralty is zero, , for all the figures.
To further explore the regulatory effect of the chiral parameter and the permittivity on the GSCF, as shown in Figure 3, we plot the additional spin–curl force on the chiral silicon sphere illuminated by linearly polarized (LP) and left/right-handed circularly polarized (LCP/RCP) light, with real permittivity and a complex chiral parameter. It shows that the GSCF scales linearly with the imaginary part of under circularly polarized light, while it remains nearly constant under linearly polarized light. The inset of Figure 3 implies that the GSCF is nonzero for linearly polarized light because of the effects of the scattered field.
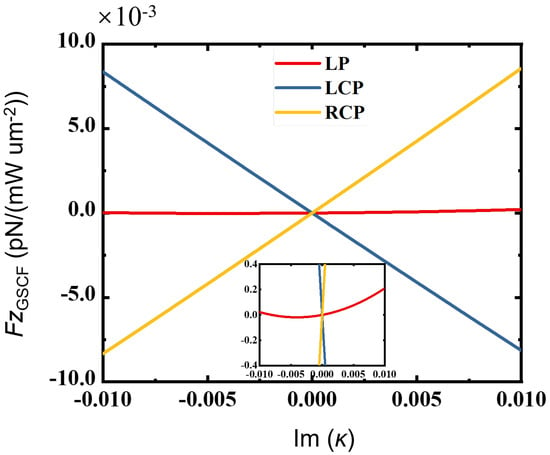
Figure 3.
The GSCFs on a chiral sphere when illuminated by linearly polarized (LP), left/righthanded circularly polarized (LCP/RCP) light with a real permittivity, and a complex chiral parameter . The inset shows the details of the GSCF varying with the imaginary part of the chiral parameter for the linearly polarized light. The other parameters are , , and .
Figure 4 shows the GSCF on a chiral silicon sphere illuminated by linearly polarized (LP), left/right-handed circularly polarized (LCP/RCP) light with complex permittivity and a complex chiral parameter. Figure 4a–f show the parts of the GSCF originating from the spin of the electromagnetic field and the chirality, respectively. Figure 4a–c show that the additional optical force is essentially the same for different polarizations and increases with the imaginary part of permittivity of the chiral sphere. Because the magnetic permeability is a pure real number of 1, the additional force in Figure 4d–f is primarily generated by electromagnetic field coupling. Figure 4g–i show the total GSCF. These show that the additional force is mainly caused by the spin. As shown above, all the numerical results are consistent with the theoretical results, further verifying the regulation of GSCF by chirality and dielectric function.
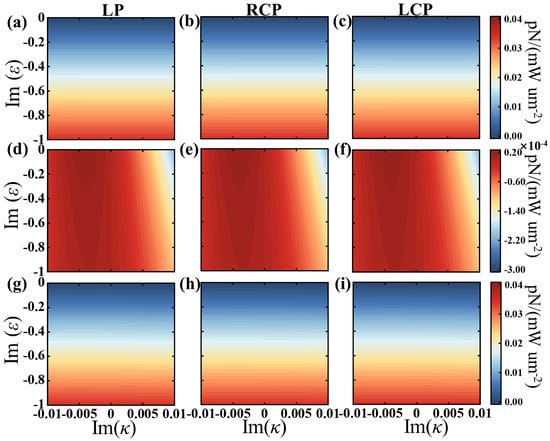
Figure 4.
The GSCFs on a chiral sphere when illuminated by linearly polarized (LP), left/right-handed circularly polarized (LCP/RCP) light with a complex permittivity, and a complex chiral parameter . (a–f) show the parts of the additional force originating from the spin of the electromagnetic field and the chiral, respectively. (g–i) shows the total additional force. The other parameters are , , and .
4. Conclusions
In summary, we have identified a generalized spin–curl force (GSCF) beyond the Minkowski stress tensor, which arises from the spin angular momentum of the electromagnetic fields and depends on the imaginary parts of the permittivity, the permeability, and the chiral parameter of the particle. Distinctly from the spin–curl force discussed in Refs. [25,26] at the case of dipole approximation, both the contributions from the electric field and magnetic field are identified for arbitrary objects and give the full origin of the spin–curl force of a light field. More importantly, the GSCF reported here is not included in the contribution of stress tensor integration. For nonabsorbing objects, the GSCF is always zero. However, for some resonant particles with proper imaginary parts of , and chirality , the amplitude of the GSCF may be comparable to the force calculated from the stress tensor integration. Though the GSCF is imperceptible due to its exact cancellation by a compensatory surface force during MST surface integration, the GSCF plays a pivotal role in critical insights into elucidating the mechanisms underlying optical momentum transfer [17,36] and internal force distribution [37,38,39] within complex media. In addition, the experimental detection of the generalized spin–curl force (GSCF) could be realized in integrated photonic or nanomechanical systems [40].
Moreover, the identification of the GSCF opens new possibilities for designing nextgeneration optical sensors and lays the groundwork for innovative sensor architectures. The explicit accounting of GSCF could inform the design of highly sensitive optical force probes capable of resolving nanoscale mechanical properties in absorbing or chiral environments, which would be invaluable in fields like nanomedicine, soft matter physics, and micro-robotics [10,27,28,29]. For example, in resonant microcavities or metasurfaces used for label-free biosensing, the internal force distribution influenced by GSCF could be exploited to improve the sensitivity to analyte concentration or chirality [27]. Furthermore, it suggests transformative applications—e.g., monitoring GSCF-mediated internal stress in specialty-fiber sensors for real-time analyte detection or designing nano-engineered probes where absorption-dependent spin–curl forces transduce biochemical interactions into mechanical readouts with high sensitivity [28,29]. Future work may explore active tuning of the GSCF via material engineering to realize highly integrated multi-parameter optical sensing platforms, and the integration of GSCF-aware models into simulation tools may accelerate the development of self-calibrating sensors, ultimately bridging the gap between theoretical electrodynamics and practical metrology.
Author Contributions
Conceptualization, T.Z. and C.L.; methodology, B.S. and R.F.; simulation, T.Z.; formal analysis, Y.C.; investigation, T.Z.; resources, W.D. and Y.F.; writing—original draft preparation, T.Z. and G.Z.; writing—review and editing, T.Z., W.D. and Y.F.; project administration, T.Z., Y.F. and W.D.; funding acquisition, Y.F. and W.D. All authors have read and agreed to the published version of the manuscript.
Funding
T. Zhu acknowledges the financial support from the National Natural Science Foundation of China (Grants No. 12104083). C. Li acknowledges the financial support from the Natural Science Foundation of Zhejiang Province (Grant No. LQ22A040010) and the National Natural Science Foundation of China (Grant No. 12304545). Y. Fang acknowledges the financial support from the National Natural Science Foundation of China (Grant No. 12274054). W. Ding acknowledges the financial support from the Heilongjiang Natural Science Funds for Distinguished Young Scholar (Grant No. JQ2022A001).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ashkin, A. Acceleration and trapping of particles by radiation pressure. Phys. Rev. Lett. 1970, 24, 156. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef]
- Chen, J.; Ng, J.; Lin, Z.; Chan, C.T. Optical pulling force. Nat. Photonics 2011, 5, 531–534. [Google Scholar] [CrossRef]
- Tanaka, Y.Y.; Albella, P.; Rahmani, M.; Giannini, V.; Maier, S.A.; Shimura, T. Plasmonic linear nanomotor using lateral optical forces. Sci. Adv. 2020, 6, eabc3726. [Google Scholar] [CrossRef] [PubMed]
- Yamanishi, J.; Yamane, H.; Naitoh, Y.; Li, Y.J.; Yokoshi, N.; Kameyama, T.; Koyama, S.; Torimoto, T.; Ishihara, H.; Sugawara, Y. Optical force mapping at the single-nanometre scale. Nat. Commun. 2021, 12, 3865. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Li, Y.; Xu, B.; Wang, X.; Zhang, L.; Chen, J.; Lin, Z.; Chan, C.T. Anomalous lateral optical force as a manifestation of the optical transverse spin. Laser Photonics Rev. 2023, 17, 2300212. [Google Scholar] [CrossRef]
- Yamanishi, J.; Ahn, H.Y.; Yamane, H.; Hashiyada, S.; Ishihara, H.; Nam, K.T.; Okamoto, H. Optical gradient force on chiral particles. Sci. Adv. 2022, 8, eabq2604. [Google Scholar] [CrossRef]
- Yamanishi, J.; Ahn, H.Y.; Okamoto, H. Nanoscopic observation of chiro-optical force. Nano Lett. 2023, 23, 9347–9352. [Google Scholar] [CrossRef]
- Li, T.; Xu, X.; Fu, B.; Wang, S.; Li, B.; Wang, Z.; Zhu, S. Integrating the optical tweezers and spanner onto an individual single-layer metasurface. Photonics Res. 2021, 9, 1062–1068. [Google Scholar] [CrossRef]
- Shan, X.; Ding, L.; Wang, D.; Wen, S.; Shi, J.; Chen, C.; Wang, Y.; Zhu, H.; Huang, Z.; Wang, S.S.; et al. Sub-femtonewton force sensing in solution by super-resolved photonic force microscopy. Nat. Photonics 2024, 18, 913–921. [Google Scholar] [CrossRef]
- Fernández, P.A.; Buchmann, B.; Goychuk, A.; Engelbrecht, L.K.; Raich, M.K.; Scheel, C.H.; Frey, E.; Bausch, A.R. Surface-tensioninduced budding drives alveologenesis in human mammary gland organoids. Nat. Phys. 2021, 17, 1130–1136. [Google Scholar] [CrossRef]
- Xin, H.; Zhao, N.; Wang, Y.; Zhao, X.; Pan, T.; Shi, Y.; Li, B. Optically controlled living micromotors for the manipulation and disruption of biological targets. Nano Lett. 2020, 20, 7177–7185. [Google Scholar] [CrossRef]
- Xin, H.; Li, Y.; Liu, Y.C.; Zhang, Y.; Xiao, Y.F.; Li, B. Optical forces: From fundamental to biological applications. Adv. Mater. 2020, 32, 2001994. [Google Scholar] [CrossRef]
- Jazayeri, A.M.; Mehrany, K. Critical study and discrimination of different formulations of electromagnetic force density and consequent stress tensors inside matter. Phys. Rev. A 2014, 89, 043845. [Google Scholar] [CrossRef]
- Antonoyiannakis, M.; Pendry, J. Electromagnetic forces in photonic crystals. Phys. Rev. B 1999, 60, 2363. [Google Scholar] [CrossRef]
- Kemp, B.A.; Grzegorczyk, T.M.; Kong, J.A. Ab initio study of the radiation pressure on dielectric and magnetic media. Opt. Express 2005, 13, 9280–9291. [Google Scholar] [CrossRef] [PubMed]
- Kemp, B.A.; Grzegorczyk, T.M.; Kong, J.A. Optical momentum transfer to absorbing Mie particles. Phys. Rev. Lett. 2006, 97, 133902. [Google Scholar] [CrossRef] [PubMed]
- Brevik, I. Experiments in phenomenological electrodynamics and the electromagnetic energy-momentum tensor. Phys. Rep. 1979, 52, 133–201. [Google Scholar] [CrossRef]
- Mansuripur, M. Electromagnetic stress tensor in ponderable media. Opt. Express 2008, 16, 5193–5198. [Google Scholar] [CrossRef]
- Mansuripur, M. Trouble with the Lorentz Law of Force: Incompatibility with Special Relativity and Momentum Conservation. Phys. Rev. Lett. 2012, 108, 193901. [Google Scholar] [CrossRef]
- Barnett, S.M. Comment on “Trouble with the Lorentz law of force: Incompatibility with special relativity and momentum conservation”. Phys. Rev. Lett. 2013, 110, 089402. [Google Scholar] [CrossRef]
- Khorrami, M. Comment on “Trouble with the Lorentz Law of Force: Incompatibility with Special Relativity and Momentum Conservation”. Phys. Rev. Lett. 2013, 110, 089404. [Google Scholar] [CrossRef] [PubMed]
- Saldanha, P.L. Comment on “Trouble with the Lorentz law of force: Incompatibility with special relativity and momentum conservation”. Phys. Rev. Lett. 2013, 110, 089403. [Google Scholar] [CrossRef] [PubMed]
- Vanzella, D.A. Comment on “Trouble with the Lorentz law of force: Incompatibility with special relativity and momentum conservation”. Phys. Rev. Lett. 2013, 110, 089401. [Google Scholar] [CrossRef] [PubMed]
- Albaladejo, S.; Marqués, M.I.; Laroche, M.; Sáenz, J.J. Scattering forces from the curl of the spin angular momentum of a light field. Phys. Rev. Lett. 2009, 102, 113602. [Google Scholar] [CrossRef]
- Ruffner, D.B.; Grier, D.G. Optical forces and torques in nonuniform beams of light. Phys. Rev. Lett. 2012, 108, 173602. [Google Scholar] [CrossRef]
- Qin, J.; Jiang, S.; Wang, Z.; Cheng, X.; Li, B.; Shi, Y.; Tsai, D.P.; Liu, A.Q.; Huang, W.; Zhu, W. Metasurface micro/nano-optical sensors: Principles and applications. ACS Nano 2022, 16, 11598–11618. [Google Scholar] [CrossRef]
- Ferreira, M.F.; Brambilla, G.; Thévenaz, L.; Feng, X.; Zhang, L.; Sumetsky, M.; Jones, C.; Pedireddy, S.; Vollmer, F.; Dragic, P.D.; et al. Roadmap on optical sensors. J. Opt. 2023, 26, 013001. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, M.; Yinguo, H.; Zhang, H.; Guo, N.; Zheng, Y. Micro-force sensing techniques and traceable reference forces: A review. Meas. Sci. Technol. 2022, 33, 114010. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Melia, F. Electrodynamics; University of Chicago Press: Chicago, IL, USA, 2020. [Google Scholar]
- Chen, H.C. Theory of Electromagnetic Waves: A Coordinate-Free Approach; McGraw-Hill Book Co.: Columbus, OH, USA, 1983. [Google Scholar]
- Lebedev, L.P.; Cloud, M.J.; Eremeyev, V.A. Tensor Analysis with Applications in Mechanics; World Scientific: Singapore, 2010. [Google Scholar]
- Berry, M.V. Optical currents. J. Opt. A Pure Appl. Opt. 2009, 11, 094001. [Google Scholar] [CrossRef]
- Neugebauer, M.; Bauer, T.; Aiello, A.; Banzer, P. Measuring the transverse spin density of light. Phys. Rev. Lett. 2015, 114, 063901. [Google Scholar] [CrossRef]
- Kemp, B.; Grzegorczyk, T.; Kong, J. Lorentz force on dielectric and magnetic particles. J. Electromagn. Waves Appl. 2006, 20, 827–839. [Google Scholar] [CrossRef]
- Mahdy, M.R.C.; Gao, D.; Ding, W.; Mehmood, M.Q.; Nieto-Vesperinas, M.; Qiu, C.W. A unified theory correcting Einstein-Laub electrodynamics solves dilemmas in the photon momenta and electromagnetic stress tensors. arXiv 2015, arXiv:1509.06971. [Google Scholar] [CrossRef]
- Sun, W.; Wang, S.; Ng, J.; Zhou, L.; Chan, C.T. Analytic derivation of electrostrictive tensors and their application to optical force density calculations. Phys. Rev. B 2015, 91, 235439. [Google Scholar] [CrossRef]
- Cui, L.; Wang, N.; Ng, J. Computation of internal optical forces using the Helmholtz tensor. Phys. Rev. A 2021, 104, 013508. [Google Scholar] [CrossRef]
- Li, M.; Pernice, W.; Xiong, C.; Baehr-Jones, T.; Hochberg, M.; Tang, H. Harnessing optical forces in integrated photonic circuits. Nature 2008, 456, 480–484. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).