RGB-Based Visual–Inertial Odometry via Knowledge Distillation from Self-Supervised Depth Estimation with Foundation Models
Abstract
1. Introduction
2. Related Work
3. Method
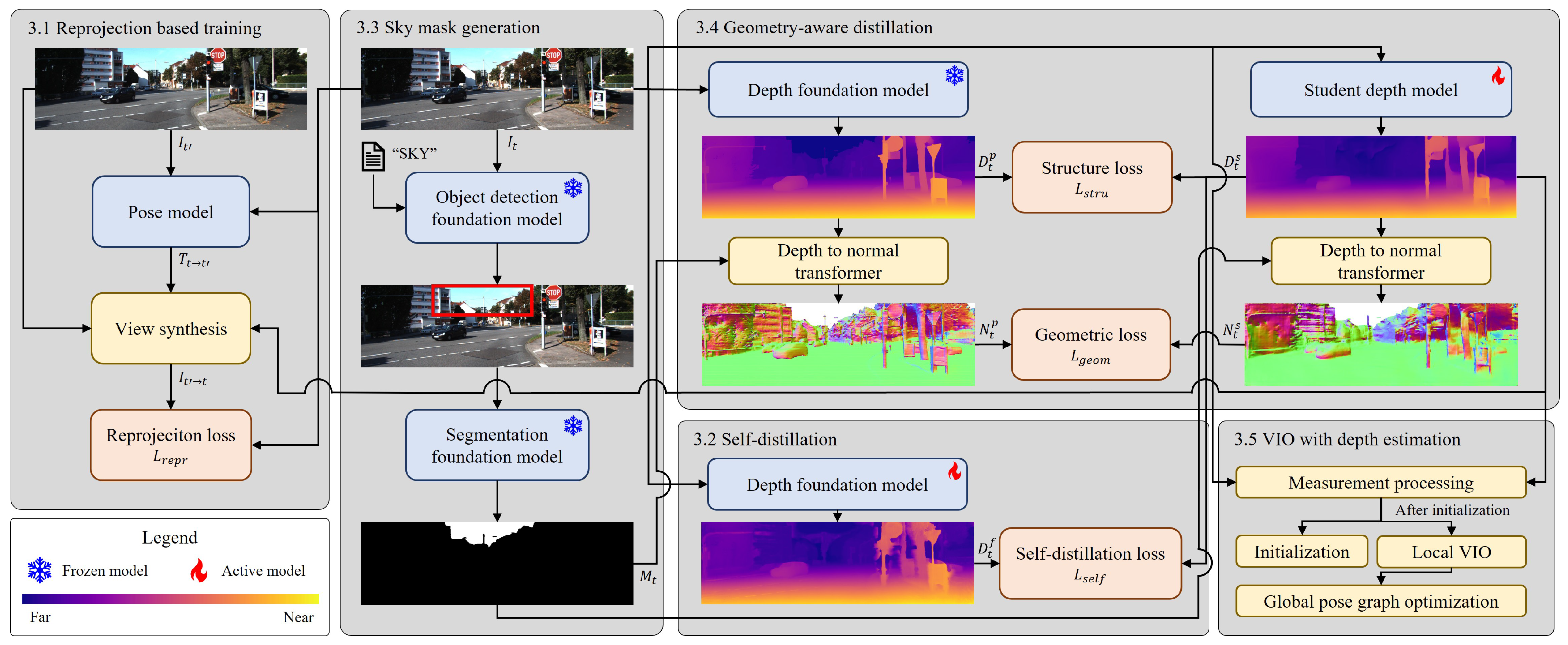
3.1. Image Reprojection Based Training
3.2. Self-Distillation of Dense Prediction Transformer
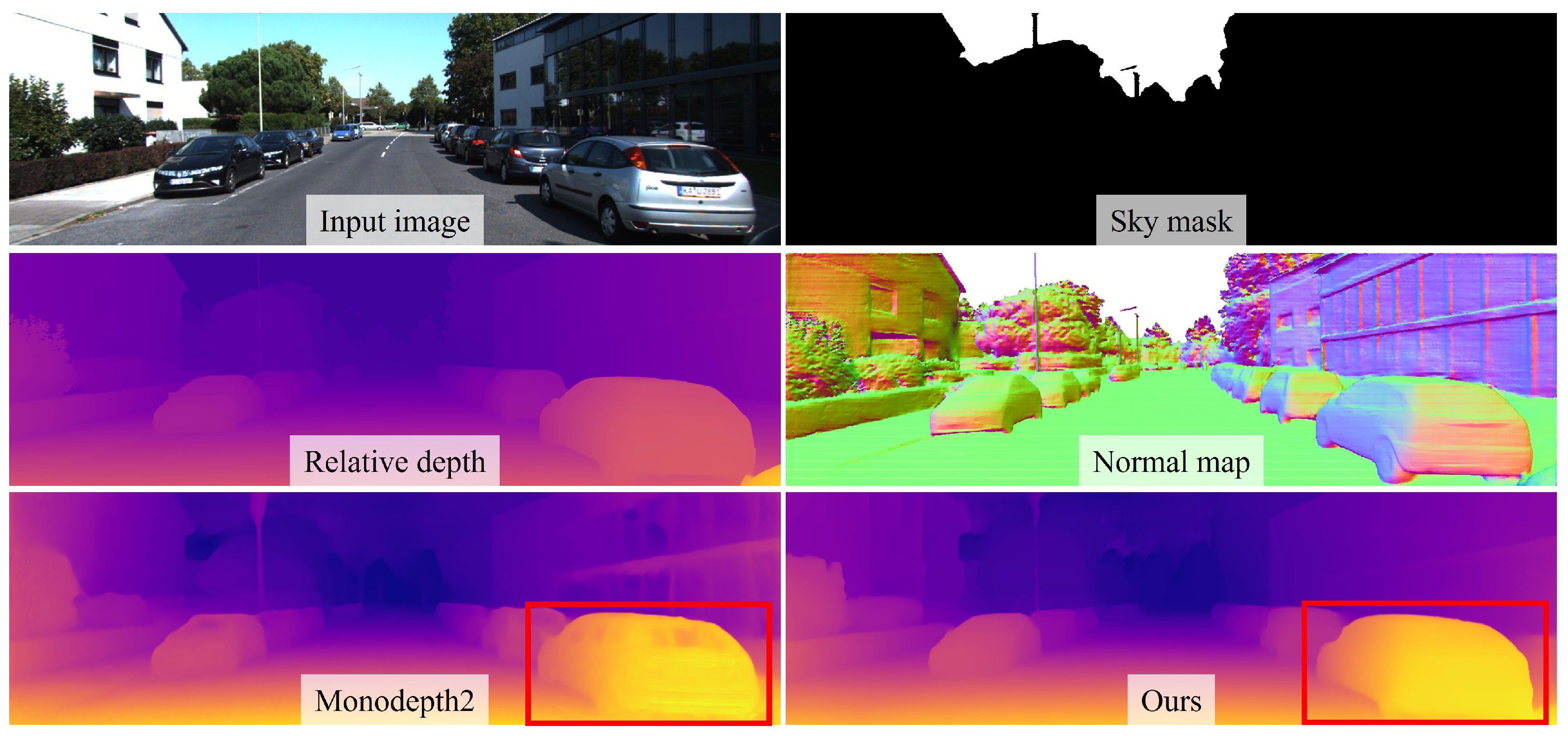
3.3. Sky Mask Generation via Foundation Model
3.4. Geometry-Aware Knowledge Distillation
3.5. VIO with Depth Estimation
4. Experiments
4.1. Experimental Setup
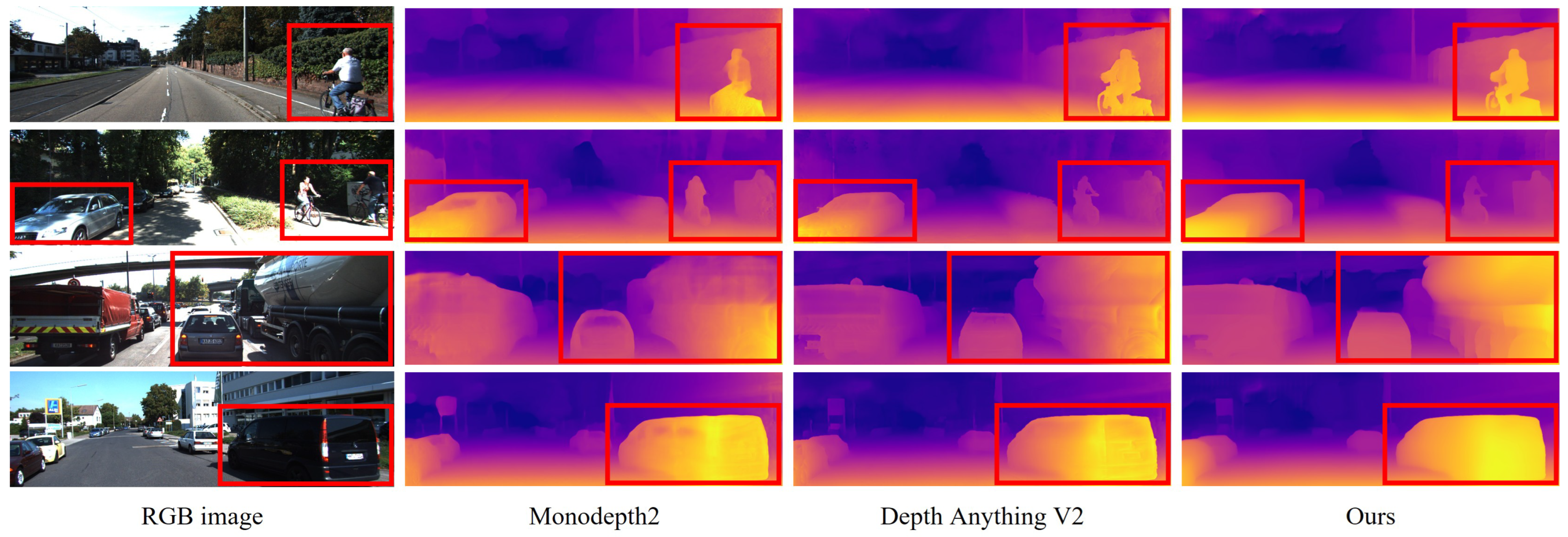
4.2. KITTI Dataset
4.3. Campus Driving Dataset
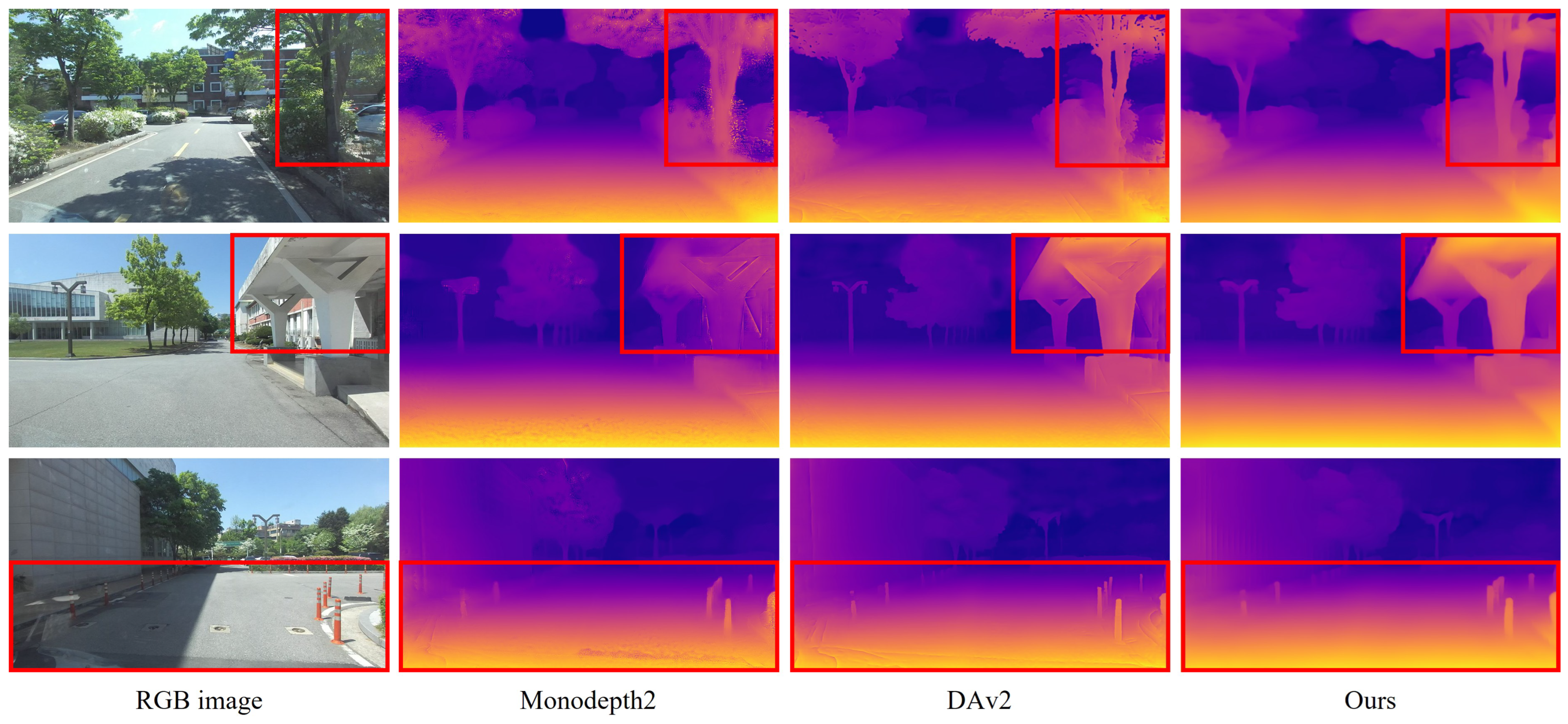
4.4. Zero-Shot Depth Estimation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zou, Z.; Chen, K.; Shi, Z.; Guo, Y.; Ye, J. Object detection in 20 years: A survey. Proc. IEEE 2023, 111, 257–276. [Google Scholar] [CrossRef]
- Minaee, S.; Boykov, Y.; Porikli, F.; Plaza, A.; Kehtarnavaz, N.; Terzopoulos, D. Image segmentation using deep learning: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3523–3542. [Google Scholar] [CrossRef]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth map prediction from a single image using a multi-scale deep network. Adv. Neural Inf. Process. Syst. 2014, 27, 2366–2374. [Google Scholar]
- Cheng, J.; Cheng, H.; Meng, M.Q.; Zhang, H. Autonomous navigation by mobile robots in human environments: A survey. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 1981–1986. [Google Scholar]
- Chang, Y.; Cheng, Y.; Manzoor, U.; Murray, J. A review of UAV autonomous navigation in GPS-denied environments. Robot. Auton. Syst. 2023, 170, 104533. [Google Scholar] [CrossRef]
- Shao, S.; Pei, Z.; Chen, W.; Zhang, B.; Wu, X.; Sun, D.; Doermann, D. Self-supervised learning for monocular depth estimation on minimally invasive surgery scenes. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 7159–7165. [Google Scholar]
- Liu, S.; Zeng, Z.; Ren, T.; Li, F.; Zhang, H.; Yang, J.; Jiang, Q.; Li, C.; Yang, J.; Su, H.; et al. Grounding dino: Marrying dino with grounded pre-training for open-set object detection. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 2 September–4 October 2024; pp. 38–55. [Google Scholar]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.; et al. Segment anything. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 4015–4026. [Google Scholar]
- Yang, L.; Kang, B.; Huang, Z.; Zhao, Z.; Xu, X.; Feng, J.; Zhao, H. Depth anything v2. Adv. Neural Inf. Process. Syst. 2024, 37, 21875–21911. [Google Scholar]
- Godard, C.; Mac, A.O.; Firman, M.; Brostow, G.J. Digging into self-supervised monocular depth estimation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3828–3838. [Google Scholar]
- Wang, Y.; Li, X.; Shi, M.; Xian, K.; Cao, Z. Knowledge distillation for fast and accurate monocular depth estimation on mobile devices. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021; pp. 2457–2465. [Google Scholar]
- Pilzer, A.; Lathuiliere, S.; Sebe, N.; Ricci, E. Refine and distill: Exploiting cycle-inconsistency and knowledge distillation for unsupervised monocular depth estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 9768–9777. [Google Scholar]
- Poggi, M.; Aleotti, F.; Tosi, F.; Mattoccia, S. On the uncertainty of self-supervised monocular depth estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 14–19 June 2020; pp. 3227–3237. [Google Scholar]
- Song, J.; Lee, S.J. Knowledge distillation of multi-scale dense prediction transformer for self-supervised depth estimation. Sci. Rep. 2023, 13, 18939. [Google Scholar] [CrossRef] [PubMed]
- Oquab, M.; Darcet, T.; Moutakanni, T.; Vo, H.; Szafraniec, M.; Khalidov, V.; Fernandez, P.; Haziza, D.; Massa, F.; El-Nouby, A.; et al. Dinov2: Learning robust visual features without supervision. arXiv 2023, arXiv:2304.07193. [Google Scholar]
- Ren, T.; Liu, S.; Zeng, A.; Lin, J.; Li, K.; Cao, H.; Chen, J.; Huang, X.; Chen, Y.; Yan, F.; et al. Grounded sam: Assembling open-world models for diverse visual tasks. arXiv 2024, arXiv:2401.14159. [Google Scholar] [CrossRef]
- Ranftl, R.; Bochkovskiy, A.; Koltun, V. Vision transformers for dense prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 12179–12188. [Google Scholar]
- Bai, C.; Xiao, T.; Chen, Y.; Wang, H.; Zhang, F.; Gao, X. Faster-LIO: Lightweight tightly coupled LiDAR-inertial odometry using parallel sparse incremental voxels. IEEE Robot. Autom. Lett. 2022, 7, 4861–4868. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.; Shen, S. Vins-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Shan, Z.; Li, R.; Schwertfeger, S. RGBD-inertial trajectory estimation and mapping for ground robots. Sensors 2019, 19, 2251. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16×16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Feng, Y.; Xue, B.; Liu, M.; Chen, Q.; Fan, R. D2nt: A high-performing depth-to-normal translator. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 12360–12366. [Google Scholar]
- Shi, J.; Tomasi. Good features to track. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 21–23 June 1994; pp. 593–600. [Google Scholar]
- Lucas, B.D.; Kanade, T. An iterative image registration technique with an application to stereo vision. In Proceedings of the International Joint Conference on Artificial Intelligence, Vancouver, BC, Canada, 24–28 August 1981; pp. 674–679. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 8024–8035. [Google Scholar]
- Bradski, G. The OpenCV Library. Dr. Dobb’s J. Softw. Tools Prof. Program. 2000, 25, 120–123. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura, Algarve, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? the kitti vision benchmark suite. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Tsai, D.; Worrall, S.; Shan, M.; Lohr, A.; Nebot, E. Optimising the selection of samples for robust lidar camera calibration. In Proceedings of the IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 2631–2638. [Google Scholar]
- Silberman, N.; Hoiem, D.; Kohli, P.; Fergus, R. Indoor segmentation and support inference from rgbd images. In Proceedings of the European Conference on Computer Vision, Firenze, Italy, 7–13 October 2012; pp. 746–760. [Google Scholar]

| Method | Params | Error Metrics ↓ | Accuracy Metrics ↑ | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SIlog | AbsRel | SqRel | RMSE | RMSEi | log10 | |||||
| Monodepth2 [10] | 14.8 M | 18.293 | 0.109 | 0.832 | 4.648 | 0.186 | 0.048 | 0.888 | 0.963 | 0.982 |
| DAv2(vits) [9] | 24.7 M | 16.994 | 0.099 | 0.740 | 4.314 | 0.173 | 0.043 | 0.908 | 0.969 | 0.985 |
| Ours | 24.7 M | 16.856 | 0.101 | 0.687 | 4.280 | 0.172 | 0.044 | 0.899 | 0.969 | 0.986 |
| DAv2(vitl) [9] | 335.3 M | 16.406 | 0.090 | 0.639 | 4.040 | 0.166 | 0.040 | 0.924 | 0.971 | 0.985 |
| SIlog ↓ | AbsRel ↓ | RMSE ↓ | ↑ | ||||
|---|---|---|---|---|---|---|---|
| ✓ | 19.688 | 0.118 | 5.230 | 0.853 | |||
| ✓ | ✓ | 18.926 | 0.120 | 5.055 | 0.852 | ||
| ✓ | ✓ | 18.872 | 0.121 | 5.067 | 0.854 | ||
| ✓ | ✓ | 18.70 | 0.115 | 5.024 | 0.861 | ||
| ✓ | ✓ | ✓ | ✓ | 18.521 | 0.119 | 5.017 | 0.861 |
| Method | Error Metrics ↓ | Accuracy Metrics ↑ | |||||||
|---|---|---|---|---|---|---|---|---|---|
| SIlog | AbsRel | SqRel | RMSE | RMSEi | log10 | ||||
| Monodepth2 [10] | 19.448 | 0.121 | 0.810 | 3.106 | 0.197 | 0.049 | 0.886 | 0.956 | 0.979 |
| DAv2(vits) [9] | 17.883 | 0.096 | 0.777 | 2.997 | 0.181 | 0.039 | 0.918 | 0.964 | 0.980 |
| Ours | 17.631 | 0.097 | 0.712 | 2.857 | 0.180 | 0.041 | 0.903 | 0.964 | 0.981 |
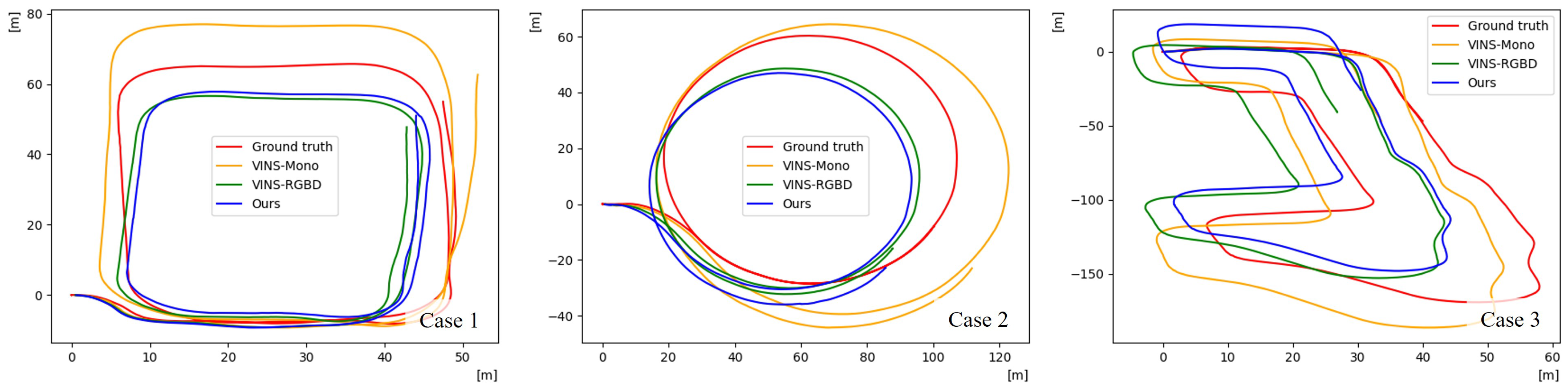
| Driving Scenario | Case 1 | Case 2 | Case 3 | Average | |
|---|---|---|---|---|---|
| Driving Distance [m] | 318.12 | 394.75 | 502.55 | ||
| RMSE of ATE [m] | VINS-Mono [19] | 4.9564 | 8.2617 | 7.8689 | 7.0290 |
| Ours | 4.1027 | 5.2186 | 7.0312 | 5.4508 | |
| VINS-RGBD [20] | 4.3050 | 4.7788 | 6.1443 | 5.0760 | |
| Translation error of RPE [m] | VINS-Mono [19] | 0.3712 | 0.6332 | 0.3648 | 0.4564 |
| Ours | 0.3993 | 0.4627 | 0.3921 | 0.4180 | |
| VINS-RGBD [20] | 0.3957 | 0.4092 | 0.3399 | 0.3816 | |
| Rotation error of RPE [deg] | VINS-Mono [19] | 0.3116 | 0.2635 | 0.3291 | 0.3014 |
| Ours | 0.3319 | 0.3666 | 0.3733 | 0.3573 | |
| VINS-RGBD [20] | 0.2975 | 0.2959 | 0.3440 | 0.3125 | |
| Method | Error Metrics ↓ | Accuracy Metrics ↑ | |||||||
|---|---|---|---|---|---|---|---|---|---|
| SIlog | AbsRel | SqRel | RMSE | RMSEi | log10 | ||||
| Monodepth2 [10] | 35.065 | 0.336 | 0.498 | 1.079 | 0.370 | 0.129 | 0.484 | 0.778 | 0.913 |
| DAv2-pre [9] | 35.086 | 0.326 | 0.787 | 1.602 | 0.365 | 0.124 | 0.515 | 0.772 | 0.981 |
| DAv2-fine [9] | 19.446 | 0.163 | 0.160 | 0.702 | 0.203 | 0.068 | 0.759 | 0.958 | 0.990 |
| Ours | 19.464 | 0.166 | 0.140 | 0.661 | 0.203 | 0.070 | 0.732 | 0.966 | 0.996 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Lee, S.J. RGB-Based Visual–Inertial Odometry via Knowledge Distillation from Self-Supervised Depth Estimation with Foundation Models. Sensors 2025, 25, 5366. https://doi.org/10.3390/s25175366
Song J, Lee SJ. RGB-Based Visual–Inertial Odometry via Knowledge Distillation from Self-Supervised Depth Estimation with Foundation Models. Sensors. 2025; 25(17):5366. https://doi.org/10.3390/s25175366
Chicago/Turabian StyleSong, Jimin, and Sang Jun Lee. 2025. "RGB-Based Visual–Inertial Odometry via Knowledge Distillation from Self-Supervised Depth Estimation with Foundation Models" Sensors 25, no. 17: 5366. https://doi.org/10.3390/s25175366
APA StyleSong, J., & Lee, S. J. (2025). RGB-Based Visual–Inertial Odometry via Knowledge Distillation from Self-Supervised Depth Estimation with Foundation Models. Sensors, 25(17), 5366. https://doi.org/10.3390/s25175366






