Investigation into the Efficient Cooperative Planning Approach for Dual-Arm Picking Sequences of Dwarf, High-Density Safflowers
Abstract
1. Introduction
- (1)
- The safflower dual-arm harvesting task is modeled as a Multiple Traveling Salesman Problem (MTSP). The K-means algorithm is used to cluster the harvesting points and divide the work areas. Combined with a load balancing strategy, tasks are assigned to the dual robotic arms, achieving cooperative path planning and zoning to reduce the risk of cross-area path conflicts.
- (2)
- A dynamic weight heuristic strategy is introduced into the Ant Colony Optimization (ACO) algorithm. By integrating heuristic information from the inverse of local distances and the inverse of node global average distances, the state transition probabilities of path planning are optimized, allowing the algorithm to dynamically balance global search and local convergence during iterations.
- (3)
- A 2-OPT local search strategy is employed to detect path crossing edges and reconstruct subpaths, eliminating redundant trajectory crossings, shortening the total length of the harvesting path, and improving the compactness and execution efficiency of path planning.
- (4)
- A parallelogram harvesting trajectory optimized based on cubic Bezier curves is designed. By adjusting the control points, the trajectory curvature continuity is optimized, smoothing discrete path points into a continuous curve, thus enhancing the trajectory smoothness and motion stability of path planning.
2. Analysis of the Picking Scenario and Design of the Dual-Arm Picking Collaborative Robot
2.1. Analysis of the Characteristics and Challenges of Safflower Picking Scenarios
- (1)
- During peak blooming, safflower distribution is random, so relying only on high-speed picking and capturing mechanisms reduces efficiency. Path planning for picking is essential.
- (2)
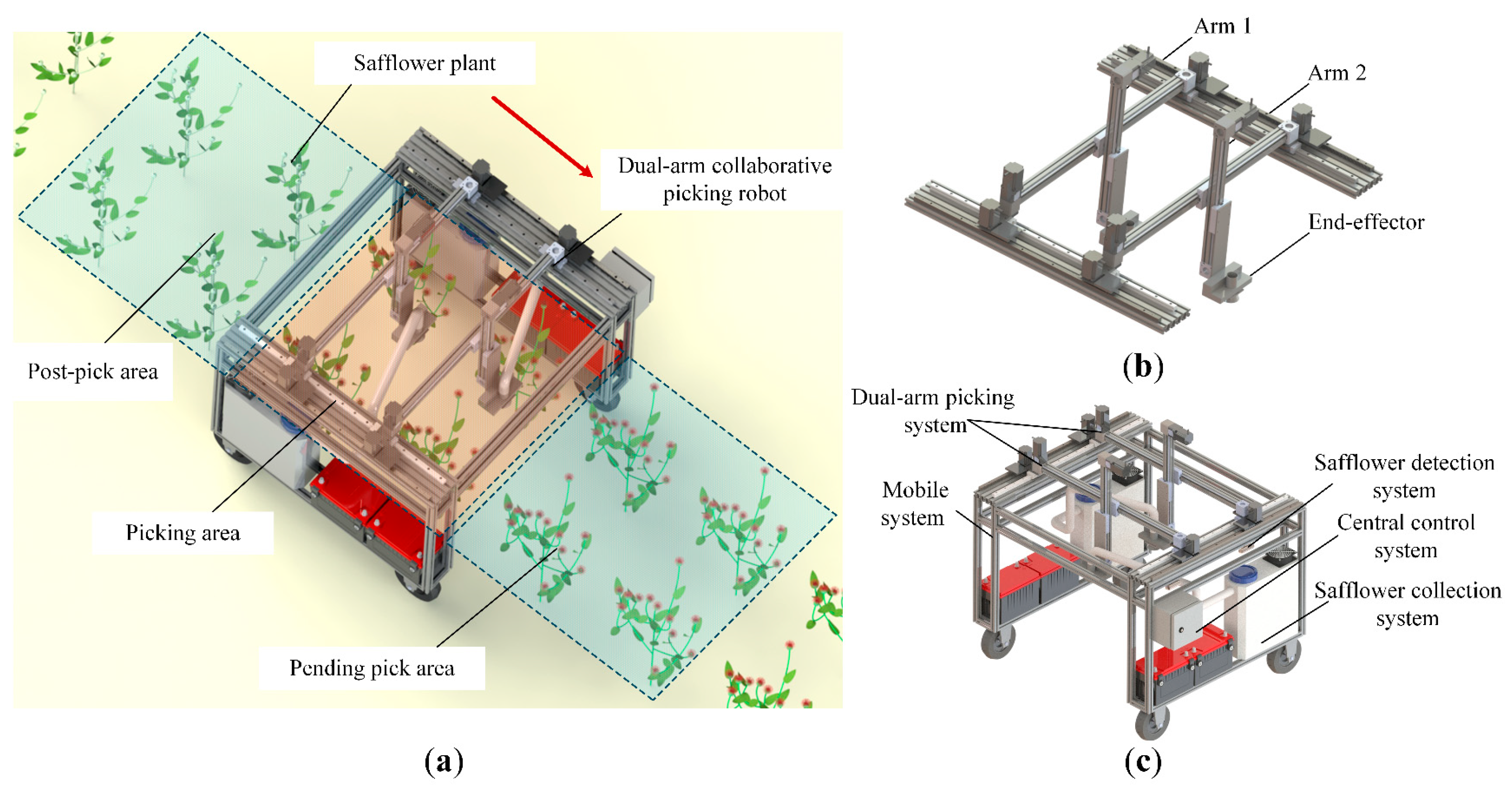
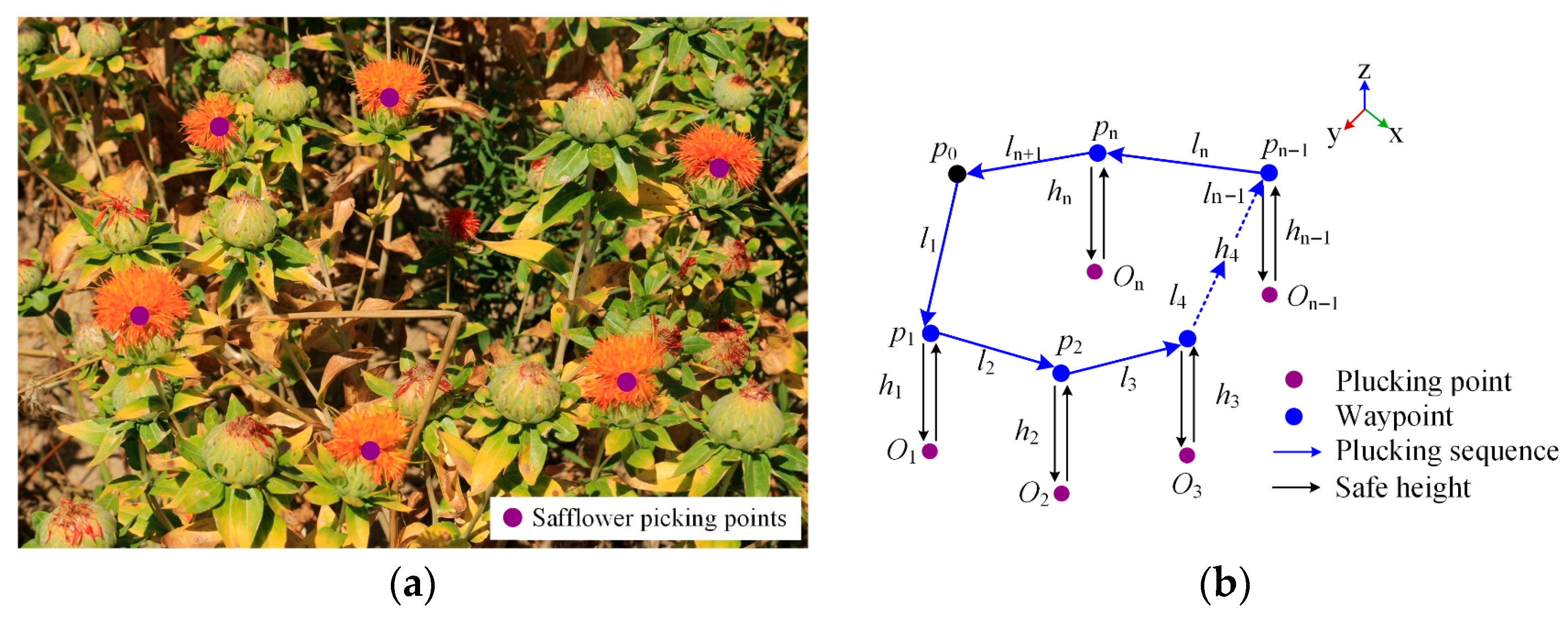
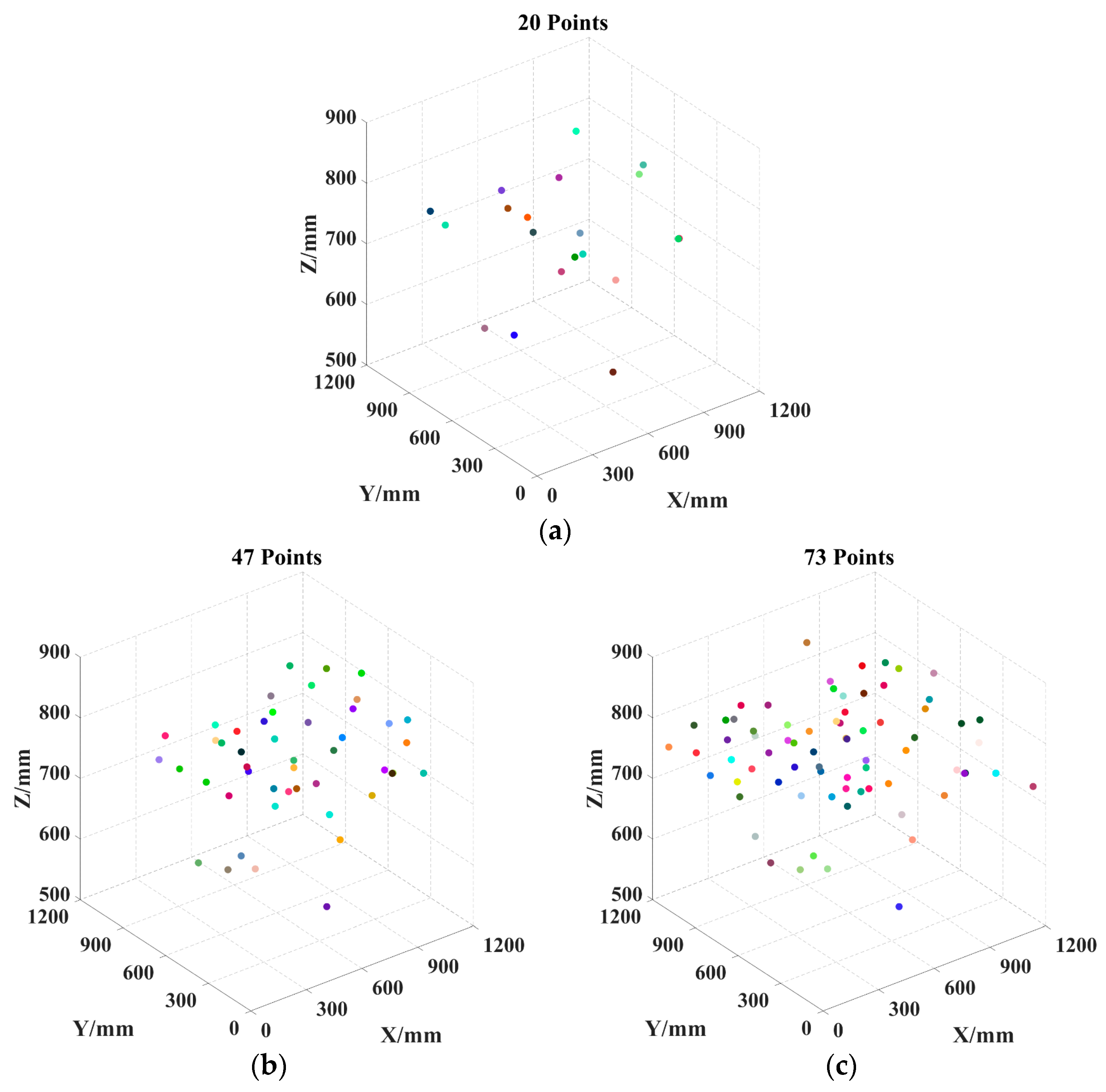
- Safflower plant height varies between 400 and 950 mm, and fruit clusters are scattered with significant height differences, as shown in Figure 1a. Single-arm picking devices struggle with multi-target picking, leading to low efficiency.
- (3)
- Safflower filaments are above the fruit clusters and scattered, requiring precise separation, as shown in Figure 1b. This scattered distribution complicates area division, causing path crossings and increasing the picking path length.
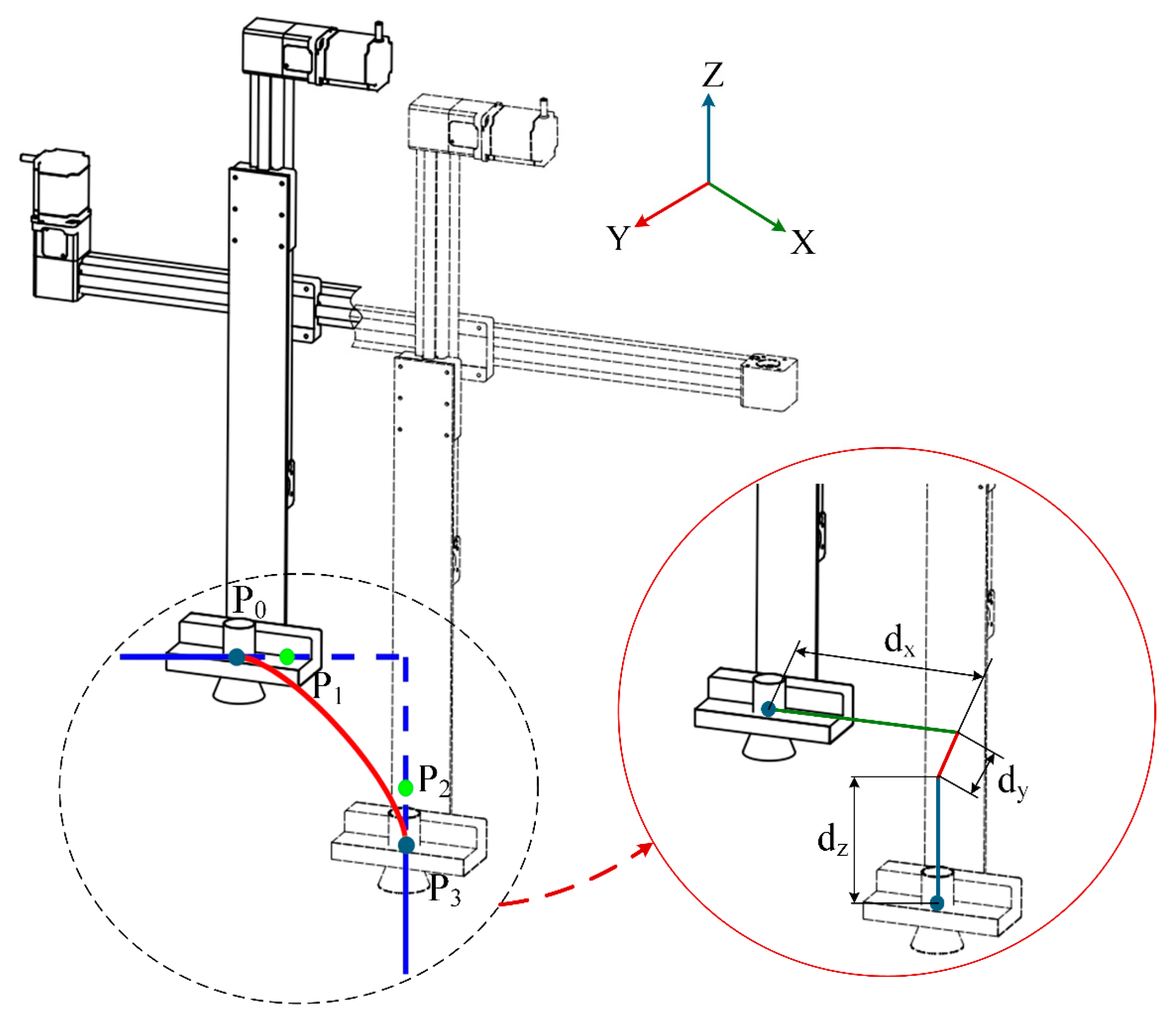
2.2. Overall Plan for the Dual-Arm Safflower Picking Robot
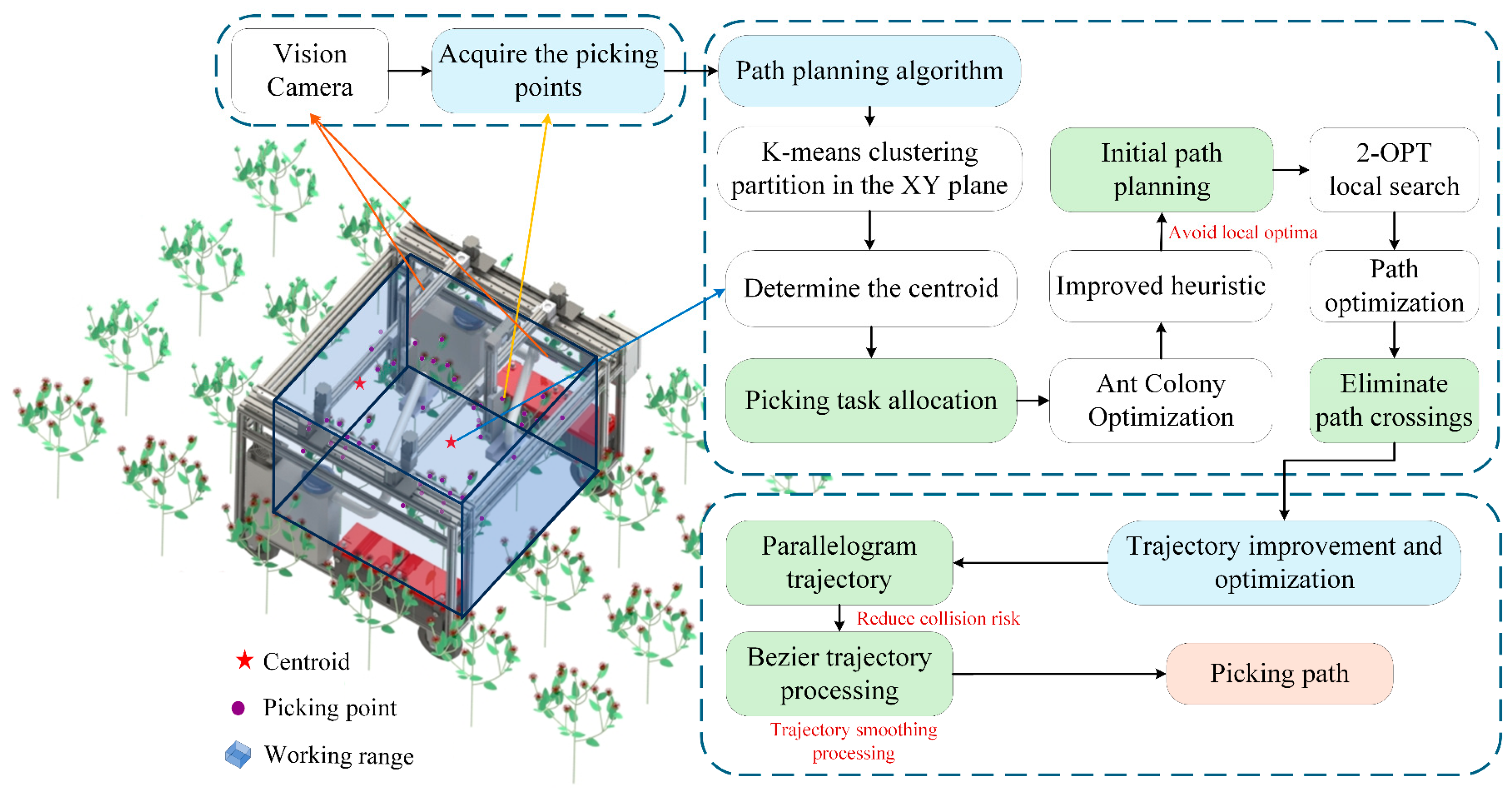
2.3. Overall Framework for Dual-Arm High-Speed Path Planning Solution
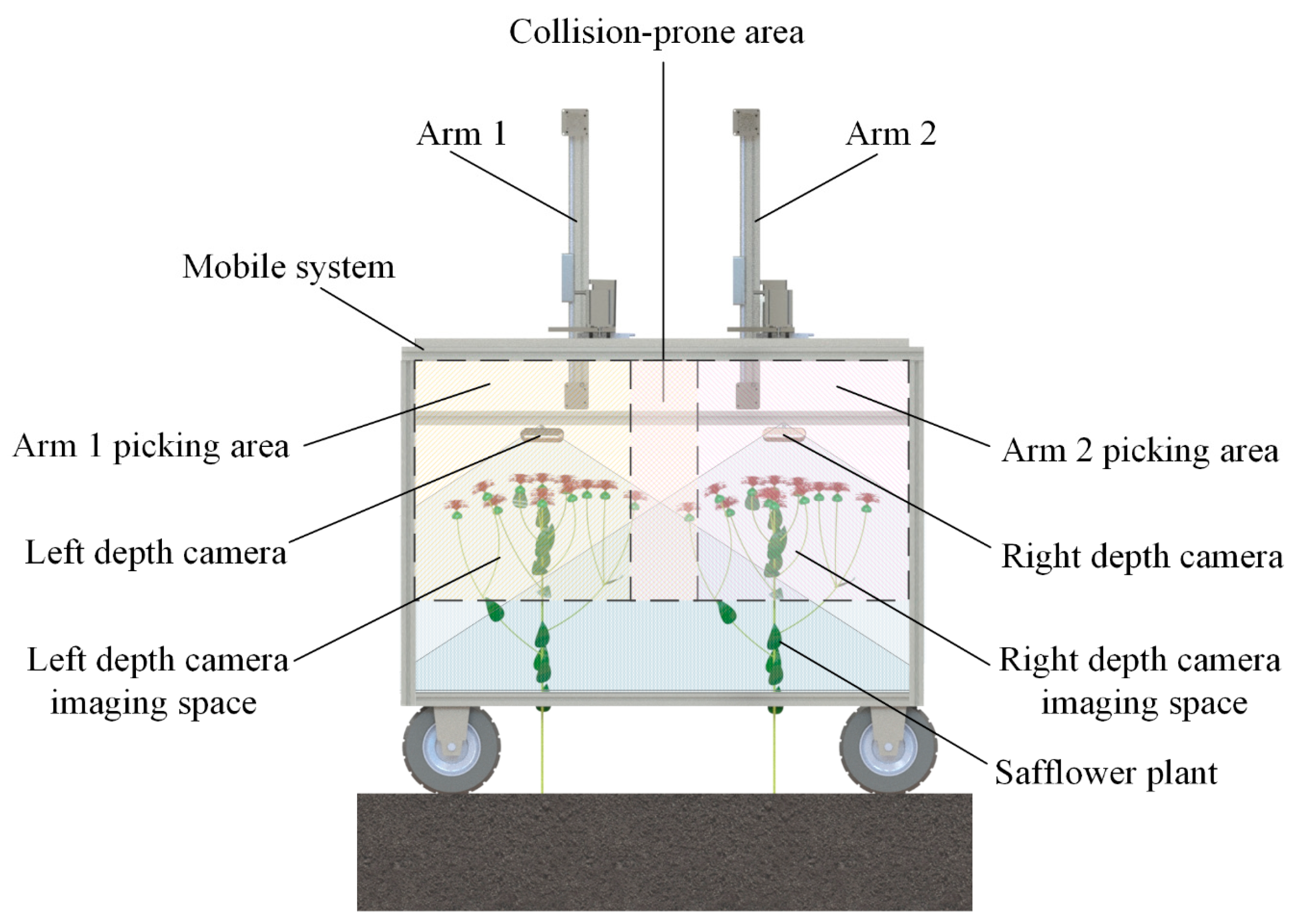
- (1)
- A region division rule is established based on safflower height fluctuations and flower cluster distribution. The work area is split into harvestable and collision-prone zones using orthogonal planes. A load balancing strategy ensures no overlap between dual-arm operations, minimizing path length and laying the groundwork for path planning.
- (2)
- The K-means algorithm clusters the discrete target points, projecting 3D points onto the x-y plane to create two sub-regions and their centroids. This enables task allocation between the robotic arms, reducing interference and providing input for the improved Ant Colony Optimization (ACO) algorithm.
- (3)
- A dynamic weight heuristic is added to improve the ACO algorithm, addressing local optimality in disorganized target points. By integrating global path information and adjusting weight factors, the path selection balances pheromone concentration and global target importance, avoiding local optima.
- (4)
- To resolve potential crossing redundancies in the preliminary paths, the 2-OPT strategy is used to optimize the path structure. By detecting crossing edges and removing/reconnecting subpaths, a better solution is generated, retaining the shortest distance options, and further enhancing the compactness and efficiency of the path.
- (5)
- A parallelogram-shaped picking trajectory is designed to reduce path distance. To address vibration issues caused by sharp turns in the path, the Bezier curve is used to smooth and optimize the parallelogram trajectory, ensuring continuous acceleration during motion and creating an efficient and stable picking trajectory.
3. Picking Sequence Planning Method
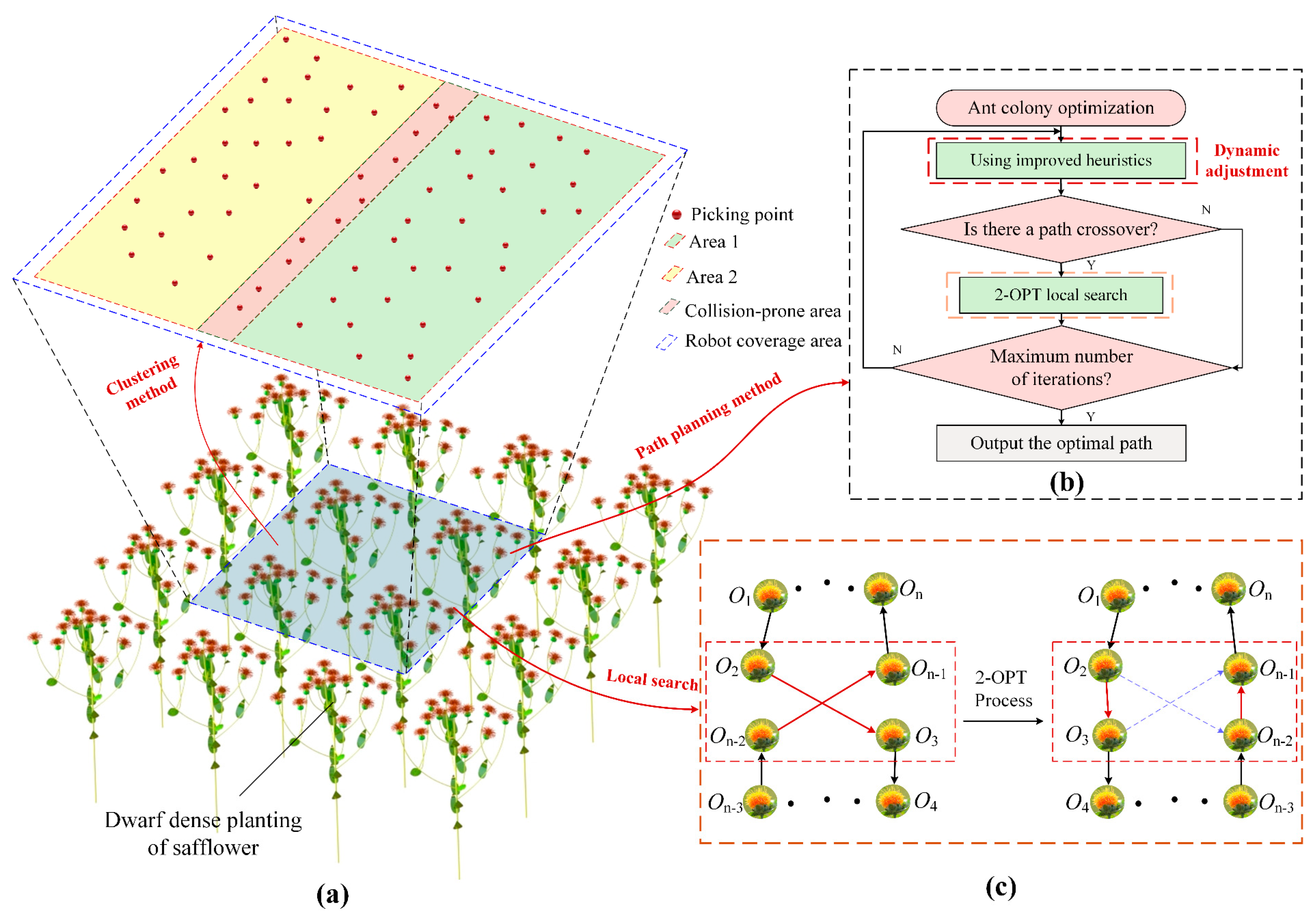
3.1. Picking Area Division Method
3.2. Safflower Picking Planning Method
3.2.1. Picking Clustering Method
3.2.2. Improved ACO Algorithm
3.2.3. 2-OPT Local Search
3.3. Improvement and Smoothing Optimization of the Picking Trajectory
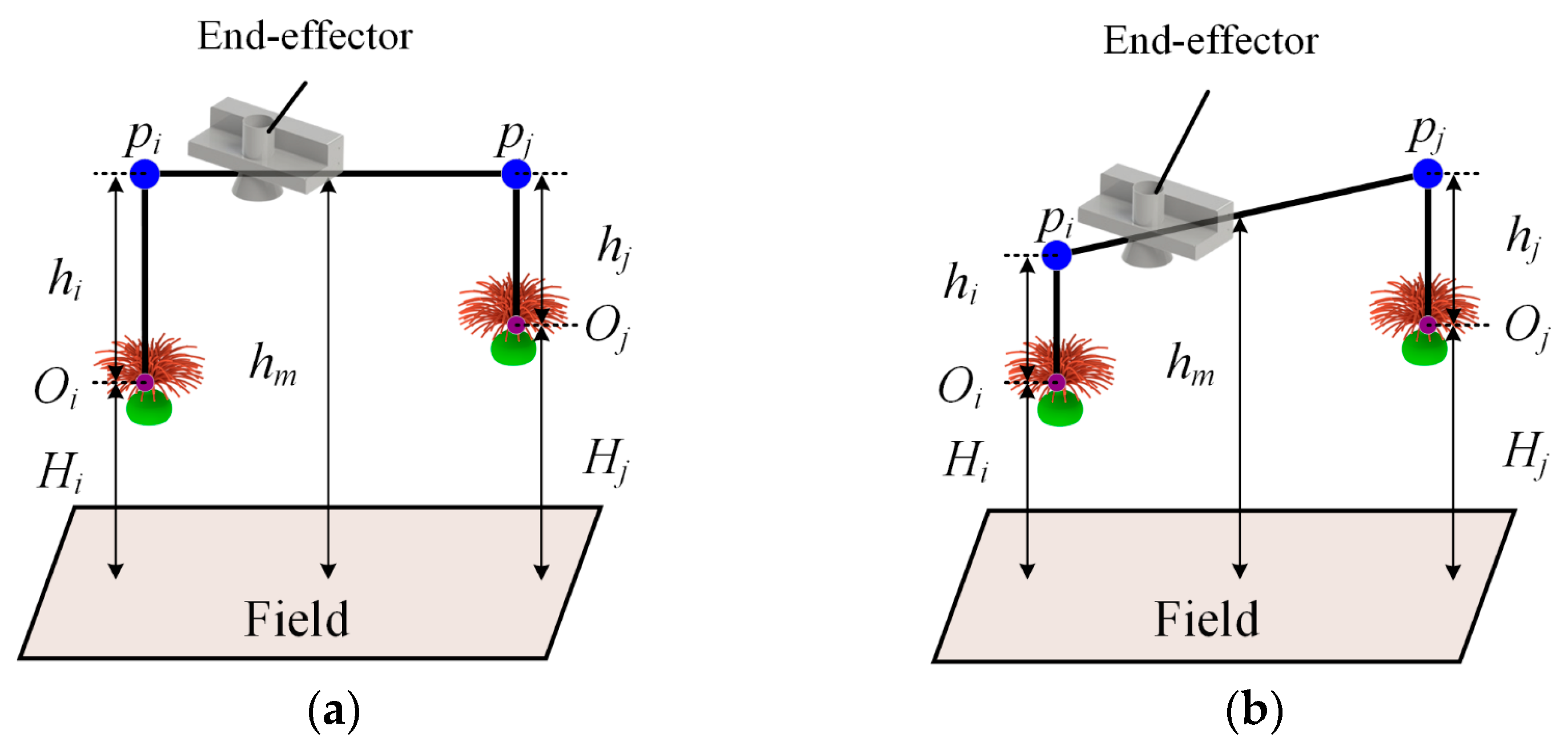
3.3.1. Improvement of the Parallelogram Trajectory
3.3.2. Cubic Bézier Curve Trajectory Optimization
3.4. Running Process of the Safflower Picking Planning Algorithm
| Algorithm 1. The LTSACO |
| Input: 3D-points, m, ρ, α, β, k, G |
| Output: Best path length, Run time |
| 1 Time start ← Run time start count |
| 2 ← K-means cluster points |
| 3 ← Euclidean distance |
| 4 ← consists distance matrix D |
| 5 for each i in [1,k] do |
| 6 Initialize heuristic matrix |
| 7 for each to G do |
| 8 Compute dynamic weight |
| 9 , , |
| 10 Compute |
| 11 |
| 12 for each ant do |
| 13 Using improved rules to improve calculations |
| 14 |
| 15 end |
| 16 Update best path, heuristic |
| 17 end |
| 18 2-OPT local search ← Remove crossing edges |
| 19 end |
| 20 Cubic Bézier cuve trajectory optimization |
| 21 Time end ← Run time stop count |
| 22 return Best path length, Run time |
- (1)
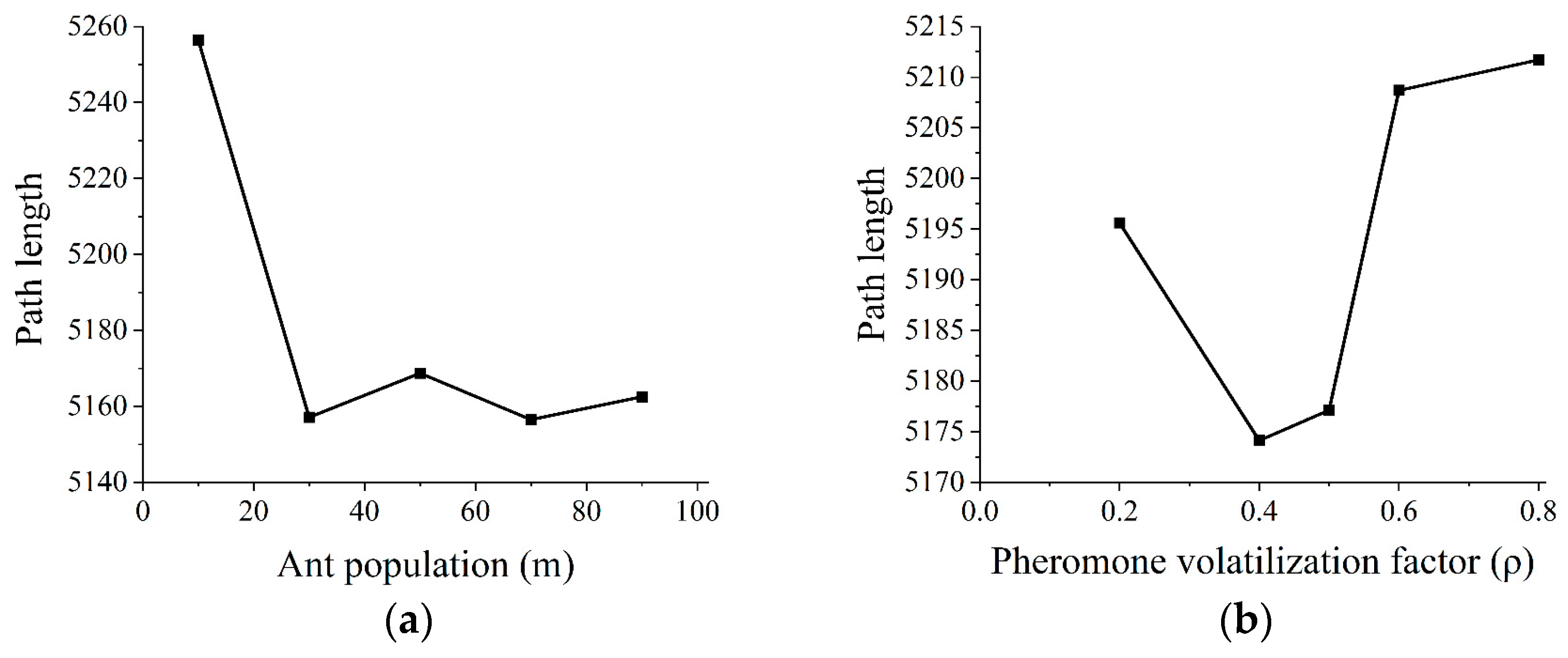
- The key parameters in the initialization algorithm are shown in Table 1.
- (2)
- Obtain the 3D coordinate data of the safflower picking points by image processing techniques, then construct a complete 3D model of the picking points based on this data to provide accurate target point information for path planning.
- (3)
- Apply the K-means clustering algorithm to divide the picking area into several sub-tasks based on the 3D Euclidean distance between picking points, with each sub-task containing multiple target picking points.
- (4)
- Optimize the decision-making process for selecting the safflower picking path by adjusting the heuristic factors, enabling the algorithm to more efficiently converge toward the optimal solution while reducing excessive pheromone concentration.
- (5)
- Use the 2-OPT local search strategy to optimize the path. By swapping two edges in the safflower picking path, this step eliminates path intersections and redundancies, shortens the total path length, and improves operational efficiency.
- (6)
- After reaching the maximum number of iterations G, output the optimized safflower picking path plan and record the optimal path information.
4. Results and Discussion
4.1. Selection of Optimal Configuration Parameters
4.2. Module Ablation Test
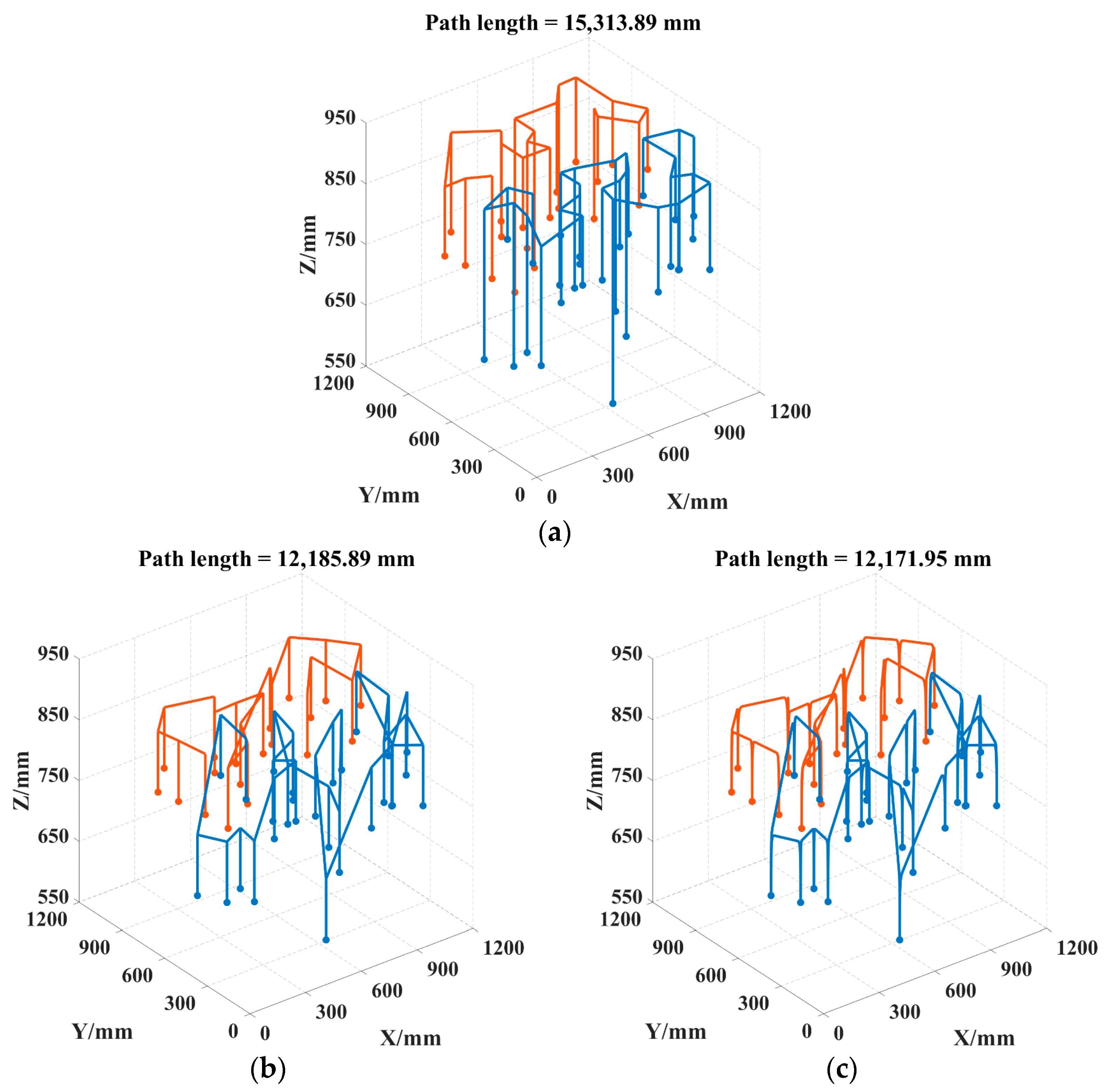
4.3. Trajectory Comparison Analysis
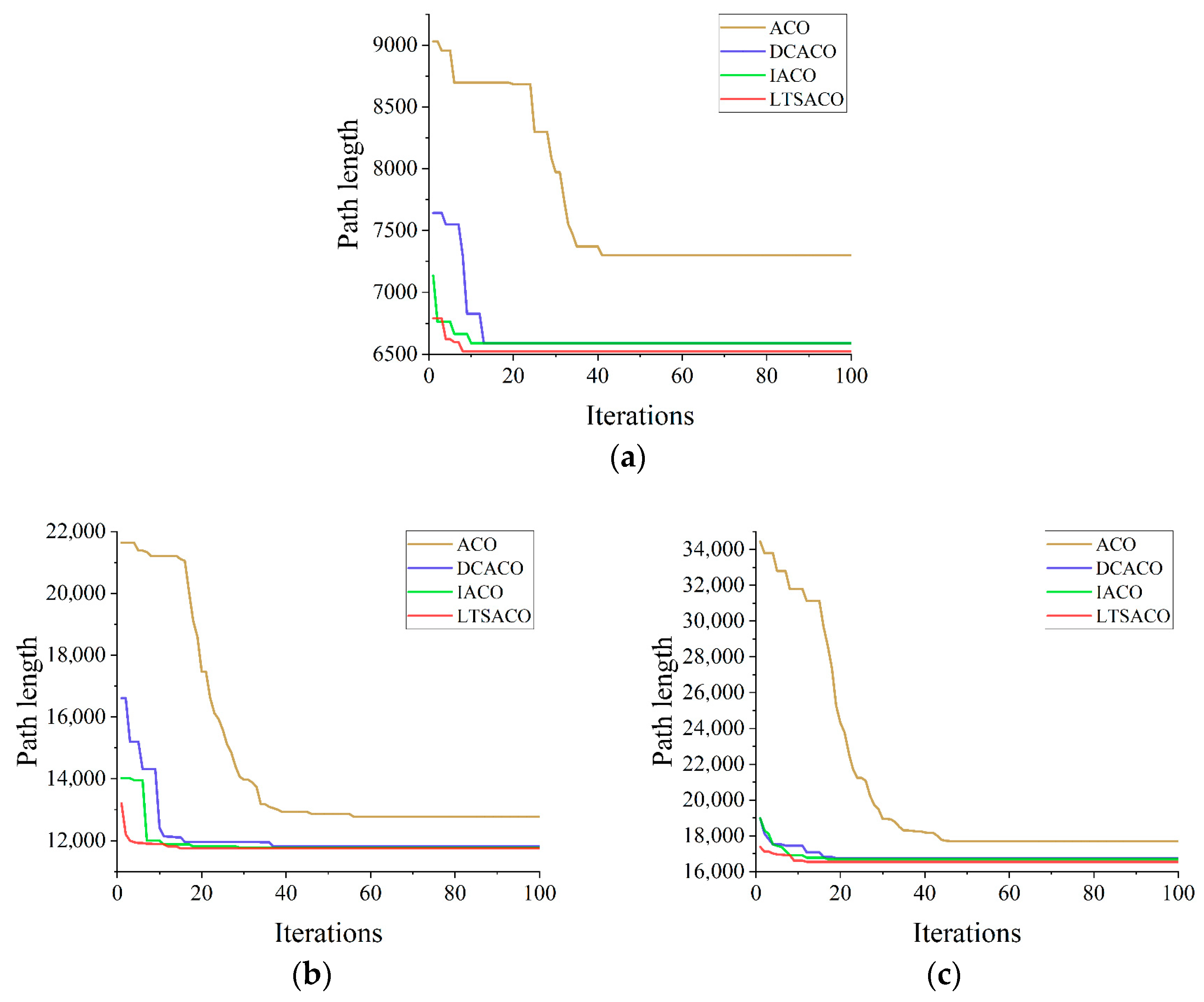
4.4. Comparison Analysis of Similar Algorithms
4.5. Picking Experiment
5. Conclusions
- (1)
- Algorithm Innovation and Optimization Effectiveness: By improving the ant colony optimization (ACO) algorithm with a dynamic weight heuristic strategy, and combining K-means clustering for task allocation with 2-OPT local search, the algorithm reduces the path length by 7.51–11.06% and shortens the picking time by 5.60% in scenarios with 20, 47, and 73 picking points. This demonstrates the effectiveness of the balance between global search and local convergence.
- (2)
- Trajectory Smoothing and Engineering Adaptation: A cubic Bézier curve is used to optimize the parallelogram trajectory, shortening the path length by 20.52% compared to the gate-shaped trajectory while ensuring curvature continuity, reducing arm vibrations, and meeting the motion stability requirements for high-density safflower picking.
- (3)
- Agricultural Scenario Adaptability: The picking task is modeled as a multi-traveling salesman problem. By incorporating 3D coordinates and load balancing strategies, the algorithm addresses challenges such as plant height differences (400–950 mm) and collision-free dual-arm collaboration. In the simulation scenarios, the standard deviation is as low as 31.64, demonstrating significant robustness.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xing, Z.; Zhang, Z.; Wang, Y.; Xu, P.; Guo, Q.; Zeng, C.; Shi, R. SDC-DeepLabv3+: Lightweight and Precise Localization Algorithm for Safflower-Harvesting Robots. Plant Phenomics 2024, 6, 0194. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Shi, R.; Xing, Z.; Guo, Q.; Zeng, C. Improved Faster Region-Based Convolutional Neural Networks (R-CNN) Model Based on Split Attention for the Detection of Safflower Filaments in Natural Environments. Agronomy 2023, 13, 2596. [Google Scholar] [CrossRef]
- Gongora, B.; de Souza, S.N.M.; Bassegio, D.; Santos, R.F.; Siqueira, J.A.C.; Bariccatti, R.A.; Gurgacz, F.; Secco, D.; Tokura, L.K.; Sequinel, R. Comparison of Emissions and Engine Performance of Safflower and Commercial Biodiesels. Ind. Crops Prod. 2022, 179, 114680. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Xu, P.; Shi, R.; Xing, Z.; Li, J. WED-YOLO: A Detection Model for Safflower Under Complex Unstructured Environment. Agriculture 2025, 15, 205. [Google Scholar] [CrossRef]
- Xing, Z.; Zhang, Z.; Shi, R.; Guo, Q.; Zeng, C. Filament-Necking Localization Method via Combining Improved PSO with Rotated Rectangle Algorithm for Safflower-Picking Robots. Comput. Electron. Agric. 2023, 215, 108464. [Google Scholar] [CrossRef]
- Williams, H.; Ting, C.; Nejati, M.; Jones, M.H.; Penhall, N.; Lim, J.Y.; Seabright, M.; Bell, J.; Ahn, H.S.; Scarfe, A.; et al. Autonomous Pollination of Individual Kiwifruit Flowers: Toward a Robotic Kiwifruit Pollinator. J. Field Robot. 2020, 37, 246–262. [Google Scholar] [CrossRef]
- Jin, T.; Han, X. Robotic Arms in Precision Agriculture: A Comprehensive Review of the Technologies, Applications, Challenges, and Future Prospects. Comput. Electron. Agric. 2024, 221, 108938. [Google Scholar] [CrossRef]
- Zhang, H.; Li, X.; Wang, L.; Liu, D.; Wang, S. Construction and Optimization of a Collaborative Harvesting System for Multiple Robotic Arms and an End-Picker in a Trellised Pear Orchard Environment. Agronomy 2024, 14, 80. [Google Scholar] [CrossRef]
- Huang, W.; Miao, Z.; Wu, T.; Guo, Z.; Han, W.; Li, T. Design of and Experiment with a Dual-Arm Apple Harvesting Robot System. Horticulturae 2024, 10, 1268. [Google Scholar] [CrossRef]
- Yin, C.; Huang, J.; Xia, Y.; Zheng, H.; Fu, W.; Zhang, B. Design, Development, Integration and Field Evaluation of a Dual Robotic Arm Mango Harvesting Robot. J. Field Robot. 2025, 24, 727–743. [Google Scholar] [CrossRef]
- Riboli, M.; Jaccard, M.; Silvestri, M.; Aimi, A.; Malara, C. Collision-Free and Smooth Motion Planning of Dual-Arm Cartesian Robot Based on B-Spline Representation. Robot. Auton. Syst. 2023, 170, 104534. [Google Scholar] [CrossRef]
- Li, T.; Qiu, Q.; Zhao, C.J.; Xie, F. Task Planning of Multi-Arm Harvesting Robots for High-Density Dwarf Orchards. Trans. Chin. Soc. Agric. Mach. 2021, 37, 1–10. [Google Scholar] [CrossRef]
- Williams, H.A.M.; Jones, M.H.; Nejati, M.; Seabright, M.J.; Bell, J.; Penhall, N.D.; Barnett, J.J.; Duke, M.D.; Scarfe, A.J.; Ahn, H.S.; et al. Robotic Kiwifruit Harvesting Using Machine Vision, Convolutional Neural Networks, and Robotic Arms. Biosyst. Eng. 2019, 181, 140–156. [Google Scholar] [CrossRef]
- Xiong, Y.; Ge, Y.; Grimstad, L.; From, P.J. An Autonomous Strawberry-Harvesting Robot: Design, Development, Integration, and Field Evaluation. J. Field Robot. 2020, 37, 202–224. [Google Scholar] [CrossRef]
- Zhang, W.; Zeng, Y.; Wang, S.; Wang, T.; Li, H.; Fei, K.; Qiu, X.; Jiang, R.; Li, J. Research on the Local Path Planning of an Orchard Mowing Robot Based on an Elliptic Repulsion Scope Boundary Constraint Potential Field Method. Front. Plant Sci. 2023, 14, 1184352. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Zou, X.; Jia, C.; Chen, M.; Zeng, Z. RRT-Based Path Planning for an Intelligent Litchi-Picking Manipulator. Comput. Electron. Agric. 2019, 156, 105–118. [Google Scholar] [CrossRef]
- Liu, C.; Feng, Q.; Tang, Z.; Wang, X.; Geng, J.; Xu, L. Motion Planning of the Citrus-Picking Manipulator Based on the TO-RRT Algorithm. Agriculture 2022, 12, 581. [Google Scholar] [CrossRef]
- Fang, C.; Wang, J.; Yuan, F.; Chen, S.; Zhou, H. Path Planning for Dragon-Fruit-Harvesting Robotic Arm Based on XN-RRT* Algorithm. Sensors 2025, 25, 2773. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Gao, B.; Hu, H.; Hong, K. Research on Path Planning of Tea Picking Robot Based on Ant Colony Algorithm. Meas. Control 2024, 57, 1051–1067. [Google Scholar] [CrossRef]
- Li, X.; Huang, T.; Chen, H.; Zhang, Y.; Xu, L.; Liu, Y. Path Planning of Mobile Robot Based on Dynamic Chaotic Ant Colony Optimization Algorithm. In Proceedings of the 2022 IEEE 10th International Conference on Information, Communication and Networks (ICICN), Zhangye, China, 23–24 August 2022; IEEE: New York, NY, USA, 2022; pp. 515–519. [Google Scholar] [CrossRef]
- Kiani, F.; Seyyedabbasi, A.; Nematzadeh, S.; Candan, F.; Çevik, T.; Anka, F.A.; Randazzo, G.; Lanza, S.; Muzirafuti, A. Adaptive Metaheuristic-Based Methods for Autonomous Robot Path Planning: Sustainable Agricultural Applications. Appl. Sci. 2022, 12, 943. [Google Scholar] [CrossRef]
- Chen, Z.; Alonso-Mora, J.; Bai, X.; Harabor, D.D.; Stuckey, P.J. Integrated Task Assignment and Path Planning for Capacitated Multi-Agent Pickup and Delivery. IEEE Robot. Autom. Lett. 2021, 6, 5816–5823. [Google Scholar] [CrossRef]
- Ali, A.; Ullah, I.; Shabaz, M.; Sharafian, A.; Khan, M.A.; Bai, X. A Resource-Aware Multi-Graph Neural Network for Urban Traffic Flow Prediction in Multi-Access Edge Computing Systems. IEEE Trans. Consum. Electron. 2024, 70, 7252–7265. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, J.; Xu, Y.; Cui, C.; Liu, Z.; Chen, J. Location of Safflower Filaments Picking Points in Complex Environment Based on Improved Yolov5 Algorithm. Comput. Electron. Agric. 2024, 227, 109463. [Google Scholar] [CrossRef]
- Zhang, H.; Ge, Y.; Xia, H.; Sun, C. Safflower Picking Points Localization Method During the Full Harvest Period Based on SBP-YOLOv8s-seg Network. Comput. Electron. Agric. 2024, 227, 109646. [Google Scholar] [CrossRef]
- Guo, H.; Qiu, Z.; Gao, G.; Wu, T.; Chen, H.; Wang, X. Safflower Picking Trajectory Planning Strategy Based on an Ant Colony Genetic Fusion Algorithm. Agriculture 2024, 14, 622. [Google Scholar] [CrossRef]
- Briot, S.; Goldsztejn, A. Singularity Conditions for Continuum Parallel Robots. IEEE Trans. Robot. 2022, 38, 507–525. [Google Scholar] [CrossRef]
- Zhang, H.; Ge, Y.; Sun, C.; Zeng, H.; Liu, N. Picking Path Planning Method of Dual Rollers Type Safflower Picking Robot Based on Improved Ant Colony Algorithm. Processes 2022, 10, 1213. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, J.; Xu, L.; Wang, J. Cooperative path planning study of distributed multi-mobile robots based on optimised ACO algorithm. Robot. Auton. Syst. 2024, 179, 104748. [Google Scholar] [CrossRef]
- Zhou, A.-H.; Zhu, L.-P.; Hu, B.; Deng, S.; Song, Y.; Qiu, H.; Pan, S. Traveling-Salesman-Problem Algorithm Based on Simulated Annealing and Gene-Expression Programming. Information 2019, 10, 7. [Google Scholar] [CrossRef]
- Uddin, F.; Riaz, N.; Manan, A.; Mahmood, I.; Song, O.-Y.; Malik, A.J.; Abbasi, A.A. An Improvement to the 2-Opt Heuristic Algorithm for Approximation of Optimal TSP Tour. Appl. Sci. 2023, 13, 7339. [Google Scholar] [CrossRef]
- Kong, F.; Liu, B.; Han, X.; Yi, L.; Sun, H.; Liu, J.; Liu, L.; Lan, Y. Path Planning Algorithm of Orchard Fertilization Robot Based on Multi-Constrained Bessel Curve. Agriculture 2024, 14, 979. [Google Scholar] [CrossRef]
- Li, G.; Liu, C.; Wu, L.; Xiao, W. A Mixing Algorithm of ACO and ABC for Solving Path Planning of Mobile Robot. Appl. Soft Comput. 2023, 148, 110868. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Z. Ant Colony Optimization for Traveling Salesman Problem Based on Parameters Optimization. Appl. Soft Comput. 2021, 107, 107439. [Google Scholar] [CrossRef]
- Sun, J.; Yu, Y.; Xin, L. Research on Path Planning of AGV Based on Improved Ant Colony Optimization Algorithm. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 7567–7572. [Google Scholar] [CrossRef]
- Wang, L.; Wang, H.; Yang, X.; Gao, Y.; Cui, X.; Wang, B. Research on Smooth Path Planning Method Based on Improved Ant Colony Algorithm Optimized by Floyd Algorithm. Front. Neurorobot. 2022, 16, 955179. [Google Scholar] [CrossRef] [PubMed]

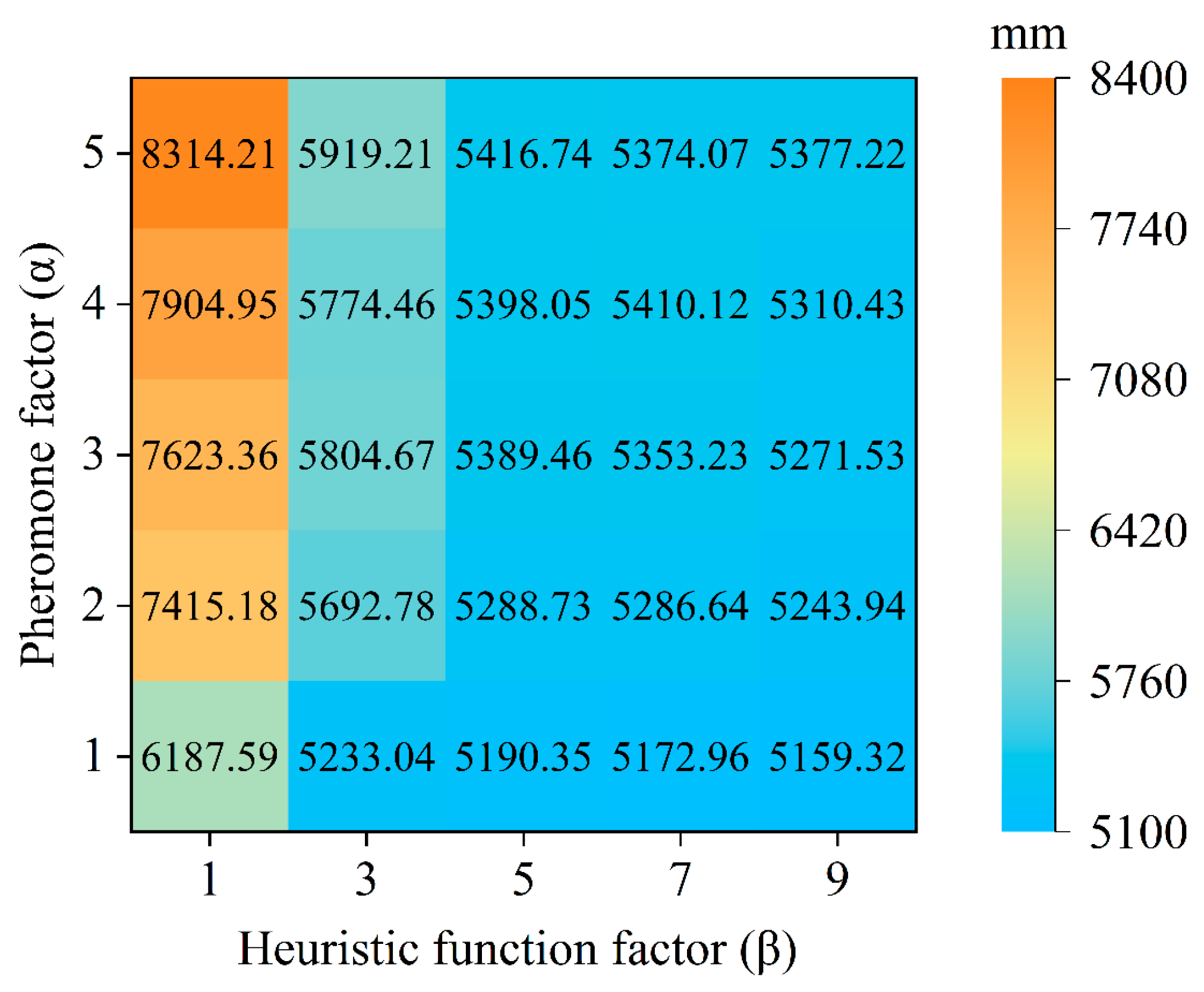


| Key Parameter | Symbol | Definition |
|---|---|---|
| Ant Population | m | Controls the diversity of the search. |
| Pheromone Volatilization Factor | ρ | Controls the rate at which pheromones decay over time. |
| Pheromone Factor | α | Adjusts the weight of pheromone concentration in path selection. |
| Heuristic Function Factor | β | Adjusts the weight of heuristic information in path selection. |
| Number of Clusters | k | Controls the expected number of clusters in the clustering algorithm. |
| Iteration Number | G | Controls the termination condition of the computation. |
| m | ρ | α | β | k | G |
|---|---|---|---|---|---|
| n | 0.4 | 1 | 9 | 2 | 100 |
| Test No. | Base Model | K-Means | Dynamic Heuristic | 2-OPT | Average Path Distance/mm | Average Runtime/s |
|---|---|---|---|---|---|---|
| 1 | √ | - | - | - | 13,115.56 | 0.5416 |
| 2 | √ | √ | - | - | 11,867.66 | 1.2535 |
| 3 | √ | √ | √ | - | 11,818.73 | 1.2659 |
| 4 | √ | √ | √ | √ | 11,780.10 | 1.2132 |
| Type | Single-Arm Picking | Dual-Arm Picking | ||
|---|---|---|---|---|
| Time | Area 1 | Area 2 | ||
| Picking Time/s | 141.00 | 57.00 | 84.00 | |
| Traversal Path Time/s | 117.79 | 48.51 | 68.98 | |
| Total Time/s | 258.79 | 152.98 | ||
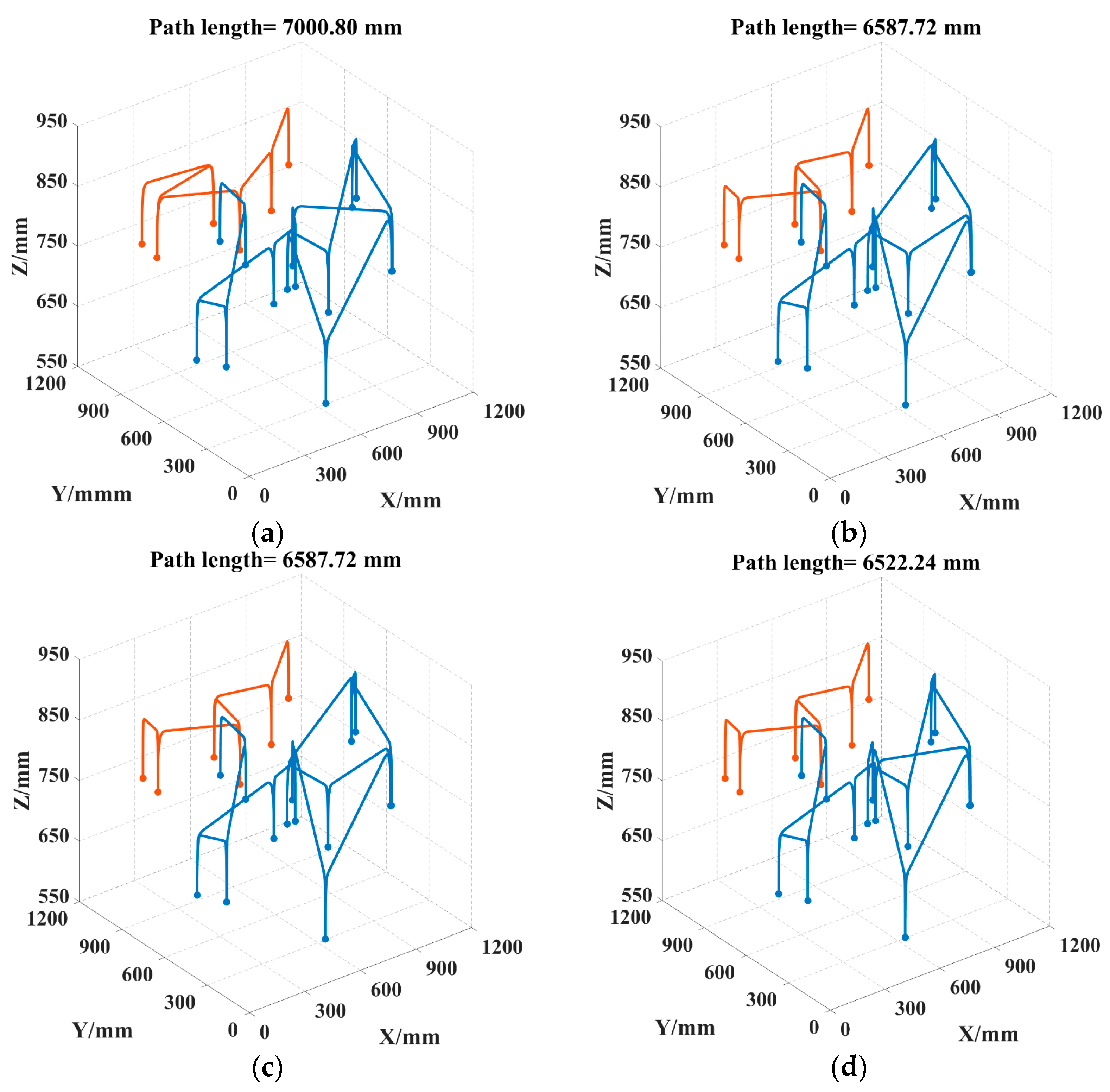
| Picking Points | Algorithm | Optimal Path Value/mm | Worst Path Value/mm | Average Path Value/mm | Path Standard Deviation | Average Iteration Time/s |
|---|---|---|---|---|---|---|
| 20 | ACO | 7000.80 | 7841.02 | 7419.99 | 351.08 | 0.3490 |
| DCACO | 6587.72 | 6983.19 | 6824.32 | 149.34 | 0.7410 | |
| IACO | 6587.72 | 6936.62 | 6677.55 | 109.51 | 0.5817 | |
| LTSACO | 6522.24 | 6861.02 | 6599.45 | 98.09 | 0.4024 | |
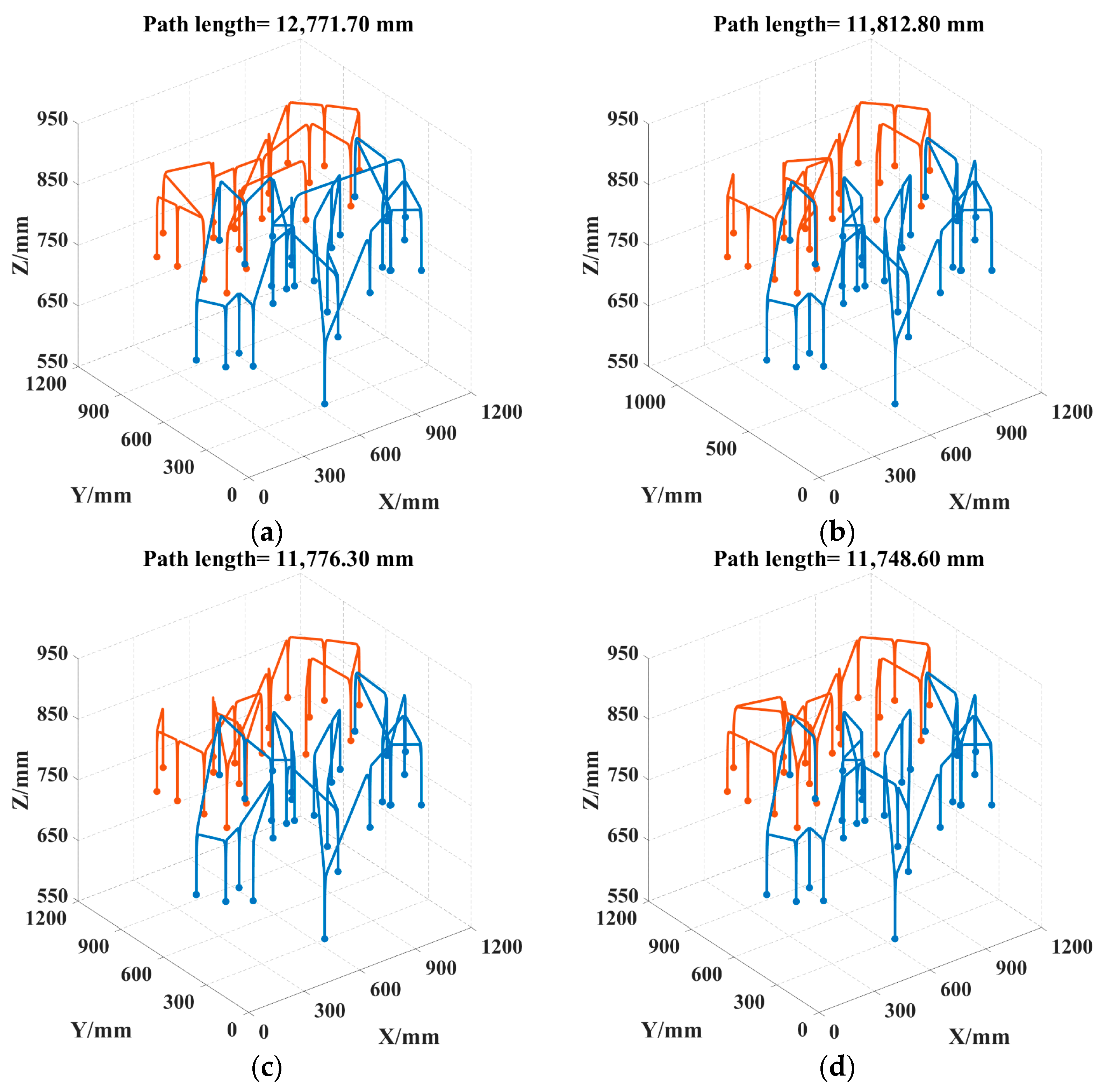
| 47 | ACO | 12,771.70 | 13,318.00 | 12,993.35 | 192.62 | 0.4546 |
| DCACO | 11,812.80 | 11,991.00 | 11,894.69 | 58.93 | 1.6147 | |
| IACO | 11,776.30 | 11,937.40 | 11,852.550 | 47.94 | 1.5985 | |
| LTSACO | 11,748.60 | 11,833.20 | 11,780.10 | 30.71 | 1.2132 | |
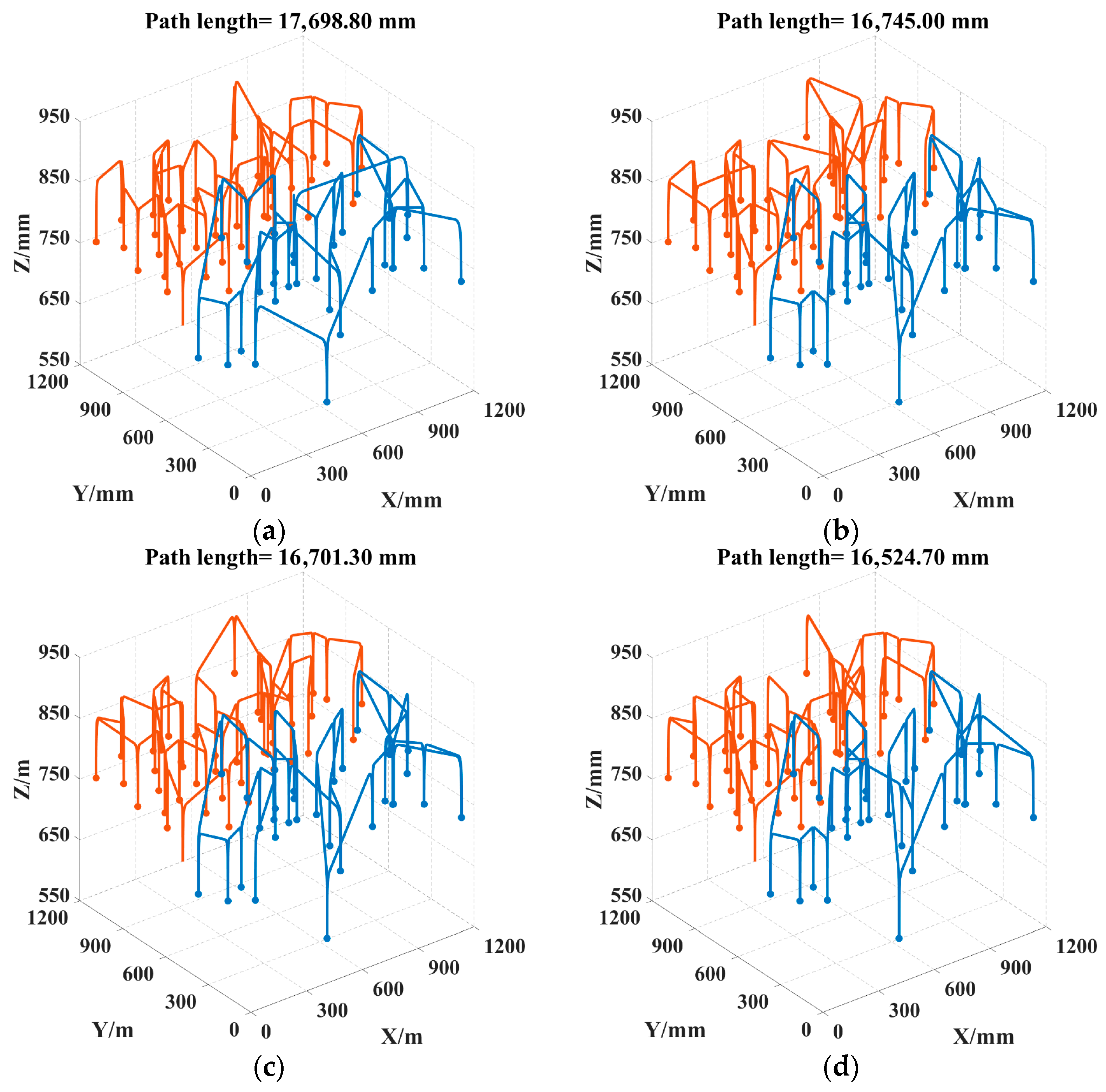
| 73 | ACO | 17,698.80 | 18,900.10 | 18,055.80 | 325.53 | 0.5478 |
| DCACO | 16,745.00 | 17,361.10 | 16,884.42 | 182.36 | 2.7024 | |
| IACO | 16,701.30 | 17,066.00 | 16,792.85 | 100.48 | 2.7080 | |
| LTSACO | 16,524.70 | 16,740.10 | 16,699.52 | 73.06 | 2.4973 |
| Algorithm | Number of Safflowers | Single Safflower Picking Duration/s | End-Effector Travel Speed/m/s | Average Path Length/mm | Path Standard Deviation | Average Picking Duration/s |
|---|---|---|---|---|---|---|
| ACO | 46 | 3 | 0.1 | 12,813.92 | 193.39 | 106.5775 |
| DCACO | 46 | 3 | 0.1 | 11,714.47 | 55.10 | 102.6384 |
| IACO | 46 | 3 | 0.1 | 11,621.15 | 41.24 | 103.3025 |
| LTSACO | 46 | 3 | 0.1 | 11,577.48 | 31.64 | 100.5926 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Xu, P.; Xie, B.; Wang, Y.; Shi, R.; Li, J.; Cao, W.; Chu, W.; Zeng, C. Investigation into the Efficient Cooperative Planning Approach for Dual-Arm Picking Sequences of Dwarf, High-Density Safflowers. Sensors 2025, 25, 4459. https://doi.org/10.3390/s25144459
Zhang Z, Xu P, Xie B, Wang Y, Shi R, Li J, Cao W, Chu W, Zeng C. Investigation into the Efficient Cooperative Planning Approach for Dual-Arm Picking Sequences of Dwarf, High-Density Safflowers. Sensors. 2025; 25(14):4459. https://doi.org/10.3390/s25144459
Chicago/Turabian StyleZhang, Zhenguo, Peng Xu, Binbin Xie, Yunze Wang, Ruimeng Shi, Junye Li, Wenjie Cao, Wenqiang Chu, and Chao Zeng. 2025. "Investigation into the Efficient Cooperative Planning Approach for Dual-Arm Picking Sequences of Dwarf, High-Density Safflowers" Sensors 25, no. 14: 4459. https://doi.org/10.3390/s25144459
APA StyleZhang, Z., Xu, P., Xie, B., Wang, Y., Shi, R., Li, J., Cao, W., Chu, W., & Zeng, C. (2025). Investigation into the Efficient Cooperative Planning Approach for Dual-Arm Picking Sequences of Dwarf, High-Density Safflowers. Sensors, 25(14), 4459. https://doi.org/10.3390/s25144459










