Selective Notch Frequency Technology for EMI Noise Reduction in DC–DC Converters: A Review
Abstract
1. Introduction
2. Fundamental DC–DC Switching Converters [1,2,3,4,5,6,7,8]
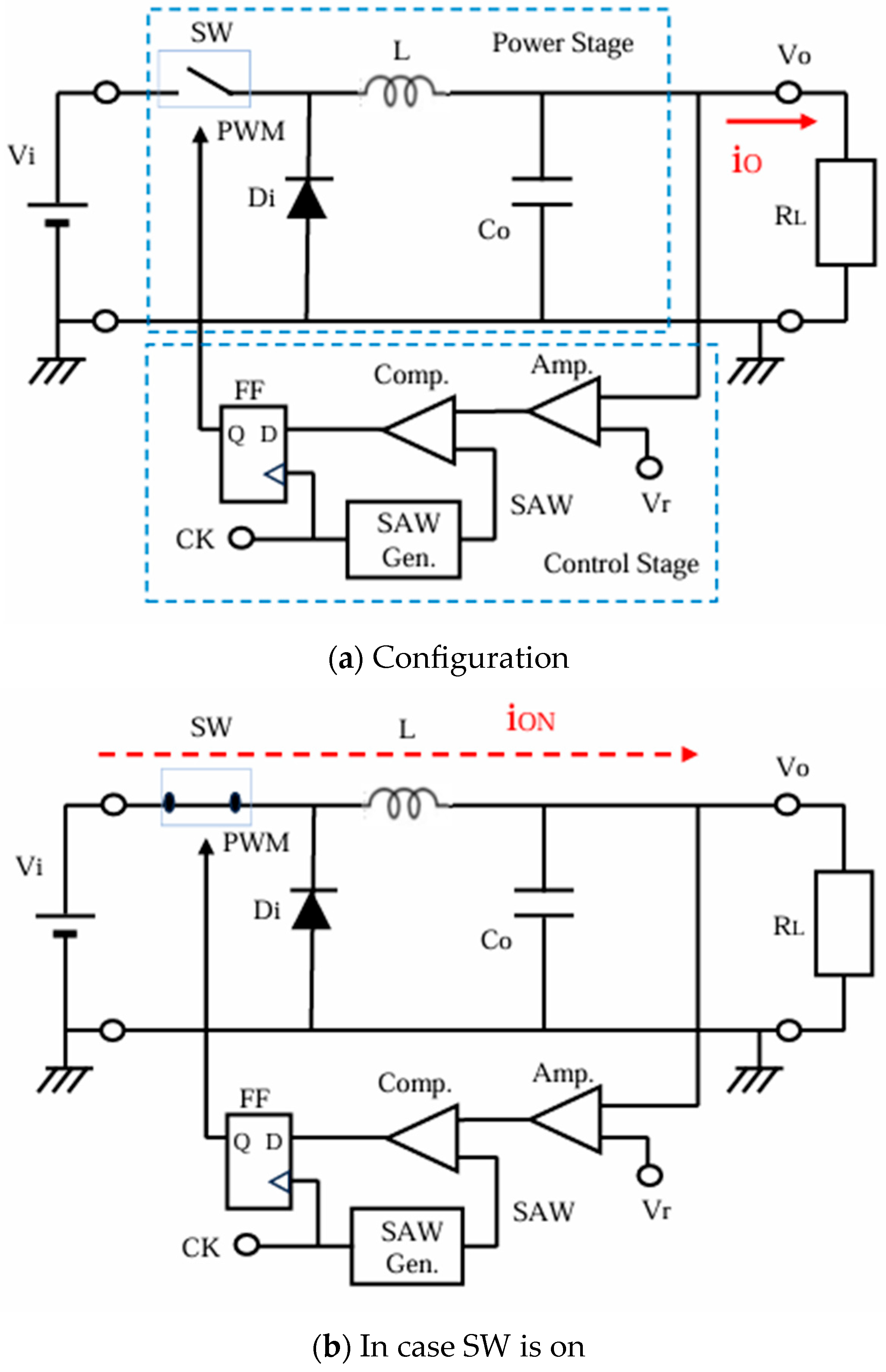
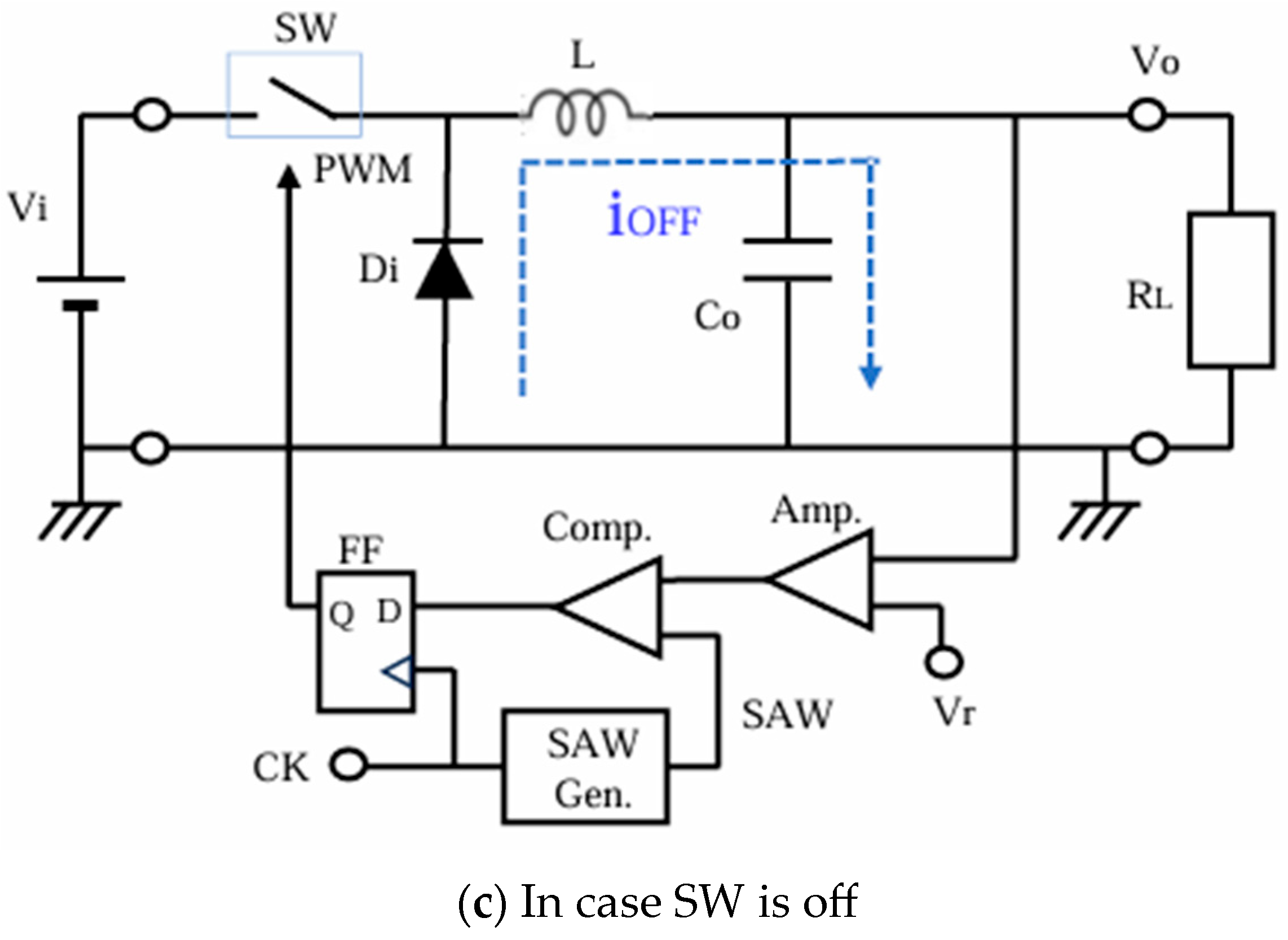
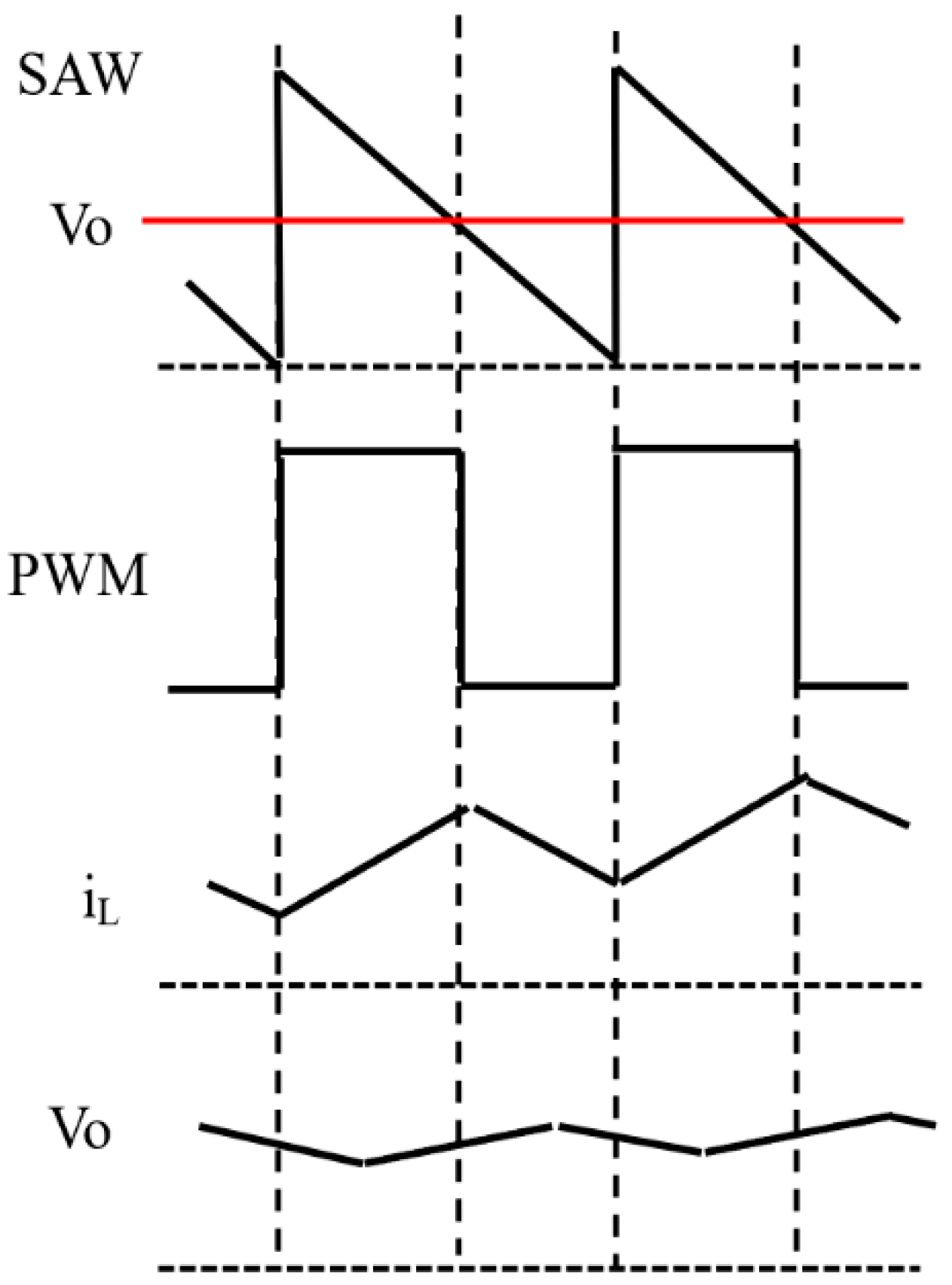
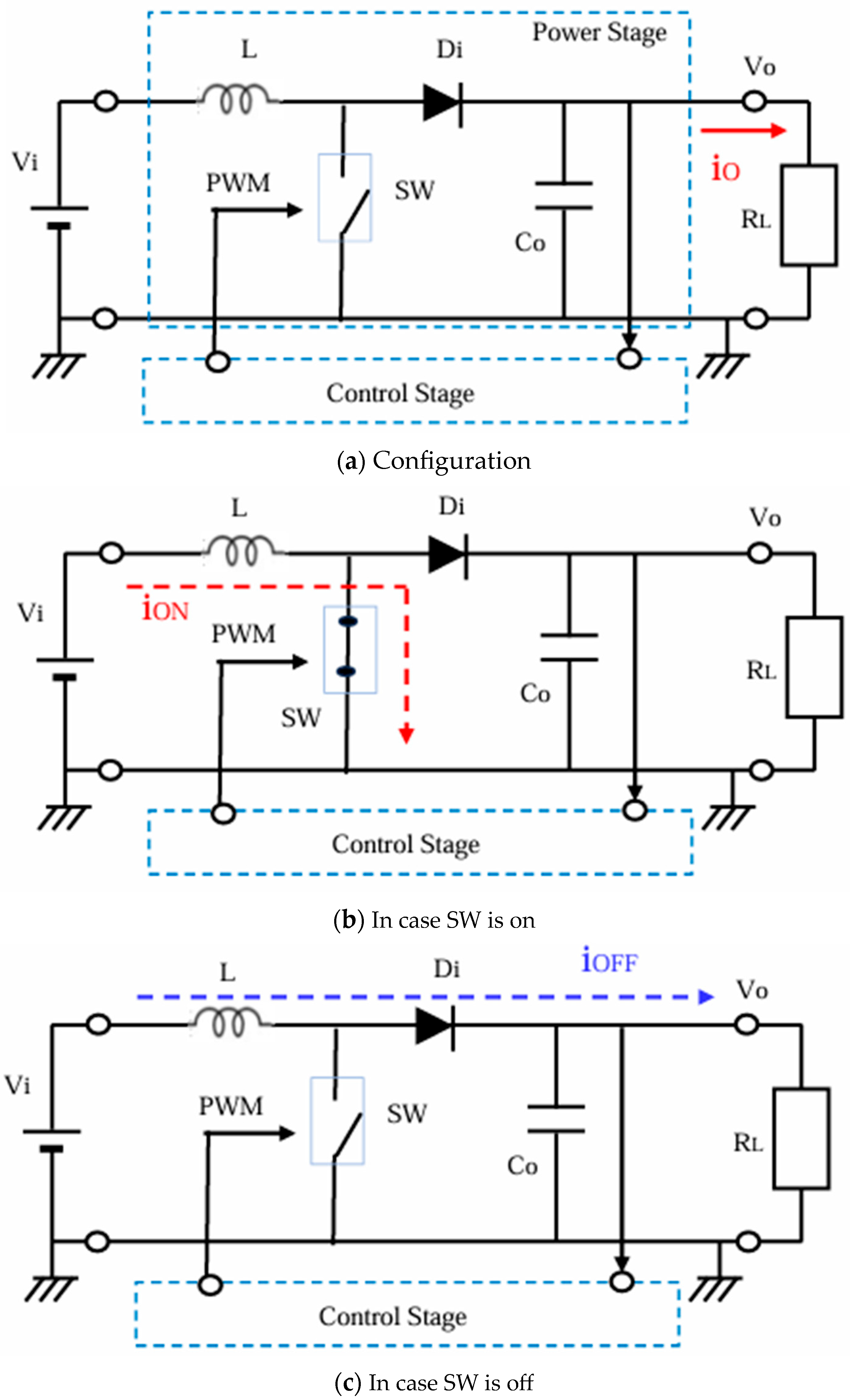
2.1. Buck Converter with PWM Control
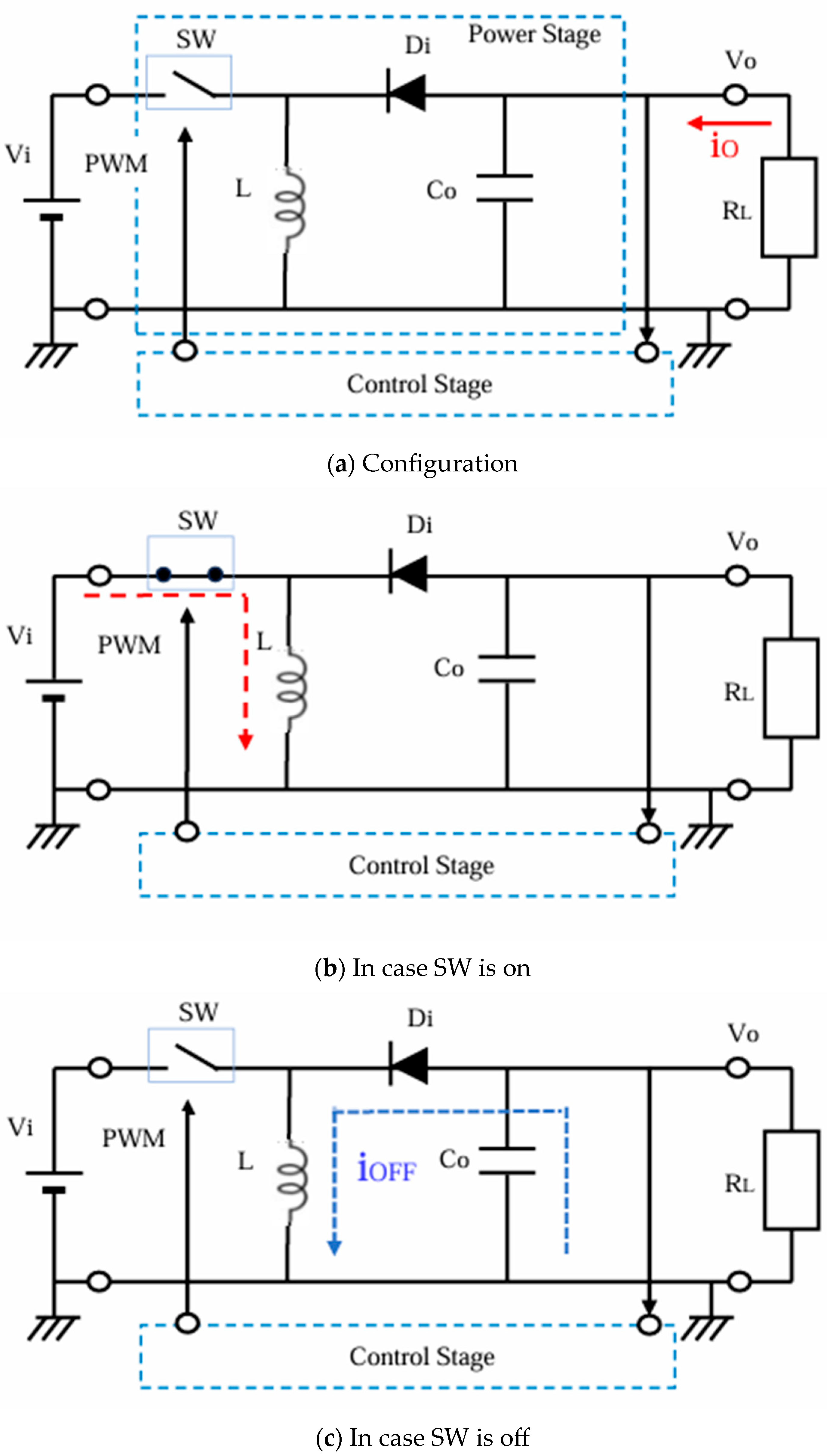
2.2. Boost Converter
2.3. Buck–Boost Converter
- (i)
- There is still room for improvement in current DC–DC converter topologies, depending on their specific applications. For example, see [34];
- (ii)
- Another type of switching-mode converter is the switched-capacitor converter, which comprises only switches and capacitors, without the need for inductors or transformers [33]. Its features are light weight, small size, high power density, and low EMI emissions. However, it has certain limitations, such as its capacity to handle only limited output current, its output voltage being step-wise rather than continuous, and its relatively low efficiency. This paper does not discuss this type of converter because of its low EMI emissions.
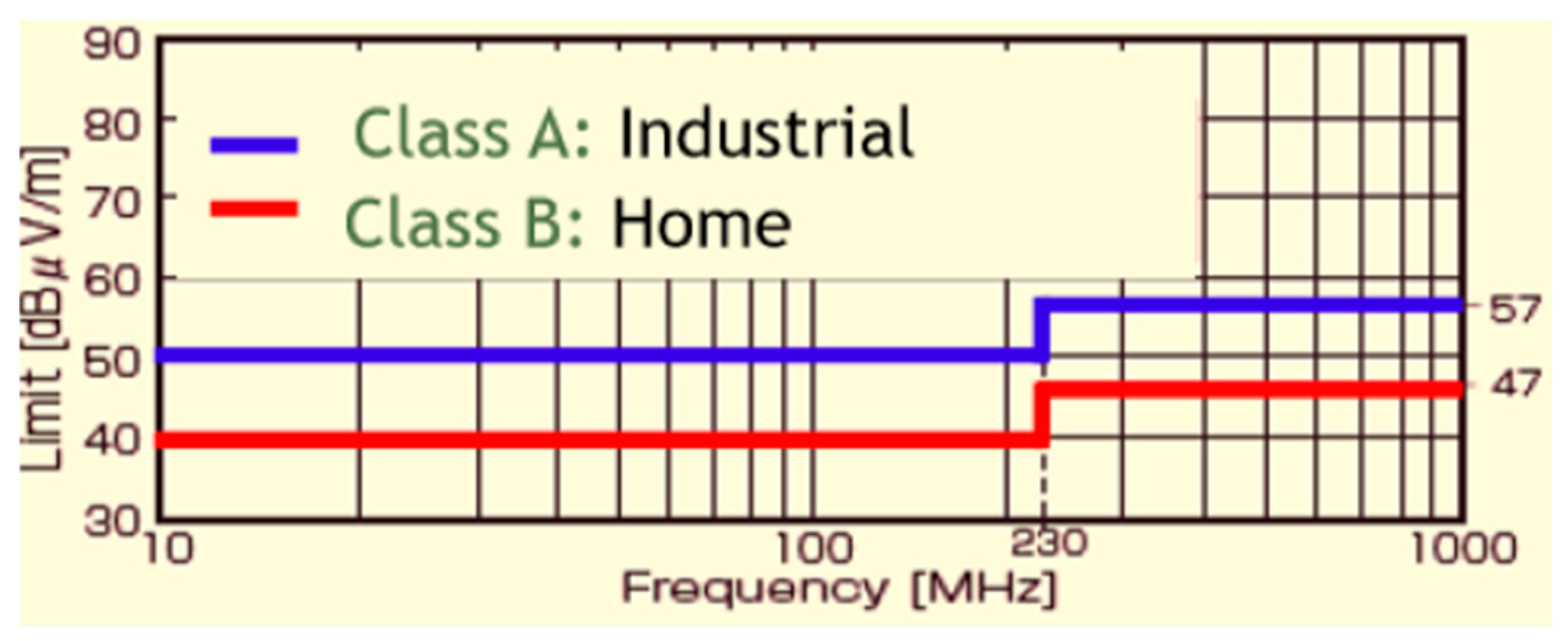
3. EMI Problems in DC–DC Converters
4. Conventional Methods of EMI Reduction with Suppressing Diffusion [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35]
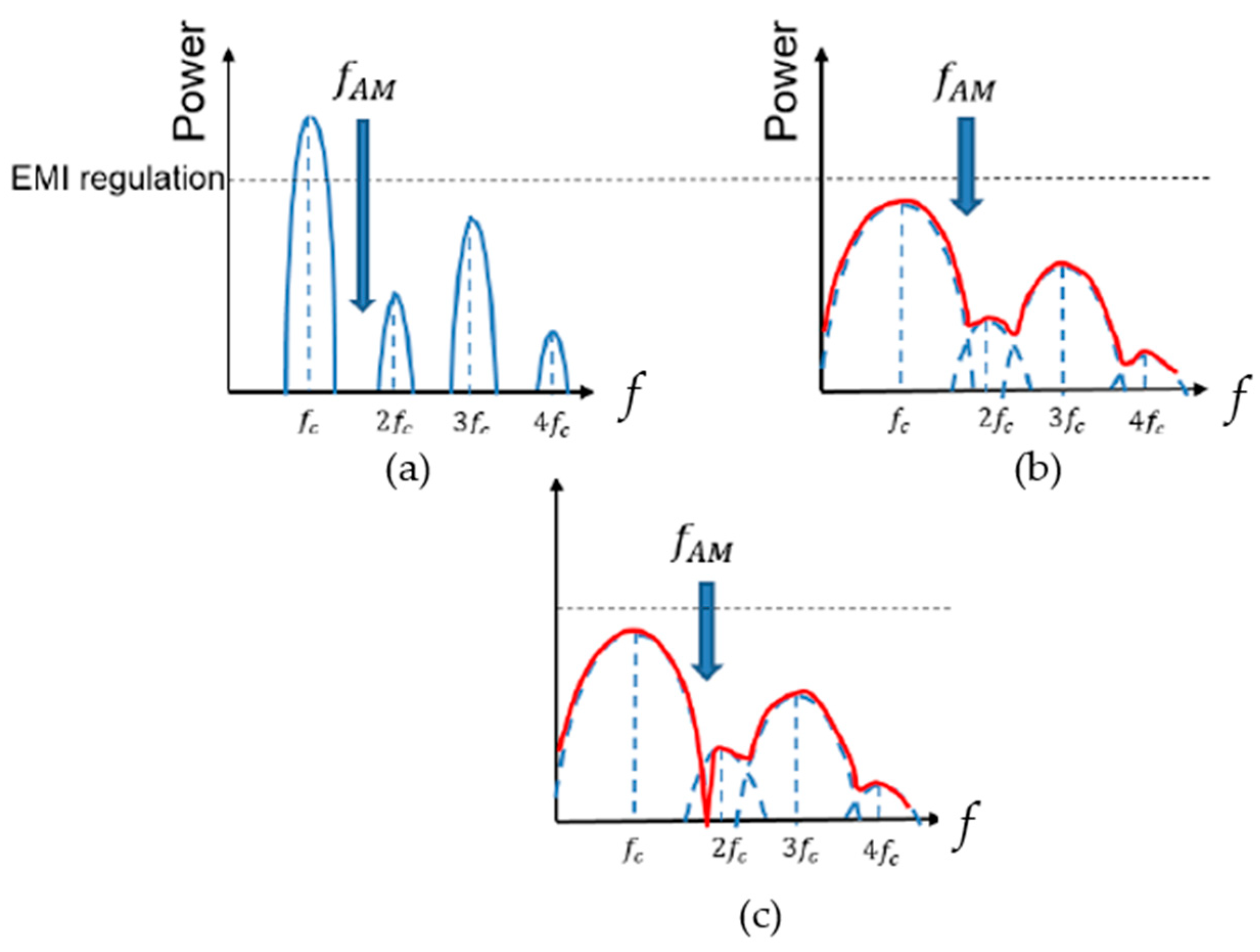
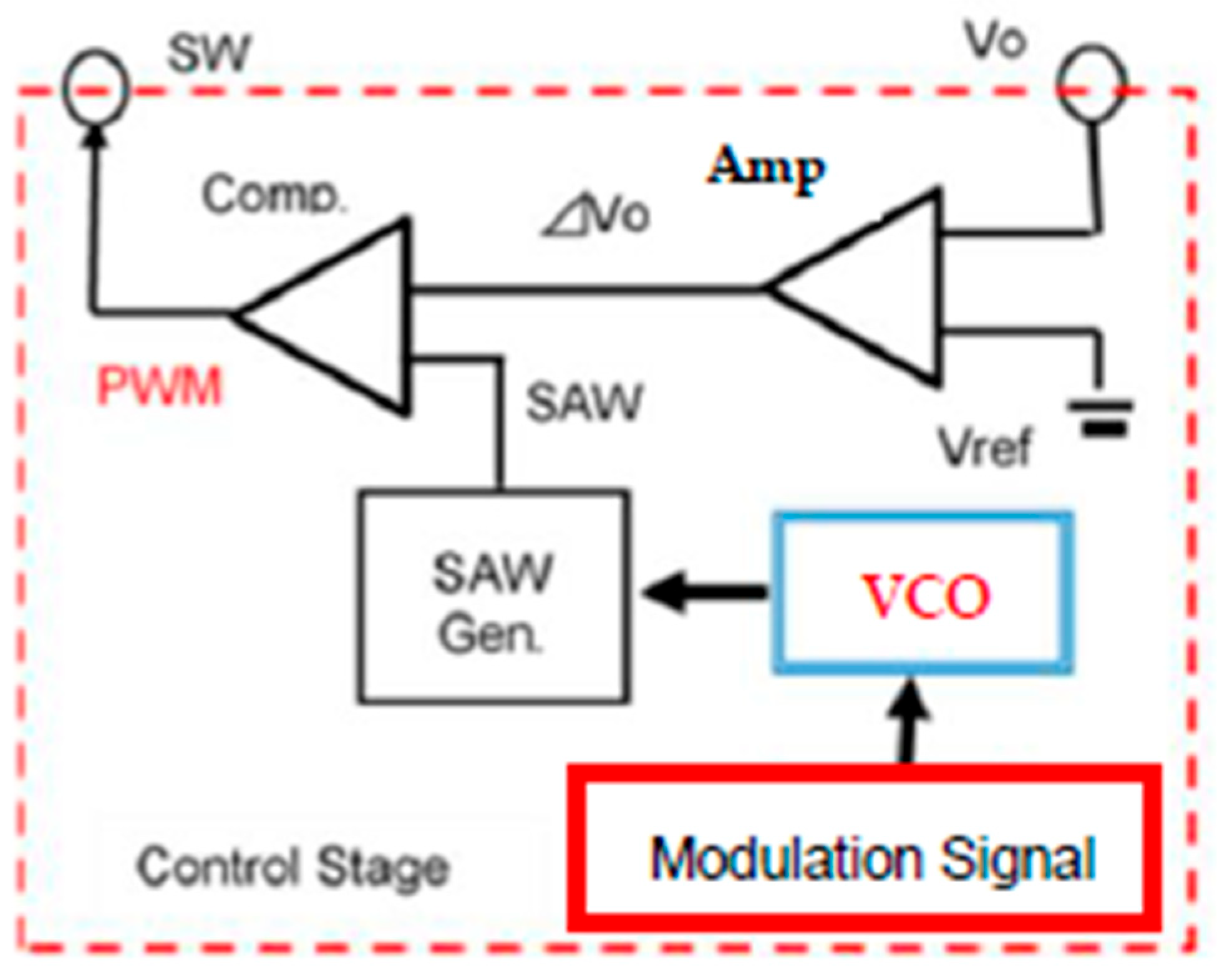
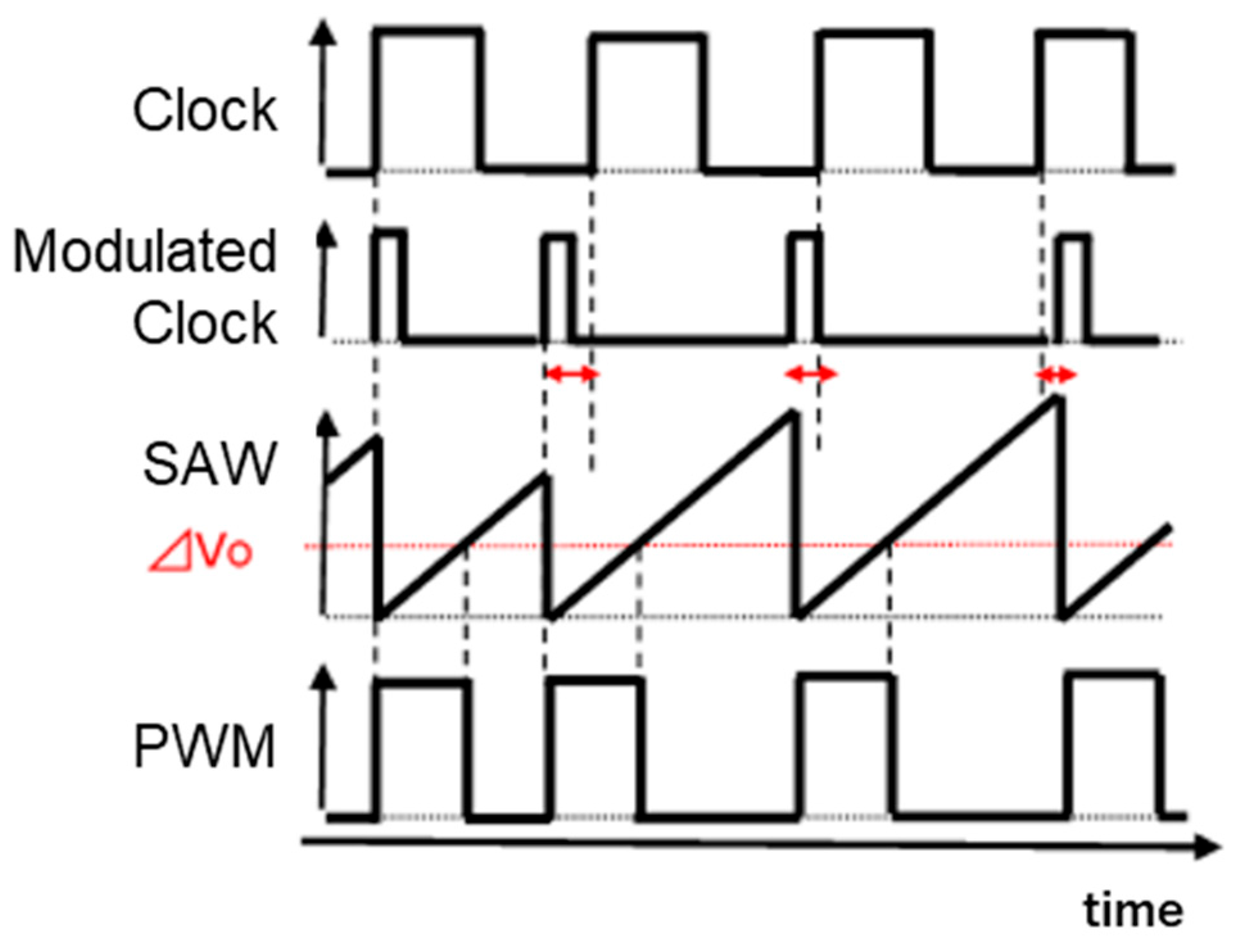
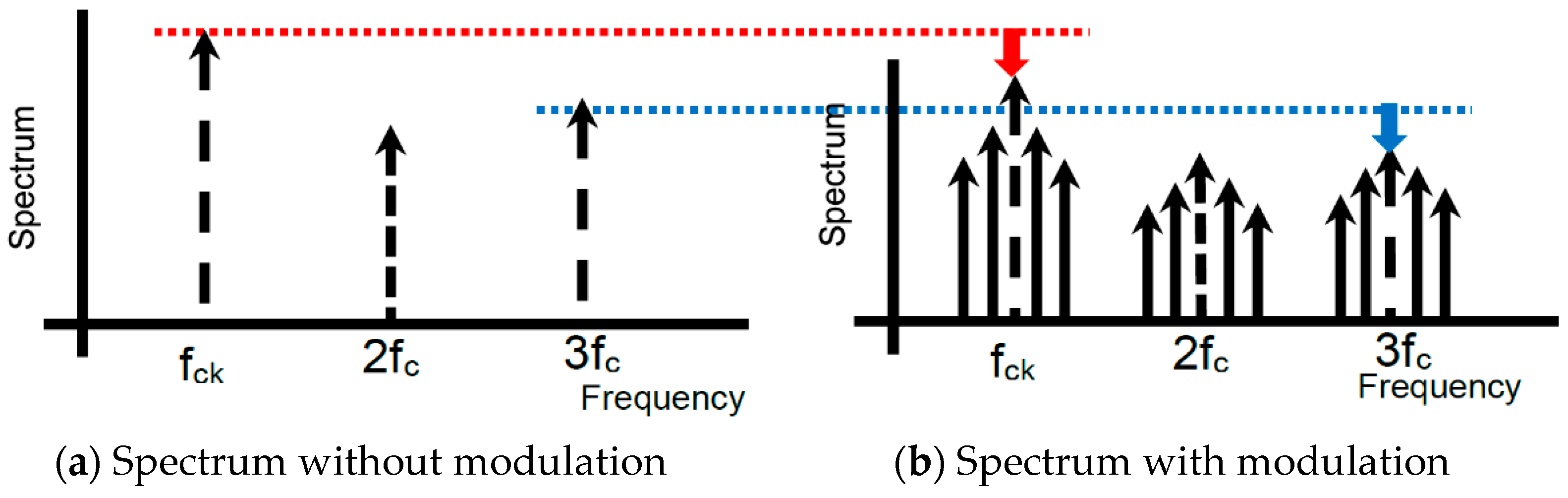
4.1. Frequency Modulation with Analog Spread Spectrum Clock Generator
4.2. Basic Digital Frequency Modulation with LFSR
4.3. Analog Noise Generators Using Bit Operation
4.4. Pattern Generator Using Bit-Inverse and Bit-Exchange and Simulation Results
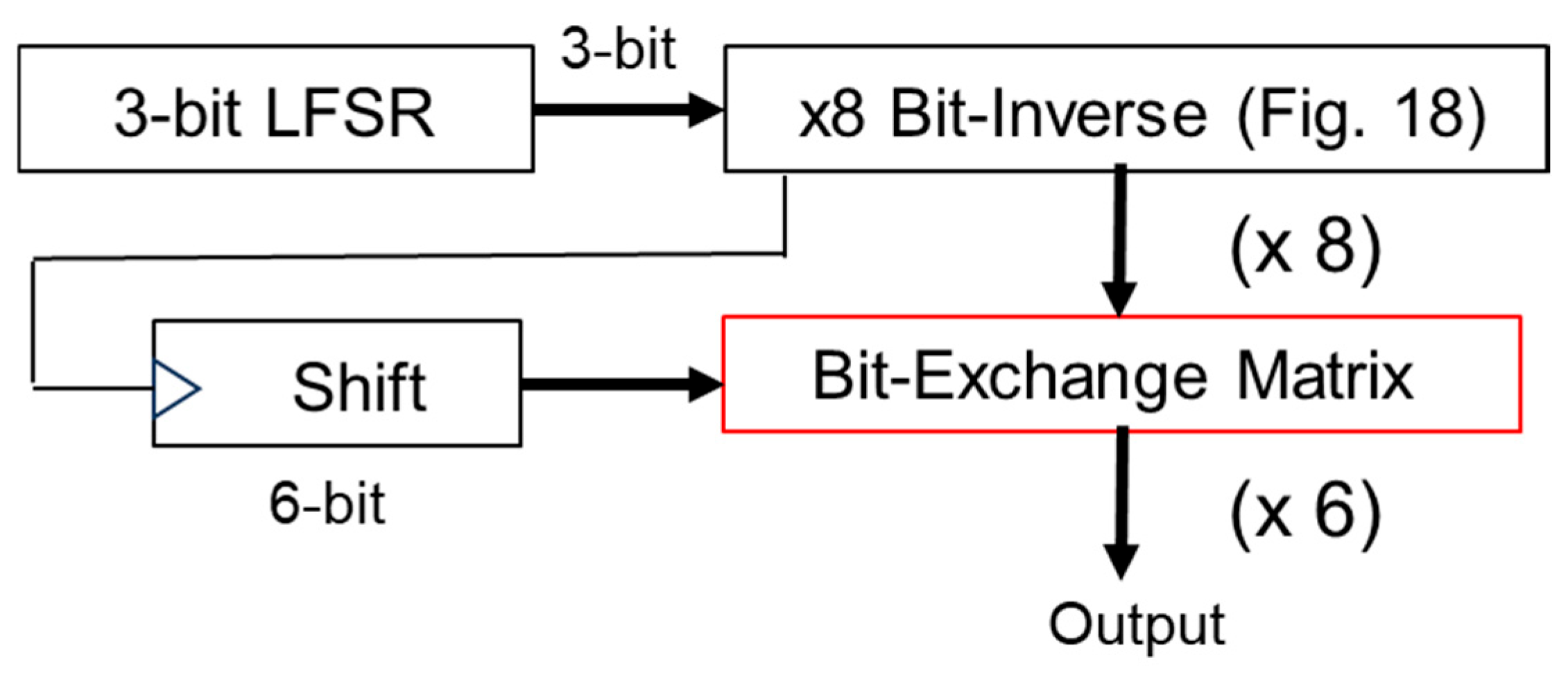
4.5. Expansion of Number of Pseudo Analog Noise Generator Bits
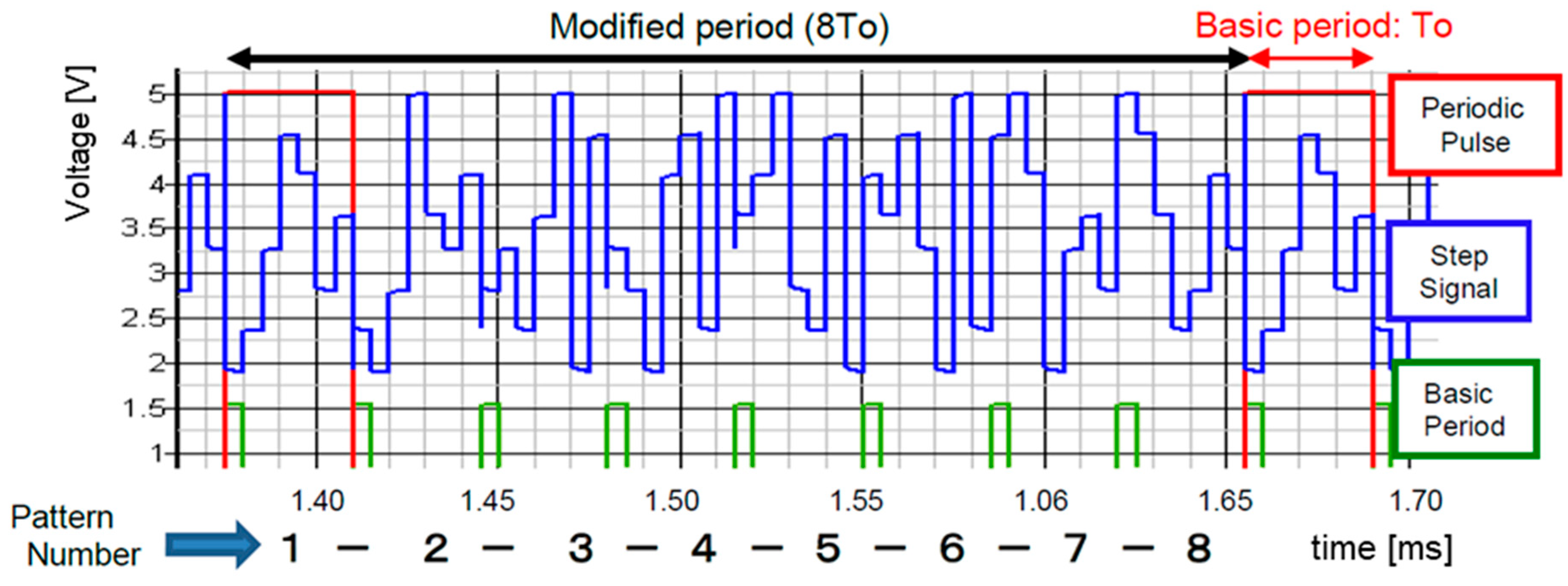
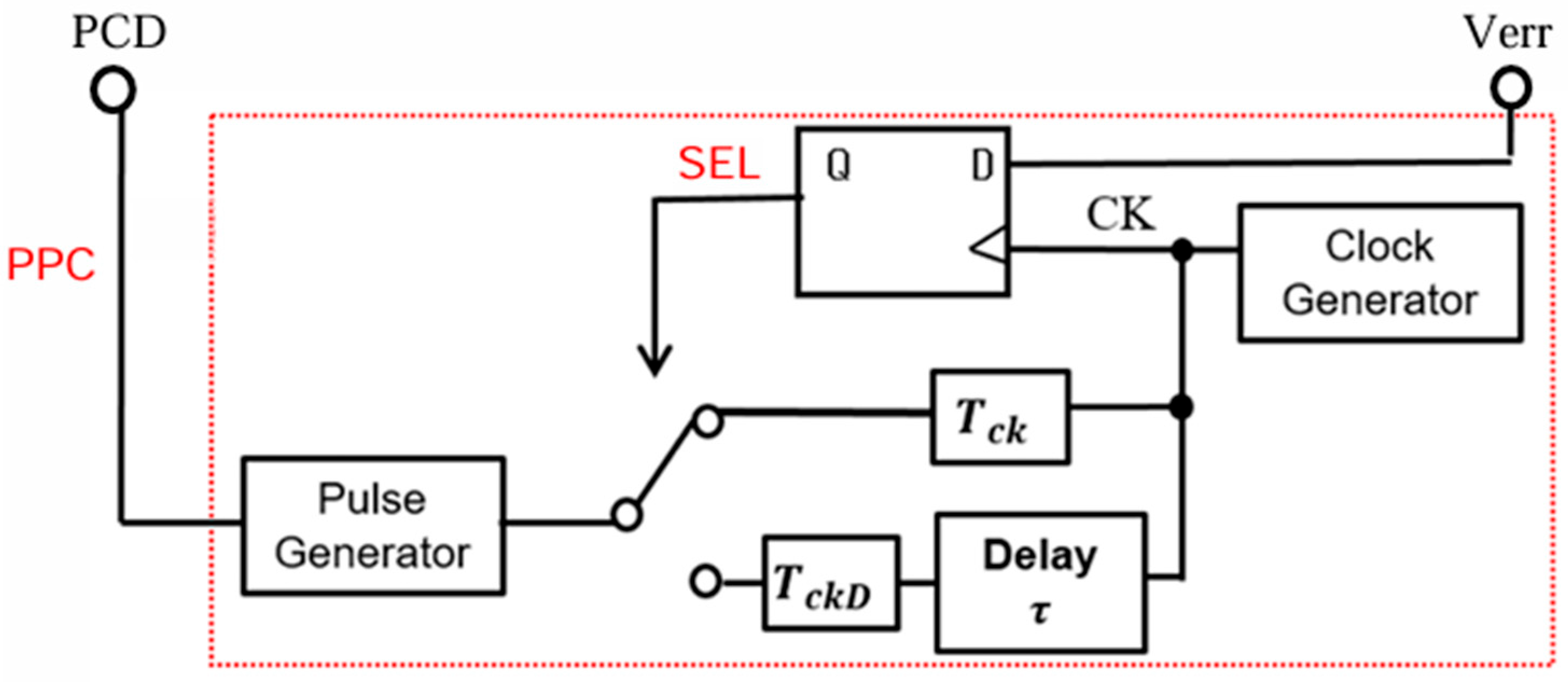
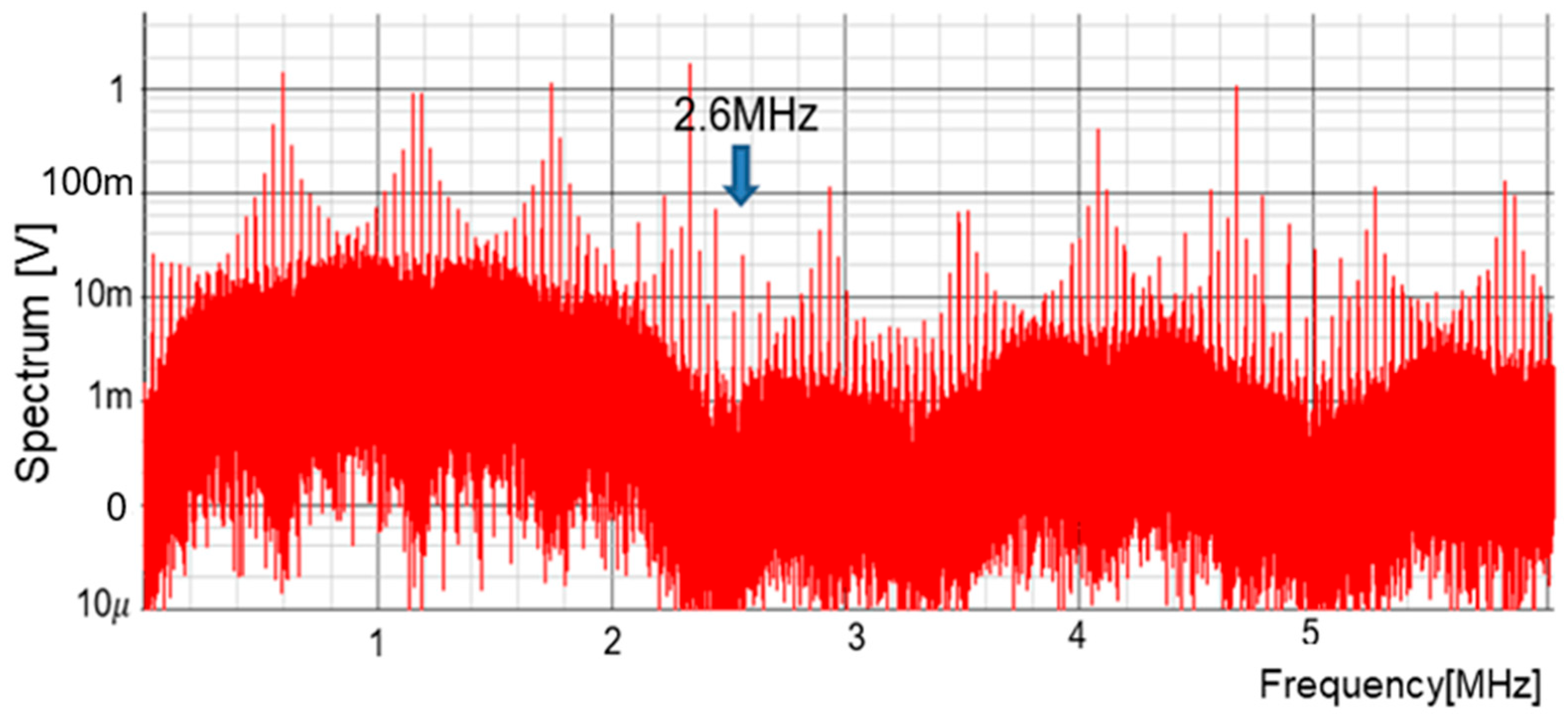
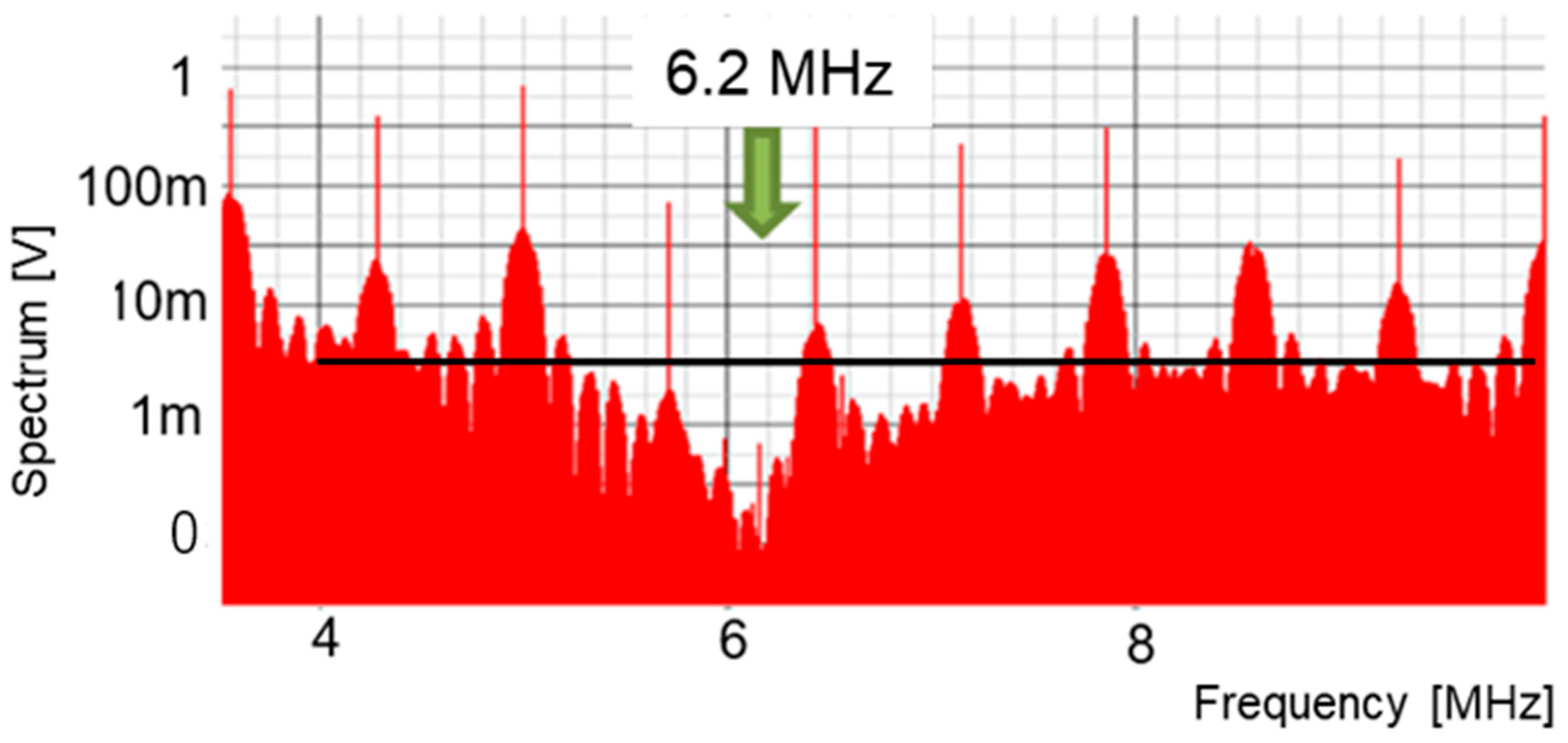
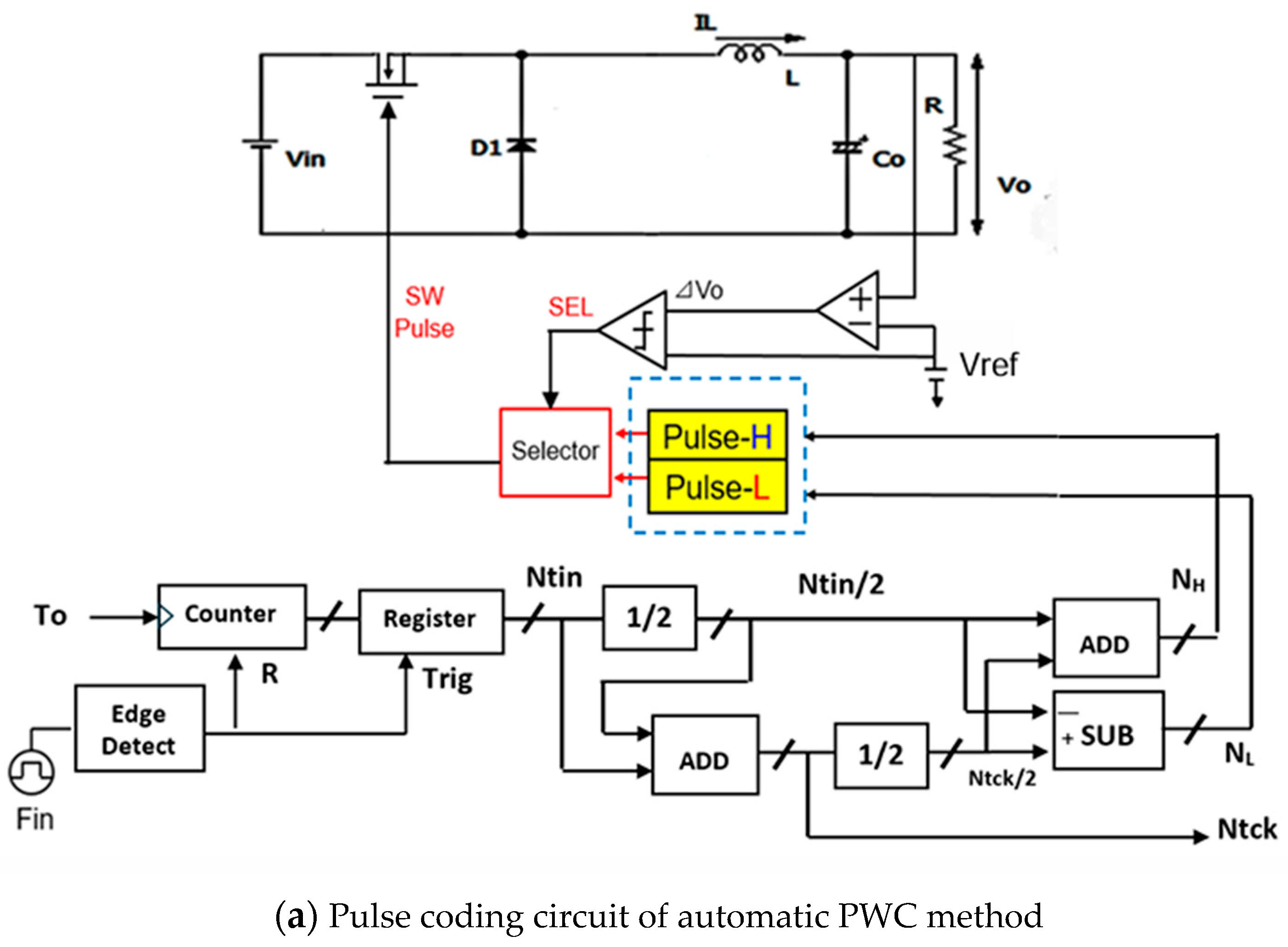
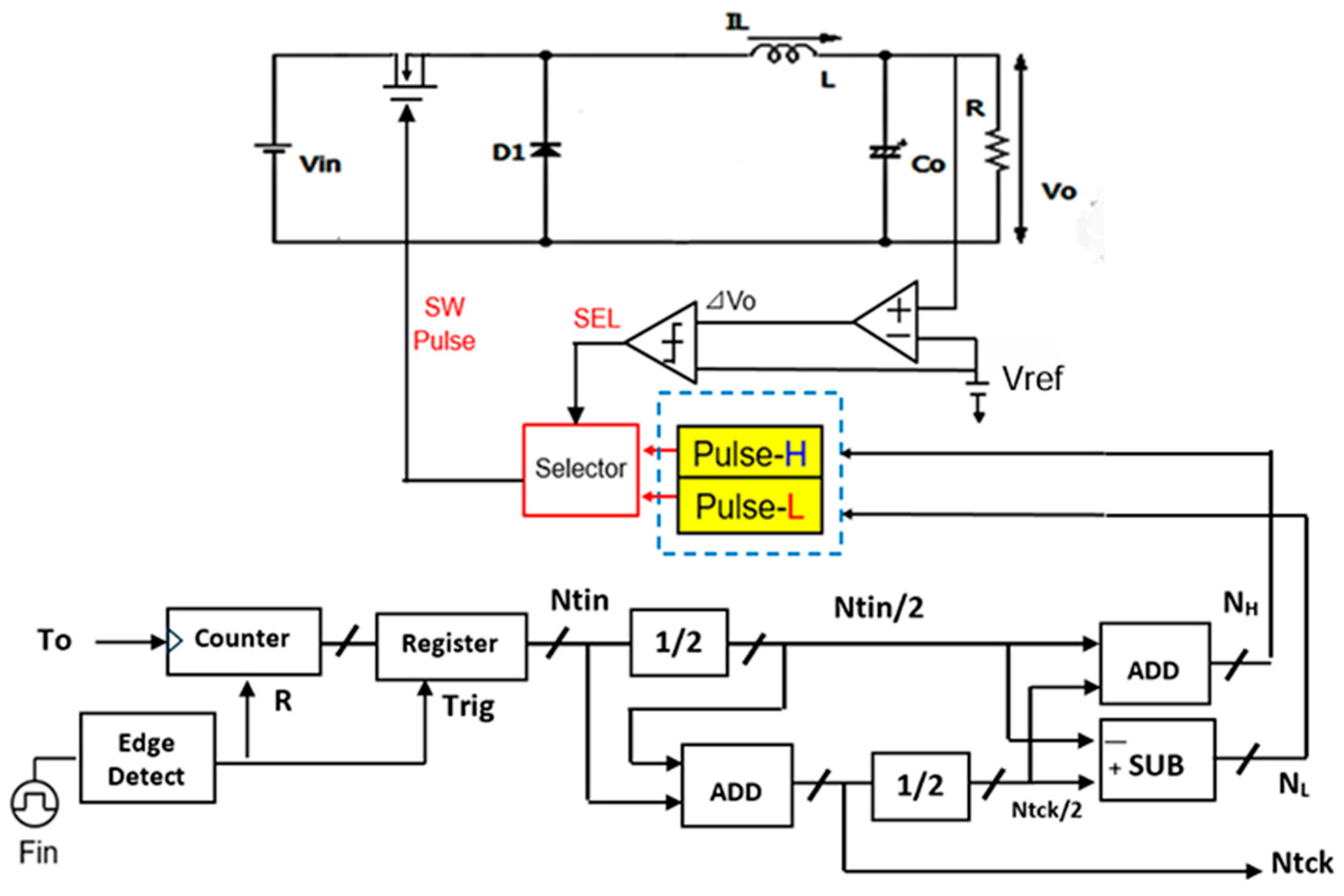
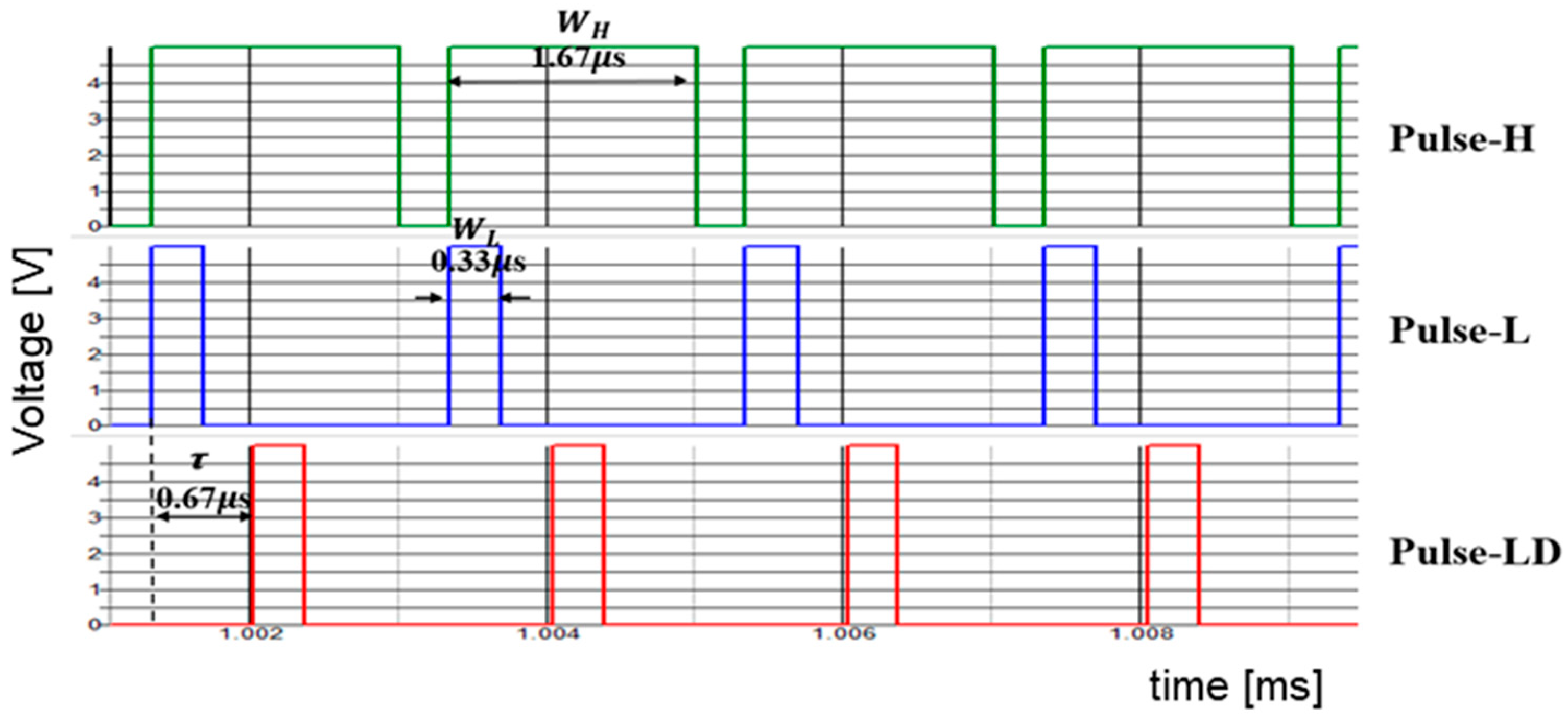
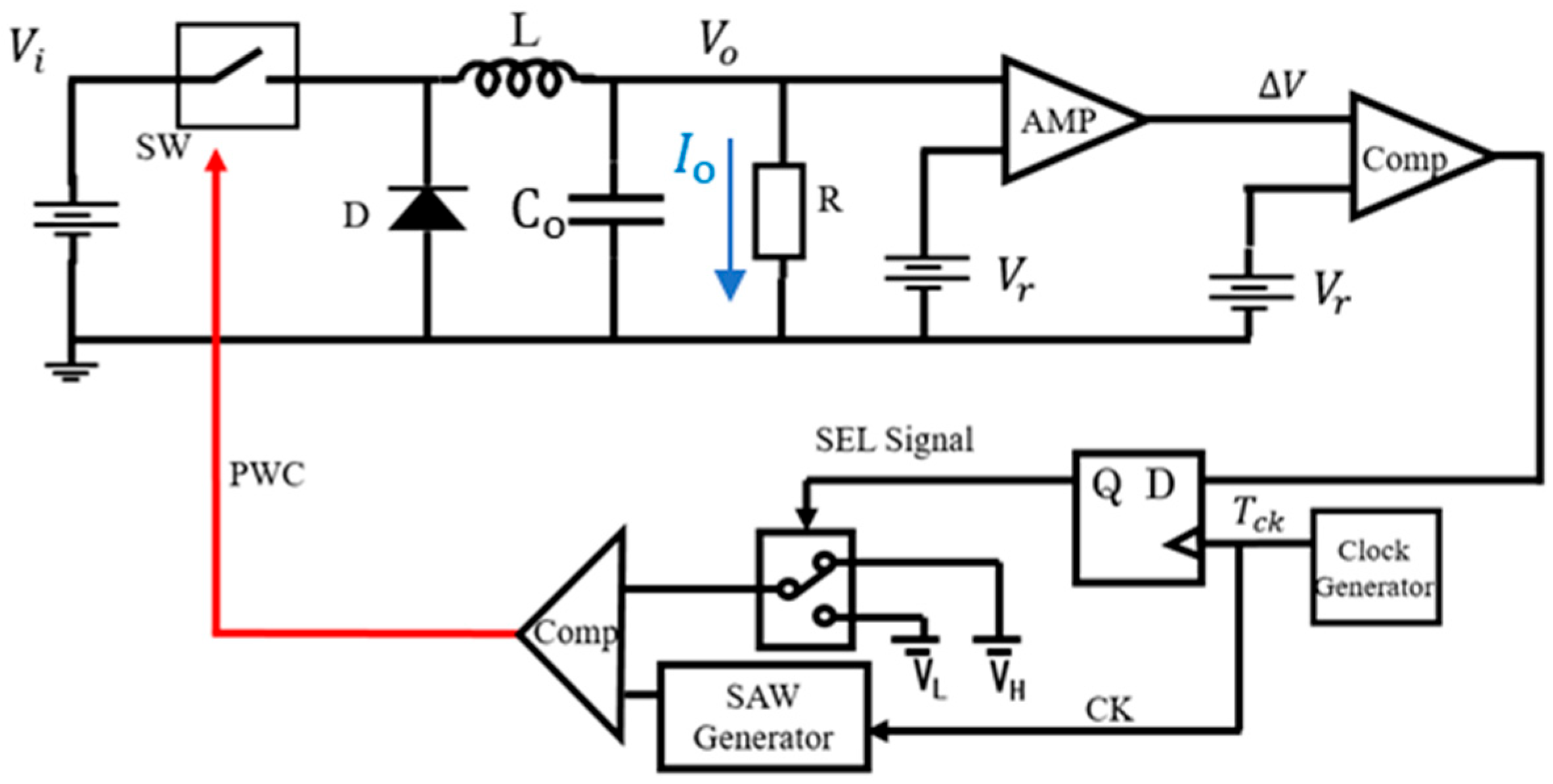
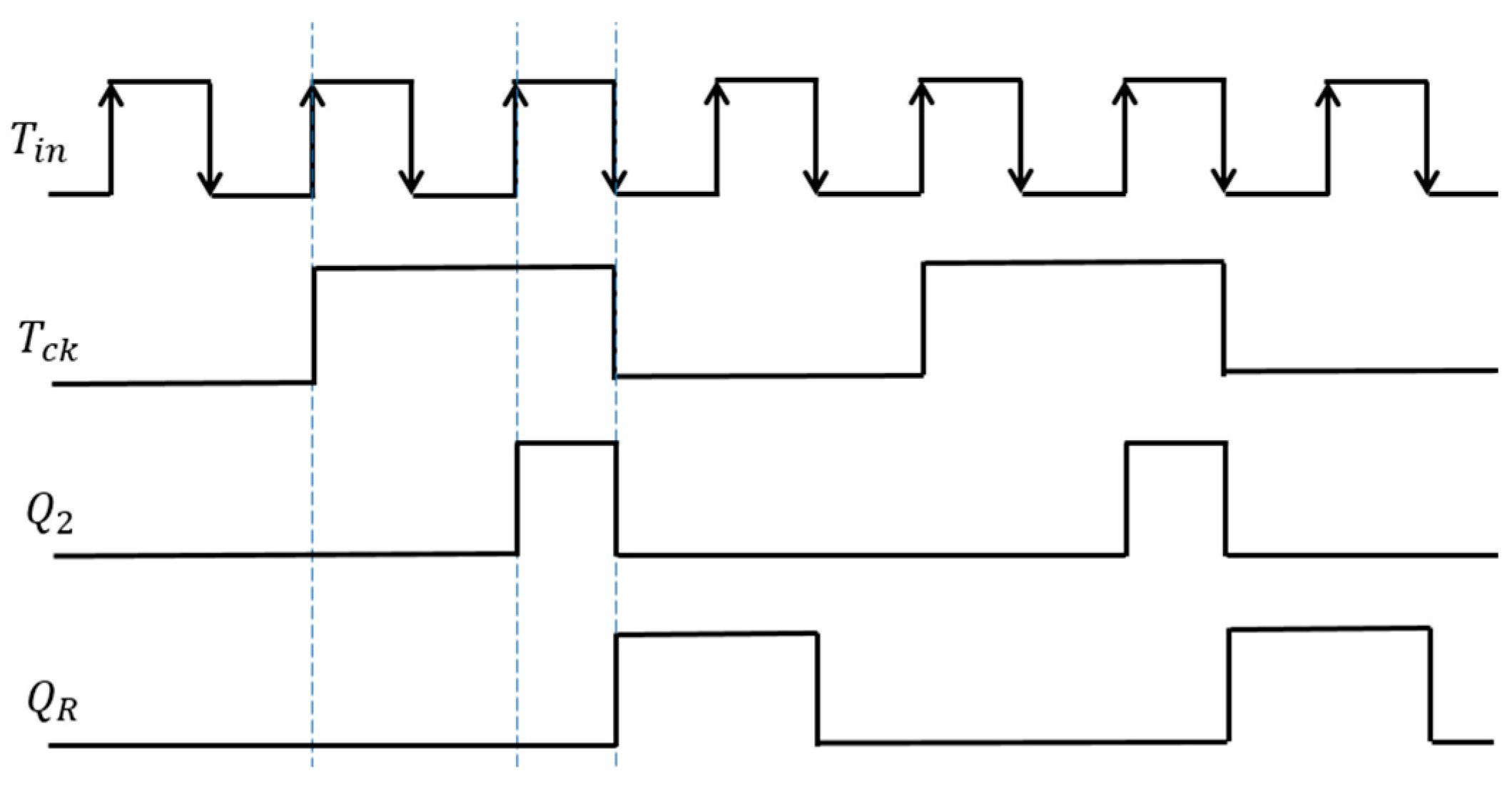
5. Notch Band Select with Pulse Coding Control [36,37,38,39]
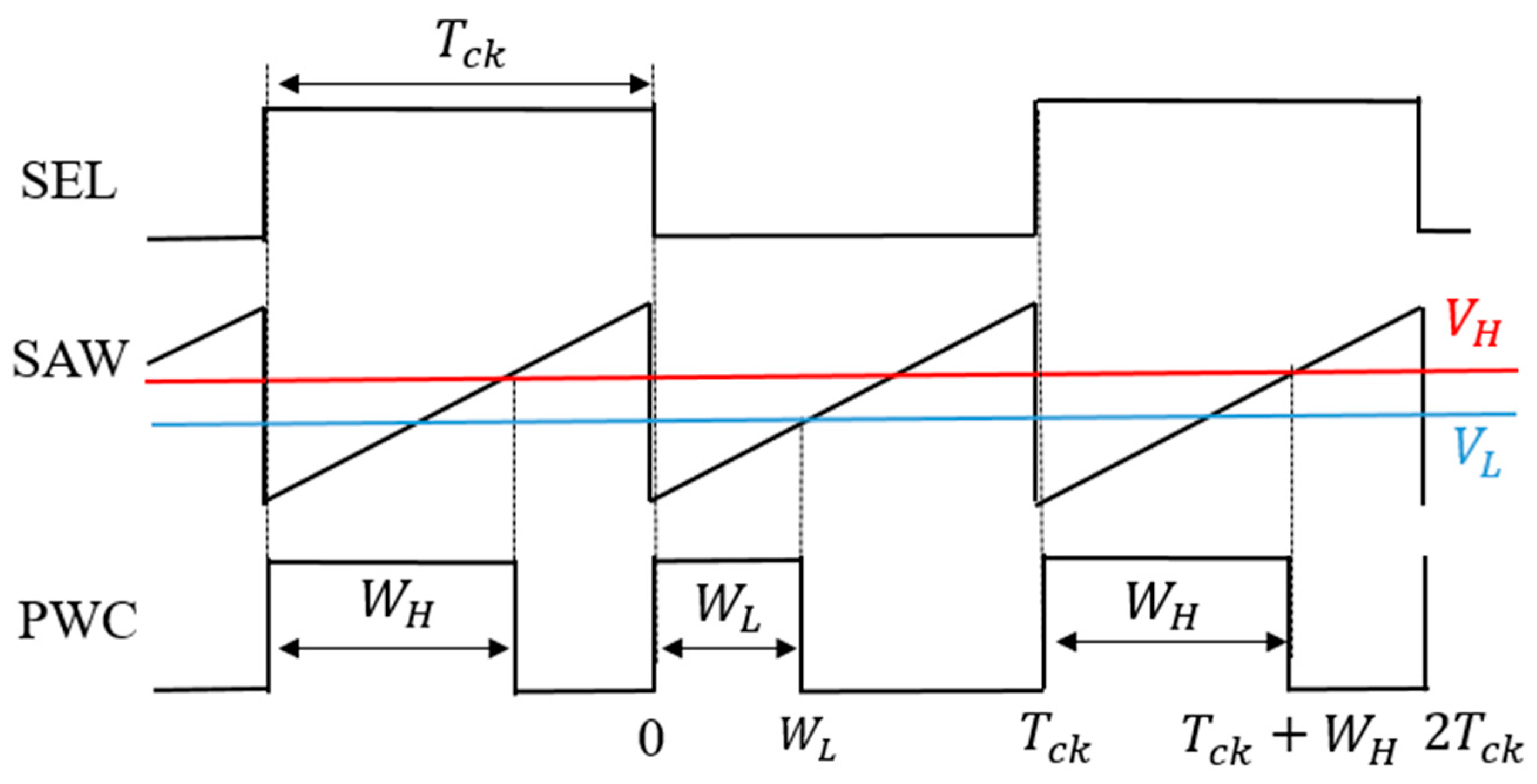
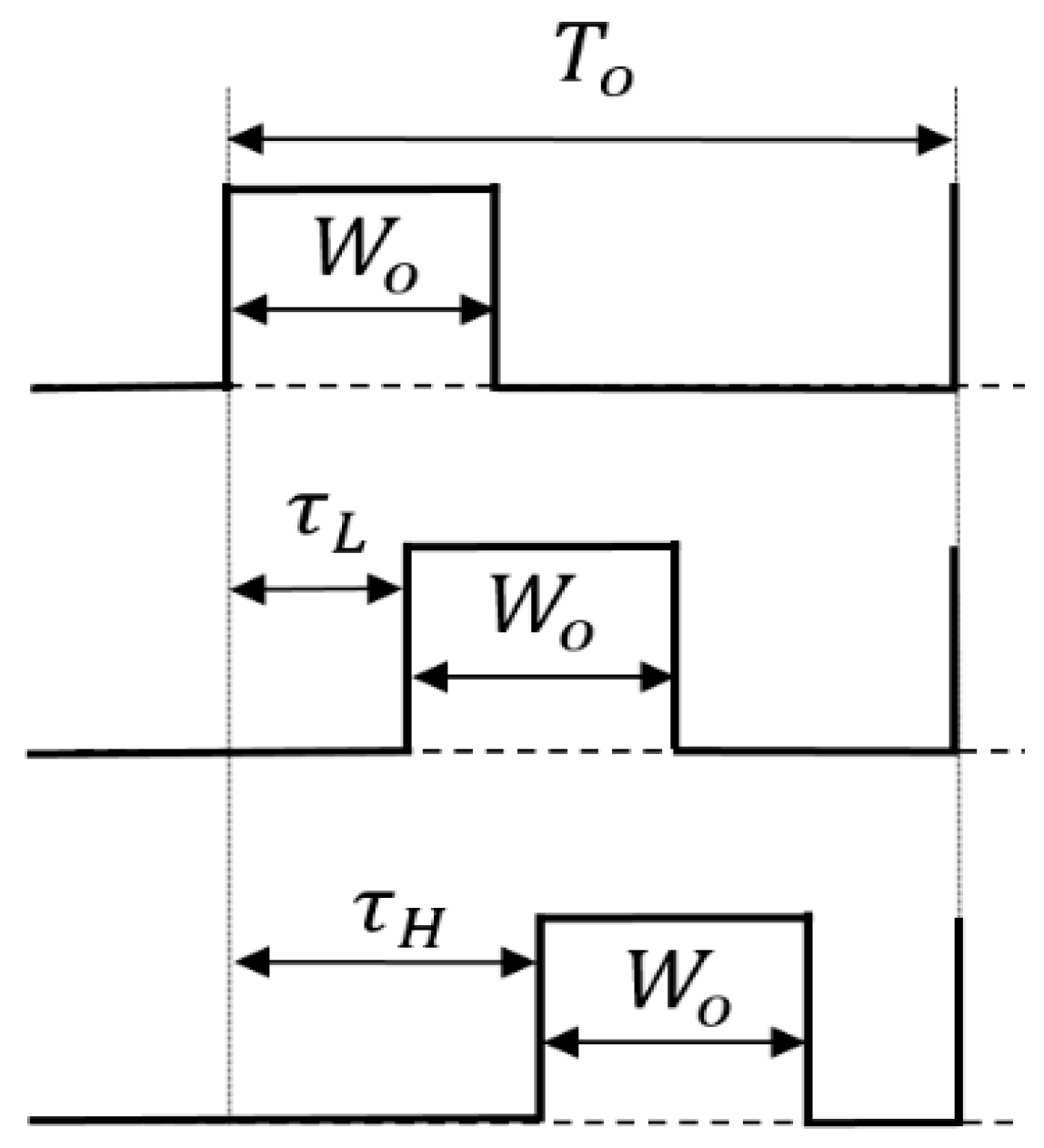
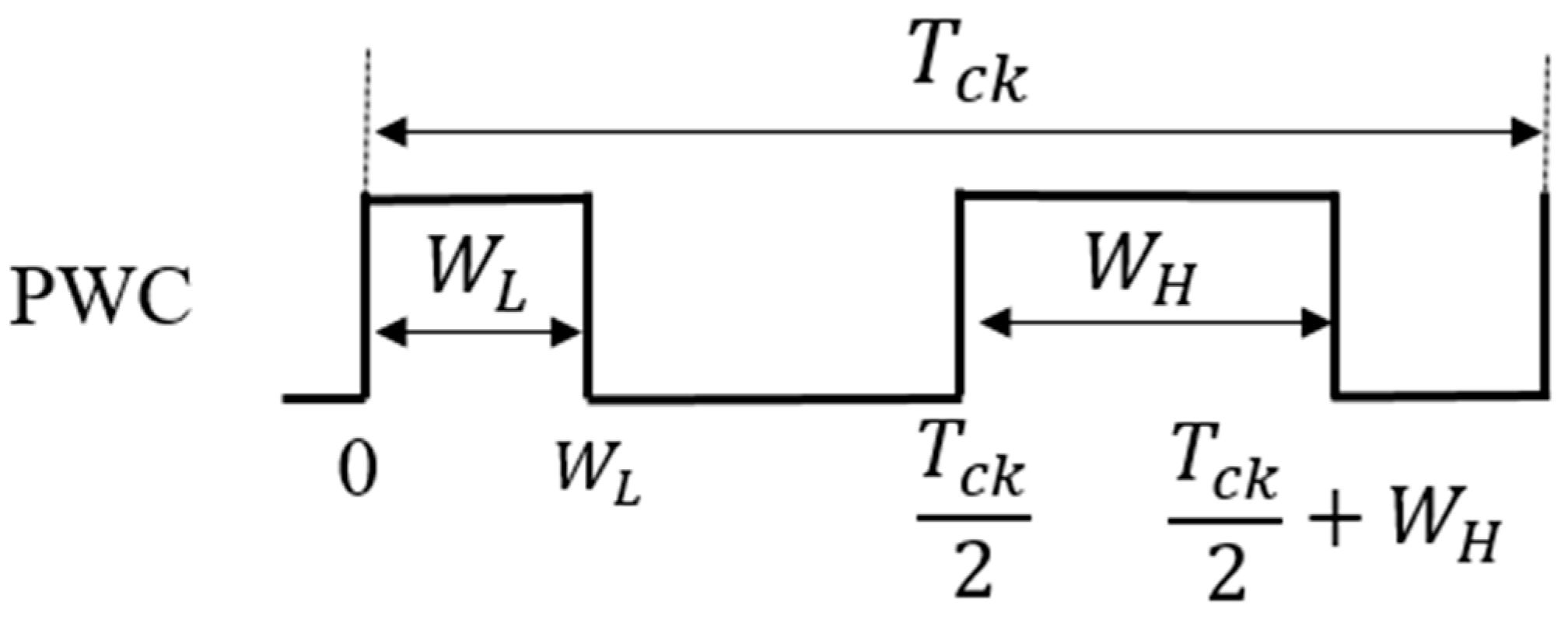
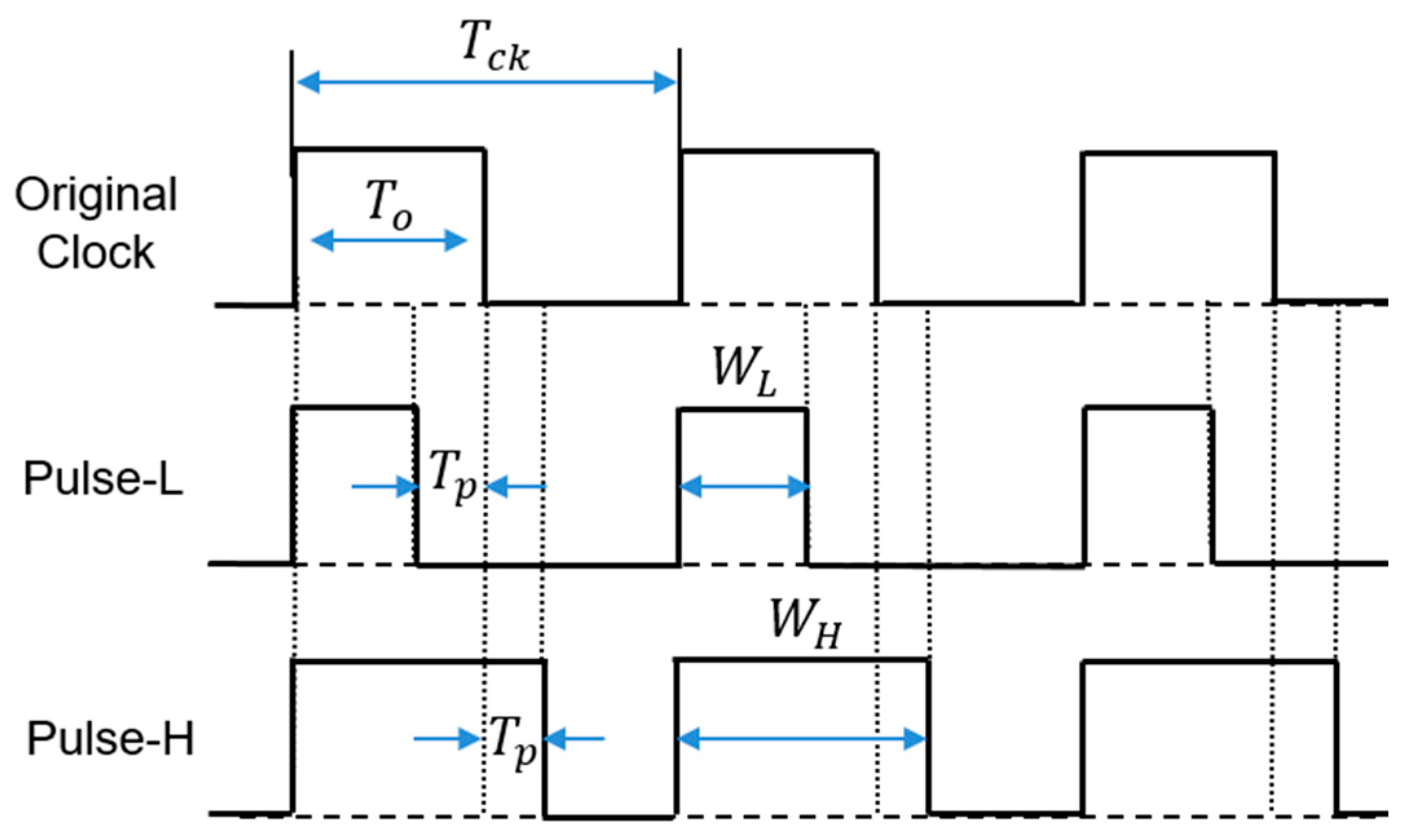
5.1. Pulse Width Coding (PWC) Control
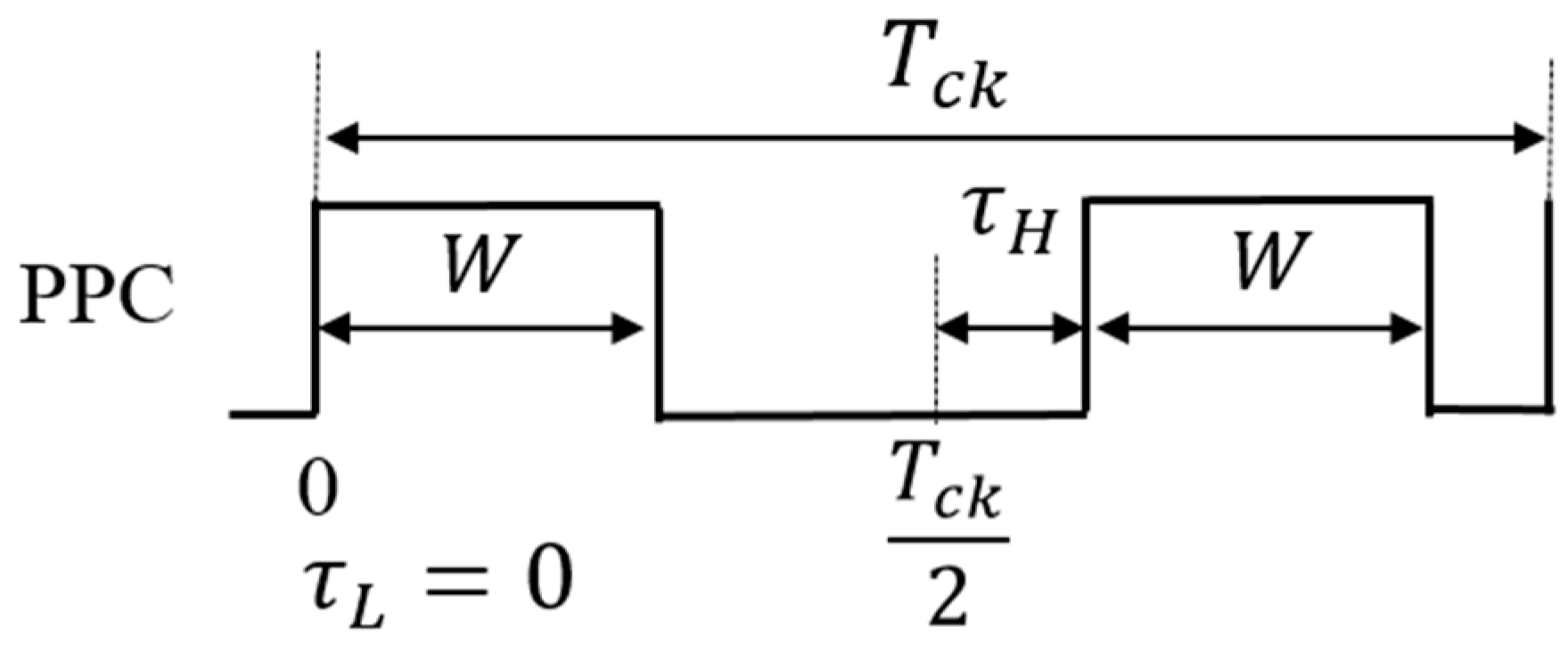
5.2. Pulse Phase Coding (PPC) Control
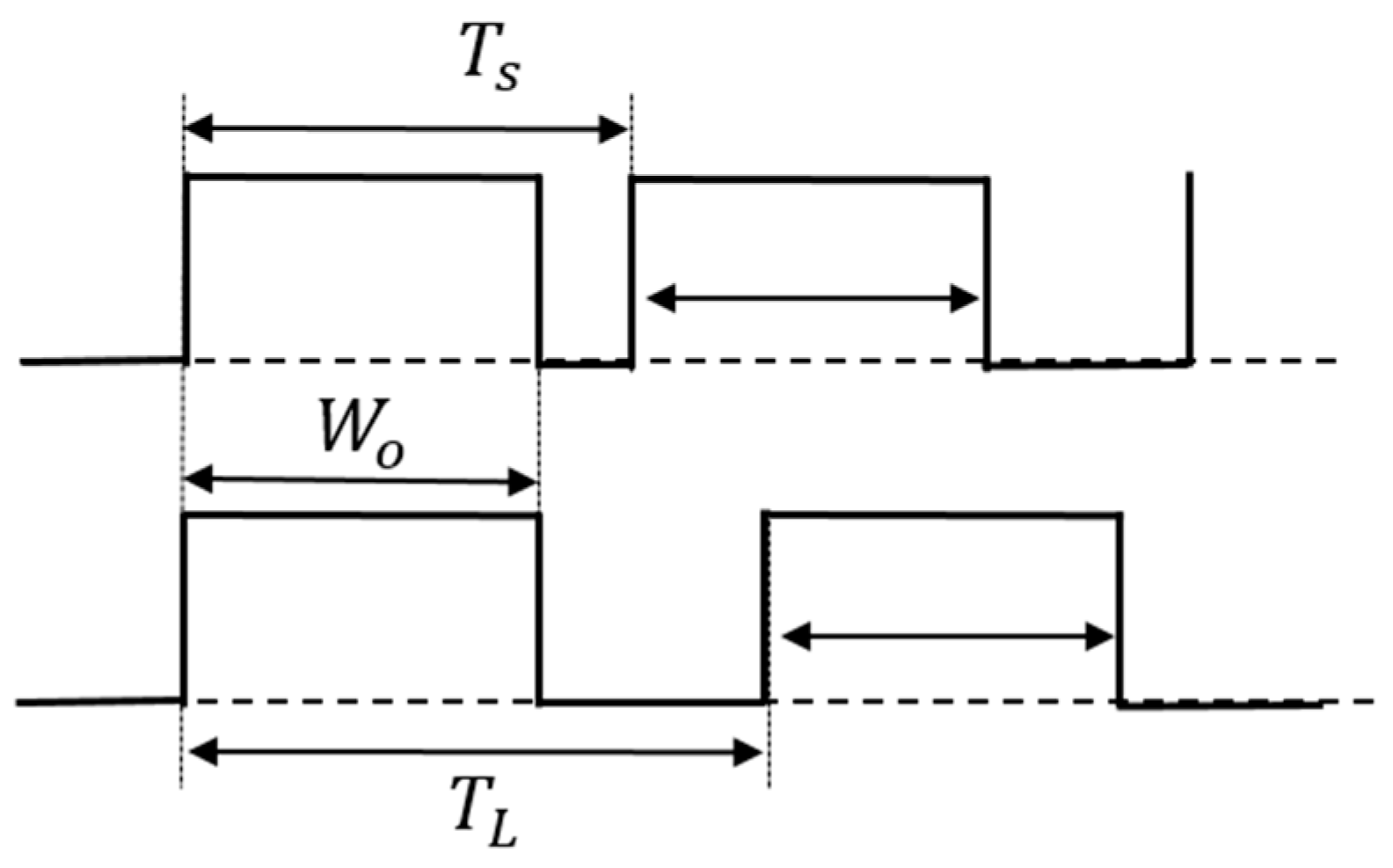
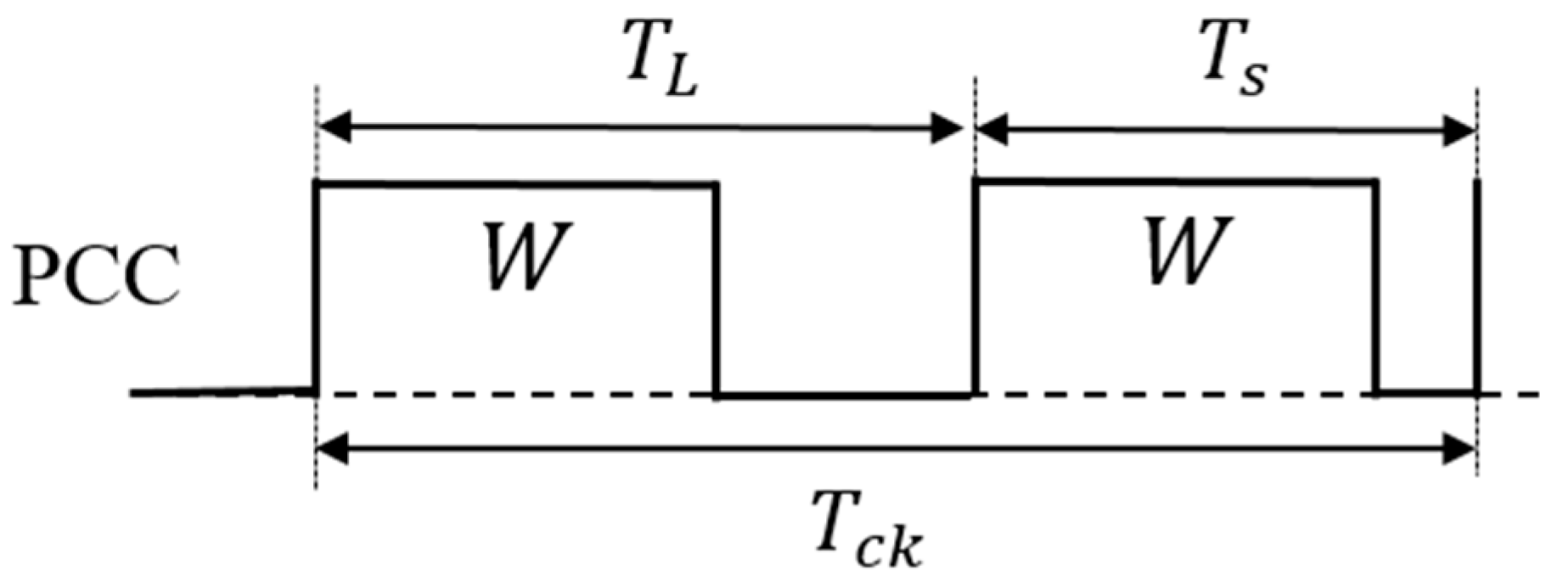
5.3. Pulse Cycle Coding (PCC) Control
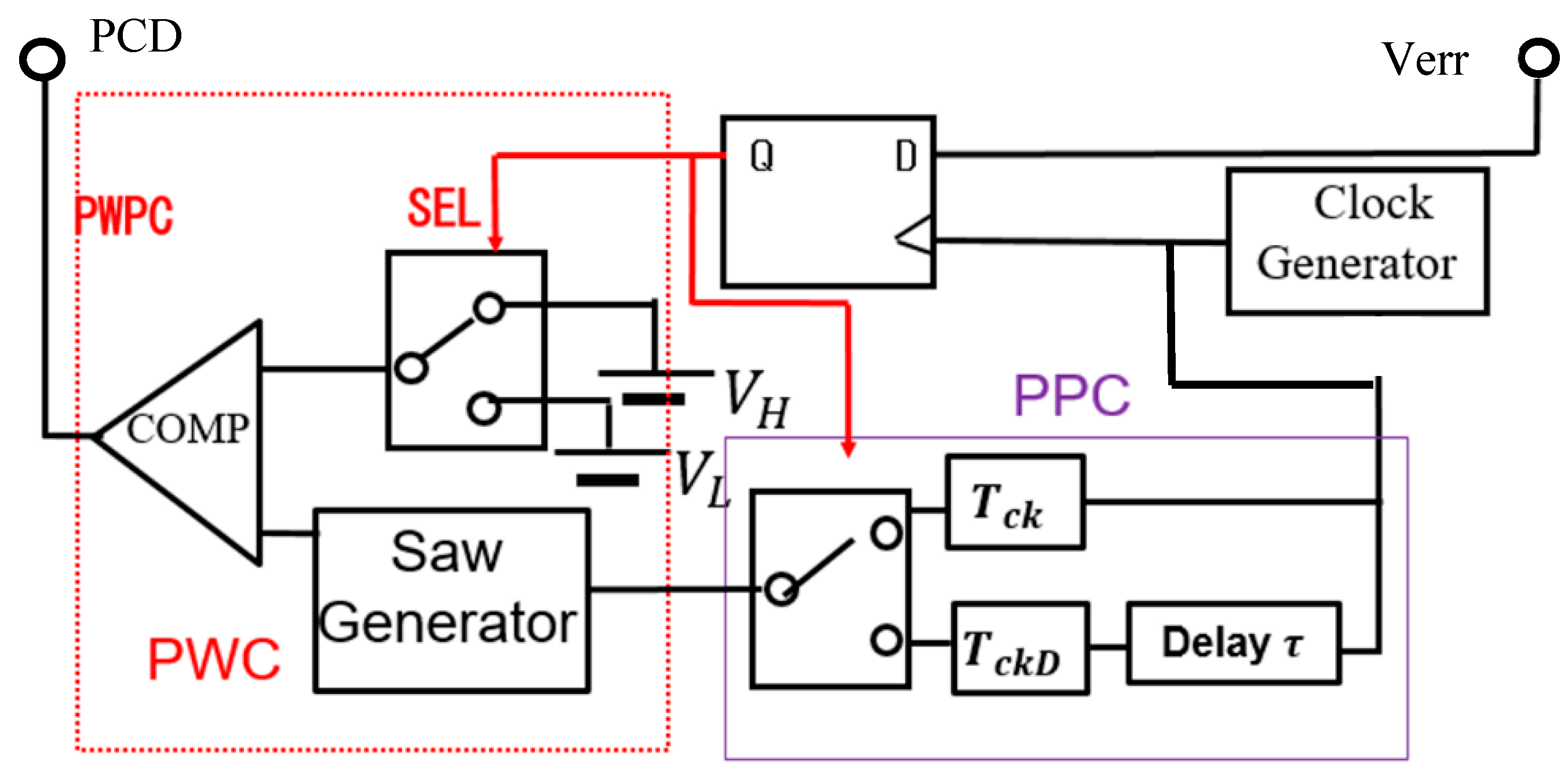
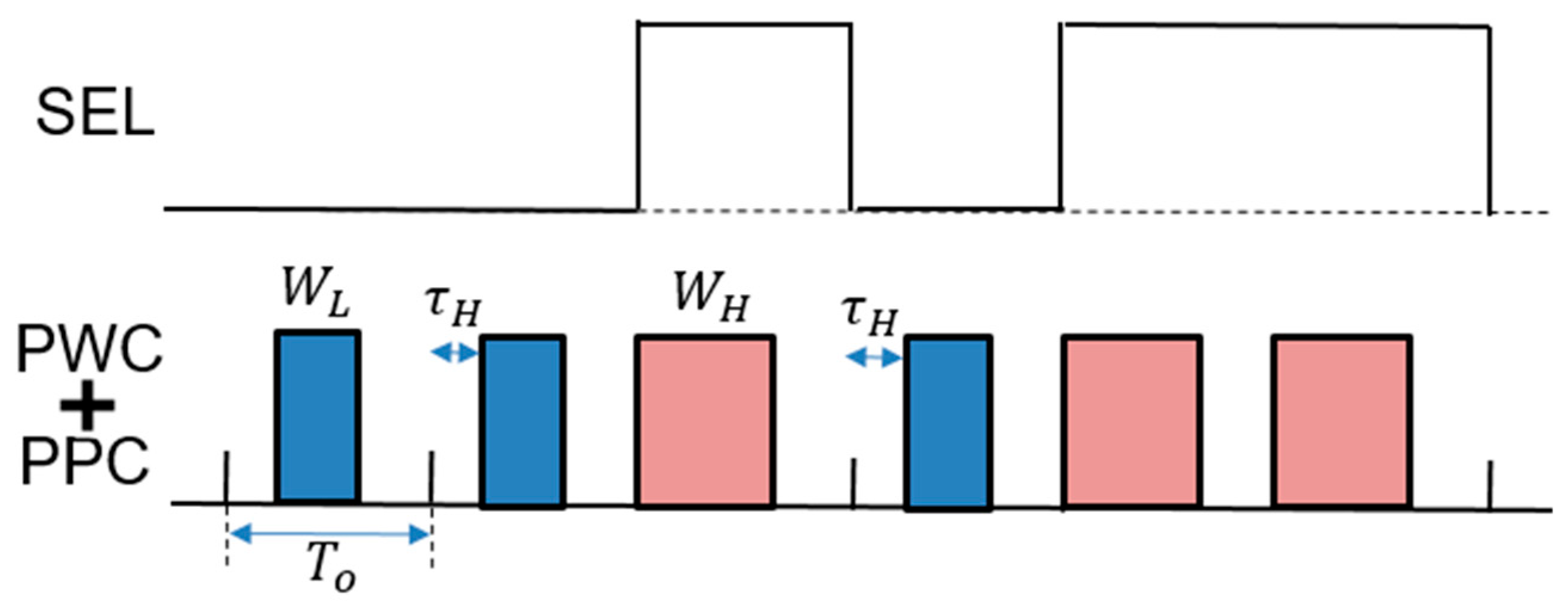
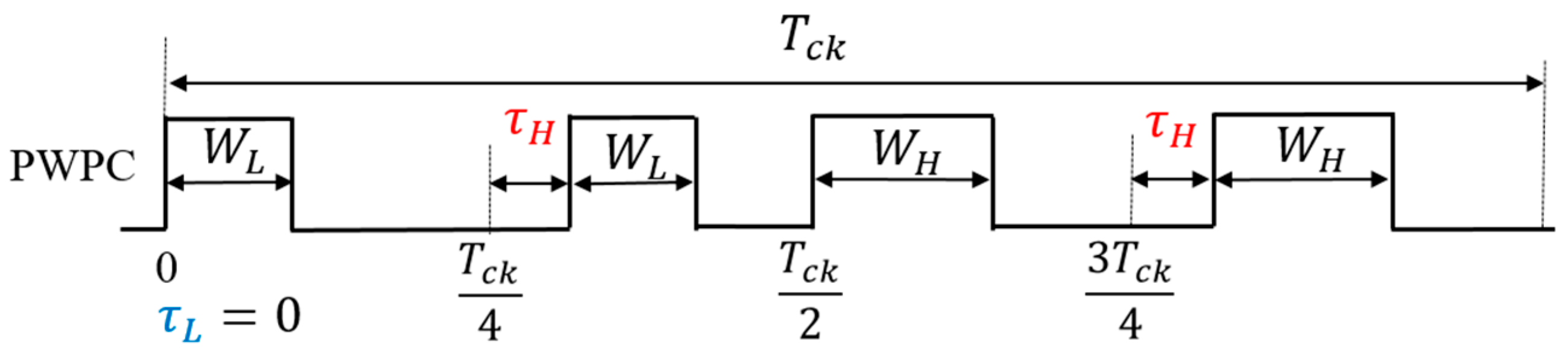
5.4. Pulse Width and Phase Coding (PWPC) Control
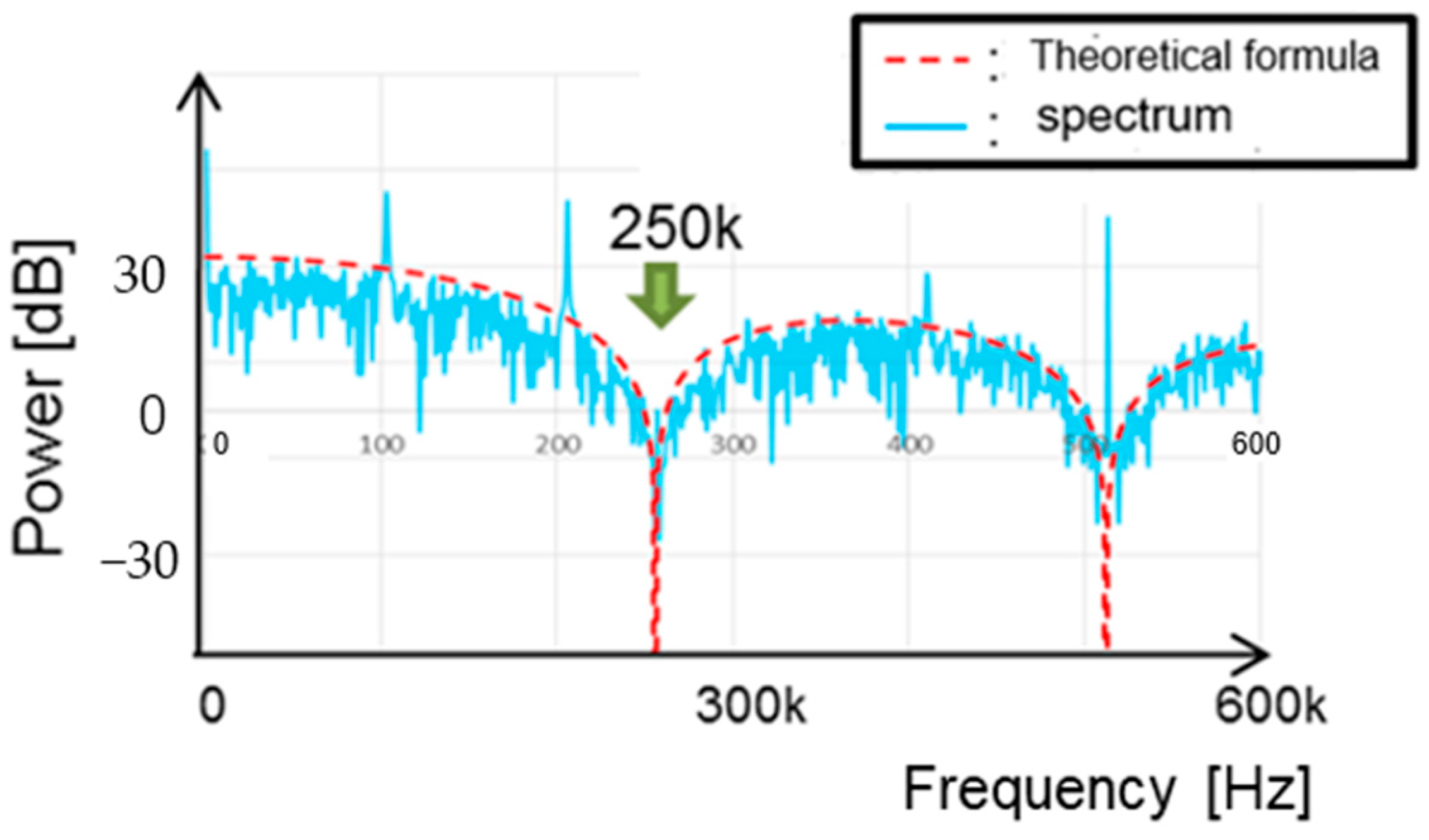
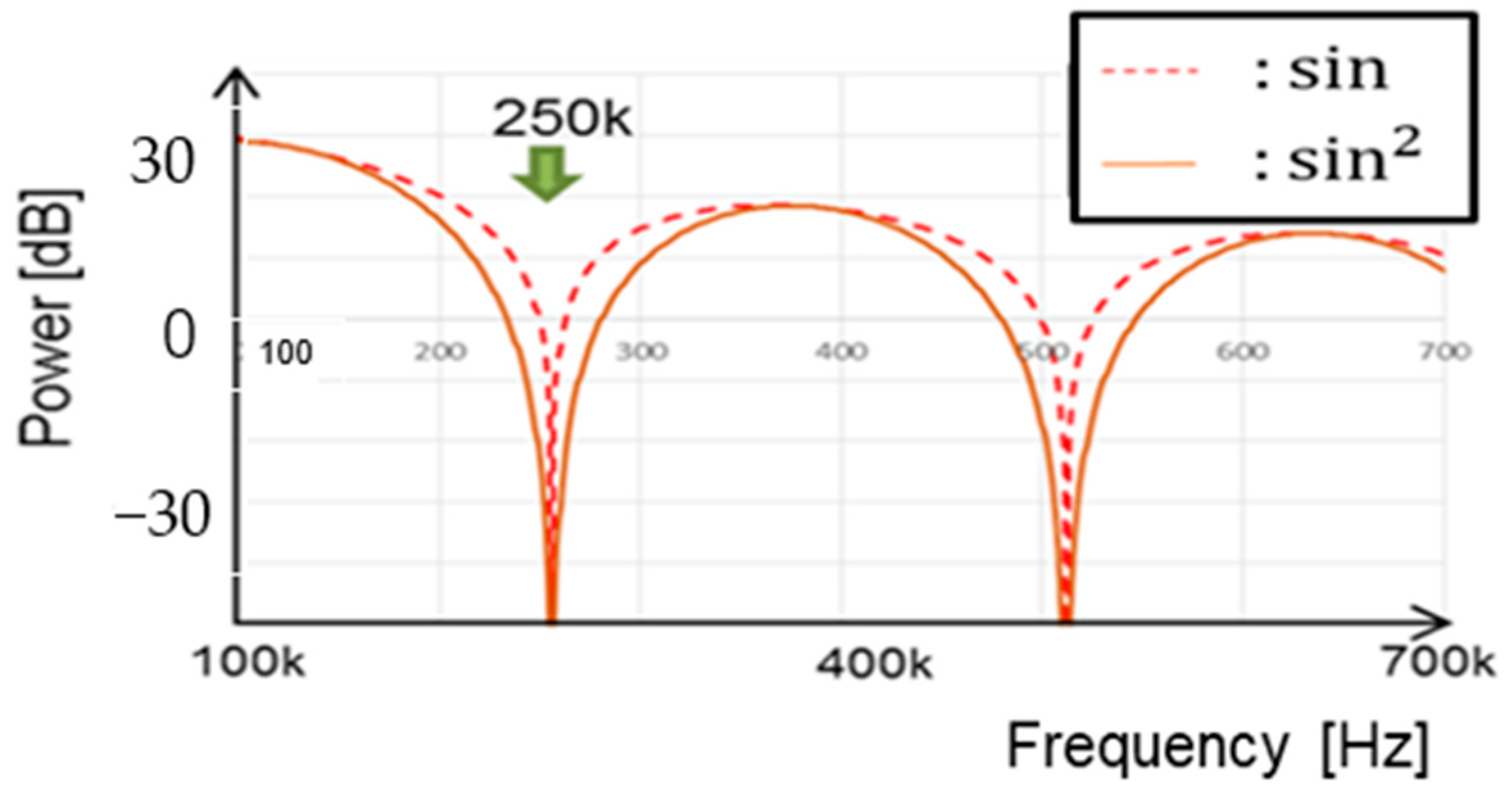
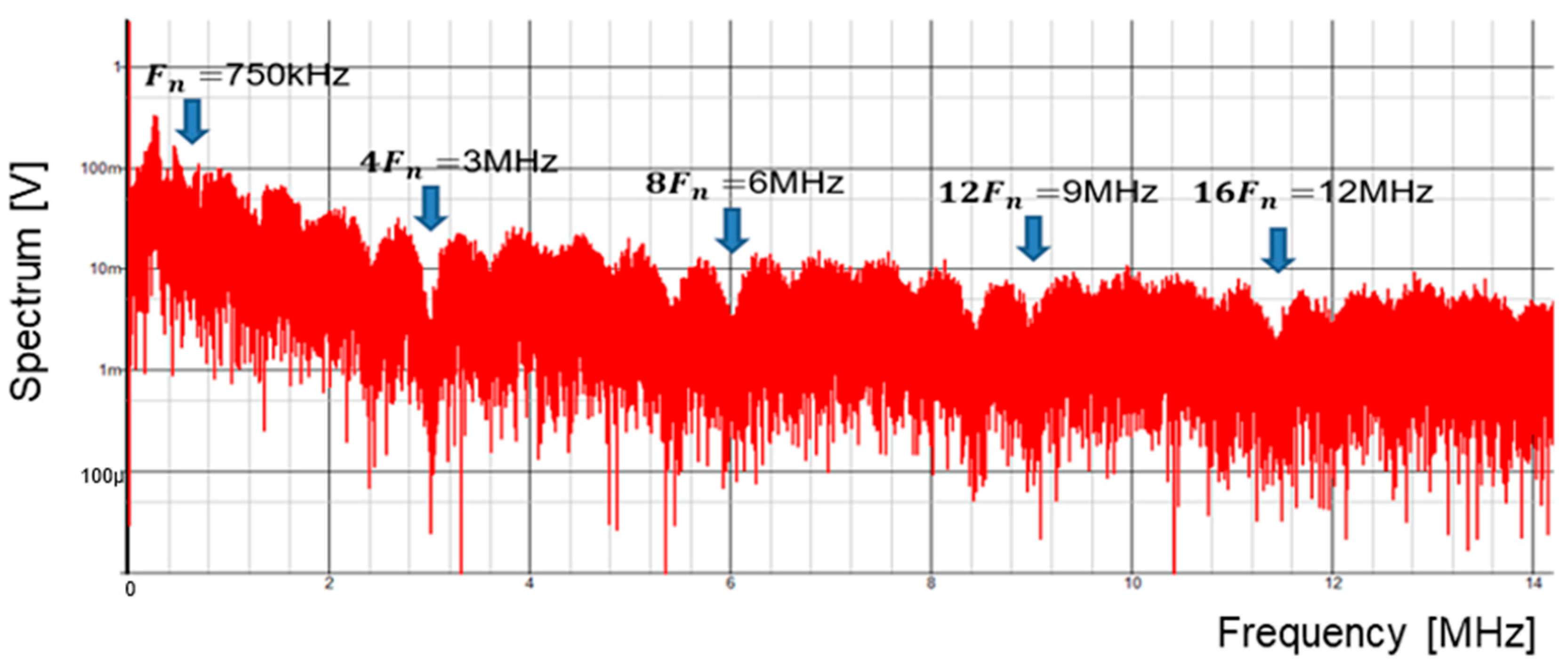
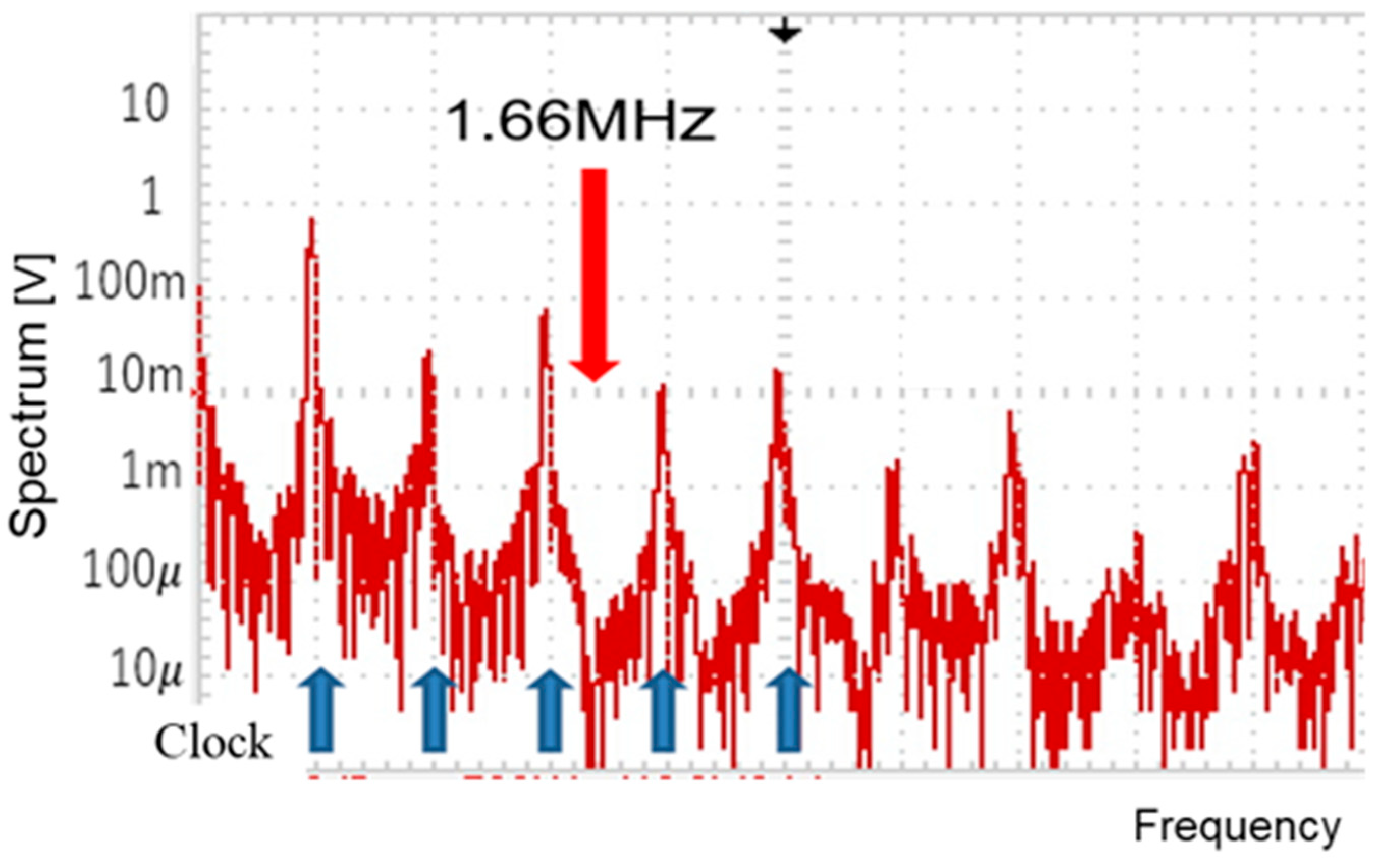
5.5. Derivation of Notch Frequency Using Fourier Transform
- (1)
- Define the signal of the pulse coding method;
- (2)
- Determine its Fourier transform;
- (3)
- Take its absolute value to obtain their spectrum characteristics;
- (4)
- Derive its zero point.
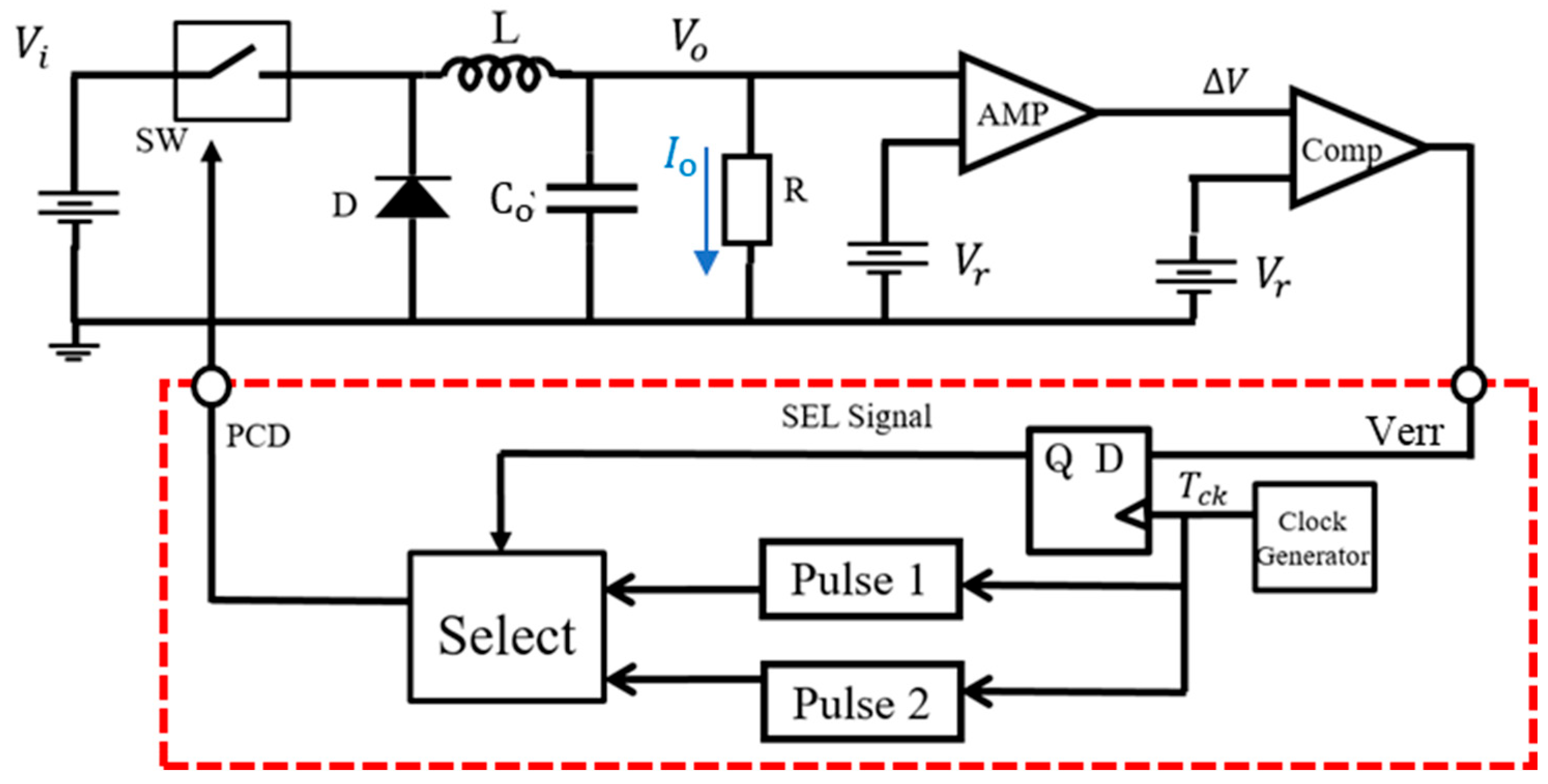
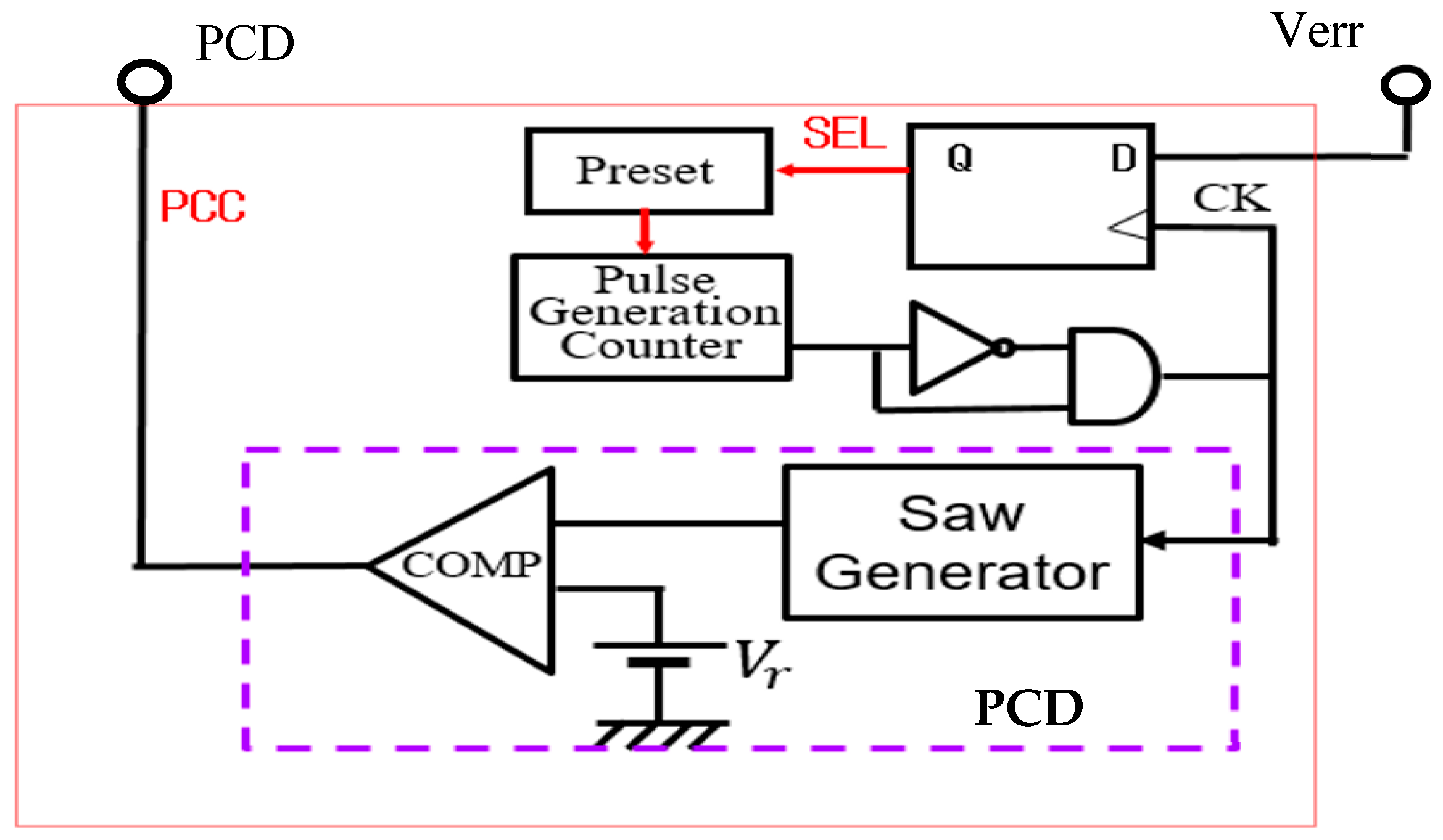
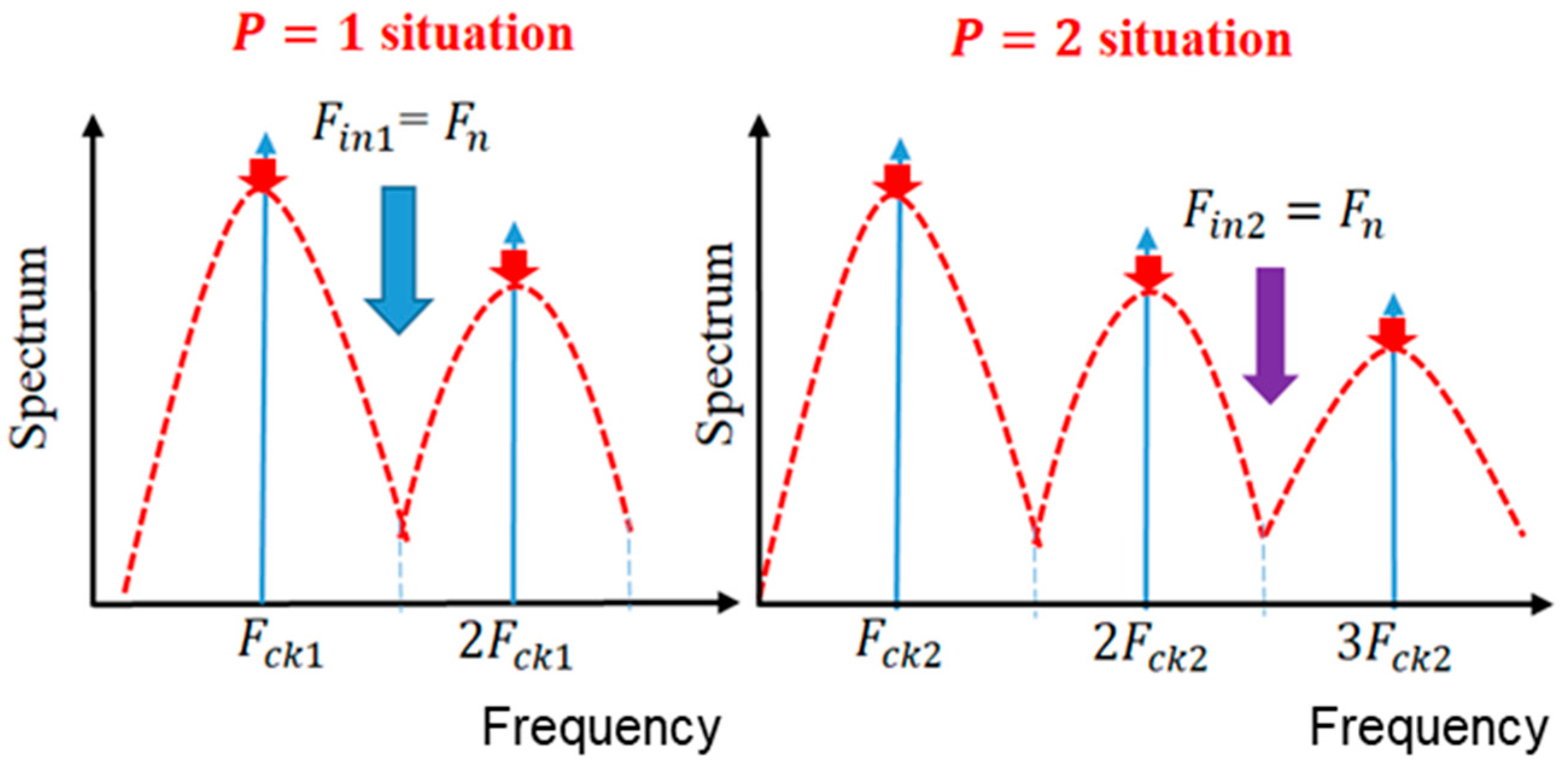
6. Automatic Notch Generation [36,37,38,39]
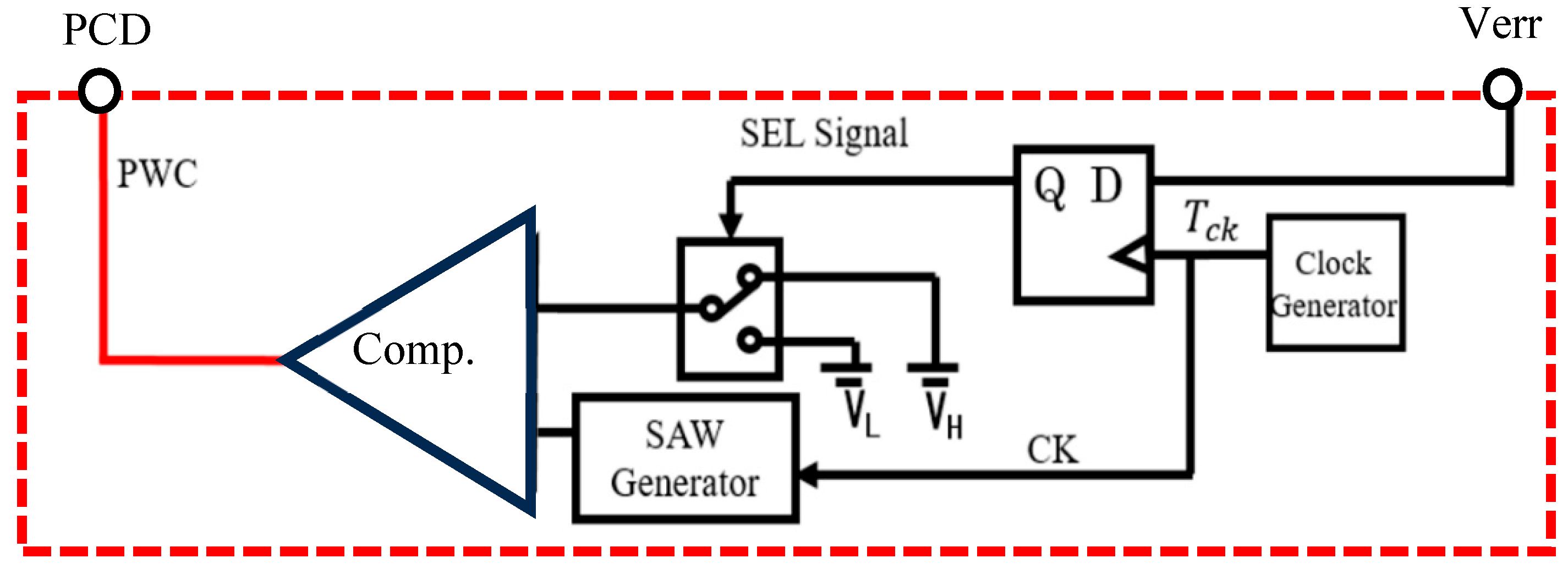
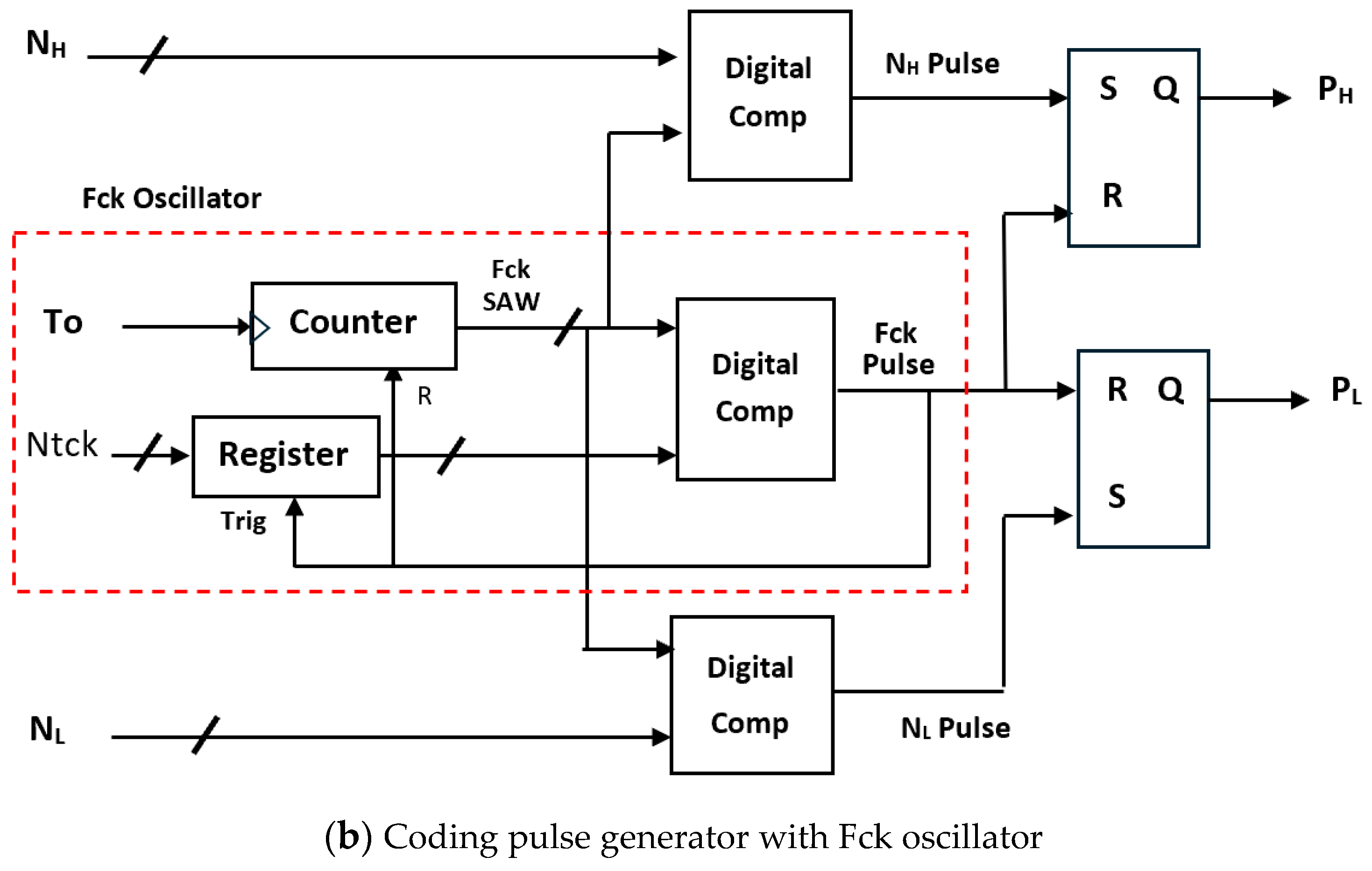
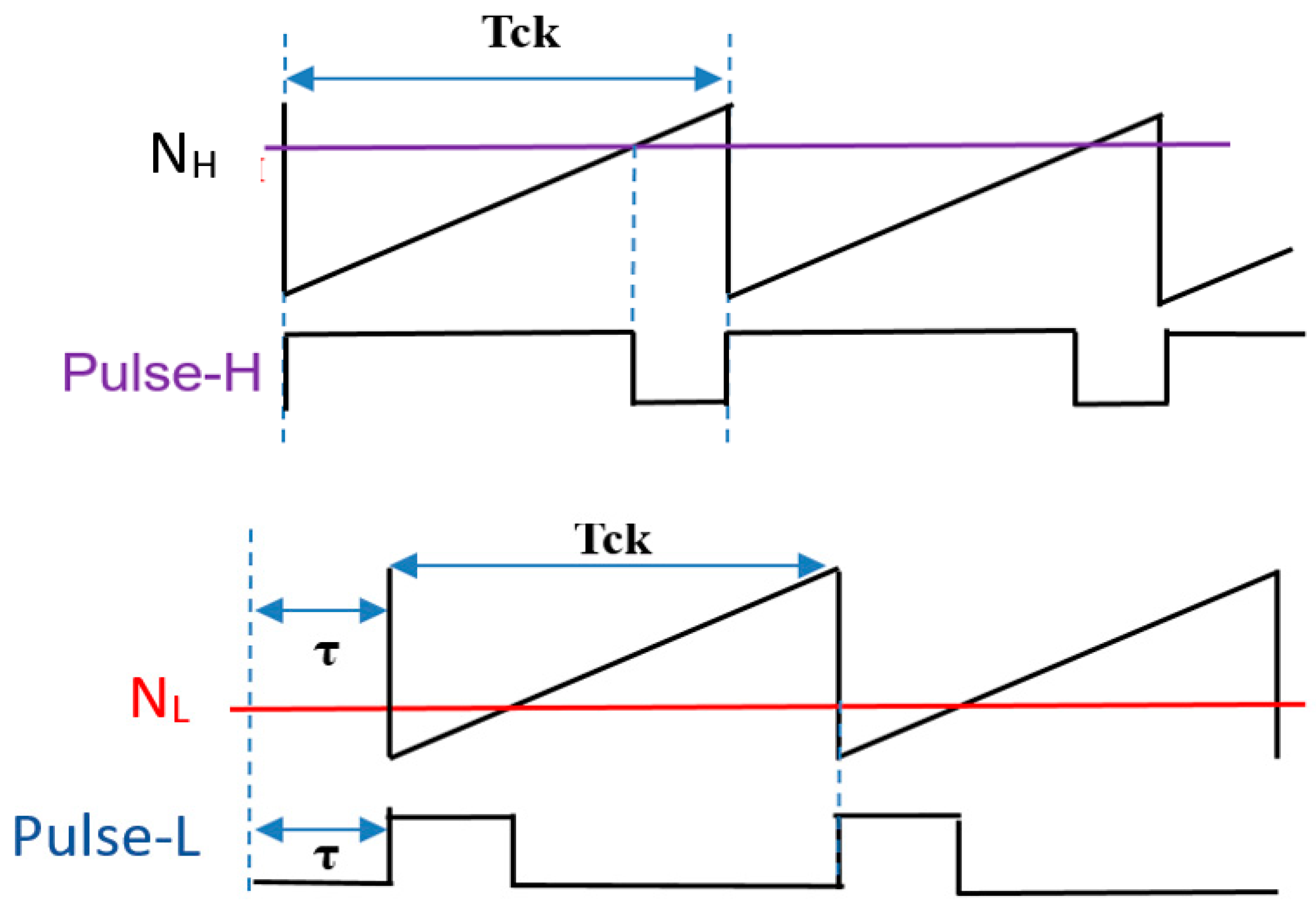
6.1. Automatic Notch Generation Using PWC Control
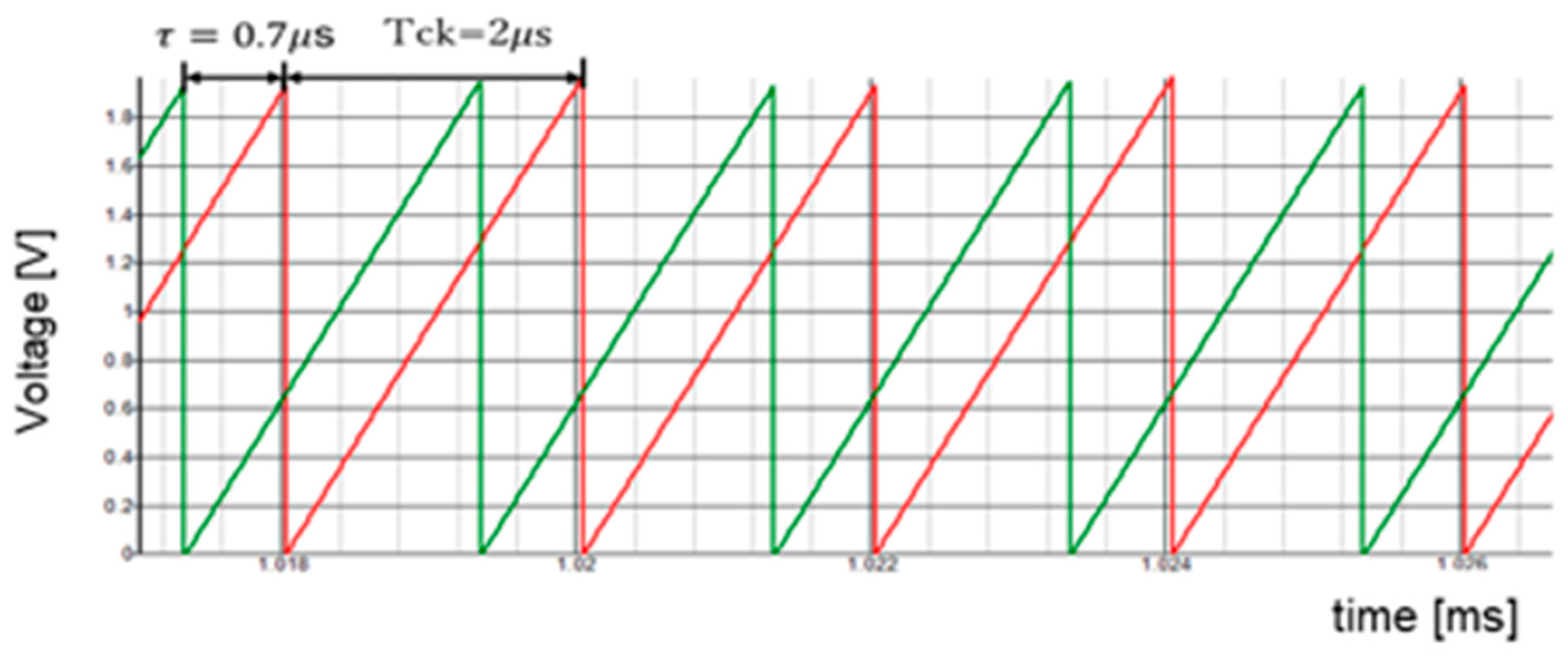
6.2. Automatic Notch Generation with PWPC Control
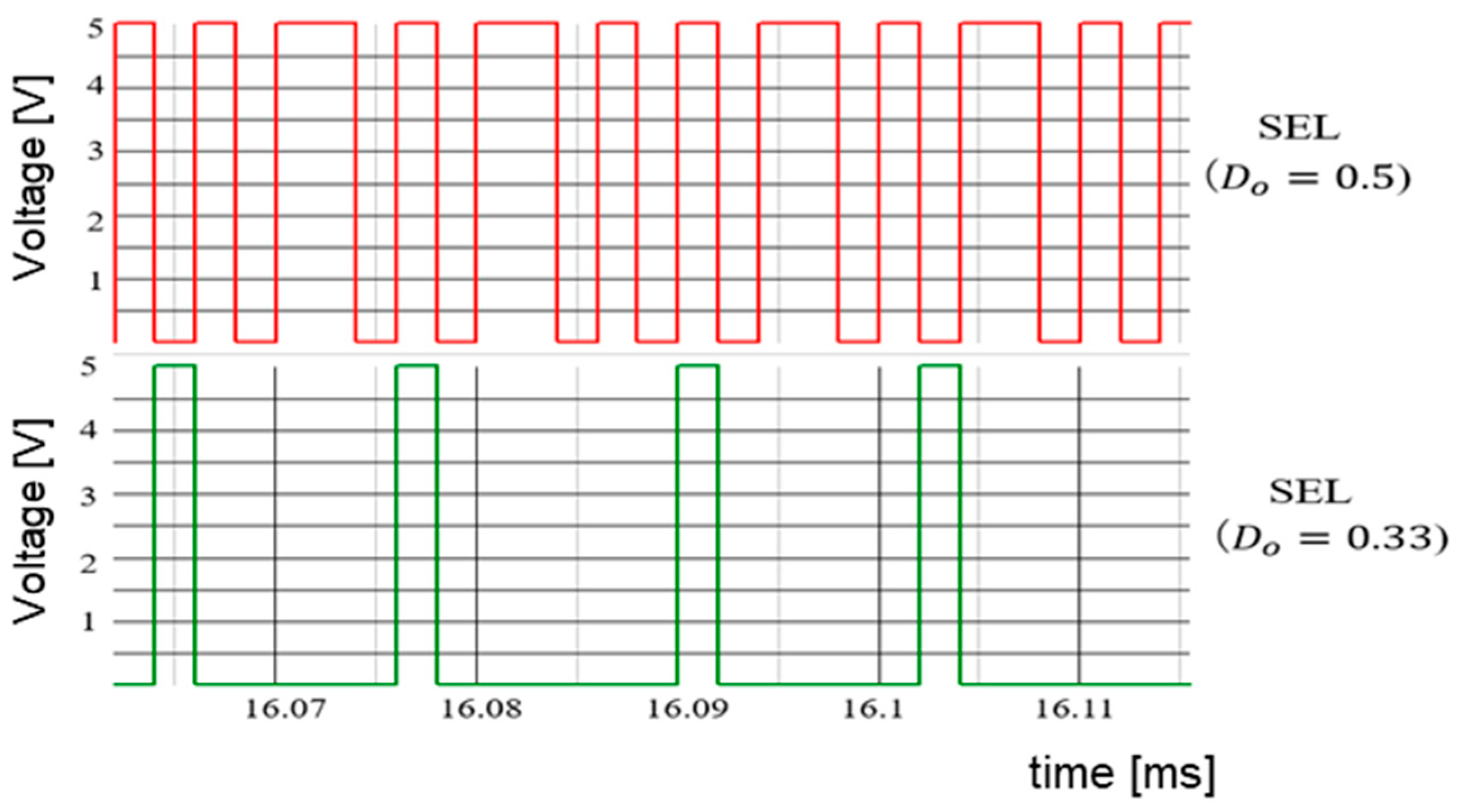
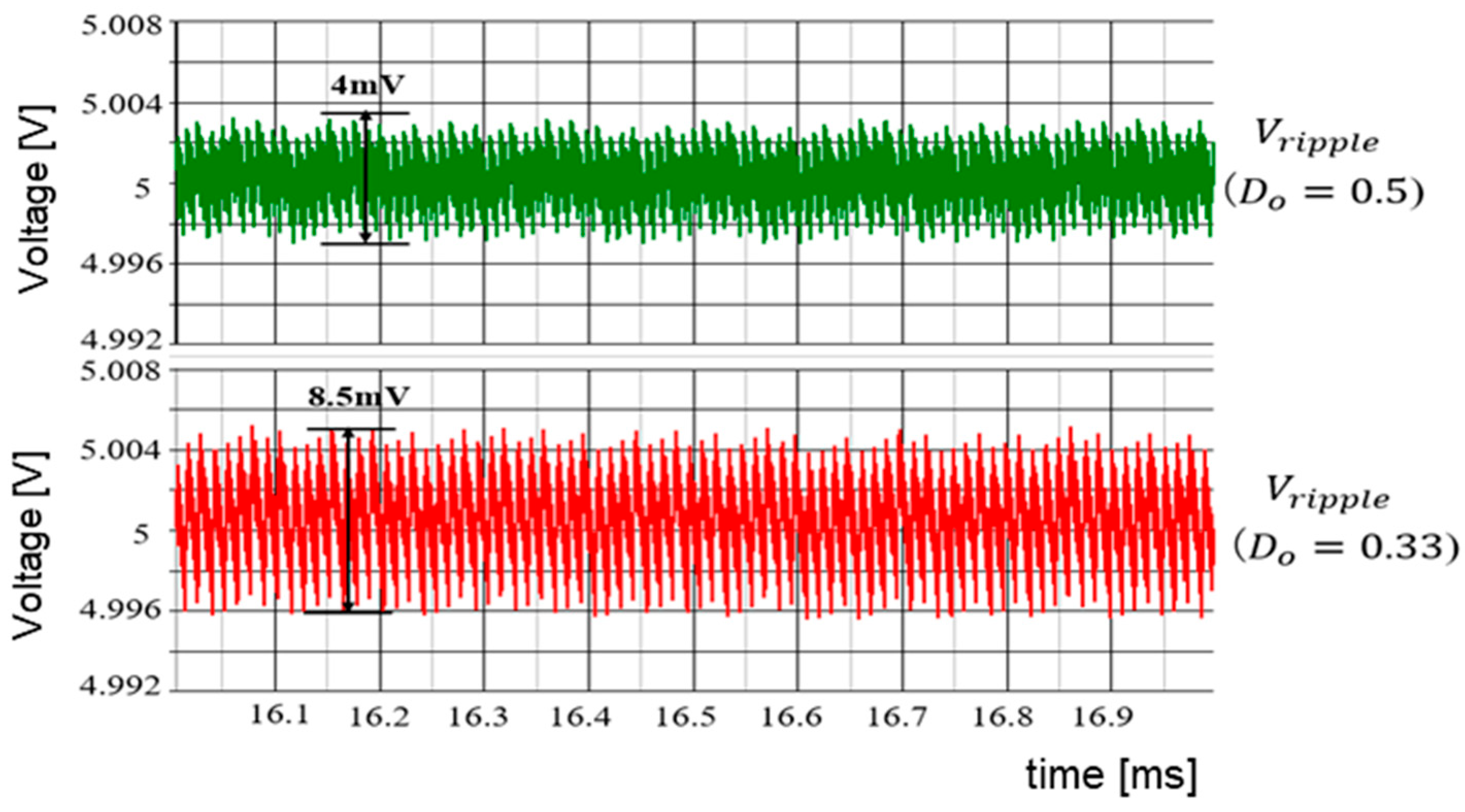
6.3. Duty Ratio Generation in Automatic Notch Generation
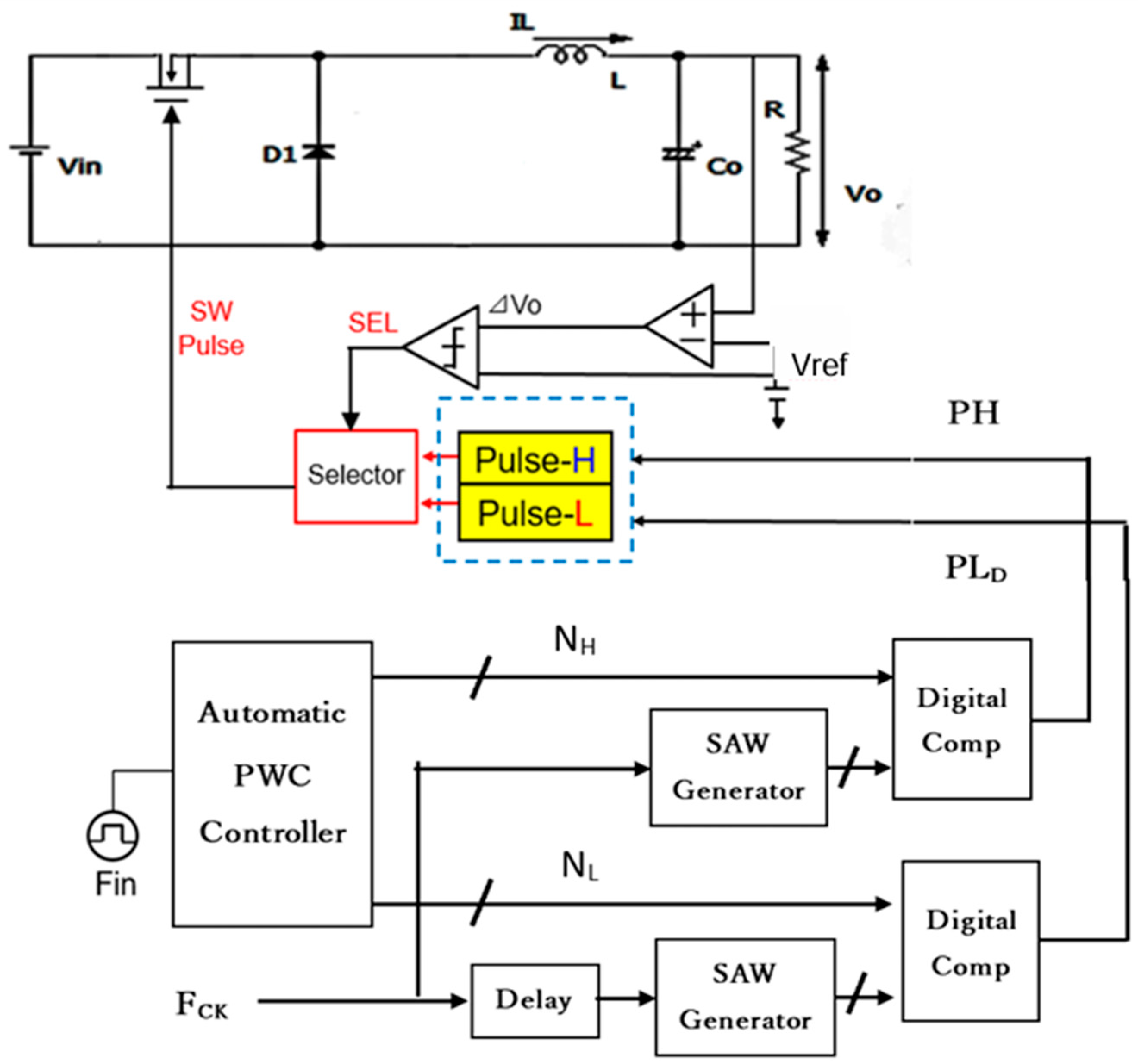
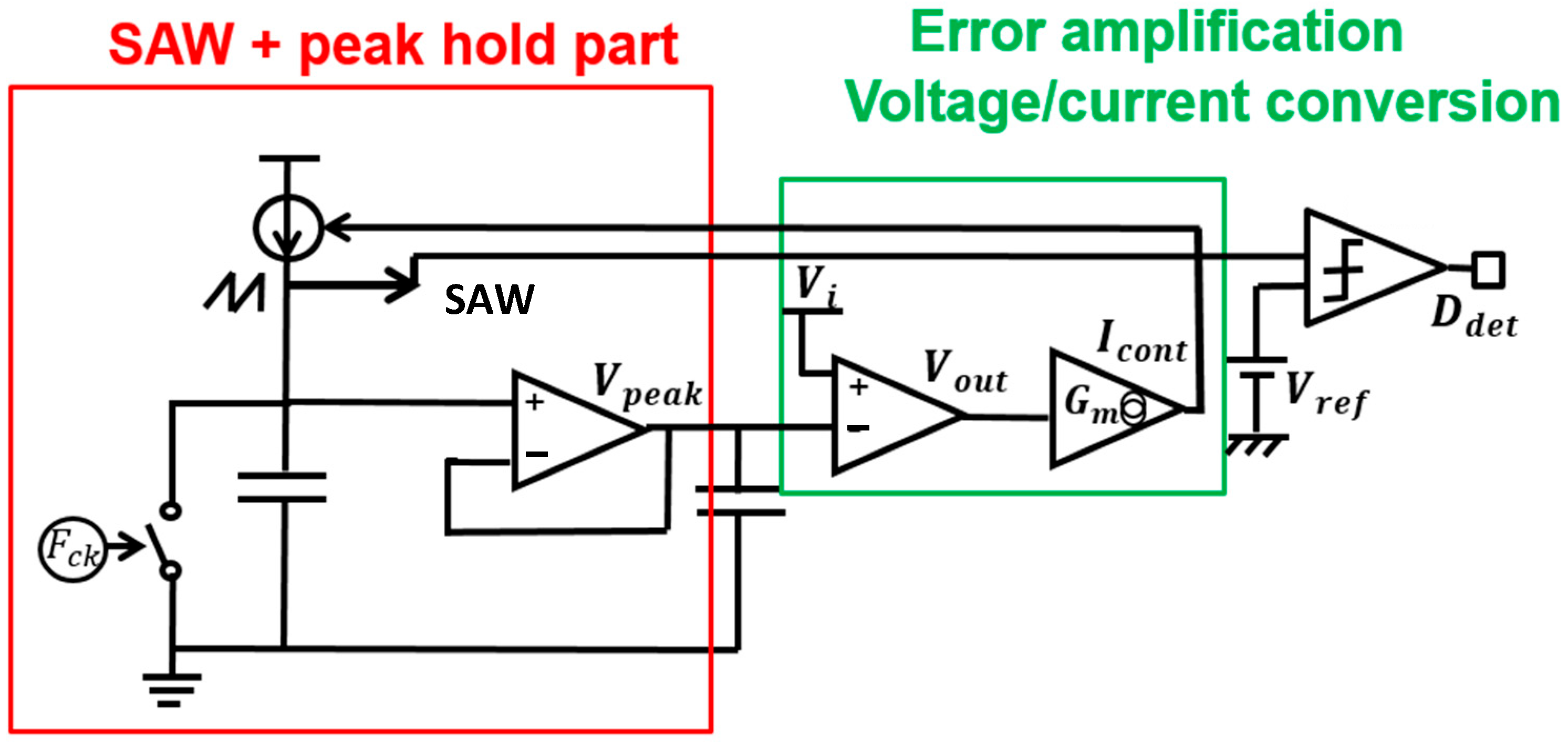
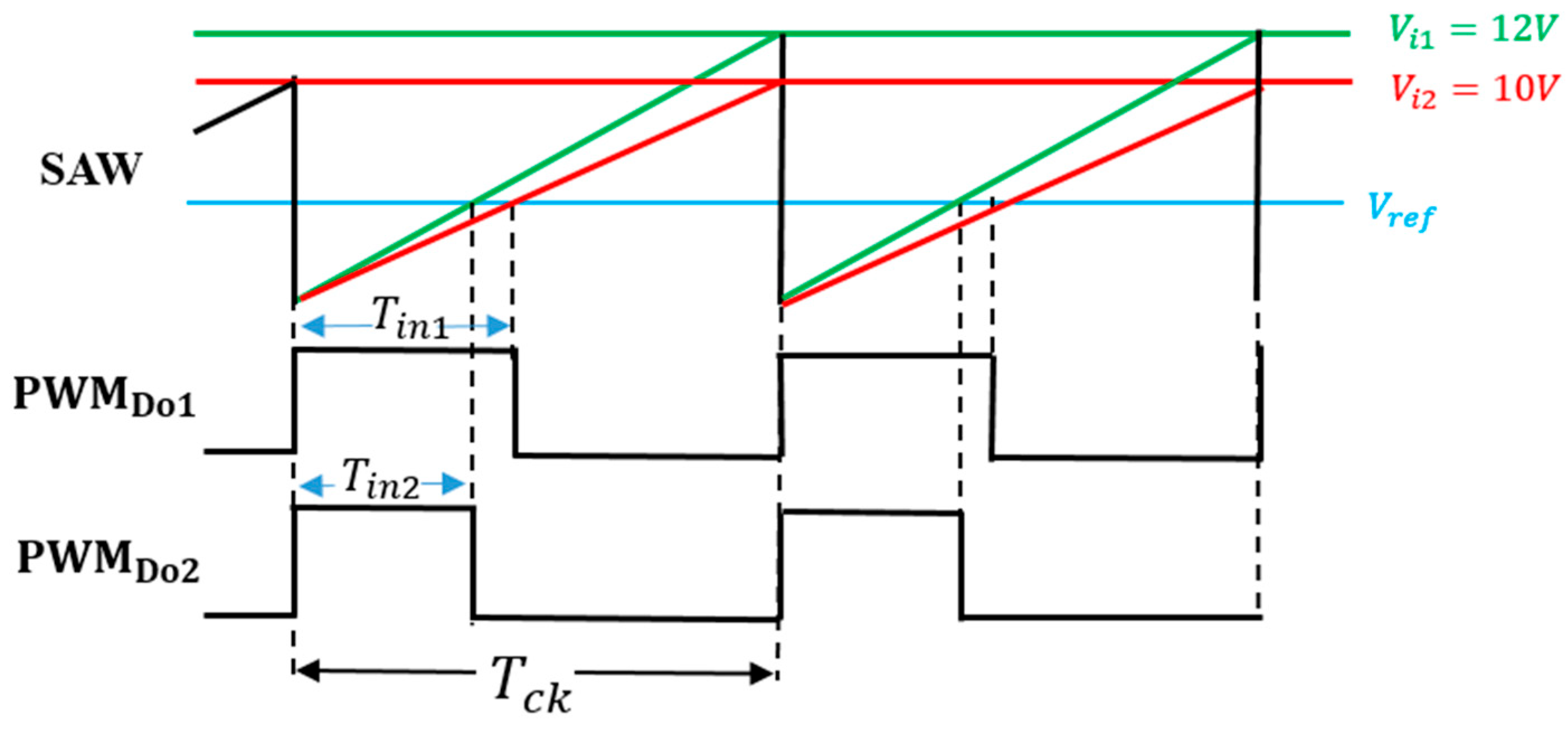
7. Implementation of PWC Controlled Converter with Notch Generation
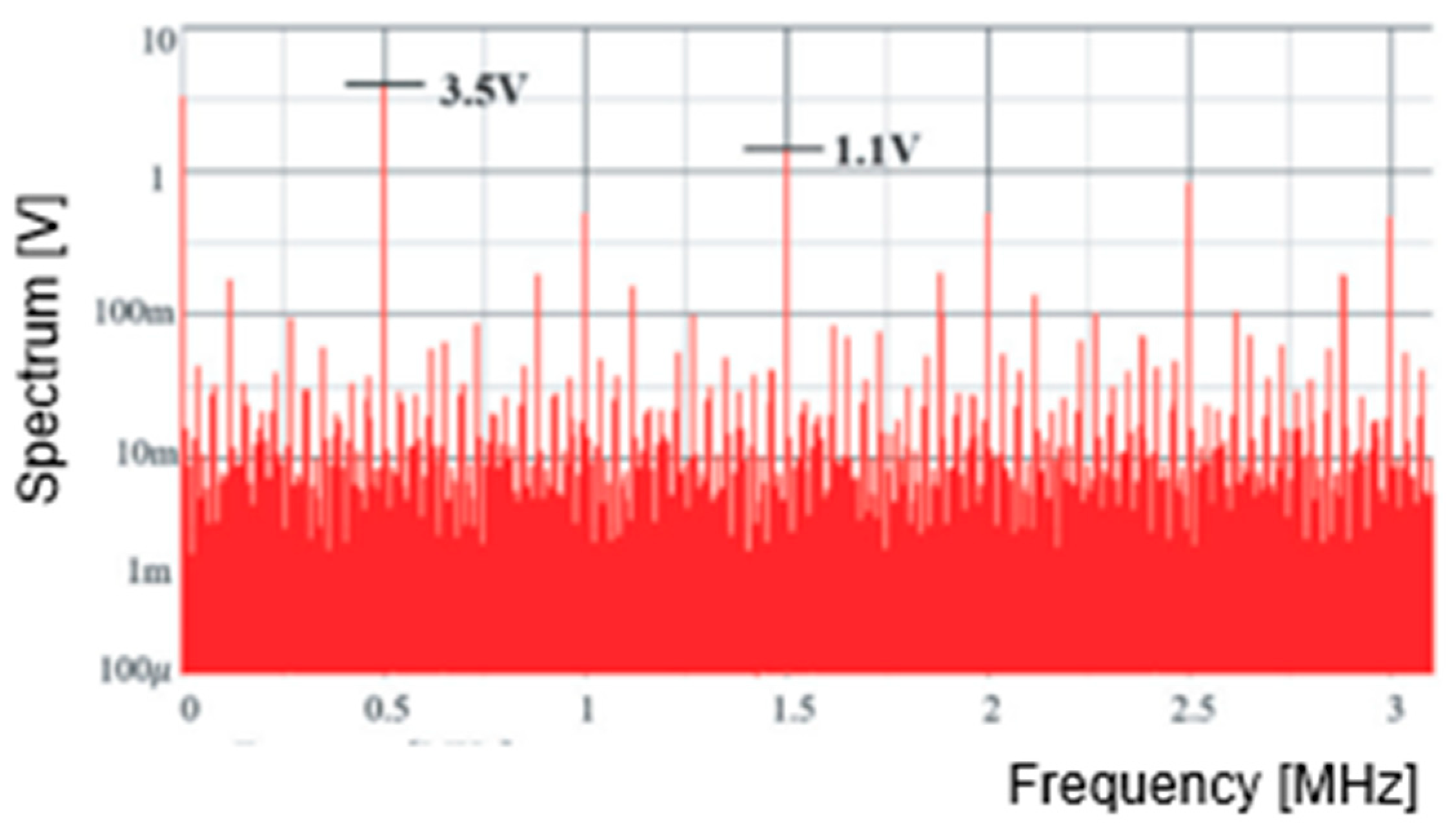
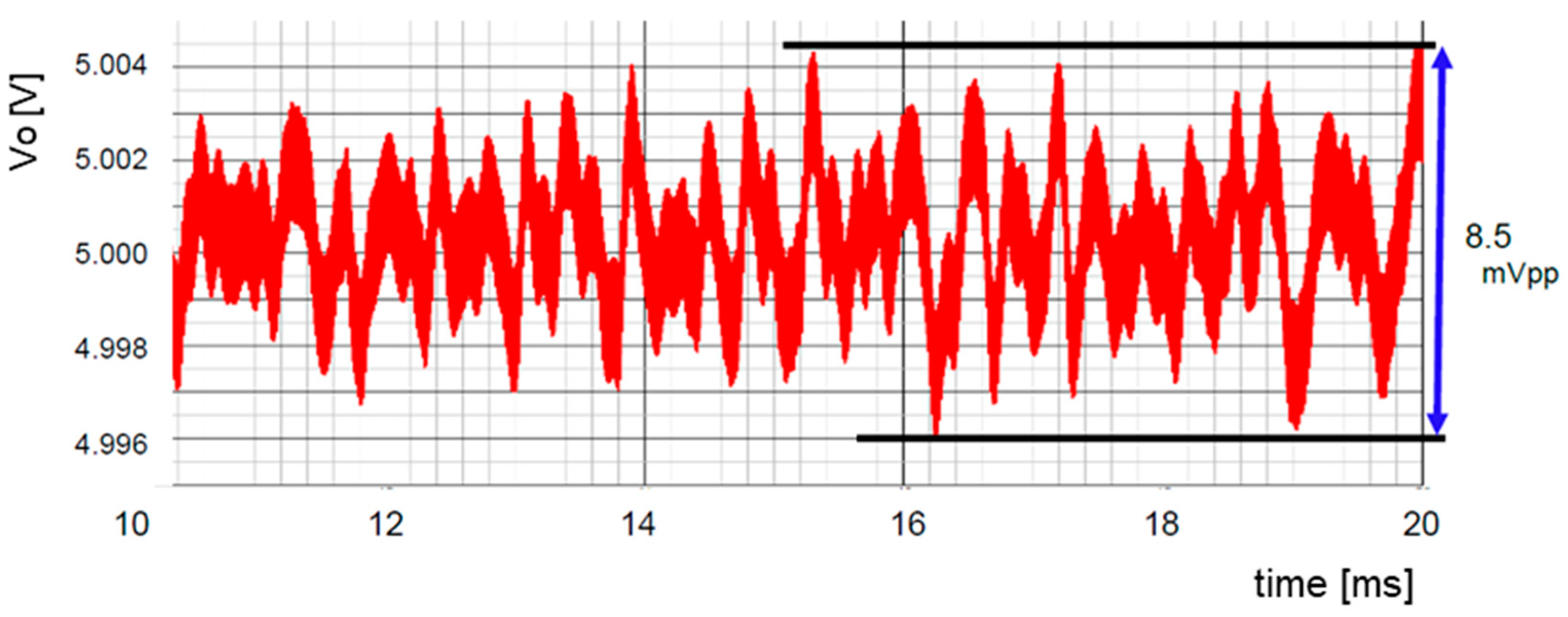
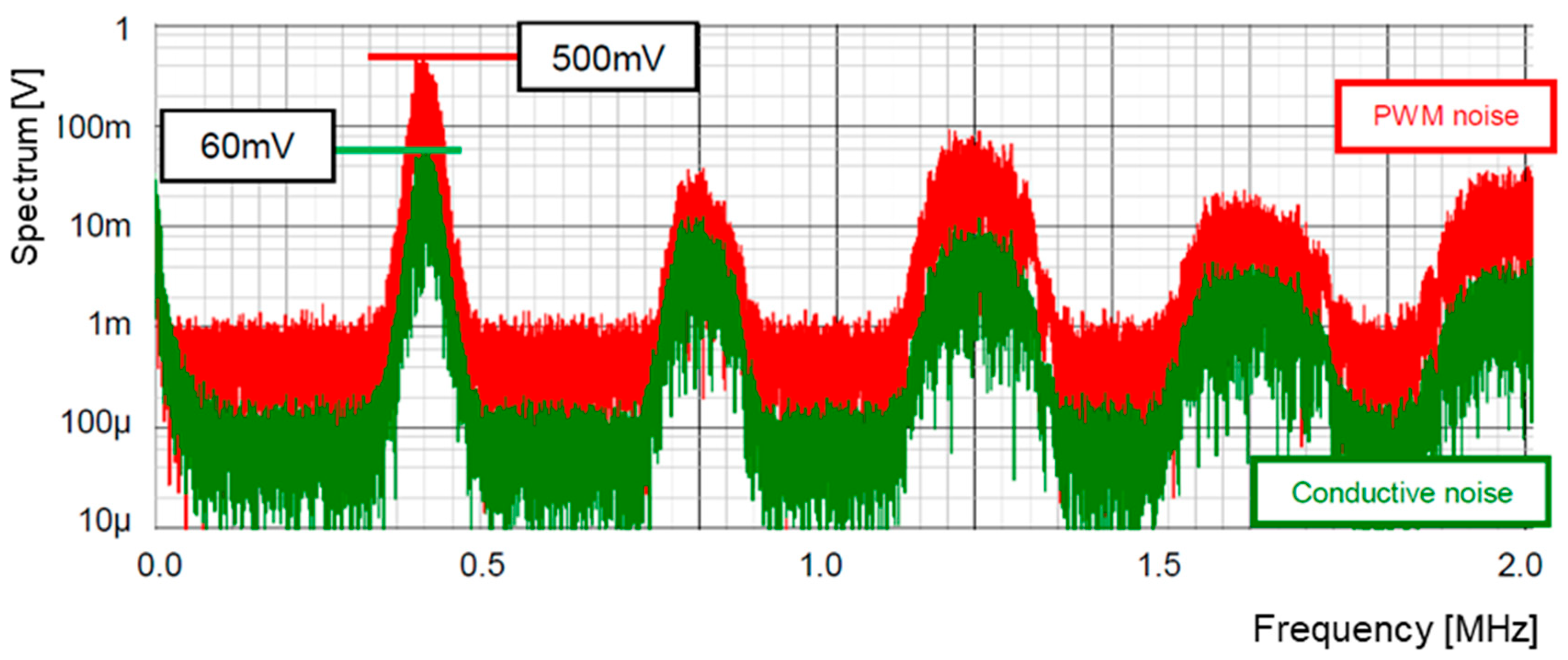
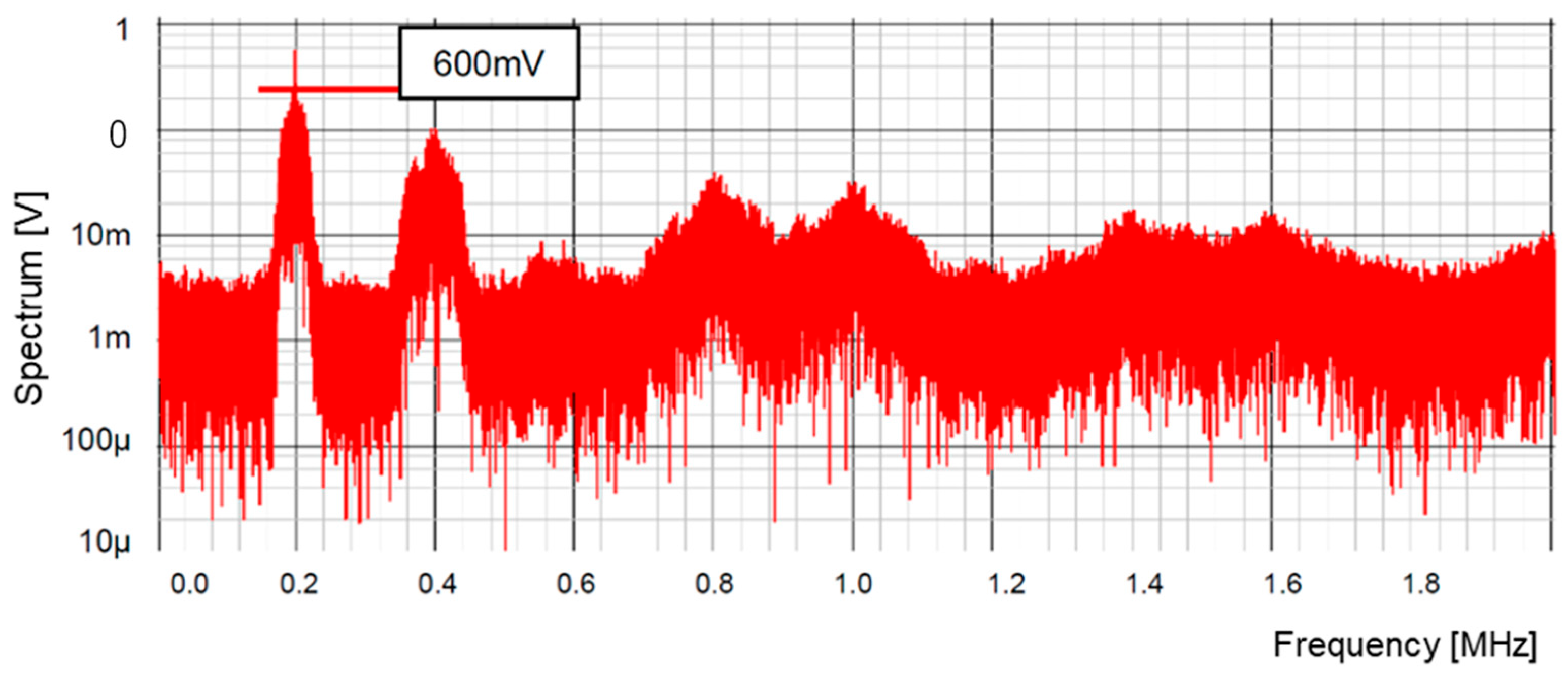
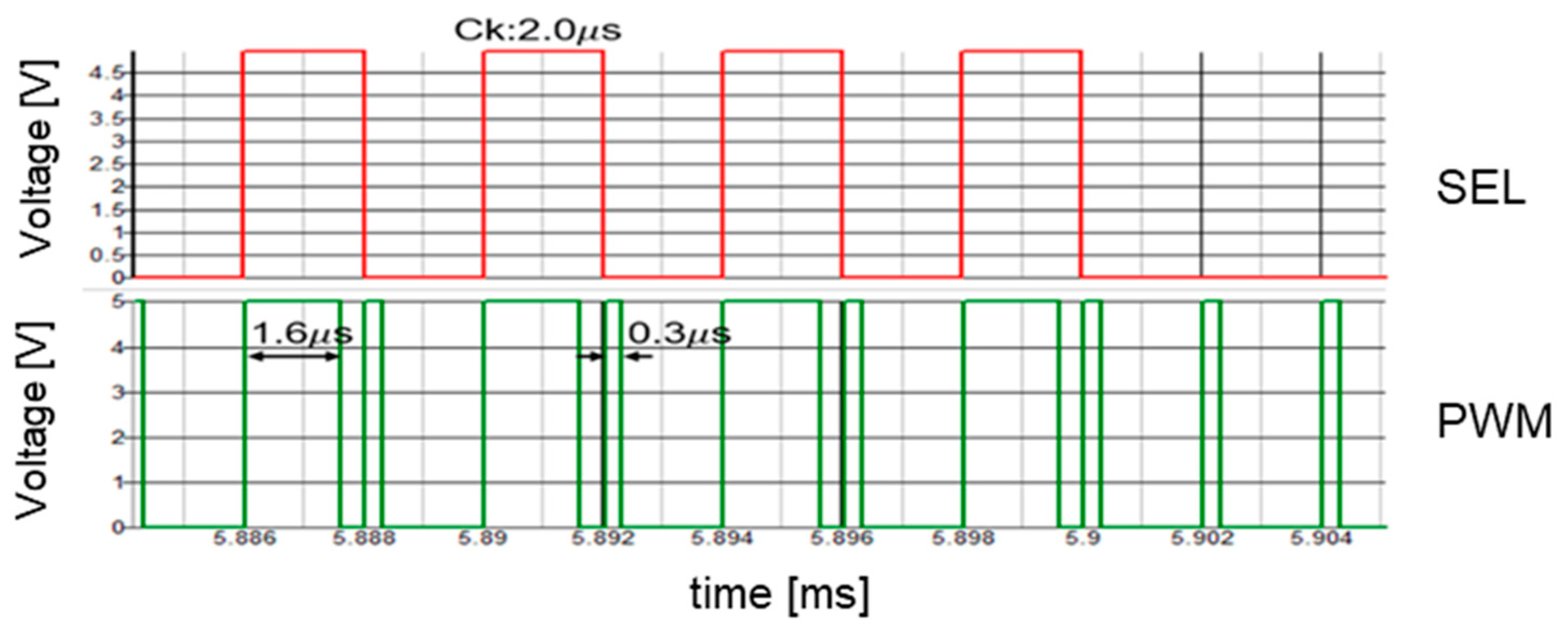
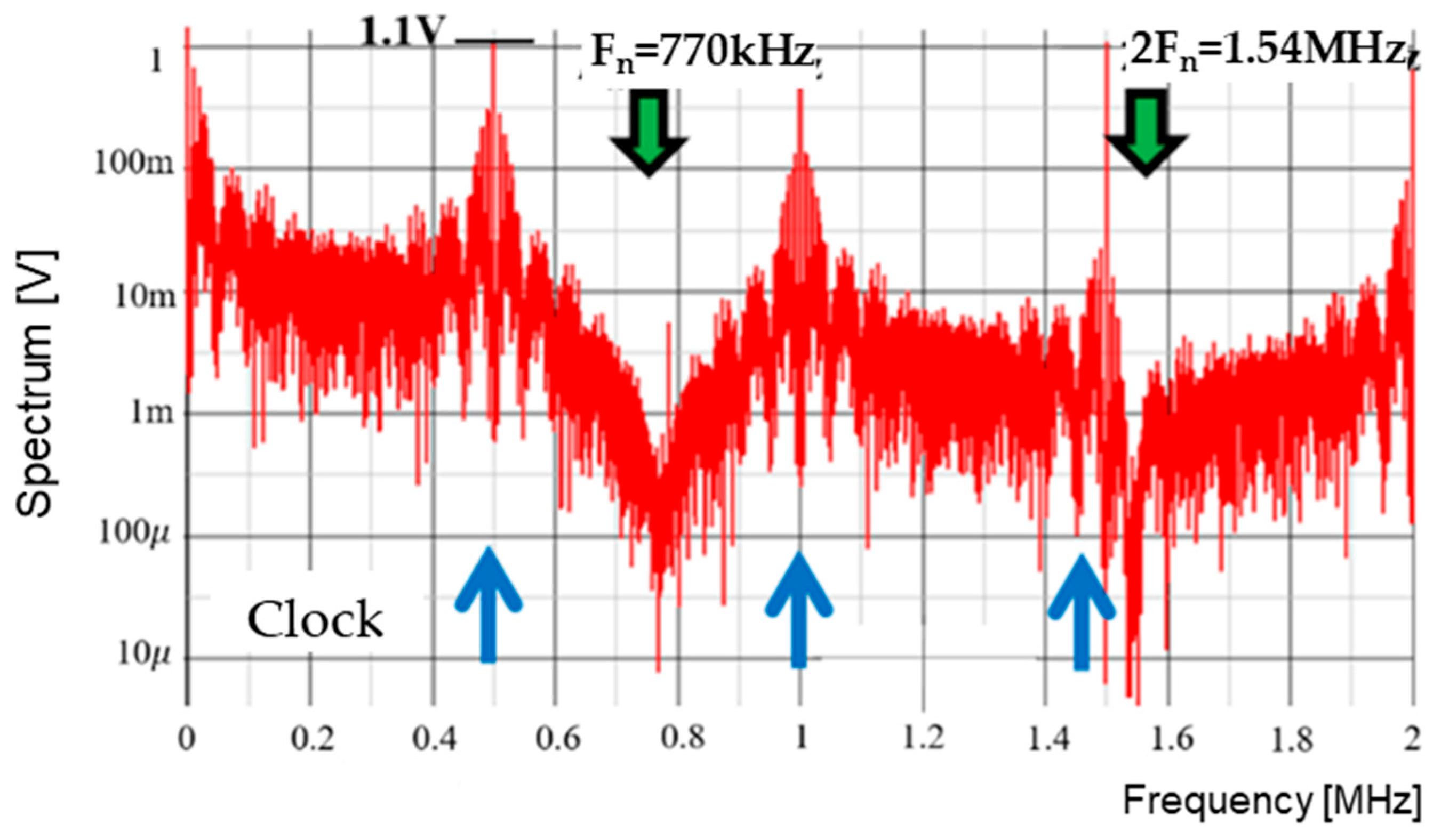
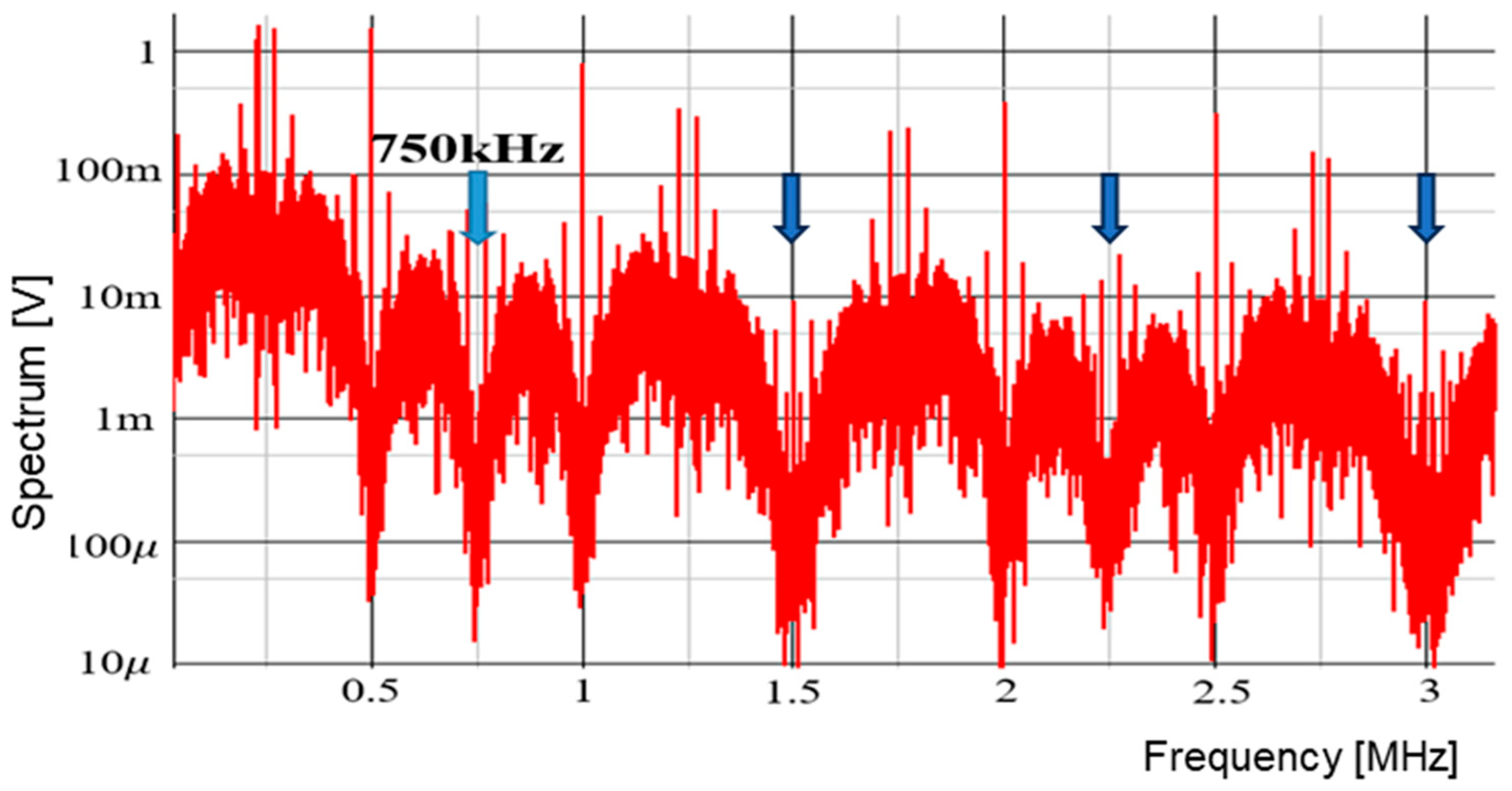
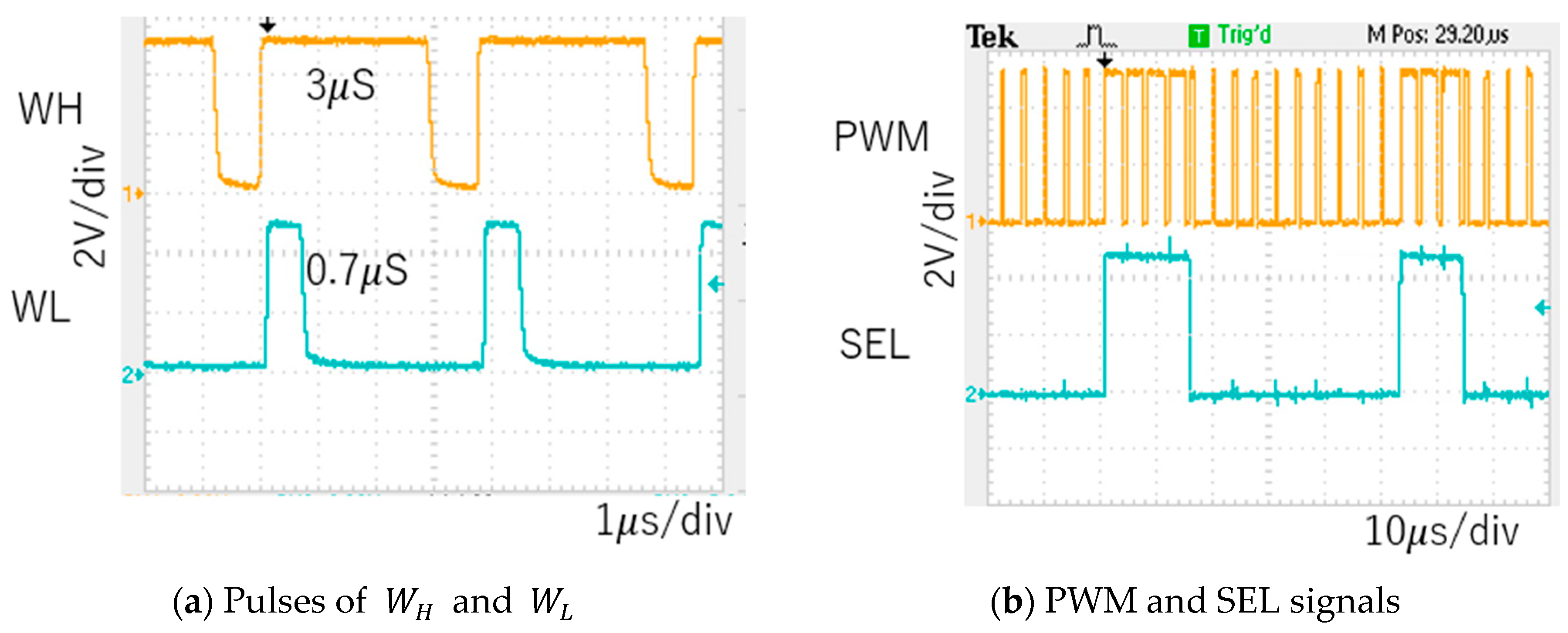
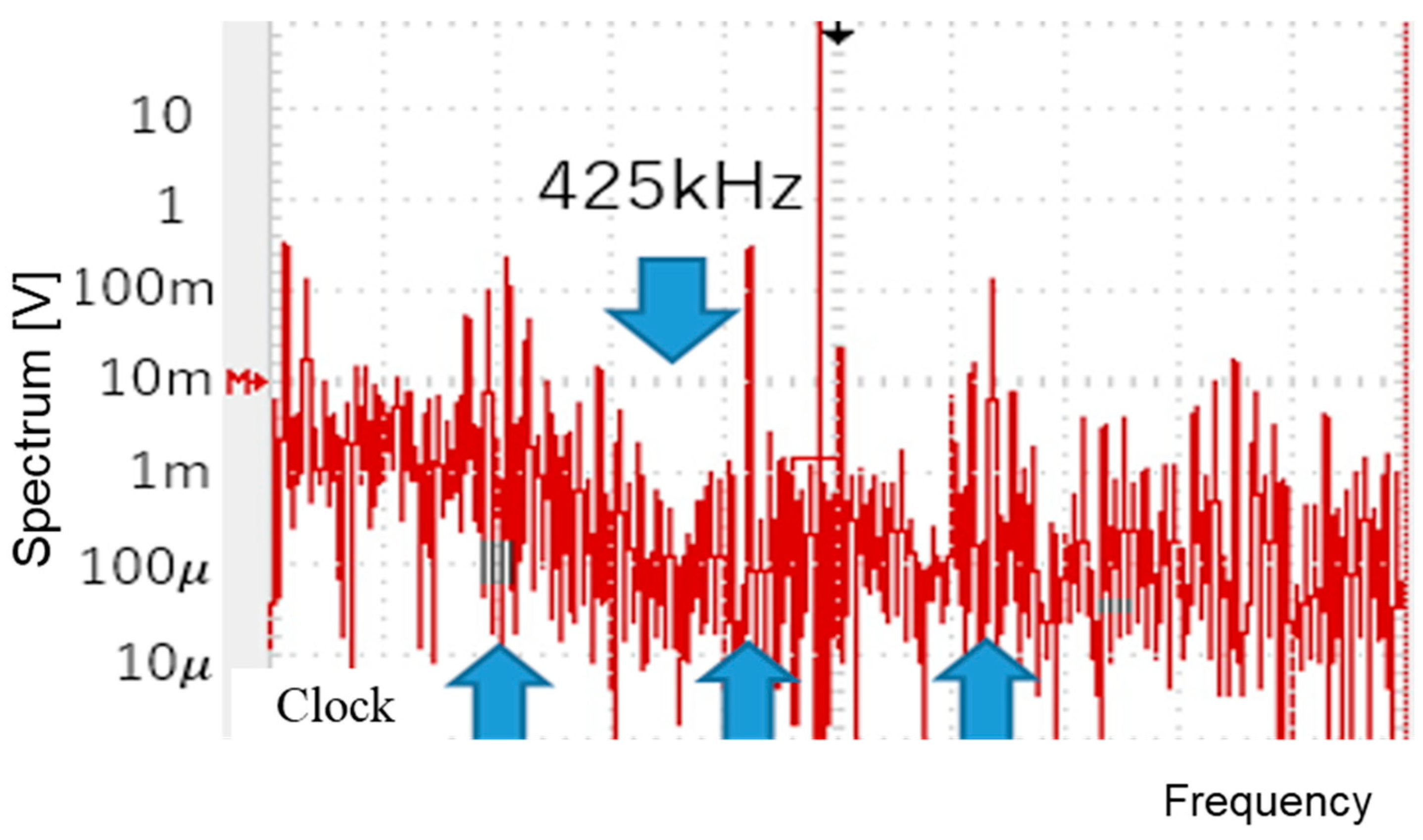
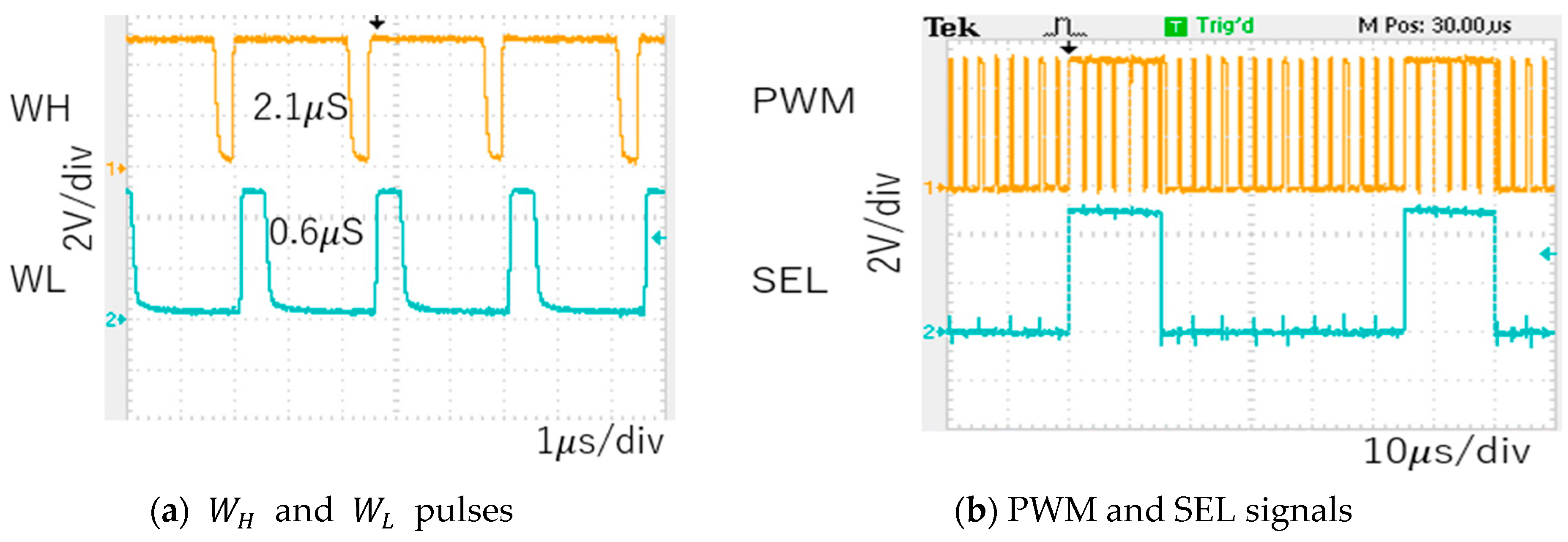
7.1. Experiment of Converter with Notch Generation
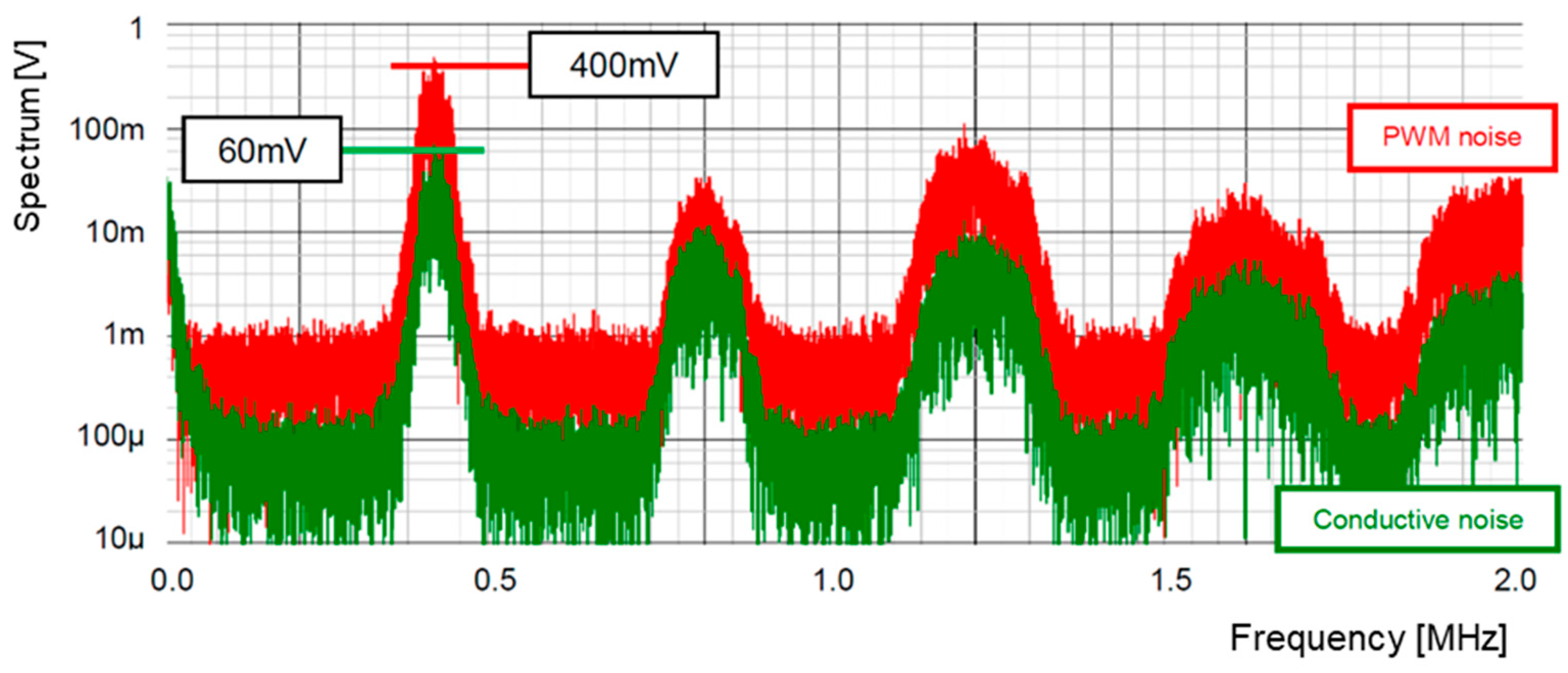
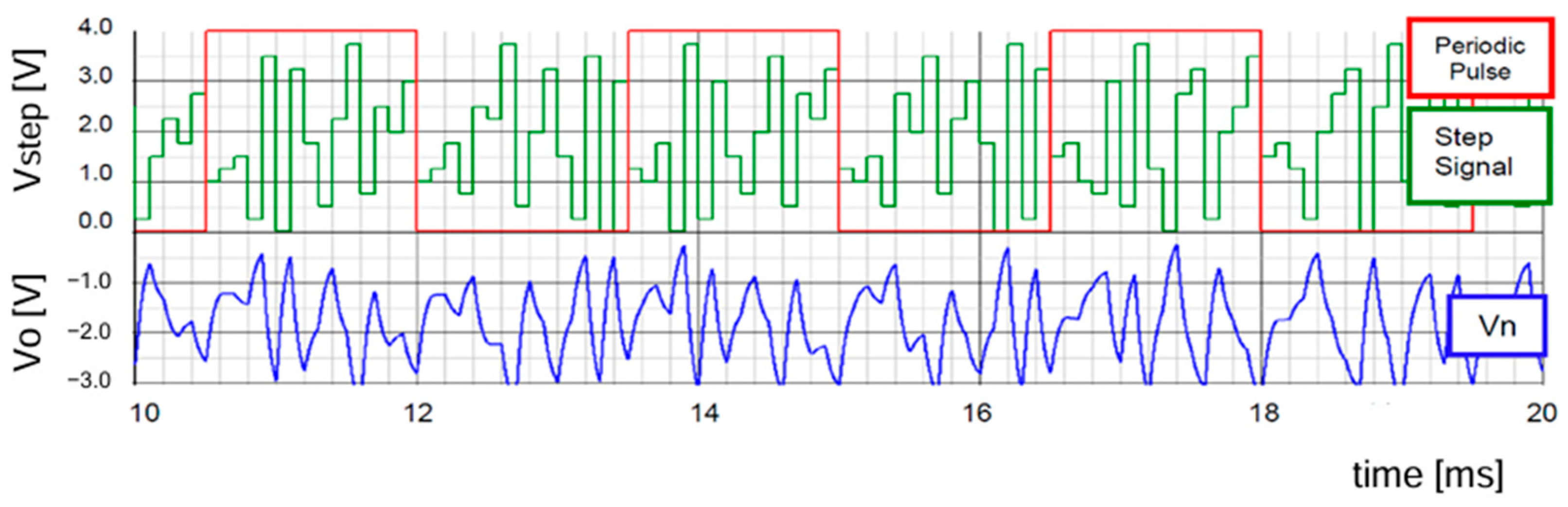
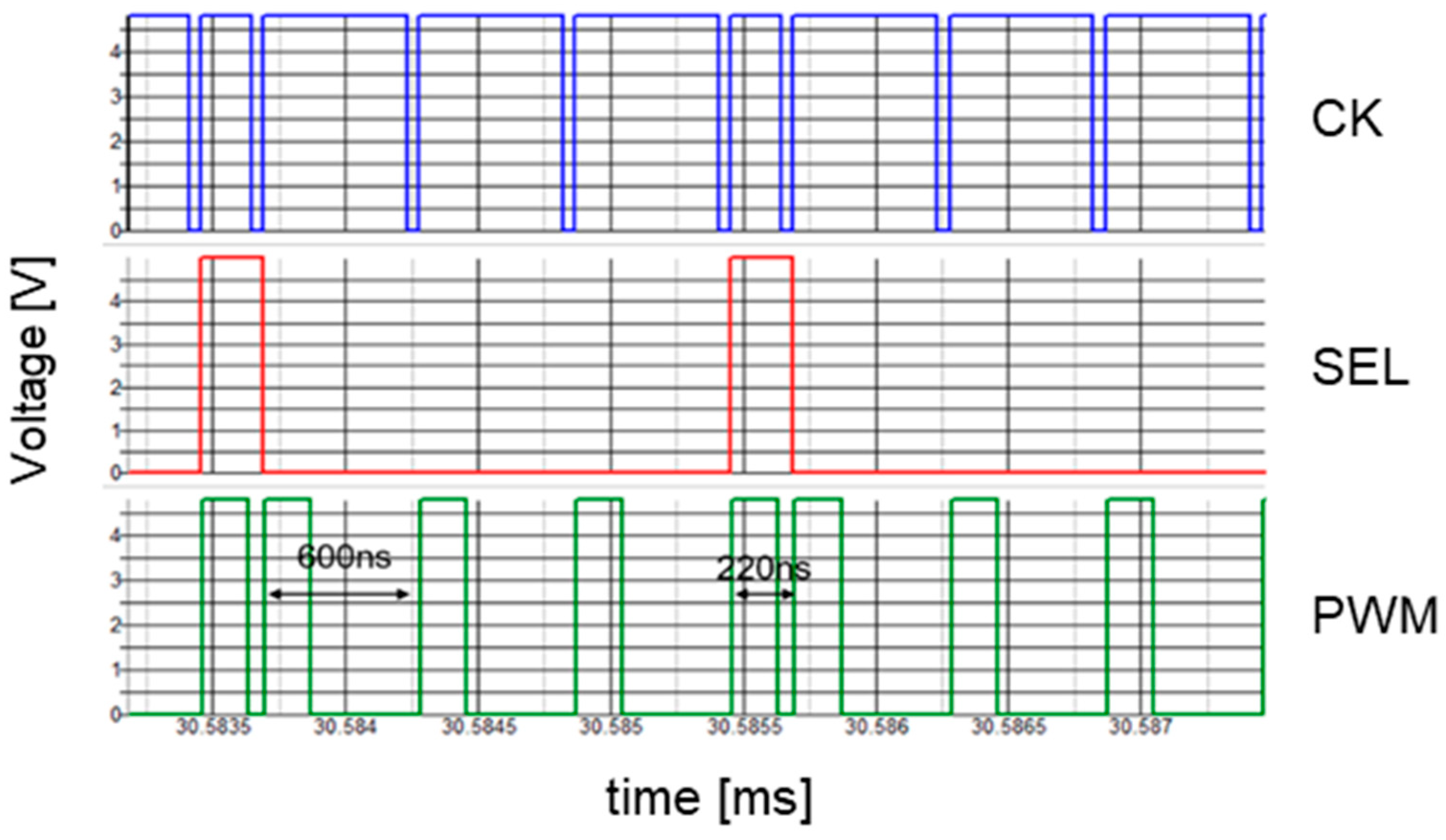
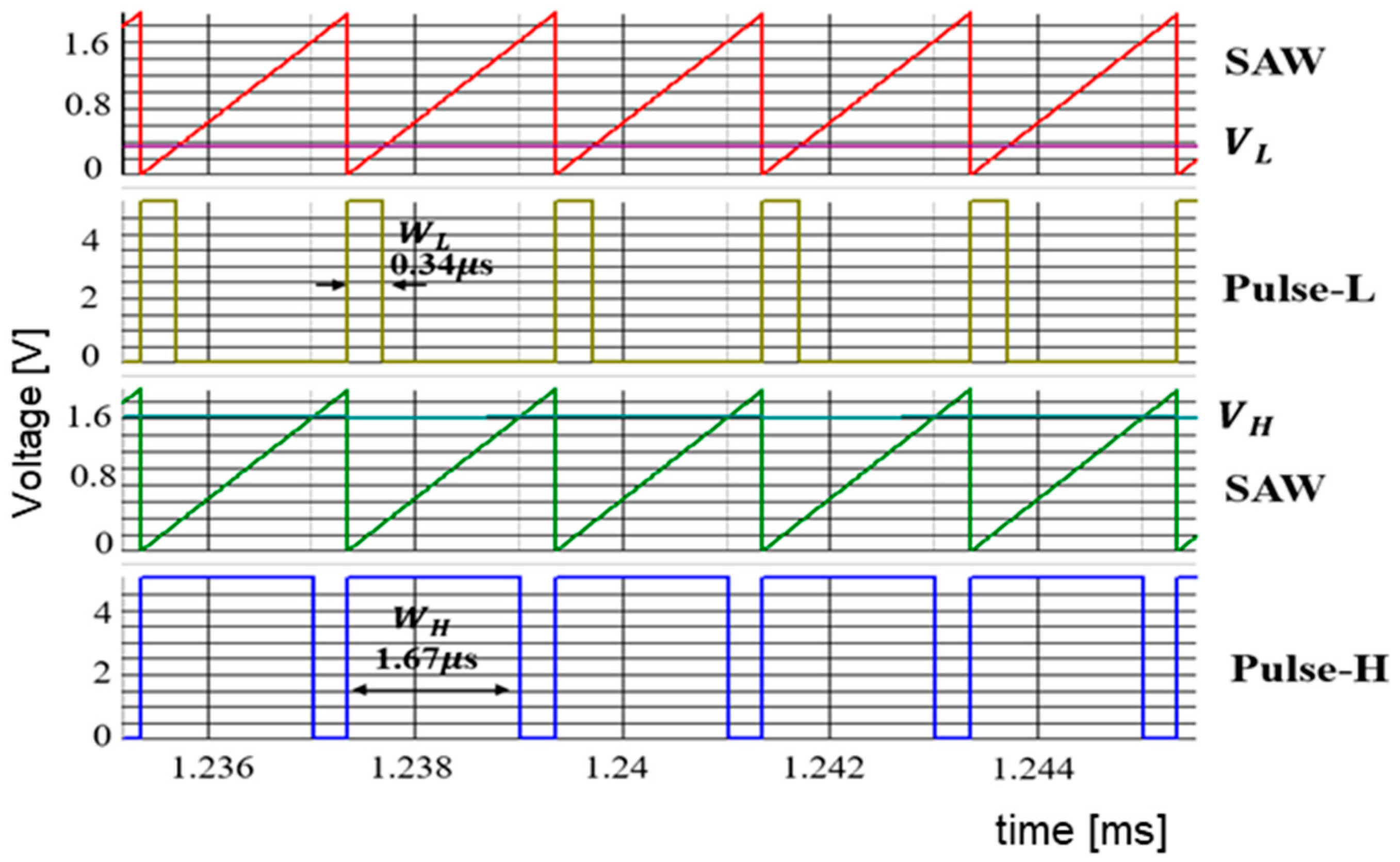
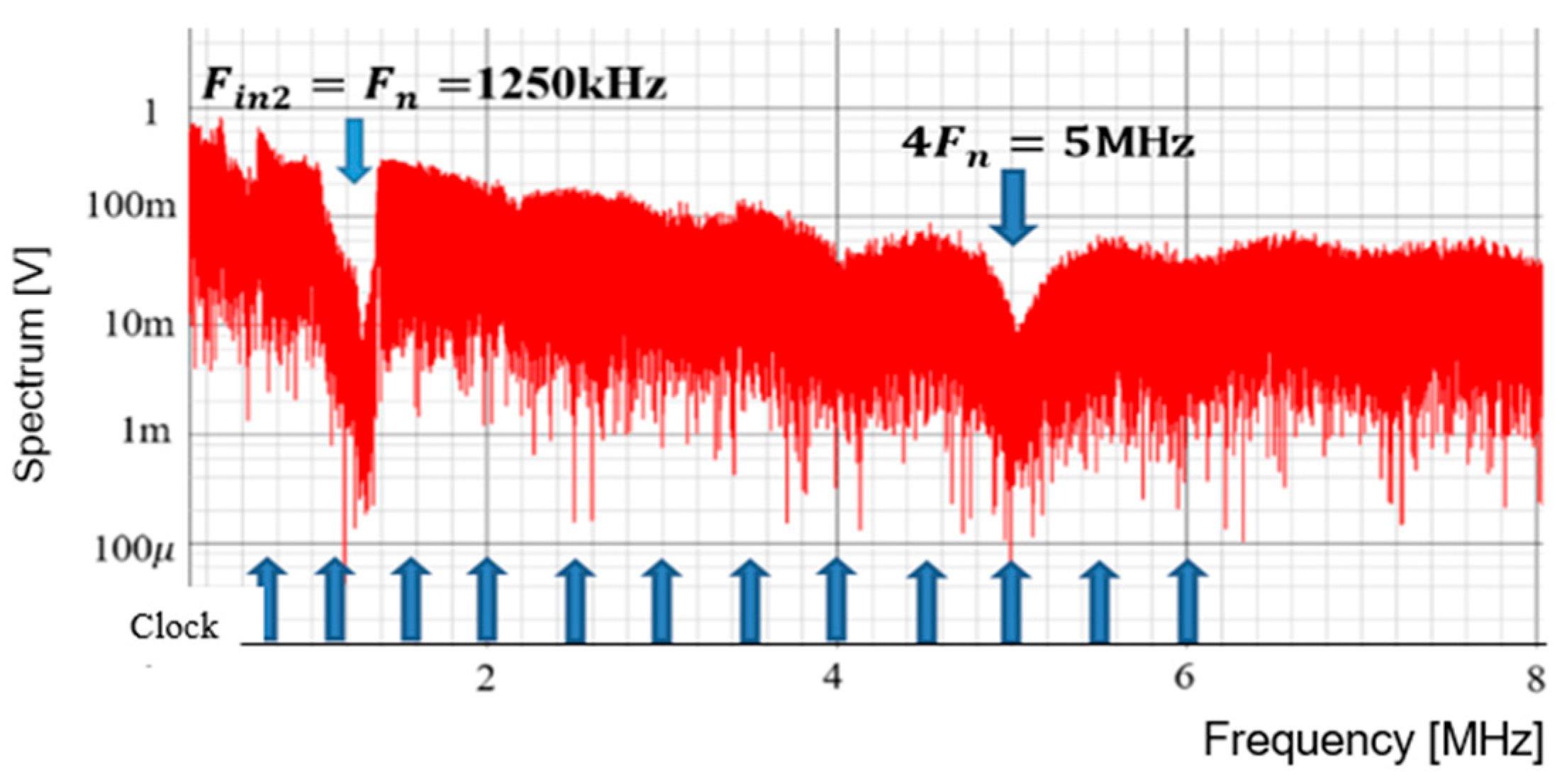
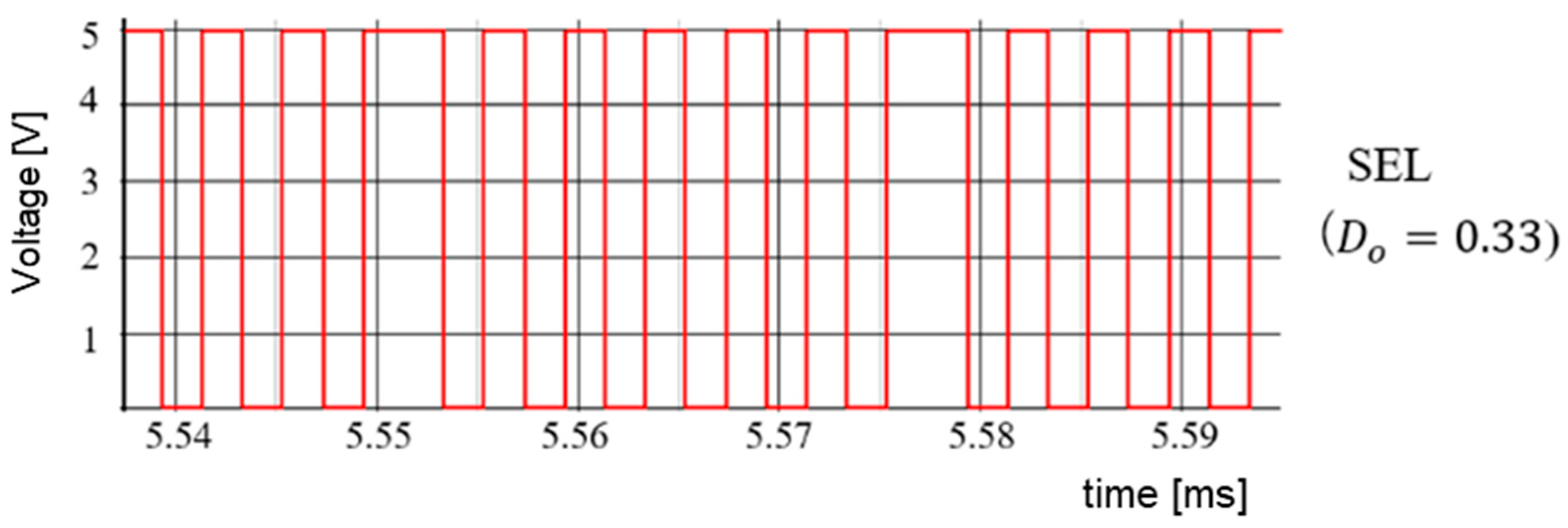
7.2. Experiment of Automatic Notch Generation
8. Discussion on Applications to Sensor Systems
- Wireless communication monitoring: small sensors are used to detect weak signals from technologies such as Wi-Fi, Bluetooth, and NFC. This allows for monitoring the health of communication environments and identifying abnormalities;
- Radio wave leakage detection: this system can be utilized in highly confidential environments to detect radio waves leaking externally and prevent information breaches;
- Frequency identification: detecting weak radio signals and pinpointing their sources or frequency bands can assist in investigations aimed at reducing radio interference;
- Smart home appliance management: an application that detects weak radio waves emitted by smart devices within the household using sensors, allowing for the management of device operational status and connection status;
- Security and surveillance system: detect suspicious signals to monitor unauthorized use of drones or communication devices, enhancing overall security;
- Healthcare: detecting environmental electromagnetic waves (e.g., EMF: Electromagnetic Field) that may affect the human body to aid in environmental management and health protection;
- Scientific investigation: detecting extremely weak signals in the environment has the potential to lead to new discoveries in fields such as space exploration, geology, and meteorology;
- IoT (Internet of Things): sensors detect the faint signals generated by IoT devices, enabling the optimization of networks and efficient energy management.
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Harada, K.; Ninomiya, T.; Gu, B. Circuit Scheme of PWM Converter in Basics of Switching Converter; Corona Publishing: Tokyo, Japan, 1992. [Google Scholar]
- Stratakos, A.J.; Sullivan, C.R.; Sandersand, S.R.; Broderson, R.W. High-Efficiency Low-Voltage DC-DC Conversion for Portable Applications in Low-Voltage/Low-Power Integrated Circuits and Systems; IEEE Press: New York City, NY, USA, 1999; Chapter 12. [Google Scholar]
- Trzynadlowski, A.M.; Wang, Z.; Nagashima, J.M.; Stancu, C.; Zelechowsk, M.H. Comparative Investigation of PWM Techniques for a New Drive for Electric Vehicles. IEEE Trans. Ind. Appl. 2003, 39, 1396–1403. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimović, D. Fundamentals of Power Electronics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Taniguchi, K.; Sato, T.; Nabeshima, T.; Nishijima, K. Constant Frequency Hysteretic PWM Controlled Buck Converter. In Proceedings of the International Conference on Power Electronics and Drive Systems (PEDS), Taipei, Taiwan, 2–5 November 2009; pp. 1194–1199. [Google Scholar]
- Lai, R.; Maillet, Y.; Wang, F.; Wang, S.; Burgos, R.; Boroyevich, D. An Integrated EMI Choke for Differential-mode and Common-mode Noise Suppression. IEEE Trans. Power Electron. 2010, 25, 539–544. [Google Scholar]
- Stankovic, A.M.; Verghese, G.C.; Perreault, D.J. Analysis and Synthesis of Randomized Modulation Schemes for Power Converters. IEEE Trans. Power Electron. 1995, 10, 680–693. [Google Scholar] [CrossRef]
- Tse, K.K.; Chung, H.S.; Hui, S.Y.; So, H.C. Analysis and Spectral Characteristics of a Spread-Spectrum Technique for Conducted EMI Suppression. IEEE Trans. Power Electron. 2000, 15, 399–410. [Google Scholar] [CrossRef]
- Giral, H.; Aroudi, E.A.; Martinez-Salamero, L.; Leyva, R.; Maixe, J. Current Control Technique for Improving EMC in Power Converters. Electron. Lett. 2001, 37, 274–275. [Google Scholar] [CrossRef]
- Yuan, B.; Liang, C.; Li, Z.; Zhang, Q. A Clock Generator with Dual Pseudo Random Spread Spectrum in DC-DC Buck Converter. In Proceedings of the IEEE International Conference on Integrated Circuits, Technologies and Applications (ICTA), Hangzhou, China, 25–27 October 2024; pp. 126–127. [Google Scholar]
- Mihali, F.; Kos, D. Reduced Conductive EMI in Switched-mode DC–DC Power Converters without EMI Filters: PWM versus Randomized PWM. IEEE Trans. Power Electron. 2006, 21, 1783–1794. [Google Scholar] [CrossRef]
- Li, H.; Tang, W.K.S.; Li, Z.; Halang, W.A. A Chaotic Peak Current Mode Boost Converter for EMI Reduction and Ripple Suppression. IEEE Trans. Circuits Syst. II Express Briefs 2008, 55, 763–767. [Google Scholar] [CrossRef]
- Kao, Y.-H.; Hung, C.-S.; Chang, H.-H.; Guo, B.; Tsai, Y. A 48V-to-5V Buck Converter with Triple EMI Suppression Circuit Meeting CISPR 25 Automotive Standards. In Proceedings of the IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 18–22 February 2024; pp. 164–166. [Google Scholar]
- Fishta, M.; Raviola, E.; Fiori, F. EMI Reduction at the Source in WBG Inverters: A Comparative Study of Spread-Spectrum Modulation and Auxiliary Switching Leg Techniques. IEEE Trans. Electromagn. Compat. 2024, 66, 1412–1419. [Google Scholar] [CrossRef]
- Stok, E.; Otten, M.; Huisman, H.; Kösesoy, Y. EMI Reduction in an Interleaved Buck Converter Through Spread Spectrum Frequency Modulation. In Proceedings of the 25th European Conference on Power Electronics and Applications (EPE’23 ECCE Europe), Aalborg, Denmark, 4–8 September 2023; pp. 1–11. [Google Scholar]
- Sun, T.-W.; Li, M.-Z.; Tsai, T.-H.; Chang, C.-C. A High-Accuracy Hysteretic DC-DC Converter Using a Spread-Spectrum EMI Suppression Technique with Double Gold Codes. In Proceedings of the 21st IEEE Interregional NEWCAS Conference (NEWCAS), Edinburgh, UK, 26–28 June 2023; pp. 1–4. [Google Scholar]
- Barbaro, A.; Fishta, M.; Raviola, E.; Fiori, F. A Comparison of Spread Spectrum and Sigma Delta Modulations to Mitigate Conducted EMI in GaN-Based DC-DC Converters. In Proceedings of the 14th International Workshop on the Electromagnetic Compatibility of Integrated Circuits (EMC Compo), Torino, Italy, 7–9 October 2024; pp. 1–6. [Google Scholar]
- Kundrata, J.; Baric, A. Clock Frequency Optimization of a Compensated Spread-Spectrum Controller in Buck Converters. IEEE Access 2024, 12, 4881–4891. [Google Scholar] [CrossRef]
- Kapat, S. Reconfigurable Periodic Bi-frequency DPWM with Custom Harmonic Reduction in DC-DC Converters. IEEE Trans. Power Electron. 2016, 31, 3380–3388. [Google Scholar] [CrossRef]
- Kundrata, J.; Barić, A. Implementation of Voltage Regulation in a Spread-Spectrum-Clocked Buck Converter. In Proceedings of the 46th MIPRO ICT and Electronics Convention (MIPRO), Opatija, Croatia, 22–26 May 2023; pp. 253–258. [Google Scholar]
- Ioinovici, A. Switched-Capacitor Power Electronics Circuits. IEEE Circuits Syst. Mag. 2001, 1, 37–42. [Google Scholar] [CrossRef]
- Li, P.; Bazzi, A.; Zhang, Z. High-Performance Control of Battery-Interfacing Cascade Buck-Boost Converter. In Proceedings of the IEEE Transportation Electrification Conference and Expo, Chicago, IL, USA, 19–21 June 2024; pp. 1–6. [Google Scholar]
- Tanaka, T.; Ninomiya, T.; Harada, K. Random-Switching Control in DC-DC Converters. In Proceedings of the IEEE PESC, Milwaukee, WI, USA, 26–29 June 1989; pp. 500–507. [Google Scholar]
- Tanaka, T.; Ninomiya, T. Random-Switching Control for DC-DC Converters: Analysis of Noise Spectrum. In Proceedings of the IEEE 23rd Power Electronics Specialists Conference, Toledo, Spain, 29 June–3 July 1992. [Google Scholar]
- Tanaka, T.; Hamasaki, H.; Yoshida, H. Random-Switching Control in DC-to-DC Converters: An Implementation Using M-Sequence. In Proceedings of the Power and Energy Systems in Converging Markets, Melbourne, VIC, Australia, 23 October 1997; pp. 431–437. [Google Scholar]
- Lin, Y.; Hsu, C.; Lin, Y.-D. A Low EMI DC-DC Buck Converter with a Triangular Spread-Spectrum Mechanism. Energies 2020, 13, 856. [Google Scholar] [CrossRef]
- Iraheta, A. Further Optimizing EMI with Spread Spectrum; Application Report; Texas Instruments: Dallas, TX, USA, 2021. [Google Scholar]
- Curtis, P.; Lee, E. EMI Reduction Technique, Dual Random Spread Spectrum; Application Note; Texas Instruments: Dallas, TX, USA, 2022. [Google Scholar]
- Pareschi, F.; Rovatti, R.; Setti, G. EMI Reduction via Spread Spectrum in DC/DC Converters: State of the Art, Optimization, and Tradeoffs. IEEE Access 2015, 3, 2857–2874. [Google Scholar] [CrossRef]
- Leonard, J. Dual Switcher with Spread Spectrum Reduces EMI. Linear Technol. Mag. 2004, 9–11. Available online: https://www.analog.com/en/resources/technical-articles/dual-switcher-spread-spectrum-reduces-emi.html (accessed on 26 April 2025).
- Zimmer, G.; Scott, K. Spread Spectrum Frequency Modulation Reduces EMI, Technical Article, Analog Devices. Available online: https://www.analog.com/en/resources/technical-articles/spread-spectrum-frequency-modulation-reduces-emi.html (accessed on 26 April 2025).
- Jaffe, S. The Pros and Cons of Spread-Spectrum Implementation Methods in Buck Regulators. Analog. Des. J. 2021, 1–6. Available online: https://www.ti.com/lit/an/slyt809/slyt809.pdf?ts=1714816631894 (accessed on 26 April 2025).
- Miki, N.; Tsukiji, N.; Asaishi, K.; Kobori, Y.; Takai, N.; Kobayashi, H. EMI Reduction Technique With Noise Spread Spectrum Using Swept Frequency Modulation for Hysteretic DC-DC Converters. In Proceedings of the IEEE International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS), Xiamen, China, 6–9 November 2017. [Google Scholar]
- Oiwa, N.; Sakurai, S.; Sun, Y.; Tri, M.T.; Li, J.; Kobori, Y.; Kobayashi, H. EMI Noise Reduction for PFC Converter with Improved Efficiency and High Frequency Clock. In Proceedings of the IEEE 14th International Conference on Solid-State and Integrated Circuit Technology, Qingdao, China, 31 October–3 November 2018. [Google Scholar]
- Kobori, Y.; Sun, Y.; Tri, M.T.; Kuwana, A.; Kobayashi, H. EMI Reduction in Switching Converters With Pseudo Random Analog Noise. J. Technol. Soc. Sci. 2020, 4, 33–48. [Google Scholar]
- Kobori, Y.; Arafune, T.; Tsukiji, N.; Kobayashi, H. Selectable Notch Frequencies of EMI Spread Spectrum Using Pulse Modulation in Switching Converter. In Proceedings of the IEEE 11th International Conference on ASIC, Chengdu, China, 3–6 November 2015. [Google Scholar]
- Sun, Y.; Kobori, Y.; Kobayashi, H. Full Automatic Notch Generation in Noise Spectrum of Pulse Coding Controlled Switching Converter. In Proceedings of the IEEE 14th International Conference on Solid-State and Integrated Circuit Technology, Qingdao, China, 31 October–3 November 2018. [Google Scholar]
- Sun, Y.; Kobori, Y.; Kuwana, A.; Kobayashi, H. Pulse Coding Controlled Switching Converter that Generates Notch Frequency to Suit Noise Spectrum. IEICE Trans. Commun. 2020, E103-B, 1331–1340. [Google Scholar] [CrossRef]
- Dong, G.; Katayama, S.; Sun, Y.; Kobori, Y.; Kuwana, A.; Kobayashi, H. Notch Frequency Generation Methods in Noise Spread Spectrum for Pulse Coding Switching DC-DC Converter. In Proceedings of the 13th Latin American Symposium on Circuits and Systems, Santiago, Chile, 1–4 March 2022. [Google Scholar]
- Gamoudi, R.; Chariag, D.E.; Sbita, L. A Review of Spread-Spectrum-Based PWM Techniques—A Novel Fast Digital Implementation. IEEE Trans. Power Electron. 2018, 33, 10292–10307. [Google Scholar] [CrossRef]
- Jankovskis, J.; Stepins, D.; Tjukovs, S.; Pikulins, D. Examination of Different Spread Spectrum Techniques for EMI Suppression in dc/dc Converters. Elektron. Ir Elektrotechnika 2008, 86, 60–64. [Google Scholar]
- Dousoky, G.M.; Shoyama, M.; Ninomiya, T. FPGA-Based Spread-Spectrum Schemes for Conducted-Noise Mitigation in DC–DC Power Converters: Design, Implementation, and Experimental Investigation. IEEE Trans. Ind. Electron. 2011, 58, 429–435. [Google Scholar] [CrossRef]
- Hegarty, T. An Overview of Radiated EMI Specifications for Power Supplies; White Paper; Texas Instruments: Dallas, TX, USA, 2018. [Google Scholar]
- Hegarty, T. An Overview of Conducted EMI Specifications for Power Supplies; White Paper; Texas Instruments: Dallas, TX, USA, 2018. [Google Scholar]
- Hegarty, T. A Review of EMI Standards, Part 2—Radiated Emissions; White Paper; Texas Instruments: Dallas, TX, USA, 2018. [Google Scholar]
- Pozar, D.M. Microwave Engineering, 4th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Razavi, B. RF Microelectronics, 2nd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 2011. [Google Scholar]
- Rappaport, T.S. Wireless Communications: Principles and Practice, 2nd ed.; Cambridge University Press: Cambridge, UK, 2024. [Google Scholar]
- Pereira, E.; Araújo, Í.; Silva, L.F.V.; Batista, M.; Júnior, S.; Barboza, E. RFID Technology for Animal Tracking: A Survey. IEEE J. Radio Freq. Identif. 2023, 7, 609–620. [Google Scholar] [CrossRef]
- Priyadharsini, S.; Renukasri, V.; Sneha, R.; Sowmiya, P.K.; Swaathi, K. Wildlife Animal Tracking System using GPS and GSM. Int. J. Eng. Res. Technol. 2020, 8, 6–8. [Google Scholar]
- Kim, S.-H.; Kim, D.-H.; Park, H.-D. Animal Situation Tracking Service Using RFID, GPS, and Sensors. In Proceedings of the IEEE Second International Conference on Computer and Network Technology, Bangkok, Thailand, 23–25 April 2010; pp. 153–156. [Google Scholar]
- Park, P.; Di Marco, P.; Nah, J.; Fischione, C. Wireless Avionics Intracommunications: A Survey of Benefits, Challenges, and Solutions. IEEE Internet Things J. 2021, 8, 7745–7767. [Google Scholar] [CrossRef]
- Sazonov, E. (Ed.) Wearable Sensors: Fundamentals, Implementation and Applications, 2nd ed.; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Wilson, J.S. (Ed.) Sensor Technology Handbook; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Roggen, D. Mobile Sensors and Context-Aware Computing; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2015. [Google Scholar]
- Khanna, V.K. IoT Sensors—An Exploration of Sensors for Internet of Things; CRC Press: Boca Raton, FL, USA, 2024. [Google Scholar]
- Pradhan, B.; Mukhopadhyay, S.; Sensors, I. AI and XAI: Empowering a Smarter World; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Vermesan, O.; Friess, P. (Eds.) Internet of Things Applications—From Research and Innovation to Market Deployment; River Publishers: Copenhagen, Denmark, 2022. [Google Scholar]
- Lee, A.T.L.; Jin, W.; Tan, S.-C.; Hui, R.S.Y. Single-Inductor Multiple-Output Converters: Topologies, Implementation, and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Rooholahi, B.; Siwakoti, Y.P.; Eckel, H.-G.; Blaabjerg, F.; Bahman, A.S. Enhanced Single-Inductor Single-Input Dual-Output DC–DC Converter With Voltage Balancing Capability. IEEE Trans. Ind. Electron. 2024, 71, 7241–7251. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, A.; Li, X.; Jiang, Y.; Martins, R.P.; Mak, P.-I. An 80W Single-Inductor DC-DC Architecture for Simultaneous Flash Charging and Dual-Output PoL Supply with 92.1% Peak Efficiency from 15V-to-28V Input to 12.6V/3.3V/1V Outputs Using 1.3 mm3 Inductor. In Proceedings of the IEEE European Solid-State Electronics Research Conference (ESSERC), Bruges, Belgium, 9–12 September 2024; pp. 61–64. [Google Scholar]
- Yeh, W.-T.; Cai, M.-X.; Tsai, C.-W.; Tsai, C.-H. A Single-Inductor Bipolar-Output DC-DC Converter With Tunable Asymmetric Power Distribution Control (APDC) for AMOLED Applications. IEEE Access 2025, 13, 6810–6819. [Google Scholar] [CrossRef]
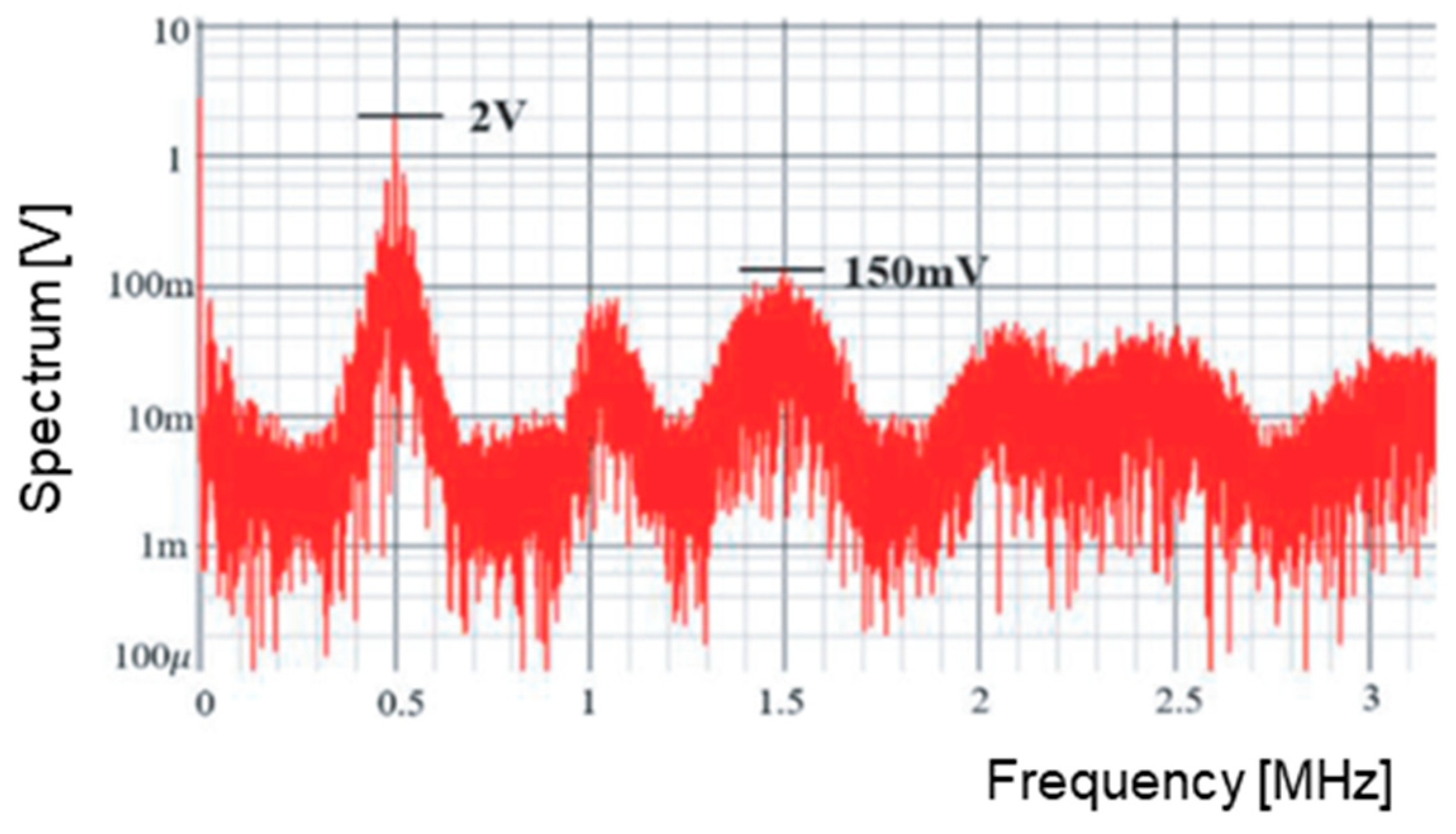
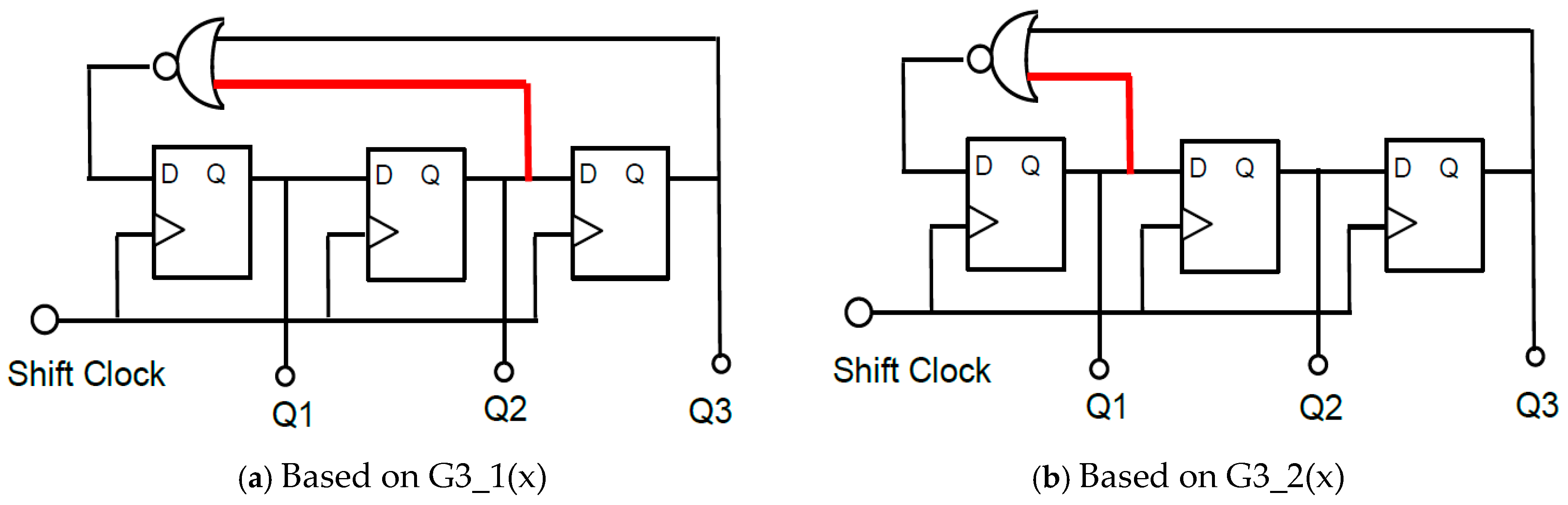
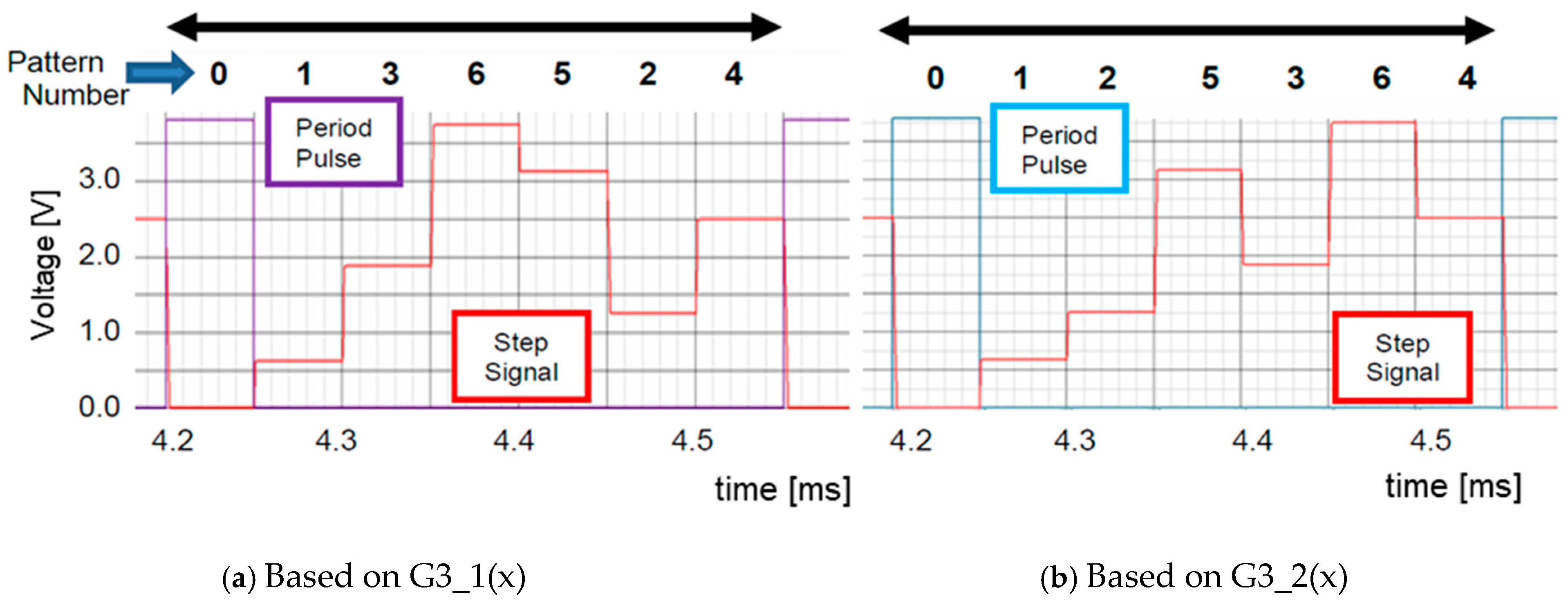
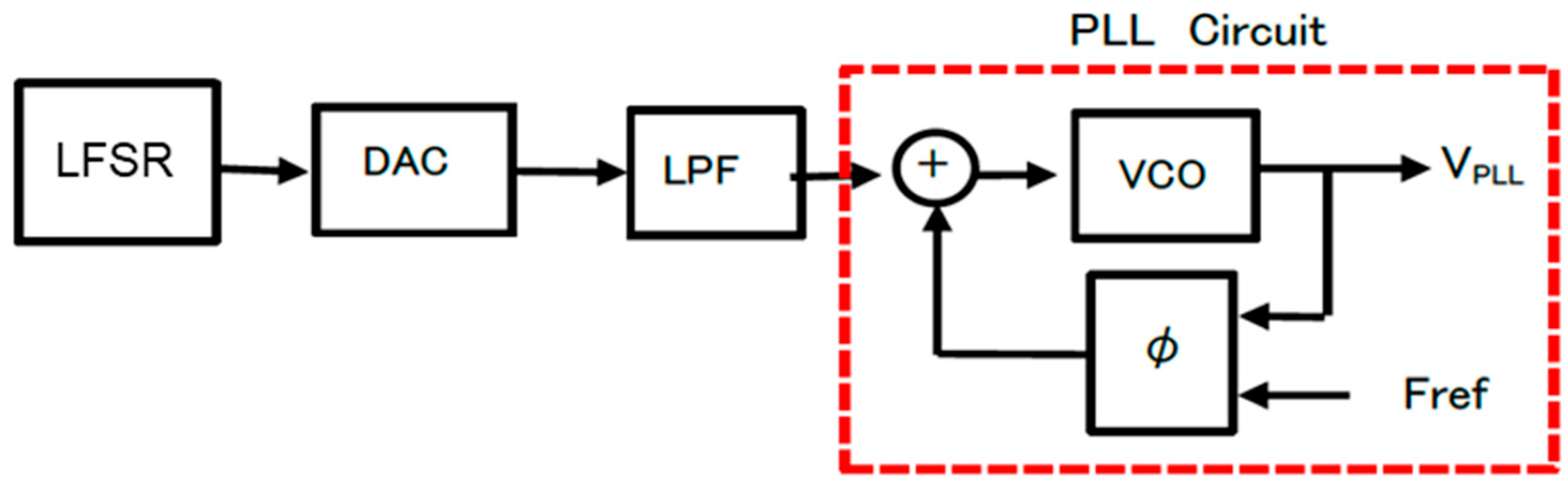
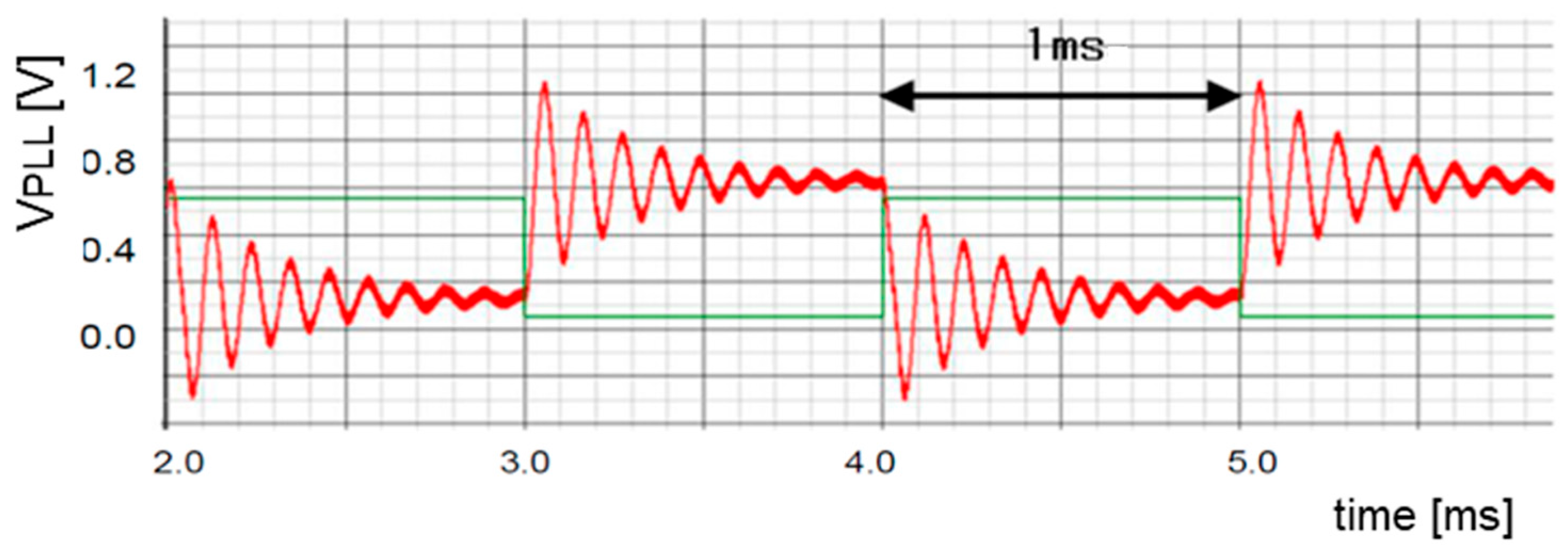
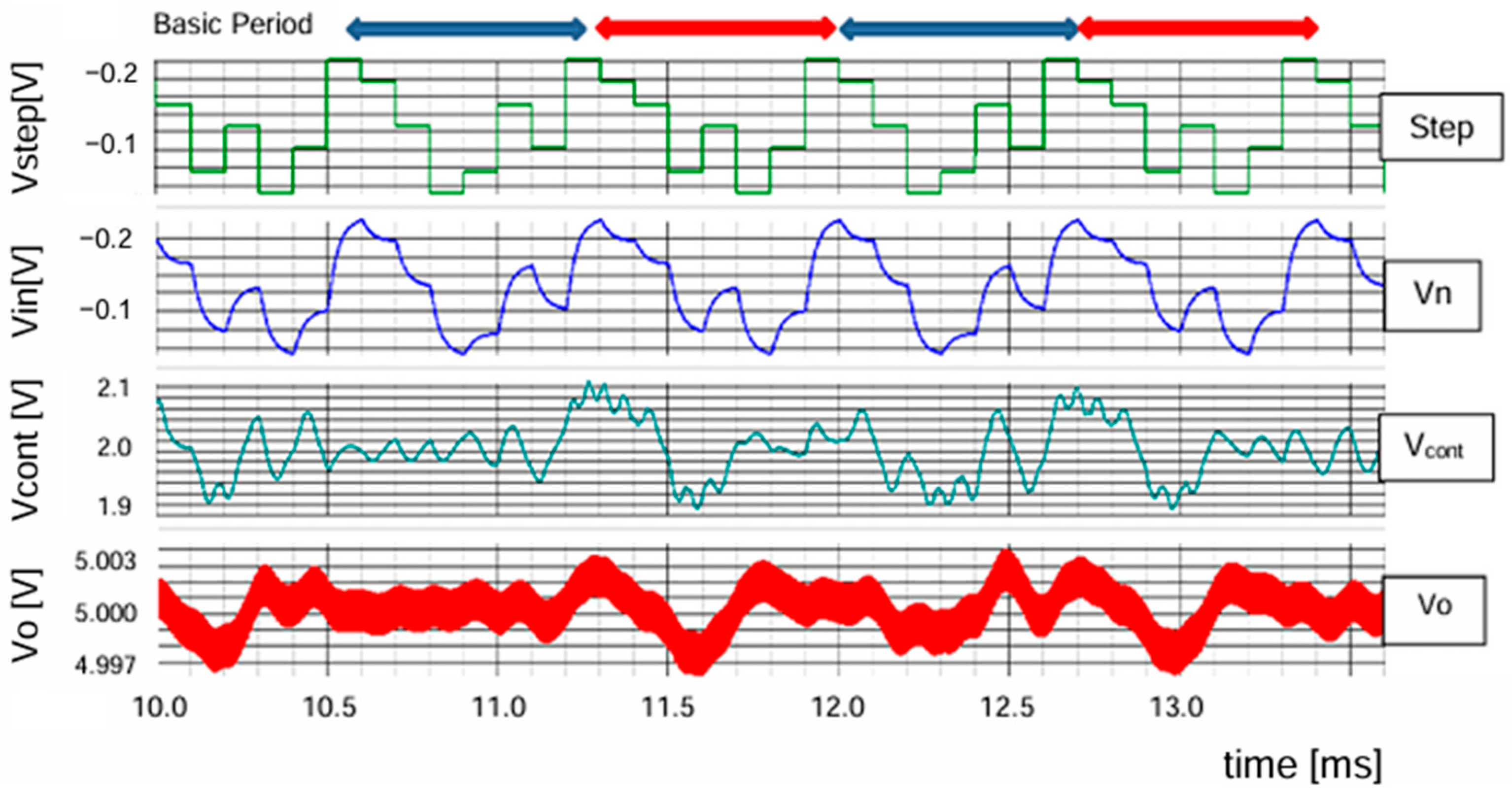
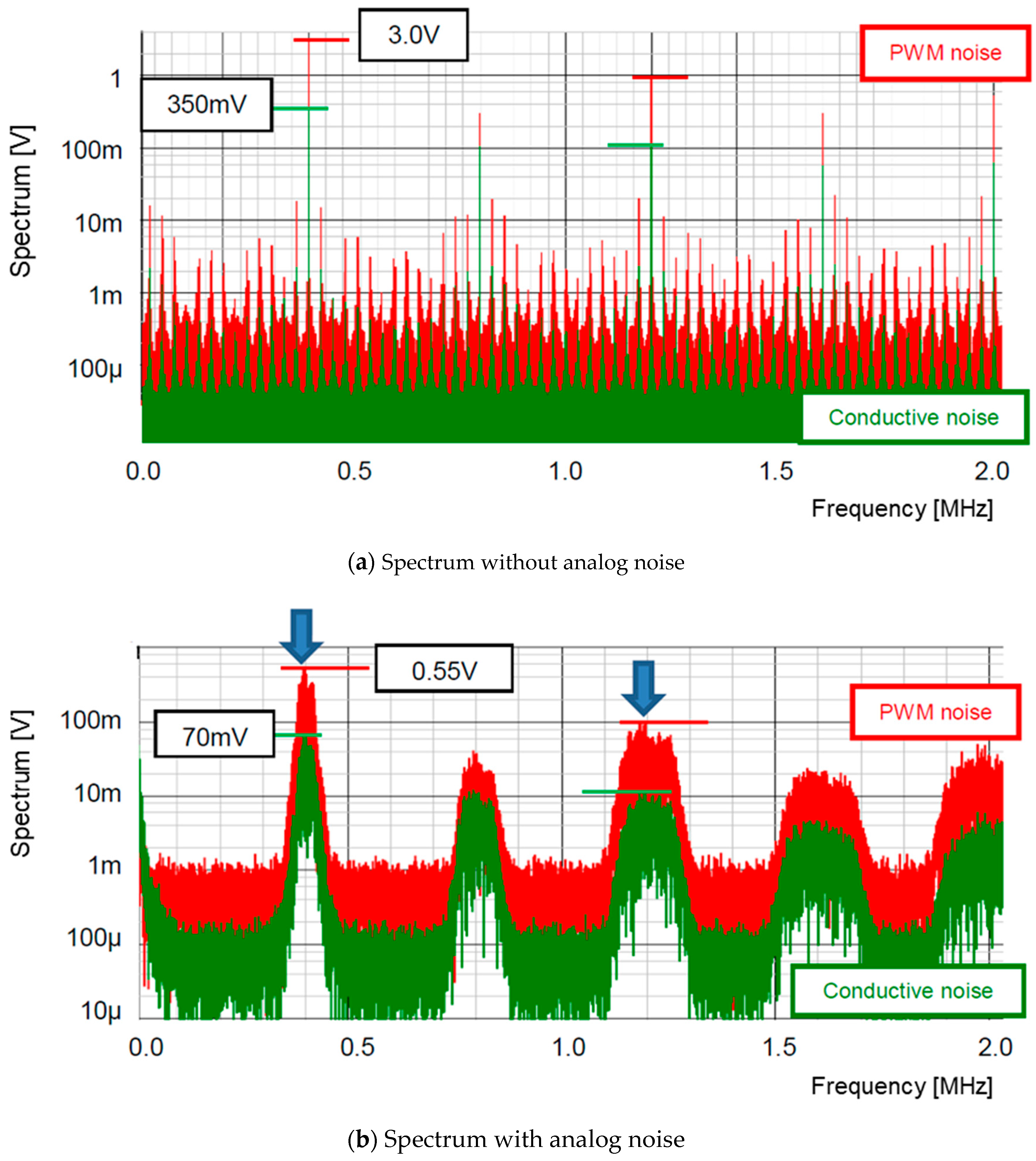
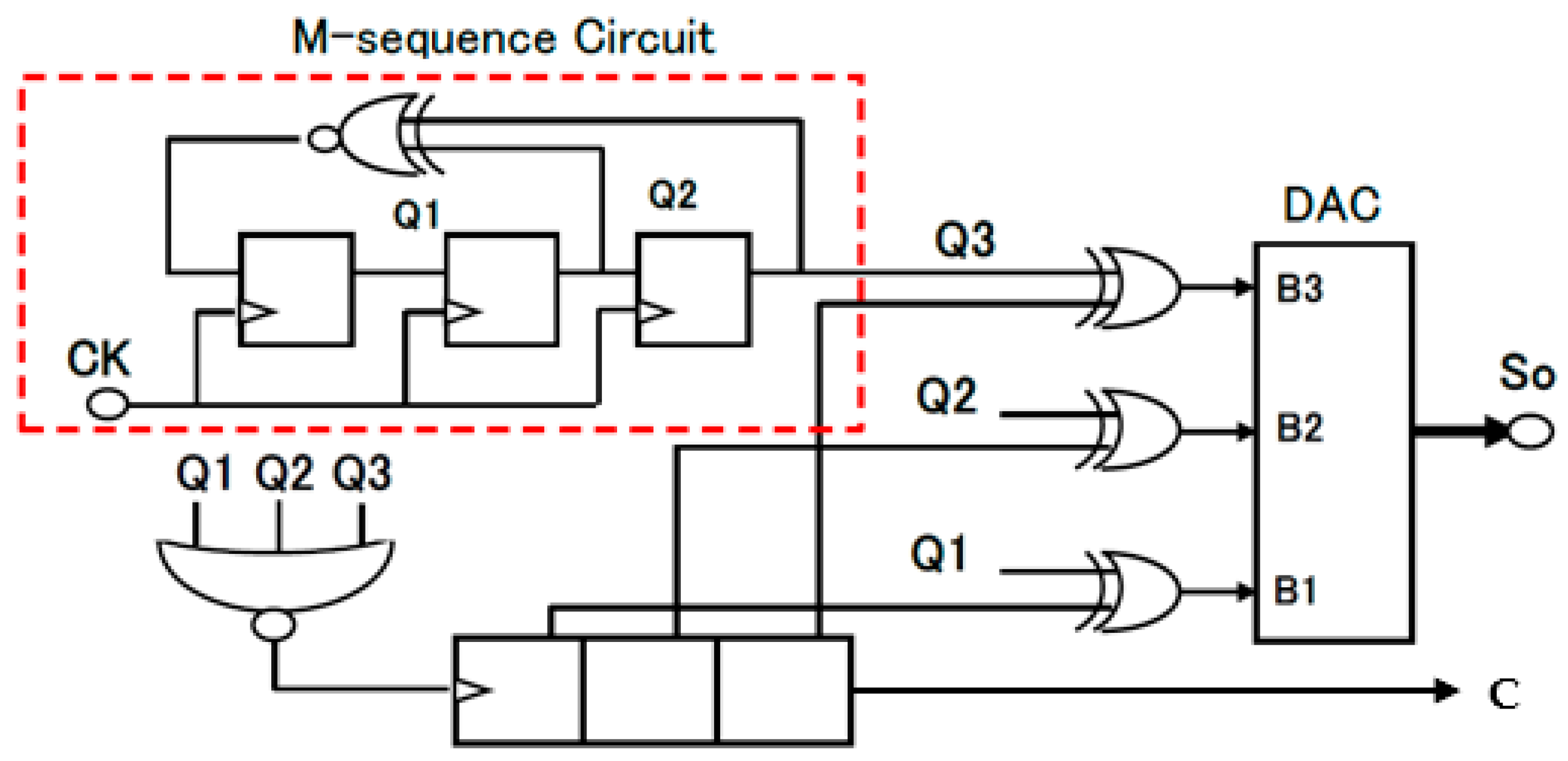


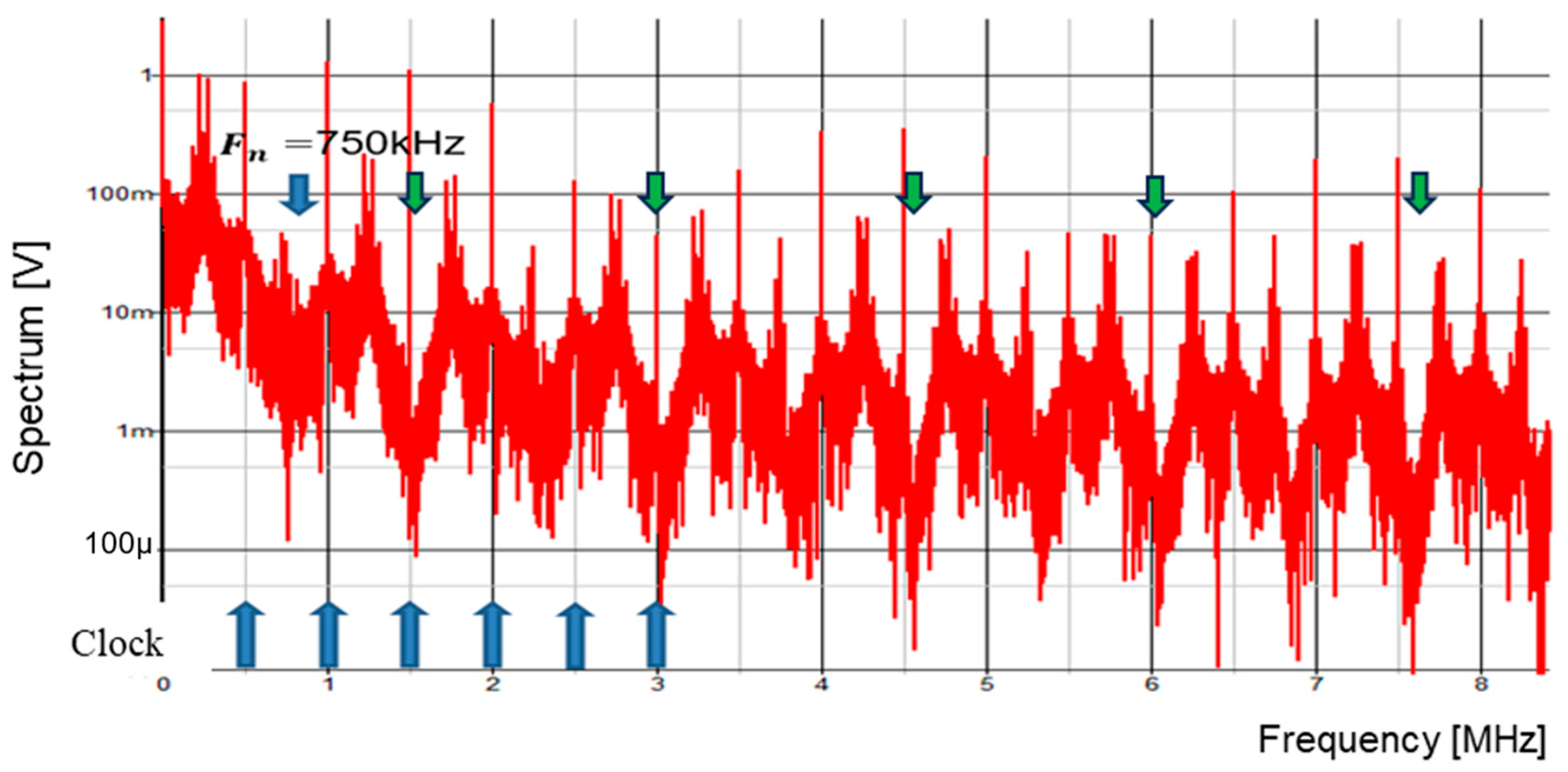
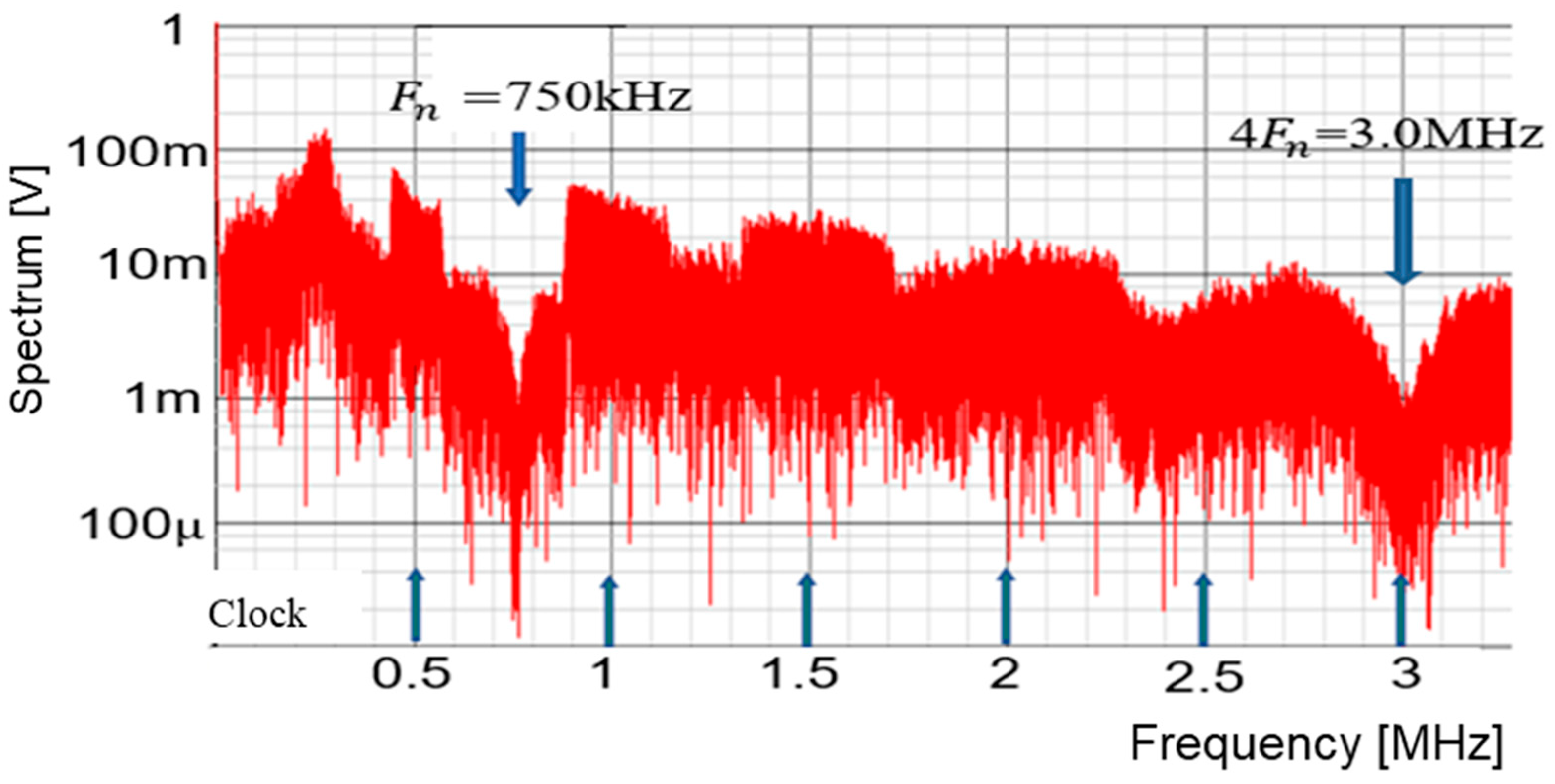
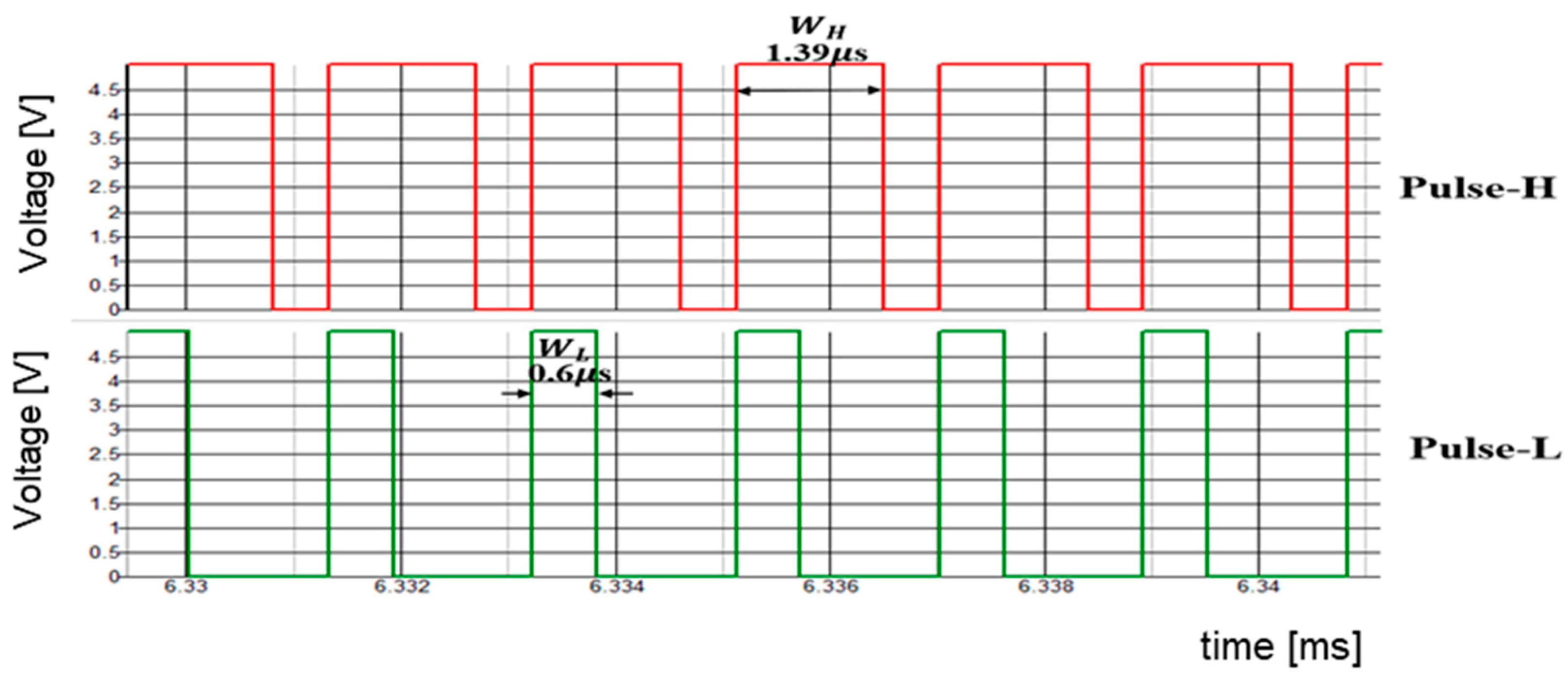
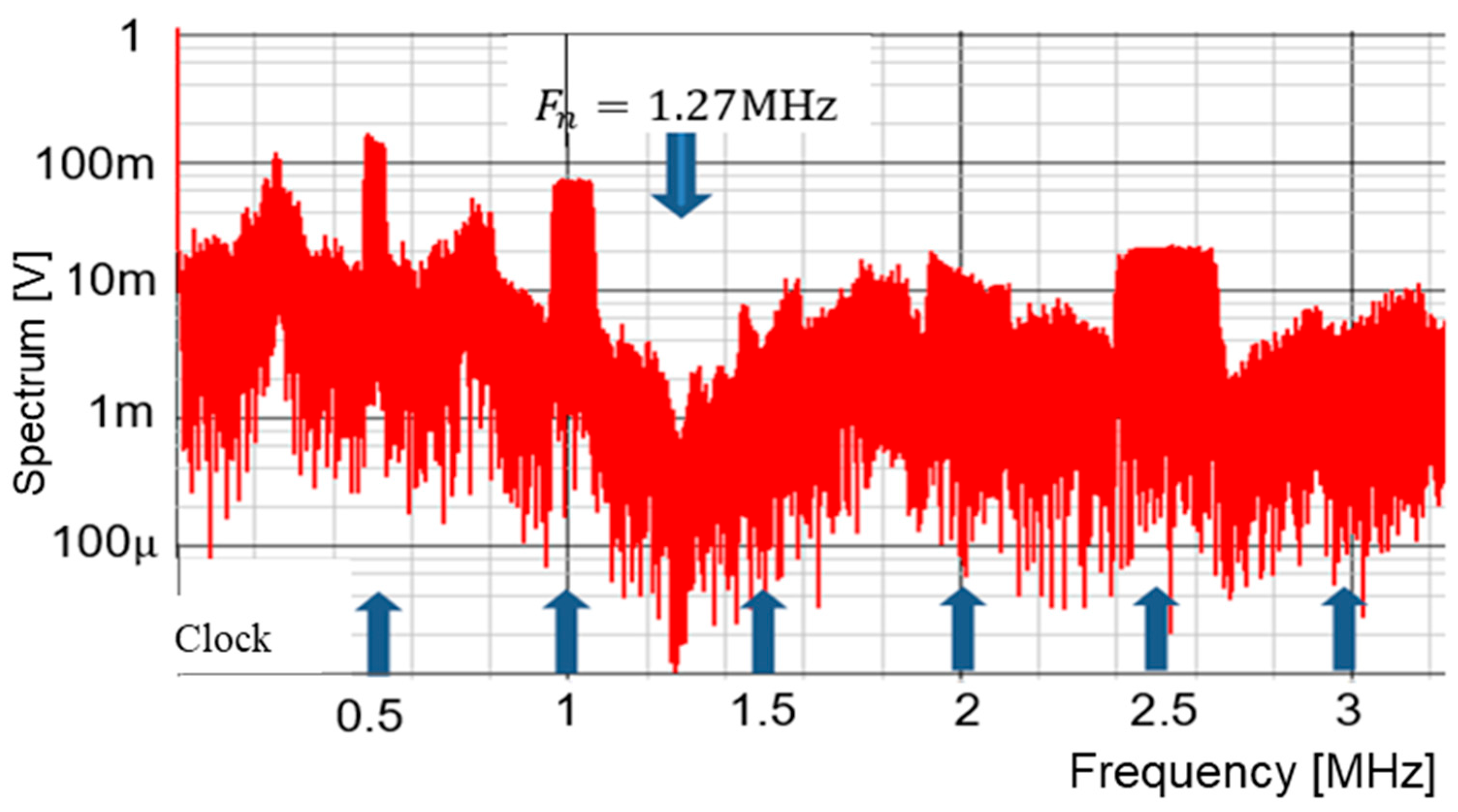
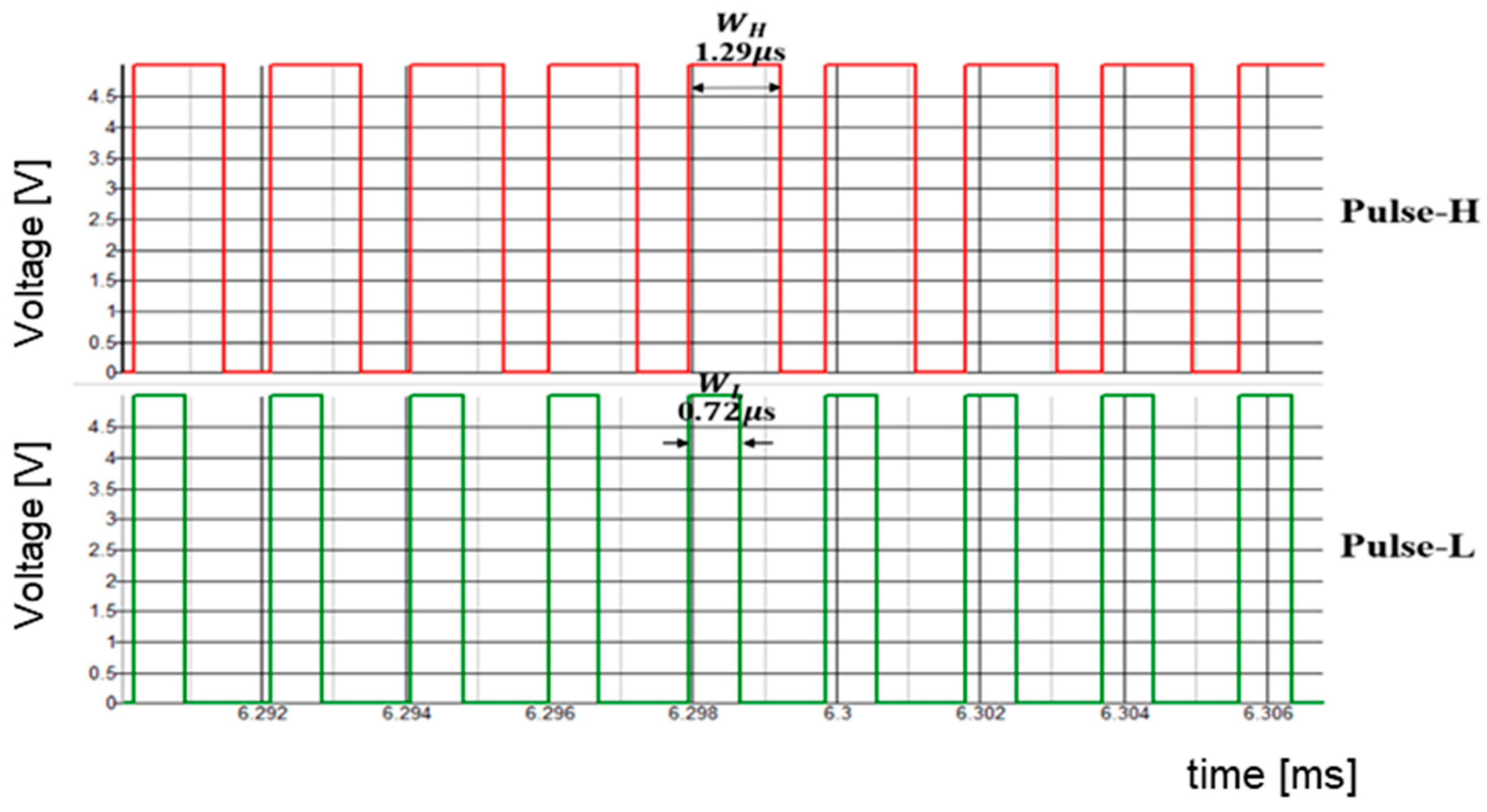
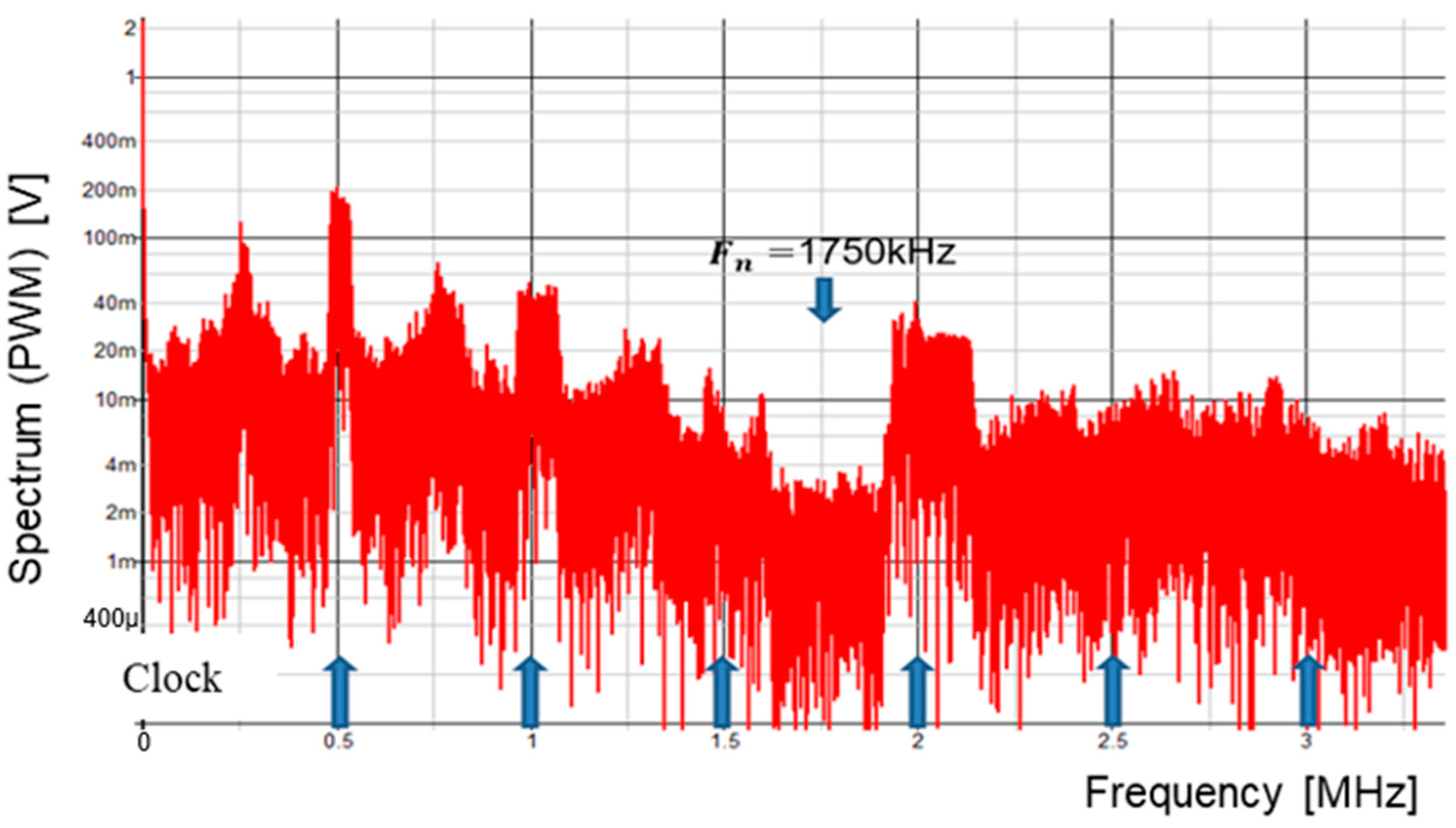
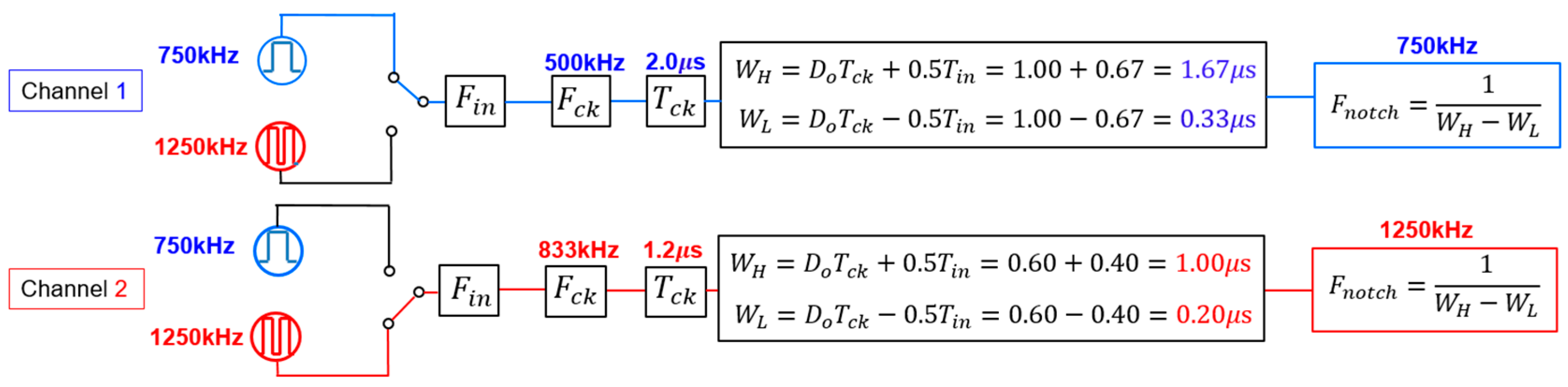
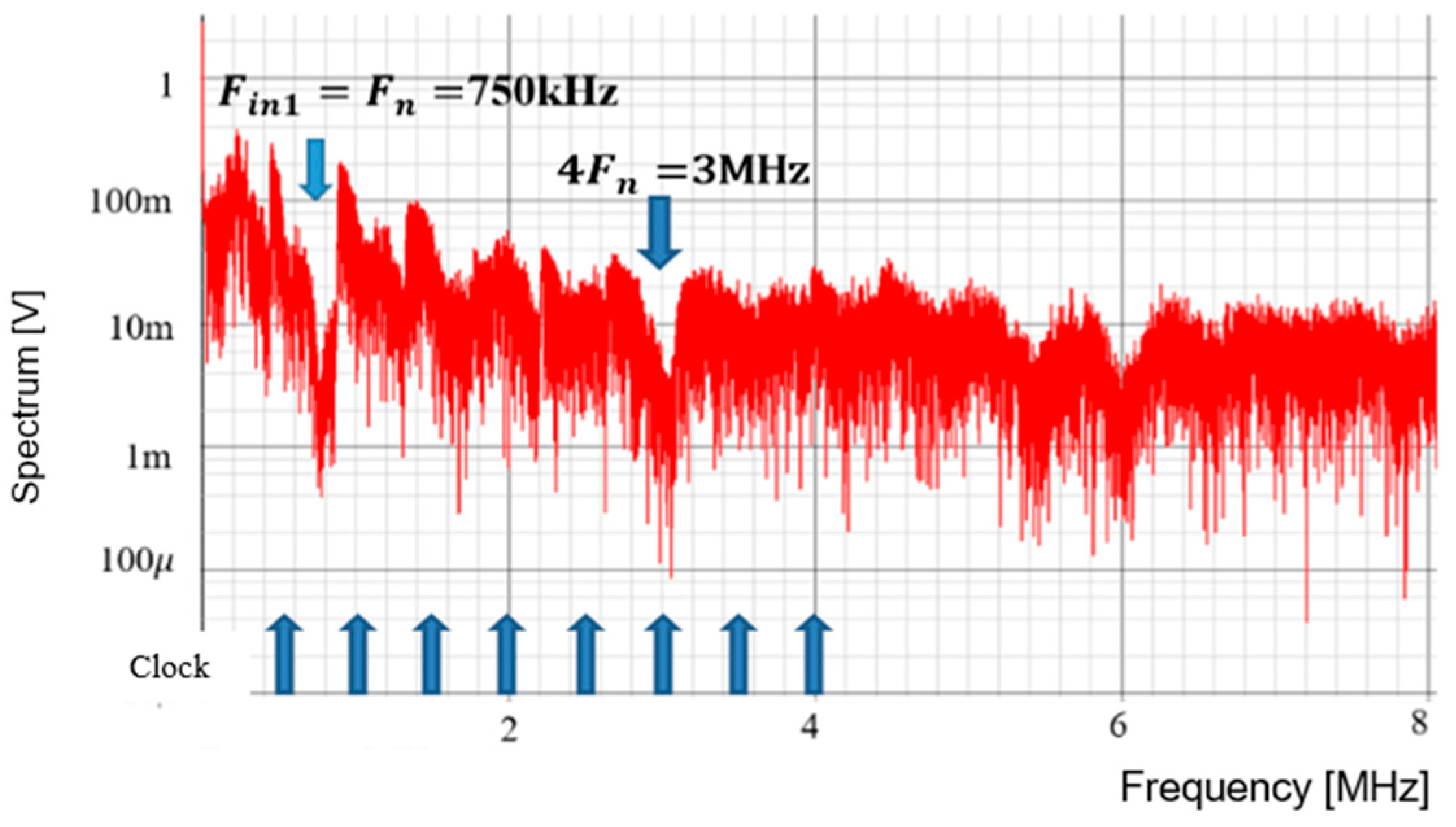
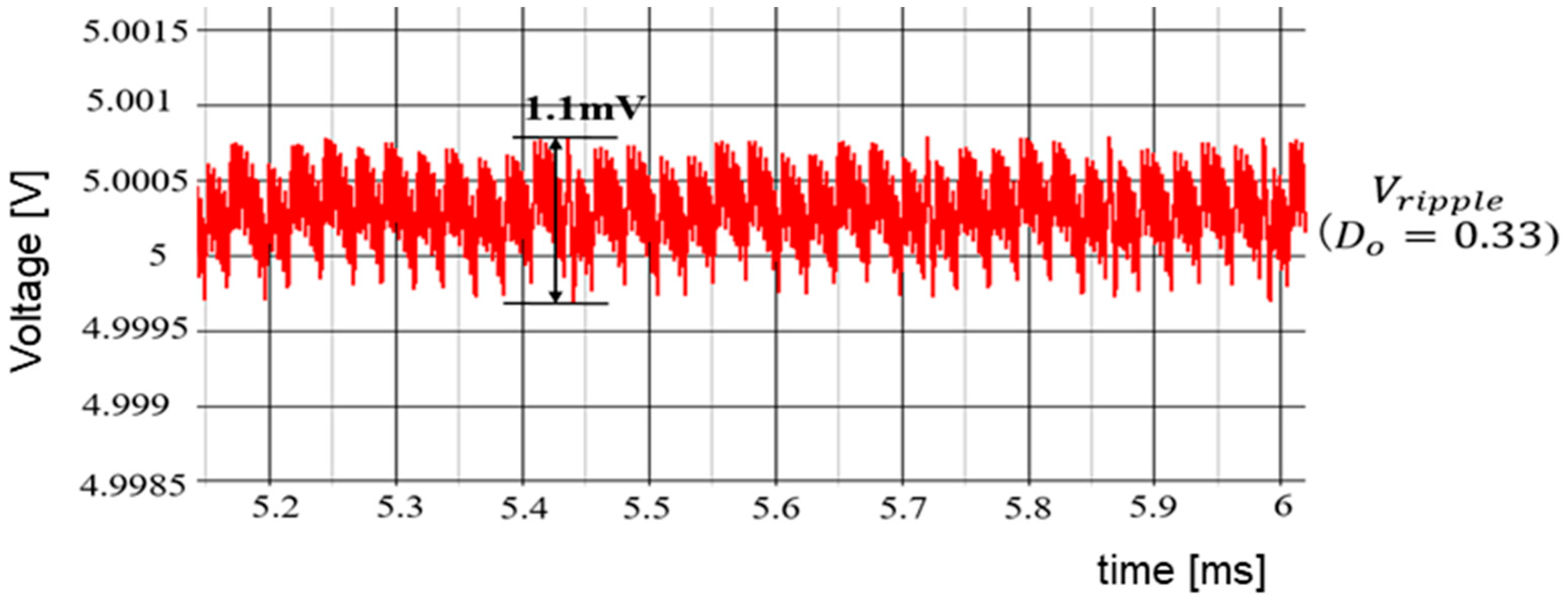

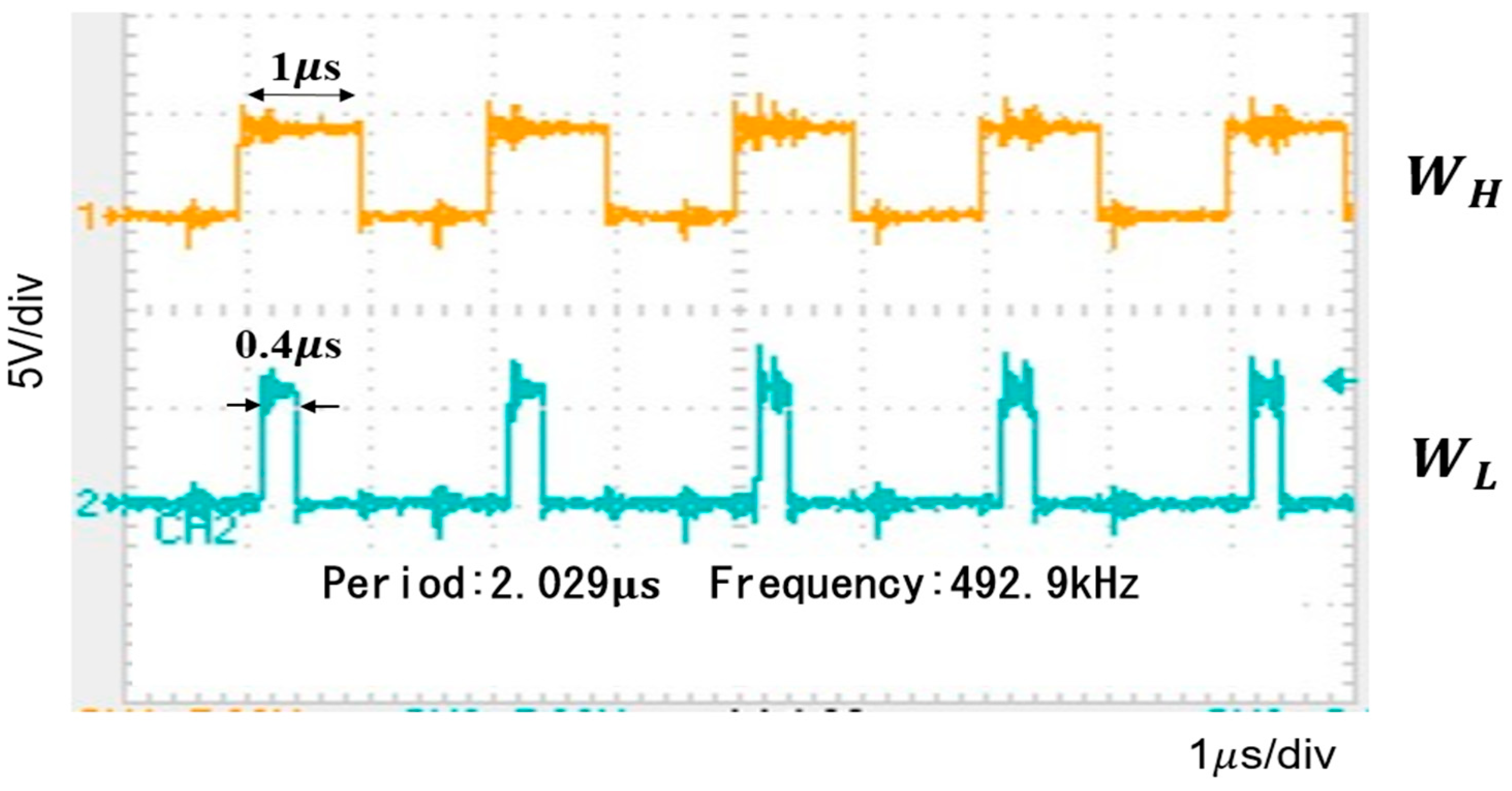

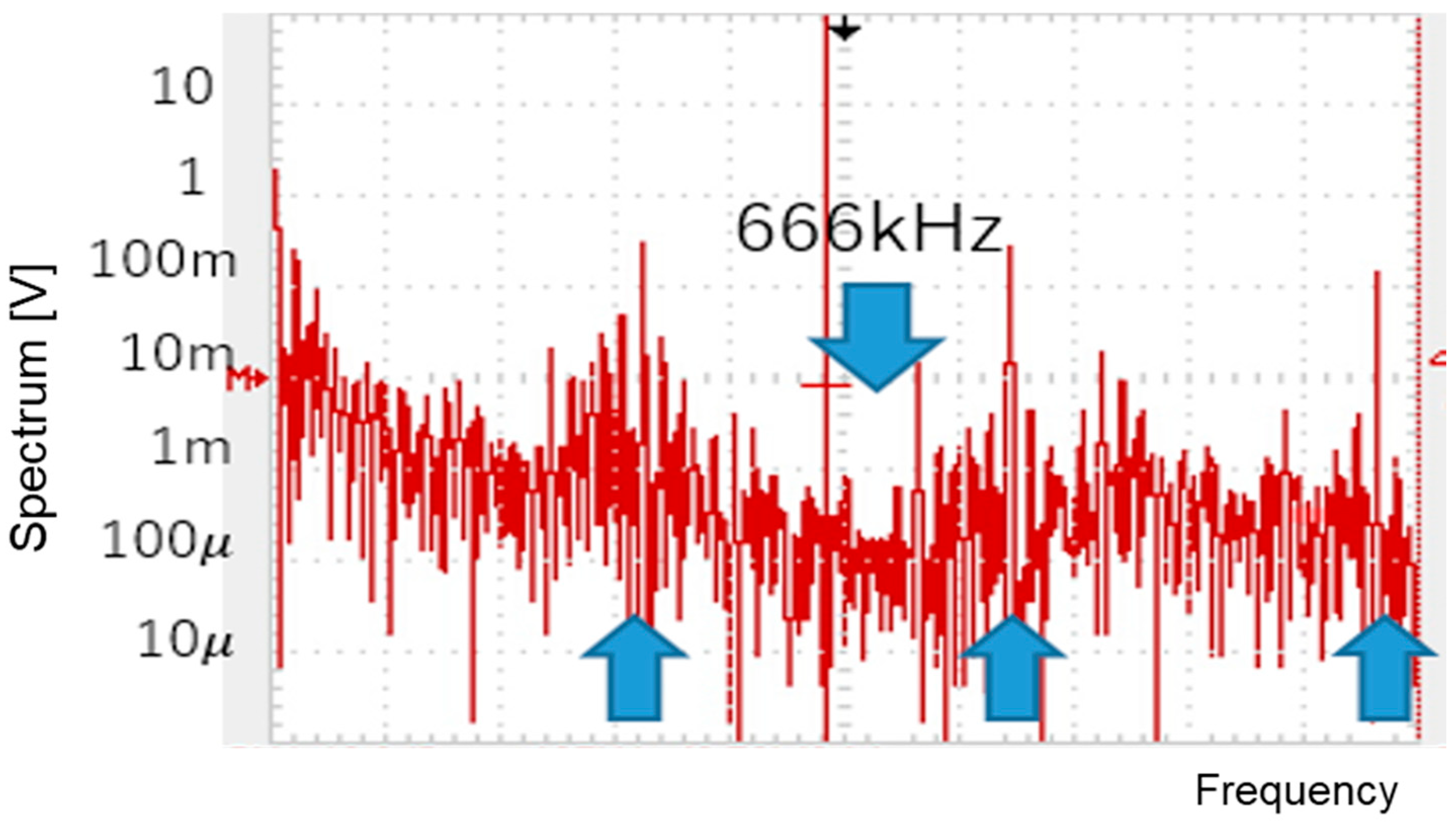
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| Vin | 10.0 V | Io | 0.5 A | Co | 470 μF |
| Vo | 5.0 V | L | 5.0 μH | Fck | 400 kHz |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| Vi | 12.0 V | L | 200 μH | WH | 1.6 μs |
| Vo | 5.0 V | C | 470 μF | WL | 0.3 μs |
| Io | 0.52 A | Tck | 2.0 μs |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| Vi | 10.0 V | L | 100 μH | TL | 600 ns |
| Vo | 3.0 V | C | 470 μF | TS | 220 ns |
| Io | 0.5 A | Wo | 170 ns |
| Parameter | Value | Parameter | Value | Parameter | Value |
| Vi | 12.0 V | Io | 0.2 A | Co | 47 μF |
| Vo | 5.0 V | L | 100 μH | Tck | 2 μs |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| Vi | 10.0 V | Io | 0.16 A | C | 570 μF |
| Vo | 3.5 V | L | 141 μH |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kobori, Y.; Sun, Y.; Kobayashi, H. Selective Notch Frequency Technology for EMI Noise Reduction in DC–DC Converters: A Review. Sensors 2025, 25, 3196. https://doi.org/10.3390/s25103196
Kobori Y, Sun Y, Kobayashi H. Selective Notch Frequency Technology for EMI Noise Reduction in DC–DC Converters: A Review. Sensors. 2025; 25(10):3196. https://doi.org/10.3390/s25103196
Chicago/Turabian StyleKobori, Yasunori, Yifei Sun, and Haruo Kobayashi. 2025. "Selective Notch Frequency Technology for EMI Noise Reduction in DC–DC Converters: A Review" Sensors 25, no. 10: 3196. https://doi.org/10.3390/s25103196
APA StyleKobori, Y., Sun, Y., & Kobayashi, H. (2025). Selective Notch Frequency Technology for EMI Noise Reduction in DC–DC Converters: A Review. Sensors, 25(10), 3196. https://doi.org/10.3390/s25103196