Novel Two-Chamber Method for High-Precision TCR Determination of Current Shunts—Part I
Abstract
1. Introduction
2. Precise Two-Chamber Method for Determination of Current Shunt TCRs
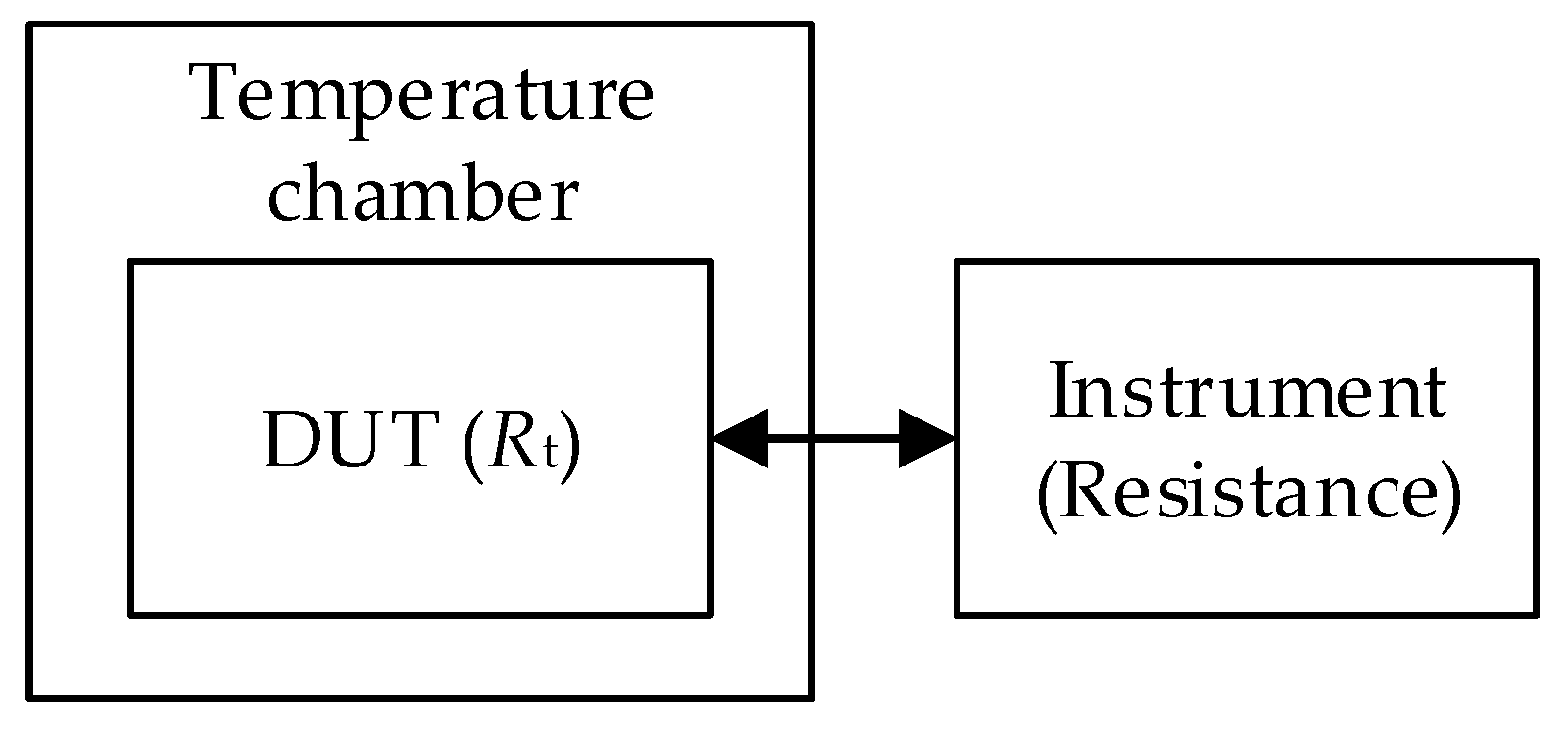
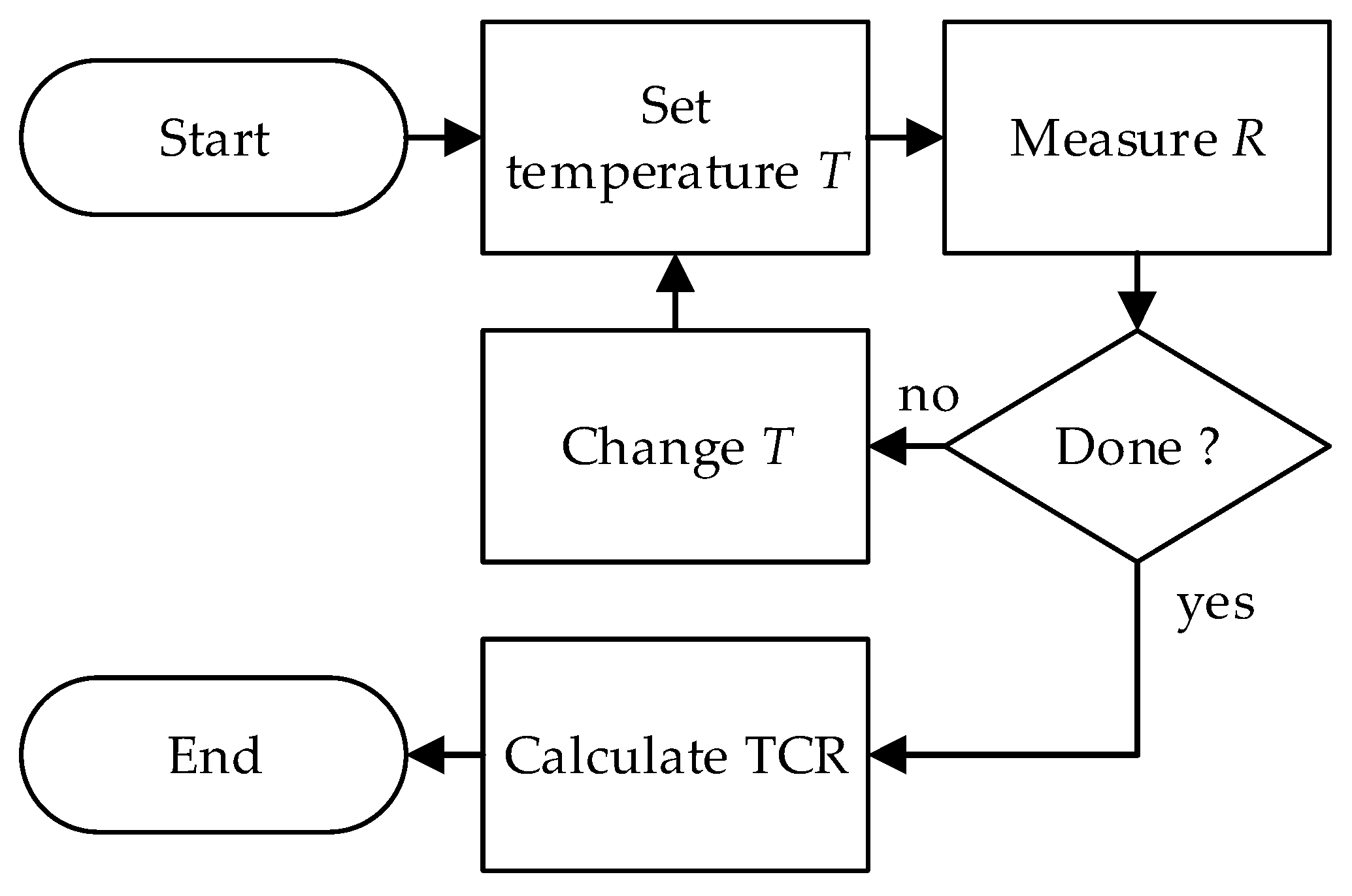
2.1. Classic Approach for Defining TCR
- -
- a precision temperature chamber that maintains a stable temperature environment for the resistor under test;
- -
- a digital multimeter (DMM) or an equivalent voltage measuring device for the high-precision measurement of resistance at certain temperatures. The DMM should have better temperature characteristics than the DUT (tested resistor , shunt, element, etc.).
- -
- set the temperature of the chamber to a specific value. You can start from the highest or lowest temperature in the area of interest and check the humidity once the temperature is stable;
- -
- start the resistance measurement, measure the resistance of the device under test and calculate the TCR as a function of ;
- -
- increase or decrease the temperature and repeat the previous steps. If is not known then add a reference temperature in the range of interest.
- -
- calculate the TCR as a function of .
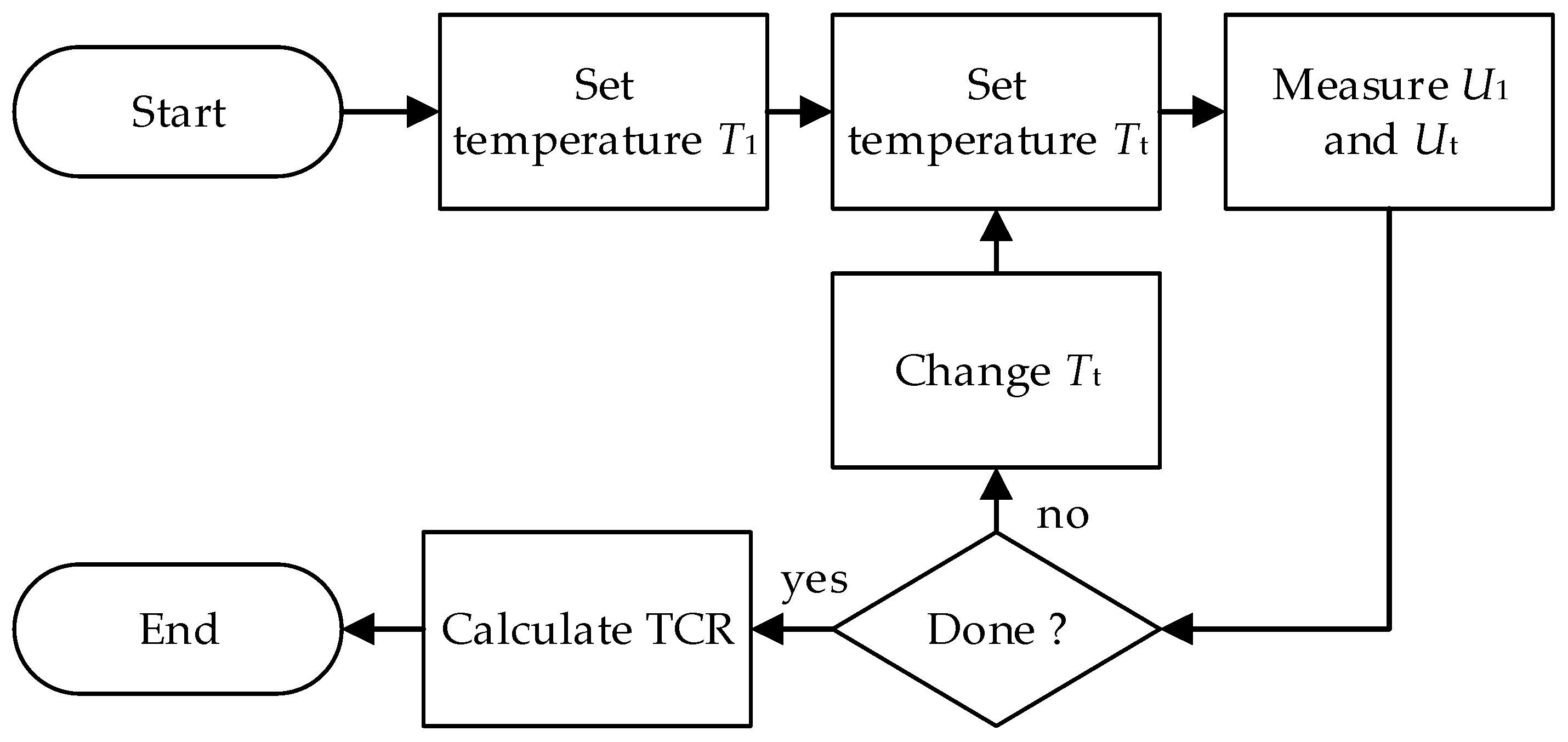
2.2. High-Precision Approach to Define TCR—Proposed New Method
- -
- two precision temperature chambers; the first chamber is used to maintain the reference temperature (23 °C) and contains a reference shunt with known (calibrated) and the second chamber with (DUT), which performs the same task as the classical approach described in the previous subchapter;
- -
- the measurement equipment consists of a reliable current source and a high-precision DMM.
- -
- set the temperature in chamber 1 to 23 °C (;
- -
- set the temperature in chamber 2 to ;
- -
- measure and using DMM;
- -
- calculate and ;
- -
- increase or decrease temperature of chamber 2 with the values within the temperature range of interest and repeat the previous steps. If is not known then add reference temperature in range of interest;
- -
- calculate the TCR as a function of .
3. Uncertainty Analysis
3.1. The Influence of Uncertainty of Parameters and Variables on the Definition of the TCR
3.2. Influence of an Inaccurate Measurement on the TCR
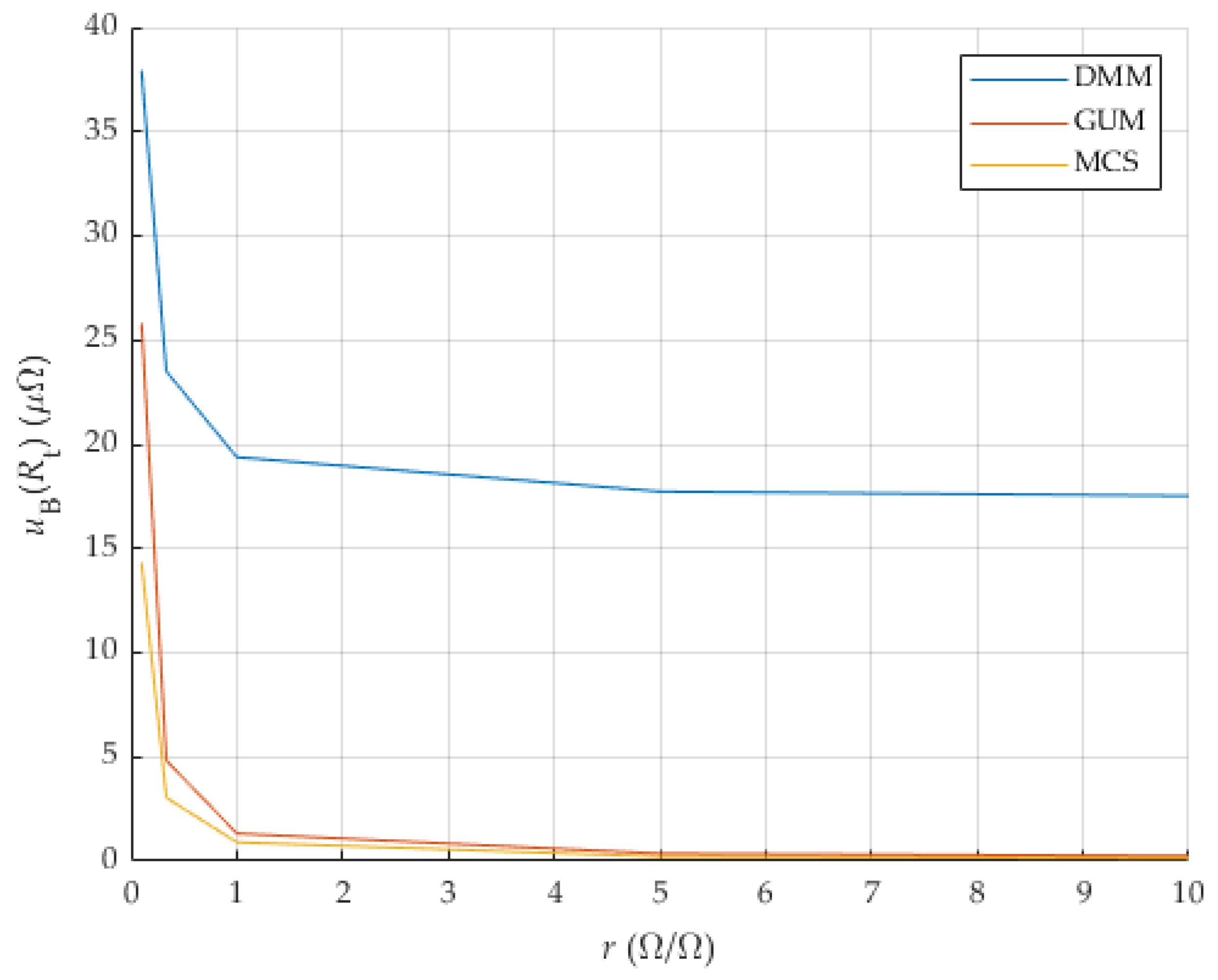
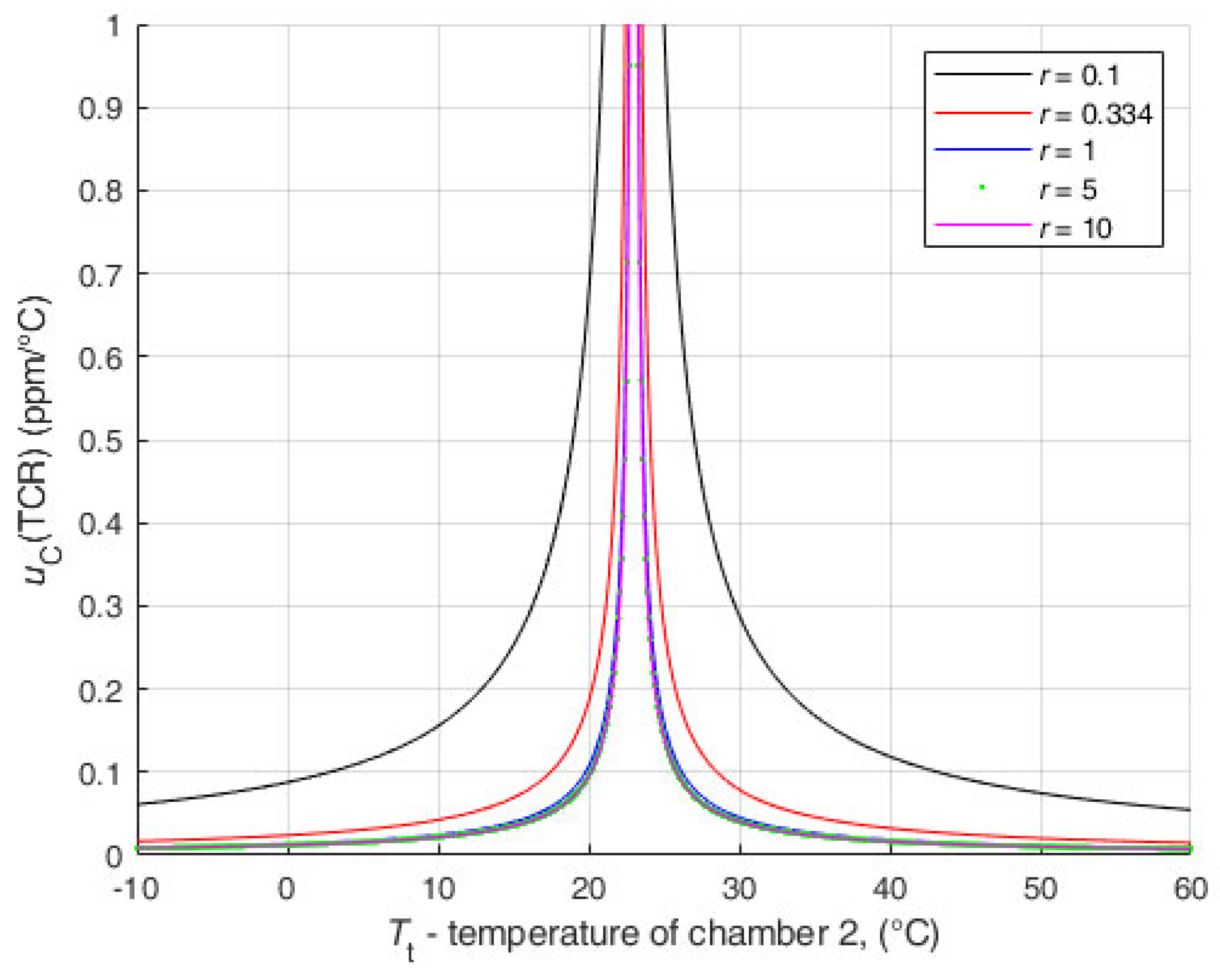
3.3. Influence of Resistance Ratio—Analysis
- -
- for four wire resistance measurements (range: ), the stability is (3 + 1) ppm/°C (of Reading + of Range) without autocalibration (ACAL procedure defined from manufacturer) or (1 + 1) ppm/°C with ACAL; accuracy for 24 h and temperature in range is (5 + 3) ppm;
- -
- for voltage measurements (range: 1 V), the stability is (1.2 + 0.1) ppm/°C without ACAL and with ACAL is (0.15 + 0.1) ppm/°C; accuracy for 24 h and temperature in range is (1.5 + 0.3) ppm.
3.4. Influence of the Calibration of the Reference Resistor on the Measurement Uncertainty
3.5. Improving DMM Accuracy by Using the Transfer Accuracy
4. Propagation of Resistance Uncertainty to TCR
4.1. Propagation of Measurement Uncertainty
4.2. Influence of Temperature Measurement Uncertainty
4.3. Application of the Proposed Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Jin, F.; Wu, D.; Lu, Y.; Pan, Z.; Gu, M.; Wang, H. La0.7Ca0.3MnO3-δ:Ag nanocomposite thin films with large temperature coefficient of resistance (TCR). J. Mater. 2022, 8, 799–805. [Google Scholar] [CrossRef]
- Liu, X.; Yan, Y.-Z.; Chen, Q.-M.; Zhang, H.; Cao, M.-G.; Zhang, S.-C.; Zhang, P.-X. High TCR (temperature coefficient of resistance) La2/3Ca1/3MnO3:Agx polycrystalline composites. Appl. Surf. Sci. 2013, 283, 851–855. [Google Scholar] [CrossRef]
- Gregory, O.J.; Chen, X. A Low TCR Nanocomposite Strain Gage for High Temperature Aerospace Applications. In Proceedings of the SENSORS, 2007 IEEE, Atlanta, GA, USA, 28–31 October 2007; pp. 624–627. [Google Scholar] [CrossRef]
- Bley, V.; Dinculescu, S.; Locatelli, M.-L.; Schlegel, B. Temperature measurement method for dielectric layer characterization in a high voltage vacuum prober. In Proceedings of the 2017 International Symposium on Electrical Insulating Materials (ISEIM), Toyohashi, Japan, 11–15 September 2017; pp. 765–767. [Google Scholar] [CrossRef]
- Gašparini, S.; Mostarac, P.; Konjevod, J.; Malarić, R. Evaluation of the Relative Phase Comparison Method at Its Limits Used for Absolute Phase Determination of an AC Cage Current Shunt Group. Sensors 2023, 23, 8510. [Google Scholar] [CrossRef] [PubMed]
- Konjevod, J.; Malarić, R.; Dadić, M.; Mostarac, P.; Hegeduš, H. Measurement of DC Properties and Relative Humidity (RH) Dependence of Wideband AC Current Shunts. Measurement 2019, 131, 1–6. [Google Scholar] [CrossRef]
- Konjevod, J.; Malarić, R.; Dadić, M.; Kunšt, I.; Hegeduš, H. Ac-Dc Characterization of Coaxial Current Shunts and Application of the Shunt in the Digital Sampling Wattmeter. J. Energy-Energ. 2018, 67, 15–18. [Google Scholar] [CrossRef]
- Koshy, J. The resistivity and temperature coefficient of resistivity of polycrystalline rhodium thin films. J. Phys. D Appl. Phys. 1980, 13, 1339–1342. [Google Scholar] [CrossRef]
- Beltrán-Pitarch, B.; Guralnik, B.; Borup, K.A.; Adelmann, C.; Hansen, O.; Pryds, N.; Petersen, D.H. Temperature coefficient of resistance and thermal boundary conductance determination of ruthenium thin films by micro four-po int probe. Meas. Sci. Technol. 2024, 35, 066012. [Google Scholar] [CrossRef]
- ASTM B84-07; Standard Test Method for Temperature-Resistance Constants of Alloy Wires for Precision Resistors. ASTM International: West Conshohocken, PA, USA, 2019. Available online: https://www.astm.org/ (accessed on 10 February 2025).
- JCGM. WG1, Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. GUM 1995 with Minor Correction. 2008. Available online: https://www.bipm.org/documents/20126/2071204/JCGM_100_2008_E.pdf (accessed on 10 February 2025).
- Capra, P.P.; Francese, C.; Galliana, F.; Lanzillotti, M.; Tet, L.R.; Sosso, A.; Durandetto, P. DMMs as Voltage Ratio Standards: A 20 Years Report. In Proceedings of the 25th IMEKO TC-4 International Symposium on Measurement of Electrical Quantities, IMEKO TC-4 2022 and 23rd International Workshop on ADC and DAC Modelling and Testing, IWADC, Brescia, Italy, 12–14 September 2022; pp. 68–72. [Google Scholar]
- JCGM. Evaluation of Measurement Data—Supplement 1 to the Guide to the Expression of Uncertainty in Measurement-Propagation of Distributions Using a Monte Carlo Method. 2008. Available online: https://www.bipm.org/documents/20126/2071204/JCGM_101_2008_E.pdf/325dcaad-c15a-407c-1105-8b7f322d651c (accessed on 10 February 2025).
- Sediva, S.; Havlikova, M. Comparison of GUM and Monte Carlo method for evaluation measurement uncertainty of indirect measurements. In Proceedings of the 14th International Carpathian Control Conference (ICCC), Rytro, Poland, 26–29 May 2013; pp. 325–329. [Google Scholar] [CrossRef]
- Farrance, I.; Frenkel, R. Uncertainty in measurement: A review of monte carlo simulation using microsoft excel for the calculation of uncertainties through functional relationships, including uncertainties in empirically derived constants. Clin. Biochem. Rev. 2014, 35, 37–61. [Google Scholar] [PubMed]



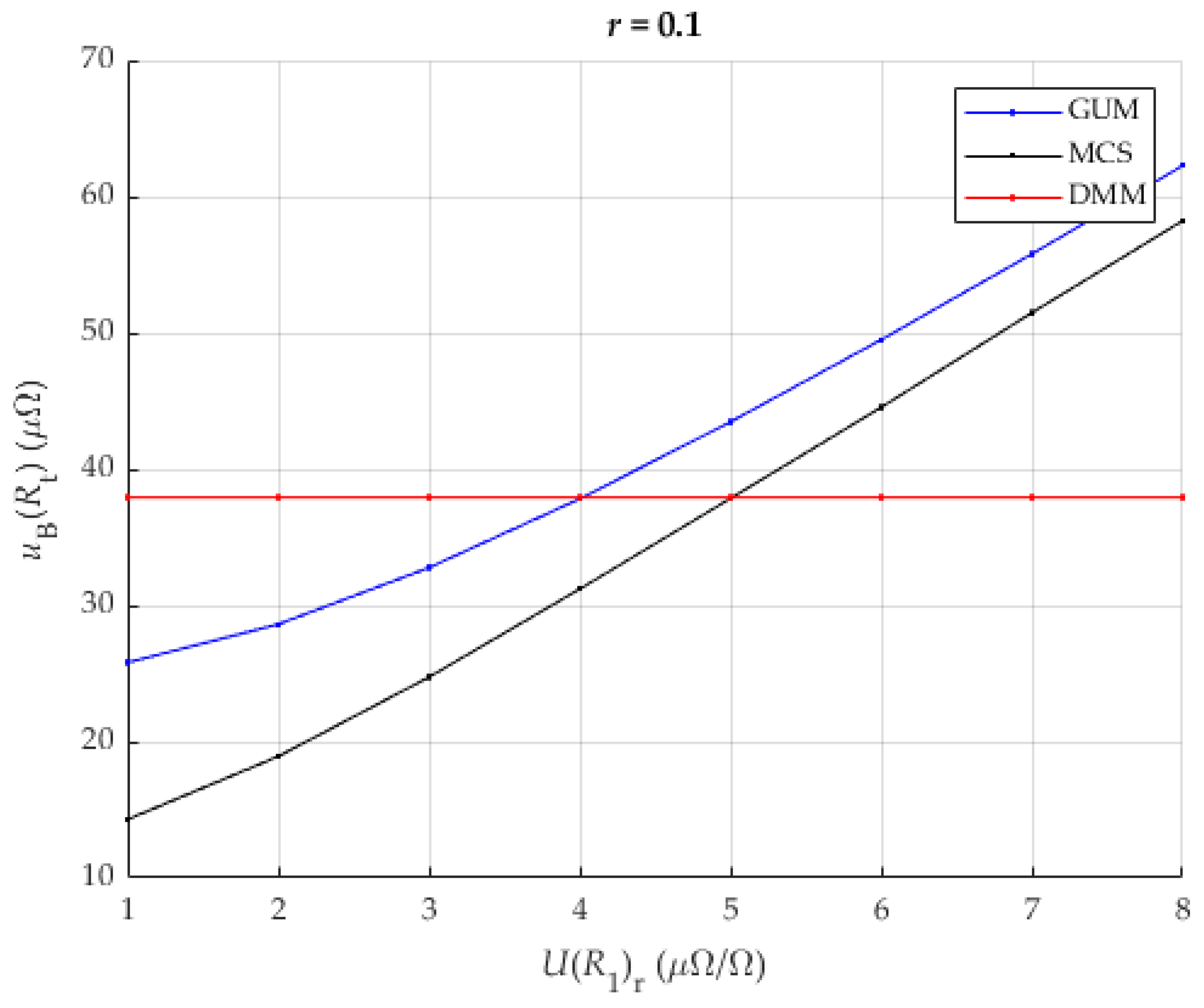
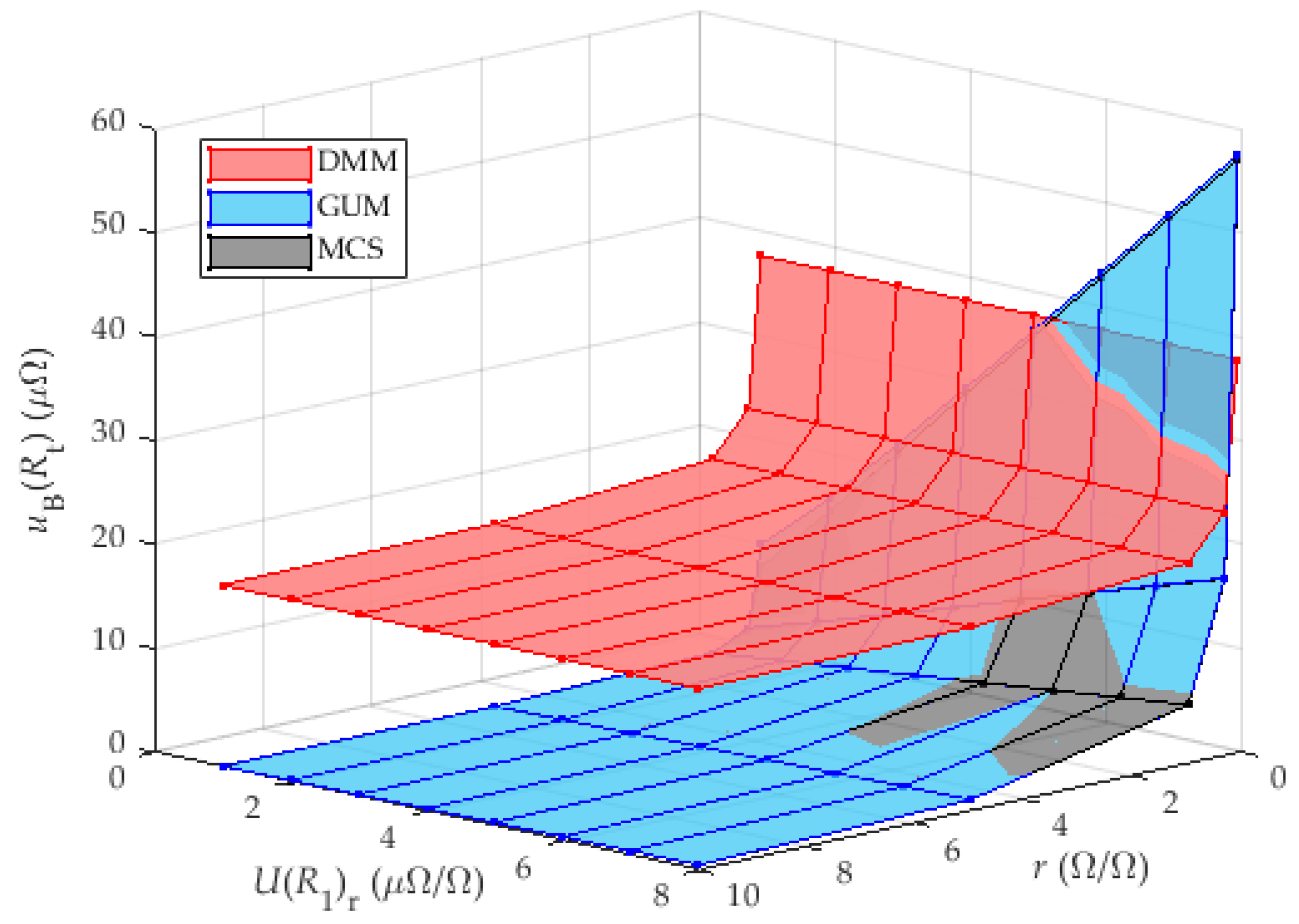
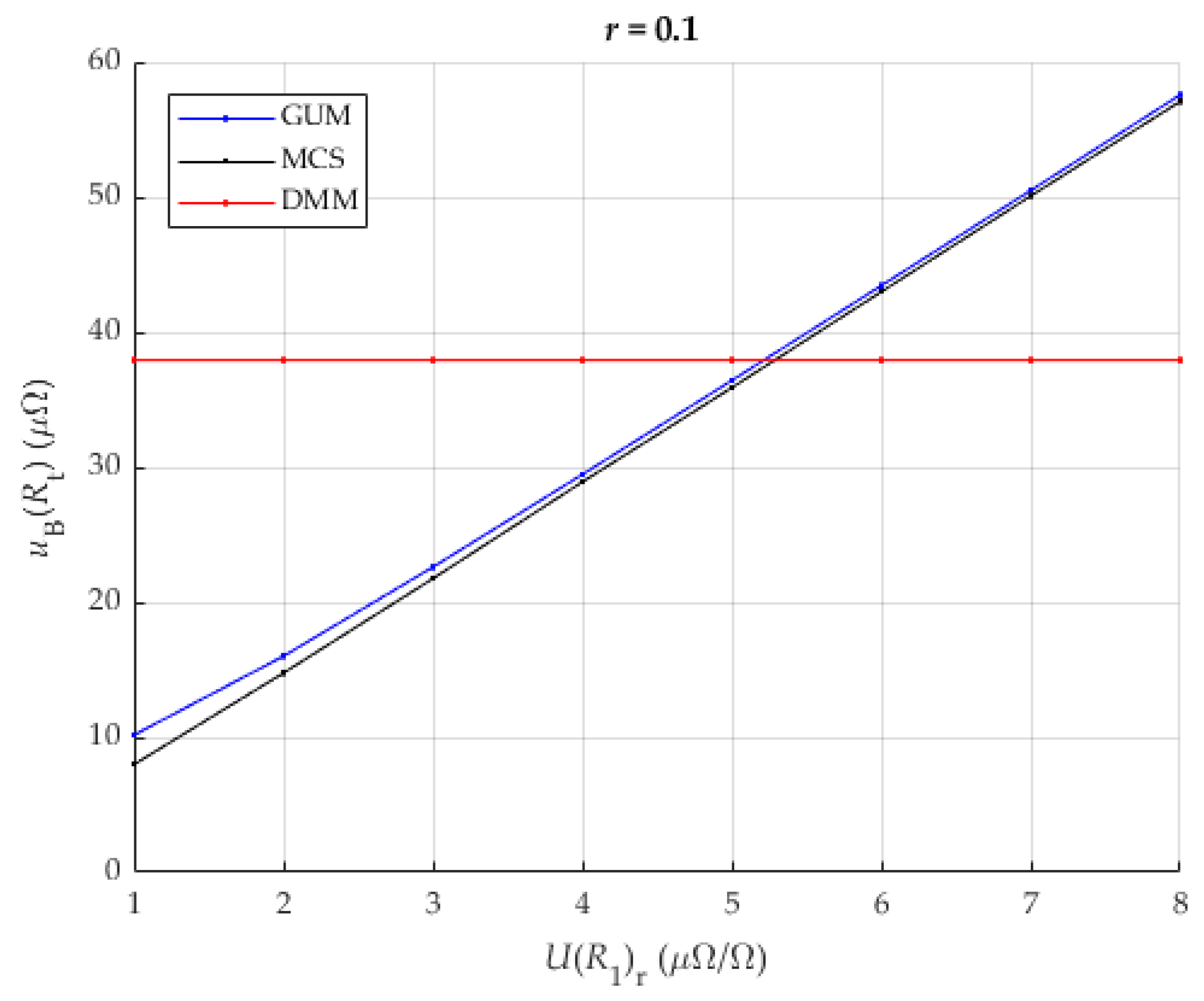


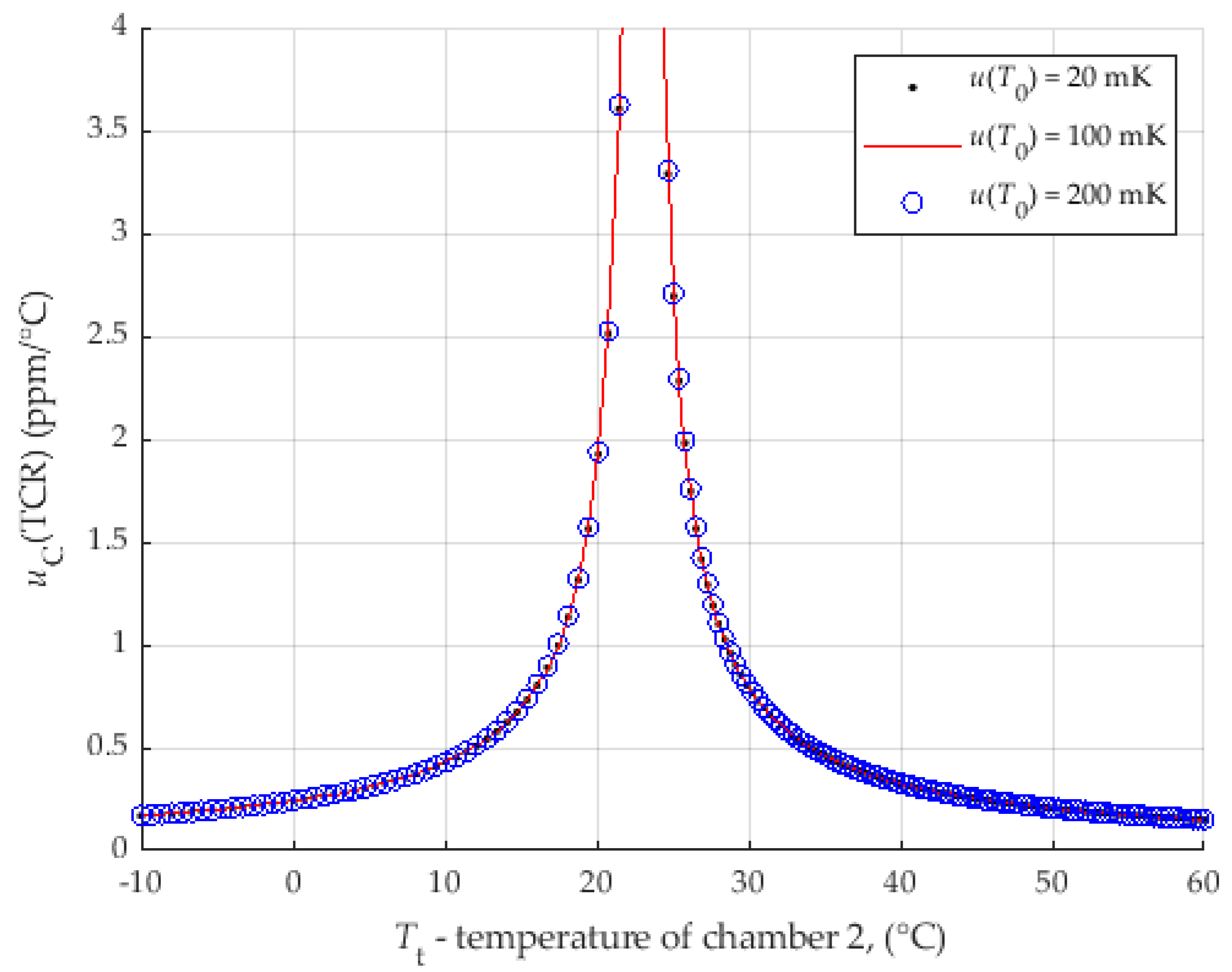
| Parameter | Value | Unit | Distribution 1/ Comment |
|---|---|---|---|
| Iteration | number of MCS iterations | ||
| 1.5 (0.3 for transfer accuracy) | rectangular | ||
| 0.3 (0.1 for transfer accuracy) | rectangular | ||
| DMM voltage range | 1 | V | DC |
| 0.01 | rectangular | ||
| 0.01 | rectangular | ||
| DMM resistance range | 10 | ||
| 0.714 | |||
| (0.0714, 0.143, 0.714, 2.14, 7.14) | at 23 °C | ||
| (10, 5, 1, 0.3, 0.1) | A | ||
| A | |||
| 1 | (1, 2, 3, 4, 5, 6, 7, 8) | normal distribution | |
| 2 | 1 | - | coverage factor |
| Parameter | Unit | Values | ||||
|---|---|---|---|---|---|---|
| 10 | 5 | 1 | 0.334 | 0.1 | ||
| A | 1 | 1 | 1 | 0.3 | 0.1 | |
| 0.714 | 0.714 | 0.714 | 0.714 | 0.714 | ||
| 0.792 | 0.792 | 0.792 | 0.359 | 0.235 | ||
| 0.235 | 0.297 | 0.792 | 0.729 | 0.792 | ||
| 0.258 | 0.366 | 1.328 | 4.830 | 25.808 | ||
| 0.143 | 0.221 | 0.908 | 3.043 | 14.322 | ||
| 17.527 | 17.733 | 19.382 | 23.498 | 37.932 | ||
| Parameter | Unit | Values | ||||
|---|---|---|---|---|---|---|
| r | 10 | 5 | 1 | 0.334 | 0.1 | |
| 0.1 | 0.2 | 0.8 | 2.4 | 10.1 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mostarac, P.; Malarić, R.; Hegeduš, H.; Šala, A. Novel Two-Chamber Method for High-Precision TCR Determination of Current Shunts—Part I. Sensors 2025, 25, 3197. https://doi.org/10.3390/s25103197
Mostarac P, Malarić R, Hegeduš H, Šala A. Novel Two-Chamber Method for High-Precision TCR Determination of Current Shunts—Part I. Sensors. 2025; 25(10):3197. https://doi.org/10.3390/s25103197
Chicago/Turabian StyleMostarac, Petar, Roman Malarić, Hrvoje Hegeduš, and Alan Šala. 2025. "Novel Two-Chamber Method for High-Precision TCR Determination of Current Shunts—Part I" Sensors 25, no. 10: 3197. https://doi.org/10.3390/s25103197
APA StyleMostarac, P., Malarić, R., Hegeduš, H., & Šala, A. (2025). Novel Two-Chamber Method for High-Precision TCR Determination of Current Shunts—Part I. Sensors, 25(10), 3197. https://doi.org/10.3390/s25103197






