1. Introduction
In recent years, with the continuous development of the Yangtze River’s smart navigation system, intelligent items of equipment, such as unmanned surface vehicles (USVs), have been increasingly used in the inland waterways of the Yangtze River. USVs have become powerful tools for inland riverine environmental surveillance, hydrological assessment, and geomorphic exploration, due to their safety, economic advantages, and other benefits. When operating in inland rivers, the primary challenge for USVs is how to achieve safe and efficient autonomous navigation. Typically, an autonomous navigation system for USVs consists of three modules: perception, path planning, and motion control [
1]. As a key technology for USVs to navigate autonomously, effective path planning is crucial in ensuring the safety and efficiency of USVs while they operate in inland waterways. The primary function of path planning is to plan a collision-free path from the starting point to the destination point of a USV, based on environmental information obtained by the USV’s perception module [
2]. Depending on the level of environmental information obtained by such perception modules, path planning can be divided into two categories: global path planning and local path planning.
Global path planning algorithms primarily plan a globally optimal path based on a priori information, including known static obstacles, channel boundaries, and water depths. In contrast to local path planning, global path planning commonly suffers from drawbacks such as poor real-time responsiveness and an inability to effectively consider real-time changes in the kinematics of USVs and the dynamic environment of the waterway. Among the widely used global-path planning algorithms are Dijkstra’s algorithm [
3], the A* algorithm [
4], the rapidly-exploring random tree (RRT) algorithm [
5], the particle swarm optimization (PSO) algorithm [
6], and neural-network-based algorithms [
7].
Dijkstra’s algorithm is a depth-first search method that is used to calculate the shortest path between a node and other nodes. Although simple and clear, Dijkstra’s algorithm has low computational efficiency and is not suitable for path planning in large scenes. The RRT algorithm replaces the directed-graph structure with a tree structure, avoiding spatial modeling. However, like Dijkstra’s algorithm, the RRT algorithm has poor real-time performance due to its uniform search characteristics, and it is difficult to obtain global optimal solutions with the RRT algorithm, due to its random-sampling nature. The PSO algorithm is an evolutionary algorithm inspired by the foraging behavior of birds. Particle swarm optimization has the advantages of fast search speed and memory, but it may be limited to local optimization due to premature convergence. Neural-network-based methods have become hot research topics in recent years, but due to their complex computations and other issues, they remain problematic for practical applications.
Compared to the above algorithms, the A* algorithm has a simple structure and operates faster than Dijkstra’s algorithm. The A* algorithm is widely used in the global path planning of USVs, due to its ability to find the globally optimal path—if such a path exists. Ding et al. [
8] utilized a complete-coverage neural-network algorithm for the global path planning of USVs vehicles and improved the A* algorithm to help the traversal algorithm escape deadlocks. Simulation experiments validated the effectiveness of their proposed algorithm. Shen et al. [
9] aimed to enhance the collision avoidance capability of USVs in open waters by utilizing the A* algorithm and combining ship-maneuvering characteristics. By fully considering navigation-experience regulations, they proposed parallel decision-making dynamic collision avoidance algorithms that only change the heading, or simultaneously change the heading and the speed. Simulation experiments and direct ship-model experiments validated the effectiveness of their proposed algorithms.
Local path planning algorithms, which are also known as local collision avoidance algorithms, are used to generate an optimal or sub-optimal local path for a USV based on real-time information obtained by its onboard sensors, such as water flow, the presence of other ships, and the presence of islands. Compared to global path planning algorithms, local path planning algorithms offer better real-time responsiveness and typically take into account the vessel’s kinematic characteristics and real-time environmental information. However, local path planning algorithms can be susceptible to becoming trapped in local optimal solutions. Common local path planning algorithms include the velocity-obstacle (VO) method [
10], the model predictive control (MPC) method [
11], the dynamic-window (DW) method [
12], and the artificial-potential-field (APF) method [
13]. The VO method, the DW method, and the APF method are widely used in local path planning, due to their real-time performances. However, while ensuring real-time performance, these algorithms have limited information considerations and are prone to being limited to local optimal solutions. In addition, the collision avoidance regulations for USVs were difficult to integrate into these algorithms.
Compared to the above algorithms, the MPC algorithm has been increasingly used in the local path planning of USVs due to its receding horizon and its ability to handle multi-input and multi-output nonlinear optimization problems. The MPC algorithm can effectively consider collision avoidance regulations during the optimization process. Johansen et al. [
14] employed the MPC algorithm to address the problem of autonomous navigation for USVs open waters. The algorithm considered various factors, such as collision avoidance regulations, water flow, and dynamic obstacles. A large-scale simulation experiment was conducted to validate the effectiveness of the proposed MPC algorithm. Similarly, Eriksen et al. [
15] utilized the MPC algorithm for local path planning in open sea environments. This algorithm can consider both moving and static obstacles simultaneously and track a reference trajectory when there is no danger. Once again, simulation experiments were conducted to verify the effectiveness of this algorithm.
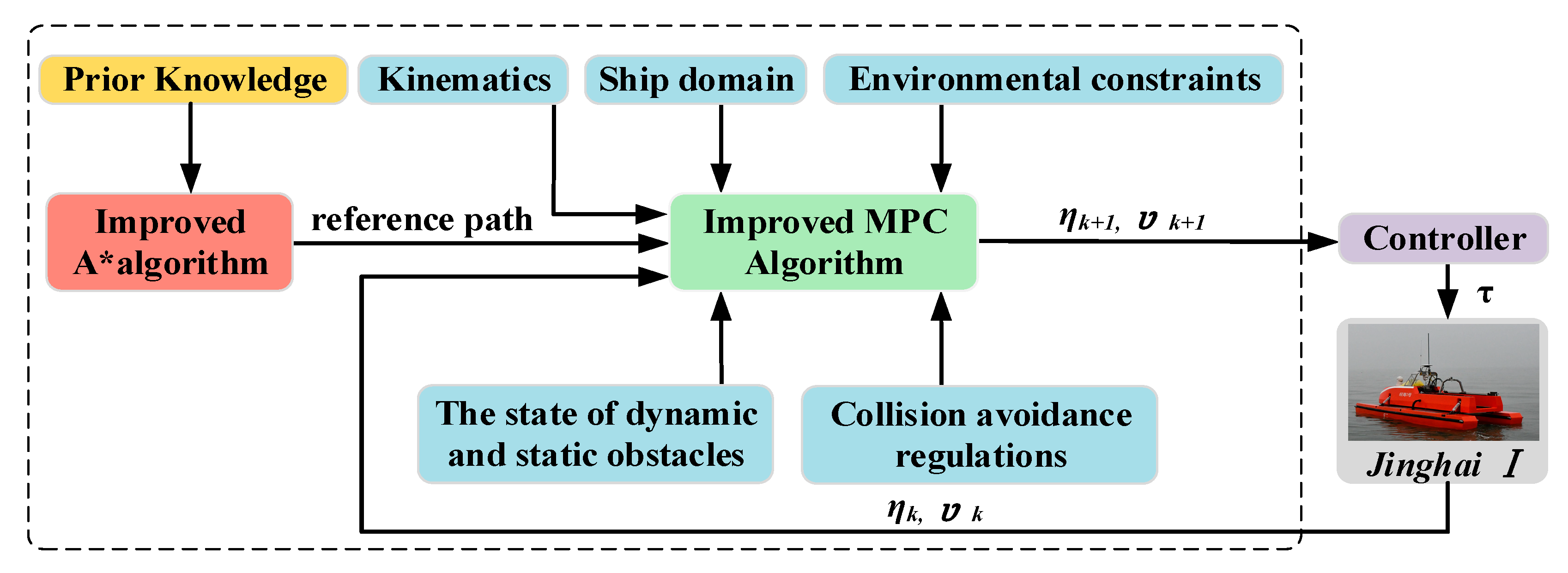
A suitable path planning algorithm should aim to achieve a global optimal solution while also accounting for the kinematics of a USV and real-time environmental information. One feasible solution is to combine a global path planning algorithm with a local path planning algorithm, achieving mutual benefit through complementary advantages. This study focuses on the path planning problem of the “Jinghai-I” USV developed by our team for inland rivers. Based on previous research, we propose a hybrid path planning method that combines an improved A* algorithm and an improved model predictive control algorithm. To meet the requirements of riverine navigation regulations, the cost functions for the improved A* algorithm and the improved model predictive control algorithm were modified accordingly. To address the issue of excessive global path turning points, a smoothing method was implemented. In order to enhance the effectiveness of local path planning using model predictive control, different planning parameters were selected, based on different encounter scenarios. The effectiveness of the hybrid path planning method was verified through simulation experiments underwater and by aquatic conditions, both with and without water-flow interference.
The remainder of this paper is organized as follows:
Section 1 introduces the research background and its significance;
Section 2 describes the basic theory of the USV motion model and hybrid path planning;
Section 3 illustrates the simulation results that were conducted;
Section 4 discusses the experimental results in detail; and
Section 5 summarizes this paper.
4. Discussion
This study proposed a hybrid path planning method that combined the improved A* algorithm and the improved MPC algorithm to solve the problem of path planning for the “Jinghai-I” USV, which was independently developed by the team for autonomous navigation in inland rivers.
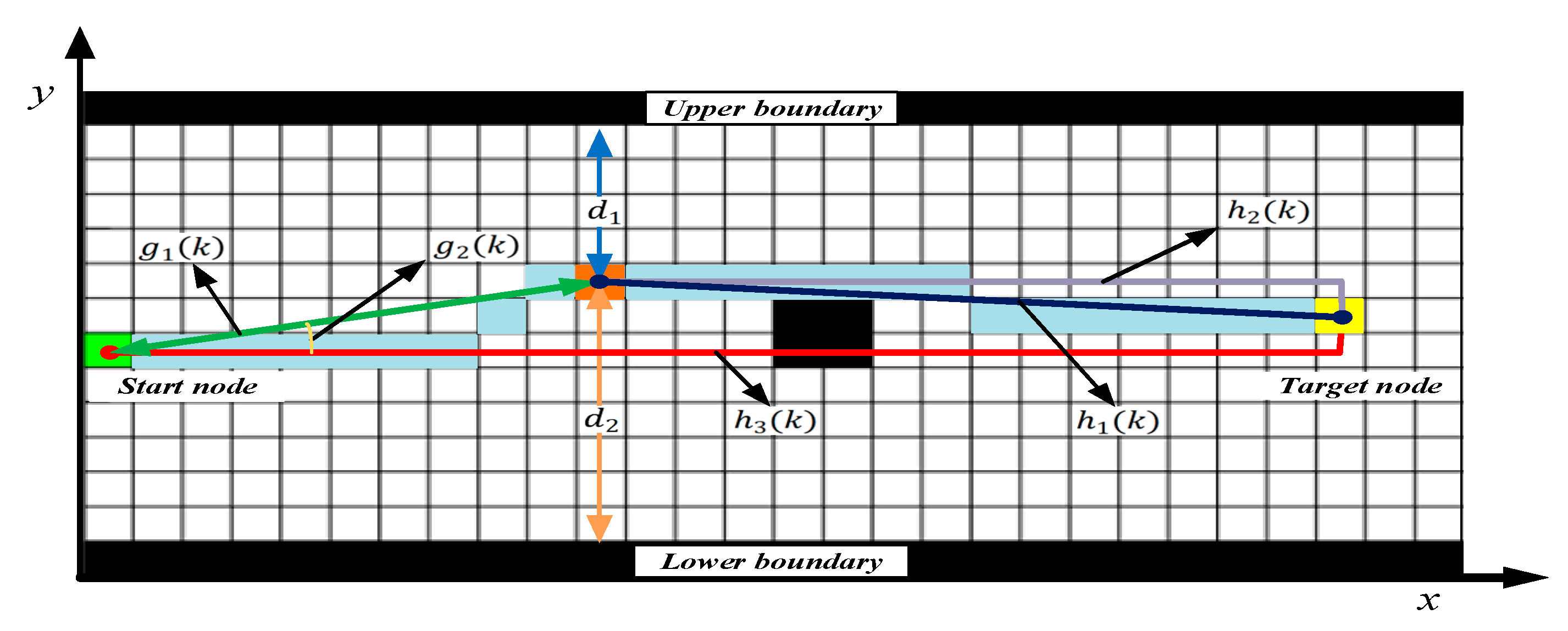
To ensure that the planned global path complied with the requirements of inland-navigation regulations for all vessels to travel as far as possible on the right side of the waterway, a cost term based on the distance from the waterway boundary was added to the cost function of the A* algorithm.
To ensure the global optimization of the path, a dynamic-adjustment heuristic method was used as the heuristic function of the improved A* algorithm, and different values of were experimented with to determine the appropriate range. In this study, the planned path by the improved A* algorithm had excessive turning angles, which did not meet the requirements of the maximum heading angle in river navigation. Finally, the global optimal path planned by the improved A* algorithm was smoothed.
When performing path smoothing, conventional curve smoothing methods such as B-spline curves and polynomial fitting were not used. Instead, unreasonable path points were removed to achieve curve smoothing. This was because, based on MPC local path planning, a more locally optimal path that conforms to the kinematics of the “Jinghai-I” USV could be planned. The improved A* algorithm only needed to plan a globally optimal path that met the maximum heading-angle requirements of river navigation, thus guiding the local path planning algorithm for tracking.
On the basis of tracking the global optimal path, the “Jinghai-I” USV used the MPC algorithm for local path re-planning. The MPC algorithm used different parameters according to different encounter situations, thus planning a more reasonable path. In response to the shortcomings of previous research, the MPC algorithm introduced a new path-deviation cost and a new yaw-angle cost, which significantly reduced the error of the algorithm in tracking the reference path and the yaw angle. Simulation experiments validated the effectiveness of the improved model predictive control algorithm.
As indicated in Formula (15), increasing the tuning coefficient increases the proportion of the corresponding cost term in the overall cost function, making the corresponding constraint more effective. However, going too far is as bad as not going far enough. An excessively large causes the algorithm to overemphasize the tracking of the reference path, affecting the actual planning efficiency and even leading to collision avoidance failure of the “Jinghai-I” USV. The selection of the reference angle is similar to the LOS method, and an excessively large will result in the “Jinghai-I” USV failing to return to the reference trajectory after avoiding obstacles. An excessively large , , , and will cause the algorithm to focus more on maintaining speed during planning, reducing the flexibility of collision avoidance. In normal circumstances, the value of is 0. Only when static obstacles are within the range of collision avoidance for the “Jinghai-I” USV will the value of be 1. At this time, the corresponding cost term will come into play and guide the “Jinghai-I” USV to avoid static obstacles. The values of and are also similar, but they will not both be 1 at the same time. For example, when static obstacle enters the collision avoidance range of the “Jinghai-I” USV at time k, assume that static obstacle is on the left side of the heading direction of the “Jinghai-I” USV and that the heading angle is positive when the “Jinghai-I” USV turns right. At this time, the value of is 1 and the value of is 0. The algorithm guides the “Jinghai-I” USV to turn right as far as possible to avoid the static obstacle. This maneuver not only reduces the collision risk of the “Jinghai-I” USV but also meets the requirements of inland-navigation regulations. When the static obstacle leaves the collision avoidance range of the “Jinghai-I” USV, the value of is 0, and other cost items will constrain the “Jinghai-I” USV to continue to follow the reference path. Similarly, the values of coefficients in Formula (16) also follow this principle.
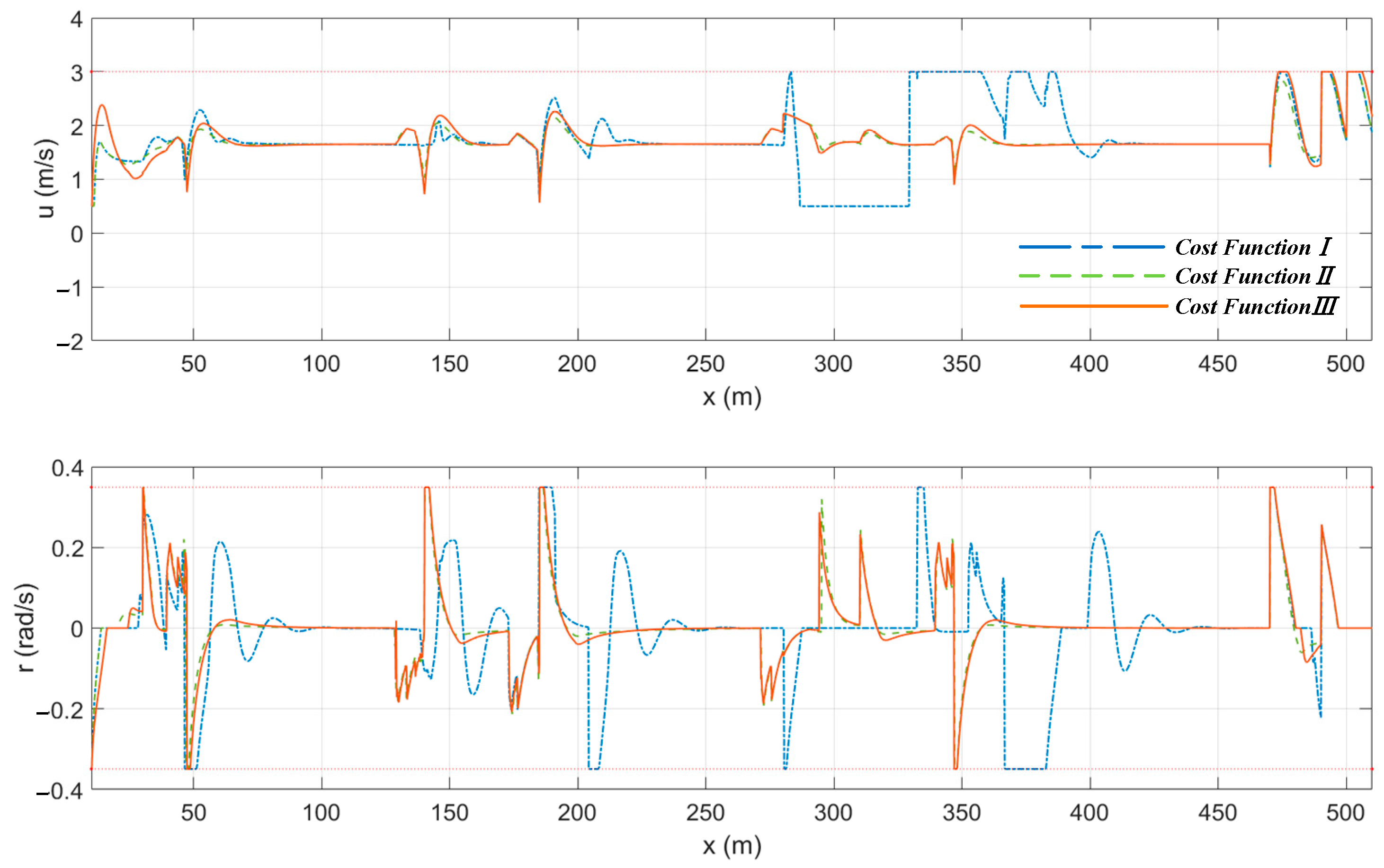
After adding the water flow term, the deviation of the planned path by cost function
I was smaller than that without water-flow interference. This was mainly because the direction of the flow was opposite to the direction that the “Jinghai-I” USV evaded. Under the influence of the flow, the deviation on the right side of the path planned by cost function
I became smaller. In addition, the gap between cost functions
II and
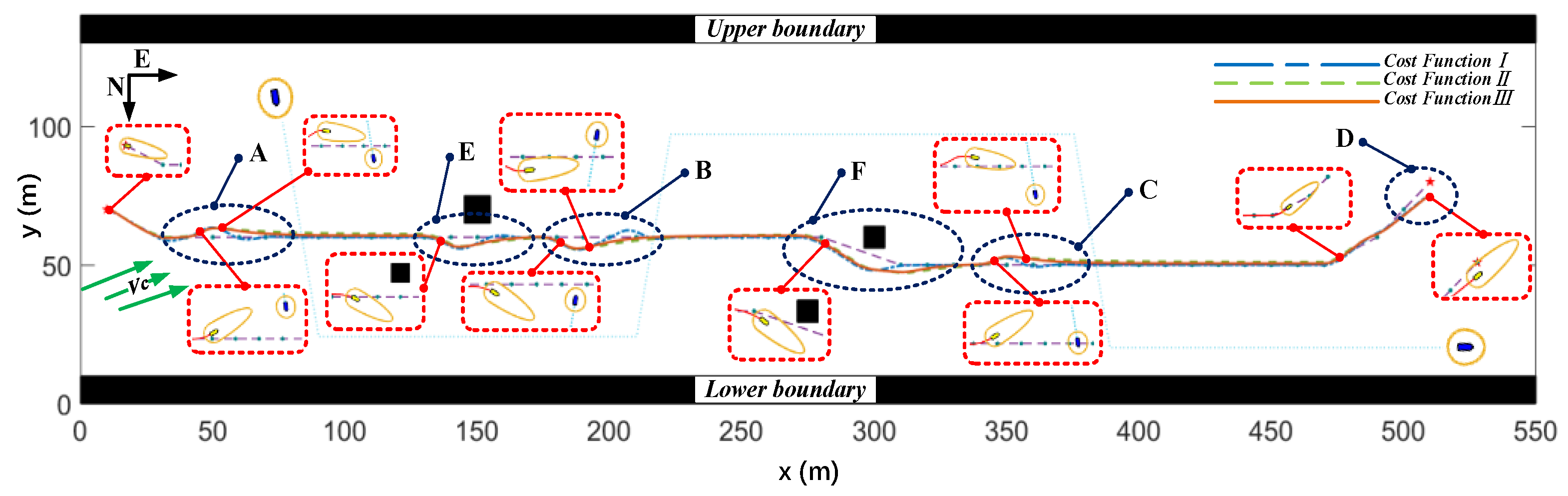
III did not seem as obvious as before, without flow interference, mainly due to the impact of the flow. For example, in scenario C shown in
Figure 13, cost function
II indicated that it was acceptable for there to be a certain path deviation. However, due to the disturbance caused by the water flow, this path deviation became even larger, making its proportion in the cost function higher. To minimize the cost function, the algorithm re-planned a more reasonable path. From another perspective, because of the receding horizon characteristic of the MPC algorithm, it has good robustness against water flow disturbances. Compared with [
16], this study removed the distance penalty term from the cost function and considered the distance factor during encounter-situation judgment. This not only did not reduce the performance of the algorithm, but also simplified the cost function and improved the efficiency of the algorithm.
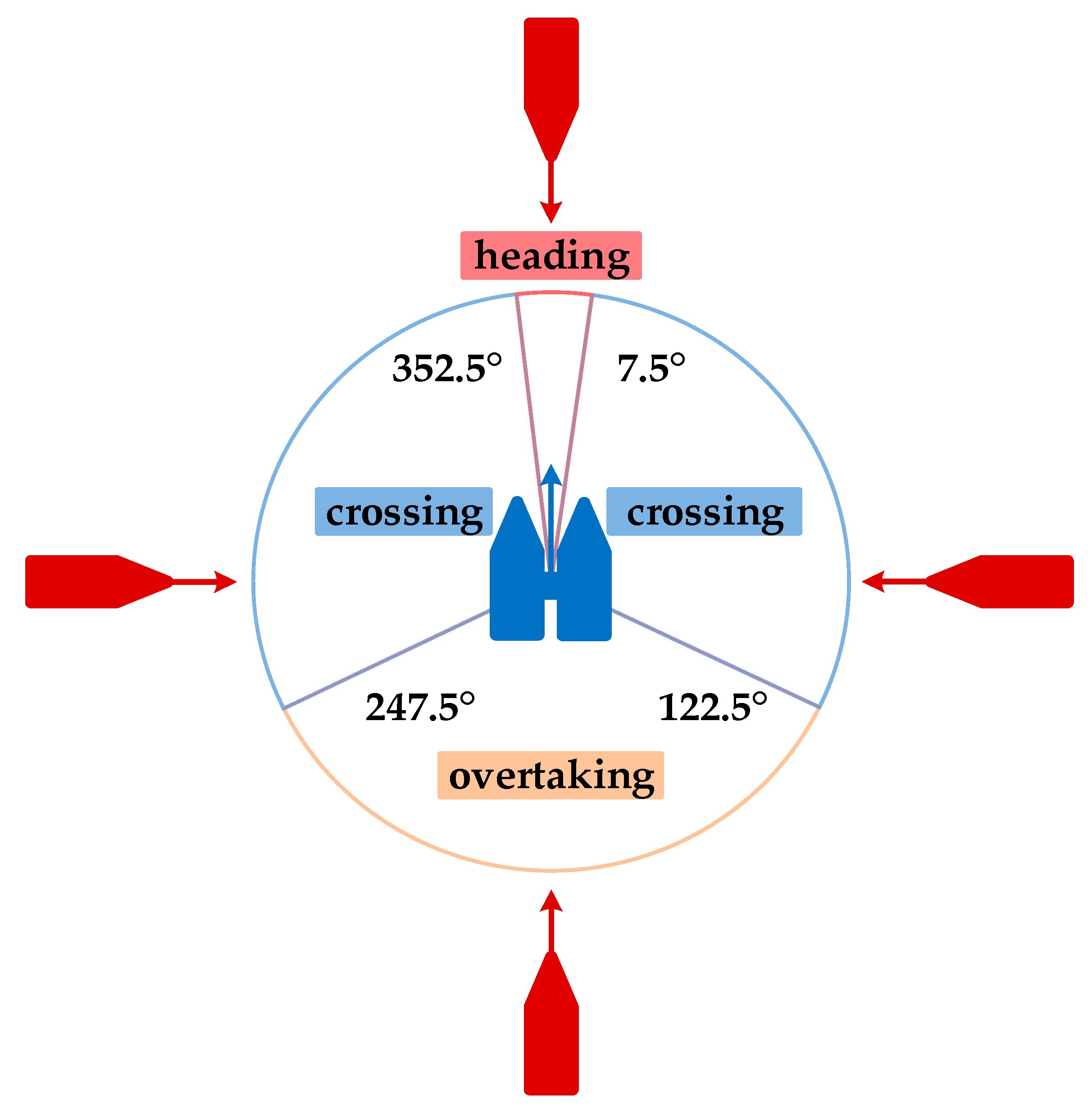
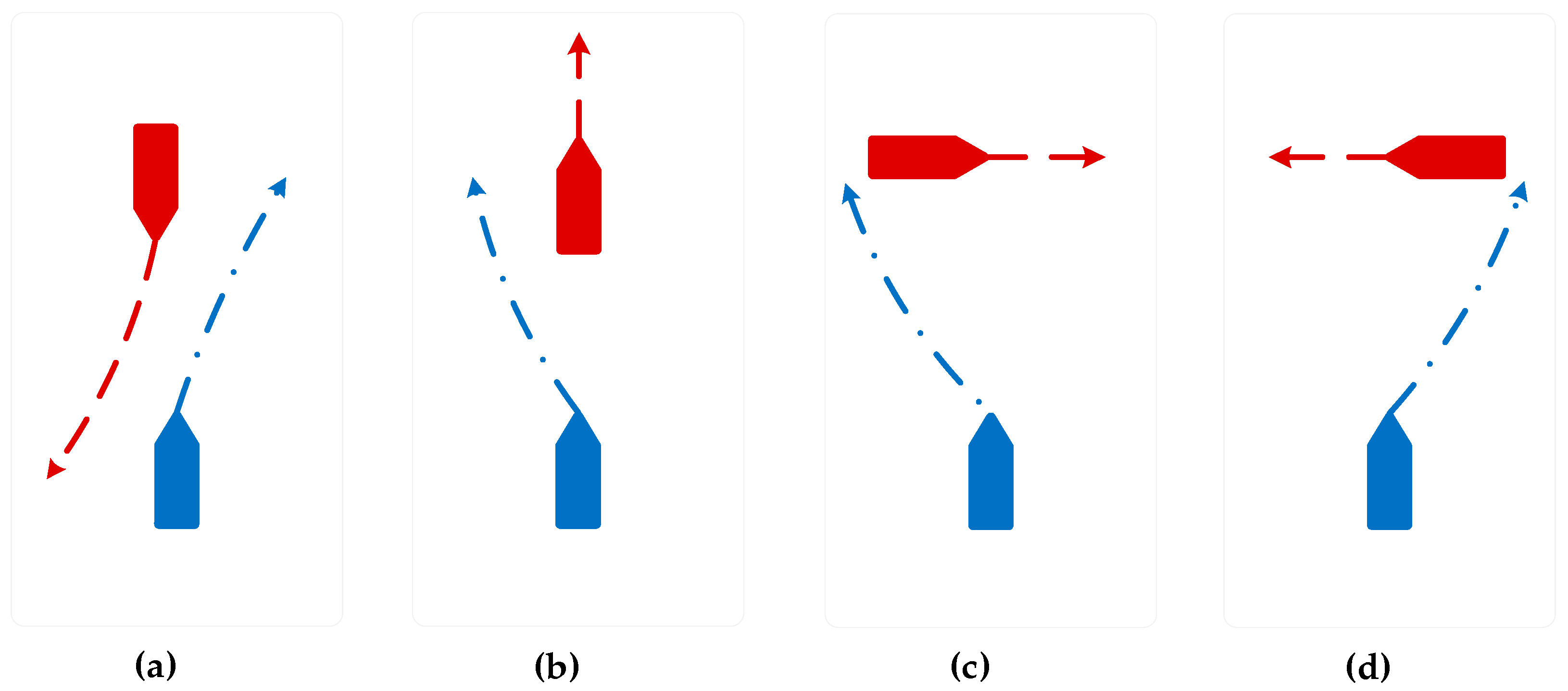
Although various encounter situations were considered in the algorithm, the main focus of the simulation was on crossing encounters, as they posed more challenges for the “Jinghai-I” USV. The speed of obstacle ships also varied during the simulation, but due to the robustness of the MPC algorithm, the “Jinghai-I” USV still effectively avoided obstacles. For the performance of the algorithm in other encounter scenarios, please refer to the authors’ previous study [
16].
5. Conclusions
In order to address the path planning problem of the “Jinghai-I” USV during autonomous navigation in inland rivers, this study proposed a hybrid path planning method that combines an improved A* algorithm with an improved model predictive control algorithm. The A* algorithm adopted a dynamic adjustment function as the heuristic function to ensure global optimization in the planned path. The cost function of the improved A* algorithm included channel boundary constraints and heading constraints, resulting in a globally optimal path that met both river-navigation regulations and local path-tracking requirements. In response to previous research limitations, the model predictive control algorithm was modified accordingly. The cost function of the MPC algorithm included a new path-deviation cost and an additional heading cost, which significantly reduced the tracking deviation and the heading-angle deviation of the algorithm. For different encounter scenarios, the MPC algorithm adopted different collision avoidance parameters, further improving local path planning performance. Finally, through simulation experiments, the effectiveness of the proposed hybrid path planning method was demonstrated.
Based on previous research, some improvements were made to the hybrid path planning algorithm in response to practical requirements. However, there is still much work to be done to truly enable the “Jinghai-I” USV to navigate autonomously in rivers. In the future, we propose the following:
Continuing to study more complex collision avoidance scenarios for the “Jinghai-I” USV in inland rivers, particularly when it encounters obstacles such as other ships, and further optimizing the collision avoidance behavior of the “Jinghai-I” USV in these scenarios;
Conducting future research to improve the applicability of the current mathematical models used to differentiate between encounter scenarios, as they are not accurate for some of these scenarios; and
Validating the research in this paper through practical testing on the “Jinghai-I” USV.