Robust Symbol Timing Synchronization for Initial Access under LEO Satellite Channel
Abstract
:1. Introduction
- We propose a robust STR scheme for a GW, which is not susceptible to a large Doppler offset caused by the LEO satellite. In the GEO satellite, most conventional schemes considered limited Doppler offset and timing uncertainty environment due to the motion of UTs. On the other hand, for LEO satellites, it is not simple to maintain network synchronization between satellite and ground UTs because the UTs are used to receive a variable Network Clock Reference (NCR) signal due to the severe Doppler offsets caused by satellite motion. Thus, UTs are required to continuously estimate the differential propagation delay based on the serving satellite’s position and velocity within a beam. Furthermore, our scheme needs to consider the scenarios when UT should support high-speed vehicles such as airplanes or when UT should have a clock oscillator with low accuracy for cost-efficiency purposes [15]. Therefore, our proposed scheme can serve as a temporary solution until novel Forward Link Signaling (FLS) information, such as DVB System Information (SI), is developed to address Doppler and timing uncertainties in the DVB-RCS2 standard work for supporting LEO satellite communication [16].
- In the case of the 3GPP NTN standard, UTs are capable to compute and pre-compensate for the delay and Doppler frequency offsets due to the LEO satellite velocity and position through ephemeris information from GW’s and UT’s positions through the GNSS receiver when triggering access to GW [17,18]. Accordingly, there is a need to update the DVB-RCS2 standard, like the 3GPP NTN standard, to accommodate LEO satellite communication [16]. Until the amendment in the DVB standard, the proposed scheme can be effective as a viable option through GW receiver implementation technology within the standard. Even in the 3GPP standard, robust time and frequency synchronization enhancement based on non-GNSS operation has been required and discussed as a candidate technology for release 19. If there are situations where NTN UT is located temporarily with improper GNSS coverage or disruptions due to jamming, it may be necessary to perform initial access without the help of GNSS operations as implementation technology. The proposed scheme in this paper can contribute to improving performance in the case of the provisional non-GNSS operation when there are a large of timing and frequency offsets in initial access from UTs to GW.
2. Transmission Model Description
2.1. Transmission Structure for DVB-RCS2 Linear Modulation and Channel Model
2.2. Demodulator Structure for DVB-RCS2 Linear Modulation
3. Robust Symbol Timing Synchronization
3.1. Previous Works
3.2. The Proposed Structure
4. Numerical Results
4.1. Simulation Condition
4.2. PER Performance Assessment
4.3. Complexity and Performance Impact
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACI | Adjacent Channel Interference |
| AVN | Absolute Value Nonlinearity |
| BCT | Broadcasting Composite Table |
| CPM | Continuous Phase Modulation |
| CB | Control Burst |
| CFO | Carrier Frequency Offset |
| COTS | Commercial On-The-Shelf |
| CR | Carrier Recovery |
| DA | Data-Aided |
| DD | Decision Directed |
| DVB | Digital Video Broadcasting |
| FDD | Frequency Division Duplexing |
| FFT | Fast Fourier Transform |
| FLS | Forward Link Signaling |
| FPGA | Field Programmable Gate Array |
| GEO | Geostationary Earth Orbit |
| GNSS | Global Navigation Satellite System |
| GPP | Generation Partnership Project |
| GW | Gateway |
| HGT | Half Guard Time |
| IF | Intermediate Frequency |
| LB | Log-on Burst |
| LEO | Low Earth Orbit |
| LTB | Long Traffic Burst |
| MCRLB | Modified Cramer–Rao Lower Bound |
| ML | Maximum Likelihood |
| NCR | Network Clock Reference |
| NDA | Non-Data-Aided |
| NTN | Non-Terrestrial Network |
| PER | Packet Error Rate |
| PLL | Phase Locked Loop |
| QAM | Quadrature Amplitude Modulation |
| QEF | Quasi Error Free |
| QPSK | Quadrature Phase Shift Keying |
| RAN | Radio Access Network |
| RCS | Return Channel via Satellite |
| SNR | Signal-to-Noise Ratio |
| SSPA | Solid State Power Amplifier |
| STB | Short Traffic Burst |
| STR | Symbol Timing Recovery |
| TDD | Time Division Duplexing |
| TDMA | Time Division Multiple Access |
| ToA | Timing offset of Arrival |
| UT | User Terminal |
| VSAT | Very Small Aperture Terminal |
Appendix A
References
- Pachler, N.; Portillo, I.-D.; Crawley, E.F.; Cameron, B.G. An Updated Comparison of Four Low Earth Orbit Satellite Constellation Systems to Provide Global Broadband. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Online, 14–23 June 2021; pp. 1–7. [Google Scholar]
- Lin, Z.; Lin, M.; Champagne, B.; Zhu, W.P.; Al-Dhahir, N. Secrecy-energy efficient hybrid beamforming for satellite-terrestrial integrated networks. IEEE Trans. Commun. 2021, 69, 6345–6360. [Google Scholar] [CrossRef]
- Lin, Z.; An, K.; Niu, H.; Hu, Y.; Chatzinotas, S.; Zheng, G.; Wang, J. SLNR-based secure energy efficient beamforming in multibeam satellite systems. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2085–2088. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; De Cola, T.; Wang, J.-B.; Zhu, W.-P.; Cheong, J. Supporting IoT with rate-splitting multiple access in satellite and aerial-integrated networks. IEEE Internet Things J. 2021, 8, 11123–11134. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; Champagne, B.; Zhu, W.-P.; Al-Dhahir, N. Secure and energy efficient transmission for RSMA-based cognitive satellite-terrestrial networks. IEEE Wirel. Commun. Lett. 2021, 10, 251–255. [Google Scholar] [CrossRef]
- 3GPP NTN. 2022. Available online: https://www.3gpp.org/news-events/partner-news/ntn-rel17/ (accessed on 30 September 2023).
- Telesat. 2022. Available online: https://www.telesat.com/blog/secure-resilient-and-accessible-how-telesat-lightspeed-pairs-with-dod-standards/ (accessed on 30 September 2023).
- ETSI TS 101 545-1 V1.2.1; Digital Video Broadcasting (DVB). Second Generation DVB Interactive Satellite System (DVB-RCS2); Part 2: Lower Layers for Satellite Standard. ETSI: Sophia Antipolis, France, 2012.
- Kim, P.; Oh, D. Low complexity phase noise mitigation for linear modulation in DVB-RCS NG standard. In Proceedings of the 29th International Communications Satellite System Conference (ICSSC), Nara, Japan, 28 November 2011. [Google Scholar]
- Kim, P.; Oh, D. Low complexity carrier phase recovery for DVB-RCS2 standard. In Proceedings of the International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Republic of Korea, 15–17 October 2012; pp. 607–609. [Google Scholar]
- Kim, P.; Oh, D. Low complexity CPM receiver based on DVB-RCS2 standard. In Proceedings of the International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Republic of Korea, 14–16 October 2013; pp. 446–447. [Google Scholar]
- Gallinaro, G.; Cecca, F.D.; Burzigotti, P. Improving frequency recovery in a DVB-RCS pilotless system via early decoding of different frequency estimation hypothesis. In Proceedings of the 16th Ka and Broadband Communication, Navigation and Earth Observation Conference, Milan, Italy, 20–22 October 2010. [Google Scholar]
- Oliver, G.; Uwe, W.; Norbert, W. Communication Performance vs. Implementation Trade-offs of Interpolation Techniques for FFT-Based Carrier Synchronization exemplified on DVB-RCS2. Adv. Radio Sci. 2021, 19, 59–80. [Google Scholar]
- Xue, Q.; Wang, J.; Chen, M.; Tang, X.; Zhu, J. Efficient Receiver for DVB-RCS2 Synchronization Problems. In Proceedings of the 4th Information Communication Technologies Conference (ICTC), Nanjing, China, 17–19 May 2023; pp. 167–171. [Google Scholar]
- Kim, P.; Lee, I.; Oh, D.; Ryu, J.-G. Robust Initial Access Technique of Spread Spectrum Based on DVB-RCS2 Standard for Mobile Application. In Proceedings of the 36th International Communications Satellite System Conference (ICSSC 2018), Niagara Falls, ON, Canada, 15–18 October 2018. [Google Scholar]
- Digital Video Broadcasting (DVB). Commercial Requirements for the Use of DVB-RCS2 in Geostationary and Non-Geostationary Systems; Document DVB Bluebook C107; DVB: Geneva, Switzerland, 2023. [Google Scholar]
- Charbit, G.; Medles, A.; Jose, P.; Lin, D.; Zhu, X.; Fu, I.-K. Satellite and Ceullar Networks Integration—A System Overview. In Proceedings of the 2021 Joint European Conference on Networks and Communications & 6G Summit (EuCNC/6G Summit), Proto, Portugal, 8–11 June 2021; pp. 118–123. [Google Scholar]
- Study on New Radio (NR) to Support Non Terrestrial Networks. Document TR 38.811, Release 15, 3GPP. September 2020. Available online: https://www.3gpp.org/ (accessed on 30 September 2023).
- Oerder, M.; Meyr, H. Digital filter and square timing recovery. IEEE Trans. Commun. 1988, 36, 605–612. [Google Scholar] [CrossRef]
- Mengali, U.; D’Andrea, A.N. Synchronization Techniques for Digital Receivers; Plenum Press: New York, NY, USA, 1997. [Google Scholar]
- Steendam, H.; Moeneclaey, M. Low SNR Limit of the Cramer Rao Bound for Estimating the Time Delay of a PSK, QAM or PAM waveform. IEEE Commun. Lett. 2001, 5, 31–33. [Google Scholar] [CrossRef]
- ETSI TR 101 545-4 V1.1.1; Digital Video Broadcasting (DVB); Second Generation DVB Interactive Satellite System (DVB-RCS2); Part 4: Guidelines for Implementation and Use of EN 301 545-1. ETSI: Sophia Antipolis, France, 2014.
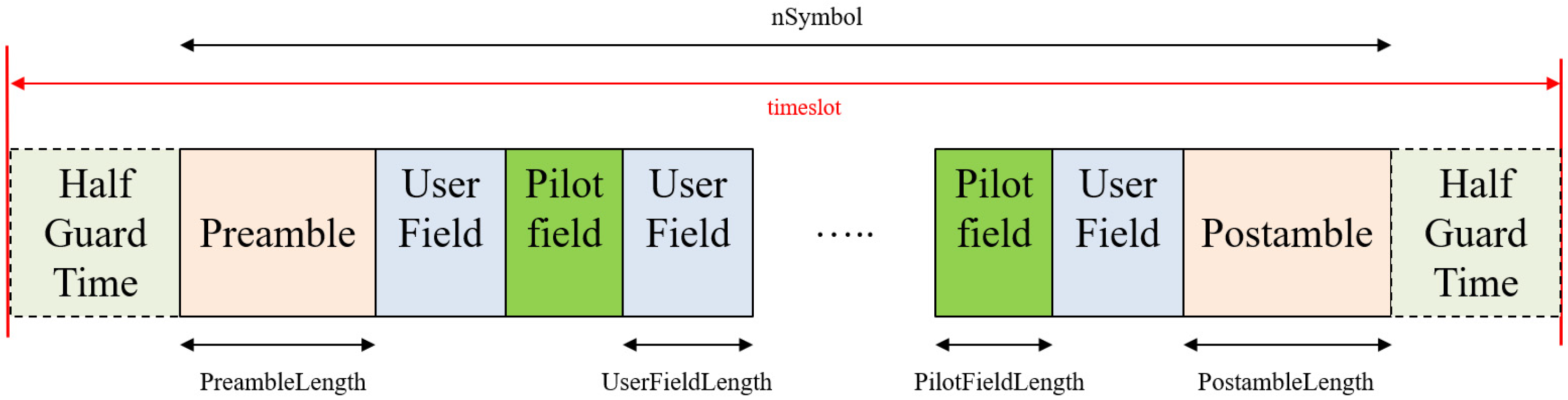


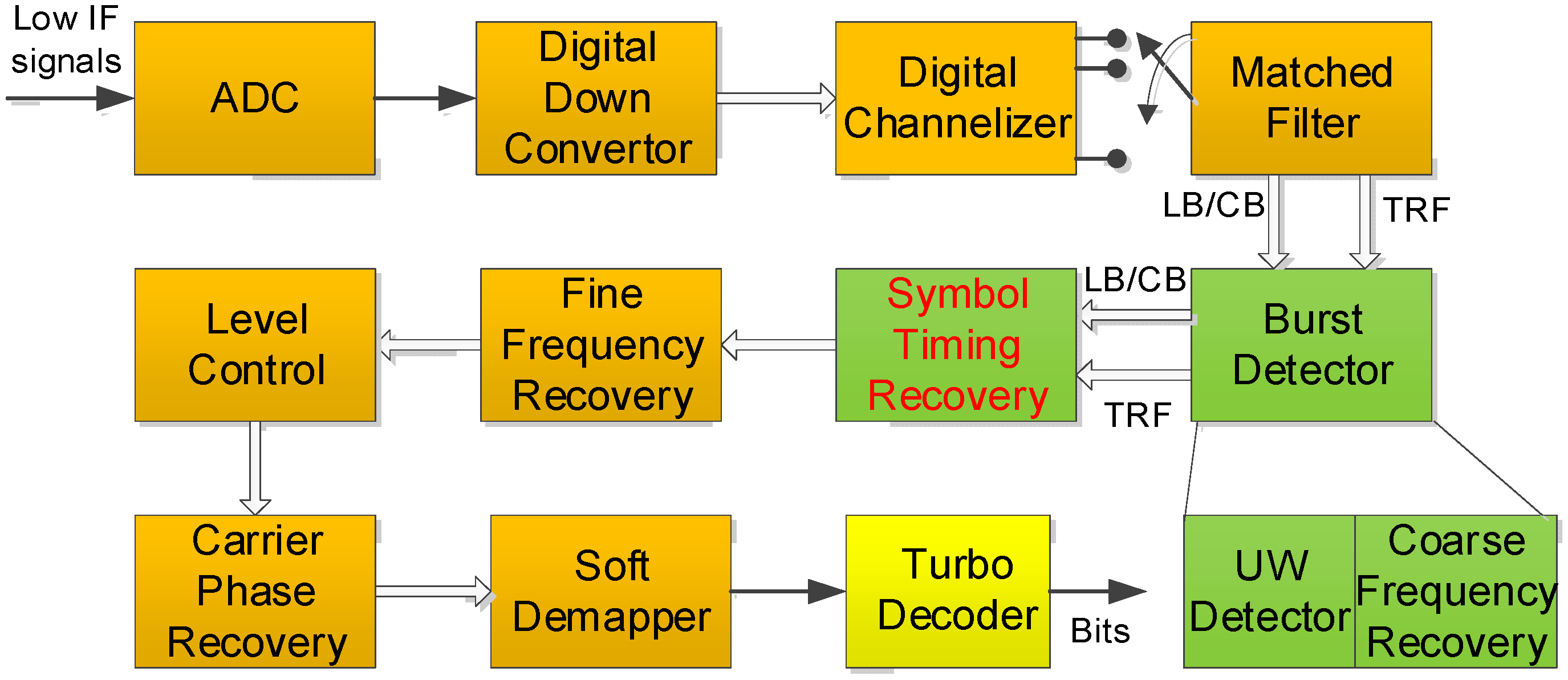
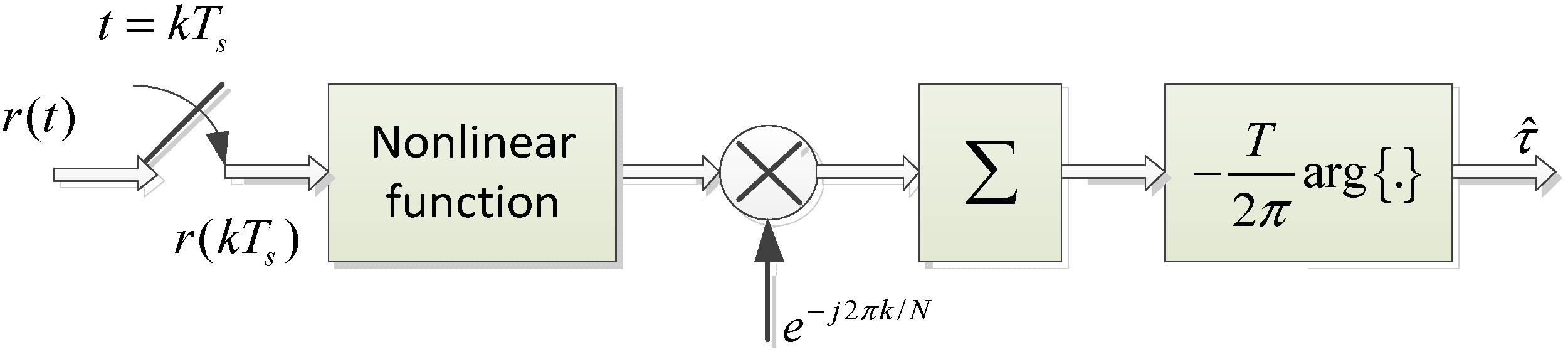
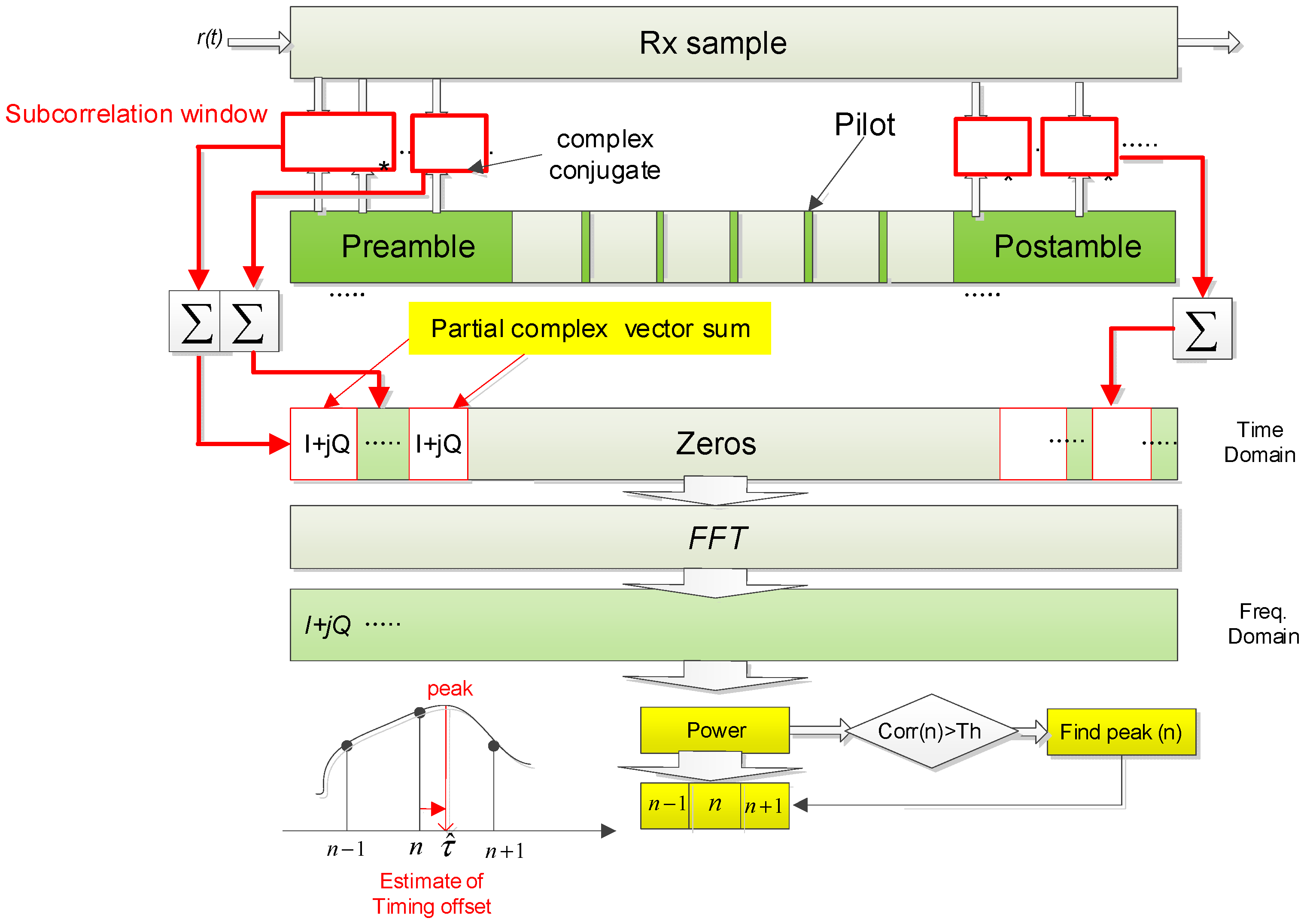


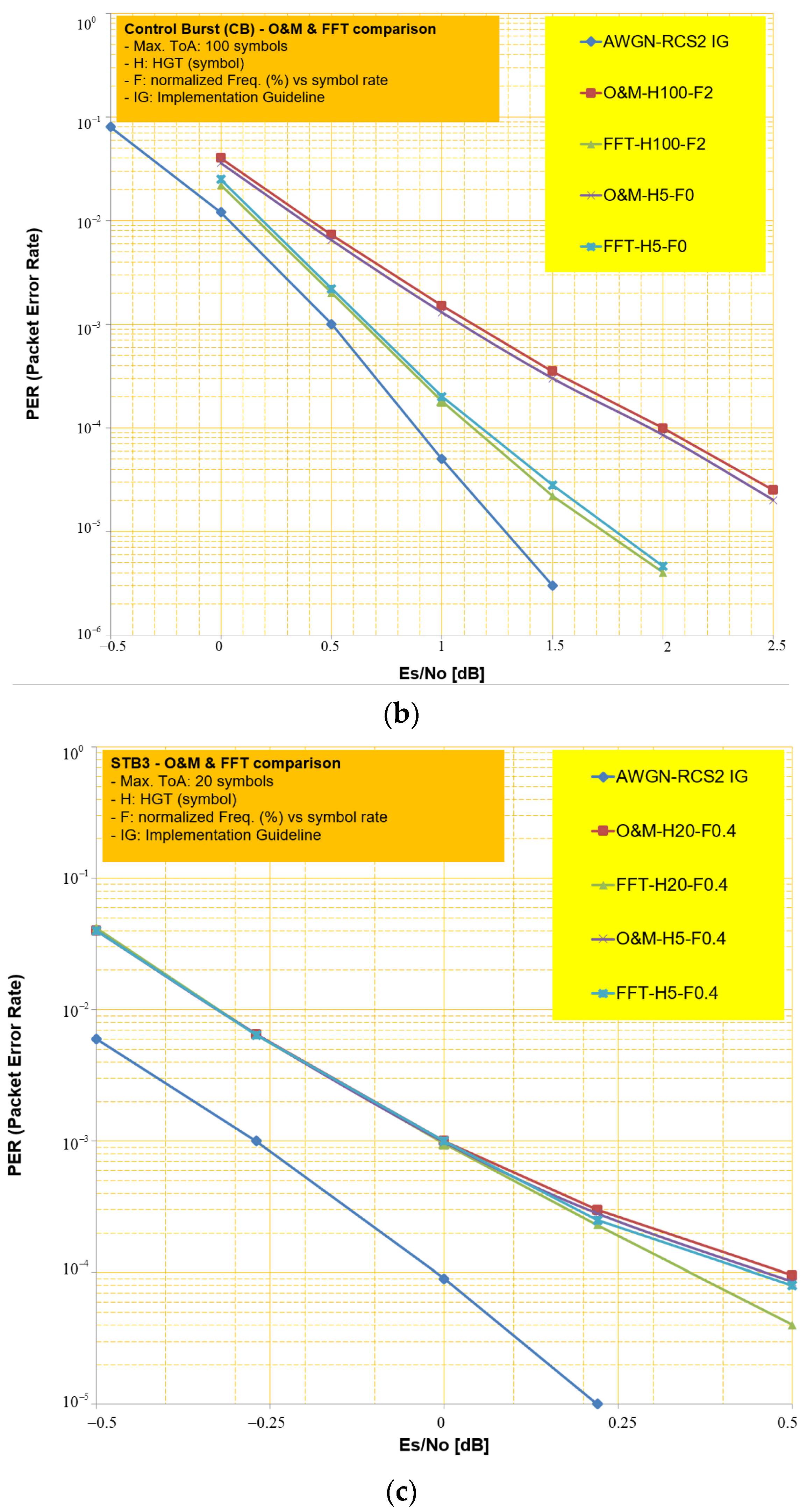
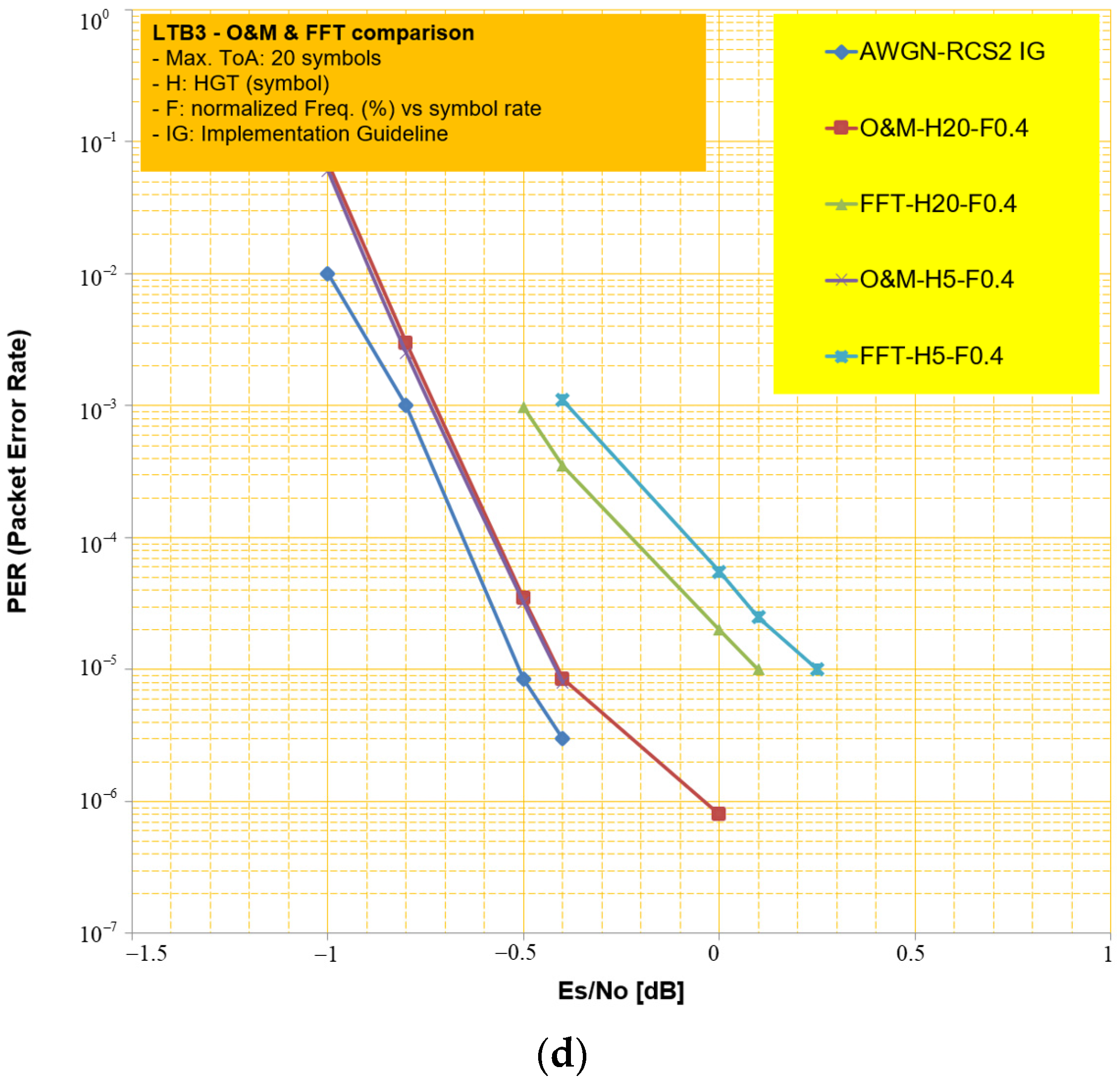
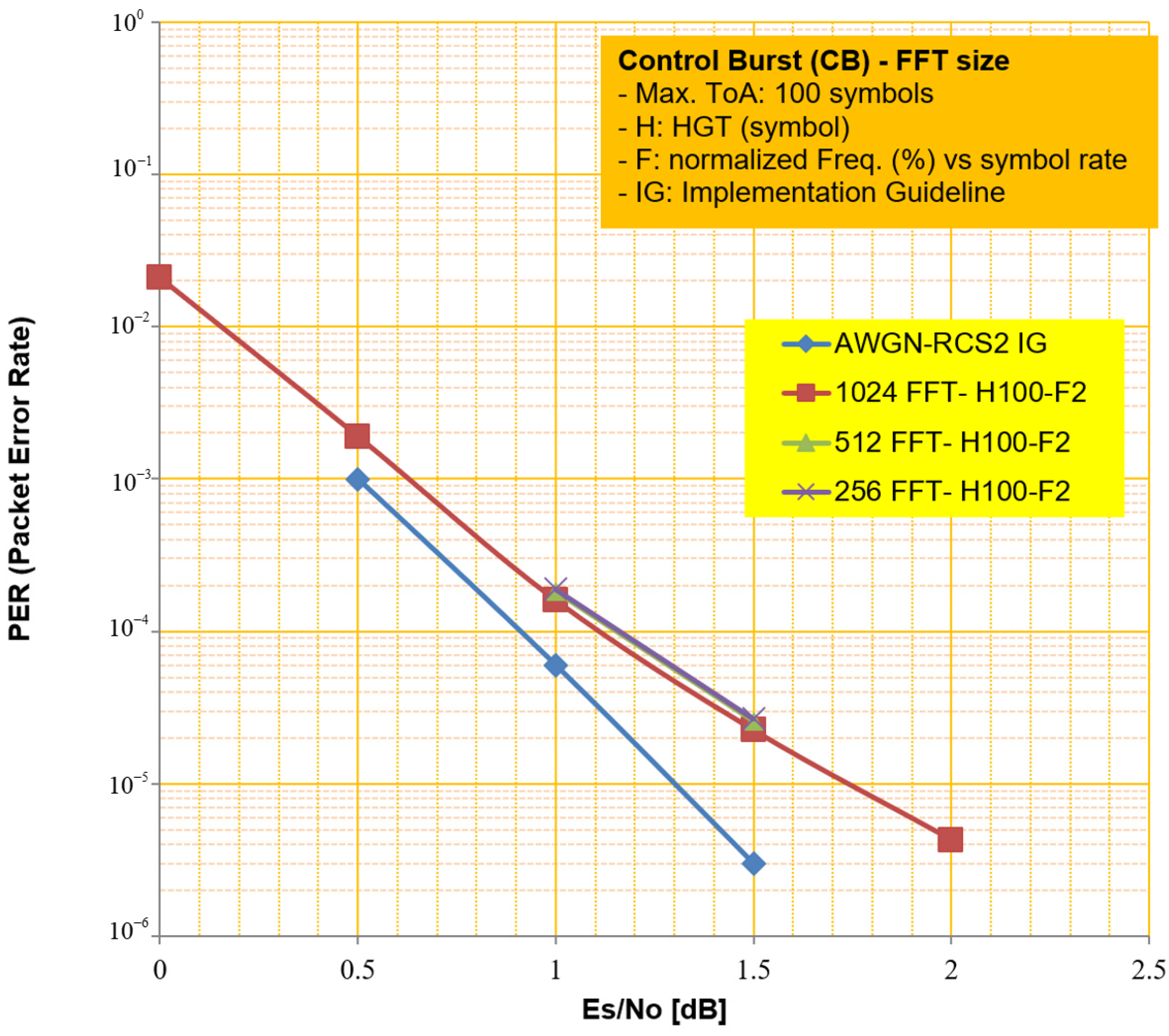

| Waveform ID | LB (ID#1) | CB (ID#2) | TB (ID#3, #13) |
|---|---|---|---|
| Maximum HGT (ToA in symbols) Uniform distribution | ±200 symbols (±20 μs in 10 Mbaud) | ±100 symbols (±10 μs in 10 Mbaud) | ±20 symbols (±2 μs in 10 Mbaud) |
| Normalized maximum CFO vs. symbol rate Uniform distribution | ±0.05 (±500 kHz in 10 Mbaud) | ±0.02 (±200 kHz in 10 Mbaud) | ±0.004 (±40 kHz in 10 Mbaud) |
| Waveform ID | Burst Length (Symbol) | Modulation | Code Rate | Known Symbol Length | The Ratio of Known Symbols in Burst |
|---|---|---|---|---|---|
| #1(LB) | 664 | QPSK | 1/3 | 208 | 31% |
| #2(CB) | 262 | QPSK | 1/3 | 94 | 36% |
| #3(STB3) | 536 | QPSK | 1/3 | 80 | 15% |
| #13(LTB3) | 1616 | QPSK | 1/3 | 140 | 9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, P.; Park, H. Robust Symbol Timing Synchronization for Initial Access under LEO Satellite Channel. Sensors 2023, 23, 8320. https://doi.org/10.3390/s23198320
Kim P, Park H. Robust Symbol Timing Synchronization for Initial Access under LEO Satellite Channel. Sensors. 2023; 23(19):8320. https://doi.org/10.3390/s23198320
Chicago/Turabian StyleKim, Pansoo, and Hyuncheol Park. 2023. "Robust Symbol Timing Synchronization for Initial Access under LEO Satellite Channel" Sensors 23, no. 19: 8320. https://doi.org/10.3390/s23198320
APA StyleKim, P., & Park, H. (2023). Robust Symbol Timing Synchronization for Initial Access under LEO Satellite Channel. Sensors, 23(19), 8320. https://doi.org/10.3390/s23198320





