Abstract
How to accurately identify unknown time-varying external force from measured structural responses is an important engineering problem, which is critical for assessing the safety condition of the structure. In the context of a few available accelerometers, this paper proposes a novel time-varying external force identification method using group sparse regularization based on the prior knowledge in the redundant dictionary. Firstly, the relationship between time-varying external force and acceleration responses is established, and a redundant dictionary is designed to create a sparse expression of external force. Then, the relevance of atoms in the redundant dictionary is revealed, and this prior knowledge is used to determine the group structures of atoms. As a result, a force identification governing equation is formulated, and the group sparse regularization is reasonably introduced to ensure the accuracy of the identified results. The contribution of this paper is that the group structures of atoms are reasonably determined based on prior knowledge, and the complexity in the process for identifying external force from measured acceleration responses is reduced. Finally, the effectiveness of the proposed method is demonstrated by numerical simulations and an experimental structure. The illustrated results show that, compared with the force identification method based on the standard l1-norm regularization, the proposed method can further improve the identified accuracy of unknown external force and greatly enhance the computational efficiency for the force identification problem.
1. Introduction
The accurate estimation of an unknown external force acting on a structure is a greatly important issue in several fields, such as structural reliability analysis and design [1,2], structural health monitoring [3,4,5,6], and fatigue life prediction [7,8]. However, it is difficult to directly measure the external force acting on the structure due to some practical issues, such as the high cost of instruments, difficulty in instrument installation, and so on [9,10,11]. Rather than directly measuring external force, structural responses can be more easily acquired. Therefore, many scholars pay attention to indirect force measurement techniques. As a useful technique, the force identification method can indirectly identify the external force from measured structural responses.
However, the force identification problem is a typical inverse problem, which means that the process of indirectly identifying unknown external force from structural responses is ill-posed. Thus, effective solution methods are important in this problem. In existing studies, the methods can be roughly divided into three categories [10,11,12,13,14,15,16], i.e., direct solution methods, regularization methods, and probabilistic/statistical methods, wherein regularization methods [11,12,13,14] often analyze the force identification problem based on deterministic methods and improve the ill-posedness of the original problem. Therefore, these methods are more popular in practical application, and different regularization methods have been introduced into the force identification problem.
In the early studies, several typical regularization methods are directly used to improve the ill-posedness, such as Tikhonov regularization, truncated singular value decomposition, generalized singular value decomposition, and so on [12,13,14,17]. For instance, as the most popular regularization method, Tikhonov regularization can preliminarily improve the identified results by penalizing the l2-norm of force vector with the Tikhonov matrix [10,13]. Many studies have been conducted on the application of the Tikhonov regularization in force identification problems [18]. However, the Tikhonov regularization method has some unavoidable limitations and disadvantages. For example, the approximate solution directly obtained from the Tikhonov regularization is too smooth, and the identified result may lack some details that the desired real solution might possess [19].
To further improve the identification accuracy, in the follow-up studies, some other regularization methods [18], such as the function expansion method [20,21,22], multiplicative regularization [23,24], sparse regularization [25,26,27,28], and so on [29,30,31,32], are introduced into the force identification problem. In particular, for the time-varying external force, it is usually not sparse in the time domain. Some regularization techniques, such as sparse regularization cannot be directly used in this problem. Meanwhile, for some other improved methods [29,30], the characteristics of time-varying force cannot be identified well. Thus, some scholars have paid attention to combining the function expansion method with a sparse regularization technique [25,26,27,33]. Based on the theory of function expansion method, the combination of discrete basis functions is represented as a dictionary, and each basis function is an atom in the dictionary. On the other hand, sparse regularization can sparsely select reasonable atoms from the dictionary to approximately express the characteristics of external force and simultaneously reduce the influences of noise [27]. For example, Qiao et al. [27] study the application of the standard l1-norm regularization with different dictionaries for both impact force identification and harmonic force identification problems, and the identified accuracy can be improved by comparing it with the traditional Tikhonov regularization method. However, the sparsity of solution obtained from the standard l1-norm regularization is considered at the independent atom level, the complexity in the process of this force identification method is high, and the solving process is time-consuming. Moreover, for time-varying external force identification, local identification results may be unsatisfactory.
Unlike the standard l1-norm regularization, the group sparse regularization method considers the sparsity of solutions in some group structures, which can reduce the complexity in the process of solving problems. In a special force identification problem, i.e., impact force identification, Qiao et al. [34] employs the prior information that the duration time of the actual impact force is quite short, and reasonable group sparsity of impact force in the time domain is considered, so group sparse regularization is reasonably introduced for impact force identification. Because the time-varying external force is usually not sparse in the time domain, the above prior information cannot be directly employed. How to introduce the group sparse regularization into the time-varying external force identification problem is an important work. If the group structures of atoms are not reasonable enough, the group sparse regularization method may not improve the identified accuracy of time-varying force. For example, the method in Ref. [35] directly uses the group number to determine the group structures of atoms; by comparing the identified results in Ref. [26], the identified accuracy of time-varying force component cannot be improved.
Considering the shortcomings above, in this study, a novel force identification method is proposed by reasonably introducing the group sparse regularization based on the prior knowledge in the dictionary. The way in which our work will contribute is by revealing the relevance of atoms in the given dictionary, and the group structures of atoms are reasonably determined for the group sparse regularization. As a result, the group sparse regularization can be reasonably introduced for identifying the time-varying external force. The complexity in the process of force identification is reduced, the computational efficiency is greatly enhanced, and the identified accuracy can be improved.
The structure of this paper is organized as follows. In Section 2, the basic theories are introduced and the proposed force identification method is explained in detail. Then, Section 3 provides several numerical validations on the proposed method, and the identified results are compared with those obtained from the standard l1-norm regularization. Furthermore, some experiments are carried out on a simply supported beam to validate the effectiveness of the proposed method in Section 4. Finally, some conclusions are drawn in Section 5.
2. Theoretical Background
2.1. Relationship between Structural Response and External Force
Firstly, an introduction about the force identification problem will be provided. For a linear time-invariant structure, it is assumed that the initial displacement and velocity responses are zeros, and m measurement points are used to acquire the structural responses. When a time-varying external force is acting on the structure, the relationship between the structural response at the i-th measurement point and the external force can be expressed as [10,12]:
where is the time-varying external force, is the structural response at the i-th measurement point, and is the impulse response function and can be calculated based on the mode superposition method.
Because accelerometers are common sensors installed in the structure and the acceleration responses are usually used for force identification, the structural response is considered as acceleration response in this study.
Assuming that N sampling points are acquired in a time interval [0, T] and the sampling time interval is , with discretization, a set of algebraic equations between the acceleration response at the i-th measurement point and the external force can be obtained from Equation (1):
Equation (2) can be simply rewritten as:
where , , the transfer matrix represents the relationship between acceleration response and external force vectors.
2.2. Function Expansion Method for Force Identification Problem
Because the time-varying external force is usually not sparse in the time domain, to effectively improve the ill-posedness of the force identification problem by using sparse regularization techniques, the function expansion method is adopted at first. As mentioned above, for the function expansion method, each basis function can be degraded as an atom, and the combination of these atoms is represented as a dictionary. Thus, the time-varying external force is represented by a dictionary and its coefficient vector , given as [20,21,22]:
where , each column of the dictionary is an atom, the i-th atom can be represented as , and the number of atoms is represented by L.
By substituting Equation (4) into Equation (3), the following equation is obtained:
where .
Because external force is difficult to be directly measured, it is necessary to indirectly identify external force from acceleration responses. If multiple accelerometers are used, a combination form of acceleration responses is considered as [11]:
where is the standard Euclidean norm.
Similarly, Equation (6) can be simply rewritten as:
where , , and .
The amplitude of time-varying force is usually different in each sampling point. Therefore, to arbitrarily express the time-varying force, the span of vector space based on the bases must be complete. That is to say, the bases in Equation (4) can be selected as some functions, such as wavelet function, cubic spline function, trigonometric function, rectangular function, and so on. Meanwhile, it should be ensured that the combination of these bases is a complete dictionary or redundant dictionary.
Compared with complete dictionaries, redundant dictionaries are more suitable for expressing the characteristics of time-varying force. Therefore, in this study, the dictionary is designed as a redundant dictionary consisting of trigonometric and rectangular functions.
In detail, the expressions of sine and cosine functions in trigonometric functions are, respectively, given in Equations (8) and (9):
where is the resolution of external force in the frequency domain, and are, respectively, represented by the numbers of atoms corresponding to sine and cosine functions, and they can be, respectively, calculated by Equations (10) and (11):
where is the floor function and is the sampling frequency.
The expression of rectangular functions is given in Equation (12):
where is a positive integer, represents the minimum value between and , and the number of atoms corresponding to rectangular functions is determined by Equation (13):
where is the ceiling function.
When and are given, with discretization, the atoms of the redundant dictionary are calculated on the basis of Equations (8)–(13) with and .
Because the coefficients of some atoms may be influenced by noise, it is necessary to define the force identification problem with reasonable constraints, such as sparse regularization techniques.
2.3. Sparse Regularization Techniques for Force Identification Problem
Sparse regularization techniques have been developed in some excellent studies. When the dictionary expression of external force is considered, the function of the sparse regularization technique is to sparsely select reasonable atoms from the redundant dictionary and to approximately express the characteristics of external force. It can effectively reduce the influences of noise. In the following context, the force identification problems proposed based on standard l1-norm regularization and group sparse regularization techniques are, respectively, introduced.
2.3.1. Force Identification Problem Based on Standard l1-Norm Regularization
Standard l1-norm regularization [28] is a popular technique for obtaining sparse solutions to inverse problems. By combining Equation (7) with standard l1-norm regularization, the l1-norm of the coefficient vector is adopted to define the force identification problem. As a result, an unconstrained optimization problem can be defined as:
where represents the l1-norm of vector and is a weight coefficient. When , the solution of Equation (14) converges to the solution obtained from the least squares method.
From Equation (14), it can be seen that the identified coefficient vector is obtained by considering a balance between the residual norm and the l1-norm of vector when the weight coefficient is given. Thus, the weight coefficient should first be determined for reasonable results, which will be introduced in the following section.
2.3.2. Force Identification Problem Based on Group Sparse Regularization
Because the standard l1-norm regularization only considers the standard sparsity of the solution, the underlying structure sparsity of the solution cannot be revealed. The structure sparsity of the solution is directly related to the underlying relevance of atoms in the given dictionary. Therefore, the underlying relevance of atoms should be analyzed at first, and the underlying structure of atoms, such as group structure, joint structure, or tree structure, can be reasonably determined. As a result, corresponding structured sparse regularization techniques can be introduced to the specific problem. That is to say, how to determine the underlying structure of atoms is an important issue for the structured sparse regularization methods.
In this study, with the help of trigonometric and rectangular functions, the underlying relevance of atoms in the redundant dictionary is analyzed, and the group structures of atoms can reasonably be determined based on this prior knowledge.
More specifically, the sine and cosine functions given in Equations (8) and (9) can be used to express a Fourier series in an amplitude-phase form. Thus, when the frequency is given, the atom coefficients and have the following relationship:
where and , respectively, represent the j-th harmonic’s amplitude and its phase shift, the corresponding atom coefficients are and , respectively.
Equation (15) indicates that the atoms corresponding to their coefficients and have obvious relevance. For each positive integer j, the atoms determined by Equations (8) and (9) are set as a group. When j = 0, the atom calculated by Equation (9) is set as an independent group.
On the other hand, the purpose of the rectangular functions defined by Equation (12) is used to approximate the local force components of the external force. In the time domain, each local force component can be considered as continuous in an extremely short time interval, so the atoms in each time interval are relevant, and they can be regarded as a group. Because the time interval for the local force component may be unknown in practice, the number of atoms in each time interval is given directly in this study.
In summary, some atoms defined by Equations (8), (9) and (12) have obvious relevance. Therefore, by defining the group structures of these atoms, the structured sparse regularization technique is introduced for force identification with the redundant dictionary, and the group sparsity of solution can be achieved.
It is assumed that the atoms in the given redundant dictionary are divided into p groups based on the above prior knowledge, and the group sparse regularization [34,35,36] is introduced to define the minimum optimization problem:
where is the j-th disjoint group and represents the atom numbers in the given dictionary. For the atoms in the same group, the corresponding coefficients tend to be zero or non-zero values simultaneously.
2.3.3. Solution Algorithm for Force Identification Problems
It should be noted that when each atom in the given dictionary is degraded as a group, the standard l1-norm regularization can be rewritten as:
It can be observed that Equations (16) and (17) have the same expression forms. In this study, the split Bregman algorithm for structured sparsity (SBSS) is adopted to solve these two optimization problems, and the detail of this algorithm can be seen in Ref. [37]. The approximate solutions in Equations (16) and (17) can be, respectively, obtained after iterations, and both identification accuracy and computational efficiency in these two problems are compared in both numerical simulation and experimental validation.
The basic flowchart for the force identification problem is shown in Figure 1. In Figure 1, for the group sparse regularization, represents the elements of vector belonging to the j-th disjoint group . For the standard l1-norm regularization, is specified as , which is the j-th element of the vector, and . is the tolerance error and is equal to 1 × 10−6.
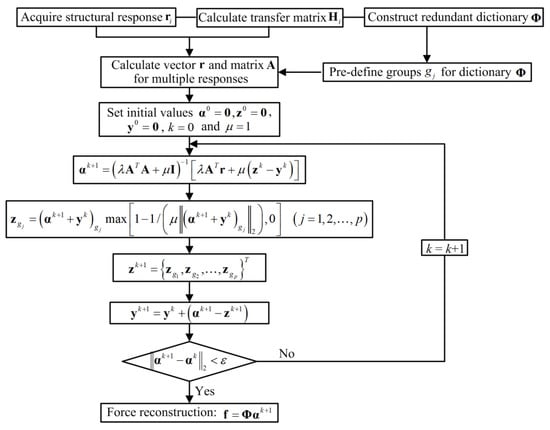
Figure 1.
Basic flowchart of force identification method based on sparse regularization and redundant dictionary.
3. Numerical Simulations
To evaluate the effectiveness of the proposed force identification method, some numerical simulations are performed in a 31-bar planar truss [38], as shown in Figure 2. The sectional dimension is b × h = 0.05 m × 0.05 m with an elastic modulus of 70 GPa and a density of 2770 kg/m3. The length is 1.52 m for horizontal and vertical components. Rayleigh damping is adopted, and the first two damping ratios are assumed to be 1%.
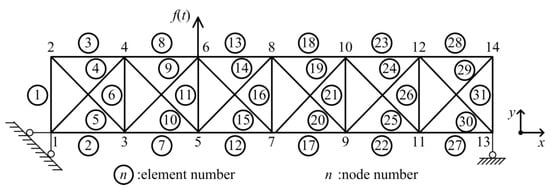
Figure 2.
Geometric configuration of 31-bar planer truss.
A time-varying external force f(t) is acting in the y direction at node 6, the signal type of the external force is random excitation, which is considered as:
where is a vector, which is first drawn from the standard normal distribution, and then filtered by a low-pass Butterworth filter, which is designed with no more than 3 dB of ripple in a passband from 0 to 160 Hz, and at least 60 dB of attenuation in the stopband, defined as being from 319 Hz to the Nyquist frequency.
Based on Equation (2), the i-th elements, respectively, in the vectors and have the following relationship:
where is the i-th element in the vector .
It is assumed that a few available accelerometers are used to acquire the acceleration responses, which are calculated based on the mode superposition method and the Newmark-β method. The first five frequencies of the planer truss, i.e., 36.4323 Hz, 76.0952 Hz, 133.8103 Hz, 223.3793 Hz, and 250.1825 Hz, are used in acceleration response calculation. The sampling frequency is fs = 640 Hz, and the sampling time is T = 1 s. As a result, the number of sampling points is N = 640.
For the redundant dictionary, the frequency resolution of the external force is , and the positive integer is set to 1. Therefore, based on Equations (10), (11) and (13), the number of atoms in the redundant dictionary can be calculated, i.e., .
To simulate polluted acceleration responses, white noise is added to each calculated response:
where and () are the i-th noiseless and noisy responses, respectively, is the noise level, is the standard deviation of vector, and is a vector drawn from the standard normal distribution.
Furthermore, to estimate the identification accuracy, the relative percentage error (RPE) between true and identified external forces is defined as:
3.1. Comparative Study between Two Force Identification Methods
Firstly, the identified results, respectively, obtained based on Equations (16) and (17) are compared. The acceleration responses in the y direction of nodes 3 and 7 are used for force identification problems, and the noise level in Equation (20) is set to 5%. For the group sparse regularization, the group structures of the atoms are given as mentioned above, and the number of atoms is set to 8. As a result, the number of groups is p = 331.
Because the SBSS is adopted for solving the optimization problems, in the iteration process of this algorithm, the weighted coefficient is needed. Meanwhile, as mentioned in the previous section, the weight coefficient is important for these two optimization problems. On the other hand, rather than selecting the weight coefficient, some posterior criteria are usually used to directly select the regularization parameter. Thus, based on Equation (16), an equivalent form is considered as:
where is the regularization parameter.
As a result, the regularization parameter can be directly selected by some posterior criteria. In this study, the L-curve criterion is adopted to select the near-optimal regularization parameter. Because the time-varying external force is identified, the L-curve is considered as a plot in log–log scales of the residual norm of the solution versus the norm of the identified force . By considering both computational efficiency and identification accuracy, the L-curve criterion is used twice to determine the parameter . For an L-curve, the optimal regularization parameter should lie on the corner of the L-curve. For values larger than the optimal regularization parameter, the residual norm of the solution increases without reducing the norm of the solution much. On the other hand, for values smaller than the optimal regularization parameter, the norm of the identified force increases rapidly without much residual decrease. Based on the above fact, in the first step, the range of regularization parameters that contains the optimal regularization parameter is determined. In the second step, the L-curve criterion is used to determine the near-optimal regularization parameter . As a result, based on the relationship between the weighted coefficient and regularization parameter , i.e., , the weight coefficient is determined by the parameter . Similarly, the weight coefficient in Equation (17) is also selected in the same way. All calculations are run on a personal computer with an AMD Ryzen 7 2700 processor and 16 GB of memory.
The selections of near-optimal regularization parameters based on the standard l1-norm regularization and group sparse regularization are, respectively, shown in Figure 3 and Figure 4.
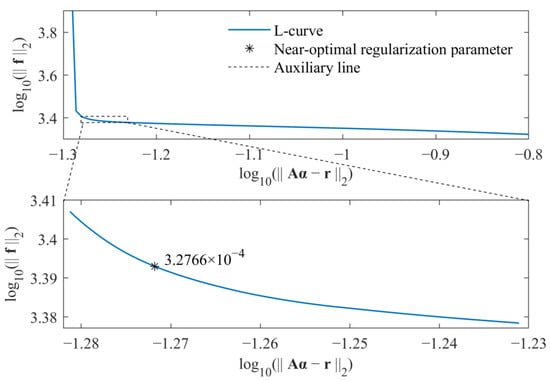
Figure 3.
Selection of near-optimal regularization parameter for standard l1-norm regularization.
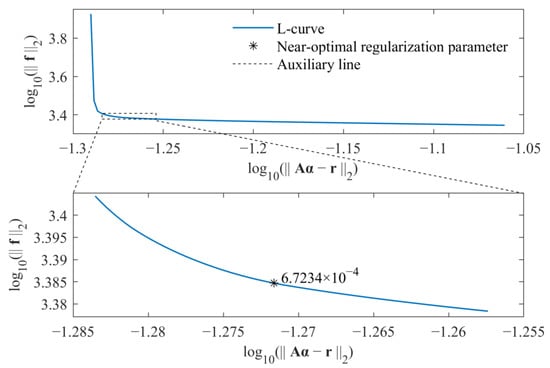
Figure 4.
Selection of near-optimal regularization parameter for group sparse regularization.
For each figure, a range near to the L-curve corner is selected at first. Then, the maximum curvature of the L-curve in the selected range is determined based on the regularization tools developed by P. C. Hansen [39], and the corresponding parameter is selected as the near-optimal regularization parameter. Finally, the weight coefficient is calculated for corresponding force identification problem, and the external force can be identified from measured acceleration responses. The comparison of identified results obtained from these two methods is given in Figure 5.
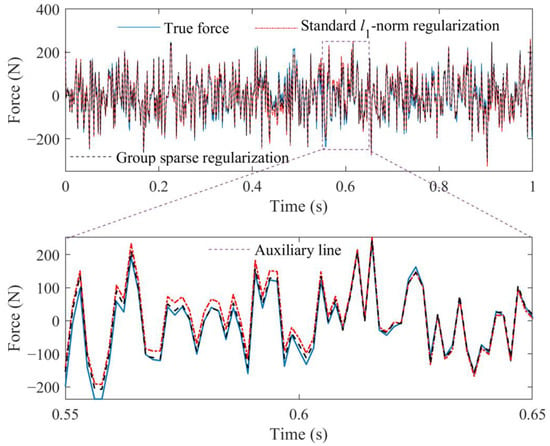
Figure 5.
Identified result, respectively, obtained from standard l1-norm regularization and group sparse regularization.
From Figure 5, it can be seen that the external force identified by the proposed method is more accurate by comparing with that identified by the standard l1-norm regularization. The RPEs of the standard l1-norm regularization and group sparse regularization are 18.4109% and 15.7292%, respectively. Because the atom coefficients and have the relationship shown in Equation (15), the local identification accuracy of the time-varying external force can be further improved. These results indicate that the way to define group structures in this study is reasonable, which can improve.
On the other hand, with the help of group structures in the redundant dictionary, the group sparse regularization can obviously reduce the complexity in the process of the SBSS algorithm. In detail, when the near-optimal regularization parameters are, respectively, given to these two regularization techniques, the computation time for the standard l1-norm regularization and group sparse regularization techniques is 65.58 s and 7.63 s, respectively. That is to say, the group sparse regularization can also effectively enhance the calculated efficiency.
Moreover, the RPEs of identified results obtained from these two regularization techniques with different weight coefficients are shown in Figure 6. From Figure 6, it can be found that more accurate results can be achieved by the group sparse regularization when the optimal weight coefficient is used. Meanwhile, the minimum values of RPE curves are, respectively, approximate to the RPEs of identified results in Figure 5, which indicates that the selection of the weight coefficient with the help of L-curve criterion in this study is reasonable.
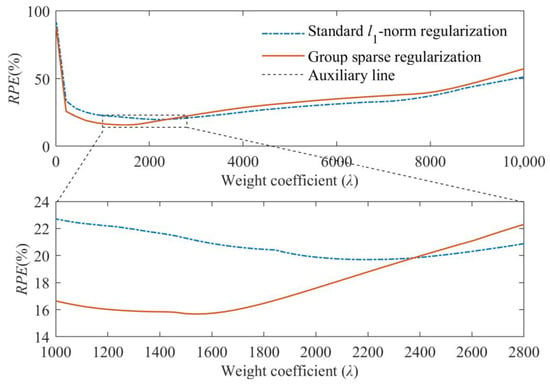
Figure 6.
Comparative results between standard l1-norm regularization and group sparse regularization under different weight coefficients.
Therefore, when reasonable weight coefficients are, respectively, selected, the proposed force identification method based on the group sparse regularization can simultaneously enhance the identification accuracy and calculated efficiency by comparing with that based on the standard l1-norm regularization.
3.2. Influence of Different Noise Levels and Measurement Points
The noise levels and measurement points of acceleration responses are important parameters for the force identification problem, which will affect the results indirectly identified from structural responses. To further investigate these influences, three noise levels, i.e., lev = 1%, lev = 5%, and lev = 10%, for the structural responses at different measurement points are adopted. With the help of the weight coefficients selected by the L-curve criterion mentioned above, the RPEs are listed in Table 1.

Table 1.
RPEs under influences of different noise levels and measurement points.
From Table 1, it can be seen that when the measurement points are given, with the increase in noise levels, the weight coefficient is decreasing and the RPE is increasing. It indicates that the RPE of the identified result is positively correlated with the noise level of acceleration response. Meanwhile, it can be found that for the same noise level, the PREs of the identified results at different measurement points have small differences, which shows that the proposed method has great ability to solve the force identification problem under different application conditions.
In summary, the proposed method can further improve the force identification results compared with the standard l1-norm regularization. It is reasonable to consider the potential group structures of atoms in the given dictionary, so the proposed method can not only further improve the identification accuracy of the external force, but also significantly enhance the calculated efficiency. This way, defining objective function can effectively accord with the prior knowledge of atom relevance in the given dictionary.
4. Experimental Verifications
4.1. Experimental Setup
To evaluate the effectiveness of the proposed method, a beam with a span of 1.2 m was adopted for force identification in the laboratory, as shown in Figure 7. The two sides of the beam were simply supported, and the corresponding diagram is shown in Figure 8. The width and height of the beam were 9.992 cm and 0.936 cm, respectively. The elastic modulus was 2.0 × 1011 N/m2. Mode testing and signal acquisition were, respectively conducted in this study, so 11 accelerometers were evenly placed on the beam, and the distance of each two adjacent accelerometers was 0.12 m.

Figure 7.
Experiment on beam structure for force identification. (a) Experimental setup. (b) Height of beam structure. (c) Width of beam structure. (d) Support of beam structure. (e) Beam structure.
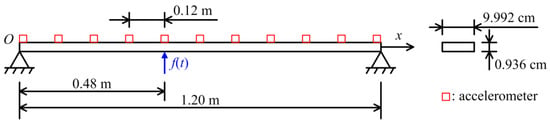
Figure 8.
Experiment diagram of beam structure.
Firstly, mode testing of the beam structure was conducted. The external force is sine sweep signal, and it acted on the beam through the exciter. The sampling frequency was set as 160 Hz, and corresponding acceleration responses were acquired by the given accelerometers.
Modal parameters of the first three orders were analyzed, and these parameters were used to calibrate the finite element model (FEM) of the beam. Because the supporting conditions of the beam were not ideal, approximate supports in the FEM were used to simulate the support conditions, as shown in Figure 9. Meanwhile, because two threaded rods were, respectively used to connect the beam structure with the supports, the density of FEM needed to be updated. As a result, the vertical spring coefficients were set as kv1 = 1.0531 × 107 N·m−1 and kv2 = 2.0495 × 107 N·m−1, respectively. Meanwhile, the rotational spring coefficients were set as kr1 = 7.5103 × 101 N·m/rad and kr2 = 6.2786 × 101 N·m/rad, respectively.

Figure 9.
Finite element model of beam structure.
The mass of the beam structure with threaded rods were measured in the laboratory, and it was equal to 9.15 kg, as shown in Figure 10. At the same time, according to the updating density of FEM and the geometric dimensions, the mass of the beam structure was equal to 8.98 kg, which was slightly smaller than the true value. This is because the length of connection between the beam structure and the threaded rods was smaller than the lengths of the threaded rods, and a part of the threaded rod was not taken as the part of beam structure. Therefore, the updating density of the FEM could be deemed as reasonable.

Figure 10.
Mass of beam structure with threaded rods measured in laboratory.
As a result, the first three frequencies calculated based on the updating FEM were equal to the measured values when the approximate values were, respectively, considered as 14.8969 Hz, 58.8586 Hz, and 131.5050 Hz. At the same time, the first three damp ratios obtained from the mode testing results, i.e., 3.7136 × 10−3, 1.8644 × 10−3, and 3.8858 × 10−3, were directly used to calculate the transfer matrix. Moreover, the comparisons on the first three mode shapes are plotted in Figure 11. For intuitive comparison, each modal shape vector is scaled by its 2-norm.
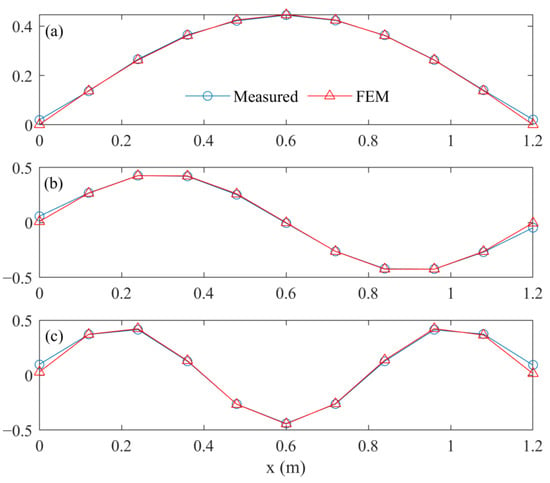
Figure 11.
Comparison on first three mode shapes. (a) First mode. (b) Second mode. (c) Third mode.
The modal assurance criterion (MAC) values between measured mode shapes and the corresponding values obtained based on the FEM are 0.9991, 0.9955, and 0.9888, respectively. The updating mode parameters of the FEM are close to the measured values. It can be deemed that dynamic similarity between the FEM and the beam structure is achieved to a certain extent.
4.2. Verification of Proposed Method
First, white noise with a frequency range from 0 Hz to 80 Hz was selected as the excitation source, which acted in the y direction of node 5. It was assumed that the external force was difficult to be directly measured; measurement points different from the location of the external force were considered. Thus, the acceleration responses at the y direction of nodes 6 and 8 were acquired for force identification problem, and the measured time-varying external force was used for comparison with the identified results. For the group sparse regularization, the group structures of the atoms were given as mentioned above. Because the sampling frequency was 320 Hz, which was half of the sampling frequency in numerical simulations, the number of atoms was set as 4.
Similarly, the near-optimal regularization parameters for the standard l1-norm regularization and group sparse regularization were selected by the L-curve criterion, as, respectively, shown in Figure 12 and Figure 13. As a result, the weight coefficients were determined, and the identified external force obtained from the proposed method was compared with that obtained from the standard l1-norm regularization, as shown in Figure 14.
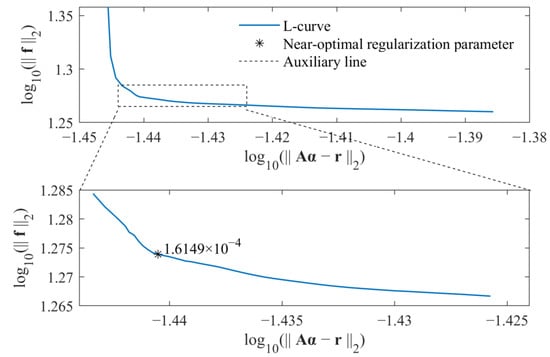
Figure 12.
Selection of near-optimal regularization parameter for standard l1-norm regularization in experimental verifications.
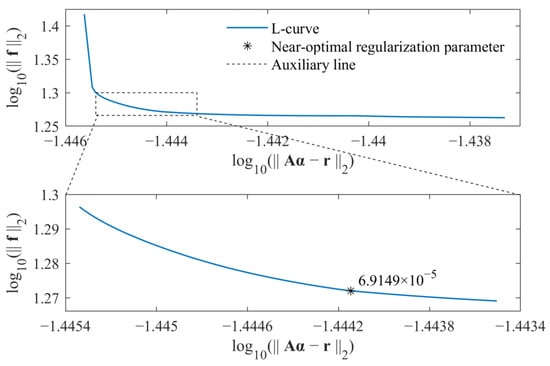
Figure 13.
Selection of near-optimal regularization parameter for group sparse regularization in experimental verifications.
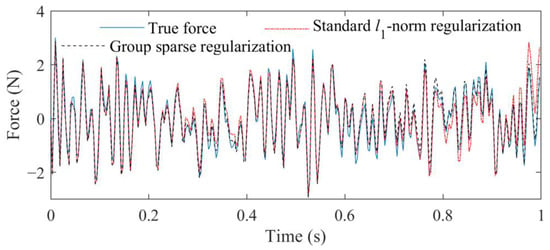
Figure 14.
Identified result, respectively, obtained from standard l1-norm regularization and group sparse regularization in experimental verifications.
In Figure 14, the RPEs obtained based on the standard l1-norm regularization and group sparse regularization are 31.56% and 21.73%, respectively. Because the updated FEM was adopted for force identification, the errors in the transfer matrix were inevitable. In this situation, by adding the regularization constraint, defined based on the group structures, the local identification accuracy obtained by the proposed method is greatly improved. It indicates the group structures of atoms are reasonable enough when updated FEM is used. Meanwhile, the computation time for the standard l1-norm regularization and the proposed method is 16.35 s and 3.59 s, respectively.
Therefore, the same conclusions can be drawn as those given in Section 3.1. The proposed method can further improve the identification accuracy and enhance the calculated efficiency for the force identification problem.
Furthermore, the acceleration responses reconstructed from the identified external force obtained from these two methods can be seen in Figure 15.
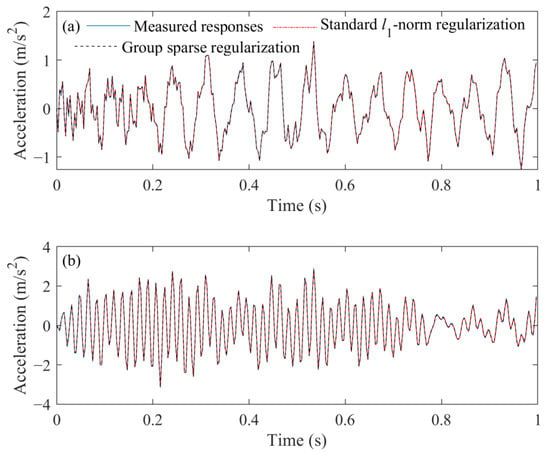
Figure 15.
Comparison of measurement and reconstructed acceleration responses at different measurement points. (a) 1/2 span. (b) 7/10 span.
It can be observed that the measured acceleration responses at 1/2 span and 7/10 span are quite different. This is because the sampling frequency is 320 Hz, only the first three modes of beam structure are contained in the measured acceleration responses, and, as shown in Figure 11b, the node of the second mode is at the middle span of the beam structure. Meanwhile, it can be observed that the reconstructed acceleration responses obtained from different regularization methods are in good agreement with the measured responses in the time domain. It indicates that the identified results can be reasonably used to reconstruct structural responses.
To further study the application of the proposed method, several response combinations with different measured cases are adopted for force identification. The corresponding force identification results based on the proposed method are shown in Table 2.

Table 2.
RPEs under different measured cases and response combinations.
In Table 2, it can be seen that despite the RPEs of the identified results fluctuating due to the influence of random noise and response combinations, the identified accuracy is acceptable. Therefore, when acceleration responses at a few measurement points are used, the proposed method can indirectly identify the time-varying external force with great identification accuracy.
5. Conclusions
In this paper, to indirectly measure time-varying external force from acceleration responses, a novel method based on the group sparse regularization is proposed. Firstly, with the help of trigonometric and rectangular functions, a redundant dictionary is constructed for the expression of external force. Then, the underlying relevance between the atoms is revealed, so the group structures of atoms in the redundant dictionary can be reasonably determined. Finally, the group sparse regularization is introduced based on the group structures, and the external force can be identified by solving the defined optimization problem. To evaluate the effectiveness of the proposed method, both numerical simulations and experimental verifications are carried out. Some conclusions are summarized as follows:
- The proposed method is an effective technique for indirectly measuring time-varying external force from acceleration responses in a few measurement points; both identified external forces and reconstructed responses are in good agreement with the measured values.
- Compared with the standard l1-norm regularization, the proposed method can further improve the force identification results in both numerical simulations and experimental verifications.
- The relevance of atoms in the redundant dictionary can obviously reduce the complexity in the process of force identification. When the same algorithm is used, the proposed method can enhance computational efficiency by comparing with the standard l1-norm regularization.
Author Contributions
Conceptualization, H.L.; methodology, H.L.; software, H.L.; validation, H.L.; formal analysis, H.L.; investigation, H.L.; resources, H.L.; data curation, H.L.; writing—original draft preparation, H.L.; writing—review and editing, H.L.; visualization, H.L.; supervision, H.M.; project administration, H.M.; funding acquisition, H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Guangdong Science and Technology Collaborative Innovation Center for Earthquake Prevention and Disaster Reduction (No. 2018B020207011), the National Key R&D Program of China (No. 2019YFC1511005), the Innovation Center of Robotics and Intelligent Equipment (No. KCYCXPT2017006), the Projects in Key Areas of Guangdong Province (No. 2019B111106001), and the Key Laboratory of Robotics and Intelligent Equipment of Guangdong Regular Institutions of Higher Education (No. 2017KSYS009).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Song, J.; Kang, W.-H.; Lee, Y.-J.; Chun, J. Structural System Reliability: Overview of Theories and Applications to Optimization. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 03121001. [Google Scholar] [CrossRef]
- Jerez, D.J.; Jensen, H.A.; Beer, M. Reliability-Based Design Optimization of Structural Systems under Stochastic Excitation: An Overview. Mech. Syst. Signal Process. 2022, 166, 108397. [Google Scholar] [CrossRef]
- Zhu, X.Q.; Law, S.S. Recent Developments in Inverse Problems of Vehicle–bridge Interaction Dynamics. J. Civ. Struct. Health Monit. 2016, 6, 107–128. [Google Scholar] [CrossRef]
- Shokravi, H.; Shokravi, H.; Bakhary, N.; Heidarrezaei, M.; Rahimian Koloor, S.S.; Petrů, M. Vehicle-Assisted Techniques for Health Monitoring of Bridges. Sensors 2020, 20, 3460. [Google Scholar] [CrossRef]
- Sujon, M.; Dai, F. Application of Weigh-in-Motion Technologies for Pavement and Bridge Response Monitoring: State-of-the-Art Review. Autom. Constr. 2021, 130, 103844. [Google Scholar] [CrossRef]
- Nie, Z.; Shen, Z.; Li, J.; Hao, H.; Lin, Y.; Ma, H. Output-Only Complete Mode Shape Identification of Bridges Using a Limited Number of Sensors. Mech. Syst. Signal Process. 2022, 178, 109246. [Google Scholar] [CrossRef]
- Kamal, M.; Rahman, M.M. Advances in Fatigue Life Modeling: A Review. Renew. Sustain. Energy Rev. 2018, 82, 940–949. [Google Scholar] [CrossRef]
- Kalayci, C.B.; Karagoz, S.; Karakas, Ö. Soft Computing Methods for Fatigue Life Estimation: A Review of the Current State and Future Trends. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 2763–2785. [Google Scholar] [CrossRef]
- Liu, J.; Li, B. A Novel Strategy for Response and Force Reconstruction under Impact Excitation. J. Mech. Sci. Technol. 2018, 32, 3581–3596. [Google Scholar] [CrossRef]
- Sanchez, J.; Benaroya, H. Review of Force Reconstruction Techniques. J. Sound Vib. 2014, 333, 2999–3018. [Google Scholar] [CrossRef]
- Liu, H.; Luo, Z.; Yu, L. A Semi-Convex Function for Both Constant and Time-Varying Moving Force Identification. Mech. Syst. Signal Process. 2021, 146, 107062. [Google Scholar] [CrossRef]
- Jacquelin, E.; Bennani, A.; Hamelin, P. Force Reconstruction: Analysis and Regularization of a Deconvolution Problem. J. Sound Vib. 2003, 265, 81–107. [Google Scholar] [CrossRef]
- Inoue, H.; Harrigan, J.J.; Reid, S.R. Review of Inverse Analysis for Indirect Measurement of Impact Force. Appl. Mech. Rev. 2001, 54, 503–524. [Google Scholar] [CrossRef]
- Li, J.; Hao, H. Substructural Interface Force Identification with Limited Vibration Measurements. J. Civ. Struct. Health Monit. 2016, 6, 395–410. [Google Scholar] [CrossRef]
- Sanchez, J.; Benaroya, H. Asymptotic Approximation Method of Force Reconstruction: Proof of Concept. Mech. Syst. Signal Process. 2017, 92, 39–63. [Google Scholar] [CrossRef]
- Yan, G.; Sun, H.; Büyüköztürk, O. Impact Load Identification for Composite Structures Using Bayesian Regularization and Unscented Kalman Filter. Struct. Control Health Monit. 2017, 24, e1910. [Google Scholar] [CrossRef]
- Chen, Z.; Chan, T.H.T. A Truncated Generalized Singular Value Decomposition Algorithm for Moving Force Identification with Ill-Posed Problems. J. Sound Vib. 2017, 401, 297–310. [Google Scholar] [CrossRef]
- Liu, R.; Dobriban, E.; Hou, Z.; Qian, K. Dynamic Load Identification for Mechanical Systems: A Review. Arch. Comput. Methods Eng. 2022, 29, 831–863. [Google Scholar] [CrossRef]
- Ren, C.; Wang, N.; Liu, Q.; Liu, C. Dynamic Force Identification Problem Based on a Novel Improved Tikhonov Regularization Method. Math. Probl. Eng. 2019, 2019, 1–13. [Google Scholar] [CrossRef]
- Liu, Y.; Shepard, W.S. An Improved Method for the Reconstruction of a Distributed Force Acting on a Vibrating Structure. J. Sound Vib. 2006, 291, 369–387. [Google Scholar] [CrossRef]
- Sun, R.; Chen, G.; He, H.; Zhang, B. The Impact Force Identification of Composite Stiffened Panels under Material Uncertainty. Finite Elem. Anal. Des. 2014, 81, 38–47. [Google Scholar] [CrossRef]
- Qiao, B.; Chen, X.; Xue, X.; Luo, X.; Liu, R. The Application of Cubic B-Spline Collocation Method in Impact Force Identification. Mech. Syst. Signal Process. 2015, 64–65, 413–427. [Google Scholar] [CrossRef]
- Aucejo, M.; De Smet, O. An Iterated Multiplicative Regularization for Force Reconstruction Problems. J. Sound Vib. 2018, 437, 16–28. [Google Scholar] [CrossRef]
- Aucejo, M.; De Smet, O. A Novel Algorithm for Solving Multiplicative Mixed-Norm Regularization Problems. Mech. Syst. Signal Process. 2020, 144, 106887. [Google Scholar] [CrossRef]
- Pan, C.; Ye, X.; Zhou, J.; Sun, Z. Matrix Regularization-Based Method for Large-Scale Inverse Problem of Force Identification. Mech. Syst. Signal Process. 2020, 140, 106698. [Google Scholar] [CrossRef]
- Liu, H.; Yu, L.; Luo, Z.; Pan, C. Compressed Sensing for Moving Force Identification Using Redundant Dictionaries. Mech. Syst. Signal Process. 2020, 138, 106535. [Google Scholar] [CrossRef]
- Qiao, B.; Zhang, X.; Wang, C.; Zhang, H.; Chen, X. Sparse Regularization for Force Identification Using Dictionaries. J. Sound Vib. 2016, 368, 71–86. [Google Scholar] [CrossRef]
- Bao, Y.; Li, H.; Chen, Z.; Zhang, F.; Guo, A. Sparse L1 Optimization-Based Identification Approach for the Distribution of Moving Heavy Vehicle Loads on Cable-Stayed Bridges. Struct. Control Health Monit. 2016, 23, 144–155. [Google Scholar] [CrossRef]
- Yang, N.; Li, J.; Xu, M.; Wang, S. Real-Time Identification of Time-Varying Cable Force Using an Improved Adaptive Extended Kalman Filter. Sensors 2022, 22, 4212. [Google Scholar] [CrossRef]
- Wang, L.; Cao, H.; Xie, Y. An Improved Iterative Tikhonov Regularization Method for Solving the Dynamic Load Identification Problem. Int. J. Comput. Methods Eng. Sci. Mech. 2015, 16, 292–300. [Google Scholar] [CrossRef]
- Song, X.; Zhang, Y.; Liang, D. Load Identification for a Cantilever Beam Based on Fiber Bragg Grating Sensors. Sensors 2017, 17, 1733. [Google Scholar] [CrossRef] [PubMed]
- Qiu, B.; Lu, Y.; Qu, X.; Li, X. Experimental Research on a Hybrid Algorithm for Localisation and Reconstruction of the Impact Force Applied to a Rectangular Steel Plate Structure. Sensors 2022, 22, 8123. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Li, K. Sparse Identification of Time-Space Coupled Distributed Dynamic Load. Mech. Syst. Signal Process. 2021, 148, 107177. [Google Scholar] [CrossRef]
- Qiao, B.; Mao, Z.; Liu, J.; Zhao, Z.; Chen, X. Group Sparse Regularization for Impact Force Identification in Time Domain. J. Sound Vib. 2019, 445, 44–63. [Google Scholar] [CrossRef]
- Zhang, L.; Liang, Y.; Yu, L. Moving Force Identification Based on Group Lasso and Compressed Sensing. Int. J. Struct. Stab. Dyn. 2022, 22, 1–28. [Google Scholar] [CrossRef]
- Feng, W.; Li, Q.; Lu, Q.; Li, C.; Wang, B. Group Relevance Vector Machine for Sparse Force Localization and Reconstruction. Mech. Syst. Signal Process. 2021, 161, 107900. [Google Scholar] [CrossRef]
- Zou, J.; Li, H.; Liu, G. Split Bregman Algorithm for Structured Sparse Reconstruction. IEEE Access 2018, 6, 21560–21569. [Google Scholar] [CrossRef]
- Liu, H.; Yu, L.; Luo, Z.; Chen, Z. Multi-Strategy Structural Damage Detection Based on Included Angle of Vectors and Sparse Regularization. Struct. Eng. Mech. 2020, 75, 415–424. [Google Scholar]
- Hansen, P.C. Regularization Tools Version 4.0 for Matlab 7.3. Numer. Algorithms 2007, 46, 189–194. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).