An Ultra-Low-Cost RCL-Meter
Abstract
:1. Introduction
2. Materials and Methods
2.1. AVR® Micro-Controllers Based RCL-Meter
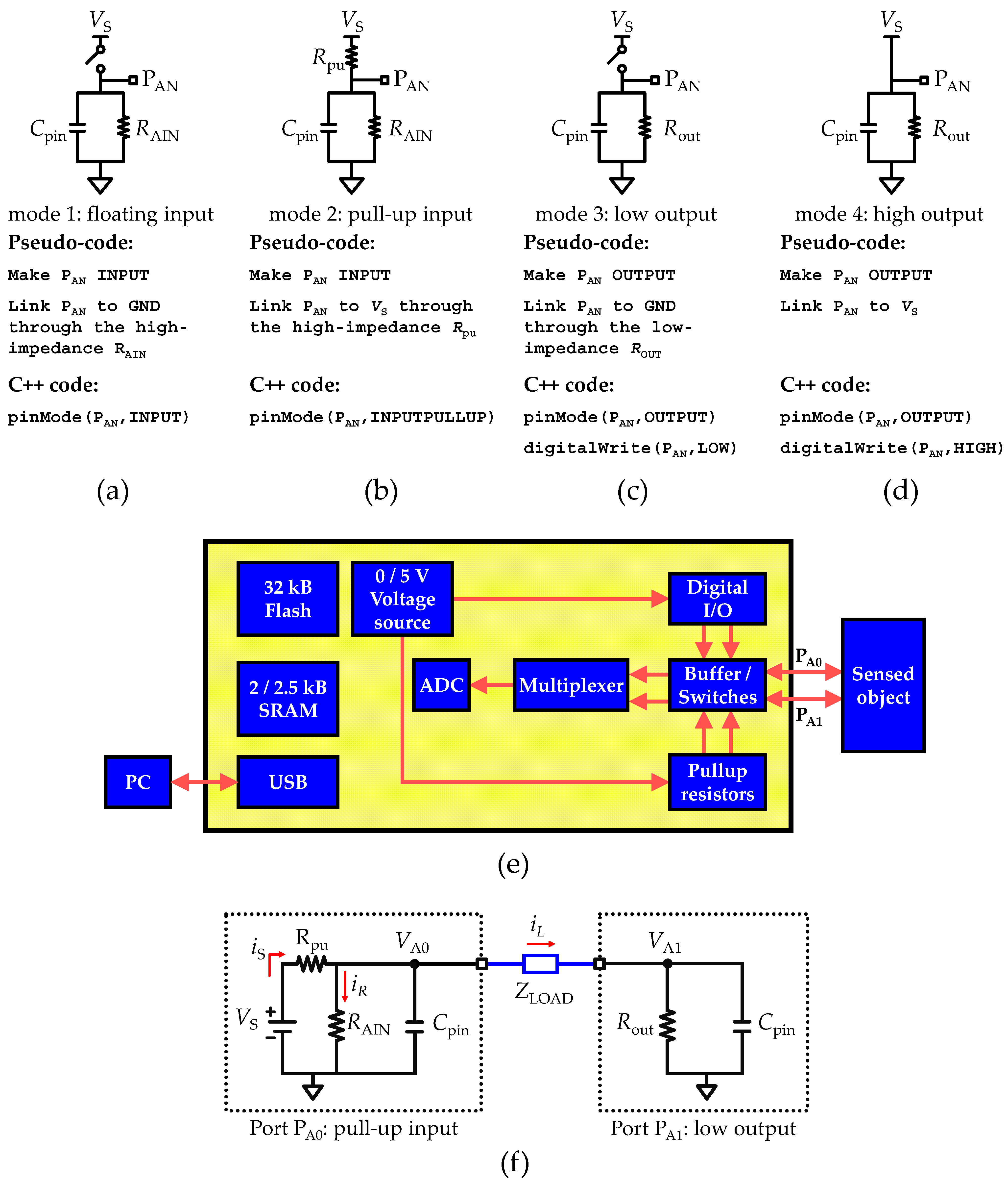
2.2. Analog I/O Operation Modes
2.3. Recording Circuit
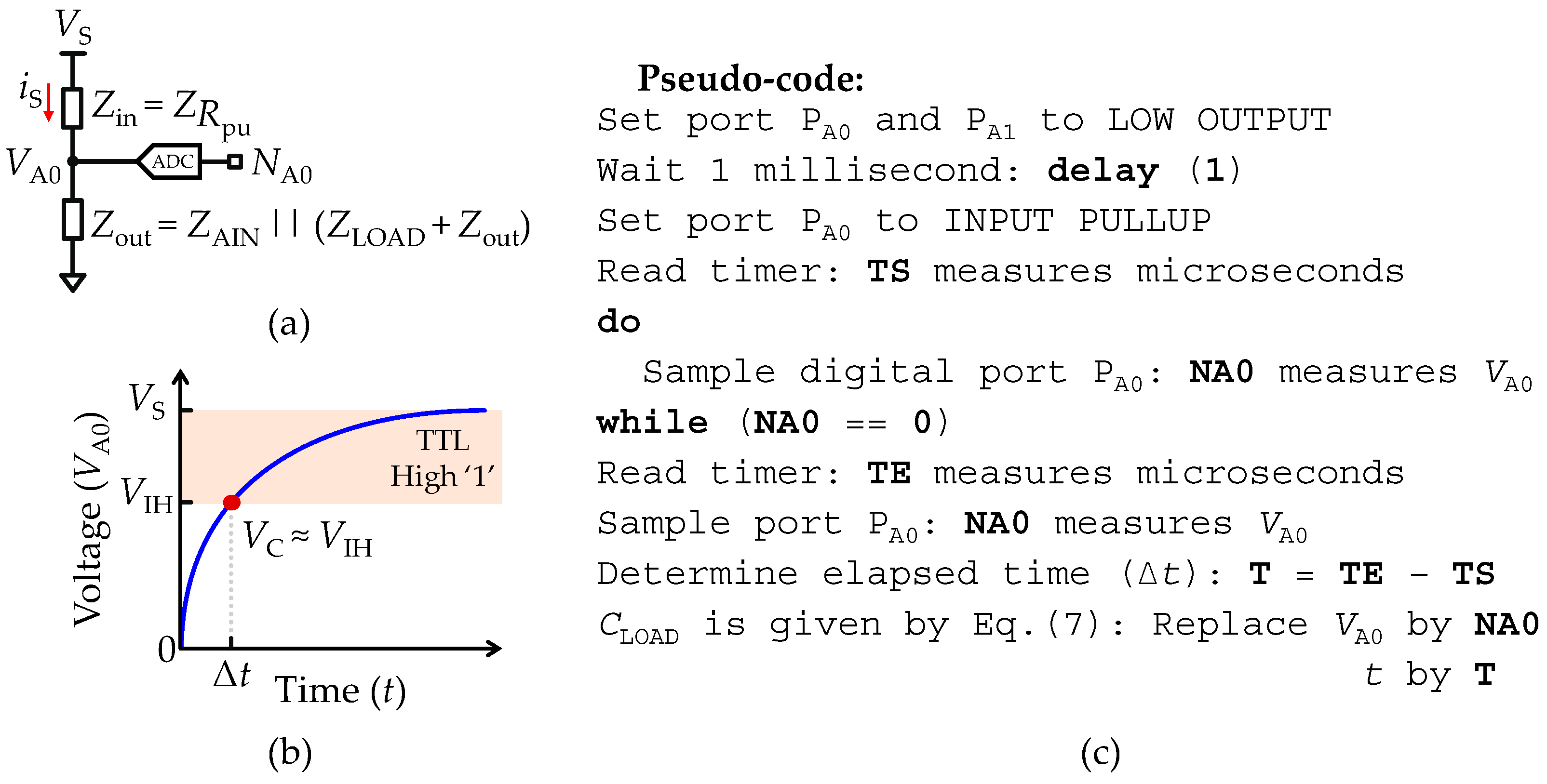
2.4. Measurements of an Isolated Load Resistance (R–Meter)
2.5. Measurements of an Isolated Load Capacitance (C–Meter)
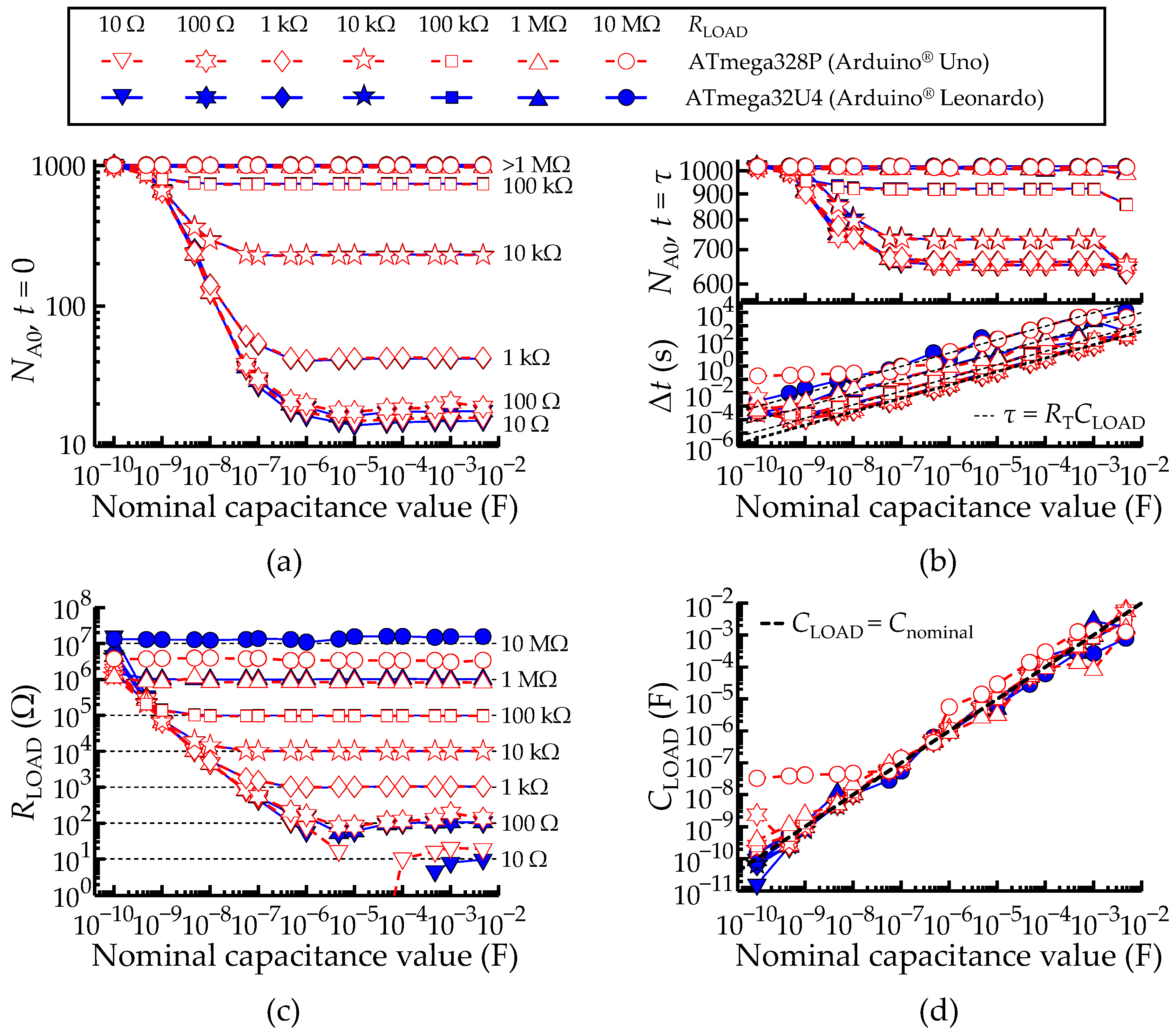
2.5.1. Fast Acquisition Mode of an Isolated Load Capacitance
2.5.2. Transient Acquisition Mode of an Isolated Load Capacitance
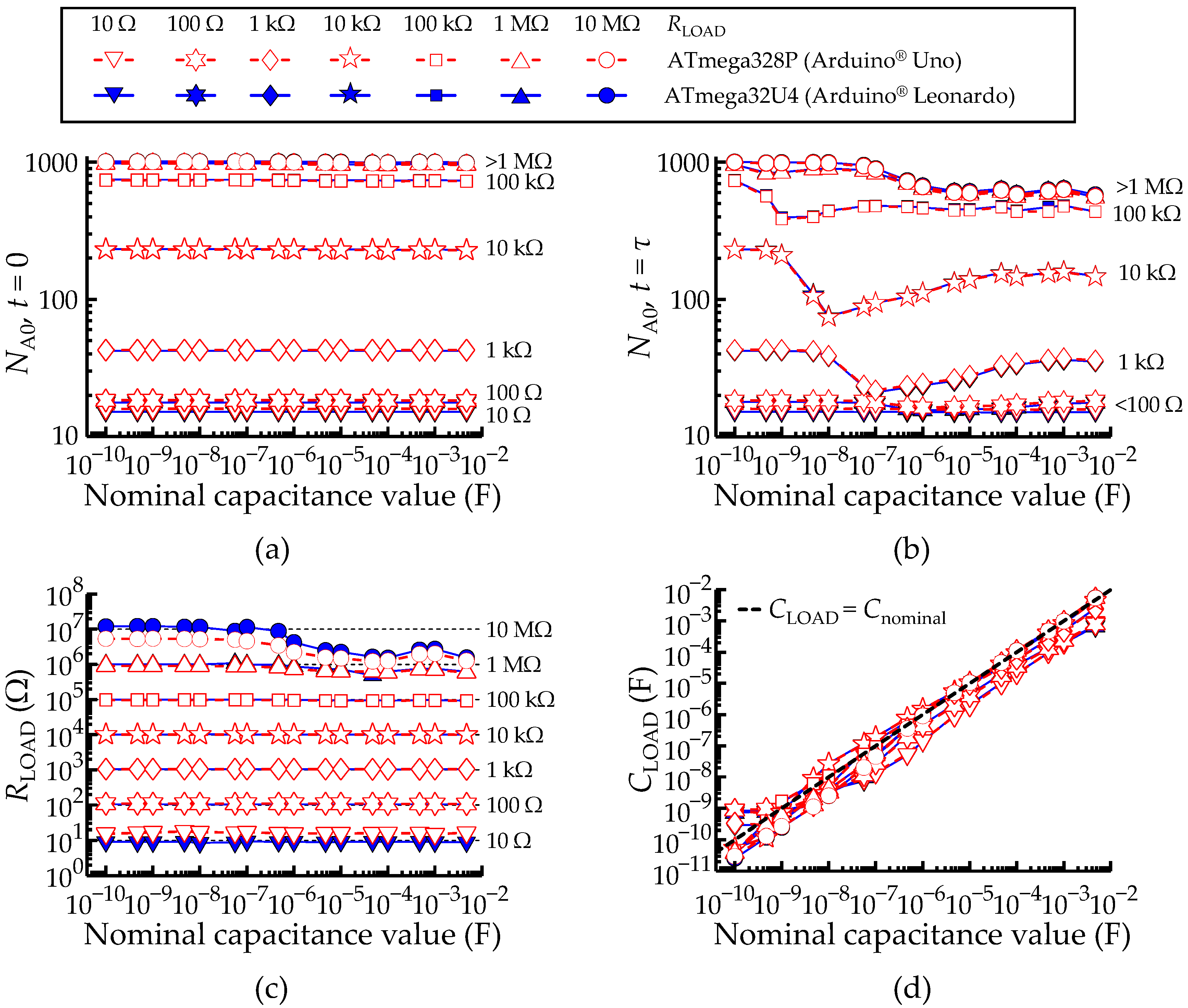
2.6. Measurements of a Serial RC Network (RC–Meter Mode)
2.7. Measurements of a Parallel RC Network (RC–Meter Mode)
2.8. Measurements of an Isolated Load Inductance (L–Meter Mode)
2.9. Data Acquisition and Analysis
2.10. Noise and Uncertainty of the Measurements
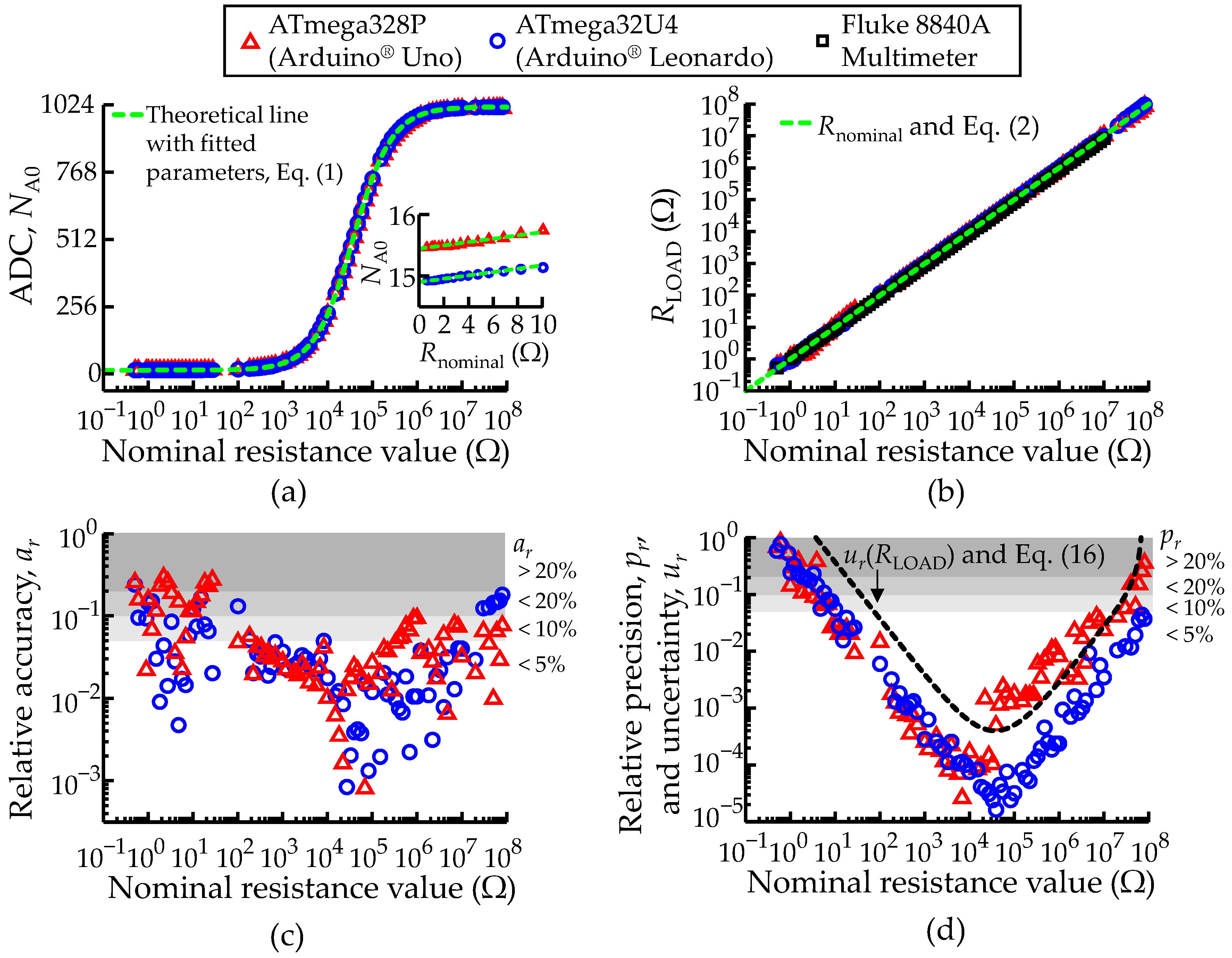
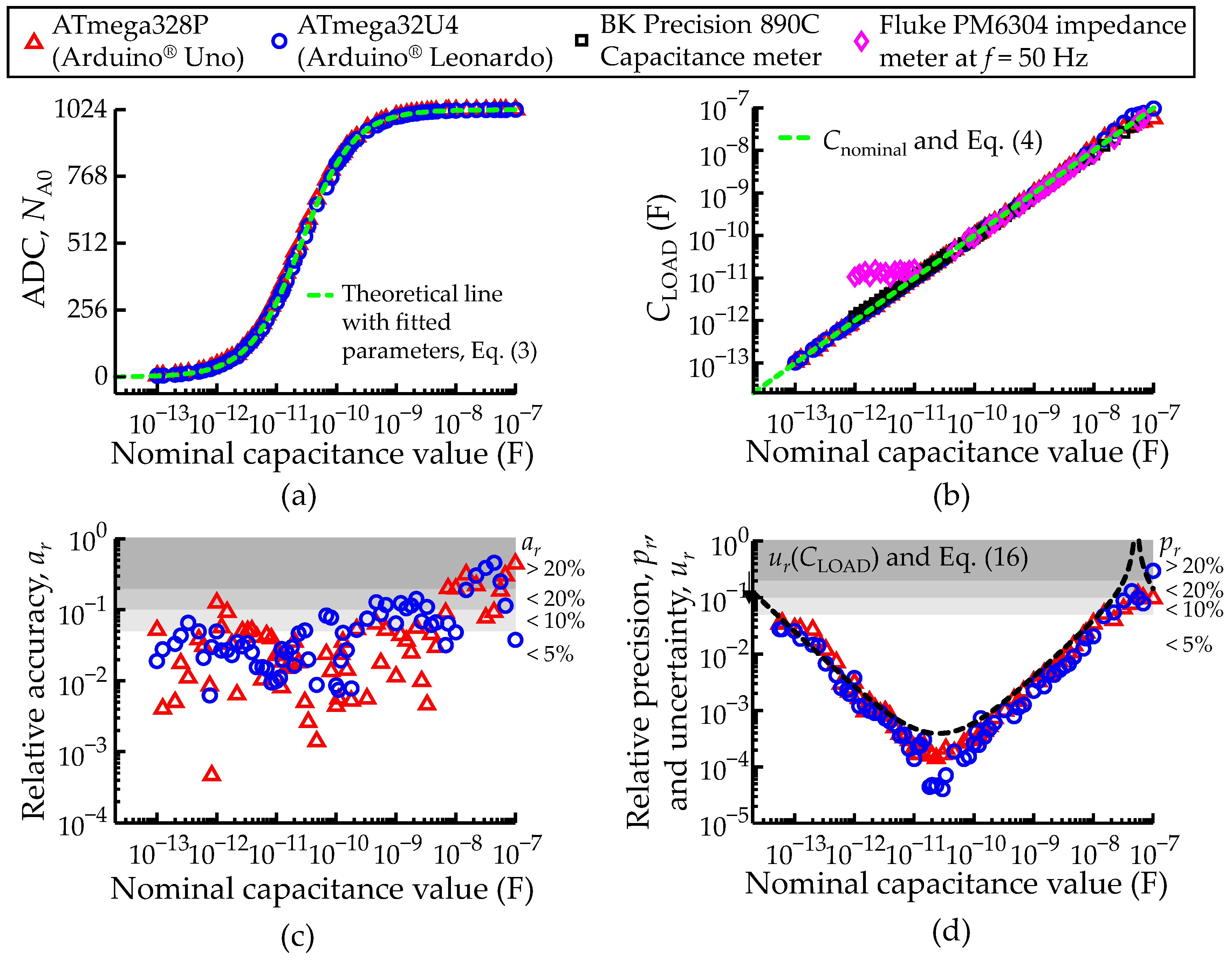
2.11. Relative Accuracy and Precision of the Measurements
2.12. Linearization of the ADC Unit
3. Results
3.1. Characterization of Isolated Resistance Measurements
3.2. Characterization of Isolated Capacitance Measurements: Fast Acquisition Method
3.3. Characterization of Isolated Capacitance Measurements: Transient Acquisition Method
3.4. Characterization of Measurements for Serial RC Networks
3.5. Characterization of Measurements for Parallel RC Networks
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cima, M.J. Next-generation wearable electronics. Nat. Biotechnol. 2014, 32, 642–643. [Google Scholar] [CrossRef] [PubMed]
- Stoppa, M.; Chiolerio, A. Wearable electronics and smart textiles: A critical review. Sensors 2014, 14, 11957–11992. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heo, J.S.; Eom, J.; Kim, Y.-H.; Park, S.K. Recent Progress of Textile-Based Wearable Electronics: A Comprehensive Review of Materials, Devices, and Applications. Small 2017, 14, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Joo, H.; Lee, Y.; Kim, J.; Yoo, J.-S.; Yoo, S.; Kim, S.; Arya, A.K.; Kim, S.; Choi, S.H.; Lu, N.; et al. Soft implantable drug delivery device integrated wirelessly with wearable devices to treat fatal seizures. Sci. Adv. 2021, 7, eabd4639. [Google Scholar] [CrossRef] [PubMed]
- Matsukawa, R.; Miyamoto, A.; Yokota, T.; Someya, T. Skin Impedance Measurements with Nanomesh Electrodes for Monitoring Skin Hydration. Adv. Healthc. Mater. 2020, 9, e2001322. [Google Scholar] [CrossRef] [PubMed]
- Chung, M.; Fortunato, G.; Radacsi, N. Wearable flexible sweat sensors for healthcare monitoring: A review. J. R. Soc. Interface 2019, 16, 20190217. [Google Scholar] [CrossRef] [PubMed]
- Boutry, C.M.; Kaizawa, Y.; Schroeder, B.C.; Chortos, A.; Legrand, A.; Wang, Z.; Chang, J.; Fox, P.; Bao, Z. A stretchable and biodegradable strain and pressure sensor for orthopaedic application. Nat. Electron. 2018, 1, 314–321. [Google Scholar] [CrossRef]
- Oren, S.; Ceylan, H.; Schnable, P.S.; Dong, L. High-Resolution Patterning and Transferring of Graphene-Based Nanomaterials onto Tape toward Roll-to-Roll Production of Tape-Based Wearable Sensors. Adv. Mater. Technol. 2017, 2, 1700223. [Google Scholar] [CrossRef]
- Giraldo, J.P.; Wu, H.; Newkirk, G.M.; Kruss, S. Nanobiotechnology approaches for engineering smart plant sensors. Nat. Nanotechnol. 2019, 14, 541–553. [Google Scholar] [CrossRef] [PubMed]
- Catini, A.; Papale, L.; Capuano, R.; Pasqualetti, V.; Di Giuseppe, D.; Brizzolara, S.; Tonutti, P.; Di Natale, C. Development of a sensor node for remote monitoring of plants. Sensors 2019, 19, 4865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mizukami, Y.; Sawai, Y.; Yamaguchi, Y. Moisture content measurement of tea leaves by electrical impedance and capacitance. Biosyst. Eng. 2006, 93, 293–299. [Google Scholar] [CrossRef]
- Li, M.Q.; Li, J.Y.; Wei, X.H.; Zhu, W.J. Early diagnosis and monitoring of nitrogen nutrition stress in tomato leaves using electrical impedance spectroscopy. Int. J. Agric. Biol. Eng. 2017, 10, 194–205. [Google Scholar] [CrossRef]
- Diacci, C.; Abedi, T.; Lee, J.W.; Gabrielsson, E.O.; Berggren, M.; Simon, D.T.; Niittylä, T.; Stavrinidou, E. Diurnal in vivo xylem sap glucose and sucrose monitoring using implantable organic electrochemical transistor sensors. iScience 2020, 24, 101966. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Martin, A.J.; Carlosena, A. Sensor signal linearization techniques: A comparative analysis. In Proceedings of the 2013 IEEE 4th Latin American Symposium on Circuits and Systems, LASCAS 2013-Conference Proceedings, Cusco, Peru, 27 February–1 March 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–4. [Google Scholar]
- Kraska, M. Digital linearization and display of non-linear analog (sensor) signals. In Proceedings of the IEEE Workshop on Automotive Applications of Electronics, Dearborn, MI, USA, 19 October 1988; IEEE: Piscataway, NJ, USA, 1988; pp. 45–51. [Google Scholar] [CrossRef]
- Islam, T.; Mukhopadhyay, S.C. Linearization of the sensors characteristics: A review. Int. J. Smart Sens. Intell. Syst. 2019, 12, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Alegria, F.; Moschitta, A.; Carbone, P.; Serra, A.D.C.; Petri, D. Effective ADC linearity testing using sinewaves. IEEE Trans. Circuits Syst. I Regul. Pap. 2005, 52, 1267–1275. [Google Scholar] [CrossRef]
- Gong, Z.; Liu, Z.; Wang, Y.; Gupta, K.; da Silva, C.; Liu, T.; Zheng, Z.H.; Zhang, W.P.; van Lammeren, J.P.M.; Bergveld, H.J.; et al. IC for online EIS in automotive batteries and hybrid architecture for high-current perturbation in low-impedance cells. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 1922–1929. [Google Scholar] [CrossRef]
- Manfredini, G.; Ria, A.; Bruschi, P.; Gerevini, L.; Vitelli, M.; Molinara, M.; Piotto, M. An ASIC-Based Miniaturized System for Online Multi-Measurand Monitoring of Lithium-Ion Batteries. Batteries 2021, 7, 45. [Google Scholar] [CrossRef]
- Crescentini, M.; De Angelis, A.; Ramilli, R.; De Angelis, G.; Tartagni, M.; Moschitta, A.; Traverso, P.A.; Carbone, P. Online EIS and Diagnostics on Lithium-Ion Batteries by Means of Low-Power Integrated Sensing and Parametric Modeling. IEEE Trans. Instrum. Meas. 2020, 70, 1–11. [Google Scholar] [CrossRef]
- Monteiro, F.D.R.; Stallinga, P. Using an Off-the-Shelf Lock-In Detector for Admittance Spectroscopy in the Study of Plants. Agric. Sci. 2020, 11, 390–416. [Google Scholar] [CrossRef] [Green Version]
- Grassini, S.; Corbellini, S.; Angelini, E.; Ferraris, F.; Parvis, M. Low-cost impedance spectroscopy system based on a logarithmic amplifier. IEEE Trans. Instrum. Meas. 2014, 64, 1110–1117. [Google Scholar] [CrossRef]
- Grassini, S.; Corbellini, S.; Parvis, M.; Angelini, E.P.M.V.; Zucchi, F. A simple Arduino-based EIS system for in situ corrosion monitoring of metallic works of art. Measurement 2018, 114, 508–514. [Google Scholar] [CrossRef]
- Campbell, S. How to Make and Arduino Capacitance Meter. Available online: https://www.circuitbasics.com/how-to-make-an-arduino-capacitance-meter/ (accessed on 17 March 2021).
- Viraktamath, S.V.; Kannur, K.; Kinagi, B.; Shinde, V.R. Digital LCR meter using arduino. In Proceedings of the 2017 International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 18-19 July 2017; pp. 805–808. [Google Scholar] [CrossRef]
- MICROCHIP. 8-Bit AVR Microcontroller with 32K Bytes In-System Programmable Flash, ATmega328P DATASHEET, Rev.: 7810D–AVR–01/15; Microchip Technology Inc.: Chandler, AZ, USA, 2015. [Google Scholar]
- MICROCHIP. 8-Bit Microcontroller with 16/32K Bytes of ISP Flash and USB Controller, ATmega16U4/ATmega32U4 DATASHEET, Rev.: Atmel-7766I-USB-ATmega16U4-32U4 07/2015; Microchip Technology Inc.: Chandler, AZ, USA, 2015. [Google Scholar]






| Voltage Source | ADC Unit | Internal Circuitry Parameters | TTL Unit | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ATmega328P | ATmega32U4 | |||||||||
| VS (V) | n | Nmax (2n − 1) | RAIN (MΩ) | Rout (Ω) | Rpu (kΩ) | Cpin (pF) | VIL (V) | VIH (V) | VIL (V) | VIH (V) |
| 5 | 10 | 1023 | 100 | 600 | 32 | 24 | −0.5–1.5 | 3.0–5.5 | −0.5–0.9 | 1.9–5.5 |
| ATmega328P | ATmega32U4 | ||||||
|---|---|---|---|---|---|---|---|
| RAIN (MΩ) | Rpu (kΩ) | Rout (Ω) | Cpin (pF) | RAIN (MΩ) | Rpu (kΩ) | Rout (Ω) | Cpin (pF) |
| 3.537 | 36.89 | 565.8 | 23.48 | 5.451 | 36.66 | 542.2 | 25.5 |
| Rnominal | ATmega328P | ATmega32U4 | Fluke 8840A | ATmega328P | ATmega32U4 | Fluke 8840A | |
|---|---|---|---|---|---|---|---|
| RLOAD ± SD | Rnominal | RLOAD ± SD | |||||
| 0.5 Ω | 0.6 ± 0.4 | 0.62 ± 0.4 | 0.548 ± 0.001 | 5.6 kΩ | 5.679 ± 0.001 | 5.7261 ± 0.0006 | 5.5390 ± 0.0002 |
| 1 Ω | 1.2 ± 0.2 | 0.86 ± 0.2 | 1.044 ± 0.001 | 8.2 kΩ | 8.539 ± 0.009 | 8.6078 ± 0.0009 | 8.1837 ± 0.0002 |
| 2.2 Ω | 1.6 ± 0.3 | 2.30 ± 0.5 | 2.247 ± 0.001 | 10 kΩ | 10.101 ± 0.002 | 10.1772 ± 0.0008 | 9.9313 ± 0.0002 |
| 5.6 Ω | 5.7 ± 0.4 | 5.70 ± 0.6 | 5.645 ± 0.001 | 22 kΩ | 21.9 ± 0.3 | 22.1858 ± 0.0008 | 21.846 ± 0.0000 |
| 8.2 Ω | 9.1 ± 0.2 | 7.72 ± 0.6 | 8.251 ± 0.001 | 56 kΩ | 55.0 ± 0.1 | 55.789 ± 0.002 | 55.8529 ± 0.0003 |
| 10 Ω | 10.5 ± 0.3 | 8.77 ± 0.5 | 10.031 ± 0.005 | 82 kΩ | 80.8 ± 0.1 | 81.891 ± 0.002 | 81.914 ± 0.002 |
| 22 Ω | 22.4 ± 0.4 | 20.1 ± 0.5 | 21.901 ± 0.002 | 100 kΩ | 97.3 ± 0.2 | 98.812 ± 0.003 | 98.622 ± 0.008 |
| 56 Ω | 59.7 ± 0.4 | 55.7 ± 0.5 | 56.023 ± 0.004 | 220 kΩ | 211.9 ± 0.4 | 217.55 ± 0.01 | 219.267 ± 0.007 |
| 82 Ω | 83.3 ± 0.3 | 83.1 ± 0.4 | 82.532 ± 0.0014 | 560 kΩ | 535 ± 5 | 549.7 ± 0.1 | 561.045 ± 0.009 |
| 100 Ω | 102.2 ± 0.3 | 101.9 ± 0.4 | 99.44 ± 0.02 | 820 kΩ | 777 ± 7 | 811.4 ± 0.2 | 824.71 ± 0.01 |
| 220 Ω | 224.3 ± 0.3 | 224.2 ± 0.4 | 220.560 ± 0.004 | 1 MΩ | 0.906 ± 0.007 | 0.9894 ± 0.0002 | 1.0140 ± 0.00004 |
| 560 Ω | 576.9 ± 0.4 | 573.6 ± 0.8 | 556.14 ± 0.01 | 2.2 MΩ | 2.14 ± 0.05 | 2.193 ± 0.004 | 2.2171 ± 0.0002 |
| 820 Ω | 835.8 ± 0.6 | 833.840 ± 0.0001 | 817.19 ± 0.03 | 6.8 MΩ | 6.3 ± 0.3 | 6.89 ± 0.01 | 6.986 ± 0.002 |
| 1 kΩ | 1.0348 ± 0.0006 | 1.0331 ± 0.0004 | 0.9945 ± 0.0001 | 8.2 MΩ | 8.8 ± 0.3 | 7.87 ± 0.05 | 8.2066 ± 0.0001 |
| 2.2 kΩ | 2.242 ± 0.001 | 2.2596 ± 0.0005 | 2.1955 ± 0.0001 | 10 MΩ | 10.3 ± 0.2 | 9.60 ± 0.03 | 10.129 ± 0.008 |
| Cnominal | ATmega-328P | ATmega-32U4 | Fluke PM6304 | BK 890C | ATmega-328P | ATmega-32U4 | Fluke PM6304 | BK 890C | |
|---|---|---|---|---|---|---|---|---|---|
| CLOAD ± SD | Cnominal | CLOAD ± SD | |||||||
| 1 pF | 1.126 ± 0.004 | 1.050 ± 0.005 | 12 ± 8 | 1.3 ± 0.6 | 560 pF | 550.0 ± 0.8 | 510.89 ± 0.05 | 526 ± 3 | 531 ± 3 |
| 1.5 pF | 1.640 ± 0.002 | 1.541 ± 0.003 | 16 ± 18 | 1.9 ± 0.3 | 680 pF | 644 ± 1 | 600.30 ± 0.05 | 678 ± 5 | 677 ± 7 |
| 2.7 pF | 2.834 ± 0.003 | 2.782 ± 0.004 | 14 ± 8 | 3.3 ± 0.6 | 1 nF | 1.012 ± 0.003 | 0.93558 ± 0.00004 | 0.999 ± 0.009 | 1.008 ± 0.004 |
| 3.9 pF | 4.101 ± 0.003 | 3.998 ± 0.004 | 12 ± 5 | 8 ± 1 | 1.5 nF | 1.445 ± 0.007 | 1.34302 ± 0.00003 | 1.493 ± 0.005 | 1.517 ± 0.002 |
| 5.8 pF | 5.860 ± 0.002 | 5.709 ± 0.003 | 17 ± 19 | 7 ± 3 | 2.2 nF | 2.08 ± 0.01 | 1.88744 ± 0.00004 | 2.185 ± 0.005 | 2.24 ± 0.01 |
| 8.2 pF | 8.527 ± 0.003 | 8.278 ± 0.003 | 17 ± 5 | 9.3 ± 0.4 | 3.3 nF | 3.29 ± 0.03 | 2.93701 ± 0.00003 | 3.314 ± 0.006 | 3.401 ± 0.003 |
| 10 pF | 10.231 ± 0.002 | 9.900 ± 0.002 | 18 ± 5 | 11.2 ± 0.3 | 6.8 nF | 7.4 ± 0.2 | 6.58318 ± 0.00003 | 7.096 ± 0.02 | 7.13 ± 0.06 |
| 20 pF | 20.711 ± 0.003 | 19.672 ± 0.002 | 25 ± 4 | 22.300 ± 0.000 | 7.5 nF | 9.0 ± 0.2 | 7.98201 ± 0.00004 | 7.56 ± 0.05 | 7.7540 ± 0.0004 |
| 47 pF | 46.934 ± 0.009 | 46.59 ± 0.04 | 49 ± 7 | 49.3 ± 0.5 | 10 nF | 12.0 ± 0.4 | 9.51585 ± 0.00003 | 10.15 ± 0.07 | 9.668 ± 0.001 |
| 82 pF | 80.88 ± 0.02 | 81.01 ± 0.02 | 89 ± 7 | 83.4 ± 0.5 | 15 nF | 20 ± 1 | 17.8541 ± 0.00004 | 15.44 ± 0.06 | 15.570 ± 0.0000 |
| 100 pF | 99.56 ± 0.04 | 100.87 ± 0.03 | 99 ± 5 | 103.183 ± 0.04 | 22 nF | 27 ± 1 | 28.6855 ± 0.00003 | 21.623 ± 0.007 | 22 ± 1 |
| 180 pF | 179.1 ± 0.1 | 178.6 ± 0.2 | 187 ± 1 | 185 ± 1 | 56 nF | 46 ± 5 | 70.0663 ± 0.00002 | 57.21 ± 0.04 | 57.2 ± 0.9 |
| 220 pF | 210.7 ± 0.2 | 208.5 ± 0.2 | 221 ± 12 | 217.6 ± 0.5 | 68 nF | 47 ± 5 | 75.7749 ± 0.00002 | 68.39 ± 0.07 | 69 ± 2 |
| 470 pF | 440.0 ± 0.7 | 409.77 ± 0.05 | 469 ± 6 | 449.9 ± 0.8 | 100 nF | 55 ± 5 | 96.2257 ± 0.00003 | 101.3 ± 0.02 | 101.536 ± 0.005 |
| Cnominal | ATmega-328P | ATmega-32U4 | Fluke PM6304 | BK 890C | ATmega-328P | ATmega-32U4 | Fluke PM6304 | BK 890C | |
|---|---|---|---|---|---|---|---|---|---|
| CLOAD ± SD | Cnominal | CLOAD ± SD | |||||||
| 100 pF | 111 ± 4 | 72 ± 1 | 99 ± 5 | 101.41 ± 0.04 | 2.2 μF | 2.259 ± 0.007 | 2.158 ± 0.006 | 2.2742 ± 0.0004 | 2.292 ± 0.005 |
| 1 nF | 0.703 ± 0.008 | 0.49 ± 0.01 | 0.999 ± 0.009 | 1.008 ± 0.004 | 4.7 μF | 4.933 ± 0.008 | 4.883 ± 0.009 | 4.24 ± 0.04 | 4.5010 ± 0.0006 |
| 2.2 nF | 1.591 ± 0.009 | 1.22 ± 0.01 | 2.185 ± 0.005 | 2.24 ± 0.01 | 6.8 μF | 6.92 ± 0.01 | 6.71 ± 0.02 | 7.1687 ± 0.0001 | 7.1870 ± 0.0001 |
| 4.7 nF | 3.99 ± 0.02 | 3.26 ± 0.02 | 4.77 ± 0.03 | 4.90 ± 0.03 | 10 μF | 10.31 ± 0.02 | 10.204 ± 0.009 | 9.76 ± 0.01 | 9.998 ± 0.02 |
| 6.8 nF | 6.10 ± 0.02 | 5.01 ± 0.05 | 7.10 ± 0.02 | 7.13 ± 0.06 | 22 μF | 23.01 ± 0.02 | 23.06 ± 0.04 | 20.98 ± 0.03 | 21.29 ± 0.03 |
| 10 nF | 9.43 ± 0.02 | 7.85 ± 0.04 | 10.15 ± 0.07 | 9.667 ± 0.001 | 47 μF | 49.10 ± 0.09 | 47.12 ± 0.09 | 42.69 ± 0.04 | 43.0 ± 0.5 |
| 22 nF | 22.10 ± 0.04 | 19.66 ± 0.04 | 21.623 ± 0.007 | 22 ± 1 | 68 μF | 70.6 ± 0.1 | 70.8 ± 0.2 | 66.39 ± 0.02 | 68.68 ± 0.06 |
| 56 nF | 56.89 ± 0.09 | 53.03 ± 0.06 | 57.21 ± 0.04 | 57.2 ± 0.9 | 100 μF | 104.2 ± 0.2 | 101.0 ± 0.3 | 98.14 ± 0.04 | 102.30 ± 0.08 |
| 68 nF | 67.22 ± 0.06 | 65.52 ± 0.05 | 68.39 ± 0.07 | 69 ± 2 | 220 μF | 225.6 ± 0.4 | 226.5 ± 0.8 | 200.29 ± 0.08 | 206.7 ± 2 |
| 100 nF | 97.2 ± 0.1 | 95.9 ± 0.2 | 101.34 ± 0.02 | 101.536 ± 0.005 | 470 μF | 491.9 ± 0.6 | 446.6 ± 0.8 | 455.7 ± 0.2 | 472.6 ± 3 |
| 220 nF | 228.3 ± 0.4 | 212.2 ± 0.2 | 221.79 ± 0.03 | 221.900 ± 0.000 | 1 mF | 1.006 ± 0.003 | 0.981 ± 0.004 | 0.9608 ± 0.0006 | 0.994 ± 0.006 |
| 470 nF | 480 ± 1 | 456 ± 1 | 468.54 ± 0.05 | 469.800 ± 0.000 | 2.2 mF | 2.240 ± 0.007 | 2.250 ± 0.007 | 2.1667 ± 0.0005 | 2.1987 ± 0.0000 |
| 680 nF | 692 ± 1 | 669 ± 2 | 665.67 ± 0.2 | 680.000 ± 0.000 | 3.3 mF | 3.62 ± 0.02 | 3.631 ± 0.009 | 3.1891 ± 0.0007 | 3.441 ± 0.002 |
| 1 μF | 1.047 ± 0.003 | 0.972 ± 0.003 | 0.983 ± 0.001 | 0.989 ± 0.007 | 4.7 mF | 4.85 ± 0.01 | 4.91 ± 0.01 | 4.6754 ± 0.0005 | 4.935 ± 0.003 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inácio, P.M.C.; Guerra, R.; Stallinga, P. An Ultra-Low-Cost RCL-Meter. Sensors 2022, 22, 2227. https://doi.org/10.3390/s22062227
Inácio PMC, Guerra R, Stallinga P. An Ultra-Low-Cost RCL-Meter. Sensors. 2022; 22(6):2227. https://doi.org/10.3390/s22062227
Chicago/Turabian StyleInácio, Pedro M. C., Rui Guerra, and Peter Stallinga. 2022. "An Ultra-Low-Cost RCL-Meter" Sensors 22, no. 6: 2227. https://doi.org/10.3390/s22062227
APA StyleInácio, P. M. C., Guerra, R., & Stallinga, P. (2022). An Ultra-Low-Cost RCL-Meter. Sensors, 22(6), 2227. https://doi.org/10.3390/s22062227








