Robust Optimization of a MEMS Accelerometer Considering Temperature Variations

1. Introduction

2. The Accelerometer

2.1. Operating Principle

The structure of the accelerometer, as shown in Figure 1, is basically a beam-mass structure. The differential capacitance detection is employed to increase output accuracy. The accelerometer has a “sandwich” structure which consists of a silicon chip and two glass substrates, as shown in Figure 1a. The silicon chip placed between the two glass substrates consists of a proof mass a supporting frame and four suspension beams. The proof mass is connected to the supporting frame by the suspension beams. The electrodes on the proof mass and fixed electrodes on glass substrate form the detection capacitors, and there is a detection capacitor on the silicon chip and each glass substrate.

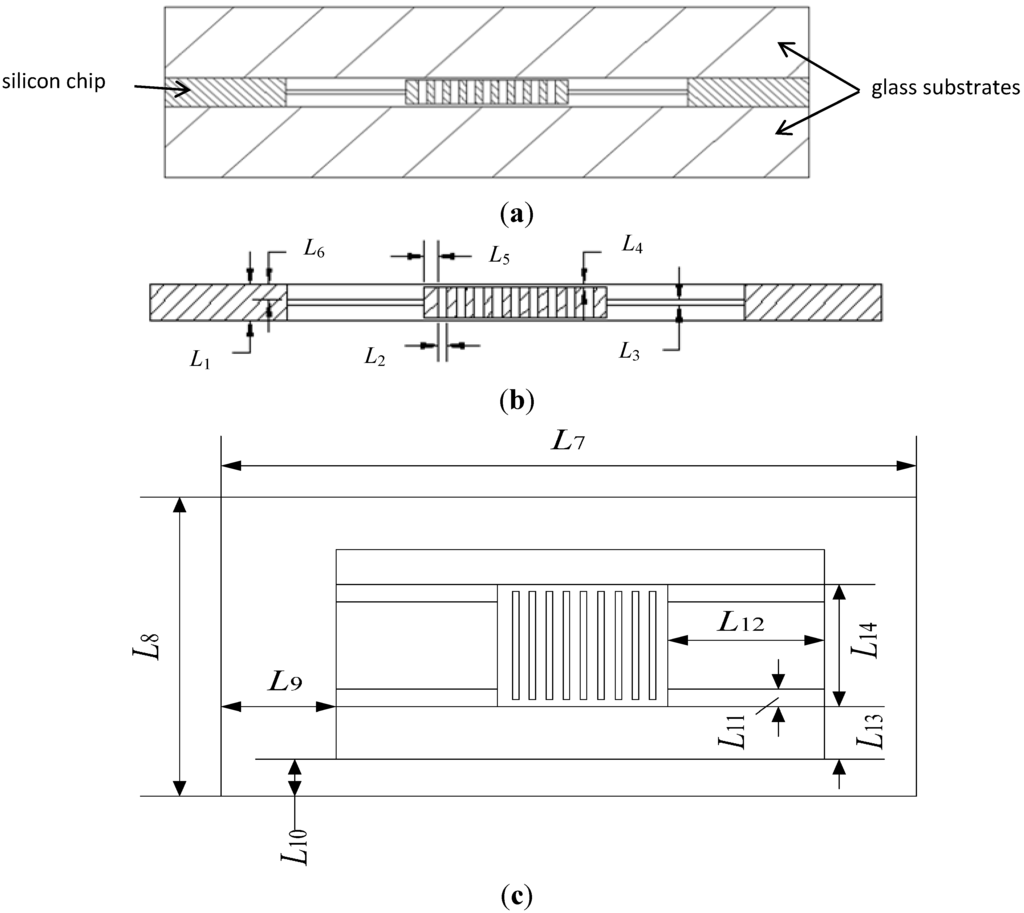
Figure 1. (a) Assembly drawing; (b) and (c) Schematic structure.

The main principle of acceleration detection is that an acceleration applied in the detection direction will cause the proof mass to move from its rest position. The proof mass connected to the supporting frame is free to move in the detection direction (Z-direction). When there is an acceleration applied in Z-direction, the proof mass of the accelerometer will move in the detection direction, and the accelerometer senses a change in electrical capacitance due to the distance change of two capacitors. The resulting capacitance change between the moving electrodes on the proof mass and fixed electrodes can be detected differentially. Accordingly the acceleration is measured. The operating mode (detection mode) is the 1st vibration mode of the accelerometer, as shown in Figure 2.

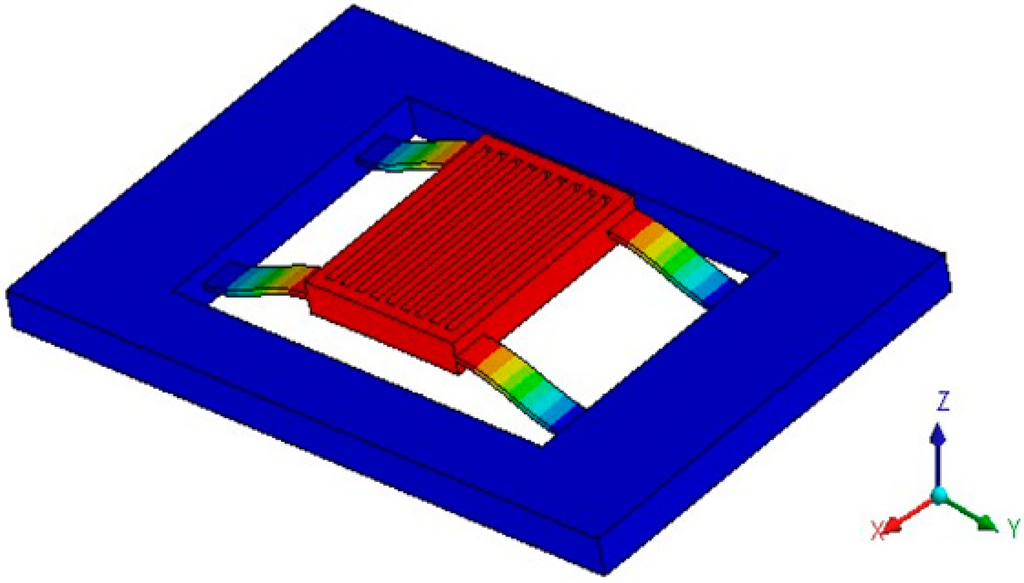
Figure 2. Detection mode of the accelerometer.

3. Effects of Temperature Variations on the Accelerometer

3.2. Resonance Frequency

As the volume of the accelerometer is very small and the material (silicon) of the accelerometer has a very high coefficient of thermal conductivity, it is assumed that the temperature of the accelerometer equals the environmental temperature. The accelerometer is assumed to be an elastic body in its working temperature −40–60 °C. Then inertial loads and uniform temperature loads are applied to the finite element model of the accelerometer and a modal analysis and thermal-mechanical coupling analysis are performed. The change of the 1st resonance frequency with temperature is shown in Figure 3.

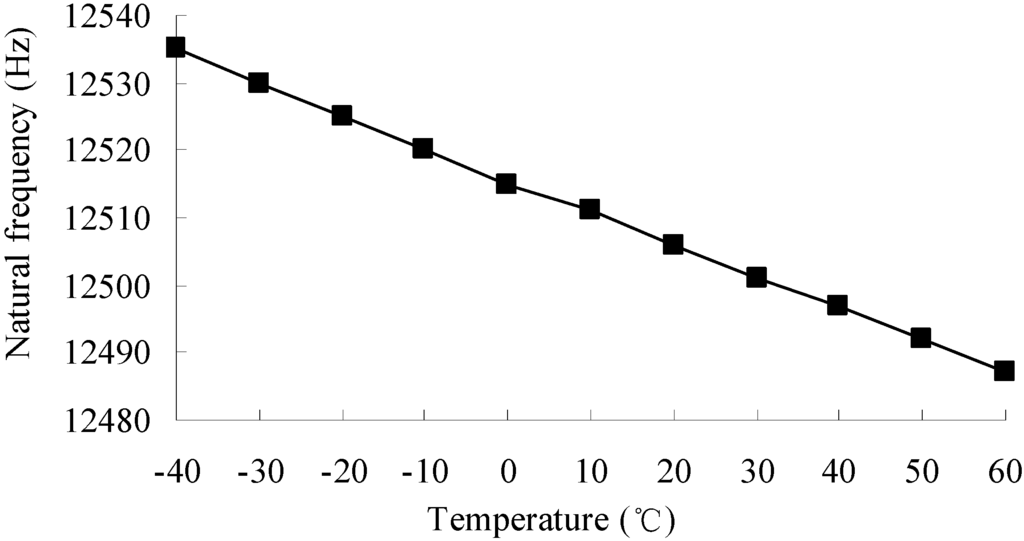
Figure 3. 1st resonance frequency vs. temperature.

The 1st mode is the detection mode of the accelerometer. It is seen that the 1st resonance frequency is inversely proportional to the temperature, and the variation of the resonance frequency with temperature is almost linear. The changes in the resonance frequency are caused by the changes in Young’s modulus. As the Young’s modulus changes with temperature linearly, so does the resonance frequency.

3.3. Thermal Deformation

Temperature variations could cause thermal deformation of the accelerometer. The acceleration detection of the accelerometer is realized through elastic deformation, so the thermal deformation may influence the output of the accelerometer.

Figure 4 shows the total deformation of the accelerometer with temperature arising from 20 °C to 40 °C when a = 0. In fact, Figure 4 is the thermal deformation of the accelerometer, as there is no acceleration input. It is seen that the thermal deformation symmetrical and non-uniform. The edge of the proof mass has the maximum deformation 0.11 µm. The suspension beams also has a relative large deformation up to 0.037 µm. The flatness of the upper and lower surfaces of the proof mass will be affected. The non-uniform thermal deformation of the proof mass means a shape change of the detection capacitors, and will eventually influence the output capacitance.

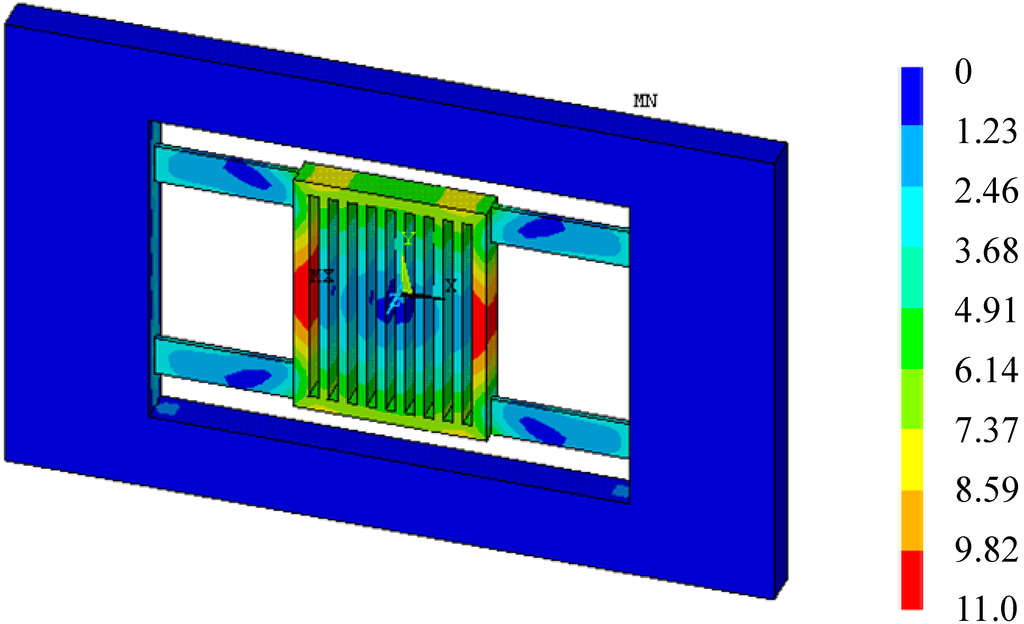
Figure 4. Deformation when temperature arising 20 °C (×10⁻⁸ m, a = 0).

After applied inertia loads and temperature loads to the FE model of the accelerometer, the total deformation of the accelerometer at 20 °C (reference temperature) and 40 °C when a = 50 m/s² can be obtained, as shown in Figure 5 and Figure 6, respectively. From Figure 5, it is seen that the deformation of the proof mass is uniform, and the deformation is caused by acceleration. From Figure 6, it is seen that the deformation of the proof mass is non-uniform, and the total deformation is a superposition of thermal deformation and mechanical deformation. Though the accelerometer’s deformation at 20 °C and 40 °C both has the maximum deformation 0.189 µm, there will be an output deviation due to the non-uniform deformation at 40 °C.

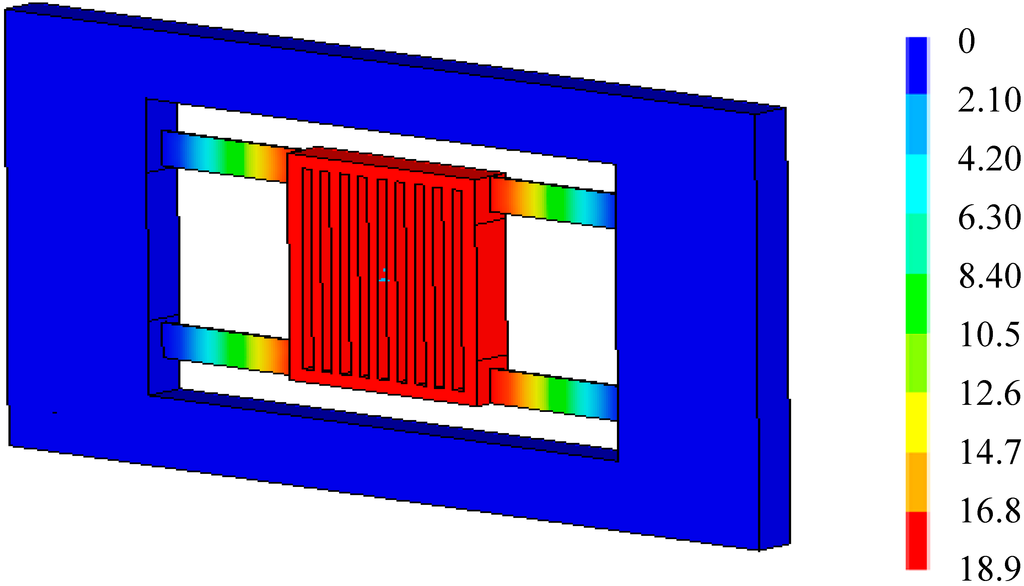
Figure 5. Total deformation at reference temperature 20 °C (×10⁻⁸, a = 50m/s²).

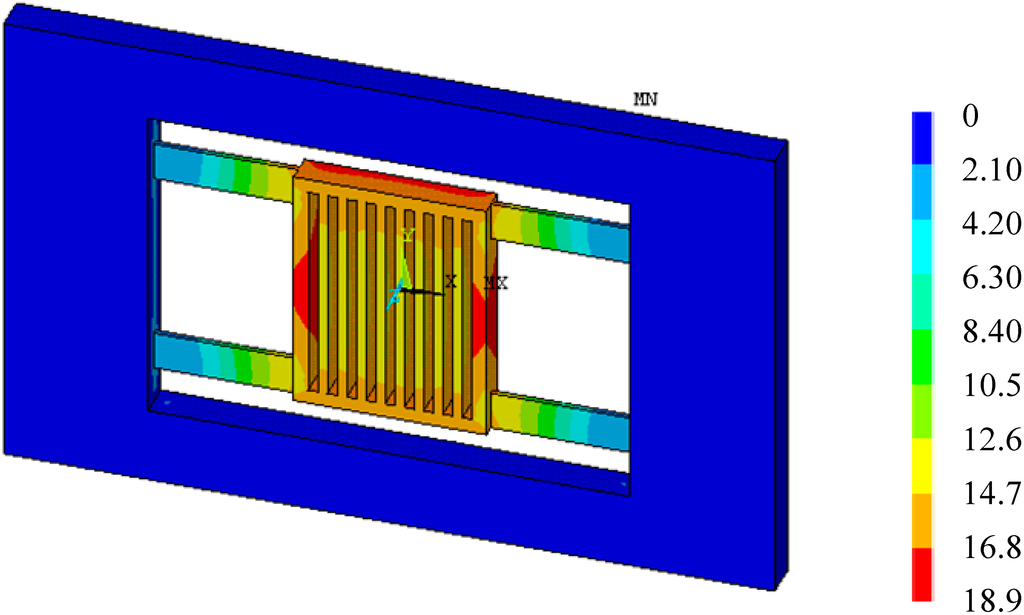
Figure 6. Total deformation at 40 °C (×10⁻⁸ m, a = 50m/s²).

3.4. Output Capacitance

Temperature variations result in output deviation due to thermal deformation and changes in material properties. The output capacitance of the accelerometer at different temperatures is shown in Figure 7. The output capacitance at reference temperature 20 °C is set to a unitary value, and the output capacitance at other temperatures is a relative value to the one at 20 °C.

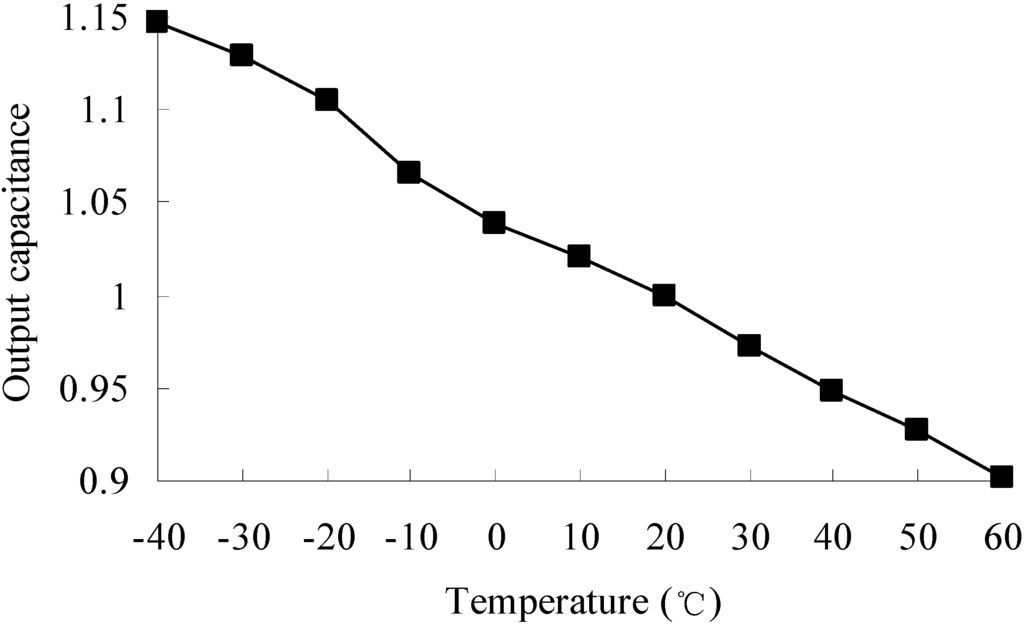
Figure 7. Output capacitance at different temperatures.

It is seen that from −40 °C to 60 °C, the output capacitance has a linear change trend. The output capacitance decreases with the increasing of temperature. The maximum output deviation can be 14.7%, which is found at −40 °C. The output deviation is mainly caused by thermal deformation and changes in Young’s modulus.

The temperature variations cause in the performance drift of the accelerometer, and eventually lead to measurement errors. Therefore, considering the environmental temperature variations and temperature-induced thermal-mechanical coupling is necessary in the design of an accelerometer. Temperature compensation method or a robust structure considering uncertainties for the design could be developed [2,25]. Figure 7 provides a reference for temperature compensation and a design objective for robust design by minimizing the influence of temperature variations in relation to the output performance of the accelerometer.

4. Sensitivity Analysis of Output Capacitance and Resonance Frequency

4.1. Sensitivity Analysis of Output Capacitance and Resonance Frequency to Structural Parameters

Nowadays, many complex MEMS devices are designed and fabricated thanks to the advances in microfabrication techniques [26]. A proper optimization process of MEMS devices is challenged by the increase in design complexity and the coupling in multiple physical domains [27]. The analysis and optimization of a MEMS device is computationally expensive. A set of factors contributes to the computational cost. Therefore, saving computational cost has become a major concern in the optimization and simulation of MEMS devices.

As shown in Figure 1, the accelerometer has 14 independent structural parameters (L₁, L₂, …, L₁₄) aside from the number of bar electrodes on the proof mass. As the optimization of the accelerometer is a nonlinear problem including thermal-mechanical coupling and may be computationally expensive, it is time-saving to reduce the dimension of the design space and increase the calculation speed. Also, it is important to find out key parameters that determine the performance of and what level of accuracy of a structural parameter is necessary, which can provide a reference for the fabrication processes.

As it is extremely difficult to measure and obtain real statistical distribution of an accelerometer in the real world, sensitivity analysis is often used to determine how “sensitive” a model is to changes in the value of the parameters of the model [28]. Sensitivity analysis of the output capacitance to structural parameters can find out key parameters that have greater influence on the output performance of the accelerometer.

The sensitivity of the output capacitance to a structural parameter $L_i$ is defined as:

$$S_c=\frac{|\mathrm{\Delta }{C}^{\prime }-\mathrm{\Delta }C|}{\mathrm{\Delta }C}$$

(8)

where $\mathrm{\Delta }{C}^{\prime }$ is the output capacitance under $\mathrm{\Delta }L$ .

The initial computational conditions and parameters of the accelerometer are shown in Table 1. The procedure of the sensitivity analysis of output capacitance to variation of structural parameters is as follows:

(1)

Calculate the output capacitance of the initial structure;

(2)

Change one of the structural parameters with $\mathrm{\Delta }{L}_i$ ( $\mathrm{\Delta }{L}_i/L_i=1\%$ ), and keep other parameters unchanged;

(3)

Calculate the sensitivity of the output capacitance to the parameter according to Equation (8);

(4)

Find out the key parameters that have greatest influence on the output capacitance.

Table 1. Computational conditions of the accelerometer.

Table 1. Computational conditions of the accelerometer.

Computational conditions	Value
Initial nodal displacements	0
Initial nodal velocities	0
Acceleration	50 m/s2
Young’s modulus	1.7×105 MPa
Poisson’s ratio	0.3
Density	2330 kg/m3
Temperature	20 °C

The sensitivity analysis of the resonance frequency $S_N$ is defined as:

$$S_N=\frac{|{\omega }^{\prime }-\omega |}{\omega }$$

(9)

where $\omega$ is the 1st resonance frequency of the accelerometer; ${\omega }^{\prime }$ is the 1st resonance frequency of the accelerometer under $\mathrm{\Delta }L$ . The procedure is similar to the one of output capacitance.

4.2. Results of Sensitivity Analysis

The results of sensitivity analysis are shown in Table 2. It is found that $L_7$ , $L_8$ , $L_9$ , $L_{10}$ , $L_{11}$ and $L_{12}$ have greater influence on the output capacitance than other parameters, and $L_7$ , $L_8$ , $L_{10}$ , $L_{11}$ and $L_{12}$ have greater influence on the 1st resonance frequency than other parameters.

Table 2. Results of sensitivity analysis.

Table 2. Results of sensitivity analysis.

Parameter	L1	L2	L3	L4	L5	L6	L6
Sc (%)	1.294	1.705	3.197	1.159	3.076	2.118	9.276
SN (%)	2.011	1.977	2.859	2.898	0.975	1.290	4.612
Parameter	L8	L9	L10	L11	L12	L13	L14
Sc (%)	14.477	3.804	4.584	4.419	4.162	2.367	1.098
SN (%)	11.401	3.172	3.913	3.121	4.166	2.339	1.901

Through the sensitivity analysis, the following conclusions can be obtained:

(1)

The six parameters that have greater influence on the output capacitance include the five parameters that have greater influence on the 1st resonance frequency, which shows a relationship between the resonance frequency and output capacitance. This can be explained by Equation (5).

(2)

The length $L_7$ and width $L_8$ of the accelerometer have the greatest influence on the performance.

(3)

The structural parameters related to proof mass also have significant influence on the performance.

(4)

The length of the suspension beams $L_{12}$ determines the stiffness of the beams, so it will influence the output capacitance and resonance frequency. However, the width $L_{11}$ and height $L_3$ of the suspension beams have a relative smaller influence on the performance of the accelerometer.

(5)

It is recommend to keep more attention on $L_7$ , $L_8$ , $L_9$ , $L_{10}$ , $L_{11}$ and $L_{12}$ in fabrication process, as they have more influence on the performance of the accelerometer.

The sensitivity of the output capacitance to fabrication variations is calculated under the condition that the percentage coefficients of all structural parameters are supposed to be 1%. It is unnecessary to know the values of percentage (or dispersion) coefficients of stochastic structural parameters in advance [15]. This means robustness can be achieved without any statistical information on the uncertainties.

5. Robust Optimization of the Accelerometer

5.4. Procedure of Robust Optimization

The procedure of the robust optimization for the accelerometer is shown in Figure 8. The robust optimization process is as follows:

(1)

Determine design variables according to the results of sensitivity analysis;

(2)

Build the solid model of the accelerometer using a 3D modeling software;

(3)

Input the solid model into a FEM software, then mesh it;

(4)

Apply constraints and loads to the FEM model, and perform FEA;

(5)

Calculate output capacitance;

(6)

Perform optimization and update design variables;

(7)

Check and evaluate the convergence criterion. If the criterion is satisfied, the process is terminated. If not so, go to the Step (2) with updated design variables.

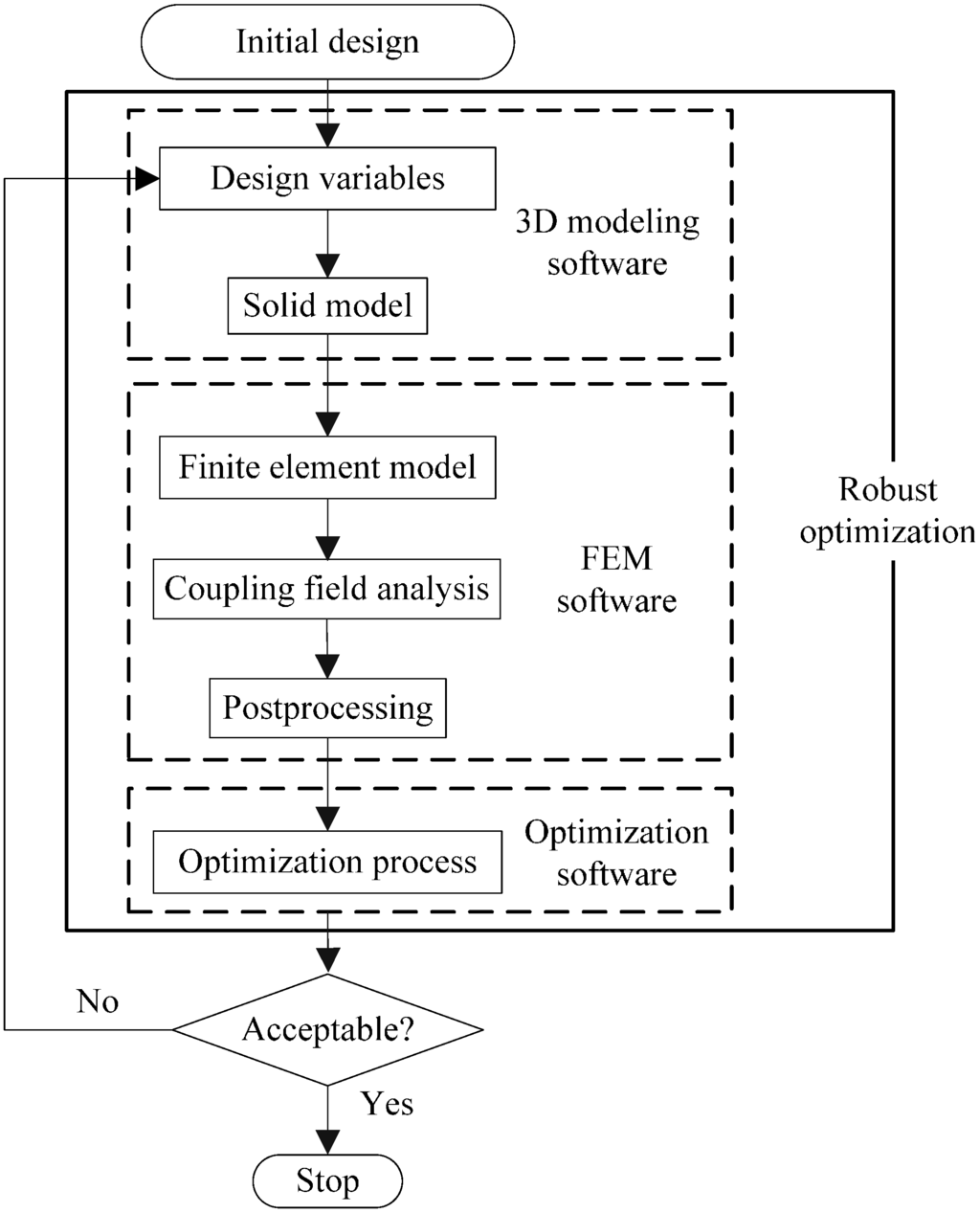
Figure 8. Procedure of robust optimization.

5.5. Results of Robust Optimization

The software iSIGHT and Multi-island Genetic Algorithm [31] are employed to solve the optimization problem. The iteration processes of the robustness constraints $h\left(X\right)$ and objective function $f(X)$ are shown in Figure 9 and Figure 10, respectively. The optimization results and comparison of initial design and robust optimization are shown in Table 3.

The optimized structure of the accelerometer is built according to Table 3. The optimized parameters are given at an accuracy of sub-nm. However, in modeling of the optimized accelerometer in a 3D modeling software, the input parameters will be reset to the default accuracy of the software automatically. We set 0.0001 mm as the default accuracy of the 3D modeling software Then a calculation of the output capacitance at different temperatures is conducted. The output capacitance at reference temperature 20 °C is set to a unitary value. The output capacitance of the optimized accelerometer at different temperatures is shown in Figure 11.

As shown in Table 3 and Figure 11, a robustness increase to temperature variations is found. The robustness constraints $h\left(X\right)$ drops by 28.2%, which means that the performance fluctuation is less than the initial structure and the robust structure has the performance against temperature variations. The sensitivity of output capacitance increases by 244.2%, and the output performance is therefore improved. The frequency difference of the 1st and 2nd resonance frequencies increases by 54.5%. We finally obtain an optimized accelerometer with high sensitivity, high temperature robustness and decoupling structure. The results show that the robust optimization can obtain not only an improved performance but also a higher yield with minimum temperature error information.

The proposed robust optimization formulation is practically applicable since no statistical information on the uncertainties is required during the optimization process in advance and can achieve robustness effectively. Considering that the temperature-induced error is one of the main error sources of the accelerometer, the robust optimization method can be valuable for practical accelerometer’s design.

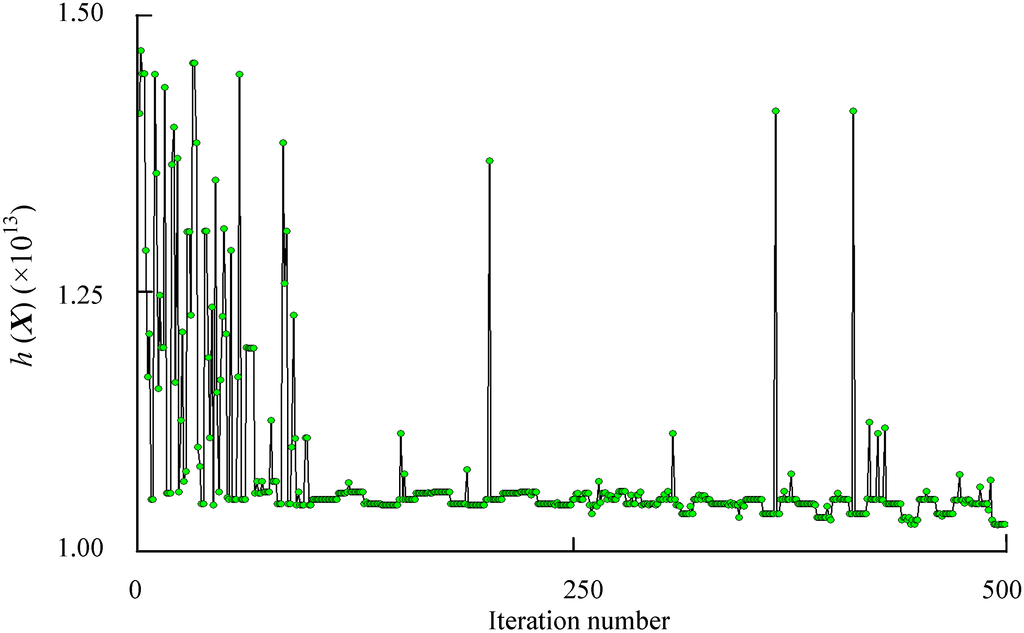
Figure 9. History of robustness constraints $h\left(X\right)$ .

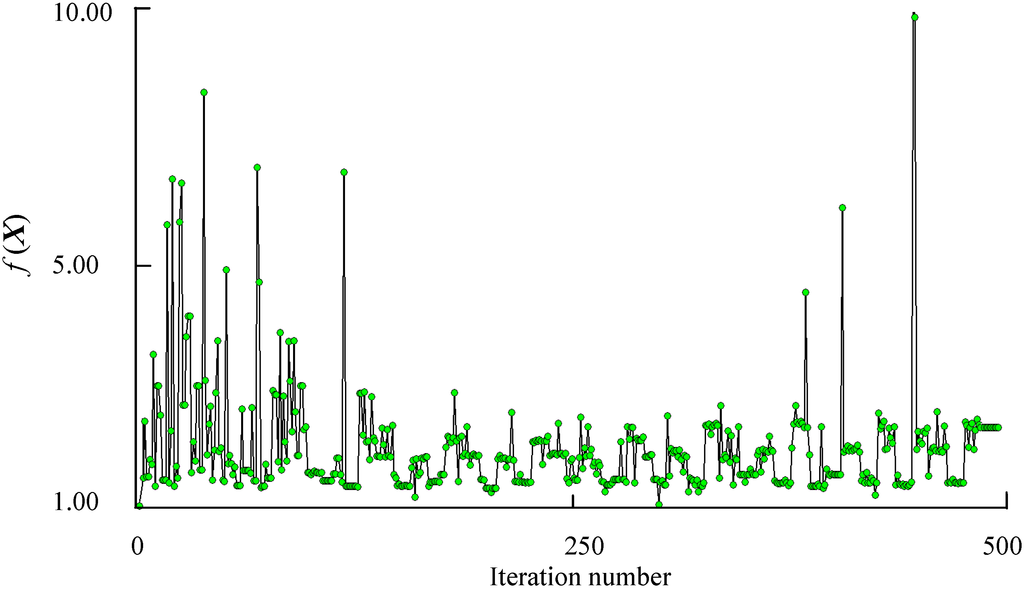
Figure 10. History of objective function $f(X)$ .

Table 3. Comparison of initial design and robust optimization.

Table 3. Comparison of initial design and robust optimization.

Description	Symbols	Initial Design	Robust Optimization
Design variables (mm)	x1	8	9.3398106
	x2	5	5.9304183
	x3	1.5	1.7980107
	x4	0.8	0.7820910
	x5	0.4	0.44435784
	x6	1.5	1.79393558
1st resonance frequency (Hz)	$\omega$	12727	16180
2nd resonance frequency (Hz)	${\omega }_2$	19184	26156
Frequency difference (Hz)	fN	6457	9976
Sensitivity of output capacitance (10−12 F/m·s−2)	K	2.5947	8.9323
Robust constraints	$h\left(X\right)$	1.4356 × 1013	1.0314 × 1013

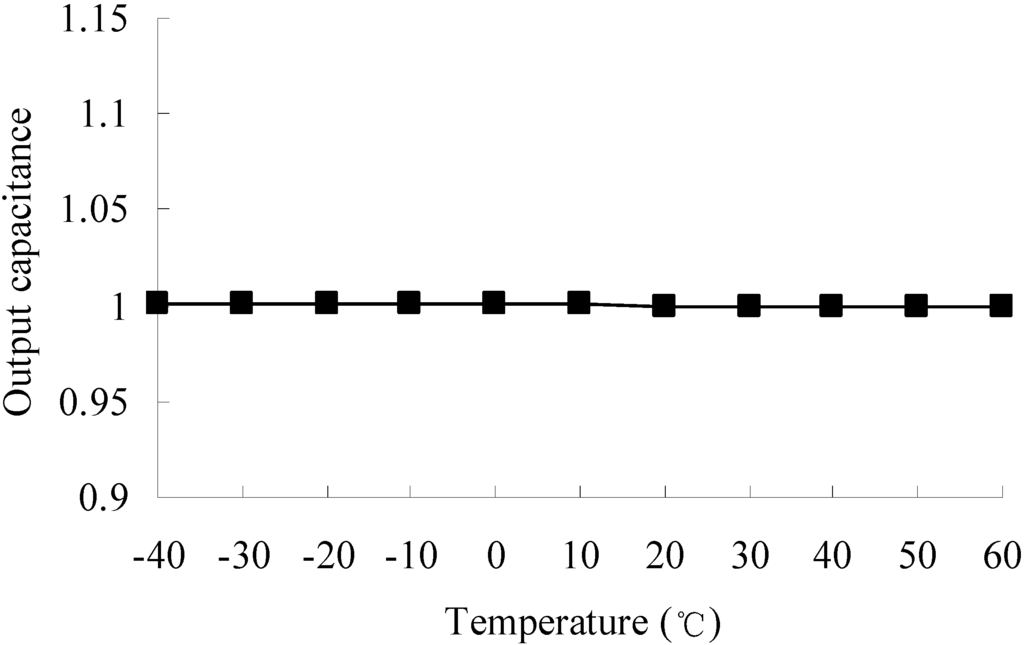
Figure 11. Output capacitance of the optimized accelerometer at different temperatures.

6. Conclusions

References

1. Yang, Z.; Li, X. Simulation and optimization on the squeeze-film damping of a novel high-g accelerometer. Microelectron. J. 2006, 37, 383–387. [Google Scholar] [CrossRef]
2. Han, J.S.; Kwak, B.M. Robust optimal design of a vibratory microgyroscope considering fabrication errors. J. Micromech. Microeng. 2001, 11, 662–671. [Google Scholar] [CrossRef]
3. Cao, H.; Li, H.; Sheng, X.; Wang, S.; Yang, B.; Huang, L. A novel temperature compensation method for a MEMS gyroscope oriented on a periphery circuit. Int. J. Adv. Robot. Syst. 2013, 10, 1–11. [Google Scholar]
4. Prikhodko, I.P.; Trusov, A.A.; Shkel, A.M. Compensation of drifts in high-Q MEMS gyroscopes using temperature self-sensing. Sens. Actuators A-Phys. 2013, 201, 517–524. [Google Scholar] [CrossRef]
5. Xu, L.; Yang, B.; Wang, S.; Li, H.; Huang, L. Research on Thermal Characteristics and on-chip Temperature-controlling for Silicon Micro-gyroscope. In Proceedings of International Conference on Information and Automation, Shenzhen, China, 6–8 June 2011.
6. Rochus, V.; Geuzaine, C. A primal/dual approach for the accurate evaluation of the electromechanical coupling in MEMS. Finite Elem. Anal. Des. 2012, 49, 19–27. [Google Scholar] [CrossRef]
7. Chang, H.; Zhang, Y.; Xie, J.; Zhou, Z.; Yuan, W. Integrated behavior simulation and verification for a MEMS vibratory gyroscope using parametric model order reduction. J. Microelectromech. Syst. 2010, 19, 282–293. [Google Scholar] [CrossRef]
8. Dai, G.; Li, M.; He, X.; Du, L.; Shao, B.; Su, W. Thermal drift analysis using a multiphysics model of bulk silicon MEMS capacitive accelerometer. Sens. Actuators A-Phys. 2011, 172, 369–378. [Google Scholar] [CrossRef]
9. Kuramochi, N.; Toshiba, K.; Mochiduki, K.; Tsuchitani, M. Application of Robust Design for the Tuning of Resistance-temperature Characteristics in Diodes. In Proceedings of International Symposium on Semiconductor Manufacturing, Santa Clara, CA, USA, 15–17 October 2007.
10. Sadeghian, H.; Doniavi, A. Analysis of quality design techniques for electrostatic actuators. J. Phys.: Conf. Ser. 2006, 34, 919–924. [Google Scholar] [CrossRef]
11. Coultate, J.K.; Fox, C.H.J.; Mcwilliam, S.; Malvern, A.R. Application of optimal and robust design methods to a MEMS accelerometer. Sens. Actuators A-Phys. 2008, 142, 88–96. [Google Scholar] [CrossRef]
12. Wu, D.H.; Tsai, Y.J.; Yen, Y.T. Robust design of quartz crystal microbalance using finite element and Taguchi method. Sens. Actuators B-Chem. 2003, 92, 337–344. [Google Scholar] [CrossRef]
13. Doltsinis, I.; Kang, Z. Robust design of structures using optimization methods. Comput. Method. Appl. M. 2004, 193, 2221–2237. [Google Scholar] [CrossRef]
14. Han, J.S.; Kwak, B.M. Robust optimization using a gradient index: MEMS applications. Struct. Multidiscip. Optim. 2004, 27, 469–478. [Google Scholar]
15. Jiang, T.; Liu, G.; Wang, A.; Jiao, J. Robust Design of a Tuning Fork Vibratory Microgyroscope Considering Microfabrication Errors. In Proceedings of the 3rd International Conference on Nano/Micro Engineered and Molecular Systems, Sanya, China, 6–9 January 2008.
16. Liu, R.; Paden, B.; Turner, K. MEMS resonators that are robust to process-induced feature width variations. J. Microelectromech. Syst. 2002, 11, 505–511. [Google Scholar] [CrossRef]
17. Kok, S.; Rahman, A.; Fauzi, M. Design Considerations of MEMS Based Piezoelectric Cantilever for Harvesting Energy. In Proceedings of IEEE Asia-Pacific Conference on Applied Electromagnetic, Melaka, Malaysia, 11–13 December 2012.
18. Martowicz, A.; Uhl, T. Reliability- and performance-based robust design optimization of MEMS structures considering technological uncertainties. Mech. Syst. Signal P. 2012, 32, 44–58. [Google Scholar] [CrossRef]
19. Li, P.; Yang, H.; Fang, Y. Robust structure design for MEMS filters in telecommunication. Chin. J. Mech. Eng. 2005, 41, 132–136. [Google Scholar] [CrossRef]
20. Corigliano, A.; Bagherinia, M.; Bruggi, M.; Mariani, S.; Lasalandra, E. Optimal design of a resonating MEMS magnetometer: A multi-physics approach. In Proceedings of the 14th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems, Wroclaw, Poland, 14–17 April 2013.
21. Bagherinia, M.; Bruggi, M.; Corigliano, A. An efficient earth magnetic field mems sensor:modeling, experimental results, and optimization. J. Microelectromech. Syst. 2014. Available online: http://doi.org/10.1109/JMEMS.2014.2357852 (accessed on 25 September 2014).
22. Zhu, Y.; Espinosa, H.D. Effect of temperature on capacitive RF MEMS switch performance—A coupled-field analysis. J. Micromech. Microeng. 2004, 14, 1270–1279. [Google Scholar] [CrossRef]
23. Liu, G.; Wang, A.; Jiang, T.; Jiao, J.; Jang, J. Effects of environmental temperature on the performance of a micromachined gyroscope. Microsyst. Technol. 2008, 14, 199–204. [Google Scholar] [CrossRef]
24. Painter, C.C.; Shkel, A.M. Structural and thermal modeling of a z-axis rate integrating gyroscope. J. Micromech. Microeng. 2003, 13, 229–237. [Google Scholar] [CrossRef]
25. Lu, X.; Li, H. Probabilistic robust design for covariance minimization of nonlinear system. Mech. Mach. Theory 2012, 52, 195–205. [Google Scholar] [CrossRef]
26. Binion, D.; Chen, X. Coupled electrothermal–mechanical analysis for MEMS via model order reduction. Finite Elem. Anal. Des. 2010, 46, 1068–1076. [Google Scholar] [CrossRef]
27. Roshanian, J.; Keshavarz, Z. Effect of variable selection on multidisciplinary design optimization: a flight vehicle example. Chin. J. Aeronaut. 2007, 20, 86–96. [Google Scholar] [CrossRef]
28. Breierova, L.; Choudhari, M. An introduction to sensitivity analysis. Massachusetts Institute of Technology: Cambridge, MA, USA, 2001. Available online: http://ocw.mit.edu/courses/sloan-school-of-management/15-988-system-dynamics-self-study-fall-1998-spring-1999/readings/sensitivityanalysis.pdf (accessed on 15 March 2015).
29. Doltsinis, I.; Kang, Z.; Cheng, G. Robust design of non-linear structures using optimization methods. Comput. Method. Appl. M. 2005, 194, 1779–1795. [Google Scholar] [CrossRef]
30. Allen, M.S.; Massad, J.E.; Field, R.V.; Dyck, C.W. Input and design optimization under uncertainty to minimize the impact velocity of an electrostatically actuated MEMS switch. J. Vib. Acoust. 2008, 130, 021009.1–021009.9. [Google Scholar] [CrossRef]
31. Su, R.; Wang, X.; Gui, L.; Fan, Z. Multi-objective topology and sizing optimization of truss structures based on adaptive multi-island search strategy. Struct. Multidiscip. Optim. 2011, 43, 275–286. [Google Scholar] [CrossRef]