Abstract
The present work has developed a methodology for studying natural ventilation in Mediterranean greenhouses by means of sonic anemometry. In addition, specific calculation programmes have been designed to enable processing and analysis of the data recorded during the experiments. Sonic anemometry allows us to study the direction of the airflow at all the greenhouse vents. Knowing through which vents the air enters and leaves the greenhouse enables us to establish the airflow pattern of the greenhouse under natural ventilation conditions. In the greenhouse analysed in this work for Poniente wind (from the southwest), a roof vent designed to open towards the North (leeward) could allow a positive interaction between the wind and stack effects, improving the ventilation capacity of the greenhouse. The cooling effect produced by the mass of turbulent air oscillating between inside and outside the greenhouse at the side vents was limited to 2% (for high wind speed, uo ≥ 4 m s−1) reaching 36.3% when wind speed was lower (uo = 2 m s−1).1. Introduction
Natural ventilation is the most common system used for greenhouse cooling and constitutes a key function in greenhouse climate control, being a major factor in their energy and mass balances, and hence in the control of crop growth and development [1,2]. Monitoring and control of the greenhouse environment play a decisive role in greenhouse production processes [3]. In order to optimise the design and operation of natural ventilation systems, one must first determine and understand, both qualitatively and quantitatively, the natural ventilation mechanisms.
The main driving forces of ventilation for a greenhouse equipped with both roof and side openings are caused by a combination of pressure differences induced by the following effects [4,5]: (1) the static wind effect due to the mean component of the wind velocity, which induces pressure differences (side wall effect) between the side and the roof openings [6] and pressure differences between the windward and the leeward parts of the greenhouse [1]; (2) the buoyancy forces (also called stack or chimney effect) generating a vertical distribution of pressures between the side and roof openings [7]; and (3) the turbulent effect of the wind, generated by pressure fluctuations of the wind velocity along and across the greenhouse openings [1,5].
The earliest studies on the circulation of air in greenhouses date back to the mid-20th century [8]. Since then, numerous researchers have shown interest in studying and understanding natural ventilation in greenhouses. Many different methods have been used for this purpose: scale models [9–11], tracer gas methods [2,4,12,13], CFD (Computational Fluid Dynamics) simulations [12,14–18] and direct in situ measurements using a variety of sensors [1,3,5,19–21].
Direct determination of the airflow through the openings of the greenhouse using sonic anemometry is the only experimental technique that allow the prediction of greenhouse air exchange rates as well as the characterisation of its components: a steady effect resulting from the combination of both mean wind-related and stack effects and a turbulent effect linked to wind speed fluctuations [1]. The relative importance of the roof and side opening areas is crucial for Mediterranean greenhouses which are characterised by a limited number of spans, small covered area, and continuous vents [4].
However, most of the studies using this technique were carried out for greenhouses equipped with only roof openings [1,20,21] or side vents [22] and there has been a lack of experimental data of ventilation airflow obtained in greenhouses equipped with both roof and side screened openings [23]. Thus, the objectives of this study were to determine the ventilation rate, air velocity and turbulence characteristics in a three-span greenhouse with continuous screened side and roof vents under natural ventilation conditions. The present work differs from previous studies in that it uses sonic anemometry to determine the flow patterns in a greenhouse with both roof and side openings and analyses the contribution of turbulent flow to greenhouse cooling.
2. Experimental Setup
2.1. Site and Greenhouse Description
The experimental work took place in the 24 × 20 m2 western half of a 1,080 m2 three-span greenhouse located at the agricultural research farm of the University of Almería (36°51′N, 2°16′W). The experimental greenhouse was physically divided into two similar sectors by a polyethylene sheet fixed to a stainless steel structure, as this allows us to study the natural ventilation of each half separately for other research projects (Figure 1).
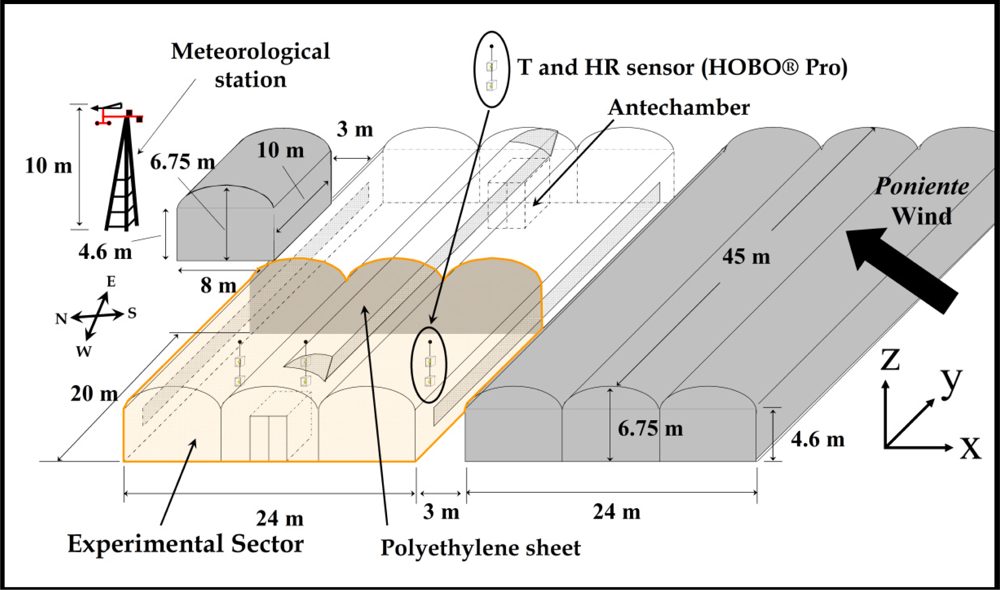
During the experiments both the side (1.05 × 17.5 m2) and roof vents (0.97 × 17.5 m2) were opened, giving an overall ventilation surface SV that represents 11.2% of the total greenhouse surface area SA (SV/SA = 0.112).
In order to prevent insects from entering the greenhouse, insect-proof screens were placed on all vents. The characteristics of the screens are as follows: 13 × 30 threads cm−2 (0.39 porosity; 164.6 μm pore width; 593.3 μm pore height; 165.5 μm thread diameter). The greenhouse contained a tomato crop (Solanum lycopersicum L. cv. Salomee) with an average height of approximately 1.38 m and a leaf area index (m2 leaf per m2 ground) of about 0.89.
2.2. Experimental and Instrumentation
Outside climatic conditions were recorded (frequency 0.5 Hz) by a nearby meteorological station placed at a height of 10 m (Figure 1). The meteorological station included a BUTRON II measurement box (Hortimax S.L., Almería, Spain) equipped with a Pt1000 temperature sensor and a capacitive humidity sensor (temperature measurement range −25 °C to 75 °C; accuracy ±0.01 °C; humidity range 0% to 100%; accuracy ±3%). Outside wind speed was measured with a Meteostation II (Hortimax S.L.), incorporating a cup anemometer (measurement range 0 to 40 m s−1; accuracy ±5%). Wind direction was measured with a vane (accuracy ±5°). Solar radiation was measured using a Kipp Solari (Hortimax S.L.) sensor (measurement range 0 to 2,000 W m−2; accuracy ±20 W m−2).
Temperature and humidity inside the greenhouse were measured (frequency 0.5 Hz) using six autonomous dataloggers (HOBO Pro Temp-HR U23-001, Onset Computer Corp., Bourne, MA, USA), protected against direct solar radiation with a passive solar radiation open shield. The dataloggers were placed in a vertical profile under the ridge of the three greenhouse spans at heights of 1 and 2 m (Figure 1). These fixed devices measure a temperature range of −40 °C to 70 °C (accuracy ±0.18 °C) and relative humidity range of 0% to 100% (accuracy of ±2.5%).
Measurement tests were carried out under prevailing Poniente southwest (SW) wind, one of the most common in the province of Almería. The outside climatic conditions remained relatively stable for the duraction of the ten measurement tests (Table 1).

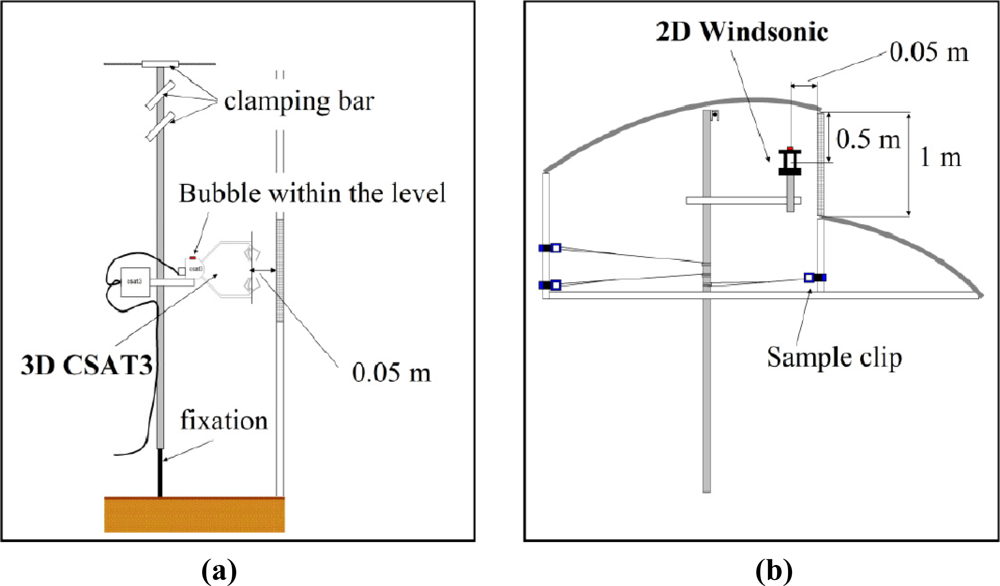
The three components of air velocity and temperature at the side vents were measured with two 3D sonic anemometers (mod. CSAT3, Campbell Scientific Spain S.L., Barcelona, Spain; accuracy ±0.04 m s−1 and ±0.026 °C). Each side vent was divided into seven equal vertical spaces and three horizontal ones (Figure 2). Air velocity was measured at the centre of each of the resulting 21 spaces, moving the trisonic anemometers from one point to another [Figure 3(a)]. At each point the sonic anemometer measured at a sampling rate of 10 Hz for 3 min.
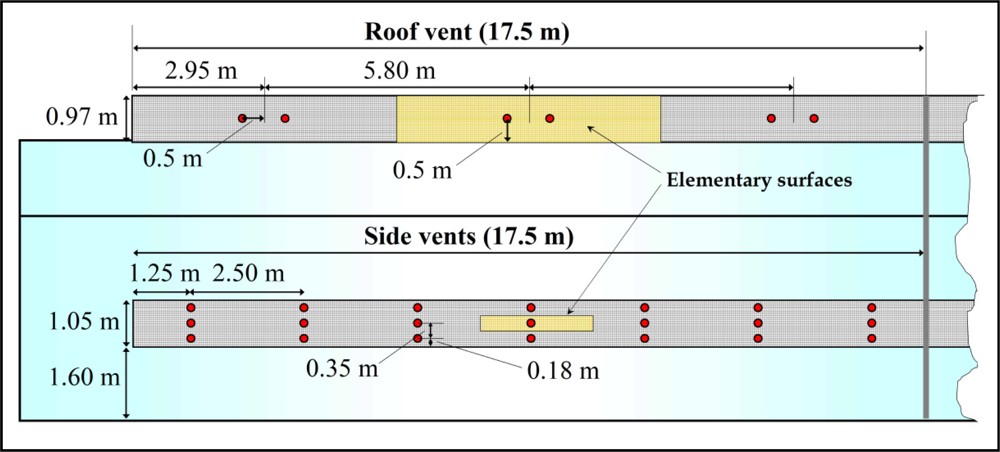
The mean surface corresponding to each measurement point at side vents was 0.9 m2. This value is less than those used to calculate the ventilation flux by other authors: through the only roof vent of a tunnel greenhouse (2.6 m2 per point) [19], in a mono-span greenhouse with two side vent openings (1.1 m2 per point) [22], in a four-span greenhouse with three roof vents (8.5 m2 per point) [20] and in a five-span Almería-type greenhouse (2.1 m2 per point) [23]. The mean surface corresponding to each equal surface in the roof vent is 5.7 m2.
As it proved difficult to displace the anemometers along the roof vent, this vent was divided into three equal surfaces and the air velocity measurements were taken continuously at the centre of each surface (Figure 2) by six 2D sonic anemometers (mod. Windsonic, Gill Instrument LTD, Lymington, Hampshire, UK; accuracy 2%) fixed to the greenhouse structure [Figure 3(b)]. Data from all sonic anemometers were recorded by two CR3000 Microloggers (Campbell Scientific Spain S.L.), with a data registration frequency of 10 Hz [21] and 1 Hz, respectively, for the 3D and 2D sonic anemometers. One 3D and three 2D sonic anemometers were connected to each micrologger.
Two 3D sonic anemometers were used to determine the air velocity at the side vents [Figure 3(a)], one per vent, and taking measurements at each point over 3 min. This time period is a compromise between a shorter one that may reduce accuracy and a longer one that may increase the overall difference with regard to outside microclimate parameters [23]. Six 2D sonic anemometers were used to measure the air velocity at the roof vent [Figure 3(b)], taking continuous measurements.
2.3. Analyses
Ultrasonic anemometers are able to determine the air velocity vector and the sonic temperature. They are instruments suitable, widely used devices to evaluate turbulent parameters such as mean air velocity, turbulence intensity and integral length scale. In this work we have calculated and studied the different parameters described below.
2.3.1. Mean and Turbulent Air Velocity
For air velocity u [m s−1] and its components (ux, uy and uz; Figure 1), the mean air velocity measured over a period Δt is [24]:
We have also calculated the average value of the two-dimensional resultant of air velocity in the XY plane (l) and in the XZ plane (v), u(t) is the instantaneous air velocity, which can be expressed as the sum of time-mean value u and a fluctuating component u′(t) [24]:
The variance of an air velocity over a period of time Δt is defined as [24]:
Turbulence intensity i is standard deviation σ divided by mean local velocity u, so [24]:
2.3.2. Turbulence Macroscale
The normalized autocorrelation function R(t) is the correlation between air velocities at a fixed position at two different instants, t and t + δt [25,26]:
As opposed to integrating R(t) to infinity, it can only be integrated to the first zero crossing (t0) to obtain tint, the integral time scale [25]:
2.3.3. Discrete Energy Spectrum
According to turbulence theory, turbulent flow can be regarded as the superposition of eddies of different scales [29]. The spectrum of energy density, E(f) [m2 s−1], gives the relationship between the frequency of a signal f and the energy of the corresponding eddies. The discrete energy spectrum E(f) is calculated by [29]:
The turbulent flow consists of a mass of eddies of different scales. The average negative slope (β value) of the logarithmic power spectrum curves is the main parameter used in the analysis of airflow. The β value can reflect the energy distribution of eddies of different scales. Its relationship with E(f) can be expressed as [24]:
A mechanically generated airflow is characterized by energy density spectra of low slope [29]. The slope of the energy spectrum for airflows generated naturally at the ventilation surfaces usually corresponds to an isotropic distribution of turbulence, β = 5/3 [30].
Total turbulence kinetic energy k [m2 s−2] can be calculated by the following expression [25]:
2.3.4. Anemometric Measurement of Volumetric Flow Rate
The mean and turbulent volumetric flow rates through the greenhouse were calculated by multiplying the scaled time-mean component uj and fluctuating component u′, respectively, of the air velocity perpendicular to the plane of the opening to the elementary surface SVj in order to describe the air circulation through the opening [19]:
With only two possible sampling positions at any one time in lateral vents, a difficulty arises from how to deal with changing external conditions over the time needed to take measurements at the different positions in the lateral vents of each sector (Figure 2). This problem can be overcome by selecting measurements for a fixed external wind direction and correcting the air velocities measured by the 3D sonic anemometers at each position j at the lateral vents uj(t) by scaling with the wind speed [23]. We have calculated a scaled air velocity in the opening, u*j(t), taking only wind effect into account, multiplying measured values of air velocity uj(t) at minute t at each point j in the greenhouse openings by the ratio between the average wind speed for the overall test period (several hours) and the instantaneous values uo(t) (average for each minute t):
The tests took 2–3 hours on average, generating a considerable amount of data. Two programmes were designed to process the air velocity data using MATLAB 7.0 [31], one for data obtained by the 3D sonic anemometers (frequency 10 Hz) and the other for data from the 2D sonic anemometers (frequency 1 Hz). These programmes allow us to analyse a complete experiment in a matter of a few minutes, while the first attempts at analysis using spreadsheets required hours of work.
2.3.5. Estimation of the Sensible Energy Flux by the Eddy Correlation Method
Local estimations of mean and turbulent flux of sensible energy across a vent opening can be obtained using eddy correlation techniques [26]. Considering the transport of heat with a velocity u normal to the vent opening, then an elemental volume of air will transport heat at a rate ρCpuT across unit surface of the opening. Now using Reynolds formulation we may write the classic formula:
Thus, the flux is composed of a mean normal flow of air (ρCpūT̄) and a part due to eddying motion ( ) proportional to the covariance between T and u denoted by . Using this approach with 3D sonic anemometers, the mean and turbulent heat fluxes can be deduced [Equation (15)].
The sensible energy flux Q exchanged between the greenhouse air and outside can be expressed by different relations as follows. Assuming the air in the greenhouse mixes well, the sensible energy flux Q can by given as a function of the air exchange rate [1,5]:
Using the normalized form described by Boulard et al. [1] and calculating the air circulation through the opening for each elementary surface SVj we can calculate the flux of sensible energy as:
From direct measurements at the vent opening we can then obtain a mean value of the total sensible heat exchange in its normalized form as [1]:
3. Results and Discussion
The methodology followed permits in-depth study of the airflow characteristics at the greenhouse vents in order to determine the ventilation airflow pattern, to estimate the air exchange rate for each experiment and to analyse the turbulence characteristics.
3.1. Airflow Characteristics
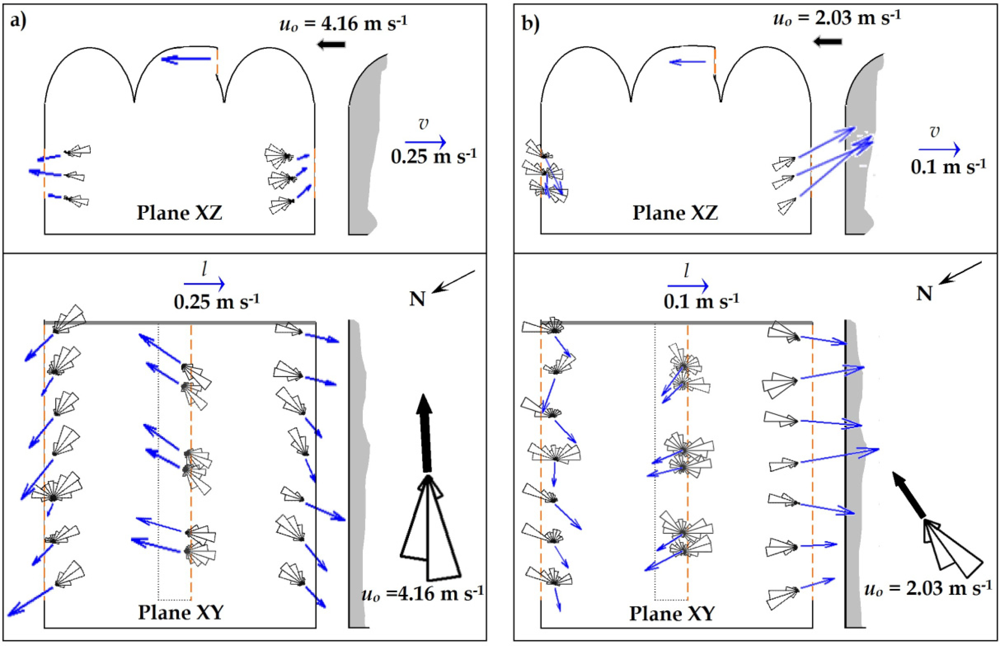
Given the particular location of the greenhouse and the placing of the vents, when natural ventilation occurs under prevailing southwesterly Poniente winds, the wind and thermal effects are contrary. The wind causes air to enter through the windward roof vent and to leave through the leeward side vent (the windward side vent is obstructed by another greenhouse). The thermal effect, on the other hand, causes warm air to rise and leave through the roof vent, favouring the entrance of air through the side vents. The polar histograms in Figure 4(b) illustrate a similar distribution of air at the roof vent in the leeward and windward direction. This illustrate the entrance and exit of air through the roof vent, providing evidence of the negative interaction of the wind and thermal effects, although the wind effect predominates, as the direction of the mean vector of velocity indicates [Figure 4(b)].
The ventilation rate of the greenhouse is affected by the buoyancy effect generated by the difference in temperature between the inside and outside air ΔTio. Several authors have pointed out that the buoyancy effect is particularly relevant for winds of less than 1.8 m s−1 [13], 1.5 m s−1 [5] or 1 m s−1 [11]. When a vertical side wall opening was added to the roof window, the temperature effect was enhanced by the so called chimney effect, linked to with the vertical distance between the two openings, in such a way that it becomes negligible only for an external wind speed of over 4 m s−1 [32]. For greenhouses with both side and roof vents the thermal effect is considered to have a major bearing when the ratio uo/ΔTio0.5 is less than 1 [4] or less than 0.3 [33].
In experiments 1, 2, and 3, when uo/ΔTio0.5 was 1.5 or greater, very little air was seen to exit through the roof vent, which is a clear indication of the predominance of the wind effect over the thermal one, with air leaving through the side vents quite consistently [Figure 4(a)].
The wind can either assist the buoyancy force or oppose the airflow [34]. For opposing winds, we can observe the alternation of positive and negative flows (entrance and exit of air, respectively) at the roof vent [Figure 4(b)]. A certain discrepancy between wind direction and the direction of airflow entering the greenhouse through the roof vent was observed in some experiments. These differences may be due to the location of the meteorological station, which recorded the characteristics of the wind once it had passed through the experimental greenhouse.
In experiment 4, with a uo/ΔTio0.5 ratio of under 1, the combination of opposing wind and thermal effects led to less uniform airflow at the vents, with alternating positive (entrance) and negative (exit) airflow at the roof vent [Figure 4(b)].
The use of sonic anemometry has allowed us to establish the ventilation pattern under different wind conditions. Under moderate-strong Poniente winds (uo ≥ 4 m s−1), the greenhouse is mainly ventilated by the wind effect, with air entering through the roof vent and leaving through both side vents. The combination of thermal and wind effects can lead to air leaving the greenhouse through the roof vent and/or entering through the side ones, although these flows which run contrary to the overall pattern occur infrequently.
Under weak Poniente winds (uo < 4 m s−1), there is a clear interaction between the thermal and wind effects at all three vents: at the roof vent air enters due to the wind effect and exits due to the stack effect, while at both the windward and leeward side vents air was also seen to enter and exit, entering in the main at the leeward side and leaving through the windward one. The airflow pattern observed is conditioned by the fact that on the windward side the greenhouse gives onto another greenhouse, without which the ventilation pattern would be completely different.
Under prevailing Poniente (SW) wind, in the experimental greenhouse a roof vent designed to open leeward (towards the North) allowed a positive interaction between the wind and stack effects, improving the ventilation capacity of the greenhouse. This result confirms that in certain circumstances (namely the obstructed windward side vent) a leeward roof vent can improve ventilation. Using CFD simulations Molina-Aiz [35] predicted a greater ventilation flux in an Almería-type greenhouse with two side openings, if the roof vents were opened towards the leeward side. Using the same method, Lee and Short [36] also observed better ventilation when the four roof vents opened towards the leeward side in a four and one-half span commercial greenhouse.
3.2. Evaluation of the Mean and Turbulent Ventilation Flows
By applying Equations (12–14), the volumetric flow rate at the three vents has been determined (leeward side vent GLS, windward side GWS and roof vent GWR), calculating the mean ventilation rate for the greenhouse GM. We have also calculated the air exchange rate from the greenhouse volume (2681.7 m3) and the mean flow (Table 2).

The accuracy of the mean values of air exchange measured can be assessed by totalling the entrance and exit flows measured at all vents. To verify to what extent the Law of Mass Conservation is met in the greenhouse [1,37], the error in the calculation of the ventilation flows has been estimated as follows:
The mean error in calculation of the airflows, EG, obtained was 16.3%. Following a similar methodology in an Almería-type greenhouse with two side and two roof vents the values of EG were between 3.0% and 37.0% [23]. Other researchers obtained errors of 2.2% and 2.6% [1] and 31.6% [37] in a multi-span greenhouse with only one roof vent.
The accuracy of this method of calculation of airflow depends mainly on the stability of the wind conditions (intensity and direction) and the influence of the thermal effect on greenhouse ventilation. Variable wind conditions or ones in which the wind or thermal effect does not clearly predominate may lead to less accuracy. The maximum error in calculating volumetric flow rate in these experiments occurred when the uo/ΔTio0.5 ratio was close to 1.5. At such a ratio, the interaction between the wind and thermal effects produces instability in the direction of the airflow in the openings and can impair the accuracy of the velocity measurements recorded with the anemometers.
3.3. Evaluation of the Mean and Turbulent Sensible Energy Flows through the Side Vents
The cooling effect produced by the mass of turbulent air oscillating between inside and outside the greenhouse at the side vent is limited to 2% for the three first experiments (Table 3). However turbulence produces about 60% of the total airflow through the greenhouse opening (Table 2). This indicates that only a small proportion of the fluctuating airflow at the side vents mixed well with the bulk of air in the greenhouse. Usually, at the side of the greenhouse turbulence causes warm air to exit through the openings and mix with the cooler outside air. However, as the mean airflow heats the side zone of the greenhouse, the air that comes out due to turbulence has a much higher temperature than in inside the greenhouse. The heat loss through the side openings due to turbulence is therefore small.

Molina-Aiz [35] also measured the sensible heat flux through the vent openings (two side openings and two roof vents) of an Almería-type greenhouse. The turbulent volumetric airflow accounted for between 31% and 45% of the overall flow, whereas the turbulent flux contributed 3–14% of the total sensible heat transfer.
In the last experiment carried out, the cooling produced by the turbulent airflow accounted for 36.3% of the overall cooling effect at the side vents (Table 3). In this case, when wind speed was lower (uo = 2.03 m s−1), air entered the greenhouse through the leeward side vent [Figure 4(b)], which does not therefore contribute to the cooling of the greenhouse (Table 3). Furthermore, the air leaving the greenhouse due to turbulence has a much lower temperature than when inside of the greenhouse, increasing the covariance and the sensible heat transfer due to eddying motion ( ). The contribution of the turbulent flux measured in this case is similar to that reported in the roof vent of a bi-span greenhouse in France: 42% [26] and 23% and 45% [1].
The total sensible heat exchange in its non-dimensional form varied from 0.017 to 0.051 (Table 3), which is similar to the values of between 0.015 and 0.028 reported in an Almería-type greenhouse, equipped with insect-proof screens [35], and lower than those estimated in a bi-span greenhouse without nets: 0.06 [26] and 0.10 and 0.13 [1].
3.4. Turbulence Flow Characteristics
3.4.1. Turbulence Intensity Levels
The turbulence intensity i at the windward side opening was similar for the four experiments, possibly due to the effect of the greenhouse close to this opening, which may impede the airflow through it. The increase in turbulence intensity caused by the outside obstacles was also observed in an Almería-type greenhouse with two side and two roof vents [23] blocked by a publicity sign 1.6 m away from a side vent.
The average levels of turbulence intensity observed at the vents (Table 4) are in some cases higher than those observed inside a mesh-covered greenhouse (83% porosity) in which i varied from 0.2–0.8 for uo < 0.5 m s−1 [38]. The turbulence intensity at the vents of a multi-span greenhouse with two side vents totally free of obstacles was greater at the windward vent than at the leeward one [22].

3.4.2. Energy Levels and Measures of Turbulence Scales
The mean values of turbulence kinetic energy k (Table 4) are greater at the roof vent (windward), where the wind has a direct impact, transmitting much of its energy to the airflow entering the greenhouse. In a tunnel greenhouse the turbulence kinetic energy was also observed to be greater on the windward than on the leeward side [26]. The presence of an obstacle at the windward side vent brings about a drastic reduction in the energy dissipated by the airflow, and as a result in its capacity to mix and transport heat and water vapour [39].
The macroscale represents the dimension of the most energetic eddies that have a significant effect on the mixture of air and therefore on ventilation [40]. The importance of studying the macroscale lies in the fact that it may be related to the geometry of the vents [40] and to the location of the vents with respect to the wind and to adjacent buildings. This parameter is slightly lower for the blocked windward side vent (Li = 0.44 ± 0.28 m) and the roof vent (Li = 0.44 ± 0.40 m) than for the leeward side vents free of obstacles (Li = 0.59 ± 0.40 m). These values are similar to those measured in the openings of an Almería-type greenhouse with insect-proof screens, between Li = 0.25 m and 0.99 m [35].
The tight-mesh insect-proof screens reduced the turbulence level and increased the spectral decay rate, which implies the generation of smaller scales of flow, since small turbulent eddies are less energetic and the dissipation of energy in these scales is faster than in large ones [41]. Small eddies also have a much lower capacity to transport heat and water vapour out of the greenhouse than large-scale ones [41]. An important reduction of the macroscale was observed in our experimental greenhouse in the simultaneous measurement of air velocity with the 3D anemometers at several points outside and inside the greenhouse at the same distance from the screen [31].
3.4.3. Discrete Energy Spectrum
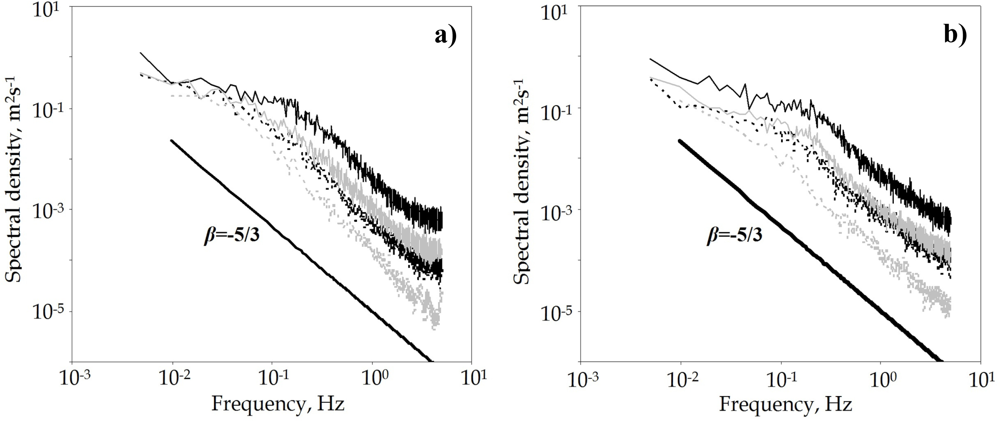
Breaking down the time series into components of frequency allows us to observe how eddies of different scales contribute to overall turbulence (Figure 5). The energy density spectra shown in the figures of this section have been obtained by calculating the average spectrum from all those obtained at the 21 points at the side vents.
 ), 2 (
), 2 (
 ), 3 (
), 3 (
 ) and 4 (
) and 4 (
 ).
).
The level of the spectrum allows us to determine under which conditions the airflow at the side vents is most turbulent and energetic: the spectrum was higher when the wind speed was greater. The most energetic eddies are those which have the most significant effect on the mixture of air and therefore on ventilation [40].
The different values of the slope of the spectrum βx for the component perpendicular to the ventilation surface (Table 5) may be due to several reasons: the geometry of the vent [40,42], the use of insect-proof screens [39] or the influence of buoyancy [43].

In experiments 1, 2 and 3, when the wind speed was moderate to high and the thermal effect ran slightly contrary to the main direction of airflow generated by the wind effect, the air left the greenhouse through the leeward side vent and through the windward one (with an obstacle). In both cases the value of the slope of the spectrum was βx < 5/3. In experiment 4, when the wind speed was low and the thermal effect had a greater influence on airflow, the air entered and exited simultaneously (observing a high fluctuation in airflow direction) through the leeward side vent, βx >> 5/3.
4. Conclusions
Using sonic anemometry techniques it has proved possible to identify the vents through which air enters and exits the greenhouse, and therefore to establish natural ventilation flow patterns. Opening the roof vent to the windward side causes a combination of contrary wind and thermal effects in natural ventilation of greenhouses. As outside air enters it circulates downwards, contrary to natural convection due to the thermal effect.
Under certain circumstances, such as an obstructed windward side vent, a leeward roof vent can improve ventilation, allowing a positive interaction between the wind and stack effects. The contribution of turbulence to the overall sensible heat transfer between inside and outside the greenhouse through the side vents increased from 2% to 36.3% when the wind speed decreased from 4 to 2 m s−1.
The methodology presented in this work has allowed us to quantify accurately the greenhouse ventilation rate under varying conditions of outside wind. It has also allowed us to characterise the turbulence of the airflow at the vents, providing useful information for future validations of simulations based on CFD. The programmes designed in MATLAB 7.0 allow a 69% reduction in the memory capacity required to store the data generated during analysis.
| Notation | |
|---|---|
| Cd | discharge coefficient |
| Cp | air thermal capacity [J kg−1 K−1] |
| Cw | wind effect coefficient |
| E(f) | spectral density [m2 s−1] |
| EG | error in the calculation of volumetric flow rate [%] |
| f | frequency [Hz] |
| EQ | wind-related ventilation efficiency coefficient deduced from heat flux measurement |
| G | ventilation volumetric flow rate [m3 s−1] |
| G′ | turbulent component of the ventilation volumetric flow rate [m3·s−1] |
| HR | relative humidity [%] |
| i | turbulence intensity |
| k | turbulence kinetic energy [m2 s−2] |
| l | two-dimensional horizontal resultant of air velocity in XY plane [m s−1] |
| Li | integral length scale [m] |
| N | number of measurement points in vents |
| Q | sensible energy flux exchanged between the greenhouse air and outside [W] |
| R | ventilation rate for greenhouse [h−1] |
| R(t) | normalized autocorrelation function [m2 s−2] |
| Rg | solar radiation [W m−2] |
| SA | greenhouse area [m2] |
| SV | surface area of the vent openings [m2] |
| T | temperature [°C] |
| T′ | fluctuating air temperature [°C] |
| t | time [s] |
| tint | integral time scale [s] |
| u | air velocity [m s−1] |
| ūj | time-mean air velocity [m s−1] |
| U′ | fluctuating component of air velocity [m s−1] |
| uo | wind speed [m s−1] |
| X(f) | Fast Fourier Transform (FFT) |
| X(t) | sample data |
| X*(f) | conjugate complex number of X |
| Greek Letters | |
|---|---|
| Δ | difference |
| β | power spectrum exponent |
| δt | time [s] |
| ɛ | turbulence energy dissipation rate [m2 s−3] |
| θ | wind direction [°] |
| λ | microscale [m] |
| σ | standard deviation |
| Subscripts | |
|---|---|
| i | inside |
| j | measurement point |
| L | leeward |
| M | average value |
| o | outside |
| R | roof vent |
| S | side vent |
| W | windward |
| x | longitudinal component |
| y | transversal component |
| z | vertical component |
Acknowledgments
This work has been financed by the Junta de Andalucía and the Ministerio de Ciencia e Innovación by means of the research grants P09-AGR-4593 and AGL2010-22284-C03-01, respectively.
References
- Boulard, T; Meneses, JF; Mermier, M; Papadakis, G. The mechanisms involved in the natural ventilation of greenhouses. Agric. For. Meteorol 1996, 79, 61–77. [Google Scholar]
- Kittas, C; Boulard, T; Mermier, M; Papadakis, G. Wind induced air exchange rates in a greenhouse tunnel with continuous side openings. J. Agric. Eng. Res 1996, 65, 37–49. [Google Scholar]
- Pawlowski, A; Guzman, JL; Rodríguez, F; Berenguel, M; Sánchez, J; Dormido, S. Simulation of greenhouse climate monitoring and control with wireless sensor network and event-based control. Sensors 2009, 9, 232–252. [Google Scholar]
- Kittas, C; Boulard, T; Papadakis, G. Natural ventilation of a greenhouse with ridge and side openings: Sensitivity to temperature and wind effects. Trans. ASAE 1997, 40, 415–425. [Google Scholar]
- Boulard, T; Baille, A. Modelling of air exchange rate in a greenhouse equipped with continuous roof vents. J. Agric. Eng. Res 1995, 61, 37–48. [Google Scholar]
- Bruce, JM. Natural convection through openings and its applications to cattle building ventilation. J. Agric. Eng. Res 1978, 23, 151–167. [Google Scholar]
- Bruce, JM. Ventilation of a model livestock building by thermal buoyancy. Trans. ASAE 1982, 25, 1724–1726. [Google Scholar]
- Morris, LG; Neale, FE. The Infra-Red Carbon Dioxide Gas Analyser and Its Use in Glasshouse Research; Technical Memorandum, number 99; National Institute of Agricultural Engineering: Silsoe, UK, 1954. [Google Scholar]
- Sase, S; Takakura, T; Nara, N. Wind tunnel testing on airflow and temperature distribution of a naturally ventilated greenhouse. Acta Hortic 1984, 148, 329–336. [Google Scholar]
- Lee, IB; Sase, S; Okushima, L; Ikeguchi, A; Choi, K; Yun, J. A wind tunnel study of natural ventilation for multi-span greenhouse scale models using two-dimensional particle image velocimetry (PIV). Trans. ASAE 2003, 46, 763–772. [Google Scholar]
- Sase, S; Takakura, T; Nara, M. Wind tunnel testing on airflow and temperature distribution of a naturally ventilated greenhouse. Acta Hortic 1984, 148, 329–336. [Google Scholar]
- Boulard, T; Feuilloley, P; Kittas, C. Natural ventilation performance of six greenhouse and tunnel types. J. Agric. Eng. Res 1997, 67, 249–266. [Google Scholar]
- Papadakis, G; Mermier, M; Meneses, JF; Boulard, T. Measurement and analysis of air exchange rates in a greenhouse with continuous roof and side openings. J. Agric. Eng. Res 1996, 63, 219–228. [Google Scholar]
- Okushima, L; Sase, S; Nara, M. A support system for natural ventilation design of greenhouses based on computacional aerodynamics. Acta Hortic 1989, 284, 129–136. [Google Scholar]
- Kacira, M. Modeling Dynamic Air Exchanges for Naturally Ventilated Sawtooth Greenhouse Designs. Ph.D. Dissertation,. The Ohio State University, Wooster, OH, USA, 1996. [Google Scholar]
- Mistriotis, A; Arcidiacono, C; Picudo, P; Bot, GPA; Scarascia-Mugnozza, G. Computacional analysis of ventilation in greenhouses at zero- and low-wind-speeds. Agric. For. Meteorol 1997, 88, 121–135. [Google Scholar]
- Boulard, T; Haxaire, R; Lamrani, MA; Roy, JC; Jaffrin, A. Characterization and modelling of the air fluxes induced by natural ventilation in a greenhouse. J. Agric. Eng. Res 1999, 74, 135–144. [Google Scholar]
- Molina-Aiz, FD; Fatnassi, H; Boulard, T; Roy, JC; Valera, DL. Comparison of finite element and finite volume methods for simulation of natural ventilation in greenhouses. Comput. Electron. Agric 2010, 72, 69–86. [Google Scholar]
- Boulard, T; Kittas, C; Papadakis, G; Mermier, M. Pressure field and airflow at the opening of a naturally ventilated greenhouse. J. Agric. Eng. Res 1998, 71, 93–102. [Google Scholar]
- Teitel, T; Tanny, J; Ben-Yakir, D; Barak, M. Airflow patterns through roof openings of a naturally ventilated greenhouse and their effect on insect penetration. Biosyst. Eng 2005, 92, 341–353. [Google Scholar]
- Shilo, E; Teitel, M; Mahrer, Y; Boulard, T. Air-flow patterns and heat fluxes in roof-ventilated multi-span greenhouse with insect-proof screens. Agric. For. Meteorol 2004, 122, 3–20. [Google Scholar]
- Teitel, M; Liran, O; Tanny, J; Barak, M. Wind driven ventilation of a mono-span greenhouse with a rose crop and continuous screened side vents and its effect on flow patterns and microclimate. Biosyst. Eng 2008, 101, 111–122. [Google Scholar]
- Molina-Aiz, FD; Valera, DL; Peña, AA; Gil, JA; López, A. A study of natural ventilation in an almería-type greenhouse with insect screens by means of tri-sonic anemometry. Biosyst. Eng 2009, 104, 224–242. [Google Scholar]
- Cebeci, T. Analysis of Turbulent Flows, 2nd ed; Elsevier Science: San Diego, CA, USA, 2004. [Google Scholar]
- Heber, AJ; Boon, CR; Peugh, MW. Air patterns and turbulence in an experimental livestock building. J. Agric. Eng. Res 1996, 64, 209–226. [Google Scholar]
- Boulard, T; Wang, S; Haxaire, R. Mean and turbulent air flows and microclimatic patterns in an empty greenhouse tunnel. Agric. For. Meteorol 2000, 100, 169–181. [Google Scholar]
- Hinze, JO. Turbulence; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Melikov, AK; Langkilde, G; Derbiszewski, B. Airflow characteristic in the occupied zone of rooms with displacement ventilation. ASHRAE Trans 1990, 96, 555–563. [Google Scholar]
- Ouyang, Q; Dai, W; Li, H; Zhu, Y. Study on dynamic characteristics of natural and mechanical wind in built environment using espectral analisis. Build. Environ 2006, 41, 418–426. [Google Scholar]
- Stull, RB. An Introduction to Boundary Layer Meteorology; Kluwer Academics Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- López, A. Contribución al Conocimiento del Microclima de los Invernaderos Mediante Anemometría Sónica y Termografía. Contribution to the Knowledge of the Greenhouse Microclimate Using Sonic Anemometry and Infrared Thermography. Ph.D. Dissertation, Almería University, Almería, Spain, 2011. Available online: http://www.ual.es/personal/alm212/ (accessed on 10 October 2011).
- Wang, S; Deltour, J. Theoretical study of natural ventilation flux in a single span greenhouse. Biotechnol. Agron. Soc. Environ 1998, 2, 256–263. [Google Scholar]
- Bot, GPA. Greenhouse Climate: From Physical Processes to a Dynamic Model. Ph.D. Dissertation,. Agricultural University, Wageningen, The Netherlands, 1983. [Google Scholar]
- Li, Y; Delsante, A. Natural ventilation induced by combined wind and thermal forces. Build. Environ 2001, 36, 59–71. [Google Scholar]
- Molina-Aiz, FD. Simulación y Modelación de la Ventilación en Invernaderos de Almería mediante Dinámica de Fluidos Computacional. Simulation and Modellisation of Ventilation in Almería Greenhouses Using Computational Fluid Dynamics. Ph.D. Dissertation,. Escuela de Ingenería, University of Almería, Almería, Spain, 2010. [Google Scholar]
- Lee, I-B; Short, TH. Two-dimensional numerical simulation of natural ventilation in amulti-span greenhouse. Trans. ASAE 2000, 43, 745–753. [Google Scholar]
- Boulard, T; Papadakis, G; Kittas, C; Mermier, M. Air flow and associated sensible heat exchanges in a naturally ventilated greenhouse. Agric. For. Meteorol 1997, 88, 111–119. [Google Scholar]
- Tanny, J; Haijun, L; Cohen, S. Airflow characteristics, energy balance and eddy covariance measurements in a banana screenhouse. Agric. For. Meteorol 2006, 139, 105–118. [Google Scholar]
- Tan-Atichat, J; Nagib, HM; Loehrke, RI. Interaction of free-stream turbulence with screens and grids: A balance between turbulence scales. J. Fluid Mech 1982, 114, 501–528. [Google Scholar]
- Tanny, J; Haslavsky, V; Teitel, M. Airflow and heat flux through the vertical opening of buoyancy-induced naturally ventilated enclosures. Energy Build 2008, 40, 637–646. [Google Scholar]
- Teitel, M. The effect of screened openings on greenhouse microclimate. Agric. For. Meteorol 2007, 143, 159–175. [Google Scholar]
- Jiang, Y; Chen, Q. Buoyancy-driven single-sided natural ventilation in buildings with large openings. Int. J. Heat Mass Transf 2003, 46, 973–988. [Google Scholar]
- Shang, XD; Xia, KQ. Scaling of the velocity power spectra in turbulent thermal convection. Phys Rev 2001, 64, 065301:1–065301:4. [Google Scholar]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).