Abstract
Materials with high hardness are critical for industrial and aerospace applications, prompting the search for novel compounds with robust covalent networks. Using a first-principles structure prediction method, we systematically explored the phase stability of Si–N compounds under high pressure. We identified two thermodynamically stable phases: Si6N with P-1 symmetry and SiN4 with space group R-3c. Phonon spectra and ab initio molecular dynamics simulations confirm the dynamical and thermal stability of R-3c SiN4 at ambient pressure and up to 2000 K. Notably, R-3c SiN4 exhibits exceptional mechanical properties with a Vickers hardness of 31 GPa, a bulk modulus of 259.53 GPa, and a Young’s modulus of 485.38 GPa. Furthermore, SiN4 possesses a high energy density (1.1 kJ·g−1) and outstanding detonation pressure and velocity (228 kbar, 7.11 km·s−1), both exceeding those of TNT, making it a potential high-energy-density materials. In addition, electronic structure analysis reveals SiN4 has a band gap of 2.5 eV, confirming its nonmetallic characteristics and strongly covalent nature. These findings provide theoretical guidance for the future synthesis of Si–N phases and establish a foundation for designing novel materials that combine high hardness with high-energy density performance.
1. Introduction
High-hardness materials combine superior hardness with excellent resistance to deformation, maintaining stable physical and chemical properties under extreme conditions such as high temperature and high pressure [1]. These features make them indispensable in advanced manufacturing, aerospace engineering, and defense applications [2,3]. Motivated by rising industrial and technological demands, researchers are devoted to exploring and developing novel multifunctional hard materials [4,5].
In recent years, experimental and theoretical research on hard materials has concentrated on compounds composed of light elements such as boron, carbon, nitrogen, and oxygen, owing to their ability to form strong covalent bonds that result in high hardness and superior resistance to deformation [6]. Among these, nitrides have been extensively studied due to their stable covalent bond structure (single bonds, 167 kJ·mol−1; double bonds, 419 kJ·mol−1) [7,8,9]. High-pressure synthesis has become a key strategy for preparing polymeric nitrogen, and various polymeric nitrogen phases have been experimentally prepared under high-pressure and high-temperature conditions [10]. However, the synthesis of pure nitrogen materials remains challenging due to the extremely high pressures (>110 GPa) required and the kinetic instability of elemental nitrogen phases. To overcome these limitations, the introduction of other elements under compression to synthesize stable nitrides at a relatively low pressure has been proven to be an effective method. The current goal is not only to obtain stable nitrides but also to achieve materials with high hardness.
Notably, the silicon-nitrogen compounds have attracted considerable attention because the Si–N bond enables the formation of covalent networks, while the incorporation of Si facilitates the stabilization and synthesis of diverse nitrides, thereby enhancing the potential for designing new high-hardness materials [11,12,13,14]. For example, theoretical investigations by Cui et al. have predicted several novel high-hardness phases of Si3N4 through first-principles calculations, namely t-Si3N4, m-Si3N4, and o-Si3N4 [15]. These phases exhibit lower energies under specific pressures than the conventional trigonal α-Si3N4 and hexagonal β-Si3N4, and possess higher Vickers hardness values [16]. Experimentally, two major Si–N stoichiometric materials, Si3N4 and SiN2, have been synthesized. Using synchrotron X-ray diffraction under high pressure, Qin et al. identified a new monoclinic phase of Si3N4, providing new insights into its high-pressure behavior [17]. In addition, α-Si3N4 (P31c), β-Si3N4 (P63/m), and γ-Si3N4 (Fd3/m) have also been reported. Weihrich et al. synthesized a pyrite-type SiN2 with a Pa-3 structure, which remains energetically stable above 15 GPa [18]. Niwa et al. further synthesized SiN2 (Pa-3) above 460 GPa and successfully recovered it at ambient conditions [19]. By contrast, Jurzick et al. synthesized SiN2 at 140 GPa [20]. Recently, dense Si3N4 ceramics were successfully fabricated via high pressure (5.5 GPa) and high temperature (900–1400 °C) [21]. Beyond these stoichiometries, recent studies have expanded the compositional and structural diversity of the Si–N system. Si-rich nitrides such as Si64N with cubic P-43m and rhombohedral R3m structures [22], as well as Cr-incorporated Si–N compounds forming bulk Cr2SiN4 phases [23] have been reported. However, these theoretical and experimental studies mainly focused on the nitrogen-rich Si3N4 and SiN2 compounds. In contrast, the existence of silicon-rich nitrides or other nitrogen-rich polymorphs in the Si–N system remains underexplored. Moreover, the potential existence of additional high-hardness structures in this system is still unknown. In addition, the systematic investigation of their mechanical and electronic properties is crucial for expanding the application potential of Si-N-based materials [24,25,26]. Therefore, exploring new Si-N structures is not only critical for discovering new materials, but also provides reliable theoretical guidance for the experimental synthesis of multifunctional Si-N compounds in the future.
In this work, we employed an ab initio structure prediction method [27,28] to comprehensively explore the high-pressure phase stability and material properties of Si–N compounds, leading to the identification of several novel thermodynamically stable phases, including SiN4 and Si6N. Phase diagram analysis indicates that Si6N becomes stable at approximately 25 GPa, while SiN4 becomes stable at around 29 GPa. Notably, R-3c SiN4 remains kinetically, dynamically, and thermally stable under both ambient and high-pressure, high-temperature conditions. Mechanical properties analysis indicates its outstanding hardness and elasticity. Furthermore, explosive performance calculations suggest that R-3c SiN4 exhibits a high detonation pressure of 228 kbar and detonation velocity of 7.11 km·s−1, underscoring its potential as a multifunctional material.
2. Results and Discussion
2.1. Stable Si−N Compounds
To assess the thermodynamic stability of the predicted structures, the relative stability of SixNy (x = 1–6, y = 1; x = 1, y = 1–6; x = 3, y = 4) compounds across varying pressures (i.e., 0, 25, 50, 75, and 100 GPa) was systematically examined through convex hull diagrams, as shown in Figure 1. The formation enthalpy per atom was obtained using the relation:
where H(SixNy) is the enthalpy of SixNy compound, H(Si) and H(N2) are the enthalpies of elemental silicon and nitrogen phases. For reference, the diamond-structured Si was adopted, while Pa-3 and P41212 molecular nitrogen were used as reference phases for computing the formation enthalpy [29,30]. As shown in the convex hull diagrams (Figure 1), the formation enthalpy per atom is obtained by dividing the total formation enthalpy of SixNγ by the total number of atoms (x + y). Solid symbols connected by solid lines denote thermodynamically stable compositions. In contrast, hollow symbols linked by dashed lines correspond to metastable or unstable phases. The negative formation enthalpy of cubic Si3N4 (Fd-3m) confirms its stability under ambient conditions (~0 GPa), consistent with previous theoretical and experimental reports demonstrating successful synthesis in a diamond anvil cell. Likewise, the predicted Pa-3 SiN2 phase remains stable under high pressure, further validating the reliability of the employed structure-search methodology [20].
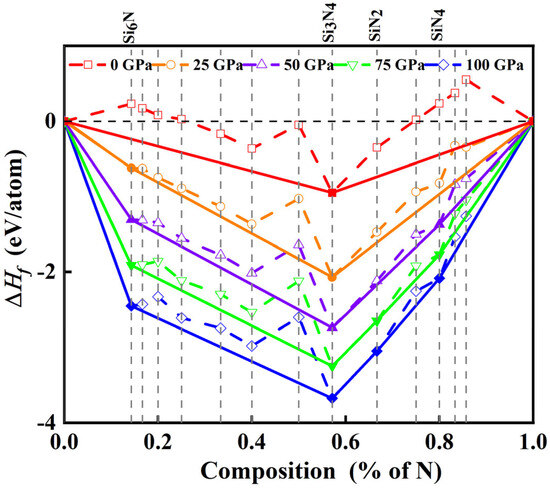
Figure 1.
Calculated formation enthalpies (ΔHf) per atom of various Si–N compounds with respect to decomposition into solids Si and N2 at 0, 25, 50, 75, and 100 GPa, respectively.
In addition to Si3N4 and SiN2, two new compositions, SiN4 and Si6N, are predicted to be thermodynamically stable. At ambient pressure, both lie slightly above the convex hull, indicating slightly metastable behavior. Upon compression, the formation enthalpy of Si6N decreases sharply, and this phase becomes thermodynamically stable above ~25 GPa, indicating that pressure effectively reduces the energetic barrier for forming this Si-rich compound. By contrast, SiN4 displays a more gradual enthalpy-pressure dependence, remaining metastable over intermediate pressures and only approaching the convex hull near 50 GPa. To determine the precise pressure, enthalpy difference calculations show that SiN4 is stabilized at ~3 GPa relative to elemental Si and N2, and at ~29 GPa relative to competing phases such as Si3N4 (see Supplemental Material, Figure S1). Overall, the enthalpy-pressure relationships indicate that the synthesis pressures for newly identified Si6N and SiN4 are below moderate pressure (~50 GPa). In contrast, nitrogen-rich compositions generally require higher stabilization pressures than Si-rich ones, reflecting the significant energetic barriers associated with breaking nitrogen’s triple bond and forming polymeric nitrogen frameworks. These results elucidate the pressure-driven stabilization pathways of both Si-rich and N-rich Si–N compounds and highlight potential routes for synthesizing novel structures.
2.2. Crystal Structures
Two SiN4 polymorphs (P-1 SiN4 and R-3c SiN4) and the Cm Si6N phase are predicted to be thermodynamically stable at high pressure. The atomic configurations of the predicted phases are shown in Figure 2. As shown in Figure 2a, the P-1 SiN4 phase crystallizes in a triclinic symmetry, where each Si atom is coordinated by six N atoms to form a structural unit. Among the coordinated N atoms, four are shared with adjacent units, while the remaining two are connected to other units through additional N linkages. The average Si–N bond length is 1.89 Å, whereas all N–N bonds maintain a uniform length of 1.31 Å at 0 GPa. In contrast, the R-3c SiN4 phase belongs to the trigonal crystal system and is stabilized by adopting a three-dimensional octahedral network. At 0 GPa, all Si–N bonds are identical, with a length of 1.91 Å, while all N–N bond lengths are 1.32 Å. These bond lengths lie within the characteristic range of stable covalent bonds. Each Si atom is bonded to six surrounding N atoms, forming an octahedral coordination geometry. Meanwhile, the ∠NSiN angle is 90 degrees, maximizing the balance of atomic repulsion. This uniform octahedral coordination imparts high bond energy, ensuring robust interatomic cohesion and compact connectivity resistant to dissociation. As shown in Figure S2, the lattice constant (a = b = c) of the R-3c SiN4 decreases continuously with increasing pressure, exhibiting an overall contraction of approximately 10% at 100 GPa. Overall, the cooperative bonding interactions effectively constrain atomic displacement, thereby reinforcing the resilience of the crystal framework.
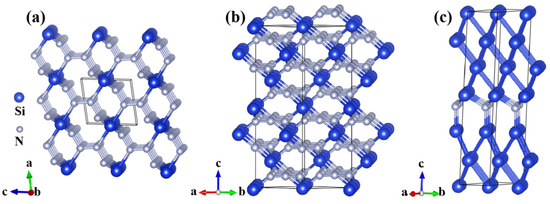
Figure 2.
(a) P-1 SiN4 at 0 GPa. (b) R-3c SiN4 at 0 GPa. (c) Cm Si6N at 25 GPa. Si atoms are shown in blue, and N atoms in gray.
For the Cm Si6N phase, which crystallizes in a monoclinic symmetry, the average Si–N bond length is 1.79 Å. In addition, Si-Si bonds have an average length of 2.51 Å at 25 GPa. Although the relatively longer bond lengths suggest lower bond energy and slightly weaker interatomic interactions, the overall configuration represents a balanced bonding state that preserves structural stability. The Si–N bonds provide supplementary connectivity channels within the crystal lattice, further reinforcing its structural stability in three-dimensional space.
2.3. Mechanical, High-Energy Density, and Electronic Properties
A quantitative assessment of hardness is critical to the theoretical design of high-hardness materials. Several semi-empirical models correlate hardness with the intrinsic properties of crystals [31,32,33,34]. Although these models employ different calculation approaches, their predicted values are generally very similar [35,36]. Among these, the Chen model is widely used and has been successfully applied to predict the hardness of many single-crystal materials, showing good agreement with experimental data [36,37,38,39,40,41,42,43]. For instance, it accurately predicts the Vickers hardness of diamond and cubic boron nitride (c-BN) in close agreement with measured values. Its broad applicability and proven reliability make it well-suited for the comparative screening of high-hardness materials, and it was therefore adopted in this study. While the model was originally formulated for polycrystalline materials, it is applied here to single-crystal structures, disregarding the influence of plastic deformation and dislocation motion. Therefore, the obtained values correspond to the intrinsic hardness of the materials under idealized conditions. Our analysis reveals that R-3c SiN4 has a Vickers hardness of 31 GPa, thereby surpassing the empirical threshold of 30 GPa that defines high-hardness materials. For the other two structures, the Vickers hardness values of P-1 SiN4 and Cm Si6N phases are 17 and 8 GPa, respectively, both much lower than that of R-3c SiN4. Evaluating elastic constants is essential for understanding the mechanical properties of the predicted Si–N compounds. The calculated elastic constants show that all values of the R-3c SiN4 satisfy the established mechanical stability criteria [44]. In addition, we computed the bulk modulus (B), shear modulus (G), Young’s modulus (E), and Poisson’s ratio (ν) to further assess the mechanical properties (Table 1). The R-3c SiN4 phase displays an exceptionally high bulk modulus of 259.53 GPa, reflecting its outstanding resistance to volume compression. Meanwhile, the shear modulus and Young’s modulus reach 204.23 and 485.38 GPa, respectively, indicating superior resistance against shape deformation and external stress. Poisson’s ratio is 0.18. Materials with a low Poisson’s ratio have very little change in lateral dimensions when subjected to axial load. These results demonstrate that the R-3c SiN4 combines remarkable hardness with extraordinary incompressibility and shear strength, making it a promising high-hardness material. The mechanical moduli of the P-1 SiN4 are listed in Table 1; all of which are inferior to those of R-3c SiN4. A comprehensive comparison integrating key properties of the R-3c and P-1 SiN4 is presented in Table S1 in the Supplemental Material.

Table 1.
Calculated mechanical moduli and Vickers hardness values of R-3c SiN4 and P-1 SiN4. Except for v, all other parameters are given in GPa.
The bulk and Young’s moduli were analyzed in spherical coordinates, and the corresponding elastic anisotropy was visualized by projecting these moduli onto selected crystallographic planes (001), (010), and (100) based on the formulations. The results for these two SiN4 polymorphs are illustrated in Figure 3. For the trigonal R-3c SiN4 phase, the contour projections of the bulk modulus on the (010) and (100) planes nearly overlap. This feature indicates that the bulk modulus is essentially isotropic in these directions. The (001) plane exhibits an almost spherical distribution with slightly higher values than those on the (010) and (100) planes. A similar trend is observed for Young’s modulus on the (001), which exhibits an isotropic distribution analogous to that of the bulk modulus and is approximately twice the magnitude of the latter. In contrast, Young’s modulus on the (010) and (100) planes deviates from a perfectly spherical pattern, displaying only weak isotropy along these directions. These results indicate that the R-3c SiN4 structure possesses excellent incompressibility and shear resistance along all three crystallographic orientations. In contrast, the triclinic P-1 SiN4 phase exhibits pronounced elastic anisotropy due to its very low crystal symmetry. Both the bulk and Young’s moduli reveal significant directional dependence across all three planes, with the (010) plane showing the most distinct anisotropy, characterized by a rod-like contour. The (001) and (100) planes also display anisotropy, though to a lesser degree. Overall, a direct comparison between the two polymorphs highlights that the elastic anisotropy of both bulk and Young’s moduli is much more pronounced in the P-1 phase than in the R-3c phase. Furthermore, the lower moduli values in the P-1 structure are consistent with its reduced hardness. These observations indicate that even at the same stoichiometric ratio, variations in atomic bonding configurations can induce substantial differences in the mechanical behavior of the structures. Although the Cm Si6N phase satisfies the mechanical stability criteria, its moderate hardness of 8.8 GPa limits its practical relevance as a hardness material; therefore, we will not discuss this structure in detail in the subsequent description of properties. Considering its high hardness, large elastic moduli, and distinctive anisotropic features, the R-3c SiN4 phase emerges as a promising high-hardness material with superior mechanical performance and was thus selected as the primary candidate for subsequent in-depth analyses.
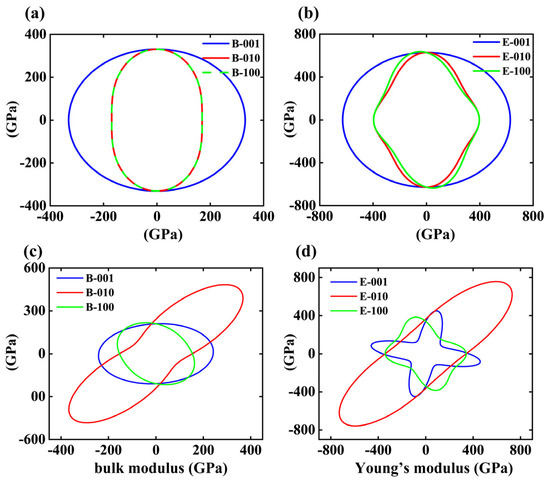
Figure 3.
Projections of bulk modulus and Young’s modulus on selected crystallographic planes for the (a,b) R-3c SiN4 and (c,d) P-1 SiN4.
As can be seen from Figure 1, R-3c SiN4 has a positive formation enthalpy, which is about 0.238 eV·atom−1 higher than the enthalpy of elemental Si plus nitrogen at 0 K and 0 GPa. After detonation, R-3c SiN4 may decompose in the following way: SiN4 (solid) → Si (solid) + 2N2 (gas). Further calculations show that R-3c SiN4 can release about 1.1 kJ·g−1 of energy, reaching the standard of high-energy-density materials (1.0 kJ·g−1). Typically, detonation velocities (Vd) and pressures (Pd) provide insights into the material’s explosive power and performance, which can be estimated based on Kamlet–Jacobs empirical equation. This method has been successfully applied to evaluate the explosive properties of nitrides and other energetic materials [45,46,47,48,49]. The corresponding expressions are given below:
Vd = 1.01(N M0.5 Ed0.5)0.5(1 + 1.30 ρ)
Pd = 1.58 ρ2 N M 0.5 Ed0.5
Herein, N, M, and ρ stand for the concentration of N2 in terms of moles per gram of explosive material (expressed as mol·g−1), the molecular weight of N2 gas (equivalent to 28 g·mol−1), and the density (measured in g·cm−3), respectively. In the above formulas, the units of gravimetric chemical energy density (Ed) should be converted to kJ·kg−1. In addition, our research results show that R-3c SiN4 releases a large amount of nitrogen upon detonation, with a detonation pressure of 228 kbar and a detonation velocity of 7.11 km·s−1—both of which exceed those of the famous explosive material trinitrotoluene (TNT, 190 kbar for detonation pressure and 6.90 km·s−1 for detonation velocity) (Table S3) [50,51]. These data demonstrate that R-3c SiN4 may be a potentially high-energy-density material that exhibits excellent detonation performance.
To systematically investigate the electronic properties and bonding characteristics of R-3c SiN4, we calculated its electronic band structure and density of states (DOS) at ambient pressure, as shown in Figure 4a,b. The band structure reveals a band gap of 2.5 eV, confirming the non-metallic nature of R-3c SiN4. Further band calculations at 100 GPa show that this structure has a band gap of 2.6 eV, which is almost the same as that at normal pressure, and still maintains non-metallic properties (Figure S3). The analysis of the total and partial DOS indicates that states near the Fermi level are primarily derived from the Si 3s and N 2p orbitals. The Si 3s states exhibit a prominent peak below the Fermi level, while the N 2p orbitals contribute significantly across a similar energy range, indicating strong s-p orbital hybridization. The hybridized orbitals suggest the formation of covalent bonds between Si and N atoms. For comparison, we also examined the P-1 SiN4 phase, which shows a semiconducting nature with a narrower band gap of 1.4 eV compared to that of R-3c SiN4 (see Figure S4 in the Supplemental Material).
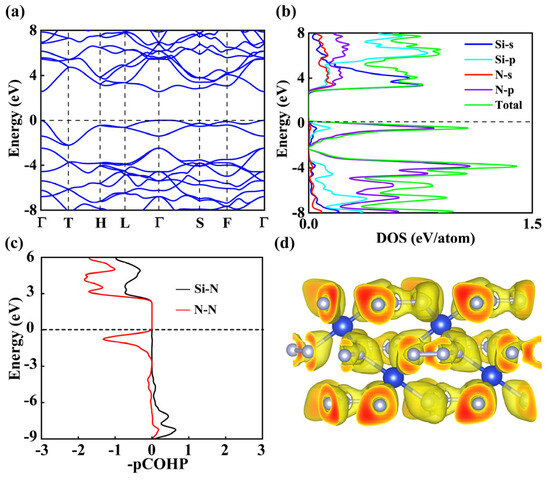
Figure 4.
(a) Electronic band structure, (b) density of states (DOS), (c) minus projected crystal orbital Hamilton populations, and (d) three-dimensional planes of electron localization function of R-3c SiN4 at 0 GPa.
To further clarify bonding and antibonding interactions, we employed the negative projected Crystal Orbital Hamiltonian population (−pCOHP), a widely used quantum chemical method. As shown in Figure 4c, a significant −pCOHP value appears below the Fermi level, confirming the existence of bonding states. Integral COHP (ICOHP) analysis of the R-3c SiN4 phase shows that the strength of the nearest-neighbor N–N bond (−14.13 eV per pair) is approximately twice that of the Si–N bond (−5.59 eV·pair−1). Similarly, the Integrated Crystal Orbital Overlap Population (ICOOP) values (0.40 eV per pair for N–N and 0.24 eV·pair−1 for Si–N) indicate that the N–N bond has greater orbital overlap and stronger covalency. The total Madelung (Ewald) energies per atom calculated using Mulliken and Rödinger charges are −4.10 eV and −3.09 eV, respectively, indicating that the contribution of ionic bonds to overall bonding is not negligible. These results indicate that N-N bonds in R-3c SiN4 dominate covalent interactions, while Si-N bonds play a relatively minor role, leading to a synergistic stabilizing effect of both covalent and ionic components. Covalent bonding behavior was also observed in the −pCOHP diagram of the P-1 SiN4 phase (Figure S5). For the P-1 SiN4 phase, the ICOHP value of the nearest-neighbor N-N bond is −14.83 eV·pair−1, approximately twice that of the Si-N bond (−5.96 eV·pair−1), with corresponding ICOOP values of 0.39 and 0.18 eV·pair−1, respectively. The calculated Madelung energies per atom are −4.18 eV (Mulliken) and −2.67 eV (Rödinger), which are nearly identical to those of the R-3c SiN4 phase. As shown in Table S1, the results suggest that these two phases have similar bonding characteristics, primarily composed of N-N covalent interactions and ionic stabilizing effects.
Further insight into the intrinsic bonding of R-3c SiN4 was obtained from the ELF (Figure 4d) and Bader charge analysis. The ELF exhibits strong localization around N atoms and along Si–N bonds, confirming the directional covalent nature of these interactions. The pronounced red regions near N highlight the concentration of electron density in these areas. Bader charge analysis showed that each Si atom donates approximately 3e, while only partial N atoms gain about 1e. This is not a complete transfer but rather a covalent sharing of electron density between Si and N atoms, primarily through covalent bonds. This charge redistribution stems from the strong electronegativity of nitrogen atoms, resulting in a shift in electron density toward neighboring N atoms. The Bader charge is consistent with the ELF results and the octahedral network observed in the R-3c SiN4 structure. These results provide consistent evidence for covalent bonding with significant ionic characteristics in R-3c SiN4. We also calculated the Bader charge of P-1 SiN4, which exhibits similar electron transfer characteristics to R-3c SiN4 as shown in Table S2.
2.4. Dynamic and Thermal Stabilities
To assess the dynamic stability of R-3c SiN4, we calculated its phonon dispersion curves at 0 and 100 GPa, as shown in Figure 5a,b. The phonon spectra exhibit no imaginary frequencies along the entire Brillouin zone, confirming the dynamic stability of R-3c SiN4 under both ambient and high-pressure conditions. Comparison of the phonon patterns reveals that increasing the pressure to 100 GPa shifts all vibration modes to higher frequencies, with a notable enhancement in the intensity of N atom vibrations in the middle and high-frequency regions. This behavior arises from the shortened interatomic distances and increased lattice stiffness under high pressure, which elevates the restoring force constants of atomic vibrations and suppresses the lattice vibrational degrees of freedom. We further computed the phonon spectra of the P-1 SiN4 phase, which confirms its dynamic stability at 0 GPa (Figure S6).
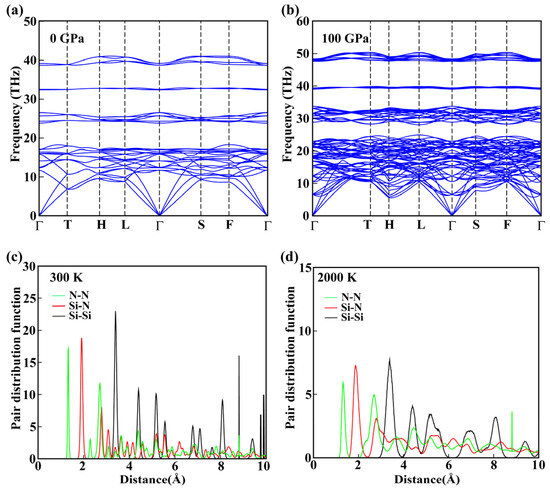
Figure 5.
Dynamical and thermal stability analysis of R-3c SiN4. Phonon spectra at (a) 0 and (b) 100 GPa, respectively. Pair distribution functions at (c) 300 and (d) 2000 K, respectively.
The thermal stability of R-3c SiN4 was evaluated using ab initio molecular dynamics (AIMD) simulations at 300 and 2000 K, as shown in Figure 5c,d. Equilibrium structures were extracted from the final steps of the AIMD runs. At 300 K, the bond length distribution for the shortest N–N bond (green line) is 1.32 Å, that for the nearest Si–N bond (red line) is 1.91 Å, and that for the Si–Si distance (black line) is 3.40 Å, which closely match those of the relaxed structure, indicating negligible deviation from the original bond lengths and confirming the stability of R-3c SiN4 at ambient temperature. At 2000 K, similar behavior is observed: the first peaks of all bond length distributions are aligned with those of the initial structure, demonstrating that the system preserves its bonding network under high-temperature conditions. As shown in Figure S7, the final structures obtained from AIMD simulations at both temperatures maintain the original bonding framework without significant deformation or distortion, confirming that R-3c SiN4 remains solid and structurally intact up to 2000 K. Pair distribution functions of P-1 SiN4 at 0 GPa and at 300 and 1000 K are presented in Figure S8. These results indicate excellent thermal stability over a wide temperature range, providing a solid theoretical basis for its potential experimental synthesis and high-temperature applications.
3. Calculation Methods and Details
The search for possible crystal structures was performed using the swarm-intelligence-based evolutionary algorithm as implemented in the CALYPSO code [27,28]. First-principles density functional theory (DFT) calculations [52] were employed to investigate the structural, electronic, elastic, and vibrational properties under high pressure, as well as to evaluate phase stability via total energy calculations. In recent years, DFT calculations, combined with the CALYPSO particle swarm optimization algorithm, have enabled the identification of thermodynamically stable structures given the chemical composition alone. These approaches provide predictive insights into phase stability and serve as a guide for experimental discovery of novel high-pressure materials [9,42,53,54,55,56]. Subsequent first-principles calculations, including structural optimization and electronic structure analyses, were carried out with the Perdew–Burke–Ernzerhof (PBE) [57] functional of the generalized gradient approximation (GGA) [58] as implemented in the Vienna Ab initio Simulation Package (VASP) [59]. The projector augmented wave (PAW) formalism [60] was employed with pseudopotentials explicitly considering the valence electrons, namely 3s23p2 for Si and 2s22p3 for N. Numerical accuracy was ensured by adopting a plane-wave cutoff energy of 700 eV and a Monkhorst–Pack k-point mesh with a reciprocal space resolution of 2π × 0.025 Å−1, resulting in a total energy convergence better than 1 meV per atom [61]. The elastic moduli were computed using the Voigt–Reuss–Hill averaging method [62,63]. The detonation velocity and pressure were estimated based on the Kamlet-Jacobs Empirical Equation [50,51]. Furthermore, the Vickers hardness was estimated using a microscopic hardness model [33]. The phonon dispersions were calculated using the direct supercell method implemented in the PHONOPY package (V.2.43.6) [64] in conjunction with the VASP code. For the R-3c SiN4 phase, 80-atom and 100-atom supercells were employed at 0 and 100 GPa, respectively. Ab initio molecular dynamics (AIMD) simulations were performed within the NpT ensemble employing a Langevin thermostat, based on the R-3c SiN4 supercell model containing 80 atoms [65]. A time step of 1 fs and a total simulation time of 8 ps were used in the molecular dynamics simulations. The electron localization function (ELF) was employed to analyze the electron localization behavior [66], and the results were displayed using the Visualization for Electronic and Structural Analysis (VESTA) software (Version 3) [67]. Chemical bonding characteristics were quantitatively analyzed through Crystal Orbital Hamilton population (COHP), Crystal Orbital Overlap Population (COOP), and Madelung energy calculations performed using the LOBSTER code with the PBEVaspFit2015 basis set [68]. The following basis functions were applied: Si: 3s, 3p and N: 2s, 2p. All calculations employed wavefunctions obtained from VASP using the PBE exchange–correlation functional and the PAW method. Additional computational details are provided in the Supplemental Material.
4. Conclusions
Using first-principles structure prediction methods, we systematically explored the high-pressure phase stability of Si–N compounds, identifying novel thermodynamically stable phases, including SiN4 and Si6N. Phase diagram analysis shows that Si6N stabilizes at ~25 GPa, while SiN4 becomes stable at ~29 GPa, indicating that their synthesis pressures are relatively low. Notably, SiN4 with R-3c symmetry remains kinetically and dynamically stable at both ambient and high pressures, and dynamically stable up to 2000 K. Mechanical evaluations reveal exceptional hardness (31 GPa) and high bulk (259.53 GPa), shear (204.23 GPa), and Young’s modulus (485.38 GPa). Its excellent explosive properties make this nitrogen-rich compound a potential high-energy-density material. Electronic structure analysis reveals a band gap of 2.5 eV, characterized by strong covalent bonds. The results demonstrate that R-3c SiN4 is a high-hardness material that combines high stability, mechanical strength, and high energy density. This work deepens our understanding of the structural, mechanical, and electronic properties of Si–N compounds and provides theoretical guidance for the synthesis of multifunctional nitride materials.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules30224357/s1, Figure S1. Calculated enthalpy differences of R-3c SiN4 relative to the mixtures of Si3N4, Si, and pure nitrogen. Figure S2. Variation of the lattice constants (a = b = c) of R-3c SiN4 the unit cell with pressure. Figure S3. (a) Electronic band structure R-3c SiN4 at 100 GPa. Figure S4. (a) Electronic band structure and (b) dos of P-1 SiN4 at 0 GPa. Figure S5. The -PCOHP of P-1 SiN4 at 0 GPa. Figure S6. Phonon spectra of P-1 SiN4 at 0 GPa. Figure S7. (a) The structure after initial optimization, (b) final structure at 300 K, and (c) final structure at 1000 K of R-3c SiN4. Figure S8. Pair distribution functions of P-1 SiN4 at 0 GPa at 300 K (a) and 1000 K (b), respectively. Table S1. Comparison of mechanical, electronic, and bonding properties of R-3c and P-1 SiN4 phases. Table S2. Charge transfer in P-1 SiN4 at 0 pressure. Table S3. Calculated energy density (Ed, kJ·g−1), detonation pressure (Pd, kbar), and detonation velocity (Vd, km·s−1) of R-3c SiN4. For comparison, the table also lists the explosion parameters of our calculated TNT and experimental TNT, where the superscript expt represents the experimental data.
Author Contributions
L.L. designed the project, supervised the calculations, analyzed the data, and wrote the manuscript. J.Q., C.D., D.W. and S.Z. performed the calculations. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the China Postdoctoral Science Foundation funded project (Grant No. 2025M773372), the National Natural Science Foundation of China (Grant No. 12404021), the Natural Science Foundation of Jiangsu Province (No. BK20233001), the Natural Science Research of Jiangsu Higher Education Institutions of China (Grant No. 23KJD140003), Innovation Training Projects for College Students in Jiangsu Province (Grant No. 202411460028Z), and the Foundation of Nanjing Xiaozhuang University (Grant No. 2022NXY25).
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gao, E.; Yang, H.; Guo, Y.; Nielsen, S.O.; Baughman, R.H. The stiffest and strongest predicted material: C2N atomic chains approach the theoretical limits. Adv. Sci. 2023, 10, 2204884. [Google Scholar] [CrossRef]
- Chen, D.; Chen, G.; Lv, L.; Dong, J.; Shang, Y.; Hou, X.; Wang, Y.; Shang, J.; Wang, S.; Yin, Y. General approach for synthesizing hexagonal diamond by heating post-graphite phases. Nat. Mater. 2025, 24, 513. [Google Scholar] [CrossRef]
- Dong, H.; Li, B.; Liu, B.; Zhang, Y.; Sun, L.; Luo, K.; Wu, Y.; Ma, M.; Liu, B.; Hu, W. Extraordinary high-temperature mechanical properties in binder-free nanopolycrystalline WC ceramic. J. Mater. Sci. Technol. 2022, 97, 169. [Google Scholar] [CrossRef]
- Wang, Y.; Csanadi, T.; Zhang, H.; Dusza, J.; Reece, M.J. Synthesis, microstructure, and mechanical properties of novel high entropy carbonitrides. Acta Mater. 2022, 231, 117887. [Google Scholar] [CrossRef]
- Chen, L.; Tai, J.; Wang, D.; Wang, S.; Liang, H.; Yin, H. High-performance solar-blind photodetector based on amorphous BN in harsh environment operations. Appl. Phys. Lett. 2024, 124, 042102. [Google Scholar] [CrossRef]
- Tian, F.; Wang, J.; He, Z.; Ma, Y.; Wang, L.; Cui, T.; Chen, C.; Liu, B.; Zou, G. Superhard semiconducting C3N2 compounds predicted via first-principles calculations. Phys. Rev. B Condens. Matter 2008, 78, 235431. [Google Scholar] [CrossRef]
- Ding, C.; Wang, J.; Han, Y.; Yuan, J.; Gao, H.; Sun, J. High energy density polymeric nitrogen nanotubes inside carbon nanotubes. Chin. Phys. Lett. 2022, 39, 036101. [Google Scholar] [CrossRef]
- Ding, C.; Yuan, J.; Wang, X.; Huang, T.; Wang, Y.; Sun, J. Single-bonded nitrogen chain and porous nitrogen layer via Ce–N compounds. Mater. Adv. 2023, 4, 2162. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, S.; Zhang, H. Pressure-driven Ne-bearing polynitrides with ultrahigh energy density. Chin. Phys. Lett. 2022, 39, 056102. [Google Scholar] [CrossRef]
- O’Sullivan, O.T.; Zdilla, M.J. Properties and promise of catenated nitrogen systems as high-energy-density materials. Chem. Rev. 2020, 120, 5682. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, G.; Cui, W.; Ge, Y.; Du, S.; Gao, Y.; Zhang, Y.; Li, F.; Chen, Z.; Du, S. Plastic deformation in silicon nitride ceramics via bond switching at coherent interfaces. Science 2022, 378, 371. [Google Scholar] [CrossRef]
- Surucu, G.; Gullu, H.H.; Candan, A.; Yildiz, B.; Erkisi, A. First-principles studies of Tin+1SiNn (n = 1, 2, 3) MAX phase. Philos. Mag. 2020, 100, 2183. [Google Scholar] [CrossRef]
- Wang, C.; Yu, G.; Zhang, S.; Zhao, Y.; Chen, H.; Cheng, T.; Zhang, X. A pressure-induced superhard SiCN4 compound uncovered by first-principles calculations. Phys. Chem. Chem. Phys. 2024, 26, 8938. [Google Scholar] [CrossRef]
- Li, Y.-L.; Liang, Y.; Zheng, F.; Ma, X.-F.; Cui, S.-J.; Sun, L. Enhanced crystallization and phase transformation of amorphous silicon nitride under high pressure. J. Mater. Res. 2001, 16, 67. [Google Scholar] [CrossRef]
- Cui, L.; Hu, M.; Wang, Q.; Xu, B.; Yu, D.; Liu, Z.; He, J. Prediction of novel hard phases of Si3N4: First-principles calculations. J. Solid. State Chem. 2015, 228, 20. [Google Scholar] [CrossRef]
- Ching, W.Y.; Xu, Y.N.; Gale, J.D.; Rühle, M. Ab-initio total energy calculation of α-and β-silicon nitride and the derivation of effective pair potentials with application to lattice dynamics. J. Am. Ceram. Soc. 1998, 81, 3189. [Google Scholar] [CrossRef]
- Qin, F.; Qin, S.; Prakapenka, V.B. High pressure behaviors and novel high-pressure phase of Si3N4 and TiN. Lithos 2020, 372, 105677. [Google Scholar] [CrossRef]
- Weihrich, R.; Eyert, V.; Matar, S.F. Structure and electronic properties of new model dinitride systems: A density-functional study of CN2, SiN2, and GeN2. Chem. Phys. Lett. 2003, 373, 636. [Google Scholar] [CrossRef]
- Niwa, K.; Ogasawara, H.; Hasegawa, M. Pyrite form of group-14 element pernitrides synthesized at high pressure and high temperature. Dalton Trans. 2017, 46, 9750. [Google Scholar] [CrossRef] [PubMed]
- Jurzick, P.L.; Krach, G.; Brüning, L.; Schnick, W.; Bykov, M. Synthesis and crystal structure of silicon pernitride SiN2 at 140 GPa. Struct. Rep. 2023, 79, 923. [Google Scholar] [CrossRef] [PubMed]
- Xiao, C.; He, S.; Chen, H.; Yu, Y.; Wang, Z.; Lu, C. Fabrication and properties of silicon nitride ceramics under high temperature and high pressure. Ceram. Int. 2025, 1. [Google Scholar] [CrossRef]
- Sluydts, M.; Pieters, M.; Vanhellemont, J.; Van Speybroeck, V.; Cottenier, S. High-throughput screening of extrinsic point defect properties in Si and Ge: Database and applications. Chem. Mater. 2017, 29, 975. [Google Scholar] [CrossRef]
- Škundrić, T.; Zagorac, D.; Schön, J.C.; Pejić, M.; Matović, B. Crystal structure prediction of the novel Cr2SiN4 compound via global optimization, data mining, and the PCAE method. Crystals 2021, 11, 891. [Google Scholar] [CrossRef]
- Mei, Z.-G.; Wang, Y.; Shang, S.; Liu, Z.-K. First-principles study of the mechanical properties and phase stability of TiO2. Comput. Mater. Sci. 2014, 83, 114. [Google Scholar] [CrossRef]
- Ying, P.; Li, Z.; Chen, S.; Li, H.; Gao, Y.; He, J.; Liu, C. First-principles study on stability, electronic and mechanical properties of 4^ 3T175 carbon allotrope. Comput. Mater. Sci. 2023, 219, 111956. [Google Scholar] [CrossRef]
- Wang, G.-M.; Zeng, W.; Tang, B.; Liu, F.-S.; Liu, Q.-J.; Li, X.-H.; Zhong, M. Structural, electronic, and mechanical properties of Y7Ru4InGe12: A first-principle study. J. Mol. Model. 2022, 28, 41. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B Condens. Matter 2010, 82, 094116. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063. [Google Scholar] [CrossRef]
- Fan, C.; Liu, S.; Liu, J.; Wu, B.; Tang, Q.; Tao, Y.; Pu, M.; Zhang, F.; Li, J.; Wang, X. Evidence for a high-pressure isostructural transition in nitrogen. Chin. Phys. Lett. 2022, 39, 026401. [Google Scholar] [CrossRef]
- Bini, R.; Ulivi, L.; Kreutz, J.; Jodl, H.J. High-pressure phases of solid nitrogen by Raman and infrared spectroscopy. J. Chem. Phys. 2000, 112, 8522. [Google Scholar] [CrossRef]
- Gao, F. Theoretical model of intrinsic hardness. Phys. Rev. B Condens. Matter 2006, 73, 132104. [Google Scholar] [CrossRef]
- Šimůnek, A.; Vackář, J. Hardness of covalent and ionic crystals: First-principle calculations. Phys. Rev. Lett. 2006, 96, 085501. [Google Scholar] [CrossRef]
- Chen, X.-Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275. [Google Scholar] [CrossRef]
- Li, K.; Yang, P.; Niu, L.; Xue, D. Group electronegativity for prediction of materials hardness. J. Phys. Chem. A 2012, 116, 6911. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, Z.; Yu, T.; Zhang, S.; Lin, J.; Yang, G. Hexagonal BC2N with remarkably high hardness. J. Phys. Chem. C 2018, 122, 6801. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Lv, J.; Zhu, C.; Li, Q.; Zhang, M.; Li, Q.; Ma, Y. First-principles structural design of superhard materials. J. Chem. Phys. 2013, 138, 114101. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Xu, B.; Zhao, Z. Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Met. Hard Mater. 2012, 33, 93. [Google Scholar] [CrossRef]
- Wang, M.; Li, Y.; Cui, T.; Ma, Y.; Zou, G. Origin of hardness in WB4 and its implications for ReB4, TaB4, MoB4, TcB4, and OsB4. Appl. Phys. Lett. 2008, 93, 101905. [Google Scholar] [CrossRef]
- Li, Q.; Zhou, D.; Zheng, W.; Ma, Y.; Chen, C. Anomalous stress response of ultrahard WB n compounds. Phys. Rev. Lett. 2015, 115, 185502. [Google Scholar] [CrossRef]
- Fulcher, B.; Cui, X.; Delley, B.; Stampfl, C. Hardness analysis of cubic metal mononitrides from first principles. Phys. Rev. B Condens. Matter 2012, 85, 184106. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, B.; Yu, D.; Ma, Y.; Wang, Y.; Jiang, Y.; Hu, W.; Tang, C.; Gao, Y.; Luo, K. Ultrahard nanotwinned cubic boron nitride. Nature 2013, 493, 385. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Lv, J.; Ma, Y. Materials discovery at high pressures. Nat. Rev. Mater. 2017, 2, 17005. [Google Scholar] [CrossRef]
- Kaner, R.B.; Gilman, J.J.; Tolbert, S.H. Designing superhard materials. Science 2005, 308, 1268. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.-J.; Zhao, E.-J.; Xiang, H.-P.; Hao, X.-F.; Liu, X.-J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B Condens. Matter 2007, 76, 054115. [Google Scholar] [CrossRef]
- Hou, J.; Weng, X.-J.; Oganov, A.R.; Shao, X.; Gao, G.; Dong, X.; Wang, H.-T.; Tian, Y.; Zhou, X.-F. Helium-nitrogen mixtures at high pressure. Phys. Rev. B 2021, 103, L060102. [Google Scholar] [CrossRef]
- Lin, J.; Wang, F.; Rui, Q.; Li, J.; Wang, Q.; Wang, X. A novel square planar N42− ring with aromaticity in BeN4. Matter Radiat. Extremes 2022, 7, 038401. [Google Scholar] [CrossRef]
- Lin, S.; Chen, J.; Zhang, B.; Hao, J.; Xu, M.; Li, Y. Lanthanium nitride LaN9 featuring azide units: The first metal nine-nitride as a high-energy-density material. Phys. Chem. Chem. Phys. 2024, 26, 3605. [Google Scholar] [CrossRef] [PubMed]
- Xia, K.; Zheng, X.; Yuan, J.; Liu, C.; Gao, H.; Wu, Q.; Sun, J. Pressure-stabilized high-energy-density alkaline-earth-metal pentazolate salts. J. Phys. Chem. C 2019, 123, 10205. [Google Scholar] [CrossRef]
- Yi, W.; Zhang, Y.; Zhang, G.; Liu, X. CuN10: A high-energy-density pentazolate with an antiferromagnetic state. Phys. Chem. Chem. Phys. 2025, 27, 5902. [Google Scholar] [CrossRef]
- Kamlet, M.J.; Dickinson, C. Chemistry of detonations. III. Evaluation of the simplified calculational method for chapman-jouguet detonation pressures on the basis of available experimental information. J. Chem. Phys. 1968, 48, 43. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Song, S.; Yang, Z.; Qi, X.; Wang, K.; Liu, Y.; Zhang, Q.; Tian, Y. Accelerating the discovery of insensitive high-energy-density materials by a materials genome approach. Nat. Commun. 2018, 9, 2444. [Google Scholar] [CrossRef] [PubMed]
- Mujica, A.; Rubio, A.; Munoz, A.; Needs, R. High-pressure phases of group-IV, III–V, and II–VI compounds. Rev. Mod. Phys. 2003, 75, 863. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Zhang, S.; Zhang, H. Pressure-stabilized GdN6 with an armchair–antiarmchair structure as a high energy density material. J. Mater. Chem. A 2021, 9, 16751. [Google Scholar] [CrossRef]
- Zhai, H.; Xu, R.; Dai, J.; Ma, X.; Yu, X.; Li, Q.; Ma, Y. Stabilized nitrogen framework anions in the Ga–N system. J. Am. Chem. Soc. 2022, 144, 21640. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Gao, P.; Zhang, C.; Lv, J.; Wang, H.; Liu, H.; Wang, Y.; Ma, Y. Data-driven prediction of complex crystal structures of dense lithium. Nat. Commun. 2023, 14, 2924. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Liu, H.; Ma, Y.; Chen, C. Direct H-He chemical association in superionic FeO2H2He at Deep-Earth conditions. Natl. Sci. Rev. 2022, 9, nwab168. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Lee, I.-H.; Martin, R.M. Applications of the generalized-gradient approximation to atoms, clusters, and solids. Phys. Rev. B 1997, 56, 7197. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Pack, J.D.; Monkhorst, H.J. “Special points for Brillouin-zone integrations”—A reply. Phys. Rev. B 1977, 16, 1748. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Wagner, J.-M.; Bechstedt, F. Properties of strained wurtzite GaN and AlN: Ab initio studies. Phys. Rev. B 2002, 66, 115202. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Crystal structure and pair potentials: A molecular-dynamics study. Phys. Rev. Lett. 1980, 45, 1196. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. Appl. Crystallogr. 2011, 44, 1272. [Google Scholar] [CrossRef]
- Dronskowski, R.; Bloechl, P.E. Crystal orbital Hamilton populations (COHP): Energy-resolved visualization of chemical bonding in solids based on density-functional calculations. J. Phys. Chem. 1993, 97, 8617. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).