Abstract
The purpose of this work is to investigate the entropy generation in a laminar, gravity-driven conducting liquid film with fully developed velocity flowing along an incline heated plate in the presence of a transverse magnetic field. The upper surface of the liquid film is considered free and adiabatic. The effect of heat generation by viscous dissipation is included in the analysis. The influence of the applied magnetic field and the viscous dissipation on velocity, temperature and entropy generation is examined.
Introduction
Entropy generation is closely associated with thermodynamic irreversibility, which is encountered in all heat transfer processes. Different sources are responsible for generation of entropy such as heat transfer and viscous dissipation [1982; 1996]. The analysis of entropy generation rate in a circular duct with imposed heat flux at the wall and its extension to determine the optimum Reynolds number as function of the Prandtl number and the duty parameter were presented by Bejan [1996; 1979]. Sahin [1998] introduced the second law analysis to a viscous fluid in circular duct with isothermal boundary conditions. In another paper, Sahin [1999] presented the effect of variable viscosity on entropy generation rate for heated circular duct. A comparative study of entropy generation rate inside duct of different shapes and the determination of the optimum duct shape subjected to isothermal boundary condition were done by Sahin [1998]. Narusawa [1998] gave an analytical and numerical analysis of the second law for flow and heat transfer inside a rectangular duct. In a more recent paper, Mahmud and Fraser [2003; 2002] applied the second law analysis to fundamental convective heat transfer problems and to non-Newtonian fluid flow through channel made of two parallel plates. The study of entropy generation in a falling liquid film along an inclined heated plate was carried out by Saouli and Aïboud-Saouli [2004]. As far as the effect of a magnetic field on the entropy generation is concerned, Mahmud et al. [2003] studied the case of mixed convection in a channel.
The purpose of this article is thermodynamics analysis of a fully developed liquid film flowing along an inclined heated plate in the presence of a transverse magnetic field. The effect of heat generation by viscous dissipation is included in the analysis. Expressions for dimensionless velocity and temperature, entropy generation number are obtained.
Problem formulation and analytical solution
The problem as shown in Fig. 1 concerns a fully developed Newtonian, laminar, gravity-driven liquid film of thickness
flowing along an inclined heated plate in the presence of a transverse uniform magnetic field . The magnetic Reynolds number
is assumed to be small, so that the induced magnetic field is neglected and the Hall effect of magnetohydrodynamics is ignored.
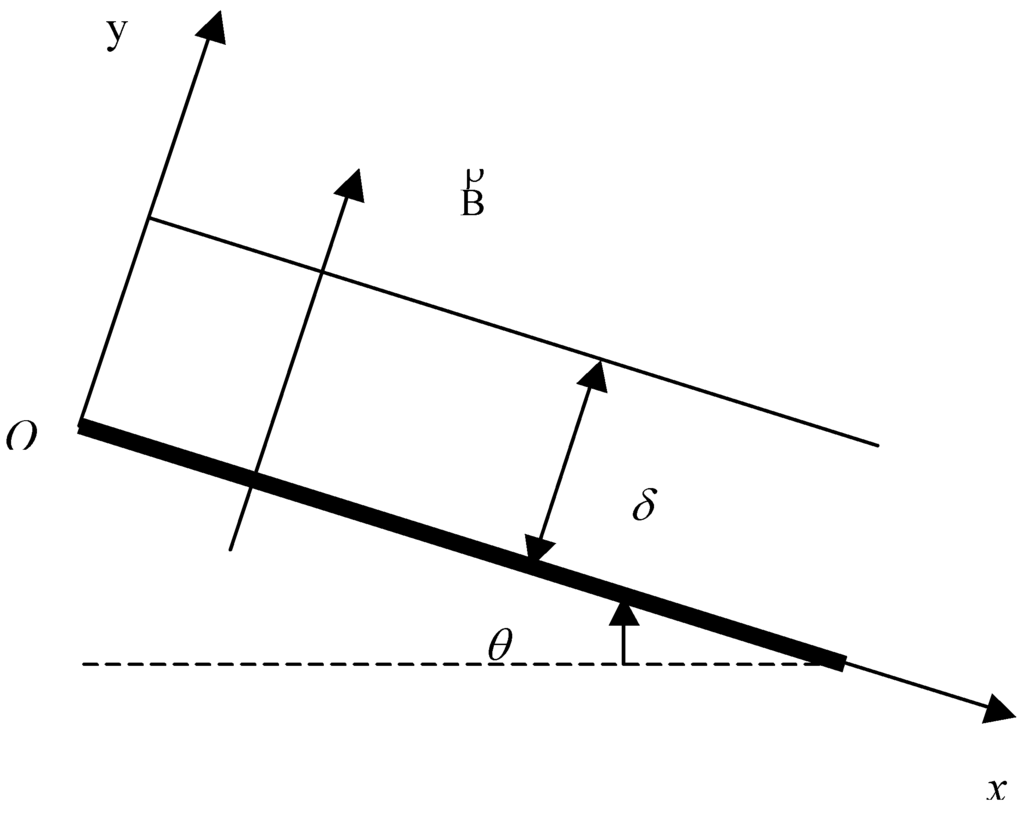
Figure 1.
Schematic diagram of the problem.
Neglecting the inertia terms in the momentum equation compared to the body force and the magnetic term, the momentum equation is then:
where
is the dynamic viscosity,
the fluid density,
the electric conductivity and
the gravity acceleration.
The boundary conditions are:
The velocity profile is obtained by integrating Eq. (1) and using the boundary conditions given by Eq. (2). It may be written:
Introducing the following dimensionless variables for the velocity and the transverse distance
,
, the dimensionless velocity becomes:
where
is the Hartman number defined as:
and
The liquid mass flow rate
is:
Substituting Eq. (3) into Eq. (7), the liquid mass flow rate is:
In absence of the magnetic field, the liquid mass flow rate is [10]:
Therefore the liquid mass flow rate may be written:
The energy equation for the present problem is:
The boundary conditions are:
Using the following dimensionless variables:
where
is a reference temperature difference defined as:
The energy equation can be written in the following dimensionless form:
subjected to the following boundary conditions:
=
is the Brinkman number.
To get a solution of Eq. (15), a separation of variables solution is assumed in the following form [10]:
The first term in the right-hand side of Eq. (17) is significant for decaying initial transition and entrance effect, the second term is significant for axial temperature rise due to accumulated wall heat flux and the third term is significant for transverse temperature variation to wall heat flux into fluid. Neglecting entrance effect and assuming that the system already passed the decaying initial transition. Then the first term at the right-hand side of Eq. (17) will disappear [8, 9]. Combination of Eq. (15) and Eq. (17) leaves two separated ordinary equations [10]. The solution of these two ordinary equations is:
where
,
and
are constants of integration.
Using the boundary conditions (16b) and (16c), it is found that:
In the above expression
, ,
and
can be defined by:
To evaluate the constant of integration
, the bulk mean temperature given in Eq. (21) is examined:
where the area element
and the area
are:
Using Eq. (21), the bulk mean temperature is:
The boundary conditions defined by Eq. (16a) leads the following condition on the bulk mean temperature:
Substituting Eq. (18) in Eq. (23) and using Eq. (24), the constant of integration is:
According to Woods [1975], the entropy generation rate is:
The dimensionless entropy generation number is defined by the following relationship:
using the dimensionless velocity and temperature, Eq.(27) can be rewritten as:
where
=
and
=
are respectively the Peclet number and the dimensionless temperature difference.
and
, are respectively the entropy generation numbers due to the conductive heat in the axial and the transverse directions.
is the entropy generation number due to the fluid friction and
is the entropy generation due to the hydromagnetic effect.
Results and discussion
The velocity profiles
are represented in Fig. 2 for various values of the Hartman number
. As it can be seen, the action of the applied magnetic field
is to flatten the velocity profile near the free surface of the liquid film. The influence of the Hartman number on the liquid mass flow rate is illustrated in Fig. 3. As the Hartman number increases, the liquid mass fluid rate decreases. This means that the mean velocity of the liquid decreases. The application of the magnetic field induces a resistive force acting in the opposite direction of the flow, thus causing its deceleration.
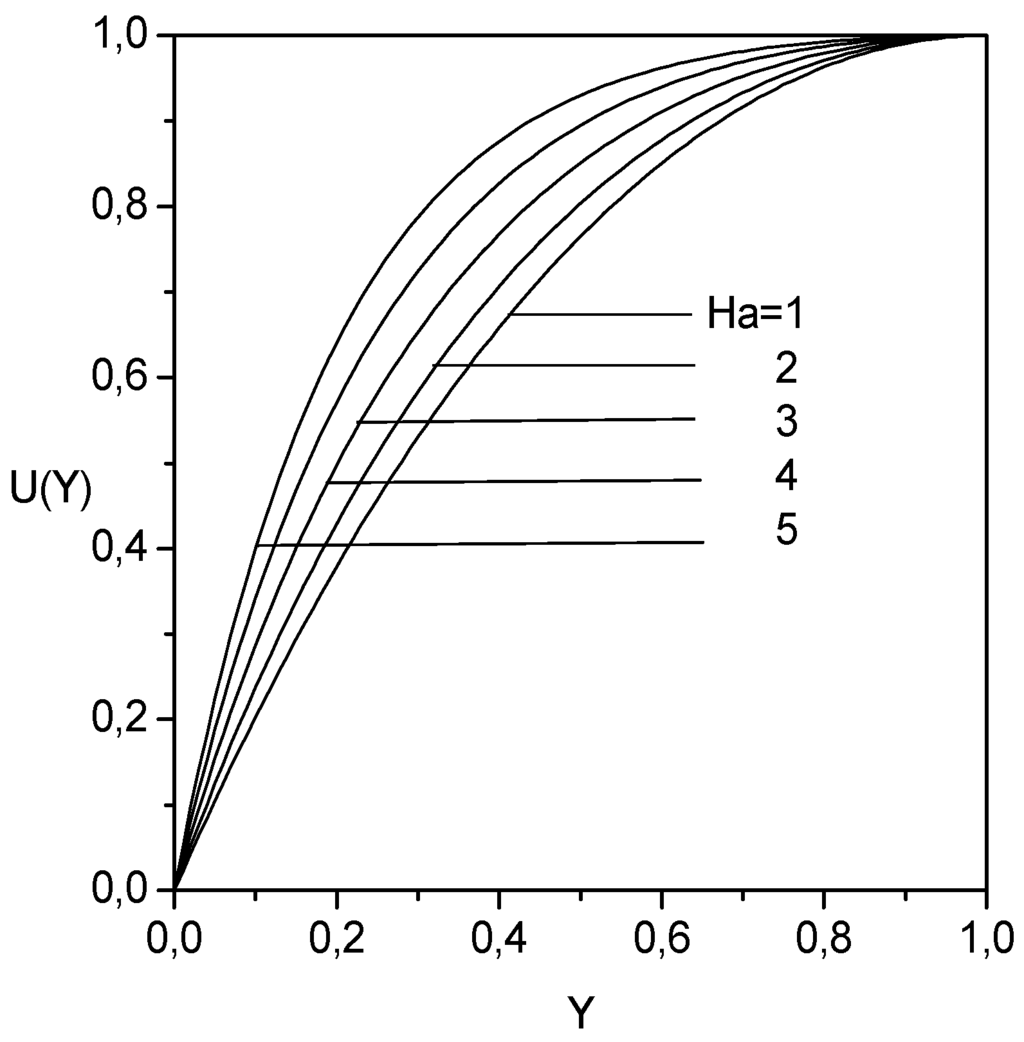
Figure 2.
Velocity Profiles as function of the transverse distance for different Hartman numbers.
Fig. 4 presents a comparison between the temperature profiles
across the liquid film without the hydomagnetic effect, with hydromagnetic effect and with hydromagnetic and viscous dissipation effects. The temperature decreases along the transverse direction. For given transverse and axial directions, the temperature increases with the application of the magnetic field and the presence of viscous dissipation because of the heat generated by the hydromagnetic and viscous dissipation effects.
For a given axial distance
and Brinkman number
, the effect of the Hartman number
on the temperature profile
is illustrated in Fig. 5. An increase of the Hartman number yields higher temperature profiles because of the heat dissipation due the action of the magnetic field.
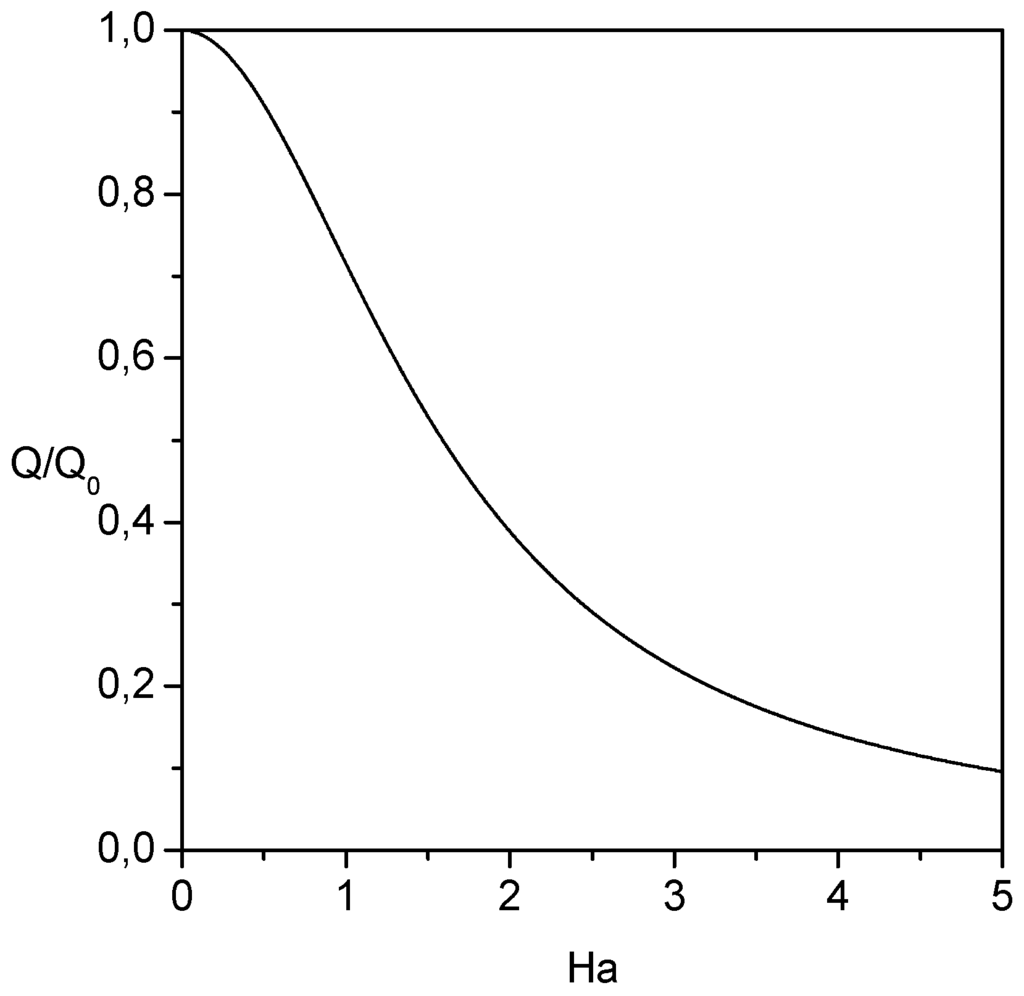
Figure 3.
Influence of the Hartman number on the liquid mass flow rate.
The action of the Brinkman number
on the temperature profiles for given axial position
and Hartman number
is illustrated in Fig. 6. As the Brinkman number increases, the temperature increases consequently because of the heat generated by viscous dissipation.
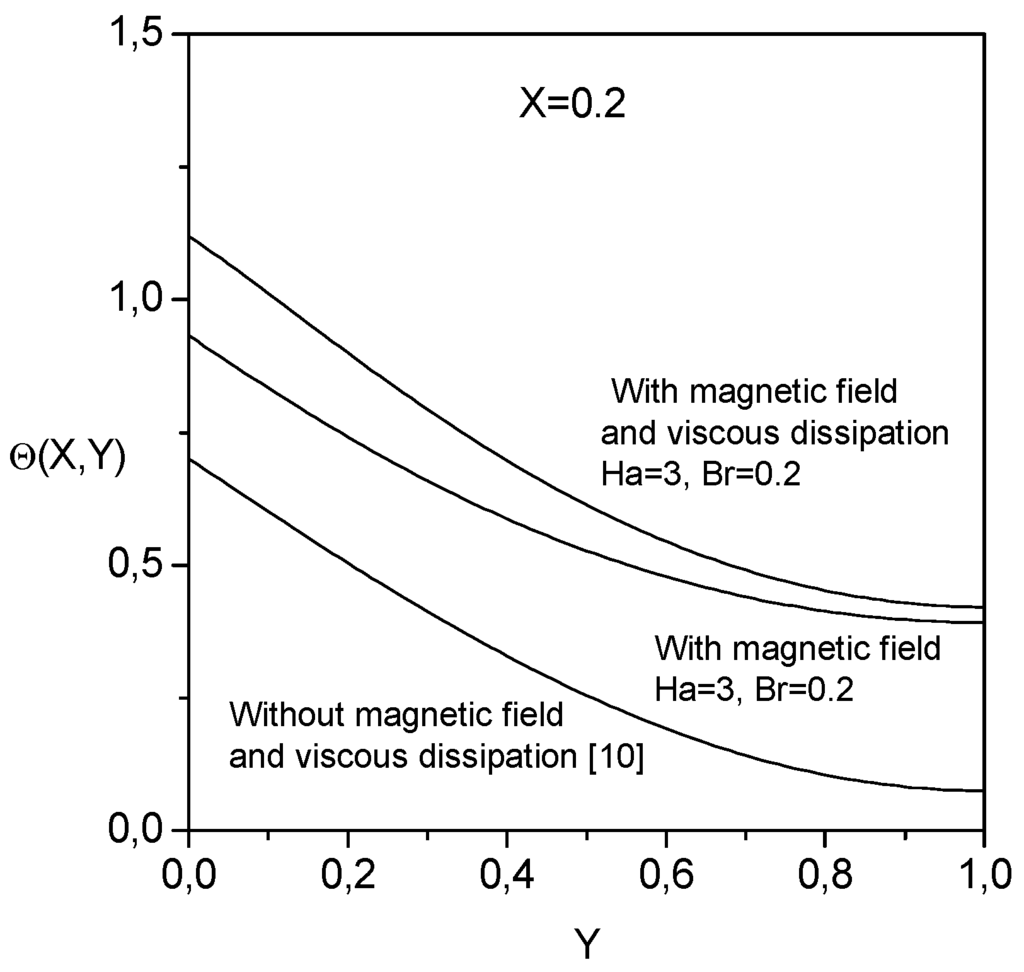
Figure 4.
Comparison between the temperature profiles across the liquid film without the hydomagnetic effect, with hydromagnetic effect and with hydromagnetic and viscous dissipation effects.
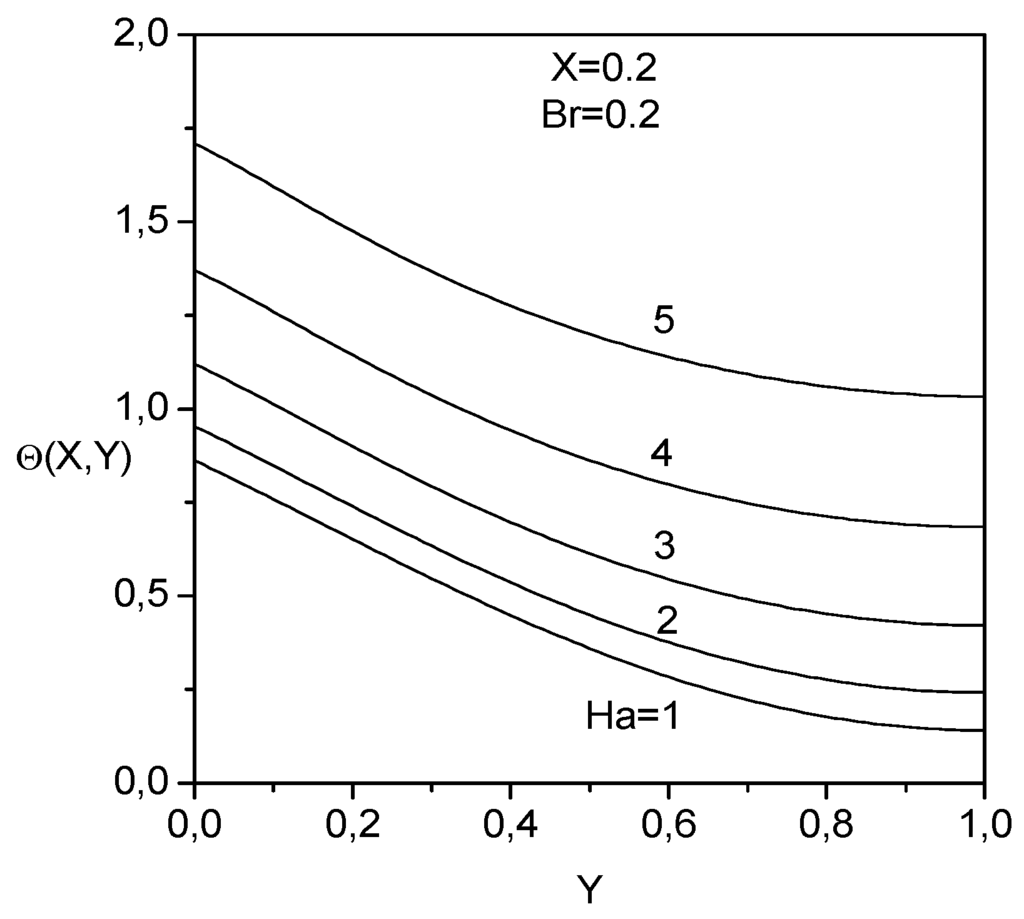
Figure 5.
Temperature profiles as function of the transverse distance at different Hartman numbers.
The effect of the Hartman number
on the transverse distribution of the entropy generation number is plotted in Fig. 7. As the Hartman number increases the entropy generation number increases in the transverse direction and a minimum in the entropy generation number appears near the heated plate. At the upper surface where both velocity and temperature are maximum (or minimum) which cause zero velocity and temperature gradients leaving no contribution to the entropy generation number ( second and third term of Eq. (28)), the entropy generation number is most sensitive to the Hartman number which is proportional to the magnetic field. The presence of the magnetic field creates additional entropy (fourth term of Eq. (28)).
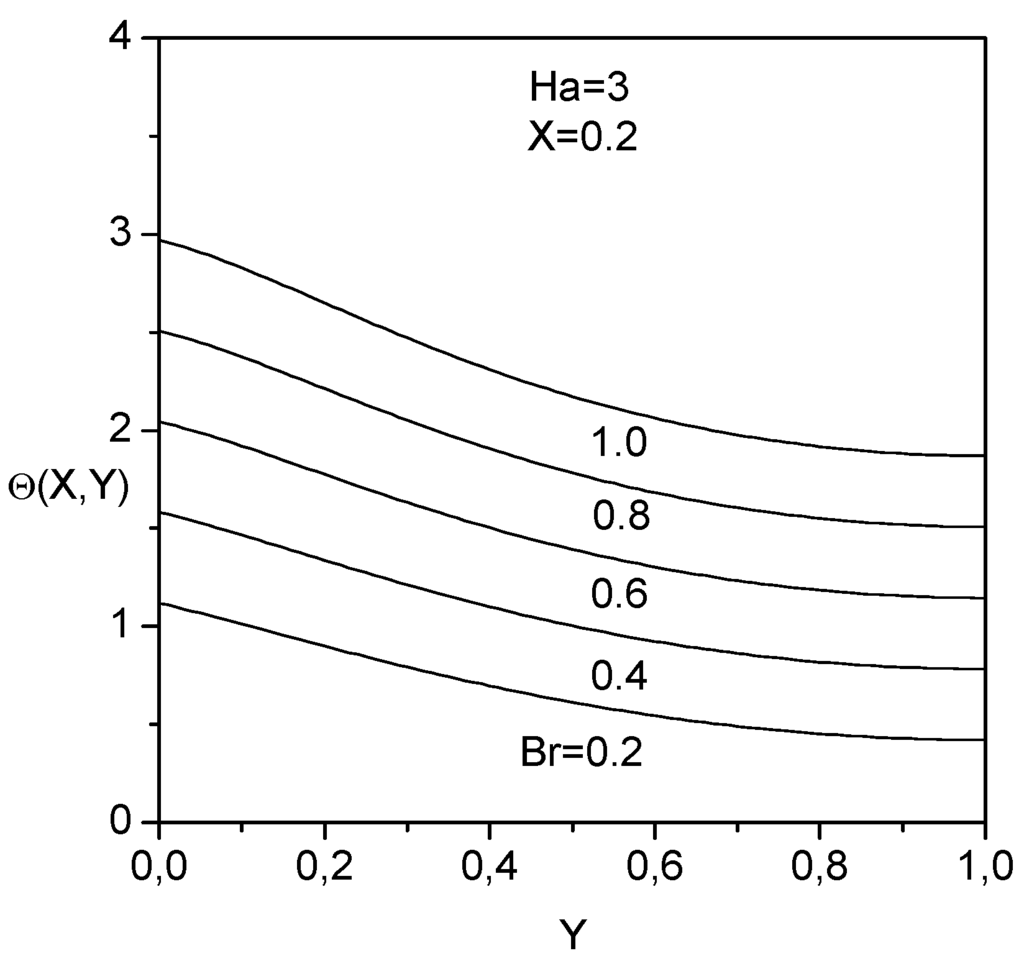
Figure 6.
Temperature profiles as function of the transverse distance at different Brinkman numbers.
Fig. 8 illustrates the effect of the Brinkman number
, for fixed Hartman number and dimensionless group, on the transverse distribution of the entropy generation number, in which there is a minimum near the heated plate. For a given transverse position, the entropy generation number is higher for higher Brinkman number. The augmentation of the Brinkman number increases the contribution of the entropy generation number due to the conductive heat in the transverse direction because of the viscous dissipation. In all cases the heated plate acts as a strong source of irreversibility.
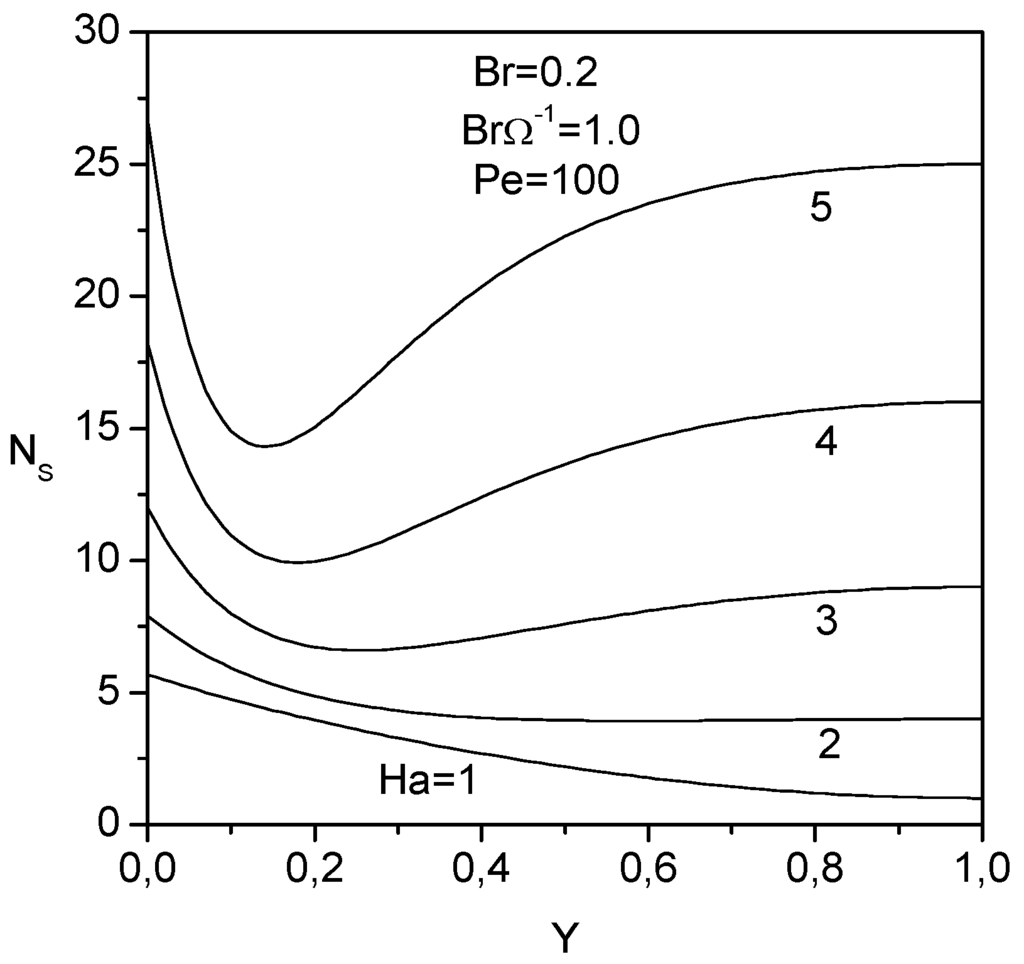
Figure 7.
Entropy generation number as function of thetransverse distance at different Hartman number.
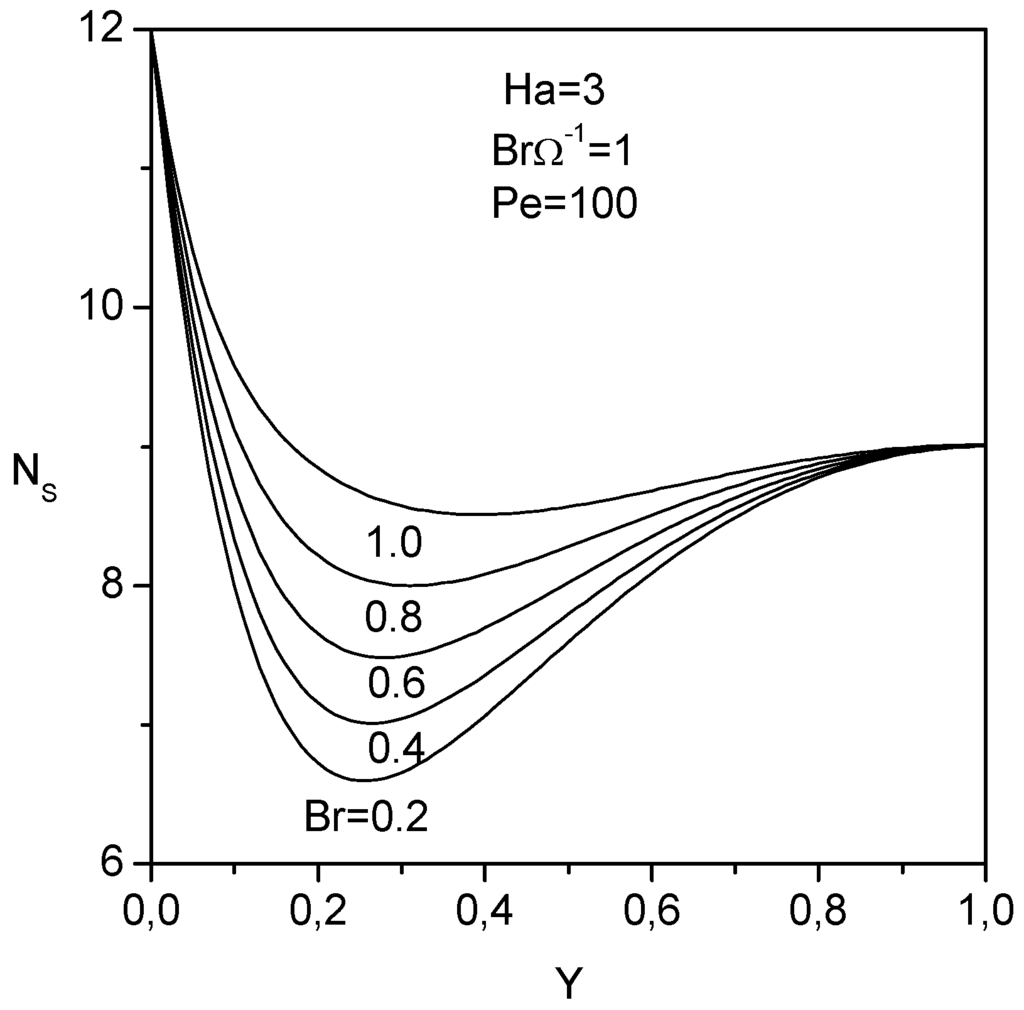
Figure 8.
Entropy generation number as function of thetransverse distance at different Brinkman numbers.
The effect of the dimensionless group
, on the transverse distribution of the entropy generation number is depicted in Fig. 9. The dimensionless group determines the relative importance of viscous effect. For small dimensionless group, the entropy generation number decreases along the transverse distance. For higher dimensionless group, the entropy generation number decreases first, then increases with increasing transverse distance. For a given transverse position, the entropy generation number is higher for higher dimensionless group. This is due to the fact that for high dimensionless group, the entropy generation numbers due to the fluid friction and to the magnetic field increase (third and fourth term of Eq. (28)).
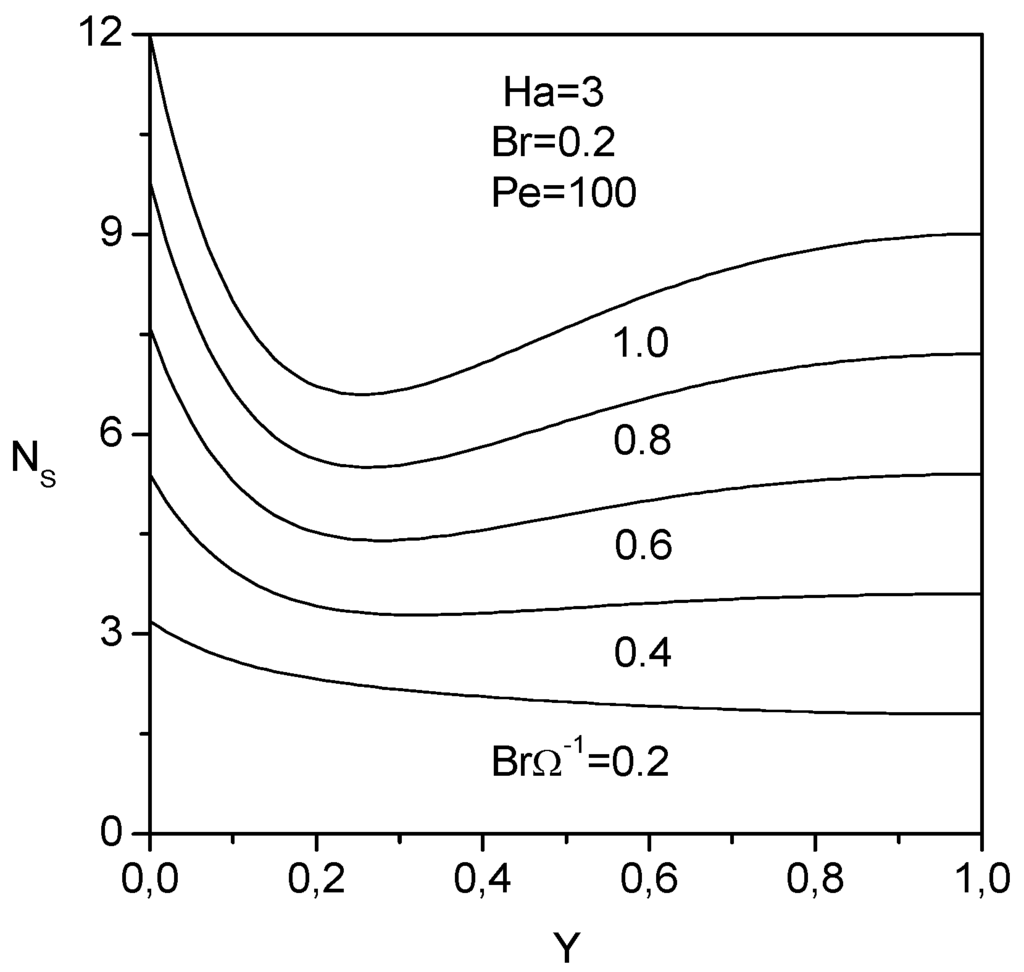
Figure 9.
Entropy generation number as function of the transversedistance at different dimensionless group.
Conclusion
This paper presents the application of the second law of thermodynamics to a gravity-driven liquid film along an inclined heated plate in the presence of a transverse magnetic field and viscous dissipation effects. The velocity and temperature profiles are obtained and used to evaluate the entropy generation number. The effects of the Hartman number, Brinkman number and the dimensionless group on velocity, temperature and entropy generation number are discussed.
From the results the following conclusions could be drawn:
Higher Hartman number causes flattened velocity profiles because the magnetic field slows down the movement of the fluid along the plate.
Temperature profiles shift to higher temperatures with increasing Hartman and Brinkman numbers because of the heat generated by magnetic and viscous dissipation.
The entropy generation number increases with Hartman number, Brinkman number and dimensionless group. As the Hartman number, Brinkman number and dimensionless group increases, the entropy generation number due respectively to the magnetic field, the conductive heat in the transverse direction and the fluid friction increases.
Nomenclature
area, (m2) | |
magnetic induction, (Wb.m-2) | |
Brinkman number,
| |
specific heat, (J.kg-1.K-1) | |
Hartman number,
| |
entropy generation number, magnetic induction | |
entropy generation, axial conduction | |
entropy generation, fluid friction | |
entropy generation number, total | |
entropy generation number, transverse conduction | |
Peclet number, | |
wall heat flux, (W.m-2) | |
liquid mass flow rate, (kg.m-1.s-1) | |
liquid mass flow rate in absence of the magnetic field, (kg.m-1.s-1) | |
Reynolds magnetic number,
| |
entropy generation rate, (W.m-3.K-1) | |
temperature, (K) | |
axial velocity, (m.s-1) | |
dimensionless axial velocity | |
axial distance, (m) | |
dimensionless axial distance | |
transverse distance, (m) | |
dimensionless transverse distance |
Greek symbols
scalar constant | |
thickness of the liquid film (m) | |
reference temperature difference,
| |
magnetic permeability, (H.m-1) | |
dynamic viscosity, (kg.m-1.s-1) | |
thermal conductivity, (W.m-1.K-1) | |
dimensionless temperature,
| |
dimensionless temperature difference,
| |
density of the fluid, (kg.m-3) | |
electric conductivity, (Ω-1.m-1) |
Subscripts
bulk value | |
maximum value | |
inlet value, reference value |
References
- Bejan, A. Second-law analysis in heat transfer and thermal design. Adv. Heat Transfer. 1982, 15, 1–58. [Google Scholar]
- Bejan, A. Entropy generation minimization. CRC Press: New York; Boca Raton, 1996. [Google Scholar]
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transfer 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Sahin, A.Z. Second law analysis of laminar viscous flow through a duct subjected to constant wall temperature. J. Heat Transfer 1998, 120, 76–83. [Google Scholar] [CrossRef]
- Sahin, A.Z. Effect of variable viscosity on the entropy generation and pumping power in a laminar fluid flow through a duct subjected to constant heat flux. Heat Mass Transfer 1999, 35, 499–506. [Google Scholar]
- Sahin, A.Z. A second law comparison for optimum shape of duct subjected to constant wall temperature and laminar flow. Heat Mass Transfer 1998, 33, 425–430. [Google Scholar]
- Narusawa, U. The second-law analysis of mixed convection in rectangular ducts. Heat Mass Transfer 1998, 37, 197–203. [Google Scholar] [CrossRef]
- Mahmud, S.; Fraser, R.A. The second law analysis in fundamental convective heat transfer problems. Int. J. Therm. Sci. 2003, 42, 177–186. [Google Scholar] [CrossRef]
- Mahmud, S.; Fraser, R.A. Thermodynamic analysis of flow and heat transfer inside channel with two parallel plates. Exergy 2002, 2, 140–146. [Google Scholar] [CrossRef]
- Saouli, S.; Aïboud-Saouli, S. Second law analysis of laminar falling liquid film along an inclined heated plate. Int. Communications in Heat and Mass Transfer 2004, 31, 879–886. [Google Scholar] [CrossRef]
- Mahmud, S.; Tasnim, S.H.; Mamun, S.A.A. Thermodynamic analysis of mixed convection in a channel with transverse hydromagnetic effect. Int. J. Therm. Sci. 2003, 42, 731–740. [Google Scholar] [CrossRef]
- Woods, L.C. Thermodynamics of fluid systems. Oxford University Press: Oxford, 1975. [Google Scholar]
© 2006 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.